Estimating relative noise to signal in DNA microarray data

Abstract

A method was proposed for estimating noise relative to signal in microarray data. A signal to noise index, SNI, was defined and used to measure the level of signal compared to the noise contained in two microarray data sets. Simulations were conducted to generate the quantitative relationship between the SNI and its measurement of relative noise. The method was applied to two well known microarray data sets. Relative noise was estimated for both data sets, and the results were consistent with the observations in the original papers, demonstrating the proposed method is reliable for estimating relative noise in microarray data.

1 Introduction

DNA microarray technology is a relatively high-throughput approach that has been widely applied for analysing gene expression patterns of whole animal genomes (Schena et al., 1995; Lockhart et al., 1996). It is, perhaps, one of the most mature high-throughput technologies, giving us hopes that the results from DNA microarray analyses could be translated into new sensitive and specific diagnostic tools leading to safer use of drugs and making personalised medicine a reality.

DNA microarray technology is based on the principle that single strand nucleic acid sequences form double strand hybrids complementarily. To make a DNA microarray, thousands of gene probes, the single strand sequences specific to particular genes, are synthesised or spotted onto a small glass or membrane support. Then, the probes can be used to detect the complementary sequences in mRNAs of genes that are labelled by a fluorescent dye. The signal is collected on a scanner and is proportional to the mRNA concentration of a gene in a sample. A DNA microarray experiment involves the following sequential steps:

• A sample is acquired, hopefully from a well-designed experiment

• RNA is extracted from the sample and purified

• The purified RNA is analysed for quality and quantity to make sure enough high quality material is available

• The RNA is Reverse Transcribed (RT) to cDNA with polyT primers with a Polymerase Chain Reaction (PCR) amplification

• A fluorescent label is added either in the RT step or in an additional step after amplification

• The labelled samples are then mixed with a hybridisation solution

• The mix is then used to hybridise with a microarray

• After hybridisation, all unbound material is washed off and the microarray is dried and scanned with a special instrument to obtain an image

• Last, the image is gridded with a template and the intensities of the features are quantified to generate raw data (the cel file) for subsequent data analysis.

One of the major concerns of microarray technology is the noisy nature of data, as each of the steps in the experiment could become a source of noise to the raw data and thus the analysis.

In the early days, a discrepancy between microarray data sets, generated from the same RNA samples but from different microarrays, was reported (Tan et al., 2003). This was followed by other similar observations (Miklos and Maleszka, 2004; Frantz, 2005). Doubts about the repeatability, reproducibility, and comparability of microarray technology have been raised (Marshall, 2004; Ioannidis, 2005), and the utility of microarray technology in biomedical sciences have also been questioned (Michiels et al., 2005; Ein-Dor et al., 2006). However, other studies, including some from the Microarray Quality Control (MAQC) consortium, demonstrated an increased and reasonably high reproducibility of microarray data (Petersen et al., 2005; Dobbin et al., 2005; Irizarry et al., 2005; Larkin et al., 2005; Kuo et al., 2006; Shi et al., 2006), alleviating concerns about microarray technology and impelling scientists to re-appraise this technology (Strauss, 2006; Ying and Sarwal, 2009). The discrepancy of different observations on the reproducibility of microarray data and the intensive debates on the reliability of microarray technology were caused in part by the noisy nature of microarray data and the lack of methods for quantitatively and accurately estimating noise in microarray data.

It was well realised eleven years ago (Kerr, 2000) that microarray data have noise. Efforts were also made to develop methods for measuring the impact of different sources of noise on microarray data (Tu et al., 2002; Balagurunathan et al., 2004; Weng et al., 2006; Takeya et al., 2007; Gopalappa et al., 2009). Most of the above-mentioned methods were developed for estimating or removing noise introduced by a specific step in a microarray experiment, such as hybridisation and image analysis. However, the noise in microarray data comes from various sources, as each of the above-mentioned steps can introduce different levels of noise into the final intensity data (the cel file). Estimating noise of some specific sources, such as hybridisation and scanning, based on the final intensity data that contain all noise, is difficult and not precise, though sample preparation, hybridisation, and scanning were reported as the major sources of noise in microarray data (Tu et al., 2002).

The ultimate goal using microarray technology is to translate discoveries, such as biomarker genes, from microarray data to diagnostic assays, enabling the use of healthcare products and incorporation into clinical practices. Therefore, a big challenge is to estimate the reliability of the microarray data used in the discovery phase. Estimating the total noise in microarray data is important for better utilisation of microarray technology in biomedical research. In this article, a statistical approach was developed to estimate the total random noise in microarray data. Simulations were conducted to derive the parameters that are needed for quantitatively estimating noise level in microarray data. The method was validated with two well-known microarray data sets (Tan et al., 2003; Shi et al., 2006).

2 Methods

A microarray data set, M, is represented as:

$$\mathbf{M}=\sum _{g=1}^n{O}_g=\sum _{g=1}^n(S_g+B_g+N_g)=\mathbf{S}+\mathbf{B}+\mathbf{N}.$$ (1)

O_g is the observed value of the probe for gene g, and n is the number of probes for all genes in a microarray. The observed value used in this article is expressed as fold changes in log2 unit, but other measurements such as intensity and p-value can be used. The observed value for gene g comprises of the biological signal, S_g, generated by gene g, the systematic bias, B_g, and the random noise, N_g, imposed on the gene. It is very difficult, if not impossible, to decompose the observed value, O_g, for a gene into its components: S_g, B_g, and N_g. However, it is hypothesised that the signal, S, and the random noise, N, are in normal distribution. The systematic bias, B, is not necessarily in the normal distribution, but is much easier to detect and control. Therefore, if the systematic bias is well controlled, B becomes very small relative to the random noise, N. It is reasonable that the sum of B and N is approximated by N and in normal distribution. For an observed microarray data set, M, it is difficult to estimate how much of the noise is relative to its signal (N/S) even if the normal distribution is true for M, N, and S. When two experiments on replicates of the same biological samples are provided, there are two observed data sets (M₁, M₂), two noise (N₁, N₂), and only one signal (biological effect is the same for the two experiments). Thus, the sum of the two noise (N₁ + N₂) relative to the signal S can be estimated from M₁ and M₂ (Figure 1).

Figure 1.

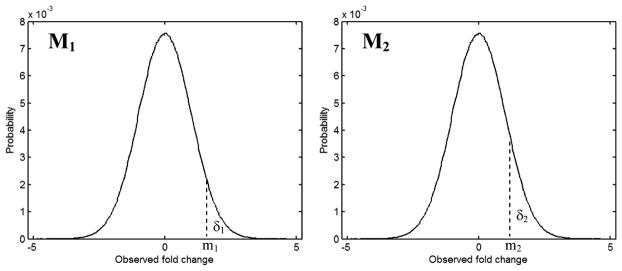
Illustration of the method for estimating noise in microarray data. The curves are the distributions of probability (y-axis) of observed fold changes (x-axis) for genes in two microarray data sets M₁ and M₂. δ₁ represents the genes with observed fold change values greater than m₁ in M₁, and δ₂ the genes with observed fold change values greater than m₂ in M₂

Let δ_i represent the number of genes of which the observed values are greater than m_i. Ideally, if there was no noise in the two data sets, and when δ₁ < δ₂, all of δ₁ would be included in the δ_2, that is δ₁ ∩ δ₂ = δ₁, as the signal in the two data sets are the same. In reality, noise is contained in the two data sets. Thus, δ₁ ∩ δ₂ = σ < δ₁ < δ₂. The subset σ depends not only on N₁/S but also on N₂/S. The bigger the noise (N₁/S + N₂/S) are, the smaller the σ. σ also depends on both δ₁ and δ₂. When δ₁ is fixed, σ depends only on δ₂ which, in turn, is determined by m₂.

For two pure random noise data sets (M₁ and M₂ have no signal), σ_n can be calculated based on the normal distribution function. For a fixed pair of δ₁ and δ₂ (or m₁ and m₂), σ_n statistically measures the expected number of common genes when no signal is contained in the two microarray data sets. Therefore, both σ and σ_n should be used for a more statistically reasonable method for measuring the amount of total noise (N₁/S + N₂/S) in the microarray data sets M₁ and M₂. As is mentioned above, both σ and σ_n depend on m₁ and m₂. To measure the amount of total noise (N₁/S + N₂/S) more precisely, the average value of estimation results calculated from all σ and σ_n for pairs of m₁ and m₂ from the whole data range, min₁ to max₁ in M₁ and min₂ to max₂ in M₂, should be used. Based on the above reasoning, an index SNI (Signal to Noise Index) was proposed to measure the noise level in the two microarray data sets. SNI is calculated as:

$$\mathit{SNI}=\frac{{\int }_{{min}_1}^{{max}_1}{\int }_{{min}_2}^{{max}_2}f{(\sigma ,{\sigma }_n)}_{m_1,m_2}\partial m_1\partial m_2}{{\int }_{{min}_1}^{{max}_1}{\int }_{{min}_2}^{{max}_2}\partial m_1\partial m_2}$$ (2)

m₁ and m₂ are the measurements of the data. They can be intensities of genes or more biologically meaningful fold changes in log2 unit of genes (the latter was used in this article). The function f(σ,σ_n) given in formulas (3) and (4) was used to numerically calculate the SNI.

$$\mathit{SNI}=\frac{1}{n_1\times n_2}\sum _{m_1=m_1^1}^{m_1=m_1^{n_2}}\sum _{m_2=m_2^1}^{m_2=m_2^{n_2}}\frac{1}{{\mu }_1}\left(\frac{1}{1+{\mathrm{e}}^{-{\theta }_{m_1,m_2}}}-{\mu }_2\right)$$ (3)

$${\theta }_{m_1,m_2}=\frac{\sigma -{\sigma }_n}{{\delta }_{min}-{\sigma }_n}\sqrt{\frac{\sigma }{{\delta }_{max}-{\delta }_{min}+1}}.$$ (4)

In more detail, the observed values in the two microarray data sets M₁ and M₂ are first divided into (n₁ + 1) and (n₂ + 1) even intervals, respectively. For each of the combinations of the n₁ observed values between min₁ to max₁ in M₁ and the n₂ observed values between min₂ to max₂ in M₂, θ_m1,m2 is calculated using formula (4). δ_min and δ_max are the minimum and maximum values among all of n₁ of δ₁ and n₂ of δ₂ values. The scaling parameters, μ₁ and μ₂, are used to scale the SNI to a number between 0 (no signal, pure random noise) and 1 (pure signal, no noise). The values of μ₁ = 0.1060 and μ₂ = 0.5019 were used in this article. They were determined by simulations on pure signal and pure random noise.

SNI measures total noise relative to signal in the two compared microarray data sets. However, the quantitative relationship between SNI and total noise (N₁ + N₂) is not linear. To quantitatively estimate noise by using SNI, simulations were conducted to quantify SNI for the microarray data with different noise relative to signal. In the simulations, for a pair of fixed amounts of noise and signal, two random noise with a length of 4000 were generated and added to the signal of the same length to mimic two microarray data sets of 4000 genes. Thereafter, the SNI was calculated using equations (3) and (4). To assess stability of the relationship, the process was repeated 2.000 times and thus, 2,000 SNI values were obtained for calculating the statistically expected SNI and its 95% confidence boundary for a specific noise-to-signal ratio.

The method was applied to two well-known microarray data sets, called Tan and Shi hereafter (Tan et al., 2003; Shi et al., 2006). The data sets were obtained from the authors directly (both also could be downloaded from the GEO database). Tan had three microarray data sets obtained from three different platforms for three experimental replicates. Each data set had 2009 genes which are common to the three platforms. All data sets from Tan were used. Shi had microarray data sets obtained from different sites for five technical replicates of each of two human RNA samples by using five platforms. All platforms were tested in three sites except for the Affymetrix platform which was tested in six sites. The microarray data sets from the first three sites and the last three sites for Affymetrix platform were separately used to derive the relative noise in the data sets from SNI values. The SNI values and the corresponding total noise relative to signal in the data for two–site combinations between each of the first three and each of the last three sites were calculated and used to test the accuracy of the estimated noise in the individual data sets. The 12091 genes shared by all of the five platforms were used. The data sets obtained and used in this study are the normalised data sets obtained directly from the authors. No further processing was applied to the data sets.

All calculations were done in MatLab (http://www.mathworks.com/).

3 Results

3.1 SNI is not dependent on the number of intervals used

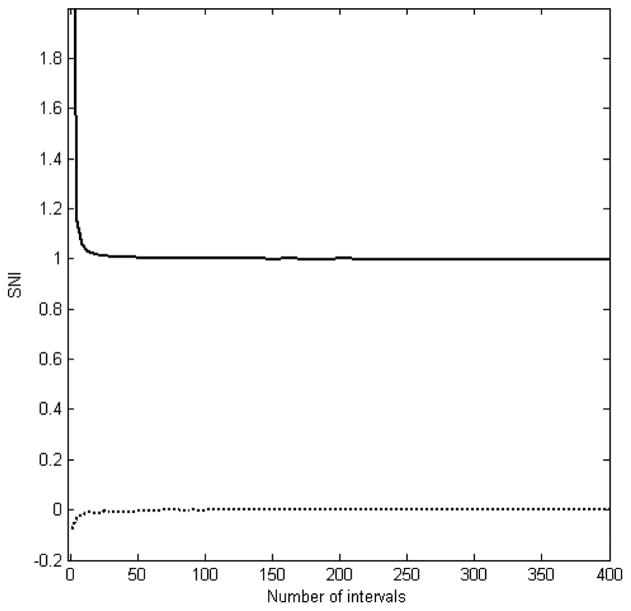
From equations (3) and (4) it can be seen that two microarray data sets are separately and evenly divided into (n₁ + 1) and (n₂ + 1) intervals, respectively, to calculate the corresponding SNI values. Therefore, the independence of the calculated SNI from the numbers of intervals in its calculation is a vital and necessary condition. To examine whether the number of intervals affects SNI and how many intervals should be used for calculating SNI, two exactly similar signals of a length of 4000 without noise and two pure random noise of the same length of 4000 without any signal were generated, respectively. Different numbers of intervals were then used to calculate the corresponding SNI values. The results were plotted in Figure 2. It was observed that when very few intervals (less than 5) were used, the calculated SNI depends dramatically on the numbers of intervals, and is not suitable for estimating the noise in the microarray data. However, when the number of intervals increases to more than 30, the SNI is not affected by the number of intervals. Moreover, the SNI for the two similar pure signals is 1, and the SNI for the two random noise is 0. Therefore, it was demonstrated that the proposed SNI is independent of the number of intervals used in its calculation, as long as a number larger than 30 is used. Sixty intervals were used in all of the calculations in this paper.

Figure 2.

Relationship between SNI and the number of intervals used in its calculation. The solid line is plotted from the calculation results on two data sets with the same pure signal, while the dotted line represents the results on two random noise without any signal

3.2 Relationship between SNI and relative noise

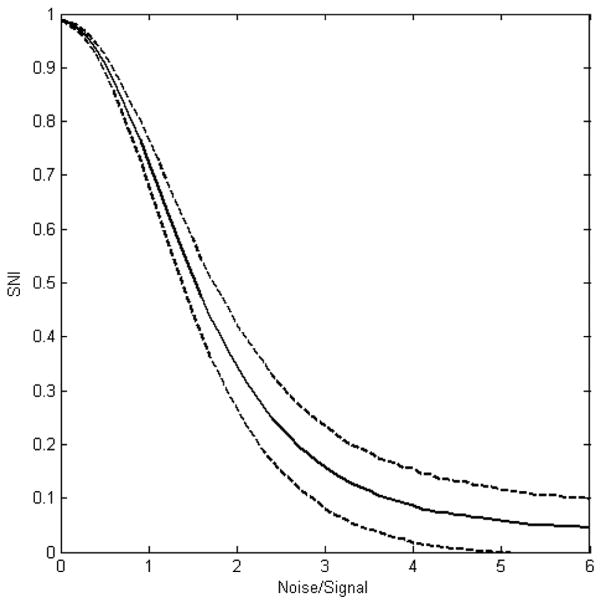
From its mathematical formula, SNI can be used to qualitatively indicate total relative noise to signal in two compared microarray data sets. The larger the SNI value, the stronger is the signal in the two microarray data sets, or the lower the noise in the data. Moreover, the relationship between SNI and relative noise is not linear. When two SNI values were calculated for two comparisons, the issue of which two microarray data sets compared had a lower noise relative to signal could only be assessed qualitatively. To quantitatively estimate the relative noise to signal in two compared microarray data sets, the quantitative relationship between SNI and relative noise has to be determined. Simulations were conducted to quantify the relationship. The simulations results were given in Figure 3. In the simulations, a signal vector with 4000 elements was mixed with two different random noise at the same noise/signal ratio with the same length of 4000 elements to mimic two microarray data sets of 4000 genes. Thereafter, a SNI value was calculated by using equations (3) and (4). The process was repeated 2,000 times and thus, 2000 SNI values were obtained for a noise/signal ratio. The mean of the 2000 SNI values and its corresponding 95% confidence boundary were calculated and plotted in Figure 3. It can be seen from the figure that the relationship is not linear. When noise is zero, the SNI reaches one, the maximum. When the noise is increased to a very big value, the SNI reaches 0, the minimum. Furthermore, it was observed that the more noise present in the two compared microarray data sets, the larger was the fluctuation in the SNI values. Alternatively, the larger the signal to noise ratio is, the more accurate the calculated SNI value is.

Figure 3.

Quantitative relationship between SNI and relative noise to signal derived from the simulations. X-axis indicates the relative noise to signal that were used in the simulations. The solid line represents the mean SNI of the 2000 simulations for a noise/signal ratio depicted at the x-axis. The dashed lines show the 95% confidence boundaries

3.3 Estimating relative noise to signal using SNI

As demonstrated by the simulations results, SNI can be used to quantitatively estimate the total noise relative to signal in two microarray data sets under comparison, not those in each data set. However, if a set of the same biological samples (same true signals) were assayed several times (replicates) using DNA microarray technology, the noise relative to the signal in each experiment could be estimated by using the SNI values calculated from the microarray data. The capability of SNI for estimating noise in microarray data was demonstrated by applying the method to two real microarray data sets.

3.4 Estimating noise in Shi data

Shi data sets were generated by the MAQC consortium (Shi et al., 2006). Two human RNA samples were profiled by using five microarray platforms. For each platform, five technical replicates of each of the two RNA samples were profiled at three different sites, except for the Affymetrix platform, which was tested at six different sites. The MAQC used the 12,091 common genes shared in all of the five microarray platforms to assess the reproducibility of microarray technology qualitatively (Shi et al., 2006). Reproducibility depends not only on the signal, but also on the noise introduced in the microarray experiments and data. Using the proposed SNI, the noise relative to the signal in the Shi data sets were quantitatively estimated. First, for each of the five platforms, total noise relative to signal were estimated in the microarray data sets between two of the three testing sites (for Affymetrix, the first three and the last three were separated) by the corresponding SNI values calculated from the data sets. Thereafter, the noise relative to signal in the data from each testing site was derived from those total noise.

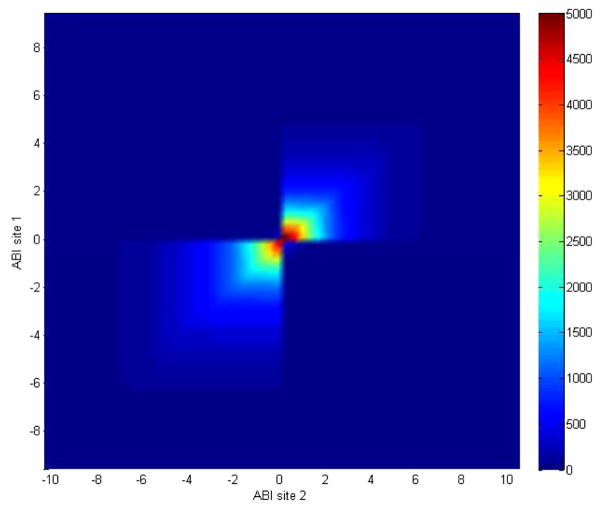
Take the ABI platform as an example. To calculate SNI from testing sites 1 and 2, the two data sets were compared by using 60 even internals to cover the data ranges. The overlapped genes, δ, selected at different data values, were calculated and shown in Figure 4. It can be seen from Figure 4 that the overlapped genes, δ, dramatically depend on the cut-off values used to select the genes for comparison. This is not a statistically stable way to assess reproducibility or to estimate noise level in the two microarray data sets. This observation supported our rationale that equation (2) should be used on whole data ranges to estimate noise or assessing reproducibility of microarray data. The SNI value for the microarray data sets generated on the ABI platform obtained from testing sites 1 and 2 was calculated as 0.9008. Mapping the SNI value of 0.9008 to Figure 3, a total noise of 0.5252 relative to the signal (N_site1/S + N_site2/S) was estimated for the two microarray data sets:

$$\frac{N_{{\mathit{site}}_1}}{S}+\frac{N_{{\mathit{site}}_2}}{S}=\mathrm{0.5252.}$$ (5)

Figure 4.

Heatmap of number of overlapped genes, δ, selected at different cut-off values of log2 (fold change) from the microarray data from testing site 1 (y-axis) and site 2 (x-axis) using the ABI platform data contained in the Shi data sets (see online version for colours)

In the same way, SNI values for microarray data sets from the ABI platform between testing sites 1 and 3 and between testing sites 2 and 3 were 0.9168 and 0.9142, respectively. By mapping those SNI values to Figure 3, the corresponding relative noise were estimated to be 0.4691 and 0.4788, respectively.

$$\frac{N_{{\mathit{site}}_1}}{S}+\frac{N_{{\mathit{site}}_3}}{S}=0.4691$$ (6)

$$\frac{N_{{\mathit{site}}_2}}{S}+\frac{N_{{\mathit{site}}_3}}{S}=\mathrm{0.4788.}$$ (7)

Combining equations (5)–(7), the noise levels relative to the signal for microarray data sets from each of the three testing sites were solved: N_site1/S = 0.2578, N_site2/S = 0.2675, and N_site3/S = 0.2114.

The same calculations were conducted for the microarray data sets from Affymetrix, Agilent, GE Healthcare, and Illumina platforms in the Shi data sets. The results were summarised in Table 1. The results showed low levels of noise relative to signal in the Shi data sets, as the noise-to-signal ratios were around 20%. Therefore, this study further confirmed the observation of inter- and intra-platform reproducibility of gene expression measurements from the MAQC (Shi et al., 2006). By further examining the relative noise of microarray data sets from different platforms, we observed that results from the Affymetrix and Illumina platforms had lower noise and thus, were of higher quality than the microarray data sets from the other three platforms. This observation is consistent with the original observations from the MAQC that the microarray data sets from the Affymetrix and Illumina platforms had lower coefficients of variation among the technical replicates, and higher correlations with the data from TaqMan assays, the gold standard method for measuring gene expression, on the two RNA samples, when compared with the microarray data from the other three platforms.

Table 1.

Calculated SNI, total relative noise in two compared microarray data sets, and relative noise derived for each individual data set in the Shi data sets

Platform	Data compared	SNI	Total noise	Data	Noise*
	Site1 ~ Site2	0.9008	0.5252	Site1	0.2578
ABI	Site1 ~ Site3	0.9168	0.4691	Site2	0.2675
	Site2 ~ Site3	0.9142	0.4788	Site3	0.2144
	Site1 ~ Site2	0.9596	0.2790	Site1	0.1722
	Site1 ~ Site3	0.9563	0.3000	Site2	0.1068
	Site1 ~ Site4	0.9667	0.2340	Site3	0.1278
	Site1 ~ Site5	0.9584	0.2866	Site4	0.1291
	Site1 ~ Site6	0.9457	0.3497	Site5	0.1291
	Site2 ~ Site3	0.9666	0.2346	Site6	0.1841
	Site2 ~ Site4	0.9687	0.2213
Affymetrix	Site2 ~ Site5	0.9668	0.2333
	Site2 ~ Site6	0.9509	0.3253
	Site3 ~ Site4	0.9643	0.2492
	Site3 ~ Site5	0.9637	0.2530
	Site3 ~ Site6	0.9537	0.3122
	Site4 ~ Site5	0.9657	0.2403
	Site4 ~ Site6	0.9497	0.3309
	Site5 ~ Site6	0.9535	0.3131
	Site1 ~ Site2	0.8474	0.6860	Site1	0.2952
Agilent	Site1 ~ Site3	0.9028	0.5188	Site2	0.3908
	Site2 ~ Site3	0.8725	0.6144	Site3	0.2236
	Site1 ~ Site2	0.9262	0.4333	Site1	0.1910
GE Healthcare	Site1 ~ Site3	0.9427	0.3637	Site2	0.2424
	Site2 ~ Site3	0.9310	0.4151	Site3	0.1728
	Site1 ~ Site2	0.9649	0.2454	Site1	0.1196
Illumina	Site1 ~ Site3	0.9649	0.2454	Site2	0.1259
	Site2 ~ Site3	0.9639	0.2517	Site3	0.1259

^*The relative noise for individual data of sites 1 to 3 were derived using the SNI from comparisons between two of the three site’s data; while those of sites 4–6 for the Affymetrix platform were from the comparisons of site 4~site 5, site 4~site 6, and site 5~site 6.

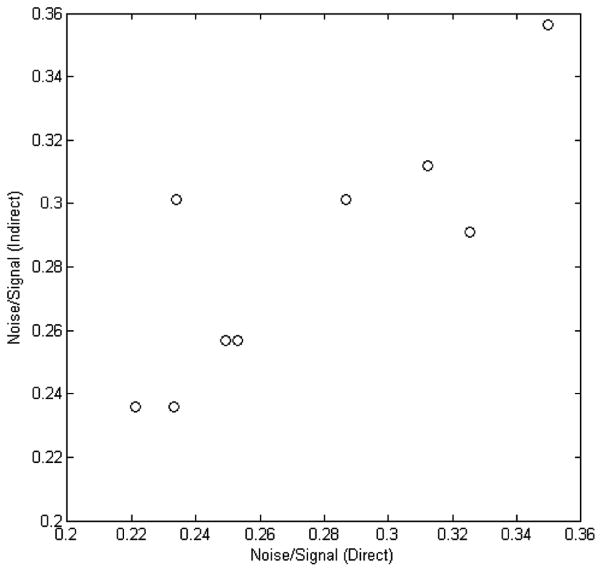
It was noted that the Shi data sets had microarray results from six testing sites on the Affymetrix platform, compared with three sites for the other platforms. The relative noise in any individual microarray data set could be derived from different combinations of the SNI values between two of the six microarray data sets. Alternatively, the total noise relative to signal of any two of the six microarray data sets could be estimated using the relative noise of individual microarray data sets that were derived from the SNI values of two other compared data sets, if the proposed SNI is reliable for estimation of relative noise. To examine the reliability and utility of the proposed SNI, the middle nine calculated SNI values in Table 1 for the microarray data sets from the Affymetrix platform were mapped to Figure 3 directly, to estimate the total noise/signal values (x-axis of Figure 5). The total noise/signal values (indirect, y-axis of Figure 5) were also estimated by adding together the relative noise of two individual microarray data sets that were derived from the other six calculated SNI values, the first three and the last three in Table 1. They were compared in Figure 5 and had a good correlation, with a coefficient of 0.824. Referring to the 95% boundary of SNI, those (direct and indirect estimation of noise) could be thought of as of very good consistency, statistically. Hence, it was further demonstrated that the proposed SNI could be a good indicator of relative noise for microarray data.

Figure 5.

Correlation analysis of the total noise relative to signal calculated directly from the SNI values (x-axis) and estimated indirectly by using the relative noise of each individual data set that were derived from the SNI values calculated by other data sets

3.5 Estimating noise in Tan Data

Tan data sets were generated for three technical replicates of RNA samples collected from PANC-1 cells grown in serum-rich medium on three microarray platforms (Tan et al., 2003). Tan data sets showed considerable divergence across the different platforms based on the correlations in expression levels of all genes and on the comparisons for significantly expressed genes. The method reported in this paper was applied to the Tan data sets to estimate the noise relative to signal in the data sets. The SNI values for the three possible combinations were calculated first. Then, the SNI values were mapped to Figure 3 to estimate the total relative noise in the compared two microarray data sets. Last, the relative noise in each of the three microarray data sets were derived. The results were listed in Table 2.

Table 2.

Calculated SNI, total relative noise in two microarray data sets, and relative noise derived for each individual data set in the Tan data sets

Data compared	SNI	Total noise	Data	Noise
Affymetrix ~ Amersham	0.4177	1.7633	Affymetrix	1.2694
Affymetrix ~ Agilent	0.4613	1.6379	Amersham	0.4940
Amersham ~ Agilent	0.7796	0.8625	Agilent	0.3696

Our results indicated that the microarray data from the Affymetrix platform in the Tan data sets were much noisier than the data from the Amersham and Agilent platforms. Our results were consistent with the original observations that the experimental error for the Affymetrix data was larger than for the Amersham data and Agilent data, and that there were only four differentially expressed genes shared by all three platforms; the number of commonly differentially expressed genes between Amersham and Agilent, 23 was much larger than those between Affymetrix and Amersham, 5, or between Affymetrix and Agilent, 9 (Tan et al., 2003). Once again, the results supported the proposition that the proposed SNI could be a reliable measurement of noise in microarray data.

It was noted that the comparisons of the Tan results were from different platforms. Thus, the systematic bias between different platforms, B in equation (1), could add noise to the observed data. Though the absolute amount of the bias is not known, it should be pointed out that it is less likely that the observed high noise (1.2694 of relative noise to true biological signal in the samples) from the Affymetrix data was mainly contributed by systematic bias, as the observed relative noise for Amersham (0.4940 of relative noise to true biological signal in the samples) and Agilent (0.3696 of relative noise to true biological signal in the samples) were both much lower, though a systematic bias should also exist for them.

4 Discussion

The DNA microarray has been widely used in biomedical research to generate testable hypotheses on biological processes which have their foundations in gene expression changes. It is a high-throughput technology that can monitor expression levels of genes of a whole genome simultaneously. However, gene expression profiling by using DNA microarray technology is a very complicated process, and each of the steps in a microarray experiment has the potential to introduce noise into the final data. Because of the nature of noisy microarray data and a lack of quantitative and accurate methods for estimating the noise, the debate on the reliability and utility of microarray technology has been intensive for a long time (Tan et al., 2003; Miklos and Maleszka, 2004; Frantz, 2005; Marshall, 2004; Ioannidis, 2005; Michiels et al., 2005; Ein-Dor et al., 2006; Petersen et al., 2005; Dobbin et al., 2005; Irizarry et al., 2005; Larkin et al., 2005; Kuo et al., 2006; Shi et al., 2006; Strauss, 2006; Ying and Sarwal, 2009). Assessing reproducibility of gene expression profiles using different data sets from different sets of samples led to the debates, as the conclusion largely depends on both the signal of the biological samples used and the noise introduced in the experiments. That is, it depends on the noise-to-signal ratio or signal-to-noise ratio. Therefore, an important aspect in microarray studies is to quantitatively and accurately estimate the noise-to-signal ratio to avoid bias in the utilisation and interpretation of the results. In this article, a method for quantitative estimation of the noise relative to the signal in microarray data was proposed and tested by applying it to two well-known microarray data sets.

Usually, microarray data not only contain random noise but also have systematic (or technical) biases, resulting from gene-specific probe sequences, different experimental protocols, different scanners and batch effects. The method proposed here is based on a pre-condition that systematic bias is zero or much lower compared to random noise in a microarray data set. Alternatively, the noise estimated using the proposed method includes the systematic bias that is assumed to be in the same distribution as the noise. Ideally, it would be an enthralling story for the biological question under study if the absolute noise in microarray data could be determined. It is a big challenge, as both the real signal and the noise are not known and the observed data are the combination of the signal and the noise. However, it should be possible to estimate the noise-to-signal ratio if the distribution of the signal and noise are both known.

In estimation of relative noise, a microarray data set, M, was represented by fold changes in a log2 unit that were used in deriving the calculation equations (2)–(4). Both signal and noise in M could be hypothesised to be in normal distribution. However, microarray data, M, could be represented in other measurements, such as intensity and p-value for genes. The proposed method could work as long as a reasonable distribution could be hypothesised for the signal and noise in other measurement metrics such as p-values and intensity.

Biographies

Huixiao Hong is a Senior Scientist at the FDA’s National Center for Toxicological Research. He received his PhD in computational chemistry in 1990. He completed his postdoctoral fellowship at Leeds University in the United Kingdom. He was an Associate Professor at Nanjing University. He worked at the National Cancer Institute, National Institutes of Health as a Visiting Scientist. He held a Research Scientist position in the Sumitomo Chemical Company in Japan. He became an FDA senior scientist in 2007. His current research interests involve developing methods for analysing and interpreting genomic, transcriptomic, proteomic, and metabonomic data.

Qilong Hong is a graduate student in the Mechanical Engineering Department at the University of Arkansas. He gained his Bachelor’s Degree in Mechanical Engineering from the University of Arkansas at Fayetteville, Arkansas. His research interests are in the areas of data mining, machine learning and simulation of mechanical engineering systems.

Jie Liu is a Graduate Student at the University of Arkansas at Little Rock/University of Arkansas for Medical Sciences Bioinformatics Graduate Program. She received her Master’s Degree in Medicine from the Peking Union Medical College, Beijing, China. From 2008 to 2010, she worked as a visiting scientist at the FDA’s National Center for Toxicological Research. Her research interests are in the areas of global microRNAs expression profiling with the use of next-generation sequencing and bioinformatics.

Weida Tong is a Senior Scientist at the FDA’s National Center for Toxicological Research. He received his PhD in chemistry from Fudan University, Shanghai, China. He did postdoctoral research at the University of Missouri, St. Louis. He held a bioinformatics group manager’s position at R.O.W. Sciences. He joined the FDA in 2002 as director of the Center for Toxicoinformatics at FDA’s National Center for Toxicological Research. His recent academic interests include the application and development of genomic and bioinformatics methods to elucidate drug-induced liver toxicity. He specialises in the field of computational modelling, chemoinformatics, and QSAR with specific interest in estrogen, androgen, and endocrine disruptors.

Leming Shi is a Senior Scientist at the FDA’s National Center for Toxicological Research. He earned a BSc Degree in analytical chemistry, MSc Degree in chemometrics, and PhD Degree in computational chemistry. He worked as a Research Associate at Case Western Reserve University (1994–1995), as a visiting fellow at the NIH’s National Cancer Institute (1995–1997), as a computational chemist at R.O.W. Sciences (1997–1999), and as a Senior Scientist at Wyeth and BASF (1999–2001). He was a co-founder and director of informatics at Chipscreen Biosciences Ltd. (2001–2003). He joined the FDA/NCTR in 2003 and has been leading the MicroArray Quality Control (MAQC) project.