Scaffold-free Tissue Engineering: Organization of the Tissue Cytoskeleton and its Effects on Tissue Shape

Abstract

Work described herein characterizes tissues formed using scaffold-free, non-adherent systems and investigates their utility in modular approaches to tissue engineering. Immunofluorescence analysis revealed that all tissues formed using scaffold-free, non-adherent systems organize tissue cortical cytoskeletons that appear to be under tension. Tension in these tissues was also evident when modules (spheroids) were used to generate larger tissues. Real-time analysis of spheroid fusion in unconstrained systems illustrated modular motion that is compatible with alterations in tensions, due to the process of disassembly/reassembly of the cortical cytoskeletons required for module fusion. Additionally, tissues generated from modules placed within constrained linear molds, which restrict modular motion, deformed upon release from molds. That tissue deformation is due in full or in part to imbalanced cortical actin cytoskeleton tensions resulting from the constraints imposed by mold systems is suggested from our finding that treatment of forming tissues with Y-27632, a selective inhibitor of ROCK phosphorylation, reduced tissue deformation. Our studies suggest that the deformation of scaffold-free tissues due to tensions mediated via the tissue cortical cytoskeleton represents a major and underappreciated challenge to modular tissue engineering.

INTRODUCTION

Scaffold-free tissue engineering aims to efficiently exploit the inherent capacity of cells to generate extracellular matrices and assemble into organized and functional 3D tissues. In many respects, the basis for scaffold-free tissue engineering can be traced back to the works of Holtfreter¹¹ and Moscona²⁴. These works showed that cells isolated from a tissue could stratify or ‘sort’ to reform an anatomically appropriate replica of the original tissue. Steinberg’s work also examined the reassociation of cells into tissues and led to his proposal of the Differential Adhesion Hypothesis (DAH) to explain the reaggregative behavior observed when dissociated cells were placed in a non-adherent hanging drop culture system^5,6,25,34,35. The organization of cells in the resulting spheroid were proposed to be driven by intercellular adhesion, surface tension, and the cells’ liquid thermodynamic properties^{1,5,6,22,28,33–36}. Expanding on these findings, Steinberg and others showed that two spheroids coalesce into a single, larger spheroid³⁴. This behavior was attributed to result from the minimization of surface area and interfacial tension and is termed ‘spheroid fusion’^5,8,34. These findings, and the fact that cells in 3D culture versus 2D culture more faithfully recapitulate cell behaviors in vivo^4,16–18, have made tissue spheroids attractive as building blocks for modular bioengineering applications.

Extending on the work of Steinberg and others, we recently showed that spheroid fusion in a non-adherent environment had no apparent limitations, as evidenced by the observation that five spheroids when placed in a non-adherent hanging drop culture system fuse to form a single larger spheroid^4,8. In order to generate tissue shapes other than spheres, we investigated culture systems that controlled the propensity of spheroid fusion to form larger spheres. In previous efforts to generate linear constructs using spheroids, spheroids were aligned and embedded in collagen-based gels²³. However, this approach failed to obtain the desired results as fusion of spheroids was incomplete and cells engaged and migrated into the embedding gel. To overcome these behaviors, work described herein investigates the utility of a scaffold-free, non-adherent mold system for the generation of tissues of varied shapes. To this end, we used agarose-based non-adherent culture molds to generate linear, toroidal, and planar constructs from spheroids and cell suspensions.

MATERIALS AND METHODS

Cell subculture

Cells were cultured in 75cm² BioLite vented culture flasks (ThermoFisher Scientific) in 37°C 5% CO₂ humidified incubators. Human umbilical vein endothelial cells (HUVECs; Lonza) and human adipose microvascular endothelial cells (HAMECs; ScienCell) were grown in M200 media supplemented with Low Serum Growth Supplement (LSGS; Gibco) and 1% Penicillin Streptomycin Solution (PS; Cellgro). Human aortic smooth muscle cells (AoSMCs; Lonza) were cultured in Medium 231 supplemented with Smooth Muscle Growth Supplement (SMGS; Cascade Biologics) and 1% Penicillin Streptomycin Solution (PS; Cellgro). Adult normal human dermal fibroblasts (NHDFs; Lonza) were cultured in high glucose Dublecco’s Modified Eagle Medium (DMEM; Gibco) supplemented with 10% Fetal Bovine Serum (FBS; Corning) and 1% Penicillin Streptomycin Solution (PS; Cellgro). Cells were passaged using 0.05% Trypsin/0.53mM EDTA (Cellgro) and harvested when confluent.

Generation of tissue spheroids

Tissue spheroids were generated using Microtissues 3D Petri Dish^Tm 24–35 Large Spheroids molds according to established procedures. Cell suspensions containing 1:1 ratio of HUVECs and AoSMCs or 1:4 HAMECs and NHDFs were seeded to form 8,000-cell spheroids. 1:1 spheroids were cultured in 1:1 M200+LSGS+PS:M231+SMGS+PS and 1:4 spheroids were cultured in 1:2 M200+LSGS+PS:DMEM+FBS+PS. Spheroids were harvested after 24 hours in culture. For ROCK inhibitor studies, cells were incubated with 10 M Y-27632 (Calbiochem) in media.

Generation of agarose molds

2% w/v agarose (Fisher Scientific) was dissolved in MilliQ water and heated until molten. Non-adherent molds were prepared by allowing molten agarose to harden around various (non-agarose) shapes within 3.5cm petri dishes. Molds were equilibrated in cell culture media (DMEM+FBS+PS) at 37°C and 5% CO₂ (humidified incubator) for 24 hours prior to use.

Generation of spheroid-based tissue constructs

For hanging drop fusion: two or more 8,000-cell spheroids (1:1 HUVEC:AoSMC) were placed within a 30 L drop of cell culture media (1:1 M200+LSGS+PS:M231+SMGS+PS) on the underside of a petri dish lid and inverted over PBS in the dish base. Hanging drops were cultured in a 37°C 5% CO₂ humidified incubator for 48 hours. For linear constructs: 8,000-cell spheroids were placed within equilibrated linear molds (~2.5×0.1×0.4cm), fully immersed in culture media, and maintained in a 37°C 5%CO₂ humidified incubator for 3 days. Where indicated, 1:1 HUVEC:AoSMC constructs were removed from molds after 24 hours in culture and allowed to continue culture submerged in media in an agarose-coated dish. Linear 1:4 HAMEC:NHDF constructs were maintained in molds for the duration of culture. For sheet constructs: 8,000-cell 1:1 HUVEC: AoSMC spheroids were placed in physical contact with adjacent spheroids within a rectangular agarose mold and allowed to culture undisturbed in a 37°C 5% CO₂ humidified incubator. Sheets were removed from molds after 24 hours in culture and allowed to continue culture submerged in media in an agarose-coated dish. 1:1 constructs were cultured in 1:1 M200+LSGS+PS:M231+SMGS+PS and 1:4 constructs were cultured in 1:2 M200+LSGS+PS:DMEM+FBS+PS. Stereo microscopic images were captured using a Dage-MTI CCD300-RC camera system and Scion ImagePC software.

Evaluation of spheroid movement during fusion

Two 8,000-cell 1:1 HUVEC:AoSMC spheroids were placed within single agarose wells, submerged in media, and imaged during culture in a humidified 37°C 5%CO₂ incubator. Time-lapse images were captured every 10 minutes for 72 hours using Dino-Capture 2.0 software (AnMo Electronics Corporation). Select time-lapse images were analyzed using ImageJ and/or Adobe Photoshop CS to assess spheroid orientation.

Generation of tissue constructs from high-density cell suspensions

Approximately 900,000 cells at 1:4 ratio (HAMEC:NHDF) were seeded into equilibrated linear molds (0.9×0.1×0.5cm) and 750,000 cells at 1:4 ratio (HAMEC:NHDF) were seeded into equilibrated toroidal molds (outer diameter 0.4cm, inner diameter 0.2cm, 0.3cm high). Molds were fully immersed in culture media and cultures maintained in a 37°C 5%CO₂ humidified incubator for 3 or 6 days. Stereo microscopic images were captured using a Dage-MTI CCD300-RC camera system and Scion ImagePC software.

Toroidal contraction and ring opening assay

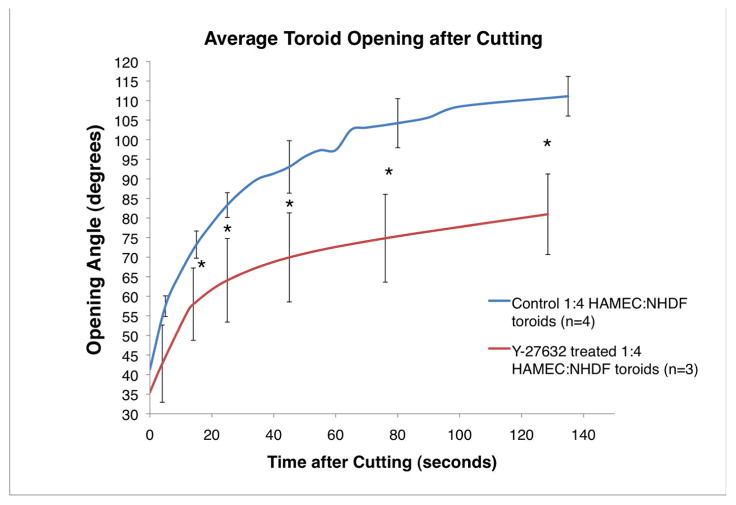
After 3 days of culture, toroids were removed from agarose molds to petri dishes of media where digital video images were recorded using an Olympus SZX16 stereo microscope. To assess contraction after removal from molds, toroids were imaged following unmolding. Our opening angle/ring assay was a modification of previous works^7,9,20,30. The annulus of an unmolded toroid was severed using forceps. The opening angle was acquired from selected video images using ImageJ software. Differences in average opening angle (degrees) between groups were assessed by Student’s t-test at a confidence level of 0.05 (Supplementary Table 1). Error bars represent standard deviations.

Biomechanical analysis

Toroids were removed from agarose molds after 3 or 6 days in culture and mounted onto a modified Bose ElectroForce 3100 testing instrument (Supplementary Figure 1). In brief: toroids were placed around two horizontal cantilevers capable of vertical-plane linear displacement (upper cantilever) and force transduction (lower cantilever). Because the toroids contracted immediately upon removal from molds, mounted toroids were stretched to their initial mold-bound dimensions by translocating the upper cantilever 1.5mm and this considered the initial state prior to undergoing a 0.1mm s⁻¹ linear ramp displacement for 2.25mm. Load data was recorded using a 50g force transducer at 100 data points per second (WinTest software). Plots of load-displacement data were analyzed to obtain engineering stress and strain as follows: _eng = F/2A_cs and _eng = L/L_o where F is the load the toroid exerts on the lower cantilever, A_cs is the initial cross-sectional area, L is the change in specimen length (corresponding to cantilever displacement), and L_o is the initial specimen length (corresponding to the initial state stretch length). Stress-strain curves were then used to calculate Young’s modulus E in the linear elastic region as follows: E = _eng/_eng. The average modulus (kPa), ultimate tensile strength (kPa), and displacement at failure (mm) were compiled and assessed using two-way ANOVA and Bonferroni post-test calculations at a significance level of 0.05. Error bars represent standard deviations. (Supplementary Tables 2 – 4).

Immunofluorescence labeling

Spheroids, linear constructs, and toroids were rinsed in phosphate buffered saline (PBS) prior to fixation in 4% paraformaldehyde. After rinsing, constructs were permeablized (0.1% Triton X-100/PBS+0.01% sodium azide) and blocked (5% Donkey Serum/3% BSA/0.1% Triton X-100/PBS+0.01% sodium azide) prior to overnight incubation at 4°C in rabbit anti-vimentin primary antibody (ab45939, Abcam) diluted in block 1:100. After rinsing, constructs were incubated overnight at 4°C in donkey anti-rabbit cy5 secondary antibody (Jackson ImmunoResearch, 7:1000), Texas Red-X-conjugated Phalloidin (Molecular Probes, 1:50), and Hoechst 33342 (Invitrogen, 1:1000). Samples were mounted whole on glass slides using Fluoro-gel (Electron Microscopy Science).

Imaging

Z-stack (1.5μM step size) image arrays were acquired on a Leica TCS SP5 AOBS Confocal Microscope System (Leica Microsystems, Inc) in sequential multichannel mode to minimize fluorescence signal mixing. Image stacks and subsets are presented as maximum projection images.

RESULTS

Generation of linear tissues from spheroids using a scaffold-free, non-adherent mold system

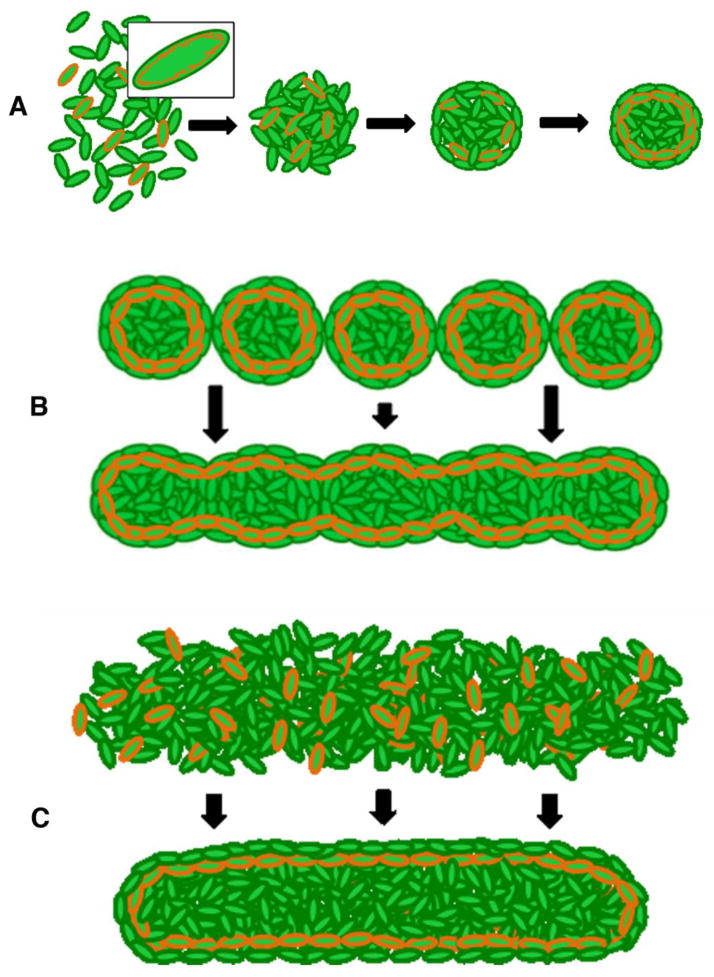
In order to generate linear tissue constructs from spheroids, we prepared rectangular agarose molds. Spheroids were arranged within the molds in a single layer so that each spheroid was in contact with at least one adjacent spheroid (Fig. 1B-Day 0) and maintained under normal cell culture conditions (submerged in media, in a humidified cell culture incubator at 37°C and 5% CO₂). After 24 hours in culture, the spheroids were observed to have undergone a limited degree of fusion as evidenced by the loss of distinct spheroid-spheroid boundaries (data not shown). To evaluate the integrity of the construct it was removed from the mold (Fig. 1B-Day 1). Unexpectedly, as illustrated in Figure 1B-Day 1, the spheroid-based construct immediately contorted upon removal from the mold. The arch of construct’s curvature increased in severity over a period of minutes until it reached a stable end point. Subsequently, a decrease in lateral length was noted during additional culture time (Fig. 1B-Day 2). Comparison of Figure 1B-Day 1 and Figure 1B-Day 2 suggests that the curvature was most pronounced during the period of minutes immediately following release of the construct from the mold. Similar tissue torsion was observed when spheroid-based tissue sheets were removed from their molds (Fig. 1C). In regards to sheets, the torsion was evident by the rolling of the edges of the construct. It is noteworthy that in the case of sheets the longer of the axes exhibited rolling. Based on these observations we hypothesized that the torsion of constructs upon release from the molds was a manifestation of spheroid-spheroid tension imposed by the dimensional constraints inherent to the molds.

Figure 1.

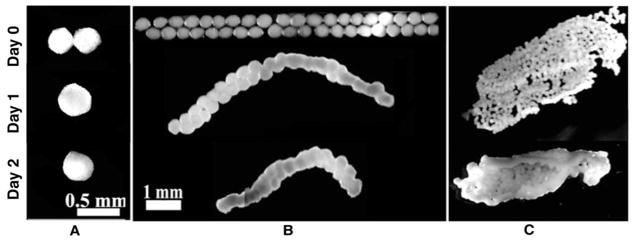
Stereo microscopic images of spheroid fusion under non-adherent unconstrained and non-adherent constrained conditions. Linear (B) and sheet-like (C) spheroid-based tissue constructs exhibit torsion upon removal from molds, whereas two spheroids in unconstrained conditions (A) fuse completely.

Culture-induced tension and the inhibition of tissue spheroid fusion

Our studies of spheroid-based constructs show that spheroid fusion is inhibited by the spatial constraints imposed by non-adherent mold culture systems during tissue generation. Evidence in support of this is the observation that spheroids in an unconstrained, hanging drop system undergo complete fusion in 24 hours, whereas spheroid fusion is incomplete at 24 and 48 hours in molds (Fig. 1). A potential mechanism underlying this behavior is that the forces which generate residual tension relieved through torsion, such as that observed in Figure 1B, can be continuously relieved in an unconstrained system. To evaluate this possibility we analyzed spheroid fusion under unconstrained conditions in real-time. We observed that two spheroids in non-adherent culture conditions exhibited 360-degree range of motion, resulting in the formation of one major spheroid (Fig. 2). Spheroids illustrated only limited + z-axis movement, which we attributed to be due to gravity. Under unconstrained conditions (i.e., hanging drop), we speculate that each spheroid is able to move, deform, and its constituent cells reorganize and coordinate sufficiently with cells of the partner spheroid to adopt one cohesive sphere shape. In contrast, under non-adherent constrained linear conditions, spheroids are limited in the directions they can move to alleviate tension. This mold-induced tension on the forming tissue as a whole underlies the observed torsion, and is the summation of the tensions of each spheroid as an individual module within the forming tissue. Each module’s tension is itself the summation of the limited range-of-motion of all the cells comprising that module (spheroid).

Figure 2.

Time-lapse images of unconstrained spheroids moving during fusion. Pairs of spheroids are denoted by boxes; lines indicate changes in spheroid orientation.

Generation of linear tissues from cells using a scaffold-free, non-adherent mold system

In light of our findings regarding spheroid-based tissue assembly, we next investigated the torsion properties of tissues generated from cells using a linear non-adherent mold system. Within 24 hours, high-density cell suspensions formed rod-like tissues within the molds (Fig. 3). In contrast to linear tissues formed from spheroids, cell-derived linear tissues did not exhibit torsion upon removal from the molds. This finding suggests that, unlike spheroids in similar culture conditions, linear tissues generated from high-density cell suspension do not retain residual tension. Similar to what we observed with spheroid-based linear constructs (Fig. 1B), the cell-based linear constructs underwent progressive lateral condensation (shortening). This illustrates that the tissue formation process was still under the influence of tension (lateral shortening); however, the lack of residual tension as evidenced from the lack of torsion upon removal from the molds suggests there is a greater capacity to resolve tension during culture using the cell-based system as compared to spheroid-based.

Figure 3.

Stereo microscopic images of high-density cell suspension cultured in linear agarose molds under non-adherent constrained conditions. Cultures form rod-like linear tissues that exhibit progressive lateral condensation.

Generation of toroidal tissues from cells using a scaffold-free, non-adherent mold system

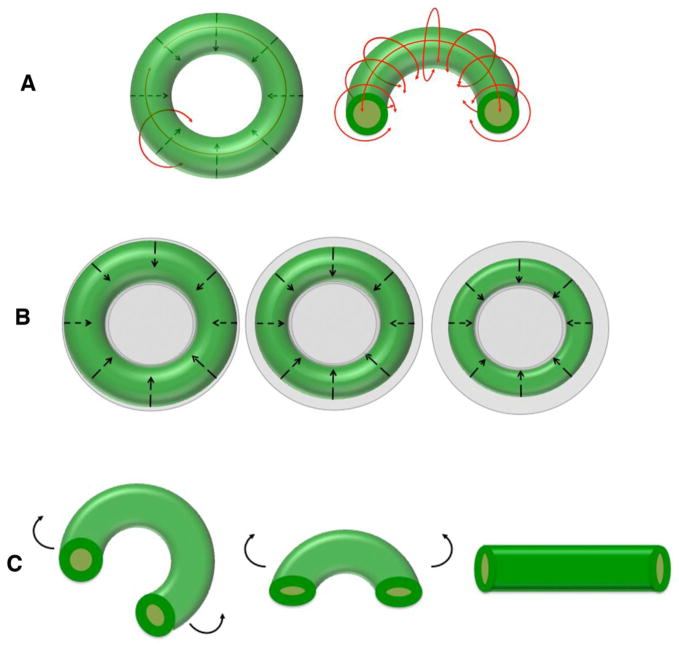
To evaluate the relationship between tissue shape and tissue deformation we generated toroid-shaped tissues using a non-adherent toroidal mold system. Within 24 hours of the addition of high-density cell suspension, toroid-shaped tissues were formed. Maintaining the toroids in culture molds over subsequent days revealed that the toroid formed increasingly tighter contraction around the central post, similar to the lateral condensation observed in rod cultures but in a radial direction (Fig. 4A). When toroid constructs were removed from molds we noted an immediate decrease in the inner diameter (Fig. 4B). Here again we interpret this activity to be the manifestation of residual radial tension induced by the culture conditions, acting to counter the propensity of the construct to form a sphere.

Figure 4.

Stereo microscopic and time-lapse images characterizing toroidal tissues generated from culture of high-density cell suspensions in agarose molds under non-adherent constrained conditions. A: Toroids exhibit progressive radial and circumferential condensation; B: Toroids decrease inner diameter upon removal from molds (black bar is constant size); C: Progressive opening of toroids following cutting.

To evaluate more extensively the tension behavior of toroid-shaped tissues, toroids were cut across the width of the annulus after removal from molds. Immediately upon cutting the toroids began to open or ‘uncurl’. At its end point this opening resulted in the tissue adopting a linear shape (Fig. 4C). We defined the tension underlying this opening behavior as circumferential since it caused a behavior distinct from that of inner diameter-decreasing tension, which we defined as radial tension. This assay revealed that the cells forming tissues in a confining toroid-shaped mold system are under the influence of both radial and circumferential tensions.

Actomyosin based contraction underlies tissue torsion and progressive condensation

Based on the studies of Dean and Morgan^2,3 investigating actomyosin-based contraction in self-assembled tissues, we investigated whether the torsion and progressive condensation we observed was actomyosin-based. We began this evaluation by immunolabeling spheroid, linear, and toroidal constructs with Texas Red X-conjugated phalloidin and an antibody to vimentin. As seen in Figure 5A phalloidin staining indicated the presence of f-actin, a known component of the cortical cytoskeleton. The vimentin immunostaining of toroidal constructs revealed regional variations in organization of the intermediate filaments. Analysis showed that the vimentin fibers underlying the outer circumference were aligned in parallel to one another and appeared to be under tension (stretched), whereas vimentin patterns observed at the center of the construct showed a loose, disorganized, coiled appearance (Fig. 5B). These observations suggest that cells comprising the outer diameter – i.e., near the cell-media interface – of the constrained toroid were under a different micromechanical environment in terms of tension than the cells at the cross-sectional center of the construct^1,22.

Figure 5.

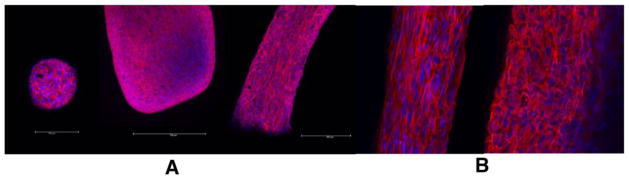
Whole-mount confocal immunofluorescence images of tissue constructs. A: Left to right: spheroid, rod-like linear, and cut toroidal tissue constructs; phalloidin (red) and Hoechst (blue) expression; 10X. B: Cut toroidal tissue construct; vimentin (red) and Hoechst (blue) expression; 40X oil. Note loose vimentin organization in inner region versus aligned and taut organization at outer/circumferential region.

To evaluate whether contraction of the actomyosin cytoskeleton contributed to either the radial or circumferential tensions observed in toroidal tissues, forming constructs were treated with Y-27632, a selective inhibitor of ROCK phosphorylation that reversibly inhibits myosin phosphorylation^3,19. Analysis of cell suspension-derived toroids treated with 10 M Y-27632 for 2 hours showed that these constructs exhibited decreased ring opening as compared to untreated (control) toroids (Fig. 6). We next investigated whether the actomyosin cytoskeleton contributed to the inhibition of spheroid fusion observed in constrained culture systems. To evaluate this we first determined whether the actomyosin cytoskeleton contributed to spheroid formation by placing cells in spheroid forming culture molds in the presence or absence of Y-27632. As seen in Figure 7A, inhibition of actomyosin via 10 M Y-27632 had no apparent effect on spheroid formation. In contrast to this observation, spheroid-based linear constructs cultured in the presence of Y-23632 exhibited decreased torsion as compared to untreated linear constructs (Fig. 7B). It is important to note that the “space” between the spheroids and molds allowed for greater range of motion than that of Figure 1. These findings suggest that actomyosin contraction is not required for spheroid formation but that actomyosin machinery is actively involved in spheroid-based tissue formation, as evident from the decreased torsion and/or condensation when cultured in the presence of Y-27632.

Figure 6.

Treatment of toroid constructs with actin-myosin contraction inhibitor Y-27632 prior to cutting reduces the opening angle. Error bars indicate standard deviation. * p<0.05 (Student’s t-test).

Figure 7.

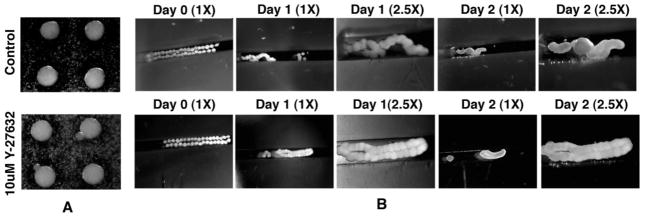
Stereo microscopic images depicting (A) that the treatment of cell cultures under non-adherent spheroid forming conditions with Y-27632 does not inhibit spheroid formation and (B) that treatment of spheroids under non-adherent linear constrained conditions with Y-27632 inhibits spheroid integration.

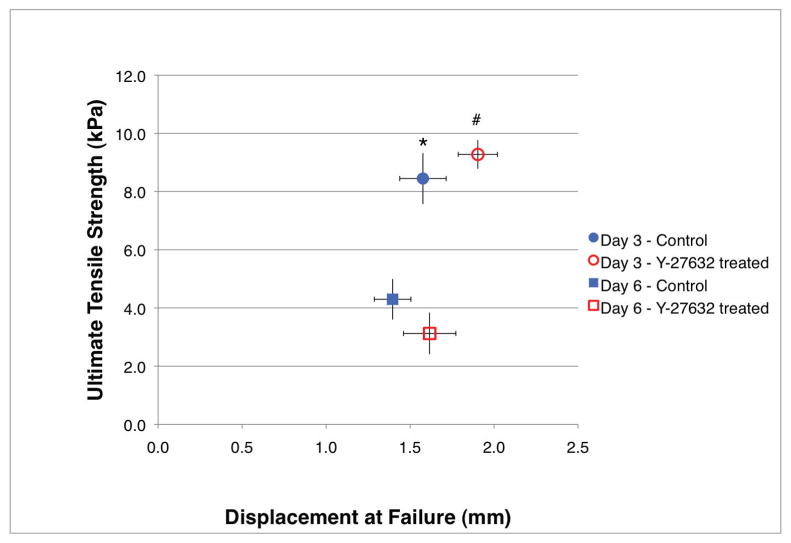
To further characterize the material properties of suspension-derived toroid-shaped tissues, we performed uniaxial tensile testing. As shown in Figure 8, both day 3 and day 6 toroids treated with 10 M Y-27632 for 2 hours prior to testing showed a trend of decrease in Young’s modulus as compared to their respective untreated day-matched toroids (15.711±1.6kPa vs. 17.378±1.49kPa and 6.001±0.38kPa vs. 8.487±1.46kPa, respectively). Duration in culture was found to inversely correlate with Young’s modulus (p<0.05). Ultimate tensile strength was significantly greater for day 3 toroids as compared to day 6 toroids, regardless of treatment, while displacement at failure was significantly greater for day 3 Y-27632-treated toroids (1.903±0.12mm) as compared to day 3 untreated (1.576±0.14mm) and day 6 untreated toroids (1.396±0.11mm) (Fig. 9).

Figure 8.

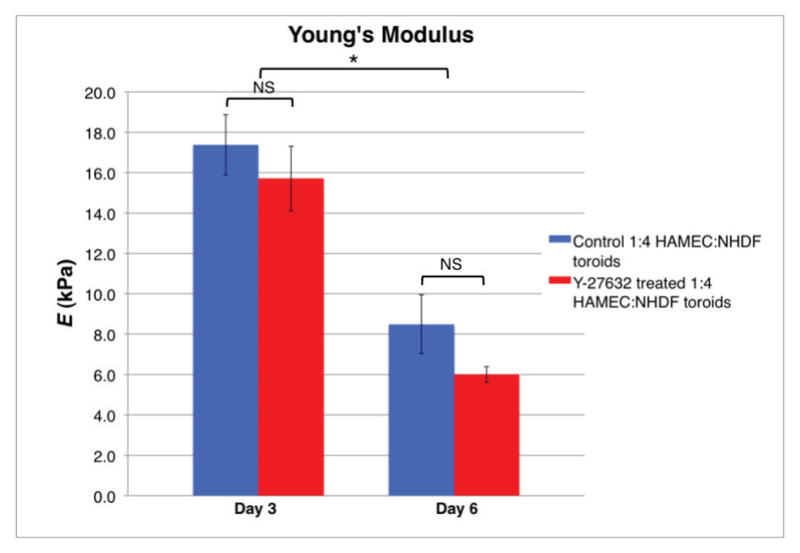
Uniaxial tensile testing illustrating toroids decrease in Young’s modulus with increased culture duration. Error bars indicate standard deviation. * p<0.05 (two-way ANOVA, Bonferroni post-test) day 3 as compared to day 6; NS – no significant difference.

Figure 9.

Biomechanical analysis indicates day 3 toroids can withstand greater deformation before failure and exhibit greater ultimate tensile strength than day 6 toroids. Treatment with Y-27632 significantly increased the displacement at failure of day 3 toroids as compared to day-matched control. Error bars indicate standard deviation. * indicates day 3 control ultimate tensile strength with respect to day 6 control and day 6 inhibitor-treated ultimate tensile strengths (two-way ANOVA, Bonferroni post-test, p<0.05); # indicates day 3 inhibitor-treated displacement at failure with respect to day 3 control and day 6 control displacements at failure, and day 3 inhibitor-treated ultimate tensile strength with respect to day 6 control and day 6 inhibitor-treated ultimate tensile strengths (two-way ANOVA, Bonferroni post-test, p<0.05).

Day 3 Y-27632-treated toroids showed differences with respect to shape of the stress-strain curves as compared to untreated day 3 toroids (Supplementary Figure 2). Specifically, the day 3 Y-27632-treated toroids showed both an elongated toe region, as noted from a delayed start to the linear region, and a longer linear region as compared to the day 3 untreated toroids. Day 6 Y-27632-treated samples showed a trend of a longer linear region than untreated day-matched samples. Among the day 6 toroids no difference between the starting-point of the linear region was noted, indicating the Y-27632-treated samples did not illustrate a modified toe region from that of the untreated samples.

DISCUSSION

In this study we utilized a mixed population of cells to generate tissue modular units (spheroids) and suspension-based tissues. Specifically, we chose a mixture of endothelial and fibroblast cells because we felt these cell types represented the minimum essential cell types necessary to build virtually all tissues. Our results suggest that cytoskeletal actomyosin machinery is not critical to initial spheroid formation. This finding supports the DAH, which attributes spheroid formation to cell-cell adhesion^5,34. According to the DAH: dispersed, dissociated cells in permissive non-adherent culture will organize into a spherical aggregate or ‘spheroid’. When multiple cell types are co-cultured under spheroid-forming conditions, cells expressing the strongest intercellular adhesions (or, greatest number of same-strength intercellular adhesions) form the center of the spheroid while those expressing less-strong (or fewer same-strength) adhesions form an outer layer³⁴. This is fitting with the property of surface tension, considering the interfacial tensions between two different liquids such as oil and water and the organization of droplets that develop in order to adopt the conformation requiring minimum energy to maintain^1,5,22,36.

Dissociated cells, stripped of extracellular matrix, have only cell surface receptors in order to establish preliminary contact. For adherent cells, contact with a substratum is required in order to survive. Thus, cells establish cell-cell adhesions as a necessity in order to survive non-adherent conditions and adopt a spheroid shape as a means to minimize interfacial tension, which is in keeping with liquid thermodynamic principles and intercellular adhesion-driven principles outlined in the DAH. It would be interesting to interrogate cell types and ratios of cells within cell suspensions and modules in order to see how cell adhesion interplays with tissue cortical cytoskeletal development and tension during tissue formation; however, adjusting the numbers and types of adhesion molecules by changing the numbers and types of cells used adds complexity to this model system. Epithelial cells, of which we utilized microvascular endothelial cells, have been shown to aggregate in relatively strong cellular adhesions primarily through E-cadherin^5,6,34, while fibroblasts are less classically attributed to cadherin-mediated aggregation due to comparatively weak (or absent) N-cadherin expression⁶. Although fibroblasts are more closely associated with cell-matrix adhesions¹⁰ and matrix synthesis, heterotypic cultures of epithelial and fibroblast cells have been shown to result in the formation of heterotypic cell adhesion complexes²⁶. While not discussed extensively in this work, there is a large body of work concerning the DAH that has investigated the role of cell adhesion molecules during initial tissue formation, particularly with respect to cell stratification or “sorting out” within tissues^{1,5,6,26,28,34,16}.

The phenomenon of spheroid fusion was based on the observation that two unconstrained spheroids coalesce into one spheroid under non-adherent conditions in order to form a composite spheroid, adopting the shape that minimizes surface area and interfacial tension. Similar to cell sorting during spheroid formation, the composite spheroid resulting from spheroid fusion contains stratified cells. Because multiple (up to 5) spheroids can be shown to fuse into one major spheroid, and because this process seems to recapitulate the process by which initial spheroids formed from cell suspension, it was assumed that the “rules” governing spheroid formation – i.e., the DAH – also govern spheroid-based tissue formation.

Our work and the work of others suggest that, once formed, spheroids undergo a number of changes as they organize from a group of associated cells into a tissue^2,3,36. These include the generation of a tissue cortical actin cytoskeleton and the production of extracellular matrix in addition to interplay between cell-cell adhesion molecules, cell-matrix adhesions, extracellular matrix molecules, and the cytoskeletal system^3,22,26,27. Together these activities act at a basal level to maintain the spheroid’s shape in response to external forces including gravity and hydrophobic-hydrophilic interactions (Fig. 10A). Though the unconstrained spheroid fusion process appears to follow liquid thermodynamic principles, our results suggest that once a spheroid has formed it is inaccurate to assume intercellular adhesion-driven DAH “rules” when predicting aggregative behavior in tissue formation²². Considering that a tissue spheroid is comprised of more components (i.e., matrix, cell-cell adhesions, cell-matrix adhesions, tissue cortical cytoskeleton) as compared to the dissociated cells that formed the tissue spheroid (i.e., cell-cell adhesions), it is reasonable that the level of complexity governing tissue formation differs when building a tissue from spheroids rather than cell suspension. In other words: it was naïve to assume that spheroid-based tissues would form according to the same process as cell suspension-based tissues. Spheroids are, themselves, small tissues.

Figure 10.

Schematic of in vitro tissue morphogenesis comparing modular and high-density cell suspension approaches. A: Cells contain cortical actin cytoskeletons (orange, higher magnification in box). Under non-adherent conditions, cell-cell adhesions and organization of cellular cortical cytoskeletons results in generation of a spheroid having a tissue cortical cytoskeleton. B: In the generation of linear constructs from individual spheroids under non-adherent constrained conditions, individual spheroid tissue cytoskeletons fuse, deform, and reassemble to generate a new linear tissue cytoskeleton. C: In the generation of linear tissue constructs from cell suspension under non-adherent linear constrained conditions, cell-cell adhesions and organization of cellular cortical cytoskeletons results in generation of a linear tissue construct with a shape-appropriate cortical cytoskeleton.

To understand that, in a scaffold-free environment, cells inherently aggregate into a sphere and all attempts to generate non-spherical tissues require inhibition of this inherent spheroidal propensity is fundamental to tissue engineering. The sphere is the “default’ tissue morphology under non-adherent conditions, having the smallest surface area per unit volume. Minimal surface area translates into minimal interfacial tension and therefore lowest energy requirement to maintain. When placed in fusion-promoting culture conditions, spheroids will deform their individual tissue cortical cytoskeletons in order to adopt the shape that requires the least expenditure of energy to maintain. As spheroids merge, individual spheroids become less discernable from the forming tissue entity. This activity reflects the ability of spheroids to act in a concerted fashion to form a larger tissue. As part of this fusion process the cortical cytoskeleton of individual spheroids must reorganize to form the cortical cytoskeleton of the newly forming tissue (Fig. 10B). When spheroids are maintained in non-adherent agarose molds of different shapes, their range of motion is limited based on the shape (dimensions and occupancy) of the mold. Accordingly, cells are limited in their ability to reorganize from each spheroid entity. The attempt to alleviate culture-induced tension by physical translocation of the spheroids is manifest as the torsion we see in linear spheroid-based constructs, most notably upon removal from molds. This transition from the default equilibrium shape of the sphere to a non-spherical shape requires time and/or energy; it is important to recognize that every modular engineering approach shares this requirement for additional time and/or energy to transition from the shape of the module to the desired tissue shape. That mold-bound spheroids remained more or less in place yet tissue morphogenesis/fusion still occurred suggests that actin-myosin based cortical cytoskeletal rearrangements are a component of tissue fusion ^3,10,31. This finding may be useful for attempts to maintain length in linear tissue engineering.

Culturing high-density cell suspension within non-adherent agarose molds results in the formation of tissues in the shape of the mold^2,39. This method of generating tissue follows the rules of the DAH and thus, unlike spheroid-based tissues, these tissues do not exhibit torsion upon removal from molds. Like spheroids and spheroid-based tissues, cell suspension-based tissues establish a tissue cortical cytoskeleton that defines the gross shape of the tissue (Fig. 10C).

We showed that spheroid, linear, toroidal, and sheet-like tissue constructs contain cortical actin cytoskeletons that define the gross shape of each tissue. The use of vimentin and phalloidin staining in concert allowed us to illustrate the presence of a multi-filamentous tissue cortical cytoskeleton containing intermediate filaments and f-actin. Additionally, vimentin staining illustrated the influence of tension on filament organization, highlighted by the loose versus taut arrangement of filaments within the inner and outer regions of the toroidal constructs, which was not apparent through visualization of f-actin alone.

While we are aware that in addition to the tissue cortical cytoskeleton the aggregative behavior of cells during tissue formation also involves cell-cell adhesions and cell-matrix adhesions, our studies using the reversible myosin phosphorylation inhibitor Y-27632 to perturb the cytoskeletal contractile system were meant to provide a foundation from which further investigations can progress. The strong interdependence between adhesion and cytoskeletal tension makes the ability to clearly distinguish whether the effects of Y-27632 act through altered tension or cell-cell cohesion difficult. By altering the intracellular mechanical environment through inhibiting myosin phosphorylation and thus ROCK-mediated contraction, we changed the relative tension of the actin cytoskeletal system. As the intracellular actin cytoskeleton is connected to cell surface receptors such as cell adhesions via protein complexes and as cell surface receptors are connected to other cells’ surface receptors and/or the extracellular environment^10,27, it is reasonable to presume that any change to the intracellular mechanical environment will be propagated to the extracellular environment and vice versa, thus altering the biomechanical properties of the tissue in its entirety in effort to establish a new homeostatic balance. It is possible, therefore, that by altering cellular contractility we may have simultaneously altered cellular cohesion³. We specifically interrogated intracellular contractile machinery through inhibition of ROCK-mediated actin-myosin contraction rather than cell surface receptors (cell-cell or cell-matrix adhesions) so as to most directly and clearly illustrate the effects of “one” of the inter-related aspects of tissue morphogenesis. As there is interplay between all factors, by perturbing one intracellular factor we recognize that we have, in fact, inevitably altered the system as a whole. In the future we intend to use this baseline as a reference point to interrogate the combinatorial and/or unique effects of cell-matrix interactions on aggregative behaviors of cells during tissue formation.

Disrupting the tension of the cytoskeleton by cutting (i.e., ring opening assay) changed both the overt shape of the tissue and the patterning of the cortical cytoskeleton (not shown). The results of our biomechanical analysis indicated that nascent cell suspension-derived toroidal tissues exhibited properties of relatively soft, inelastic tissues. By inhibiting actin-myosin contraction through treatment with the ROCK inhibitor Y-27632 we saw a decrease in opening angle as well as a decrease in Young’s modulus, which is compatible with our working model in which tissues utilize cortical cytoskeletal contractile machinery to attempt to alleviate culture-induced tension. The differences in the shape of the stress-strain curves – particularly the toe region – among the day 3 Y-27632-treated and untreated toroids (Supplementary Figure 2) illustrate the dynamic nature of the nascent tissue and its ability to use the tissue cortical cytoskeleton to modulate culture-induced tension. Though it was somewhat surprising that the day 6 toroids illustrated a significant decrease in Young’s modulus and ultimate tensile strength as compared to the day 3 toroids, the relative scale of the magnitude of values at both time points is in line with those measured from embryonic tissues. This shift in biomechanical properties over a relatively short period of time reflects underlying changes to the tissue as a whole which are not appreciable from gross macroscopic comparison and suggests further that, given that the process of tissue morphogenesis encompasses cell-cell adhesion, cell-matrix adhesion, cytoskeletal, and extracellular matrix-mediated factors acting in concert, the balance between which factor is dominant may change as a function of time. We intend to investigate the dynamic nature of scaffold-free tissue engineering over a more extensive time course in the future.

Overwhelmingly, our results indicate that tissue morphogenesis is greatly influenced by the effects of culture-induced tension and that an active actin-myosin cytoskeleton is used to contract in response to tension (Figure 11)^{12–15,27,31,37–39}. We believe the following parameters explain the ‘rules’ governing self-assembly of tissue constructs and as such should be kept in consideration when undertaking tissue engineering endeavors: 1) globally, the laws of physics determine the ultimate shape of the tissue and also provide the impetus driving fusion. Cells will become a sphere under unconstrained, non-adherent conditions. By altering the dimensions of the culture conditions (i.e., providing constraints through agarose molds) we inhibit the cells’ ability to move and establish cell-cell contacts, and therefore perturb their inherent drive to form a sphere. 2) Locally, the ability for cells to interact to form tissue constructs is mediated by cell-cell and cell-matrix interactions, and is influenced by existing tissue cortical cytoskeleton^{21,22,26,27,29,31,32}. Differences in the numbers and types of cell-cell and cell-matrix receptors and relative ability to synthesize and organize matrix (and/or types of matrix molecules) among cell types may account for the stratification of cells, in agreement with DAH principles². When using spheroids as the modular units to generate tissues, the established spheroid tissue cortical cytoskeletons inhibit the cells’ inherent propensity to form a new sphere. Presence of matrix may also serve to prevent integration into a uniform tissue in spheroid-based engineering.

Figure 11.

Schematic illustrating the influence of tension on in vitro cell-based toroidal tissue formation under non-adherent constrained conditions. A: Forming toroidal tissues generate radial and circumferential tension during culture and (B) exhibit progressive condensation. C: Toroids “opening” upon cutting relieves residual circumferential culture-induced tension.

In summary, we speculate that the development of the cortical actin cytoskeleton is the rate-limiting step that defines in vitro tissue engineering. In modular tissue engineering approaches, it is necessary to keep in mind that each module’s cortical cytoskeleton must be disassembled and reassembled in a coordinated fashion in order to achieve an integrated tissue construct of desired shape in which cells can act dynamically in a concerted fashion. The ability for each module to fuse and integrate into the desired tissue shape is influenced by tension induced by the culture parameters (i.e., mold dimensions and tolerance/fit within the mold) and achieved through both cell-cell adhesion-based cellular rearrangements and active actin-myosin cytoskeletal contraction.

Supplementary Material

10439_2014_986_MOESM1_ESM

Supplementary Figure 1. Diagram depicting toroid loading onto Bose ElectroForce 3100 uniaxial testing apparatus and initial dimensions of toroid. A1: Toroid is removed from agarose mold using forceps and placed around two horizontal cantilevers; A2–3: top cantilever is translocated 1.5mm vertically to establish initial state, in which toroidal internal diameter matches that of the agarose mold central post (2.5mm). Initial force mounted toroid exerts on cantilevers (avg: 0.09 0.017g) is set to zero at this time. B: Enlarged front-view of mounted toroid. Initial toroid length L_o was set as 2.5mm, corresponding to the internal diameter at initial state. Cross-sectional area was obtained from measuring the cross-sectional diameters of intact, paraformaldehyde-fixed toroids and by imaging the fixed cross-sections and measuring cross-sectional diameters on the images. The average value 0.566mm² (n=7) was used for all calculations. C: Example of stress-strain plot denoting locations from which values for ultimate tensile strength, Young’s modulus, and displacement at failure calculations were obtained.

Supplementary Figure 2. Stress-strain plots obtained from load-displacement data acquired during uniaxial tensile testing of day 3 toroids. Day 3 Y-27632-treated toroids (bottom plot) showed elongated toe and linear elastic regions as compared to day-matched control samples (top plot).

Supplementary Table 1. Summary of results of Student’s t-test analysis of toroid ring opening experiments corresponding to Figure 6 (p<0.05). Confidence Intervals are expressed as absolute values ( ). Based on F-test, assumption of equal variance among samples was valid for all except T2. Significance level p<0.05.

Supplementary Table 2. Summary of data used to calculate two-way ANOVA corresponding to biomechanical characterization of toroids in Figures 8 and 9. As listed from top to bottom, each cell contains mean, variance, standard deviation, and standard error. Units for mean Young’s modulus and ultimate tensile strength are kPa; mean displacement at failure is reported in mm.

Supplementary Table 3. Summary of results of two-way ANOVA (two factors, two levels each: Y-27632 treatment vs. control and 3 vs. 6 days in culture) corresponding to biomechanical characterization of toroids in Figures 8 and 9. SS – sum of squares; df – degrees of freedom; MS – mean square. Significance level p<0.05.

Supplementary Table 4. Summary of results of post-test calculations with Bonferroni correction corresponding to biomechanical characterization of toroids in Figures 8 and 9. ‘3’ or ‘6’ indicates culture duration (i.e., day 3 or day 6, respectively); ‘C’ or ‘I’ indicates treatment (i.e., control or Y-27632-treated, respectively). Significance level p<0.05.