Using GRAPPA to improve auto-calibrated coil sensitivity estimation for the SENSE family of parallel imaging reconstruction algorithms

Abstract

Two strategies are widely used in parallel MRI to reconstruct subsampled multi-coil image data. SENSE and related methods employ explicit receiver coil spatial response estimates to reconstruct an image. In contrast, coil-by-coil methods such as GRAPPA leverage correlations among the acquired multi-coil data to reconstruct missing k-space lines. In self-referenced scenarios, both methods employ Nyquist-rate low-frequency k-space data to identify the reconstruction parameters. Because GRAPPA does not require explicit coil sensitivities estimates, it needs considerably fewer auto-calibration signals than SENSE. However, SENSE methods allow greater opportunity to control reconstruction quality though regularization and thus may outperform GRAPPA in some imaging scenarios. Here, we employ GRAPPA to improve self-referenced coil sensitivity estimation in SENSE and related methods using very few auto-calibration signals. This enables one to leverage each methods’ inherent strength and produce high quality self-referenced SENSE reconstructions.

Introduction

Parallel MR imaging methods reconstruct an image from sub-sampled k-space data acquired in multiple coils, and can be organized in two basic classes. One class reconstructs the image directly, using all the subsampled data and explicit estimates of the receiver coil sensitivities. The other class of methods estimates the missing data in each coil, implicitly using correlations in the data across all the coils, and then combines this synthesized coil data set to obtain a final result. In this work, we refer to the first class as combine-then-reconstruct (CtR), the simplest form of which is (Cartesian) SENSE (1). We have shown in (2) that a number of methods, including Cartesian SENSE, SPACE RIP (3), and Generalized SMASH (4) are special cases of the CtR Generalized SENSE approach, and indeed the same linear system problem formulation can be used to describe each of them. The second class, which we refer to here as reconstruct-then-combine (RtC), includes the GRAPPA (5) approach, as well as other variable-density auto-calibrated approaches (2).

RtC and CtR approaches are often seen to be competing. For example, (6) seeks to answer the question of “which method is better?” in particular imaging scenarios. In this work we look instead to combine the two approaches to leverage their distinct advantages. We present a method which uses an idea borrowed from the RtC philosophy to address one of the limitations of CtR methods. In particular, CtR methods require numerical estimates of the differing spatial sensitivities of the multiple coils. A common way to obtain these coil sensitivities is to measure a set of lines near the origin of k-space and use them to construct estimates of the coil sensitivies (7).

However, as we illustrate below, CtR methods can be sensitive to the accuracy of these sensitivity estimates. High-acceleration acquisitions in particular need very accurate coil sensitivity estimates. In self-referenced scenarios, accuracy can be increased through acquisition of more auto-calibration signal (ACS) lines, although this decreases the total achievable acceleration. Here we suggest a method by which the RtC approach can be used to greatly improve the accuracy of coil sensitivity estimates using a very small number of ACS lines, at very modest additional computational cost. To illustrate, we focus on a specific RtC method, GRAPPA, and leverage it to improve our LSQR-Hybrid CtR method (13). We present examples using both uniform and non-uniform subsampling strategies.

Theory

In CtR methods, the signal acquisition model for all coils is discretized and then combined to form a linear system that models the mapping of the excited spin density (the imaged object) to the output. As we describe in (2), the full spectrum of CtR methods can be described analytically by the same linear system of equations. One strength of this class is that system regularization approaches can be easily employed, which has been used for example to limit noise amplification (8), maintain spatial-domain smoothness (9), and maintain specific phase profiles (10).

A primary point of weakness in this class of methods, however, is that they rely explicitly on estimates of the coil sensitivities. Good estimates can be difficult to obtain, especially without measuring additional low-frequency lines, with its consequent cost in reduced acceleration. Furthermore, reconstruction accuracy is highly dependent on the degree to which the coil sensitivity estimates match the measured data. A number of approaches for creating coil sensitivity estimates have been proposed, including the use of a prescan step and/or polynomial estimation of low-frequency data (1), joint estimation of both the sensitivity information and the reconstructed image (11), and self-referenced/auto-calibrated methods (7).

In contrast to CtR methods, RtC methods first explicitly estimate the unsampled k-space data in each coil, and then form an image by combining the measured and estimated k-space data. The estimate is based on a model that assumes the measured data result from a convolution in k-space (12) between the excited spin density and the coil sensitivities—which are assumed to be band-limited to lower-frequencies and smoothly varying spatially. The convolution model parameters are typically found through a least-squares fit to a densely sampled set of low-frequency ACS measurements. A significant strength of RtC methods is the ability to produce accurate estimations of missing k-space data when limited ACS data is available.

In this paper we propose to leverage the strength of the RtC class to improve coil sensitivity estimates in self-referenced CtR approaches. Specifically, we propose using GRAPPA-enhanced sensitivity maps for SENSE reconstructions (GEYSER). We first identify a low-frequency region of k-space large enough to ensure sufficient coil sensitivity estimates. To enhance acceleration, however, rather than measure all the lines in that region at the Nyquist rate, we subsample part of that region and use GRAPPA to estimate the missing lines. Combining sampled and GRAPPA-estimated lines, we calculate coil sensitivities which are then used with CtR algorithms to reconstruct the image.

Methods

Sampling strategy and reconstruction approaches

The examples presented below use the following data acquisition strategy: As illustrated in Fig. 1, we divided the low-frequency “central” region of k-space into “inner” and “outer” subregions. In particular, we acquired a small number of lines in the inner low frequency region at the Nyquist rate (1Δk) for a specified image resolution. This inner region typically spans 4 to 6 lines, although SNR-limited applications such as perfusion or diffusion imaging may require more. In the outer central region, a number of lines spaced (2Δk) or (3Δk) apart were acquired. At frequencies beyond the central low-frequency region, higher local acceleration factors were employed.

Figure 1.

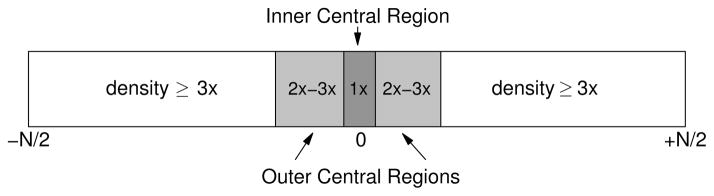
Sampling density distribution along the phase encode direction in k-space. Numbers shown in the boxes report the spacing of acquired lines in units of (1Δk). The density in the box labeled as ≥3x can be chosen as desired, for instance according to the exponential density Z_ed = exp(−|βk_y|).

The CtR image reconstruction then proceeded in three stages: (I) a GRAPPA estimate of the missing data in the outer-central k-space regions of each coil, (II) coil sensitivity estimation using both the inner central and the GRAPPA-enhanced outer central regions, and (III) an LSQR-Hybrid reconstruction(13), of the original data using the coil sensitivity estimates from step (II). Step (I) employed a 2×3 kernel, estimating a given k-space data point from 3 points along the readout direction on two neighboring phase encode lines. Thus, the number of available ACS lines for GRAPPA calibration was two less than the number of (1Δk) lines. In step (II), the coil sensitivity estimates were calculated from the GRAPPA enhanced coil data set, similar to (7). A Gaussian window, f(k) = exp(−0.5|αk/(N/2)|²) with α the window width and N as the number of k-space coordinates to span, was applied to ensure smoothness in the coil sensitivity maps. Along the readout dimension, the width of the window was specified as α = 10. Along the phase encode dimension, the width of the window was α = 2.5, and the k-space coordinate span was set to cover both the inner and the outer central regions in the GRAPPA enhanced data set. After windowing, the data from each coil was transformed to the spatial domain. The composite view of the coil array was estimated by computing the root-sum-of-squares of the complete set. This composite view was then used to normalize the spatial domain representation of each coil estimate. The complete process is illustrated in Fig. 2.

Figure 2.

Coil sensitivity estimation data flow.

The resulting coil sensitivity estimates were then employed with the original acquired data to reconstruct an image using an iterative algorithm known as LSQR-Hybrid (14). This algorithm is similar to the conjugate gradient (CG) approach(15), although we prefer it over CG because it is more stable numerically and allows very efficient selection of good Tikhonov regularization values(13). In the examples shown below, we refer to the CtR reconstructions as LSQR-Hybrid, regardless of the sampling pattern employed. Through appropriate regularization settings, one can ensure that the regularized pMRI solution found via LSQR-Hybrid will be nearly identical to solutions found via more traditional regularized CG-SENSE or a pseudo-inverse approach (2).

For comparison, we also performed reconstructions by replacing steps (II) and (III) above with a second pass of the GRAPPA algorithm. This second pass employed a 4×5 kernel and ACS lines drawn from both the inner and outer central region. We note that the linear system used to identify GRAPPA reconstruction parameters grows larger as the number of ACS lines increase, which significantly increases the parameter estimation time.

Evaluation of the Reconstructions

To map the CtR results back to RtC results for comparison, we apply the coil sensitivity estimates to the CtR reconstruction to create estimates of each individual coil acquisition. One can then replace some of this estimated coil data with the actual measured lines (17). This ensures that reconstructions from both classes contain the same acquired data in the same data locations and that any errors present in the coil sensitivity estimates affect only the CtR-class reconstructions. Images shown in the figures are derived from a root-sum-of-squares operation on each multi-coil estimate.

In the phantom imaging example, where an unaccelerated data set is available, three metrics are used to evaluate the reconstructions. The relative mean square error (rms err) is calculated as ||I_est−I_true||₂/||I_true||₂ to give a measure of the normalized difference between the estimated and the fully sampled data. The maximum pixel error (max err), ||I_est−I_true||_∞, is used to measure the maximum deviation between the estimate and the true image. Finally, we calculate the standard deviation (std dev), $\sigma =\sqrt{{\sum }_{i=1}^M{\sum }_{j=1}^N{(I_{\text{est}}(i,j)-I_{\text{true}}(i,j))}^2/(NM)}$, of the re-construction error to measure the noise amplitude.

Data acquisition

The phantom images presented below represent one slice of the American College of Radiology (ACR) phantom acquired with a FSE sequence (TR/TE:500ms/20ms, slice thickness:5mm, FOV:25cm, matrix size:256×256) on a 1.5T GE Excite (GE Medical Systems) scanner using a standard 8-channel head coil. We note that this slice can be challenging to reconstruct accurately, as there is significant information content in the high-frequency coordinates of k-space.

An accelerated acquisition of this data was simulated by sampling every third line along the phase encoding dimension. In addition, four auto-calibration lines were retained, giving a total of 6 central k-space lines sampled at the Nyquist frequency. That is, the sampled lines were k_y = {−127, −124, ···, −7, −4, −2, −1, 0, 1, 2, 3, 5, 8, ···, 125, 128}. The six inner central lines provided 4 ACS lines to each of the three GRAPPA patterns employed by a 2×3 kernel, {*x*,*xo*,*ox*}, where * represents a phase-encode line, o represents an unsampled phase-encode line, and x is a reconstruction target point.

The in-vivo example shows a 256×256 image reconstructed from accelerated data acquired using an standard 8-channel cardiac coil on a 1.5T GE Scanner (GE Medical Systems). The data was provided by a healthy volunteer after informed consent. The FGRE sequence (TR: 3.95 msec, TE: 1.78 msec, flip-angle: 45°, slice thickness: 8 mm) employed was cardiac gated, and the k-space sub-sampling scheme used 6 (1Δk) lines in the inner central region. The outer-central region employed phase-encode steps of (2Δk), and spanned the phase encoding dimension from −26 to +26 Δk steps from the coordinate system origin. After the application of GRAPPA in the outer-central region there were 52 lines available to estimate coil sensitivities; 6 (1Δk), 22 odd (2Δk) measured lines and 24 even-indexed GRAPPA estimated lines. Beyond the outer-central region, the sampling density was exponentially weighted (Z_exp(k_y) = exp(−|0.9k_y|)), growing from (3Δk) in the mid-frequency range to (8Δk) in the high-frequency range. A total of 72 lines, out of 256, were acquired, giving an effective acceleration factor of almost 3.56x.

Results

Figure 3 shows reconstructed phantom and error images for three different central region sizes. On the left of the figure, three LSQR-Hybrid SENSE reconstructions are shown. On the right are three comparable GRAPPA-only reconstructions, using either a single- or double-pass as applicable. For the LSQR-Hybrid reconstructions, one can see a dramatic improvement in image quality as one increases the number of ACS lines used for coil sensitivity estimation. Similar improvement can be seen the GRAPPA images, although the change is less dramatic due to the robustness of GRAPPA when using limited ACS data.

Figure 3.

Reconstructions and error images of a simulated acquisition employing uniform subsampling. (Subsampled by 3 plus 4 additional lines for an effective acceleration of 2.87×). (a–c) LSQR-Hybrid SENSE reconstructions using auto-calibrated coil sensitivity estimates from (a) 6 ACS lines, (b) 24 ACS lines, and (c) 64 ACS lines. (d–f) comparable GRAPPA reconstructions using the same ACS lines. (Note that the error images of (a) and (d) are shown at different scales.)

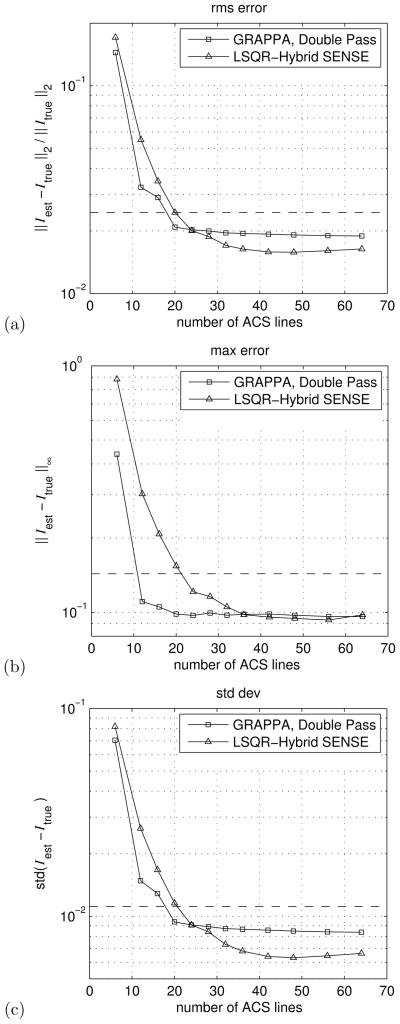
Fig. 4 illustrates graphically the rms err, max err, and std dev of the reconstructions for a number of central-region sizes. These figures reflect the dramatic decrease in artifact and noise present in the LSQR-Hybrid reconstructions as the number of ACS lines available increases. Notably, the error in LSQR-Hybrid reconstructions approaches that of a single-pass GRAPPA reconstruction with a relatively small GRAPPA-enhanced central region, i.e. ≈ 20 ACS lines. And as the central region grows beyond 30 lines, the error metrics surpass that of the double-pass GRAPPA approach. This is reflected in images (c) and (f) of Fig. 3, where the LSQR-Hybrid reconstruction shows less speckle noise than the comparable GRAPPA reconstruction.

Figure 4.

Graphic comparison of (a) root-mean-square error, (b) maximum error, and (c) standard deviation of the error between the Double Pass GRAPPA, and LSQR-Hybrid SENSE reconstructions and the fully-sampled phantom image. Each of the error metrics is defined in the labels on the vertical axis of each panel. For comparison, the error metrics for Single Pass GRAPPA using 6 ACS lines is shown as a dashed line on each graph.

Reconstructions of the in-vivo data are shown in Fig. 5. Fig. 5(a) shows the LSQR-Hybrid reconstruction using only the 6 ACS lines available in the original measured data. Fig. 5(b) shows a reconstruction of the same acquired data, but this time using GRAPPA-enchanced coil sensitivity estimates from a total of 52 (28 measured + 22 GRAPPA estimated) ACS lines. The artifacts visible in (a) are markedly reduced in (b). For comparison, Fig. 5(c) shows a reconstruction from the same acquired data using a single pass GRAPPA reconstruction with 6 ACS lines. Consistent with the simulated example, the GEYSER + LSQR-Hybrid image in (b) exhibits significantly less noise than the GRAPPA image of Fig. 5(c). This is quantified by the measured standard deviation of the data in the boxes of (b) and (c), as well, with σ = 0.0094 for LSQR-Hybrid with GEYSER and σ = 0.0286 for GRAPPA.

Figure 5.

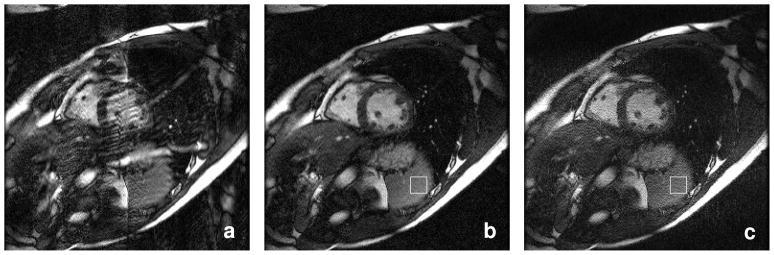
Reconstructions of 3.56x accelerated data using (a) LSQR-Hybrid with self-referenced coil sensitivity maps from 6 ACS lines, (b) LSQR-Hybrid with GEYSER using 52 (28 measured + 24 GRAPPA estimated) auto-calibration lines to estimate coil sensitivity, and (c) a single pass GRAPPA reconstruction. The acquired data for all images is identical. The improved quality visible in (b) compared to (a) is attributed to the use of GRAPPA to improve the coil sensitivity estimates. The measured standard deviation in the boxes is (b) LSQR-Hybrid:0.0094 and (c) GRAPPA:0.0286.

Discussion and Conclusions

In this work the particular sampling strategy, the LSQR-Hybrid reconstruction algorithm used for the CtR method, and the choice of GRAPPA as the RtC method for enhancing coil sensitivity estimates, should all be seen as convenient but not required choices. Any reconstruction strategy from the CtR class which relies on explicit coil sensitivity estimates could potentially benefit from our approach. Any linear system solver that can perform the reconstruction with an acceptable computational delay could be used. And any member of the RtC family, with an appropriate sampling scheme, could be used to estimate missing low frequency lines for use in coil sensitivity calculations.

Aside from image quality, completing the reconstruction in a clinically usable time is a prevailing concern in developing algorithms to reconstruct subsampled pMRI data. Thus, it may first appear counterintuitive to combine two pMRI algorithms. Our method avoids long reconstruction times in two ways. First, the GRAPPA estimation step can be performed using a small GRAPPA kernel and a very small number of ACS lines. Since both the kernel size and the number of ACS lines contribute to the size of the linear system used to find the GRAPPA reconstruction parameters, keeping both small enables us to find the parameters very quickly. Second, as we are interested in reconstructing k-space data to be used only for coil sensitivity estimation, only a narrow region around the origin of k-space needs to be reconstructed.

Of course, GRAPPA reconstructions using small kernels and a very small number of ACS lines are more prone to reconstruction errors, as visible when comparing Figs. 3(d) and (e). This is mitigated some in our approach due to the filtering that occurs during coil sensitivity estimation. In practice, one needs to balance the obtainable acceleration against a sufficient central region size to provide adequate data for sensitivity estimation. Currently, we limit the acceleration in the outer-central region to ≤3x, and only reconstruct 1/4 of the full k-space range. This allows GRAPPA-enhancement, Step (I), in roughly the same time as coil sensitivity calculation, Step (II), which is significantly less than the time required to reconstruct the final image in Step (III), whether using LSQR-Hybrid or GRAPPA with a 4×5 kernel.

The method we presented here leverages the fact that RtC methods can quickly provide sufficient coil sensitivity estimation data from very few ACS lines. This allows one to use CtR methods in imaging scenarios where good coil sensitivity estimates have previously been difficult or costly (in acquisition time) to obtain. We demonstrated the advantages of this approach in cardiac imaging, and we anticipate it will bring substantial benefit to the use of CtR reconstruction methods in real-time imaging applications.