Statistical methods for assessing agreement between double readings of clinical measurements

Abstract

Statistical analysis of data is crucial in cephalometric investigations. There are certainly excellent examples of good statistical practice in the field, but some articles published worldwide have carried out inappropriate analyses.

Objective

The purpose of this study was to show that when the double records of each patient are traced on the same occasion, a control chart for differences between readings needs to be drawn, and limits of agreement and coefficients of repeatability must be calculated.

Material and methods

Data from a well-known paper in Orthodontics were used for showing common statistical practices in cephalometric investigations and for proposing a new technique of analysis.

Results

A scatter plot of the two radiograph readings and the two model readings with the respective regression lines are shown. Also, a control chart for the mean of the differences between radiograph readings was obtained and a coefficient of repeatability was calculated.

Conclusions

A standard error assuming that mean differences are zero, which is referred to in Orthodontics and Facial Orthopedics as the Dahlberg error, can be calculated only for estimating precision if accuracy is already proven. When double readings are collected, limits of agreement and coefficients of repeatability must be calculated. A graph with differences of readings should be presented and outliers discussed.

INTRODUCTION

Clinical measurements are generally imprecise because they cannot be measured directly (such as an organ size), or they are difficult to achieve (such as knee joint circumference). Hence, different methods of measuring the same phenomenon or different ways of measuring the same variable on different types of physical records have been proposed. However, even when a method is universal, double readings of the same quantity by the same method and the same operator in order to confirm that readings agree well enough are advised.

By definition, repeatability is the closeness of agreement between successive readings obtained by the same method on the same material and under the same condition (same operator, same apparatus, same setting and same time). Reproducibility is the closeness of agreement between individual readings obtained by the same method on identical testing material, but under different conditions (different operator or different apparatus or different setting or different time). Lack of precision means that repeated measures of the same value under specified conditions are spread out or scattered.

In Orthodontics, locating the same point on the same image in repeated acts of landmark location is always a daunting task. Midtgard, et al.⁷ (1974), in a classical paper, compared the positions of 15 landmarks calculated by the same observer from two lateral cephalometric radiographs taken consecutively on each of 25 children and found statistically significant differences for all of them. Difficulties in landmark identification are emphasized by Houston, et al.⁴ (1986). According to those authors, the greatest errors arise in point identification rather than in measurement, but Silveira and Silveira⁸ (2006) performed various cephalometric measurements three times using 40 digital radiographs and concluded that differences among triple readings were significant for most of the cephalometric measurements analyzed. Hence, repeatability must be evaluated.

On the other hand, different methods of measuring the same phenomenon need to be carefully compared. So, reproducibility must be studied. Battagel¹ (1993) reviewed the literature related to the assessment of measuring cephalometric radiographs and provided some suggestions for estimating all types of errors. Martelli Filho, et al.⁶ (2005) studied statistical methods for evaluating reproducibility of quantitative measurements in Orthodontics and also offered many suggestions.

The aim of this paper is to suggest that when repeatability needs to be assessed, a control chart for means should be set up if a patient's records are traced on the same occasion, which is a common practice. A control chart gives limits of agreement, identifies possible outliers, makes the calculation of a coefficient of repeatability straightforward and shows it when a serial correlation exists. If the order in which the records were measured was randomized in a way that prevented the researcher from knowing which patient he/she was measuring or re-measuring, the well-known plot proposed by Bland and Altman² (1986) should be set up.

MATERIAL AND METHODS

The data used in this study are from Houston⁵ (1983), a classical paper cited worldwide when repeatability, reproducibility or precision in Orthodontics are mentioned. For analyzing repeatability, Houston⁵ (1983) used Pearson's correlation coefficients and paired t-tests, as shown in Table 1.

Table 1.

Data analysis for upper-arch length projected onto the midsagittal plane in millimeters measured from models and cephalometric radiographs, each on two separate occasions (in mm)

Statistics	Radiographs			Models
	Time 1	Time 2	Difference	Time 1	Time 2	Difference
Sample size	30	30		30	30
Mean	44.08	44.32	0.24	39.05	39.21	0.15
Variance	26.73	29.32	0.33	21.78	21.30	0.22
Standard deviation	5.17	5.42	0.59	4.67	4.61	0.47
Standard error	0.944	0.989	0.11	0.85	0.84	0.09
p-value for paired t-test			0.03			0.09
Correlation coefficient	0.99			0.99

Source: Houston⁵ (1983)

In this paper, scatter plots and regression lines both for radiographs and models were also drawn. Control charts for differences between readings were constructed and out-of-control points were counted. Upper and lower limits and coefficients of repeatability were calculated. For discussion, standard deviations of the means assuming that mean differences are zero, which have been popularized in Orthodontics and Facial Orthopedics as the Dahlberg error, were also calculated.

RESULTS

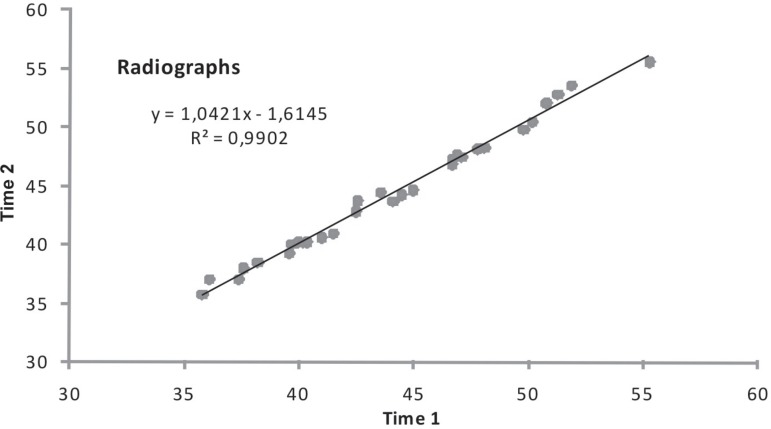
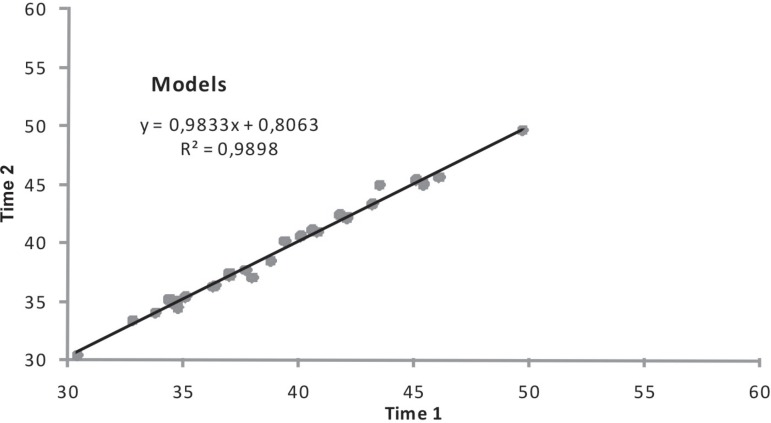
A scatter plot of the two radiograph readings with the regression line is shown in Figure 1, and a scatter plot of the two model readings with the regression line is shown in Figure 2. Intercept coefficients are not significantly different from zero (p=0.0736 for radiographs and p=0.2854 for models), and slopes are significantly different from 1 for radiographs (p=0.0401) and non significant for models (p=0.3821).

Figure 1.

Double readings of radiographs with the line of equality

Figure 2.

Double readings of models with the line of equality

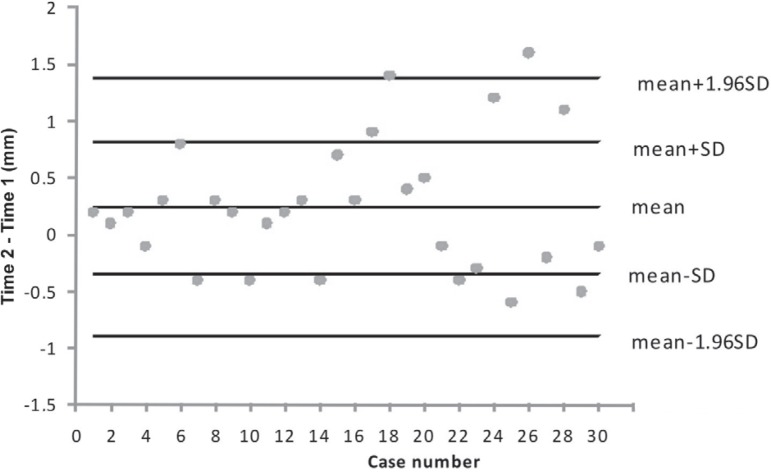
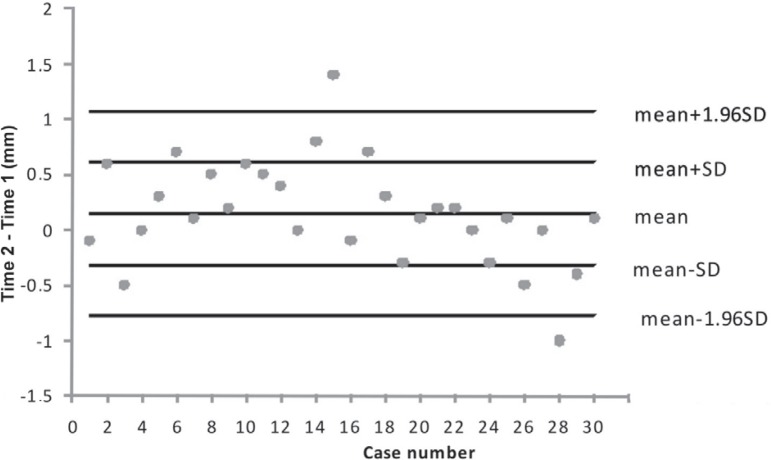
Control charts for the mean of the differences between radiograph readings are shown in Figure 3 and for models in Figure 4. An error analysis for Houston´s data of upper arch length onto the midsagittal plane in millimeters measured from models and cephalometric radiographs are given in Table 2. Coefficients of repeatability⁷ were calculated by the following equation:

Figure 3.

Control chart for the mean of differences between radiographs readings

Figure 4.

Control chart for the mean of differences between models readings

Table 2.

Error analysis for upper-arch length projected onto the midsagittal plane in millimeters measured from models and cephalometric radiographs

Statistics	Radiographs	Models
Mean of difference between readings	0.24	0.15
Confidence interval: lower limit	0.04	-0.02
Confidence interval: upper limit	0.45	0.32
Coefficient of repeatability	1.13	0.92
Number of points in the warning zone	9	6
Number of out-of-control points	2	2

$\mathrm{CR}\mathrm{=}\mathrm{1}\mathrm{.}\mathrm{96}\mathrm{\times }\sqrt{\frac{\Sigma {\left(\mathrm{d}-\stackrel{─}{\mathrm{d}}\right)}^{\mathrm{2}}}{\mathrm{n}-1}}\mathrm{(}\mathrm{1}\mathrm{)}$

In Health Sciences, differences within mean±SD are generally considered clinically unimportant. Differences between mean±SD and mean±1.96 SD are in a warning zone and differences out of these limits are out-of-control points. Their percents are shown in Table 2 for both methods of measuring upper-arch length projected onto the midsagittal plane.

DISCUSSION

The correlation coefficients shown in Table 1 look impressive, but they do not mean agreement. Agreement is perfect only when the points lie along the regression line, which means, a line with equation Y=X, while correlation is perfect when the points lie along any straight line. For radiographs, although the correlation coefficient is 0.9951, the slope is significantly different from 1. Houston⁵ (1983) has pointed out there was a significant difference between measurements of radiographs and considered standardization was a requirement for better results. Houston⁵ (1983) also calculated the correlation coefficient between the averaged measurements (Time 1 and Time 2) from models and radiographs, which is 0.971 even the percent of radiograph enlargement is approximately 13%.

A control chart for analyzing errors in double readings is a better statistical tool, since it is used to detect excessive process variability. It serves to determine whether the extent of variation of errors in double readings does not exceed that which is expected, that means, an average not different from zero and, even considering the natural statistical variability of the process, a coefficient of repeatability small in relation to the measurement taken.

Differences within mean±SD are clinically unimportant. Differences between mean±SD and mean±1.96 SD are in a warning zone and differences out of these limits are out-of-control points. Out-of-control points are uncertain and a risk of adverse results in treatment or diagnosis. Therefore, the clinician should look for them and decide whether they are in an acceptance zone, considering they should be zero. Number of points in the warning zone and number of out-of-control points are shown in Table 2 for both methods of measuring upper arch length projected onto the midsagittal plane. It has to be noted that averages both from radiographs and models are above zero and there are out-of-control points more than 2 SD far from means.

It has to be pointed out that many papers consider precision can be estimated by a statistic known in Orthodontics and Facial Orthopedics under the name of Dahlberg error³. It is well known that when readings are independent, identically distributed random variables, sums or differences between readings are independent, identically distributed random variables with mean zero and variance:

${\mathit{S}}_{\mathit{X}}=\sqrt{\frac{\Sigma ^{\mathit{d}}{}^{}}{2\mathit{n}}}\mathrm{(}3\mathrm{)}$

If a large number of readings are performed by the same operator and the same method on the same material (such as a blood sample or an oil sample), it can be assumed that measurements are distributed closely to the true value. If readings are performed in duplicates and the difference between a duplicate is calculated, it can be seen as a difference between two values taken at random from the same probability curve. When another duplicate is read by the same method and the same operator on another sample of the same material, these two readings can also be seen as two values chosen at random from another probability curve of the same type as that of the previous one. By continuing the process, a series of differences is obtained that conforms to the series of differences which would be obtained by choosing, at random and repeatedly, two values from one and the same probability curve. Under such circumstances, an estimate of the standard deviation is calculated by adding the squares of the differences (because the mean is zero), dividing the sum by two times the number of differences (because the variance of the difference is 2s2) and extracting the root of the resulting figure, that is, by calculating:

${\mathit{S}}_{\mathit{X}}=\sqrt{\frac{\Sigma ^{\mathit{d}}{}^{}}{2\mathit{n}}}\mathrm{(}3\mathrm{)}$

This estimate of the standard deviation is a measure of dispersion (and, inversely, precision) when double readings are performed on the same material (a standard practice in laboratories, which can be assumed as independent and identically distributed variables). This is not the case in cephalometric investigations, where double readings, known as paired observations, are performed on the same radiograph. Therefore, radiographs taken from different patients not only imply measurement errors, but also take into account the variability of patients.

Anyway, the standard deviation using the Dahlberg equation is s_x=0.437 mm for radiographs and s_x=0.345 mm for models, which does not have a straightforward interpretation. In other areas, such as Chemistry, where a gold standard is always provided, the uncertainty of the measurement can be tested by an F-test. On the other hand, it is easy to interpret that the expected percent of differences between double readings bigger than mean±SD is approximately 37% for radiographs and approximately 27% for models.

CONCLUSION

In the study of repeatability, neither the correlation coefficient nor the regression analysis is appropriate. The standard deviation Dahlberg³ (1946) gives in his textbook can be used only when readings are independent and identically distributed random variables and differences between readings are on average zero, which is not the case in cephalometric investigations.

In clinical practice, when double readings are taken, a t-test should be carried out for testing whether differences between double readings are on average zero or there is a systematic error. Standard deviation is of course a measure of dispersion (or, inversely, precision) and so is the coefficient of repeatability, but a control chart should also be used for detecting outliers. Measurements made in out-of-control points are uncertain and a risk of adverse results in treatment or diagnosis.