From action to abstraction: Using the hands to learn math

Abstract

Previous research has shown that children benefit from gesturing during math instruction. Here we ask whether gesturing promotes learning because it is itself a physical action, or because it uses physical action to represent abstract ideas. To address this question, we taught third-grade children a strategy for solving mathematical equivalence problems that was instantiated in one of three ways: (1) in the physical action children performed on objects, (2) in a concrete gesture miming that action, or (3) in an abstract gesture. All three types of hand movements helped children learn how to solve the problems on which they were trained. However, only gesture led to success on problems that required generalizing the knowledge gained. The results provide the first evidence that gesture promotes transfer of knowledge better than action, and suggest that the beneficial effects gesture has on learning may reside in the features that differentiate it from action.

There is ample experimental evidence that performing actions on the external world affects our internal representations (e.g., James, 2010; Kontra, Beilock & Goldin-Meadow, 2012; Sommerville & Woodward, 2010; Wilson, 2002). Recently, there has been growing interest in a special kind of action–the actions we produce when we talk, often called “gestures” (McNeill, 1992). Both action and gesture involve movements of the body, but actions have a direct effect on the world; gestures do not (e.g., twisting a jar lid results in an open jar; gesturing a twisting movement does not). Yet we know that gestures, like other forms of action, can have profound effects on thinking and learning (Goldin-Meadow, 2003). These observations raise questions about how the fundamental differences between gesture and action affect learning. Here we compare the consequences of learning a concept by directly acting on objects vs. gesturing about those objects. Our goal is to better understand how these two types of movements affect learning.

One critical feature of action-based learning is that it often involves manipulating or interacting with physical objects. For example, a child using base-ten blocks to learn how to carry addends in an addition problem literally carries the blocks from one column to another. Traditional theories of cognitive development suggest that children can often succeed in solving problems with physical objects before they succeed with symbolic representations (Bruner, Olver & Greenfeild, 1966; Piaget, 1953). External symbols can be acted upon, allowing motor processes to be integrated with abstract ideas (Lakoff, & Nunez, 2000). Yet despite the theoretical benefits of action, encouraging learners to act on concrete objects has received mixed support (see Sarama & Clements, 2009; Mix, 2010; McNeil & Uttal, 2009). Children can become preoccupied with irrelevant details of perceptually rich symbols (McNeil, Uttal, Jarvin, & Sternberg, 2009), or see their actions as relevant only to the objects on which they were trained rather than to a more general concept (Uttal, Scudder & DeLoache, 1997). If physical objects focus a child’s attention on irrelevant aspects of a procedure rather than on the concept underlying the procedure, then the child may not be able to generalize what she has learned to a new context (Mix, 2010). Action may thus be helpful in teaching children to solve a particular problem, but may fare less well in teaching them to extend that knowledge to new problems.

Gesture, like action, is an act of the body but, unlike action, it does not involve directly manipulating objects. Rather, gestures are representational hand movements that vary in how veridically they represent actions. Gestures can represent many aspects of the action they reference (e.g., pantomiming twisting a jar lid) or they can selectively represent only the movement of the action (e.g., tracing the circular path of the lid). On a mental rotation task, Chu and Kita (2008) examined how people spontaneously produced different types of gesture while explaining their rotation strategies. Adults initially used mimetic gestures, miming the act of rotating the object but, over the course of the experimental session, they used more and more abstract gestures, tracing the path of the object as it rotates. Chu and Kita hypothesized that this shift reflected an internalization of the action strategy, which had become less tied to the concrete rotation action and thus more abstract.

Goldin-Meadow, Cook and Mitchell (2009) used an abstract gesture to help 9- to 10-year-old children solve mathematical equivalence problems such as 4+3+6= __+6. Children were taught to produce a V-point gesture to the first two numbers (the 4 and the 3 in this instance) followed by a point at the blank. These movements, which were modeled after the spontaneous gestures of children who know how to solve these problems correctly (Perry, Church & Goldin-Meadow, 1988), were designed to help students see that the problem can be solved by grouping and adding the two numbers on the left side of the equation that do not appear on the right side, and putting the sum in the blank. Children who were asked to produce these hand movements during a math lesson were able to extract the grouping strategy despite the fact that they were never explicitly told what the movements represented. Surprisingly, even children who were trained to make a V-point to the “wrong” addends (3 and 6 in the example above) learned grouping, although less well than children trained to point to the correct numbers. Gesture’s power as a teaching tool may thus reside not only in its ability to focus children’s attention on a specific aspect of a problem, but also in its ability to convey substantive ideas about the relational structure of the problem.

These findings make it clear that children can glean novel insights from an abstract gesture. But we do not yet know whether abstract gesture can support generalization beyond the particular problem on which it was taught, nor do we know whether abstract gesture is more (or less) effective as a teaching tool than concrete action. Our study was designed to address these questions.

We used the procedure from Goldin-Meadow, Cook and Mitchell (2009) to investigate whether varying the concreteness of the actions children were trained to produce during a math lesson would influence their ability to generalize the knowledge they had gained to new problem forms. Each child was assigned to one of three training conditions: (1) In the action condition, children were taught to pick up magnetic number tiles, which had been placed over the first two numbers in the problem, group them in one hand, and then hold the hand over the blank. (2) In the concrete gesture condition, children were taught to mime the action of picking up, grouping, and moving the number tiles, but without ever actually touching the tiles. (3) In the abstract gesture condition, children were taught to produce a V-point gesture to the first two number tiles followed by a point at the blank. If action-based instruction is the best way to scaffold learning an abstract concept, then we ought to see higher rates of learning on trained problems in the action condition than in either of the gesture conditions. But if the procedure instantiated in action is too tied to the particulars of the problem, then we might expect children in the action condition to fail to generalize. In contrast, if abstract gesture focuses attention on the aspects of the procedure particularly relevant to solving the problem (and away from aspects that are irrelevant), we would expect gesture to be effective not only in teaching children how to solve the problems on which they were trained, but also in helping them generalize this knowledge to new problem forms. Finally, we were agnostic about concrete gesture. Concrete gesture replicates many of the features of action and therefore may behave like action, tying knowledge to the particular problem on which it was learned. On the other hand, concrete gesture is not produced on objects, freeing knowledge from a particular context so that it can be more easily generalized to new problem forms.

Method

Participants

One hundred forty-two third-grade children were tested in their elementary schools in the Chicagoland area; third-grade children were studied because children of this age typically fail to solve mathematical equivalence addition problems correctly, making them an ideal population within which to explore the impact of different types of instruction on learning. To insure that the participants in all conditions were equally naïve with respect to the mathematical equivalence problems, we excluded all of the children who solved any of the 6 problems on the pretest correctly (n = 44).¹ In addition, 1 child was excluded due to a language barrier, and 7 were excluded due to experimenter error. The remaining 90 children (60 females) ranged in age from 8.46 to 10.48 years (M= 9.23 years, SD=.38) and were racially and ethnically diverse. All participants were tested in the schools they attended, which were recruited through phone calls and e-mails to principals. Children’s parents had submitted written consent prior to their child’s participation in the study. Children were randomly assigned to one of three conditions: Action (n=30), Concrete Gesture (n=31), or Abstract Gesture (n=29). Children received a pencil, stickers, and a certificate for participating, and the teachers of participating classrooms received a $40 gift certificate to a local learning store.

Materials

Math problems were written on a white, portable, dry-erase magnetic board in black marker. During training, black magnetic number tiles were placed over each of the numbers in the problem. There were two forms of math problems administered at pretest and posttest. In the ABC form, the last number on the left side of the equation (c) was repeated on the right side, (e.g., a+b+c=__+c) and in the PQR form, the first number on the left side (p) was repeated on the right side, (e.g., p+q+r=p+__).

Design and Procedure

Children were tested individually in an unused room at their school. The procedure was divided into 5 parts: pretest, pre-instruction, instruction, posttest, and generalization. Experimenter A administered the pretest, posttest, and generalization Experimenter B administered the pre-instruction and instruction. Experimenter A was not present during instruction and therefore blind to the training condition.

Pretest

All children first completed a written pretest containing 6 problems, 3 in the ABC form and 3 in the PQR form. After the child solved the written pretest problems, Experimenter A wrote each problem on the whiteboard one at a time and asked children to explain how they got each answer.

Training

Pre-instruction

The purpose of the pre-instruction (3 problems in ABC form) was to teach the child the words and hand motions he or she would be asked to repeat during instruction. In all conditions, the experimenter first wrote a sample problem on the board, 2+9+4=__+4, and covered all the numbers with black magnetic number tiles. Children in all conditions were taught to look at the problem and say, “I want to make one side equal to the other side,” the equalizer strategy (Perry et al., 1988). They were also taught hand movements, which differed by training condition (see Figure 1). On each of the 3 pre-instruction problems, the experimenter demonstrated the words and hand movements and then asked the child, “Can you say those words and do those hand movements for me?” Neither the experimenter nor the child actually solved any of the pre-instruction problems.

Figure 1.

Demonstrations of the hand movements taught during the pre-instruction phase of the training procedure to children in the Action, Concrete Gesture, and Abstract Gesture conditions.

Instruction

During instruction, the experimenter and child alternated solving 12 ABC problems on the white board; we refer to problems of this form as trained problems. During the experimenter’s turn, she wrote a problem on the board, covered the numbers with magnetic tiles, and wrote the correct answer in the blank. She then explained how to solve the problem using the equalizer strategy, but did not move her hands at all. For example, for the problem 6+3+8=__+8, the experimenter put 9 in the blank and said, “I want to make one side equal to the other side. You see, 6 plus 3 plus 8 is 17, and 9 plus 8 is 17, so one side is equal to the other side.”

The experimenter then wrote a new problem on the board, and covered all the numbers with the magnetic tiles. Children were asked to produce the words and hand movements they were taught in pre-instruction, and were then asked to solve the problem. Children were told whether their answer was right or wrong, but if the answer was incorrect, they were not given the correct answer. The child’s solution was then erased, and the child was asked to repeat the words and hand movements taught during pre-instruction.

Posttest

After instruction, the child was given a second 6-question paper-and-pencil test (with 3 ABC and 3 PQR problems and thus comparable to the pretest) to measure immediate improvement.² As in the pretest, children first completed the problems and then explained their solutions at the white board. Because the PQR problems were seen only in pretest and posttest and not during training, we refer to them as near-transfer problems.

Generalization

Following posttest, each child was given a paper and pencil generalization test. The test contained two problems that could not be solved using the grouping strategy but required a deeper understanding of mathematical equivalence (i.e., 2+5+3=__+6 where none of the addends on the left side of the equation was repeated on the right). We refer to these problems as far-transfer problems.³

Coding

Videos of children explaining their answers were transcribed and coded for speech according to a previously established coding system (Perry et al., 1988). Three independent coders determined whether or not the equalizer strategy was used in explanations of posttest trials. Each post-test trial was coded by two of the three coders and each coder coded two thirds of the total trials. Reliability was between 94% and 97% for all three pairs of coders (Kappa’s ranged from .88 to .93).

Results

Figure 2 displays histograms of the number of problems solved correctly by children in the three conditions combined; children are categorized according to the number of trained (left graph), near-transfer (middle graph), and far-transfer (right graph) problems they solved correctly after instruction (recall that no problems were solved successfully before instruction). Because the distribution for each of the three problem forms was non-normal and bimodal (i.e., children tended to either get the problems completely wrong or completely right), we classified children as learners or non-learners for each problem form (trained, near-transfer, far-transfer). To be coded as a learner for a problem form, a child had to produce a correct answer, or an answer that was off by 1 but accompanied by a correct explanation, on all exemplars of that problem form.

Figure 2.

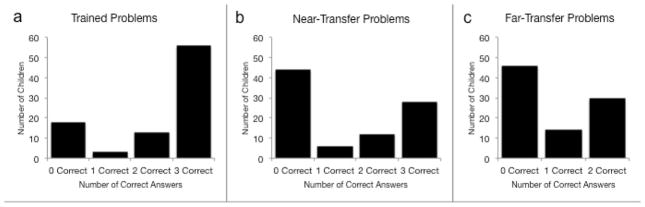
The number of problems each child solved correctly on the (a) trained, (b) near-transfer, and (c) far-transfer problems after instruction (across all conditions).

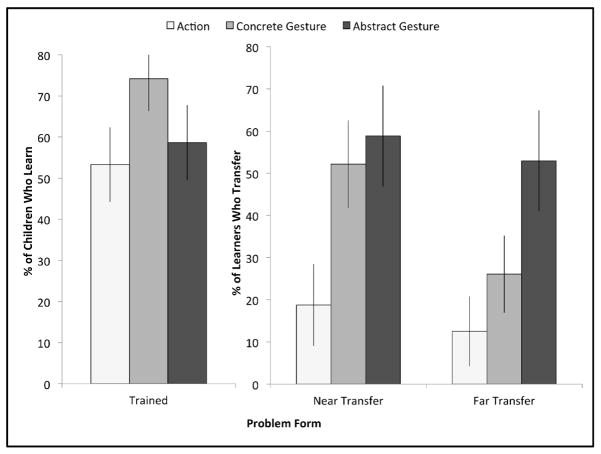
Children in all three conditions were equally likely to succeed on the trained problems after instruction (Figure 3, left graph). We used condition (action, concrete gesture, abstract gesture) to predict success on the trained problems using a fixed-effects binomial logit model (abstract gesture was used as the baseline estimate group as it was likely to have the lowest rates of learning). There was no effect of condition on success on trained problems (for action, β = −0.22, z = −0.41, p = 0.68; for concrete gesture, β = 0.71, z = 1.27, p = 0.20), indicating that children did not display significantly different odds of succeeding on the trained problem forms as a function of condition. Releveling the model with action as baseline also resulted in no differences between action and abstract gesture (β = 0.22, z = 0.41, p = 0.68) but a marginal difference between action and concrete gesture (β = 0.92, z = 1.68, p = 0.09).

Figure 3.

The left-most graph shows the percentage of all children we succeeded on trained problems (learners). The middle graph shows the percentage of learners who also succeeded on near-transfer problems. The right graph shows the percentage of learners who succeeded on both near-transfer and far-transfer problems. Error bars represent the standard error of the percentages.

We next focused on learning near- and far-transfer problems, and did so only for children who had successfully learned the trained problem forms (N = 16 for action training, N = 23 for concrete gesture training, N = 17 for abstract gesture training). Focusing first on near-transfer problems (Figure 3, middle graph), we used a fixed-effects binomial logit model to predict children’s probability of becoming a learner on both trained and near-transfer problems. We found a main effect of training condition–children in the action condition had significantly lower odds of mastering near-transfer problems than children in the abstract gesture condition (β = −1.58, z = −1.97, p = 0.049), but children in the concrete gesture condition did not differ from children in the abstract gesture condition (β = −0.031, z = −0.05, p = 0.962). Releveling the model to make the action condition the baseline, we found that children in both the concrete (β = 1.55, z = 2.03, p = 0.04) and abstract (β = 1.58, z = 1.97, p = 0.049) gesture conditions performed significantly better than children in the action condition. Overall, children in the action condition were less likely to generalize the knowledge they had gained on the trained problems to the near-transfer problems than children in either gesture condition, but there was no difference between children in the two gesture conditions.

Finally, we examined performance on the far-transfer problems (Figure 3, right graph). We again used a fixed-effects binomial logit model to predict the log-odds of becoming a learner on all three problem forms (trained, near-transfer and far-transfer). We again found a main effect of training condition–children in the action condition had significantly lower odds of success on all three problem forms than children in the abstract gesture condition (β = −2.06, z = −2.30, p = 0.02), and children in the concrete training condition had marginally lower odds of success than children in the abstract gesture condition (β = −1.15, z = −1.71, p = 0.09). When we releveled the model to make the action condition the baseline, we found that concrete gesture was not statistically different from action (β = 0.90, z = 1.01, p = 0.31), but abstract gesture was significantly better than action (β = 2.06, z = 2.30, p = 0.02). The pattern of results displayed in Figure 3 suggests that abstract gesture was the most effective in encouraging learners to generalize the knowledge they had gained during instruction, action the least effective, and concrete gesture somewhere in between.

To further explore the impact of gesturing on children’s understanding of the principle underlying mathematical equivalence, we examined children’s explanations on the posttest. Children in all three conditions were trained during pre-instruction to parrot the words of the equalizer strategy (a strategy based on the principle that the two sides of an equation must be equivalent). We asked whether the hand movements children produced along with the words they parroted influenced how likely they were to glean meaning from those words. We correlated the number of times a child said the equalizer strategy on the posttest with the child’s success on the posttest problems (0=no success on any problems; 1=success on only trained problems; 2=success on trained and near-transfer problems; 3=success on trained, near-transfer, and far-transfer problems). We found a significant positive relation between the two measures only if the child had repeated the equalizer strategy while producing a concrete (R=.76, p<.001) or abstract (R=.64, p<.001) gesture during instruction, and not if the child had repeated the words while acting on the numbers (R=.25, p=0.17). These results suggest that the children gleaned meaning from the words they were trained to say if they were required to produce gestures (but not actions) along with those words.

Discussion

From previous research, we know that action and gesture support learning across a variety of ages and contexts. Here we exploited the similarities and differences between action and gesture to compare their effects on learning. We found that acting gave children a relatively shallow understanding of a novel math concept, whereas gesturing led to deeper and more flexible learning. Furthermore, the form of the gesture mattered–abstract gesture facilitated generalization whereas concrete gesture, which mimicked the hand movements of action, brought learners to an intermediate stage of conceptual understanding. Learning in this task was thus correlated with the “concreteness” of the hand movements children produced during training. The more concrete movements seemed to tie the knowledge gained to the training context, suggesting that the beneficial effects gesture has on learning may stem, not only from its base in action, but also from its ability to abstract away from action.

Our findings are consistent with the literature on abstraction. For example, the “concreteness fading” theory proposes that learning is best supported by first introducing concrete representations and then transitioning learners to more symbolic or abstract representations (Goldstone & Son, 2005; McNeil & Fyfe, 2012). This theory raises the possibility that the movement-based learning in our mathematics paradigm could have been even more successful had we done a within-subjects training design in which we provided learners with increasingly abstract representations of the grouping strategy. Would children have learned even better had they begun with action and then moved to gesture in a second training session? A fading technique of this sort might be particularly effective with children who are struggling with the concept.

Action did not promote generalization on our math task. But manipulating concrete symbols may not be ideal for learning in a domain as symbolic and abstract as mathematics. The utility of teaching ideas through action on objects may depend on whether an answer can be “read off” of the manipulative (see Clements & Samara, 2009). Consider, for example, a mental rotation task where doing the action gives the answer (i.e., once the object is rotated, one can see whether it is the same object in a different orientation or a different object). Using action to teach a task like mental rotation might be more effective than using gesture to teach such a task. Recent evidence from a study of mental transformation in kindergarten children provides some support for this hypothesis–training children to rotate the objects led to greater success immediately after instruction than training them to gesture the rotation (although children who were trained to gesture did catch up at a one-week follow up, Levine, Goldin-Meadow, Carlson, & Hemani-Lopez, 2013). The age of the learner might also have an impact on the relative effectiveness of action vs. gesture. Young children are not only believed to internalize ideas through action experience (Vygotsky, 1978), but they also find gesture to be more difficult to interpret than action (Novack, Goldin-Meadow & Woodward, under review). Thus, although we found here that gestures were better than action in promoting generalization, additional research is needed to determine the pervasiveness of this effect across domains and ages.

Why does gesture promote the kind of learning that leads to generalization? Our findings suggest that gesture may play a role in helping learners process the words it accompanies less superficially. In this study, we trained children to produce the equalizer strategy in speech and children in all three conditions followed our instructions, producing the words on every problem they attempted to solve. However, repeating these words led to deep learning (i.e., generalization to near- and far-transfer problems) only when they were produced along with gesture, either concrete or abstract. Children in the action condition repeated the words of the equalizer strategy while continuing to answer problems incorrectly, suggesting that they did not really understand what they were saying. Our findings thus lead to the intriguing hypothesis that saying words while gesturing may help a learner integrate and internalize those words, whereas saying words while acting may not (see also Cook, Mitchell & Goldin-Meadow, 2008).

In sum, our findings provide the first evidence that gesture not only supports learning a task at hand but, more importantly, leads to generalization beyond the task. Children appear to learn underlying principles from their actions only insofar as those actions can be interpreted symbolically. Although gesture can be thought of as simulated action (Hostetter & Alibali, 2008), the features of gesture that differentiate it from action may be precisely what makes it useful for generalization. On a continuum of “action to abstraction” gesture is more abstract than action but still less abstract than verbal language. Perhaps it is this comfortable middle ground, with one foot in the concrete and one foot in the abstract, that makes gesture such a powerful tool for learning.