Redefining Relative Biological Effectiveness in the Context of the EQDX Formalism: Implications for Alpha-Particle Emitter Therapy

Abstract

Alpha-particle radiopharmaceutical therapy (αRPT) is currently enjoying increasing attention as a viable alternative to chemotherapy for targeting of disseminated micrometastatic disease. In theory, αRPT can be personalized through pre-therapeutic imaging and dosimetry. However, in practice, given the particularities of α-particle emissions, a dosimetric methodology that accurately predicts the thresholds for organ toxicity has not been reported. This is in part due to the fact that the biological effects caused by α-particle radiation differ markedly from the effects caused by traditional external beam (photon or electron) radiation or β-particle emitting radiopharmaceuticals. The concept of relative biological effectiveness (RBE) is used to quantify the ratio of absorbed doses required to achieve a given biological response with alpha particles versus a reference radiation (typically a beta emitter or external beam radiation). However, as conventionally defined, the RBE varies as a function of absorbed dose and therefore a single RBE value is limited in its utility because it cannot be used to predict response over a wide range of absorbed doses. Therefore, efforts are underway to standardize bioeffect modeling for different fractionation schemes and dose rates for both nuclear medicine and external beam radiotherapy. Given the preponderant use of external beams of radiation compared to nuclear medicine in cancer therapy, the more clinically relevant quantity, the 2 Gy equieffective dose, EQD2(α/β), has recently been proposed by the ICRU. In concert with EQD2(α/β), we introduce a new, redefined RBE quantity, named RBE2(α/β), as the ratio of the two linear coefficients that characterize the α particle absorbed dose-response curve and the low-LET megavoltage photon 2 Gy fraction equieffective dose-response curve. The theoretical framework for the proposed new formalism is presented along with its application to experimental data obtained from irradiation of a breast cancer cell line. Radiobiological parameters are obtained using the linear quadratic model to fit cell survival data for MDA-MB-231 human breast cancer cells that were irradiated with either α particles or a single fraction of low-LET ¹³⁷Cs γ rays. From these, the linear coefficient for both the biologically effective dose (BED) and the EQD2(α/β) response lines were derived for fractionated irradiation. The standard RBE calculation, using the traditional single fraction reference radiation, gave RBE values that ranged from 2.4 for a surviving fraction of 0.82–6.0 for a surviving fraction of 0.02, while the dose-independent RBE2(4.6) value was 4.5 for all surviving fraction values. Furthermore, bioeffect modeling with RBE2(α/β) and EQD2(α/β) demonstrated the capacity to predict the surviving fraction of cells irradiated with acute and fractionated low-LET radiation, α particles and chronic exponentially decreasing dose rates of low-LET radiation. RBE2(α/β) is independent of absorbed dose for α-particle emitters and it provides a more logical framework for data reporting and conversion to equieffective dose than the conventional dose-dependent definition of RBE. Moreover, it provides a much needed foundation for the ongoing development of an α-particle dosimetry paradigm and will facilitate the use of tolerance dose data available from external beam radiation therapy, thereby helping to develop αRPT as a single modality as well as for combination therapies.

INTRODUCTION

Advances in the targeted delivery of radionuclides and radionuclide conjugation chemistry, and the increased availability of alpha emitters appropriate for clinical use, have recently led to a resurgence of preclinical studies and a number of clinical trials using radiopharmaceuticals labeled with these radionuclides (1–5). The same characteristics that make these radiopharmaceuticals attractive for targeting disseminated disease, namely the high-linear energy transfer (LET) and short range (<80 μm in water) of the α particles, also render their dosimetry complex. This is a serious issue as one of the major advantages of radiopharmaceutical therapy over chemotherapy is the ability to tailor treatment to a higher level of personalization. This is often done by quantitative imaging of a pretherapeutic quantity of radiopharmaceutical or an imaging surrogate in the patient at several time points to determine organ activities as a function of time. These data are used to calculate average organ absorbed doses per unit administered activity and ultimately the maximum tolerable activity that can be administered safely. However, because of the short range of α particles, nonuniformity in the activity uptake at the suborgan or functional subunit level will result in a nonuniform absorbed dose distribution, which may lead to localized toxicities that affect the organ as a whole in a manner inconsistent with radiotoxicity predicted by estimations of the average absorbed dose. In recognition of this fact, the Medical Internal Radiation Dose (MIRD) Committee has recommended the use of small-scale and/or microdosimetry for α-particle emitters and other radionuclides that impart high-LET type damage (6, 7), and efforts are ongoing in this direction (8–11) that attempt to translate macroscopically measured activity to cell- and subunit scale dosimetry.

Efforts are also currently underway to standardize a framework for bioeffect modeling of different fractionation schemes in external-beam radiation therapy, differing absorbed dose rates in nuclear medicine therapy and different LET radiations used in external beam therapies and nuclear medicine (i.e., protons, carbon ions, Auger electrons, α particles). The equieffective dose, EQDX(α/β), has recently been proposed by the International Commission on Radiation Units and Measurements (ICRU) as the standard quantity for bioeffect modeling of responses to therapeutic applications of ionizing radiation (12); in this notation, X is the fraction size and α/β is the ratio of the linear-quadratic model of cell survival parameters that characterize cell type response to low-LET radiation. The commonly used biologically effective dose (BED) (13, 14), represented by EQD0(α/β) in the EQDX(α/β) notation, would seem to be a natural choice for such standardization from a theoretic standpoint, as it uses the already existing linear parameter from the linear-quadratic formalism. However, most clinically relevant tissue responses have been characterized with acutely delivered 2 Gy fractions of low-LET radiations and consequently clinicians are well versed in tissue responses to 2 Gy fractions. In this context, the ICRU (12) recommends using the EQD2(α/β) form of the equieffective dose. Regardless of which reference is used in the EQDX(α/β) formalism, the lethal effects of low-LET radiation are exponentially dependent on EQDX(α/β). This means that cell survival curves are a log-linear function (i.e., single exponential) of EQDX(α/β) for low-LET radiation. At absorbed doses and dose-rates relevant to radionuclide and external-beam therapy, cell survival curves for α-particle radiation are a log-linear function of absorbed dose. Therefore, we propose defining the α-particle relative biological effectiveness RBE2(α/β) as the ratio of the two linear coefficients that characterize the α-particle absorbed dose-response curve and the low-LET megavoltage photon 2 Gy fraction equieffective dose-response curve. In other words, the low-LET equieffective (2 Gy fraction equivalent) dose for α-particle radiation can be obtained by simply multiplying the absorbed dose (from α-particle radiation) by the same RBE2(α/β) value, no matter the absorbed dose. Further, we recommend reporting RBE2(α/β) instead of the conventionally defined RBE, which does vary with absorbed dose.

METHODS

Conventional Definition of Relative Biological Effectiveness for High-LET Radiation with Exponential Dose Response

According to the widely-accepted linear-quadratic model (15), which forms the basis for radiobiological modeling for most irradiation conditions except extremely high dose rates, the surviving fraction (SF) of cells receiving an absorbed dose from low-LET radiation, D_L, is:

$$\text{SF}=e^{-\mathrm{\alpha }{D}_{\mathrm{L}}-\mathrm{\beta }{D}_{\mathrm{L}}^2}$$ (1)

The parameters α and β are known, respectively, as the linear and quadratic radiobiological parameters and are in principle specific to a given cell type. However, for α particles [or DNA-incorporated Auger electron emitters (16, 17), another high-LET type radiation], the response to the absorbed dose, D_H, is exponential (i.e., linear on a semilog plot):

$$\text{SF}=e^{-\mathrm{\kappa }{D}_H}$$ (2)

here, κ is the radiobiological parameter that characterizes the response of a given cell line to α-particle irradiation. The relative biological effectiveness is designed to relate the absorbed dose of the reference radiation (often low-LET delivered acutely) and absorbed dose of the test radiation (in this case high-LET α particles) that are required to cause equal biological effect (18): either a same surviving fraction of cells for cellular in vitro studies or a same measure of toxicity or therapeutic efficacy in organs or tumors, respectively. The basic equation that defines this concept is:

$$\text{RBE}={\frac{D_L}{D_H}|}_{SF}$$ (3)

This principle is illustrated in Fig. 1, where a same given surviving fraction of cells from the same cell line is obtained after delivery of an absorbed dose from either a high-LET radiation such as an α particle (D_H) or a low-LET radiation (D_L), given as a single fraction. The ratio between the two doses is the RBE. However, it is apparent that this ratio depends on the surviving fraction of cells chosen, or equivalently on the absorbed doses D_H and/or D_L.

FIG. 1.

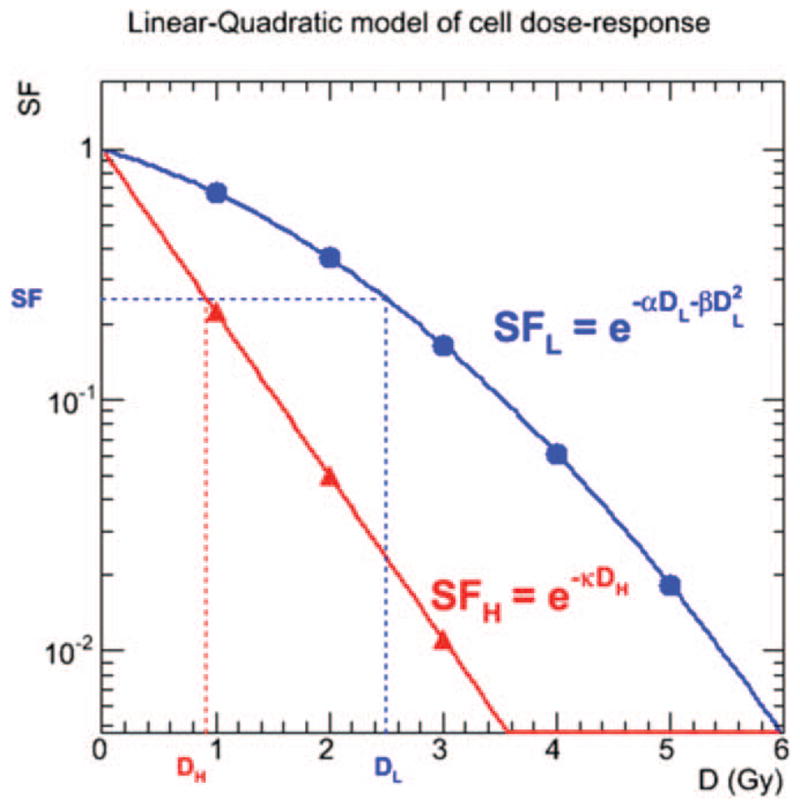
Semilog plot of theoretical cell survival curves for low-LET radiation such as β particles (linear-quadratic, blue symbols) and high-LET radiation such as α particles (linear, red symbols). For a given surviving fraction SF, the RBE is the ratio of the respective absorbed doses D_L and D_H corresponding to the SF.

No dose-independent resolution for the value of RBE is possible (Fig. 2); RBE is potentially equal to a range of values for the same cell line and is most often reported as such. The conundrum caused by the range of RBE for a given cell line is made concrete by establishing RBE_min (19) and RBE_max (20) for dose-response modeling. In that approach, the RBE_min such as it has been defined formulaically is undefined for cell survival curves for α-particle radiation. Consequently, in practice RBE_min and RBE_max are often taken as the limits of the measured RBE values, which may or may not correspond to the theoretical limits. By setting Eq. (1) equal to Eq. (2), a relationship between D_H and D_L is established:

$$D_L=\frac{-\mathrm{\alpha }\pm \sqrt{{\mathrm{\alpha }}^2+4\mathrm{\beta }\mathrm{\kappa }{D}_H}}{2\mathrm{\beta }}$$ (4)

FIG. 2.

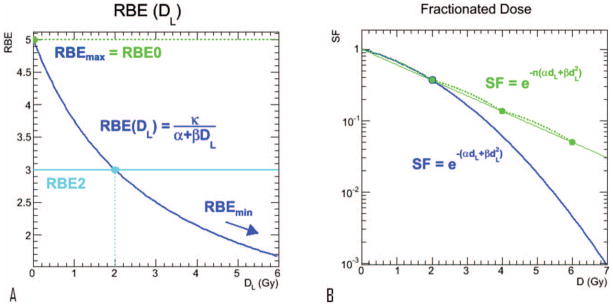
Panel a: Relative biological effectiveness [as defined by Eq. (6)] as a function of absorbed dose from low-LET radiation. RBE(D_L → 0) = RBE_max = κ/α. Panel b: Illustration of Eq. (7), the surviving fraction of cells for a fractionated dose regimen (d_L = 2 Gy, green) compared to a single fraction (blue).

Substituting Eq. (4) into Eq. (3), the RBE can be expressed as a function of D_H:

$$\text{RBE}=\frac{-\mathrm{\alpha }\pm \sqrt{{\mathrm{\alpha }}^2+4\mathrm{\beta }\mathrm{\kappa }{D}_H}}{2\mathrm{\beta }{D}_H}$$ (5)

Alternatively, by expressing RBE as a function of D_L, a more useful equation is established:

$$\text{RBE}=\frac{\mathrm{\kappa }}{(\mathrm{\alpha }+\mathrm{\beta }·D_L)}$$ (6)

For a fractionated regimen of low-LET radiation, when the time interval between fractions is short relative to the doubling time of the cells, the surviving fraction of cells is given by:

$$\text{SF}={(e^{(-\mathrm{\alpha }{d}_L-\mathrm{\beta }{d}_L^2)})}^n=e^{n(-\mathrm{\alpha }{d}_L-\mathrm{\beta }{d}_L^2)}=e^{-D_L(\mathrm{\alpha }+\mathrm{\beta }{d}_L)},$$ (7)

for a number, n, fractions of d_L absorbed dose per fraction (Fig. 2b). The RBE can be derived in a similar manner for a fractionated low-LET regimen by setting Eq. (2) equal to Eq. (7), and for an equivalent surviving fraction of cells, we have:

$$-\mathrm{\kappa }{D}_H=-D_L(\mathrm{\alpha }+\mathrm{\beta }{d}_L)$$ (8)

And the RBE for a reference fractionated low-LET regime is:

$$\text{RBE}=\frac{\mathrm{\kappa }}{(\mathrm{\alpha }+\mathrm{\beta }·d_L)}$$ (9)

The conventional definition of the RBE given by Eq. (6) poses problems when it is used to predict biological response primarily because it depends on absorbed dose. It also assumes that the reference radiation is a single fraction of low-LET radiation (e.g., ¹³⁷Cs γ rays) that is delivered acutely, and that all low-LET radiations are equally effective. This definition of reference radiation is often not well suited for the external beam therapy community and even less so for nuclear medicine. Indeed, outside of stereotactic radiosurgery and high dose brachytherapy, single fractions of high dose delivered punctually have little basis as a frame of reference; consequently reporting values relating α-particle dose to such a regimen makes little practical sense. A more universal, more easily understandable reference radiation would clearly be advantageous. The fractionated formalism given by Eq. (9) has this potential, assuming a standard dose per fraction can be adopted.

The EQDX(α/β) Framework

Two major schools of thought have emerged in radiation therapy for dose response modeling that accounts for dose rate or fractionation differences, BED and EQD2(α/β). These are rooted in radiobiology. The BED has been used most often in nuclear medicine, yet both approaches account for absorbed dose delivered over the time frames specific to radiopharmaceutical therapy. However, recently the ICRU has promulgated the use of the equieffective dose EQDX(α/β) for bioeffect modeling of radiation responses (12). EQDX(α/β) is defined as the total absorbed dose delivered by the external beam reference treatment plan of fraction size X that leads to the same biological effect as a test treatment plan that is conducted with absorbed dose per fraction d_L and total absorbed dose D_L according to a relation adapted from the Withers formula (21):

$$\text{EQDX}\mathrm{\alpha }/\mathrm{\beta }=D_L\frac{d_L+\mathrm{\alpha }/\mathrm{\beta }}{X+\mathrm{\alpha }/\mathrm{\beta }}$$ (10)

It was proposed that 2 Gy fractions of megavoltage X rays, EQD2(α/β), should be the reference (12). Accordingly, given this new standard, the RBE should be redefined with EQD2(α/β) as the reference radiation. In this formalism, the BED is the same as EQD0(α/β). While not as elegant or natural as the use of BED [or EQD0(α/β)] from a theoretic standpoint, the rationale behind this choice is that 2 Gy fractions are the most common standard for external beam radiotherapy and thus the biological effects are best understood by the treating physicians and by the radiotherapy community in general; it is, simply put, a more clinically relevant standard. From a linearity standpoint, which is the primary concern when addressing the issue of RBE for high-LET (α particle) radiations, the two choices [BED or EQD2(α/β)] are equivalent. Normal organ toxicity has often been correlated with BED; for example, this has been used in the context of renal toxicity caused by targeted radionuclide therapy (22, 23). However, since the BED and EQD2(α/β) are related by a constant coefficient for a given cell line, tissue or organ, the response relationships correlated to the BED will also exist for EQD2(α/β).

RBE2(α/β) for HIGH-LET Radiations in Radiopharmaceutical Therapy

Since the EQDX(α/β) has been chosen as the standard on the basis of being the common denominator of understanding, a logical step is to accommodate high-LET radiations (α particles, DNA-incorporated Auger electron emitters) in the EQDX formalism:

$$\text{EQDX}(\mathrm{\alpha }/\mathrm{\beta })=\text{RBE}·{\mathrm{D}}_{\mathrm{H}}\frac{d_L+\mathrm{\alpha }/\mathrm{\beta }}{X+\mathrm{\alpha }/\mathrm{\beta }}$$ (11)

By substituting Eq. (9) for RBE into Eq. (11):

$$\text{EQDX}(\mathrm{\alpha }/\mathrm{\beta })=\frac{\mathrm{\kappa }}{(\mathrm{\alpha }+\mathrm{\beta }{d}_L)}·D_H\frac{\mathrm{\alpha }+\mathrm{\beta }{d}_L}{\mathrm{\alpha }+\mathrm{\beta }X}=D_H\frac{\mathrm{\kappa }}{\mathrm{\alpha }+\mathrm{\beta }X}$$ (12)

Eq. (12) establishes a linear relation between EQDX(α/β) and D_H; the coefficient of proportionality is named RBEX(α/β):

$$\text{EQDX}(\mathrm{\alpha }/\mathrm{\beta })=\text{RBEX}(\mathrm{\alpha }/\mathrm{\beta })·D_H$$ (13)

Where, equivalent to Eq. (11),

$$\text{RBEX}(\mathrm{\alpha }/\mathrm{\beta })=\frac{\mathrm{\kappa }}{(\mathrm{\alpha }+\mathrm{\beta }X)}$$ (14)

And, more specifically:

$$\text{RBE}2(\mathrm{\alpha }/\mathrm{\beta })=\frac{\mathrm{\kappa }}{(\mathrm{\alpha }+2\mathrm{\beta })}$$ (14b)

The interpretation of this result is that the EQD2(α/β) standard is understood not as the “2 Gy fraction equivalent” specific to a particular modality, but as the “2 Gy fractions of low-LET megavoltage external beam equivalent” as the standard for all radiation types. The visual clarification of this EQDX(/) formalism is shown in Fig. 3. With respect to this standard, the relative biological effectiveness of the high-LET α particles is constant for the specified cell line or tissue; this constant is denoted RBE2(α/β).

FIG. 3.

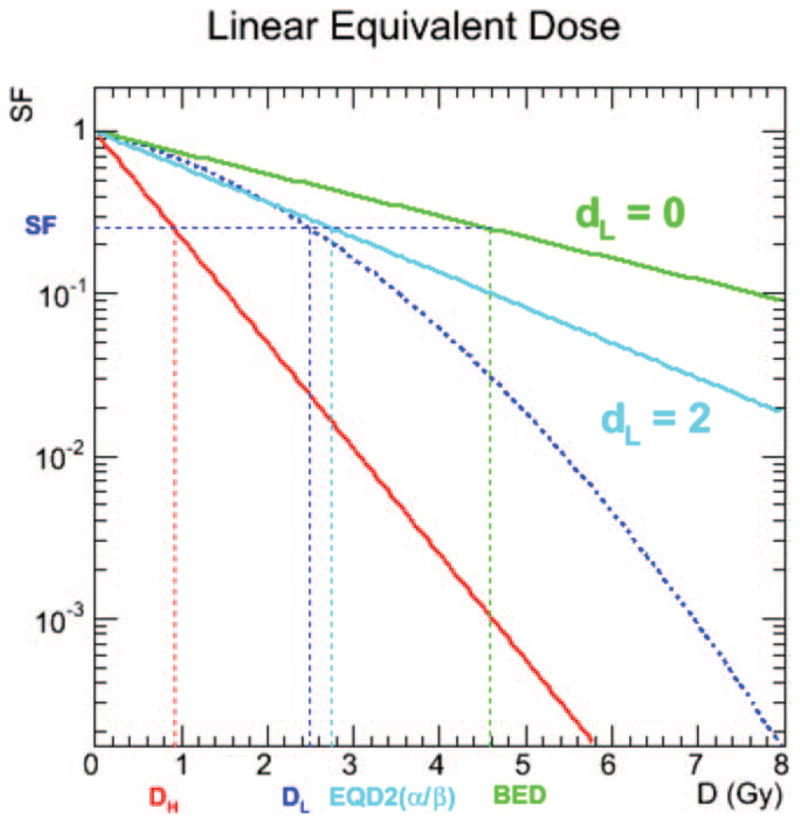
Graphical interpretation of the RBE0(α/β) and RBE2(α/β) concepts on a semilog plot. The red line represents the linear response to high-LET radiations such as α particles (Eq. 2), while the other three curves relate to the low-LET response. The dotted dark-blue line is the linear quadratic dose-response curve for low-LET radiations such as X rays and β particles (Eq. 1), the green line is the linear dose-response to infinitely small fraction size and the light-blue line is the linear dose-response to a fraction size of 2 Gy. The values of D_H, D_L, EQD2(α/β) and BED for a given SF are denoted on the abscissa. RBE0(α/β) is the ratio between D_H and EQD0(α/β), RBE2(α/β) is the ratio between D_H and EQD2(α/β); these values are constant for all D_H, D_L and SF.

Potentially, the RBE_max could also be used as a linear conversion constant in a manner analogous to the proposed RBE2(α/β) quantity; in fact in the EQDX(α/β) schema the RBE_max would logically be renamed “RBE0(α/β)”. Should the BED, rather than the EQD2(α/β) be deemed a more appropriate standard, the RBE0(α/β) quantity would follow as the more appropriate linear conversion for high-LETα-particle radiation.

$$\mathit{RBE}0(\mathrm{\alpha }/\mathrm{\beta })={\mathit{RBE}}_{\mathit{max}}=\frac{\mathrm{\kappa }}{\mathrm{\alpha }}$$ (15)

Application to Cell Lines

The survival curves for a human breast cancer cell line MDA-MB-231, exposed to α-particle radiation or low-LET ¹³⁷Cs gamma-ray radiation (0.5 Gy/min) were measured by colony formation assay. Details regarding the cell culture, radiolabeling, colony formation and dosimetry have been previously published (24, 25). Briefly, for α-particle radiation, MDA-MB-231 cells were exposed to nonspecific Rituximab-labeled ²¹³Bi (concentration range from 2.0 to 40.0 μCi/ml). Cells were incubated overnight, washed with PBS and transferred to Petri dishes for colony growth. The radiation absorbed doses from ²¹³Bi (range from 0.21–4.3 Gy) were estimated assuming the non-targeting α-particle radiation to be uniformly distributed and absorbed in the volume containing the cells.

Comparison with Low-LET Preclinical Radiopharmaceutical Therapy Studies

There are examples in the literature wherein an RBE is derived by comparing the biological effect, in vivo, of low-LET radiation delivered by a β-emitter labeled radiopharmaceutical (i.e., the reference radiation) characterized by a linear-quadratic cell survival curve in a semilog plot with an α-emitter labeled radiopharmaceutical (26, 27). In such a circumstance, RBEXα/β is not directly available, but may be calculated by first converting the absorbed dose from low-LET RPT, D_RPT, to an EQDX(α/β) and then by applying the developed formalism. The conversion to D_RPT from EQDX(α/β) has been previously described in the context of combination external beam-RPT therapy (28) and is derived in a manner analogous to the Wither’s formula (Eq. 10), namely by equating the BED for the different modalities to each other. The BED for external beam therapy is:

$$\text{BED}=D_{\mathit{XRT}}\left(1+\frac{d_{\mathit{XRT}}}{\mathrm{\alpha }/\mathrm{\beta }}\right)$$ (16)

where D_XRT is the total absorbed dose from external beam (XRT) and d_XRT is the absorbed dose per fraction. The formula for BED using low-LET RPT is (14, 29):

$$\text{BED}=D_{\mathit{RPT}}\left(1+\frac{G(\infty )·D_{\mathit{RPT}}}{\mathrm{\alpha }/\mathrm{\beta }}\right)$$ (17)

where G(T) is the Lea-Catcheside G-factor in the LQ response which accounts for DNA repair that occurs during chronic irradiation, as is the case in low-LET RPT where the absorbed dose is delivered continuously over a period of several hours or days. The expression for the G-factor is given by:

$$G(T)=\frac{2}{D^2}{\int }_0^T\stackrel{.}{D}(t)dt{\int }_o^t{e}^{-\mathrm{\mu }(t-w)}·\stackrel{.}{D}(w)dw$$ (18)

where t and w are integration variables representing time, and T is the integration limit time point, i.e., the integral is from 0 to T in time. For simple dose rate kinetics, such as mono-exponential fits, this equation reduces to simpler analytic forms; however, even in its most general form the G-factor may be resolved numerically (30). Using the BED as a bridge and setting Eq. (16) equal to Eq. (17) with the dose per fraction d_XRT = 2 Gy and therefore D_XRT = EQD2(α/β), we obtain:

$$\text{EQD}2(\mathrm{\alpha }/\mathrm{\beta })=D_{\mathit{RPT}}\frac{G(\infty )·D_{\mathit{RPT}}+\mathrm{\alpha }/\mathrm{\beta }}{2+\mathrm{\alpha }/\mathrm{\beta }}$$ (19)

As shown in Eq. (19), the EQD2(α/β) expression for a low LET-emitter labeled radiopharmaceutical is a function of the radiopharmaceutical absorbed dose, D_RPT, and the G-factor. The G-factor, in turn, depends on a radiobiological parameter, μ, which represents the rate of DNA single-strand break (SSB) repair, assumed exponential, and on the dose-rate kinetic profile during the irradiation duration. The dependencies shown in Eq. (19) underscore the fact that the ratio between the low-LET and high-LET RPT absorbed doses, and therefore an RBE defined as such, depends on the absorbed dose as well as the dose rate. However, once EQD2(α/β) has been calculated, the invariant RBE2(α/β) value may be obtained by combining Eq. (13), where D_H is the absorbed dose for the alpha-emitter labeled radiopharmaceutical calculated with Eq. (19):

$$\text{RBE}2(\mathrm{\alpha }/\mathrm{\beta })=\frac{D_{\mathit{RPT}}}{D_H}·\frac{G(\infty )·D_{\mathit{RPT}}+\mathrm{\alpha }/\mathrm{\beta }}{2+\mathrm{\alpha }/\mathrm{\beta }}$$ (20)

More specifically, while the ratio of D_RPT and D_H, sometimes reported as the RBE value in the literature (26, 27) depends on the absorbed dose and dose rate, and the ratio of EQD2(α/β) to low-LET RPT absorbed dose, D_RPT, also depends on those same factors, the product of those dependencies shown in Eq. (20) does not depend on either factor and RBE2(α/β) is indeed invariant.

RESULTS

Application to Cell Lines

The surviving fraction of MDA-MB-231 cells is plotted in Fig. 4. The error bars indicate the standard deviation for the two studies. The data were plotted using the ROOT physics analysis software (31) and fit with the Migrad algorithm inherited from the Minuit libraries (32). The parameters to the linear-quadratic fit to the low-LET data are: α = (0.187 ± 0.020) Gy⁻¹ and β = (0.0408 ± 0.0054) Gy⁻² with a fit correlation of R² = 0.99, while the high-LET parameter value is κ = (1.21 ± 0.02) Gy⁻¹ with a fit correlation of R² = 0.99. From these values, the derived quantities and their uncertainties were calculated: α/β = (4.6 ± 1.1) Gy, RBE0(4.6) = (6.5 ± 0.8), and RBE2(4.6) = (4.5 ± 0.6), while the traditional RBE value varies from 2.4 to 6.0.

FIG. 4.

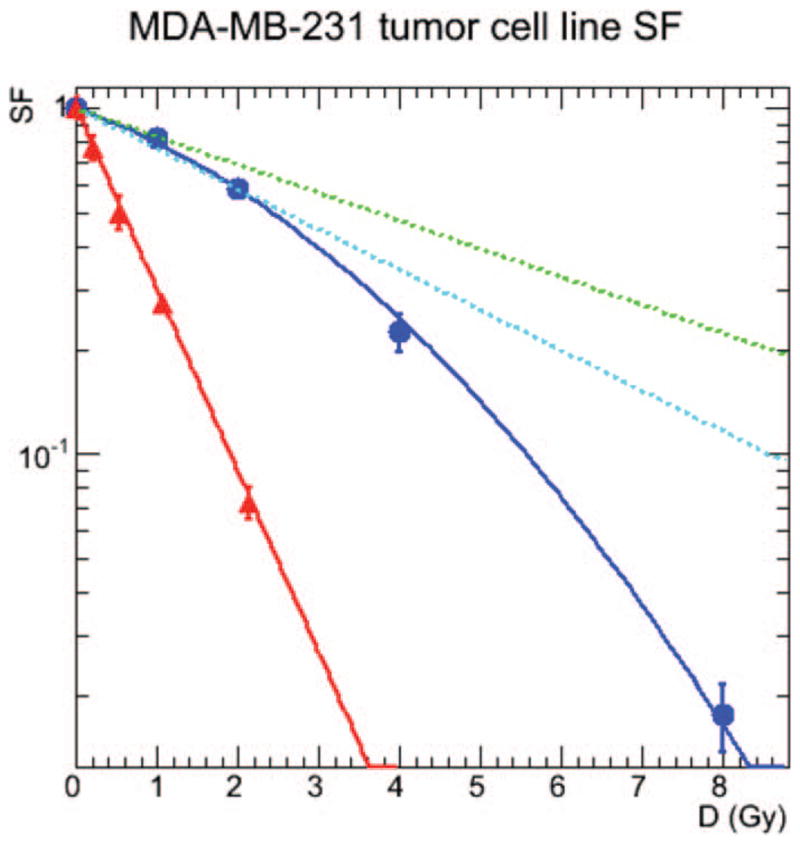
Measured response of cells that were acutely irradiated with ¹³⁷Cs γ rays (blue circles) or α particles from ²¹³Bi (red triangles). Data were least squares fitted to Eq. (1) (dark-blue lines) or Eq. 2 (red lines). Using the experimental values of α, β and κ, the green line is the projected linear dose-response to infinitely small fraction size [Eq. (9), d_L = 0] and the light-blue line is the linear dose-response to a fraction size of 2 Gy [Eq. (9), d_L = 2 Gy]. Results are presented for MDA-MB-231, a human breast cancer cell line.

Illustration of EQDX(α/β) Equivalence

To illustrate the impact of the formalism presented here, surviving fraction values were calculated for different patterns of delivering absorbed dose from different radiation types: (1) acute (single fraction) external beam; (2) 2 Gy per fraction external beam; (3) high-LET αRPT; and (4) and traditional (low-LET) β-particle RPT. The radiobiological parameters for the MDA-MB-231 cell line were used for all cases. However, in the case of traditional β-particle RPT, a simple exponential decrease in the dose rate with a half-life, T_λ, of 8 h and a repair half-life, T_λ, of 0.5 h were assumed. For a simple exponential fit to the dose rate, Eq. (18) reduces to:

$$\mathrm{G}(\infty )=\frac{T_{\mathrm{\mu }}}{T_{\mathrm{\mu }}+T_{\mathrm{\lambda }}}$$ (21)

Consequently, for the chosen parameters, G(∞) = 0.0588, for the β-particle RPT. The resulting SF values were plotted as a function of absorbed dose in Fig. 5a. The absorbed doses were then converted to EQD2(α/β) using Eq. (10) for the acute radiation; Eq. (12) for the α-particle radiation; and Eq. (19) for the β-particle RPT radiation and plotted in Fig. 5b. As expected, the EQD2(α/β) results all fall along a same line in the semilog plots, demonstrating the utility of the EQDX(α/β) formalism and the advantage of correlating response with EQD2(α/β).

FIG. 5.

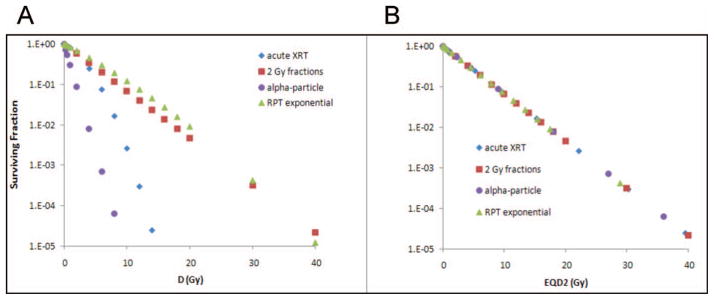
Dose-response curves for MDA-MB-231 cells for different radiation delivery patterns and types when plotted as a function of D (panel A) and EQD2(α/β) (panel B). The curves in panel A are plotted using Eqs. (1) and (2). This demonstrates the convergence of the dose response when surviving fraction is plotted as function of EQDX(α/β).

DISCUSSION

The purpose of this article is to develop and recommend a consistent manner of presenting α-particle RBE values to the scientific and clinical communities. The 2 Gy fraction equivalent of external beam radiation formalism proposed herein would discourage the use of giving RBE values for a range of doses that may or not be relevant (may or may not include a theoretical RBE_max) and that may be subsequently taken and applied out of context (for a different dose range than for those published) by the community. Historically, attempts have been made to report only single values of RBE for ease of application (16); however, no single standard emerged successfully and the choice of basis varied between D₅₀, D₃₇ or D₁₀. Most authors stated the endpoint – although not always and because of the lack of consistency, the RBE value would be extracted from the article and the endpoint lost in the process. With the advent of an official standard and nomenclature, we hope that the proposed single value formalism will enjoy widespread acceptance.

According to the strict definition of relative biological effectiveness (18), the test and reference radiations should be delivered in an identical manner with the exception of the radiation type. However, this is often experimentally difficult, particularly in the context of targeted radionuclide therapies. Implicit in the RBEX(α/β) formalism proposed here is the separation of dose rate and LET effects. This is logical given that the dose-rate dependence of the response to low-LET radiation is already implicit within the “2 Gy equivalent” concept for this type of radiation. More generally, as pointed out by the ICRU (12), the EQD2(α/β) standard should be considered not just the standard for external beams of low-LET radiations, but for all radiation types, in which case the α-particle RBE, re-named the RBE2(α/β), an absorbed dose-independent quantity, should also be the standard. By such a definition, importantly, reported values for use by the general community gain significantly in transparency and enable straightforward application of documented results.

While this treatise focuses mainly on α particles, the proposed use of RBE2(α/β) as the relevant reported RBE value is eminently logical for other high-LET radiations used in nuclear medicine, such as Auger electrons, which present similar log-linear dose-response curves when the Auger emitter is incorporated into DNA in the cell nucleus, as well as those encountered in external beam, such as protons or carbon ion (33) radiations, which are characterized by a linear-quadratic response curve. Much work has already been done by Dale and colleagues (19, 20, 34) incorporating RBE into the BED formalism; however, still within the context of an absorbed dose-dependent RBE between two extreme limits RBE_max at low absorbed dose per fraction and RBE_min at very high absorbed dose per fraction.

From the perspective of αRPT, a single RBE value to convert absorbed dose to equieffective dose would facilitate progress towards an effective paradigm for bioeffect modeling in αRPT. Specifically, such a tool would be used to validate the RBE-adjusted equivalence of normal organ radiotoxicity thresholds in pre-clinical and clinical cases, as has been done for kidney toxicity in β-emitter RPT and external beam therapy using the BED as a standardizing quantity (22, 23). This in turn along with the spatial macro-to-micro conversion methodology would provide the justification for combination dosimetry for combination therapies, which include αRPT. This is a highly desirable goal as αRPT is especially suited for micro-metastases, which are not identified in external beam therapy and often receive sub-therapeutic doses from β-emitting radiopharmaceuticals. Combination strategies using different β emitters (35, 36) or using β-emitters in conjunction with external beam have been proposed (28); however, for optimal therapy targeting as large a range of tumor sizes as possible, αRPT would be the ideal complement to other therapies. In general, accurate dosimetry is fundamental to radiation therapies to ensure an optimal, safe and effective treatment. The use of population averaged standard anatomy based approaches that provide a single absorbed dose value, is detrimental to the effective treatment of the individual patient, especially if one considers the nonlinearity of tumor cell kill and response to administered therapeutic quantities.

The present formalism assumes that the linear-quadratic (LQ) and linear models are valid for the photon/β-emitter dose response and α-particle dose response, respectively. While the LQ model is generally recognized as valid and forms the basis for much of the normal organ dose-toxicity thresholds that have been established, it is also generally recognized that high dose rates or fractions such as those present in high dose rate brachytherapy, hypofractionated therapy or stereotactic radiosurgery have cellular responses that can depart from the linear-quadratic model. Several supplementary or alternative models have been proposed to account for these high dose rates (37–39). To date none have commanded unequivocal consensus. Similarly, the log-linear quality of the α-particle dose-response curve is suspect at higher dose; the α-particle curves tend to be concave up on the semilog plots. This is possibly due to the statistical fluctuations and the stochastic nature of the α-particle energy deposition or due to the different relative distributions of the radionuclide (40). Additionally, a theoretical quadratic term should exist in the α-particle cell survival curve, since an important fraction of the damage is delivered by delta-ray electrons. However, to date this has not been observed experimentally, and departures from the log-linear curve tend to be concave up as noted previously, rather than concave down. In all cases, the formalism presented here is amenable to variations in the models used to describe the cellular dose-response curves, as the fundamental principle of defining and reporting RBE with respect to EQD2(α/β) remains.

In the ²¹³Bi experiments conducted in this article, we have assumed that the mean absorbed dose to the cultured cells is equal to the mean absorbed dose to the culture medium from ²¹³Bi. Given that (1) the individual cells are much smaller than the range of the α emissions, (2) the antibody does not bind to the cells and (3) the cells exist as individuals in suspension in the medium, this is a reasonable approximation that has been substantiated by Monte Carlo simulations (data not shown). However, there are imprecisions in activity measurement and assumptions in the methodology that may influence the data presented in Fig. 4. Dose-response measurements using a broad beam of α particles would give cleaner, more accurate results (41). It should also be noted that RBE2(α/β) (or generic RBE) values can be sensitive to experimental conditions such as temperature, pressure, CO₂ concentration, pH, cell cycle phase, etc. Every effort should be made to control these variables as tightly as possible. Nevertheless, as a proof of principle, the results presented here illustrate the concept and potential value of an absorbed dose-independent, dose-rate-adjusted relative biological effectiveness parameter.

Particular attention should be made to the issue of dose nonuniformity when applying the model to larger scale collections of cells, such as in tumors or normal organs. The relative short range of α particles means that any nonuniformity of uptake will most likely result in nonuniformity of absorbed dose. Just as a single absorbed dose value may not well represent the complexity of the absorbed dose distribution or the biological response, the single RBE2(α/β) value may not be sufficient. In the case of tumors, the equivalent uniform dose (42) has shown promise as a single value more representative of biological response (43, 44), but a more diverse representation such as a dose-volume histogram with associated RBE2(α/β) values may still present a clearer picture. In the case of normal organs, as previously mentioned, the MIRD Committee has recommended micro- or small-scale dosimetry (6), and models exist where absorbed dose values are calculated for different compartments corresponding to different cell types or spatial distributions (8, 9) (e.g., proximal tubules and glomeruli for the kidney) to which RBE2(α/β) values may be attributed.

On a similar note, for protracted therapies, such as with ²²⁵Ac, which has a 10-day half-life, additional modifications to the formalism that allow for cellular repopulation may be relevant and this has not been taken into account. However, here too, this is probably best addressed by incorporating the repopulation factor into the small-scale modeling which attributes the absorbed dose values to the cell population and only subsequently calculates the respective RBE2(α/β) values.

A significant practical consideration concerns the origin of the α, β and κ values necessary for the calculation of RBE2(α/β). Although there is substantial documentation regarding the radiobiological parameters in the literature, the picture is far from complete. If the radiobiological parameters are unknown, it may still be necessary to compare efficacy over a range of absorbed doses from high-LET and low-LET radiations to identify the radiobiological parameters. Concerning the conversion of RPT-derived RBE values to the RBEX(α/β) formalism, once α, β, D_RPT and G are known, as is often the case, Eq. (14) may be used to calculate, κ and in so doing, link in vivo response end points to a cell-line surviving fraction end point. In general, the proposed RBE2(α/β) does not immediately resolve any outstanding issues regarding the validity of in vitro vs. in vivo radiobiological parameter values, however, by reducing the RBE to a single dose-independent quantity, the formalism does eliminate one of the confounding factors. Consequently, this will better enable the identification of potential radiobiological differences between in vitro and in vivo end points.

Finally, we have not considered the dependence of RBE2(α/β) on the energy of the α-particles emitted by the radionuclide. Because RBE depends on LET and LET depends on the α-particle energy, the RBE differs for particles emitted by different radionuclides (45). A number of possibilities can account for this dependence, for example: (1) RBE2(α/β) is determined experimentally as a function of initial α-particle energy over the range of energies emitted by the various α emitters (~2–10 MeV) (45) or (2) a more theoretical microdosimetric approach where RBE2(α/β) takes into account the changes in LET as the α-particles traverse the cell population.

CONCLUSIONS

Consistent with the ICRU framework for bioeffect modeling with EQD2(α/β), the α-particle relative biological effectiveness RBE2(α/β) is defined as the ratio of the two linear coefficients that characterize the α-particle absorbed dose-response curve and the low-LET megavoltage photon 2 Gy fraction equieffective dose-response curve. RBE2(α/β) thus defined, is independent of absorbed dose and provides a more logical formalism than the conventional absorbed dose-dependent definition of RBE. Moreover, RBE2(α/β) provides a much needed foundation for the ongoing development of an α-particle bioeffect modeling paradigm as well as for rational (i.e., safe and effective) dosimetrically-based combination therapies.