Abstract
Förster resonance energy transfer (FRET) experiments are often used to study interactions between integral membrane proteins in cellular membranes. However, in addition to the FRET of sequence-specific interactions, these experiments invariably record a contribution due to proximity FRET, which occurs when a donor and an acceptor approach each other by chance within distances of ∼100 Å. This effect does not reflect specific interactions in the membrane and is frequently unappreciated, despite the fact that its magnitude can be significant. Here we develop a computational description of proximity FRET, simulating the cases of proximity FRET when fluorescent proteins are used to tag monomeric, dimeric, trimeric, and tetrameric membrane proteins, as well as membrane proteins existing in monomer-dimer equilibria. We also perform rigorous experimental measurements of this effect, by identifying membrane receptors that do not associate in mammalian membranes. We measure the FRET efficiencies between yellow fluorescent protein and mCherry-tagged versions of these receptors in plasma-membrane-derived vesicles as a function of receptor concentration. Finally, we demonstrate that the experimental measurements are well described by our predictions. The work presented here brings additional rigor to FRET-based studies of membrane protein interactions, and should have broad utility in membrane biophysics research.
Introduction
Approximately one-third of the open reading frames in the human genome encode for membrane proteins in the form of receptors, transporters, and channels, to name a few. The function of many of these proteins is regulated by their interactions with partners in the membrane. For instance, some membrane proteins are active as dimers or higher-order oligomers, but are inactive in the monomeric state (1–3). In other cases, activity of a protein is controlled by its heterointeraction with a structurally unrelated partner (4,5). Although such interactions are critical for normal biological function and are implicated in many diseases, our knowledge of membrane protein interactions is often qualitative and rudimentary, and lags far behind the knowledge of soluble protein interactions.
Many of the label-free techniques that are commonly used to study soluble protein interactions cannot be extended to membrane proteins in their native environment. Instead, fluorescence methods, particularly approaches that rely on Förster resonance energy transfer (FRET), are often used (6-10). A major advantage of the FRET-based assessment of molecular interactions in the membrane is that experiments can be performed in cells or in a cell-derived system, without the need for membrane protein extraction and purification.
FRET involves the nonradiative transfer of energy from an optically excited donor to an appropriate acceptor molecule (11). In FRET experiments, the membrane proteins of interest are tagged with genetically encoded donor and acceptor fluorescent proteins such as cyan fluorescent protein, green fluorescent protein, yellow fluorescent protein (YFP), and mCherry (12–14). The steady-state FRET efficiency in this case can be easily measured in a standard fluorescence microscope. However, quantitative assessment of the strength of interactions between the tagged membrane proteins remains a challenge, partially because of the unknown proximity-FRET contribution to the steady-state FRET efficiency. Proximity FRET occurs when a donor and an acceptor approach each other by chance within distances of about two Förster radii and does not reflect specific interactions between the tagged membrane proteins (15). The magnitude of this effect is significant, because the fluorophores are confined in two dimensions. Without a correction for proximity FRET, the results of a FRET-based measurement of membrane protein interactions can be incorrect and misleading. Thus, it is critical that the effect is understood and reliably predicted even in cases when it is not directly measurable.
Wolber and Hudson developed a model for FRET in two dimensions that accounts for random encounters of donors and acceptors, assuming that the size of donors and acceptors is negligible (15). This theoretical model has been shown to explain FRET data in lipid bilayers when the donor and the acceptor are small organic molecules (16–18). However, the model is not applicable to large β-barrel fluorescent proteins used in cellular studies because of their rather large finite size (∼3–4 nm), which limits the distance of closest approach between donors and acceptors. A model that is useful in this case was developed by Snyder and Freire, who used computer simulations to predict proximity FRET for monomeric fluorophores with finite size that are confined to a plane in two dimensions (19). However, the case of proximity FRET for fluorophores attached to membrane proteins that form constitutive oligomers or exist in a monomer-dimer equilibrium has never been considered in the literature. Such a proximity-FRET contribution can be expected to occur, but its exact magnitude is unknown.
Along with the challenges in developing reliable predictions of proximity FRET, there have also been challenges in the experimental assessment of the effect. There have been no rigorous measurements of proximity FRET as a function of concentration with fluorescent protein-tagged, noninteracting membrane proteins. In fact, as the protein interaction networks in cellular membranes are not yet well defined, there are no definitive negative controls for noninteracting proteins. Usually, unrelated membrane proteins are assumed to be noninteracting, without rigorous tests for the lack of such interactions.
Here, we address all the above issues by providing a computational description of proximity FRET, and by identifying several integral membrane proteins that do not interact and allow for experimental characterization of proximity FRET. First, we revisit the simulations of Snyder and Freire, which were carried out for a limited number of fluorophore concentrations and distances of closest approach (20). We improve upon their numerical results by simulating monomeric fluorophores over a wider range of exclusion radii and acceptor concentrations. Second, we calculate the theoretical proximity contribution for oligomeric arrangements of fluorophores, accounting for their finite size and geometric arrangement. We demonstrate that both the distance of closest approach between fluorophores and their oligomeric state affect the magnitude of the proximity-FRET contribution. Furthermore, the monomer predictions that we generate allow us to identify integral membrane proteins from the receptor tyrosine kinase (RTK) family that do not interact in mammalian membranes and thus can be used as negative controls in FRET experiments in cellular systems. We measure the FRET signatures of these proteins, tagged with YFP and mCherry fluorescent protein, in plasma-membrane-derived vesicles. We accomplish this with the help of the quantitative-imaging FRET (QI-FRET) method (21,22), which yields not only the FRET efficiency but also the donor and acceptor concentrations. By fitting the model to the experimental data, we obtain the distance of closest approach between fluorophores for the different RTK/fluorescent protein pairs studied here.
Numerical Methods
Proximity FRET
When confined to two dimensions, even at relatively low concentrations, donors and acceptors can randomly approach each other such that the energy of an excited donor can be transferred to an acceptor. This type of random proximity FRET will occur even in the absence of sequence specific interactions.
As shown by Wolber and Hudson (15), in a static quenching experiment, the relative quantum yield for a donor surrounded by a random configuration, β, of N acceptor molecules is
| (1) |
In Eq. 1, Ri is the distance from the ith acceptor molecule to the donor and R0 is the Förster Radius, a property of the donor-acceptor FRET pair. The Förster radius is the donor-acceptor distance, R0, at which resonance energy transfer efficiency, E, is decreased to 50% (11). Therefore,
| (2) |
The ensemble average of Eq. 1 over all configurations of acceptor molecules equals the ratio of the donor quantum yield in the presence (QDA) and absence (QD) of the acceptor molecule (15):
| (3) |
The proximity FRET depends only on the acceptor concentration (15), and thus it can be predicted based on quantum yield calculations for a single donor surrounded by a random configuration of acceptors. However, certain cases are more complex (see below), and configurations of multiple donors may need to be considered. As shown by Snyder and Freire (19), if multiple excited donors, ND, are available to transfer their energies to a random configuration of acceptors, the ratio of quantum yields shown in Eq. 3 becomes
| (4) |
The proximity-FRET transfer efficiency, E, for a given acceptor concentration is then given by Eq. 5:
| (5) |
Wolber and Hudson developed analytic equations to calculate proximity FRET as a function of acceptor concentration (15). These equations, however, are valid for point fluorophores only, and break down when the excluded volumes of donor and acceptor molecules become relevant, as in the case of fluorescent proteins with diameters of ∼3 nm and Förster radius of ∼5.4 nm. Snyder and Freire used computer simulations and the equations above to determine proximity FRET (19) that is valid for monomers of finite size. As discussed below, we improve here upon their numerical result by simulating over a wider range of exclusion radii and a finer grid of acceptor concentrations. We also calculate, for the first time to our knowledge, the proximity-FRET contribution as a function of the oligomeric state and geometry of the membrane protein complexes.
In our simulations, we specifically model the case of integral membrane proteins that are labeled with fluorescent proteins at their termini. We assume that the attachment of the fluorescent proteins is through an intrinsically disordered linker, and thus the fluorophores adopt random orientations. Furthermore, the fluorescent proteins are confined to the two-dimensional (2-D) region in the immediate vicinity of the membrane. Thus, we can forego simulations of the complicated membrane environment and focus solely on the generation of random 2-D configurations of fluorophores with limited distances of closest approach, L. The simulation is performed in 2-D, and the fluorophores are modeled as circles of a fixed exclusion radius, r. In the case when donor and acceptor molecules are fluorescent proteins fused to identical membrane proteins, this distance of closest approach, L, is twice the exclusion radius, 2r, of the 3-D volume sampled freely by the fluorescent protein.
Proximity FRET for monomeric membrane proteins
To simulate proximity FRET for monomeric membrane proteins, a lone donor molecule is placed in the center of a 2-D, square simulation region (Fig. S1 in the Supporting Material). For each simulated acceptor concentration, the number of acceptor molecules is calculated and acceptors are placed one by one into the simulation region until the desired surface density is reached. For each acceptor molecule to be placed, a random position is chosen within the simulation region and evaluated against the condition of no overlap. If no overlap occurs between the newly placed acceptor and any other previously placed molecule, including the central donor molecule, the position is chosen as acceptable. If not, then a new random position is chosen and the position is evaluated again against the condition of no overlap. This is repeated until all of the acceptor molecules are successfully placed without overlap within the simulation region. Equation 1 is then used to calculate the quantum yield of the central donor in the presence of the random configuration of acceptors. After this is done for a large ensemble of such configurations, Eqs. 3 and 4 are used to calculate the simulated proximity FRET as a function of acceptor concentration.
The case of proximity FRET in the case of noninteracting fluorophores with finite volume has been considered previously by Snyder and Freire, with the only difference being the method of molecular placement (20). They used an elegant Monte Carlo approach to generate the various acceptor configurations, from which curves of QDA/QD were generated for different values of L/R0 (19). Each curve was fitted to an exponential function of acceptor concentration per R02, [c], and the dependence of the best-fit parameter on L/R0 was modeled with a third-order polynomial function. The equations used were
| (6) |
where
| (7) |
and
| (8) |
With ai determined by fitting A as a function of L/R0, this form of the relative quantum yield can be used in any nonlinear least-squares fitting algorithm to determine the best-fit value of L for a data set, when R0 is known.
Since the publication of these results, 30 years have passed, during which computer power has increased immensely. As such, we performed monomer-only simulations over a much finer mesh of acceptor concentrations and exclusion radii than was possible previously. We found, in agreement with previous work, that the relative quantum yields, as a function of acceptor concentration, were modeled well as an exponential function of the form shown in Eq. 6. Employing a finer mesh of simulated exclusion radii allowed us to confirm that A was indeed a smooth function of the exclusion radius. The finer mesh of acceptor concentrations used in the simulations, which determines the value of A in a least-squares sense, showed that a fifth-order polynomial more accurately models the dependence of A as a function of the fluorophore exclusion radius. The inclusion of additional terms did not significantly improve the quality of the fit. Thus, our refined prediction for the relative quantum yield is given by Eq. 6, where
| (9) |
and
The proximity-FRET contribution due to random approach of monomeric fluorophores was simulated on a 150 × 150 nm2 2-D plane (see Fig. S1). Acceptor concentrations ranging from 0 to 0.01 acceptors/nm2 were used in the simulations, and the simulations were run for exclusion radii ranging from 0 to 4 nm, in 0.02 nm steps. These simulations were performed for N = 40,000 different configurations at each acceptor concentration. The Förster radius for the YFP-mCherry FRET pair of 5.4 nm was utilized in the generation of the curves of relative quantum yield. In Fig. 1, we show the results of a simulation when the distance of closest approach is 2.8 nm, corresponding to an effective exclusion radius of 1.4 nm.
Figure 1.
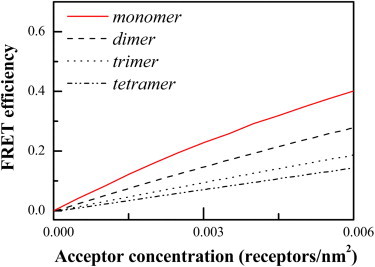
Predictions for proximity FRET for monomers, dimers, trimers, and tetramers, as a function of acceptor concentration.
Proximity FRET for oligomeric membrane proteins
The cases of constitutive oligomers confined to two dimensions are more complex than the monomer case, as the oligomers can have a specific orientation within the plane of the membrane (see angle ϕ in Fig. S2 B). The total number of fluorophores is calculated from the acceptor concentration and the donor/acceptor ratios. Next, the number of oligomers is calculated based on the total concentration. A central oligomer is placed in the center of the simulation region and assigned a random orientation angle, ϕ. Random (x,y) positions are assigned for the locations of the centers of the remaining oligomers, and orientation angles are chosen with a random number generator. The positions of the fluorophores are calculated based on the orientation angle and the position of the center of the oligomer. The fluorophore positions within each oligomer are compared to the positions of all the previously placed oligomers to ensure that no overlap with any other previously placed fluorophore has occurred. If no overlap occurs, this location is chosen as an acceptable oligomeric position. Conversely, if overlap has occurred with another molecule, a new position and orientation angle are chosen until a no-overlap position is identified. Once all the oligomers have been placed, one of the central oligomeric fluorophores is randomly selected to be a donor, hereafter called the central donor. Next, some fluorophores are randomly assigned to be donors, based on the donor fraction. Once all of the donors have been selected, the remaining fluorophores are assigned to be acceptors. Equations 4 and 5 are then applied to determine the relative quantum yield of the donor for that specific configuration of fluorophores for all of the acceptor molecules not assigned to the central oligomer. This yields proximity FRET between oligomers, as there are no intraoligomeric donor-to-acceptor distances used in the calculations.
The proximity-FRET contributions due to random approach of dimers, trimers, and tetramers were simulated on a 150 × 150 nm2 2-D plane (Figs. S2–S4). Acceptor concentrations ranging from 0 to 0.01 acceptors/nm2 were used in the simulation, and the simulations were run for four donor/acceptor ratios: 0.1, 0.2, 0.3, and 0.4. These simulations were performed for N = 40,000 times at each acceptor concentration and each donor/acceptor ratio. The Förster radius for the YFP-mCherry FRET pair of 5.4 nm was utilized in all simulations. The distance between the fluorophores in the oligomers was fixed at d = 50 Å. This distance corresponds to an intrinsic FRET efficiency of 0.6 for a dimer labeled with a donor and an acceptor.
Proximity FRET for membrane proteins in monomer-dimer equilibrium
This case is more complex than the previous cases, as a lone donor placed in the center of the simulation region can exist either as a monomer or as part of a dimeric arrangement. For this reason, in this set of simulations we did not calculate the quantum yield of a single acceptor-quenched donor; instead, we calculated the quantum yield of all excited donors randomly placed within a 50 × 50 nm2 central region centered within the 150 × 150 nm2 simulation region (see Fig. S5). Wolber and Hudson (15) used a similar central-region approach, which offers the advantage of avoiding edge effects experienced with donor placement near the edge of the simulation region. The FRET efficiency due to proximity is calculated using Eqs. 4 and 5 for all donor molecules within the central region. Thus, FRET is averaged over donors in both the monomeric and dimeric configurations in this simulation. If an acceptor molecule is in a dimer with a donor molecule in the central region, that intermolecular distance is not used in Eq. 5, since this acceptor is not contributing to the proximity FRET, but instead is engaging in FRET due to sequence-specific dimerization.
During each trial, the predetermined acceptor concentration and donor/acceptor ratio are used to calculate the total number of molecules, the number of acceptors, and the number of donors to be placed within the simulation region. Based on a given dimerization free energy, ΔG° = −RT ln(K), where K is the equilibrium association constant for the two-state model, the fraction of dimers as a function of total fluorophore concentration is calculated. Based on the total number of simulated molecules, the number of molecules to be placed in a dimeric configuration is then determined, also yielding the number of monomeric fluorophores. In all trials, the first molecule (monomer or dimer) to be placed is assumed to be a donor fluorophore and is placed randomly within the region of interest inside the simulation region. The probability that this molecule is a dimer is equal to the fraction of dimers designated for that trial. A random number between 0 and 1 is chosen, and if this number is between 0 and the expected fraction of dimers, then the first molecule placed is a dimer. Otherwise, the first molecule placed in the region of interest is a monomer. The purpose of placing the first molecule within the region of interest, as opposed to randomly within the entire simulation region is to ensure that at least one donor molecule is excited and can transfer its energy to an acceptor configuration.
After placement of the first monomer or dimer, the remaining dimers are placed randomly within the simulation region and are given a random orientation, ensuring that no spatial overlap takes place between all previously placed fluorophores. The remaining monomers are then placed randomly within the simulation region, and again the condition of no overlap between the newly placed fluorophore and all previously placed fluorophores is enforced. Once all the monomers and dimers have been placed in the simulation region without overlap for a particular trial, the fluorophores are randomly assigned to be either donors or acceptors. After completion of all trials for a given acceptor concentration and donor/acceptor ratio, Eqs. 4 and 5 are used to calculate the theoretical proximity FRET.
Monomeric fluorophores were modeled as circles of radius r = 1.4 nm and dimeric structures consisted of two circles of radius r = 1.4 nm separated by an intramolecular distance d = 5 nm. Acceptor concentrations were varied from 0 to 0.01 acceptors/nm2, and donor/acceptor ratios of 0.1, 0.2, 0.3, and 0.4 were used in the simulations, with 30,000 trials per simulated acceptor concentration and donor/acceptor ratio. Predictions were created for different values of the dimerization free energy, ΔG°.
Experimental Methods
Plasmid constructs
The pRSETB-mCherry plasmid was a gift from Dr. R. Tsien (University of California, San Diego) and the YFP plasmid was a gift from Dr. M. Betenbaugh (Johns Hopkins University, Baltimore, MD). The plasmid encoding human wild-type fibroblast growth factor receptor (FGFR)1/IIIc in the pRK5 vector was a gift from Dr. M. Mohammadi (New York University, New York). All of the plasmids used for mammalian expression were constructed in the pcDNA 3.1(+) vector (Invitrogen, Carlsbad, CA), and all primers for FGFR1 were purchased from Invitrogen. The primers used for ErbB1 (epidermal growth factor receptor) and ErbB2 (human EGFR 2) cloning were purchased from Integrated DNA Technologies (Coralville, IA).
Six plasmid constructs (pcDNA-receptor-YFP and pcDNA-receptor-mCherry) were subcloned for these experiments (see Fig. 3). The two FGFR1 constructs, pcDNA-FGFR1-YFP and pcDNA-FGFR1-mCherry encoded the FGFR1 signal peptide, the FGFR1 extracellular domain, the FGFR1 transmembrane (TM) domain, a 15 amino acid (GGS)5 flexible linker, and a fluorescent protein (YFP or mCherry) replacing the intracellular domain of the receptor. The two ErbB1 plasmid constructs, pcDNA-ErbB1-YFP and pcDNA-ErbB1-mCherry, encoded sequences for the signal peptide of human ErbB1; the extracellular and TM domains of ErbB1, a 15 amino acid (GGS)5 linker, and YFP/mCherry fused at the C-terminus. The two ErbB2 plasmid constructs, pcDNA-ErbB2-YFP and pcDNA-ErbB2-mCherry encoded sequences for the signal peptide of human ErbB2, the extracellular domain and TM domains of ErbB2, and YFP/mCherry attached to the C-terminus of the TM domain via a 15 amino acid (GGS)5 linker. The oligonucleotide sequence for the 15 amino acid linker was identical for all six plasmid constructs.
Figure 3.
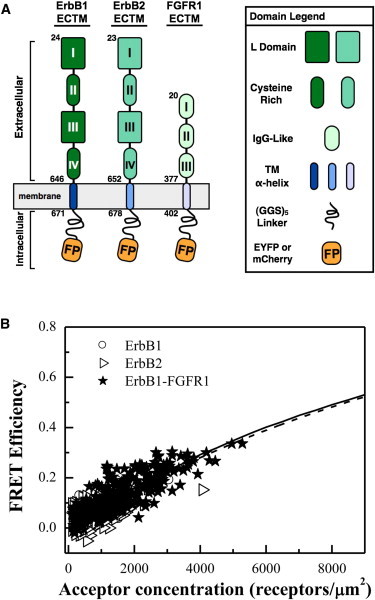
(A) RTK constructs, identified here as the non-interacting controls. (B) Measured FRET efficiencies for i), truncated ErbB1 labeled with either YFP or mCherry in CHO derived vesicles, ii), truncated ErbB2 labeled with either YFP and mCherry in HEK 293T derived vesicles, and iii), truncated ErbB1 labeled with YFP and truncated FGFR1 labeled with mCherry in CHO derived vesicles. All the measured FRET efficiencies fall close to the prediction for monomers. (Solid line) our prediction for L = 2.8 nm. (Dashed line) prediction of Snyder and Freire (19) for L = 2.8 nm.
Cell culture and transfection
Chinese hamster ovary (CHO) cells were a kind gift from Dr. M. Betenbaugh (Johns Hopkins University, Baltimore, MD). Human Embryonic Kidney (HEK293T) cells were a gift from Dr. D.Wirtz (Johns Hopkins University). The cells were cultured in Dulbecco’s modified Eagle medium at 37°C with 5% CO2 for 24 h. Transfection was carried out using Fugene HD transfection reagent (Roche Applied Science, Penzberg, Germany) according to the manufacturer’s protocol. HEK293T and CHO cells were cotransfected with 5 μg and 7 μg, respectively, of total DNA. The DNA encoded either 1), the pcDNA-FGFR1-mCherry and pcDNA-ErbB1-YFP; 2), the pcDNA-ErbB1-YFP and pcDNA-ErbB1-mCherry; or 3), the pcDNA-ErbB2-YFP and pcDNA-ErbB2-mCherry.
Production of mammalian plasma membrane vesicles
We used two types of vesiculation buffers. The vesiculation buffer developed by Scott (23) was used to vesiculate HEK293T cells, and the chloride salt buffer (24) was used to produce plasma-membrane-derived vesicles from CHO cells. We have demonstrated that the method of vesicle production has no statistically significant effects on the measured FRET efficiencies (25).
HEK293T cells were rinsed once with phosphate-buffered saline (PBS), pH 7.4, containing 0.75 mM calcium chloride and 0.5 mM magnesium chloride (CM-PBS), and incubated with 1 mL of vesiculation buffer for 2 h at 37°C. The vesiculation buffer consisted of CM-PBS with 25 mM formaldehyde, 0.5 mM 1,4-dithiotreitol, and a protease inhibitor cocktail (complete mini EDTA-free tabs, Roche Applied Science). To quench the formaldehyde after vesiculation, glycine solution in PBS was added to the vesiculation buffer to a final concentration of 0.125 M. A large number of vesicles were produced after 1.5 h.
CHO cells were rinsed twice with 30% PBS (pH 7.4), and incubated with 1 mL of chloride salt vesiculation buffer overnight at 37°C. The vesiculation buffer consisted of 200 mM NaCl, 5 mM KCl, 0.5 mM MgSO4, 0.75 mM CaCl2, 100 mM bicine, and protease inhibitor cocktail (complete mini-EDTA-free tabs, Roche Applied Science) adjusted to a pH of 8.5. After 12 h, the vesicles were transferred into four-well chambered coverslips (Nunc Lab-Tek II, Sigma-Aldrich, St. Louis, MO) for imaging.
Fluorescence image acquisition
Vesicles were imaged using a Nikon Eclipse confocal laser scanning microscope using a 60× water immersion objective. All the images were collected and stored at a 512 × 512 resolution. Each vesicle was imaged in three distinct scans: donor, FRET, and acceptor scans. The donor scan was used to excite YFP at 488 nm and to collect YFP emission in the 500–530 nm range. The acceptor scan was used to excite the acceptor at 543 nm and its emission spectrum was collected in the range >650 nm. For the FRET scan, YFP was excited and the emission of mCherry was collected in the 565–615 nm range. The imaged vesicles exhibited uniform fluorescence intensities, which allowed us to determine the concentrations of the fluorescent proteins in the membrane using solutions of purified YFP and mCherry solutions of known concentration. The fluorescent protein solutions were prepared as described previously (21,26). They were imaged in the microscope using the same settings as above, to allow direct comparison of solution and vesicle intensities. The FRET efficiencies in each vesicle were determined using the QI-FRET method, as described in detail previously (22,27,28), and are shown as a function of acceptor concentration (see Figs. 3 and 4). The FRET efficiencies for each vesicle were calculated using Eq. 10,
| (10) |
Figure 4.
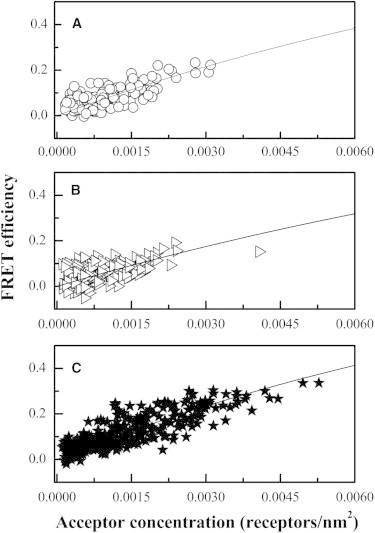
Fits of the model for monomer proximity FRET to the measured FRET efficiencies, yielding the optimal distances of closest approach, L, shown in Table 1. (A) truncated ErbB1 labeled with either YFP or mCherry in CHO derived vesicles, (B) truncated ErbB2 labeled with either YFP and mCherry in HEK 293T derived vesicles, and (C) truncated ErbB1 labeled with YFP and FGFR1 labeled with mCherry in CHO derived vesicles.
The intensities ID, IFRET, and IA, are the intensities measured for each vesicle in the donor, FRET, and acceptor channels, respectively. The parameters βD and βA are the donor and acceptor bleed-through coefficients, obtained by imaging the purified YFP and mCherry solutions, as described elsewhere (29). The gauge factor, GF, relates the sensitized emission of the acceptor to the quenching of the donor and is calculated by analyzing vesicles loaded with a soluble linked YFP-mCherry construct (21).
Results and Discussion
Predictions for proximity FRET
The proximity contribution to FRET measurements of interactions between membrane proteins in cellular membranes is quite substantial, and it needs to be accounted for. Although the proximity-FRET contribution has been characterized in lipid bilayers when the donor and the acceptor are small organic molecules (17,30), there are no assessments of this effect when bulky fluorescent proteins are used. Steady-state FRET measurements of membrane protein interactions using fluorescent proteins are often performed (8,9,31,32), and thus the lack of understanding of proximity FRET in this case is a major obstacle for future progress. To start bridging this gap, we calculate here the theoretical proximity contribution while accounting for the finite size of the fluorophores and the oligomeric state of the membrane protein complexes. We create the predictions as a function of acceptor concentration, as this is the relevant parameter (for fixed d, R0, and L) that determines the magnitude of the proximity FRET (15). We accomplish this by generating 40,000 different configurations for each acceptor concentration and applying Eqs. 1–5, accounting for the interoligomeric donor-to-acceptor distances.
In Fig. 1, we show the simulations for proximity FRET for monomers (solid line), dimers (dashed line), trimers (dotted line), and tetramers (dash-dotted line). Predictions are for monomers with an exclusion radius of 1.4 nm and for dimers, trimers, and tetramers with an exclusion radius of 1.4 nm and a distance of 5 nm between fluorophores. We see that in all cases, the proximity FRET increases when the acceptor concentration is increased. An important novel result of this simulation is the fact that the proximity contribution decreases with the oligomer size. This effect is substantial, as the contribution for a tetramer is less than half the contribution of the case of monomeric proteins. We can rationalize these results with the simple notion that the large oligomer acts as a barrier to the close approach of the acceptors contributing to proximity FRET. Thus, the distances between these acceptors and the central donor are larger than in the case of the monomer, and the proximity-FRET contribution is lower.
Fig. 2 shows the predictions for the case of monomer-dimer equilibrium. Predictions were generated for different values of the dimerization free energies. As the free energies of dimerization vary from −1 kcal/mole to −5 kcal/mole, the predictions move from a monomer-like proximity to a dimer-like proximity. Thus, the proximity contribution is a function of the dimerization propensity.
Figure 2.
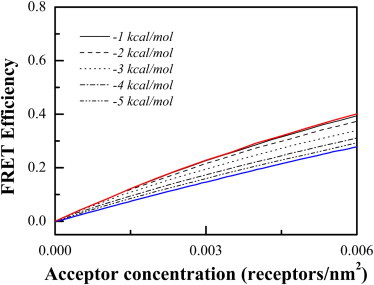
Predictions for proximity FRET in the case of monomer-dimer equilibrium, for different values of the dimerization Gibbs free energy. (Red line) 100% monomer. (Blue line) 100% dimer.
As discussed in Materials and Methods, simulations for all cases shown in Figs. 1 and 2 were carried out for various donor/acceptor ratios, and here we show the averaged results. Our simulations (not shown) reveal a very weak dependence on this ratio (results were within 3%). Thus, like in the monomer case (15), the acceptor concentration is the principal parameter that controls the magnitude of the proximity FRET in the oligomeric cases.
Comparison with experiments: the monomer case
The QI-FRET method, which has been described in detail previously (22,25,27,28,33), allows rigorous measurements of FRET efficiencies as a function of concentration. The method yields the FRET efficiency and the donor and acceptor concentrations in each vesicle. In these experiments, mammalian cells are transfected with plasmids encoding for the membrane proteins of interest, tagged with fluorescent proteins. After expression, vesicles are produced, derived from the plasma membranes of the cells, as discussed in Materials and Methods. We analyze 200–600 individual plasma-membrane-derived vesicles in each experiment, imaging a thin slice through the equator of each vesicle. Because the distribution of the membrane proteins in the vesicles is homogeneous, the fluorescence of the vesicles can be compared to the fluorescence of solutions of purified fluorescent proteins, allowing the determination of the donor and acceptor concentrations and the FRET efficiency. Therefore, this method can be used for the experimental assessment of proximity FRET in plasma-membrane-derived vesicles.
Using this technique, we sought to verify the proximity-FRET calculations presented in this article. A direct verification of the predictions can be carried out for monomeric proteins, as the measured FRET in this case will be equal to the proximity FRET. In this case, one needs to measure FRET between two proteins that do not interact, when one is labeled with a donor and the second with the acceptor. These proteins can be identical and have the property to not self-associate into dimers or higher-order oligomers, or they can be two different noninteracting proteins. A problem arises, however, in that currently there are no known adequately characterized monomeric membrane proteins. Historically, in this field of research, the TM domain of glycophorin A (GpA) has been used as a control for a constitutive dimer, whereas a G83I mutant of GpA has been used as a weakly interacting control (34). However, this behavior is derived from studies in detergents or pure lipid bilayers, and GpA dimerization was recently shown to be very sensitive to lipid composition (35). In fact, GpA is a rather weak dimer in mammalian membranes, and the G83I mutation does not cause a strong dimer destabilization in the complex plasma membrane environment (L. Chen, S. Sarabipour, P. Byrne and K. Hristova, unpublished). Thus, it is not clear what proteins should be selected as monomeric controls in the experiments.
As we work with RTKs, we searched for RTK constructs that do not form homodimers or heterodimers. We engineered plasmid DNA constructs that encoded for the extracellular and TM domains of different RTKs, tagged with donor or acceptors, and we determined the FRET efficiencies with the QI-FRET method. We sought pairs that 1), give FRET that is lower than the FRET for other proteins we have worked with; 2), give FRET that is close to the monomer prediction; and 3), give similar FRET. In three cases—1), truncated ErbB1 labeled with either YFP or mCherry; 2), truncated ErbB2 labeled with either YFP or mCherry; and 3), truncated ErbB1 labeled with YFP and FGFR1 labeled with mCherry—we observed FRET that satisfied these requirements. In all three cases, the intracellular domains of these receptors were removed, and substituted with either YFP or mCherry, connected via a flexible linker to the TM domain. Protein constructs are shown in Fig. 3 A, and the measured FRET efficiency for the three experiments is shown in Fig. 3 B. All three cases display overlapping measured FRET efficiencies as a function of acceptor concentration. Furthermore, FRET is lower when compared to other interacting RTK proteins that we have studied in the past with quantitative FRET techniques (25,28,33). Thus, the measured FRET efficiencies strongly suggest that the truncated ErbB1 and ErbB2 constructs do not homodimerize, and that the truncated ErbB1 and FGFR1 constructs do not heterodimerize.
Next, we fitted each individual data set while optimizing for the distance of closest approach between fluorophores, L, using Eqs. 6, 8, and 9. The data and the fits are shown in Fig. 4. The best-fit values of L are shown in Table 1, along with the average. The minimum distance of closest approach should depend on 1), the size of the fluorescent proteins, and 2), the size and shape of the RTKs to which the fluorophore is linked. The optimal values in Table 1 are ∼3 nm, comparable to the size of the fluorescent proteins. Thus, it appears that the extracellular glycosylated domains of the RTKs do not significantly affect the measured distance of closest approach, L, with the possible exception of ErbB2 (see Table 1).
Table 1.
Distances of close approach, L, that yield the best fit of the model to the experimental data
In Table 1, we show the fit when our model, given by Eqs. 6, 8, and 9, is used, along with the fit produced by the model of Snyder and Freire, given by Eqs. 6–8. We see that the fit results are very similar and within experimental error, suggesting that both models can be used in future work.
In this study, we employed ErbB proteins comprising only the extracellular and transembrane domain, ErbB1-ECTM and ErbB2-ECTM, and excluded the intracellular domain. Full-length ErbB1 and ErbB2 have been reported to form clusters and preformed homodimers in the absence of ligand (36–42). However, dimerization is believed to be mediated by the intracellular domain, which is excluded here (43,44). This is consistent with the observations that the purified extracellular regions of ErbB1 and ErbB2 do not form dimers at high concentration in solution or in x-ray crystal structures (45–48). The ErbB1 extracellular domain takes on a tethered conformation in the absence of ligand and functions in an autoinhibitory manner. For the case of ErbB2, the extracellular domain adopts an extended conformation that likely inhibits homodimerization (49). Although one study (50) reports on reversible dimerization of ErbB1 lacking the intracellular domain in CHO cells, the majority of the published structural, biochemical, and functional studies suggest that ErbB receptors that lack intracellular domains are monomeric in the absence of ligand, consistent with our results.
Conclusion
Here, we present predictions for proximity FRET, for the cases of membrane monomers, dimers, trimers, and tetramers, and we verify this approach by measuring the proximity FRET for monomeric membrane proteins in plasma-membrane-derived vesicles. The predictions that we present here can be used to correct the measured FRET efficiencies when fluorescent proteins are used in steady-state FRET experiments, such that the efficiencies do not contain contributions due to nonspecific interactions. The computational tools described in this article advance the FRET-based methodologies used to study interactions between membrane proteins. As membrane protein interactions underlie many important cellular processes, these tools should have a broad utility in membrane protein research.
Acknowledgments
We thank Dr. Moosa Mohammadi for the FGFR1 plasmid.
This work was supported by National Institutes of Health grants GM095930 to K.H. and GM099321 to D.L., and by a National Science Foundation Graduate Research Fellowship (DGE-1232825) to C.K.
Footnotes
Christopher King and Sarvenaz Sarabipour contributed equally to this work
Supporting Material
References
- 1.Schlessinger J. Cell signaling by receptor tyrosine kinases. Cell. 2000;103:211–225. doi: 10.1016/s0092-8674(00)00114-8. [DOI] [PubMed] [Google Scholar]
- 2.He L., Hristova K. Physical-chemical principles underlying RTK activation, and their implications for human disease. Biochim. Biophys. Acta. 2012;1818:995–1005. doi: 10.1016/j.bbamem.2011.07.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lemmon M.A., Schlessinger J. Cell signaling by receptor tyrosine kinases. Cell. 2010;141:1117–1134. doi: 10.1016/j.cell.2010.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Shi Y., Karon B.S., Thomas D.D. Phospholamban-dependent effects of C12E8 on calcium transport and molecular dynamics in cardiac sarcoplasmic reticulum. Biochemistry. 1996;35:13393–13399. doi: 10.1021/bi9614085. [DOI] [PubMed] [Google Scholar]
- 5.Young H.S., Jones L.R., Stokes D.L. Locating phospholamban in co-crystals with Ca2+-ATPase by cryoelectron microscopy. Biophys. J. 2001;81:884–894. doi: 10.1016/S0006-3495(01)75748-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kenworthy A.K., Edidin M. Distribution of a glycosylphosphatidylinositol-anchored protein at the apical surface of MDCK cells examined at a resolution of <100 Å using imaging fluorescence resonance energy transfer. J. Cell Biol. 1998;142:69–84. doi: 10.1083/jcb.142.1.69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kenworthy A.K., Petranova N., Edidin M. High-resolution FRET microscopy of cholera toxin B-subunit and GPI-anchored proteins in cell plasma membranes. Mol. Biol. Cell. 2000;11:1645–1655. doi: 10.1091/mbc.11.5.1645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Singh D.R., Mohammad M.M., Raicu V. Determination of the quaternary structure of a bacterial ATP-binding cassette (ABC) transporter in living cells. Integr Biol (Camb) 2013;5:312–323. doi: 10.1039/c2ib20218b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Raicu V., Stoneman M.R., Saldin D.K. Determination of supramolecular structure and spatial distribution of protein complexes in living cells. Nat. Photonics. 2009;3:107–113. [Google Scholar]
- 10.Chen H.M., Puhl H.L., 3rd, Ikeda S.R. Estimating protein-protein interaction affinity in living cells using quantitative Förster resonance energy transfer measurements. J. Biomed. Opt. 2007;12:054011. doi: 10.1117/1.2799171. [DOI] [PubMed] [Google Scholar]
- 11.Förster T. Intermolecular energy migration and fluorescence. Ann. Phys. 1948;2:55–75. [Google Scholar]
- 12.Shaner N.C., Steinbach P.A., Tsien R.Y. A guide to choosing fluorescent proteins. Nat. Methods. 2005;2:905–909. doi: 10.1038/nmeth819. [DOI] [PubMed] [Google Scholar]
- 13.Rizzo M.A., Springer G.H., Piston D.W. An improved cyan fluorescent protein variant useful for FRET. Nat. Biotechnol. 2004;22:445–449. doi: 10.1038/nbt945. [DOI] [PubMed] [Google Scholar]
- 14.Piston D.W., Kremers G.J. Fluorescent protein FRET: the good, the bad and the ugly. Trends Biochem. Sci. 2007;32:407–414. doi: 10.1016/j.tibs.2007.08.003. [DOI] [PubMed] [Google Scholar]
- 15.Wolber P.K., Hudson B.S. An analytic solution to the Förster energy transfer problem in two dimensions. Biophys. J. 1979;28:197–210. doi: 10.1016/S0006-3495(79)85171-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wimley W.C., White S.H. Determining the membrane topology of peptides by fluorescence quenching. Biochemistry. 2000;39:161–170. doi: 10.1021/bi991836l. [DOI] [PubMed] [Google Scholar]
- 17.Posokhov Y.O., Merzlyakov M., Ladokhin A.S. A simple “proximity” correction for Förster resonance energy transfer efficiency determination in membranes using lifetime measurements. Anal. Biochem. 2008;380:134–136. doi: 10.1016/j.ab.2008.05.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.You M., Li E., Hristova K. Förster resonance energy transfer in liposomes: measurements of transmembrane helix dimerization in the native bilayer environment. Anal. Biochem. 2005;340:154–164. doi: 10.1016/j.ab.2005.01.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Snyder B., Freire E. Fluorescence energy transfer in two dimensions. A numeric solution for random and nonrandom distributions. Biophys. J. 1982;40:137–148. doi: 10.1016/S0006-3495(82)84468-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Freire E., Snyder B. Quantitative characterization of the lateral distribution of membrane proteins within the lipid bilayer. Biophys. J. 1982;37:617–624. [PMC free article] [PubMed] [Google Scholar]
- 21.Li E., Placone J., Hristova K. Quantitative measurements of protein interactions in a crowded cellular environment. Anal. Chem. 2008;80:5976–5985. doi: 10.1021/ac800616u. [DOI] [PubMed] [Google Scholar]
- 22.Chen L., Novicky L., Hristova K. Measuring the energetics of membrane protein dimerization in mammalian membranes. J. Am. Chem. Soc. 2010;132:3628–3635. doi: 10.1021/ja910692u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Scott R.E. Plasma membrane vesiculation: a new technique for isolation of plasma membranes. Science. 1976;194:743–745. doi: 10.1126/science.982044. [DOI] [PubMed] [Google Scholar]
- 24.Del Piccolo N., Placone J., Hristova K. Production of plasma membrane vesicles with chloride salts and their utility as a cell membrane mimetic for biophysical characterization of membrane protein interactions. Anal. Chem. 2012;84:8650–8655. doi: 10.1021/ac301776j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Sarabipour S., Hristova K. Glycophorin A transmembrane domain dimerization in plasma membrane vesicles derived from CHO, HEK 293T, and A431 cells. Biochim. Biophys. Acta. 2013;1828:1829–1833. doi: 10.1016/j.bbamem.2013.03.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sarabipour S., King C., Hristova K. Uninduced high-yield bacterial expression of fluorescent proteins. Anal. Biochem. 2013;449C:155–157. doi: 10.1016/j.ab.2013.12.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Placone J., Hristova K. Direct assessment of the effect of the Gly380Arg achondroplasia mutation on FGFR3 dimerization using quantitative imaging FRET. PLoS ONE. 2012;7:e46678. doi: 10.1371/journal.pone.0046678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Sarabipour S., Hristova K. FGFR3 transmembrane domain interactions persist in the presence of its extracellular domain. Biophys. J. 2013;105:165–171. doi: 10.1016/j.bpj.2013.05.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bowie J.U. Membrane protein folding: how important are hydrogen bonds? Curr. Opin. Struct. Biol. 2011;21:42–49. doi: 10.1016/j.sbi.2010.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wimley W.C., White S.H. Designing transmembrane α-helices that insert spontaneously. Biochemistry. 2000;39:4432–4442. doi: 10.1021/bi992746j. [DOI] [PubMed] [Google Scholar]
- 31.Kim M., Carman C.V., Springer T.A. Bidirectional transmembrane signaling by cytoplasmic domain separation in integrins. Science. 2003;301:1720–1725. doi: 10.1126/science.1084174. [DOI] [PubMed] [Google Scholar]
- 32.Kenworthy A.K. Imaging protein-protein interactions using fluorescence resonance energy transfer microscopy. Methods. 2001;24:289–296. doi: 10.1006/meth.2001.1189. [DOI] [PubMed] [Google Scholar]
- 33.Chen L., Placone J., Hristova K. The extracellular domain of fibroblast growth factor receptor 3 inhibits ligand-independent dimerization. Sci. Signal. 2010;3:ra86. doi: 10.1126/scisignal.2001195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Russ W.P., Engelman D.M. TOXCAT: a measure of transmembrane helix association in a biological membrane. Proc. Natl. Acad. Sci. USA. 1999;96:863–868. doi: 10.1073/pnas.96.3.863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hong H., Bowie J.U. Dramatic destabilization of transmembrane helix interactions by features of natural membrane environments. J. Am. Chem. Soc. 2011;133:11389–11398. doi: 10.1021/ja204524c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Low-Nam S.T., Lidke K.A., Lidke D.S. ErbB1 dimerization is promoted by domain co-confinement and stabilized by ligand binding. Nat. Struct. Mol. Biol. 2011;18:1244–1249. doi: 10.1038/nsmb.2135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Gadella T.W.J., Jr., Jovin T.M. Oligomerization of epidermal growth factor receptors on A431 cells studied by time-resolved fluorescence imaging microscopy. A stereochemical model for tyrosine kinase receptor activation. J. Cell Biol. 1995;129:1543–1558. doi: 10.1083/jcb.129.6.1543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Martin-Fernandez M., Clarke D.T., Jones G.R. Preformed oligomeric epidermal growth factor receptors undergo an ectodomain structure change during signaling. Biophys. J. 2002;82:2415–2427. doi: 10.1016/S0006-3495(02)75585-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Sako Y., Minoghchi S., Yanagida T. Single-molecule imaging of EGFR signalling on the surface of living cells. Nat. Cell Biol. 2000;2:168–172. doi: 10.1038/35004044. [DOI] [PubMed] [Google Scholar]
- 40.Nagy P., Claus J., Arndt-Jovin D.J. Distribution of resting and ligand-bound ErbB1 and ErbB2 receptor tyrosine kinases in living cells using number and brightness analysis. Proc. Natl. Acad. Sci. USA. 2010;107:16524–16529. doi: 10.1073/pnas.1002642107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Van de Vijver M.J., Kumar R., Mendelsohn J. Ligand-induced activation of A431 cell epidermal growth factor receptors occurs primarily by an autocrine pathway that acts upon receptors on the surface rather than intracellularly. J. Biol. Chem. 1991;266:7503–7508. [PubMed] [Google Scholar]
- 42.Clayton A.H., Orchard S.G., Burgess A.W. Predominance of activated EGFR higher-order oligomers on the cell surface. Growth Factors. 2008;26:316–324. doi: 10.1080/08977190802442187. [DOI] [PubMed] [Google Scholar]
- 43.Jura N., Endres N.F., Kuriyan J. Mechanism for activation of the EGF receptor catalytic domain by the juxtamembrane segment. Cell. 2009;137:1293–1307. doi: 10.1016/j.cell.2009.04.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Thiel K.W., Carpenter G. Epidermal growth factor receptor juxtamembrane region regulates allosteric tyrosine kinase activation. Proc. Natl. Acad. Sci. USA. 2007;104:19238–19243. doi: 10.1073/pnas.0703854104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lemmon M.A., Bu Z.M., Schlessinger J. Two EGF molecules contribute additively to stabilization of the EGFR dimer. EMBO J. 1997;16:281–294. doi: 10.1093/emboj/16.2.281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Ferguson K.M., Berger M.B., Lemmon M.A. EGF activates its receptor by removing interactions that autoinhibit ectodomain dimerization. Mol. Cell. 2003;11:507–517. doi: 10.1016/s1097-2765(03)00047-9. [DOI] [PubMed] [Google Scholar]
- 47.Cho H.S., Leahy D.J. Structure of the extracellular region of HER3 reveals an interdomain tether. Science. 2002;297:1330–1333. doi: 10.1126/science.1074611. [DOI] [PubMed] [Google Scholar]
- 48.Burgess A.W., Cho H.S., Yokoyama S. An open-and-shut case? Recent insights into the activation of EGF/ErbB receptors. Mol. Cell. 2003;12:541–552. doi: 10.1016/s1097-2765(03)00350-2. [DOI] [PubMed] [Google Scholar]
- 49.Cho H.S., Mason K., Leahy D.J. Structure of the extracellular region of HER2 alone and in complex with the Herceptin Fab. Nature. 2003;421:756–760. doi: 10.1038/nature01392. [DOI] [PubMed] [Google Scholar]
- 50.Chung I., Akita R., Mellman I. Spatial control of EGF receptor activation by reversible dimerization on living cells. Nature. 2010;464:783–787. doi: 10.1038/nature08827. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


