Abstract
We invent a simple method for fabricating high-aspect-ratio, hierarchical and dynamically tunable surface patterns by harnessing localized-ridge instabilities in gold nanofilms coated on elastomer substrates (a); develop a theoretical model to calculate the critical parameters (e.g. wavelength and amplitude) for designing the new patterns (b); and demonstrate novel applications of the patterns as super-hydrophobic coatings (c) and biomimetic cell-culture substrates (d) capable of on-demand tunability.
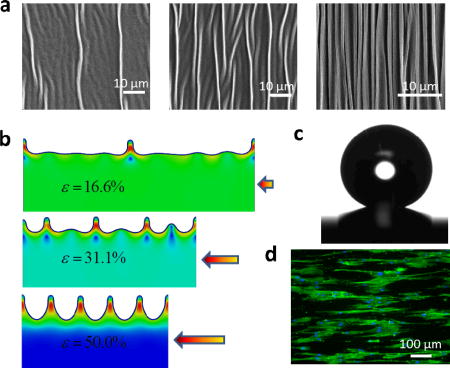
Keywords: Localized ridge, instability, hierarchical patterns, superhydrophobicity, cell alignment
Topographical patterns are of fundamental importance to materials science, physics, chemistry and biology, impacting applications as diverse as antifouling, microfluidic device design, tissue engineering, and functional surface with extraordinary adhesive, wetting and optical properties.[1–13]As a convenient and low-cost method, mechanical instabilities of thin films compressed on substrates have been intensively investigated to generate surface patterns, in which the most prominent examples include wrinkling, folding, creasing and delaminated buckling.[14–20] Despite the great promise of these instability patterns, they still suffer from a number of limitations:(i) The aspect ratios (i.e. amplitude over wavelength) of wrinkles, folds and creases are relatively small, which hinders their applications in areas that require high-aspect-ratio patterns such as super-hydrophobic coatings.[11, 14, 15, 19](ii) While delaminated buckles can have relatively high aspect ratios, the generation of delaminated patterns usually requires complicated fabrication processes such as micro-patterning adhesive regions on substrates and/or multi-step transfer of films.[10, 16, 21](iii) Most importantly, the morphologies of instability patterns are usually fixed in their final states during fabrication;[5, 22] however, in many cases it is highly desirable to be able to dynamically tune the morphologies of surface patterns. Since these limitations have significantly hampered the potential of instability patterns, it is a crucial task to invent new methods to generate large-area high-aspect-ratio patterns capable of dynamic tunability. Furthermore, hierarchy is another desirable feature for surface patterns due to the synergic effects of hierarchical structures across multiple length scales.[10, 23–27]
Here we report a simple method to fabricate larger-area high-aspect-ratio hierarchical surface patterns capable of dynamic tunability and multifunctionality. By depositing metallic nanofilms (i.e., gold, silver and aluminum) on a highly pre-stretched elastomer substrate and then relaxing the substrate in controlled manners, we can generate a rich variety of hierarchical patterns with feature sizes ranging from nanometers to micrometers. The patterns are based on a new mode of mechanical instability that combines nano-scale wrinkles and micro-scale localized ridges. The aspect ratio of the new patterns is much larger than those of wrinkles, creases, and folds. As a result, the hierarchical patterns give extremely stretchable (i.e., over 100% biaxial strain) super-hydrophobic surfaces with water contact angle over 150° and roll-off angle less than 10°.[28]Additionally, because the length scales of the hierarchical patterns are similar to those of physiologically cellular environments, the patterned surface can be used for alignment of stem cells as biomimetic cell-culture substrates. By simply stretching the elastomer substrate, one can dynamically tune the hierarchical patterns to vary the surfaces’ wettability, transmittance, and cell alignments on demand. In addition, we develop a theoretical model to calculate the initiation and evolution of localized ridges and derive scaling laws for their wavelengths, amplitudes and aspect ratios. The theoretical results can be used to guide future design of high-aspect-ratio surface patterns by harnessing localized ridges.
Figure S1 illustrates the procedure for fabricating hierarchical surface patterns. A square-shaped elastomer film, VHB acrylic 4910 with thickness of 1 mm (3M Inc., US), was stretched along two orthogonal in-plane directions by pre-strains of εpre1 and εpre2 which are defined as change in length over the undeformed length of the elastomer. Notably, either or both of the pre-strains were set to high values, ranging from 100% to 300%. The pre-strained elastomer film was then sputter-coated with a thin layer of gold film (Figure S1). The thickness of gold film can be tuned from 4nm to 31nm by varying the sputter-coating time from 30 s to 300 s (Figure S2). Thereafter, the pre-strains in the elastomer substrate were relaxed uniaxially or biaxially. As a result, the macroscopic lateral dimensions of the gold film were reduced by the same ratio as the substrate (Figure S1). Remarkably, such a simple low-cost fabrication can generate a variety of high-aspect-ratio hierarchical patterns with feature sizes ranging from nanometers to micrometers.
In order to discuss the instability patterns, we first define the strains in the film and the substrate. Denote the lateral dimensions of the gold film along two pre-strained directions as L1 and L2 at the as-deposited state and as l1 and l2 at a relaxed state. The nominal compressive strains in the gold film are defined as εf1 = (L1 − l1)/L1 and εf2 = (L2 − l2)/L2. Further denote the tensile strains in the substrate at a relaxed state as εs1 and εs2. Therefore, the nominal compressive strains in the gold film and the tensile strains in the substrate are related by εf1 = (εpre1 − εs1)/(εpre1 + 1) and εf2 = (εpre2 − εs2)/(εpre2 +1). When the substrate is fully relaxed (i.e., εs1 = εs2 = 0), the nominal compressive strains in the gold film reach maximum values of εpre1/(εpre1 + 1) and εpre2/(εpre2 + 1).
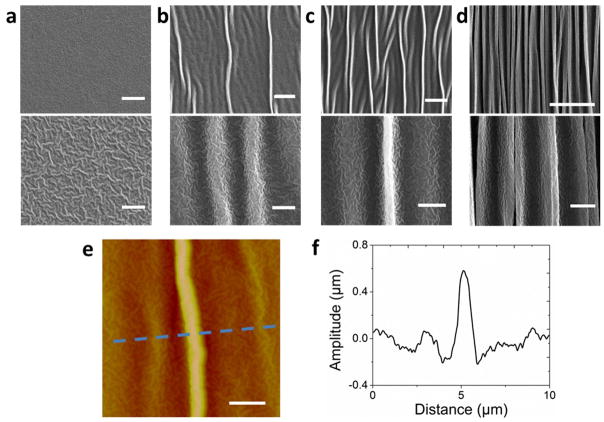
We now discuss the pattern of hierarchical ridges in a gold film of 13±1 nm generated by relaxing a uniaxially pre-strained elastomer substrate (i.e., εpre1 = 200% and εpre2 = 0). As shown in Figure 1a, the as-deposited gold film on the pre-strained elastomer substrate has already formed a random pattern of first-level wrinkles with wavelength of 110~160 nm. We find that the first-level wrinkles can also form on elastomer substrates without pre-strains and the wavelength of the wrinkles is independent of the thickness of the gold films (Figure S3). These observations indicate that the first-level wrinkles are possibly caused by modification of the elastomer surfaces by sputtered ions.[29]Thereafter, as the uniaxial pre-strain in the substrate is relaxed, the gold film reduces its width macroscopically by the same ratio as the substrate. Microscopically, when the nominal compressive strain in the gold film εf1 exceeds a critical value, a second level of wrinkles with wavelength much larger than that of the first-level wrinkles set in (Figure 1c). The wavelength of the second-level wrinkles can be calculated as[16, 30]
Figure 1. Evolution of hierarchical surface pattern of gold film on uniaxially pre-strained elastomer substrate.
The thickness of the gold film is 13±1 nm and the uniaxial pre-strain in the substrate is 200%. SEM images (top panel low resolution, bottom panel high resolution) of the gold film under nominal compressive strains of 0% (a), 5% (b), 20% (c) and 67% (d). The scale bars are 10 μm in top panels and 2 μm in bottom panels of (a)–(d). AFM image (e) of the first- and second-level wrinkles and second-level localized ridge on the gold film, and a cross-section (f) of the AFM image. The amplitude of the second-level localized ridge is significantly larger than those of adjacent second-level wrinkles. The scale bar is 2 μm in (e)
| (1) |
where Hf, μf and υf are the thickness, shear modulus, and Poisson’s ratio of the gold film, μs the shear modulus of the elastomer substrate taken to be a neo-Hookean material, and Λ = [1+(1+εpre1)2(1+εpre2)]/2(1 + εpre2). Taking Hf = 12.6 nm, μf = 27.4 GPa, υf = 0.44, εpre1 = 200 %, εpre2 = 0 %, μs= 20 kPa,[31] we obtain λwrinkle ≈ 2.91 μm, consistent with the experimental observation (Figure 1b). Since the amplitude of the first-level wrinkle is relatively small (Figure 1e and f), we assume it will not significantly modify the modulus and thickness of the gold film.
As the nominal compressive strain εf1 further increases, the amplitude of some second-level wrinkles increase more dramatically than others (Figure 1c). Now the surface pattern ceases to follow the uniform sinusoidal shape, but features a combination of second-level wrinkles and localized ridges (Figure 1c, 1f, and 1g). With further increment of εf1, more ridges form on the surface and the amplitude of the ridges increases (Figure 1d). Once the substrate is fully relaxed, a pattern of localized ridges with wavelength ~1 μm eventually develops on the surface (Figure S4). It should be noted that the localized-ridge instability is distinctly different from the period-doubling or quadrupling instability formed on substrates with relatively low pre-strains (i.e., εpre1<40%).[30, 32]Remarkably, the aspect ratio of the ridges can readily reach above 1.0 (Figure S5), much higher than those of common wrinkles, creases and folds. Furthermore, by sectioning the ridge patterns,[33] we find that the elastomer substrate deforms together with the gold film at the ridges (Figure S5). In addition, the first-level wrinkles maintain superimposed on the second-level ridges, giving a hierarchical pattern with nano-scale wrinkles and micro-scale ridges (Figure 1d).
While the localized-ridge instability has been reported before,[16, 17, 30, 34] the wavelengths λridge and the amplitudes Aridge of localized-ridge patterns have not been studied. However, both λridge and Aridge are critical parameters for the design of high-aspect-ratio surface patterns. In order to better understand the localized-ridge instability and the corresponding parameters, we develop a finite-element model for the film-substrate system with software package ABAQUS 6.11. Since the metal film is much more rigid than the elastomer substrate, the deformation in the film is relative small and in the elastic region. Therefore, we take both the film and the substrate to be neo-Hookean materials with shear moduli, μf and μs, undergoing plane-strain deformation.[30]The film–substrate systems are modeled with the hybrid quadratic elements (CPE8MH) in ABAQUS. The pseudo-dynamic method is adopted and a very small initial geometric imperfection is introduced into the model for post-buckling analysis.[30, 34] The width of the model is taken to be at least 5 times of the wavelengths of the initial wrinkles, while the depth of the substrate is taken to be more than 10 times of the wavelength. The displacement-control loading condition is used to apply pre-strains in the substrate and then to control the relaxation of the film-substrate system. The vertical displacement and the shear traction are prescribed to be zero on the bottom surface of the substrate; and the shear traction is prescribed to be zero at the vertical sides of the model.
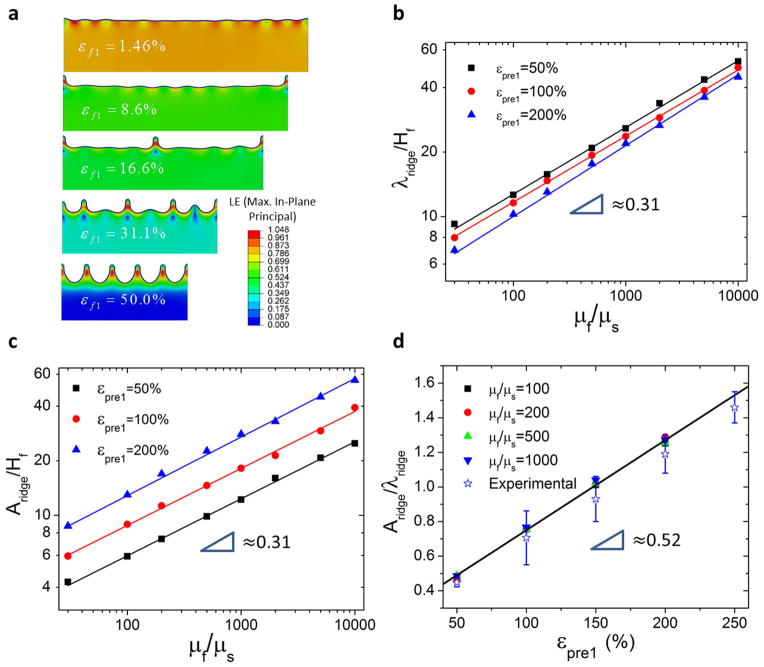
The initiation and evolution of ridges are calculated for the film-substrate system with various modulus ratios μf/μs and pre-strains εpre1. Figure 2a presents the modeling results of a film-substrate system with μf/μs = 1000 and εpre1 = 100%. The localized ridges emerge when a pattern of wrinkles is further compressed due to the relaxation of highly pre-strained substrate (Figure 2a). This is consistent with previous reports that high pre-strain of the substrate (i.e., εpre1 > 40 %) is required for the formation of localized ridges.[30, 34]Figure 2b and 2c give the calculated λridge and Aridge for film-substrate systems with substrates at the fully relaxed state (see Figure S6 for the finite-element calculation). It can be seen that the wavelengths of ridges on fully relaxed substrates approximately follow a scaling of
Figure 2. Evolution of localized ridges with the relaxation of uniaxially pre-strained substrate, and the wavelengths, amplitudes and aspect ratios of the ridges calculated by finite-element model.
The calculated evolution of the ridges in a film-substrate system with shear modulus ratio μf/μs = 1000 and pre-strain εpre1 = 100 % (a). The contour in (a) represents the maximum in-plane principal strain. The calculated wavelengths (b), amplitudes (c) and aspect ratios (d) of ridges on fully relaxed substrates as functions of μf/μs and εpre1. The experimentally measured aspect ratios of ridges match consistent with the prediction from the calculation.
| (2) |
It is interesting to observe that the scaling of λridge is similar to that of wrinkles of thin films compressed on substrates, i.e., λwrinkle/Hf ∝ (μf/μs)1/3. Furthermore, the wavelength λridge decreases with the pre-strain εpre1, so that a higher pre-strain of the substrate induces a shorter wavelength of ridges. Remarkably, the amplitudes of ridges on fully relaxed substrate also follow the scaling of
| (3) |
Consequently, the aspect ratios of ridges on fully relaxed substrates are independent of μf/μs (Figure 2d). Furthermore, we find the aspect ratio of ridges is approximately linearly related with the pre-strain, i.e.
| (4) |
Therefore, while a pre-strain over 40% in the substrate is required to induce localized ridges,[30, 34] a pre-strain over 150%can give ridges with aspect ratios over one (Figure 2d). To validate the aspect ratio predicted by Eq. (4), we measure the aspect ratios of ridges formed on fully relaxed substrates withεpre1 = 50%~250% (Figures S5); and compare the experimental and theoretical results in Figure 2d. It can be seen that the theoretical prediction matches with the experimental results consistently. The theoretical results can be used to guide the design of high-aspect-ratio patterns by harnessing the localized-ridge instability.
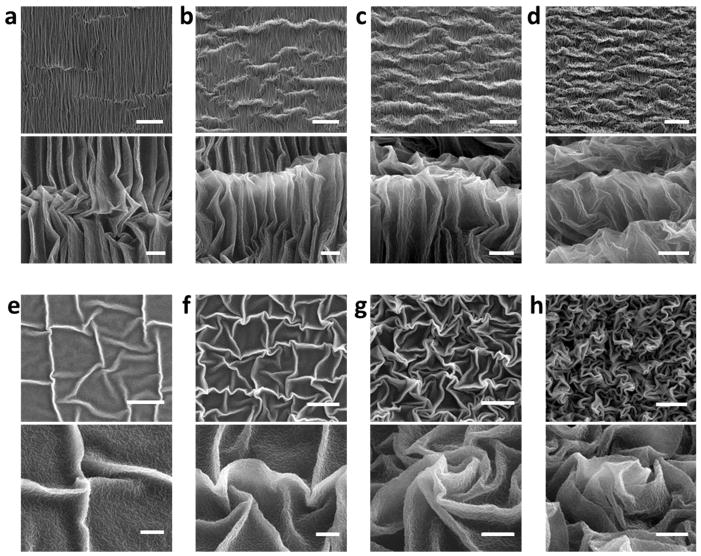
We next discuss the hierarchical patterns generated in gold films of 13±1nm by relaxing biaxially pre-strained elastomer substrates (i.e., εpre1 = εpre2 = 200 %). The first-level wrinkles with wavelength of 110~160 nm also develop in the as-deposited gold film on biaxially pre-strained elastomer substrate (Figure 1a). The biaxial pre-strains in the substrate are relaxed either sequentially or simultaneously along the two orthogonal pre-strained directions (Figure S1).[16, 35]During sequential relaxation of the substrate, the pre-strain in one direction (i.e. εpre1) is first relaxed, so that a pattern of second-level ridges develop on the film (Figure 3a). When the pre-strain in the other direction is relaxed subsequently, the pattern of parallel ridges will be deformed as an effective layer with thickness higher than the film, leading to a pattern of third-level ridges orthogonal to the previous second-level ridges (Figure 3b–d). When the pre-strain in the second direction is fully relaxed, the wavelength of the third-level ridges reaches around 8 μm and the amplitude 2~4 μm, much larger than those of the second-level ridges.
Figure 3. Evolution of hierarchical surface pattern of gold films on biaxially pre-strained elastomer substrates.
The thickness of the gold film is 13±1 nm and the biaxial pre-strains in the substrates are 200%. SEM images (top panel low resolution, bottom panel high resolution) of gold film on a substrate under sequential relaxation with εf1 = 67% and εf2 = 3% (a), 20% (b), 50% (c) and 67% (d). SEM images (top panel low resolution, bottom panel high resolution) of gold film on a substrate under simultaneous relaxation with εf1 =εf2 = 5% (e), 30% (f), 50% (g) and 67% (h). The scale bars are 10 μm in top panels and 2 μm in bottom panels of (a)–(h).
On the other hand, simultaneously relaxing the substrate generates a hierarchical surface pattern significantly different from the sequentially-relaxed one. As the biaxial pre-strains are relaxed simultaneously, second-level wrinkles and ridges develop along different directions (Figure 3e). The intersection of two ridges generates a vertex with a sharp tip (Figure 3e). Under further compression, the ridges are buckled and collapsed, which also induces more sharp vertices (Figure 3f and g). As the biaxial pre-strains are fully relaxed, the surface is featured with a pattern of buckled ridges together with sharp vertices almost evenly distributed on the surface (Figure 3g). Similar patterns have also been generated in other metallic films such as silver and aluminum by simultaneously relaxing biaxially pre-strained substrates, demonstrating the generality of our method (Figure S8a and b). It is interesting to note that these hierarchical patterns of ridges generated on highly pre-strained substrates (200%) are drastically different from the hierarchical folds caused by moderate film-substrate mismatch strain (~8%) reported before.[36] The contrast indicates that the magnitude of pre-strains in the substrates plays an important role in generating instability patterns.
Furthermore, since these high-aspect-ratio hierarchical patterns are generated on compliant elastomer substrates, they can be dynamically tuned by simply stretching the elastomer substrates along the pre-strained directions. Stretching the substrate will reduce the amplitude of the ridges and increase their wavelength, thereby reducing the aspect ratio of the pattern (Figure S7). However, once the stretched substrate is relaxed again, the previous high-aspect-ratio hierarchical pattern can be restored. In addition, as long as the applied strains on the substrate are significantly lower (e.g.,100%) than the pre-strains, the gold film can maintain its integrity over multiple stretch-relaxation cycles in applications, leading to dynamic tunability of the hierarchical patterns.
A combination of high aspect ratio, nano-micro-hierarchy, dynamic tunability, and giant stretchability promises extraordinary functions of the new surface patterns. We next discuss the application of the new patterns as biomimetic cell-culture substrates to present dynamic topographical cue to the culture of stem cells. The study of cell behavior in response to surface topography has important implications in tissue engineering and regenerative medicine.[37–43] Native extracellular matrix abounds with nano-micro-scale topographical features that vary over time.[44]Existing works on cell behaviors in response to surface topography are mostly based on surface patterns that are fixed over time.[5, 42, 45–47] A recent study reported that varying wrinkles on polydimethylsiloxane (PDMS) can control stem cell alignments, but the wavelength of the wrinkles is ~27.2 μm and the aspect ratio only ~0.184.[7]However, patterns with higher aspect ratios and multi-scale biomimetic topography can potentially provide a microenvironment to enhance cell alignment, increase cell density on scaffold and improve cell-cell contact.[48, 49]
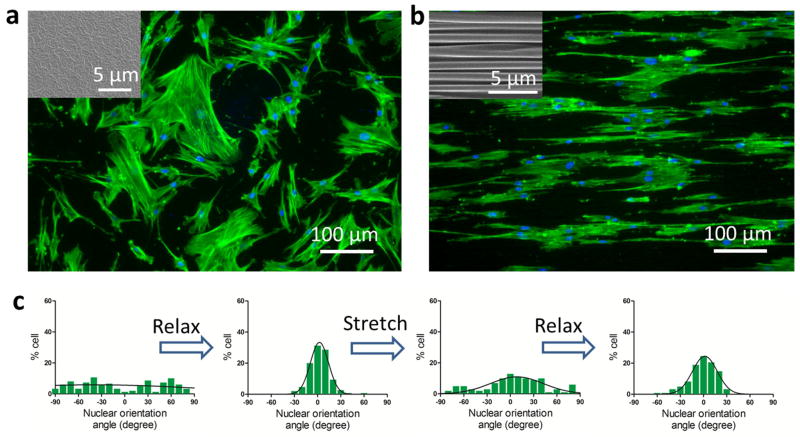
Here we show that the high-aspect-ratio hierarchical patterns can dynamically tune the alignment of stem cells by reversibly stretching and relaxing the substrate. A gold film of 13±1 nm was deposited on a uniaxially pre-strained elastomer substrate (i.e. εpre1 = 100 % and εpre2 = 0). Human mesenchymal stem cells (hMSC) were cultured on the gold film at 37°C for 2 days while maintaining the substrate at the pre-strained state. On the flat gold film, the hMSC were randomly orientated (Figure 4a and c). When the pre-strain in the substrate was relaxed and the hMSC cultured further for 2 days, the hMSCs elongated and aligned along the hierarchical ridges, with the long axis of their nuclei seldom deviating more than ~15° from the ridge direction (Figure 4b and c). The hMSC alignment is consistent with previous findings of cell alignments on PDMS nanogratings.[47]Zyxin has been identified as one of the molecular players involved in the underlying mechanism of altering the focal adhesion remodeling of hMSC in response to the nanogratings.[50]In addition, the random and aligned orientations of the hMSC could be repeatedly manipulated by simply stretching and relaxing the substrate (Figure 4c). Furthermore, since the dimensions of the hMSC extend beyond 10 μm in both the short and long axes and the wavelength of the ridges is ~1 μm, the cells grow across multiple ridges in the current study. This could be significantly different from the case in Ref 7, where cells may grow within wrinkles with wavelength of ~27.2 μm.
Figure 4. Dynamically tuning stem-cell alignment on the hierarchical pattern by uniaxially stretching and relaxing the elastomer substrate.
Optical microscopic images of stem cells on flat (a) and hierarchically patterned (b) surfaces. Stem cells are randomly oriented on the flat gold film, but aligned along the ridges of the hierarchical pattern. The distribution of the nuclei orientation of stem cells on the gold film on relaxed or stretched substrate (c). By relaxing or stretching the substrate, one can reversibly generate or eliminate the hierarchical surface pattern, thereby aligning stem cells or randomizing their orientations on demand.
The new patterns can also be used as stretchable coatings capable of superhydrophobicity and tunable wettability and transmittance. We generated the pattern by simultaneously relaxing biaxially pre-strained substrates (Hf = 13 ± 1 nm and εpre1 = εpre2 = 250 %), so that the resultant pattern, combining nano-scale wrinkles, high-aspect-ratio micro-scale ridges and sharp vertices, potentially mimicked the surface structures of superhydrophobic leaves.[1] To enhance its hydrophobicity, the as-deposited gold film was also hydrophobilized by (heptadecafluoro-1,1,2,2-tetrahydrodecyl) trichlorosilane, prior to relaxing the substrate.[9]Figure 5a shows that water drops placed on the pattern have an average static contact angle of 162° and roll-off angle of 2°, indicating the pattern indeed gives a super-hydrophobic coating. Video S1 further supports that water drops placed on the patterns can easily roll off under small tilting angles of the surface. In addition, we biaxially stretch the fully relaxed substrate and then place water drops on the deformed pattern. Remarkably, when the biaxial strain in the substrate is within 100%, the static contact angle of water drop is kept above 150° and roll-off angle below 10° (Figure 5a), meaning that the new super-hydrophobic coating is extremely stretchable. While many previous studies attempted to create superhydrophobic surfaces using thin-film instabilities;[10, 11, 16] to our knowledge, such a combination of high contact and low roll-off angles and giant stretchability have not been achieved.
Figure 5. Super-hydrophobicity, tunable wettability and transmittance of the hierarchical pattern of gold film on biaxially pre-strained substrate with simultaneous relaxation.
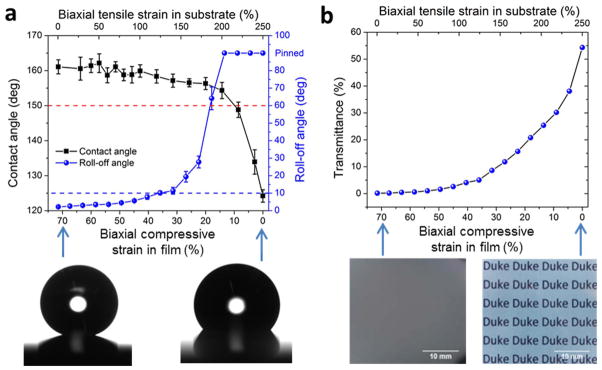
The thickness of the gold film is 13±1 nm and the biaxial pre-strains in the substrates are 250%. The static contact and roll-off angles of water drops on the pattern as functions of the biaxial compressive strain in the gold film or tensile strain in the substrate (a). The transmittance of the pattern on substrate as a function of the biaxial compressive strain in the gold film or tensile strain in the substrate (b).
If the substrate is biaxially stretched beyond 100% strain, the contact angle of water drops would quickly decrease to 124° (Figure 5a) while the roll-off angle increases to 90°, due to significant diminishment of the hierarchical pattern (Figure S7). Notably, this dramatic variation of contact and roll-off angles can be controlled by simply stretching the substrate, leading to coatings with dynamically tunable wettability. Furthermore, while the as-deposited gold film is optically semi-transparent, the patterned surface is non-transparent due to the absorption of incident light by the hierarchical structure. Similarly, the transmittance of the hierarchical structure can be tuned from 0.2% to 54.3% by biaxially stretching the substrate (Figure 5b). To demonstrate the generality of the current method, we further show that other metallic films such as silver on highly pre-strained elastomer substrates can also give similar superhydrophobicity and tunable wettability (Figure S8c).
In summary, we demonstrate a simple low-cost method to generate high-aspect-ratio hierarchical surface patterns. The new patterns are achieved by harnessing the wrinkling and localized-ridge instabilities of gold films coated on highly pre-strained elastomer substrates. The high aspect ratio and nano-micro-hierarchy of the new patterns lead to extraordinary functions including biomimetic cell-culture substrates and stretchable super-hydrophobic coatings. Mechanical stretch of the elastomer substrate can vary the surface patterns, thereby tuning cell alignment, wettability, and optical transmittance of the surfaces on demand. We further develop a theoretical model to calculate the initiation and evolution of localized ridges in film-substrate systems with various modulus ratios and pre-strains. We find that the wavelength and amplitude of the ridge patterns follow the same scaling law and the aspect ratio of the ridges is linearly related to the pre-strain. The experimental and theoretical results presented here will guide future design of novel surface patterns by harnessing mechanical instabilities.
Experimental Section
Fabrication of hierarchical surface patterns
The hierarchical surface patterns were fabricated using an elastomer film (VHB 4910, 3M Inc., US) and a thin layer of gold film. The VHB film was cut into square substrates with dimensions of 5cm by 5cm. Thereafter, the substrate is stretched along two orthogonal in-plane directions to specified pre-strains of εpre1 and εpre2. The pre-strained elastomer substrate was then sputter-coated with a layer of gold film using Vacuum Sputter Coater (Denton Desk IV, USA) for 30s, 60s, 100s or 300s. After coating, the pre-strained sample was relaxed uniaxially or biaxially following Figure S1.
Characterization of the morphology of hierarchical surface patterns
To characterize the surface patterns, we performed scanning electron microscope (SEM) and atomic force microscope (AFM) on the prepared samples. The SEM images were obtained with 2000–50000 magnifications, 3–20 kV beam, and 10–12 mm working distance (FEI XL30 SEM-FEG, USA). The AFM images were taken in tapping mode with Digital Instrument as dimension 3100, Bruker, Germany. The software used for data acquisition and analysis is NanoScope Analysis (Bruker, Germany). To determine the wavelength of the ridges, we performed two-dimensional fast Fourier transform of SEM images of ridge patterns using MATLAB (Figure S4). To measure the amplitude of the ridges, we used either AFM images of ridge patterns (Figure 1e) or SEM images of cross-section of ridge patterns (Figure S5). The amplitude was calculated as an average of amplitudes of over 10 ridges.
Sample preparing and measurement of water contact angle
The super-hydrophobic hierarchical films were prepared by immersing the as-deposited gold/silver/aluminum films into the saturated vapor of (heptadecafluoro-1,1,2,2-tetrahydrodecyl) trichlorosilane for at least 2 hours and then relaxing the biaxial pre-strains in the elastomer substrate simultaneously. The static contact angles and roll-off angles were measured using a Ramé-Hart goniometer equipped with a dispensing needle. A water droplet (5 μL) was firstly generated by the manually dispensing needle close to sample surface. The sessile droplet was formed by moving the substrate to slowly approach the droplet. The water drops were gently removed by compressive air to dry the film surface for repeated contact angle experiments. The contact angle was analyzed and calculated automatically by the software embedded in Ramé-Hart goniometer. For each data point in the figures, at least five drops at different locations were measured and the mean values and stand derivations were calculated. The roll-off angles were captured by tilting the stage very slowly until water droplets (10 μL) started rolling on the sample surface.
Transmittance measurement
The transmittance of gold film on elastomer films are measured using a UV-VIS-NIR Spectrophotometer (Shimadzu UV-3600, USA) at a wavelength of 550 nm in visible range.
Human mesenchymal stem cell culture
Bone marrow–derived hMSCs were provided by Tulane University Health Sciences Center. Cells were cultured in α-minimum essential medium with 20% fetal bovine serum and 1% penicillin/streptomycin at 37 °C and 5% CO2. The 4–6th passages of hMSCs were used in this study. Before cell seeding, the film was sterilized with 70% ethanol and coated with bovine skin collagen solution (Sigma Aldrich, USA) at 20μg/cm2. Cells were seeded on relaxed gold-sputtered elastomer film at 5000 cells/cm2 after pre-stretch. The sputtering time was either 100s or 200s and the pre-strain was 0%, 100% or 200%. For dynamically switching patterns in situ, cells were cultured on one pattern for 2 days before a custom-designed stretcher was used to change the pattern from flat to patterned or vice versa.
Cell staining, Imaging, and Quantification of nuclear orientation angle
Cells were fixed with 4% paraformaldehyde at room temperature for 30 min before permeabilized with 1% triton X-100 (Sigma Aldrich, USA) and stained for F-actin with FITC-phalloidin (Invitrogen, USA) and nuclei with DAPI (Invitrogen, USA) for another 30 min. Three sets of images across each sample were taken using Nikon Eclipse TE2000-U fluorescence inverted microscope for green (F-actin) and blue (nuclei) channels. Cell alignment was analyzed by measuring the orientation angle of the long axis of the nuclei relative to the ridge direction (in the case of patterned surface) or any direction (in the case of flat surface) using NIH ImageJ software. More than 50 nuclei were analyzed in each image. The frequency distribution of >100 nuclear orientation angles was plotted with GraphPad Prism software and Guassian fits were created for the distributions.
Supplementary Material
Acknowledgments
The work was supported by NSF CAREER Award CMMI-1253495, NIH UH2 TR000505 and NIH Common Fund for the Microphysiological Systems Initiative. K.W.L. acknowledged the financial support from NIH EB015300. C.C. acknowledged the financial support from the Australian National Universality.
References
- 1.Neinhuis C, Barthlott W. Annals of Botany. 1997;79:667. [Google Scholar]
- 2.Long CJ, Finlay JA, Callow ME, Callow JA, Brennan AB. Biofouling. 2010;26:941. doi: 10.1080/08927014.2010.531390. [DOI] [PubMed] [Google Scholar]
- 3.Shivapooja P, Wang Q, Orihuela B, Rittschof D, López GP, Zhao X. Advanced Materials. 2013;25:1430. doi: 10.1002/adma.201203374. [DOI] [PubMed] [Google Scholar]
- 4.Ohzono T, Monobe H, Shiokawa K, Fujiwara M, Shimizu Y. Soft Matter. 2009;5:4658. [Google Scholar]
- 5.Chen A, Lieu DK, Freschauf L, Lew V, Sharma H, Wang J, Nguyen D, Karakikes I, Hajjar RJ, Gopinathan A, Botvinick E, Fowlkes CC, Li RA, Khine M. Advanced Materials. 2011;23:5785. doi: 10.1002/adma.201103463. [DOI] [PubMed] [Google Scholar]
- 6.Vajpayee S, Khare K, Yang S, Hui CY, Jagota A. Advanced Functional Materials. 2011;21:547. [Google Scholar]
- 7.Guvendiren M, Burdick JA. Advanced Healthcare Materials. 2013;2:155. doi: 10.1002/adhm.201200105. [DOI] [PubMed] [Google Scholar]
- 8.Chan EP, Smith EJ, Hayward RC, Crosby AJ. Advanced Materials. 2008;20:711. [Google Scholar]
- 9.Shu Y, Krishnacharya K, Pei-Chun L. Advanced Functional Materials. 2010;20:2550. [Google Scholar]
- 10.Zhang Z, Zhang T, Zhang YW, Kim KS, Gao H. Langmuir. 2011;28:2753. doi: 10.1021/la203934z. [DOI] [PubMed] [Google Scholar]
- 11.Lin PC, Yang S. Soft Matter. 2009;5:1011. [Google Scholar]
- 12.Genzer J, Groenewold J. Soft Matter. 2006;2:310. doi: 10.1039/b516741h. [DOI] [PubMed] [Google Scholar]
- 13.Wang Q, Tahir M, Zang J, Zhao X. Advanced Materials. 2012;24:1947. doi: 10.1002/adma.201200272. [DOI] [PubMed] [Google Scholar]
- 14.Bowden N, Brittain S, Evans AG, Hutchinson JW, Whitesides GM. Nature. 1998;393:146. [Google Scholar]
- 15.Kim J, Yoon J, Hayward RC. Nature Materials. 2009;9:159. doi: 10.1038/nmat2606. [DOI] [PubMed] [Google Scholar]
- 16.Zang J, Ryu S, Pugno N, Wang Q, Tu Q, Buehler MJ, Zhao X. Nature Materials. 2013;12:321. doi: 10.1038/nmat3542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ebata Y, Croll AB, Crosby AJ. Soft Matter. 2012;8:9086. [Google Scholar]
- 18.Mei H, Landis CM, Huang R. Mechanics of Materials. 2011;43:627. [Google Scholar]
- 19.Wang Q, Zhang L, Zhao X. Physical Review Letters. 2011;106:118301. doi: 10.1103/PhysRevLett.106.118301. [DOI] [PubMed] [Google Scholar]
- 20.Chung JY, Nolte AJ, Stafford CM. Advanced Materials. 2011;23:349. doi: 10.1002/adma.201001759. [DOI] [PubMed] [Google Scholar]
- 21.Rogers JA, Someya T, Huang Y. Science. 2010;327:1603. doi: 10.1126/science.1182383. [DOI] [PubMed] [Google Scholar]
- 22.Fu CC, Grimes A, Long M, Ferri CG, Rich BD, Ghosh S, Ghosh S, Lee LP, Gopinathan A, Khine M. Advanced Materials. 2009;21:4472. [Google Scholar]
- 23.Efimenko K, Rackaitis M, Manias E, Vaziri A, Mahadevan L, Genzer J. Nature Materials. 2005;4:293. doi: 10.1038/nmat1342. [DOI] [PubMed] [Google Scholar]
- 24.Su Y, Ji B, Zhang K, Gao H, Huang Y, Hwang K. Langmuir. 2010;26:4984. doi: 10.1021/la9036452. [DOI] [PubMed] [Google Scholar]
- 25.Tokudome Y, Suzuki K, Kitanaga T, Takahashi M. Sci Rep. 2012;2:683. doi: 10.1038/srep00683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Yin J, Lu C. Soft Matter. 2012;8:6528. [Google Scholar]
- 27.Vandeparre H, Gabriele S, Brau F, Gay C, Parker KK, Damman P. Soft Matter. 2010;6:5751. [Google Scholar]
- 28.Lafuma A, Quere D. Nature Materials. 2003;2:457. doi: 10.1038/nmat924. [DOI] [PubMed] [Google Scholar]
- 29.Moon MW, Lee SH, Sun JY, Oh KH, Vaziri A, Hutchinson JW. Proceedings of the National Academy of Sciences. 2007;104:1130. doi: 10.1073/pnas.0610654104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Cao Y, Hutchinson JW. Journal of Applied Mechanics. 2012;79:031019. [Google Scholar]
- 31.Zhao X, Koh SJA, Suo Z. International journal of applied mechanics. 2011;3:203. [Google Scholar]
- 32.Brau F, Vandeparre H, Sabbah A, Poulard C, Boudaoud A, Damman P. Nature Physics. 2010;7:56. [Google Scholar]
- 33.Sun J-Y, Xia S, Moon M-W, Oh KH, Kim K-S. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science. 2012;468:932. [Google Scholar]
- 34.Zang J, Zhao X, Cao Y, Hutchinson JW. Journal of the Mechanics and Physics of Solids. 2012;60:1265. [Google Scholar]
- 35.Yin J, Yagüe JL, Eggenspieler D, Gleason KK, Boyce MC. Advanced Materials. 2012;24:5441. doi: 10.1002/adma.201201937. [DOI] [PubMed] [Google Scholar]
- 36.Kim P, Abkarian M, Stone HA. Nature Materials. 2011;10:952. doi: 10.1038/nmat3144. [DOI] [PubMed] [Google Scholar]
- 37.Yim EK, Pang SW, Leong KW. Experimental Cell Research. 2007;313:1820. doi: 10.1016/j.yexcr.2007.02.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.McMurray RJ, Gadegaard N, Tsimbouri PM, Burgess KV, McNamara LE, Tare R, Murawski K, Kingham E, Oreffo RO, Dalby MJ. Nature Materials. 2011;10:637. doi: 10.1038/nmat3058. [DOI] [PubMed] [Google Scholar]
- 39.Bettinger CJ, Langer R, Borenstein JT. Angewandte Chemie International Edition. 2009;48:5406. doi: 10.1002/anie.200805179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.McNamara LE, McMurray RJ, Biggs MJ, Kantawong F, Oreffo RO, Dalby MJ. Journal of Tissue Engineering. 2010;1:120623. doi: 10.4061/2010/120623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Zhao F, Veldhuis JJ, Duan Y, Yang Y, Christoforou N, Ma T, Leong KW. Molecular Therapy. 2010;18:1010. doi: 10.1038/mt.2010.21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Dalby MJ, Gadegaard N, Tare R, Andar A, Riehle MO, Herzyk P, Wilkinson CD, Oreffo RO. Nature Materials. 2007;6:997. doi: 10.1038/nmat2013. [DOI] [PubMed] [Google Scholar]
- 43.Kulangara K, Leong KW. Soft Matter. 2009;5:4072. doi: 10.1039/B921206J. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Midwood KS, Williams LV, Schwarzbauer JE. The International Journal of Biochemistry & Cell Biology. 2004;36:1031. doi: 10.1016/j.biocel.2003.12.003. [DOI] [PubMed] [Google Scholar]
- 45.Kim DH, Lipke EA, Kim P, Cheong R, Thompson S, Delannoy M, Suh KY, Tung L, Levchenko A. Proceedings of the National Academy of Sciences. 2010;107:565. doi: 10.1073/pnas.0906504107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Chen CS, Mrksich M, Huang S, Whitesides GM, Ingber DE. Science. 1997;276:1425. doi: 10.1126/science.276.5317.1425. [DOI] [PubMed] [Google Scholar]
- 47.Yim EK, Darling EM, Kulangara K, Guilak F, Leong KW. Biomaterials. 2010;31:1299. doi: 10.1016/j.biomaterials.2009.10.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Yeong WY, Yu H, Lim KP, Ng KLG, Boey YCF, Subbu VS, Tan LP. Tissue Engineering Part C: Methods. 2010;16:1011. doi: 10.1089/ten.TEC.2009.0604. [DOI] [PubMed] [Google Scholar]
- 49.Luna JI, Ciriza J, Garcia-Ojeda ME, Kong M, Herren A, Lieu DK, Li RA, Fowlkes CC, Khine M, McCloskey KE. Tissue Engineering Part C: Methods. 2011;17:579. doi: 10.1089/ten.TEC.2010.0410. [DOI] [PubMed] [Google Scholar]
- 50.Kulangara K, Yang Y, Yang J, Leong KW. Biomaterials. 2012;33:4998. doi: 10.1016/j.biomaterials.2012.03.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.