Abstract
Computationally efficient statistical tests are needed in association testing of large scale genetic markers for survival outcomes. In this study, we explore several test statistics based on the Cox proportional hazards model for survival data. First, we consider the classical partial likelihood-based Wald and score tests. A revised way to compute the score statistics is explored to improve the computational efficiency. Next, we propose a Cox-Snell residual based score test, which allows us to handle the controlling variables more conveniently. Incorporation of these three tests into a permutation procedure to adjust for the multiple testing is also illustrated. In addition, we examine a simulation-based approach proposed by Lin (2005) to adjust for multiple testing. Comparison of these four statistics in terms of type I error, power, family-wise error rate and computational efficiency under various scenarios are presented via extensive simulation.
Keywords: Survival outcome, Cox proportional hazard model, Cox-Snell residuals, multiple testing, genetic markers
1. Introduction
The availability of robust technologies for genotyping single nucleotide polymorphisms (SNPs) has stimulated large-scale genetic association studies of complex human diseases [1, 2]. The large amount of genetic data underscore the need for tools beyond existing computational resources and analytic methods [3]. Genetic association testing can go far beyond the comparison of single marker genotypes or allele frequencies between cases and controls. In addition to the need for adjustments for patient, disease, or therapeutic factors, many studies also involve censored time-to-event data. For these survival outcomes, there is a need to determine appropriate statistical methods that are computationally more efficient.
One distinct feature of studies with survival outcomes is right censoring. The proportional hazards model of Cox [4] has been widely used to handle right censored survival data in the presence of covariates. Various tests such as the partial likelihood-based likelihood ratio, Wald, and score tests have been proposed as association tests using the Cox proportional hazards model [5]. However, comparison of these tests in genetic association testing of large scale genetic markers has not been fully explored.
The current work was motivated by a genetic study conducted by Petersdorf et al. [6] which sought to identify SNPs within the major histocompatibility complex (MHC) that affect clinical outcome after hematopoietic stem cell transplantation. Information on 1,120 SNPs was available for 2,492 patients who received first allogenenic transplants from HLA-A, -C, -B, -DRB1, -DQB1 allele-matched unrelated donors for malignant and non-malignant blood disorders. The clinical outcomes included overall survival, disease-free survival etc., which were traditionally modeled by the Cox proportional hazards model [4]. The impact of each SNP was evaluated separately with adjustments for other clinical, patient or donor risk factors that influenced the outcomes.
One major challenge in the transplantation genetic association study is how to appropriately control for the family-wise error rate (FWER) due to multiple tests of the 1,120 SNPs. Classical Bonferroni correction or Holm's step-down procedure [7] are known to be conservative in controlling the FWER as they do not take into account the correlation structure between the SNPs. Alternatively, the permutation approach by Churchill and Doerge [8] is widely considered to be the gold standard for multiple testing correction in genetic association studies. However, the permutation approach often requires intensive computation. Several methods have been proposed to improve its computational efficiency or as alternatives to the classical permutation approach (e.g. [9], [10], [11], [12], [13]). Most of these methods, however, are limited to case-control studies using generalized linear models (GLM). For survival data, the classical partial-likelihood based Wald and score tests for the proportional hazards model can be incorporated within the permutation procedure. Lin [14] also proposed a Monte-Carlo approach to control the FWER without relying on permutation. Lin's method can be applied to GLMs as well as survival outcomes using the Cox model.
In this paper, we first review the classical partial likelihood based Wald and score tests for the Cox proportional hazards model and describe a way to improve the computational efficiency for the score test when testing a large number of SNPs. We further propose a novel score test based on the Cox-Snell residuals [15]. We discuss the pros and cons of this new statistic versus the partial likelihood-based Wald and score statistics. Implementation of the Wald, the score and the Cox-Snell residual based score statistics within the permutation procedure to adjust for multiple testing of SNPs is illustrated. In addition, we consider Lin's Monte-Carlo approach, which is based on approximating the joint distribution of the test statistics of all SNPs via Monte-Carlo simulation. Comparison of these four testing methods in terms of their type I error, power, FWER and computational efficiency are performed through extensive simulations.
2. Methods
For each subject i, let Ti be the observed on study time and δi be the death indicator (=1, if Ti is a death time; =0, if Ti is a censoring time); Zj is a vector of length p of clinical covariates that may affect the time-to-event outcome such as patient age, gender, disease type, disease stage, etc. We assume that censoring is non-informative. In addition, we have typed genotypes gik at a set of genetic markers k = 1, 2,…, M. For biallelic markers such as SNPs, we typically have three genotypes at each marker locus, say BkBk, AkBk and AkAk with Bk being the common allele at marker locus k. Let G0k, G1k, G2k be the three indicator variables for these three genotype groups, respectively. By choosing one of the genotype groups (e.g., the homozygous genotype BkBk of the common allele) as the baseline group, the genotype covariates for marker locus k can be defined as Gik = (G1k(gik), G2k(gik))T, with G1k(gik) = 1 if gik = AkBk and 0 otherwise; and G2k(gik) = 1 if gik = AkAk and 0 otherwise. At each marker locus k, we can then test for association of the observed genotypes gik with the survival outcome using the following proportional hazards model
| (1) |
where λ(t|Zi, Gik) denotes the hazard function for individual i at time t given the covariates Zi and Gik, λ0(t) is an unspecified baseline hazard function, α is a p-dimensional vector of risk effects for the clinical covariates, and βk is a qk-dimensional vector of risk effects for the genotypes at marker locus k. Here qk = 2 for Gik = (G1k(gik), G2k(gik))T, or qk = 1 if the homozygous genotype group AkAk of the rare allele is too small and excluded at marker locus k (see Section 2.3). We are mainly interested in finding significant markers after controlling for the clinical covariates via testing the null hypothesis H0 : βk = 0 for k = 1, 2,…, M.
Let L(α, βk) be the usual partial likelihood for the Cox proportional hazard model (1) (cf., [5]). We can estimate (α, βk) by solving the partial score equations Uα(α, βk) = 0 and Uβk(α, βk) = 0 for α and βk, where Uα(α, βk) and Uβk(α, βk) are the first partial derivatives of log L(α, βk) with respect to α and β, respectively.
To construct the test statistics, we calculate the observed information matrix I(α, βk), which is the matrix of the second partial derivatives of the negative log partial likelihood function. We write this matrix as a partitioned matrix:
where, for example, Iαα(α, βk) is the p × p submatrix of the second partial derivatives of -log L(α, βk) with respect to α. In the same way, we also represent the inverse of I(α, βk) as a partitioned matrix:
| (2) |
where denotes the upper p × p submatrix of I(α, βk)−1.
2.1. The Wald and score statistics
To test the null hypothesis of H0 : βk = 0 in model (1) for k = 1, 2,…, M, we consider two standard partial-likelihood based tests − the Wald and the score tests. A third common test is the likelihood ratio test, which we will not further explore since its performance does not differ much from the Wald test and it is computationally less efficient. It is well known that all the three statistics are asymptotically identical.
Let α̂ and β̂k be the partial maximum likelihood estimates of α and βk in model (1). The Wald statistic for testing H0 : βk = 0 is given by
| (3) |
which under H0 asymptotically has a chi-squared distribution with qk degrees of freedom. For each marker k = 1,…, M, as β̂k and α̂(β̂k) depend on the observed genotypes gik, we need to refit the model to obtain estimates of β̂k, α̂(β̂k) and recompute the information matrix and its inverse before we can calculate the test statistic .
The score statistic for testing the null hypothesis H0 : βk = 0 is defined as
| (4) |
which under H0 asymptotically also has a chi-squared distribution with qk degrees of freedom. To compute (4), we only need to calculate the partial maximum likelihood estimate α̂0 of α once under H0, as this estimate does not depend on the marker locus k.
In testing multiple SNPs using score statistics, one way to improve the computational efficiency is to calculate by (see [16])
| (5) |
As the estimates β̂0 and the matrix are the same across all marker loci, they only need to be calculated once. In general, it is computationally more efficient to use the score test than the Wald test especially when a large number of SNPs are being tested.
2.2. A Cox-Snell residual based test
In the following, we introduce a modified score test based on the Cox-Snell residuals [15]. Let X be the true event time, S(x∣Z) the survival function of X, and Λ(x∣Z) the cumulative hazard function of X for subjects with covariates Z. It is well known that Λ(X∣Z) follows an exponential distribution with a hazard rate of 1. Note that under the proportional hazards model λ(t∣Z) = λ0(t) exp {αTZ}, the cumulative hazard function is .
When βk = 0, the Cox-Snell residuals based on (Ti, δi, Zi, Gik), i = 1,…, n, are defined as
| (6) |
where is Breslow's estimator of the baseline cumulative hazard function and α̂0 is the partial maximum likelihood estimator of α under H0. If the proportional hazards model (1) with βk = 0 is correct and the estimates Λ̂0(t) and α̂0 are close to the true values, the Cox-Snell residuals Ri should behave like a censored sample from the exponential distribution with a hazard rate of 1. These residuals are commonly used as a diagnostic tool for assessing the goodness-of-fit of a proportional hazards model.
Now, if the true model is actually , then has an exponential distribution with a hazard rate of 1. Or, alternatively, Λ1(X) exp {αTZ} follows an exponential distribution with a hazard rate of . By using the estimates Λ̂0(Ti), α̂0 to approximate Λ1(X) and α, the Cox-Snell residuals Ri given in (6) would approximately follow an exponential distribution with hazard rate at least under the null. An intercept β0 is added on because the cumulative hazard Λ1(t) refers to a particular baseline genotype group at maker locus k while Λ0(t) does not. Here we also assume that Λ1(t) is proportional to Λ0(X), i.e., Λ1(t) = exp{β0}Λ0(t). We can then test the SNP association via testing the null hypothesis of H0 : βk = 0 versus the alternative H0 : βk ≠ 0.
By assuming that the underlying distribution of (Ri, δi), i = 1,…, n, is exponential with hazard rate λR(r∣Gk), the likelihood function becomes
| (7) |
Let
where the latter equation is from (5) and , , and are the second partial derivatives of -log L(β0, βk). The score statistic based on the Cox-Snell residuals Ri to test the null hypothesis H0 : βk = 0 is then given by
| (8) |
which under the null has a chi-squared distribution with qk degrees of freedom for k = 1,…, M. Here, β̂0 = ln(Σ δi/Σ Ri) is the maximum likelihood estimate of β0 under the null. The explicit formulas for the expressions in (8) are given in the supporting web material (Section 1).
Similar to the previous partial likelihood based score test, here we only need to estimate α̂0 and compute the Cox-Snell residuals Ri (i = 1, ⋯, n) once under H0. One major advantage of using the Cox-Snell score test instead of the regular score test is that the score equations as well as the information matrix used in computing the Cox-Snell score statistic are from simple parametric models and have a much simpler form. Moreover, we only need to adjust for covariates and stratified variables once in calculation of the Cox-Snell residuals Ri, i = 1, ⋯, n. After that, there is no need to account for them in the remaining association tests of the SNPs.
The assumption that the Cox-Snell residuals asymptotically follow an exponential distribution only holds if the proportional hazards model is correct and the estimates Λ̂0(t) and α̂0 in (6) are close to the true values. Lagakos [17] showed that this approximation might be questionable for small sample sizes. Moreover, the assumption that Λ1(t) is proportional to Λ0(t) could be relieved by fitting a Cox proportional hazards model (without the intercept term β0) to the Cox-Snell residuals instead of the parametric exponential model. However, this would be at a cost of increased computation time. It should be pointed out that the Cox-Snell residuals Ri, i = 1,…, n, as transformed from the original survival data, are no longer independent. It would be more appropriate to make inference based on the empirical distributions of testing statistics rather than the asymptotic chi-squared distributions.
2.3. Incorporation with permutation to adjust for multiple testing
When hundreds to thousands of SNPs are being tested in genetic association studies, one statistical challenge is how to appropriately control for FWER and adjust for the multiple testing. Some simple criteria such as Bonferroni and Sidak methods have been developed to tackle this issue. However, these methods are known to be conservative in controlling for FWER especially when the test statistics are positively correlated, which is often the case for SNPs in high linkage disequilibrium (LD). Alternatively, some data-driven methods such as the permutation approach can provide empirical estimates of the critical values with more flexible assumptions [18, 8]. To test for association between a phenotypic trait and marker genotypes, a basic permutation procedure will shuffle the trait values randomly and then re-assign them to the original genotype data. For each shuffled data set, we then compute the test statistics for all the markers. Under the null hypothesis of no association between the traits and the marker genotypes, this random shuffling of the trait values across all individuals should not alter the distribution of the test statistics. So, by computing the values of the test statistics in all the shuffled data sets, we essentially obtain a random sample of all the test statistics for the set of markers which allows us to estimate the joint distribution of all the test statistics under H0.
In association tests of genetic markers, quite often we may have to adjust for some clinical variables as well. We adopt here a strategy that binds the clinical covariates and the survival outcomes (Ti, δi, Zi), i = 1,…, n, together to be shuffled and then re-assigns them to the marker genotypes. Meanwhile, all the marker genotypes gik (or Gik) for i = 1,…, n are also bound together to keep their LD structure the same across all the permutation data sets. Lin [14] noted that this permutation approach could inflate the type I error when the genetic markers are correlated with some of the clinical covariates (e.g., disease type). This is true in terms of the direct association of genetic markers with the survival outcomes. In our bone marrow transplantation study, however, we are mainly interested in finding genetic markers that are associated with survival outcomes after controlling for the clinical covariates. In this case, the binding strategy above satisfies the exchangeability assumption for the permutation (see our further comments on this issue in the Discussion).
As the degrees of freedom for the test statistics between different markers might be different, we adopt the minimum of p-values instead of the maximum of test statistics as the summary statistic to control for FWER [8]. That is, for the b-th permutation data set, we first compute the p-values pkb, k = 1,…, M, of all the M markers. Then, we calculate the minimum of these p-values overall the markers for b = 1,…, B. Finally, the B minimum p-values { , b = 1,…, B} are ordered and the 100(α)-th percentile is chosen as our empirical estimate of the critical value P for controlling the overall FWER at a significance level α.
The permutation approach based on the Wald statistic consists of the following procedure:
For the original data set, fit model (1) and compute the observed Wald statistic using (3) and its corresponding p-value pk0 for each marker k = 1,…, M.
For each permuted data set b = 1,…, B: (i) fit model (1) and compute the Wald statistic using (3) and its corresponding p-value pkb for each marker k = 1,…, M; (ii) compute .
Compute the empirical threshold P as the 100(α)-th percentile of { , b = 1,…, B}. Markers with the observed pk0 < P will be declared as significant at FWER level of α.
As we pointed out before, for the Wald test, we need to refit model (1) for each marker k = 1,…, M in each permutation data set.
The permutation approach based on the regular score statistic consists of the following steps:
Estimate α̂0 and compute once under H0.
For the original data set as well as each permuted data set b = 1,…, B: (i) use in equation (5) to calculate , and compute the score statistic according to (4) with its corresponding p-value for each marker k = 1,…, M; (ii) compute .
Compute the empirical threshold P as the 100(α)-th percentile of { , b = 1,…, B}. Markers with the observed pk0 < P will be declared as significant at FWER level of α.
Unlike the Wald based permutation, this score statistic based permutation approach avoids the repeated estimation of α and βk and the repeated computation of . Instead, we only need to compute once and then use (5) to compute .
Under the linear model setting, several residual based permutation strategies have been proposed for dealing with covariates [19]. Similarly, we can perform permutation on the Cox-Snell residuals from the Cox model. The permutation procedure using the Cox-Snell residual based score statistic includes the following steps:
Estimate α̂0, calculate the Breslow's estimate Λ̂0(t) of the cumulative hazard function, and the Cox-Snell residuals Ri, i = 1,…, n, once under H0.
For the original data set as well as each permuted data set b = 1,…, B: (i) calculate the Cox-Snell score statistic defined in (8) for all markers k = 1,…, M. Calculate their corresponding p-value pkb either based on the asymptotic chi-squared distributions or their empirical distributions; (ii) compute .
Compute the empirical threshold P as the 100(α)-th percentile of { , b = 1,…, B}. Markers with the observed pk0 < P will be declared as significant at FWER level of α.
Note that we need to compute the Cox-Snell residuals Ri (i = 1,…, n) only once for all permutation data sets. For each permutation data set, the calculation of the Cox-Snell score statistics , k = 1,…, M, is then based on simple parametric models without any further covariates or stratification variables being involved except for the marker genotype covariates. When all the score statistics for different permutation sets b = 1,…, B at a marker k have the same degrees of freedom, we can actually use these score statistics to approximate the empirical distribution of the test statistic at marker k and calculate the p-value pkb, b = 1,…, B based on this empirical distribution. In practice, however, the score statistics , b = 1,…, B at the same marker k may have different degrees of freedom. Due to varying minor allele frequencies (MAFs), some MAFs are so rare that the genotype groups of homozygous rare alleles are quite small such that very few events will be observed in some permutation data sets. In this case, if by chance all the events in this small category occur before the events in other categories, it could lead to an artificially large value of the test statistic. This could cause problems in the permutation procedure and lead to unreliable results. To avoid this problem, we eliminate a genotype group if it has less than a threshold E (e.g., E=5 or 10) of events. For each test statistic, we then compute its corresponding p-value using the asymptotic chi-squared distribution with 1 or 2 degrees of freedom. This is more efficient than using the empirical distribution because we do not need to store all the score statistics. In our simulation study, we found that it gives similar results as using the empirical distribution when the sample size is large (see Section 3.1).
2.4. A simulation approach to adjust for multiple testing
Lin [14] proposed a Monte-Carlo approach to adjust for multiple testing based on approximating the joint distribution of the test statistics for all the markers via simulation. Many of the common test statistics for testing the kth null hypothesis H0 : βk = 0, k = 1,…, M can be written as , where and with Uki being the so-called efficient score function of the ith subject for βk [20]. If the null hypothesis is true, then Sk has approximately a chi-squared distribution with degrees of freedom equal to the length of Uk. Moreover, under the null hypothesis, the set of statistics (U1,…, UM) is asymptotically multivariate normal with mean zero and estimated covariance between Uj and Uk, j, k = 1,…, M [21].
Define and , where G1,…,Gn are independent standard normal random variables. Since (Ũ1,…, ŨM) has the same joint distribution as (U1,…, UM), (S̃1,…,S̃M) has the same joint distribution as (S1,…,SM). Lin [14] proposes to obtain realizations for the joint distribution of (S1,…,SM) by repeatedly generating normal random variables G1,…,Gn while keeping Uki and the same as obtained from the observed data. To adjust for multiple testing, Lin [14] adopts a step-down procedure based on a large number (e.g. 10,000) of the realizations of (S̃1,…, S̃M). Specifically, let s(1),…, s(M) be the ordered observed values of the test statistics from the observed data with corresponding hypotheses H(1),…, H(M). Starting with hypothesis H(1), the kth hypothesis H(k) is rejected if P(maxk≤j≤MS̃j ≥ s(k)) ≤ α, given that H(1),…, H(k−1) have been rejected, for k = 1,…, M.
As pointed out in the Appendix of Lin [14], different expressions for Uki can be found for different models. For the proportional hazards model, derived from the formula given in Lin and Wei [22] and geared towards our needs, we have Uki = Wiβk(α̂0, 0), where α̂0 is obtained by fitting a proportional hazards model under the null hypothesis and Wiβk (α, βk) is given in the supporting web material (Section 2).
Lin's approach is computationally more efficient than the previously discussed permutation approaches. It mainly involves the simulation of i.i.d. random numbers variables from the standard normal distribution and does not require the repeated analysis of shuffled data sets. We only need to estimate α̂0 and calculate the quantities Uki and once for each k = 1,…, M. The calculation of Ũk and S̃k is rather trivial.
3. Simulation and Example
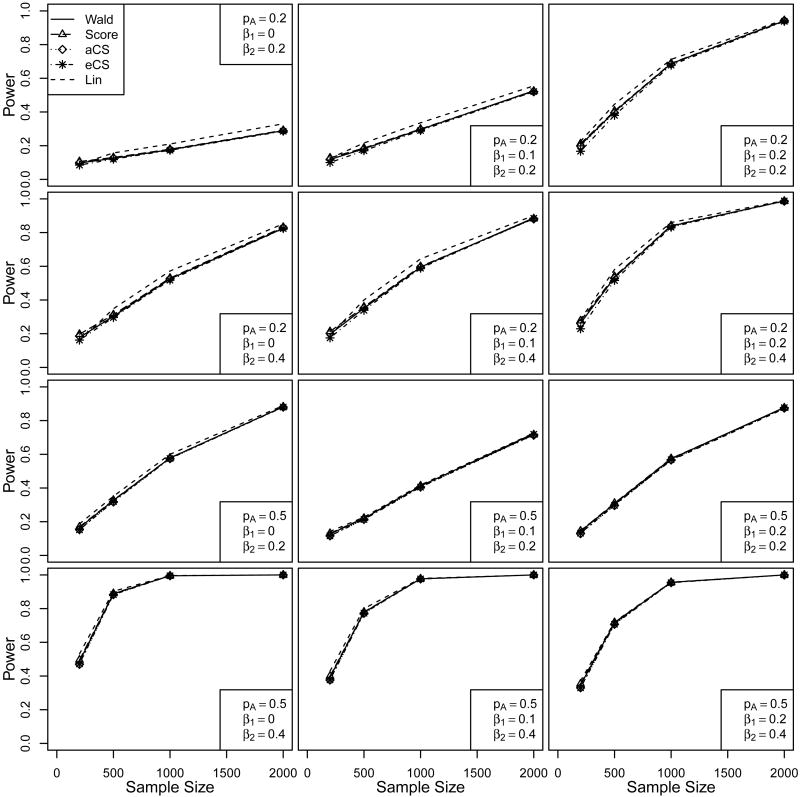
In this section, we perform simulation studies to compare the performances of the regular Wald and score tests, the Cox-Snell residual based score test, and Lin's simulation approach in various scenarios. First, we look at the type I error and power when only one genetic marker is present. We consider scenarios where the proportionality assumption is satisfied and scenarions were is it violated. We also consider scenarios with population stratification. Second, we look at FWER and power in testing multiple markers. Third, we compare the computing time of the four statistics in testing multiple markers. Finally, we apply the Wald and Cox-Snell residual based score tests in a real genetic study conducted by Petersdorf et al [6]. In the following, all tests were performed using our own programs which were implemented in C.
3.1. Type I error and power in testing a single marker
In this single marker case, we first consider a biallelic locus with allele frequencies pA = 0.2 or 0.5 and pB = 1 − pA. The genotypes AA, AB and BB are generated based on a multinomial distribution with the genotypic frequencies , P(AB) = 2pApB and (i.e., under Hardy-Weinberg equilibrium (HWE)). The survival times are generated from the following proportional hazards model
where Z1 and Z2 are two independent binary covariates with identical Bernoulli(0.5) distribution and effects α1 = α2 = 0.5. The baseline hazard is set to be constant with λ0(t) = 1. The genotype covariates G1 and G2 are defined as G1 = 1 if AB and 0 otherwise, while G2 = 1 if AA and 0 otherwise, with BB being the baseline category. We consider several combinations for the effects of G1 and G2 including β1 = 0, 0.1, 0.2 and β2 = 0, 0.2, 0.4. Exponential censoring is superimposed on the survival times such that roughly 30% of the event times are censored.
As mentioned in section 2.2, the Cox-Snell Residuals Ri are no longer independent and consequently the asymptotic chi-squared distribution of the test statistic might be questionable. Therefore, in addition to using the asymptotic chi-squared distribution, we also use the empirical distribution of the test statistic based on 1,000 permutations to calculate the p-value and assess the type I error and the power. For Lin's approach, we use Sk as the test statistic and calculate p-values based on the asymptotic chi-squared distribution. We noticed that the simulation results are very similar if we calculate the p-values based on the empirical distribution from the simulated S̃k's.
We consider different sample sizes of n = 200, 500, 1000, 2000. In each case, we perform 10,000 simulations to compute the type I error and power. To assess the type I error, we set β1 = β2 = 0 and record how often the test rejects H0 : β1 = β2 = 0. For the power, we set β1 ≠ 0 and/or β2 ≠ 0 and again count how often H0 is rejected. In both cases, we perform the tests at the 5% significance level. The simulation results for type I error estimates are summarized in Table 1, where aCS denotes the Cox-Snell score test using the asymptotic chi-squared distribution and eCS denotes the Cox-Snell test based on the empirical distribution from 1000 permutations.
Table 1.
Estimated type I error for the partial likelihood-based Wald and score tests, the asymptotic and empirical distribution based Cox-Snell score tests, and Lin's approach based on 10,000 simulations.
| n | pA | Wald | Score | aCS | eCS | Lin |
|---|---|---|---|---|---|---|
| 200 | 0.2 | 0.062 | 0.068 | 0.062 | 0.049 | 0.062 |
| 0.5 | 0.056 | 0.058 | 0.051 | 0.052 | 0.067 | |
| 500 | 0.2 | 0.056 | 0.058 | 0.054 | 0.050 | 0.063 |
| 0.5 | 0.052 | 0.053 | 0.049 | 0.050 | 0.057 | |
| 1000 | 0.2 | 0.051 | 0.051 | 0.052 | 0.049 | 0.058 |
| 0.5 | 0.050 | 0.050 | 0.048 | 0.050 | 0.054 | |
| 2000 | 0.2 | 0.054 | 0.054 | 0.053 | 0.052 | 0.059 |
| 0.5 | 0.050 | 0.051 | 0.049 | 0.050 | 0.052 |
For the type I error rate, we first compare the partial likelihood-based Wald and score tests and the Cox-Snell residual based score test. It has been known that the partial likelihood-based score test tends to have slightly inflated type I error rate for small sample sizes [23]. We make a similar observation for n = 200 and 500 not only for the score test but also for the Wald test. The asymptotic Cox-Snell score test also has an inflated type I error for n = 200 and 500 when the MAF is small (pA = 0.2) but for large MAF (pA = 0.5) the type I error is close to the nominal value of 0.05. For larger sample sizes of n = 1000 or 2000, all three tests control the type I error rate appropriately. The Cox-Snell test using the empirical distribution has better control of the type I error rate as compared to the Cox-Snell test using the asymptotic distribution, especially for smaller sample sizes. For larger n, both the asymptotic and the empirical Cox-Snell tests give similar results in terms of type I error. Hence, for large sample sizes it seems reasonable to use the asymptotic chi-squared distribution for the Cox-Snell based test. Finally, the test based on Lin's test statistic appears to have inflated type I error rates even for large sample sizes.
The simulation results for the power comparisons are summarized in the supporting web material (Section 3) and plotted in Figure 1. As one would expect, the power increases as the sample size increases, and the power is lower when the MAF is small (pA = 0.2) as compared to large MAF (pA = 0.5). Overall, Lin's approach appears to have slightly higher power especially when the MAF is small. However, this could be due to the inflated type I error rates. The other four tests give quite comparable results in all scenarios. Since the Cox-Snell residual based score test using the asymptotic distribution performs similar to the one using the empirical distribution, we again conclude that it is reasonable to use the asymptotic chi-squared distribution to make inference. We also performed similar simulation studies under a stratified proportional hazards model setting. The overall performance of the five tests are very similar to that in the no stratification setting. Details of the simulation setting and simulation results can be found in the supporting web material (Section 4).
Figure 1.
Powers of the partial likelihood-based Wald and score tests, the asymptotic and empirical distribution based Cox-Snell score tests, and Lin's approach.
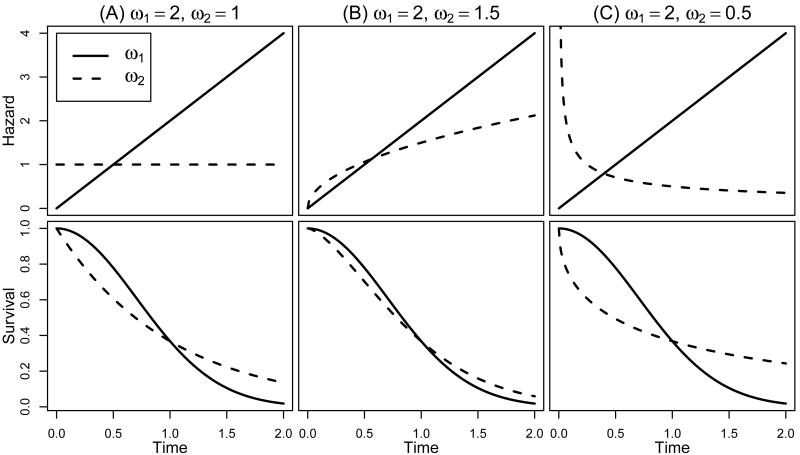
Next, we examine the performance of the tests when the proportionality assumption is violated. We generate genotype categories AA, AB, BB according to HWE with pA = 0.5. The genotype covariate is defined as: G = 1 for genotype AA; =0, otherwise. Survival times are simulated from the following model:
where α1 = α2 = 0.5 are the effects of the two binary covariates Z1, Z2 ∼ Bernoulli(0, 0.5), and
Both baseline hazards are Weibull(γ, ω) with scale parameter γ = 1 and shape parameter ω = ω1 or ω2. We consider three combinations of (ω1, ω2)=(2,1), (2,1.5) and (2, 0.5). The corresponding hazard and survival functions are shown in Figure 2. Exponential censoring is superimposed to give roughly 30% censoring.
Figure 2.
The non-proportional hazards and their corresponding survival functions.
We consider four different sample sizes of n = 200, 500, 1000, 2000. In each case, we perform 10,000 simulations to estimate the power. For each simulation data, we ignore the non-proportionality and fit the following model to the survival data:
We would like to see how robust the four statistics are against violation of the proportionality assumption in terms of their power. The estimated powers are summarized in Table 2. In this non-proportional hazard case, only Lin's approach is claimed to be robust against non-proportionality [22]. Although the power estimates from Lin's method may need some minor adjustment due to the slightly inflated type I error, the other tests appear to be slightly lower powered than Lin's test especially for small sample size. The partial likelihood-based Wald and score tests and the Cox-Snell residuals based tests are comparable in most scenarios with only around 2% power differences.
Table 2.
Estimated power for the partial likelihood-based Wald and score tests, the asymptotic and empirical distribution based Cox-Snell score tests, and Lin's approach based on 10,000 simulations.
| Cases | n | Wald | Score | aCS | eCS | Lin |
|---|---|---|---|---|---|---|
| ω1 = 2, ω2 = 1 | 200 | 0.224 | 0.228 | 0.207 | 0.213 | 0.343 |
| 500 | 0.560 | 0.562 | 0.545 | 0.544 | 0.723 | |
| 1000 | 0.882 | 0.882 | 0.874 | 0.875 | 0.948 | |
| 2000 | 0.995 | 0.995 | 0.995 | 0.994 | 0.999 | |
|
| ||||||
| ω1 = 2, ω2 = 1.5 | 200 | 0.059 | 0.061 | 0.054 | 0.057 | 0.075 |
| 500 | 0.094 | 0.095 | 0.091 | 0.093 | 0.126 | |
| 1000 | 0.169 | 0.170 | 0.166 | 0.169 | 0.223 | |
| 2000 | 0.325 | 0.326 | 0.322 | 0.321 | 0.405 | |
|
| ||||||
| ω1 = 2, ω2 = 0.5, | 200 | 0.801 | 0.805 | 0.778 | 0.776 | 0.924 |
| 500 | 0.998 | 0.998 | 0.997 | 0.997 | 1.000 | |
| 1000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | |
| 2000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | |
Finally, we look at the performance of the tests under population stratification. Survival times are generated from two different sub-populations. The genetic marker has genotype categories AA, AB, BB with HWE and allele frequencies pA = 0.8 in sub-population 1, and pA = 0.7 in sub-population 2. The genotype covariate is defined as: G = 0 for genotype AA; =1, otherwise. The survival times in sub-population j are simulated from the following model:
where λj(t) = ωjtωj−1 is from the Weibull(γ, ωj) distribution with scale parameter γ = 1 and shape parameter ωj, j = 1, 2. Z1, Z2 ∼ Bernoulli(0, 0.5) are two binary variables with α1 = α2 = 0.5. Censoring is exponential such that about 30% are censored. The combined sample has a 50:50 percent mixture of the two sub-population samples.
For the effects of the genotype covariates, we consider 3 situations: (β1, β2) = (0, 0), (log(1.2), log(1.2)), (0, log(1.5)) and the shape parameters (ω1, ω2)=(1,1), (2,1) or (2,1.5). So totally there are 9 combinations, and in each case we consider total sample sizes of n=200, 500, 1000 and 2000. Assuming the population sub-structure is known, we first fit a stratified Cox model with stratification on populations 1 and 2. Then we also fit a Cox model by ignoring the population substructure. The estimated powers with and without stratification are summarized in the supporting web material (Section 5) Table 4 and Table 5, respectively. In general, when the population sub-structure is known and stratified in a Cox model, the power estimates are expected to be closer to the true values, although the stratified Cox model still does not account for the distribution and effect differences of the genetic marker in the two sub-populations. In fact, from the simulation results we see that the type I error is better controlled when a stratified Cox model is used and we also achieve higher power in most cases. Comparing the five tests, the power is similar in most of the cases. However, it appears that the Cox-Snell score tests may be a little conservative in terms of the type I error, while Lins approach has slightly inflated type I error rates. When the population sub-structure is ignored and a Cox-Model without stratification is used, the type I errors and the power of the five methods are fairly close with only about 1-2% differences.
Table 4.
Power results of the Cox-Snell residuals based score test and Lin's Monte Carlo based approach (2000 simulations).
| SNP | Excluding categories with < 5 events | Excluding categories with < 10 events | ||
|---|---|---|---|---|
| Cox-Snell | Lin | Cox-Snell | Lin | |
| SNP 1 | 0.91 | 0.96 | 0.94 | 0.96 |
| SNP 2 | 1.00 | 1.00 | 1.00 | 1.00 |
| SNP 3 | 0.10 | 0.20 | 0.16 | 0.22 |
| SNP 4 | 0.14 | 0.31 | 0.22 | 0.30 |
| SNP 5 | 0.22 | 0.44 | 0.29 | 0.44 |
Table 5.
CPU time needed to run the permutation approach for one data set using the Wald, the regular score, the Cox-Snell score tests and Lin's Monte-Carlo based test (all implemented in C).
| Simulation settings | Methods | Number of clinical covariates | |||
|---|---|---|---|---|---|
|
| |||||
| 1 | 2 | 5 | 10 | ||
|
| |||||
| 1) n = 1000, M = 10, B = 100 | Wald | 21 sec | 36 sec | 109 sec | 5 min |
| Score | 5 sec | 6 sec | 10 sec | 15 sec | |
| Cox-Snell | < 0.5 sec | < 0.5 sec | < 0.5 sec | 1 sec | |
| Lin | < 0.5 sec | < 0.5 sec | < 0.5 sec | < 0.5 sec | |
|
| |||||
| 2) n = 2000, M = 100, B = 1000 | Score | 15 min | 17 min | 29 min | 41 min |
| Cox-Snell | 21 sec | 22 sec | 24 sec | 24 sec | |
| Lin | 11 sec | 11 sec | 11 sec | 12 sec | |
|
| |||||
| 3) n = 2000, M = 1000, B = 10000 | Cox-Snell | 31 min | 31 min | 32 min | 32 min |
| Lin | 10 min | 10 min | 10 min | 10 min | |
|
| |||||
| n = 1000, M = 1046, B = 1000 | Cox-Snell | 2 min | 2 min | 2 min | 2 min |
| n = 1000, M = 1046, B = 10000 | Lin | 6 min | 6 min | 6 min | 6 min |
3.2. FWER and power in testing multiple markers
In this multiple marker case, we compare the permutation approach based on the Cox-Snell score statistics and Lin's Monte-Carlo based method in terms of controlling the FWER as well as the power via simulation. We won’t consider the Wald and the regular score statistics in this setting since those two are computationally inferior to the Cox-Snell score statistic and Lin's Monte-Carlo based method, as we will see in section 3.3.
We use the observed genotype data of genetic markers (SNPs) from our real data (see Section 3.4) to simulate genotypes. This will guarantee that we have correlated genetic markers as one would expect to see in real genetic data. Our data set consists of 2,492 subjects with 1,120 SNPs. First, we exclude SNPs that meet one of the following criteria: less than three categories, missing genotype information for more than 40 subjects, or MAF less than 0.05. This results in a total of 1,046 genetic markers. Missing genotypes for the remaining SNPs were imputed using a multinomial distribution based on the allele frequencies and assuming Hardy-Weinberg equilibria. Each SNP consists of three genotypic categories (AkAk, AkBk,BkBk) and is coded by two dummy variables as described earlier: G1k = 1 if the genotype at SNP k is AkBk, and 0 otherwise; G2k = 1 if the genotype at SNP k is AkAk, and 0 otherwise. The homozygous genotype BkBk of the common allele is chosen as the baseline category.
Out of the 1,046 genetic markers, we assign effects on survival to 5 SNPs. These five genetic markers (named SNP 1 to SNP 5) are selected such that they are not strongly correlated (i.e., not in strong linkage disequilibrium) with each other. The minor allele frequencies, genotype counts in the original data and effects of the 5 SNPs on survival are summarized in Table 3. The survival times are generated from the following Cox model
Table 3.
Minor allele frequencies (MAF) and genotype category frequencies in the original data and effects of the five SNPs on survival for the simulation study.
| SNP | Frequency | MAF | β1 | β2 | ||
|---|---|---|---|---|---|---|
| AA | AB | BB | ||||
| SNP 1 | 17 | 373 | 2102 | 0.08 | log(2) | log(2) |
| SNP 2 | 368 | 1172 | 952 | 0.38 | log(2) | log(2) |
| SNP 3 | 24 | 350 | 2118 | 0.08 | log(1.5) | log(1.5) |
| SNP 4 | 483 | 1232 | 777 | 0.44 | log(1.5) | log(1.5) |
| SNP 5 | 436 | 1135 | 921 | 0.40 | −log(1.5) | −log(1.5) |
where the baseline hazard λ0(t) = 1, Z1 and Z2 are two independent binary covariates with identical Bernoulli(0.5) distribution and effects α1 = α2 = 0.5. The censoring time is exponentially distributed such that about 30% of the event times are censored.
We only consider a fixed sample size of n = 1000. For each simulation data set, the genetic markers are obtained from our real data set by randomly selecting 1000 subjects out of the total of 2,492 available subjects with replacement, where each subject carries the same 1,046 genetic markers as in the real data set. The total number of simulation data sets is 2000. For each simulation data set, we adjust for multiple testing using the Cox-Snell residuals based permutation approach with B = 1, 000 permutations and Lin's Monte Carlo based approach with B = 10, 000 normal samples. We record which genetic markers are found to be significant using a nominal FWER of 5%.
The permutation approach based on the Cox-Snell score statistic is executed as described in Section 2.3. As we have pointed out, special care needs to be taken with regard to the small genotype groups with very few events. Let E be the minimum number of events that we require per category. For the Cox-Snell score test, we use all observed subjects to compute the Cox-Snell residuals and to generate the permutations in order to guarantee that the permutation data sets are consistent across all markers. Then, separately for each marker k = 1,…, M, we eliminate subjects belonging to a category with less than E events for the observed as well as each permutation data set. As a result, at the same marker the test statistics from different permutations could have different degrees of freedom. Instead of deleting subjects, one could also collapse categories with small event counts with one of the other two categories. However, this strategy artificially assumes that the collapsed categories share the same effect, and we feel that it is more reliable to exclude small category subjects instead of collapsing the categories. For Lin's Monte Carlo based approach, we can exclude subjects in categories with less than E events in computating Uik by simply assigning Uik = 0 (for any k) to those deleted subjects [21]. This ensures that the set of normal variables G1,…, Gn are consistent across all the markers. To assess the impact of selecting E, we compare using E = 5 and E = 10.
First, we examine the FWER which is defined as the probability of making at least one false discovery among a set of hypotheses. We estimate the FWER by setting the effects of the five genetic markers on survival equal to zero. For the Cox-Snell score statistics, using the permutation approach to adjust for multiple testing (with E = 5), we obtain an estimated FWER of 0.06 with 95% CI (0.05, 0.07). On the other hand, Lin's Monte-Carlo based procedure gives an estimated FWER of 0.09 (0.08, 0.10). The permutation approach based on the Cox-Snell score test controls the FWER error rate significantly better than Lin's Monte-Carlo approach in this case. We obtain approximately the same results and have the same conclusion when increasing the minimum number of events per category to E = 10 events.
The results of the power analysis are summarized in Table 4. We notice that the power of the Cox-Snell score test is higher when using a minimum of E = 10 events per category compared to using E = 5 events. The reason might be due to the instability of the test statistic when E = 5. On the other hand, Lin's method seems to be less sensitive to the minimum number of events required per category. When the effect size is large (e.g., SNP1 and SNP2), both tests have a high power regardless of the MAF. Lin's approach performs slightly better than the Cox-Snell score permutation method in the low MAF case (SNP2: 0.94 vs 0.96 for E = 10). For moderate effect sizes (SNP3-5), we see that the power of Lin's test is higher than the power of the Cox-Snell score permutation method. However, a fair comparison of the two approaches in terms of power is difficult due to the inflated FWER of Lin's method. Also, as we expected, SNP 4 has slightly higher power than SNP 3 even though they have the same effect size, likely due to the fact that the MAF of SNP3 is smaller than that of SNP 4.
3.3. Computational performance
We examine the computational efficiency of the partial likelihood-based Wald and score tests and the Cox-Snell score test in the permutation setting as well as Lin's Monte-Carlo approach. We generate survival times from a proportional hazards model , where the baseline hazard λ0(t) = 1, Zi,…,Zp are independent and identically Bernoulli(0.5) distributed covariates, and p is the number of covariates we would like to adjust for. We considere p = 1, 2, 5, 10 with effects α2i−1 = 0.5 and α2i = −0.5 for i = 1,…, 5. Additionally, we have M bi-allelic markers whose effects on survival need to be assessed. Since here we are mainly interested in comparing the computational time, we set no effects for all the markers. The marker genotypes are generated independently for k = 1,…, M, with each having the same genotype distribution: , P(AB) = 2pApB and , where pA = 0.5. For each marker k = 1,…, M, the genotype covariates G1k, G2k are coded in the same way as before. Censoring is exponential such that about 30% of the event times are censored.
Let n be the sample size, M be the number of markers, and B be the number of permutations. We first consider three settings: (i) n = 1000, M = 10 and B = 100; (ii) n = 2000, M = 100 and B = 1000; (iii) n = 2000, M = 1000 and B = 10000. For Lin's approach, the number of permutations B refers to the number of realizations of S̃k, k = 1,…, M. In order to make a fair comparison of the four testing procedures, all tests including the estimation of α0 and βk (by Newton-Raphson method) were implemented in C. The programs were executed on a Notebook with Windows 7, Intel i5 M580 CPU with 2 cores and 4 threads (@ 2.66 GHz clock speed), and 8.00 GB RAM.
The CPU time for each of the four procedures for a different number of clinical covariates is given in Table 5. In the first setting, as expected, using the score test is faster than using the Wald test. The Cox-Snell based score test and Lin's approach are computationally faster than the other two tests. In the second setting, we did not run our implementation of the Wald test due to its slow speed. We can see that the Cox-Snell residual based score test is approximately 100 times faster than the regular score test with 10 clinical covariates. Lin's approach is still computationally the most efficient with less than half of the CPU time used by the Cox-Snell test. In the third setting with a large number of genetic markers and a large number of permutations, we only ran our proposed Cox-Snell permutation approach and Lin's approach. We see that Lin's approach is about 3 times faster than the permutation approach based on the Cox-Snell residuals.
Lastly, we consider a fourth setting. It is the same setting that we have used in the simulation study for the FWER and the power in Section 3.2. The sample size is n = 1000, the number of genetic markers is M = 1046, and the number of permutations is B = 1000 for the Cox-Snell based permutation approach and the number of Monte-Carlo samples is B = 10, 000 for Lin's method. We see that the Cox-Snell based permutation approach performs better in controlling the FWER even though we only used B = 1000 permutation. Here we see that running the Cox-Snell permutation with B = 1000 is about 3 times faster than running Lin's approach with B = 10000.
3.4. Real example
The data set analyzed by Petersdorf et al. in [6] includes 2,492 patients transplanted from HLA-A, -C, -B, -DRB1, -DQB1-matched unrelated donors. In total, 1228 SNPs were typed within the major histocompatibility complex region, and among them 1,120 passed quality control. 1,076 of the 1,120 SNPs have minor allele frequency MAF>5% among Caucasians in this cohort of patients. The typical outcomes included overall survival (OS), disease-free survival (DFS), relapse, treatment related mortality (TRM), acute grades 2-4 graft-versus-host disease (aGVHD2), acute grades 3-4 graft-versus-host disease (aGVHD3), and chronic graft-versus-host disease (cGVHD). For each SNP, we also consider 3 forms of genotype covariates: the patient genotype, the donor genotype and the match vs. mismatch between patient's and donor's genotype.
For each outcome, we first test clinical variables for the proportional hazard assumption using the time dependent covariate approach [5]. Variables that did not satisfy the proportional hazards assumption are adjusted for through stratification. We subsequently perform stepwise forward/backward model selection procedures to identify significant clinical variables at a 5% significance level. For example, for the primary outcome overall survival, the stratification variables included graft type (bone marrow vs. peripheral blood), Karnofsky performance score (90-100 vs. 10-80), myeloablative conditioning regimen (myeloablative vs. reduced intensity/nonmyeloablative), GvHD prophylaxis and year of transplantation (≥2004 vs. 2000-2003 vs. 1995-1999 vs. <1995), while the adjusted covariates included disease type, disease stage, patient age, total body irradiation (TBI) in conditioning regimen, and time from diagnosis to transplant for patients with chronic myeloid leukemia (CML). For aGVHD2, the stratified variable was conditioning regimen and the adjusted covariates were disease type, graft type, GvHD Prophylaxis, donor age, TBI in conditioning regimen, Karnofsky performance score and year of transplantation. For aGVHD3, the stratified variables included conditioning regimen by group and Karnofsky performance score, while the adjusted covariates included disease type, disease stage, GvHD prophylaxis and year of transplantation. We built separate models for each of the seven outcomes. Based on these preliminary models, we then tested the SNP association for each of the 1,120 SNPs in the 3 different forms separately with an adjustment for the selected clinical covariates.
We initially performed 1,000 permutations using the partial likelihood-based Wald test to compute empirical threshold values for all seven outcomes and the 3 sets of genotype forms by fitting Cox models to the cause-specific hazard functions. The targeted FWER was 5%. A given SNP was statistically significant if its observed overall p-value was smaller than the empirical threshold value. The empirical threshold values for all the seven outcomes and three forms of SNP genotype covariates are summarized in Table 6 below. Based on these thresholds, only one SNP (rs2859091) in donor genotypes was found to be significantly associated with both aGVHD2 and aGVHD3. The observed p-values of this SNP were 1.3 × 10−5 for aGVHD2 and 4.0 × 10−6 for aGVHD3, which were also significant based on the Bonferroni threshold of 0.05/1120 = 4.5 × 10−5. Although for this particular data set we did not find additional significant SNPs using these empirical thresholds, most of the empirical threshold values were larger than the Bonferroni threshold value and therefore less conservative.
Table 6. The empirical threshold values from the minimum p-value approach based on B = 1000 permutations.
| Outcomes | Patient genotype | Donor genotype | Patient-donor mismatch |
|---|---|---|---|
|
| |||
| OS | 6.3 × 10−5 | 6.0 × 10−5 | 2.3 × 10−5 |
| DFS | 4.5 × 10−5 | 5.8 × 10−5 | 2.1 × 10−5 |
| Relapse | 3.5 × 10−5 | 2.8 × 10−5 | 6.9 × 10−6 |
| TRM | 4.8 × 10−5 | 5.4 × 10−5 | 3.1 × 10−5 |
| aGVHD2 | 3.9 × 10−5 | 5.1 × 10−5 | 2.0 × 10−5 |
| aGVHD3 | 5.3 × 10−5 | 2.9 × 10−5 | 1.1 × 10−5 |
| cGVHD | 4.1 × 10−5 | 5.6 × 10−5 | 1.4 × 10−5 |
It should be pointed out here that the adjustment for multiple testing was performed on the seven outcomes and three forms of SNP genotypes independently. A more thorough adjustment should also take into account the correlation among the seven outcomes and the three forms of SNP genotypes all together, which could be made by evaluating the overall minimum p-value across all the seven outcomes as well as the three sets of SNP genotype covariates for each permutation data. The 100(α)-th percentile of these overall minimum p-values from all the permutation data sets provides an empirical estimate of the critical value for controlling the FWER over the seven outcomes as well as the three sets of SNP genotypes at a significance level α.
We also used the Cox-Snell residual based permutation procedure for two outcomes: overall survival and DFS. We did not consider the other outcomes as they have competing risks, and the Cox-Snell residuals are not well defined for competing risks data. The empirical threshold values were slightly different from the ones obtained using the Wald test. For example, in running 10,000 permutations, we obtained the empirical threshold values of 3.1 × 10−4 in patient genotypes for overall survival and 7.8 × 10−5 in patient genotypes for DFS. We did not find additional significant SNPs using these threshold values.
4. Discussion
In this study, we explored several different statistics for genetic association analysis of survival outcomes. In addition to the classical partial likelihood-based Wald and score statistics, we also proposed a Cox-Snell residuals based score statistic. In association tests of large scale genetic markers for time-to-event outcomes, this new test has an advantage in terms of computational efficiency over the partial likelihood-based Wald and the score tests in that the adjustments for covariates, stratified variables or tied event times only need to be made once in the computation of the Cox-Snell residuals. This is especially the case when there are many adjusted clinical covariates involved and a permutation procedure is being used to adjust for the multiple testing. Our simulation studies demonstrate that the Cox-Snell residual based permutation approach can provide appropriate control for the type I error and FWER even for moderate sample sizes, and it is significantly faster than the Wald or the score test based permutation approach. We suggest, however, that the Cox-Snell residual based permutation approach should be used mainly for identifying significant SNPs. Point estimates for the effect size, hazard ratios and confidence intervals at significant markers should be obtained by fitting the Cox model to the original survival outcomes. Although in our simulation study we focused on single marker analysis only, extension to other analysis such as haplotypes or gene-gene interactions could be feasible as well.
In the Cox-Snell residual based permutation approach, we suggest binding the clinical covariates and the survival times together to be shuffled and then re-assigned to the SNP genotypes. As pointed out in Lin [14], the exchangeability of the observations under the null hypothesis of no SNP effects is a key assumption for permutation testing. If we are interested in testing the null hypothesis of no direct association of genetic markers with the survival outcomes regardless of the clinical covariates, then binding covariates with survival times together is problematic. This is because under the null hypothesis of no association between the SNPs and survival outcomes, the SNP genotypes could still be correlated with certain covariates and perhaps the censoring as well. If this is the case, the observations are not exchangeable. In our transplantation study, however, we are mainly interested in identifying genetic markers that can predict survival outcomes in addition to the known clinical covariates. Here our null hypothesis is of no association of the SNPs with the survival outcomes given the covariates and the censoring mechanism. In this case, the observations are exchangeable under the null hypothesis and the permutation with the clinical covariates and the survival outcomes bound together is a valid approach.
Although the Cox-Snell residual based permutation approach is computationally promising, it has some limitations. First, the proposed Cox-Snell score test should not be used in the competing risks setting since the survival function depends not only on the cause-specific hazard but also on the hazards from other competing risks [24]. Moreover, as pointed out by Dudbridge [25], the permutation approach is suitable for testing the global association of the SNPs after adjustment for other clinical covariates. However, it cannot be used to test for gene-environmental interactions. Furthermore, in genome-wide association studies, several hundreds of thousands of SNPs are interrogated. A larger number of permutations might be needed in order to achieve sufficient accuracy for the empirical estimates of the threshold p-values. Due to limitations on our computing resources, our simulation did not achieve that scale. Further assessment on the performance of this approach in support of large scale genome-wide association studies is needed in the future.
Another quite promising method is Lin's simulation approach, which is computationally very efficient and seems more robust to non-proportionality situations. Lin also proposes a step-down procedure to adjust for multiple comparisons, which gives very similar results as the p-minimum adjustment. From our simulation study, however, we found that Lin's simulation approach may have slightly inflated type I error rate and FWER. A modification of Lin's simulation approach might be needed in order to control the type I and FWER appropriately.
With the current high-throughput SNP genotyping techniques, it is typical to have numerous missing genotypes across various SNPs. Common remedies for this problem include creating a separate category for missing genotypes, imputing the missing genotypes, or simply excluding patients with missing genotypes. Creating a separate category for missing genotypes can easily be performed and allows us to include all the patients in the analysis. However, this approach could lead to spurious association of SNPs where the SNP effect mainly comes from the difference from the missing genotype group. Alternatively, genotype imputation for a SNP can be made based on its neighboring haplotype information. It has been known that the imputation of missing genotypes could improve the statistical power in certain circumstances. So ideally we could perform imputation on missing genotypes prior to the permutation especially when the SNPs are in high linkage disequilibria. However, in our transplantation data, one should be cautious about choosing the appropriate imputation method because the patient sample may not represent a random sample from the general population. Another way to handle missing genotypes is to simply exclude the patients with missing genotypes. For example, in our permutation setting for testing multiple SNPs, we can start with the entire patient population. When each SNP is tested for association in a permutation data set, patients with missing genotypes at that particular SNP can be excluded. By excluding the patients with missing genotypes in this way, the spurious association caused by artificially creating the ‘missing’ genotype group can be avoided. One disadvantage, however, is a loss of power compared to the imputation approach.
Errors in SNP genotyping error could affect the results in genetic association studies. Quality control measures used in our transplantation study included 233 inter- and intra-experiment duplicate samples with a 0.997 concordance rate. A total of 65 samples (1.3%) that failed genotyping and 30 samples (0.6%) that failed duplicate controls were excluded. In addition to quality control for SNP genotyping, robust statistics may reduce type I errors in association analysis. Further exploration on the robustness of the four statistics to genotyping errors might be an interesting research topic in the future.
Supplementary Material
Acknowledgments
This research work is partially supported by grant AI069197 (E.W.P., M.M., T.W., F.M.) from the National Institutes of Health.
References
- 1.Carlson CS, Eberle MA, Kruglyak L, Nickerson DA. Mapping complex disease loci in whole-genome association studies. Nature. 2004;429:446–452. doi: 10.1038/nature02623. [DOI] [PubMed] [Google Scholar]
- 2.Need AC, Goldstein DB. Whole genome association studies in complex diseases: where do we stand? Dialogues in Clinical Neuroscience. 2010;12:37–46. doi: 10.31887/DCNS.2010.12.1/aneed. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ziegler A, König I, Thompson J. Biostatistical aspects of genome-wide association studies. Biometrical Journal. 2008;50:8–28. doi: 10.1002/bimj.200710398. [DOI] [PubMed] [Google Scholar]
- 4.Cox DR. Regression models and life-tables (with discussion) Journal of the Royal Statistical Society, Series B. 1972;34:187–220. [Google Scholar]
- 5.Klein JP, Moeschberger ML. Survival Analysis: Techniques for Censored and Truncated Data. 2nd. Springer; New York: 2003. [Google Scholar]
- 6.Petersdorf EW, Malkki M, Gooley TA, Spellman SR, Haagenson MD, Horowitz MM, Wang T. Mhc-resident variation affects risks after unrelated donor hematopoietic cell transplantation. Science Translational Medicine. 2012;4:144ra101. doi: 10.1126/scitranslmed.3003974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Holm S. A simple sequentially rejective bonferroni test procedure. Scandinavian Journal of Statistics. 1979;6:65–70. [Google Scholar]
- 8.Churchill GA, Doerge RW. Empirical threshold values for quantitative trait mapping. Genetics. 1994;138:963–971. doi: 10.1093/genetics/138.3.963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Schaid DJ, Rowland CM, Tines DE, Jacobson RM, Poland GA. Score tests for association between traits and haplotypes when linkage phase is ambiguous. The American Journal of Human Genetics. 2002;70:425–434. doi: 10.1086/338688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Seaman S, Müller-Myhsok B. Rapid simulation of P values for product methods and multiple-testing adjustment in association studies. American Journal of Human Genetics. 2005;76:399–408. doi: 10.1086/428140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Conneely KN, Boehnke M. So many correlated tests, so little time! Rapid adjustment of P values for multiple correlated tests. The American Journal of Human Genetics. 2007;81:1158–1168. doi: 10.1086/522036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Browning B. PRESTO: Rapid calculation of order statistic distributions and multiple-testing adjusted P-values via permutation for one and two-stage genetic association studies. BMC Bioinformatics. 2008;9(1):309. doi: 10.1186/1471-2105-9-309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Han B, Kang HM, Eskin E. Rapid and accurate multiple testing correction and power estimation for millions of correlated markers. PLoS Genetics. 2009;5:e1000 456. doi: 10.1371/journal.pgen.1000456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lin DY. An efficient Monte Carlo approach to assessing statistical significance in genomic studies. Bioinformatics. 2005;21:781–787. doi: 10.1093/bioinformatics/bti053. [DOI] [PubMed] [Google Scholar]
- 15.Cox DR, Snell EJ. A general definition of residuals (with discussion) Journal of the Royal Statistical Society, Series B. 1968;30:248–275. [Google Scholar]
- 16.Schott JR. Matrix Analysis for Statistics. 2nd. Wiley; 2005. [Google Scholar]
- 17.Lagakos SW. The graphical evaluation of explanatory variables in proportional hazard regression models. Biometrika. 1981;68:93–98. [Google Scholar]
- 18.Fisher RA. The Design of Experiments. Olyver and Boyd Edinburgh; 1935. [Google Scholar]
- 19.Anderson MJ, Legendre P. An empirical comparison of permutation methods for tests of partial regression coefficients in a linear model. Journal of Statistical Computation and Simulation. 1999;62:271–303. [Google Scholar]
- 20.Bickel PJ, Klaassen CA, Ritov Y, Wellner JA. Efficient and Adaptive Estimation for Semiparametric Models. Springer; New York: 1998. [Google Scholar]
- 21.Lin DY. On rapid simulation of P values in association studies. American Journal of Human Genetics. 2005;77:513–514. doi: 10.1086/432817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lin DY, Wei LJ. The robust inference for the cox proportional hazards model. Journal of the American Statistical Association. 1989;84:1074–1078. [Google Scholar]
- 23.Li YH, Klein JP, Moeschberger ML. Effects of model misspecification in estimating covariate effects in survival analysis for small sample sizes. Computational Statistics and Data Analysis. 1996;22:177–192. [Google Scholar]
- 24.Klein JP. Competing risks. Wiley Interdisciplinary Reviews: Computational Statistics. 2010;2:333–339. [Google Scholar]
- 25.Dudbridge F. A note on permutation tests in multistage association scans. American Journal of Human Genetics. 2006;78:1094–1095. doi: 10.1086/504527. author reply 1096. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.