Dimensionality Reduction in Controlling Articulated Snake Robot for Endoscopy Under Dynamic Active Constraints

Abstract

This paper presents a real-time control framework for a snake robot with hyper-kinematic redundancy under dynamic active constraints for minimally invasive surgery. A proximity query (PQ) formulation is proposed to compute the deviation of the robot motion from predefined anatomical constraints. The proposed method is generic and can be applied to any snake robot represented as a set of control vertices. The proposed PQ formulation is implemented on a graphic processing unit, allowing for fast updates over 1 kHz. We also demonstrate that the robot joint space can be characterized into lower dimensional space for smooth articulation. A novel motion parameterization scheme in polar coordinates is proposed to describe the transition of motion, thus allowing for direct manual control of the robot using standard interface devices with limited degrees of freedom. Under the proposed framework, the correct alignment between the visual and motor axes is ensured, and haptic guidance is provided to prevent excessive force applied to the tissue by the robot body. A resistance force is further incorporated to enhance smooth pursuit movement matched to the dynamic response and actuation limit of the robot. To demonstrate the practical value of the proposed platform with enhanced ergonomic control, detailed quantitative performance evaluation was conducted on a group of subjects performing simulated intraluminal and intracavity endoscopic tasks.

I. Introduction

IN robot-assisted minimally invasive surgery (MIS), the development of articulated tools to enhance a surgeon’s dexterity combined with intelligent human–robot interaction has significantly improved the consistency and accuracy of surgery. However, the use of traditional long rigid laparoscopic instruments still limits the access and effective workspace of MIS. For this reason, optimal port placement is important, and in some cases, the advantages of MIS are undermined by awkward patient positioning and complex instrument manipulation due to the difficulty of following curved pathways to reach the target anatomical region. The importance of flexible access also becomes evident in the context of emerging surgical techniques, such as natural orifice transluminal endoscopic surgery (NOTES), which aims to accomplish scarless surgical operations through transluminal pathways. One key requirement for NOTES instrumentation is adequate articulation to ensure no tissue damage during insertion and a wide visual exploration angle of the operative site including retroflection [1].

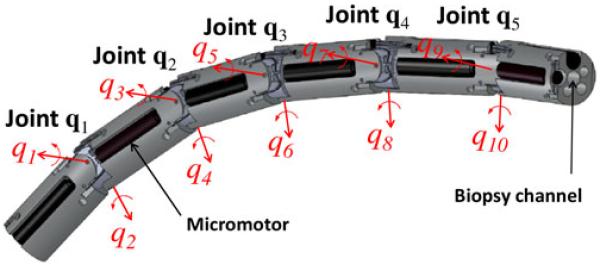
In order to meet these requirements, we developed a lightweight universal-joint-based articulated flexible access platform [2], which has been tested in in vivo trials, as shown in Fig. 1. Fig. 2 illustrates the structure of our snake-like robot prototype that comprises a series of identical link units. Each link embeds two micromotors, which provide angular actuation between two adjacent joints generating relative rotations along perpendicular axes. Hence, the rigid robot links are connected by universal joints, each providing two-degree-of-freedom (DoF) rotational movement within ±q_max = ±45°. Independent actuation of each provides typical hyper-redundant kinematic structure [3]. Furthermore, the robot uses a modular hybrid micromotor-tendon joint design that allows for the integration of multiple internal instrument channels [4]. Although the presence of a large number of DoFs enhances the flexibility and dexterity of the robotic platform, the practical control of the hyper-redundant structure can be difficult because of the large number of possible joint configurations. Most traditional approaches to redundancy resolutions are based on computing the pseudoinverse of the Jacobian matrix, describing the relationship between the desired velocities in the task space, and the angular velocities in the robot joint space. These methods are, therefore, subject to trajectory reconstruction errors, especially in the vicinity of singular configurations, where the Jacobian is rank deficient and the resulting joint velocities can be beyond the physical limit of the robot [5]. To overcome this problem, techniques that are based on augmented [6] or extended [7] Jacobians have been proposed to solve kinematic redundancy by assigning additional tasks together with the end-effector task so that all the available DoFs become necessary. However, these methods are still subject to algorithmic singularities. In addition, the specification of such a large number of additional constraints can be challenging, especially to implement shape conformance tasks that are not only limited to the end-effector motion, but also to the entire length of the robot.

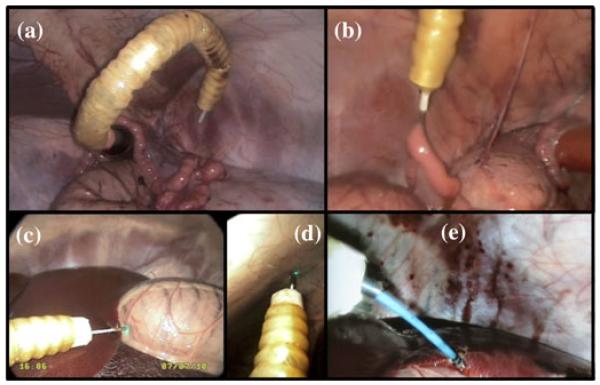
Fig. 1. In vivo trials of the snake robot on a porcine experiment.

(a) and (b) Full retroflexion for grasping the uterine horn. (c) and (d) Probe-based confocal laser endomicroscopy (pCLE) images acquired on the stomach and peritoneum. (e) Endoscopic diathermy conducted on the liver.

Fig. 2. Schematic illustration of the robot showing the articulated joint structure.

Many of the snake-like systems for surgery that have been developed to date are based on tendon-driven or shape memory alloy (SMA) actuation. This simplifies the control complexity by coupling multiple DoFs. Some of the example platforms along with their respective technical features are listed in Table I.

TABLE I. Snake-Like Robots for Minimally Invasive Surgery.

Sources [ref]	Design	Control	Comments
Ikuta et al. [8]	5 segments actuated by SMA wires	SMA actuation for bending in one plane	High currents for actuation, slow forward motion
NeoGuide System Inc. [9]	Flexible endoscope made of identical electromechanically controlled segments	“Follow-the-leader” motion according to pre-recorded tip movements	Difficult ergonomics, complex control and potential endoscope instability
Choset et al. [10]	Two concentric tubes consisting of a series of cylindrical links connected by spherical joint units	“Follow-the-leader” motion by alternating the rigidity of the two tendon-actuated concentric tubes	The joints cannot be actuated independently, slow forward speed and large external feeding mechanism required
Simaan et al. [11]	4 degrees-of-freedom snake-like arms actuated by SMA wires	SMA actuation according to master manipulator motion	Complex control and modelling of SMA actuators, flexibility limited by length and diameter

For procedures such as NOTES, the use of pre- and intraoperative imaging to ensure safe navigation and tissue manipulation is important. When a snake robot is used for such applications, the major technical hurdles to be tackled include

1. path following and shape conformance to anatomical constraints using real-time proximity queries (PQs);

2. motion modeling and parameterization to ensure the ease of control of the robot with standard interfacing devices that typically have a low number of DoFs;

3. matching visual-motor control with the dynamics of the robot to ensure seamless human–robot interaction.

Recent advances in real-time registration [12] and remodeling [13] with the consideration of potential anatomical changes of the model have enabled real-time haptic guidance under active constraints [14] or virtual fixtures (VFs) [15]. A prerequisite of such approaches is the computation of PQs, which is a challenging problem for haptic rendering because of its intrinsic complexity and high update rate required (>1 kHz). Well-known methods including Gilbert–Johnson–Keerthi [16], V-Clip [17], and Lin–Canny [18] require object representation as convex polyhedra to guarantee global convergence. Enhanced approaches have been proposed recently to achieve the required haptic update rate with low Big-O complexity [19], [20]. Under this scheme, the objects have to be represented in more specific formats such as spheres, torus, or convex implicit surfaces. As all of the reported PQ methods require iterative-based algorithms to find the shortest distance between a pair of objects, in order to compute penetration depth whenever the two objects overlap, the computational burden is further increased by the need to estimate the minimum translation required to separate the objects. This makes real-time implementation of the methods difficult and hinders the practical use of VFs to constrain the motion of an entire robot body, which is especially important for a snake robot to conform to curved anatomical pathways during surgical navigation. Thus far, almost all the reported studies on VFs [14], [15], [21], [22] are designed to constrain only a single end-effector. There was no attempt to consider the interaction of the robot body with the surrounding anatomical regions explicitly, except for [23] by Li et al., which modeled the robot instrument as a series of line segments surrounded by a bone cavity. Their PQs were conducted by searching in a covariance tree data structure that cannot be updated if the anatomical geometry is changed intraoperatively since the time to build the tree is relatively long (in minutes), thus limiting its real-time application.

In order to address some of the aforementioned challenges, we have proposed dynamic active constraints (DACs) to navigate generic articulated MIS instruments using accurate forward kinematics [24], [25]. Under this framework, a real-time modeling scheme is used to construct a volumetric pathway that is able to adapt to tissue deformation, thus providing an explicit safety manipulation margin for the entire articulated device, rather than only the tip of the robot.

To extend our previous work, we present in this paper a real-time control framework for a snake robot with hyper-kinematic redundancy for MIS. A new PQ formulation is proposed to compute the deviation of the robot outside the constraint pathway defined by a 3-D anatomical model. The method is generic as it can be applied to any robot shape represented as vertices and not restricted to a convex polygon or other continuity properties. The proposed PQ formulation is also implemented on a graphic processing unit (GPU) computational platform to permit fast update for haptic rendering above 1 kHz. Furthermore, we demonstrate that the robot joint space can be characterized into a lower dimensional space for the optimization of robot articulation within the constrained anatomical pathway. This optimization can be implemented in real time, and a novel motion parameterization in polar coordinates is used to describe the motion transition, thus allowing direct manual control of the robot using only a limited number of DoFs.

Under the proposed framework, the correct alignment between visual and motor axes is also provided. Haptic guidance is provided, not only to ensure safe navigation within the anatomical constraints, but also to enhance smooth pursuit movement by matching the input motion of the manipulator with the dynamic response of the robot based on its physical actuation capabilities. To demonstrate the practical value of the proposed platform, detailed quantitative performance evaluation has been conducted by a group of subjects performing simulated intraluminal and intracavity endoscopic tasks.

II. Clinical Motivation

The drive to reduce patient trauma has led to the development and introduction of minimally invasive techniques such as laparoscopy [26] and single-port surgery, both of which demonstrate significant benefits over the open surgical approach with enhanced recovery for an earlier return to work. With increasing demand on endoscopes, both in terms of routine screening colonoscopy, as well as the emerging NOTES and single-port access techniques, the difficulties of their realization, particularly surrounding the ergonomics, have become increasingly apparent.

In endoscopy, the traditional rear drive mechanism often creates a potential problem where the leading end of the endoscope remains still and the tail is forced into a loop. This causes stretching of the bowel and its attachments, which results in pain. Visual disorientation within the lumen is also significant. An inherent lack of effective instrumental control coupled with a lack of sufficient haptic feedback presents potential patient safety risks. The ability to provide an instrument that maintains the flexibility of the endoscope to enable navigation within the tortuous endoluminal channel constrained through haptic feedback will lead to a more reliable, comfortable and safe diagnostic, or interventional procedure.

Another unique feature of fully articulated MIS instrument is that it enables target sites to be accessed through a single incision distant from the operative site with instruments that are capable of performing minor interventional procedures presented to the target through biopsy channels. This has the potential to expose a platform upon which new surgical treatment options, such as drug delivery or accurate stem cell placement, could capitalize.

Intervention within these spatial environments, however, exposes a further problem. The force that is required to biopsy tissues or drive needles using endoscopic instruments causes the endoscope to move away from the interventional target. This is again associated with the uncontrollable flexibility of the currently used conventional endoscopes. Providing a more stable platform will enable more effective instrumentation delivery, but this has to be provided without compromising the flexibility [1]. All these considerations have led to the exploration of fully controllable flexible devices such as snake robots.

III. Methods

In order to meet the clinical demand, as stated in Section II, detailed technical approaches to address the engineering challenges mentioned earlier will be provided in this section. More specifically, they will address 1) shape conformance and real-time PQs; 2) motion modeling, parameterization, and control of the snake robot; 3) visual-motor and haptic interaction of the robot under DACs.

A. Shape Conformance and Proximity Queries

1) Shape Conformance to Parametric Curve

Given a snake robot with the generic configuration, as shown in Fig. 2, the homogeneous transformation of link i relative to link i − 1 is determined by a joint-angle pair q_i := [q_2i−1, q_2i]^T. This can be expressed as ${}_i{}^{i-1}T\left({\mathbf{q}}_i\right){\forall }_i=\{1,\dots ,L\}$, where L is the total number links forming the robot. To position the robot in the safest region inside a constraint pathway, the robot configuration in joint space has to be computed so that all the joint centers are aligned along the centerline [24], [25]. This is particularly important for transluminal navigation so that the robot is able to kinematically conform to the curvature of the channel to ensure accurate path following. For this paper, the centerline is defined as a curve P(s) with continuous tangent M(s). It is parameterized based on the time-varying control points P_k(t) predefined on a dynamic tissue model. The center of joint i is adjusted to lie on the centerline at point $\mathit{P}\left({\stackrel{‒}{s}}_i\right)$. By implementing the shape-inverse approach that is proposed in [3], we can obtain the robot configuration $\tilde{\mathbf{q}}≔{[{\tilde{\mathbf{q}}}_1,{\tilde{\mathbf{q}}}_2,\dots ,{\tilde{\mathbf{q}}}_L]}^T\in {\Re }^{2L\times 1}$ closest to the centerline. The angular joint limits are also considered so that the joint space solution $\tilde{\mathbf{q}}$ will not exceed the range ±q_max. The transformation of link i relative to the world coordinate frame {w} can be expressed as ${}_i{}^{w}T\left({\tilde{\mathbf{q}}}_{1\dots i}\right)$, where ${\tilde{\mathbf{q}}}_{1\dots i}≔{[{\tilde{\mathbf{q}}}_1,\dots ,{\tilde{\mathbf{q}}}_i]}^T\in {\Re }^{2i\times 1}$. The solution $\tilde{\mathbf{q}}$ is then used as a reference for the optimization of robot configuration during surgical navigation.

2) Formulation of Proximity Queries

To ensure that the robot operates within the prescribed anatomical constraint, real-time PQs need to be performed. The proposed constraint is modeled as a volumetric pathway. Fig. 3(a) shows a single segment Ω_j that comprises two adjacent contours C_j and C_j+1 ${\forall }_j\in [1,\dots ,{\tilde{N}}_C]$. The center of the contour C_j is at the point P_j on the centerline with tangent M_j. The parameterized centerline of the luminal structure can be found using some of the well-established techniques in vascular modeling [27]. These give the intuitive definition of the pose [P(s), M(s)] as well as the radii R(s) of the numerous contours modeled along the navigation pathway. The lower the parameter interval Δs, the higher the resolution of the contour segments. Together with the tessellation of the 3-D boundary to facilitate navigation, PQs between the robot and the constraint pathway are provided for haptic guidance. In addition, these queries are used to define conditions for the optimization of robot configuration within the pathway.

Fig. 3.

(a) Basic structure of a single segment enclosed by two adjacent contours. (b) Portion of cross-sectional region extracted. Four regions to which the points [x₀, x₁, x₂, x₃] belong yield different distance calculations.

In this study, points and segments are considered as primitive components to represent the boundary of the robot body and the constraint pathway, respectively. Therefore, it is necessary to formulate the calculation of distance between a point on the robot body and a constraint segment. In Fig. 3(a), an arbitrary point x on a particular part of the robot body is given, from which the shortest distance δ_j to the segment boundary Ω_j has to be computed. Note that this convex segment is not a conical shape with explicit mathematical expression, but it is a connection of two contours with different poses. Therefore, it is not possible to derive a single closed-form solution for such a distance query. Instead, a computation procedure is proposed as follows.

Step 1: Find the normal of a plane containing points x, P_j, and P_j+1

$${\mathbf{n}}_j=({\mathit{P}}_j-\mathbf{x})\times ({\mathit{P}}_{j+1}-\mathbf{x})$$ (1)

where the symbol “×” denotes a cross product of two vectors in 3-D. This applies when point x ∈ ℜ^3×1 is not collinear with the line segment. Otherwise, simpler distance calculation can be used.

Step 2: Calculate vectors ρ_j and ρ_j+1 that are, respectively, perpendicular to tangents M_j and M_j+1 and both parallel to the plane with normal n_j

$${\rho }_j={\mathbf{n}}_j\times {\mathit{M}}_j,{\rho }_{j+1}={\mathbf{n}}_j\times {\mathit{M}}_{j+1}$$ (2)

Step 3: Determine a four-vertex polygon that is a part of the cross section of segment Ω_j. This section is cut by a plane containing the point x and the line segment P_j → P_j+1. As shown in Fig. 3(b), ^jv_i=1…4 ∈ ℜ^3×1 are the four vertices of the section arranged in a particular order as follows:

$$\begin{array}{cc}\hfill {}_{}{}^j\mathbf{v}_1& ={\mathit{P}}_j,{}_{}{}^j\mathbf{v}_2={\mathit{P}}_j+\left[R_j\right({\widehat{\rho }}_j\left)\right]{\widehat{\rho }}_j\hfill \\ \hfill {}_{}{}^j\mathbf{v}_4& ={\mathit{P}}_{j+1},{}_{}{}^j\mathbf{v}_3={\mathit{P}}_{j+1}+\left[R_{j+1}\right({\widehat{\rho }}_{j+1}\left)\right]{\widehat{\rho }}_{j+1}\hfill \end{array}$$ (3)

where the caret ^ denotes that the vector is normalized with respect to its length. As shown in Fig. 3(a), the contour can be a complex polygon that is represented in polar coordinates by the radial function $R_j\left({\widehat{\rho }}_j\right)$; therefore, the resultant distance calculated in step 6 will become an approximation of the actual value, but without affecting the correctness of the procedure in step 4. For the anatomical structure of the lumen, a constant function $R_j\left({\widehat{\rho }}_j\right)=r_j$ is used so that the contour results in a circle.

Step 4: As point x lies on the same plane formed by the four vertices ^jv_i=1…4, the procedure to determine whether the point is inside the polygon can be simplified by projecting the points in 2-D coordinates. This simplification allows faster computation of the queries without loss of generality. The projection is simply onto one of the 2-D planes of XY, YZ, or ZX, implying that one of the coordinate elements X, Y, or Z can be neglected. To avoid projecting the polygon into a very narrow structure like a line segment, which adversely affects the accuracy of the query, the normal n_j = [n_xj, n_yj, n_zj]^T of the plane containing x and ^jv_i=1…4 is used as an indicator to determine which coordinate has to be neglected. Let ${{}^j\stackrel{‒}{\mathbf{v}}}_i=[{{}^j\stackrel{‒}{v}}_{xi},{{}^j\stackrel{‒}{v}}_{yi},{{}^j\stackrel{‒}{v}}_{zi}]$ be the vertices offset by x, i.e., ${{}^j\stackrel{‒}{v}}_i={{}^j\mathbf{v}}_i-\mathbf{x}$. Based on the coordinates of n_j, for example, if |n_zj| = max {|n_xj|, |n_yj|, |n_zj|} the determinant λ_i of the adjacent 2-D vertices i and i + 1 can be computed as follows:

$${\lambda }_{i=1,\dots ,4}={}_{}{}^j\stackrel{‒}{v}_{x(i+1)}\cdot {}_{}{}^j\stackrel{‒}{v}_{yi}-{}_{}{}^j\stackrel{‒}{v}_{xi}\cdot {}_{}{}^j\stackrel{‒}{v}_{y(i+1)}$$ (4)

where ^xv₅ := ^xv₁. Referring to [28], we can determine whether point x is inside the polygon by looking at the sign of λ_i, as in (5). The shortest distance δ_j from point x to segment Ω_j will then be considered as zero if the point is inside the polygon; otherwise, δ_j > 0 and the algorithm will move to the next step

$${\delta }_j\left(\mathbf{x}\right)=0,\text{if}\forall {\lambda }_{i=1\dots 4}\ge 0\text{or}\forall {\lambda }_{i=1\dots 4}\le 0$$ (5)

Step 5: When point x is outside the polygon, the closest point on the segment Ω_j lies on the segment boundary, particularly on the line segment between vertices ^jv₂ and ^jv₃. Therefore, if point x is outside the polygon, the parameter ^jμ ∈ ℜ from (6) is used to linearly interpolate the line segment ^jv₂ → ^jv₃ so that x′ = (1 − ^jμ)^jv₂ + ^jμ · ^jv₃, where x′ is the perpendicular projection of x on the line segment

$${}_{}{}^j\mu =-\frac{\text{dot}\left\{\right({}_{}{}^j\mathbf{v}_2-\mathbf{x}),({}_{}{}^j\mathbf{v}_3-{}_{}{}^j\mathbf{v}_2\left)\right\}}{{\parallel {}_{}{}^j\mathbf{v}_3-{}_{}{}^j\mathbf{v}_2\parallel }^2}$$ (6)

Step 6: For point x′ lying between ^jv₂ and ^jv₃ so that ^jμ ∈ [0, 1], the shortest distance to segment Ω_j is obtained as the point-to-line distance [see Fig. 3(b)]

$${\delta }_j\left(\mathbf{x}\right)=\parallel \mathbf{x}-\left[\right(1-{}_{}{}^j\mu ){}_{}{}^j\mathbf{v}_2+{}_{}{}^j\mu \cdot {}_{}{}^j\mathbf{v}_3]\parallel$$ (7)

For ^jμ < 0, δ_j=∥x − ^jv₂∥, while if ^jμ > 1, then δ_j = ∥x − ^jv₃∥.

Step 7: As explained previously, the robot is represented by a set of surface vertices. Let the vertex coordinates be ${\mathbf{x}}_i^l$, i = 1, …, V_l, where V_l is the number of vertices on link l. The deviation distance of a single coordinate ${\mathbf{x}}_i^l$ from the constraint segments {Ω_k+1, …, Ω_k+Δk} can be computed as follows:

$${{}_i{}^l\delta }_{k,\Delta k}=\underset{j}{\min }\left\{{\delta }_{k+1}\right({\mathbf{x}}_i^l),{\delta }_{k+2}({\mathbf{x}}_i^l),\dots ,{\delta }_{k+\Delta k}({\mathbf{x}}_i^l\left)\right\}$$ (8)

where Δk is the number of segments involved in the calculation. The maximum deviation among all the vertices on robot link l, which is also called penetration depth, is then finally obtained as follows:

$$d_l^{k,\Delta k}=\underset{i=1,\dots ,V_l}{\max }\left\{{{}_i{}^l\delta }_{k,\Delta k}\right({\mathbf{x}}_i^l\left)\right\}$$ (9)

3) Proximity Queries Accelerated by GPU

The proposed PQ algorithm is intrinsically parallel, and the computation time can be significantly reduced when using a parallel architecture such as a GPU. The GPU employs the single-instruction multiple data architecture and contains multiple processors. Each processor consists of multiple floating point units (FPUs) and is able to execute multiple threads with the same instruction stream but different input data. In this study, we develop a parallel GPU-based design system to accelerate our PQ algorithm. The process in (1)-(7) is repeated for all the constraint segments and for every vertex on the boundary. Equations (8) and (9) are used to find the min/max values after all distances are computed. The computation kernel is outlined in the pseudocode.

All geometry computations are based on 3-D vectors in IEEE-754 double-precision format in order to achieve sufficient accuracy. The inner loop body contains 115 ADD/SUB/MULT operations, two DIV operations and three SQRT operations. Solving the performance bottleneck for n × m iterations becomes our main objective to implement an efficient GPU design. The acceleration is mainly achieved by distributing computations to different threads and executing GPU’s processors in parallel. Thus, the workload partitioning scheme has a significant effect on the final performance. Only the outer loop is partitioned such that each thread will process a few vertex points. The number of threads assigned to GPU’s processors depends on the resource utilization of our kernel. In the first kernel, we load the data of the constraint segment into the shared memory within each GPU’s processor before the computation starts. Since these data are referenced multiple times throughout the kernel, the use of this low latency and high-performance shared memory will significantly reduce memory access overhead. Various techniques, such as data reuse and common expression sharing, are also employed in this kernel to improve performance.

The results of the first kernel are written back to the external memory of the GPU card. The global memory space allows the second kernel to use these results directly without data transfer overhead between the host PC and the GPU. In the second kernel, we assign the computation of one link to a single-GPU processor. This eliminates the need of synchronization between processors. A parallel algorithm with complexity O (log₂(n)), which is similar to the parallel reduction design from nVidia [29], is used to find the maximum values in (9). The results are also stored in the external memory for the host to read.

B. Motion Modeling, Parameterization, and Control

1) Characterization of Robot Bending

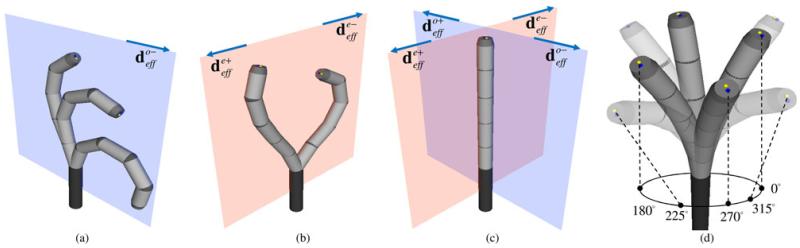
A common requirement of endoscopic navigation is to ensure that the tip is fully articulated to provide both forward vision and direct inspection of the wall from a nearly perpendicular configuration. By exploiting the kinematic redundancy of our robot, we take advantage of different bending configurations to obtain optimal visualization of the deforming anatomical structure. Provided with a serial kinematic structure, such a configuration can be mathematically characterized by the gradual change of joint values from proximal to distal joints. We consider that only a certain number of distal joints $\stackrel{⌢}{L}$ are directly manipulated by the user, while the proximal joint values are determined through the shape conformance algorithm introduced in Section III-A as ${\tilde{\mathbf{q}}}_{L-\stackrel{⌢}{L}+1\dots L}$. The optimal configuration of the distal joints is instead denoted by $\Delta \mathbf{q}≔{[\Delta {\mathbf{q}}_1,\dots ,\Delta {\mathbf{q}}_{\stackrel{⌢}{L}}]}^T\in {\Re }^{2\stackrel{⌢}{L}\times 1}$, where Δq_i = [Δq_2i−1, …,Δq_2i]^T and $L\ge \stackrel{⌢}{L}$. As shown in Fig. 2, each universal joint comprises two DoFs with odd and even joint indices. Since the corresponding joint axes are parallel to each other when the robot is in a straight configuration, actuation of either odd or even joint angles along the robot structure yields a planar motion, as shown in Fig. 4(a) and (b). These two motion planes are orthogonal to each other, as shown in Fig. 4(c). For panoramic exploration, the linear combination of such independent odd- and even-joint angles actuation can generate a wide range of configurations in different bending directions, as shown in Fig. 4(d). Each of these configurations can be represented by a linear gradient. The main advantage of this model is that only two parameters, namely the slope m and the intercept of angular value q_c, are required to control the amount of bending. Therefore, to conform to different parts of the navigation channel, the joint values Δq are modeled and adjusted by the two variables (m, q_c) according to

$$\Delta q_i^e(m,q_c)=\{\begin{array}{cc}m(i-2\stackrel{⌢}{L})+q_c,\hfill & \text{if}i\text{is even}\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$ (10)

where $\Delta {\mathbf{q}}^e={[\Delta q_1^e,\Delta q_2^e,\dots ,\Delta q_{2\stackrel{⌢}{L}}^e]}^T$ represents the bending configuration applied to the joint angles with even indices and contains all zeros for the joint angles with odd indices. Assuming the robot is in a straight configuration when $\tilde{\mathbf{q}}=\overrightarrow{0}$, we can derive the end-effector position ^lx_eff ∈ ℜ³ relative to the link frame $\{l=L-\stackrel{⌢}{L}\}$ given by Δq^e as follows:

$${[{}_{}{}^l\mathbf{x}_{\mathrm{eff}},1]}^T={}_L{}^{l}T\left(\Delta {\mathbf{q}}^e\right(m,q_c\left)\right){[\overrightarrow{0},1]}^T$$ (11)

The corresponding displacement of the end-effector can then be expressed as follows:

$${\mathbf{d}}_{\mathrm{eff}}={}_{}{}^l\mathbf{x}_{\mathrm{eff}}\left(\Delta {\mathbf{q}}^e\right(m,q_c\left)\right)-{}_{}{}^l\mathbf{x}_{\mathrm{eff}}\left(\Delta {\mathbf{q}}^e\right(0,0\left)\right)$$ (12)

With m = 0 and a small value ±ε assigned to q_c, we have

$${\mathbf{d}}_{\mathrm{eff}}^{e\pm }={\mathbf{d}}_{\mathrm{eff}}\left(\Delta {\mathbf{q}}^e\right(0,q_c\left){\mid }_{q_c=\pm \epsilon }\right)$$ (13)

Fig. 4(b) shows that the two resultant configurations are bending in opposite directions. With the condition of i being odd applied to (10)-(12), this odd-index bending effect spans perpendicularly to the one given by even angles, as shown in Fig. 4(a). In total, four basic displacements $\{{\mathbf{d}}_{\mathrm{eff}}^{e+},{\mathbf{d}}_{\mathrm{eff}}^{o+},{\mathbf{d}}_{\mathrm{eff}}^{e-},{\mathbf{d}}_{\mathrm{eff}}^{o-}\}$ are defined to determine the optimal amount of bending in }different quadrants [see Fig. 4(d)], thus allowing panoramic exploration by manipulating the camera at the robot tip.

Fig. 4.

(a) Three sets of variables (m, q_c): (−0.13, −55°), (−0.23, −109.7°), and (−0.18, −119.7°) generate three bending configurations with ascending curvature through the of odd joint axes in one direction. (b) Two bending configurations corresponding to the actuation of even joint angles in opposite directions, parameterized as +ve: (0.31°, 112.9°), −ve: (−0.11, −34.7°). (c) Motion planes spanned by even and odd joint angle actuation are perpendicular to each other. Their intersection is aligned with the robot axis in the straight configuration $\stackrel{⌢}{\mathbf{q}}=\overrightarrow{0}$. Four primitive bending directions are indicated. (d) Four primitive bending configurations with (m, q_c) = (0, ±5°) are represented in solid color. The other four configurations displayed in semitransparent color are generated between the four primitive configurations by assigning (α, β) = (0.25, 3.35).

2) Constrained Optimization of Robot Configuration

In addition to panoramic exploration, robot bending must be confined within the anatomical channel to avoid discomfort [30], [31] to the patient, especially during unsedated endoscopy. The constraint pathway closely fitting with the anatomical structure can be implemented as a safety margin to optimize the bending angles, thus providing diversified viewing directions while ensuring safe navigation. The search of values for variables (m, q_c) within the range of optimal bending can be formulated as a minimization problem. Although a number of metrics could be used to define the objective function to minimize, we notice that the position of the robot end-effector with respect to the reference frame attached at the robot base is only determined by the particular bending configuration. Specifically, the cost function can be simply represented by the z-coordinate of ^lx_eff, namely ^lz_eff, normalized by its maximum value z_max when the robot is straight $(\stackrel{⌢}{\mathbf{q}}=\overrightarrow{0})$:

$$(\stackrel{⌢}{m},\stackrel{⌢}{q_c})=\arg \underset{m,q_c}{\min }\left\{\frac{1}{z_{\max }}{}_{}{}^{l}z_{\mathrm{eff}}\left(\Delta {\mathbf{q}}^e\right(m,q_c\left)\right)\right\}$$ (14)

where $z_{\max }={{}^{l}z}_{\mathrm{eff}}\left(\overrightarrow{0}\right)$. This is valid assuming that the z-axis of the end-effector frame is aligned with the positive z-axis of the base coordinate frame $\{l=L-\stackrel{⌢}{L}\}$ when the robot is in a straight configuration so that the smaller the value of ^lz_eff, the greater the robot bending necessary to retroflex the end-effector toward the robot base. In addition, the bending configuration is limited by the permitted deviation from the constraint pathway. This deviation range is applied to the minimization process as a nonlinear constraint. Therefore, the search for appropriate values of m and q_c in (14) is aimed to find the maximum allowable robot bending within the spatial constraint. The deviation distance is calculated using the fast PQ algorithm that is proposed earlier. To minimize the computational cost, this query involves only the constraint segments possibly enclosing the distal links from $L-\stackrel{⌢}{L}+1$ to L. Once the series of segments {Ω_k+1, …, Ω_k+Δk} is selected, the distance from the constraint is calculated, as in (8).

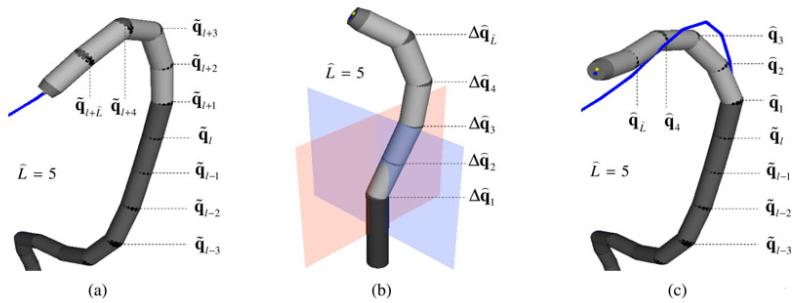
The positions of the surface vertices evenly covering robot link l can be automatically selected from the CAD model. They are only affected by the joint values q_1…l = [q₁, q₂, …, q_2l]^T; therefore, the maximum deviation d_l deduced from (9) will also be determined by joint values q_1…l. When considering the deviation caused by the distal $\stackrel{⌢}{L}$ links when the bending configuration Δq_i is applied to the corresponding joint values ${\tilde{\mathbf{q}}}_{L-\stackrel{⌢}{L}+1\dots L}$, as shown in Fig. 5(a), the robot vertices ${{}^{l+i}\mathbf{x}}_{i=1\dots V_l}^{l+i}$ on link l + i relative to link frame {l + i} will be transformed to the world frame {w} as follows:

$${[{\mathbf{x}}_{i=1\dots V_l}^{l+i},1]}^T={}_l{}^{w}T\left[{}_{l+i}{}^{l}T\right({\tilde{\mathbf{q}}}_{l+1\dots l+i}+\Delta {\mathbf{q}}_{1\dots i}\left)\right]{[{}_{}{}^{l+i}\mathbf{x}_{i=1\dots V_l}^{l+i},1]}^T$$ (15)

Therefore, the distance constraint for the distal links $i=1,\dots ,\stackrel{⌢}{L}$ can be expressed as follows:

$$D_i^{k,\Delta k}=d_{l+i}^{k,\Delta k}\left({\mathbf{x}}_{j=1\dots V_l}^{l+i}({\tilde{\mathbf{q}}}_{l+1\dots l+i}+\Delta {\mathbf{q}}_{1\dots i})\right)$$ (16)

where $l=L-\stackrel{⌢}{L}$. Note that every element of (${\tilde{\mathbf{q}}}_{l+1\dots l+i}+\Delta {\mathbf{q}}_{1\dots i}$) will be limited by the physical bounds ±q_max. The deviation function $D_i^{m,\Delta m}$ determined by the bending configuration is bound by real values b_i, which define the range of minimization constraints. These values can be set depending on the risk of tissue damage correlated with the specific surgical procedure. Usually, the value $b_{\stackrel{⌢}{L}}$ for the last distal link is low compared with other links in order to avoid tissue perforation caused by the tip of the robot [32]. Combined with the requirement for the robot to bend in the direction of ${\mathbf{d}}_{\mathrm{eff}}^{e+}$, a nonlinear constraint that is defined as follows needs to be applied to the minimization in (14)

$$\{\begin{array}{cc}{D}_i^{k,\Delta k}({\tilde{\mathbf{q}}}_{l+1\dots l+i}+\Delta {\mathbf{q}}_{1\dots i}^e(m,q_c\left)\right)\le b_i,\hfill & i=1,\dots ,\stackrel{⌢}{L}\hfill \\ {\mathbf{d}}_{\mathrm{eff}}\left(\Delta {\mathbf{q}}^e\right(m,q_c\left)\right)\cdot {\mathbf{d}}_{\mathrm{eff}}^{e+}>0\hfill & \hfill \end{array}$$ (17)

The corresponding optimal bending configuration is finally obtained as $\Delta \stackrel{⌢}{\mathbf{q}}{}^{e+}(\stackrel{⌢}{m},\stackrel{⌢}{q_c})$. Following the same procedure, we can determine four basic optimal configurations {$\Delta \stackrel{⌢}{\mathbf{q}}{}^{e+}$, $\Delta \stackrel{⌢}{\mathbf{q}}{}^{e-}$, $\Delta \stackrel{⌢}{\mathbf{q}}{}^{o+}$, $\Delta \stackrel{⌢}{\mathbf{q}}{}^{o-}$}, corresponding to opposite bending directions in the even and odd joint axes motion planes, respectively.

Fig. 5.

(a) Configuration $\tilde{\mathbf{q}}$ conforming to a part of the pathway along the colon below the splenic flexure. (b) Bending configuration $\Delta \stackrel{⌢}{\mathbf{q}}(\alpha ,\beta )$ is a combination of odd and even joint angle values; therefore, it spans a different motion plane from the ones shown in Fig. 4(c). It is also one of the optimized configurations within the spatial constraint. (c) By superposing the two configurations in (a) and (b), the resultant configuration $\stackrel{⌢}{\mathbf{q}}={\tilde{\mathbf{q}}}_{l+1\dots l+\stackrel{⌢}{L}}+\Delta {\mathbf{q}}_{1\dots \stackrel{⌢}{L}}$ is obtained, which determines the bending of the last $\stackrel{⌢}{L}$ links due to external manipulation. The remaining joints are fixed as ${\tilde{\mathbf{q}}}_{1\dots l}$ to ensure conformance to the constraint pathway.

Except for the deviation constraint D_i, the minimization is not affected by the spatial constraints adapting to the anatomical environment, but mainly by the number of links $\stackrel{⌢}{L}$ involved in the manipulation. This is because both the cost function in (14) and the displacement function d_eff only depend on the distal joint variables Δq. As the cost function is well formulated and its gradient can be computed as a closed-form expression, the search can be efficiently performed by a number of general solvers such as branch and bound algorithms [33]. The search strategy used in this study and its performance will be discussed in detail in Section IV-B.

3) Robot Shape Parameterization

To simplify the navigation of the robot end effector along a 3-D surface, it is possible to represent the surface using only two variables by calculating a 2-D interpolation of the control points in ${\Re }^{2\stackrel{⌢}{L}}$. However, many existing methods, such as 2-D splines, require the control points to be arranged on a regular 2-D grid [34]. Such an arrangement highly restricts the flexibility in choosing the control points, especially when describing nonuniform surfaces. The correct fusion of modeled high-dimensional patches is also an important concern to provide a smooth motion transition when varying the two parameters. In particular, we require that the resultant interpolation is globally continuously differentiable in C^∞ so that the smoothness of the manipulation is guaranteed also at the joint velocity and acceleration level. Therefore, we propose a modified Hermite interpolation method that parameterizes the optimal bending configuration in the polar coordinates (r, ϑ).

To ensure that the robot body conforms to the constraint pathway when external manipulation is not enabled, the optimal bending configuration is superimposed on the initial configuration ${\tilde{\mathbf{q}}}_{l+1\dots L}$ determined by the shape conformance algorithm so that $\stackrel{⌢}{\mathbf{q}}={\tilde{\mathbf{q}}}_{l+1\dots L}+\Delta \text{q}$ denotes the resultant robot configuration. By adding the optimal configurations {$\Delta \stackrel{⌢}{\mathbf{q}}{}^{e+}$, $\Delta \stackrel{⌢}{\mathbf{q}}{}^{o+}$, $\Delta \stackrel{⌢}{\mathbf{q}}{}^{e-}$, $\Delta \stackrel{⌢}{\mathbf{q}}{}^{o-}$} to ${\tilde{\mathbf{q}}}_{l+1\dots L}$, we obtain four $(=\stackrel{⌢}{n})$ corresponding control bending configurations {$\stackrel{⌢}{\mathbf{q}}{}^{e+}$,$\stackrel{⌢}{\mathbf{q}}{}^{o+}$, $\stackrel{⌢}{\mathbf{q}}{}^{e-}$, $\stackrel{⌢}{\mathbf{q}}{}^{o-}$} either clockwise or anticlockwise within the motion planes of even and odd joint axes. Again, the range of joint movement is also considered so that each $\stackrel{⌢}{q}{}_i$ is limited by ±q_max. These four bending configurations can be represented in polar form for our interpolation as $\stackrel{⌢}{\mathbf{q}}{}^{(1,{\vartheta }_{j=1\dots 4})}=\{\stackrel{⌢}{\mathbf{q}}{}^{(1,0)},\stackrel{⌢}{\mathbf{q}}{}^{(1,\pi ∕2)},\stackrel{⌢}{\mathbf{q}}{}^{(1,\pi )},\stackrel{⌢}{\mathbf{q}}{}^{(1,3\pi ∕2)}\}$, corresponding to four viewing directions separated by 90° rotation with the assignment of r = 1 for a circular constraint. However, for some complex anatomical structures, in which the spatial constraint cannot be approximated by segments with simple circular contours, we represent contours in polar coordinates so that more control configurations can be used to describe the corresponding more complicated transition. By averaging two consecutive optimal bending configurations $\Delta \stackrel{⌢}{\mathbf{q}}{}^{(r,{\vartheta }_j)}$ and $\Delta \stackrel{⌢}{\mathbf{q}}{}^{(r,{\vartheta }_{j+1})}$, we obtain

$$\begin{array}{cc}\hfill \Delta {\stackrel{‒}{q}}^{(r,{\varphi }_j)}& =\frac{1}{2}\left(\Delta \stackrel{⌢}{\mathbf{q}}{}^{(r,{\vartheta }_j)}+\Delta \stackrel{⌢}{\mathbf{q}}{}^{(r,{\vartheta }_{j+1})}\right),j=1,\dots ,\stackrel{⌢}{n}\hfill \\ \hfill s.t.{\vartheta }_{\stackrel{⌢}{n}+1}& ≔{\vartheta }_1\text{and}{\varphi }_j≔\frac{1}{2}({\vartheta }_j+{\vartheta }_{j+1})\hfill \end{array}$$ (18)

Finally, by introducing two parameters (α, β) to scale every value of $\Delta {\stackrel{‒}{\mathbf{q}}}^{(r,{\varphi }_j)}$, we can devise a new bending configuration Δq^(r,ϕ_j) as

$$\begin{array}{c}\hfill \Delta q_i^{(r,{\varphi }_j)}=\left[(\beta -\alpha )\frac{i}{2\stackrel{⌢}{L}}+\alpha \right]\Delta {\stackrel{‒}{q}}_i^{(r,{\varphi }_j)}\hfill \\ \hfill i=1,\dots ,2\stackrel{⌢}{L},\alpha >0\text{and}\beta >0\hfill \end{array}$$ (19)

By restricting α and β to be positive, we ensure that the new configuration will bend in a consistent direction between the two consecutive control bending configurations. Fig. 4(d) shows four intermediate bending configurations at polar angles ϕ_j of 45°, 135°, 225°, and 315°. The optimal parameters α and β can be found by minimizing the same cost function as in (14) and considering the deviation constraint (17) but performing the search in a different domain

$$\begin{array}{cc}\hfill & (\stackrel{⌢}{\alpha },\stackrel{⌢}{\beta })=\arg \underset{\alpha ,\beta >0}{\min }\left\{{}_{}{}^{l}z_{\mathrm{eff}}\right(\Delta {\mathbf{q}}^{(r,{\varphi }_j)}(\alpha ,\beta )\left)\right\}\hfill \\ \hfill & s.t.D_i^{k,\Delta k}({\tilde{\mathbf{q}}}_{l+1\dots l+i}+\Delta {\mathbf{q}}_{1\dots i}^{(r,{\varphi }_j)}(\alpha ,\beta \left)\right)\le b_i,i=1,\dots ,\stackrel{⌢}{L}\hfill \end{array}$$ (20)

where the same optimization solver used to find (m, q_c) is adopted. With a new bending configuration $\Delta \stackrel{⌢}{\mathbf{q}}{}^{(r,{\varphi }_j)}(\stackrel{⌢}{\alpha },\stackrel{⌢}{\beta })$ optimized as in Fig. 5(b), a list of control bending configurations $\left\{\stackrel{⌢}{\mathbf{q}}{}^{(r,{\vartheta }_j)}\right\}$ will then be updated by adding $\stackrel{⌢}{\mathbf{q}}{}^{(r,{\varphi }_j)}={\tilde{\mathbf{q}}}_{l+1\dots L}+\Delta \stackrel{⌢}{\mathbf{q}}{}^{(r,{\varphi }_j)}$ so that $\stackrel{⌢}{n}$ will be increased by 4. Fig. 5(c) shows a resultant bending configuration. Once the number of control configurations is fixed, we can describe the motion transition among them for panoramic visualization using cubic Hermite spline interpolation. For example, within the domain of ν, the vector of Hermite basis functions in the interval [ϑ_i, ϑ_i+1] can be denoted by

$$\begin{array}{cc}\hfill & H_{{\vartheta }_i}^{{\vartheta }_{i+1}}\left(\vartheta \right)≔{\left[h_1\right(u),\dots ,h_4(u\left)\right]}^T\in {\Re }^{4\times 1}\hfill \\ \hfill & s.t.u={\frac{\vartheta -{\vartheta }_i}{{\vartheta }_{i+1}-{\vartheta }_i}\mid }_{{\vartheta }_i\le \vartheta \le {\vartheta }_{i+1}}\in [0,1]i=1,\dots ,\stackrel{⌢}{n},{\vartheta }_{\stackrel{⌢}{n}+1}≔{\vartheta }_1\hfill \end{array}$$ (21)

Given the parameter r, the parametric configuration in the domain of ν can be expressed as

$$\begin{gathered} {ϴ}_r\left(\vartheta \right)=[\stackrel{⌢}{\mathbf{q}}{}^{(r,{\vartheta }_i)},(\stackrel{⌢}{\mathbf{q}}{}^{(r,{\vartheta }_{i+1})}-\stackrel{⌢}{\mathbf{q}}{}^{(r,{\vartheta }_{i-1})}),\stackrel{⌢}{\mathbf{q}}{}^{(r,{\vartheta }_{i+1})},(\stackrel{⌢}{\mathbf{q}}{}^{(r,{\vartheta }_i)}-\stackrel{⌢}{\mathbf{q}}{}^{(r,{\vartheta }_{i+2})}\left)\right]\cdot H_{{\vartheta }_i}^{{\vartheta }_{i+1}}\left(\vartheta \right) \\ i=1,\dots ,\stackrel{⌢}{n} \end{gathered}$$ (22)

where $[{\vartheta }_{\stackrel{⌢}{n}+1},{\vartheta }_{\stackrel{⌢}{n}+2},{\vartheta }_0]≔[{\vartheta }_1,{\vartheta }_2,{\vartheta }_{\stackrel{⌢}{n}}]$ and ${ϴ}_r\in {\Re }^{2\stackrel{⌢}{L}\times 1}$. As the control bending configurations $\stackrel{⌢}{\mathbf{q}}{}^{(1,{\vartheta }_i)}$ are arranged on the radius coordinate at r = 1, ϴ_{r = 1}(ϑ) is exploited to construct their cubic Hermite spline interpolation on the basis of (22). The 2-D polar Hermite function varying for r ∈ [0, 1] and ν ∈ [0, 2π) is then defined as follows:

$$\mathbf{Q}(r,\vartheta )=[\stackrel{⌢}{\mathbf{q}}{}^{(0,0)},({ϴ}_1\left(\vartheta \right)-{ϴ}_1(\vartheta -\pi )),{ϴ}_1(\vartheta \left)\right({ϴ}_1\left(\vartheta \right)-\stackrel{⌢}{\mathbf{q}}{}^{(0,0)}\left)\right]\cdot H_0^1\left(r\right)$$ (23)

Therefore, the value of r represents the bending curvature so that $\stackrel{⌢}{\mathbf{q}}{}^{(0,0)}={\tilde{\mathbf{q}}}_{l+1\dots L}$.

C. Visual-Motor and Haptic Interaction Under Dynamic Active Constraints

Once the anatomical constraints and the controlled articulation of the robot are defined, it is important to ensure a seamless visual motor control of the robot with haptic feedback. To this end, it is necessary to consider visual-motor coordination and matched dynamic response of the robot with haptic interfaces.

1) Incorporation of Visual-Motor Coordination

The visual field is determined by the miniaturized camera placed at the tip of the flexible instrument. The relative pose of the camera is affected by the joint configuration during motion. During surgical navigation, it is also important to ensure stable visual-motor coordination in order to avoid disorientation. Disorientation can in fact pose significant challenges on the robot control, especially when the instrument is articulated. Since the camera is integrated at the robot tip, a constant transformation representing a small linear translation of the camera frame relative to the robot end-effector frame can be expressed as ${}_C{}^{L}T$. The camera position relative to the link frame $\{l=L-\stackrel{⌢}{L}\}$ is, therefore, given as

$${[{}_{}{}^l\mathbf{x}_C,1]}^T={}_C{}^{l}T\left(\stackrel{⌢}{\mathbf{q}}\right){[\overrightarrow{0},1]}^T$$ (24)

where ${}_C{}^{l}T\left(\stackrel{⌢}{\mathbf{q}}\right)={}_L{}^{l}T\left(\stackrel{⌢}{\mathbf{q}}\right){}_C{}^{L}T$ and ${{}^l\mathbf{x}}_C={[{{}^{l}x}_C,{{}^{l}y}_C,{{}^{l}z}_C]}^T$. To provide intuitive manipulation of the camera pose without causing disorientation, 2-D input motions by the operator have to be mapped to the coordinates of the camera plane. The gradients of the camera 3-D position with respect to the joint space are denoted by

$$\nabla {}_{}{}^l\mathbf{x}_C\left(\stackrel{⌢}{\mathbf{q}}\right)=\left[\frac{\partial {}_{}{}^l\mathbf{x}_C}{\partial \stackrel{⌢}{q}{}_1},\cdots ,\frac{\partial {}_{}{}^l\mathbf{x}_C}{\partial \stackrel{⌢}{q}{}_{2\stackrel{⌢}{L}}}\right]\in {\Re }^{3\times 2\stackrel{⌢}{L}}$$ (25)

These gradient vectors are also considered as the 3-D camera displacement yielded by fine adjustment of every joint value. Since they are computed relatively to the link frame $\{l=L-\stackrel{⌢}{L}\}$, the transformation to camera frame {C} is required for the purpose of manipulation

$$\nabla {}_{}{}^C\mathbf{x}_C={}_l{}^C\mathbf{R}\left(\stackrel{⌢}{\mathbf{q}}\right)\nabla {}_{}{}^l\mathbf{x}_C\left(\stackrel{⌢}{\mathbf{q}}\right)$$ (26)

where ∇^Cx_C = [∇^Cx_C, ∇^Cy_C, ∇^Cz_C]^T, and ${}_l{}^C\mathit{R}\left(\stackrel{⌢}{\mathbf{q}}\right)={}_C{}^l{\mathit{R}}^T\left(\stackrel{⌢}{\mathbf{q}}\right)$ is the rotation matrix of ${}_C{}^{l}T\left(\stackrel{⌢}{\mathbf{q}}\right)$ in (24). In the parameter space, the gradient of the parameterized bending configuration is denoted by

$$\nabla \mathbf{Q}(r,\vartheta )=\left[\frac{\partial \mathbf{Q}}{\partial r},\frac{\partial \mathbf{Q}}{\partial \vartheta }\right]\in {\Re }^{2\stackrel{⌢}{L}\times 2}$$ (27)

The closed form of the partial derivatives can be obtained by differentiating the vectors of Hermite basic functions in (22) and (23). Since the basic functions h_i=1,…4(.) are all globally continuously differentiable in C^∞, both $\partial H_{{\vartheta }_i}^{{\vartheta }_{i+1}}\left(\vartheta \right)∕\partial \vartheta$ and $\partial H_0^1\left(r\right)∕\partial r$ are well defined. Assuming that the principal axis of the camera is along the z-axis of the camera frame, the 2-DoF input motion only needs to be mapped to the movement along the image plane. The inverse Jacobian from the input motion (δ^C x_C, δ^C y_C) to the output configuration that determines the robot bending due to manipulation can be obtained as

$$\begin{array}{cc}\hfill \left[\begin{array}{c}\hfill \delta r\hfill \\ \hfill \delta \vartheta \hfill \end{array}\right]& =J^{-1}(r,\vartheta )\left[\begin{array}{c}\hfill {\delta }^C{x}_C\hfill \\ \hfill {\delta }^C{y}_C\hfill \end{array}\right]\hfill \\ \hfill s.t.J(r,\vartheta )& =\left[\begin{array}{cc}\hfill {\nabla }^C{x}_C\left(\stackrel{⌢}{\mathbf{q}}\right)\frac{\partial \mathbf{Q}}{\partial r}\hfill & \hfill {\nabla }^C{x}_C\left(\stackrel{⌢}{\mathbf{q}}\right)\frac{\partial \mathbf{Q}}{\partial \vartheta }\hfill \\ \hfill {\nabla }^C{y}_C\left(\stackrel{⌢}{\mathbf{q}}\right)\frac{\partial \mathbf{Q}}{\partial r}\hfill & \hfill {\nabla }^C{y}_C\left(\stackrel{⌢}{\mathbf{q}}\right)\frac{\partial \mathbf{Q}}{\partial \vartheta }\hfill \end{array}\right]\in {\Re }^{2\times 2}\hfill \end{array}$$ (28)

where $\stackrel{⌢}{\mathbf{q}}=\mathbf{Q}(r,\vartheta )$. At every time step Δt of the high-frequency (>1 kHz) iteration, the incremental movement (δ^C x_C, δ^C y_C) input by the operator is small and yields a new (δr, δϑ) based on the mapping in (28) such that r(t + Δt) = r(t) + δr and ϑ(t + Δt) = ϑ(t) + δϑ. To avoid singularity at r = 0 causing $\partial \mathbf{Q}(0,\vartheta )∕\partial \vartheta =\overrightarrow{0}$, a small value ε⁺ is set as a lower bound for the parameter r

$$r(t+\Delta t)=\{\begin{array}{cc}{\epsilon }^{+},\hfill & \text{if}\mid r\left(t\right)+\delta r\mid <{\epsilon }^{+}\hfill \\ r\left(t\right)+\delta r,\hfill & \text{otherwise}\hfill \end{array}$$ (29)

In order to keep the value of r in the positive range, the symmetry of the polar form interpolation is imposed so that for r(t) + δr < 0, where r(t) ≥ ε⁺, not only the new parameter r(t + Δt) is updated to ε⁺, but ±π is also added to the polar angle so that ϑ(t + Δt) = ϑ(t) + δϑ ± π is still within [0, 2π).

2) Resistance Forces for Visual-Motor Synchronization

For practical applications, the dynamic response of the robot also needs to be considered to prevent the manipulation from exceeding the actuation limits of the robot. Given the amount of input motion and the mass of each robot link, the required torque $\tau ={[{\tau }_1,\dots ,{\tau }_{2\stackrel{⌢}{L}}]}^T\in {\Re }^{2\stackrel{⌢}{L}\times 1}$ can be computed using inverse dynamics. The kinematics simplicity, e.g., each joint consists of two rotational axes perpendicular to each other with no offset, implies simple formulation of robot dynamics, thus yielding a closed form of inverse dynamics, as reported in [3].

The motion interpolation function $\stackrel{⌢}{\mathbf{q}}=\mathbf{Q}(r,\vartheta ,t)$ is actually time varying since the optimal control bending configurations $\stackrel{⌢}{\mathbf{q}}{}^{(1,{\vartheta }_i)}\left(t\right)$ are also updated intraoperatively, while the constraint pathway is dynamically adapting to tissue deformation [24], [25]. However, the configuration changes due to constraint deformation are slow compared with the ones generated by input manipulation, especially when the deformation is mainly due to respiratory motion. The resultant joint velocity and acceleration vectors considering both effects are calculated as follows:

$$\begin{array}{cc}\hfill \underset{\mathbf{q}}{\overset{\cdot }{⌢}}& =\nabla \mathbf{Q}(r,\vartheta ,t)\left[\begin{array}{c}\hfill \stackrel{.}{r}\hfill \\ \hfill \stackrel{.}{\vartheta }\hfill \end{array}\right]+\stackrel{.}{\mathbf{Q}}(r,\vartheta ,t)\hfill \\ \hfill \underset{\mathbf{q}}{\overset{\cdot \cdot }{⌢}}& =\nabla \mathbf{Q}(r,\vartheta ,t)\left[\begin{array}{c}\hfill \stackrel{\cdot \cdot }{r}\hfill \\ \hfill \stackrel{\cdot \cdot }{\vartheta }\hfill \end{array}\right]+{\nabla }^2\mathbf{Q}(r,\vartheta ,t)\left[\begin{array}{c}\hfill \stackrel{.}{r}\hfill \\ \hfill \stackrel{.}{\vartheta }\hfill \end{array}\right]+\stackrel{\cdot \cdot }{\mathbf{Q}}(r,\vartheta ,t)\hfill \end{array}$$ (30)

The variation of (^Cx_C, ^Cy_C) on the image plane is obtained from a haptic device manipulated by the operator in 2-DoF and correlated with parameters (r, ν), as devised in (28). Resistance forces are generated against excessive motion caused by the manual control, thus matching the dynamic response of the robot end-effector to the input manipulation. As reported in [25], the accuracy of manual control is significantly improved when such a force is applied in order to synchronize visual-motor perception. The maximum angular speed and torque ${\stackrel{.}{q}}_{\max }$ and τ_max are dictated by the actuation limitations of each motor and can be considered as actuation margins for defining the magnitudes of damping force f_b and inertia resistance force f_I

$$\begin{array}{cc}\hfill f_b& =c_b\left(b^{-1}\right(\underset{\mathbf{q}}{\overset{\cdot }{⌢}})-{\stackrel{.}{q}}_{\max }^{-1})\hfill \\ \hfill f_I& =c_I\left(I^{-1}\right(\underset{\mathbf{q}}{\overset{\cdot \cdot }{⌢}})-{\tau }_{\max }^{-1})s.t.\{\begin{array}{c}b\left(\underset{\mathbf{q}}{\overset{\cdot }{⌢}}\right)={\stackrel{.}{q}}_{\max }-\underset{i}{\max }\{\mid \underset{{\mathbf{q}}_i}{\overset{\cdot }{⌢}}\mid \}\hfill \\ I\left(\underset{\mathbf{q}}{\overset{\cdot \cdot }{⌢}}\right)={\tau }_{\max }-\underset{i}{\max }\{\mid {\tau }_i\mid \}\hfill \end{array}\hfill \end{array}$$ (31)

where $i=1,\dots ,2\stackrel{⌢}{L},c_b,c_I$ are positive scalar constants, and $b,I:{\Re }^{2\stackrel{⌢}{L}}\to {\Re }^1$ are the differences between the actuation margins (${\stackrel{.}{q}}_{\max }$, τ_max) and the instantaneous angular dynamics (|$\underset{q_i}{\overset{\cdot }{⌢}}$|, |τ_i|). When the velocity or torque of one of the joints reaches the safety margin, stronger damping or inertia force is generated to resist the hand motion before b → 0 or I → 0. Due to the physical limitations of haptic devices, thresholds f_bmax and f_Imax are set as upper bounds for the damping and inertia force, respectively; however, the prevention of excessive robot dynamics is still ensured. The resultant resistance force applied by the master manipulator against the hand motion is finally obtained by

$${\mathbf{F}}_r=\frac{-f_I}{\sqrt{{}_{}{}^C\stackrel{\cdot \cdot }{x}{}_C{}^2+{}_{}{}^C\stackrel{\cdot \cdot }{y}{}_C{}^2}}\left[\begin{array}{c}\hfill {}_{}{}^C\stackrel{\cdot \cdot }{x}{}_C{}^{}\hfill \\ \hfill {}_{}{}^C\stackrel{\cdot \cdot }{y}{}_C{}^{}\hfill \end{array}\right]+\frac{-f_b}{\sqrt{{}_{}{}^C{\stackrel{.}{x}}_C^2+{}_{}{}^C{\stackrel{.}{y}}_C^2}}\left[\begin{array}{c}\hfill {}_{}{}^C{\stackrel{.}{x}}_C\hfill \\ \hfill {}_{}{}^C{\stackrel{.}{y}}_C\hfill \end{array}\right].$$ (32)

3) Haptic Interaction With Constraint Pathway

The proposed DACs not only provide a condition for the optimization of robot bending configuration in (17) and (20) but also apply manipulation margins for the entire robot body, rather than just the end-effector. With high update rate (>1 kHz) of the PQ accelerated by GPU, it is possible to generate a continuous haptic force for guiding the operator in navigating the robot within the constraint pathway. Most importantly, our first clinical concern is to avoid the application of excessive forces on the vessel wall, which would likely cause perforation.

To this end, sensitivity thresholds are defined as $\mathbf{a}=[a_1,\dots ,a_{\stackrel{⌢}{L}}]:\forall a_i\ge 0$ so that the haptic force is enabled when $a_i<D_i^{m,\Delta m}$. The motion of each robot link $i=1,\dots \stackrel{⌢}{L}$ could cause a deviation from the sensitivity threshold s.t. $D_i^{m,\Delta m}-a_i>0$. We assign the spring force constants of each link to be $\mathbf{k}=[k_1,\dots ,k_{\stackrel{⌢}{L}}]:\forall k_i\ge 0$. Usually, $k_{\stackrel{⌢}{L}}$ is set to a greater value than the others so as to generate the strongest haptic force when deviation is due to the distal link, since the instrument tip can cause tissue perforation. Hence, the resultant haptic force magnitude is given by the sum of the spring forces proportional to their deviation offsets

$$f_h=\underset{i=1}{\overset{\stackrel{⌢}{L}}{\Sigma }}\Gamma \left(D_i^{k,\Delta k}\right(\stackrel{⌢}{\mathbf{q}})-a_i)\cdot k_i\left[D_i^{k,\Delta k}\right(\stackrel{⌢}{\mathbf{q}})-a_i]$$ (33)

where Γ: ℜ → ℜ is a step function s.t. if u > 0, then Γ(u) = 1; otherwise, Γ(u) = 0. Again, the haptic force magnitude will be limited by the physical upper bound f_hmax. To prevent the operator from increasing the deviation from the constraint during the robot surgical navigation, it is necessary to determine the particular direction of motion from the manual control which would generate a lower degree of robot bending and, therefore, decrease the value of the parameter r. To this end, the rate of change of r has to be negative, e.g., Δr = −1, without affecting the polar angle (Δϑ = 0). With the Jacobian defined in (28), the instantaneous direction of the haptic force can subsequently be calculated

$$\left[\begin{array}{c}\hfill {\Delta }^C{x}_h\hfill \\ \hfill {\Delta }^C{y}_h\hfill \end{array}\right]=J(r,\vartheta )\left[\begin{array}{c}\hfill -1\hfill \\ \hfill 0\hfill \end{array}\right]$$ (34)

The resultant haptic force is then obtained as

$${\mathbf{F}}_h=\frac{f_h}{\sqrt{{\Delta }^C{x}_h^2+{\Delta }^C{y}_h^2}}\left[\begin{array}{c}\hfill {\Delta }^C{x}_h\hfill \\ \hfill {\Delta }^C{y}_h\hfill \end{array}\right]$$ (35)

where the instantaneous motion direction is normalized to a unit vector and scaled by the magnitude f_h. The net force generated by the master device against the motion of the operator is finally given by F = F_r + F_h.

D. Summary of the Key Steps for Controlling the Snake Robot Under Dynamic Active Constraints

For controlling the snake robot under DACs, the main steps of the proposed methods are summarized in Fig. 6. In this figure, we have also listed the inter-relationship of different technical sections detailed previously. It is important to note that only the robot bending parameterization and subsequent optimization is specific to a hyper-redundant robot comprising numerous universal joints. Excluding this part, the framework is generally designed for any robotic mechanism. In particular, the PQs procedure can be applied to any kind of robot object represented by a set of vertex points. The role of vertex points and contours to represent the robotic device and the tissue is actually interchangeable. Similarly, the robot shape parameterization describes the motion transitions in joint space by means of reference robot configurations based on the task requirement. This is also applicable to other robot kinematics with continuous and convex joint-space domain. Finally, the impedance/reaction forces generated by haptic interaction are calculated based on the well-formulated robot kinematics but not limited to the one considered in this study.

Fig. 6. Diagrammatic overview of the proposed control framework under DACs.

IV. Results

In this section, the performance of the overall framework is evaluated according to the three main technical challenges outlined previously. First, the real-time response of the proposed GPU-based PQ computation is demonstrated. Subsequently, the optimized robot configurations are determined for two exemplar constraint models. Finally the effectiveness of continuous haptic interaction enabled by real-time PQ update is shown. To demonstrate the practical use of the proposed closed-loop feedback control under motion constraints, detailed evaluation of user performance is conducted for both simulated intraluminal and intracavity endoscopic tasks.

A. Proximity Query Computational Performance

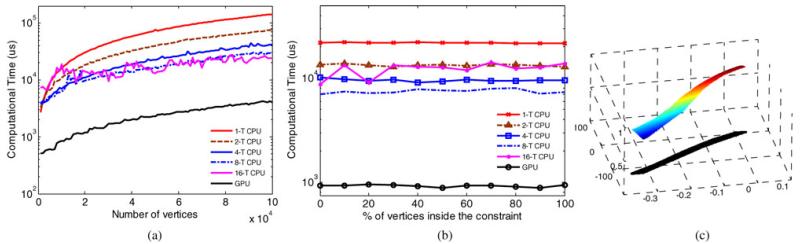
For PQ computational performance evaluation, a standard GPU platform, i.e., nVidia S2070, is used. This platform has 224 double-precision FPUs. The design is programmed using CUDA C framework v.4. The existing narrow phase PQ algorithms can only handle objects in primitive or convex shape. In our case, deviation depth to the inner surface of the constraint pathway is required. Outer part of the pathway will then be considered as the object to calculate such a depth with the robot. The process for decomposing this outer part is difficult, especially when the contours of the pathway are complex. Most of the existing approaches cannot be implemented in GPU without preprocessing [35], which would significantly deteriorate the performance. Therefore, comparison with such conventional algorithms is not attempted in this paper. Instead of comparing with those CPU-based PQs, the acceleration of the proposed GPU PQ is used to demonstrate its performance advantage. To this end, we provide a CPU-based C reference implementation with detailed kernel source code. The reference design is compiled using Intel Compiler version 11.1 and executed in a dual 6-core Intel Xeon X5650 server. The “-fast” compiler flag is used and the program is multithreaded using OpenMP.

After compiling the kernels, it is shown that the first kernel uses 62 registers. The experiment platform is equipped with a 32-k-entry register file, and thus, a configuration with 512 threads per group is used to maximize the parallelism. The performance profiler shows that the first GPU kernel contributes to over 78% of the total GPU based process time, while the second kernel represents less than 2% of that. The rest of 20% GPU time is spent on data communication and alignment. Due to software overhead, the kernel computation time is about 64% of a complete PQ function call time. This suggests that, for any further acceleration of the GPU kernels, the application performance improvement is limited mainly by this factor.

Twenty (=Δk) constraint segments are involved in the PQ process, sufficient to enclose an entire five-link snake robot. Fig. 7(a) shows the time consumption increasing with the number of robot vertices. To obtain a high update rate above 1 kHz required for high fidelity haptic interaction, 14 800 vertices at the 1-ms margin is shown as the maximum vertex number to represent the robot in our setup. The log scale for computational time indicates that the GPU design is an order of magnitude faster than the state-of-the-art multithreaded CPU counterparts. It shows that the 16-thread result does not provide further performance improvement over the eight-thread results. In this case, thread-based parallelism reaches the physical limit of the multi-core system. Fig. 7(b) shows the measured performance in different percentage of those 14 800 vertices inside the constraint pathway in various processing configurations. It is observed that both CPU and GPU kernels are insensitive to the portion of robot vertex being outside the constraint pathway, even if there are two more calculations in (6) and (7) involved. This stable performance is essential for maintaining smooth feedback control under different query conditions.

Fig. 7.

(a) Computational time for a PQ update with 20 constraint segments against the number of vertex describing the robot. (b) Computational time for a single PQ update corresponding to different percentages of the 14 800 vertices being inside the constraint pathway. (c) Cost function for the optimization of robot bending ($\stackrel{⌢}{L}=5$) above an example constraint polytope (in black), which can be approximated as a convex polygon. The optimal ($\stackrel{⌢}{m},\stackrel{⌢}{q}{}_c$) is found at the shape edge of level cost value.

B. Results of Robot Configuration Optimization

It has been found that without other instruments integrated onto the robot tip, 500 vertices are sufficient to describe the entire five-link robot in our application. The boundary of each link can be described as a union of a sphere and a cylinder. Other than performing PQ for haptic interaction, a portion of the GPU threads is spared to search the optimal control bending configurations $\stackrel{⌢}{\mathbf{q}}{}^{(1,{\vartheta }_i)}$. Fig. 7(c) depicts the objective function devised in (14), showing an example polytope based on a particular portion of the constraint pathway in the colon. If more links $\stackrel{⌢}{L}$ are involved in bending, then the higher scale is applied on the variable domain (m, q_c) to the cost value. The function itself is simply concave and globally convergent. The problem is considered as a concave minimization over a polytope, which is a feasible region confined by (17) on the variable domain. The solution will reach the edge of the constraint polytope quickly after a few iterations. The search time mainly relies on the number of PQ constraint function (16) evaluations. Therefore, by limiting the number of evaluations, we can standardize the search time for every optimization trial. It also allows the same number of kernels operating on a stream of data required in different trials. In fact, such robot bending optimization is not necessary to perform as frequently as the haptic update. The optimization to update the control bending configurations is only required when the robot configuration is close to ${\tilde{\mathbf{q}}}_{l+1,\dots L}$ with the motion parameter r being small such as below 0.15. Therefore, the current configuration does not need to be completely modified in real time when a new set of control bending configurations is applied. This is because the manual control is mainly guided by the haptic interaction with constraint pathway that keeps varying due to tissue deformation. The maximum r_max is normally set to be >1 (i.e., 1.4) to allow higher degree of bending for the haptic interaction.

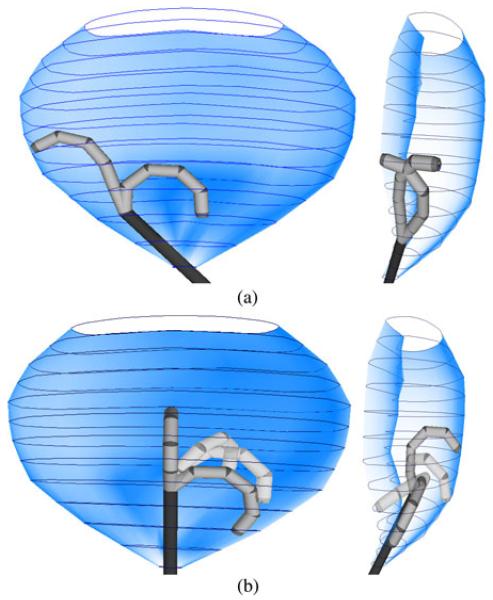
By limiting PQ evaluation number to 100, one can obtain four or eight optimal control bending configurations in parallel just within 30 ms. Fig. 8(a) and (b) shows the optimization results with four and eight optimal bending configurations. All these bending configurations are within the spatial constraint defined inside an abdominal cavity. It comprises 13 complex-shaped contours and each has 28 polar coordinates in 2-D.

Fig. 8.

(a) Four ($=\stackrel{⌢}{n}$) control bending configurations optimized inside a complex-shaped constraint, where the robot base is inclined to one side. Two of them are bent, with even-number joint indices in front view (left), while the other two are with odd-number indices in side view (right). (b) Eight $=\stackrel{⌢}{n}$ optimal control bending configurations with the robot base pointing upward. The four transparent configurations are optimized in the domain of (α, β) based on the other four configurations in solid color.

C. Results of Subject Tests With Visual-Motor and Haptic Interaction

To investigate how the proposed control scheme can enhance surgical manipulation, two endoscopic procedures are simulated and performed by a virtual articulated flexible access robot in the OpenGL environment. Subject tests are carried out to validate the clinical value of the technique in detail. Such simulated tasks provide sufficient information to analyze the efficiency, accuracy, and safety of the proposed control scheme for surgical navigation. A virtual camera with a field of view of 70° mounted at the tip provides adequate range of visualization of the tissue under simulated endoscopic lighting. Its relative pose is changed simultaneously with the movement of the articulated robot. For master–slave control of the robot with haptic interaction, a haptic input device (PHANToM Omni, SensAble Tech., Woburn, MA) is used in the experiments. Appropriate values for interaction force are assigned based on the specific capabilities of the robot and the haptic device (see Table II). Twelve subjects (age ranging from 25 to 40) were invited to participate in the experiments to evaluate the performance with and without the proposed control approach. Three of them are clinicians with endoscopy experience, whereas the others are from a technical background. The two studies are designed to assess both intraluminal and intracavity endoscopy.

TABLE II. Variable Assignment for Human-Robot Interaction.

Variable types	Assigned values	Equ.
Robot actuation limits	τmax = 75.6mNm and ${\stackrel{.}{q}}_{\max }={36}^{°}{\mathrm{s}}^{-1}$	(31)
Haptic force limits	[fbmax,fImax = [0.88,3.30]N	(31)
Resistance force constants	[cb,cI] = [1,3] × 10−3	(31)
Spring force constants	k = [7,7,7,7,45] × 10−2 N/mm	(33)

1) Study I (Intraluminal Endoscopy)

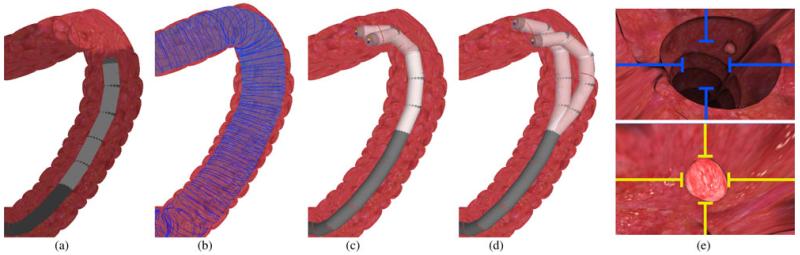
A 3-D colon model with 43 598 triangular meshes is obtained from high-resolution CT imaging data [see Fig. 9(a)]. Based on this preoperative model, a centerline along the luminal structure can be easily predefined by the operator in the GUI. The constraint pathway with numerous contours is closely adapted to the luminal structure [see Fig. 9(b)]. The simulated colonoscopy task consists in visualizing multiple virtual polyps extruding from the colon wall inside the lumen by navigating the robot in three translational DoFs using the haptic device. Since each link is 28 mm in length (=ℓ), 30 (=L) links in total are required for the robot to reach the ascending colon. During the task, only the endoscopic camera view is provided. The subject has to handle the bending of the five most distal robot links ($\stackrel{⌢}{L}=5$) by moving the device’s end-effector in a 2-D plane: left-and-right and up- and-down. Robot dynamics is only considered for this five-link robot. We assume that the rest of the links (denoted in dark gray-color) are capable of accurately following the centerline of the constraint within their angular joint motion limits (i.e., ±45°). The five-link robot configuration is locked when the user presses a button on the haptic device stylus; meanwhile, the subject can adjust the insertion of the entire robot along the colon by moving the stylus forward and backward. With our proposed method, the last five universal joints are actuated simultaneously to vary the robot bending configuration in different parts of the colon. Fig. 9(c) and (d) shows four exemplars optimized bending configurations computed according to the specific constraint pathway. Haptic interaction is also provided when the robot deviates from the constraint pathway. In the control experiment for comparison, manual control is performed by actuating one universal joint at a time. By pressing the second button on the manipulator stylus, the subject can choose either one of the last two distal joints for actuation. The left-and-right and up-and-down motions of the haptic manipulator are directly mapped to the two angular values of the chosen universal joint. The angular values of the remaining joints are automatically adjusted to follow the centerline.

Fig. 9.

(a) Robot conforms along the centerline of the CT colon model used to simulate colonoscopy. Endoscopic lighting is also simulated and projected on the splenic flexure. (b) Fifty (=N_C) circular contours with varied radii are fitted manually to the whole colon model. One hundred and ninety-seven ($={\tilde{N}}_C$) contours are interpolated to smoothen the constraint pathway (in blue). (c) and (d) Four control bending configurations optimized inside the flexure for viewing polyps on the transverse colon wall. (e) Polyp is clearly visualized within the camera view under sufficient endoscopic lighting. The color of the aiming marker is changed gradually based on the targeting accuracy. (Top, in blue): Out of the viewing range. (Bottom in sharp yellow): Very accurate targeting.

During the task, experimental data including time, robot configuration, target pose relative to the camera, deviation from the constraint pathway, and input motions of the haptic device are all recorded for offline analysis. The performance can be assessed on three different aspects: task efficiency, targeting accuracy, and manipulation safety. Detailed quantitative results are shown in Table III, where the performance indices are classified according to the above evaluation categories. With the proposed control scheme, the performance improvement is always higher than 30%, and most of the measures are shown to be very significant with p-values less than 0.05. Detailed analysis of the data in Table III is reported in the following paragraphs.

TABLE III. Measured Performance Indices Averaged Across the 12 Subjects in Study I.

	w/o DAC		with DAC		Improv.
Task efficiency	Mean	SD	Mean	SD	% *p-val.
Complet. Time (sec)	333.8	94.78	143.9	11.15	57 *.0001
Aver. Trav. Dist. (mm)	543.5	191.0	114.9	22.60	79 *.0000
No. of Polyps Missed	0.33	0.65	0	0	100*.104
Targeting error	Mean	SD	Mean	SD	% *p-val.
Aver. Dist. Err. (mm)	2.63	0.67	1.68	0.40	36 *.0004
Aver. Ang. Err. (°)	7.64	1.76	4.76	0.81	38 *.0001
No. of Times Missed	1.87	0.90	1.20	0.50	36 *.0314
Deviation	Mean	SD	Mean	SD	% *p-val.
No. of Times	63.08	27.39	34.00	7.05	46 *.0025
Max. Depth (mm)	33.66	6.22	10.72	4.98	68 *.0000
Aver. Depth (mm)	7.30	2.30	2.21	0.81	70 *.0000
Aver. Time (sec)	3.99	2.46	0.43	0.12	89 *.0004
Max. Time (sec)	54.08	35.13	3.07	2.55	94 *.0004
Total Length (mm)	4268	1585	372.9	144.6	91 *.0000

a) Task efficiency

Ten identical polyps are placed along the colon wall from the rectosigmoid junction, through the splenic flexure into the ascending colon. The task is completed when the robot has reached the ascending colon. The mapping between the 2-D input motion and the camera motion is not static and keeps changing with the robot configuration. Without stable visual-motor coordination, even when a single distal joint is actuated at each time, the subject finds it particularly challenging to target the polyp. A high number of joint repositioning maneuvers are, therefore, required in the control experiment, as demonstrated by the much larger completion time and average distance per polyp traveled by the end-effector measured during the trials. Due to spatial disorientation, three of the subjects were not able to target one or more polyps. The task is completed in an easier and more efficient way when the correct visual-motor alignment is provided.

b) Targeting accuracy

Accurate manipulation is desirable for tissue examination tasks such as biopsy. During such tasks, the subject is expected to visualize every polyp at a proper viewing distance and angle for the ease of examination. As shown in Fig. 9(e), the target marker superimposed on the camera view helps subjects locate the polyp precisely relative to the end-effector for surgical investigation. The polyp has to be correctly visualized inside the square frame at the center of the image plane. The color of the marker changes according to the viewing accuracy. Bright yellow indicates that the polyp is correctly visualized in terms of viewing distance and angle. This visual reference allows us to evaluate the ability of the subject in maneuvering the robot with and without our proposed control. The reference values of the viewing angle and distance are preset as 15 mm and 0° such that the principal axis of the camera exactly points at the center of the polyp, i.e., it is correctly placed inside the aiming marker. The tolerance ranges are set to 15 ± 7 mm and ±20° for viewing distance and angle, respectively. The polyp will disappear when it has been visualized with accuracy within the preset ranges for 7 s. Once the camera pose is within the tolerance ranges, the deviations from the reference values are computed and recorded to assess the targeting error. The number of times these ranges are exceeded is also recorded for each polyp. Using our proposed interface, it was observed that subjects were able to meet the desired targeting accuracy quickly and steadily without any disorientation caused by visual-motor coordination. As a result, both average errors per polyp in viewing distance and angle are reduced. On the other hand, in the control experiment, subjects have to reach the correct targeting position by manually adjusting the robot configuration through actuation of the two distal universal joints. Under the influence of spatial disorientation, frequent adjustments of each joint position are required to meet the desired targeting accuracy. Inevitably, this increases the chances to exceed the viewing tolerance ranges and miss a number of targets.

c) Manipulation safety

As the constraint pathway is modeled and adapted tightly to the inner surface of the colon model, deviation of the robot body outside the pathway can be correlated with the physical force applied on the colon wall. The larger the deviation, the higher the chance to cause tissue injury. Such deviation caused by the robot distal links is measured during the experiment. With haptic feedback based on the DACs, subjects are able to realize if the robot is beyond the safety margin. This helps minimizing the number of times deviation occurs. Sensitivity thresholds a_i are all set to zero. The spring constant of the last link is set to $k_{\stackrel{⌢}{L}}=0.45$, which is 6.4 times higher than the others. Much stronger forces are applied to the distal link to stop any movement that would cause deviation in order to prevent intestine perforation, which is mostly caused by the end-effector. The maximum deviation depth is highly reduced because of these strong forces. Small value in average deviation depth also indicates the effectiveness of haptic guidance on the subjects to guide safe navigation by sensing the manipulation margin. Long deviation time indicates subjects having great difficulty in maintaining the robot within the colon lumen due to disorientation. The maximum deviation time usually occurs when the robot is navigated around the colon flexures. The deviation length is defined as the distance traveled by the robot tip outside of the constraint pathway. High deviation length and depth values both increase the chance to cause damage to the tissue due to the high contact force applied.

2) Study II (Intracavity Endoscopy)

In Fig. 10(a), a set of 3-D organs from CT imaging data is integrated into a simulator model. The model represents an accurate reconstruction of the adult human abdominal cavity during surgery, thus providing a spatial workspace for the simulated task of endoscopic diathermy. The robot base is fixed and inserted in the cavity via transvaginal access. To investigate the proposed framework, the subject has to approach multiple targets located at different anatomical features by manipulating the bending and retroflexion of a five-link robot ($L=\stackrel{⌢}{L}=5$). The spatial constraint, as shown in Fig. 8, is defined by an experienced surgeon. It geometrically adapts to the abdominal cavity. There are totally six circular labels with a diameter of 33 mm positioned to replicate a diagnostic laparoscopy, a surgical procedure required for diagnostic purposes. As shown in Fig. 10(b), each label contains a 20-mm-long arrow on which a thin cylindrical object is superimposed. Each arrow is placed at a different orientation and distance relative to the camera. Since currently there is no formal intra-abdominal endoscopic training available, the labels have been designed to simulate the precision of the virtual robot at its distal end-effector. Clinically, the need for precise cutting can be reflected to cutting blood vessels, nerves or indeed removing tumors which require a greater precision of cutting. Only the endoscopic camera view is provided during the task. The camera is assumed to be fixed relative to the diathermy tool. A marker is provided in the camera view to guide accurate aim at one extremity of the object [see Fig. 10(b)] so that the subject can shorten the object while pressing a button on the haptic device. One diathermy task is considered successful when the object is completely eliminated and the end of the arrow on the label is reached. The task is, therefore, designed to simulate a focal diathermy along a straight pathway with the diathermy electrode turned ON and placed in contact with the tissue target.

Fig. 10.

(a) Simulated intracavity endoscopy in the abdomen. (b) (Top) Endoscopic view of the labels with different poses. The aiming marker guides the straight-path following. (c) Parameterized bending configurations for subject manipulation to approach the six label targets. (d) Cartesian end-effector trajectory traveled by one of the subjects performing the task. The portions in red represent the tool being enabled for straight-line diathermy on that label.

Once the eight control bending configurations are found and optimized inside the spatial constraint, as shown in Fig. 8(b), the joint-space parameterization provides diversified bending configurations according to the manual control. Fig. 10(c) shows different configurations to visualize the six labels. Fig. 10(d) shows an example of the end-effector trajectory traveled by a subject while performing the task. The smooth trajectory profile (in blue) demonstrates easy and intuitive manipulation between the labels. Straight path lengths (in red) are followed along the diathermy targets. Note that such path-following control cannot be accomplished by manual joint actuation; therefore, no control experiment was conducted in this study.

Table IV summarizes the accuracy and efficiency in performing the diathermy task on the six labels with different poses corresponding to various levels of difficulty. The time required to complete a straight-line diathermy on each label is shown. The position of the center of the aiming marker projected on the label was also recorded during the experiment. Other than the viewing angle error in targeting the diathermy object, the distance between the projected marker and the arrow can also be calculated to compute the deviation from the straight diathermy line. Both errors are shown to be very low in average, i.e., <1.7° and <0.5 mm. Low values in standard deviation (SD) of the completion times and targeting errors for each subject indicate high performance repeatability under our control framework. After completion of a diathermy task, the traveled distance while searching for the next label is also measured. High SD of these distance values is due to different searching behaviors performed by the subjects.

TABLE IV. Measured Performance Indices Averaged Across the 12 Subjects in Study II.

Performance		Label Index
		1	2	3	4	5	6
Compl. Time	Mean	21.4	18.1	21.0	15.6	18.7	23.3
(sec)	SD	9.17	3.69	3.21	2.33	3.30	5.46
Ang. Err.	Mean	1.36	1.34	1.68	0.99	1.50	1.67
(°)	SD	0.35	0.27	0.27	0.24	0.23	0.19
Dist. Err.	Mean	0.37	0.33	0.30	0.41	0.28	0.38
(mm)	SD	0.16	0.09	0.07	0.14	0.08	0.06
Trav. Dist.	Mean	N/A	134	108	63.6	103	143
(mm)	SD	N/A	45.7	91.0	24.9	103	138

V. Conclusion and Future Work

This paper presents a real-time PQ implementation and dimensionality reduction scheme to control an articulated snake robot under DACs. The development of a novel lightweight articulated snake robot allows large-area exploration in vivo. Compared with standard laparoscopic manipulation, its flexibility offers significant advantages to endoscopic surgery, for which enhanced control ergonomics is essential. The relative merit of the proposed framework can be summarized as follows.

A. Efficient Proximity Queries

To ensure shape conformance to anatomical constraints and real-time PQs, we have proposed a new PQ formulation to compute the penetration depth between the robot and the constraint pathway. In contrast with existing methods, our PQ computational structure is highly parallel and, therefore, particularly suitable for GPU implementation. For the proposed algorithms, no specific object constraints are required, thus facilitating its use for generic, subject-specific anatomical models. The proposed computational technique is shown to be highly customizable such that the parameters that control the parallelism can be easily adjusted for performance analysis. Without having to preprocess the input PQ data, as in [23] and [35], the data of both the constraint pathway and the robot structure can be updated dynamically for each PQ sampling. This is especially useful in soft tissue surgery, which provides time-varying registered computer tomography models. The accelerated computational performance is so promising that it allows sufficient fast update for haptic rendering at a rate higher than 1 kHz. This allows the framework of our DACs to provide haptic guidance, visual-motor synchronization, and real-time robot shape optimization.

For future improvement of our GPU-based PQ computation, large overhead of the data transfer will be compensated for by overlapping the processing and transferring tasks. It will potentially reduce the effective turn around time by 50%. Investigation regarding the requirement of data precision will also be conducted. It is envisioned that mixed precision technologies can be applied by taking the advantage of the larger single-precision FPU resources.

B. Robot Motion Parameterization

For application to endoscopic navigation, we have proposed a method to characterize the robot bending in joint space in a 2-D domain. This allows us to simplify the control of the articulated robot when using a master manipulator with limited DoFs. Optimal robot bending configurations are devised online to adapt to dynamic spatial constraints. The bending motion is then parameterized in polar coordinates. With the high flexibility of having nonuniform arrangement of control points, further studies will be conducted to investigate the effect of optimizing more control bending configurations with different values of the parameter r < 1, giving rise to a large permutation of motion transitions. This would allow us to describe complicated path-following trajectories within a more complex geometry.

The motion parameterization generates a 2 × 2 full-rank Jacobian. Only a 2-DoF manual input is required to control the robot bending or retroflexion in alignment with the camera view. We have ensured that visual and motor coordination is always obtainable without having to deal with the presence of reduced-rank Jacobian singularities. Compared with existing methods [5]-[7], it eliminates the need of solving the inverse kinematics, for which the valid specification of the input pose and dynamic of end-effector is not guaranteed.

C. Enhanced Visual-Motor Coordination and Haptic Interaction

For controlled performance evaluation, subject tests have been performed within a simulation environment. The experimental results have shown that visual-motor coordination and haptic guidance are particularly important when using a flexible robotic instrument. They also demonstrate the significant clinical value of the proposed control in terms of efficiency, accuracy, and safety. It is worth noting that only the proposed characterization of robot configuration is specific to our snake robot structure and is still valid for a major category of hyper-redundant robots comprising rigid links and universal joints. On the other hand, the proposed PQ computation and motion parameterization are general and can be applied to other existing surgical platforms, e.g., the bending of the flexible continuum catheter. Online haptic guidance can also be incorporated into its 2-DoF manual control. In addition, by inverting the role of robot and constraint in the PQ procedure described for intraluminal navigation, more complex tissue geometry can also be represented by numerous vertex points, while the constraint can be fitted to the robot geometry.

D. Conclusion

In summary, we presented a real-time navigation and dimensionality reduction scheme to control an articulated snake robot under DACs. The evaluation of the proposed framework demonstrates its potential to address the three technical challenges in terms of shape conformance, motion modeling, and visual-motor coordination to control a flexible robot for seamless, safe surgical navigation. Shape conformance to anatomical constraints is obtained by providing continuous haptic guidance through the implementation of a real-time PQ algorithm. Intuitive control of multiple DoFs is achieved through dimensionality reduction, and visual-motor coordination is provided for seamless human–robot interaction.

Biographies

Ka-Wai Kwok received the B.Eng. and M.Phil. degrees from the Chinese University of Hong Kong, Hong Kong, in 2003 and 2005, respectively, and the Ph.D. degree from the Department of Computing, Imperial College London, London, U.K., in 2012.

He is currently a Postdoctoral Research Associate with the Hamlyn Centre for Robotic Surgery, Imperial College London. His research interests include image-guided surgical navigation, robot motion planning, human–robot interface, and high-performance parallel computing. His main research objective is to fill the current technical gap between medical imaging and surgical robotic control.

Kuen Hung Tsoi received the Ph.D. degree from the Department of Computer Science and Engineering, The Chinese University of Hong Kong, Hong Kong, in 2007.

He is currently a Postdoctoral Research Associate with the Custom Computing Group, Department of Computing, Imperial College London, London, U.K.

Valentina Vitiello (M’09) received the B.Eng. and M.Eng. degrees in medical engineering from the University of Rome Tor Vergata, Rome, Italy, in 2004 and 2007, respectively, and the Ph.D. degree in medical robotics from Imperial College London, London, U.K., in 2012.

She is currently a Research Associate with the Hamlyn Centre for Robotic Surgery and the Department of Computing, Imperial College London. Her main research interests include kinematic modeling and control of articulated robots for surgical applications, as well as human–robot interaction in robotic surgery. Specifically, her research is currently focused on the ergonomic control of multiple degrees-of-freedom systems through perceptually enabled modalities, such as the human motor and visual systems.

James Clark received the B.Sc. and MBBS degrees from Imperial College London, London, U.K., and received the qualification of MRCS from the Royal College of Surgeons of England.

He is currently a General Surgical Registrar and Visiting Lecturer at Imperial College London. Over the past five years, his role as a lead member of the clinico-technological collaboration clinically defined the design and engineering of flexible articulated robotic platforms for surgical application. His main academic interest is in exploring the potential for flexible robotics for future medical application.

Gary C. T. Chow received the B.Eng. and M.Phil. degrees from the Department of Computer Science and Engineering, The Chinese University of Hong Kong, Hong Kong, in 2005 and 2007, respectively. He is currently working toward the Ph.D. degree with Imperial College London, London, U.K.

His research interests include heterogeneous multicore systems with multiple types of processing elements.

Wayne Luk (F’09) received the D.Phil. degree in computer science from the University of Oxford, Oxford, U.K.

He currently directs the Computer Systems Section and the Custom Computing Research Group, Imperial College London, London, U.K. His main research interests include architectures, design methods, languages, tools, and models for customizing computation, particularly those involving reconfigurable devices such as field-programmable gate arrays, and their use in improving design efficiency and designer productivity for demanding applications, such as high-performance financial computing and embedded biomedical systems.

Dr. Luk is a Fellow of the Royal Academy of Engineering and the Institution of Engineering and Technology.

Guang-Zhong Yang (F’11) received the Ph.D. degree in computer science from Imperial College London, London, U.K.

He is the Director, Co-Founder, and currently chairs the Hamlyn Centre for Robotic Surgery, Imperial College London. His main research interests include biomedical imaging, sensing, and robotics.

Dr. Yang is a Fellow of the Royal Academy of Engineering, the Institution of Engineering and Technology, and the American Institute for Medical Biological Engineering.