Regularized Rare Variant Enrichment Analysis for Case-Control Exome Sequencing Data

Abstract

Rare variants have recently garnered an immense amount of attention in genetic association analysis. However, unlike methods traditionally used for single marker analysis in GWAS, rare variant analysis often requires some method of aggregation, since single marker approaches are poorly powered for typical sequencing study sample sizes. Advancements in sequencing technologies have rendered next-generation sequencing platforms a realistic alternative to traditional genotyping arrays. Exome sequencing in particular not only provides base-level resolution of genetic coding regions, but also a natural paradigm for aggregation via genes and exons. Here we propose the use of penalized regression in combination with variant aggregation measures to identify rare variant enrichment in exome sequencing data. In contrast to marginal gene-level testing, we simultaneously evaluate the effects of rare variants in multiple genes, focusing on gene-based LASSO and exon-based sparse group LASSO models. By using gene membership as a grouping variable, the sparse group LASSO can be used as a gene-centric analysis of rare variants while also providing a penalized approach toward identifying specific regions of interest. We apply extensive simulations to evaluate the performance of these approaches with respect to specificity and sensitivity, comparing these results to multiple competing marginal testing methods. Finally, we discuss our findings and outline future research.

INTRODUCTION

Genome-wide association studies (GWAS) have been conducted for a large number of phenotypes on the principle that complex diseases are the result of multiple common single nucleotide polymorphisms (SNPs), known as the common disease common variant hypothesis (CD-CV) [Reich and Lander 2001]. While much success has been achieved in identifying a large number of common risk-associated loci for various complex diseases [Hindorff, et al. 2009], the reported SNP associations are generally of low effect sizes and explain a modest proportion of the total estimated heritability [Manolio, et al. 2009]. This has prompted investigators to extend association analysis beyond the scope of CD-CV and consider other sources of genetic variation, notably with respect to rare variants [Pritchard 2001]. While traditional genotyping microarray chips are generally not designed to capture rare variation, recent advancements in next-generation sequencing technologies, such as whole-exome sequencing (WES), have made large-scale interrogation of rare variation logistically plausible. These assays have resulted in an invigorated evaluation of rare variant analysis for complex traits, with multiple associations identified [Holm, et al. 2011; Nejentsev, et al. 2009; Rivas, et al. 2011].

Unlike common polymorphisms, traditional single marker analyses for rare variants are often underpowered for typical sequencing study sample sizes due to low minor allele frequencies (MAFs) [Li and Leal 2008] and specialized statistical methods are required for association analysis. It has been noted that multiple causal variants may aggregate in biologically relevant functional domains, such as genes [Bansal, et al. 2010]. This has led to multi-marker analysis strategies that evaluate the aggregate effect of multiple variants within a given region of interest (ROI), rather than at the individual variant level. These modes of analysis amount to identifying regions of rare variant enrichment, indicating incidence disparity of rare variation in the ROI across affected status. There have been recent developments of multiple statistical methods to detect such clustering of rare variation. Burden testing, such as the Madsen-Browning weighted sum statistic (WSS) [Madsen and Browning 2009], collapses all of the variants in the ROI into a single variable of interest,. Collapsing methods will suffer if there is a presence of both risk and protective variants in the ROI, since the effects will be canceled out in the collapsing measure. To address this, variance component tests such as C-alpha test [Neale, et al. 2011] and the sequence kernel association test (SKAT) [Kwee, et al. 2008; Wu, et al. 2011], a generalized form of the C-alpha, were developed to evaluate the association of a genomic ROI with a trait. Other methods include scan-based clustering approaches, which use a sliding window to localize variant clustering over a much larger genomic segment [Fier, et al. 2012; Ionita-Laza, et al. 2012; Schaid, et al. 2013].

Given that disease risk may be the result of contributions from many genes, there is interest in jointly modeling the effects of rare variants across multiple genes simultaneously. Such a model may result in more powerful detection of associations in contrast to marginal ROI analyses [Ayers and Cordell 2013; Clayton 2012]. However, regression models attempting to simultaneously assess all potential rare variant risk associations will be grossly underdetermined for any typical sequencing study sample size, requiring some form of model selection. Exhaustive combinatorial searches over the model space in conjunction with a model selection criterion would be computationally infeasible for most applications. An alternative strategy is to apply regularized regression methods, such as the least absolute shrinkage and selection operator (LASSO) [Tibshirani 1996], to simultaneously perform model selection and parameter estimation. Regularized regression approaches are not uncommon in genomic data analysis due to the vast feature sets, with applications proposed for microarray [Gui and Li 2005], GWAS [Liu, et al. 2011], and methylation data [Sun and Wang 2012]. Basu et al. [Basu, et al. 2011] explored global testing using penalized regression models and permutation for common variation. Recently, a number of methods have been proposed [Ayers and Cordell 2013; Zhou, et al. 2011; Zhou, et al. 2010] using group penalties on individual rare (and common) variation based upon prior biological information (i.e., gene structure) for large-scale applications on multiple genes.

Due to rapid population expansion and weak purifying selection, rare variation is actually quite common with respect to the number of identified polymorphic sites in a given study. Recent work by Nelson et al. [Nelson, et al. 2012] revealed that variant sites occurred every 21 bp on average across 12,514 subjects of European ancestry, with a vast majority observed in one or two subjects. For a ~30 Mb exome capture, this variant density would yield over 1 million variants for simultaneous consideration, which could be computationally taxing for complex penalties. Alternatively, gene structures can be used to inform the formulation of collapsing measures, corresponding to weighted sums of minor allele counts over predefined regions such as genes or exons. This approach also defines the maximal model dimensionality, since the quantity of unique ROIs is fixed a priori.

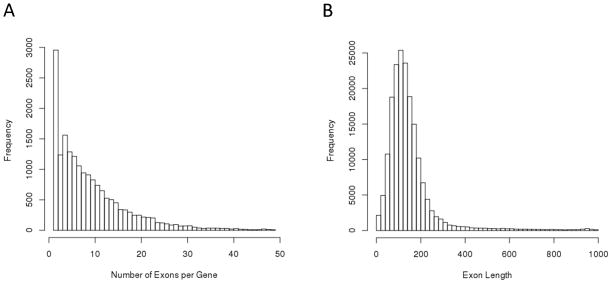
Examination of the latest build (hg19) of the consensus coding sequence (CCDS) regions [Pruitt, et al. 2009] reveals the human exome consists of 18,305 protein coding genes corresponding to ~180,000 unique exons in the human genome. While genes tend to be favored for ROI definition as a base biologically functional unit, WES also provides a natural alternative through using multi-marker collapsing measures of variants with respect to individual exons. Collapsing rare variation at the exon-level strikes a compromise between gene-level aggregations and no collapsing altogether, resulting in a fine partitioning of the exome. Examination of the CCDS data reveals that, with rare exception, exon length ≤ 1000 bp and has a median value equal to 126 bp. Figure 1 illustrates the distributions of exon lengths and number of exons per gene across the genome. There is also strong evidence that exons are correlated with functional domains in proteins for complex organisms [Kolkman and Stemmer 2001; Liu and Grigoriev 2004], supported by the “exon shuffling” theory [Gilbert 1978; Gilbert 1985]. Thus, it is possible that rare variants may not only cluster in genes, but that a given complex disease may be the result of specific alteration in protein activity by disrupting functional domains through localized exon-specific rare variation. A notable example of such a phenomenon is exon 11 in BRCA1, which harbors multiple variants associated with increased risk of breast and ovarian cancers [Risch, et al. 2001]. Biologically, exon 11 in BRCA1 encodes two putative nuclear localization signals [Chen, et al. 1996] and contains a domain that interacts with the DNA damage repair gene RAD51 [Zhang and Powell 2005]. Another example of acute localization was found in the rare variant analysis of DISC1 exon 11 for schizoaffective disorders [Green, et al. 2011], which identified multiple case-only missense RVs.

Figure 1.

Histograms depicting distributions of (A) number of exons per gene and (B) individual exon length for ~180,000 exons constituting 18,305 genes in CCDS data for the hg19 human genome build. The right tails of each figure are censored, excluding approximately with 0.8% and 1.5% of the distributions, respectively.

Given that exons naturally group to form genes, it may be reasonable to expect the existence of an effect for a given exon to be potentially related to other exons within its respective gene, a hierarchical relationship which can be exploited in regularized modeling procedures. It is also possible that only certain exons within a gene may be enriched for RVs. Use of the sparse group LASSO [Friedman, et al. 2010a] can impose sparsity both across groups and within groups, which accommodates rare variant enrichment localized to specific domains within a gene. This strategy is of particular relevance to sequencing studies, and naturally accommodates WES data analysis.

In this paper, we explore the use of the penalized regression with variant collapsing measures to assess rare variant enrichment for case-control WES studies, which we respectively refer to as gene-based LASSO (GB-L) and exon-based sparse group LASSO (EB-SGL). We analyze their performance under a variety of disease model scenarios via simulation study, characterizing sensitivity and specificity and comparing gene-level performance against existing methods. We conclude with a discussion of the benefits and shortcomings of these approaches, as well as outline future research directions.

MATERIALS AND METHODS

Aggregation Measures

Consider an exome sequencing study dataset involving J genes on N = N_C + N_D subjects, where N_C (N_D) is the number of controls (cases) and each gene consists of K_j exons (j = 1, …, J) for a total of $p={\mathrm{\sum }}_{j=1}^J{K}_j$ exons. Define a set of genetic positions within a given exon designated to be rare by some minor allele frequency (MAF) threshold criterion (e.g., MAF ≤ 0.05), whereby the vector g_ijk = (g_ijk1, g_ijk2, …)′ represents the minor allele count of these variants for subject i, gene j, exon k. This vector can in turn be summarized using a scalar collapsing measure, z_ijk, which is a univariate summary of g_ijk and can be considered a “super-variant.” Although there are many options for z_ijk as a function of g_ijk [Dering, et al. 2011a; Dering, et al. 2011b], we consider the Madsen and Browning weighted-sum (WS) genetic score [Madsen and Browning 2009], which up-weights positions based upon the empirical rarity in the control cohort. The aggregation measure is then defined such that

$$z_{\mathit{ijk}}=z({\mathit{g}}_{\mathit{ijk}})=\frac{1}{2L_{jk}}{\mathrm{\sum }}_l^{L_{jk}}{w}_{\mathit{jkl}}{g}_{\mathit{ijkl}}\text{where}{w}_{\mathit{jkl}}=\frac{1}{\sqrt{{Nq}_{\mathit{jkl}}(1-q_{\mathit{jkl}})}}\text{and}{q}_{\mathit{jkl}}=\frac{\mathrm{\sum }{g}_{\mathit{ijkl}}^C+1}{2N_C+2},$$

where L_jk is total number of variant positions in g_ijk and $\mathrm{\sum }{g}_{\mathit{ijkl}}^C$ is the sum of control subject alternative alleles at position l. The discriminative value of z_ijk is thus a function of the underlying MAF distribution, sample size, and number of true risk RVs for the given exon. We can similarly define a gene-based measure where exon membership is ignored and collapsing is conducted at the gene level, resulting in $z_{ij}^{\ast }=z({\mathit{g}}_{\mathit{ij}})$, where g_ij = (g_ij1, …, g_ijKj)′. Alternative weighting schemes could be used that take advantage of any additional annotation, including functional prediction tools such as SIFT [Kumar, et al. 2009] or Polyphen2 [Adzhubei, et al. 2010].

Penalized Models

Let y be a vector of binary disease status indicators, such that y_i is 1 if the i^th subject is a case and 0 if a control, and define X to be an N × m matrix of additional confounding covariate data, such as age or sex. For EB-SGL, let Z be an N × p matrix of aggregation measures, such that the i^th row of Z is z_i = (z_i11, z_i12, …)′. We similarly define the N × J matrix Z^* with i^th row ${\mathit{z}}_{\mathit{i}}^{\ast }={(z_{i1}^{\ast },z_{i2}^{\ast },\dots )}^{\prime }$ for GB-L. We use logistic regression on these data in order to detect differences in the collapsing measures across case-control status. Under this model, we apply a logit link on the probability of affected status for subject i, Pr(y_i = 1|x_i, z_i) = μ_i, such that for EB-SGL

$$log\left(\frac{{\mu }_i}{1-{\mu }_i}\right)={\eta }_i={\beta }_0+{\mathit{x}}_{\mathit{i}}^{\prime }\mathit{\beta }+{\mathit{z}}_{\mathit{i}}^{\prime }\mathit{\theta }$$

where x_i is the i^th column of X, β the respective model parameters corresponding to X, and θ the corresponding parameters to Z. Model fitting can then be conducted by maximizing the log-likelihood, which can be written as

$$lnL(\mathbf{\Theta };\mathit{y})=ln\left(\prod _{i=1}^N{\mu }_i^{y_i}{(1-{\mu }_i)}^{1-y_i}\right)=\sum _{i=1}^N{y}_i{\eta }_i-ln(1+exp({\eta }_i))$$

where Θ = (β₀, β, θ) is the full set of model parameters. In order to induce sparsity at both the gene and exon level for EB-SGL, we apply the sparse group LASSO penalty, such that the criterion for the penalized model fit is given as

$$\underset{\mathit{\theta }\in {\mathcal{R}}^p}{min}\left(-\frac{1}{N}lnL(\mathbf{\Theta };\mathit{y})+{\lambda }_1\sum _{j=1}^J\sqrt{K_j}{\Vert {\mathit{\theta }}_j\Vert }_2+{\lambda }_2{\Vert \mathit{\theta }\Vert }_1\right)$$

where $\sqrt{K_j}$ is correction factor accounting for the group size of gene j, θ_j = θ_j1, θ_j2, …)′ is a vector of exon-level parameters for a given gene, and $\mathit{\theta }={({\mathit{\theta }}_{\mathbf{1}}^{\prime },\dots ,{\mathit{\theta }}_{\mathit{J}}^{\prime })}^{\prime }$ is the complete p-length exon regression coefficient vector. In this formulation β₀ and β are unpenalized parameters, but β could be also included in the LASSO penalty if desired.

For GB-L, the regression model is very similar to EB-SGL, except that no group penalty is included and the model fitting criterion is given as

$$\underset{\mathit{\theta }\in {\mathcal{R}}^p}{min}\left(-\frac{1}{N}lnL({\mathbf{\Theta }}^{\ast };\mathit{y})+\lambda {\Vert {\mathit{\theta }}^{\ast }\Vert }_1\right)$$

where L(Θ^*, y) is the model likelihood regressing affected status on Z^* rather than Z and θ^* is the J-length vector of regression coefficients corresponding to the gene-level collapsing measures.

Model fitting for G-BL was conducted in R using the glmnet package [Friedman, et al. 2010b], which employs cyclical coordinate descent algorithms. To implement model fitting for EB-SGL, we utilized a blockwise descent (BD) algorithm put forth by Simon et al. [Simon, et al. 2013] provided in the R package SGL. The BD algorithm takes advantage of the group-level separability of the penalty function by cyclically iterating over the covariate groups, performing generalized gradient steps for each group with at least one non-zero regression coefficient.

Tuning Parameter Selection

Specific to EB-SGL, previous work by Zhou et al. [Zhou, et al. 2010] applying mixtures of group and traditional LASSO penalties for association analysis indicated that framing the relationship $\frac{{\lambda }_2}{{\lambda }_1+{\lambda }_2}=c$ is an effective strategy for identifying disease associations. This also reduces the path space for tuning parameter selection by fixing the value of c a priori, such that optimization corresponds to identifying a proper value of λ = λ₁ + λ₂ where λ₁ = (1 − c)λ and λ₂ = cλ. Based upon empirical evidence under various simulation conditions, we conducted our analyses with c fixed at 0.80.

Many strategies exist in general for selecting an appropriate value of λ in penalized regression. One option is to define a fine grid of values for λ and apply cross-validation, although this may be a very computationally demanding process. If we can assume a very sparse set of true associations, an efficient alternative approach is to employ a bracketing and bisection algorithm [Wu, et al. 2009] to identify a set of values for λ that result in small additions to the active set of covariates. Let θ_λ indicate the vector of non-zero coefficients under a model fit for a given value of λ, such that these coefficients correspond to the active set of n_λ = ||θ_λ||₀ covariates. If we a priori fix the maximum possible size of n_λ to be very small n_θ, we can iteratively fit penalized models by reducing λ until n_λ exceeds n_θ. This is a particularly appealing strategy in exploratory analyses when a small set of ROIs is desired for further investigation. This approach can be combined with a model selection criterion, such as the Bayesian Information Criterion (BIC) [Schwarz 1978], which is defined as

$$\mathit{BIC}(\mathbf{\Theta };\lambda )=-2ln{L}_{\lambda }(\mathbf{\Theta };\mathit{y})+d·lnN$$

where d is the model degrees of freedom and L_λ(Θ, y) is the model likelihood specific to the value of λ. The minimization of BIC(Θ; λ) can then be used to select a value of λ over the path of values in order to yield a final fit such that the size of θ_λ is equal to n_λ ≤ n_θ. The calculation of d requires that the model selection procedure be taken into consideration. For the LASSO procedure, this is equivalent to the size of the active set [Zou, et al. 2007]. An approximation for EB-SGL can be shown (see Appendix) to reduce to the trace of the smoother hat matrix of the model fit, which can be written as

$$d=tr\left({\mathit{W}}^{\frac{\mathbf{1}}{\mathbf{2}}}\stackrel{\sim }{\mathit{X}}{({\stackrel{\sim }{\mathit{X}}}^{\prime }\mathit{W}\stackrel{\sim }{\mathit{X}}+\mathbf{\Omega })}^{-\mathbf{1}}{\stackrel{\sim }{\mathit{X}}}^{\prime }{\mathit{W}}^{\frac{\mathbf{1}}{\mathbf{2}}}\right)$$

where W = diag(μ_i(1 − μ_i)), X̃ = [1 X Z_λ], Z_λ is a subset of Z corresponding to the nonzero subset of θ, θ_λ, for a given value of λ, and Ω = diag(ω), where the first m + 1 elements of ω are 0 since they correspond to unpenalized parameters (β₀, β), and the remaining n_λ are penalty weights corresponding to θ_λ and equal to $\frac{c\lambda }{\mid {\theta }_{jk}\mid }+\frac{(1-c)\lambda \sqrt{K_j}}{\sqrt{{\mathrm{\sum }}_j{\theta }_{jk}^2}}$.

Model criteria based in part upon prediction performance may result in a large number of false positives, which stands in contrast to the prevailing objective of identifying a confident subset of associated genes for follow-up analyses. If we are instead interested in gene-level control of the false positive rate, we may employ the permutation-based method described in Ayers et al. [Ayers and Cordell 2010], which selects λ by repeatedly permuting case-control status and identifying values that result in the first covariate (i.e., false positive) entering the active set. For EB-SGL, translating this procedure to gene-level association is complicated by defining what constitutes a false positive result. We adopt a minor modification that is based upon admittance of covariates at the group level, such that we record smallest values of λ that allow exon-level measures into the active set from at most one gene. We focus on this mode of tuning parameter selection for the remainder of the paper, as we foresee it being of greatest utility for large-scale sequencing studies (e.g., whole exome).

Data Simulation

To base our simulations on realistic exome sequence data characteristics, we downloaded the empirical distribution of rare (MAF≤0.05) variants from the NHLBI-ESP Exome Variant Server (release ESP6500). We isolated the European American minor allele frequencies for all observed polymorphic sites on chromosome 1, which we then annotated with exon membership information from the CCDS data (including appended 10bp flanking regions for potential splice site variation). Finally, we excluded genes exhibiting minimal variation, such that for all included genes the sum of MAFs across all variants in a given gene ≥ 0.005 and the total number of variants ≥ 10. Our final variant list consisted of a total of 28,552 unique sites on 6000 exons in 597 genes, with median values of 3 variants per exon and 37 variants per gene. The corresponding MAFs ranged from 0.00012 to 0.05, with a mean value of 0.00121. We generated genotype data for 30,000 simulated individuals, assuming Hardy-Weinberg equilibrium proportions and independence between variant sites.

For our disease models, we selected five unique genes to harbor causal variants, concentrating on moderately sized genes with a variety of exon distributions and total variant counts (see Table I). While some of these genes have a relatively large number of variants, the vast majority of these variants are very rare and unlikely to be observed on an individual basis in any given simulation replicate. To simulate phenotypes based upon genotypes, we applied a logistic regression approach whereby the Bernoulli probability of affected status conditional on genotype is given as

Table I.

Description of disease-related genes used in the simulation study, characterizing gene size, quantity of exons and variants, as well as MAFs of variants.

Gene	Length (bp)	Total Exons	# Var.	Mean MAF	Dist. of All Variants by MAF
					0.05–0.01	0.01–0.001	<0.001
1	2083	11	87	0.0012	3	6	78
2	1062	6	37	0.0019	1	7	29
3	3754	17	82	0.0009	2	3	77
4	1592	7	43	0.0004	0	3	40
5	3052	17	114	0.0017	4	10	100

$${\mu }_i=\frac{exp({\beta }_0+{\mathrm{\sum }}_{j}ln({OR}_j)g_{ij})}{1+exp({\beta }_0+{\mathrm{\sum }}_{j}ln({OR}_j)g_{ij})}$$

where OR_j is the odds ratio associated with variant j, g_ij the corresponding minor allele count for subject i, and β₀ is an intercept adjusted to result in a population prevalence of approximately 5%.

Since the success of specific rare variant association methods depends largely upon the underlying assumptions of the disease model, we examined a variety of potential scenarios in our simulation study. We considered models where approximately 20% or 40% of the total number of variants are deleterious, such that the corresponding OR_j > 1. To define each OR_j, we considered two different approaches: a uniform, or fixed, effect model where OR_j = 3.0 for all causal variants regardless of population allele frequency, and an MAF-dependent scheme where $ln({OR}_j)=\frac{ln(10)}{4}\mid {log}_{10}{\mathit{MAF}}_j\mid$, akin to settings in Wu et al. [Wu, et al. 2011]. Deleterious variant selection was also conducted using two different approaches. We first considered causal variants to be randomly sampled uniformly from the total set of variants, regardless of exon membership. The second method selected causal variants from a subset of variants defined by falling within designated causal exons. These exons were selected to capture approximately 50% of the total number of variants, enforcing localization of causal variation to a fraction of the total exons for each gene. Table II details the causal variants for each gene by derived MAF across these scenarios. A total of 1000 cases and 1000 controls were sampled from the population of 30,000 subjects for each simulation replicate, with 500 replicates conducted per unique set of simulation conditions. In total, we evaluated eight distinct simulation scenarios to examine performance under a variety of underlying causal variant models.

Table II.

MAF distribution of causal rare variants by four unique variant sets.

Causal Variant %	Selection Method	Distribution of Causal Variants by MAF [0.050 – 0.010] [0.010 – 0.001] [<0.001]
		Gene 1			Gene 2			Gene 3			Gene 4			Gene 5
40	Random	2	2	31	0	3	12	1	0	32	0	1	16	2	4	40
	Exon	0	0	34	1	1	12	0	2	30	0	1	16	1	3	41
20	Random	0	0	17	1	0	6	0	0	16	0	0	9	0	0	23
	Exon	0	1	16	0	3	4	1	0	15	0	1	7	1	2	19

Comparison with Other Methods

We have framed the application of EB-SGL and GB-L with respect to hypothesis testing via variable selection, with non-zero coefficients corresponding to significantly associated genes. While no other explicit exon-based methods exist to our knowledge, there is interest in how EB-SGL compares to current gene-based testing approaches that are agnostic to the additional exon structure information. We denote gene-level significance in the context of variable selection in EB-SGL such that gene j is said to be associated with the response if ||θ_j||₂ > 0 for a given value of λ.

We compared gene-level power of EB-SGL and GB-L to a number of leading omnibus tests: C-alpha; the sequence kernel association test SKAT; SKAT-O [Lee, et al. 2012], an optimized combination of SKAT and burden-based testing; the Madsen-Browning WSS test; and the Cohort Allelic Sums Test (CAST) [Morgenthaler and Thilly 2007]. We applied SKAT and SKAT-O under the linear weighted kernel using the SKAT package in R, p-values from the WSS testing were derived with the approximation method under 100 permutations, and the C-alpha and CAST tests were performed using code from the AssotesteR package reporting asymptotic p-values. All remaining settings were set to the default values for the respective tests, with statistical significance for each test determined based upon p-values using a Bonferroni-corrected Type I error level of α = 0.05 (i.e, 0.05/597 ≈ 8.38e-05).

To achieve a comparably sized testing for GB-L and EB-SGL at the gene-level, we applied the previously described permutation-based approach for a priori selecting the tuning parameter λ. In the interest of computational cost for our simulation study, we approximated this procedure by assuming that the same values of λ were applicable across all simulation replicates for a given scenario, since the sampled population and causal variation were identical across replicates. We conducted 500 initial simulation replicates for each scenario, permuting case-control status once prior to computing Z and Z^*, and ran EB-SGL and GB-L on the respective permuted datasets. We selected the λ value that admitted a total of 25 false positive genes across all replicates for each unique simulation scenario, resulting in a comparable Type I error rate (25/(500*597) = 0.05/597).

Finally, for both EB-SGL and GB-L, we noted in our preliminary simulation studies that the presence of singletons often led to poor statistical power. Although the mechanism behind this issue has not yet been fully resolved, we nonetheless present simulation results for both approaches with singletons either included or filtered prior to analysis. Since previous work [Ladouceur, et al. 2013] has illustrated that removal of singletons in general leads to decreases in power in the competing gene-level tests, these methods were applied solely to the unfiltered data.

RESULTS

We first examined the Type I error rate control across the various testing procedures, presented in Table III. Surprisingly, these varied greatly across methods, but were relatively stable within methods across simulation scenarios. The C-alpha testing results yielded highly elevated Type I error rates, generally two orders of magnitude larger than the nominal level, indicating possible issues with asymptotic assumptions. SKAT, SKAT-O, and CAST generally exhibited near nominal Type I error control and tended toward being conservative, while GB-L and WSS results were slightly liberal and comparable in value. EB-SGL Type I error rates were also elevated, although moreso than GB-L and WSS and often close to an order of magnitude increase relative to the nominal level. With respect to both of the penalized approaches, the exclusion of singletons led to differing impacts on Type I error rates, with EB-SGL exhibiting larger scale effects than GB-L, although these impacts were relatively modest overall.

Table III.

Empirical false positive rates across simulation replicates for gene-wise testing at Bonferroni corrected α = 0.05 (0.05/597 ≈ 8.38e-05) for all simulation scenarios and methods.

Scenario			Methods
			EB-SGL	EB-SGL (no sing)	GB-L	GB-L (no sing)	SKAT	SKAT-O	WSS	C-alpha	CAST
Causal Variant %	OR model	Causal variants
40	Fixed	Random	5.92e-04	6.40e-04	3.00e-04	3.44e-04	5.85e-05	6.22e-05	1.06e-04	5.69e-03	4.02e-05
		Exon	6.29e-04	7.64e-04	3.07e-04	2.89e-04	2.92e-05	6.94e-05	1.39e-04	5.78e-03	5.11e-05
	Var.	Random	4.79e-04	7.17e-04	2.63e-04	1.83e-04	2.55e-05	4.75e-05	1.06e-04	5.48e-03	2.92e-05
		Exon	7.50e-04	5.78e-04	1.79e-04	2.05e-04	6.21e-05	6.94e-05	1.57e-04	5.70e-03	6.58e-05
20	Fixed	Random	6.69e-04	5.78e-04	2.82e-04	2.27e-04	6.94e-05	7.31e-05	2.05e-04	5.86e-03	8.41e-05
		Exon	5.81e-04	5.78e-04	3.55e-04	2.52e-04	6.94e-05	7.67e-05	1.54e-04	5.94e-03	4.75e-05
	Var.	Random	7.09e-04	5.74e-04	3.25e-04	3.22e-04	4.39e-05	8.04e-05	1.90e-04	6.00e-03	5.12e-05
		Exon	8.00e-04	6.00e-04	4.13e-04	3.95e-04	5.85e-05	9.51e-05	1.83e-04	5.98e-03	6.94e-05

Simulation results with respect to overall power (Table IV) indicated that EB-SGL and GB-L performed very poorly when the variant-level effect sizes were not dependent upon the underlying MAF, especially relative to the competing gene-level methods. This is somewhat unsurprising, since the weighting scheme explicitly places more weight on rarer variation. A similar pattern was observed with respect to the WSS test, which uses the same weighting scheme, although the overall power for this approach was much higher relative to GB-L and EB-SGL. Statistical power was also in general higher for each given method when the true causal proportion was higher and when the effect sizes were MAF-dependent rather than uniform across variants. SKAT-O and WSS tended to perform the best across all scenarios, taking into account proper control of Type I errors.

Table IV.

Empirical power across simulation replicates for gene-wise testing at Bonferroni corrected α = 0.05 (0.05/597 ≈ 8.38e-05) for all simulation scenarios and methods. The methods with the highest power per scenario are highlighted in bold (C-alpha was ignored due to its high Type I error rate).

Simulation Scenario			Methods
			EB-SGL	EB-SGL (no sing)	GB-L	GB-L (no sing)	SKAT	SKAT-O	WSS	C-alpha	CAST
Causal Variant %	OR model	Causal variants
40	Fixed	Random	0.002	0.088	0.102	0.231	0.635	0.661	0.533	0.744	0.394
		Exon	0.012	0.081	0.065	0.135	0.349	0.369	0.390	0.440	0.008
	MAF	Random	0.080	0.297	0.538	0.722	0.754	0.903	0.802	0.787	0.767
		Exon	0.198	0.339	0.516	0.676	0.398	0.614	0.561	0.540	0.228
20	Fixed	Random	0.001	0.007	0.000	0.004	0.184	0.177	0.200	0.205	0.000
		Exon	0.001	0.023	0.006	0.029	0.383	0.378	0.370	0.416	0.004
	MAF	Random	0.004	0.008	0.115	0.259	0.129	0.130	0.186	0.206	0.004
		Exon	0.040	0.137	0.142	0.400	0.432	0.500	0.401	0.491	0.113

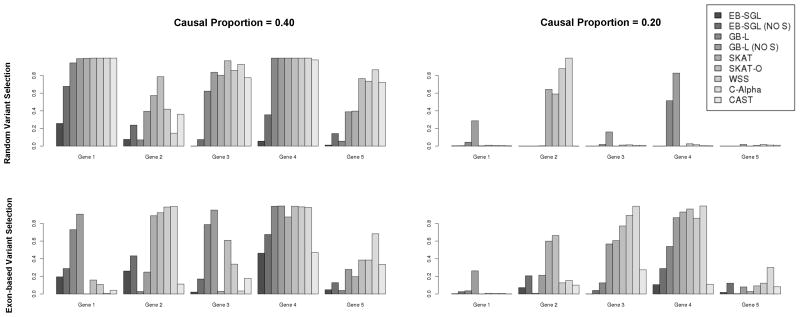
Focusing on gene-specific power under the MAF-dependent effect models (Figure 2), illustrates that the performance of the penalized methods was highly dependent upon the underlying causal variation. Overall, GB-L exhibited higher power over EB-SGL in every scenario except for the results for gene 2 under the exon-based variant selection model. Interestingly, the gene-wise power for the penalized approaches were much more powerful than the competing tests in isolated instances, while in others the opposite was observed. For example, from Figure 2 we observe that GB-L performed well for genes 1, 3, and 4 across all scenarios, with the version excluding singletons often exhibiting comparable, or better, power relative to the competing approaches. However, these competing approaches grossly outperform GB-L for gene 2. Examination of the results relative to the underlying causal variation for each scenario indicates that the penalized approaches tend to perform better when both the causal and neutral variant MAFs are relatively low (<0.005).

Figure 2.

Barplots indicating statistical power for detecting individual disease genes harboring causal variants OR_j across various methods and simulation conditions where the are defined using the MAF-dependent scheme. Analysis results using EB-SGL and GB-L where singletons have been removed are indicated by “NO S” in the legend.

DISCUSSION

In this paper, we have extended existing work for penalized regression on sequencing data by combining LASSO and sparse group LASSO logistic regression with variant collapsing to identify rare variant enrichment in case-control exome sequencing studies. While collapsing methods for rare variant analysis are commonplace for omnibus testing, our approaches explore simultaneous assessment of multiple collapsing measures in a regression framework, which can also accommodate adjustment for confounding variables. We considered a gene-based method using a simple LASSO logistic regression model, GB-L, where rare variants within individual genes are summarized by a univariate weighted sum for each subject. Motivated by biological principles of the coding content of exons within genes, we also examined an exon-based sparse group LASSO approach, EB-SGL, which may provide more acute localization of rare variant associations in contrast to gene-level testing by operating on an ROI definition with finer granularity.

Overall, our simulation results indicated that the power of EB-SGL to be quite poor unless causal variation is highly localized with multiple causal variants. This may in part be attributable to the exon structure of the genes we modeled, which we observed to be often composed of multiple very small exons. Given that much of the observed variation in the ESP6500 data is very rare or private, this resulted in most exons in our simulations harboring ≤ 1 variant, rendering any collapsing measure over exons superfluous. In this context, these results agreed with Ayer et al. [Ayers and Cordell 2013], who noted similarly poor performance for variant-level sparse group LASSO. As gene-wise functional domain annotation for coding proteins improves, however, it may be worthwhile to revisit this type of sub-gene aggregation.

The simulation performance of the GB-L penalized regression approach was much more encouraging, and was the highest powered method in two of our eight simulation scenarios. Although the Type I error rate was slightly elevated relative to the nominal level, this may be potentially due to the approximation approach we employed to select the tuning parameter λ. Of greater interest was the wide variety of gene-specific performance observed across simulation scenarios, as seen in Figure 2, with some instances where the power for GB-L was dramatically greater than the competing testing procedures. Examination of these cases indicated this disparity to be dependent upon the MAF distribution of the causal variation, as we observed GB-L to be relatively more sensitive when the causal variants were very rare. It was also interesting to note the sizable increases in power for both GB-L and EB-SGL by filtering out singletons in the model fitting procedure while maintaining comparable Type I error rates. This may be due in part to issues of quasi-complete separability in the regression model for genes with minimal variation, and further evaluation of filtering mechanisms may be necessary prior to model fitting.

From a computational perspective, the source of the computational burden for both EB-SGL and GB-L largely stems from running the permutation fits necessary to select the value of λ, although this is an easily parallelizable process. Final model fits completed in < 2 minutes for either approach on a modern Linux workstation equipped with a Quad-Core AMD Opteron^™ Processor and 16 Gb of RAM. Methods based upon iterative model fits, particular bracketing and bisection algorithms, require considerably more computational time. This is particularly true for EB-SGL, where the burden of such model fits is heavily dependent upon the maximum desired model size, n_θ.

One caveat of variant collapsing approaches is that they implicitly presume that the direction of the effects in the ROI is uniform (i.e., all protective or all risk), an issue left unexplored in this paper. Reductions in statistical power can arise if a mixture of both types occurs in a given ROI, resulting in a “canceling” of effects. This is clearly a pitfall for GB-L, and an issue shared by other collapsing procedures. EB-SGL does not completely avoid this problem, but it does allow for the effects of aggregation measures at specific exons to be either risk or protective oriented. A possible remedy would be to apply the sign assignment procedure used by Hoffman et al. [Hoffmann, et al. 2010], where the weighted sum collapsing measure takes into account whether a given variant is observed more often in cases or controls. Evaluation of this approach when both protective and risk variants are observed in a given gene is the focus of future work.

While we have presented these approaches with respect to detecting rare variant clustering in case-control studies, they can be extended to other response types, such as quantitative traits or censored survival responses under appropriate variant weighting schemes. We can also extend GB-L to take advantage of available gene set annotation by reintroducing group-level penalties, which can accommodate overlapping groups in the penalty function. This circumvents the common problem of pathway-based analyses which result in dependent pathway-specific test statistics if genes are shared across multiple pathways. More work is necessary to further evaluate and build upon these penalized regression variant collapsing methods.

APPENDIX

Approximating the degrees of freedom for the EB-SGL model fit

An approximation for the degrees of freedom d for a LASSO linear regression model fit was provided by Tibshirani [Tibshirani 1996], noting that the LASSO penalty can be written as a ridge regression problem by redefining the penalty term as $\mathrm{\sum }\mid {\beta }_i\mid =\mathrm{\sum }\frac{{\beta }_i^2}{\mid {\beta }_i\mid }$. This results in the LASSO estimator being defined as ridge estimator, such that

$$\stackrel{\sim }{\mathit{\beta }}={({\mathit{X}}^{\prime }X+\mathbf{\Omega })}^{-\mathbf{1}}{\mathit{X}}^{\prime }\mathit{y}$$

where $\mathbf{\Omega }=\mathit{diag}\left(\frac{\lambda }{\mid {\beta }_i\mid }\right)$. The hat matrix is then given as H = X(X′ X + Ω)⁻¹X′, and Tibshirani approximates the effective number of parameters d by tr(H).

Consider a traditional logistic regression model

$$\mathit{logit}(\mathit{\mu })=\mathit{\eta }=\mathit{X}\mathit{\beta }$$

where X is some design matrix, β is the corresponding vector of regression coefficients, and μ the vector of success probabilities associated with binary response vector y. Recall that the iteratively reweighted least squares (IRWLS) estimator of regression coefficients β in traditional logistic regression is given as

$$\widehat{\mathit{\beta }}={({\mathit{X}}^{\prime }\mathit{WX})}^{-\mathbf{1}}{\mathit{X}}^{\prime }{\mathit{Wy}}^{\ast }$$

where $y_i^{\ast }={\eta }_i+(y_i-{\mu }_i)/({\mu }_i(1-{\mu }_i))$ is the working response and W = diag(μ_i(1 − μ_i)). The hat matrix for y^* is then given as

$$\mathit{S}={\mathit{W}}^{\frac{\mathbf{1}}{\mathbf{2}}}\mathit{X}{({\mathit{X}}^{\prime }\mathit{WX})}^{-\mathbf{1}}{\mathit{X}}^{\prime }{\mathit{W}}^{\frac{\mathbf{1}}{\mathbf{2}}}$$

Now, consider the penalized logistic regression model posed in our EB-SGL approach, which can be written similarly as

$$\mathit{logit}(\mathit{\mu })=\mathbf{1}{\beta }_0+\mathit{X}\mathit{\beta }+\mathit{Z}\mathit{\theta }$$

with a model fit criterion is given by

$$\underset{\alpha \in R^p}{min}\left(-\frac{1}{N}log(L(\mathbf{\Theta };\mathit{y}))+{\lambda }_1\sum _{j=1}^J\sqrt{K_j}{\Vert {\mathit{\theta }}_j\Vert }_2+{\lambda }_2{\Vert \mathit{\theta }\Vert }_1\right)$$

First, note that the lasso penalty term can be rewritten in the same fashion proposed by Tibshirani, such that

$${\lambda }_2{\Vert \mathit{\theta }\Vert }_1={\lambda }_2\sum _{j=1}^J\sum _{k=1}^{K_j}\frac{{\theta }_{jk}^2}{\mid {\theta }_{jk}\mid }$$

Similarly, the group penalty term can be rewritten such that

$${\lambda }_1\sum _{j=1}^J\sqrt{K_j}{\Vert {\mathit{\theta }}_j\Vert }_2={\lambda }_1\sum _{j=1}^J\sqrt{K_j}\sqrt{\sum _{k=1}^{K_j}{\theta }_{jk}^2}={\lambda }_1\sum _{j=1}^J\sqrt{K_j}\frac{{\mathrm{\sum }}_k{\theta }_{jk}^2}{\sqrt{{\mathrm{\sum }}_k{\theta }_{jk}^2}}={\lambda }_1\sum _{j=1}^J\sum _{k=1}^{K_j}{\alpha }_{jk}^2\frac{\sqrt{K_j}}{\sqrt{{\mathrm{\sum }}_i{\theta }_{jk}^2}}$$

Thus, the full penalty can be rewritten as

$${\lambda }_1\sum _{j=1}^J\sum _{k=1}^{K_j}{\theta }_{jk}^2\frac{\sqrt{K_j}}{\sqrt{{\mathrm{\sum }}_i{\theta }_{jk}^2}}+{\lambda }_2\sum _{j=1}^J\sum _{k=1}^{K_j}\frac{{\theta }_{jk}^2}{\mid {\theta }_{ij}\mid }=\sum _{j=1}^J\sum _{k=1}^{K_j}{\theta }_{jk}^2\left(\frac{{\lambda }_2}{\mid {\theta }_{jk}\mid }+\frac{{\lambda }_1\sqrt{K_j}}{\sqrt{{\mathrm{\sum }}_i{\theta }_{jk}^2}}\right)$$

Notice that the penalty function is now in the form of a ridge penalty with weights defined by the nature of the sparse group penalty. Thus, we can frame our calculation of the degrees of freedom of the EB-SGL model fit in the context of a ridge-type penalized model fit, where the diagonal penalty matrix Ω = diag(ω) for a penalty weight vector ω consisting of m + n_λ + 1 elements. The first m + 1 elements of ω are 0, corresponding to the unpenalized parameters β₀ and β, while the remaining n_λ parameters correspond to θ_λ and are defined as $\frac{{\lambda }_2}{\mid {\theta }_{jk}\mid }+\frac{{\lambda }_1\sqrt{K_j}}{\sqrt{{\mathrm{\sum }}_i{\theta }_{jk}^2}}$. If we assume that λ = λ₁ + λ₂ and $c=\frac{{\lambda }_2}{\lambda }$ for some fixed value of c, then this reduces to $\frac{c\lambda }{\mid {\theta }_{jk}\mid }+\frac{(1-c)\lambda \sqrt{K_j}}{\sqrt{{\mathrm{\sum }}_i{\theta }_{jk}^2}}$. Approximating the degrees of freedom then amounts to

$$d=tr\left({\mathit{W}}^{\frac{\mathbf{1}}{\mathbf{2}}}\stackrel{\sim }{\mathit{X}}{({\stackrel{\sim }{\mathit{X}}}^{\prime }\mathit{W}\stackrel{\sim }{\mathit{X}}+\mathbf{\Omega })}^{-\mathbf{1}}{\stackrel{\sim }{\mathit{X}}}^{\prime }{\mathit{W}}^{\frac{\mathbf{1}}{\mathbf{2}}}\right)$$

such that X̃ = [1 X Z_λ], where Z_λ is a submatrix of Z with columns corresponding to the nonzero subset of θ, θ_λ, for a given value of λ.