Abstract
Quantum mechanical (QM) calculations of noncovalent interactions are uniquely useful as tools to test and improve molecular mechanics force fields and to model the forces involved in biomolecular binding and folding. Because the more computationally tractable QM methods necessarily include approximations, which risk degrading accuracy, it is essential to evaluate such methods by comparison with high-level reference calculations. Here, we use the extensive Benchmark Energy and Geometry Database (BEGDB) of CCSD(T)/CBS reference results to evaluate the accuracy and speed of widely used QM methods for over 1200 chemically varied gas-phase dimers. In particular, we study the semiempirical PM6 and PM7 methods; density functional theory (DFT) approaches B3LYP, B97-D, M062X, and ωB97X-D; and symmetry-adapted perturbation theory (SAPT) approach. For the PM6 and DFT methods, we also examine the effects of post hoc corrections for hydrogen bonding (PM6-DH+, PM6-DH2), halogen atoms (PM6-DH2X), and dispersion (DFT-D3 with zero and Becke–Johnson damping). Several orders of the SAPT expansion are also compared, ranging from SAPT0 up to SAPT2+3, where computationally feasible. We find that all DFT methods with dispersion corrections, as well as SAPT at orders above SAPT2, consistently provide dimer interaction energies within 1.0 kcal/mol RMSE across all systems. We also show that a linear scaling of the perturbative energy terms provided by the fast SAPT0 method yields similar high accuracy, at particularly low computational cost. The energies of all the dimer systems from the various QM approaches are included in the Supporting Information, as are the full SAPT2+(3) energy decomposition for a subset of over 1000 systems. The latter can be used to guide the parametrization of molecular mechanics force fields on a term-by-term basis.
Introduction
Noncovalent interactions are of fundamental importance to biomolecular systems, as they help determine the structures and functions of proteins and nucleic acids and play a central role in molecular recognition. A reliable representation of noncovalent interactions therefore is critically important to computational modeling of biomolecules, with applications that include rational drug design and protein engineering.1,2 In molecular simulations, noncovalent interactions are typically modeled by the nonbonded terms in an empirical force field.3−9 These account for electrostatic and van der Waals interactions and may also include terms to account for time-varying changes in electronic polarization during the simulation.10 Although the parameters in an empirical force field are typically adjusted to optimize agreement with experimental data, growing computer power and a shortage of suitable experimental data are also driving increased use of quantum mechanical (QM) calculations to parametrize and test force fields.11−15 In addition, concerns regarding the accuracy of empirical force fields16,17 are motivating the direct application of QM methods to the study of noncovalent binding in host–guest18,19 and protein–ligand20−22 systems.
It would be ideal if such applications could take advantage of the highly accurate QM approach often viewed as the gold standard for computing noncovalent interactions, that is, counterpoise-corrected couple-cluster theory with single, double, and perturbative triple excitations extrapolated to the completed basis set limit.23 However, the computational demands of such CCSD(T)/CBS CP calculations make them too time consuming for routine use in force field parametrization and prohibit direct application to biomolecular systems. As a consequence, a range of other QM methods have been developed. Because all of these methods make approximations for the sake of computational efficiency, it becomes essential to evaluate their accuracy. While there are many studies that rely on high accuracy reference results for relevant molecular systems,24−28 there is still a need for broader comparative validation studies that will provide users and developers with a perspective of the strengths, weaknesses, and trade-offs among the various QM approaches and their applicability to specific classes of noncovalent interactions.
Here, therefore, we contribute a systematic assessment of accuracy and speed for a range of QM methods using a reference data set of over 1200 gas-phase dimers, for which CCSD(T)/CBS CP reference energies are publicly available in the Benchmark Energy and Geometry Database (BEGDB).29 The categories of the QM method examined are semiempirical, density functional theory (DFT) with and without dispersion corrections, and symmetry-adapted perturbation theory (SAPT). The semiempirical PM630 and PM731 methods, the most computationally efficient methods tested here, rely on empirically adjustable parameters and are often combined with additional interaction terms. We examine the PM6 method, with post hoc corrections for dispersion and hydrogen bonding interactions (PM6-DH2,32,33 PM6-DH+34), and halogen interactions (PM6-DH2X35). The PM7 method, which is based on PM6, is also included without additional corrections, as its parametrization strategy accounts for such interactions. We test the widely used DFT functionals B3LYP,36,37 B97-D,38 and M062X,39 with and without added dispersion corrections,40 as well as the ωB97X-D41 functional, which includes its own correction for dispersion. Finally, we test SAPT,42 which is distinct from the PMx and DFT approaches in that it is applicable only to the calculation of noncovalent interactions (e.g., it cannot be applied to geometry optimizations) and that it provides an informative decomposition of the overall interaction energy into electrostatic, induction, exchange, and dispersion components. In SAPT, the interaction energy is computed as an expansion of perturbative terms, and we examine the SAPT0, SAPT2, SAPT2+, SAPT2+(3), and SAPT2+3 truncations.26 We also explore the potential for the fast SAPT0 (fSAPT0) method to afford accurate results through empirical scaling of its energy terms, much as done previously in a smaller study,43 and make available the detailed energy decompositions afforded by SAPT across all of the test systems, as these can be useful to guide force field parametrization.44 The present study provides a unique perspective of the reliability and efficiency of a broad range of QM methods and should be a useful guide to their selection and further improvement.
Methods
Benchmark Data Sets
A growing collection of benchmark data sets provides high quality geometries and interaction energies for noncovalent complexes.26 Here, we use several data sets (Table 1) from the BEGDB to explore the accuracy of various QM methods for noncovalent interactions spanning a range of system types and sizes. We study a total of 1266 dimers, ranging in size from 20 electrons in 4 atoms to 478 electrons in 101 atoms (Figure 1). These various BEGDB data sets probe different classes of noncovalent interactions. In particular, the S22×545 and S66×846 data sets both contain noncovalent complexes categorized as hydrogen bonded (electrostatics dominated), dispersion dominated, or mixed electrostatic and dispersive. X40×1047 focuses on complexes with halogen interactions. Ionic48 contains systems with charged hydrogen bonds. SCAI49 and JSCH23 contain amino acid and nucleic acid complexes. The L750 data set contains even larger extended complexes; all of them containing greater than 200 electrons. Several of these data sets, S22×5, S66×8,46 X40×10,47 and Ionic, contain geometries generated along a dissociation path relative to the equilibrium geometry and thus include many nonequilibrium conformations. Because the aug-cc-pVTZ basis set51−54 used in the present study is not applicable to iodine, we omit the nine iodine-containing complexes in X40×10 and term the reduced data set X31×10. Lastly, we also include the A2455 data set, which contains small complexes sized to enable comparisons of more accurate approaches that would otherwise be unfeasible for larger complexes. BEGDB provides counterpoise-corrected CCSD(T)/CBS interaction energies for all of these data sets, except for JSCH, which contains energies evaluated using CCSD(T)/CBS and MP2/CBS without counterpoise (CP) correction, and L7, which uses QCISD(T)/CBS CP. It is also worth noting that there are variations within and across these BEGDB data sets in both the basis sets and extrapolation schemes employed to obtain the CBS results. Such details are not trivial and can produce discrepancies as large as 0.7 kcal/mol, as elaborated in the Results section.
Table 1. BEGDB Data Sets Used in the Present Studya27.
|
equilibrium data sets | ||||
|---|---|---|---|---|
| data set | description | number of structures | geometry optimization level | reference energy level |
| A2455 | small complexes of 7–11 atoms | 24 | CCSD(T)/CBS CP or noCP | CCSD(T)/CBS CP |
| S2223 | small complexes of 8–26 atoms | 22 | MP2/cc-pVTZ CP noCP or CCSD(T)/cc-pV(T/Q)Z noCP | CCSD(T)/CBS CP |
| S6646 | small complexes of 6–18 atoms | 66 | MP2/cc-pVTZ CP | CCSD(T)/CBS CP |
| X4047 | complexes with halogenated molecules | 40 | MP2/cc-pVTZ CP | CCSD(T)/CBS CP |
| SCAI49 | amino acid side-chain complexes of 22–32 atoms | 24 | DFT TPSS/TZVP noCP | CCSD(T)/CBS CP (D→T) |
| JSCH23 | 124 nucleobase complexes and 19 amino acid complexes of 29–41 atoms | 143 | artificial geometries, NMR structures, crystal structures, X-ray structures, MP2/cc-pVTZ noCP, or MP2/TZVPP noCP | CCSD(T)/CBS noCP or MP2/CBS noCP |
| L750 | large complexes of 48–112 atoms | 7 | DFT-D TPSS-D/TZVP or other | QCISD(T)/CBS CP or CCSD(T)/CBS CP |
|
nonequilibrium data sets | ||||
|---|---|---|---|---|
| data set | relative displacements | number of structures | geometry optimization level | reference energy level |
| S22×545 | 0.9, 1.0, 1.2, 1.5, 2.0 | 110 | MP2/cc-pVTZ CP or CCSD(T)/cc-pV(T/Q)Z noCP | CCSD(T)/CBS CP |
| S66×846 | 0.90, 0.95, 1.00, 1.05, 1.10, 1.25, 1.50, 2.00 | 528 | MP2/cc-pVTZ CP | CCSD(T)/CBS CP |
| X40×1047 | 0.80, 0.85, 0.90, 0.95, 1.00, 1.05, 1.10, 1.25, 1.50, 2.00 | 400 | MP2/cc-pVTZ CP | CCSD(T)/CBS CP |
| Ionic48 | 0.90, 0.95, 1.00, 1.05, 1.10, 1.25, 1.50, 2.00 | 120 | MP2/cc-pVTZ CP | CCSD(T)/CBS CP |
Note that the names match those on the BEGDB Web site, which are not necessarily consistent with the corresponding publications. For example, the X40, X40×10, and Ionic data sets have also been referred to as “Halogens”, “Halogensx10”, and “Charged HB”.
Figure 1.
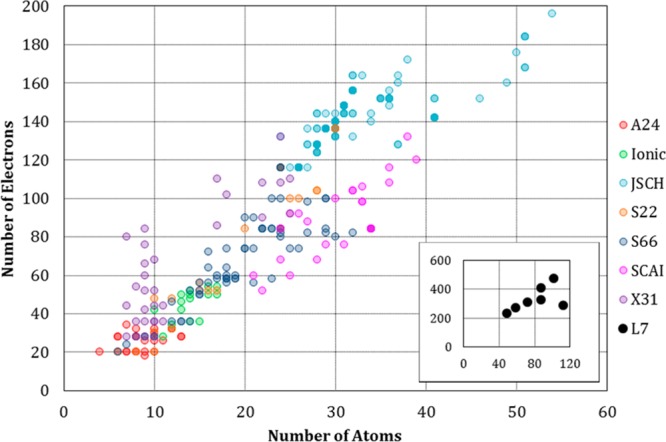
Sizes of dimers studied. For nonequilibrium data sets, only one point is shown per dimer system. The larger L7 data set is included in the inset.
Computational Methods
Semiempirical PMx energy calculations were carried out with MOPAC2012.56 The PM630 methods were examined with corrections for dispersion, hydrogen bonding, and halogen interactions. PM6-DH232 and PM6-DH+34 differ in the hydrogen-bonding correction used, with the latter having improved long-range behavior. PM6-DH2X35 adds an empirical repulsive correction for halogen interactions to the same dispersion and hydrogen-bonding corrections implemented in PM6-DH2. The more recent PM731 method is parametrized against a larger reference data set than that used for PM6 and includes its own terms to account for dispersion and hydrogen bonding.
The DFT calculations with CP correction were carried out with the aug-cc-pVTZ basis set in revision C.01 of Gaussian 09.57 Where SCF calculations failed to converge using default run parameters, the keyword Integral = (Acc2E = 12) was used to increase the two-electron integral accuracy. B3LYP,36,37 B97-D,38 M062X,39 and ωB97X-D41 functionals were selected based on previously assessed performance for noncovalent interactions.58 The D3 dispersion correction was applied using DFT-D3, version 3.0,40 to B3LYP, B97-D, and M062X using the default parameters. These were optimized using a different basis set, (aug-)def2-QZVP. However, we have found that for the S22 data set, aug-cc-pVTZ and (aug-)def2-QZVP, without any dispersion correction, give results that are within 0.18 kcal/mol RMSE of each other, across all of the methods examined in the present study. We also observed that using the DFT-D3 parameters optimized for (aug-)def2-QZVP reduced the RMSE across all data sets by up to 0.12 kcal/mol, compared with using those optimized for (aug-)def2-TZVPP, the only other basis set option currently available. Becke–Johnson damping for the D3 correction59 (D3BJ) was also tested for B3LYP and B97-D using parameters optimized for (aug-)def2-QZVP; there is no such correction available for M062X. The original “zero-damping” D3 corrections are so-called because they employ a damping function for which the dispersion energy approaches zero with small internuclear separations. We note that, with the exception of B3LYP, all the functionals already contain some treatment of dispersion. B97-D is the B97 functional with the D2 dispersion correction. M062X is already parametrized to account for dispersion. ωB97X-D utilizes its own specialized empirical dispersion correction.
The SAPT42 energy calculations at varying orders (SAPT0, SAPT2, SAPT2+, SAPT2+(3), SAPT2+3) were carried out with PSI4.60 In SAPT, the total interaction is computed as a sum of energy terms that are each classified as resulting from electrostatic, exchange, induction, or dispersion effects. The specific truncations of the SAPT expansion are detailed in Table S1 of the Supporting Information. Due to memory limitations, only lower order SAPT calculations were completed for larger systems. Thus, L7 was evaluated only with SAPT0. SCAI was evaluated at orders through SAPT2+. JSCH was evaluated through SAPT2 with the exception of nine amino acid pair geometries (F30–K46, F30–L33, F30–Y13, F30–F49, F30–Y4, F49–K46, F49–V5, F49–W37, and F49–Y4) taken from a rubredoxin crystal structure61 (PDB 1RB9), for which only SAPT0 calculations were completed. On the opposite end of the system size spectrum, SAPT orders up to SAPT2+3 were calculated for A24. All other data sets (S22×5, S66×8, Ionic, and X31×10) were evaluated through SAPT2+(3).
Evaluation of Accuracy and Computational Speed
We use the root mean squared error (RMSE) as the primary metric of error in comparing the various computational methods. However, the mean signed error (MSE) is also provided to further characterize the performance of each method; a negative MSE indicates that a method overestimates the attractive interactions of a noncovalent dimer. Relative error is often reported in the literature, presumably because errors are thought to increase with interaction energy. Here, however, we saw no correlation between error and interaction (R2 < 0.2 for all methods), so relative errors are not reported.
Timing studies were carried out on eight CPUs of a 16-CPU node, which was dedicated entirely to the calculation being timed. The timings of DFT and SAPT methods were examined by applying them in triplicate to each system in the A24 data set and noting the shortest of the three wall-clock times reported as elapsed “real” time by the Unix time command. This timing approach accounts for the efficiency with which each method uses the eight available CPUs. The timings for DFT with D3 dispersion correction are recorded without the add-on correction, as it requires negligible resources compared to the main calculation.
Linear Scaling of SAPT0 Energy Terms
The SAPT0 interaction energy is the sum of seven energy terms, as detailed in Table S1 of the Supporting Information. In the fSAPT0 schemes a separate scaling factor is applied to some or all of these terms. The linear scaling factors for the SAPT0 energy terms were determined by randomly splitting the systems in all combined data sets, except L7, into two equal subsets. One subset was used for training and the other for testing. Thus, we applied multiple linear regression of the SAPT0 energy terms to the corresponding CCSD(T)/CBS CP reference energies for the training set to obtain a set of fitted coefficients. We then used these coefficients to compute interaction energies for the test set and computed correlation coefficients and RMSE for the test set results. This procedure was repeated 1000 times, with different random selections of the training and testing subsets. Three different fitting schemes were tested: fSAPT0(1) scales all SAPT0 energy terms; fSAPT0(2) scales only the two dispersion terms, Edisp(20) and Eexch–disp, treated independently; and fSAPT0(3) scales only the sum of the two dispersion terms, Edisp(20) and Eexch–disp. We also tried applying scaling factors to SAPT2 thru SAPT2+(3), but this did not lead to significant improvements in accuracy.
Results
We tested a spectrum of quantum mechanical methods, spanning semiempirical (PMx), DFT, and SAPT, by comparing their results with reference interaction energies for a collection of noncovalent complexes in the gas phase. The reference collection, which comprised the A24, Ionic, JSCH, L7, SCAI, S22×5, S66×8, and X31×10 data sets from BEGDB, totals 1266 entries and includes a variety of molecules—nonpolar, polar, ionized, and halogenated—in equilibrium and nonequilibrium geometries. The Supporting Information provides the interaction energies, calculated using the various QM methods for all the systems studied, along with the corresponding BEGDB reference energies.
The present quantum mechanical results were compared with the highest-accuracy reference energies available in the BEGDB for the data sets used. These were generated with CCSD(T)/CBS calculations including counterpoise corrections, except as noted in the Methods section. It is worth noting that the reference energies in the S2223 and S6646 data sets, which are more limited versions of the S22×5 and S66×8 data sets used here, were recently revised based on larger basis sets, additional points for the CBS extrapolation, or both. The more rigorous results differ from those originally published by 0.2 and 0.1 kcal/mol RMSE, respectively, with maximum unsigned errors of up to 0.7 kcal/mol. Given that the reference energies were not computed at such a high level, they also presumably have errors similar in magnitude. This uncertainty in the reference energies implies that the present study cannot meaningfully resolve errors less than about 0.2 kcal/mol.
The following subsections provide an overview of the results, followed by more detailed discussions of the PMx, DFT, and SAPT approaches. Timing comparisons are then given for the DFT and SAPT methods. Finally, we show that a simple scaling of SAPT0 energy components offers substantially improved accuracy at minimal computational cost.
Overview
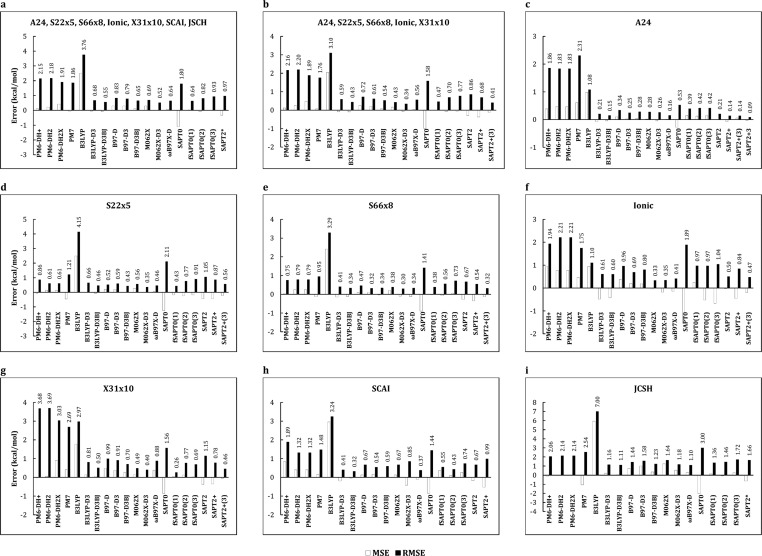
As shown in Figure 2 and tabulated in Table 2, the RMSE values of the various quantum methods averaged across all data sets range from 0.52 to 3.76 kcal/mol. The methods that yield the lowest overall errors are SAPT2+(3) and M062X, both with and without its dispersion correction, but a number of methods also yield overall RMSE values within 1 kcal/mol. The methods that yield the highest overall errors are the semiempirical (PMx) methods, B3LYP without dispersion correction, and SAPT0. The MSE values are more informative; they show that both the PMx and DFT methods without dispersion corrections tend to provide interaction energies more positive (less favorable) than the reference results, while the SAPT methods tend to provide interaction energies more negative (more favorable) than the reference results. As expected, supplementing the DFT methods with negative dispersion energy terms reduces the tendency to overestimate the interaction energy; the resulting improvement is particularly striking in going from B3LYP to B3LYP-D3.
Figure 2.
Evaluation of QM methods for combined and individual benchmark data sets. Errors evaluated relative to CCSD(T)/CBS CP energies. SAPT2 calculations were only evaluated for 134 out of 143 of the JCSH systems.
Table 2. Ranking of QM Methods by RMSE (kcal/mol) for Combined and Individual Benchmark Data Setsa.
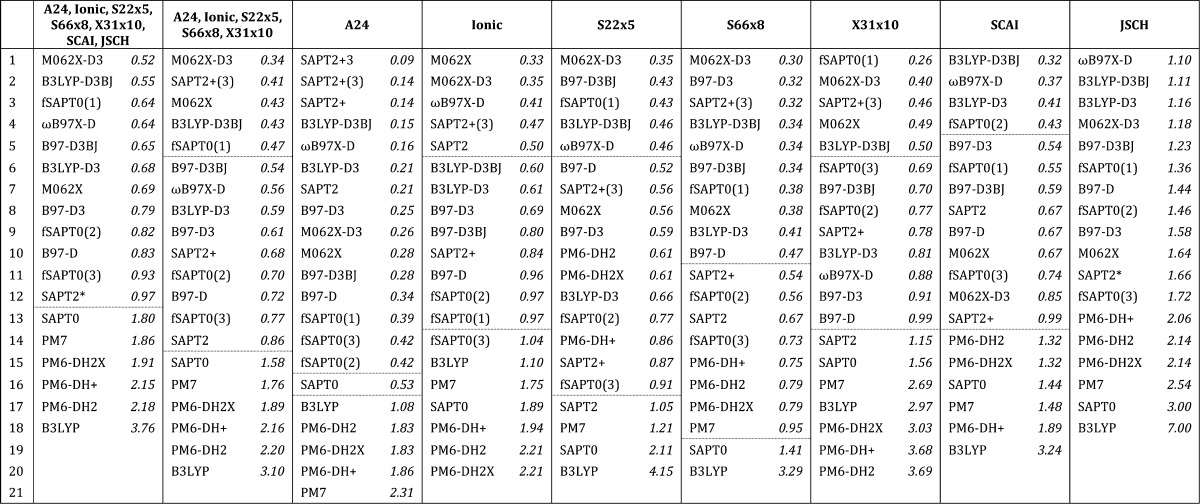
Dashed lines mark RMSE levels of 0.50 and 1.00 kcal/mol. Higher orders of SAPT calculations were not completed for some data sets due to memory limitations. A24 was evaluated at orders through SAPT2+3, SCAI through SAPT2+, JSCH through SAPT2, and all other data sets through SAPT2+(3).
SAPT2 calculations were only evaluated for 134 out of 143 of the JCSH systems.
The performance of the quantum approaches varies significantly across the data sets, as shown in Figure 2. Perhaps most striking is that the PMx methods provide substantially better relative results for the S22×5, S66×8, SCAI, and JCSH data sets and worse results for A24, Ionic, and X31×10. The problems for A24 and X31×10 appear to arise largely from errors associated specifically with halogenated molecules. The Ionic data set includes no halogens, however, and we speculate that the errors here may trace to the lack of ionized hydrogen-bonded complexes in the data sets used to parametrize the PMx methods. In addition, the minimal basis sets used in the PMx methods may have difficulty accounting for the strong polarization effects present in such ionized complexes. Other than B3LYP, lower-order SAPT, and PMx, all methods are within 1 kcal/mol RMSE of the reference energies for all sets except JSCH. For JSCH, all approaches yield larger errors (note the scale of the vertical axis in Figure 2c). This is perhaps not surprising because the JSCH data set contains the largest dimer systems, and one may expect larger systems to effectively include more interactions, each potentially associated with some level of error (Figure 1). Ranking the methods according to their overall accuracy and their accuracy on each data set (Table 2) shows that although certain methods remain near the top of the rankings across the board, the detailed ordering of the methods varies across data sets.
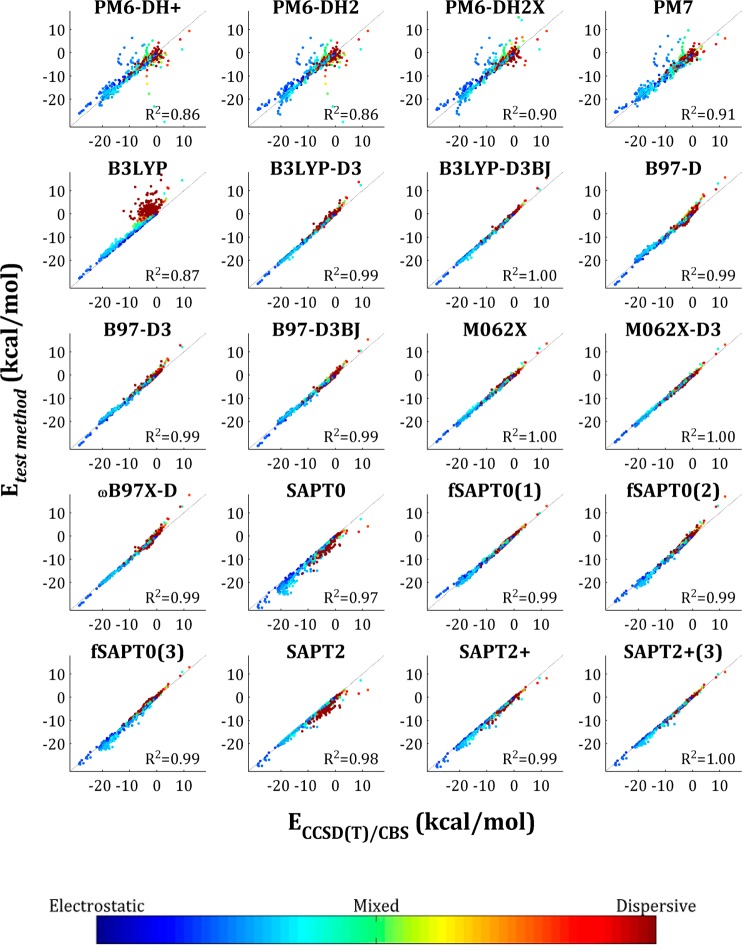
The scatter plots in Figure 3 provide further insight into the performance of the various approaches. All the methods tested provide excellent correlation with the reference energies (R2 > 0.86), and not surprisingly, those with the largest RMSE values (Figure 2) also yield the lowest R2 values (Figure 3). This analysis also allows further characterization of the errors associated with some of the methods. First, the PMx scatter plots include outliers arranged in smooth arcs. Further analysis indicates that each arc corresponds to the dissociation curve of one dimer system, and the dimer systems that generate these arcs are ones for which the PMx method yields idiosyncratically high errors, as discussed below. Second, most of the errors of the B3LYP method are associated with dimer systems whose interactions are primarily dispersive, as indicated by the red cluster of off-diagonal points. These errors are largely corrected by addition of the D3 dispersion correction. In contrast, the tendency of the SAPT methods to overestimate dimer affinities is largely independent of interaction type, as points of all colors are found below the lines of identity in the SAPT scatter plots. Third, adding a dispersion correction to the DFT methods uniformly improves the correlation, and the D3 correction performs somewhat better than D2, where the comparison is made (B97-D versus B97-D3). Finally, the DFT methods have a weak tendency to overestimate the unfavorable energy of the most repulsive interactions, while the PMx and SAPT methods tend to assign overly favorable energies in these cases. These repulsive interactions tend to have intermediate electrostatic dispersive character, as indicated by the cyan color of these points.
Figure 3.
Correlation of QM methods with CCSD(T)/CBS CP. We present only those data sets to which all methods could be applied, i.e., A24, Ionic, S22×5, S66×8, and X31×10. Each entry is colored by interaction type character (see spectrum below), which is defined as |Edisp/Eelst|, where Edisp and Eelst are the total electrostatic and dispersion energy components taken from the SAPT2+(3) calculations.
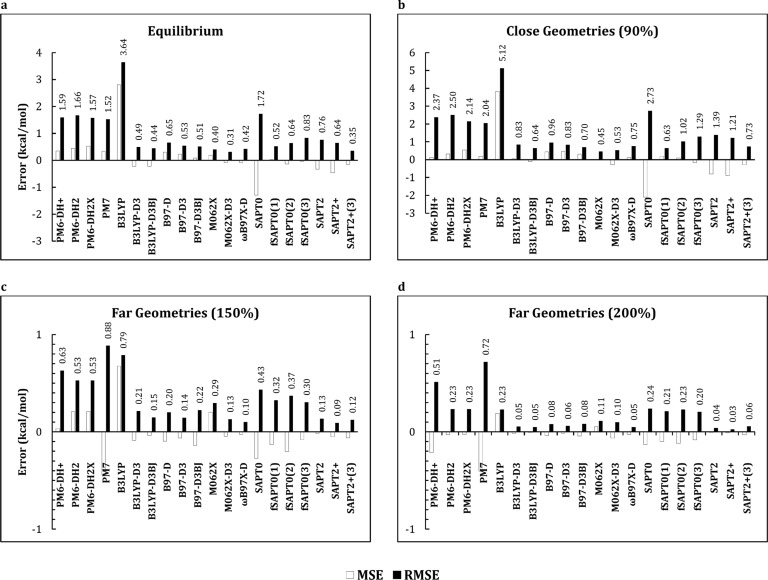
It is of interest to examine how the performance of the various methods depends on whether they are applied to equilibrium versus nonequilibrium geometries. Data sets S22×5, S66×8, X31×10, and Ionic make such comparisons possible, as they contain dissociation curves for a total of 134 dimer systems (see Methods). Figure 4 compares the MSE and RMSE for each method at close, equilibrium, and far separations, defined here as 90%, 100%, and 200% of the equilibrium separations, respectively. The rankings of the methods for equilibrium geometries correlate well with the rankings for the close geometries but poorly with rankings at far separations (Table 3).
Figure 4.
Evaluation of QM methods for equilibrium and nonequilibrium geometries.
Table 3. Ranking of QM Methods by RMSE (kcal/mol) for Equilibrium and Nonequilibrium Geometriesa.

Dashed lines mark RMSE levels of 0.5 and 1.0 kcal/mol.
Given that the long-range interactions are smaller in absolute terms, this observation suggests that a study of equilibrium geometries suffices to determine which methods work best overall. On the other hand, the errors rise at a short distance for all methods, so that none provide excellent accuracies for the close geometries, and only M062X has an RMSE below 0.5 kcal/mol. At far separations, all methods are within 1.0 kcal/mol RMSE, and several fall under 0.2 kcal/mol RMSE, which is comparable to the size of errors associated with basis set choice in computing the CCSD(T) correction, as discussed above.
Semiempirical PMx Methods
The semiempirical PMx methods are roughly comparable in accuracy to the DFT-D3 and higher-order SAPT methods for the S22×5, S66×8, and JSCH data sets but is considerably less accurate for A24, Ionic, and X31×10, much as previously noted.27 We conjecture that this difference stems in part from the fact that the PMx methods considered here, as well as their corrections (e.g., DH+), were parametrized using systems similar in character to those in the S22×5, S66×8, and JSCH data sets. In addition, as suggested by the scatter plots in Figure 3, some of the larger errors of the PMx methods are associated with specific systems for which they give idiosyncratically poor results. In particular, the PMx methods supply problematic results for bromobenzene···trimethylamine and systems containing HF, i.e., HF dimer, HF···methane, HF···methanol, and HF···methylamine. Accordingly, omitting these problematic cases significantly improves the RMSE of the PMx methods by 0.8–1.8 kcal/mol for the A24 and X31×10 data sets and by 0.2–0.7 kcal/mol across the full reference collection of data sets, as shown in Table 4. The bromine–nitrogen problem, as found here in the bromobenzene···trimethylamine system, is a known issue for the PM6 method and is improved by the halogen (“X”) correction for PM6 or by going to the PM7 method. However, we have not found previous comments on the issue for HF, and we are not aware of a correction for it. The fact that HF is problematic for all of the PMx methods is evident from the fact that the corresponding RMSE values for the A24 data set, which lacks the bromobenzene···trimethylamine system, improve by 0.5–0.9 kcal/mol when only the HF systems are omitted. When the bromobenzene···trimethylamine and HF-containing systems are omitted from the PMx results, their RMSE values across all systems fall to 1.4–1.6 kcal/mol (Table 4, bottom row, right). However, this improvement does not significantly change their position in the rankings in Table 2.
Table 4. Evaluation of PMx Methods with and without Problematic Dimer Casesa.
| original |
no bromobenzene
trimethylamine or HF |
|||||||
|---|---|---|---|---|---|---|---|---|
| PM6-DH+ | PM6-DH2 | PM6-DH2X | PM7 | PM6-DH+ | PM6-DH2 | PM6-DH2X | PM7 | |
| A24 | 1.86 | 1.83 | 1.83 | 2.31 | 0.88 | 0.82 | 0.82 | 0.93 |
| X31×10 | 3.68 | 3.69 | 3.03 | 2.69 | 1.88 | 1.92 | 2.26 | 1.72 |
| all | 2.16 | 2.20 | 1.89 | 1.76 | 1.44 | 1.48 | 1.59 | 1.52 |
Errors are presented as RMSE values, in kcal/mol.
No single PMx method emerges as the most reliable from these data. For example, although PM7 has a slightly better RMSE across the entire data collection than the corrected PM6 methods, it is not clear how significant this difference is, as its relative performance is quite inconsistent across the separate data sets (Figure 2). The PM6-DH2 and PM6-DH2X methods are equivalent for all systems except those containing halogens and thus produce identical results for S22×5, S66×8, Ionic, SCAI, and JSCH data sets. As expected, using PM7 or applying the “X” correction provides significant improvement in RMSE for the halogen-containing X31×10 data set. However, removing the specific problem systems mentioned in the prior paragraph essentially eliminates the advantage of these more advanced methods. The utility of the “X” correction, which is specifically designed to improve the treatment of halogens, may be examined more closely by comparing the various PMx methods for the full X40×10 data set, for which all systems contain at least one halogen atom, and which includes both equilibrium and nonequilibrium distances. PM6-DH2X is more accurate than PM6-DH2 at all distances, except that the “X” correction generates a particularly large error (22.6 kcal/mol RMSE) for dimers at 80% of their equilibrium distances, as shown Table S2 of the Supporting Information. Interestingly, when the iodine-containing systems are omitted, to create the X31×10 subset of X40×10, the “X” correction yields improved or equal results at all distances, and the anomalously high error at short range is absent. Thus, although the “X” correction yields an overall improvement, it seems problematic for the particular case of short-ranged interactions involving iodine. The PM7 method lacks this short-range anomaly but is somewhat less accurate for the iodinated compounds at longer ranges.
DFT with and without Dispersion Corrections
The DFT methods that incorporate some treatment of dispersion show good overall performance, with RMSE values ranging from 0.52 to 0.83 kcal/mol. In contrast, uncorrected B3LYP yields a rather large RMSE of 3.76 kcal/mol, and its largest errors are associated chiefly with dispersive systems (red in Figure 2), for which the method underestimates the attractive forces. Supplementing B3LYP with attractive D3 dispersion corrections markedly improves the overall RMSE across all test systems to 0.68 kcal/mol with D3 and to 0.55 kcal/mol with D3BJ. For the B3LYP functional, the BJ-damped version of the D3 correction typically produces results closer to reference compared with zero-damped D3. Interestingly, there is no marked improvement going from the two-body D2 correction to the three-body D3 correction in the context of the B97-D method, even for the larger systems in the JSCH and SCAI data sets, where three-body contributions are expected to be more important. Furthermore, while B97-D3BJ has a lower overall RMSE across all systems compared with B97-D3 (0.65 kcal/mol compared to 0.79 kcal/mol), the former produces higher RMSE values for the Ionic and SCAI data sets. Thus, it is difficult to gauge the benefit of applying BJ-damping over zero-damping for B97-D. The uncorrected M062X method performs equally well for electrostatic and dispersive systems (Figure 3), but its accuracy appears to be slightly improved by supplementing it with the D3 dispersion term (Figure 2). The ωB97X-D method includes its own dispersion correction distinct from D2 or D3, and this method ranks well across all the data sets. It is perhaps worth noting that the counterpoise corrections for all for DFT methods (B3LYP, B97-D, M062X, and ωB97X-D) are small, averaging 0.15 kcal/mol across all methods and systems. The mean correction rises only slightly to 0.21 kcal/mol for nonequilibrium systems at close range (90% of equilibrium separation). These corrections are small, in the sense that they are similar in magnitude to the uncertainty in the reference energies used here, as discussed above. Finally, it is worth noting that the low errors observed for D3-corrected DFT functionals in S22×5 are, perhaps, unsurprising, because the same molecules in similar geometries were included in the data set used to parametrize DFT-D3.
SAPT
The accuracy of the SAPT approach tends to increase with order, as expected, and the higher orders are comparable in accuracy to the best DFT methods (Figure 2). The trend of increased accuracy with increased order holds for all individual data sets, except Ionic, for which SAPT2 yields a lower RMSE than SAPT2+. Because SAPT2+ differs from SAPT2 by only two dispersion terms, it is interesting that the inclusion of these terms seemingly degrades accuracy here. Perhaps the excellent performance of SAPT2 for this particular data set results from a fortuitous cancellation of errors. It is worth noting that all orders of SAPT tend to overestimate attractive forces, regardless of system character, as evident from the negative MSE values in Figure 2 and by inspection of the scatter plots in Figure 3. This overestimation is particularly marked for SAPT0, suggesting the presence of a systematic error that might be mitigated by a post-calculation correction. Finally, because the SAPT energy components can be useful for tuning individual force field terms,44 we provide in the Supporting Information the detailed SAPT2+(3) decompositions for all the dimer systems studied here.
Timing Analysis
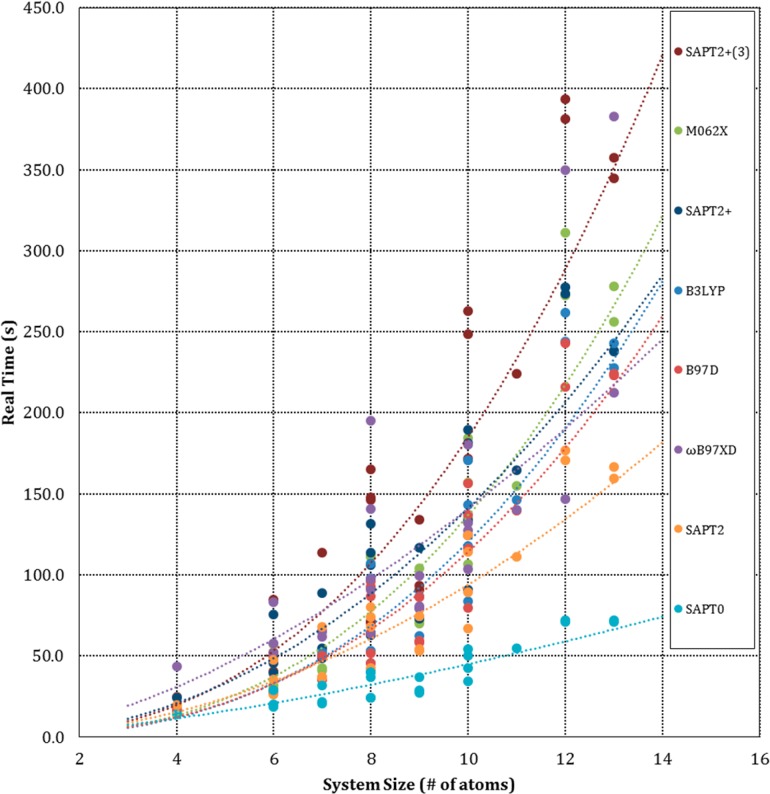
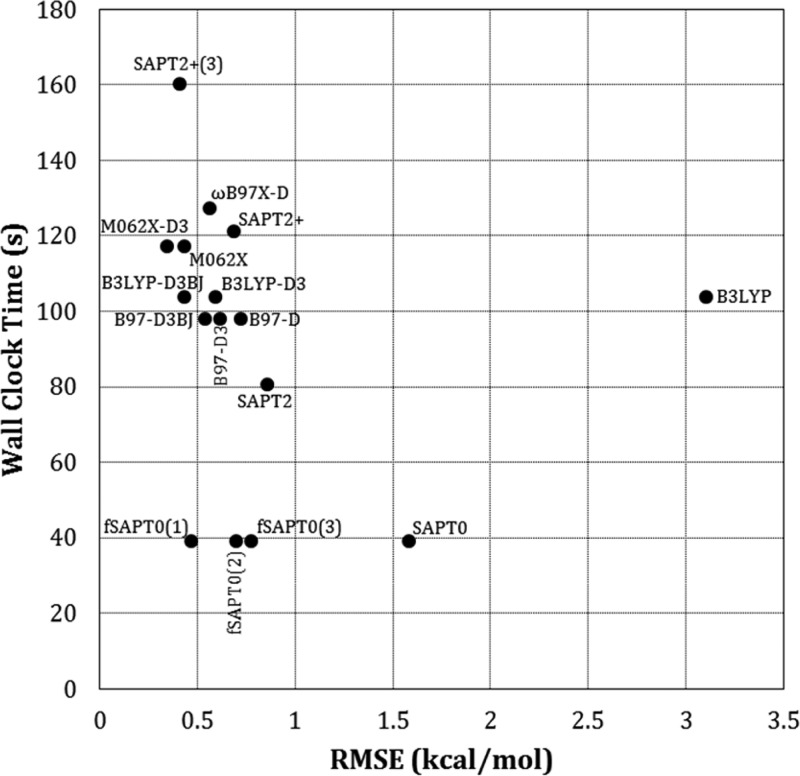
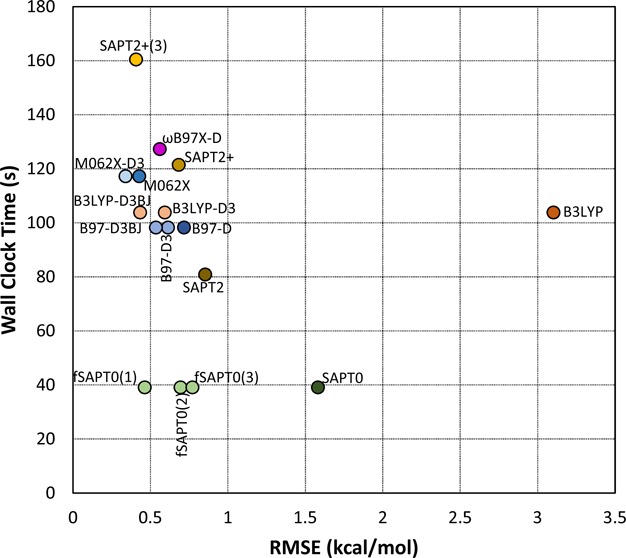
We used the A24 data set to compare the computational speeds of the various methods. The PMx methods all finished in less than 0.02s real (wall clock) time on a single CPU, making them over 1000 times faster than the DFT or SAPT methods. The latter were timed for all A24 systems on eight dedicated CPUs. Figure 5 plots real time against system size, as measured by the number of atoms, while Figure 6 plots the trade-off between accuracy and computer time. Overall, SAPT0 is clearly the fastest approach, SAPT2+(3) is the slowest, and the DFT timings are rather similar to each other and to SAPT2+. The level of accuracy broadly correlates with computer time, except in the case of uncorrected B3LYP.
Figure 5.
Scaling of calculation time with system size. Results are presented for the A24 data set, where system size is measured by the number of atoms in each dimer.
Figure 6.
Trade-off between accuracy and calculation time. Accuracies are presented as RMSE across the A24, Ionic, S22×5, S66×8, and X31×10 data sets, while calculation times are averaged for the A24 data set alone. Note that the post hoc D3 dispersion corrections and the SAPT0 fitting require negligible calculation time.
The scaling of computer time with system size was examined by fitting the timings for each method to a power model of the form t = anb, where t is real time and n is the number of atoms or electrons. The curve fits are detailed in Table S3 of the Supporting Information. As shown in Figure 5, all of the DFT methods except ωB97X-D have exponents of about 2.5 and prefactors of about 0.4. The ωB97X-D DFT method appears to scale rather differently, as its exponent and prefactor are 1.65 and 3.13, respectively. On the other hand, the R2 value of its fit to the power model is only 0.67, so its scaling behavior is not clearly defined by these data. The exponents for the SAPT methods increase with order. SAPT0 scales as the number of atoms to the power 1.49, while the SAPT2+(3) time varies as the 2.44 power. Analogous trends across the methods are observed when one fits the timings to the number of electrons in the system, rather than the number of atoms. Perhaps surprisingly, however, the R2 values of the fits are much lower, as evident in Table S3 of the Supporting Information.
Linear Scaling of SAPT0 Energy Terms
Of the methods tested here, SAPT0 is faster than all but the semiempirical PMx methods, as detailed above. The fact that it decomposes the total dimer interaction energy into seven contributions, which capture aspects of electrostatics, exchange, induction, and dispersion, provides an opportunity to try generating a fast method with improved accuracy by scaling these contributions, as detailed in Methods. Table 5 lists the means and standard deviations of the resulting scaling coefficients for the SAPT0 terms across the 1000 different training sets and the mean and standard deviations of the RMSE and R2 values when the trained coefficients are applied to the respective test sets. Most of the scaling coefficients are near unity; the term that requires the most scaling is the Eexch–disp(20) term. Scaling all terms in fSAPT0(1) produces the lowest test set RMSE, followed by scaling the dispersion terms individually in fSAPT0(2), and then by scaling the summed dispersion terms in fSAPT0(3). The fact that these results are obtained on test sets not used to set the coefficients means that the improvement in performance for the more highly parametrized models do not reflect overfitting. The accuracy of the three scaling schemes is also compared with the various QM methods in Figures 2 and 3 and Tables 2 and 3. Across all data sets, except L7, applying scaling factors to the SAPT0 terms reduces the RMSE from 1.58 kcal/mol to as low as 0.47 kcal/mol and corrects the tendency of SAPT0 to overestimate the attractive nature of the dimer interactions. Indeed, the fitted SAPT0 results approach the accuracy of the DFT methods, with the differences within the estimates of CCSD(T)/CBS basis set choice errors (above). Note that this improvement in SAPT0, through the application of simple scaling factors, incurs negligible additional computational cost, so that the fSAPT0 scaling methods provide a particularly favorable combination of efficiency and accuracy, as shown in Figure 6. Figure S1 of the Supporting Information furthermore examines the accuracy of fSAPT0, as well as the other QM methods, for the large noncovalent complexes of the L7 data set; the results are generally consistent with those obtained for the other data sets. The energy components of the fitted SAPT0 method still correlate well with the corresponding energy components calculated at the SAPT2+(3) level, as detailed in Table S4 of the Supporting Information. The good agreement suggests that the energy decomposition derived using the scaled terms is still physically meaningful.
Table 5. Linear Scaling Factors for SAPT0/aug-cc-pVTZ Energy Termsa.
| fSAPT0(1) | fSAPT0(2) | fSAPT0(3) | |
|---|---|---|---|
| Eelst,r(10) | 1.01 ± 0.02 | 1.00b | 1.00b |
| Eexch(10) | 1.02 ± 0.02 | 1.00b | 1.00b |
| Eind,r(20) | 0.76 ± 0.08 | 1.00b | 1.00b |
| Eexch–ind,r(20) | 0.70 ± 0.08 | 1.00b | 1.00b |
| δEHF,r(2) | 1.06 ± 0.08 | 1.00b | 1.00b |
| Edisp(20) | 0.93 ± 0.01 | 0.96 ± 0.02 | 0.76c ± 0.01 |
| Eexch–disp(20) | 1.7 ± 0.2 | 2.1 ± 0.2 | 0.76c ± 0.01 |
| test RMSE | 0.66 ± 0.06 | 0.82 ± 0.05 | 0.93 ± 0.04 |
| test R2 | 0.995 ± 0.009 | 0.993 ± 0.001 | 0.992 ± 0.001 |
Three different fitting schemes were tested: fSAPT0(1) scales all terms; fSAPT0(2) scales only the two dispersion terms, Edisp(20) and Eexch–disp, treated independently; and fSAPT0(3) scales only the sum of the two dispersion terms, Edisp(20) and Eexch–disp. The scaling factors were determined over 1000 iterations of multiple linear regression on randomly selected training subsets of the dimer systems, while RMSE and R2 were evaluated over the same iterations using test subsets comprising all dimer systems not included in the training subset. Training and test subsets were equal in size.
Not fitted.
Both dispersion terms share a single fitted coefficient.
Discussion
The present study systematically evaluates the accuracy and speed of a broad range of electronic structure methods for estimating noncovalent interaction energies. Methods spanning PMx, DFT, and SAPT were applied to over 1200 geometries of gas-phase dimers drawn from the BEGDB resource, which is tailored to probe a variety of interaction motifs relevant to biomolecules and drug-like compounds. These results offer useful guidance regarding which methods are most suitable for various types of applications where “gold-standard” CCSD(T)/CBS CP calculations are too time consuming or impractical, as now discussed.
The PMx methods studied here are dramatically faster than both the DFT and SAPT approaches, and they are more readily applied to larger molecules. However, they are in general less accurate, particularly for halogenated and ionic molecules, as well as for a few types of systems with idiosyncratic results.62 Perhaps surprisingly, none of the various PMx methods tested here are clearly superior to the others in terms of overall accuracy. The DFT methods are slower and more difficult to apply to large systems, but they can achieve high accuracy, so long as dispersion is accounted for, either implicitly, as in M062X, or via an add-on term, as in B97-D3. The performance of the SAPT approach depends strongly on the order of the SAPT expansion. The SAPT2+ and SAPT2+(3) orders span the range of accuracy seen for the dispersion-corrected DFT methods. However, while the speed of the SAPT2+ method is comparable to that of the DFT methods, the more accurate SAPT2+(3) is considerably slower. It is also worth noting that, at least in the current PSI4 software, the memory requirements of SAPT at orders higher than SAPT0 can become problematic for the larger systems examined here. The lowest order of SAPT, SAPT0, is similar in accuracy to the PMx methods but significantly slower. However, we find that a simple empirical scaling of one or more SAPT0 energy terms leads to accuracy approaching that of the best DFT methods, at far less computational cost. With further development, an empirically adjusted SAPT0 approach might provide a powerful alternative to DFT methods for the study of noncovalent interactions in larger systems.
The results of this study have implications for improving the treatment of noncovalent interactions in molecular modeling, as QM calculations are used to guide the development of force fields for simulation and may even replace force fields in some applications. The more accurate DFT and DFT-D3 methods maybe most suitable for force field parametrization given their reliability and consistency across many types of molecular systems and the fact that their moderate computational cost is not a major liability for this application. Despite the high speed of the PMx methods, their lower accuracy, especially for ionic systems and halogens, along with occasional idiosyncratic performance, makes them less suitable for parametrization of force fields. However, continued development of such semiempirical methods, including training on broader data sets, remains promising. In addition, these methods may already be more accurate than typical simulation force fields, so their high speed makes them a reasonable choice for direct modeling of biomolecular systems. The higher order SAPT methods are about as accurate as DFT but are relatively slow, while SAPT0 is fast but inaccurate. Interestingly, the scaled SAPT0 method offers a promising blend of accuracy and computational speed, especially for larger molecular systems. In addition, the present scaling approach is relatively simple, and more sophisticated schemes that account for geometry and chemistry might be even more accurate at minimal computational cost.
Acknowledgments
This work was supported in part by Grants R01GM61300 and T32EB93803 from the NIH. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH. Computing resources were supported by the NSF XSEDE program (Gordon and Trestles systems at the SDSC) and by the NIGMS (P41GM103426) of the NIH (computing cluster hosted by NBCR). The authors thank Dr. David Sherrill and his group for their help with PSI4, the Gaussian support team for their help with Gaussian 09, and Dr. Jan Jensen for valuable comments and suggestions.
Supporting Information Available
Material as mentioned in the text. This material is available free of charge via the Internet at http://pubs.acs.org.
Author Present Address
§ H. S. Muddana: Dart Neuroscience LLC, 12278 Scripps Summit Drive, San Diego, California 92131, United States.
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- Wang W.; Donini O.; Reyes C. M.; Kollman P. A. Biomolecular simulations: Recent developments in force fields, simulations of enzyme catalysis, protein–ligand, protein–protein, and protein–nucleic acid noncovalent interactions. Annu. Rev. Biophys. Biomol. Struct. 2001, 30, 211–243. [DOI] [PubMed] [Google Scholar]
- Gainza P.; Roberts K. E.; Georgiev I.; Lilien R. H.; Keedy D. A.; Chen C.-Y.; Reza F.; Anderson A. C.; Richardson D. C.; Richardson J. S.; Donald B. R. OSPREY: Protein design with ensembles, flexibility, and provable algorithms. Methods Enzymol. 2013, 523, 87–107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lifson S. Consistent force field for calculations of conformations, vibrational spectra, and enthalpies of cycloalkane and n-alkane molecules. J. Chem. Phys. 1968, 49, 5116–5129. [Google Scholar]
- Levitt M.; Lifson S. Refinement of protein conformations using a macromolecular energy minimization procedure. J. Mol. Biol. 1969, 46, 269–279. [DOI] [PubMed] [Google Scholar]
- Hagler A. T.; Huler E.; Lifson S. Energy functions for peptides and proteins. I. Derivation of a consistent force field including the hydrogen bond from amide crystals. J. Am. Chem. Soc. 1974, 96, 5319–5327. [DOI] [PubMed] [Google Scholar]
- Jorgensen W. L.; Tirado-Rives J. The OPLS [optimized potentials for liquid simulations] potential functions for proteins, energy minimizations for crystals of cyclic peptides and crambin. J. Am. Chem. Soc. 1988, 110, 1657–1666. [DOI] [PubMed] [Google Scholar]
- Cornell W. D.; Cieplak P.; Bayly C. I.; Gould I. R.; Merz K. M.; Ferguson D. M.; Spellmeyer D. C.; Fox T.; Caldwell J. W.; Kollman P. A. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 1995, 117, 5179–5197. [Google Scholar]
- Ponder J. W.; Case D. A. Force fields for protein simulations. Adv. Protein Chem. 2003, 66, 27–85. [DOI] [PubMed] [Google Scholar]
- Mackerell A. D. Empirical force fields for biological macromolecules: Overview and issues. J. Comput. Chem. 2004, 25, 1584–604. [DOI] [PubMed] [Google Scholar]
- Shi Y.; Xia Z.; Zhang J.; Best R.; Wu C.; Ponder J. W.; Ren P. Polarizable atomic multipole-based AMOEBA force field for proteins. J. Chem. Theory Comput. 2013, 9, 4046–4063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paton R. S.; Goodman J. M. Hydrogen bonding and pi-stacking: How reliable are force fields? A critical evaluation of force field descriptions of nonbonded interactions. J. Chem. Inf. Model. 2009, 49, 944–55. [DOI] [PubMed] [Google Scholar]
- Sherrill C. D.; Sumpter B. G.; Sinnokrot M. O.; Marshall M. S.; Hohenstein E. G.; Walker R. C.; Gould I. R. Assessment of standard force field models against high-quality ab initio potential curves for prototypes of pi-pi, CH/pi, and SH/pi interactions. J. Comput. Chem. 2009, 30, 2187–93. [DOI] [PubMed] [Google Scholar]
- Huang L.; Roux B. Automated force field parameterization for nonpolarizable and polarizable atomic models based on ab initio target data. J. Chem. Theory Comput. 2013, 9, 3543–3556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayne C. G.; Saam J.; Schulten K.; Tajkhorshid E.; Gumbart J. C. Rapid parameterization of small molecules using the force field toolkit. J. Comput. Chem. 2013, 34, 2757–2770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yilmazer N. D.; Korth M. Comparison of molecular mechanics, semi-empirical quantum mechanical, and density functional theory methods for scoring protein–ligand interactions. J. Phys. Chem. B 2013, 117, 8075–84. [DOI] [PubMed] [Google Scholar]
- Muddana H. S.; Varnado C. D.; Bielawski C. W.; Urbach A. R.; Isaacs L.; Geballe M. T.; Gilson M. K. Blind prediction of host-guest binding affinities: A new SAMPL3 challenge. J. Comput.-Aided. Mol. Des. 2012, 26, 475–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muddana H. S.; Gilson M. K. Prediction of SAMPL3 host-guest binding affinities: Evaluating the accuracy of generalized force-fields. J. Comput. Aided. Mol. Des. 2012, 26, 517–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grimme S. Supramolecular binding thermodynamics by dispersion-corrected density functional theory. Chem.—Eur. J. 2012, 18, 9955–9964. [DOI] [PubMed] [Google Scholar]
- Muddana H. S.; Gilson M. K. Calculation of host-guest binding affinities using a quantum-mechanical energy model. J. Chem. Theory Comput. 2012, 8, 2023–2033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fanfrlík J.; Bronowska A. K.; Rezác J.; Prenosil O.; Konvalinka J.; Hobza P. A reliable docking/scoring scheme based on the semiempirical quantum mechanical PM6-DH2 method accurately covering dispersion and H-bonding: HIV-1 protease with 22 ligands. J. Phys. Chem. B 2010, 114, 12666–12678. [DOI] [PubMed] [Google Scholar]
- Raha K.; Merz K. M. Large-scale validation of a quantum mechanics based scoring function: predicting the binding affinity and the binding mode of a diverse set of protein–ligand complexes. J. Med. Chem. 2005, 48, 4558–4575. [DOI] [PubMed] [Google Scholar]
- Ilatovskiy A. V.; Abagyan R.; Kufareva I. Quantum mechanics approaches to drug research in the era of structural chemogenomics. Int. J. Quantum Chem. 2013, 113, 1669–1675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jurecka P.; Sponer J.; Cerný J.; Hobza P. Benchmark database of accurate (MP2 and CCSD(T) complete basis set limit) interaction energies of small model complexes, DNA base pairs, and amino acid pairs. Phys. Chem. Chem. Phys. 2006, 8, 1985–1993. [DOI] [PubMed] [Google Scholar]
- Korth M.; Grimme S. “Mindless” DFT benchmarking. J. Chem. Theory Comput. 2009, 5, 993–1003. [DOI] [PubMed] [Google Scholar]
- Burns L. A.; Vázquez-Mayagoitia A.; Sumpter B. G.; Sherrill C. D. Density-functional approaches to noncovalent interactions: A comparison of dispersion corrections (DFT-D), exchange-hole dipole moment (XDM) theory, and specialized functionals. J. Chem. Phys. 2011, 134, 084107. [DOI] [PubMed] [Google Scholar]
- Hohenstein E. G.; Sherrill C. D. Wavefunction methods for noncovalent interactions. WIREs Comput. Mol. Sci. 2012, 2, 304–326. [Google Scholar]
- Hostaš J.; Řezáč J.; Hobza P. On the performance of the semiempirical quantum mechanical PM6 and PM7 methods for noncovalent interactions. Chem. Phys. Lett. 2013, 568–569, 161–166. [Google Scholar]
- Dilabio G. a; Johnson E. R.; Otero-de-la-Roza A. Performance of conventional and dispersion-corrected density-functional theory methods for hydrogen bonding interaction energies. Phys. Chem. Chem. Phys. 2013, 12821–12828. [DOI] [PubMed] [Google Scholar]
- Řezáč J.; Jurečka P.; Riley K. E.; Černý J.; Valdes H.; Pluháčková K.; Berka K.; Řezáč T.; Pitoňák M.; Vondrášek J.; Hobza P. Quantum chemical benchmark energy and geometry database for molecular clusters and complex molecular systems (www.begdb.com): A users manual and examples. Collect. Czechoslov. Chem. Commun. 2008, 73, 1261–1270. [Google Scholar]
- Stewart J. J. P. Optimization of parameters for semiempirical methods V: Modification of NDDO approximations and application to 70 elements. J. Mol. Model. 2007, 13, 1173–1213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stewart J. J. P. Optimization of parameters for semiempirical methods VI: More modifications to the NDDO approximations and re-optimization of parameters. J. Mol. Model. 2013, 19, 1–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korth M.; Piton M.; Pitoňák M.; Řezáč J.; Hobza P. A transferable H-bonding correction for semiempirical quantum-chemical methods. J. Chem. Theory Comput. 2010, 6, 344–352. [DOI] [PubMed] [Google Scholar]
- Řezáč J.; Fanfrlík J.; Salahub D.; Hobza P. Semiempirical quantum chemical PM6 method augmented by dispersion and H-bonding correction terms reliably describes various types of noncovalent complexes. J. Chem. Theory Comput. 2009, 5, 1749–1760. [DOI] [PubMed] [Google Scholar]
- Korth M. Third-generation hydrogen-bonding corrections for semiempirical QM methods and force fields. J. Chem. Theory Comput. 2010, 6, 3808–3816. [Google Scholar]
- Řezáč J.; Hobza P. A halogen-bonding correction for the semiempirical PM6 method. Chem. Phys. Lett. 2011, 506, 286–289. [Google Scholar]
- Becke A. D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar]
- Lee C.; Yang W.; Parr R. G. Development of the Colle–Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [DOI] [PubMed] [Google Scholar]
- Grimme S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [DOI] [PubMed] [Google Scholar]
- Zhao Y.; Truhlar D. G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other function. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Grimme S.; Antony J.; Ehrlich S.; Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [DOI] [PubMed] [Google Scholar]
- Chai J.; Head-Gordon M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [DOI] [PubMed] [Google Scholar]
- Jeziorski B.; Moszynski R.; Szalewicz K. Perturbation theory approach to intermolecular potential energy surfaces of van der Waalscomplexes. Chem. Rev. 1994, 94, 1887–1930. [Google Scholar]
- Řezáč J.; Hobza P. Extrapolation and scaling of the DFT-SAPT interaction energies toward the basis set limit. J. Chem. Theory Comput. 2011, 7, 685–689. [DOI] [PubMed] [Google Scholar]
- McDaniel J. G.; Schmidt J. R. Physically-motivated force fields from symmetry-adapted perturbation theory. J. Phys. Chem. A 2013, 117, 2053–2066. [DOI] [PubMed] [Google Scholar]
- Gráfová L.; Pitoňák M.; Řezáč J.; Hobza P. Comparative study of selected wave function and density functional methods for noncovalent interaction energy calculations using the extended S22 data set. J. Chem. Theory Comput. 2010, 6, 2365–2376. [DOI] [PubMed] [Google Scholar]
- Rezáč J.; Riley K. E.; Hobza P. S66: A well-balanced database of benchmark interaction energies relevant to biomolecular structures. J. Chem. Theory Comput. 2011, 7, 2427–2438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Řezáč J.; Riley K. E.; Hobza P. Benchmark calculations of noncovalent interactions of halogenated molecules. J. Chem. Theory Comput. 2012, 8, 4285–4292. [DOI] [PubMed] [Google Scholar]
- Řezáč J.; Hobza P. Advanced corrections of hydrogen bonding and dispersion for semiempirical quantum mechanical methods. J. Chem. Theory Comput. 2012, 8, 141–151. [DOI] [PubMed] [Google Scholar]
- Berka K.; Laskowski R.; Riley K. E.; Hobza P.; Vondrášek J. Representative amino acid side chain interactions in proteins. A comparison of highly accurate correlated ab initio quantum chemical and empirical potential procedures. J. Chem. Theory Comput. 2009, 5, 982–992. [DOI] [PubMed] [Google Scholar]
- Sedlak R.; Janowski T.; Pitoňák M.; Rezáč J.; Pulay P.; Hobza P. The accuracy of quantum chemical methods for large noncovalent complexes. J. Chem. Theory Comput. 2013, 9, 3364–3374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunning T. H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007. [Google Scholar]
- Kendall R. A.; Dunning T. H.; Harrison R. J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796. [Google Scholar]
- Woon D. E.; Dunning T. H. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358. [Google Scholar]
- Wilson A. K.; Woon D. E.; Peterson K. A.; Dunning T. H. Gaussian basis sets for use in correlated molecular calculations. IX. The atoms gallium through krypton. J. Chem. Phys. 1999, 110, 7667. [Google Scholar]
- Řezáč J.; Hobza P. Describing noncovalent interactions beyond the common approximations: How accurate is the “gold standard,” CCSD(T) at the complete basis set limit?. J. Chem. Theory Comput. 2013, 9, 2151–2155. [DOI] [PubMed] [Google Scholar]
- Stewart J. J. P. MOPAC2012. http://openmopac.net/. [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H. P.; Izmaylov A. F.; Bloino J.; Zheng G.; Sonnenberg J. L.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Rega N.; Millam J. M.; Klene M.; Knox J. E.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Martin R. L.; Morokuma K.; Zakrzewski V. G.; Voth G. A.; Salvador P.; Dannenberg J. J.; Dapprich S.; Daniels A. D.; Farkas Ö.; Foresman J. B.; Ortiz J. V; Cioslowski J.; Fox D. J.. Gaussian 09, Revision C.01. Gaussian, Inc: Wallingford, CT, 2009, 34. [Google Scholar]
- DiLabio G. A.; Johnson E. R.; Otero-de-la-Roza A. Performance of conventional and dispersion-corrected density-functional theory methods for hydrogen bonding interaction energies. Phys. Chem. Chem. Phys. 2013, 15, 12821–12828. [DOI] [PubMed] [Google Scholar]
- Grimme S.; Ehrlich S.; Goerigk L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [DOI] [PubMed] [Google Scholar]
- Turney J. M.; Simmonett A. C.; Parrish R. M.; Hohenstein E. G.; Evangelista F. a.; Fermann J. T.; Mintz B. J.; Burns L. a.; Wilke J. J.; Abrams M. L.; Russ N. J.; Leininger M. L.; Janssen C. L.; Seidl E. T.; Allen W. D.; Schaefer H. F.; King R. a.; Valeev E. F.; Sherrill C. D.; Crawford T. D. Psi4: An open-source ab initio electronic structure program. WIREs Comput. Mol. Sci. 2012, 2, 556–565. [Google Scholar]
- Vondrásek J.; Bendová L.; Klusák V.; Hobza P. Unexpectedly strong energy stabilization inside the hydrophobic core of small protein rubredoxin mediated by aromatic residues: correlated ab initio quantum chemical calculations. J. Am. Chem. Soc. 2005, 127, 2615–2619. [DOI] [PubMed] [Google Scholar]
- Accuracy within MOPAC2012. http://openmopac.net/Manual/PM6_accuracy.html.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.