Constant pH Replica Exchange Molecular Dynamics in Explicit Solvent Using Discrete Protonation States: Implementation, Testing, and Validation

Abstract

By utilizing Graphics Processing Units, we show that constant pH molecular dynamics simulations (CpHMD) run in Generalized Born (GB) implicit solvent for long time scales can yield poor pK_a predictions as a result of sampling unrealistic conformations. To address this shortcoming, we present a method for performing constant pH molecular dynamics simulations (CpHMD) in explicit solvent using a discrete protonation state model. The method involves standard molecular dynamics (MD) being propagated in explicit solvent followed by protonation state changes being attempted in GB implicit solvent at fixed intervals. Replica exchange along the pH-dimension (pH-REMD) helps to obtain acceptable titration behavior with the proposed method. We analyzed the effects of various parameters and settings on the titration behavior of CpHMD and pH-REMD in explicit solvent, including the size of the simulation unit cell and the length of the relaxation dynamics following protonation state changes. We tested the method with the amino acid model compounds, a small pentapeptide with two titratable sites, and hen egg white lysozyme (HEWL). The proposed method yields superior predicted pK_a values for HEWL over hundreds of nanoseconds of simulation relative to corresponding predicted values from simulations run in implicit solvent.

1. Introduction

Solution pH often has a dramatic impact on biomolecular systems. By modulating the protonation state equilibria of various, titratable functional groups present in the system, small changes in solution pH can affect the charge distribution within the biomolecule. This charge distribution, in turn, often has a profound impact on the fundamental structure and function of biomolecules. This effect can be so pronounced that some proteins’ native states are stable only in a narrow pH range, even denaturing completely in extreme pH environments.^1,2

Because biomolecular behavior can depend very strongly on the pH-dependent protonation states of various titratable residues, accurate computational models designed to treat such systems must somehow account for pH effects. While the traditional approach of assigning a fixed protonation state for each titratable residue at the beginning of the simulation is still the most common approach, numerous methods have been developed in an attempt to treat pH effects in biomolecules more quantitatively.³

Of particular interest in this study is the constant pH molecular dynamics (CpHMD) technique, of which there are several variants.⁴⁻⁸ CpHMD is a method that leverages the ability of classical molecular dynamics to sample conformational space while simultaneously sampling from the available protonation states according to the semigrand canonical ensemble.⁵ By adopting this approach, CpHMD simulations can overcome the limitations imposed by constant-protonation MD simulations by constructing an ensemble whose protonation state distributions are properly weighted via the thermodynamic constraint imposed by a constant chemical potential of hydronium ions.

Within the myriad of available CpHMD methods, there are two fundamentally different approaches—continuous protonation states^6,8−11 and discrete protonation states.^5,7,12−14 In the former, a continuous ‘titration coordinate’ describing a fictitious ‘titration particle’ is introduced at each protonable site that is propagated as part of the standard MD according to a pH-dependent force acting on this particle.^6,8 Discrete protonation state models, on the other hand, employ occasional Metropolis Monte Carlo (MC) exchange attempts between different protonation states throughout the course of the MD simulation.^5,7 For the purposes of this study, we will focus on CpHMD models using discrete protonation states—specifically as implemented in the AMBER software suite.⁷

In the original AMBER implementation of CpHMD, the molecular dynamics is propagated treating solvent effects implicitly via the Generalized Born (GB) method.⁷ Periodically throughout the dynamics, a trial move changing the protonation state of either one or two closely interacting titratable residues is evaluated based on the difference in electrostatic and solvation energies calculated via GB, after which the coordinates are propagated according to this same potential.

Recently, however, Machuqueiro and Baptista raised concerns about pK_a predictions inheriting problems related to the model compound definition and inaccuracies in the underlying force field.¹⁵ In particular, force field deficiencies have been shown to result in incorrect—even unphysical—global minima.¹⁶⁻²⁰ So far, reported applications of Mongan et al.’s method have shown good results because the simulations were too short to reveal the full extent of the weaknesses in the Generalized Born model being used.^7,12,21−24 When we implemented Mongan et al.’s method on graphics processing units (GPUs) in order to run long simulations, the unphysical states sampled over long time scales degraded the pK_a predictions of the hen egg-white lysozyme (HEWL). This erroneous sampling may be addressed to some extent by using an explicit representation of the solvent to propagate the dynamics.

While most of the physics-based methods designed to describe a biomolecular system at constant pH use an implicit solvent representation of the solvent, several CpHMD methods have been extended to sample, at least conformations, in explicit solvent with both the discrete⁵ and continuous⁹⁻¹¹ protonation models. The methods proposed by Baptista et al.⁵ and Wallace and Shen⁹ use an implicit solvent potential to sample protonation states while the methods developed by Goh et al.¹⁰ and Donnini et al.¹¹ perform λ-dynamics on the titration coordinate directly in explicit solvent. A more recent approach by Wallace and Shen uses a λ-dynamics approach in pure explicit solvent and adds a counterion whose charge is changed simultaneously with a titratable residue in order to maintain charge neutrality in the unit cell.²⁵

Discrete protonation methods use molecular dynamics to propagate the spatial coordinates, while occasionally interrupting the dynamics to attempt changes to the protonation states of the titratable residues using a Metropolis Monte Carlo criteria. The CpHMD method implemented in AMBER⁷ (and later implemented in CHARMM¹²) performs MD in GB solvent, periodically attempting to change the protonation state of one or two interacting residues roughly every 10 fs.⁷ In the stochastic titration method described by Baptista et al., dynamics is run in explicit solvent for 2 ps,²⁶ after which a cycle of protonation state change attempts are evaluated using the Poisson–Boltzmann (PB) equation to treat solvation effects for every titratable residue and interacting titratable residue pair. About 40 000 full cycles are attempted each time protonation state changes are attempted.²⁷ Afterward, the solute is held fixed while MD is propagated on the solvent to reorganize the solvent distribution to the new set of protonation states.

Implicit solvent models—in this case GB and PB—average over all solvent degrees of freedom, thereby instantly incorporating the effects of solvent relaxation around discrete protonation state changes. Therefore, MC moves in which a protonation state change is attempted have a reasonable probability of succeeding when the solution pH is set close to the pK_a of the titratable group. When explicit solvent molecules are present, however, the solvent orientation around any solvent-exposed, titratable residue will oppose any protonation state changes. On average, the solvent distribution tends to resist protonation state changes by imposing a barrier on the order of 100 kcal/mol as estimated by measurements in our lab and in others’,⁹ making titration with discrete protonation states difficult directly in explicit solvent.

In this study, we present a new method of performing CpHMD simulations in explicit solvent using discrete protonation states. This method is similar in some regards to that used by Baptista et al.,⁵ and we evaluate its performance on the model compounds, a pentapeptide, and the HEWL protein. To enhance the sampling capabilities of this new CpHMD method, we use replica exchange in the pH-dimension (pH-REMD), whose theory and performance were discussed previously in the context of implicit solvent calculations.^12,24 This paper is organized as follows: We will first describe the method and its implementation in the Theory and Methods section, followed by a description of the calculations we performed in the Calculation Details section. Afterward, we will evaluate its performance as well as sensitivity to the method’s tunable parameters in the Results and Discussion section.

2. Theory and Methods

In this section, we will discuss the details of our proposed method and highlight how it differs from the approach used by Baptista et al.⁵ The theoretical foundation of our CpHMD method is described in detail, as well as the pH-REMD method we used in our simulations.

2.1. Conformational and Protonation State Sampling

In CpHMD, structures are sampled from the semigrand canonical ensemble, whose probability distribution function is given by

1

where β = 1/k_BT, μ* is the chemical potential of hydronium (directly related to the solution pH), q is the generalized coordinates of the system particles, p is the conjugate momenta, and n is the total number of titratable protons present in that state. When bold, n refers to the protonation state vector, specifying not only the total number of protons present but on which titratable sites those protons are located. The denominator in eq 1 is the partition function of the semigrand canonical ensemble.

To sample from the probability function ρ in eq 1, discrete protonation state methods use MD with a fixed set of protonation states to sample coordinates and momenta coupled with a MC-based protonation state sampling at fixed conformations throughout the trajectory. Baptista et al. showed that standard MD, which samples ρ(q,p|n), used in conjunction with MC moves on protonation states, which samples from ρ(n|q,p), properly samples from the desired probability distribution function ρ(q, p, n).⁵ In this notation, ρ(q,p|n) is the conditional probability function of the positions and momenta with fixed protonation states whereas ρ(n|q,p) is the conditional probability function of the protonation state vector at a fixed protein conformation.

In explicit solvent, ρ(n|q,p) is difficult to sample directly, since the solvent orientation is relaxed with respect to the current protonation state vector. Following the arguments of Baptista et al., the system coordinates (and momenta) can be separated into solute and solvent degrees of freedom.⁵ The protonation state sampling is then performed according to the conditional probability

2

where q_solvent and p_solvent are relaxed solvent distributions of positions and momenta around the protonation state vector, n.⁵ The energy differences resulting from the relaxed solvent distributions around the different protonation states are quantities that implicit solvent models strive to reproduce. Therefore, the distribution function ρ′ in eq 2 can be approximated using continuum models, such as the PB or GB equations, thereby avoiding the otherwise costly solvent relaxation calculation associated with each attempted protonation state change. Performing relaxation MD on the solvent degrees of freedom should be done after protonation state changes to generate the uncorrelated, relaxed solvent distribution required by eq 2. While using MD to generate relaxed solvent distributions violates detailed balance—microscopic reversibility is no longer preserved—Manousiouthakis and Deem have shown that simply satisfying the weaker balance condition is valid.²⁸

Contrary to the stochastic titration method that calculated solvation free energies using the PB equation to evaluate protonation state changes,⁵ we chose to use the GB implicit solvent model for three main reasons. First, AMBER has numerous GB models readily available,²⁹⁻³³ allowing us to use the existing code to evaluate protonation state change attempts. Second, results from the original GB-based CpHMD implementation by Mongan et al., and from a number of previous studies using the method, have been promising.^7,22,24,34 Furthermore, GB was shown to be effective when used in a hybrid solvent method with continuous protonation states,⁹ is computationally cheaper than PB, and GB is more easily parallelizable, allowing longer simulations to be performed in the same amount of time.

2.2. Explicit Solvent CpHMD Workflow

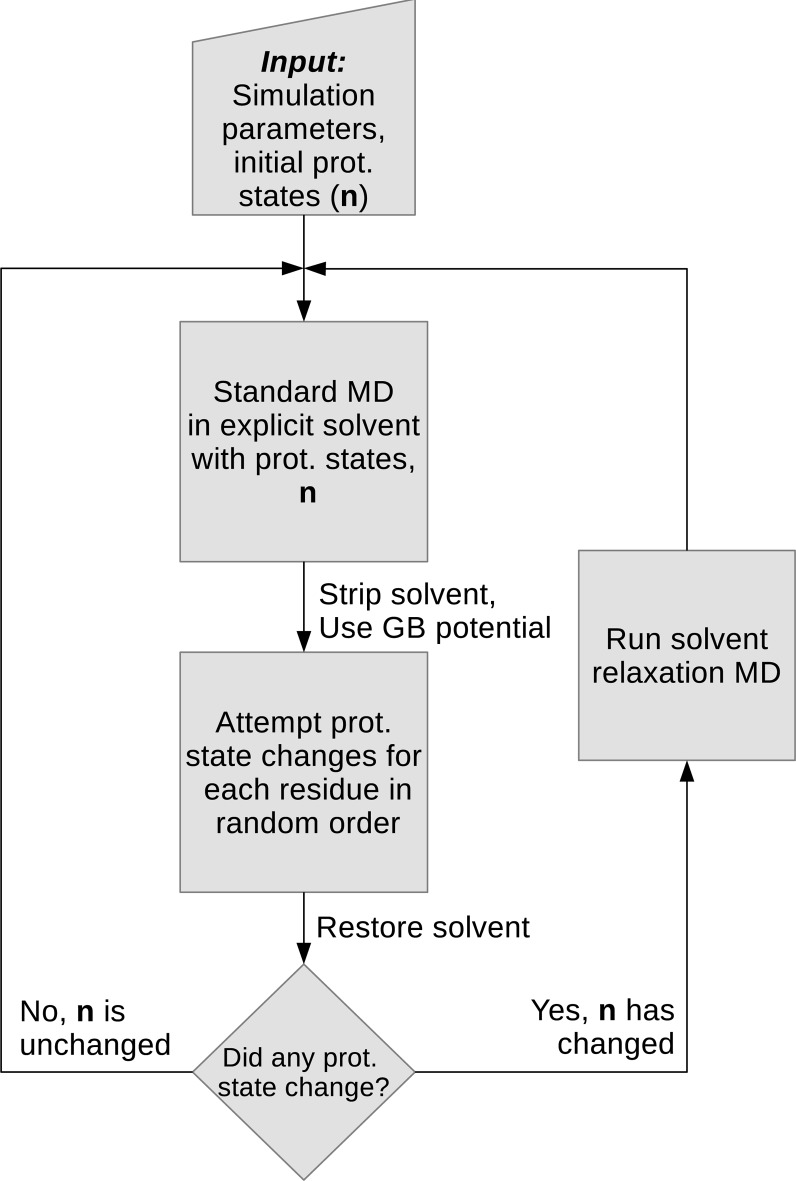
The process of the CpHMD method presented here can be divided into three repeating steps, summarized in the workflow diagram in Figure 1. This workflow is very similar to the one presented in ref (5) (Figure 2), although the nature of the MC protonation state move is different.

Figure 1.

Workflow of the proposed discrete protonation CpHMD method in explicit solvent. Following the standard MD, the solvent, including all nonstructural ions (as determined by user-input), are stripped and the protonation state changes are evaluated in a GB potential. After that, the solvent and the original settings are restored for the remaining steps.

In the proposed method standard MD in explicit solvent is carried out using a constant set of protonation states (an initial set must be provided at the start of the simulation). At some point the MD is stopped, the solvent (including any nonstructural ions) are stripped, the potential is switched to an available GB model, and a set of N protonation state changes are attempted where N is the number of titratable residues. While in principle the MD can be stopped randomly with a predetermined probability at any step, in this iteration of our proposed method we run MD for a set time interval, τ_MD, similar to the stochastic titration method.⁵

After the MD is halted and the solvent stripped, protonation state changes are proposed for each titratable residue once, in random order, choosing from the available protonation states of that residue excluding the currently occupied state. The electrostatic energy difference between the proposed and current protonation states, as well as the MC decision regarding whether or not to accept the proposed state, are calculated the same way as in the original GB implementation.⁷ If the protonation state change is accepted, the ‘current’ state is appropriately updated, and the next residue, chosen at random without replacement, is titrated with this new state.

For each residue that is titrated, there is a 25% chance that a so-called multisite titration will occur with a neighboring residue; that is, the proposed change will involve changes to the protonation state of both the residue and its neighbor. Two titratable residues are considered ‘neighbors’ if any two titrating hydrogen atoms are within 2 Å from each other. If either residue has more than one titrating proton, the two residues are neighbors if the minimum distance between any pair of titrating hydrogens meets the cutoff.

Including multisite protonation state jumps is important for systems that have closely interacting titratable residues. Without these multisite moves, proton transfers between adjacent titratable residues involved in a hydrogen bond would never occur due to the high penalty of disrupting the interaction by adding another proton or removing the proton involved in the hydrogen bond. This feature was actually present in the initial GB CpHMD implementation, and while no mention of it was made in the original paper, a small note was made in the AMBER Users’ manual.⁷

If any of the protonation state change attempts were accepted, the solute is frozen while MD is performed on the solvent (and any ions) to relax the solvent distribution around the new protonation states. The length of this relaxation is a tunable parameter of the method, which we will call τ_rlx. After the relaxation is complete, the velocities of the solute atoms are restored to their values prior to the relaxation and the standard dynamics is continued.

It is worth noting that as the protonation states change during the course of the CpHMD simulations, so too does the net charge on the system. Because we are using periodic boundary conditions with a lattice-sum method to compute electrostatics, finite-size effects involving the changing charges are introduced.^35,36 The investigations focusing on charge-dependent finite-size effects have identified artifacts affecting primarily computed free energies and pressure and are larger for smaller unit cells.³⁵ In the proposed method, the protonation state changes are attempted in implicit solvent with a GB potential, which is entirely unaffected by these finite-size effects. Furthermore, since replica exchange simulations in AMBER require the use of constant volume, no pressure corrections are required, either.

2.3. pH-based Replica Exchange

The underlying theory behind replica exchange in pH-space with MD run in explicit solvent is unchanged from the version we implemented in implicit solvent earlier.^12,24 Replicas are ordered by their solution pH parameter, and adjacent replicas attempt to exchange their pH periodically throughout the MD simulations.

The probability of accepting these replica exchange attempts, given by eq 3, depends only on the difference in the number of titrating protons present in each replica and their respective difference in pH.²⁴

3

where N_i is the total number of titratable protons ‘present’ in state i.

Because the probability of accepting replica exchange attempts depends only on the number of titratable protons that are present in the system, the number of replicas necessary to obtain efficient mixing in pH-space does not increase as explicit solvent is added. This, coupled with the more accurate sampling found with explicit solvent simulations,²⁴ makes pH-REMD an effective tool for explicit solvent CpHMD.

3. Calculation Details

To evaluate the performance of the proposed method, we applied it to the amino acid model compounds, a small pentapeptide (ACFCA), and a protein commonly used in pK_a calculation studies-the hen egg-white lysozyme (HEWL).

3.1. Implicit Solvent Simulations

In order to allow simulations to be run for hundreds of nanoseconds, we implemented Mongan et al.’s CpHMD method with pH-REMD²⁴ on GPUs in GB implicit solvent.³⁷ We used the HEWL structure solved in PDB code 1AKI(38) as our starting structure. The carboxylate residues were initially set in the deprotonated state, and histidine 15 was started in the double-protonated state according to AMBER defaults.

The structure was minimized using 10 steps of the steepest descent algorithm followed by 990 steps of conjugate gradient with 10 kcal/mol·Å² . The minimized structure was then heated for 1 ns, varying the target temperature linearly from 10 to 300 K over 667 ps. Positional restraints (5 kcal/mol·Å²) were placed on the backbone atoms. The temperature was controlled using Langevin dynamics with a 5 ps^–1 friction coefficient.

The heated structure was then equilibrated at 300 K for 2 ns using Langevin dynamics with a friction coefficient of 10 ps^–1 with 0.1 kcal/mol·Å^–2 positional restraints on the backbone. We then ran 500 ns of pH-REMD, attempting to change protonation states every 10 fs and attempting replica exchanges every 20 fs. We used 14 replicas spanning the pH range 1–7.5 with a 0.5 pH-unit spacing between adjacent replicas. No nonbonded cutoff was used for any implicit solvent simulation.

3.2. Model Compounds

Absolute pK_a values are very difficult to calculate in solution; they are impossible using classical force fields. As a result, every physics-based CpHMD method uses the idea of a model compound whose experimental pK_a is easy to measure with a high level of accuracy. An empirical parameter—the reference energy—is then added so that CpHMD reproduces the experimental pK_a values of these compounds. The reference energy must be set for the solvation model that is used during the simulations, which was the same GB^OBC model that Mongan et al. used in their study.⁷

The model compounds have the residue sequence ACE-X-NME, where ACE is a neutral acetyl capping residue, X is the titratable residue, and NME is a neutral methyl amine capping residue.⁷ The available titratable residues in AMBER are aspartate (AS4), glutamate (GL4), histidine (HIP), lysine (LYS), tyrosine (TYR), and cysteine (CYS), which are all defined as described by Mongan et al.⁷ A 10 Å TIP3P³⁹ solvent buffer was added in a truncated octahedron around each model compound that we simulated. The aspartate model compound was also simulated with larger box sizes—15 Å and 20 Å buffers—to determine if it had any effect on the calculated pK_a.

After the system topologies were generated, each system was minimized using 100 steps of steepest-descent minimization followed by 900 steps of conjugate gradient minimization. They were then heated at constant pressure, varying the target temperature linearly from 50 to 300 K over 200 ps. The solvated model compounds were then run for 2 ns at constant temperature and pressure.

Each model compound system was simulated at constant pH and volume for 2 ns, setting τ_rlx = 200fs. Each simulation employed pH-REMD using six replicas with the solution pH set to pK_a ± 0.1, pK_a ± 0.2, and pK_a ± 1.2. To evaluate the effect of the solvent relaxation time, the cysteine model compound was run with τ_rlx set to 10 fs, 40 fs, 100 fs, 200 fs, and 2 ps.

3.3. ACFCA

A pentapeptide with the sequence Ala-Cys-Phe-Cys-Ala (ACFCA) was solvated with a 15 Å buffer of TIP3P molecules around the solute in a truncated octahedron.

The system was minimized using 100 steps of steepest descent minimization followed by 900 steps of conjugate gradient. The minimized structure was heated by varying the target temperature linearly from 50 to 300 K over 200 ps at constant pressure. The resulting structure was then simulated at 300 K at constant temperature and pressure to stabilize the system density and equilibrate the solvent distribution around the small peptide.

The resulting structure was then used in simulations at six different solution pH values—7.1, 8.1, 8.3, 8.7, 8.9, and 9.9. These pH values were chosen because the pK_a of the cysteine model compound is 8.5, so the two cysteines of ACFCA were expected to titrate in this pH range. To demonstrate the effect that pH-REMD had on the titration of ACFCA, two sets of simulations were run—CpHMD with no exchanges and pH-REMD—with each replica being run for 2 ns.

3.4. Hen Egg White Lysozyme

We used the structure solved in PDB code 3LZT as the starting structure for our simulations.⁴⁰ All eight aspartate residues were renamed AS4, both glutamate residues were renamed GL4, and histidine 15 was renamed HIP in preparation for the pH-REMD simulations.

All disulfide bonds were added manually in tleap, and the system was solvated with a 10 Å TIP3P water buffer surrounding the protein in a truncated octahedron. We added 26 sodium ions and 11 chloride ions in random locations in the simulation cell to provide an ionic atmosphere and neutralize the system in its initial, default protonation states.

The system was minimized using 1000 steps of steepest descent minimization followed by 4000 steps of conjugate gradient, with 10 kcal/mol·Å² positional restraints applied to the backbone. The structures were then heated at constant volume, varying the target temperature linearly from 10 to 300 K over 400 ps using Langevin dynamics with a 5 ps^–1 friction coefficient. The heated structures were then equilibrated for 4 ns at constant temperature and pressure using Langevin dynamics with a 2 ps^–1 friction coefficient to maintain the temperature and 2 ps^–1 coupling constant for the Berendsen barostat. The system was then subjected to 112 ns of equilibration MD at constant volume and temperature using Langevin dynamics with a 2 ps^–1 friction coefficient to maintain a constant temperature of 300 K.

Following the setup stages of the simulations, two sets of pH-REMD simulations were carried out for 122 and 150 ns with 12 replicas spanning the pH range from −3 to 8 at 1 pH-unit intervals to characterize the acidic-range titration behavior of HEWL.

3.5. Simulation Details

All systems were parametrized using the AMBER FF10 force field, which is equivalent to the AMBER FF99SB force field for proteins.¹⁹ The tleap program of the AmberTools 12 program suite was used to build the model compound and ACFCA molecules, to add hydrogen atoms HEWL and to solvate each system that was run in explicit solvent.

All simulations were performed using either the sander or pmemd module of a development version of AMBER 12.⁴¹ Langevin dynamics was used in every simulation to maintain constant temperature with collision frequencies varying from 1 ps^–1 to 5 ps^–1, and the random seed was set from the computer clock to avoid synchronization artifacts.^42,43 The Berendsen barostat was used to maintain constant pressure for the equilibration dynamics with a coupling constant of 1 ps^–1.

All molecular dynamics, including the solvent relaxation dynamics, are run with a 2 fs time step, constraining bonds containing hydrogen using SHAKE.^44,45 Replica exchange attempts between adjacent replicas were made every 200 fs for all pH-REMD simulations. Protonation state changes were attempted every 200 fs for all constant pH simulations.

Long-range electrostatic interactions were treated with the particle-mesh Ewald method^46,47 using a direct-space and van der Waals cutoff of 8 Å. Defaults were used for the remaining Ewald parameters. The GB model proposed by Onufriev et al., indicated by the parameter igb = 2 in sander,³¹ was used to evaluate the protonation state change attempts to be consistent with the original implementation in implicit solvent.⁷ The intrinsic solvent radius of the carboxylate oxygen atoms was reduced from the standard value of 1.5 Å to 1.3 Å to compensate for the effect of having 2 dummy protons present on each oxygen in the syn- and anti-positions in the explicit solvent simulations.⁷

The deprotonation fraction (f_d) and pH for each simulation—and each window of the running averages—was fitted to the Hill equation (eq 4) using the Levenberg–Marquardt nonlinear least-squares algorithm implemented in SciPy to compute the pK_a and Hill coefficient (n). All pK_a values reported for titratable residues in this paper correspond to the value computed by fitting f_d from the simulations at every pH to eq 4 over the specified time interval.

4

4. Results and Discussion

First, we will analyze the long simulations in implicit solvent that demonstrate the weaknesses of implicit solvent models. Next, we will analyze our proposed CpHMD and pH-REMD methods as well as ways to optimize its overall performance. We will start by discussing the behavior of the model compounds when the size of the unit cell and the length of the relaxation dynamics (τ_rlx) is varied. We will follow this discussion with a similar analysis on a slightly larger system—ACFCA—before discussing the application of our proposed method to HEWL.

4.1. Long GB Simulations

Long simulations are required to observe rare events or phenomena that occur on long time scales, but often expose deficiencies in a computational model that are frequently missed in shorter simulations.⁴⁸ Therefore, we ran CpHMD GB simulations of HEWL for 600 ns—more than an order of magnitude longer than what has previously been published—to determine if these calculations were stable and could be used to study the dynamical behavior of proteins over long time scales.

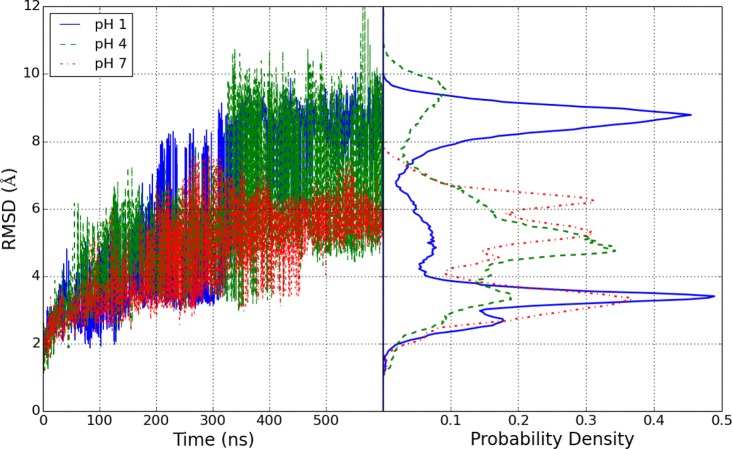
The backbone RMSD with respect to the starting crystal structure, shown in Figure 2 for the replicas at pH 1, 4, and 7, reaches as much as 10 Å at lower pH values, suggesting that the native state is unstable in GB implicit solvent at long time scales. As the lysozyme is active at the lysosomal pH around 4.5, CpHMD simulations near this pH should reflect this stability. As the backbone RMSD from the crystal structure increases, the predicted pK_a value worsens. We computed the root mean squared error (RMSE) of the computed acidic residue pK_a values compared to experiment. The predicted pK_a was computed for each residue by taking a running average with a 10 ns window of the deprotonation fraction for each residue at each pH in the pH-REMD simulation. The RMSE of the calculated pK_a values from experiment averaged over all titratable residues is shown in Figure 3.

Figure 2.

RMSD compared to the 1AKI crystal structure for the ensembles at pH 1, 4, and 7. The time series is shown on the left with the normalized histograms shown on the right.

Figure 3.

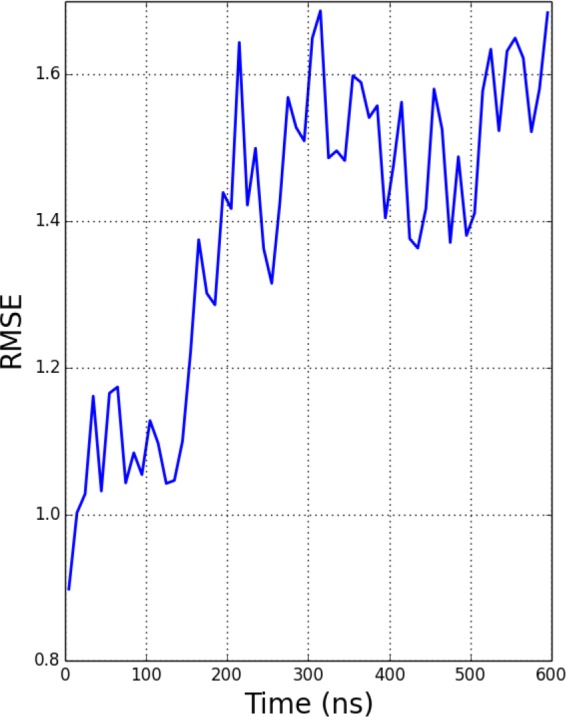
RMSE of all acidic titratable residue pK_a values compared to experiment⁴⁹ during the course of the simulation. A 10 ns window was used for the running average of the computed pK_a.

4.2. Explicit Solvent Simulations

4.2.1. Box Size Effects

To study the effect that the unit cell size has on titrations in our proposed method, we prepared three simulations of the aspartate model compound with different TIP3P solvent buffers surrounding it. We prepared systems with a 10 Å, 15 Å, and 20 Å TIP3P solvent buffer around the model aspartate.

Because protonation state sampling takes place in GB solvent without periodic boundary conditions, any effect of the box size on calculated pK_a values can only arise due to alterations of the structural ensembles induced by artifacts from the box size. The calculated pK_a values of the three systems were 4.02 ± 0.07, 4.05 ± 0.08, and 4.12 ± 0.07 for the 10 Å, 15 Å, and 20 Å solvent buffer systems, respectively. To estimate the uncertainties we divided each simulation into 100 ps chunks and took the standard deviation of the set of 20 pK_a values calculated from those segments.

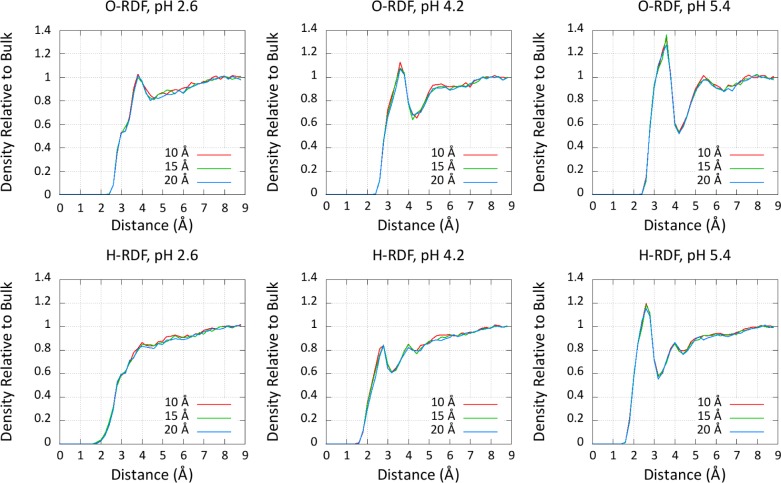
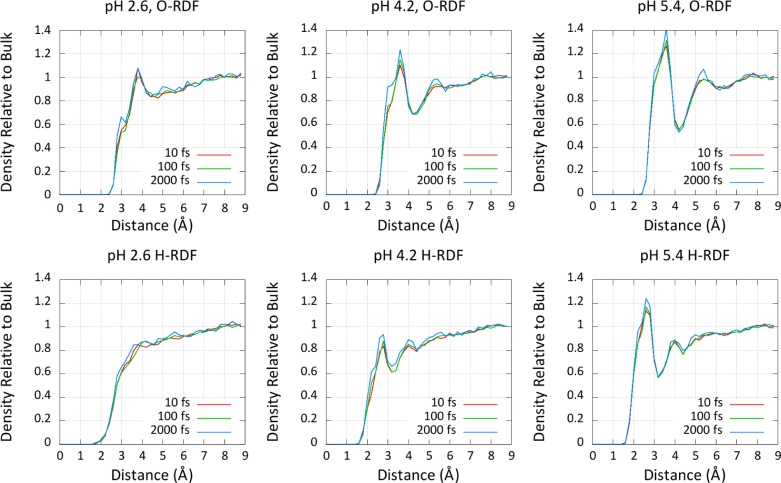
To further demonstrate the insensitivity of box size to pH-REMD titrations, we plotted the solvent radial distribution functions (RDFs) around the center of mass of the carboxylate functional group in Figure 4. The insensitivity of the pK_a and solvent structure with respect to the model compound provides strong evidence that no undue care is necessary when choosing the size of the solvent buffer for these types of simulations.

Figure 4.

Radial distribution functions (RDFs) of solvent oxygen atoms (O) and hydrogen atoms (H) with different unit cell sizes. The shown measurements—10, 15, and 20 Å—represent the size of the solvent buffer surrounding the solute. RDF plots for three different pHs are shown, highlighting the pH dependence of the solvent structure around the carboxylate of the aspartate model compound and its invariance to box size.

4.2.2. Effect of Solvent Relaxation Time (τ_rlx)

An important approximation in the proposed method is that the protonation state sampling ρ′ from eq 2 can be replaced using an implicit solvent model followed by relaxation MD to generate the relaxed solvent positions and momenta. The question then becomes how long this relaxation dynamics should be run.

To address this, 2 ns of constant protonation molecular dynamics simulations were run on the model cysteine compound in both protonation states—protonated and deprotonated—after the same minimization and heating protocols were used as for the other model compound simulations. The protonation state was then swapped for the final structures of both simulations, and MD was performed while constraining the solute position for 20 ns, equivalent to the relaxation dynamics protocol in our proposed method.

The optimum value for τ_rlx is the time after which the energy of the relaxation trajectory stabilizes and the simulation loses all memory of its initial configuration. To be truly equivalent to having been chosen at random, the final, relaxed solvent distribution must be completely uncorrelated from the initial distribution at the time the protonation state was changed.

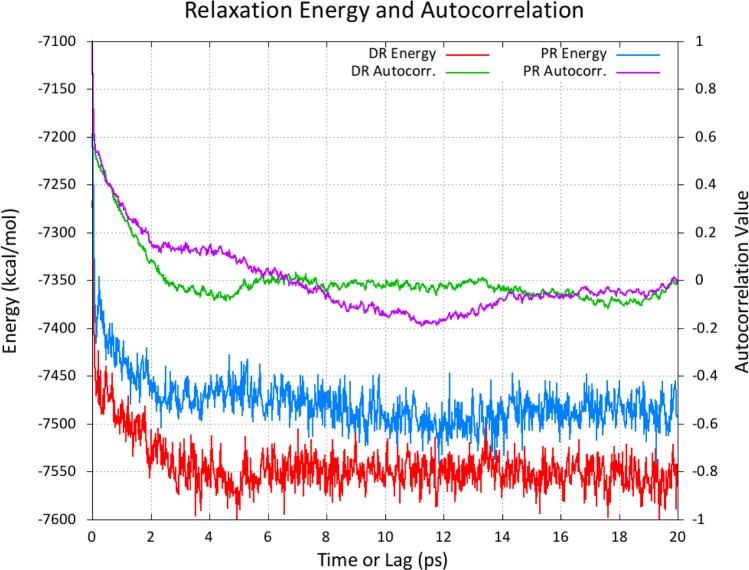
To probe the necessary time scales for these relaxation dynamics, the energy of each snapshot in the relaxation trajectory is plotted alongside the autocorrelation function of that energy in Figure 5 to clearly demonstrate the ‘appropriate’ value of τ_rlx for this model system.

Figure 5.

The relaxation of the protonated state, starting from the protonated trajectory, is shown in blue with its autocorrelation function shown in purple. The relaxation of the deprotonated state from an equilibrated snapshot from the protonated ensemble is shown in red with its autocorrelation function shown in green. Here, PR and DR stand for Protonated-Relaxation and Deprotonated-Relaxation, respectively.

We chose the cysteine model compound for this test for two reasons. First, the model compounds are fully solvent-exposed due to their small size, which results in a worst-case scenario in terms of the number of water molecules that must be reorganized during the relaxation dynamics. The optimum τ_rlx value for model compounds is expected to be an upper-bound on the values required for larger systems. Second, cysteine is the smallest and simplest of the titratable amino acids, eliminating potential complications from tautomeric states compared to aspartate, glutamate, and histidine.

The relaxation energies plotted in Figure 5 begin to stabilize after 4 to 6 ps of relaxation dynamics and are largely uncorrelated within that same time scale. However, because 4 ps of MD—corresponding to 2000 steps of dynamics with a 2 fs time step—adds dramatically to the cost of CpHMD simulations in explicit solvent, we will analyze the approximation of using a significantly smaller value for τ_rlx.

Both the relaxation energies and autocorrelations drop very sharply at the start of the relaxation dynamics, so the majority of the benefit gained by relaxing the solvent is realized within the first few steps.

For both simulations, the first 200 fs of relaxation dynamics resulted in 70% of the total relaxation energy in calculations. The correlation of the relaxation energy decays similarly, so the assumption that the relaxed solvent distribution is uncorrelated from its starting point is a reasonable approximation.

To validate the use of a shorter τ_rlx, we titrated the aspartate model compound using pH-REMD with five different values for τ_rlx—10 fs, 40 fs, 100 fs, 200 fs, and 2 ps. The calculated pK_a for each simulation was 4.10, 4.08, 4.07, 4.10, and 4.05, respectively, for the listed relaxation times. Furthermore, comparing the solvent radial distribution functions of the different solvent relaxation times (Figure 6) shows little dependence of the solvent distribution on the value of τ_rlx.

Figure 6.

RDFs of water oxygen atoms (O) and hydrogen atoms (H) around the center-of-mass of the carboxylate group of the model aspartate molecule at different solution pHs.

4.2.3. ACFCA: CpHMD vs pH-REMD

The small peptide chain ACFCA, described in section 3.3, was chosen as a test due to its small size and predictable titration behavior. The simplicity of the system makes it an ideal test; its small size mitigates the conformational sampling problem, and the simple titrating behavior of cysteine further simplifies protonation state sampling. Unlike aspartate and glutamate, which have the four defined tautomeric states defined by anti- and syn-protonation on each of two carboxylate oxygens, and histidine which has two tautomeric states on the imidazole, cysteine has only one protonated and one deprotonated state, presenting fewer degrees of freedom that must be exhaustively sampled.

Each cysteine is in a slightly different microenvironment due to the different charges of the N- and C-termini. Due to its proximity to the N-terminus, Cys-2 is expected to experience a negative pK_a shift with respect to the model compound due to the electrostatic interactions with the positively charged terminus. Cys-4, on the other hand, is expected to experience a pK_a shift in the opposite direction due to the electrostatic interactions with the negatively charged C-terminus.

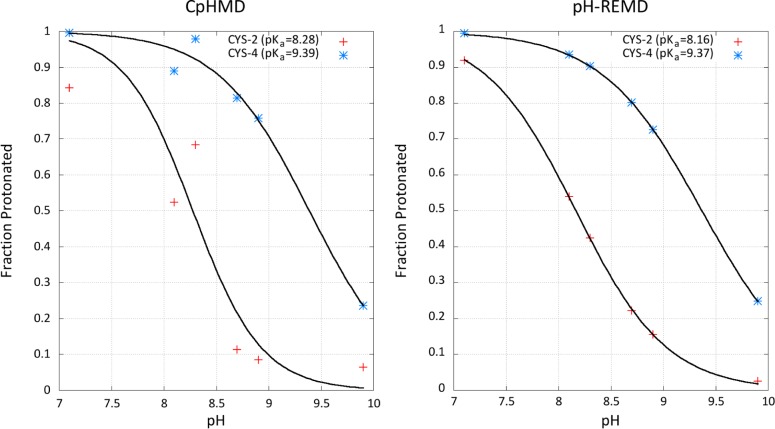
We ran simulations at pH 7.1, 8.1, 8.3, 8.7, 8.9, and 9.9 to sufficiently characterize the titration behavior of both cysteine residues around their pK_a values. One set of replicas was run with pH-REMD while the other set was run using CpHMD (i.e., without attempting exchanges between the replicas). The titration curves for both sets of simulations, shown in Figure 7, demonstrate the importance of using pH-REMD in constant pH simulations in explicit solvent. As expected, the pH-REMD simulations revealed pK_a shifts of −0.2 pK units for Cys 2 and +0.9 pK units for Cys 4 with respect to the model Cys compound.

Figure 7.

Titration curves of Cys-2 and Cys-4 in the ACFCA pentapeptide. Results from CpHMD (no replica exchange attempts) and pH-REMD are shown in the plots on the left and right, respectively.

Even for a simple system such as ACFCA, using pH-REMD on top of standard CpHMD simulations results in a drastic improvement in titration curve fit—a result of improved protonation state sampling. The residual sum of squares (RSS), a quantity that measures how well an equation fits a data set, shows drastic improvement using pH-REMD. The RSS for Cys-2 and Cys-4 using CpHMD was 9 × 10^–2 and 7 × 10^–3, respectively. For the pH-REMD simulations, on the other hand, the RSS was reduced by several orders of magnitude to 7 × 10^–5 and 9 × 10^–6 for Cys-2 and Cys-4, respectively.

4.2.4. Hen Egg White Lysozyme

HEWL is a common benchmark for pK_a calculations because it has been studied extensively both experimentally⁴⁹⁻⁵¹ and theoretically,^{7,9,24,26,34,52} and it has a large number of titratable residues—some with a marked pK_a shift compared to the isolated model compound.

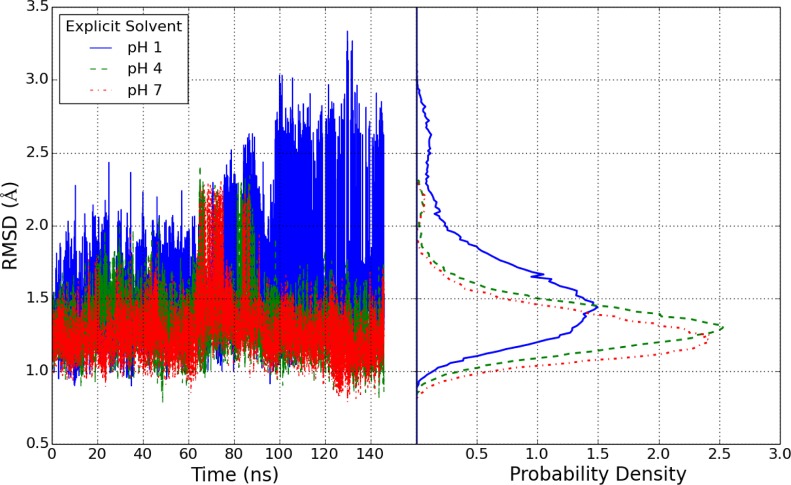
The simulations run in explicit solvent revealed far more stable trajectories over all pH values than their analogs run in implicit solvent over the 150 ns time scale of the explicit solvent simulations. In Figure 8, the plots of backbone RMSDs are bounded below 3.5 Å for the duration of the ca. 150 ns simulation. The RMSD distributions from the second 120 ns simulation are very similar.

Figure 8.

Backbone RMSD distributions for HEWL simulations in explicit solvent with solution pH set to 1, 4, and 7. Time series are shown on the left and histograms are shown on the right.

The predicted pK_a values for the titratable residues, summarized in Table 1 for both sets of simulations, show good agreement to experiment. The agreement is significantly better than the predictions from the implicit solvent calculations over a similar time scale. With the exception of aspartate 119 (and aspartate 52 in the 150 ns simulation), the predicted pK_a values of all residues were within 1 pK unit from the experimental values given in ref (49).

Table 1. Calculated pK_a Values for Acid-Range Titratable Residues in HEWL Using the Proposed Method for a ca. 150 ns Simulation and a ca. 120 ns Simulation^a.

simulation
residue	150 ns	120 ns	implicit	experiment
Glu 7	3.37	3.31	3.85	2.6
His 15	6.38	6.32	5.79	5.5
Asp 18	2.83	2.89	2.49	2.8
Glu 35	6.27	6.32	3.65	6.1
Asp 48	2.31	1.92	2.47	1.4
Asp 52	2.24	2.63	3.37	3.6
Asp 66	1.87	1.81	1.50	1.2
Asp 87	2.02	2.06	2.98	2.2
Asp 101	4.36	4.25	2.32	4.5
Asp 119	1.53	1.53	1.74	3.5
RMSE	0.92	0.82	1.32

^aExperimental values are taken from ref (49). Implicit solvent results are shown for comparison. (Results are shown for the final 500 ns of the 600 ns implicit solvent simulation).

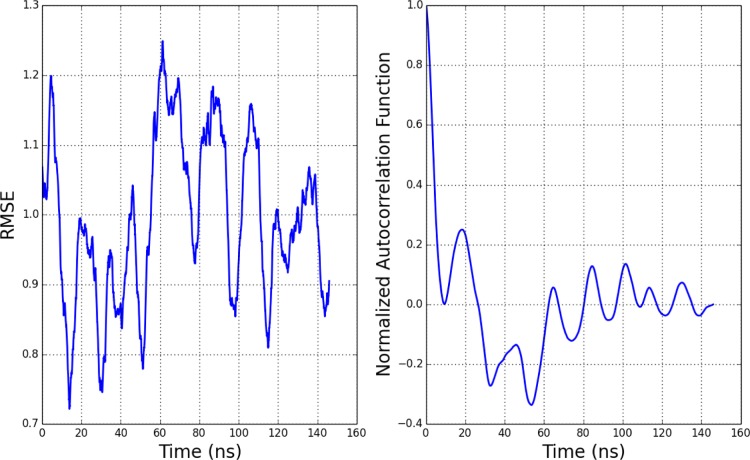
Furthermore, the large fluctuations in the RMSE throughout the course of the simulation—between 0.70 and 1.25 seen in Figure 9—suggest that differences in reported RMSE around 0.1 pK units are statistically insignificant for short CpHMD and pH-REMD simulations on the order of 10 ns. The standard deviation of the pK_a RMSE plotted in Figure 9 is 0.12 pK units with a correlation time of roughly 25 ns. The standard error of the mean, given by (σ/N)^1/2 where σ is the variance and N is the number of independent samples, is 0.05 pK units over 150 ns. Therefore, there is no statistically significant difference between methods with reported pK_a RMSEs within 0.10 pK units of each other (±0.05 pK units for each simulation) over 150 ns.

Figure 9.

(left) Plot showing the RMSE of all acidic titratable residue pK_a values compared to experiment⁴⁹ during the course of the simulation. A 5 ns window was used for the running average of the computed pK_a. (right) Plot showing the autocorrelation function of the RMSE time series, showing that the correlation time between statistically independent samples is roughly 25 ns.

Unlike the implicit solvent calculations, the quality of the predicted pK_a values in the proposed method does not appear to degrade over time in long simulations. The deviation of each residue compared to experiment and the total RMSE is shown in Figure 9. The pK_a at each time step is computed from a running average of deprotonation fraction for replicas at each pH using a window size of 5 ns and fitting to eq 4 the same way as described for Figure 3.

The smaller backbone RMSD and drastically improved pK_a predictions are strong evidence that the current method improves conformational sampling by employing an explicit representation of the solvent. Because the protonation state sampling is performed with the same GB potential in both the original and proposed methods, any differences in the predicted pK_a values must be caused by differences in conformational sampling. Given the rigorous nature of the experimental measurements,⁴⁹ this provides strong evidence that the proposed method improves significantly upon the original by improving conformational sampling with an explicit solvent representation.

5. Conclusion

We have extended the constant pH molecular dynamics method developed by Mongan et al.⁷ so that the dynamics can be run in explicit solvent. We tested a wide range of parameters in our proposed method for their effect on the conformational and protonation state sampling of small test systems. Because these test systems are small and their titratable sites are completely solvent-exposed, they likely represent the highest level of sensitivity to these various parameters.

In particular, we found that the box size of the unit cell had no discernible effect on the titration behavior of the aspartate model compound, given cell sizes that ranged from 20 Å in diameter—one of the smallest sizes permissible when using the minimum image convention with an 8 Å cutoff—to 40 Å in diameter.

Another key aspect of the current method is the necessity to relax the solvent around any new protonation state selected by the MC moves carried out in GB. By analyzing the decay of the potential energy in the solvent relaxation dynamics, we determined that 4 ps of MD was sufficient to stabilize the energy of the solvent distributions and generate relaxed solvent conformations whose energies are uncorrelated from the initial arrangements. However, given the expense of such a long relaxation period, we investigated using fewer relaxation steps to increase the simulation efficiency and found shorter times—down to 0.2 ps—had no measurable effect on the calculated pK_a and very little effect on the solvent distribution around the model cysteine compound.

Further tests on a small pentapeptide test system with two titratable sites (ACFCA) showed the importance of using pH-REMD over conventional CpHMD with the proposed method. While we showed that the enhanced protonation state sampling of pH-REMD results in smoother titration curves for complex proteins in implicit solvent,²⁴ even the simplest systems in explicit solvent require pH-REMD to obtain a smooth titration curve.

We tested the proposed method on HEWL, a very common pK_a benchmark system. We found that the proposed method of using GB implicit solvent to evaluate protonation state changes and explicit solvent to propagate dynamics yielded stable trajectories whose predicted pK_a values agreed well with experiment. Our results show that using the proposed method leads to a significant improvement in how systems are modeled at constant pH compared to the original method that used GB to propagate system dynamics.

Often, the most interesting titratable residues in biological systems have a large pK_a shift compared to the model compound. These highly perturbed residues have environments drastically different than the one provided by bulk solvent, and the conformational sampling must be both accurate and extensive to yield accurate pK_a predictions. In future work we will explore the use of enhanced sampling techniques in conjunction with pH-REMD in an attempt to improve the efficiency of the conformational sampling in explicit solvent, such as accelerated MD and temperature-based REMD.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States