Abstract
The crucial prerequisite for proper biological function is the protein’s ability to establish highly selective interactions with macromolecular partners. A missense mutation that alters the protein binding affinity may cause significant perturbations or complete abolishment of the function, potentially leading to diseases. The availability of computational methods to evaluate the impact of mutations on protein–protein binding is critical for a wide range of biomedical applications. Here, we report an efficient computational approach for predicting the effect of single and multiple missense mutations on protein–protein binding affinity. It is based on a well-tested simulation protocol for structure minimization, modified MM-PBSA and statistical scoring energy functions with parameters optimized on experimental sets of several thousands of mutations. Our simulation protocol yields very good agreement between predicted and experimental values with Pearson correlation coefficients of 0.69 and 0.63 and root-mean-square errors of 1.20 and 1.90 kcal mol–1 for single and multiple mutations, respectively. Compared with other available methods, our approach achieves high speed and prediction accuracy and can be applied to large datasets generated by modern genomics initiatives. In addition, we report a crucial role of water model and the polar solvation energy in estimating the changes in binding affinity. Our analysis also reveals that prediction accuracy and effect of mutations on binding strongly depends on the type of mutation and its location in a protein complex.
Introduction
Proteins recognize specific targets and bind them in a highly regular manner. The specificity of interactions is mostly determined by structural and physico-chemical properties of interfaces of interacting proteins.1 Proteins highly similar in sequence can participate in different interactions, and even a small number of amino acid substitutions or insertions/deletions at binding interfaces can lead to different interaction partners or different binding modes.2 Introducing mutations at protein–protein interfaces can quite effectively modulate binding affinity or specificity, and site directed mutagenesis has been successfully used in rational protein design and directed evolution to create novel protein complexes.3−6 In some cases, the redesign of protein–protein interactions may yield new binding partners with differences in specificities of at least 300-fold between the cognate and the noncognate complexes.7 Missense disease mutations may also directly affect protein–protein interactions and lead to Mendelian diseases or cancer.8−11
One possible way to assess the effect of mutation on protein binding affinity is to experimentally measure it. However, although site-directed mutagenesis methods are inexpensive and fast, surface plasmon resonance, isothermal titration calorimetry, FRET and other methods used to measure binding affinity can be time-consuming and costly. Therefore, the development of reliable computational approaches to predict changes in binding affinity upon mutation is urgently required. It is especially true in light of the rapid development of next generation sequencing technologies, which are producing overwhelming amounts of data on polymorphisms and disease mutations. There have been many studies aiming to develop potentials for protein ligand binding12−16 (see references within). According to some studies, the burial of polar groups should not be penalized in the case of hydrophilic protein–protein interfaces. At the same time, the contribution of electrostatic interactions might be more pronounced when switching from protein folding to protein–protein interaction potentials.17 In addition, water-mediated protein–protein interactions should be taken into account in the development of the potentials.18 Many models have been proposed that try to estimate binding affinities of protein–protein complexes, yet they cannot reproduce experimental binding data with satisfactory accuracy. This happens mostly due to the difficulties associated with modeling of conformational changes upon binding, estimating the entropy changes and long-range noninterfacial interactions.13 Moreover, most of the approaches are largely tuned to predict the effect of alanine-scanning mutations defined as substitutions of residues into alanine.
Energy functions used to describe and predict interactions governing protein–protein binding linearly combine several energy terms and the coefficients in front of each term can be optimized using datasets of experimentally measured binding affinities or changes in binding affinity due to missense mutations. Several approaches have recently been proposed that predict the effects of point mutations on binding energy. They include coarse-grained predictors based on statistical or empirical potentials,19−21 molecular mechanics force fields with different solvation models22−24 and others. For example, the molecular mechanics Poisson–Boltzmann surface area (MM-PBSA) method has been shown to yield good agreement with experimental studies in determining protein stability, binding affinity and ranking docking templates.25,26 Certain methods specifically investigate the impact of mutations on binding in relation to function or different environmental conditions. For example, recently an in silico mutagenesis method was proposed to calculate the effect of mutation at various pH,27 whereas another approach predicted the mutations’ ability to shift the allosteric conformational equilibrium with consequences for functional regulation.28 Although many of these methods report reasonable root-mean-square error (RMSE) values, their applicability is biased toward very limited sets of proteins and mutations (on an order of a dozen protein complexes and up to several hundreds of mutations) used for training and parametrization. Despite their limitations, methods that estimate changes in affinity produced by mutations show somewhat better performance compared to computational approaches to predict absolute affinities. It can be partially attributed to counterbalancing of errors, produced by energy calculations or conformational sampling, between the wild-type and mutant structures, under an assumption that structures do not undergo large changes upon mutations.29−33
Here we introduce a new approach to assess the impact of single and multiple missense mutations on protein binding affinity. It uses a modified MM-PBSA energy function, statistical scoring function and efficient energy minimization protocol. Our protocol is parametrized on a large set of several thousands of mutations and their corresponding experimental binding free energy changes assembled from the scientific literature.34 We find that the choice of water model is very important for the quality of prediction and a simulation protocol with explicit water without restraints on the backbone atoms gives the best results. We show that the conformational sampling by molecular dynamics simulations does not help to achieve better quality predictions for NM set (see Methods), and further analyses are needed to prove or disprove this observation for larger sets of mutations. In addition, we describe how prediction accuracy depends on the type of amino acid substitution and its location in the complex. Compared to several available computational protocols, our approach achieves very good accuracy and speed. It is benchmarked against a large and independent experimental dataset and shows high correlation coefficients between predicted and experimental values of 0.69 and 0.63 with root-mean-square errors of 1.20 and 1.90 kcal mol–1 for single and multiple mutations, respectively. At the same time, it can efficiently handle the large amount of data generated by modern genomics techniques.
Methods
Datasets
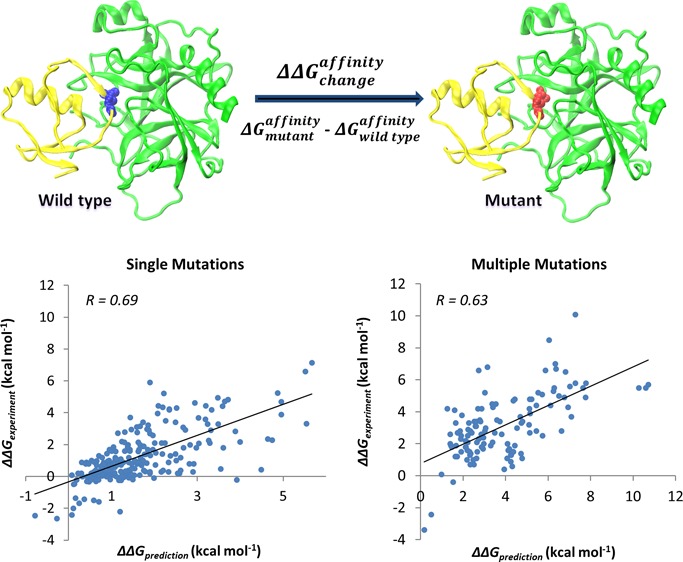
We use two datasets of experimentally determined values of changes in standard binding free energy upon mutations (denoted as ΔΔG in the paper), which are calculated as the difference between binding affinities of mutant (ΔGmut) and wild-type (ΔGWT) complexes and are derived from the scientific literature for protein–protein complexes with experimentally determined wild-type structures. One set is taken from the paper of Bockmann et al.22 and includes 242 single mutations and 123 multiple mutations from nine wild-type protein–protein complexes (one mutation was excluded because it had two inconsistent experimental data values). It will be referred to as the “NM set” hereafter. Another dataset was compiled from the SKEMPI database.34 We retained only structures of wild-type proteins, eliminated redundant entries and made sure that the SKEMPI set did not overlap with the NM set. We also excluded ten single and eight multiple mutants having initial VMD35 models (see next section) with unrealistically large steric clashes between the substituted and adjacent residues that could not be fixed by the minimization procedure (Table S1, Supporting Information). As a result, our second experimental set included 1844 single and 574 multiple mutations from 81 wild-type protein–protein complexes (it will be referred to as the “SKEMPI set” hereafter). Results for our and other methods and main scripts for running the programs are accessible through ftp://ftp.ncbi.nih.gov/pub/panch/Mutation_binding.
Simulation Protocol
An energy minimization procedure is used to compute the equilibrium configuration and find a minimum of the potential energy of the system. Here we use a conjugate gradient algorithm implemented in NAMD,36 which finds a nearest minimum to the starting point, repairs distorted geometries and removes steric clashes. The initial crystal structures of wild-type protein–protein complexes were obtained from the Protein Data Bank (PDB);37 only protein chains were retained in the calculations and missing heavy side chain atoms and hydrogen atoms were added using the VMD (version 1.9.1) program.35 The procedure for adding atoms in VMD is based on the topology file from CHARMM27 force field. We tested several simulation protocols (Figure S1, Supporting Information) (1) with and without restrains on the backbone atoms upon minimization using explicit TIP3P water model (2) with an unconstrained molecular dynamics (MD) simulations with TIP3P explicit water model38 and (3) with the minimization using the Generalized Born implicit solvent model39 for both wild-type and mutant structures. MD simulations were performed for 242 single mutants from the NM set. A simulation protocol that used minimization without restraints on the backbone atoms in explicit water showed the best agreement with the experiments (see Results). We will introduce this protocol in detail below.
All models were immersed into rectangular boxes of water molecules extending up to 10 Å from the protein in each direction. To ensure an ionic concentration of 150 mM and zero net charge, Na+ and Cl– ions were added by VMD. The distribution of the system size including water molecules and ions is shown in Figure S2 (Supporting Information). All wild-type protein complexes were minimized using a 40 000-step energy minimization procedure to make all wild-type protein complexes fully optimized for further binding energy calculation and the preparation of the initial mutant structures. This 40 000-step energy minimization procedure included an initial 5000-step minimization that was carried out using harmonic restraints (with the force constant of 5 kcal mol–1 Å–2) applied on the backbone atoms of all residues, followed by a 35 000-step energy minimization on the whole system.
We used the final minimized models of wild-type protein complexes to produce the mutant structures (Figure S1, Supporting Information); namely, we introduced an amino acid substitution using the “mutator” plugin of the VMD and kept the rest of the system invariant including the water box and ions. Then we performed an additional 1000-step minimization of the mutant (altogether 40 000 steps for wild-type and 1000 steps for mutant minimization) and showed that the agreement with the experimental data increases as the number of steps increases but reaches a plateau after 300–500 steps for single mutations. Figure S3 (Supporting Information) shows that increasing the number of minimization steps for a mutant above 300–500 does not improve the agreement with the experiments. Moreover, we showed that even very large complexes did not require more than 300–500 minimization steps for mutants (Figure S4, Supporting Information). The minimized models of mutant protein complexes after 300 minimization steps were used in our further analysis. Minimization was done only for the protein complexes, and protein structures of monomers were extracted from the minimized complexes for the following energy calculation. Consistent with the previous studies,8,10,40−42 this approach was more accurate and faster than when minimization was done for complexes and monomers separately.
The energy minimization and MD simulation were carried out with the NAMD program version 2.936 using the CHARMM27 force field.43 Periodic boundary conditions and a 12 Å cutoff distance for nonbonded interactions were applied to the systems. The Particle Mesh Ewald (PME) method44 was used to calculate the long-range electrostatic interactions. Lengths of hydrogen-containing bonds were constrained by the SHAKE algorithm.45 Unlike minimization, MD simulation generates atomic trajectories and may be used to generate conformational ensemble and determine macroscopic properties of the system by ensemble averages. In addition, MD simulations can in principle explore conformations which are not accessible via energy minimization protocol because of the energy barriers between different conformational states.
Binding Energy Calculation
Binding energies were calculated based on the MM-PBSA method that combines the molecular mechanical terms with the Poisson–Boltzmann continuum representation of the solvent46 calculated using the CHARMM force field. The total free energy in MM-PBSA is expressed as the following:
| 1 |
Here EgasMM corresponds to the molecular mechanical energy and is calculated as a sum of the internal energy of the molecule, the van der Waals and Coulomb electrostatic interactions in the gas-phase. Gsolv is the polar contribution to the solvation free energy of the molecule calculated using the Poisson–Boltzmann (PB) equation, which is the difference between the electrostatic energy of solute in the solvent environment and in the reference environment (gas phase in our study).47−49Gsolvnp is the nonpolar solvation energy, which is proportional to the solvent-accessible surface area (SA) of a molecule50 and TS corresponds to the entropy of solute. As entropy calculations are very computationally expensive and might not be very accurate,13 we did not perform entropy calculations in our analysis. Moreover, as was discussed in previous studies, entropy terms may cancel each other later in eq 3, especially for cases when structures do not undergo large changes upon mutations in the minimization simulation protocol.29−33 The binding energy in MM-PBSA approach is usually calculated as a difference between the average energies of the complex and each monomer:
| 2 |
Then the change of the binding energy due to a mutation can be calculated as the following:
| 3 |
We performed a multiple regression fitting procedure to model the linear relationship between the response (dependent) variable, which is, in our case, experimental values of changes in binding affinity, and different dependent variables. We tried different types of energy functions composed of different energy components (see Results section) and estimated the optimal model parameters (the weight factors for each energy term) using the NM and SKEMPI experimental sets. We assessed the accuracy of predictions (Tables 2 and 3) and found that energy function Pred1 had the best agreement with experiments for both datasets and had only four parameters and three energy terms, all of which were derived from CHARMM:
| 4 |
Here ΔΔEvdw is the change of van der Waals interaction energy and ΔΔGsolv is the change of polar solvation energy of solute in water. ΔSAmut represents a term proportional to the interface area of the mutant complex (if we choose the wild-type complex interface area, the results are not significantly different from those where mutant interface area is used). Nonpolar solvation energy and other terms did not contribute significantly to the model quality (p-value > 0.01) and were not used in our model.
Table 2. Comparison of Methods’ Performance for Different Training and Test Sets for Single Mutations Using Minimization Protocola.
| method/energy function | training/test set | R(RCV) | RMSE (kcal mol–1) | slope |
|---|---|---|---|---|
| Pred1 | NM/NM | 0.63(0.61) | 1.22 | 1.00 |
| NM/SKEMPI | 0.52 | 1.66 | 0.97 | |
| SKEMPI/SKEMPI | 0.53(0.52) | 1.62 | 1.00 | |
| SKEMPI/NM | 0.62 | 1.27 | 0.60 | |
| Pred2 | NM/NM | 0.70(0.67) | 1.12 | 1.00 |
| NM/SKEMPI | 0.57 | 1.61 | 0.95 | |
| SKEMPI/SKEMPI | 0.58(0.58) | 1.55 | 1.00 | |
| SKEMPI/NM | 0.69 | 1.20 | 0.97 | |
| Pred4 | NM/NM | 0.74(0.68) | 1.05 | 1.00 |
| NM/SKEMPI | 0.37 | 2.39 | 0.31 | |
| CC/PBSA | NM/NM | 0.71 | 1.13 | 1.13 |
| FoldX | test: NM | 0.47 | 1.60 | 0.53 |
| test: SKEMPI | 0.37 | 2.14 | 0.42 | |
| BeAtMuSiC | test: NM | 0.52 | 1.36 | 0.86 |
| test: SKEMPI | 0.40 | 1.82 | 0.80 |
R is the Pearson correlation coefficient between experimental and predicted ΔΔG values and RCV is the five-fold cross-validated correlation coefficient. The last column shows the slope of the regression line between predicted and experimental values. CC/PBSA results were taken from the previous paper.22 All correlation coefficients are statistically significant (p-value ≪ 0.01).
Table 3. Comparison of Methods’ Performance for Different Training and Test Sets for Multiple Mutationsa.
| method/energy function | training/test set | R(RCV) | RMSE (kcal mol–1) | slope |
|---|---|---|---|---|
| Pred1 | NM/NM | 0.74(0.72) | 1.33 | 1.00 |
| NM/SKEMPI | 0.49 | 2.81 | 0.80 | |
| SKEMPI/SKEMPI | 0.55(0.54) | 2.66 | 1.00 | |
| SKEMPI/NM | 0.63 | 1.90 | 0.60 | |
| Pred3 | NM/NM | 0.90(0.85) | 0.90 | 1.00 |
| NM/SKEMPI | 0.46 | 3.11 | 0.58 | |
| CC/PBSA | NM/NM | 0.74 | 1.37 | 0.83 |
| FoldX | test: NM | 0.53 | 3.42 | 0.33 |
| test: SKEMPI | 0.38 | 3.45 | 0.53 |
R is the Pearson correlation coefficient between experimental and predicted ΔΔG values and RCV is the five-fold cross-validated correlation coefficient. The last column shows the slope of the regression line between predicted and experimental values. CC/PBSA results were taken from the previous paper.22 All correlation coefficients are statistically significant (p-value ≪ 0.01).
For the PB calculation47,48 dielectric constants ε = 1, 2, 4 and different ion concentrations were tested on single mutations of NM set using the optimized minimization protocol and energy function Pred1 (the testing results are shown in Table S2, Supporting Information). As a result, ε = 2 for the protein interior,51−54 ε = 80 for the exterior aqueous environment and ion concentration of zero were used for further energy calculations. All PB calculations were performed with the PBEQ module;48,55,56 the van der Waals interaction energy was calculated with the ENERGY module, and molecular surface area was obtained with the SASA module of the CHARMM program.57 The atomic Born radii were previously calibrated and optimized to reproduce the electrostatic free energy of the 20 amino acids in MD simulations with explicit water molecules.56
Prediction of Binding Energy Change by Other Methods
We also estimated binding energy change using three independent methods. The FoldX method19 calculates the effect of mutations on protein stability using an empirical force field. It optimizes the side chain configurations without taking into account the backbone conformational movements. We tested two different protocols using FoldX: the RepairPDB module applied to protein crystal structures and the RepairPDB module applied to the minimized structures. We choose the first FoldX protocol for comparison as it gave us better correlation with experimental values. To calculate binding energy by FoldX, we used eq 2 and calculated the unfolding free energy of the whole complex and each monomer separately.
The second method, BeAtMuSiC21 is specifically trained to calculate the change in binding affinity produced by single missense mutations. It uses residue based statistical potentials that were previously optimized to discriminate native from decoy complexes.58 In addition, the BeAtMuSiC energy function has terms accounting for packing defects and for the effect of mutations on the unfolding free energy of the whole complex in cases where unbound monomers could be considered disordered. BeAtMuSiC is not designed to estimate changes in binding energy for multiple mutations. The third method, CC/PBSA,22 applies the Concoord approach to sample the protein configurational ensemble and the PB approach to calculate the solvent contribution to the binding free energy.
Statistical Analysis
We used two main measures to estimate the quality of the agreement between experimental and predicted values. First, we calculated the Pearson correlation coefficient and tested a null hypothesis about the equality of the correlation coefficient to zero. All correlation coefficients reported in the paper were significantly different from zero with p-values of less than 0.01. Another measure was the root-mean-square error (RMSE), which is the square root of the sum of the differences between values predicted by a model and experimental values divided by the number of cases. Five-fold cross validation was done on training sets where the data was randomly partitioned into five subsets of approximately equal size, and one subset was used for testing the model and the remaining four subsets were used as training data. To diminish similarity between training and testing sets and ensure the accuracy of cross-validated correlation coefficients, protein complexes from the same similarity cluster, provided by the SKEMPI database, were used only for training and not for testing. Then correlation coefficients were averaged over different cross-validated sets.
Results
Testing Different Simulation Protocols
Our goal is to construct a computational protocol that would yield good prediction accuracy for a diverse and large set of missense mutations. We obtained a new energy function with weighting factors in front of each terms based on eq 3 (see Methods) by applying a multiple linear regression procedure. This model was fit to the experimental data of the differences in binding affinities produced by mutations. Because several mutations can interact with each other and exhibit cooperativity and positive epistasis,59 we performed the fitting procedure separately for single and multiple mutations. Our results showed that the separate parameter optimization for single and multiple mutations yielded a better agreement with experiments than if we combined them. Table 1 (Table S2, Supporting Information, has more detailed information) shows results for different simulation protocols for 242 single mutants from the NM set with the 5-fold cross-validation using the Pred1 energy function. As can be seen from Table 1, minimization in explicit water without restrains on the backbone atoms shows the highest correlation which indicates how important the water model is for the quality of prediction. Moreover, minimizing the structures of mutants results in a better quality of ΔΔG estimates than a protocol where the VMD in silico model is used without minimization (see zero minimization step in Figure S3A–D, Supporting Information). However, increasing the number of minimization steps after about 300 does not significantly improve the average prediction performance. The exception is the minimization for multiple mutations from the SKEMPI set where the shorter minimization procedure in general produces better results (Figure S3D, Supporting Information).
Table 1. Correlation between Predicted and Experimental Values of ΔΔG for Different Simulation Protocolsa.
| simulation method | water model | flexibility | R(RCV) | RMSE (kcal mol–1) |
|---|---|---|---|---|
| minimization | explicit water | flexible backbone | 0.63(0.61) | 1.22 |
| restrained backbone | 0.62(0.61) | 1.23 | ||
| implicit water | flexible backbone | 0.50(0.48) | 1.36 | |
| MD simulation | explicit water | flexible backbone | 0.40(0.26) | 1.48 |
All calculations were performed with Pred1 energy function. R, the Pearson correlation coefficient between experimental and predicted ΔΔG values, RCV, the five-fold cross-validated correlation and RMSE, the root-mean squared error are each shown for the case of training/testing on single mutations of NM set. This table only shows the results with dielectric constant of two and ion concentration of zero. More detailed results are shown in Table S2 (Supporting Information).
We executed 1 ns MD simulations for 242 single mutants from nine protein complexes of the NM set. No significant conformational changes were observed in most cases in terms of RMSD from the starting mutant complex that was minimized for 1000 steps prior to MD simulation. Relatively large conformational changes between the wild-type and mutant proteins were observed in a few cases (RMSD of more than 2.5 Å), although the average backbone RMSD was less than 1.5 Å (Figure S5, Supporting Information). We observed even smaller backbone conformational changes during the minimization procedure (data not shown). As can be seen from Table 1 and Figure S3(E,F) (Supporting Information), MD simulation over 1 ns yields a maximum correlation of 0.40 between experiments and predictions for cases when MD simulations were done for both mutant and wild-type complexes (Figure S3F, Supporting Information). Nevertheless, it is considerably lower compared to the protocol when only minimization procedure is used.
Tables 2 and 3 compare our approach with other methods for single and multiple mutations, respectively. First, we tested two energy functions: Pred3 and Pred4 with 11 and 13 parameters for single and multiple mutations, respectively (energy functions are defined in the Supporting Information). Pred4 and Pred3 were applied to single and multiple mutations of the NM set (Tables 2 and 3) and produced very good agreement with the experiment (cross-validated correlation coefficient of 0.68 and 0.85 for Pred4 and Pred3, respectively, applied to single and multiple mutations), but they showed rather poor results on the large representative set of SKEMPI mutations with the correlation coefficients of 0.37 and 0.46 for single and multiple mutations, respectively. It should be mentioned that, unlike the correlation coefficient, RMSE values are scale dependent and can only be compared for different methods for the same test set, not between different sets. It is known that if parameters are tuned to overminimize mean squared errors and overfit the model, this can lead to decreased generalization performance.
Taking all this into account, we have constructed a model and ensured that it was trained on one large representative set (SKEMPI) and yielded a good agreement with experiments when tested on another independent set (NM). Our energy function Pred1 (see Methods, eq 4) had four parameters and three energy terms. Energy terms with statistically significant contribution to the quality of multiple regression model are listed in Table S3 (Supporting Information) together with their corresponding coefficients/weights. As can be seen from Tables 2 and 3, the Pred1 function gives a correlation coefficient of 0.62 and 0.63 and RMSE values of 1.27 and 1.90 kcal mol–1, if trained on SKEMPI and tested on the NM set for single and multiple mutations respectively. Interestingly, the energy function Pred1 trained on a set of SKEMPI multiple mutations showed better results for multiple mutations compared to using the energy function Pred1 trained on SKEMPI single mutations set (correlation coefficient of 0.55 versus 0.49).
Comparison with Other Methods
We compared our approach with three other independent methods, FoldX, BeAtMuSiC and CC/PBSA. BeAtMuSiC cannot be applied to multiple mutations whereas CC/PBSA is not very efficient for large sets like SKEMPI because of its slow computation time. As can be seen from Table 2, BeAtMuSiC overall yields better results than FoldX whereas the Pred1 model gives a better agreement with the experiments compared to both of these methods (correlation of 0.62, 0.52 and 0.47 for Pred1, BeAtMuSiC and FoldX, respectively, for testing on the NM set). Limited FoldX capacity can be attributed to the fact that the FoldX empirical energy function was parametrized on the experimental changes of unfolding free energy, not the binding affinity. The comparison of their computational speed will be reported in another section. Given the relatively high algorithm efficiency of the FoldX and BeAtMuSiC methods, we decided to combine their scoring schemes with our Pred1 energy function.
| 5 |
The performance of the combined model (Pred2) exceeded the performances of the individual Pred1 (p-value < 0.01, see Table S3, Supporting Information), FoldX and BeAtMuSiC methods and returned the correlation coefficient of 0.69 with an RMSE of 1.20 kcal mol–1. Importantly, the slope of the regression line for Pred2 is very close to 1 (0.97), which indicates that predicted values are on the same scale as experimental ones. In addition, we used the CC/PBSA server and managed to obtain the results for 66 single mutations randomly selected from the SKEMPI set. After excluding five mutations with very high predicted energies of ΔΔGCC/PBSA > 100 kcal mol–1, the correlation between experimental and calculated values for remaining 61 mutations was found to be R = 0.23 (p-value = 0.07) using the CC/PBSA method and R = 0.47 (p-value < 0.01) using the Pred2 energy function.
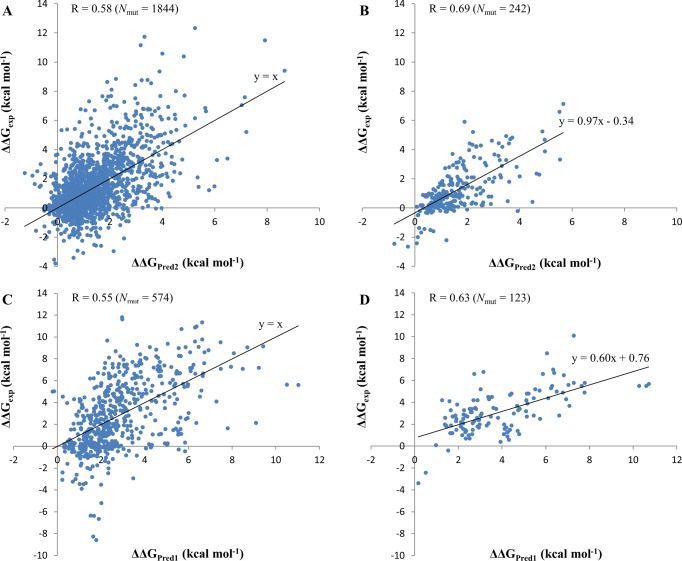
We further compared the accuracy separately for mutations that stabilized (ΔΔGpred < 0) or destabilized (ΔΔGpred > 0) the protein–protein binding. Mutations were also subdivided into binding hot spots (|ΔΔGpred| ≥ 2 kcal mol–1) or others (|ΔΔGpred| < 2 kcal mol–1). The prediction accuracy was defined as a percentage of correctly identified mutations out of the total number of mutations (TP + TN)/total, where TP denotes true positives and TN corresponds to true negatives. Sensitivity was defined as TP/(TP + FN) and specificity was calculated as TN/(TN + FP) (FN, false negative; FP, false positive). Table 4 shows that the Pred2 energy function has very high prediction accuracy for destabilizing mutants but low accuracy for stabilizing mutants. Stabilizing mutants are not well predicted by any of the methods used in this study and the FoldX method provides the highest prediction accuracy for stabilizing mutants. The specificity of predictions of binding hot spots is almost 100% for all methods although the sensitivity is compromised for all of them. We did not have enough data to perform a similar analysis for multiple mutations. Figure 1 shows experimental and predicted ΔΔG for single and multiple mutants for the SKEMPI training set and the NM test set. We can see that only a few stabilizing mutants are predicted as stabilizing whereas the majority of them are predicted as destabilizing.
Table 4. Prediction Accuracy of Destabilizing/Stabilizing Mutations and Binding Hot Spots for Single Mutations.
| destabilizing | stabilizing |
binding
hot spot |
||||
|---|---|---|---|---|---|---|
| method | training/test set | accuracy | accuracy | accuracy | sensitivity | specificity |
| Pred2 | SKEMPI/SKEMPI | 0.95 | 0.11 | 0.80 | 0.51 | 0.91 |
| SKEMPI/NM | 1.00 | 0.07 | 0.81 | 0.64 | 0.87 | |
| CC/PBSA | NM/NM | 0.99 | 0.32 | 0.84 | 0.48 | 0.97 |
| FoldX | test: NM | 0.72 | 0.48 | 0.77 | 0.37 | 0.91 |
| test: SKEMPI | 0.67 | 0.41 | 0.76 | 0.30 | 0.94 | |
| BeAtMuSiC | test: NM | 0.95 | 0.23 | 0.77 | 0.33 | 0.92 |
| test: SKEMPI | 0.90 | 0.18 | 0.77 | 0.30 | 0.95 | |
Figure 1.
Comparison between experimental ΔΔGexp and predicted changes in binding affinity ΔΔG. Training is performed on SKEMPI single (A, B) and multiple (C, D) mutation sets. A: Testing on SKEMPI single mutation set. B: Testing on NM single mutation set. C: Testing on SKEMPI multiple mutation set. D: Testing on NM multiple mutation set. Nmut is the number of mutations in the dataset. R is the Pearson correlation coefficient between experimental and predicted ΔΔG values. All correlation coefficients were significantly different from zero with p-values ≪0.01.
Comparison of Speed Performances
We compared the computational speed of different methods. BeAtMuSiC has the shortest processing time and calculation for one mutation takes less than a second on its webserver (http://babylone.ulb.ac.be/BeAtMuSiC/). FoldX is also very fast and takes about 5 min for a protein of about 300 residues when calculations are performed on an Intel Core Duo2 2.8 GHz processor. If we consider the parallel CPU calculation ability, our minimization protocol with NAMD uses 15 min of CPU time for a protein of 160 residues and 10 Å water box, altogether of about 23 900 atoms on 16 processors (with a 2.8 GHz Intel EMT64). There is no need to redo the long wild-type minimization procedure if several mutations of one protein are analyzed. In our study, we utilized the high computational capabilities of the Biowulf Linux cluster at the National Institutes of Health. For the binding free energy calculation using CHARMM, it takes about 10 min on one processor for about 160 residues protein (2.6 GHz AMD Opteron). The CC/PBSA approach uses the conformational sampling method and has long processing time (249 min for 149 residue protein on a 3.2 GHz Intel Xeon processor, as reported in ref (22)). However, the CC/PBSA webserver (http://ccpbsa.biologie.uni-erlangen.de/ccpbsa/) takes much longer to process one mutation and is not practically applicable for large datasets.
Contribution of Different Energy Terms to the Quality of the Model
On the basis of our previously mentioned results, we decided to use SKEMPI as a representative training set for the multiple regression fitting procedure. The resulting coefficients/weights in front of each energy terms and standardized coefficients in front of standardized variables (variable with the variance equal to one) are listed in Table S3 (Supporting Information). The standardized coefficients show relative contributions of different energy terms. As can be seen from this table, the polar solvation energy term calculated using Poisson–Boltzmann equation (ΔΔGsolv) and the van der Waals (ΔΔEvdw) terms have largest contributions to the total change in binding energy ΔΔGPred1 for single mutants (standardized coefficients of 0.40 and 0.34, respectively). Interface area (ΔSA) makes a relatively minor contribution. Interestingly, for multiple mutations, ΔΔGsolv becomes twice as important as for single mutations whereas the role of interface area diminishes. If we use the Pred2 model, then the largest contribution also comes from the polar solvation energy term (standardized coefficient of 0.31). The BeAtMuSiC score (ΔΔGBM) has a relatively high impact, whereas FoldX and interface area make smaller contributions to the quality of the model (standardized coefficients of about 0.15). However, all above terms contribute significantly to the agreement between experiments and predictions with p-values of less than 0.01.
Factors Influencing Prediction Accuracy
In this section, we consider several factors that might influence the quality of the prediction for single mutations. Importantly, all of these factors represent features of studied mutation sites that can be derived either from sequences or protein structures a priori.
Amino Acid Types of Substituted Amino Acids
First, we analyzed the effect of the type of residue substitutions on prediction accuracy. Figure 2 shows the boxplots of prediction errors for wild-type and mutant residue types, respectively. In each box, the central line is the median, the edges of the box are the 25th and 75th percentiles, the whiskers extend to the most extreme data points and outliers are plotted with circles. The median signed error for most wild-type amino acids is close to zero with two notable exceptions of overprediction, for Met and Pro. On the other side of the spectrum are Glu, Tyr and Thr, which produce underprediction errors but not as prominently as Met and Pro. As to the mutant residue type, Pro is again found to be exceptionally error-prone causing overprediction. The cyclic structure of proline’s side chain introduces constraints on the main-chain dihedral angles and can be structurally important for stability or binding. As can be seen from Figure S6 (Supporting Information), substitutions from/into Pro might cause relatively large local conformational changes compared to other substitution types. Moreover, substitutions of other amino acids into proline can result in significant destabilization of complexes (Figure S7, Supporting Information).
Figure 2.
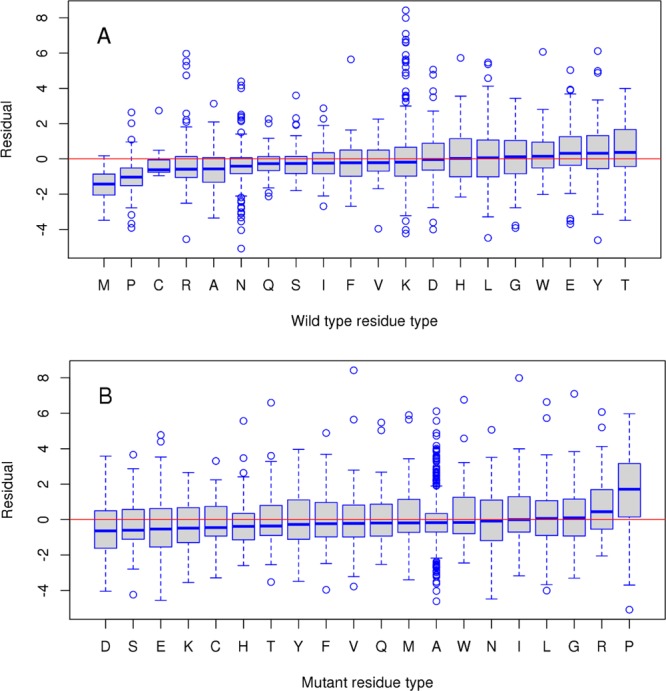
Boxplots of prediction error (residual) for different wild-type (A) and mutant (B) residue types for single mutants from SKEMPI training set. The residual is calculated as a difference between experimental ΔΔGexp and predicted ΔΔGPred2 values.
Physico-Chemical Properties of Substituted Amino Acids
As was previously shown, mutations resulting in amino acid substitutions with similar physico-chemical properties may not drastically alter the stability of a protein or a complex.8,10 We examined the performance of our model Pred2 in relation to the change in charge and volume of side chains produced by mutations (Tables S4 and S5, Supporting Information). One can see from Table S4 (Supporting Information) that the majority of substitutions are neutral-into-neutral, whereas the minority of them change the charge of amino acids. Positive-into-negative and neutral-into-negative amino acid substitutions are characterized by notable correlations (not enough statistics to estimate negative-into-positive charge changing substitutions). If we consider changes in the amino acid volume, then the highest correlation is observed for substitutions of small-into-large amino acids (Table S5, Supporting Information). As can be seen from Figure S6 (Supporting Information), small-into-large substitutions also cause largest conformational changes unlike large-into-small substitutions, which usually do not produce steric clashes.
Structural Locations of Substituted Amino Acids
The location of mutations in protein structures is another important feature, and even neighboring mutations might produce very different effects on binding affinity.60 All mutations can be classified into five types depending on their locations with respect to interface and surface (see ref (61) and the Supporting Information for definition). Figure 3 shows how mutation location may influence the experimental and predicted (not shown, but the effect is very similar) ΔΔG values. Mutations located in the core of the interface (COR) produce the largest changes in binding energy followed by the interface mutations partially exposed to the solvent (RIM and SUP). This is consistent with previous observations.13 Noninterface mutations (INT and SUR) affect binding the least. On the basis of these observations, one might conclude that majority of single mutations from the SKEMPI set do not lead to long-range allosteric effects and only those located directly at the interface regions make the largest contribution to the change in binding energy. Nevertheless, the effect of noninterface mutations is not negligible.
Figure 3.
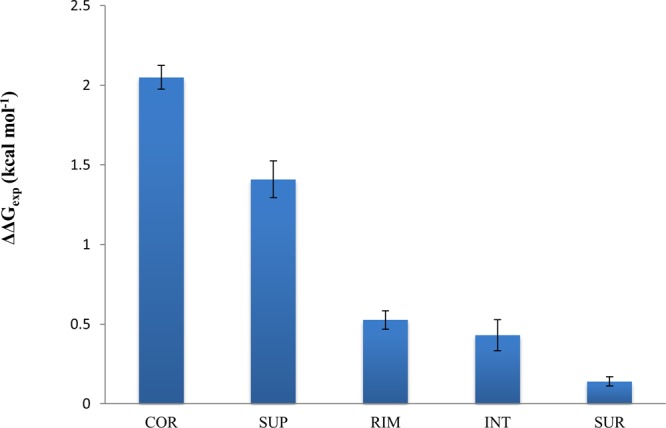
Effect of structural location of mutation on experimental ΔΔGexp. COR, RIM and SUP are the core, rim and support regions of the interface and INT and SUR are the solvent accessible regions. Definitions of regions are provided in the Supporting Information.
Case Study: Accounting for Protein Flexibility
The effect of protein flexibility on binding cannot be ignored and in some cases can improve or deteriorate the predictions. Here we describe two examples where we account for conformational changes in complex structures when the mutation is introduced.
Figure 4 compares two structures obtained by minimization and MD simulation for mutant alpha-chymotrypsin A/turkey ovomucoid third domain protein complex (PDB code: 1CHO); the Leu15Glu mutation is introduced into turkey ovomucoid third domain (chain I). If we compare the minimized structure and the complex conformation after MD simulation, we can see the changed conformation after MD simulation where side chains of Ser217 and Ser190 from alpha-chymotrypsin A protein flip over to form four extra hydrogen bonds with mutated residue Glu15; moreover, Ser195 moves closer to Glu15 to form another hydrogen bond (Figure 4 and Table S6, Supporting Information). This might enhance the interaction between the two partners and results in a smaller destabilizing ΔΔGPred1 values (1.13 kcal mol–1) for the MD simulation protocol compared to minimization protocol (4.32 kcal mol–1) and experimental value (6.6 kcal mol–1). This example illustrates that although MD simulation does allow for larger conformational changes, these transitions might not take place in a native protein.
Figure 4.
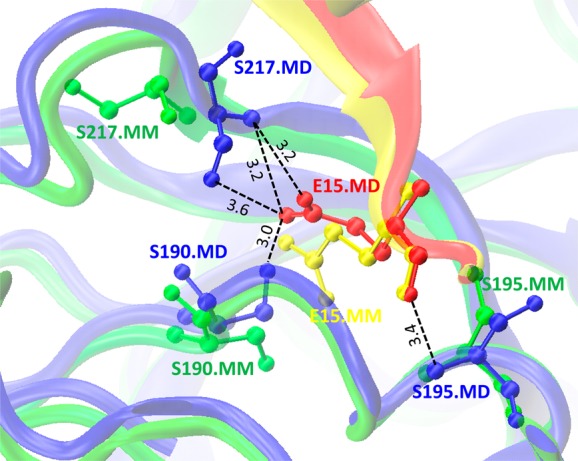
Difference between conformations of Leu15Glu mutant for α-chymotrypsin A/turkey ovomucoid third domain protein complex (PDB code: 1CHO) obtained by minimization (MM) and MD simulation (MD). Complex between turkey ovomucoid third domain (chain I) and α-chymotrypsin A (chains F and G) for MM structure are shown in yellow and green, respectively. Complex between chains I and F/G for MD are shown in red and blue, respectively. Black dotted lines correspond to the hydrogen bonds formed between Glu15 of chain I and Ser217, Ser190 and Ser195 of chain G (ball-and-stick model) in the MD simulated structure.
In the case of interleukin-4/receptor α chain protein (PDB code: 1IAR), the Arg85Ala mutation was introduced into interleukin-4 (chain A). MD simulation protocol made a relatively better prediction compared to the minimization protocol (ΔΔGexp = 0.43 kcal mol–1, ΔΔGPred1_MM = 4.57 and ΔΔGPred1_MD = 1.89 kcal mol–1). The mutant minimized structure loses seven hydrogen bonds between Arg85 and Asp67 and Asp125 compared to the wild-type minimized structure (Table S6, Supporting Information) whereas the mutant MD simulated structure loses only three hydrogen bonds compared to the MD simulated wild-type structure (Table S6, Supporting Information).
Discussion
In this study, we attempt to design an efficient computational protocol in order to estimate the impact of single and multiple missense mutations on protein binding affinity. Our analysis showed that the choices of simulation procedure and energy function are both important for achieving accurate predictions. We demonstrated that using an unconstrained minimization procedure in explicit solvent yielded a better agreement with experiments compared to implicit solvent, which is consistent with a previous study on a smaller dataset62 We used a modified MM-PBSA energy function and optimized its parameters on the experimental data of several thousands of mutations. We showed that even with the 5-fold cross-validation, it is possible to attain a very high correlation coefficient (R = 0.85) with the experimental data using a model with eleven parameters. However, these energy functions do not perform well when applied to an independent set of mutations. It points to the fact that such a model can be overtrained and biased toward certain groups of proteins or mutations. Therefore, one should be very cautious in interpreting the results using only one limited dataset for fitting and testing even if cross-validation is done.
Our approach with an all-atom force field model, explicit water minimization protocol and energy function with only four parameters yielded a reasonable correlation coefficient (R = 0.62) and RMSE values (RMSE = 1.27 kcal mol–1) between experimental and predicted values after training was done on a representative SKEMPI set and testing was performed on an independent and nonoverlapping set of single mutations. Consistent with another study, the MM-PBSA energy function displayed superior performance compared to statistical and empirical potentials.22 Moreover, including statistical scores from FoldX and BeatMusic into the model produced significantly better agreement with experiments (p-value < 0.01) with a correlation coefficient of 0.69 and RMSE of 1.20 kcal mol–1. We showed that the largest significant contribution that explained the largest proportion of experimental data variation came from the polar solvation energy term. This result once more points to the extreme importance of the solvent model and solvation effects. We also would like to spotlight the drawback of our model that underestimates the contribution of stabilizing mutations. This, in turn, could be the result of an insufficient number of stabilizing amino acid substitutions in the experimental training set.
To assess the effect of multiple mutations, we investigated two models trained on single and multiple mutations, respectively. Interestingly, we found that the model trained on a set of multiple mutations showed better results for multiple mutations compared to the model trained on single mutations. Indeed, nonadditivity of the effect of multiple mutations on binding was observed previously for alanine scanning and disease mutations.59,63 It was partially attributed to the modular structure of the binding interface and cooperativity of amino acids within each binding site cluster.63
It is difficult to assess the conformational changes of monomers occurring upon binding and the effect of flexibility on prediction accuracy. Although we did not estimate conformational changes upon binding (in many cases, no unbound states were available), we tried to account for conformational changes in complex structures produced by mutations. As we showed, conformational sampling of mutant structures by molecular dynamics simulations on a 1 ns time scale did not help to achieve better agreement with experiments compared to the protocol when only one minimized mutant complex structure was used. This is consistent with several previous studies demonstrating that averaging over an MD-generated ensemble of conformations had a negligible effect on the quality of binding affinity predictions, on estimating the effect of mutations on binding23,24 and on homology model refinement.64 It was previously shown that backbone sampling can do more harm than good when estimating the effects of mutations on protein stability in cases where structural changes are negligible.65 It implies that either our single minimized conformation dominated a native conformational ensemble or we sampled inaccessible conformations during the unconstrained MD simulations. In any case, even without conformational sampling, we were able to achieve similar or better prediction accuracy on a much faster time scale compared to one of the best currently available method (CC/PBSA).22 This is especially important for high-throughput virtual screening studies because the conformational sampling is very time-consuming.
Finally, we found that the highest correlation was observed for substitutions that changed either charge or side chain volume. We also observed that missense mutations located directly in the core region of interfaces had the largest effect on binding affinity and long-range effects from noninterface mutations were relatively minor. All these distinctive realistic patterns and the reasonable agreement with experiments validates the use of atomic force fields, statistical potentials or combinatorial scoring schemes for estimating the effects of single and multiple missense mutations on protein–protein binding affinity.
Acknowledgments
We thank Thomas Madej for insightful discussions. This work was supported by the Intramural Research Program of the National Library of Medicine at the U.S. National Institutes of Health. M.P. and E.A. were supported in part by National Institutes of Health, National Institute of General Medical Sciences, grant number R01GM093937.
Supporting Information Available
Ten single and eight multiple mutants with unrealistic VMD initial models; correlation between predicted and experimental values of ΔΔG for different simulation protocols; optimal fitting coefficients and standardized coefficients for multiple linear regression performed on SKEMPI set; accuracy of prediction for different types of amino acid substitutions categorized by their charge; accuracy of prediction for different types of amino acid substitutions categorized by the side chain volume; residue–residue pairs that have hydrogen bonds and salt bridges formed in the final minimized structure for wild type (WT-MM), 500-step minimized structure for mutant (Mutant-MM), average structure obtained using 1 ns of MD simulations for wild type (WT-MD) and mutant (Mutant-MD); schema of the simulation protocols; distribution of the system size for 83 protein–protein complexes; dependence of correlation coefficient between experimental ΔΔGexp and predicted ΔΔGPred1 on the number of minimization steps and number of frames in MD simulations; correlation between experimental and predicted Pred1 ΔΔG values for each protein complex for 500 and 10 000 minimization steps for single mutants from NM set; distribution of the Root mean square deviation (RMSD, Å) of backbone atoms for 242 single mutants from NM set; average local heavy atom RMSD values between the minimized mutant structure and the initial non-minimized mutant models for different types of amino acid substitutions categorized by charge, side chain volume and Proline; average values of experimental ΔΔGexp for different types of amino acid substitutions categorized by charge, side chain volume and Proline; definitions of models Pred3 and Pred4; definitions of regions for different locations of mutations for Figure 3; definition of standardized regression coefficients. This material is available free of charge via the Internet at http://pubs.acs.org.
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- Nooren I. M. A.; Thornton J. M. Structural Characterisation and Functional Significance of Transient Protein–Protein Interactions. J. Mol. Biol. 2003, 325, 991–1018. [DOI] [PubMed] [Google Scholar]
- Hashimoto K.; Panchenko A. R. Mechanisms of protein oligomerization, the critical role of insertions and deletions in maintaining different oligomeric states. Proc. Natl. Acad. Sci. U. S. A. 2010, 107, 20352–20357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dahiyat B. I.; Benjamin Gordon D.; Mayo S. L. Automated design of the surface positions of protein helices. Protein Sci. 1997, 6, 1333–1337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shifman J. M.; Mayo S. L. Exploring the origins of binding specificity through the computational redesign of calmodulin. Proc. Natl. Acad. Sci. U. S. A. 2003, 100, 13274–13279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen T. S.; Keating A. E. Designing specific protein–protein interactions using computation, experimental library screening, or integrated methods. Protein Sci. 2012, 21, 949–963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin H.; Slusky J. S.; Berger B. W.; Walters R. S.; Vilaire G.; Litvinov R. I.; Lear J. D.; Caputo G. A.; Bennett J. S.; DeGrado W. F. Computational Design of Peptides That Target Transmembrane Helices. Science 2007, 315, 1817–1822. [DOI] [PubMed] [Google Scholar]
- Joachimiak L. A.; Kortemme T.; Stoddard B. L.; Baker D. Computational Design of a New Hydrogen Bond Network and at Least a 300-fold Specificity Switch at a Protein–Protein Interface. J. Mol. Biol. 2006, 361, 195–208. [DOI] [PubMed] [Google Scholar]
- Teng S.; Madej T.; Panchenko A.; Alexov E. Modeling Effects of Human Single Nucleotide Polymorphisms on Protein-Protein Interactions. Biophys. J. 2009, 96, 2178–2188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yates C. M.; Sternberg M. J. E. The Effects of Non-Synonymous Single Nucleotide Polymorphisms (nsSNPs) on Protein–Protein Interactions. J. Mol. Biol. 2013, 425, 3949–3963. [DOI] [PubMed] [Google Scholar]
- Nishi H.; Tyagi M.; Teng S.; Shoemaker B. A.; Hashimoto K.; Alexov E.; Wuchty S.; Panchenko A. R. Cancer Missense Mutations Alter Binding Properties of Proteins and Their Interaction Networks. PLoS One 2013, 8, e66273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei Q.; Wang L.; Wang Q.; Kruger W. D.; Dunbrack R. L. Testing computational prediction of missense mutation phenotypes: Functional characterization of 204 mutations of human cystathionine beta synthase. Proteins: Struct., Funct., Bioinf. 2010, 78, 2058–2074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chothia C.; Janin J. Principles of protein-protein recognition. Nature 1975, 256, 705–708. [DOI] [PubMed] [Google Scholar]
- Kastritis P. L.; Bonvin A. M. J. J. Molecular origins of binding affinity: seeking the Archimedean point. Curr. Opin. Struct. Biol. 2013, 23, 868–877. [DOI] [PubMed] [Google Scholar]
- Marsh J. A.; Teichmann S. A. Relative Solvent Accessible Surface Area Predicts Protein Conformational Changes upon Binding. Structure 2011, 19, 859–867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moal I. H.; Agius R.; Bates P. A. Protein-protein binding affinity prediction on a diverse set of structures. Bioinformatics 2011, 27, 3002–9. [DOI] [PubMed] [Google Scholar]
- Kastritis P. L.; Bonvin A. M. J. J. Are Scoring Functions in Protein–Protein Docking Ready To Predict Interactomes? Clues from a Novel Binding Affinity Benchmark. J. Proteome Res. 2010, 9, 2216–2225. [DOI] [PubMed] [Google Scholar]
- Sharabi O.; Dekel A.; Shifman J. M. Triathlon for energy functions: Who is the winner for design of protein–protein interactions?. Proteins: Struct., Funct., Bioinf. 2011, 79, 1487–1498. [DOI] [PubMed] [Google Scholar]
- Papoian G. A.; Wolynes P. G. The physics and bioinformatics of binding and folding—an energy landscape perspective. Biopolymers 2003, 68, 333–349. [DOI] [PubMed] [Google Scholar]
- Guerois R.; Nielsen J. E.; Serrano L. Predicting Changes in the Stability of Proteins and Protein Complexes: A Study of More Than 1000 Mutations. J. Mol. Biol. 2002, 320, 369–387. [DOI] [PubMed] [Google Scholar]
- Schymkowitz J. W. H.; Rousseau F.; Martins I. C.; Ferkinghoff-Borg J.; Stricher F.; Serrano L. Prediction of water and metal binding sites and their affinities by using the Fold-X force field. Proc. Natl. Acad. Sci. U. S. A. 2005, 102, 10147–10152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dehouck Y.; Kwasigroch J. M.; Rooman M.; Gilis D. BeAtMuSiC: prediction of changes in protein–protein binding affinity on mutations. Nucleic Acids Res. 2013, 41, W333–W339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benedix A.; Becker C. M.; de Groot B. L.; Caflisch A.; Bockmann R. A. Predicting free energy changes using structural ensembles. Nat. Methods 2009, 6, 3–4. [DOI] [PubMed] [Google Scholar]
- Kuhn B.; Gerber P.; Schulz-Gasch T.; Stahl M. Validation and Use of the MM-PBSA Approach for Drug Discovery. J. Med. Chem. 2005, 48, 4040–4048. [DOI] [PubMed] [Google Scholar]
- Rastelli G.; Rio A. D.; Degliesposti G.; Sgobba M. Fast and accurate predictions of binding free energies using MM-PBSA and MM-GBSA. J. Comput. Chem. 2010, 31, 797–810. [DOI] [PubMed] [Google Scholar]
- Okimoto N.; Futatsugi N.; Fuji H.; Suenaga A.; Morimoto G.; Yanai R.; Ohno Y.; Narumi T.; Taiji M. High-Performance Drug Discovery: Computational Screening by Combining Docking and Molecular Dynamics Simulations. PLoS Comput. Biol. 2009, 5, e1000528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z.; Wang L.; Gao Y.; Zhang J.; Zhenirovskyy M.; Alexov E. Predicting folding free energy changes upon single point mutations. Bioinformatics 2012, 28, 664–671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spassov V. Z.; Yan L. pH-selective mutagenesis of protein–protein interfaces: In silico design of therapeutic antibodies with prolonged half-life. Proteins: Struct., Funct., Bioinf. 2013, 81, 704–714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinkam P.; Chen Y. C.; Pons J.; Sali A. Impact of Mutations on the Allosteric Conformational Equilibrium. J. Mol. Biol. 2013, 425, 647–661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Massova I.; Kollman P. A. Computational Alanine Scanning To Probe Protein–Protein Interactions: A Novel Approach To Evaluate Binding Free Energies. J. Am. Chem. Soc. 1999, 121, 8133–8143. [Google Scholar]
- Huo S.; Massova I.; Kollman P. A. Computational alanine scanning of the 1:1 human growth hormone–receptor complex. J. Comput. Chem. 2002, 23, 15–27. [DOI] [PubMed] [Google Scholar]
- Moreira I. S.; Fernandes P. A.; Ramos M. J. Unraveling the Importance of Protein–Protein Interaction: Application of a Computational Alanine-Scanning Mutagenesis to the Study of the IgG1 Streptococcal Protein G (C2 Fragment) Complex. J. Phys. Chem. B 2006, 110, 10962–10969. [DOI] [PubMed] [Google Scholar]
- Gohlke H.; Kiel C.; Case D. A. Insights into Protein–Protein Binding by Binding Free Energy Calculation and Free Energy Decomposition for the Ras–Raf and Ras–RalGDS Complexes. J. Mol. Biol. 2003, 330, 891–913. [DOI] [PubMed] [Google Scholar]
- Zhang Z.; Teng S.; Wang L.; Schwartz C. E.; Alexov E. Computational analysis of missense mutations causing Snyder-Robinson syndrome. Hum. Mutat. 2010, 31, 1043–1049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moal I. H.; Fernández-Recio J. SKEMPI: a Structural Kinetic and Energetic database of Mutant Protein Interactions and its use in empirical models. Bioinformatics 2012, 28, 2600–2607. [DOI] [PubMed] [Google Scholar]
- Humphrey W.; Dalke A.; Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996, 1433–827–8. [DOI] [PubMed] [Google Scholar]
- Phillips J. C.; Braun R.; Wang W.; Gumbart J.; Tajkhorshid E.; Villa E.; Chipot C.; Skeel R. D.; Kale L.; Schulten K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berman H. M.; Westbrook J.; Feng Z.; Gilliland G.; Bhat T. N.; Weissig H.; Shindyalov I. N.; Bourne P. E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foloppe N.; MacKerell A. D. All-atom empirical force field for nucleic acids: I. Parameter optimization based on small molecule and condensed phase macromolecular target data. J. Comput. Chem. 2000, 21, 86–104. [Google Scholar]
- Tanner D. E.; Chan K.-Y.; Phillips J. C.; Schulten K. Parallel Generalized Born Implicit Solvent Calculations with NAMD. J. Chem. Theory Comput. 2011, 7, 3635–3642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee M. S.; Olson M. A. Calculation of Absolute Protein-Ligand Binding Affinity Using Path and Endpoint Approaches. Biophys. J. 2006, 90, 864–877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bradshaw R. T.; Patel B. H.; Tate E. W.; Leatherbarrow R. J.; Gould I. R. Comparing experimental and computational alanine scanning techniques for probing a prototypical protein–protein interaction. Protein Eng. Des. Sel. 2011, 24, 197–207. [DOI] [PubMed] [Google Scholar]
- Li M.; Zheng W. Probing the Structural and Energetic Basis of Kinesin–Microtubule Binding Using Computational Alanine-Scanning Mutagenesis. Biochemistry (Moscow) 2011, 50, 8645–8655. [DOI] [PubMed] [Google Scholar]
- MacKerell A. D.; Bashford D.; Bellott M.; Dunbrack R. L.; Evanseck J. D.; Field M. J.; Fischer S.; Gao J.; Guo H.; Ha S.; Joseph-McCarthy D.; Kuchnir L.; Kuczera K.; Lau F. T. K.; Mattos C.; Michnick S.; Ngo T.; Nguyen D. T.; Prodhom B.; Reiher W. E.; Roux B.; Schlenkrich M.; Smith J. C.; Stote R.; Straub J.; Watanabe M.; Wiorkiewicz-Kuczera J.; Yin D.; Karplus M. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [DOI] [PubMed] [Google Scholar]
- Deserno M.; Holm C. How to mesh up Ewald sums. I. A theoretical and numerical comparison of various particle mesh routines. J. Chem. Phys. 1998, 109, 7678–7693. [Google Scholar]
- Hoover W. G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [DOI] [PubMed] [Google Scholar]
- Kollman P. A.; Massova I.; Reyes C.; Kuhn B.; Huo S.; Chong L.; Lee M.; Lee T.; Duan Y.; Wang W.; Donini O.; Cieplak P.; Srinivasan J.; Case D. A.; Cheatham T. E. Calculating Structures and Free Energies of Complex Molecules: Combining Molecular Mechanics and Continuum Models. Acc. Chem. Res. 2000, 33, 889–897. [DOI] [PubMed] [Google Scholar]
- Russell S. T.; Warshel A. Calculations of electrostatic energies in proteins: The energetics of ionized groups in bovine pancreatic trypsin inhibitor. J. Mol. Biol. 1985, 185, 389–404. [DOI] [PubMed] [Google Scholar]
- Im W.; Beglov D.; Roux B. Continuum Solvation Model: computation of electrostatic forces from numerical solutions to the Poisson-Boltzmann equation. Comput. Phys. Commun. 1998, 111, 59–75. [Google Scholar]
- Jo S.; Vargyas M.; Vasko-Szedlar J.; Roux B.; Im W. PBEQ-Solver for online visualization of electrostatic potential of biomolecules. Nucleic Acids Res. 2008, 36, W270–W275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connolly M. Analytical molecular surface calculation. J. Appl. Crystallogr. 1983, 16, 548–558. [Google Scholar]
- Olson M. A.; Reinke L. T. Modeling implicit reorganization in continuum descriptions of protein-protein interactions. Proteins 2000, 38, 115–9. [DOI] [PubMed] [Google Scholar]
- Gilson M. K.; Honig B. H. The dielectric constant of a folded protein. Biopolymers 1986, 25, 2097–119. [DOI] [PubMed] [Google Scholar]
- Sharp K. A.; Honig B. Electrostatic interactions in macromolecules: theory and applications. Annu. Rev. Biophys. Biophys. Chem. 1990, 19, 301–32. [DOI] [PubMed] [Google Scholar]
- Sharp K. A.; Honig B. Calculating Total Electrostatic Energies with the Nonlinear Poisson-Boltzmann Equation. J. Phys. Chem. 1990, 94, 7684–7692. [Google Scholar]
- Roux B. Influence of the membrane potential on the free energy of an intrinsic protein. Biophys. J. 1997, 73, 2980–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nina M.; Beglov D.; Roux B. Atomic radii for continuum electrostatics calculations based on molecular dynamics free energy simulations. J. Phys. Chem. B 1997, 101, 5239–5248. [Google Scholar]
- Brooks B. R.; Bruccoleri R. E.; Olafson B. D.; States D. J.; Swaminathan S.; Karplus M. Charmm - a Program for Macromolecular Energy, Minimization, and Dynamics Calculations. J. Comput. Chem. 1983, 4, 187–217. [Google Scholar]
- Dehouck Y.; Gilis D.; Rooman M. A New Generation of Statistical Potentials for Proteins. Biophys. J. 2006, 90, 4010–4017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hashimoto K.; Rogozin I. B.; Panchenko A. R. Oncogenic potential is related to activating effect of cancer single and double somatic mutations in receptor tyrosine kinases. Hum. Mutat. 2012, 33, 1566–1575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li M.; Shoemaker B. A.; Thangudu R. R.; Ferraris J. D.; Burg M. B.; Panchenko A. R. Mutations in DNA-Binding Loop of NFAT5 Transcription Factor Produce Unique Outcomes on Protein–DNA Binding and Dynamics. J. Phys. Chem. B 2013, 117, 13226–13234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy E. D. A Simple Definition of Structural Regions in Proteins and Its Use in Analyzing Interface Evolution. J. Mol. Biol. 2010, 403, 660–670. [DOI] [PubMed] [Google Scholar]
- Weis A.; Katebzadeh K.; Söderhjelm P.; Nilsson I.; Ryde U. Ligand Affinities Predicted with the MM/PBSA Method: Dependence on the Simulation Method and the Force Field. J. Med. Chem. 2006, 49, 6596–6606. [DOI] [PubMed] [Google Scholar]
- Reichmann D.; Rahat O.; Albeck S.; Meged R.; Dym O.; Schreiber G. The modular architecture of protein–protein binding interfaces. Proc. Natl. Acad. Sci. U. S. A. 2005, 102, 57–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chopra G.; Summa C. M.; Levitt M. Solvent dramatically affects protein structure refinement. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 20239–20244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kellogg E. H.; Leaver-Fay A.; Baker D. Role of conformational sampling in computing mutation-induced changes in protein structure and stability. Proteins: Struct., Funct., Bioinf. 2011, 79, 830–838. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.