Emergent complexity of the cytoskeleton: from single filaments to tissue

Abstract

Despite their overwhelming complexity, living cells display a high degree of internal mechanical and functional organization which can largely be attributed to the intracellular biopolymer scaffold, the cytoskeleton. Being a very complex system far from thermodynamic equilibrium, the cytoskeleton's ability to organize is at the same time challenging and fascinating. The extensive amounts of frequently interacting cellular building blocks and their inherent multifunctionality permits highly adaptive behavior and obstructs a purely reductionist approach. Nevertheless (and despite the field's relative novelty), the physics approach has already proved to be extremely successful in revealing very fundamental concepts of cytoskeleton organization and behavior. This review aims at introducing the physics of the cytoskeleton ranging from single biopolymer filaments to multicellular organisms. Throughout this wide range of phenomena, the focus is set on the intertwined nature of the different physical scales (levels of complexity) that give rise to numerous emergent properties by means of self-organization or self-assembly.

1. Introduction

Most parts of what we feel is “the world we live in” consist of many intertwined levels or scales leading to an incredible complexity. Especially what we call “life” exists far from thermodynamic equilibrium and comprises an almost uncountable number of interacting elements. This might explain why physicists stayed away from soft and especially living matter for such a long time. The incredibly successful achievements in physics up to the middle of the twentieth century simply seem to be impossible to repeat for the case of living organisms. It appears that a purely reductionist approach (which was and still is extremely successful in physics) is unable to fully investigate soft matter [1–3].

The grand achievements of early twentieth century physics tell us little about how to deal with complex systems yet “the world we live in” seems nothing but a complex system. The most fundamental living entity, the cell, exists on a physical scale that is largely governed by electrostatic interactions (e.g. Van der Waals interactions and hydrogen bonding) and entropy. Yet the huge number of interacting elements makes it impossible to derive from fundamental electrostatics how the cell manages to organize its interior. The cell remains in a highly organized state despite its many components and avoids the restrictions of thermodynamic equilibrium through permanent energy dissipation.

Obviously, we need radically new methods and concepts to tackle this complexity, a need we share with many different disciplines, ranging from physics to sociology. This goes along with a certain vagueness of the term complex system which can be associated with anything from a few molecules to macroeconomics. Luckily, it turns out that analytical tools developed to address complex systems are highly versatile.

Not until the 1940s were substantial efforts made to address complex systems giving birth to completely new scientific fields like cybernetics, chaos theory, or nonlinear dynamics. Along came a growing awareness of complexity as a fundamental property of our world we necessarily have to deal with.

In this context, the concepts of emergence, as well as self-organization and self-assembly became increasingly popular and are commonly applied in many scientific disciplines. Not surprisingly, these concepts attracted a particularly wide interest in biophysics since they give rise to the formation of complex structures from simpler elements. Classical examples are the formation of beautiful, regular patterns in numerous biological systems from the molecular level up to plants and animals as well as collective or swarm-like behavior [4,5]. But not only ordering (in form of patterns) or collective behavior can emerge. The concept also holds for the emergence of new material properties that are absent on the single component level. An important example is the mechanics of polymer solutions and networks.

In this review, the mentioned concepts will be discussed by focusing on the cytoskeleton, the underlying biopolymer scaffold of living cells. The cytoskeleton's ability to organize itself is absolutely essential for the cellular morphology, its mechanical properties, as well as biological key processes like cell division, neuroplasticity, wound healing, and metastasis. As reflected by its substantial biological relevance, the cytoskeleton and its emergent organization lie at the heart of the structural and functional organization of living matter.

In the following sections, we systematically move along the different levels of complexity starting with a single filament perspective (Section 2) forming the basis for the cellular level (Section 3) up to whole interacting cytoskeleton in multicellular bodies (Section 4). Across these scales, our main focus lies on both ordering and emerging mechanical properties (Figure 1).

Figure. 1.

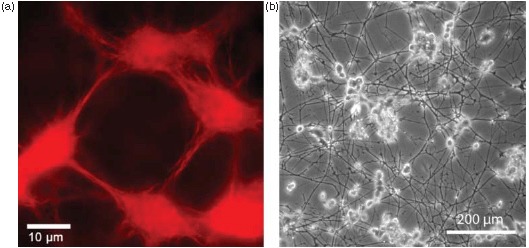
Two examples of complex organization based on cytoskeletal elements. (a) On the subcellular level, reconstituted systems of actin filaments with molecular myosin motors form networks connected by aggregated actin centers (asters). The image was taken using fluorescence microscopy and actin was labeled with a rhodamine dye. (b) On amulticellular level, neuron-like PC12 cells form extensive networks of MT-rich neurites. The image was taken using phase contrast microscopy and cells were cultured on a laminin-coated surface. Images were taken by David Smith (a) and Steve Pawlizak (b), image (a) also appeared in [148].

1.1. The cytoskeleton

The cytoskeleton is a polymer fiber-based scaffold spanning the cell's interior which apart from its biological importance is particularly fascinating, thanks to two key features. First, cytoskeletal systems are highly dynamic, enabling rapid adaptive organization and yet they remain well-ordered. This is only possible due to permanent energy dissipation. Second, although the fundamental building blocks are almost the same in every animal cell, their cytoskeleton-induced morphology differs substantially. The same extreme variability is found within single cells where the cytoskeleton organizes locally into many different structures. Different functional modules (Section 1.2.2) can hence be constructed out of similar sets of ingredients reflecting the multifunctionality of essential cytoskeletal components.

The fundamental building blocks are three different biopolymer materials, actin, microtubules (MTs), and intermediate filaments (IFs), all of which form micrometer long fibers or filaments that are comprised of many individual monomers [6] (Figure 2). Differences in the filaments’ internal architecture result in a wide variation of their bending rigidity. MTs are very rigid polymer tubes that typically appear as individual fibers. They are commonly associated with intracellular transport, mitosis, and organelle positioning. Actin filaments are semiflexible polymers (see Section 2.1) appearing in the form of various cross-linked networks. Actin filaments form the most dynamic of all cytoskeleton structures and consequently actin networks are able to undergo rapid changes. They determine the shape of the cell and are essential for cell migration. IFs are a more heterogeneous class of biopolymers forming extended networks that substantially contribute to the mechanical properties of living cells.

Figure. 2.

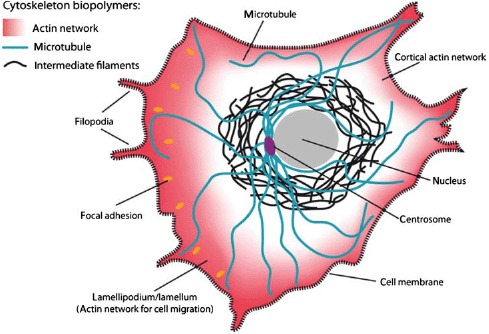
Schematic of a crawling cell on a 2D substrate to show the most prominent locations for the three types of cytoskeleton biopolymers. MTs are typically nucleated at the centrosome and span most parts of the cell. IFs are most commonly around the cell nucleus whereas actin filaments form dense networks close to the cell membrane. Particularly dense and dynamic actin networks are found at the leading edge of migrating cells (forming lamellipodia and filopodia).

Organization and dynamics of these three polymer materials are largely determined by the complex interplay with numerous accessory proteins which can nucleate, sever, cross-link, weaken, strengthen, or transport individual filaments (Figure 3) [6]. Despite the large variety of different cytoskeletal reactions only two essential processes drive the cytoskeleton in a dissipative manner being fueled by adenosine triphosphate (ATP) or guanosine triphosphate (GTP): Hydrolysis powered de-/polymerization of filaments and molecular motor-driven filament/motor transport.

Figure. 3.

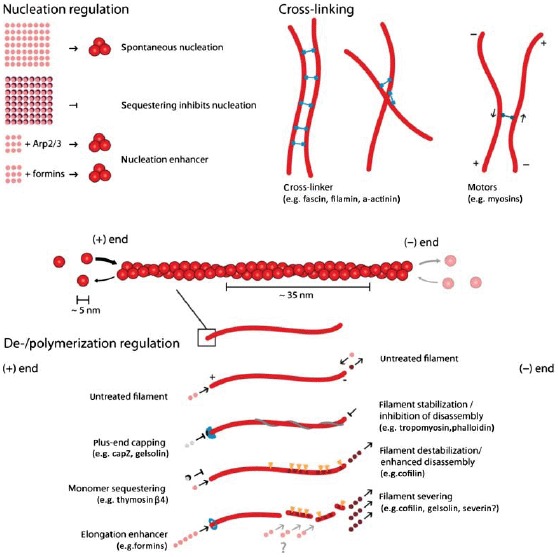
Actin filaments are helical polar structures with a plus and a minus-end and are built from actin monomers. Various ways have been discovered how accessory proteins modify actin filament dynamics. In this sketch, representative accessory proteins are classified according to their function into the three categories “Nucleation regulation,” “Cross-linking,” or “Polymerization regulation”.

Actin and MTs are polar structures with a plus – and a minus – end (unlike IFs). ATP or GTP hydrolysis provides different critical concentrations at the two ends leading to unsymmetrical polymerization and depolymerization dynamics (treadmilling). Treadmilling is an active process and hence reflects an inherent non-equilibrium state. Furthermore, it enables filaments to produce significant pushing forces [7]. Molecular motors on the other hand move along polar filaments in a directed fashion. Again, the directional and persistent motion is only possible due to ATP hydrolysis and can be utilized to transport cargo but also to move or pull on filaments [8].

Actin filament turnover and molecular motor dynamics are permanent processes in biological matter and, due to the high actin content of most cells and its fast turnover dynamics, result in substantial energy consumption. In mammalian cells, this can reach up to ∼50% of the total ATP consumption [9,10] indicating that minimal energy consumption might not have been the most dominant evolutionary factor.

Apart from molecular motors, all other actin accessory proteins influence the filament or network properties without consuming ATP or GTP. Their regulative functions can roughly be classified as modification of either polymerization dynamics, cross-linking, or filament nucleation (see Figure 3).

All three polymer types undergo growth and shrinkage by addition or subtraction of monomers or oligomers. Thus, the length (and for IFs or actin bundles also the diameter) is dynamically adjustable and typically subject to permanent stochastic fluctuations [11–13].

Nature found many ways to alter this polymerization process via accessory proteins (Figure 3). The concentration of monomers available is an essential factor regulating polymerization and is typically controlled by specific sequestering proteins. Some proteins are able to directly weaken or stabilize filaments, while others block the polymerizing or depolymerizing ends.

Another class of accessory proteins is the cross-linkers that bind together filaments. Cross-linkers can either bind (quasi-)permanently or transiently and can imply or favor different binding geometries. Naturally, cross-linking dramatically influences the mechanical properties of the cytoskeleton [14].

Finally, nucleation of new filaments is tightly controlled in cells from two sides. Sequestering suppresses spontaneous nucleation and specific addressable nucleators allow spatial as well as temporal control over filament generation [15].

Proper regulation of the cytoskeleton by the use of accessory proteins is only possible when additional feedback-loops and signaling-cascades control parts of this system. Often functional units possess one or few key elements that are biochemically switchable and have an active and an inactive state such as Arp2/3, a common actin nucleator [16]. These elements are incorporated into a signal chain that allows triggering. Once activated, however, the functional units tend to work autonomously without further external regulation [17].

Looking at the persistent, cooperative functioning of hundreds of different proteins, one often tends to think of cells as highly complex machines which can be misleading as some authors pointed out [18,19]. Whereas a machine is designed to fulfill a specific task, an organic system designs itself. Machines are built, organisms build themselves. This is exactly what makes life robust and possible. Albeit our manner of speaking often sounds differently, cells do not control every detail and in the same way they do not depend on them. Cells continue to migrate even after blocking their molecular motors [20]. Knockout or knockdown of important cellular proteins still results in nearly unchanged behavior in many cases [21,22].

In reconstituted bottom-up systems, the difference becomes particularly striking. When a number of interacting elements are simply “thrown together,” highly organized cooperative behavior suddenly appears without any rational design.

1.2. Concepts

Self-organization, emergence, and complexity are terms that today are used from gases to socio-economic systems and from particles to galaxies. During the last decades, not only the philosophical debate on what complexity and life has advanced, but also the scientific means which are inseparably connected with a rapid evolution of computational and experimental techniques.

Due to the many different disciplines involved and the fields’ novelty, many important terms or concepts are used in different ways such that precise interdisciplinary terms are not yet established, nor is there any common consensus on how to gain knowledge out of excessively complex systems delivering masses of data. In the following sections, explanations and definitions of the key terms along which this article is structured are given.

1.2.1. Coarse-graining as hierarchical reduction

Although it is widely agreed on among scientists that the world in its essentials is held together by fundamental physical laws and although, from a physics perspective, the fundamental material properties are astonishingly well known today, we still seek out for chemists when we want to know how to oxidize a given substance and we still consult a physician when we are sick.

At this point, we do not want to enter the intensive debate conducted in philosophy and science concerning the question whether or not the entire world could at least “in principle” be described based on fundamental physics. If new, orders of magnitude faster computers facilitate the modeling of a gas from quantum mechanics (or elementary particle physics), the only thing to learn is that the discovered fundamental laws are sufficient to obtain what is observed on the larger scale. To our understanding, the more important knowledge is gained by condensing the statistical behavior through introducing the quantities temperature, pressure, and volume to describe the gas.

Exceedingly complex systems resist an intuitive understanding and inhibit further abstraction of the system. Both steps, however, are essential for a physicist's approach. In this context, it is commonly referred to levels of complexity which directly refers to physical scales in order to avoid circular argumentation when we later on use the term emergence [23]. Typically, the higher level contains the lower level which is why the complexity necessarily increases. Comparing only two levels of complexity, it is also adequate to refer to a respective micro- and macro-state.

Going from smaller to larger scales (i.e. from lower to higher levels of complexity), reveals entirely new properties [1]. Based thereupon, the term hierarchical reductionism refers to the description of a given system only on the basis of the next underlying level of complexity [24,25].

Adapting the language common for computer simulations and favored by the statistical mechanician, this reduction could also be called as coarse-graining, i.e. the resolution is reduced on purpose to lose the details of the lowest levels. To understand how a program works and what it does, it is enough to look at it on the level of the programming language. Considerations including every single transistor would not only make it substantially more complicated, it would not even result in a better understanding of the programs outcome.

If a fundamental understanding is the ability to trace back the highest scale behavior to the fundamental laws on the lowest scale, it should, in general, be sufficient to dissect (i.e. reduce) the hierarchy of levels into smaller subsystems. These subsystems need to be closed in the sense that its highest level is entirely determined by its lower levels. We will consequently call them “causally reducible systems”. Let L_i be different scales, the larger and more complex, the higher the index giving

If L₂ is completely described by laws of L₁, L₃ by laws of L₂, and L₄ by laws of L₃, then level L₄ is fundamentally understood in terms of laws of L₁. This, however, does not require directly describing L₄ in terms of L₁. In such an ideal system, the hierarchy of levels can be reduced to the level of interest plus its next lower one.

Unfortunately, in many cases, the choice of an adequate subsystem for reduction is far from trivial. Usually, a level L_i is not entirely determined by the laws from L_i-1. While it is true that single molecule behavior need not be considered to understand most hydrodynamic effects [26], single molecule arrangements will determine the shape of a macroscopic snow flake. Thus, in certain cases, one encounters direct links that span more than one layer of complexity.

Hence, one can coarse-grain the system of choice as long as one does not miss substantial lower level effects. Knowledge is also accessible from open sub-systems, yet it will not be sufficient to build a complete fundamental picture.

Since this work's focus lies on the cytoskeleton, a possible hierarchy could look like

Each higher level is formed by lower-level elements and the properties of every level vary from their respective lower level [27]. This article is roughly structured along three major cytoskeletal scales, the subcellular, cellular, and tissue level. Further sublevel hierarchies will be discussed in the respective synopsis sections (Sections 2.3, 3.4, and 4.6).

1.2.2. Functional modules

The concept of functional modules (or functional units) attracted much attention since the 1980s and has become a common term in many scientific fields, notably in biology and philosophy of science. More recently, the term seems to gain importance in the cytoskeleton-related soft matter community as well [28,29]. Modularity is closely related to the hierarchical reductionism introduced before, although it largely represents a different perspective and both descriptions typically result in a very different model language.

Hierarchical reductionism features an intra-modular perspective, whereas the functional modularity focuses more on the inter-modular perspective. In this sense, both concepts can largely be used complementarily (Figure 4).

Figure. 4.

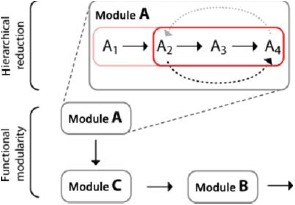
Different perspectives of functional modularity and hierarchical reductionism. While hierarchical reduction aims at dissecting a module's function according to different physical scales, the functional modularity perspective is focused on inter-module interactions regardless of their respective level of complexity.

According to Raff [30], modules in biology can be defined using four basic criteria being autonomy, hierarchical structure (possibly part of an even larger hierarchical entity), physical location, and connections to other modules. Following the first two criteria, a functional module to some extent corresponds to an aforementioned causally reducible system. Physical location as well as connections to other modules, however, only matter for functional modularity.

Whereas hierarchical reductionism aims at finding the minimal level that serves as a basis for a loss-free microscopic description of the system, the modularity concept establishes the functional module as an autonomous entity independent of its microscopic structure. As their name suggests, functional modules are chosen for and at the same time characterized by their function within a larger context. This means that the main focus clearly lies on the module's function and not so much on the module's internal architecture. Following the common usage, however, the distinction between functional modularity and hierarchical reductionism is far from being clear-cut and can in some cases even refer to the same approaches.

By reduction to interacting functional modules, it becomes possible to strongly reduce the complexity of a given system which nicely applies to biological systems [28]. In contrast to the hierarchical reductionism, a full microscopic understanding is not the most important aim but the more intuitive understanding of a bigger system.

1.2.3. Emergence

Whenever the concept of emergence is broken down to a single sentence explanation, people tend to adapt Aristotle's “the whole is more than the sum of its parts”. This is also the point where the consensus ends. When looking for more precise definitions, it quickly becomes apparent that they vary strongly between different fields but also from author to author [31,32]. For the purpose of this work, it suffices to define emergent properties as being present in the respective macrostate but absent on the underlying microstate. Emergence then is the process leading to novel emergent properties [23]. Here, micro- and macro- do not refer to any definite length scale but to different levels of complexity or different levels of abstraction (Section 1.2.1).

It should, however, be mentioned that numerous authors further distinguish different types or classes of emergent properties which sometimes helps to better delineate emergent phenomena [18,23,27,32].

On an intuitive level, emergence can be illustrated by numerous examples. The terms temperature or pressure commonly known from thermodynamics do make little sense when looking only at a single atom just like a single fish will never show swarm behavior. A very instructive illustration for emergent properties that goes beyond the most intuitive level is the cellular automata.

The microstates are the single cells which follow well-defined rules like in the famous “game of life” [33] (Figure 5). And even given an understanding of single-cell behavior, the interaction of several hundreds of cells leads to complex and unexpected behaviors. Many different algorithms are capable of producing highly complex patterns out of very simple rules (Figure 5) so that cellular automata became a common model for emerging complexity [34].

Figure. 5.

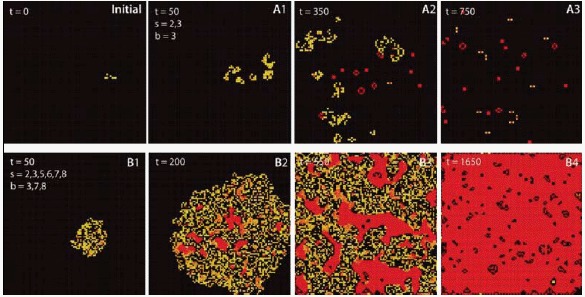
Cellular automata as an example for emergent behavior. The frames show the state of the system for two algorithms at different times and originate from the same initial state (initial). Squares (cells) are activated (born) when they have b neighbors and survive as long as they have s neighbors. Frames A1–A3 were obtained with Conway's Game of Life algorithm (s = 2, 3; b = 3), frames B1–B4 follow the Coagulation algorithm (s = 2, 3, 5, 6, 7, 8; b = 3, 7, 8). Images were generated with MJcell v1.5. Cells are color coded along their age with yellow for novel cells and red for old cells.

A similar analogy can be found in reaction–diffusion systems where again simple rules quickly lead to surprisingly complex behavior [35]. With both systems being highly complex and chaotic as well as regularly ordered patterns can be generated and both systems can be of dissipative as well as non-dissipative nature. Energy dissipation is directly linked to our understanding of self-organization and self-assembly.

1.2.4. Self-organization and self-assembly

Unfortunately, the two terms are often used interchangeably or are understood differently in the various disciplines. The rising importance of complex systems, however, demands a clear distinction of both terms. For the present work, we agree with the definitions given by Halley and Winkler [36] where the main distinction between the two terms is energy dissipation. While self-organization creates order on a macroscopic level through permanent energy dissipation, self-assembly refers to a decrease of the free energy of a given system (or sub-system).

In the field of biophysics, classical examples for self-assembly are phospholipid-based membrane and vesicle formation [37] as well as liquid–crystalline pattern in biopolymer solutions [38]. Well-known examples of self-organization are bacteria or mold pattern formation [39] but also include active cytoskeleton-based processes such as spindle organization [40], all of which constantly dissipate energy.

2. Subcellular level

The subcellular level of a cell reveals the full complexity of cellular organization. Although order is facilitated by the formation of intracellular compartments and functional units, cytoplasm and cytosol contain hundreds or thousands of different macromolecules and proteins which are subject to random, diffusive motion. So what exactly is meant by the commonly found statements describing cells as “highly organized” systems? Not in the least does this refer to precisely determined locations for single proteins or molecules. Instead the high order in cells is of stochastic nature where single elements undergo Brownian motion, and randomly bind, unbind, phosphorylate, etc. The ensemble of elements, however, maintains spatially and temporally well-located functional units and assures persistent compartmental organization.

A major source of intracellular organization is the cytoskeleton leading to spatial and mechanical structures. Even though it comprises hundreds of accessory proteins, the last decades, nevertheless, proved that already very simplified systems, ignoring most of the regulative mechanisms, give us surprisingly general insights into cytoskeletal functioning.

Coarse-grained approaches are particularly successful when applied in systems containing only few components which often allow strong hierarchical reduction. A good example is pure F-actin solutions where mechanical properties as well as spatial ordering can both be explained as emergent from the filament level. Both theory and experiments developed within the last 20 years finally led to the current fundamental understanding of semiflexible polymers like actin [41,42].

As soon as the system is no longer fully reducible to very few length scales, the situation quickly becomes exceedingly difficult. To date, we are not yet close to a fundamental understanding of the mechanics of transiently cross-linked networks. This is mostly because these systems resist extensive coarse-graining. Molecular elements like motors and transient cross-linkers directly affect the overall network properties and are at the same time network conformation and tension dependent.

2.1. Mechanics of semiflexible polymers

2.1.1. Semiflexible polymers

Polymers are repetitive macromolecular structures that are usually distinguished in three differing stiffness regimes: flexible, semiflexible, and stiff. At non-zero temperature, the polymer configuration is subject to thermal fluctuations. To properly characterize the polymer's resistance against thermal fluctuations, tangent vectors are introduced to each point on the polymer's contour s. The correlation of tangent vectors along the polymer contour decays exponentially with l_p as the decay constant:

For persistence lengths that are small in comparison to the polymer contour length L, polymers are considered to be flexible. Their resistance against thermal bending is low which leads to highly coiled random configurations. If l_p and L are roughly on the same order, the polymer is considered to be semiflexible and stiff enough to prevent coiling. When l_p is much longer than the contour length, the polymer appears as a stiff rod with only minor fluctuations of the polymer's configuration. Nature provides model polymers for all three regimes ranging from highly flexible DNA strands to comparatively rigid MTs (Figure 6).

Figure. 6.

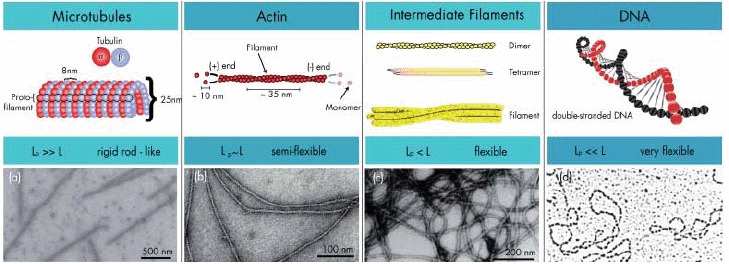
Stiffness regimes of the three major cytoskeletal components and DNA illustrating that mechanical responses highly depend on the filaments architecture. Electron microscopy images were taken from [45-48] with permission from Macmillan Publishers Ltd (a), US National Academy of Sciences (b), John Wiley & Sons (c), and the American Society for Biochemistry and Molecular Biology (d).

Unlike DNA or most synthetic polymers, the cytoskeleton biopolymers are fundamentally different in their mechanical properties since entropic or enthalpic interactions along their backbone increase their bending rigidity [43]. Modeling this type of polymers (or “filaments”) is highly demanding and assembled filaments cannot be easily described as a sequence of independent, non-self-avoiding monomers like in a freely jointed chain [44]. The differing stiffness regimes observed are far from trivial since protein backbones are almost identical in their molecular assembly with only the filament architecture as the main factor for the resulting mechanical properties.

Since the persistence length is a directly observable property, it is especially suitable for first characterizations. Isambert et al. [49], for instance, derived l_p for actin filaments from the analysis of either the tangent-cosine correlation function or the average transverse fluctuations of a series of recorded shapes of filaments. Actin filaments display a persistence length of around 10 μm [50,51], whereas MTs show a much longer persistence length, typically in the range of few millimeters [52].

Since l_p is temperature dependent, it is usually not considered as a material-defining constant. Thus, a new parameter called the bending stiffness κ is introduced by multiplying the thermal energy k_BT to the persistence length lp: κ = k_BTl_p. This material constant is essential to explain dynamic polymer chains within the worm-like chain model (WLC), a concept envisioning a homogeneous, isotropic, continuously flexible rod characterized by the bending stiffness κ [53]. By using this parameter, the polymer can be described as a differentiable curve r(s), where statistical properties are determined by the effective free energy [54]:

where κ is the bending stiffness and t(s) = ∂r(s)/∂s the tangent vector at the arc length s.

The question is why evolution chose semiflexible polymers to build up structures like the cytoskeleton. In contrast to very flexible polymers, semiflexible polymers arrange already for low volume fractions in a mechanically stabilizing fashion. This property can be described in analogy to a tent where relatively stiff rods with a low volume fraction result in a mechanically stabilized system. In addition, the polymers’ extended configuration allows myosin motors to move freely along the rather straight polymer backbone.

Of the three major classes of cytoskeletal polymers – MTs, actin filaments, and IFs – we will in the following mostly focus on actin and MTs although not without briefly discussing the role of IFs (Section 2.1.4). One reason is that actin and MTs are considered to be more dynamic structures that are more prominently involved in the overall cytoskeletal dynamics. Another reason, however, is that IFs are still much less understood in their functioning and their role for cellular processes (Section 2.1.4).

2.1.2. Assembly of actin filaments and MTs

In general, proteins are often described as polymers with an amino acid backbone, but in contrast to synthetic polymers, proteins are not randomly folded and their functioning highly depends on their well-defined tertiary structure.

Actin is a highly conserved protein that occurs ubiquitously in eukaryotic cells. Actin monomers (G-actin) have a molecular weight of 42 kDa and are divided into two halves by a central cleft with each of the halves containing two subdomains. In the cleft, either triphosphate (ATP) or diphosphate (ADP) adheres complexed with a divalent ion (Mg²⁺ or Ca²⁺). Under physiological salt conditions G-actin polymerizes into long, helical filaments. This filamentous form is called F-actin and the filaments are about 10 nm in diameter and in the absence of regulating factors have an exponential length distribution with a mean of 6–7 μm [55].

Because actin monomers carry a functional polarity, actin filaments generate a functional polarity as well. The two ends are called plus (or barbed) and minus (or pointed) end. The terms barbed and pointed end stem from the arrowhead-like appearance of heavy meromyosin labeled F-actin under transmission electron microscopy. The ability to undergo fast polymerization and depolymerization provides the opportunity to dynamically influence shape, and functions of a cell.

Energy dissipation through the decay of ATP to ADP allows the two filament ends to maintain different chemical conformations. This effectively renders actin filaments a polar structure in terms of their growth dynamics [12]. Since ADP-actin has a reduced binding affinity to neighboring monomers, the critical concentration at the minus-end is higher than at the plus-end. This allows a hypothetical steady state, where subunits dissociate from the minus-end and assemble at the plus-end at the same rate. Newly added monomers travel through the filament like on a treadmill until reaching the minus-end where they dissociate (treadmilling) [56]. Treadmilling hence illustrates a self-organizing non-equilibrium which can be altered or regulated by actin-associated proteins like illustrated in Figure 3 or reviewed by Bugyi and Carlier [57]. It should be noted, however, that the rates are generally a bulk (i.e. average) quantity, whereas growth and shrinkage of single filament ends undergo strong fluctuations in proximity to the critical concentrations. Vavylonis et al. [12] related growth rates and dynamics in simulations to ATP-actin and ADP-Pi-actin within filaments. For the plus-end at c_crit, they found a short ATP cap and a long ADP-Pi cap, which stabilizes length fluctuations and related these findings to the cap structure and dynamics. Near c_crit filaments alternate between ATP capped and uncapped states and the length fluctuation is pronounced, a mild version of the dynamic instability of growing MTs (see below).

Similar to actin, MTs represent another major constituent of the cytoskeleton able to undergo rapid growth and shrinkage processes. These stiff biopolymers clearly are an exception concerning their filamentous structure as well as their mechanical properties. Two types of heterodimers forming subunits, α- and β-tubulin, and organize into a head-to-tail fashion into polar protofilaments (PFs) [58]. Unlike actin and IFs, typically 13 or 14 (numbers from 8 to 20 have been observed) of these PFs assemble in sheets which eventually fold to form tubular superstructures termed MTs [59]. The tubular architecture is also responsible for a comparably high stiffness (three orders of magnitude larger than for actin).

MTs further display highly dynamic behavior. Nucleation of MT polymerization requires a third monomer type (γ-tubulin) forming a circular base for further dimer attachment. During polymerization, GTP bound to the β-tubulin subunits is hydrolyzed. The remaining GDP reduces binding constants, thereby destabilizing the MT and can only be substituted by GTP in free dimers after depolymerization. Binding and unbinding rates also differ at both ends of the MTs resulting in highly (plus) and less dynamic (minus) ends. Since GDP cannot be replaced within polymerized filaments, the so-called catastrophe events occur when hydrolysis proceeds faster than the addition of new GTP-decorated dimers. Connections between PFs break up and, due to conformational changes upon GTP hydrolysis, the free filaments bend outwards (Figure 7). After this process, single PFs can remain in stable ring-shaped or helical configurations, a first hint that longitudinal interactions are more stable than inter-PF bonds [60]. The subsequent detachment of tubulin monomers and thus shrinkage of the MT can only be reversed when new GTP carrying dimers bind and cap the filament in a process named rescue. Several investigations have aimed to reveal details of the capping process and the underlying molecular events. It has become clear that the process of capping is crucial for MT polymerization and presumably a few layers of GTP-tubulins at the growing end of an MT are sufficient to prevent catastrophe (see [61] and references therein). This fast alternation of growth and depolymerization phases, termed dynamic instability [62], leads to highly dynamic changes observed for MTs in vitro and in vivo.

Figure. 7.

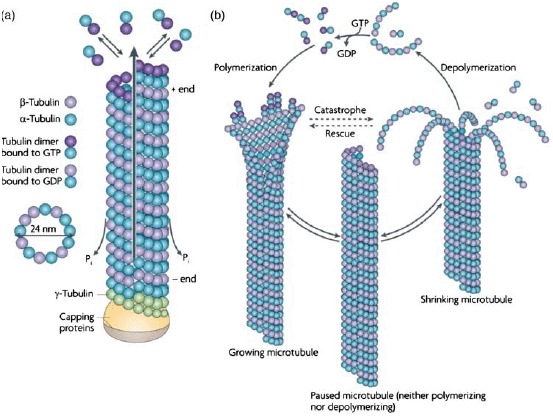
Assembly and dynamic instability of MTs. (a) In a GTP bound state, tubulin heterodimers polymerize into an oriented sheet of usually 13 PFs which eventually closes and forms a hollow tube. Upon polymerization, GTP hydrolysis occurs. (b) As soon as the free GTP-dimer concentration drops below a critical concentration, GDP-decorated dimers disassemble and the MT shrinks (catastrophe). This process can only be reversed by an increase of GTP-tubulin providing a capping layer (rescue) (Reprint from Conde et al. [63] with permission from Macmillan Publishers Ltd: Nature Reviews Neuroscience 10, 241, ©2009).

2.1.3. Mechanics of MTs

The internal structure of MTs was already described in the 1960s [64]. But only recent insights gained from advanced cryoelectron microscopy measurements allowed for a detailed understanding of the internal organization and the resulting mechanical behavior of MTs [65,66]. As mentioned before, dynamic polymer chains are often described by the WLC. This model, however, would oversimplify the anisotropic three-dimensional (3D) interactions between neighboring protein monomers that contribute to the macroscopic mechanical properties of the tubular filament. Various experiments provide evidence for non-isotropic responses to mechanical stress. From high resolution scanning force microscopy (SFM) measurements of fixed MTs, it is known that the radial stiffness of an MT is slightly higher when probed between PFs than on top of one individual filament [67]. Recent studies further reported a filament length-dependent persistence length for mirotubules deviating from the simplified worm-like chain behavior with short filaments appearing more flexible than long ones [68,69]. These findings are ascribed to anisotropies in the spatial alignment of the molecular monomers as well as in the binding strength between these subunits. The combination of high lateral deformability and longitudinal stiffness is an inherent property of assembled MTs and is crucial for their structural stability under in vivo conditions [66].

In general, measurements of an MT flexural rigidity can lead to very different results depending on the applied technique or the history of the MTs examined. Values for the persistence length of MTs hence range from hundreds of micrometers to several millimeters, thereby even exceeding values measured for carbon nanotubes [70]. Detailed reviews on techniques and results can be found in [71,72]. It was determined that not only a large family of microtubule-associated proteins (MAPs) or (de-)stabilizing drugs like taxol but also parameters as simple as polymerization speed can significantly influence the mechanical properties of MTs [52]. In the latter case, a higher flexibility was attributed to structural defects in the tubulin lattice, which are more likely to occur during fast polymerization phases.

Obviously, MTs are complex structures and up-to-date, there is no theoretical model that satisfyingly describes their mechanical properties on all scales. Departing from the WLC, different approaches have been pursued in order to fit experimental data from fluctuation and deformation measurements. As mentioned before, the simple worm-like chain assumes an elastic, homogenous rod and hence cannot account for the highly non-homogenous internal architecture of MTs. A convincing model describing MT mechanics was developed by Heussinger and co-authors [73–76]. They modified their worm-like bundle (WLB) model, which was initially applied to describe actin bundle mechanics and dynamics (Section 2.1.6).

In vivo interactions between MTs and other proteins are abundant and make MTs a versatile cellular machinery. A large variety of cross-linkers and other associated proteins has been identified which can cause bundling, influence polymerization speed, or (de-)stabilize the whole filament via altered binding and unbinding dynamics. The most important of these proteins are the family of MAPs, including the Tau protein. As an example, MAP2 and Tau share a common tubulin-binding domain and are typically found in neuronal cells where they cause MT bundling and support the initiation of axon (Tau) and dendrite (MAP2) outgrowth. Thus, they play a key role in neuronal development and malfunctions in Tau phosphorylation have been associated to Alzheimer's disease. A detailed description of the most important MAPs will follow in Section 2.2.3.

2.1.4. Interaction with IFs

Another main component of the cytoskeleton is named intermediate filaments (IFs) according to their diameter lying in between the diameter of actin and MTs (Figure 6).

Unlike actin and MTs, IF form a very diverse class of biopolymers [77]. While actin and MTs both include binding sites for nucleoside triphosphates resulting in structural polarity, cytoskeletal IFs show very different growth and shrinkage behavior.

IFs are formed by rod-shaped subunits that self-assemble in the absence of ATP and GTP into parallel dimers. Once polymerized, they remain stable even under conditions that would easily dissolve actin or MTs [78]. In contrast to actin and MTs, the subunits of IFs are not globular and the exchange of subunits occurs along the entire length of polymerized IFs [79].

Investigations of mechanical properties of individual IFs can be realized by atomic force microscopy. This revealed that many IFs have an unusual extensibility and show a strong resistance against breakage with individual filaments resisting strains up to 300% [80]. The resistance against breakage is dominated by strain hardening occurring above a certain threshold, which is different for each filament type [13]. This very particular characteristic of certain IFs was further observed to strongly effect the high-strain response of IF networks [81]. Presumably, those properties enable cells to bear large stresses and deformations.

At first, many of the more dynamic cellular processes such as cell migration and division are mostly attributed to the more dynamic actin and MT structures (Sections 3.2 and 3.3). IFs, however, display a highly complex interplay with actin and MTs [13,77]. Already the simple presence of IF networks was shown to render MTs more resistant against forces by lateral reinforcement [82]. Further, mixtures of entangled vimentin IFs and actin filaments yield a significantly greater dynamic shear modulus than their individual suspension at the same total protein concentration [83].

In addition to these rather indirect, passive interactions, various motors and linkers lead to more specific crosstalk of IFs with actin and MTs [77]. Based thereupon, IFs are essentially involved in many dynamic cellular processes such as elongating invadopodia in invasive cancer cells [84].

Although this illustrates that the cellular cytoskeleton is a compound material of actin, MTs and IFs, the key cytoskeletal biopolymers have largely been studied individually in the past. The complex cytoskeletal crosstalk, however, remains poorly understood and future research on compound structures will be necessary to better elucidate the close interplay between different biopolymer types in living cells.

2.1.5. Mechanics of actin networks

Although filament properties can directly be related to the monomeric level [85,86], it is not essential to take this lower level into account to properly handle terms like semiflexibility, or filament fluctuations. Starting from a mostly filament-level-based description, it is possible to further explore assembled structures on a larger scale. Depending on the filament density, one typically distinguishes between dilute, semi-dilute, and concentrated (or liquid–crystalline) solutions. In dilute solutions, filaments show all forms of translational and rotational motions nearly without any interactions. In the semi-dilute solution, however, these movements are confined by other filaments, which due to the dense-packing cross and entangle each other. In concentrated solutions, filaments start to show liquid–crystalline phases with increasing orientational order (Section 2.2.1).

The focus in this section will be on isotropic actin networks which fall into the semi-dilute regime. We will distinguish three fundamentally different situations: entangled networks formed in the absence of specific cross-linkers, rigidly cross-linked networks showing permanent connection points, and transiently cross-linked networks allowing cross-linkers to bind and unbind. A common tool to characterize biopolymer networks is to investigate their mechanical behavior by rheological measurements. Janmey et al. [87], for instance, were able to show mechanical differences for these biopolymers providing the possibility to relate them to their respective cellular functions. To investigate semiflexibility, homogenous actin structures are especially suitable since actin is considered a model for semiflexible polymers and hence will be discussed in this section.

In the absence of cross-linkers, single filament fluctuations are restricted only by the surrounding filaments forming a confining cage or tube (Figure 8). This is the core idea of the tube model providing an elegant phenomenological description of the complicated topological constraints in entangled solutions [44,88].

Figure. 8.

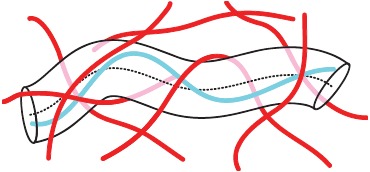
The tube model proposes that a polymer's movement within a semi-dilute solution is confined by other filaments. These confinements restrict the polymer's movement into a tube-like region.

While the tube at first began as a theoretical concept, its actual existence could even be visualized in experiments on semi-dilute F-actin solutions [89]. Experiments also proved that the tube displays substantial heterogeneities regarding the tube radius. This was taken into account by computer simulations [90] as well as by a systematic theory of tube radii fluctuations [91]. Consequently, this theory presents a more comprehensive characterization of the structural and elastic properties of stiff polymer solutions than conventional mean-field theory [92].

Entanglement notably restricts the filaments’ motion. Although filaments can freely reptate within the confining tube, it takes a comparatively long time (minutes to hours) before a filament fluctuates out of its original confining tube, strongly depending on its length [38,89,93].

When filament density increases further, the solution undergoes a transition from the isotropic or entangled phase to a nematic phase. Single filament diffusion within nematic regions was shown to be qualitatively different from entangled network diffusion [94]. Rod-like polymers show accelerated longitudinal diffusion in the nematic phase which can possibly be assigned to the tube dilation effect [44,95]. Actin solutions, however, display decreased longitudinal filament diffusion within the nematic phase which could be explained by orientational imperfections such as hairpins [94] or an abnormal slowdown due to counterions [95].

The remarkably slow diffusive motion of single filaments in both entangled and nematic phases results in extremely slow relaxation dynamics. Even below the critical density threshold for nematic ordering, actin solutions form nematic domains. At room temperature, these domains remain stable for weeks or months [94,96].

The entanglement results in trapped states leading to viscoelastic behavior, such that relaxation of imposed stress is strongly delayed [97,98]. With regard to in vivo situations, this at first seems counterproductive. Cells need to respond quickly in their morphology to external situations. An efficient way to circumvent the temporal restrictions imposed by filament entanglement is the use of molecular motors which induce active sliding of filaments past each other. In vitro experiments proved that active myosin motors can quickly fluidize entangled networks with drastic effects on the macroscopic behavior of biopolymer solutions [97] (Figure 9).

Figure. 9.

Tilted cuvettes filled with an actin gel allow to observe the gel's flow behavior. Left side: ATP depleted conditions lead to non-motile myosin motors that essentially function as cross-linkers. Right side: in the presence of ATP, the motors are active and increase the filament transport making the gel significantly more fluid-like [97].

Another possibility to avoid getting trapped in a highly viscous entangled state is to ensure a very fast filament turnover (i.e. fast depolymerization and polymerization of filaments). In cells, this is achieved by numerous accessory proteins addressing the polymerization dynamics [99,100].

Entangled networks of semiflexible polymers show very interesting physical properties. Unlike flexible polymer solutions which display viscoelastic properties that can largely be explained by entropic effects for a wide frequency range [44], semiflexibility gives rise to a more complex behavior of entangled networks [101]. Commonly, three different regimes are reported.

In case of very slow perturbations (i.e. for low frequencies), filaments have the time to partially leave their confinement and viscous flow dominates. For an intermediate regime of applied stresses on relatively short timescales, the entanglements resemble fixed cross-links and the network behaves elastic obeying Hooke's law (the so-called rubber plateau regime). At very high frequencies, an anomalous power-law increase of both storage and loss modulus was reported [102,103]. Hence, these different mechanical regimes arise only from arrangements of actin filaments without any cross-linking involved and can consistently be explained using the tube picture (Figure 8) [92,98].

Beyond the basic tube model, it has been shown that small variations in temperature, salt concentration, polymer length, and concentration can dramatically alter the network properties, especially in long-term equilibrium dynamics and nonlinear rheology [104]. Semmrich et al. distinguished three differing response regimes: for low stresses, the creep compliance is approximately constant, showing a linear stress–strain relation. Above a critical strain, a strain-hardening regime arises (elasticity increases with pulse amplitude) followed by an abrupt decrease of elasticity at a certain point. At this point, the response of the system ceases to be reversible and the system starts to deform in an irreversible fashion. This behavior is explained by an exponential stretching of the single-polymer relaxation spectrum of the classical WLC, which leads to the observed glass-like behavior during deformations (see below).

In particular, the newer, more refined theoretical models, for instance considering tube heterogeneities [91] or filament stickiness [104], result in a remarkable agreement between theory and experiment. These examples illustrate the major advances in certain areas of biological physics that clearly go beyond a first qualitative understanding.

While entangled networks depend on only few parameters (filament density, persistence length), the system's complexity increases notably as soon as additional filament–filament interactions are introduced, e.g. in form of rigid cross-linkers. Changes in cross-linker density strongly influence the overall mechanical response of actin networks (Figure 10) [14].

Figure. 10.

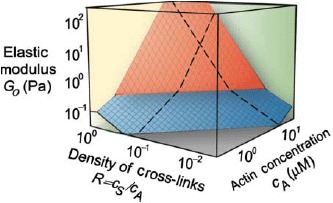
State diagram showing variations of elasticity due to changes of the actin concentration or changes of the cross-linker density (c_s represents the concentration of the cross-linker scruin). By varying these factors, the elastic modulus can be varied by more than three orders of magnitude. The elasticity can be distinguished in two different regimes: a linear regime arises for small values of R and c_A up to large strains without any stiffening effects (blue plane). A nonlinear regime arises for large values of R and c_A even under small deformations (red plane). The elasticity increases under increasing strain. Reprint from Gardel et al. [14] with permission from AAAS.

A popular approach toward understanding permanently cross-linked actin networks was presented by MacKintosh et al. [105]. This approach refers to the rubber plateau regime mentioned above and focuses on chain segments between two entanglement (or cross-linking) points. As a major difference to entangled solutions, rigid cross-links allow for longitudinal deformations of individual filaments under strain [101]. Since semiflexible polymers show anisotropic response to applied forces [54], affine deformations are no fully valid assumption which clearly complicates the question of how stresses and strains are transmitted within networks [106]. Cross-linked networks further differ from entangled solution in their internal architecture. Whereas in the absence of cross-linkers, the distance between entanglements (entanglement length) is determined by persistence length and filament density [98], the number of filament–filament-links as well as their spatial organization are additional quantities in cross-linked networks. Cross-links typically imply highly non-isotropic network architectures [107] that differ substantially from isotropic networks as assumed in the case of entangled solutions. This renders mean-field approaches difficult. Thus, most microscopic modeling attempts were performed using two-dimensional (2D) (e.g. [106,108,109]) or 3D computer simulations (e.g. [110–112]).

In the simplest case, the cross-linker itself does not contribute to the viscoelastic response of the network and some cytoskeletal cross-linker like scruin can indeed be considered to induce rigid cross-links [14,113]. Experiments on reconstituted actin systems demonstrated that the mechanical properties of the actin networks are highly sensitive to a changing cross-linker density (Figure 10) [14,113]. Varying the cross-linker density at constant actin filament concentration, the low-frequency elastic modulus was observed to span several orders of magnitude (from 0.1 to 300 Pa) [113].

In general, however, parameters like binding affinity, cross-linker length or stiffness can be expected to significantly alter the network behavior. Kasza et al. [114] reported a qualitative difference of elastic responses of networks formed by large, compliant and small, rigid cross-links, respectively. Their experimental data revealed that the elasticity of networks formed by long, compliant cross-links can support large shear stresses due to their pronounced nonlinear strain-stiffening and differs notably from networks formed by rigid cross-links. This work was complemented by theoretical modeling using an effective medium approach [115]. In contrast to rigid cross-links, the mechanical properties of flexible binding proteins have to be accounted for when considering the properties of the whole network. At a certain strain, they become effectively rigid leading to a stiffening effect. For even greater forces DiDonna and Levine [116] reported an additional state where the network is softening under shear as a result of stress-induced domain unfolding of several cross-linkers.

Stiffness variations due to cross-linking proteins describe a passive behavior correlated to properties of the involved components. A very intriguing additional possibility is active alteration of network properties by employing molecular motors such as actin-associated myosins. These biopolymers can bind to actin and generate forces of order 1–10 pN [117] by hydrolyzing ATP. This activity enhances the longitudinal filament fluctuations until the ATP reservoir is depleted. At this point, an abrupt transition to a passive rigor state can be observed and a second steady state arises with rheological characteristics of passive semiflexible networks. Due to myosin motor activity, the network is in a non-equilibrium state leading to unusual mechanical properties that were first approached using active viscoelastic theories [118–120]. Experiments revealed drastic effects of motor activity, including enhanced fluidization [97] or in the presence of additional passive cross-links a 100-fold stiffening (together with highly nonlinear elastic responses) [117,121]. Therefore, the motor activity can dramatically increase the network's bulk elasticity moduli by tensile stress [121]. Cross-linking proteins provide sites for mechanical anchorage and enable the buildup of internal tension by myosin motors. The resulting pre-stress induces strain hardening of networks and actively alters mechanical properties.

In addition to the cross-linker structure (and stiffness), cross-linking proteins in most cases only bind transiently to binding sites and differing cross-link concentrations lead to various larger-scale architectures (Section 2.1.7). Binding is followed by unbinding events depending on the on- and off- rate of each cross-linker type. These events, however, are force-sensitive and hence depend on the applied external shear or internal motor activity [122]. This force or strain-dependent binding behavior results in another closed feedback loop between the molecular level (cross-links) and the network level which essentially complicates a reduction of the system. Precisely, these complex feedback mechanisms further imply a complicated dependence of the network behavior (and architecture) on its mechanical history. Certain aspects, however, appear to be accessible to further abstraction [123,124]. First, entanglements in semi-dilute filament solutions can also be regarded as transient cross-links (depending on the frequency range).

A more sophisticated way of approaching transient cross-links represents the glassy worm-like chain (GWLC) model developed by the group of Klaus Kroy. The GWLC is based on the WLC but further includes interactions of the test polymer with the surrounding network [125]. This can, for instance, be a sticky, attractive potential. Although of phenomenological origin, this stickiness could be interpreted as transient linking. The predicted network behavior is characterized by WLC dynamics on very short timescales and a subsequent stretched logarithmic relaxation [123]. Interestingly, the GWLC hence potentially allows describing the transitions from filamentous solutions to permanently cross-linked networks. An additional extension of the model accounts for nonlinear inelastic mechanics due to bond-rupture which result in network fluidization at large strain pulses [123,126].

Similar to the aforementioned analogy between entanglements and rigid cross-links for fast deformations, this reduction to the filament level naturally cannot fully account for cross-linking as an independent parameter. Due to the reduced complexity, the number of cross-links is related to the filament density and stiffness. Working with a mean-field approach, it is furthermore necessary to ignore the network's anisotropic architecture.

In summary, transient networks are still far from being entirely understood and to date there is no fully comprehensive picture able to relate the network behavior to the microscopic level.

2.1.6. Actin bundles

Isotropic networks are only one possible arrangement for actin filaments into higher structures. Filaments can further be grouped into anisotropic bundles showing a very different behavior in comparison to networks. In living cells, bundles are commonly observed in different contexts fulfilling various key functions, including the generation and transmission of contractile forces (stress fibers), and the sensing of chemical or mechanical cues (filopodia) (Figure 11).

Figure. 11.

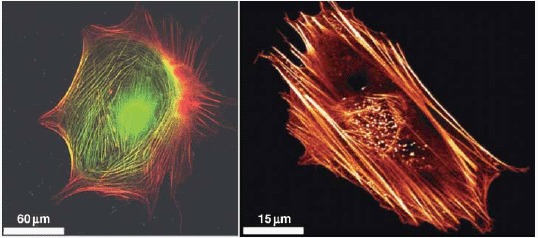
Actin stress fibers in living cells (left side: a fibroblast with labeled myosin (green) and actin (red), right side: a fibroblast with labeled actin) fulfill important tasks like mechanical stabilization. The development of cellular stress fibers is preferred by 2D cell cultures. Images were taken by Thomas Fuhs and Daniel Koch.

The WLC, with κ as the defining property, has become the standard model for semiflexible polymers like actin (Section 2.1.1). Filament bundles, i.e. bundles of WLCs, however, cannot be reproduced trivially from this model. The theory had to be refined leading to the worm-like bundle model (WLB). In addition, the anisotropy of the bundles does not allow for rheological bulks measurements and micro-rheological methods need to be applied.

Bundles are usually formed by various types of cross-linking proteins adding a new parameter to the material-defining properties. Bathe et al. [74] showed that the bending stiffness κ_b is state-dependent and derives from a generic interplay between the high stiffness of individual filaments and their rather soft sliding motion, indicating a sensitive dependency on time and length scales for responses against external influences [75,76]. The WLB model connects the effective stiffness of the bundle with parameters of its components namely bending and stretching stiffness of the individual filaments as well as density and shear stiffness of cross-linkers and inter-filament spacing [75].

Within the WLB model, the actin-binding proteins (ABPs) are classified as fully coupled or decoupled cross-linkers. In the fully coupled state cross-links resist shear stress and rigidly glue filaments together, leading to a bundle's response dominated by filament stretching. The filament-stretching displacement increases linearly through the bundle cross-section like in a homogeneous beam and κ_b shows a quadratic dependency on the number of filaments forming the bundle (κ_b ∝ N²). In the decoupled state, filaments are bent independently under stress, because the cross-links provide no resistance to shear and can freely tilt or stretch causing a linear dependence of κ_b on N (κ_b ∝ N²). κ_b can be determined by the thermal fluctuation of the bundle [127], a measurement that can be used to investigate the crossover between the decoupled and fully coupled regime.

The properties of the accessory proteins significantly influence the actin structure itself. Strehle et al. [128] demonstrated that deformed actin bundles adapt to their stressed configuration by rearrangement of the transient cross-linkers through binding/unbinding events (Figure 12).

Figure. 12.

Actin bundles formed by α-actinin are time-dependent mechanically stabilized in their deformed position due to rearrangements of the dynamic cross-linker within the bundled structure (scale bar 5 μm). For a deformation time of 5 s, the bundle relaxes to its original position since the time is not sufficient for considerable rearrangements while for a 1000 s deformation, the bundle is observably stabilized in the deformed state [128].

Apart from addressing the mechanical properties of actin bundles, the WLB model can be used to describe MTs as bundles of PFs arranged in a hollow cylinder geometry [76]. The model suggests that the previously determined dependency of MT stiffness on the length of the filament [68] can be explained as a secondary effect of the mode dependence of κ_b.

2.1.7. Composite structures

Depending on density, packing, and cross-linker characteristics, bundle and network structures show a very broad range of mechanical behavior. Further opportunities to tune the mechanical properties of biological matter result when combining networks and bundled structures. The resulting structural polymorphism depends on concentrations of involved constituents and not just on the type of these constituents. Lieleg et al. [129] illustrate that a broad range of mechanical response is achieved by various arrangements on the molecular level. These structures comprise networks, bundles, and combinations of both elements. Since modeling transiently cross-linked networks is already extremely complicated (Section 2.1.5), modeling composite conformations is likely to be possible only for very limited cases.

Hence, higher ordered network structures display a large spectrum of mechanical properties depending on only few generic underlying structures like actin filaments and molecular agents like cross-linkers or motor proteins. This enables a cell to cover a broad range of tasks with only few basic, highly tunable components. Therefore, complexity due to various interactions between different levels is lucrative for nature in many ways although difficult to model for scientists as it obstructs simple abstraction (see also Section 1.2.1).

In addition, and unlike synthetic polymers, different biopolymers further allow polymer mixtures enabling the formation of compound structures, which further increases the system's complexity remarkably as illustrated in Section 3.1. Although certainly present in the cellular context [77,130], compound structures comprising combinations of actin, MTs, and IFs are only beginning to be studied in bottom-up systems.

2.2. Complex pattern formation

On the subcellular level, many different forms of spatial and temporal orders need to be created out of a vaste reservoir of molecular building blocks. This is done by either self-assembly or self-organization (Section 1.2.4). Within the last decades, advanced imaging techniques as well as reconstituted systems revealed many important examples for both self-assembled and self-organized structures within living cells [131,132]. Prominent examples which will not be reviewed in this text include membrane systems. Reviews on these topics can, for instance, be found in [37,133].

Here, the focus will lie on cytoskeletal pattern formation, i.e. the emergence of cytoskeletal order. As soon as the emerging order can directly be associated with network architecture, this will naturally affect the mechanical properties as well, i.e. structure formation and structure mechanics are closely related. Yet biopolymer networks have so far mainly been investigated using rheological means (Section 2.1.5) and much less is known concerning structure formation and dynamics [96,134].

Early in vitro examples for pattern formation were liquid–crystalline order and regular stripe pattern found in both purified actin and MT solutions [135–137]. The variety of accessible patterns dramatically increases when integrating molecular motors and cross-linkers and includes the spontaneous formation of complex structures like asters, spindles, vortices, or regular networks.

2.2.1. Random networks and nematic phases

Despite being strongly reduced with respect to cell-like situations, pure biopolymer solutions already possess a multi-faceted behavior which constitutes the fundamental basis for cytoskeletal systems of higher complexity. Properties like orientational order or viscoelastic behavior can only be assigned to the network or filament solution level but are absent on the underlying single filament level, therewith they are clearly emergent properties. Pure polymer solutions without accessory proteins have the advantage that details from the molecular level can largely be ignored and ordering phenomena can be studied on the basis of the single filament level.

The aforementioned rigidity of biopolymers like actin, results in a mainly extended configuration. In a first-order approximation the polymers in solution can consequently be approximated by rigid rods. Since they typically possess a large length-to-diameter ratio, liquid–crystalline behavior can be expected even at moderate volume fractions. This was indeed among the first ordering phenomena observed with purified biopolymer systems. In both concentrated actin and MT solutions, nematic order could be detected via polarized light microscopy [136,137].

Usually liquid–crystalline order is described using an order parameter S that is defined based on the second-Legendre polynomial. The polynomial includes the angle between the elements and the local director which is a vector pointing in the preferred direction of the surrounding elements [38,138]. Polarized light is one possible measure to directly probe local alignment of filaments and to access S. Other methods to determine the order parameter experimentally are single filament imaging and X-ray scattering [139].

For ideal liquid–crystalline materials of rigid rods, a clear-cut first-order transition between isotropic (I) and nematic (N) phase is expected when going from lower to higher densities [38]. Semiflexible actin filaments do not show such ideal liquid–crystal behavior. Recent studies revealed the importance of filament length on the nature of the phase transitions. For actin filaments longer than 2 μm, a continuous I–N-phase transition is observed, while for shorter filaments, an authentic first-order transition occurs [140]. It was hypothesized that this might be due to suppressed relaxation of individual filaments in entangled solutions or filament length polydispersity [139,140].

The onset concentration for nematic ordering strongly correlates with filament length [135,140–142] and various boundary conditions. Flow or shear stress generally tend to align filaments and hence strongly reduce the onset concentration [143,144]. The same is true for surface effects which drastically increase the tendency for nematic local alignment [145]. The basic nematic ordering is established by self-assembly, but what about more complex patterns observed in liquid–crystalline biopolymer solutions?

Commonly observed distortions of the nematic director are the so-called zebra stripes with periodic alterations of the director angle. Zebra stripes have been reported for both actin and MT systems [135,146]. While there has been some speculation that active mechanisms could lead to such order [147], experiments soon could show that zebra stripes can be formed in non-dissipative systems [135]. Gentry et al. [143] indeed showed that zebra stripe patterns originate from shear flow, hence active processes are not necessary for stripe formation. Therefore, these patterns are self-assembled, too. Fluorescence imaging in combination with polarization microscopy revealed that zebra stripes consist of alternating domains of highly bent filaments that correspond to low filament density and low nematic order next to domains of straight filaments at comparatively large filament density and nematic order [143].

2.2.2. Linker and motor-induced networks

In vitro experimental evidence like network fluidization or MT pattern formation both in the presence of molecular motors demonstrate that active elements result in entirely different qualitative behavior and ordering [40,97,148,149]. It has consequently been described as a new class of materials often named active soft matter or active systems [119,150,151].

The previously described entangled networks or liquid–crystalline systems were all non-dissipative. More complex patterns such as the mentioned zebra stripes arise when we apply forces such as shear stress or flow. These forces, however, are applied at the boundaries, thus the system itself remains passive. In active systems, energy uptake is located on the scale of the single elements.

At high filament density, addition of active molecular motors creates the so-called active nematics which differ profoundly from the aforementioned passive nematics [150,152]. Early theoretical studies found that pure nematic order of uniform orientation as in passive systems becomes unstable in active systems [152,153]. This results in long-wavelength fluctuations of the axis of orientation, e.g. in the form of a splay or bend pattern [150,153]. When focusing on a more local order, it was shown that motor-induced filament transport in 2D and 3D generates a higher tendency for local alignment [154,155]. In vitro experiments using a myosin-coated surface and actin filaments in solution indeed confirmed these predictions and revealed a spontaneous formation of domains of highly oriented filaments. At low filament densities, the phase remains disordered and filaments perform random-walk like motion, whereas above a critical density threshold a transition to an ordered state was observed [5,156]. Schaller et al. [5] in addition report that actin filaments form active polar patterns above a critical density, which are not seen in the results reported by Butt et al. [156]. These patterns include formation of spirals or swirls in agreement with theoretical predictions made for active polar gels [157]. Moreover, depending on the filament density complex dynamic patterns form as, for example, swarm-like moving clusters and density waves [5] (Figure 13).

Figure. 13.

Depending on the filament density different dynamic patterns emerge when actin filaments move over a myosin-coated surface. Few characteristic examples are shown here: swirl (a), swarm (b), and waves (c). Figure was adapted from [5] (with permission from Volker Schaller and Macmillan Publishers Ltd: Nature Reviews Neuroscience 467, ©2010).

A more classical case for a self-organizing system in the cytoskeleton is the MT aster or spindle formation that is part of cell division (see also Section 3.2). Spontaneous aster formation of MTs with molecular motors was already observed in early in vitro experiments [149]. Asters are assemblies of many biopolymers or biopolymer bundles radially pointing outwards from the aster center. Several scenarios further lead to polar asters where equal polymer ends point either in- or outwards. The robust self-organization into aster-like structures is of great importance to further understand the cellular processes involved in cell division (Section 3.2). Later experimental studies revealed that in addition to asters, reconstituted MT-motor systems allow formation of other complex patterns like vortices [40,158].

Theoretical studies approached biopolymer-motor mixtures using different continuum models [119,155,159,160] or microscopic descriptions [154,158]. The models developed show a large variability and form an instructive example of hierarchical reduction or coarse-graining (Section 1.2.1).

Arguably, the most intuitive approaches are microscopic models that typically form the basis for computer simulations [154,158] (Figure 14(a)). Although microscopic models typically contain more low level details than continuum models, rigorous abstraction is still quintessential for a proper use as a model system.

Figure. 14.

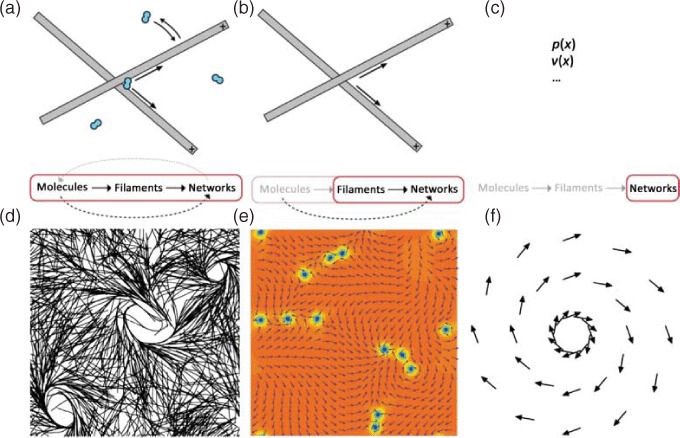
The interplay between MTs and respective motor proteins can be modeled on different scales. Microscopic models (left panel) allow tracing back the network level behavior to molecular interactions but do not reach the level of abstraction needed for a fully analytical description. Macroscopic models (right panel) are much more phenomenological in their origin but they are able to deliver analytical descriptions. A certain kind of compromise is presented by mesoscopic models (center panel) that start from the molecular level but use strong coarse-graining, (d) was adapted from [161], (e) was taken from [159] (with permission from Igor Aronson), (f) was inspired by [157].

A second class of models applied in this context also originates from the microscopic level. The respective equations are then coarse-grained to go from a single element description to a continuum description. Filament and motor density together with mean orientation replace individual elements (Figure 14(b)). Thus, the higher complexity level description is derived from lower level equations [134,159,162].

In contrast, hydrodynamic theory starts on large length and time scales. It depends on phenomenological parameters and hence is largely independent of microscopic details [157,163] (Figure 14(c)). Theories derived from microscopic properties are mostly restricted to their respective macroscopic system, i.e. the next higher level of complexity. Hydrodynamic theories on the other hand are generic and have successfully been applied to a large variety of situations, with a wide variation in the size of the components from system to system [157,163,164] (see Section 3.3.3 for their use on the cellular level). This, however, goes along with the main limitation of hydrodynamic descriptions. Due to their large-scale perspective, macroscopic behavior cannot be traced back directly to microscopic elements (Figure 14(c)).

Aster formation was obtained in both MT and actin in vitro systems and could in most cases be attributed to motor activity. Since both systems are built from polymer fibers and molecular motors that move along the filaments with defined direction, this seems to suggest that both systems function in a completely analogous way. Surprisingly, however, a closer look at available experimental data indicates significant differences between MT and actin systems. While for MT systems, aster formation was observed in the presence of active molecular motors, i.e. as a dissipative phenomenon [40], actin–myosin solutions remain isotropic [148]. In actin systems, myosin motors can only create asters in the presence of cross-linkers, be it ATP depleted myosin [148] (Figure 15) or an additional cross-linking protein [165]. An analogous situation arises for MTs when two opposing classes of motors interact with MTs [158].

Figure. 15.

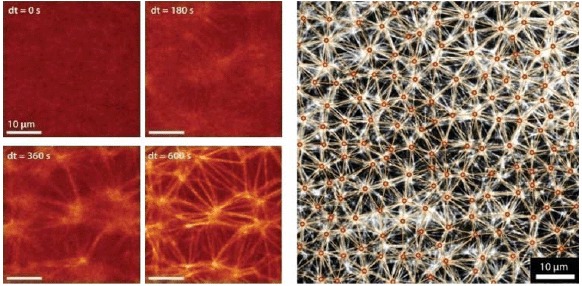
Counterion-induced formation of aster-based actin bundle networks in confined droplets. Left side: snapshots showing the transition from an actin filament solution (at dt = 0 s) to a stable actin bundle network following a slight increase in counterions above their critical concentration for inducing filament aggregation. Right side: aster-based bundle networks obtained by counterion-condensation appear highly regular regarding the average aster distances. Images were taken using confocal microscopy (left side) and epi-fluorescence microscopy (right side). Figure was adapted from [144].

Very recent bottom-up experiments, however, demonstrate that active motor-based systems are not even necessary to form aster structures [144]. Using counterions as switchable model cross-linkers, it was possible to generate regular aster-based bundle networks in the complete absence of molecular motors (Figure 15). Asters can hence not only form by self-assembly but also by non-dissipative self-assembly. Further, the study shows that initial anisotropies in the filament solution prior to cross-linking imply significant changes of the final network architecture [144].

The following section will further focus on various possible internal feedback loops for cytoskeletal self-regulation.

2.2.3. Inherent self-regulation of the cytoskeleton

Robust self-assembly or self-organization of ordered structures is a key feature of cytoskeletal organization. The formation and disassembly of such constructs, however, must somehow be regulated to allow communication and response. As argued earlier [166], the overall organization cannot solely be established by straightforward top-down actions. The enormous complexity resulting from the large number of MT or actin-related proteins demands inherent self-regulative mechanisms. Altogether, these inherently contained feedback loops permit autonomous functional units in the form of actively responding polymer systems as illustrated by experiments on cell fragments [17] (Section 3.3.3).

Both MTs and actin assembly and disassembly are not only regulated by monomer concentration and available triphosphates but strongly react to numerous associated proteins termed ABPs and MAPs.

In the case of actin, polymerization dynamics are drastically affected by end-capping proteins, polymerization enhancers (e.g. formins) or filament stabilizers (e.g. tropomyosins), depolymerization enhancers (e.g. cofilin), and induced filament severing, (as depicted in Figure 3). Numerous MAPs can induce similar effects for MTs, again including stabilization (e.g. MAP2, MAP4 [167,168]), destabilization (e.g. oncoprotein-18 [169]), or severing (e.g. katanin, spastin, and fidgetin [170]). Depending on the accessory proteins, biopolymers can display very high turnover dynamics, a unique characteristic when compared to synthetic polymers.

In addition to the accessory proteins that influence the polymerization dynamics, and the aforementioned cross-linking proteins, motor proteins form another fundamental class of actin or MT-related proteins. Those motors are molecular machines consuming energy from ATP hydrolysis that are able to actively move along actin filaments or MTs. Motors have a drastic influence on the spatial organization of actin and MT systems (see also Sections 2.2.2 and 3.2) and are further essential for intracellular cargo transport and cellular force production.

Keeping in mind that the so far mentioned actin and MT modifying factors only represent a small excerpt in comparison to a typical in vivo situation, it is obvious to ask how these interactions are orchestrated. It cannot be expected that this could easily be achieved by production and recruitment of new protein material since this would be too slow and inflexible. Localized trigger mechanisms are more likely to initiate coordinated cytoskeleton response. Molecular mechanisms of that kind have indeed been revealed by in vivo and in vitro experiments.

For all known cellular systems actin polymerization, for instance, is triggered in a comparable way. Spontaneous, uncontrolled nucleation is strongly suppressed by accessory proteins (e.g. profilin, thymosins) which allow monomeric actin and other building blocks to remain freely available at high concentrations at all times. The bottleneck of actin nucleation is then utilized by at least two types of highly efficient nucleation initiators, Arp2/3 and formins [57,99].

Arp2/3 can be present in a passive and an activated form. Activation was found to be triggered by various signaling pathways, thus Arp2/3-induced actin polymerization can directly be linked to chemical cascades that potentially connect to higher level actions [171].

One might be tempted to look for similar signaling pathways for all pronounced spatial and temporal forms of cytoskeleton organization. These signaling pathways correspond to a top-down hierarchy meaning that higher levels trigger specific reactions on the molecular scale. This might appear intuitive because it resembles man-made machineries. However, mammalian cells only include about 20 different members of the Rho-family of signaling molecules [171], not enough to exclusively trigger each of the many more ABP and MT-binding protein. Hence not every little detail will be directly addressable by an own specific signaling pathway.

Therefore, our picture of cytoskeletal organization is somewhat different. Directly triggered activation pathways are restricted to few key mechanisms (like nucleation), and most organization is based on inherent self-organization or assembly [166]. Inherent here means that structural elements display at the same time regulative functions, thereby implementing closed feedback loops. This supports the common view that molecular complexity can often be reduced to largely autonomous functional units that interact via specific chemical pathways connected to few key regulators. The signaling pathways hence are predominantly used to trigger entire functional entities and certainly play an essential role in initiating large-scale cytoskeleton response [57,171,172]. In the following, however, signaling pathways will be largely ignored since they are usually not encoded inherently within the cytoskeleton's functional components. For a further classification following Huber and Käs [166], we want to summarize fundamental principles of inherent self-regulative organization (Figure 16). These mechanisms all originate from the subcellular level and in the form of numerous combinations of these mechanisms, they seem to account for much of the higher level behavior.

Figure. 16.

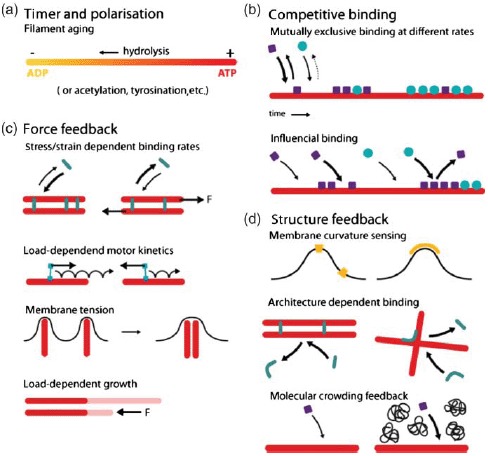
Sketch presenting the five fundamental regulative principles we focus on. For each principle, one or more generic examples are illustrated. Figure was adapted from [166].

2.2.3.1. Timer mechanisms and polarization

A very common key regulator for organizing the cytoskeleton is triphosphate (ATP or GTP) hydrolysis. Hydrolysis results in slightly changed monomer configurations for the unhydrolysed (new) compared to the hydrolysed (older) state. These differing configurations de facto act as a timer mechanism since many accessory proteins have strongly altered-binding behavior for the different nucleotide-bound monomer states [57]. Several ABPs like cofilin or Arp2/3 either avoid the newer monomers (e.g. cofilin) or the older monomers (e.g. Arp2/3) of a filament. Others behave very differently when bound to either new or hydrolysed subunits (e.g. coronin) [173]. This subunit sensitive protein-binding behavior or functioning allows to specifically discriminate the faster growing end from the rest of the filament. Especially for MTs, where disassembly occurs in the form of characteristic catastrophes, end tracking is a key issue.

An important subgroup of MAPs is ubiquitous in eukaryotic cells and shows specific activity at the dynamic ends of MTs and is hence termed plus-end tracking proteins (+TIPs). A number of structurally unrelated families of +TIPs have been identified including motor, non-motor, and transmembrane proteins [174]. Two fundamentally different concepts can be distinguished, polarity based and timer based. Using the MT's polarity, some MAPs actively follow the growing ends, such as kinesin8 regulating MT length by actively supporting depolymerization at the plus-end. Single kinesin8 molecules reside at the tip until another one arrives and pushes them off. The detaching molecule removes one or two tubulin subunits thus enhancing depolymerization. The flux of kinesins toward the plus-ends depends on the overall length of the MT and contributes to a length-dependent depolymerization rate [175].

Other MAPs undergo repeated binding and unbinding cycles with a higher affinity for newly polymerized tubulin and thus remain at the very tip, unaffected by polymerization-dependent growth. In the diverse group of +TIPs, each member has, according to its function, a characteristic MT-binding domain. +TIP function and activity range from influence on tubulin assembly to the transport of functional complexes toward cellular adhesion sites using polymerizing MTs as carriers. It is believed that many +TIPs bind competitively. They can also bind to each other and mutually influence their accumulation at plus-ends.

A quite unique way of coupling load to the dynamic ends of MTs can be observed during mitosis of yeast cells where the Dam1 complex connects kinetochores to MT tips through phases of assembly and disassembly [176]. The ability of the Dam1 kinetochore complex to stably attach to the dynamic end of a MT assumingly results from its geometric features with ring-shaped structures clasping around the tubule. Due to the curling of PFs during depolymerization phases and the closure of the tubulin sheet during polymerization, these rings move back and forth with the tip. Less familiar than triphosphate hydrolysis are post-translational modifications forming another important class of aging mechanisms that just as well influence the binding of MAPs [177,178]. These modifications are caused by removal or addition of amino acids from or to tubulin subunits. Thereby, tubulins are differentially marked and binding affinities for certain MAPs are altered.

Prominent examples are axonemal structures in cilia and centrioles, where extensive modifications lead to the assembly of double- or triple-MTs. Spindle MTs in mitotic cells are also highly modified and can be clearly distinguished from native astral MTs. For a more detailed description of post-translational modifications and their biological function, see [178].

2.2.3.2. Competitive and cooperative binding

Interactions between different accessory proteins as well as interactions between accessory proteins and the filament often lead to competitive or cooperative binding. Competitive binding occurs in many different ways. It can be a powerful tool to create gradients and functionally distinct subsections, in particular when combined with a timer mechanism or newly polymerized material. Different binding kinetics of accessory proteins in combination with mutually exclusive binding already induce pattern formation, for instance, in the actin networks of migrating cells [179]. Another mechanism for competitive binding can be influential binding (Figure 17) meaning that one species of accessory proteins alters the binding or unbinding characteristics of another species.

Figure. 17.

Basic reaction kinetics can already enable the formation of a large variety of two or more overlaying temporal gradients. In conjunction with polar structures such as MT or actin filaments, these gradients translate into spatial gradients. Figure was taken from [166].

A variety of studies revealed the importance of competitive binding in cellular processes. At the leading edge of migrating cells, different network sub-domains with their characteristic dominance of particular accessory proteins can thereupon be explained without a need for further external triggering [179,180]. In addition, it was discovered that in yeast, competitive binding of fimbrin and tropomyosin further determines functioning of cofilin and myosins, leading to entirely different actin-based functional units [181,182].

Analogously, MAP binding to MTs is modulated by regulative proteins (mapmodulin, MARK family of kinases). Mapmodulin is a phospho-protein and affects tubulin-MAP interactions by binding to the tubulin-binding sites of MAP2, MAP4, and tau. It assembles in trimers and is mainly found in the cytosol, but only at low concentrations in the cortex [183]. The microtubule affinity regulating kinase (MARK) family of enzymes is another fundamental regulator of MAP activity. Like other protein kinases, they are able to transfer phosphate groups from donors like GTP to a specific substrate, in this case, tau and related MAPs. MARKs regulate MT dynamics and polarization in neurons and play a key role in cell-cycle regulation, intracellular signaling, and transport [184].

An intriguing example of cooperative binding was found in the case of cofilin binding to actin filaments. Cofilin alters the helical twist of an actin filament [185] and thereby facilitates further binding of cofilin to neighboring subunits [186]. Since cofilin's binding cooperativity is mediated by the filament's twist, it can also be considered a structure-sensing mechanism.

2.2.3.3. Force feedback

It appears trivial that forces will influence the cellular organization. We will later come to the response to external forces, i.e. mechanosensitivity (Section 3.3.6). First, the focus is on closed intracellular loops, where forces indeed function as self-regulative mechanisms. They originate from the cytoskeleton and influence it at the same time. These intracellular forces are generated by molecular motors or assembly/disassembly of filaments and closely interplay with numerous cytoskeletal force feedback mechanisms.

Both actin and MT growth dynamics are regulated by forces acting on the polymerizing filament. Opposing forces can result in a strongly decreased or even stalled growth velocity [7,187]. While for single actin filaments the force-dependent dynamics can be described by the Brownian ratchet model [188,189], multiple growing filaments make the situation substantially more complicated [190–192]. Particularly for MTs similar force-sensing assembly dynamics seem to be extremely important for cellular regulation. Dynamic instability is typically characterized by the rate of catastrophe events and the filament polymerization speed. These parameters are directly influenced by opposing forces as observed in experiments with MTs growing against micro-barriers [193] or optically trapped beads [194]. Longer filaments tend to buckle when a critical threshold is reached, keeping counterforces constant. They keep switching between growth and shrinkage phases, but undergo catastrophes significantly more often than free filaments under the same conditions [187]. For in vivo situations, this means that in addition to biochemical parameters, simple mechanical factors (e.g. obstacles) influence polymerization dynamics. To exert or transmit forces over long distances, MTs can also bundle or couple to other components of the cytoskeleton [130]. Interestingly, forces actively exerted by MTs are not limited to pushing forces. Depolymerization can cause remarkable pulling forces when PFs curl outward after they detach from the neighboring filament. Curled PF shapes become energetically favored after conformational changes of α-/β-tubulin dimmers induced by GTP hydrolysis. This stored energy is released during MT shrinkage when PFs are no longer forced into the straight conformation by neighboring contacts. Depolymerization forces can exceed forces generated by a single MT-associated motor protein by a factor of ten [195]. Recent bottom-up experiments could further show that MTs growing against a dynein-coated wall results in both pushing and pulling forces [196]. Laan et al. [196] show that the combination of these pushing and pulling forces allows MT asters to actively maintain a robust center-position in microfabricated chambers.

A further force feedback originates from binding rates which we expect, in general, to be force sensitive. Force-dependent unbinding of cross-linkers is one particularly important aspect [122]. This can have severe consequences for cytoskeleton networks since it directly feeds back to the network's mechanical properties [197]. Recently, it was shown that the Arp2/3-induced formation of actin branches preferentially takes place at the convex side of bent filaments, making it sensitive to compressive forces [198]. Force-dependent binding and unbinding can further modulate the movement of molecular motors. Experiments indeed revealed strong load-dependent characteristics for these motors responding to either pulling or pushing forces [199].

As described before (Section 2.2.2), forces also directly influence cytoskeletal structures by inducing orientational order [5] or even more complex patterns [5,158]. In the same context, it was found that membrane tension can have a strong impact on filament organization. Filaments growing against a membrane experience a force due to the membrane's tension. Whenever two such filament-driven membrane extensions are sufficiently long and close, tension-based forces will automatically initiate filopodia-like bundle formation [200].

2.2.3.4. Structure feedback

Simple reversed energetic arguments on cross-linker binding already lead to structure feedbacks. A commonly described cross-linker characteristic is their preference to either predominantly bundle filaments or to assemble extended networks. The respective preference should in principle also manifest in binding affinities that are sensitive to the available geometries. Thus, fascin displays a high affinity for parallel actin filaments, whereas filamin does not. In a way cross-linkers both sense and promote particular network geometries and thereby function auto-catalytically since they facilitate binding of further cross-linkers with the same binding preferences. Additionally, it was found that strong cross-linkers influence the actin filament twist in densely packed bundles which has similar consequences for further cross-linker binding [201]. This situation is directly comparable to the cooperative binding of cofilin which is mediated by cofilin-induced changes of the actin filament twist [185,186]. Both examples show a closed feedback loop resulting in cooperative-binding behavior [201,202]. Moreover, these mechanisms are well suited to hinder or promote binding of further accessory proteins, thus providing a powerful link between competitive binding and structure feedback.

A bit more abstract, but nevertheless a structural effect, is molecular crowding which appears to be a largely underestimated effect in cells. Crowding promotes spontaneous alignment of elongated objects and can even induce sorting [203,204]. It is further a well-known property of common crowding agents to induce formation of tightly packed actin bundles [141,205]. Apart from affecting filament ordering or bundling molecular crowding is generally able to drastically alter reaction kinetics [206]. Crowding sensitive actin polymerization, for instance, is as an important cytoskeleton-related phenomenon [207].

2.2.4. Bringing regulation to the cellular level

Many of the examples mentioned so far directly translate into organization and regulation on the cellular level which will be discussed in more detail in the following part of the review. It is this complex self-regulative nature which makes the cytoskeleton a key regulator of cellular behavior. Actin and MTs are persistently interacting with their complex molecular and physical environment giving cells the ability to properly react to various conditions on short timescales (when compared to regulation by gene expression). Actin is commonly associated with force production and the mechanical response of living cells [15]. MTs are far more rigid and elongated structures and are essentially involved in establishing cell polarity [208] and internal transport [209,210].

Dense, actively pushing actin networks (lamellipodia) and sensitive actin bundles (filopodia), for instance, represent highly dynamic actin structures that largely govern cellular migration (Section 3.3). Another example for actin-driven organization on the cellular level is contractile ring formation during cytokinesis, the last phase of cell division, and leads to a final separation of the cells (Section 3.2).

Being one of the most rigid structures within a cell, MTs have the ability to withstand high-pressure loads and to actively push or pull with forces in the range of several pN [211,212]. Originating from MT organizing centers, MTs are responsible for the correct positioning of cellular organelles, the mitotic spindle during cell division [213], and the nucleus (Section 3.2). The sensitivity of the MT network relies on dynamic instability allowing individual MTs to explore target regions and retract in case they do not reach the according site of activity. The large-scale functions on the cellular level can hence not be understood without understanding MT tip regulation and growth dynamics on the single-biopolymer scale.

2.3. Synopsis and open questions

Regarding the cell's functioning, the introduced self-regulative nature of the cytoskeleton components is certainly a key feature of living matter. The large number of different accessory proteins comprises a large toolbox for cytoskeletal regulation which is used in the form of various functional modules existing in parallel. This means using the same proteins in different ways. Permutative use and functional redundancy leads to robust emergent properties which is likely to be a cause for evolutionary stability. A clear manifestation of the variable, multifunctional use of the cellular building blocks can be seen in numerous knock-out or knock-down experiments where one or more elements are genetically removed. Even after removal of assumingly essential elements, cells in many cases show the ability to maintain most of their functions. A prominent example is gelsolin-null mice displaying roughly unchanged embryonic development [21].

Applying the hierarchical reduction perspective as introduced before (Section 1.2.1), it becomes apparent how quickly very basic cytoskeleton components give rise to highly complex systems that resist trivial modeling attempts (Figure 18). On the subcellular level, an intense exchange of theoretical models and advancing experimental design clearly lead to a very fundamental understanding of some strongly reduced reconstituted systems such as entangled actin solutions or kinesin-driven suspensions of bundled MTs [214]. Statistical physics provides powerful tools for these systems comprised of multiple elements of the same kind. Here, numerous models mentioned in this chapter successfully describe or explain various key phenomena of the cytoskeleton, both in terms of its mechanical properties as well as in its structural organization. When approaching more physiological systems, the combination of a heterogeneous, multi-component structure (and non-affine deformations), complex feedback mechanisms down to the molecular scale (e.g. force-dependent cross-links), and out-of equilibrium properties (e.g. motors or polymerization) drastically complicates a profound understanding of network mechanics and organization.

Figure. 18.

Depending on the system of interest, the involved levels of complexity are intertwined differently. (a) The properties of individual biopolymer filaments can be explained by its respective monomer level and reconstituted biopolymer solutions forming entangled networks are understood from a single filament level (b). As soon as elements start to bridge more levels of complexity, the situation quickly becomes more complicated. (c) Cross-linked actin networks, for instance, are more difficult to model than entangled solutions. Closed feedback loops across multiple levels (d), such as transiently cross-linked actin networks, inhibit further coarse-graining and hence make it a demanding task for theoretical modeling.

However, recently developed mean-field models are already able to account for inelastic effects due to bond breakage and allow a fundamental qualitative understanding of a broad range of generic features of cytoskeleton mechanics [123,124]. In addition, microscopic, simulation-based models make it possible to approach the mechanical behavior of heterogeneous and compound networks as well as non-affine deformations [108,112,215]. Active elements and inherent feedback loops remove the cytoskeletal networks even more from close-to equilibrium modeling representing a major task for theoreticians in the near future.

By adding more network influencing accessory proteins, one commonly expects to gain a better understanding of cytoskeletal behavior on the cellular level. It should be noted, however, that any additional component included into theoretical modeling approaches increases the number of parameters usually risking a broadening of a model's accessible outcome. In a similar way, the difficulty of reconstituted in vitro experiments rises drastically with the number of components since every component contributes an additional source of error, making any fully operating experimental run less likely.

We further observe a similarly (if not more) severe limitation of the current models and experimental setups. To date, most experiments as well as theoretical models largely ignore three key features of the actual cellular situation: the polyelectrolyte nature of the biopolymers, the high degree of molecular crowding, and solvent effects.

Experimental data already existing for both polyelectrolyte and molecular crowding effects strongly suggests a very high impact on the cytoskeletal behavior. Polyelectrolyte effects are known to induce filament bundling at high counterion concentrations [216], but also strongly affect filament solutions far below such high densities [620]. In particular, the recent finding that counterions can already induce the formation of regular aster-based networks [144] illustrates their broad range of potential effects on biopolymer network formation. Incorporation of generic filament stickiness could prove to be one possibility to theoretically account for such effects [125]. Molecular crowding can have very similar bundling effects [141,203] and moreover induces drastic changes of the reaction kinetics [206] such as the polymerization rate of actin [207]. So far, molecular crowding effects are neither considered in most theoretical models nor are they deliberately included in reconstituted experimental systems. Future studies, however, will need to further incorporate these influences in order to properly relate the subcellular level to the cellular level.

Finally, the investigation of the subcellular cytoskeleton is still mostly divided into separate communities focusing on either actin, MTs, or far too seldom, IFs. In living cells, however, these three biopolymer types naturally interact in various ways, mechanically as well as biochemically [130], hence clearly demanding a better fundamental understanding of the biopolymer crosstalk.

3. Cellular level

Already on the subcellular level, many organelles and functional units make it a difficult task to fully understand their behavior since coarse-graining is often limited by strong interactions across multiple levels of complexity. Hence, coming from a subcellular point of view it might appear counterintuitive that whole cell behavior should be reducible to two or three levels at all. It turns out, however, that many substantial cellular phenomena can be described and understood in a strongly coarse-grained manner.

Cell mechanics close to equilibrium are part of this class. As long as active effects and long-term transitions are left out, cellular mechanics can indeed be understood as an emergent consequence from the cytoskeletal network level. Moreover, using very fundamental hydrodynamic-based descriptions, active soft matter theory is capable of explaining key aspects of cell migration [163] or cell shape [164] without considering details from the filament or the molecule level.

The situation becomes notably more complicated with increasing nonlinearity and multiple-level interactions. Why is the cell's mechanical strength so little affected by certain types of MT or actin modifications but so strongly affected by others? Why can substantial amounts of myosin motors be blocked without inhibiting cell migration [20]? In many situations, the cellular response to experimentally applied perturbations appears unpredictable or counterintuitive. Developments of experimental techniques that permit better control and reproducibility might help to further address cellular key processes more systematically. One step in this direction might be the synchronization of the cellular shape via adhesive substrate patterns [217].

On the cellular level, the question arises again as to how the lower level elements give rise to spatial and temporal distinction between functional units. How do filopodia, lamellipodia, and lamella find their right location and dimension? These different structures form without any membrane separation, i.e. they per se arise from the same pool of cytosolic elements.

3.1. Cell mechanics

Biological cells can structurally be regarded as polymer-filled entities. Unlike synthetic polymers, however, the comparably stiff nature of a biopolymer leads to mechanical integrity already at much lower volume fraction or mesh sizes, thereby still allowing molecular transport. As described previously, these biopolymers arrange into various higher order structures like networks or bundles. Already on the subcellular level, it became apparent that the given set of (evolutionarily largely conserved) cytoskeleton-related building blocks can give access to a broad variety of different material characteristics. On the cellular level, the many degrees of freedom in creating such a higher order structure lead to an incredibly rich pool of structural appearances and mechanical properties of cells, as illustrated in Figure 19.

Figure. 19.

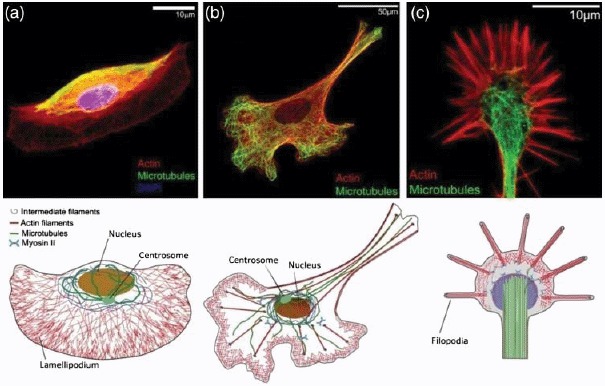
Fluorescently labeled cytoskeleton of three different types of adhering cells with actin marked in red and MTs marked in green. (a) Fish keratocytes, (b) fibroblast, and (c) neuronal growth cone. These three cell types illustrate the large diversity of cytoskeletal architectures which is likely to result in very different mechanical characteristics. The cytoskeleton architecture of the respective cells is further illustrated below the fluorescence images. Similar figure already appeared in [372].

The linear elastic modulus of most cells is surprisingly low [218] and ranges between some hundred Pa in glial cells or neuronal cells [219] and tens of kPa in human thrombocytes [220]. The broad range of elastic moduli already indicates that cells as a material are highly variable and adaptive in their properties in contrast to conventional synthetic materials. But since all the different cells of one organism share the same DNA, the genes alone do not suffice to explain the buildup of elastic strength. During the past years, the picture evolved that the non-genetic level is of greater importance to cells and their internal organization than initially believed. An explanation was found in epigenetics, the heritable changes in gene expression. But even for one and the same cell both appearance and mechanical structure do not persist over time allowing the cell to dynamically adapt to its changing periphery – on a timescale much faster than typical for epigenetic pathways, indicating an inherent ability of the cytoskeleton for complex self-regulation (Section 2.2.3).

Cell mechanics play a key role for a proper functioning of cells [221–225]. This includes mitosis, where cells need to change their internal cytoskeletal structure as well as their mechanical properties to facilitate cell division [226] (Section 3.2). Other examples are mechanosensitivity (Section 3.3.6) and cell migration demanding drastic changes of cytoskeletal networks over time (Sections 3.3.2 and 3.3.3).

The dynamic internal reorganization of cells is consequentially reflected in their viscoelastic properties. For decades, it has been a subject of research whether (and to what extent) cells actually behave like polymer gels. This would open the questions as to how their behavior compares to simplified, reconstituted biopolymer networks (Section 2.1.5) and if material properties from single cells can be utilized for novel applications. Answering these questions might help to find differences between various cell types, which are of invaluable importance for medical sciences. One very prominent example is cancer where a cell's malignant transformation, including the capability for uncontrolled, competitive growth, is reflected in an altered phenotype also affecting the cytoskeleton [225,227–230]. Modeling mechanical cell behavior, for instance, would allow early stage cancer diagnosis if it is combined with measurement of cell mechanics (see also Section 4.5). The growing interest for mechanical properties of single cells has led to the establishment of many rheological methods.

3.1.1. Studying cell mechanics

Cell rheology probes the reaction of a cell to an external mechanical disturbance to restore its original state or to adapt to new configurations. A variety of probing methods (described below, Table 1) have been developed to determine the mechanical properties such as elasticity, viscosity, plasticity, glass-like behavior or, relaxation behavior. These properties can be expressed by quantities such as complex shear modulus and the Poisson ratio of cells. But so far it has proved difficult to produce comparable, consistent results. The major difficulty in single-cell rheology certainly is the high structural heterogeneity of cells. Depending on their state, cells consist of many different compartments displaying large mechanical variations. As described earlier, the cytoskeleton is made of three different classes of polymers and a large number of associated modifying factors (Section 2.2.3). So the first question when probing cells is what exactly is probed and which elements of the cell respond to the specific mechanical disturbance. Application of mechanical disturbances with various frequencies might help to elucidate the contribution of different cellular entities to the overall mechanical behavior. But things become more complicated as soon as the geometry of the cell is taken into account. A cell adhered to a hard substrate like a culture dish clearly shows stress fibers of bundled actin spanning the entire cell. These stress fibers gradually vanish in isolated cells that grow on softer substrates but they reappear as soon as cell–cell-contact is established [231]. In a single suspended cell, stress fibers are entirely absent and most polymerized actin is present as a cortical network right below the membrane [232,233]. It remains an open question whether (and how) results obtained for adhered and suspended cells compare.

Table 1.

Schematic representation of different methods to characterize cellular viscoelastic behavior.

Technique	Range of application	References
Micropipette aspiration	Local or global probing depending on diameter Time range 1–1000 s	[235,236]
SFM indentation	Low and high strains possible Local or averaged probing Frequency range 1–300 Hz Force range pN–nN Low and high strains possible	[220,237,238]
Active & passive optical-trap rheology	Probing of the overall force and fraction of that force transmitted to the environment	[239]
Passive bead rheology	Passive method Local properties	[240] [241,242]
Magnetic bead rheology	Local probing Frequency range 10−2–103 Hz Torques up to 130 Pa linear	[243,244]
Optical stretcher	Local or global probing Stresses (Pa) Forces 10−10 N Small strains	[225,233,245–247]

3.1.1.1. Probing techniques

One of the earliest methods to characterize mechanical properties of cells has been micropipette aspiration [234]. In this case, blood cells were used, which are naturally in a suspended state without adhering to other cells or any hard substrate. Micropipettes with varying diameter are used to exert more or less local suction pressures on cells. Depending on the pipette size, local properties of the cell membrane are probed or even the entire suspended cell is sucked into the pipette. Timescales range from seconds to several thousands of seconds [235] and deformations far from the linear regime can be obtained. Later, also cells isolated from tissue were probed with micropipette aspiration [236].

Another method to determine the cell's mechanical properties is scanning force microscopy (SFM), which can probe adherent cells as well as cells of mostly spherical shape in the early stages of spreading. Depending on the tip geometry, the whole cell can be compressed with a flat cantilever [248] or the cell can be indented with a sharp tip to probe properties very locally [221].A spherical tip averages the mechanical properties of a certain region of the cell [219,237,249]. The timescales of indentation can range from milliseconds to hundreds of seconds. Furthermore, an oscillating cantilever can induce oscillatory stress with small amplitude resulting in a complex shear modulus [238,250]. With an SFM, large deformations can be obtained, but since adherent cells are relatively thin substrate effects which potentially affect the results have to be considered [237]. Deformations like stretching can also be achieved by allowing the cell to establish connections to the cantilever that is subsequently pulled away [251]. Similar experiments are performed using microplates instead of SFM cantilevers. A cell is allowed to briefly attach between a fixed and a movable microplate and is subsequently deformed by moving the microplate. Deformations can be very large thus probing nonlinear aspects of cell elasticity [252,253].

While presenting a very direct way of probing mechanical properties of cells, the above-mentioned micropipette and SFM-based techniques are inherently slow due to comparably long preparation or measurement times for each cell. To circumvent this bottleneck, other techniques aim at simultaneously preparing many cells for mechanical probing, for instance, by incorporating probing or tracing beads. Currently, many different techniques exist to infer the mechanical properties of living cells from the Brownian motion of embedded tracer particles (passive microrheology) or from the response to active bead displacements (active microrheology) [254]. A common method in passive microrheology is to cross-correlate the motion of different tracer particles to correct for local heterogeneities [242,255]. Passive methods can even be applied in a non-invasive manner when using tracers which are naturally present in a cell such as storage granules, mitochondria, or other submicron particles [241,256].

For active microrheology of living cells, one of the most commonly applied techniques is magnetic twisting cytometry which employs magnetic beads that respond to an external magnetic field [243,244,257].A direct application of an oscillatory force field can probe the cytoskeleton of many cells at once over four decades of frequencies. However, variations of the bead's magnetic moment, bead–bead interactions as well as uncertainties concerning the precise magnetic field strength applied might notably limit the measurement accuracy.

Due to the small size of the beads (compared to the cell's size) both passive and active microrheological methods are able to give access to local mechanical properties of cells. This, however, comes with the drawback of a very high dependence on the type and strength of linkages between the particles and the local cellular structures [254,258]. It remains highly non-trivial to account for effects from varying indentation depth [258] and a precise control of binding behavior and localization of the beads is not yet feasible [254].

All methods mentioned so far are suitable for probing cells in an at least weakly adhered state. In general, both geometry and type of contacts can be expected to influence cellular responses and should ideally be taken into account when comparing results obtained with different methods. This also applies to techniques using optical forces on probing beads [239]. However, using optical manipulation techniques, it is possible to measure single suspended cells avoiding direct contacts, simply by taking advantage of a difference in refractive indices between the surrounding medium and the cell [259]. Employing the optical stretcher, it is thereby possible to globally deform suspended cells with a step stress of duration between 0.1 s and tens of seconds to conduct a compliance measurement [245,246]. The global stress originates from optical forces caused by two divergent laser beams of two opposing fibers (Figure 20). This allows trapping of individual suspended cells and deformation by increasing the laser power [233]. Applied stresses depend on the setup geometry and are in the order of Pa corresponding to forces below 1 nN. Oscillatory stress, however, can only be applied with an offset since the optical stretcher cannot squeeze a cell. Embedded in a microfluidic setup, the optical stretcher allows serial measurements of many cells and subsequent sorting, which can be challenged by the inherently broad stiffness distributions [260]. Moreover, potential problems due to laser-induced heating need to be considered and are best avoided by limiting laser power or stretch duration [261]. A related technique able to deform cells in a similar contact-free manner is based on hydrodynamic instead of optical forces [262].

Figure 20.

Schematic principle of the optical stretcher. (a) Two opposing laser fibers emit a non-focused Gaussian beam acting as an optical trap for dielectric objects (cells) with refractive index higher than the surrounding medium. The cell is centered between the laser fibers. (b) At increased laser power, the cell is deformed along the laser axis due to mechanical stress induced at its surface. (c) The stress at the cell surface is caused by a momentum transfer occurring when light with a momentum p₀ is transmitted from a medium with refractive index n₀ into the cell medium with refractive index n₁ > n₀, where it has a momentum p₁ > p₀. Momentum conservation demands that a momentum p_x1 perpendicular away from the surface acts on it. At exit, another momentum transfer p_x2 occurs, again directed perpendicular away from the surface.

A further comparison of the different commonly applied probing techniques can be found in [218,254,263–266].

Measuring the mechanical properties of a cell might at first give a rough estimate of the general nature of its material properties. For a deeper understanding concerning their origin, however, it is essential to access cytoskeletal key parameters in order to elucidate their contribution to cell mechanics. While reconstituted systems (Section 2.1.5) have the tremendous advantage of precise control of the individual component concentrations, cellular parameter changes are very delicate due to numerous inherent cytoskeletal feedback mechanisms (see Section 2.2.3). Direct insertion of proteins into cells (e.g. via micropipettes) is difficult to reproduce and strongly limited to few individual cells. The most accessible way to strongly alter the cellular cytoskeleton lies in the application of cytoskeletal drugs allowing to selectively target individual cytoskeletal components. Colchicine and nocodazole disrupt MTs [267], whereas taxol stabilizes them [268]. Phalloidin stabilizes polymerized actin [269] and hinders its depolymerization, whereas cytochalazin D inhibits actin polymerization [270]. Other drugs commonly applied to alter the cytoskeleton are latrunculin, jasplakinolide, blebbistatin, and ML7. Their efficient functioning is based on their ability to pass the cell membrane. This renders them poisonous at high doses but generally makes their use simple at lower doses. The drugs are widely used to investigate cell functions such as cell migration [271–273], or to explore cell mechanics (e.g. [274,275]).

One major drawback of most cytoskeletal drugs is the unspecific side effects in living cells because they might interfere with a whole set of signaling pathways that are not yet known. Modern genetic engineering provides an alternative way of manipulating cellular systems and in principle allows to specifically add or remove single cytoskeleton components. RNA interference, for instance, hinders the expression of certain proteins and is, therefore, able to more specifically target the expression of single cytoskeletal elements. A remaining difficulty in cells is to overcome possible redundancy effects which is a characteristic and inalienable property of life. Nevertheless, these genetic approaches would allow more controlled and more versatile parameter changes, but they still have not found their way into the biological physicist's standard repertoire. Adaptation of modern high throughput methods [276] might help to get a clearer picture of the microscopic basis of cell elasticity.

3.1.1.2. Rheological measurements

The large number of experimental techniques is complemented by a broad range of resulting data, most particularly when it comes to quantitative comparison of cell stiffness. Differing cell responses can be expected already from cell shape variations between adherent and suspended state, as well as between resting and migrating cells. Moreover, the different rheological approaches either probe local cellular features or entire cells. Even when focusing on one single technique and one well-defined cell type, measured cell stiffness seems to inherently display a very broad, non-Gaussian spread [260] (some approach this problem by averaging over many cells using larger samples [277]). Figure 21 shows typical measurement curves for a selection of four different methods.

Figure 21.

Characteristic measurement curves for four selected rheological techniques as an example for active probing methods on suspended (a), adherent (b, c) and for a passive method on adherent cells (d). (a) Example graph of a step-stress compliance experiment with the optical stretcher. Cells are held at trap power for 1 s, then stretched with 1.2 W for 2 s and subsequently monitored at trap power for another 2 s. Shown here is the relative deformation of cells along the laser axis over time. This graph is an average of 167 cells. (b) Shear moduli extracted from magnetic twisting rheology plotted versus twisting frequency [243]. (c) Frequency dependence of the storage modulus G′ (filled symbols) and the loss modulus G″ (open symbols) measured on A549 cells (N = 12) at different oscillation frequencies using an SFM [238]. (d) Mean square displacement of a single particle (solid symbols) and two particles (open symbols). With the two particles method superdiffusive behavior is found [256]. Data were reproduced with permission from Ben Fabry (b), Jordi Alcaraz (c), and Tom Lubensky (d).

With the optical stretcher, it is possible to perform a variety of pulling experiments; most prominently a step stress experiment [233,245–247,278] where a constant stress is applied and a creep curve of the cellular deformation is monitored. In Figure 21(a), a typical deformation of the cell along the laser axis is shown. During the trap time before stretching, almost no deformation is observed, but during stretching the value first increases with a steep slope which changes to a constant value illustrating viscous behavior. After the stretch, a fast recovery to a remaining deformation is seen in comparison to its original state. This behavior was first interpreted in terms of a simple spring-dashpot model and a single relaxation time [233] but at closer inspection is better described by a power law [279] (general resemblance shown in Figure 22).

Figure. 22.

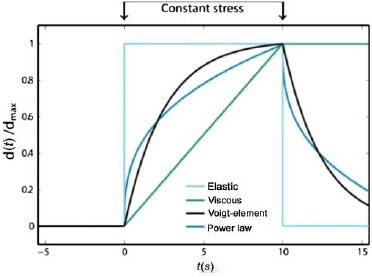
Comparison of different archetypes of response to applied step stress. Viscoelastic behavior is characterized by combining both elastic and viscous properties. The simple phenomenological descriptions by linear viscoelastic models (here: Voigt element) as well as the soft glassy rheology model (power-law) show viscoelastic behavior.

Using magnetic twisting rheology, it is possible to directly apply an oscillatory stress with a broad frequency range from 10-² to 10³ Hz [243]. From these experiments, a complex elastic modulus 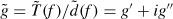can be derived with a complex torque being torque per bead volume and the complex bead displacement . From , the traditional storage modulus G′ and the loss modulus G″ can be calculated by the incorporation of a geometric factor derived from finite element calculations () [243,258]. The method was checked for linearity by applying varying torques to cells resulting in constant G′ and G″ for torques up to 130 Pa [244]. Probing the cells with different frequencies yielded a power law, i.e. G′, G″ ∝ exp(x − 1), with G″ < G′ for f < 1000 Hz. Since both moduli obey the same power-law exponent, their ratio remains constant over frequency. This behavior is known as structural damping or simply power-law behavior and was seen before in biological tissue [280,281] as well as in a large variety of soft materials [282]. In addition to the passive deformation, some cells are also mechanoactive and apparently exhibit contractile behavior [225,256].

SFM rheology data are shown in Figure 21(c). The moduli were obtained with cyclic indentation at a preset small force on an adherent cell. The frequency dependence of the storage modulus G′ (filled symbols) and the loss modulus G″ (open symbols) was determined for the human alveolar epithelial A549 cell line at different oscillation frequencies. This curve form resembles data measured with magnetic twisting rheology.

Figure 21(d) shows mean square displacement curves obtained with the passive microrheology. The displacement curves for single particles display a linear relationship between time and mean square displacement as one would expect for ordinary diffusion. Cross-correlating the motion of two particles, however, reveals superdiffusion behavior with an exponent greater than 1, indicating the presence of nonthermal fluctuations.

Since single cells display a largely heterogeneous, multi-component cytoskeleton architecture, it is little surprising that they are often characterized by a substantial variability that only represents the multiple realizations of their internal polymer scaffold. In this respect, the large quantitative spread of cellular stiffness is already a very important and robust finding which indicates the ability of single cells to easily vary with respect to their own mechanical properties.

It is meanwhile possible to qualitatively compare cell rheological data obtained with different experimental techniques and the overall understanding of cell mechanics has clearly advanced due to the complementary aspects of the various methods [218,254]. However, a proper quantitative comparison of different cell types (including different conditions and internal modifications), especially across different rheological methods, remains a very demanding task for the nearest future. Two key issues on this way will be good enough statistics and more standardized measurement protocols.

Many current methods render it difficult to obtain enough data points to account for the inherently broad spread within even well-defined cell lines. Proper statistics will in most cases demand measuring hundreds of cells which rather remains an exception in the current literature. The second aim should be to achieve better ways of standardizing cellular samples. It is well known that multiple factors have a very strong influence on cellular stiffness even including the phase within the cell cycle or the passage number. Possibilities to obtain more homogeneous samples could be a better cell-cycle synchronization, but also well-defined adhesion patterns to better synchronize major parts of the cytoskeleton [217]. Finally, the different rheological techniques probe different parts of cells, at different stages (e.g. adhered versus in suspension). Thus, a complete picture of cell mechanics will most likely rely on combining several different methods.

3.1.2. Interpreting cell mechanics

While in some cases the large variety of probing techniques available complicates the direct comparison of data on cell mechanics, their diversity on the other side reflects the wide spectrum of different situations. Depending on whether cells are probed globally or locally very different behavior can be expected. Deformation as a response to applied forces will depend on cellular shape, exact position (if probing locally), and the applied strain regime. From a physicist's perspective, the main interest lies in a deeper theoretical understanding of the observed mechanical behavior. In the following, some of the most commonly used models will briefly be introduced.

Already on the subcellular level, it is an inevitable necessity to apply suitable coarse-graining as explained earlier (see Section 1.2.1). All models aiming at describing the cell's reaction to external perturbation and at predicting its mechanical behavior need to strongly simplify the enormous complexity of cells. Geometries typically need to be strongly simplified and anisotropies such as the variable position of the nucleus and other organelles have to be neglected. Furthermore, all cells are internally defined by a multi-component structure, whereas current theoretical models typically assume isotropic systems of one single biopolymer type. Therefore, the models presented here tend to be first-order approximations leaving out many facets of the cells’ nonlinear behavior. Nevertheless, these models have been able to explain some of the mechanical reactions by employing different assumptions.

Neutrophils, a subtype of white blood cells, for instance, have been described by several continuum models namely the Newtonian liquid drop model and viscoelastic solid models [235,283]. Another approach described subsequently is the tensegrity model assuming the cell as a pre-stressed cable network [82]. Finally, a more micro-rheological approach describing cells as soft glassy material will be presented. These three models are of phenomenological nature and contain little or no microscopic details (Figure 23).

Figure. 23.

Different phenomenological models commonly used to describe cell mechanics. (a) Voigt element as one possible representation of mechanical equivalent circuits that combine springs and dashpots in various arrangements. (b) The tensegrity model describes the cell as a pre-stressed network consisting of cables and struts. (c) The soft glassy rheology models assume a complex energy landscape with wells of different depth ΔE such that spontaneous transitions form one to another well have a very low probability.

More microscopic models still aim mostly at describing lower levels of complexity (e.g. reconstituted systems) and have largely been introduced in Section 2.1.5. They could form a valid base for first microscopic models able to describe cellular behavior. To date, they already point out the possible microscopic origins of some key features seen on the cellular level as described by the purely phenomenological models [218].

3.1.2.1. Linear viscoelasticity

Cells under external stress deform neither purely elastic nor purely viscous but behave like a mixture of both characteristics which is commonly referred to as viscoelastic behavior. A rather obvious first approach to better characterize this behavior lies in mechanical equivalent circuits, employing a combination of viscous elements (dashpots) and elastic elements (springs) (Figure 23(a)).

Different arrangements of these elements have been used to describe the stress-strain relationship of a cell. The simplest viscoelastic solid is a spring and a dashpot in parallel (Voigt-Kelvin element), the simplest viscoelastic fluid is a spring and a dashpot in series (Maxwell element). As a further extension of spring-dashpot models, plasticity can be introduced by incorporation of a rupturing element [284]. Here, depending on external stress, the cell can follow two distinct ways of deformation: if the plastic element does not break, the cell will entirely relax to its initial form. If the plastic element breaks, there will be a remaining deformation after a step-stress experiment. In principle, these circuits formed of springs, dashpots, and further elements can be designed to any desired complexity, resulting in very large numbers of element parameters. Overall, the composition of viscous, elastic, and plastic elements certainly helps to increase the accordance between data and theory, yet only at the price of an increasing arbitrariness.

Rubber elasticity in living cells has been reported by Wottawah et al. [233] based on cells in suspension probed with the optical stretcher. Rubber elasticity in living cells at first seems unexpected since cells are multi-component structures and likely to exhibit more than one relaxation time. Already on the level of actin bundles, different relaxation times exist depending on the type of cross-linker used [128]. Suspended cells, however, do not show prominent actin bundles in the form of stress fibers. Nevertheless, more recent studies with the optical stretcher seem to suggest that even suspended cells show multi-relaxational behavior meaning that they have to be regarded as complex, multi-component systems [279].

3.1.2.2. Tensegrity

Very likely inspired by images of stained cytoskeletal networks (such as in Figure 19), the tensegrity model includes some quasi-microscopic assumptions and describes cells as a pre-stressed network consisting of cables and struts (Figure 23) [285]. Cellular structures under tension have indeed been reported with traction force microscopy as an excellent tool to visualize tension inside cells [286,287]. The tensegrity model assumes actin stress fibers as cables, whereas MTs can bear compressive loads of considerable size [82] illustrating struts. Apart from rather loose microscopic analogies, however, the structure equivalents largely remain of symbolic nature so that the tensegrity model is mostly regarded a phenomenological model [218].

The model is able to describe a number of properties observed in cells such as pre-stress, strain hardening, and changes in deformability after cell spread [288]. These effects are mainly explained by geometrical rearrangement of the cables and struts. Yet, it is a completely static model with fixed connections between cables and struts unable to describe any frequency dependency. Up to now, adaptations of the tensegrity model incorporating dynamic elements have not reproduced the observed power law for the shear moduli G′ and G″. It should further be noted that several other models are just as well able to explain the variations of cell stiffness due to pre-stress [218].

3.1.2.3. Soft glassy rheology

Glassy behavior is typically associated with some degree of structural disorder and metastable states [282]. An obvious way to model this lies in considering energetic “traps” (i.e. metastable states) often formed by one element's direct neighbors. These traps can have differing depths ΔE, hence implying an energy barrier necessary to leave one particular metastable state (Figure 23(c)). While earlier studies on glassy materials assumed that elements pass the energy barriers of their current metastable states by thermal fluctuations [289], the soft glassy rheology theory considers a much higher trap depth [282]. This higher trap depth renders spontaneous transitions from one state to another very unlikely and instead of thermal fluctuations interactions between coupled elements drive the movement of elements within the energy landscape. This non-thermal driving is represented by an effective temperature or noise level x with the glass transition at x = 1.

Above the glass transition (x > 1), the theory displays the most interesting regime at 1 < x < 2, where both G′ and G″ show a frequency dependence of ∼ ø^x-1 and hence remain at a constant ratio [282,290]. This fits very well into the power-law behavior observed for many biological materials, using different techniques [218].

In the picture of the different energetic wells (Figure 23), the material behaves elastic at a low effective temperature x = 1, because the individual elements remain trapped in their metastable states. At a high effective temperature of x = 2, the elements are not restricted by energy barriers anymore which results in purely viscous dynamics. As described before, cells show elastic as well as viscous properties and are described best by effective temperatures of 1.1 to 1.5 [218]. Interestingly, unlike in classical polymer research where temperature is known to have a strong effect on viscoelastic behavior, the role of temperature on cell mechanics or biopolymer networks is not well studied.

While the soft glassy rheology theory agrees well with large parts of available experimental data on cell rheology, many open issues remain. The theory does not include effects of active, contractile elements or pre-stress and furthermore fails to describe high frequency behavior. Complimentary approaches might be able to resolve some of these fundamental problems [291].

Another approach aiming to unify some of the observations was proposed by Hoffman et al. [240]. They report a general trend in most literature reporting effective temperatures of either around 1.26–1.29 or 1.17, which made it possible to describe dynamic shear moduli from a majority of studies as a sum of two power laws. This finding is interpreted as contributions from two distinct network compartments, one being the cortical lamellar and the other being the deep intracellular space [240,254].

Although the soft glassy rheology theory is a phenomenological model, it is nevertheless able to indicate some interesting features of possible microscopic origins for the observed behavior. The existence of a power-law distribution of relaxation times was proposed as a reason for the observed power-law behavior [282]. While the theory cannot deliver the microscopic details leading to such a broad distribution of energy barriers their existence, however, is very plausible considering the enormous complexity of cytoskeletal structures. Power-law behavior strongly indicates that the cell's mechanical properties do not result from few major components (such as a few “springs” and “dashpots”) since this would imply a comparably low number of relaxation times. To properly trace back cellular behavior to lower level components, more microscopic models are necessary. One possible direction to further elucidate the microscopic basis of power-law behavior might be on the basis of the glassy WLC [123,292].

3.1.3. Potential modeling directions

Over the decades, many different types of experiments have been designed to shed some light on the mechanical behavior of soft biological matter. Along with experiments employing different mechanical and chemical manipulations, numerous models were created to explain and predict the complex variety of cellular behavior. All models face limitations as biological cells are heterogeneous structures far from equilibrium. Blood cells have been an early subject of mechanical studies since they are easy to access and per se single cells. For these cells, viscoelastic models have been established and are able to describe some of the cells’ mechanical properties [220,293]. Underlying viscoelastic models can also describe deformation behavior of individual, suspended cells as shown with the optical stretcher. Being purely phenomenological, the viscoelastic models do not provide a causal link between the subcellular and the cellular level. Hence, they might be adequate for material classification but they allow no fundamental understanding of the material properties’ origins. Moreover, viscoelastic models fail for the case of adherent cells probed with a wide range of techniques [218]. Here, no intersection of storage and loss modulus over a large frequency range could be observed. This cellular behavior was explained assuming cells to be close to glass transition. The soft glassy rheology model provides a good description of those material properties but remains a phenomenological model. This is also true for the tensegrity model. Hence all models presented here are unable to consistently derive cellular behavior from subcellular level properties.

Regarding the glassy properties observed in power-law rheology, similar general behavior can, for instance, be described based on the filament level by the glassy WLC [125,292]. To date, however, most models largely refer to reconstituted systems that lack the high anisotropies and multi-component nature of living cells. For a more microscopic insight in cell elasticity, one would potentially need compound models to account for the heterogeneous, multi-component structure of the cytoskeleton. Unfortunately, this is already very complicated on lower scales as shown in Section 2.1 and additional complexity comes with the cytoskeleton's ability to respond actively (e.g. through molecular motors). Apart from this general difficulty to build models from extensive and highly intertwined systems far from equilibrium, another considerable problem is the necessary limitation of free model parameters. Models with excessive numbers of parameters often do not promote a more intuitive understanding and risk producing arbitrary results. Using the generalized Maxwell model, where more and more springs and dashpots are added, it might be possible to describe any viscoelastic behavior, but in the end, this will reveal no more fundamental understanding than a spline fit.

3.2. Cell division

Cell division, or mitosis in technical terms, is a stable and well-organized process and since cells always originate from other cells by their division, all mechanisms involved must be highly reliable. This is particularly remarkable since cell division involves drastic shape changes (Figure 24) that are mechanically induced by the active interplay of multiple cytoskeleton modules. Blocking these force generating modules is a very common way to disturb cell division, for instance, in cancer therapy (e.g. using taxol to stall MT growth).

Figure. 24.

Fluorescence images of cell division phases: interphase, prophase, metaphase, late anaphase, and cytokinesis (EMBL, Heidelberg).

Mitosis is reoccurring in almost the same form in all organisms (although the underlying biochemical processes can vary drastically). The two prominent structures involved in mitosis are the mitotic spindle and the cytokinetic ring. Spindles consist of two centrosomes organizing a set of MTs to a bipolar apparatus. Their major task is to equally distribute DNA to both daughter cells. The DNA is organized in a set of chromosomes, which have in their duplicated form two identical subunits, called chromatids, that are held together by a centromere (not to be mixed up with centrosome). The cytokinetic ring, also called contractile ring, consists of a combination of actin and its associated motor protein myosin, and serves to cleave the cell in half along the cell equator.

In eukaryotic cells, mitosis can be described by five phases (Figure 25) starting with the prophase, when duplicated centrosomes migrate around the nucleus. In the prometaphase, the nuclear envelope breaks down and allows chromosomes translocation to the equator of the cell. During subsequent metaphase, chromosomes are oriented along the equator with chromatids facing opposite poles. MTs are organized into different sets with specific characteristics, each fulfilling an own task in the division of the chromosomes. In anaphase A, the chromosomes are separated and the chromatids are transported to opposite poles. Later, in anaphase B, the distance between poles increases and finally the division plane is defined. A contractile ring is formed from actin and myosin II at the equator and begins to contract. Within the telophase, nuclear envelopes reassemble around the decondensing chromatids. The contractile ring contracts further, forming a barrier between both cell bodies. During abscission, the furrow seals, completely separating both daughter cells. A more detailed review on that topic is given by Scholey et al. [294].

Figure 25.

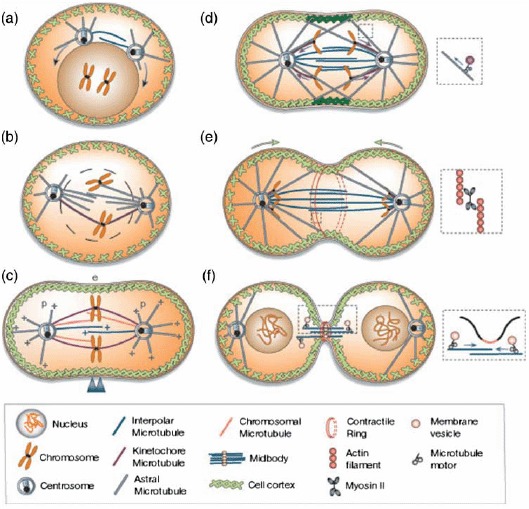
(a) Prophase. Duplicated centrosomes migrate around the nucleus. (Centrosomes, consisting of a pair of previously replicated centrioles surrounded by pericentriolar material, nucleate MT assembly and organize spindle poles.) (b) Prometaphase. The nuclear envelope breaks down allowing MTs to move chromosomes to the equator (e) in a process termed congression. (c) Metaphase. Sister chromatids (double arrowheads) face opposite poles (p). MTs are oriented with their plus-ends distal to the poles, and are organized into four sets, namely: astral MTs linking spindle poles to the cell cortex; chromosomal MTs linking chromosome arms to poles; kMTs linking poles to kinetochores; and ipMTs linking the two poles. (d) Anaphase A. Chromatids are moved to opposite poles (segregation). (e) Anaphase B. Pole–pole spacing increases. During late anaphase, the division plane is determined by a mechanism involving spindle–cortex interactions and the cleavage furrow containing a contractile ring assembles from actomyosin II and begins to contract. (f) Telophase/cell–cell scission. Nuclear envelopes reassemble around decondensing segregated sisters. The contractile ring contracts (furrow ingression) developing a barrier between the daughter cells and constricting the spindle mid-zone (the array of ipMTs lying between separated chromatids) into a structure called midbody (the remnant of the mid-zone). During abscission, the furrow “seals” and separates the daughter cells, apparently involving vesicle transport/exocytosis. Reprint from Scholey et al. [294] with permission from Macmillan Publishers Ltd: Nature 422, ©2003.

Spindle and cytokinetic ring formation are closely interacting self-organized processes [131]. The cytokinetic ring is triggered by the spindle and eventually cuts the cell into two daughter cells. Both mechanisms are highly dynamic and characterized by cooperative mechanisms. Therefore, they are good examples for emergent complexity of the cytoskeleton.

Mitosis further represents an important example of intertwined MT- and actin-based functional modules: MTs (Section 2.1.2) form a large part of the spindle apparatus that is responsible for spatial organization of chromosomes and their segregation. The contractile ring in the cleavage furrow that separates the two daughter cells is formed by actin and myosin motors (Section 2.1.2). The previous sections introduced force production by addition or loss of subunits as well as through molecular motors. On a larger scale, within the mitotic spindle or the contractile ring, the resulting forces are some orders of magnitude higher than on the single filament level. Spindle fibers precisely move the chromosomes and chromatids over tens of microns through the cell with forces in the nN-range [295]. An interaction of many components and cooperative effects is necessary for such achievements. As it is not our aim to explain the whole process of cell division, the focus will lie on two events with major participation of the cytoskeletal proteins: first, the organization of the mitotic spindle and second, the formation of the contractile ring for separating the daughter cells.

3.2.1. Mitotic spindle

The fundamental condition for equitable distribution of cellular material is symmetry breaking. There is no obvious polarity in animal cells, so the symmetry in the local environment of many mitotic processes needs to be broken to create spatial orientation. Cells achieve symmetry breaking by creating a structure that has already an inherent asymmetry originating from the tubulin dimers having a plus and a minus-end [296]. Principles of MT polymerization and their organization by directed motor proteins and bipolar structures have been described above (Section 2.2.2). Most animal spindles are constituted from kinetochore microtubules (kMTs), interpolar microtubules (ipMTs), and astral microtubules (aMTs). Although these three kinds are all assembled from the same subunits (tubulin), they differ in architecture, dynamics, and function [297].

aMTs are nucleated at the centrosomes, where gamma-tubulin caps their minus-ends. They radially emerge from the centrosome and a large part points to the cortex of the cell. One of their main tasks is to position the spindle apparatus within the cell. These aMTs are characterized by a pronounced dynamic instability, their plus-ends growing and shrinking at rates of ∼10–15 μm/min [298]. These dynamics allow aMTs to explore the space for kinetochores or other types of MTs to establish connections to chromosomes or other MTs.

All MTs that lie between the poles of the spindles and are not connected to the kinetochores of chromosomes are named ipMTs (or non-kMTs). These ipMTs form thin but long bundles of 2–6 MTs with an inter-filament spacing of about 30–50 nm [299]. Both, astral and ipMT types show a very dynamic behavior. They rapidly polymerize and depolymerize and have an average lifetime of about 20 s. In order to stably organize chromosomes, some more consistent structures are required.

kMTs are MTs attached with their plus-ends at the kinetochore, the central part of the chromosomes, and extend continuously to the poles where they bind with their minus-ends at or near the poles. Typically, each kinetochore is connected to 10–30 kMTs, which form together with an equal number of ipMTs the kinetochore fibers (k-fibers) – structures that can be visualized in light microscopy [300]. These kMTs are much more stable than the other MT population probably due to the capping at both ends. Their turnover has a half-life of about seven minute in metaphase [301].

Two mechanisms for kMT formation have been proposed. One is the attachment of astral MTs to bivalent kinetochores, called the search-and-capture model and is based on the MT dynamic instability (Section 2.1.2). By alternating cycles of growth and shrinkage, they randomly explore space until they capture a kinetochore, leading to a suppression of the MTs dynamics [302]. This mechanism appears rather inefficient with mathematical models predicting several hours to capture all 92 kinetochores in a human cell exceeding by far the time of less than one hour that is experimentally observed [303]. In the 1960s, Inoue and Sato proposed a second mechanism where k-fibers are nucleated and organized by kinetochores [304]. It helped explaining how mitotic spindles can be organized in cells lacking centrosomes. At first thought, this model seems counterintuitive since MTs that are nucleated at the kinetochore would have their plus-ends growing away from it in contrast to the actual orientation in the spindle. However, Witt et al. [305] found an explanation by observing nucleation of MTs in close vicinity to kinetochores, which then capture MTs’ plus-ends. Local nucleation of MTs is promoted by a gradient of a small GTPase (Ran-GTP) [306,307] that is present around mitotic chromosomes [308] and is established by the activity of a chromosome-associated factor [309]. Apparently, kMTs bind to the kinetochore via a fibrous network or kinetochore fibrils in a fashion that they can still grow or shrink while remaining attached to the kinetochore [310]. It is not yet understood how kinetochores control the dynamics of kMTs. Using electron tomography, it has been shown that kinetochore attachment prevents rapid disassembly of kMT plus-ends that are in the disassembly conformation [310].

This means that the chromosomes do not sit and wait to be found by the astral MTs but actively contribute by forming a centrosomal kMTs. At this point, the search and capture model comes into play again. Astral MTs do not search and capture only kinetochores, but also the loose ends of kMTs. They act as a highway to the centrosome, where kMTs are incorporated into the forming spindle. In conclusion, there are a number of cooperative mechanisms leading to efficient and robust self-organization of the mitotic spindle. The occurrence of multiple nucleation sites for MTs increase the probability of chromosomes to be integrated into the spindle apparatus. This is further enhanced by a Ran-GTP gradient, which not only promotes MT nucleation but also stabilizes microtobules, increasing the likeliness of astral MTs in proximity of kMTs (see also [311]).

3.2.2. Forces in the mitotic spindle

Here, only a short overview of forces involved in spindle organization will be given; a more detailed description can be found in Dumont and Mitchison [297].

The most prominent forces in the mitotic spindle result from polymerization dynamics of MTs and from motor proteins, which are both active (i.e. dissipative) processes (Sections 2.1.2, 2.2.2, 3.3). A pulling force due to MT depolymerization is thought to be involved in dragging chromosomes polewards. To generate such a pulling force, the MT must be coupled to an object [195] (Section 2.2.3). Regarding the connection of MTs to the kinetochore of the chromosomes, several model hypotheses were formulated [310]. For motor-related force generation, cells use up to 10 different motor proteins. As described before (Section 2.2.2), motors actively move along MTs, which is either used to transport objects, or to organize and orient MTs with respect to each other. In addition, they influence MT growth and shrinkage dynamics [196,312]. Interesting effects result from motor proteins with opposing directionality that pull on the same object. Force-dependent detachment rates create a positive feedback so that the antagonistic motors can amplify small spontaneous oscillations, as observed in the case of spindle positioning [313,314]. The oscillatory behavior hence results from the involved feedback mechanisms, which inherently coordinate the action of the opposing motors. Grill et al. [315] further showed by optically induced centrosome disintegration (Figure 26) that there are no specific force-generating cortical regions illustrating the ability of the system to self-organize.

Figure. 26.

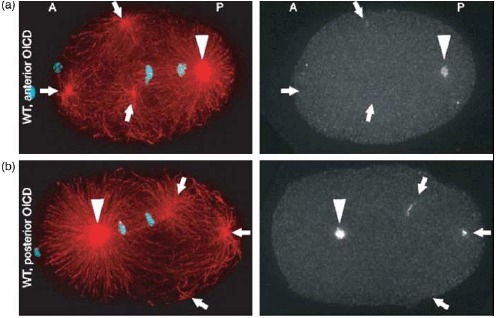
(a) Anterior and (b) posterior optically induced centrosome disintegration. MTs asters were visualized by indirect immune-fluorescence to tubulin (red) in the left panels and γ-tubulin in the right panels. DNA is stained blue. Arrows point to aster fragments, arrowheads to unirradiated centrosomes. Reprint from Grill et al. [315] with permission from AAAS.

When stalled or inactive, motors can act as cross-linkers that generate friction. To allow movement of objects, such as MTs or chromosomes through a gel of cross-linked filaments, the gel needs to be reorganized, meaning that many bonds are transiently stretched or broken. This results in friction rising with the velocity of the moving object. If objects move faster than the timescale of bond-dissociation, they are limited by the rupture rates in the system [297] which might explain the comparably slow movements in the spindle.

3.2.3. Spindle positioning and asymmetric cell division

As seen above, the formation of the mitotic spindle is a complex process depending on well-coordinated interaction of many components. The spindle structure not only needs to be organized, but also has to be positioned properly. Forces for active spindle positioning result from MT growth and molecular motors. Regulatory mechanisms and feedbacks can result, for instance, from the dynamic instability of MTs (Section 2.1.2), MT bending, or collective motor effects. While the antagonistic forces from MT bending and growth can already result in dynamic spindle positioning, in many cases positioning seems to be driven mainly by pulling forces from molecular motors located at the cortex [61,196]. Bottom-up experiments further confirmed that a combination of dynein-mediated pulling forces and MT growth-driven pushing forces leads to a more effective and reliable spindle positioning. In combination with theoretical modeling, the experiments show that the benefit of having both pushing and pulling MTs largely stems from the fact that pulling forces are independent of MT length, whereas pushing forces are not (e.g. limited by length-dependent MT buckling) [196].

Directly related to spindle positioning is asymmetric cell division. It is required for a variety of cells and tissues in a developing organism [8]. Due to a shifted position of the spindle apparatus, cells divide into two cells of different size and content. Asymmetric division in the worm Caenorhabditis elegans was explained by oscillations of the spindle arising from cortical forces acting on the MTs. If the number of cortical force generators, such as dynein, is increased beyond a critical value, their statistical binding and unbinding from MTs together with the elasticity of MTs make the spindle poles oscillate [313,314]. It was shown that coordination between opposing motors is an inherent property, resulting from load-dependent detachment rates of the motors, creating constellations where one motor type is pulling while the opposing motor type stays detached. Cytokinesis takes place in the plane through the center of the spindle, so the off-centered spindle apparatus results in an asymmetric cell division. Additionally, different mechanisms for asymmetric cell division in stem cells have been observed. In the neuroblastoma of Drosophila, for example, two unequal centrosomes form an asymmetric spindle [316]. Also human stem cells divide asymmetrically, producing two different daughter cells. One keeps the stem cell properties, while the other becomes a differentiated cell. The cell fate is determined by a series of polarization determining proteins, although it has been proposed that centrosomes carry the polarity information organizing the distribution of cell fate determinants [317]. This would mean that the process of generating the diversity of cell types in an organism also depends on the cytoskeleton, in this case, the centrosomes and MTs.

During division, the orientation of the spindle becomes very important for determining the position and orientation of the two daughter cells. Théry et al. [318] presented a detailed study on spindle orientation with mammalian cell lines cultured on micro-patterned substrates. They observed that spindle orientation depends on the spatial distribution of the extracellular matrix (ECM; proteins secreted by cells, forming a fibrous meshwork around the cells) which can give rise to shape anisotropies during cell rounding in mitosis. But the final orientation is arising from cortical cues. The cell “memorizes” its interphase shape by cortical marks originating from the segregation of cortical proteins in membrane ruffles (motile lamellipodial regions with freshly polymerized actin filaments). They presumably contain MT-stabilizing proteins and motors such as dynein. Therefore, it has been suggested that these cortical regions selectively attract the spindle poles via the astral MTs [318].

A very interesting property of metaphase spindles is their adaptive size. Spindles measure between 5 and 50 μm, which in many cells correlates with cell size [297,319]. Extrinsic factors could be a direct translation of cell size on spindle size through connections to the cortex of the cell. Moreover, the mass of available building blocks scales with the mass of the cell and might be a size-limiting factor in smaller cells. However, in large cells, it was observed that spindle size reached a plateau around 60 μm [319] indicating intrinsic regulatory mechanisms. Many potential intrinsic mechanisms have been proposed on the basis of polymerization dynamics, MT treadmilling, opposing motors, the highly controversial spindle matrix, centrosome size, and MT gliding [297,320]. Recent experiments in conjunction with computer simulations further revealed MT severing as a mechanism able to consistently explain the scaling of spindle length in Xenopus [321]. None of these mechanisms are exclusive, making it likely to be a combination of several processes in the end, where some might possibly be responsible for coarse adjustment, while others are more involved in fine tuning.

3.2.4. Positioning the cleavage furrow

Once the chromosomes are segregated and the genetic material equally distributed to both poles, the cell is cleaved into two parts. The fact that the cleavage furrow repositions within minutes upon disturbance of the spindle position further illustrates the dynamic, yet robust nature of this system [322]. In many cells, the spindle midzone is more than 5 μm away from the cell cortex, thus signals have to travel over large distances. Cells seem to cope with this problem by establishing a local phosphorylation gradient defining the future cleavage site [322]. Such gradients that are established by positive feedback loops, as described below in more detail, fit very well to self-organizing pattern formation concepts proposed by Turing [323]. The enzymatic part of the chromosome passenger complex, Aurora B kinase, is supposed to play a key role in establishing the phosphorylation gradient [322]. Aurora B influences the concentration of Rho A, a protein that recruits myosin II motors (Figure 27) [324]. Furthermore, Aurora B is involved in many other processes in cell division, for example, the bi-orientation of chromosomes at the equator, the spindle assembly checkpoint, as well as in chromosome condensation and cohesion [296].

Figure. 27.

(left) Centrosomal and cytoplasmic Aurora B complexes are transported to the midzone along midzone MTs and astral MTs, respectively (middle). There, Aurora B is involved in the Rho A flux, a constant activation and deactivation of Rho A leading to an accumulation of Rho A at the equatorial plane. The effectors of Rho A – formins and Rho kinase are key players in the formation of the contractile actin ring (right).

Prior to anaphase, Aurora B is only transiently bound to centrosomes leaving substantial amounts in the cytoplasm [325]. At the onset of anaphase, the centrosomal Aurora B is bound to the midzone MTs by a highly possessive motor transporting it to the midzone of the spindle. The cytoplasmic Aurora B, however, is transported to the midzone by a similar mechanism but along astral MTs [325]. There are two independent pathways for Aurora B transport to the equatorial plane. Binding of Aurora B to MTs initiates a structure-based feedback loop. Aurora B auto-activates during anaphase and activation is localized to midzone MTs [326]. It actually stabilizes midzone MTs which then again catalyze Aurora B activation [296]. Such stabilization of MTs has not only been observed in the midzone of the mitotic spindle, but also for stable astral MTs [327]. In contrast, dynamic astral MTs rather suppress cortical activation [328]. This suggests that depending on their state, MTs exert opposite effects via the same regulator, a hypothesis supported by computational modeling [329].

The Aurora B concentration presumably is the basis for the local Rho A gradient along the future cleavage site established by a continuous flux of Rho A through activation and deactivation [324]. Active Rho A binds and activates formins as well as Rho kinase, which are key players in cytoskeleton remodeling for cytokinesis. Further, the active Rho A is held in the zone of contractile ring formation through this rapidly driven flow of Rho A [324].

Myosin II seems to localize at the cortex in spots that may correspond to myosin filaments [330]. It is possible that upon phosphorylation by Rho kinase myosin II assembles into thick filaments which help localizing motors to the equatorial cortex [331]. Actin is recruited by formin nucleation producing unbranched filaments. When it comes to keeping myosin II at the equator F-actin is indispensable. Two downstream Rho A effectors, formin and profilin, are necessary to maintain the motors in the equatorial region. They both mediate a nucleation of unbranched actin filaments [332] (unlike branched Arp2/3-based networks). Unbranched filaments facilitate parallel arrangements in the form of bundles resulting in a higher binding affinity of myosin motors, which are, therefore, retained near the equator (see also [333]).

The assembly of the contractile ring has been intensively studied for fission yeast due to their comparatively simple geometry and composition. Some theories suggest that in those cells actin filaments are nucleated by cortical nodes containing the actin polymerization protein formin [334]. These filaments are supposed to form a network between the nodes. This way myosin II motors can pull on the nodes to form a ring structure [330]. Numerical simulations have shown that such rings can be formed on the condition that connections between the nodes are transient [334]. This can be accounted to breakage of filaments or dissociation of myosin II. The model has been named the Search, capture, pull, and release model, but is not fully accepted since substantial doubts arose concerning the relevance of the incorporated nodes [335,336]. Yeast cells lacking cortical nodes still display proper contractile ring formation [335]. This rather supports the leading actin cable model, where actin polymerization starts at a single site in both directions. Electron microscopy studies with myosin II-decorated actin filaments have shown that at early mitosis, the ring seems to be composed of two actin bundles with opposite polarity from the same origin [337] (Figure 28).

Figure. 28.

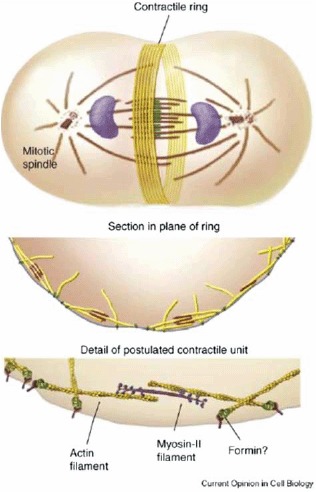
Scheme of contractile ring in cytokinesis and contractile units postulated by Pollard. Reprint from [330] with permission from Elsevier.

While future research on living cells will be essential to reveal the precise road to contractile ring formation, additional insight into the fundamental mechanisms might also come from very simplified model systems. Bottom-up experiments reported the robust self-organization of actin ring structure in the presence of only actin filaments, myosin motors, and cross-linkers [165]. Other studies reported the formation of 3D foci rather than 2D rings [338], so that it remains unclear how the observed rings relate to contractile rings in living cells. Additionally, the actual contraction of the cytokinetic ring is not well understood yet. Its actin–myosin composition often led to suggestions of a muscle-like mechanism, resembling ordered contractile structures, the sarcomeres. But so far, sarcomere-like units have not been reproducibly observed in the cytokinetic ring [339]. One proposed mechanism to explain non-sarcomeric contractions is based on depolymerization of actin filaments in combination with end-tracking cross-linkers [339]. Recently, however, bottom-up experiments [340] together with theoretical modeling [341] also demonstrated that contractile behavior is a very inherent property even of non-sarcomeric actin–myosin bundles.

3.3. Cell migration

3.3.1. Cilia and flagella

In our body, many physiologically relevant functions involve a directed displacement of individual cells called cell motility. Due to the low Reynolds number regime, all motion is over-damped and inertia becomes irrelevant. As a consequence, migrating cells have to permanently produce forces in order to translocate. For swimming motion, it needs to be considered that there is no net fluid flow for time reversible motions.

This is done in a number of different ways. Many less complex prokaryotic organisms as well as sperm cells use flagella or cilia to propel themselves, which is a highly interesting physical process. Moreover, cilia and flagella are highly specific functional modules that resemble nano-machines. Another basic type of cell locomotion that will only be discussed briefly in this article is based on cell blebbing and allows migration of cells through pores or 3D matrices without the need to form thin, polar actin networks termed lamellipodia (see, e.g. [342]). Our main focus, however, lies on eukaryotic cells and their most common type of migration: crawling motion. Crawling motion is obtained by dynamic changes in cellular morphology in conjunction with corresponding local modulations of the friction.

Motile flagella and cilia are thin MT-based extensions which undergo beating or a rotating movement. This is used for motility, e.g. to drive sperm, or for transport of mucus [343]. While the structure and assembly of these motor-driven systems is a fascinating task [344], it is the beating mechanism which attracted most attention from physicists [345]. Physical models revealed that the oscillatory nature of beating itself results from cooperation of many molecular motors [343,346].

Built in a similar fashion, cilia and flagella are often distinguished by their beating pattern which are asymmetric for cilia and show a symmetric wave form for flagella [347]. For the shape of the beating cilia or flagella, the properties of the surrounding medium play a dominant role. The different waveform patterns have been studied theoretically by Fu et al. [347]. Further studies investigated the nonlinear dynamics of the beating [348] as well as hydrodynamic coupling of several oscillators [349,350]. Cilia- and flagella-driven propulsion at low Reynolds numbers further inspired researcher to explore general concepts for possible microswimmers [351,352]. In addition, cilia and flagella motion inspired researchers to adapt similar concepts for micro-fluidic assemblies, for instance, for mixing [353]. For such a purpose, Vilfan et al. [354] developed artificial biomimetic cilia in the form of chains of spherical superparamagnetic particles. Experiments with cilia under load revealed that beating frequency is not strongly affected by applied forces but by the beating amplitude [355]. The same study experimentally revealed force production by motile cilia of about 60 pN. More detailed reviews on cilia and flagella-based motion and dynamics are recommended to the interested reader [356,357].

3.3.2. Blebbing motility and 3D cell migration

Going from prokaryotes to eukaryotes, the type of motion changes dramatically. Cilia and flagella represent very specific, autonomous functional modules that can be understood on a rather mechanistic level. Eukaryotic motion is far more complex and one and the same cell usually possesses various different migration modes. In contrast to the precisely assembled nano-machines of cilia and flagella, the very same cytoskeletal-building blocks, in this case, are involved in various functional modules that hence show a high degree of overlap. This is certainly a fundamental reason for the highly adaptive nature of eukaryotic cell migration.

The key feature of this type of motility is the constantly changing cell morphology. Protrusive forces during cell migration are, in most cases, produced by the actin–myosin cytoskeleton, although MT growth might also contribute to force generation in certain cell types (Section 3.3.5). The most common principles for active cell protrusions by the actin–myosin cytoskeleton are expanding actin networks at the cell front (i.e. crawling motion, see Section 3.3.3) or pressure-driven protrusions (the so-called blebs) that follow active network contractions [358]. Many cells such as Dictyostelium are able to apply both crawling and blebbing motion, whereas others exclusively use one type of protrusions [342,358,359]. In particular for cancer cells transitions between both migration modes are well-known and relate to cancer metastasis [360–362]. Crawling motion, however, received far more attention in biological physics so far (Section 3.3.3), while the use of blebs for cell migration just started to attract substantial interest [342,363].

Bleb formation is driven by intracellular pressure from actin–myosin contractions [364]. Blebs start to form after local rupturing of the actin cortex [364,365] or dissociation of the membrane from the actin cortex, for instance, at sites of lower membrane-cortex adhesion [342]. Initially, blebs lack a visible actin–myosin cortex [365,366]. Cortex reassembly was shown to be able to stop (and retract) bleb protrusions [367] and apparently determines the time of bleb growth [364,366]. Applying an elastic model to experiments with controlled induction of bleb formation revealed that the bleb size, however, strongly depends on cortical tension [364].

While crawling motion is often associated with a more controlled type of cell migration (Section 3.3.3), blebbing motility might allow for faster migration particularly in porous, 3D environments [342,360]. The minor importance of blebbing motion on flat 2D substrates is certainly a main reason for the dominance of research on the crawling motion within the last decades. 3D cell migration undoubtedly is extremely relevant to cells in multicellular organisms constantly facing a complex 3D environment such as dense fiber networks (ECM). Crawling cell migration often demands local degradation of these surrounding matrices. Blebbing motion, in contrast, allows to even squeeze through very narrow gaps and is independent of matrix degradation [360,368].

It could now be argued that flat 2D substrates represent a rather artificial situation, but they are simply much better accessible in experiments both regarding their visualization and their comparability. Technical advances slowly start to give access to a better 3D visualization, but the incredible diversity of possible 3D environments still makes it a difficult task to compare different studies. While a 2D substrate is sufficiently defined by its viscoelastic properties and biochemical coating, 3D matrices further differ in their internal architecture and structure usually representing highly anisotropic materials. At present, 3D cell migration hence remains a poorly understood subject with many key characteristics of cell migration differing substantially between flat 2D surfaces and different 3D environments [342,358,362,368].

3.3.3. Crawling motion

The most commonly investigated type of eukaryotic cell migration is crawling motion on 2D substrates. This is often described by decomposition into three core processes. First, the leading edge is propelled forward by polymerization forces from directed growth of flat actin network structures. This extending actin network adheres to the exterior via formation of adhesion sites. Second, at the rear of the cell contacts are reduced and active contractions lead to a detachment from the substrate. Finally, contractile forces directed toward the cell body pull the cell forward (Figure 29). All three mechanisms take place in parallel. To initiate cell migration, two different scenarios can be found. Either the front starts by lamellipodial outgrowth, or the rear first starts to contract. Both mechanisms aim at breaking the cell's symmetry [369].

Figure. 29.

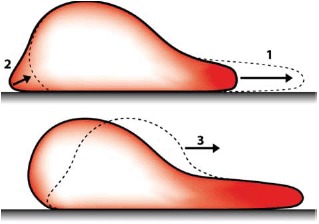
Illustration of the “standard model” of crawling cell migration on flat substrates [6,370]. It commonly is reduced to three processes taking place in parallel: (1) A comparatively thin actin gel protrusion extends the leading edge and adheres to the substrate. (2) The rear end actively retracts and detaches from the substrate. (3) The cell body is pulled forward.

Apart from this common working principle, the structure and dynamics of lamellipodia-like network outgrowth differs strongly between cell types. Different combinations of the most relevant leading edge entities – lamellipodia, filopodia, adhesions, and MTs from the back – lead to fundamentally different types of motion. The spectra of motile behavior ranges from persistent, continuous migration of lamellipodia-dominated keratocytes to highly fluctuating motion of neuronal growth cones where the rate of actin gel formation is highly stochastic [371] (Section 3.3.5). A quantitative analysis of the fluctuations of the actin gel growth rate gives a clear signature of different types of motility [372]. In addition to the fluctuation characteristics, cells also strongly differ in their overall translocation rates with a typical maximum value for fish keratocytes of 10–15 μm/min [372]. The arising actin network formed at the leading edge is transported backwards, driven by polymerization itself and contractile elements further back [373,374].

This actin gel rearward transport with respect to the substrate is the retrograde flow and is a generic property in crawling cells. The vectorial sum of retrograde flow and growth rates is the protrusion rate as indicated in Figure 30. Retrograde flow, protrusion rate, and growth rate hence are no independent quantities. However, retrograde flow and growth rate can be accessed separately. The retrograde flow strongly depends on the adhesion strength to the substrate, whereas the growth rate can be tuned using a large set of actin accessory proteins [372].

Figure. 30.

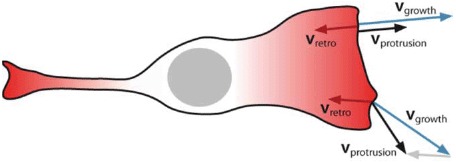
Sketch of a crawling fibroblast-like cell. The local protrusion rate (v_protrusion) of the leading edge is the vectorial sum of retrograde flow (v_retro) and gel growth velocity (v_growth).

From a physicist's point of view, it was a substantial discovery that the lamellipodial machinery at the leading edge acts as a largely autonomous system with respect to the cell body. Verkhovsky et al. [17] demonstrated that fragments of living cells continue to migrate by exactly the same type of crawling motion with nearly unchanged characteristics. On the other end of the experimental spectrum, bottom-up in vitro approaches proved that highly reduced systems consisting only of a small percentage of cellular proteins are sufficient to mimic fundamental properties of migrating cells [375–378].

While a simplified textbook picture of cell migration (Figure 29) [6,370] at first seems to suggest that cell motility might be governed by principles that are universal to all crawling cells, today's more detailed understanding of the underlying processes results in substantial doubts concerning this hypothesis. On a very abstract level, we will certainly find common principles, however, it remains unclear whether or not all crawling cells address their cytoskeleton in a similar way. It is possible, for instance, that neuronal growth cone motility is not entirely driven by actin protrusions but by MTs. Still all cellular migration remains driven by the cytoskeleton.

3.3.3.1. Leading edge protrusion

At the leading edge of a crawling cell, actin is permanently transformed between its monomeric and filamentous state by persistent polymerization and depolymerization [379]. Polymerization in the front part leads to network or gel expansion creating a pressure that gives rise to forward forces. Although depending on cell type and environmental conditions, cell migration differs substantially in its characteristics, two actin-based structural key features are commonly recognized at the front part of moving cells: filopodia and lamellipodia.

Filopodia are densely packed, oriented actin bundles generally perpendicular to the leading edge with the actin plus-ends pointing outwards that can be found in many different cell types at various stages of development. Their functions include exploring the cellular environment in search of cell–ECM or cell–cell adhesion sites as well as supporting the alignment and adhesion of opposing sheets of epithelial cells during embryogenesis and wound healing [380].

The lamellipodium in contrast is an extended, flat network of predominantly oriented actin filaments [381,382]. Most cells are reported to form lamellipodia, but unfortunately the term itself is not very well defined. Usually, further distinction between lamellipodium and lamellum is made. Already very early studies on crawling cells distinguished between the very thin front part, the lamellipodium and the following thicker part, the lamellum [383]. Common criteria include the filament length and the degree of branching, with short, branched filaments in the lamellipodium and longer unbranched filaments in the lamellum. Many other criteria can be added to distinguish both structures, however, this further distinction remains vague and no generally accepted definition exists [179,384].

Due to their little changing morphology and a persistent lamellipodia-based type of migration in the absence of filopodia formation, fish keratocytes have become a central model system to study the lamellipodium. While the actual actin network growth velocity during protrusion is comparable with other common cells types, only keratocytes show persistent forward motion. Other cell types such as fibroblasts or neurons display strong stochastic fluctuations in their lamellipodial dynamics [372]. These fluctuations significantly reduce the overall velocity of migrating cells, but at the same time they allow more adaptive and sensitive movements.

Keratocytes typically assemble their front actin network at a speed of around 10 μm/min corresponding to 60–90 actin monomers per second and the growing filament. Early in vitro studies using reconstituted actin revealed steady-state conditions (i.e. net polymerization equals net depolymerization) with growth rates far too slow to account for the observations made in migrating cells [385]. It quickly became evident that the cellular situation is characterized by a highly complex interplay of many actin accessory proteins that strongly alter actin polymerization and nucleation dynamics. A complete biochemical picture of the regulative interaction partners is still far away. There are, however, fundamental principles and mechanisms that underwent few or no changes within the last years despite many newly discovered accessory proteins. In this review, we will not aim to fully cover the current knowledge of all interacting elements, but we want to focus on key underlying mechanisms that led to both reconstituted model systems and theoretical models elucidating essential parts of lamellipodial migration.

The lamellum and even more the lamellipodium were subjects of very intense research during the last decades. Advances in electron- and fluorescence microscopy revealed many details on its internal architecture and composition. Electron microscopy pictures discovered a dendritically branched actin network at the very leading edge [382]. Roughly at the same time reconstituted in vitro experiments showed that the Arp2/3 protein complex initiated similar actin branches after activation [386]. Electron microscopy studies of lamellipodia confirmed the existence of Arp2/3 at actin branching points [387,388] and recently even revealed the detailed branch structure and 3D network architecture [388].

Of great importance for cellular regulation is the finding that Arp2/3 needs to be activated by Arp2/3 activating factors in order to function properly [100]. In addition to these activating factors, a bound actin monomer and a mother filament are necessary for effective branching [389]. Arp2/3 activating factors play a key role in cytoskeletal organization since they are all embedded in signaling pathways and hence can be directly triggered by either internal or external signals [100,172] (Section 2.2.3). Although the Arp2/3 activation pathway seems understood to a large extent, it is still not fully resolved why the activating factor preferentially remains at the very leading edge [390,391]. And is it already enough to activate Arp2/3 at the leading edge to form lamellipodial network formation in cells?

Much of what follows Arp2/3 activation was learned based on another major breakthrough which was the discovery of the close relationship between listeria motion and lamellipodia-like motion [392] and its following in vitro imitation [375,376,378].

Listeria monocytogenes is a bacterium that protrudes within cells by using the cell's lamellipodial proteins. Actin assembly is initiated at the bacterium's surface resulting in forward propulsion through the host cell [392]. A major step to fully understand the principle of Listeria motion was the step-wise reconstitution of mimicking systems. It was found that Listeria moves at physiological rates within a well-controlled mixture of reconstituted proteins instead of cytosol [377]. This was a major advance since it drastically reduced the set of key proteins involved. Another important step was the use of Arp2/3 activator-coated beads as a model bacterium instead of real Listeria [376,378]. Combining both approaches created a fully accessible bead motility assay allowing for full control over all its constituents [375]. This experimental system proved to be highly versatile and much of our current understanding of Arp2/3-driven propulsion was gained using similar setups.

Before the directed overall movement of the spherical beads takes place, symmetry needs to be broken. Apart from slight variations in the initial distribution of activators, the actin gel starts to grow rather homogeneously on all sides of the bead forming a dense network layer covering the entire bead surface. Since the network is radially growing outwards, its circumference increases and sets up an elastic stress. At a critical thickness of the gel, the actin layer fractures like a classical polymer gel [393,394]. Once the spherical symmetry breaks upon actin gel fracture, the actin gel continues to grow off the bead forming a so-called actin comet tail. In addition to being a fascinating physics problem and a fundamental element of bacteria locomotion, the actin network rupture itself can be regarded as a model system for the inverse case of a rupturing cortex during bleb formation [395] (Section 3.3.2). Using glass needles [396] or SFM cantilevers [397], it was possible to determine the forces produced by the growing Arp2/3-based actin network tail and its reaction to opposing forces or stall force measurements. Micrometer-sized objects were found to produce significant forces in the nN range. In contrast to propulsion through cilia and flagella (Section 3.3.1), propulsion in this case is entirely based on polymerization forces. Most commonly, polymerization forces are explained by a Brownian ratchet mechanism [188] or rather by mechanisms based thereupon [398]. The general idea lies in a way to bias the system's inherent stochastic fluctuations to generate forces [398,399].

A qualitatively different motile behavior was obtained upon replacing the spherical beads by lipid vesicles [400,401] or oil droplets [402]. Both vesicles and droplets are relatively soft and the object deformation can be used as a direct measure for the compressive forces of the actin comet tail [400–402]. In contrast to polystyrene or glass used previously, both vesicles and droplets allow surface-bound diffusion of Arp2/3 activators. Depending on the Arp2/3 concentration, this can lead to a periodic saltatory regime besides a previously observed continuous regime [403]. Additional aspects were revealed by analyzing the actin-based propulsion of non-spherical objects [404] (Figure 31).

Figure. 31.

Actin network growth from a polystyrene bead functionalized with an Arp2/3 activator (VCA). Functionalized beads were immersed in a solution that besides actin and Arp2/3 contained few other regulative proteins (here: gelsolin, cofilin, and profilin). The bead size was about 2 μm and images were taken with phase contrast (left) and fluorescence microscopy (right). Actin was labeled with a rhodamine dye. Images were taken by Björn Stuhrmann.

The bead motility assay consequently delivered important insights into the mechanical properties of Arp2/3-based networks and regulatory functions of its key components. This was of fundamental importance for a further understanding of lamellipodial organization since both systems bear a surprising resemblance in their molecular composition. Valid for both cases, the core proteins of the lamellipodial network were brought together in the conceptual framework of the array treadmilling model [15,386]. Core aspects of this model picture are still valid to date, although more recent modifications and recently discovered inconsistencies demand a further revision of this framework (discussed in the next subsection). Analogto single filament treadmilling (Section 2.1.2), the array treadmilling is essentially driven by material addition at the front and material loss toward the rear. At the front, the network is formed by Arp2/3-based branching, filament elongation and subsequent capping while further back branches and filaments are disassembled (Figure 32) [57]. Of growing interest is the role of tropomyosin which was suggested to determine the transition from lamellipodium to lamellum by stabilizing filaments further back in the actin network [57,180] (Figure 32).

Figure. 32.

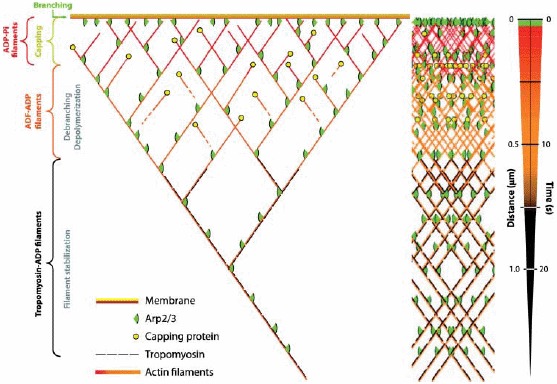
Model picture of the self-organizing actin network within lamellipodia. ATP-hydrolysis acts as a timer mechanism resulting in distinguishable zones dominated by different actin accessory proteins. Branching and hence nucleation of new filaments is driven by Arp2/3 at the front while in the middle zone debranching and depolymerization dominate. At the rear of the network filaments, start to be hindered from fast depolymerization by tropomyosin binding. Illustration was taken from [57] with permission of Marie-France Carlier.

In the context of this article, the bead motility assay is a very instructive example of emergent behavior. Taken individually, none of the protein components show overall directed motile behavior. By simply throwing together all ingredients, entirely new properties emerge. Due to the structure's permanent turnover, i.e. energy dissipation, the highly organized, polar actin gel [405] nicely represents a self-organized structure. With respect to the motile cell, this means that a single signaling pathway activating Arp2/3 is sufficient to switch from a passive state to a persistent lamellipodia turnover since the network itself forms an autonomous functional unit.

Although many molecular details remain to be elucidated in the future, the reconstituted bottom-up assays suggest that we already possess a very basic picture of lamellipodia-based cell migration on the molecular level. This creates an exciting space for modeling crawling motion from the microscopic to the macroscopic level. So it is hardly surprising that a large number of different theoretical models for lamellipodial migration can be found. Fortunately, the strong modeling activity in this field already resulted in highly recommendable review articles [189,406–408].

The existing models can roughly be classified along different axes. In particular, our focus on the different scales suggests a distinction between microscopic and more macroscopic and phenomenological models. Microscopic models originate from microscopic details, whereas macroscopic models do not account for these details. It is clear that a macroscopic model will not reveal any microscopic details, but it might give a new language or formalism to better describe and understand the macroscopic level. In contrast, a microscopic model will help to understand molecular interplay, but it will probably not lead to a new macroscopic formalism.

A second distinction could be made between stochastic, discrete and deterministic, continuous models. The first one is typically realized using Monte Carlo-like methods, while the later one is normally based on sets of differential equations with continuous densities [189]. Table 2 aims at classifying several different modeling approaches according to their scope and the explicitly modeled levels of complexity. Another approach lies in combining differently coarse-grained models, for instance, a microscopic mean-field description for the very leading edge of the lamellipodium and a macroscopic, hydrodynamic description for the rear part of lamellipodium (and lamellum) [191,192].

Table 2.

Overview and classification of different models aiming at describing crawling, lamellipodia-based cell migration.

Modeling approach	Scope	Modeled levels of complexity	Examples
All protein models (stochastic-discrete)	Lamellipodium (+lamellum)		[180,393,409–411]
Microscopic mean-field models (deterministic-continuous)	Lamellipodium (+lamellum)		[179,412]
	Whole cell		[413–415]
Filament-based models (stochastic-discrete)	Lamellipodium (+lamellum)		[416]
Macroscopic/hydrodynamic models (deterministic-continuous)	Lamellipodium (+lamellum)		[417]
	Whole cell		[418,419]

Notes: The models are classified according to their modeling scope and their different inherent hierarchical reductions (Section 1.2.1). Red encircled scales represent the levels of complexity covered by the respective models. Feedback loops, i.e. arrows pointing from higher to lower levels, are not drawn explicitly.

Arguably the smallest level that allows meaningful modeling cellular actin networks starts at the monomer level. Molecular dynamics simulation on a lower all-atom level are quickly advancing with growing computational power, but the largest systems still only comprise small exerts of MT or actin filaments [86]. While such all-atom simulations help to understand the mechanical properties of filaments from a sub-molecular level, we doubt that they will substantially contribute to our understanding of higher level phenomena like cell motility. In the framework of the following sections, many different modeling approaches will be presented and discussed in close conjunction with experimental data from whole-cell studies as well as from reconstituted systems.

3.3.3.2. Self-organization into oriented branches

The current cartoon picture of the lamellipodia network (Figure 32) was strongly influenced by the branched structure seen under electron microscopy [382]. One major weakness of this array treadmilling model is that it does not directly explain the leading edge orientation of actin filaments. By accepting that Arp2/3 induces 70° branches close to the leading edge, it still does not explain why they automatically should orient in a way that necessarily leads to the well-known angular distribution peaked at ±35°. What feedback loops can potentially discriminate filaments pointing to the leading edge from filaments pointing backwards?

An early modeling attempt by Maly and Borisy [420] suggested an orientation-dependent nucleation and capping rates to explain the dominant ±35° orientation. A later, more detailed microscopic model by Schaus et al. [421] found that a zone at the leading edge where branching is allowed and capping forbidden already leads to the assumed orientational pattern. In addition, the existence of +70/0/-70° patterns was reported which recently were analyzed in more detail [422]. Interestingly, another computational model by Schreiber et al. [416] only restricts branching to the front zone, but does not assume any other particular orienting mechanism and still they observe a tendency of filaments to orient at ±35°. Recent experiments further revealed the ability of Arp2/3 to sense filament curvature which seems to induce a preference for branches pointing forwards [198].

Naturally, the way forces can be exerted by the leading edge filaments is directly related to their orientational organization. In terms of migrating cells, it is particularly fascinating to look at the response of this leading edge actin network to opposing forces or perturbations. While Brownian ratchet models were already suggested many years ago to explain the force production of single-polymerizing filaments (see also “leading edge protrusion”) [407], they could not simply be adapted to protrusive actin networks showing a very different force-dependent behavior [397,423,424]. Recently, several models intended to explain the respective force-velocity curves, in general by using more complete models that incorporate many facets of the growing actin network.

Taking into account excluded volume effects of branched actin filaments in addition to a Brownian ratchet mechanism, Schreiber et al. [416] could reproduce the force-velocity relation of migrating cells. Able to describe even the response of migrating cell to drug application, another model by Zimmermann et al. is based on the interplay of a semiflexible network region near the leading edge with a gel-like actin network further back which is constantly advancing through ongoing crosslinking [191,192]. Weichsel et al. [422] in contrast suggest that the transitions between a ±35° and a +70/0/-70° filament orientation might account for the force-velocity relations observed in migrating cells.

Although generally, a lot of things can be learned by the presented models, it should be noted that many of these models have to rely on current research hypothesis. This comes along with a persistent risk of new experimental evidence disproving parts of the models’ basis. The relevance of Arp2/3 branches itself has long been under debate [425], but their existence is meanwhile well documented and accepted [388]. However, many other aspects of the early array treadmilling picture underwent major revisions. A number or recent findings have challenged the initial belief that protrusion forces are generated by many short filaments directly pushing the leading edge with their growing ends. Based on the reconstituted bead motility assay, the need for having oriented filaments directly pointing at the bead was recently questioned [426,427]. This is in agreement with a stochastic simulation model which takes care of excluded volume effects and shows perfectly fine lamellipodial dynamics even in the absence of well-oriented filaments [416]. Both studies point at gel expansion as the driving mechanism, so that even in cells filaments do not necessarily have to directly grow against the membrane in order to allow protrusion. This would also be consistent with the observation that growing actin plus ends can be found throughout a broad section of the lamellipodium network [388]. This puts a question mark to many previous models and will certainly lead to an interesting debate since, in principle, it shows that oriented filaments are not prerequisite for forward propulsion [426].

3.3.3.3. Regulation of the actin dynamics

With a detailed biochemical picture at hand, it is possible to model the complex interplay of actin and its accessory proteins. Many different microscopic models have been developed on the basis of the bead motility assay (e.g. [393,409,410,426]) or on the basis of keratocyte lamellipodia [180,412]).

Early stochastic microscopic models showed that measured rates for growth, capping, and depolymerization are consistent with the formation of an actin comet tail on coated beads [409,410]. The very detailed model by Alberts and Odell [410] already includes G-actin diffusion and thus a feedback loop linking polymerization and depolymerization.

An important analysis of the array treadmilling hypothesis was performed by Mogilner and Edelstein-Keshet [412] on the basis of a deterministic microscopic model. Here, many known reactions up to actin sequestering were included resulting in a complex set of differential equations revealing the complex interplay of actin accessory proteins. Other stochastic [180] as well as deterministic [179] models further investigated the biochemical self-organization of the actin dynamics using a slightly different set of accessory proteins. Even though all these models had to strongly reduce the number of interacting agents, they were nevertheless able to reproduce many key features of lamellipodial actin networks. The models further show good quantitative agreement with actin and accessory protein profiles obtained for living keratocytes (Figure 33). Using such reaction rate-based models, it is also possible to investigate filament length and distribution [180,428,429]. To determine the mechanisms for orientational order, however, mechanic interactions need to be considered in detail [416,420,421].

Figure. 33.

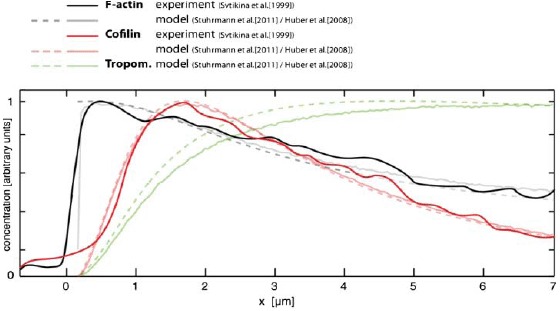
Comparison of experimental data from migrating keratocytes (taken from [387] with theoretical result obtained from computer simulation (taken from [180]) and mathematical modeling (taken from [179]). The depicted curves show concentration profiles of F-actin as well as cofilin and tropomyosin along the lamellipodial network starting at the leading edge (x = 0). For both F-actin and cofilin, theory and experiments are in good agreement.

Complementary to microscopic models, a more phenomenological, macroscopic approach leads to a further abstraction of lamellipodial motility. Treating the lamellipodial actin network as an active gel, it was possible to approach both the lamellipodial shape and dynamics [163,417]. Here, molecular motor-based contractile forces are included in the form of an active stress.

3.3.4. Substrate adhesion and network contraction

Regarding lamellipodia-based protrusion, there is already a detailed working picture of its functioning. The situation is different for the necessary counterparts of force transduction: adhesion and contraction.

Physically all three systems, protrusion, adhesion, and contraction, are directly linked by forces. Polymerization-driven forces at the leading edge need to be balanced by adhesion (or friction) to result in forward movement. The cell body can only follow the movement of the front if it is able to move against the backward actin gel flow, meaning that contractile elements need to constantly pull it forward with the leading edge machinery.

An experimental tool that quickly became essential when it comes to contraction and adhesion is traction force microscopy. The most common way to measure the forces that cells exert on a soft substrate is by analyzing the displacement of tracer beads embedded in the soft substrate. Today this allows working with various gel substrates and very high spatial resolution [430] (see also Section 3.3.6).

3.3.4.1. Contractility, retraction, disassembly

In cells, two fundamental principles can lead to contractile forces. Most obvious are active contractile elements based on dissipative molecular motors such as myosins. In addition, however, network disassembly or restructuring can also result in contractile forces that might play an important role in cell migration as well [407].

Interestingly, up to now network disassembly attracted considerably less attention than assembly. Although the array treadmilling model (Figure 32) in principle includes assembly and disassembly, it cannot explain the so-called convergence zone in the rear of the lamellum [179]. Following the array treadmilling model, the Arp2/3-based actin networks will gradually thin out toward the rear. The current picture of tropomyosin stabilizing filaments in the back is only further slowing down network disassembly. A basic microscopic model able to account for both filament reorientation and network disintegration is still missing.

Regarding contractility, it turns out that the network's disintegration toward the rear is inseparably linked to contraction. By affecting the network structure on the one hand, active contractile elements like molecular motors might contract the network more efficiently. On the other hand, network disintegration by itself is already a possibly contractile mechanism [431]. Cross-linking filaments can suppress their thermal fluctuations. This can be interpreted as stored elastic energy. Cutting or disassembling parts of those networks can in turn increase filament fluctuations, which results in a shortening of their effective end-to-end distance and thereby leads to overall contraction. In particular, it was shown that this mechanism applies to nematode sperm cells where a gel based on non-polar fibers in the absence of molecular motors still retracts [432,433]. How far this mechanism really applies to other types of crawling cells remains an open question [407,431]. Very early experiments blocking several types of myosin motors at least suggest that network contractions show substantial redundancies on the microscopic level [434].

Whether almost exclusively or in addition to network disintegration, in most common cell types myosin-based activity is decisively involved in cell retractions. Among the many different myosin motors, myosin II plays a dominant role in network contraction. Studies made on migrating fish keratocytes could show that myosin II motors are preferentially located toward the rear of the lamellum [17,382]. The respective distribution of myosin can be explained by a combination of diffusion and drift in form of transient binding to a treadmilling actin network. While myosin concentration increases toward the rear, the actin network thins out due to continuous disassembly. This apparently allows motors to contract the actin mesh into actin–myosin bundles [382]. The microscopic details, however, are still not understood [189]. Some of these missing details can potentially be drawn from simplified one-dimensional (1D) models such as an analytical approach by Kruse and Jülicher [435].

Combining fluorescence live cell imaging with image analysis techniques, Schaub et al. [436] determined scalar maps of actin and myosin activity for migrating keratocytes. Their results confirm that myosin-driven contractions take place toward the rear of the lamellipodial network. Adachi et al. [437] went one step further and measured the direction of the network contractions in migrating keratocytes. They found that the network's strain is positive close to the leading edge and negative (i.e. compressive) further back. In addition, it is shown that the contraction only takes place along the direction of migration. This is in good agreement with early proposition on lamellipodial network contraction [17,382]. Consistent with the model, the network contractions become more pronounced for increased motor activity and can be suppressed upon myosin inhibition [20]. For the case of fish keratocytes, the network contractions are most dominant within the cell wings (Figure 34).

Figure. 34.

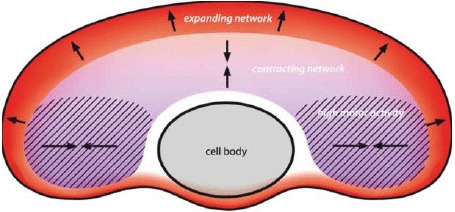
Sketch of a crawling keratocyte. The front region is characterized by fast actin gel growth, whereas the part further back disassembles and contracts. The flanks of the cell display particularly strong contractions that to a large extent depend on myosin motor activity.

An important next step to understand entire contracting networks are again in vitro experiments that revealed that network contraction only works efficiently within a certain range of cross-linker concentrations [438].

3.3.4.2. Substrate adhesion

All in all, polymerization-driven protrusion in conjunction with disintegration and contraction creates a closed turnover cycle and polar gel flow. However, to translate this into a forward movement, friction between cell and substrate is needed. Rather than having simple fluid friction, cells specifically adhere to substrates via non-permanent adhesions. Using highly specific adhesion mechanisms, cells do not adhere to the full surface area but rather establish discrete cell–substrate connections [439]. For a physicist, the processes that control cellular adhesion are at the same time fascinating and frightening. Its enormous biochemical complexity [440] makes detailed, microscopic modeling approaches a difficult task while, for instance, its response to exerted forces and their use for environmental sensing makes them physically very appealing to study [440,441] (Section 3.3.6).

Although these findings clearly show that substrate adhesion is a rather complicated process, for certain conditions it nevertheless can be described adequately as simple velocity-dependent friction [417]. Mostly, however, the modulation of adhesive strength is described by the molecular clutch model [442,443].A clutch is realized by a tunable complex of adhesive proteins linking the actin cytoskeleton to the substrate [100]. When the clutch is engaged, coupling between substrate and cytoskeleton is strong and the actin network growth directly translates into leading edge protrusion. The disengaged state leads to slippage of the cytoskeleton (retrograde flow, Figure 30) and the forward propulsion of the leading edge is strongly reduced.

The force transmission characteristics not only depend on substrate and cell type, but in addition can differ substantially between different regions of migrating cells. For keratocytes, it was shown that the front substrate and cytoskeleton are strongly coupled showing very little retrograde flow while at the sides slipping behavior was observed [445]. In terms of the clutch model, adhesions at the front are mostly engaged whereas adhesions at the sides are mostly disengaged. A slightly extended clutch model incorporating motor driven retrograde flow was successfully tested by combining microscopic simulations with experimental data on neurons [444]. Notably, this motor clutch model inherently includes a mechanism to sense the mechanical properties of the substrate and to respond to it (Section 3.3.6).

A different, very detailed mathematical model by Kuusela and Alt [415] incorporates (force-dependent) integrin binding and unbinding to the cytoskeleton and the substrate as well as integrin diffusion to model substrate adhesion.

Ignoring most of the molecular details, an interesting 2D mesoscopic model was developed by Shemesh et al. to study the interplay between a growing elastic actin gel and maturing adhesion sites [446]. Their findings on the formation of the lamellipodium-lamellum interface indicate that adhesion in 2D qualitatively differs from a 1D case since the focal adhesion distribution directly affects the network architecture.

Understanding more and more fundamental properties of all three essential components for cell migration – protrusion, contraction, and adhesion – a way to integrate these components is needed to model larger parts of migrating cells. This has been done in a number of ways. Some models combining at least two components were already mentioned, such as protrusion and adhesion [415,417,444,446]. Some of them even include contractile elements, however, none of them presents an entirely closed system that reflects a whole cell.

1D models combining all three components have already been developed about 20 years ago [447]. More recent 1D models put more emphasis on the viscoelastic properties of the actin gel and account for actin assembly and disassembly [418]. As previously seen for the case of adhesion sites and force transduction, the 2D situation shows qualitative differences when compared to the 1D reduction. Naturally, important aspects of cell migration such as cell shape and cell turning need at least two modeling dimensions.

Using different multiscale 2D models, it became possible to reproduce the keratocyte shape and type of movement [413,414]. The fan-like shape of migrating keratocytes, however, can even be explained by simpler models only based on a conservation of the cells’ area and an observed F-actin gradient along the leading edge [448]. Another possibility to reproduce the keratocytes shape is by phenomenological rule-based models [449]. For further details, we also recommend another review on the cell shape in migrating cells [450].

Having keratocytes in mind, it seems that one rapidly approaches a complete picture of their type of motion. However, this only represents a very particular case of cell migration. First, it is a representative for 2D cell migration (see Section 3.3.2). Second, keratocyte movement is very particular in its characteristics and in fact was chosen as a model system precisely for this reason. Keratocytes are the prototype cell for fast, directed, persistent, lamellipodia-based motion. Most cells, however, are far more complicated in their migration dynamics (Figure 35) [372]. A complete picture of whole cell migration that includes filopodia and/or MT dynamics remains a long way to go.

Figure. 35.

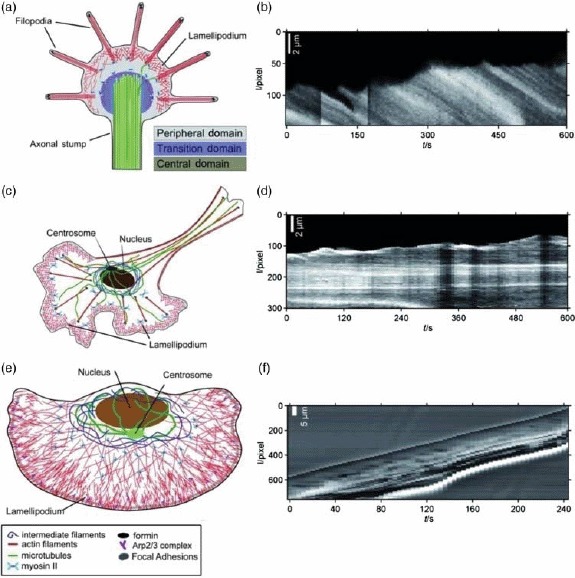
Different cell types do not only differ in morphology and cytoskeletal architecture (illustrated on the left side) but further display distinct migration characteristics. Kymographs of the leading edge of three different cell types are shown on the right (b, d, f) with the signature of persistent forward motion in the case of keratocytes (f) and significant edge fluctuations for neuronal growth cones (b) and fibroblasts (d). Image was adapted from [372].

3.3.5. Making cells sensible – the role of filopodia and MTs

It seems clear that the presence of filopodia is related to the ability of motile cells to sense adhesion gradients and guidance cues [380]. Fibroblasts and neuronal growth cones, two other common model systems for cellular motility which are going to be presented show both characteristic filopodia formation. While some details of the underlying mechanisms regarding filopodia formation remain elusive, important insights have been gained concerning their composition and assembly. The process of filopodia initiation was investigated using GFP-tagged structural proteins as markers [451]. They found that in murine melanoma cells most filopodia emerge from lambda-shaped actin structures forming in the lamellipodium (A-precursors). In contrast to previous assumptions, the filament nucleating protein Arp2/3 seems not to participate in the formation of these structures. Other proteins abundant in filopodia like the cross-linker fascin and the capping inhibitor VASP were detected in A-precursors indicating a central role for the formation of filopodia. VASP enriched regions of the leading edge merge to single spots indicating the fusion of multiple fast growing filaments into filopodial bundles. Other findings support the idea of specific protein complexes first assembling in the vicinity of the cell membrane and eventually initiating filopodia formation [452,453]. In addition, it was shown in a minimal system of branched actin networks growing against a lipid membrane that already free energy minimization leads to the formation of bundled actin structures that resemble filopodia [200].

The relation between filopodia dynamics and cellular detection of guidance cues is very complex and includes mechanical sensing (durotaxis) and chemical sensing (chemotaxis). Both variants require specific interactions between receptor proteins for various signaling and adhesion molecules enriched in filopodia and the cellular environment. In the case of durotaxis, a mechanism involving molecular clutches has been proposed by Chan and Odde [444] (Figure 36). Integrins located in the membrane envelope of filopodia establish transient connections between filopodial actin bundles and the substrate. These connections as well as the substrate itself are modeled as Hookean springs with force-dependent binding and unbinding rates. In agreement with experimental data from chick neurons their model predicts an influence of the substrate deformability on internal actin transport. According to their data, filopodia show the highest sensitivity to substrate stiffness in a range from 730 to 1300 Pa. The clutch model for filopodia traction dynamics is capable of explaining the so-called inverse durotaxis of neuronal growth cones, showing an increase in motility on softer substrates (see Section 3.3.6).

Figure. 36.

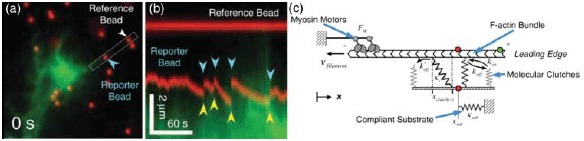
The movements of growth cone filopodia on compliant substrates (a and b) observed by Chan and Odde [444] can be explained by a motor-clutch model (c). Images were taken from Chan and Odde [444] with permission from AAAS.

A very common type of filopodia-based motility is found in fibroblasts that are responsible for the assembly of the ECM. They also play a role in tissue remodeling as well as wound healing processes. Before moving, fibroblasts polarize and form a small lamellipodium toward the direction of motion. Unlike keratocytes, fibroblasts autonomously switch from motile to stationary phases and are able to retract and rebuild their lamellipodium at any given direction. This flexibility is achieved by variations in actin polymerization speed. As long as polymerization exceeds retrograde flow, the leading edge moves forward. Down-regulated polymerization causes retraction of the lamellipodium. Switching between polymerization on and off states results in edge fluctuations which most likely help the cell to better detect external stimuli and to readjust the motility machinery accordingly [371,372,454].

While it is generally accepted that actin-based filopodia are fundamental elements in cell migration, the role of MTs attracted much less attention. In motile fibroblasts, MTs occasionally explore the periphery of the fluctuating lamellipodium where they target new adhesion sites to influence their maturation [455].

MTs hold a much more dominant function in another type of cellular motility represented by the growth cones of neuronal cells. Neurons are highly specialized cells that have to accurately follow a large number of overlapping guidance cues during the development of the central nervous system. Any deviation from the designated route will lead to malfunctions or disabilities of the respective organism and thus nature had to endow neurons with a sensitive and robust detection system for all kinds of signaling cues. After differentiation, the neuron undergoes a process of extensive morphological and structural changes. External signals induce the selective stabilization of certain populations of MTs resulting in a symmetry break and polarization of the cell [302]. In the periphery of the cell, MTs get “captured” by components in the cell cortex. This leads in most neurons to the development of multiple processes, usually one axon and several dendrites which are later able to send or receive electric signals, respectively. Axonal MTs are rich in tau and show parallel orientation with the highly dynamic plus-ends pointing toward the distal end of the process. In contrast, MTs in the MAP2-rich dendrites can be oriented in both ways. Already at the point of initial stabilization, the future fate of a neuronal process (neurite) is determined by the specific way MTs are stabilized and oriented. Once the outgrowth of a neurite from the soma has begun, MTs get bundled in order to build a stable shaft. This is achieved by a combination of biochemical cross-linking through MAP activity and mechanical compression by contractile actin bundles (actin arcs) that exert radial forces on the internal MT network [63]. The growth cone is located at the end of the neurite and appears as a flat fan shaped structure responsible for outgrowth and path finding (Figure 37). The growth cone center is dominated by the large MT bundle with a sub-population of dynamic MTs exploring the peripheral domain (Figure 35(a)). The peripheral domain comprises a pronounced lamellipodium together with numerous filopodia radially pointing outwards reaching beyond the lamellipodium (Figure 35(a), Figure 37).

Figure. 37.

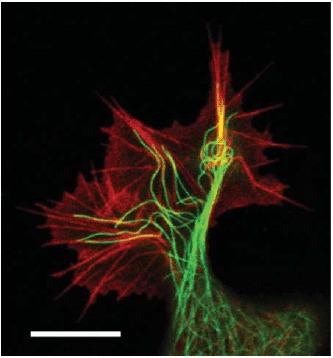
Emerging neurite of an NG-108 15 neuronal cell with overlapping growth cones. Actin networks and bundles (red) form the lamellipodium and filopodia of the cone, respectively. MTs (green) are bundled in the neurite shaft and explore the periphery of the growth cone, most likely to target adhesion sites. Confocal laser scanning image, scale bar: 10 μm.

Actin–MT interaction in the peripheral domain apparently plays a crucial role for growth cone path finding [63,130,456]. MTs preferential extend along filopodia apparently serving as polymerization guides [457]. However, it has been shown that in growth cones MTs can also advance into filopodia depleted lamellipodia [458]. In many cases cross-linking proteins seem to induce a direct physical coupling of MTs to the actin cytoskeleton [130,457,459]. In addition, active stiffening of MTs by the surrounding actin–myosin medium was proposed as a mechanism to guide MTs into filopodia [460]. Recent work even demonstrates that microtubules substantially contribute to the total protrusion force of growth cones [621].

Realizing that growth cones are more or less made of the same components than other motile cells, it is not obvious at first why they detect guidance cues in a noisy environment more efficiently. Interestingly, the reason is not only the presence of specialized receptors, but the way these receptors interact with the dynamic cytoskeleton. The edge of the lamellipodium performs steady fluctuations correlated to local switching between actin polymerization on and off states [372]. These fluctuations may improve the precise detection of environmental stimuli due to their stochastic nature.

A process known as stochastic resonance is believed to help improving the signal to noise ratio allowing the detection of signals close to the background noise. It was shown that these complex fluctuations can be very well described by relatively robust mathematical means [371]. Assuming a stochastic bistable process behind the lamellipodium dynamics of the growth cone edge led to a more detailed understanding of the underlying processes. Switching rates between growth and retraction phases correspond to jump processes in a potential landscape that is tuned by the cell in response to external signals. Directed protrusion occurs when jumps toward a growth phase become favored. On the cytoskeletal level, these jumps are implemented through changes in the actin polymerization rate at the growth cone edge. Parameters derived from the experimental data are in excellent agreement with Kramers’ model for bistable stochastic processes.

However, the way external signals are subsequently translated into cytoskeletal reconstruction is still under investigation. Very likely small external gradients are amplified by numerous internal mechanisms in order to cut off noise for further signal processing [461]. In the same context, sensing external signals is not limited to the detection of chemical substances but further includes mechanosensitivity enabling cells to react to mechanical properties of their environment.

3.3.6. Mechanosensitivity and mechanotransduction

The very adaptive nature of living cells does not only manifest in the form of active cell migration (Section 3.3.3) or highly robust cell division (Section 3.2), but further includes the cell's ability to recognize and respond to its surrounding. At any given time, cells face a multitude of external stimuli, mainly of biochemical but also of mechanical nature. Signaling cascades triggered by these environmental influences can lead to a variety of different changes in cell morphology, dynamics or gene expression or even cause apoptosis. In recent years, it has become clear that in addition to biochemical signals, forces and mechanical properties act as main regulators for a large variety of cellular processes [462,463]. Among these are polarization and motility (Section 3.3.3), the regulation of cell behavior during development, and embryogenesis (Section 4) as well as gene expression resulting in the differentiation of stem cells into specific cell lineages. Also tissue physiology and a number of diseases have been shown to be related to the mechanosensing abilities of cells.

But how does mechanosensitivity work? Many components are believed to function as mechanosensors or to contribute to the force sensing mechanisms of cells: ECM-molecules, the cytoskeleton (Section 2.2.3), transmembrane proteins (e.g. integrins), proteins at the membrane-phospholipid interface, elements of the nuclear matrix, chromatines and the lipid bilayer membrane itself [463,464]. Hence, mechanosensitivity can result from many interrelated processes (Figure 38).

Figure. 38.

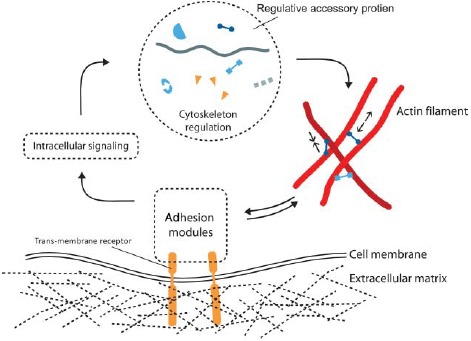
Schematic illustrating the interplay of the actin cytoskeleton with focal adhesions. A feedback loop including trans-membrane receptors that are connected via a rather complex adhesion module to intracellular signaling pathways relates ECM properties (chemistry, mechanics) to cytoskeleton regulation. Receptor modules (e.g. integrins) transmit signals to protein complexes responsible for signaling or actin dynamics. In turn the cytoskeleton influences the maturation and configuration of focal adhesion complexes. Image inspired by Geiger et al. [440].

An essential mechanism for sensing lies in the translation of mechanical into biochemical signals (mechanotransduction) with a key role ascribed to the sites of adhesion where cells connect to a substrate, the ECM or other cells [465]. Cell–substrate contacts comprise elaborate protein complexes termed focal adhesions or focal adhesion complexes (FACs) mechanically coupling the cell exterior to intracellular components of the cytoskeleton. Integrin family proteins span the cell membrane and act as receptors for extracellular adhesion molecules. Integrins cover a wide range of possible binding sites on both sides of the membrane enabling biochemical inter-membrane communication. This makes them the most important transductional elements of bi-directional intercellular signaling [466]. On the cytoplasmic side, they recruit a number of adhesion-related proteins like zyxin, vinculin, talin and α-actinin which establish a mechanical link to the contractile intracellular actin network. Thus, forces generated or applied at one site can be transmitted to distant areas of the cell such as the nucleus where related signaling cascades may be triggered.

After an initial contact to the substrate or the ECM has been established, the fate of focal adhesions is governed by force-dependent signaling and a close cross-talk between focal adhesion proteins and the actin and MT cytoskeleton. Small focal adhesions containing only several bonds to the substrate grow in a force-dependent manner [467]. A two-spring model was proposed as a convincing and simple way to relate applied forces and substrate elasticity to the maturation or degradation of adhesion complexes [468]. Direction and magnitude of applied forces, either external or generated by the cell itself, directly influence the size and orientation of FACs in living cells on a timescale of tens of seconds to minutes [469]. A linear relation between force and FAC was observed for cells with fluorescently labeled FACs growing on micro-patterned elastic substrates [470]. Effects of substrate patterning, however, are not limited to protein recruitment. Also gene expression levels do change depending on nano-scale structures on the substrate [471].

In many cases, the actual conversion of mechanical into biochemical signals seems to be accomplished by mechano-induced changes in protein conformation and resulting variations in molecular binding capacities and rates. Locally altered affinities for signaling and adhesion molecules allow the cell to regulate the fate of individual adhesion sites depending on environmental influences. There is evidence that the adhesion-related proteins focal adhesion kinase and zyxin show stretch-dependent affinities for binding to the cytoskeleton and other components of the adhesion complexes in adherent cells [469].

Another important regulation pathway for cellular adhesions is the biochemical and mechanical interplay of adhesion molecules with the cytoskeleton. An active myosin-actin network covers the whole cell, capable of forming force generating and transmitting structures. Thus, the cell itself is able to exert forces on adhesion sites which in turn regulate the formation of contractile actin structures. Both, self-generated pre-stress as well as external mechanical stimuli influence the active or passive behavior of adherent cells. This results in a feedback mechanism that leads to an adaptation of the cell's stiffness to the stiffness of its environment. Fibroblasts cultured on substrates of variable stiffness, mimicking soft tissue environments, automatically increase their own rigidity to match substrate stiffnesses ranging from 500 to 40,000 Pa [472]. In addition to the ability to adapt to the mechanical properties of their environment, a number of cell types show clear preferences for substrates with certain mechanical characteristics [473]. Fibroblasts cultured on 2D substrates with a rigidity gradient preferentially move toward the stiffer region, a phenomenon that was termed durotaxis [474]. Durotaxis has been observed in many cases, mostly for tissue cells that are subject to mechanical changes in the ECM they are embedded in. A different type of mechanosensitivity, termed inverse durotaxis was found in neurons which seem to prefer very soft environments [475,476]. Apparently this is closely related to the fact that in nerve tissue neurons are surrounded by very soft glial cells potentially supporting neuronal growth and plasticity [219]. Complementing chemical guidance cues, durotaxis on elastic substrates regulates neuronal outgrowth and helps to selectively stabilize or retract neuronal processes [477]. The physiological surrounding of cells, however, is typically not composed of purely elastic components. Cytoskeleton and ECM meshworks clearly show elastic behavior when sufficiently cross-linked, but especially on longer timescales viscous behavior notably influences the overall mechanical properties of biological materials. The question arises whether cellular mechanosensing solely depends on elastic responses of the environment or if viscous adhesion substrates like the membranes of neighboring cells also contribute to the mechano-chemical signaling process. Artificial lipid membranes that have been modified to serve as cell adhesion substrates were applied to investigate the behavior of motile cells in a surrounding that provides only viscous response to cellular forces. Depending on the actual viscosity of the substrate, these cells showed remarkable changes in their internal organization of the actin cytoskeleton. This indicates that cellular adhesion and force transmission are possible even when substrate responses hardly differ from that of the cell's own membrane.

Interestingly, cross-talk between adhesion sites and the cytoskeleton does not necessarily include direct mechanical interactions. In polarized motile cells where FACs undergo a cycle of initiation, maturation, and disassembly, specific biochemical interactions between single MTs and adhesion molecules have been observed. Individual MTs were reported to specifically target newly generated FACs [478] and to play a crucial role for focal adhesion turnover [479]. It is very likely that MTs directly influence focal adhesion sites by delivering specific proteins either through motor-driven transport or in form of MT-bound regulators [479–481].

In addition to local modifications of the size and orientation of adhesion complexes and influences on the cytoskeleton, mechanical stimuli can also have a profound impact on the genetic development of cells. The mechanisms through which force signals are mediated to the nucleus eventually altering gene expression are not fully understood yet. The consequences of these processes, however, are clearly visible and shine a new light on the importance of physical aspects of stem cell differentiation and tissue engineering. Mesenchymal stem cells can differentiate into a number of different tissue cells, including brain, muscle and bone tissue, each of which has characteristic mechanical properties. When stem cells are exposed to an environment mimicking the elastic properties of one of those tissue types, they preferably differentiate into the corresponding cell type. On substrates with an elastic modulus of 0.1 to 1 kPa, matching that of brain tissue, an increase of neurogenic marker level has been observed. The same behavior can be seen for muscle (8–17 kPa) and bone-associated tissue (25–40 kPa) [224]. Of course, mechanical stimuli are not the only trigger for stem cell differentiation or the adaption of cells to their physiological environment. However, there is more and more evidence that the proper development of tissue and organisms strongly depends on mechanical influences and that disorders in the mechanosensing machinery of the cell are closely related to defective developments and diseases.

3.4. Synopsis and open questions

Since many years, the field of cell mechanics attracted a lot of attention among physicists, probably because mechanical properties are obviously close to physical criteria. In contrast to most synthetic materials, however, cells issue a fundamentally new challenge to physics. In several aspects, cells represent an entirely new class of material combining highly anisotropic, compound structures with non-equilibrium. This might already serve as an explanation for the dominance of mostly phenomenological models describing cellular mechanics (see Section 3.1). To bridge the existing gap between cellular and subcellular level, it will be necessary to trace back the mechanical properties of cells to a more microscopic cytoskeletal level. Only a more microscopic theory will give access as to why and how cytoskeletal changes correlate to changes in cell mechanics (Figure 39).

Figure 39.

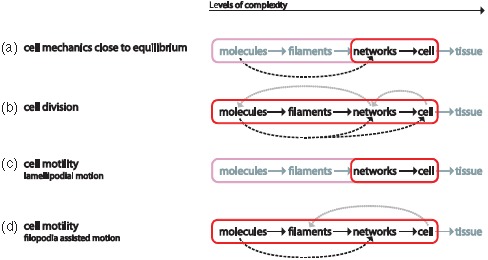
The ability for coarse-graining varies strongly among the different phenomena studied on the cellular level. (a) So far, the mechanical behavior of cells on shorter timescales is mostly described by phenomenological models. A decent microscopic understanding might already result from models originating from the underlying network level. By comparing to the subcellular level, however, one has to expect that compound and transient networks will be most relevant demanding some adaptation of even lower levels. (b) Cell division involves the interplay of numerous different proteins and includes several internal feedback loops which makes it less accessible to coarse-graining. (c + d) Various model approaches aim at further understanding cell motility. Lamellipodial motion is particularly accessible to coarse-graining and hence attracted most attention from physicists (c). Whereas some models start from the molecular level others further coarse-grain the problem to the network, i.e. the actin gel level. (d) As soon as filopodia or MTs significantly influence the cellular migration, the filament can no longer be ignored.

In its full complexity, cell division appears similarly complicated and in addition has not been in focus of physicists for so long. Recently, more physical models start to evolve and due to the highly fascinating physics taking place during cell division much more attention can be expected in the near future. Again, a main problem seems to be the difficulty to coarse-grain underlying processes due to a highly intertwined level structure (see Section 3.2). It is still not fully resolved how cells are able to undergo a geometrically well-defined division with very high accuracy despite being in a highly anisotropic environment. Cells need a robust length measure which functions properly independent of variations of the external pressure (from surrounding tissue) or available space. In its accuracy and precision, cell division resembles a perfectly designed mechanistic process, yet inherently it originates from stochastic self-organization.

A very general problem (which we noted for instance in the context of cell migration) is the insufficient distinction between long-term hypotheses and well-founded theoretical models. The array treadmilling picture or the Brownian ratchet models, for instance, certainly represent very valuable working hypotheses, but in both cases important open questions remain (Section 3.3.3). Very often models are primarily used to consistently explain a set of experimental observation but too often seem to have only little predictive power. This is usually the case when models remain too vague (e.g. too many parameters or arbitrary numbers of possible additional elements).

In general, we notice that reconstituted mimicking systems clearly become increasingly important on the cellular level and already contributed substantially to our current understanding of fundamental functional modules with particular success regarding cell motility and the reconstruction of lamellipodia-like network growth in vitro (see Section 3.3). Currently, much emphasis is put on the integration of dynamic actin networks into membrane enclosed vesicles as one possible way to further mimic even larger cellular modules [482–484]. On a longer perspective, an important future goal will most likely be to rebuilt or to synthetically construct autonomously migrating entities. These bottom-up approaches can, in principle, nicely be complemented by using the available genetic toolbox. More frequent use of modern cell biological methods might allow to systematically probe physical models on the cellular level.

4. Multicellular level

4.1. Cells collaborate tightly

Presumably all cells are able to sense external signals and to react to it. Cells are also able to produce the corresponding cues intended for stimulating other cells (e.g. release of signal molecules), thereby presenting a closed feed-back loop establishing the basis for intercellular communication. In this context, bacteria invented quorum sensing as an efficient method for reacting collectively to external cues [485]. This apparently was a new way in evolution to compete successfully by responding collectively. Furthermore, those signals represent the bacterial production of a common good which results in cooperative behavior again being evolutionary favorable in certain cases [486].

Mostly, however, bacteria conserved an autonomous, individual life form until today. The collective organization was further deepened with the appearance of a totally new cell type, the eukaryotic cell. This new cell type was able to use oxygen, poisoning most of the bacteria. A second important “invention” is a less protective but more communicative cellular membrane which got reduced to a simple lipid bilayer stabilized by a flexible and controllable actin cortex instead of passive two bilayers (biderm) or one bilayer plus a rigid cell wall (monoderm). The chromosomes became protected by an additional inner nuclear membrane. This opened the door to a new emergent level of complexity, the tightly organized cellular community named tissue with entirely new possibilities comprising simultaneous response to external cues resulting in significantly improved resistance to hostile living conditions. The price of collective organization, however, is that the cell's existence becomes submitted to the requirements of the larger entity. An efficient conjoined action brings many survival advantages of which only few may be mentioned here: faster locomotion (crawling, walking), specialized cells allowing for increased survival probability (e.g. immune system, vision, bones), exploitation of new sources of nutrients (animals, plants), and penetration into new habitats (land, air) initially still free from competitors. In terms of selection, it appears that the advantages of an integration into a tissue opens a new niche characterized by a large spatial and temporal scale providing the possibility to escape the conditions of the microscopic world dominated by surface forces and thermal fluctuations. Statistical mechanics teaches us that with increasing system size N relative fluctuations of physical quantities as, e.g. the energy, δE/N ∼ 1/sqrt(N), decrease which provides structural stability. Structural stability allows more complex and fragile systems with more specific response but also implicates a slower adaptation to external conditions. Following this way, eukaryotic cells link their fate irreversibly to the fate of the entire community. Despite the fact, that multicellular organisms are all based on the same fundamental units – single cells – the variety of morphologies and dynamics is stunning. This comprises a huge class of organisms, which we will of course not be able to cover completely. However, we assume that a rather small number of more general biophysical and biochemical mechanisms apply to a wide range of tissue formation and regulation processes. By restriction to few species, we try to develop a consistent picture of mechanical and biochemical aspects according to the present-days knowledge.

In this context, the amoeba Dictyostelium discoideum represents a remarkable model system bridging the gap between unicellular and multicellular organisms. Its cells prefer to live isolated until upon nutrition shortage they start diffusing the messenger molecule cAMP (cyclic adenosine monophosphate) into the environment. Nearby cells may detect the signal and move in direction of its gradient. In turn, those cells start producing and secreting cAMP. Once a cell produces cAMP, the detection sensitivity has to be reduced in order to avoid signal saturation. As a consequence, the cAMP release and sensing appears consecutively in periods and creates an outwards moving spiral [487]. The cells migrate toward the center of the principal spiral and form spores or slugs being able to escape the starvation thread much better than a single cell. Other species do not provide an isolated cell state anymore and their tissues got far more specialized. The embryonic development of those species involves a cellular ensemble from the very beginning: an oocyte or a bud. The question arises as to how cells organize such organisms during development and which factors mainly regulate this organization.

Active and passive mechanical cell properties, cell–cell adhesion, signaling, and genetic control are the principal factors acting in a coordinated manner in order to organize tissues from simple embryonic cell clusters to filigree structures and well organized tissues. Since the topic is vast and little is really understood, we will mainly restrict our review to two species, Hydra vulgaris, a simple sweetwater polyp and zebrafish (Danio rerio) as a more complex representative belonging to the vertebrates. Why is Hydra interesting being so apparently different than higher evolved organisms, notably the human organism? The reasons are its structural and cellular simplicity and uniformity (though its genome size is comparable to the human genome size) allowing to discern more easily different phenomena. Its transparency significantly facilitates microscopic 2D and 3D observation (this also applies to other model organisms such as C. elegans or zebrafish). A further reason is its outstanding regenerative tissue plasticity raising many questions concerning tissue engineering and regeneration research [488]. Regarding tumorigenesis, the relation of hydra development and the tumoral epithelial-mesenchymal transition is of high interest as both are based on the same signaling Wnt pathway. In comparison to tumor tissues, Hydra growth is equally perpetual, but the resulting shape seems more organized and controlled than in tumors but definitely less controlled than in more complex tissues (e.g. in drosophila or zebrafish). It can be speculated that Hydra tissue is a partially organized tumor or a tissue deprived of proliferation arrest mechanisms probably similar to a benign tumor. Both possess stem cell populations which proliferate slowly but without limitations [489]. Literature comparing Hydra and tumors is rare and the topic may give rise to new interesting research projects.

Zebrafish is one of the most common model organisms for investigating embryogenesis, due to its advantage of producing transparent eggs in large numbers. As a vertebrate, it shows many features of the more complex development of higher organisms. The development of an early embryo is quite rapid (few hours) displaying several interesting stages. Zebrafish eggs are protected by a shell (chorion) and consist of a very large yolk cell carrying the blastomere at the animal pole. The cleavage period shows a perfectly synchronous sequence of divisions up to 1024 cells. Subsequently, synchronization gets lost and the circular bastodisc, of which the cell number is not counted anymore, begins flattening after little more than three hours after fertilization. Afterwards, yolk cells begin bulging (formation of a “dome”) toward the animal pole and epiboly begins. The spherical symmetry is broken leading to a sequence of complex rearrangements resulting in the fish embryo [490]. This development is surprising with a discrete-continuous transition leading to spherical symmetry which finally is broken again to allow more complex structures. It is intriguing and poorly understood how this cellular ballet is organized.

4.1.1. Intercellular communication

In the early days of tissue research, when chemical signaling was still far from being discovered, morphogenesis was understood as a purely mechanical phenomenon [491]. Later, Spemann and Mangold investigated the role of implants in the differentiation of the surrounding tissue and assumed a cellular cause driving differentiation [492]. Holtfreter surprised by bringing denatured tissues (heated or exposed to 70% ethanol) into contact to a developing alive tissue observing that induction of differentiation still takes place. He showed that development can also be triggered by other factors and assumed chemical cues [493,494]. It took a long time, however, before the molecular components and the corresponding mechanisms were identified.

Theory was faster and in 1952, the mathematician Alan Turing proposed a strategy to describe spatio-temporal patterns by differential equations. The question is how spatio-temporal patterns arise in a featureless medium [323,495]. Mathematical models showing instable features lead to a description of pattern-formation by reaction-diffusion equations. Regarding biological morphogenesis Turing postulated a system of chemical signaling with “substances, called morphogens sensed by the cells reacting specifically and diffusing across the tissue” [323]. Not knowing the nature of those substances, Turing proposed hormons or genes, though not diffusing, and skin pigments. The approach considers two cross-coupled, spatio-temporal fields, an activator and an inhibitor field acting in opposite ways. Hydra was suggested as a model organism being sufficiently simple for a mathematical description.

Hydra shows a quite simple morphology presenting an advantage for modeling attempts. It mainly consists of a digestive tube, termed gastric column, ending up with the head surrounded by 4 to 7 tentacles on one side (Figure 40) and a basal disk on the other enabling Hydra to attach to various substrates. Its reproduction versatility is particularly remarkable. Besides sexual proliferation, it shows spore formation and complete regeneration from tissue fragments. Bud formation in the column, however, is the predominant way.

Figure. 40.

(a) Grafting experiments showed the effect of the homeostatic flow and the high level of versatility of Hydra tissues [496]. (b) Image of H. vulgaris depicting its most prominent parts. Hydras morphology is simple: a gastric column ends in a head (hypostome) surrounded by tentacles and a basal disk at the other side. (c) Hydra cells can be cut into pieces or even be entirely disassembled and re-aggregated to form a new organism. Within this process, first a hollow sphere is formed. This sphere passes through several phases of pulsations before a new small hydra finally emerges. Figure (a) was adapted from [496], figure (c) was inspired by [497].

The hollow gastric column is confined by an epithelial double-layer separated by an ECM structure (mesoglea membrane). Hydras contain about 20 cell types and three different stem cell lineages able to proliferate without limitation [498]. At the extremities, most tentacle and hypostome cells as well as the basal disk cells are more differentiated and lost division capabilities. 85% of the proliferating gastric column cells are directed to the bud. This process allows the organism to maintain a constant size. In contrast to the amoeboid Dictyostelium, Hydra cells are not capable to live as individual cells and depend at least on the presence of a mesoglea supporting and stabilizing the tissue mechanically [499].

The gastric column cells proliferate constantly to renew the whole organism. Cells flow from the inner part toward the two opposite extremities and differentiate irreversibly [500]. Each cell of the organism is replaced after four days [501]. Hydra was, therefore, described as an eternal embryo which does not show a final state with arrested cells as it is the case, for example, for zebrafish or the human body. Hence, fate maps describing the functional and positional destination of cells during embryonic development do not fully cover the cellular dynamics. The apparent similarity to tumor growth may render Hydra particularly interesting to tumor and regeneration research. Cellular tissue invasion is studied by placing cells into different parts of a growing organism (grafting), which may serve as a model system for metastasis and wound healing. Hydras have even been observed over a period of four years in which somatic epithelial cells may have divided at least 300 times meaning the whole organism may have been fully replaced at least 60 times [502]. No significant mortality rate could be stated meaning that Hydra may have escaped mortality. The lack of senescence could only be observed in primitive organisms as Hydra or planarians so far [503,504]. Besides the differentiation grade, the body symmetry suited for scaling may be a prerequisite for the advantageous regeneration capability.

Hydra displays total regeneration of a new organism based on re-aggregation of single cells (Figure 40(c)). This gives rise to the fundamental question of how the global tissue organization can arise from local information.

Numerous classical grafting experiments on hydra such as found in Mutz [496] (Figure 40(a)), revealed that structures are integrated or suppressed depending on their relative position in the organism (Figure 41). The cells of this organism are permanently replaced due to homeostatic flow. It remains unclear how hydra conserves its size, which seems to require precise coordination of cellular differentiation and apoptosis.

Figure. 41.

Systematic grafting experiments revealed the importance of the provenience and the destination position of the tissue fragment. Head cells are supposed to segregate head inhibitors. Inserting a head fragment close to a head inhibits new head formation (a). Only at distal inserting positions a head is formed since the inhibitor level is low there (b). Grafts of distal origins also show only weak head formation even if inserted at a distal position as the activator level is small (a). (c) The activator activates head formation but at the same time raises the inhibitor level while the inhibitor in turn suppresses the activator and consequently the head formation [505,506]. Figures (a) + (b) were adapted from Müller [505] with permission from Elsevier.

An important approach to understand the formation of a single-body axis was elaborated by Gierer and Meinhardt [507] describing semi-quantitatively the grafting experiments with Hydra [508–510]. Short-range activators were introduced triggering the activation of head formation, while long-range inhibitors suppress it. Although the molecular realization of these activators and inhibitors is still not fully resolved, activation seems to be a consequence of the expression of HyWnt (Hydra Wnt) genes triggering a consecutive cascade of different Wnt genes related to beta-catenin [511].

A fundamental question aims at the influence of differentiation (process by which cells become more specialized cells) versus migration during morphogenesis, distinguishing between constant and variable lineages. Constant lineage cells, as found in nematodes, are determined by their origin [512] resulting in malformations upon cell removal (e.g. using laser ablation to irreversibly remove cells). In Drosophila cell fate is not determined a priori and cell removal results in replacement by other cells as long as those cells belong to the same compartment. Even mammalian cells stay entirely variable during early phases of embryonic development. These cells are determined by their position and not by their origin. They further show extensive cell migration enabling a significantly higher plasticity and compensation capacity in case of cellular loss or damage during early development [512]. In zebrafish, the primordial germ cells, initially dividing in a perfectly ordered manner, undergo a transition to motile cells. This transition correlates with cadherin expression and presumably calcium gradients, but the underlying mechanisms remain unexplained [513]. In the simpler model organism Hydra, cells migrate and differentiate simultaneously. Cell-migration in Hydra is particularly increased after having grafted new cells into the organism. To a small percentage cells even migrate opposite to the homeostatic flow direction and bulk movement has been observed after grafting [514].

How do cells know about the required degree of differentiation or migration direction corresponding to their current position in such an agile environment? This fact implies that cells have access to positional information, for instance by measuring the local concentration of morphogens using a threshold, a concept introduced by Wolpert [515]. Although at first, this approach appears simple, it encounters the problem that cells do not possess calibrated sensors that are precise enough. Even worse, sensing is exposed to thermal and concentration fluctuations being considerable at a molecular scale as well as fluctuations due to active cellular movements. The dynamic nature of cells is, in fact, rather an advantage when registering differential signals in time or space (e.g. expression rate, degradation rate, gradients) instead of absolute levels.

Therefore, Turing's nonlinear approach based on self-organization appears to be better suited and has consequently been developed further and substantially refined for Hydra mainly by Gierer and Meinhardt [516,518]. Their model is a nonlinear spatio-temporal field theory ignoring the cellular nature of tissues including mechanical cues. Two coupled time and space-dependent fields with corresponding diffusion constants were introduced representing the concentrations of a short-range activator and a long-range inhibitor as well as a spatial source density distribution for each field. Numerical simulations revealed that slightly asymmetric source density distributions produce stable patterns when starting from uniform distributions of activator and inhibitor fields [495,507,517]. The hope was to reveal the diffusive properties of the actual molecular signaling components based on the proposed reaction-diffusion model [518]. So far, however, these morphogens have not been clearly identified [506].

At least for Drosophila, different transcription factors determining the anterior-posterior axis formation by gradients were indeed identified [519]. In its early stage, the drosophila embryo is a cell with multiple dividing nuclei (syncytium). Nuclear divisions in this phase are accompanied by the formation of several different morphogen gradients triggering local gene expression [519,520]. The mechanism for establishing the respective gradients differ substantially between morphogens [520]. A stable gradient of the transcription factor Bicoid is formed by continuous production and degradation of corresponding proteins and is responsible for establishing the anterior-posterior axis [520,521]. It has been shown that both the gradient and the local readout are very precies, close to the limits set by basic physical principles [521]. This is an instructive example for gradient-induced patterning confirming the relevance of reaction-diffusion systems for development. Nevertheless, it remains unknown to what extent morphogen gradients are involved in tissue organization in multicellular non-syncytial embryos and tissues. It might be asked if sensing of global gradients is already sufficient to organize more complex tissues and fine structures as the zebrafish lateral line. If a typical signaling-gradient spreads over 10⁴ cells, a relative and temporally stable sensitivity on the order of 10⁻⁴ would be enough to determine the relative position with a resolution on the cellular scale. In general, such precision is not easily feasible to biological systems since they are strongly submitted to drift and noise. Hence, it must be assumed that a subsequent post-gradient refinement and resharpening process takes place to comply with the requirements for the observed delicate and precise patterns [522]. The initial gradient is then required to give an initial coarse cue to the tissue to break the symmetric situation and to give rough global positional information. Subsequent local nonlinear sharpening mechanisms enable the creation of locally fine-tuned patterns. Temporal modulation of signaling molecules propagating within the tissue leads to stripe pattern generation facilitating the positioning problem. A prominent example is the segmentation clock of zebrafish responsible for the morphogenesis of these vertebrates [522].

Other phenomena in contrast seem barely accessible to a reaction-diffusion-based description such as the bulk movement in zebrafish lateral line morphogenesis. Gradients are without doubt a major principle in development. However, it is difficult to imagine stable global gradients to entirely control development in the heterogeneous and highly dynamic environment of growing tissues. Direct cell–cell communication provides an additional alternative. Transmembrane proteins establish intercellular junctions serving as communication paths by allowing molecule exchange but also transmission of mechanical stress (see also Section 3.3.6).

Signaling pathways, for instance, control molecules from the cadherin family in adherens junctions joining actin networks of adjacent cells. One type of junctions, the desmosomes, organizes IFs to the cell membrane and tethers them to neighbor cells. Tight junctions (claudins and occludins) provide sealing against liquid leakage [6]. Gap junctions provide a direct intercellular path accessible to electrical or chemical signaling (Figure 42(a)) [6]. Electrical signaling is the fastest, however, it is lacking specificity and an efficient de-exciting control. Chemical signals are much slower but can address very specific receptors and antagonists may control the signal increase and suppression. A gap junction channel is composed of two connexons located in the two adjacent membranes and consists of connexins. Only if the connexons are coaxially aligned, the pore is opened for molecular exchange (Figure 42(a)). The permeability of gap junctions can be controlled by pH (voltage gated channels) and calcium ions [523–525]. This permits cells to dynamically modulate rapid and long range communication paths suited for fast and complex cellular rearrangements during morphogenesis and in myocytes [524,526]. Gap junctions can conduct molecules of sizes below 5 kDa [6] suited for translocation of signaling molecules but no larger proteins and enzymes.

Figure. 42.

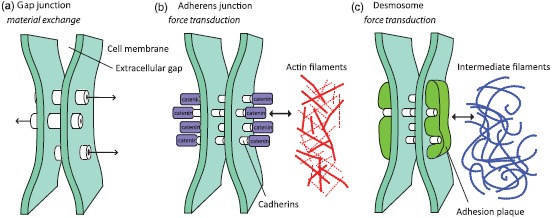
Different types of cell–cell junctions allow different means of intracellular communication. Gap junctions (a) allow cells in a tissue to directly exchange signaling molecules and ions. Other junction types such as adherens junctions (b) or desmosome junctions (c) establish direct links between the cytoskeletal networks of two neighboring cells. While adherens junctions link to actin filaments, the desmosome connects IFs (keratins).

In addition to gap-junctions, alternative ways of intercellular communication exist. Other mechanisms for intercellular exchange of molecules, e.g. vesicle exchange (transcytosis) or ligands externally hopping between cell receptors have been discussed in the literature [527–530].

Knowing that cells are in mutual communication, one could ask for the scaling properties of information exchange. Is a nearest neighbor communication sufficient to realize complex gradients? It is known from physics of critical phenomena that local interactions limit the range of accessible phenomena of the critical system [531]. In contrast to the nearest neighbor interaction in purely physical systems, cell-to-cell communication can be actively sustained against signal degradation and communication may take place across several cells. Membrane nanotubes extending from the cell surface (cytonemes) are suitable for connecting cells over longer distances. Individual myeloid cells, for example, can support up to 75 nanotubes [525,532]. Many cell types including neuronal cells, T cells, NK cells, and virally infected fibroblasts are able to form such connections [532]. It was found that cytonemes carry protein traffic in Drosophila wing discs and between dendritic cells in mouse corneas [533]. Since most investigations focused on in vitro systems, the role of membrane protrusions for tissues is not well-understood [532]. To which extent and under which conditions those tubes may be formed in tissues and how far the intracellular communication is based on these physical pathways remains an important open question.

4.2. Mechanical interactions and cellular displacement

4.2.1. Physical consequences of cell–cell adhesion: cell assemblies as liquids

Morphogen patterns and chemical signals discussed in the previous section are able to direct cellular migration and development in order to regulate tissue formation. In addition to this chemical signal-based communication, cells interact via physical connections. This can take place in form of direct cell–cell adhesions (Figure 42(b) and 42(c)), or indirectly by transmission through a surrounding (partially) elastic medium, for example the ECM (see also Section 3.3.5). Mechanical signals are very fast and can range from local interactions to very long-ranged signals depending on material properties and signal type [534,535]. Mechanotransduction allows translating incoming mechanical signals into intracellular, chemical signaling (Section 3.3.6). Alternatively, mechanical signals also have a direct mechanical influence on essential cellular components (e.g. cytoskeletal networks) that are responsible for sensing and signaling as well (see, e.g. p. 33).

Tissue formation will certainly depend to a notable degree on purely mechanical crosstalk. Already unspecific intercellular forces in form of mutual pulling and pushing, directly result in cooperative behavior during collective cell migration [535–537]. Unlike collectively migrating cells, cells in tissue use specific cell–cell adhesions to establish stable links between their cytoskeletal networks (Figure 42(b) and 42(c)). This can virtually be regarded as a partial fusion of multiple cytoskeleton to form a mechanically stable and well-connected multicellular entity. A profound analysis of the self-organized nature of cell–cell force transmission and production can further be found in Lecuit et al. [538].

A comparably simple form of intracellular communication through physical connections between cells can be found in cell aggregates or clusters. Early observations of demixing cells in clusters containing different cell types were assigned to different intercellular affinities [539]. This hypothesis was developed further in the form of the differential adhesion hypothesis, which was explained and experimentally tested by Steinberg and Foty [540–542]. Meanwhile criteria have been defined to distinguish between adhesion dominated and cortical-tension dominated regimes [543]. The differential adhesion hypothesis was further strengthened by different modeling approaches [544,545].

It was observed that interactions between cells in cell culture can be compared to chemical bonds or molecular interactions in mixtures of fluids [539]. The concepts of surface and interface tensions could be transferred to describe the dynamics of cell clusters in terms of wetting and mixing and indeed, cell clusters as well as tissue excisions typically round up like droplets in the absence of adhesive surfaces [546]. If cells with different mutual adhesion strengths are mixed, cells with stronger adhesion assemble and define the center and less adhesive cells build an external layer around this center as non-miscible liquids in contact would do under zero gravity conditions [542]. In addition to cell–cell adhesions, actin-myosin-induced activity influences the effective surface tension which was shown to directly correlate with the ratio of adhesion to cortical tension [543].

Fluctuations due to cellular random movements, resembling cellular diffusion, can originate from active cell migration as well as from processes of cell division and apoptosis [547]. In close analogy to liquids, where molecules or atoms are incessantly in motion due to thermal fluctuations, cellular diffusion allows to rearrange positions as well as forces and to find an arrangement that is thermodynamically favored. Depending on the energetic barrier for leaving trapped states, metastable states might occur instead of perfect demixing (e.g. few red cells remaining in the center of a shell of green cells in Figure 43(b)).

Figure. 43.

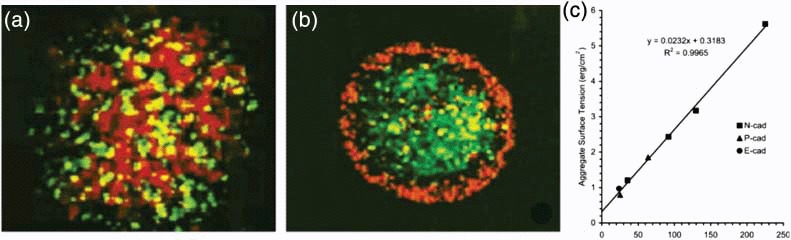
Foty and Steinberg [542] showed that cell–cell adhesion is an essential factor for cell sorting in re-aggregates. The surface tension of the cluster appears to be a linear function of the Cadherin expression level. Figures were adapted from Foty and Steinberg [542] with permission from Elsevier.

Further, the dependence of the aggregate surface tension on cell–cell adhesion strength yields an affinity hierarchy of cells of different provenience (Figure 43) [542]. The differential adhesion hypothesis is not only supposed to be a major mechanism of embryogenesis but also may have important implications for tumorigenesis, currently a field of intensive research activity (Section 4.5).

Despite the fundamental nature of cell sorting experiments, similar experiments might only relate to few particular phases during embryogenesis and tissue development. Tissues often grow by a sequence of organized cell divisions and display a specific structure including highly ordered states. In zebrafish embryos, animal cells divide several times in a directed way (Figure 44) [490]. The first cell divisions are highly organized and periodic with 12 synchronized cell cycles until the 1024 cell state when slight asynchrony appears [490]. Only then, the cell clusters become unordered and the animal pole seems to behave fluid-like.

Figure. 44.

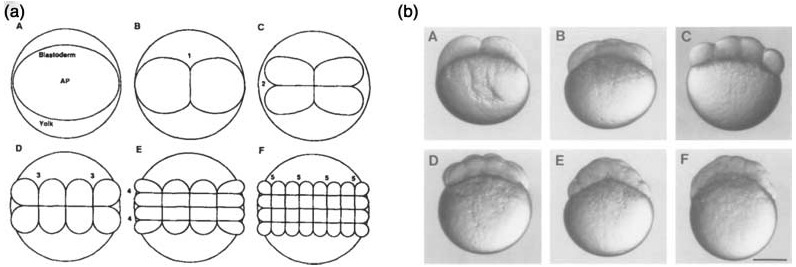
Zebrafish embryogenesis starts with a pair of cells: one animal and one vegetal (yolk) cell. The animal cell divides synchronously without much growth and follows a definite protocol for the first divisions. Left: top view of the first divisions. Right: side view of selected states: A 2-cell state, B 4-cell state, C 8-cell state, until F, where the synchronous division gets disordered and cells start behaving individually. As a consequence, the cell cluster becomes a droplet behaving similar to a fluid. Figures were taken from Kimmel et al. [490] with permission from John Wiley & Sons.

This fluid cell droplet is attached to the big nutrient-filled yolk cell and forms a round cap restoring axial symmetry (Figures 44 and 45(a)). Arguably, this is a result of the surface tension now dominating the structure. Subsequently, a process of coordinated cell movement called epiboly terminates this process. The cell droplet starts contracting asymmetrically along an axis and extends perpendicular to it (Figure 45). It was shown that the symmetry breaking is based on mRNA migrating from the bottom of the yolk cell upwards. This process is described as being controlled by a MT network as origin of an mRNA-based organizer (shield). The axis is defined by the position of this shield and might be formed spontaneously. A complex sequence of flow patterns eventually results in a small fish embryo. Artificial cell aggregates, in contrast, are to our knowledge not able to display a similarly complex evolution.

Figure. 45.

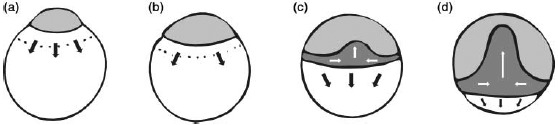
The animal cell droplet of Zebrafish further spreads over the yolk cell similar to a water droplet wetting a hydrophilic surface. Eventually, the cells show global organization as they break symmetry during epiboly (last two pictures). A complex flow scenario results in a fish embryo wrapped band-like around the yolk cell. Image was adapted from Keller et al. [548] with permission from Elsevier.

This drastic physical remodeling of the cellular compound involves a remarkably fast concerted displacement. Several thousand cells move simultaneously and the front moves at a speed of a few μm/min during the transition to the epiboly-state. Recently, advanced microscopic techniques lead to precisely measured single-cell trajectories during early zebrafish development potentially allowing a more detailed analysis of the different developmental stages in the future [549].

Early embryogenesis follows a precise series of first stages in most model organisms, including zebrafish. In this respect, Hydra presents an interesting exception since new organisms can be regenerated from random cell re-aggregates provided by grown organisms. Further investigations will need to evaluate the different possible trajectories in phase space toward a single state, a fully grown organism. Regarding Hydra, this can start either from low-level organized cell aggregates or from higher organized tissue fragments.

4.2.2. Cellular flow and forces during development

As seen in the case of cell sorting in reconstituted aggregates and even more in the case of zebrafish embryogenesis (Section 4.2.1), cells embedded in tissue are subject to substantial rearrangements. This is crucial for many developing species and requires complex coordination of different dynamical factors: cell migration, cell flow (flow of groups of cells), change of cell shape or their visco-elastic properties, cell–cell adhesion, signaling, and cell division. For long-term dynamics cell division and apoptosis have antagonistic consequences and influence shape formation considerably [547]. All these phenomena are linked in a way that is still not understood well enough to successfully design reliable quantitative models. Local cell deformation can result in different possible global shape transformations. An overview of fundamental changes is depicted in Figure 46. By pushing a tissue it becomes wavy, a process which can be reversed by pulling again without changes on the cellular scale. Cells may as well rearrange to minimize surface tension and to recover a flat tissue geometry again (Figure 46, c→g). This process is irreversible as cellular order is not conserved. A rearrangement of a 2D sheet may also shift cells into the third direction (Figure 46, b→a). Reversible and irreversible processes work in concert to realize complex reshaping.

Figure 46.

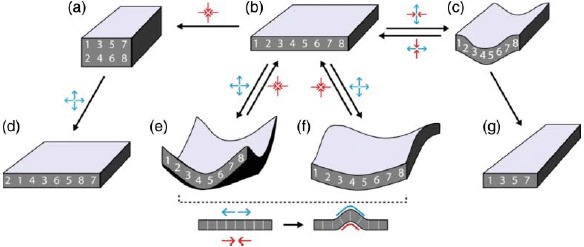
Tissue remodeling requires reversible (both directions of arrows) externally triggered deformation and irreversible (only one direction of arrows) relocalization of the cells. The colored arrows indicate the cell flow at the center of the layer (red = pushing, blue = pulling). Transitions from one state to another can be reversible when a return to the original cell order is possible (e.g. by removing the external cue. Irreversible transitions, in contrast, imply a change in intrinsic cell order (a return to the original overall shape is still possible, though). Several modes are depicted here: x-contraction and y-extension (b→c) leads to tissue bending (c) and after relaxation to tissue elongation called epiboly (g) which is often combined with tissue spreading and thinning. x- and y-contraction leads to evagination (e) or may end up in tissue thickening after rearranging the cells (a) based on transversal intercalation. The inverse process leads to tissue thinning and again to a flat state (d) similar to (b) which happens often in conjunction with epiboly. Bending of tissues is always linked to an asymmetrical cellular deformation. (e, f) A deformation can be the cause or the result of the tissue bending depending if the process is triggered from the surrounding tissue or actively driven by local cells implying their cytoskeleton force generation machinery. Further transformations are possible and thinning and rearrangements can, for instance, be combined to transform a sheet to a tube (see, e.g. [550]).

In the case of single-cell migration, movement is mainly driven by forces exerted by the cytoskeleton onto the extracellular structure via adhesion sites (Section 3.3.4). In embryonic tissues, the other cells and the ECM represent the substrate. Cells further react to forces transmitted by the surrounding tissue, hence forming a feedback loop coupling mechanical stimulation exerted by a cell onto its neighbors back onto the cell of origin. This may explain why complex fluctuations and oscillations are frequently observed in developing tissues. One may speculate that the function of such fluctuations might be the fluidization of the tissue allowing cells to better adapt to a particular structure similar to the role of thermal fluctuations during melting processes. Similarities to glass transition in supercooled colloidal and molecular fluids have been reported for long-term confluent cell cultures at high enough cell densities [551].

During embryonic development, cell polarization and substantial cellular rearrangement (gastrulation) is observed. These tissue level processes are based on cellular symmetry breaking, extension and intercalation all depending directly on the inherent biomechanical design of the individual cells [548,550,552]. The initially symmetric protrusive activity of cells is becoming dipolar. Stiffening adhesions generate traction driving the intercalation process aiming at altering the cellular arrangement and thereby determining the number of junctional interfaces [548,553,554].

4.3. Genetic control

Up to this point, most systems described in this review are based on self-organization and self-assembly of a fixed set of building blocks. Type and amount of these components was hence considered to be conserved. The genetic level is able to contribute fundamentally new mechanisms since gene expression is able to dynamically vary the amount and type of the contained components.

Having gained access to the genome within the last decades appeared like having found the cell's construction plan. After closer inspection, however, it became clear that this is precisely the point where a machine analogy is breaking down. The genome only delivers a list of available building blocks. This resembles handing over a bag full of gearwheels instead of a fully assembled watch. Unlike man-made machines, living cells are not the result of a fully determined construction plan with well-defined positions and functions assigned to each of its components. Moreover, molecules of the same kind are not restricted to one particular function and can be included in several processes at the same time possibly leading to many interconnected functional modules (Section 1.2.2). However, cells are able to regulate gene expression (gene regulation) as well as to modify proteins after translation from the genome. It is thereby possible to access and alter the type and number of available building blocks which can be used to address one or several functional modules. Those alterations of the cellular machinery are often based on signaling pathways.

To date several important pathways are known to access gene expression. A very prominent example regarding embryonic development and regeneration is the Wnt/β-catenin signaling pathway [555–557]. This pathway further plays a fundamental role for the transition from a collective cell compound (epithelial) to individually moving (mesenchymal) cells in tumor development [558]. Transgene Hydra over-expressing β-catenin in all cells show multiheaded morphology and implants display a strong potential for axis formation. So far, however, it has not been fully elucidated how activation of this pathway is translated into a morphological change. It is clear that β-catenin substantially contributes as it plays a double role as signaling molecule and as linking element of the calcium ion-dependent cadherin-mediated cell adhesion system (Figure 47). In absence of the Wnt ligand, the β-catenin destruction complex (Axin + APC + GSK3β + CK1α, Figure 47) and β-TRCP triggers β-catenin degradation. In the presence of Wnt the β-catenin destruction complex is disassembled and β-catenin concentration increases as the synthesis continues. The protein eventually enters the nucleus triggering the expression of several target genes that cause a transition from epithelial to more mesenchymal cells [559]. In addition, β-catenin is known to be part of the bridge between membrane bound E-cadherin and the actin cytoskeleton. Microsopic details, however, often remain contradictory in literature.

Figure 47.

The canonical (yellow background) and non-canonical (red background) Wnt/β-catenin signaling pathways are related to mechanical elements and actions responsible for cell polarization, migration and tissue organization. Blue background stands for membrane bound receptors. β-catenin is a major player and is permanently created and degraded by the APC complex. It is important for linking the cytoskeleton to the cell membrane and to neighboring cells but also as a gene transcription factor. If it is over-expressed or if APC is not working properly developmental genes are activated and the cell is less adhesive and the epithelial-mesenchymal transition is induced with cell migration and proliferation. These are features of malignant tumors. The Wnt pathway is further directly linked to pathways controlling the activity and structure of the cytoskeleton: Rac, Cdc42, and Rho. It was recently discovered that IPGAP1 has a major regulatory function for actin and MT cytoskeleton. This is also the case for the APC-Asef complex. The illustration combines different sources as indicated by numbers on a white background. 1: [560], 2: [561], 3:[559], 4: [562,563], 5: [564].

The E- and N-cadherin proteins, part of the cadherin superfamily comprising over 100 members [565], are responsible for cell–cell adhesion [566,567]. Mechanical stress onto adhesion sites leads to increasing phosphorylated β-catenin concentrations in the cytoplasm through mechanical destruction of cadherin adhesion sites. Once entering the nucleus, the mentioned regulation genes are activated [559,568]. Furthermore, the tumor suppressor protein adenomatous polyposis coli (APC), a co-factor for the β-catenin destruction complex, interacts with the plus-ends of MTs in membrane protrusions [560,569]. APC is also connected to the actin cytoskeleton by means of IQGAP1 (Figure 47). IQGAP1 and APC proteins are essentially involved in cell polarization and directional migration [560,562]. APC deficiency results in an over-activation of Asef contributing to aberrant migration behavior presumably relevant for tumor progression and invasiveness. Many further links seem to exist between the Wnt pathway and cytoskeletal dynamics as well as formation of tight junctions and cadherin based cell–cell junctions resulting in very complex feedback loops [562].

Tissue cells are not viable when suspended in fluids and need a substrate and other cells. In this context, mechanosensitivity discussed in Section 3.3.6 reveals a direct connection between substrate properties and cellular behavior. Discher and co-authors [462,570–572] showed that the cells respond in a specific manner to the stiffness of the substrate. Even more, cells differentiate according to the substrate stiffness [573,574] (Section 3.3.6). This reveals that adjacent cells may form a coupled closed-loop system mutually influencing their physical properties by mechanical as well as chemical cues.

In addition, the extracellular matric (ECM) presents an integral and non-negligible part in tissue dynamics and regulation. A mixture of polysaccharide gels and glyco-protein fibers (mostly collagen based) leads to superior mechanical stability and elasticity of the tissue when compared to only tissue cells. Here again, closed feedback-loops can easily be established. While the ECM will clearly influence cellular behavior (e.g. via mechanosensitivity, Section 3.3.6), it is at the same time influenced by the embedded cells. This ranges from purely mechanical effects such as local gel compaction through active cellular force production [575] to complex biochemical matrix alterations. Furthermore, cells modulate mechanical properties by secreting specific enzymes. As its components are also capable to serve as signaling molecules (e.g. collagens, laminins, and fibronectin bind to the integrin-receptor family), the ECM also directly takes part in cellular signaling. Epithelial cells bind strongly to the laminin whereas mesenchymal cells attach to fibronectin fiber networks [576]. Tissue cells are even facing apoptosis once detached from the ECM and regeneration is linked to the presence of corresponding ECM receptors. This partially explains the difficulty to culture tissue cells in vitro as discussed for Hydra by several authors [577,578].

So far, an important signaling pathway controlling cell–cell adhesion was described as an example. The Wnt pathway crosstalks to the GTPase regulating system including Rho, Rac, and Cdc42 which further regulate assembly and organization of the actin cytoskeleton. These pathways are cooperating during cell polarization as well as migration and control MT polarity. Hence a combined Wnt/GTPase pathway model has been suggested [564]. However, many molecular aspects as well as the link to mechanical cues of tissue cells remain largely unknown, even for the canonical Wnt pathway [561]. Another component is IFs, which –in comparison to MTs and actin – are far less understood and studied regarding their role in cell mechanics (Section 2.1.4). On the tissue level, the problem of having many different types of IFs again complicates a proper understanding of their role in tissues and clearly demands further substantial research efforts [13,47]. Concluding, one may get the misleading impression that signaling is superordinated to the physico-chemical self-organizing machinery of the cytoskeleton. As discussed in Section 2.2.3, however, it must be interposed that many functional units of the cytoskeleton self-organize independently of classical signaling pathways. Moreover, it was shown that the link between signaling and mechanics is not one way. Mechanical stimulation triggers gene expression [568,579]. Rendering the control gene APC deficient it could be shown that even short and weak mechanical compression of mouse intestinal tissues up-regulates the expression of master developmental genes (Myc and Twist1 via the Wnt pathway) [568]. It is further known that these genes are involved in cell division and development in Drosophila acting as precursors of colon tumorigenesis [6].

4.4. Biological development as a critical phenomenon?

Critical phenomena are classically describing the transition of a physical system in which the divergence of quantities describing the system's state is characterized by scaling laws. A prominent example is the Ising model revealing a second-order phase transition. Such transitions can also be observed in non-equilibrium systems as, for instance, the rising convection patterns in Rayleigh-Bénard cells [495]. It turned out that a scaling law could even be found in polarization of Hydra cell aggregates, the very first step of axis formation which can be observed during embryogenesis.

Hydra's regeneration capabilities from tissue fragments or even entirely dissociated cells [580–582] allow studying a true symmetry breaking scenario unlike other embryos where the axis may be induced by sperm entry (Xenopus) or an attachment location (placenta) [515,583]. It turned out that regeneration from those cellular spheres is accompanied by saw tooth pulsations [497,584] presumably due to osmotic swelling and pressure release [585]. Temporal dynamics have been studied using Fourier analysis of a time series of the cell ball contour in (Figure 48(a)) [584] and angular distributions (Figure 48(b)) [497].

Figure 48.

During the regeneration of H. vulgaris, a cellular cluster first establishes a spherical arrangement consisting of a hollow cellular double layer. This spheroid's regeneration can be described by three phases with saw tooth like oscillations – the radius and the second, third Fourier modes are depicted in (a). The transition from phase II to III shows a transition to non-uniform tissue elasticity as the pressurized cell ball is stronger deformed (red line) as the relaxed one (blue line). (b) Orientation of the hydra head with respect to the direction of a temperature gradient across the cell aggregate. During the transition from phase I to II, the axis is locked. Small temperature gradients applied from the beginning are sufficient to significantly affect the orientation of the head (yellow squares, red triangles) which is a signature of the system's critical state. Later, application of a temperature gradient does no longer result in an overall reorientation (blue circles). Images were adapted from [584] (a) and [497] (b) (with permission from Albrecht Ott).

During regeneration of Hydra three phases of pulsations could be distinguished and related to axis formation. In phase I, large pulsations are present and the possibility to reorient the development axis in a weak temperature gradient indicates that the differentiation has not been locked yet. Only after switching to small oscillations in phase II the axis is irreversibly locked and cannot be reoriented anymore. Analysis of the spatio-temporal gene expression pattern of the ks1 gene-specific for head generation [586] shows fluctuations and revealed a scaling law of the gene expression pattern of ks1 close to the transition moment (after 25 h) [497] (Figure 48).

This discovery relates fluctuations and gene expression patterns during the axis formation of developing tissues to critical phenomena. Experiments revealed that the axis cannot be properly reoriented as soon as the frequency has changed in phase II. This suggests that the mechanical oscillations are linked to the genetic level [587]. Furthermore, it was shown that expression level of a head-related gene ks1 is correlated with the oscillation frequency [497]. In phase III, the elasticity of the hydra sphere becomes inhomogeneous explaining the inversion of the relaxed state (Figure 48, blue line) and tensed state (Figure 48, red line) of the deformation. This suggests that certain processes during development may also be classified as a critical phenomenon showing symmetry breaking with transient fluctuations. The transition from phase II to III indicates a second level of symmetry breaking in epithelial elasticity. The Gierer–Meinhardt model was investigated with respect to critical states and symmetry breaking scenarios on a spherical geometry including oscillatory and non-oscillatory bifurcations. Apparently, more biochemical investigations are required to decide about the relevance of this model in competition to an alternative pace-maker model where a part of the embryo (micromere) generates waves organizing the entire tissue [588].

Oscillations were reported for other species as well [589,590]. Somitogenesis (segment formation becoming organs and the ribs later) of zebrafish and the dorsal closure of Drosophila [589] is based on the segmentation clock generating a periodic signal spreading along the tissue (pre-somitic mesoderm) resulting in a wave corresponding to the oscillator-wave model by Cooke and Zeeman [591]. This was described by a coupled phase oscillator model which originates from the description of coupled pendula. The delay of the coupling required for oscillatory behavior was attributed to the Delta-Notch pathway [592].

4.4.1. Mitosis and apoptosis

While mitosis (cell division) obviously contributes to embryonic development and other tissues, apoptotic (programmed cell death), autophagic (self-disassembling), and necrotic (death caused by poisoning or starvation) cell deaths are not less important processes to sculpt the developing embryo. Signals from the outside are actually required to inhibit apoptosis even for cells in mature tissues [593]. This explains why cell culture of tissue cells needs additional factors in the provided medium. External cues may come from other cells, from the medium or from the ECM [593].

Programmed cell death describes the driven disassembly of cells caused by external or internal signals and is frequently observed during tissue development and regeneration. In embryogenesis, programmed cell death has not been observed in vertebrate embryos other than mammals prior to gastrulation [594,595]. In a later stage, however, apoptosis plays a crucial role for sculpting, for example, fingers and toes from a continuous tissue or cavities as the epiblast formation and morphogenesis of lungs [596,597]. In the much simpler case of Hydra, apoptosis becomes prominent during spheroid formation (the first step of regeneration of Hydra), especially if the movement is hindered by a gel or obstacles. This resembles observations made for tumor spheroids displaying strongly altered growth dynamics when embedded into elastic gels [598–600]. Later, hollow sphere formation and rounding up in Hydra again involves apoptosis. The concerned cells are rejected by the organisms by pumping through contractions as observed during formation of Hydra spheres.

On a more abstract level, cell apoptosis and mitosis can be interpreted as two rates of removing and adding cells to tissue. On long time scales (comparable or larger to the typical times for apoptosis or division) apoptosis and mitosis introduce fluctuations resulting in viscoelastic fluid-like behavior with the respective rates controlling the relaxation time [547]. Certainly, these rates are not constant and depend on numerous factors such as the level of nutrition or chemical cues. However, rates also vary according to the direct physical environment and cell aggregate growth was reported to strongly depend on applied mechanical stresses [547,598–600]. Interestingly, in vitro experiments revealed that mechanical pressure has little impact on apoptosis [601] but greatly reduces division rates [599,601]. In particular, in the core region of tumor spheroids, cell growth was found to be slowed down by up to two orders of magnitude as a consequence of external pressure, making apoptosis the dominating process [599,601].

4.4.2. Compartments

Development of more complex tissues (Hydra is too simple) is based on common differentiation of multicellular sub-units forming compartments [602]. Compartment cells co-develop and work together in a coordinated way. Cells being proximal and attributed to the same function may totally differ ontogenetically and be of different compartments. In the context of the liquid-analogy of cellular aggregates (Section 4.2.1), compartments could be described as immiscible groups of cells [554]. Representing a reduction to the cellular level the differential adhesion hypothesis succesfully explains compartment formation in simplified cell aggregates [542,543]. However, in the more complex situation of compartment formation in many living organisms, it is not yet entirely clear to what extend differential adhesion applies [554,603] and how other complementary mechanisms help to establish stable compartment boundaries or to orchestrate tissue dynamics over time (see [554]).

In living organisms, it is not always evident where the compartment border is located. In Drosophila, for example, the border crosses the wing disk as a straight line in the middle [604]. So far, the high structural stability of this line is not fully understood. It was found that cell–cell communication through gap junctions across compartment borders is restricted [605]. The border may be stabilized by a signaling feedback or long-term memory inside the concerned cells. Moreover, it was reported that the boundary region exhibits an altered cytoskeletal composition [606]. Unlike liquid-analogy-based sorting models these results seem to suggest a more boundary-focused view. Following the differential adhesion hypothesis, boundary formation results in inherent properties of all participating cells, while the so-called “fence” hypothesis [554,606] emphasizes the role of the boundary cells for establishing spatial separation.

Although many open questions remain regarding formation, function, and dynamics of compartment boundaries, simple physical models clearly allow deciphering fundamental underlying mechanisms. In many cases shape changes and compartment formation can already be explained based on cell–cell adhesiveness and cortical tension [543,587,603].

In addition, it is becoming increasingly clear that results from developmental research have important medical implications: surgery of tumors is still the most consequent and successful therapeutic method as long as metastasis has not occurred. However, lacking better knowledge arbitrary determination of tumor boundaries as usually done by surgeons could not avoid tumor recurrence to a significant percentage [607,608]. It was further discovered by Höckel and coworkers that cervical carcinoma growth is restricted to the developmental compartment for tumor progression. The recommendation is to remove the entire tumor-containing compartment at best without affecting adjacent compartments even if adjacent to the tumor. This method is favorable in comparision to removing a spherical volume surrounding the tumor (total mesometrial resection). Hence, the relapse rate of cervical tumors could be reduced substantially. The five years survival probability of patients with cervix carcinoma could be increased from 70% to 85% to over 95%. An according viability for other tumors is currently investigated. This is probably the first example showing the direct relevance of developmental biology research in medical research.

4.5. Physics of cancer

As expressed by Erwin Schrödinger's quote “The working of an organism requires exact physical laws” [3], physicists strive to explain nature by precise mathematical equations, which could bring a truly new perspective to cancer research. It has already triggered worldwide efforts to decipher the potential physical aspects of cancer. A major problem, not only for physicists, is that cancer is not a single disease with a certain etiology and one cure. DNA repair as well as damage tolerance are not only relevant for carcinogenesis but also for genetic diversity. Therefore, mutations are necessary for biological enhancements and cannot be classified into desirable and undesirable events.

Cancer arises through a catastrophic event as a result of a succession of randomly occurring mutations. The stochastic nature of these mutations results in an extreme molecular diversity in tumors on top of the inherently complex molecular networks on the subcellular scale of any human cell (Chapters 2 and 3). Thus, a mathematical model solely describing the processes in a very specific tumor is hardly a physical law. However, this should not give the wrong impression that physics cannot contribute to oncology. Statistical physics, for instance, has already created tools effectively describing stochastic progression. Furthermore, despite molecular diversity, tumor progression and metastasis require characteristic changes in tumor cells’ material properties to meet physical criteria imposed by the surrounding tissue [361,362].

A holistic approach listing the precise molecular interactions in tumor cells may make it hard to detect underlying laws emerging from the stochastic, random processes on the molecular scale (Section 1.2.1). Consequentially, functions which are crucial for the survival of tumor cell need to be identified. Intracellular elements, i.e. modules, to accomplish these functions may show molecular redundancy and diversity. Nevertheless, as a starting point for the physics of cancer we expect that required cell functions for tumor initiation, progression, and metastasis, depend on particular material properties of tumor cells to perform specific physical processes. Thus, an abstract (or coarse-graining) physics perspective is needed to explain intracellular functional modules, such as uncontrolled proliferation, growth against the surrounding tissue matrix, and tumor cell migration across the body. The physical laws underlying solid tumor progression are rooted in soft matter physics and will help to define what unifies cancer despite tumor diversity. The concepts of functional modules and coarse-graining (Sections 1.2.1 and 1.2.2) will greatly facilitate our understanding of the laws that govern cancer. From a molecular network's perspective, the door handle is the most important part to drive a car since it is the first step to drive a car. In terms of functional modules, the engine is the central element.

In tumor cells, the functional modules may not show identical molecular architectures, but the same physical principals are essential for their functions. Changes in a tumor cell's active and passive biomechanics, for instance, are required for functional modules involved in metastasis [360,361,609]. During tumor progression, the proportion of cancer cells with a high compliance under small deformations increases. These softer cells also indicate increased contractile behavior (Figure 49). Tumor cells that readily deform to squeeze through narrow spaces and easily switch between mesenchymal or amoeboid motion are optimized to invasively migrate through the body [360–362,610].

Figure. 49.

Cell biomechanics could be very useful for cancer diagnosis, e.g. using the optical stretcher, illustrated in (A). Average deformation and relaxation curves of benign cells and breast tumor cells from early and late stage tumors (G1 and G3) are shown in (B). With increasing tumor aggressiveness, the cells become more compliant. Despite the higher deformability, i.e. weaker elastic strength, late stage tumor cells show a stronger relaxation behavior. This relaxation behavior of softer tumor cells can only be explained by increased cell contractility since the passive viscoelastic properties only permit a weaker relaxation behavior. Illustration in (A) by courtesy of Steve Pawlizak, data in (B) kindly provided by Franziska Wetzel.

Furthermore, cells within a tissue can still move leading to a viscous behavior on long-time scales. Describing these tissue dynamics will be a significant part in the novel area of active soft matter physics [150,151]. In this course, the question arises why a tumor initially grows as a collective and why cells can eventually transgress its boundary? According to Mal Steinberg's differential adhesion hypothesis, compartment boundaries between tissues are stabilized through a new type of surface tension [542]. This surface tension cannot be solely described by intercellular adhesion and cell contractility has to be taken into account [543]. Additionally, at higher packing densities cells in tissues behave very similar to soft colloids and have difficulties passing by each other. Therefore, tissues can be regarded as a glass-like state, potentially helping to stabilize tumor boundaries [551,611].

The physics of cancer is still in its infancy and it may need a decade until a translational impact will become truly visible (see also Section 4.4.2). Nevertheless, in diagnosis, single tumor cell biomechanics provides some unparalleled advantages. Deformability of cells obtained from cytobrushes of the mouth may serve as a screen for oral cancer [612]. Moreover, biomechanical characterization could solve a dilemma in the staging of breast cancer. Currently, surgical treatment of breast cancer includes the removal of the sentinel lymph nodes to determine whether the primary tumor is metastatic or not. However, sentinel lymph node dissection correlates with deterioration in the patient's prognosis [613]. Therefore, direct biomechanical detection of metastatic cells from the resected tumor may be an alternative to the removal of the lymph nodes.

In terms of a more long-term translational perspective, an essential part that will be provided by the physics of cancer is a new perspective for drug targets and therapies. The most common chemotherapy agents act by suppressing cell division which is particularly fast in most cancer cells. Newer anticancer drugs act directly against abnormal proteins in cancer cells – this is termed targeted therapy – or inhibit tumor angiogenesis. In all these cases, the goal is to destroy the solid tumor. Usually the primary tumor can be removed in most cases by surgery and radiation. It is the remaining tumor cells as well as their ability to transgress boundaries that have to be hindered since they determine the long-term survival. Changes in tumor cells’ physical and material properties that disrupt the functional modules required for metastasis could provide a much broader treatment option which is not limited to few solid tumors.

4.6. Synopsis and open questions

Formation of multicellular tissues relies on mechanical (stiffness and adhesion), genetic, and signaling cues that are all highly interwoven. It is, therefore, necessary to further investigate how these factors interact and to select potentially dominant contributions for individual processes during development. It is clear that gene expression, being a slow process, cannot be involved in tissue fluctuations on a time scale in the range of seconds, but it controls many aspects of long-term development. In addition, tissues show fluid-like behavior on long timescales, which is certainly not true for short time scales. So, on one particular time scale certain regulative elements can be neglect due to their apparent weakness, but they may nevertheless dominate the system on a different scale. Furthermore, cellular organization in many cases is governed by physical and chemical self-organizing mechanisms dramatically reducing the number of degrees of freedom to be controlled. A good example is the cytoskeleton which is controlled by few key elements but triggers complex cellular shapes and movement through many adaptive, partly autonomous functional modules. This means that local interactions may lead to global, potentially highly complex patterns. Similarly, axis formation in embryonic tissues is based on local amplification of signaling molecules in adjacent cells. Gene expression is in turn influenced by chemical and mechanical cues closing a feedback loop between different scales.

In contrast to the subcellular level (and at least more severe than on the cellular level), a unifying model of morphogenesis is very ambitious, not to say unrealistic. The broad spectrum of regulative mechanisms originating from very different levels of complexity and acting on very different time scales strongly limits coarse-grained modeling. Apparently, it becomes a prerequisite to dissect embryogenesis into different stages in order to separate the different time scales. Many of these stages then indeed allow substantial coarse-graining and the development of physical models (Figure 50). Dorsal closure in drosophila embryogenesis, for instance, can be described and understood by physics models [554,615,616] but the same models can naturally not account for the developmental phases before and after dorsal closure. It will be difficult to find the right balance in between dissecting into too many different sub-models which might not allow understanding large tissue transformations and more global but too strongly coarse-grained models that will lose important details of tissue dynamics.

Figure 50.

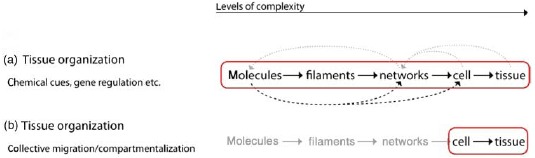
Tissue organization includes a tremendous variety of different phenomena. Some show a very high complexity with feedback-loops ranging from the molecular scale up to the multicellular level (a). This includes examples involving complex signaling cascades or gene regulation. Gene regulation, for instance, is able to alter cytoskeletal components, which will affect its network architecture and thereby cellular properties and behavior. At the same time, the resulting interactions on a cellular level or above can involve signaling cascades down to the molecular or genetic level hence forming a multi-scale feedback-loop. In such cases, coarse-graining becomes a very difficult endeavor. Other examples, however, demonstrate nicely that very prominent phenomena on the tissue level can even be described on the cellular scale such as cell sorting in cellular aggregates [542], collective cell migration [536] or epithelial tissue dynamics [554,614].

A further cytoskeleton specific problem on the tissue level is the role of IFs and the ECM. Both systems are poorly understood since most fundamental modeling and bottom-up experiments focus on the actin and MT cytoskeleton exclusively. The ECM can indeed be largely ignored on the lower levels but substantially contributes to the tissue level. IFs, however, are playing an important role on the lower levels as well. We already note an increasing interest in IFs as well as ECM suggesting that these fields could soon become much more relevant.

5. Conclusions

The stochastic large-number character of biological systems lies at the very heart of biological physics and is so dominant that the emergence of “new” laws of physics on higher levels of complexity was already claimed in the early 1940s [3]. Roughly 70 years after “What is life?” many more physical principles have indeed been discovered in biological physics. Along this article, we tried to outline much of the current physical picture of the cytoskeleton including numerous emergent properties which are absent on lower scales.

One aim of this article is to illustrate how the different scales from macromolecules up to tissue are intertwined and how a physics approach helps to understand key processes taking place on these levels. Within this framework, coarse-graining obviously represents a major component of the physics perspective on biological matter. It allows a degree of abstraction necessary for developing mathematically treatable models and to filter for basic physical principles. The incredible complexity of biological matter resulting from multi-component systems largely dominated by highly nonlinear out-of-equilibrium states demands very delicate balancing acts between over-simplification and over-abstraction. To some extent, the fascination of biological matter for physicists certainly lies exactly in its challenging nature requesting entirely new models.

Despite the challenge and the relative novelty of this research area, a physics approach already proved to be very successful in revealing fundamental concepts of cytoskeleton organization and behavior. A very instructive example is the physics of semiflexible polymers, which already gave birth to new, fundamental theoretical models. In this context, it becomes clear that the physics approach is not limited to the mere assistance for biological or medical research. Moreover, these efforts are able to result in new physics with the related example of polyelectrolyte physics as a new field of research. A very apparent and even more general tendency is the increasing importance of systems out-of-equilibrium representing an essential characteristic of living matter. This is represented, for instance, by the emerging field of active soft matter physics.

In addition, one should not underestimate the potential physiological or medical benefits of a physics approach. Based on a better understanding of mechanosensitvity and the resulting phenomena of durotaxis and inverse durotaxis (Section 3.3.6), it is possible to further understand why nerve regeneration is such a delicate process. Even more prominent is the growing number of physics contributions to cancer research. Cancer is a highly heterogeneous class of diseases with several hundred different types of tumors often displaying hundreds of mutations. Despite their substantial variations in molecular composition, cancer cells often display similar functional modules and similar overall emergent properties consisting in uncontrolled growth, tissue invasion and sometimes metastasis. These altered emergent properties hence cannot trivially be traced back to few molecular components, but it might be possible to find underlying physical explanations. Supposing this is true, one could even hope to find cancer treatments based on a more fundamental physical picture of cancer cells.

During the last decades, the characterization of all available macromolecular building blocks was strongly emphasized. This should not hide the fact that knowing all building blocks will not automatically reveal the resulting emergent properties on higher levels. For illustrative purposes one can consider a classical higher level example of emergence: consciousness. We do not doubt that the brain's functions are anchored in molecular interplay. Unfortunately, this statement contains no real understanding of what consciousness is, not even when adding a detailed list of proteins and molecules forming the brain. It appears as senseless as understanding thoughts by mass spectroscopy.

The different levels described within this article clearly reveal the importance of the cytoskeleton as an essential element in neuron migration and interaction (Section 3.3.5) but also in tissue formation and dynamics (Section 4). Hence, cytoskeleton-based effects even strongly influence the behavior on comparatively large scales and might play a fundamental role in higher tissue functioning. Of particular interest are various level bridging connections (arrows in Figure 51). They allow to choose the right frame for future modeling approaches and to determine the right language level to properly treat, for instance, consciousness.

Figure. 51.

Possible level hierarchy from molecules to consciousness. A detailed picture of the levels’ connections is likely to result in a highly intertwined structure.

There is little doubt that we are still far away from answering Schrödinger's book title question and to date a general physics picture of the individual living cell does not exist. At large, the available physics models are strongly characterized by incoherence and very high specificity. There is not only nothing like a unifying theory of biological matter, but it is even unclear whether such a theory will ever exist. Along this article, however, it becomes apparent that our current understanding of many cytoskeleton-related phenomena advanced substantially due to physics approaches.

Naturally, systems comprising only few different constituents such as reconstituted biopolymer solutions or simpler motor-filament mixtures are particularly prone to physical modeling attempts. For many-component systems that cannot be divided further into autonomous subsystems, modeling turns out to be less intuitive but not necessarily impossible.

We note a more general limitation to physical modeling when looking at the introduced levels of complexity. The semiflexible nature of an actin filament can be derived when starting from the single monomer level (Section 2.1.2). Going to much larger scales such as entangled filament solutions, it is possible to correctly describe the system on the basis of single filaments, for instance using WLCs (Section 2.1.5). In this example, hierarchical reduction nicely works, the filament level can be explained in terms of the underlying monomer level and the network level by the underlying filament level (see Section 1.2.1). Hence, the network is understood on the basis of the single molecule level although the network itself is not directly described in molecular level language (Figure 52). Analogously, a pressure rise upon temperature increase can be described by the ideal gas law, which in turn can be traced back to the gas molecule level. Here too, the pressure rise is understood on a molecular basis although it is not necessarily modeled on this basis.

Figure. 52.

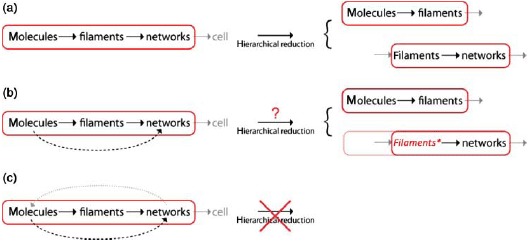
A given system comprised of several levels of complexity can only be reduced further, i.e. split into smaller subsystems if no loss of lower level details occurs. (a) For strictly hierarchical order, further reduction is possible without apparent loss of causal understanding. If interactions bridge one or more levels, the reduction becomes difficult but remains possible (b) as long as no inherent multi-level feedbacks occur (c). The bridging interactions in (b) must be included in form of suitable modifications of the bridged level. Here, filaments* is a modified form of filaments that, for instance, considers “sticky” filaments to account for molecular cross-linkers.

As soon as direct links spanning more than one layer of complexity start to interfere, hierarchical reduction is limited by potential loss of substantial lower level effects (Figure 52(c)). Multi-layer connections in the upwards direction (Figure 52(b)) present an exception and can still allow hierarchical reduction with minor modifications. As presented in Section 2.1.5, filaments can be described as sticky in order to account for molecular cross-linker effects.

Multi-layer connections pointing downwards enable more complicated feedback loops that can no longer be simply attributed to an intermediate level. Transiently cross-linked networks are such an example. Network deformations directly influence the individual cross-linkers which in turn alter the network properties. It comes as no surprise that analytical models on transiently cross-linked networks largely remain work in progress. So far, they have mostly been described by computer simulations which more easily span several levels of complexity (Section 2.1.7).

Apart from the fact that the classification into different levels remains subjective and will depend on the system of interest (a “filament” or “cell” level would not be chosen in solid state physics), the question of down to which level reduction is necessary directly leads into very complex philosophical controversies.

Two main arguments caused Laughlin and Pines [2] to provocatively speak of an “End of Reductionism” in physics. First, reductionism based on proper analytical deduction is technically impossible for systems comprised of larger numbers. Deductive logic ends where approximations start. Second, one has no means to be sure of having found the most fundamental microscopic level as the ultimate, most basic level for successive reductions. If there is a level below, the fundamental basis would immediately become a purely phenomenological description. In this context, the authors refer to strong reductionism demanding full reduction down to the most fundamental levels (see [31] for further details on the reductionism debate).

Compared to elementary particle physics or quantum mechanics, these two objections against strong reductionism appear less controversial in biological physics. The second argument is far away from the core focus of biological or soft matter physics since here the lowest scale one cares about usually lies in between the atomic or molecular level. In contrast, the first argument is clearly beyond dispute because all systems of interest are multi-atomic rendering a certain degree of coarse-graining unavoidable which precludes any full reduction to the most fundamental physical laws.

For biological matter, there is little doubt that a quantum mechanical description of a living cell will never make it. In the present article, the conceptual idea of hierarchical reduction was shortly introduced (Section 1.2.1). Does this compensate the impossibility of full reduction to the most fundamental physical laws? To some extent, we think it does, since it circumvents the technical problem of full reduction down to the most fundamental levels by dissecting the system into causally reducible subsystems. The epistemological problem coming along with the missing full reduction, however, cannot entirely be circumvented by hierarchical reduction and we notice two major problems arising.

First, even if one divides a chosen system in several subsystems that are small enough to be treated theoretically, how can one know that they are really causally reducible (i.e. without further direct links to levels of complexity other than the lowest or highest level already accounted for; see Section 1.2.1)? This is the same problem physicists commonly face when using approximations and can only be finally answered in comparison to empirical data. If a gas does not behave like an ideal gas then essential parts are missing, e.g. effects emerging from a lower level.

Second, to what level does one need to reduce a system in order to properly call it “understood”? In biological physics, there are typically no (or very little) causal links directly connecting to sub-molecular or smaller scales which is why sub-molecular levels are largely ignored in this field. Implicitly, this indicates that the sub-molecular scales form a causally reducible system with respect to the questions posed in biological physics (Section 1.2.1). This does by far not mean, however, that there would be a general agreement on the molecular scale as the fundamental level of interest. Whereas some authors claim that “all biology is now about molecules” [617], others strongly disagree with this position (for a direct objection to Epstein's point of view, see e.g. [618]).

From our perspective, Epstein's statement appears to be highly problematic. No doubt that a living cell functions based on a complex interplay of numerous different molecules, but the inherent complexity will technically and principally inhibit a full understanding of a living cell in purely molecular language. We would even question the attempt per se, since we are not aware of any convincing criteria to properly distinguish “more fundamental” from “less fundamental” scales. The most intuitive understanding of a phenomenon rather seems to originate from an understanding of the respective “core” level that accounts for the major emergent properties.

We feel, for instance, that we understand entangled actin solutions although ignoring or coarse-graining the filaments’ detailed molecular structure. Thus, there are clearly numerous examples where a molecular description will add nothing to deepen the understanding. The frame for modeling attempts should hence be scaled according to the questions posed and will vary significantly depending on whether one looks at single filament properties (Section 2.1.2) or embryonic development (Section 4). An all-atom simulation of a glass of water tipping over will still result in water flowing out.

Applying Moore's law known from computer sciences, Vendruscolo and Dobson [619] predict all-atom simulations of entire bacteria on a nanosecond scale for the year 2050. Apart from technological or methodical superlatives, we should not be too excited regarding this scenario. Yes, it will be an even more versatile and powerful tool than it already is right now. But it will by no means solve our fundamental biological questions and it will not explain to us what life is.