Energy Landscape of the Michaelis Complex of Lactate Dehydrogenase: Relationship to Catalytic Mechanism

Abstract

Lactate dehydrogenase (LDH) catalyzes the interconversion between pyruvate and lactate with nicotinamide adenine dinucleotide (NAD) as a cofactor. Using isotope-edited difference Fourier transform infrared spectroscopy on the “live” reaction mixture (LDH·NADH·pyruvate ⇌ LDH·NAD⁺·lactate) for the wild-type protein and a mutant with an impaired catalytic efficiency, a set of interconverting conformational substates within the pyruvate side of the Michaelis complex tied to chemical activity is revealed. The important structural features of these substates include (1) electronic orbital overlap between pyruvate’s C₂=O bond and the nicotinamide ring of NADH, as shown from the observation of a delocalized vibrational mode involving motions from both moieties, and (2) a characteristic hydrogen bond distance between the pyruvate C₂=O group and active site residues, as shown by the observation of at least four C₂=O stretch bands indicating varying degrees of C₂=O bond polarization. These structural features form a critical part of the expected reaction coordinate along the reaction path, and the ability to quantitatively determine them as well as the substate population ratios in the Michaelis complex provides a unique opportunity to probe the structure–activity relationship in LDH catalysis. The various substates have a strong variance in their propensity toward on enzyme chemistry. Our results suggest a physical mechanism for understanding the LDH-catalyzed chemistry in which the bulk of the rate enhancement can be viewed as arising from a stochastic search through an available phase space that, in the enzyme system, involves a restricted ensemble of more reactive conformational substates as compared to the same chemistry in solution.

A bimolecular chemical reaction occurring in water is best viewed as a stochastic event. The two reacting molecules must “hunt” through the available phase space until the two are close enough in space and attain the correct geometry for reaction. Moreover, the solvent molecules may also transiently make any structural and electrostatic contacts to provide sufficient momentum to the solvent–molecule system to carry the system over the reaction barrier. The phase space describing this system is very large. Hence, a reaction in water might take years despite the fast characteristic clock time for searching through this phase space, on the femtosecond to picosecond time scale.

Similar considerations can be applied to enzyme-catalyzed reactions. It has long been recognized that a protein does not occupy a unique folded three-dimensional array of atoms. Rather, a protein’s structure is best described as a hierarchy or ensemble of interconverting conformations on all time scales from picoseconds to minutes, and the spatial extent from small atom displacements to large scale domain motions. This physical picture flows from the nature of the folded structure, whose stability and structural integrity are dictated by a large number of weak forces acting together. The exact role of a protein’s dynamical nature in function is directed by its so-called “energy landscape” (e.g., ref (1)). While some of the rate enhancement may be caused by differences in the nature of the characteristic clock,²⁻⁴ the basic job of an enzyme in catalyzing a chemical reaction is to “guide” the enzyme–substrate Michaelis complex toward a quite restricted set of reactive conformations so that the search can be completed in the ∼1 ms time that typically characterizez enzymatic catalysis. This is accomplished via specific interactions between the substrate and the enzyme protein and also within the protein itself that may be partly revealed by X-ray structural and other spectroscopic studies as well as computational approaches. However, how such interactions drive the enzyme system along the reaction coordinate to achieve catalysis is not well understood.⁵⁻⁹ The ensemble of structures of the enzyme–substrate Michaelis complex imposes a specific energy landscape that guides the search. The actual nature of the landscape and its relationship to catalysis may be quite complex.¹⁰ The propensity toward on-enzyme chemistry may vary quite substantially among the substates (i.e., varying effective k_cat values). Moreover, the dynamics of interconversion among the substates is almost certainly complex, with varying interconversion times and free energies of activation.

Here, we investigate how (pig heart) lactate dehydrogenase (phLDH) guides the on-enzyme reaction pathway as the system goes from LDH·NADH·pyruvate to LDH·NAD⁺·lactate. Our goal is to determine the phase space carved out of the subpopulation of the substate ensemble of the LDH·NADH·pyruvate Michaelis complex that is along the reaction coordinate. We look for the population of substates of the protein ensemble, trying to determine which ones, if any, are more reactive toward the chemical step than others.

Figure 1 shows the reaction catalyzed by LDH, hydride transfer chemistry with H^– and H⁺ transfers occurring simultaneously on the ∼20 fs time scale.¹¹ It has been concluded that three structural factors are responsible for the 10¹⁴ M rate enhancement of the pyruvate·NADH to lactate·NAD⁺ interconversion catalyzed by LDH, compared to the uncatalyzed chemistry in water (i.e., comparing the on-enzyme rate with the solution rate for 1 M solutes).¹²⁻¹⁴ (1) Approximately 10⁴–10⁶ M comes from bringing the reacting molecules close together in a favorable position for reaction. (2) An enzyme-imposed restriction of the ring geometry of bound NADH toward an “activated” conformation brings about another factor of at least 10 in rate enhancement.^15,16 (3) Specific electrostatic interactions at the active site contribute as much as 10⁶ M to reaction rate acceleration.¹⁷ This dissection is very useful but does not yield any physical insight into the dynamical nature of the chemical reaction.

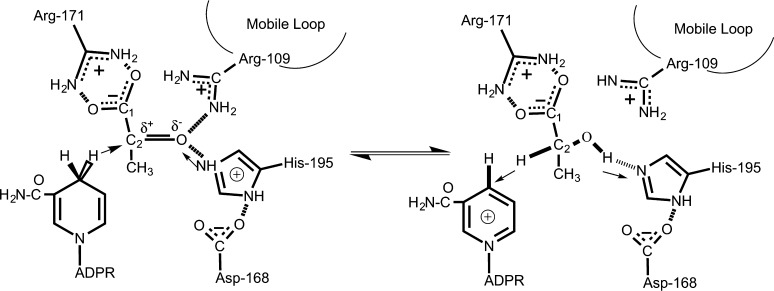
Figure 1.

Active site contacts of pyruvate and NADH (left) and lactate and NAD⁺ (right) bound to LDH with key active site residues as determined by X-ray crystallography. The substrate is placed near the nicotinamide ring of the NADH and key protein residues, His195, Arg106, and Arg171. The C₂=O bond of the bound pyruvate forms hydrogen bonds with His195 and Arg106. The catalytically key surface loop (residues 98–110), accompanied by the motions of mobile areas in the protein,³⁹ has the effect of closing over the ligand, bringing residue Arg109 within hydrogen bond contact with ligand; water leaves the pocket, and the pocket geometry rearranges to allow for favorable interactions between the cofactor and the ligand that facilitate on-enzyme catalysis. It is generally accepted that the hydride transfer and proton transfer occur virtually simultaneously, with both approximately halfway through their motion at the transition state; the C₂=O group is thus very polar at the transition state.

While of major interest, it is notoriously difficult to characterize the specific ensemble of conformational substates of an enzyme and determine the propensity toward on-enzyme chemistry of a particular member. Crucially, the part of the distribution of the substate ensemble of the LDH·NADH·pyruvate Michaelis complex that is key to the reaction coordinate can be characterized in part by measuring the C₂=O stretch frequency of the bound pyruvate molecule. Previous temperature-dependent vibrational measurements and ab initio calculations on hydrogen donor–acceptor pairs that include a C=O group have revealed simple linear correlations between the C=O stretch frequency and the interaction energy (enthalpy of hydrogen bond formation).^18,19 For a simple molecule such as acetone, the correlation coefficient is ∼0.5 (the 2 cm^–1 C=O stretch frequency shift corresponds to a 1 kcal/mol H-bond energy change).¹⁸ Pyruvate bound to LDH forms hydrogen bonds (an enthalpy of interaction of ∼15 kcal/mol) with specific residues at the active site (Figure 1) much stronger than that normally found in an aqueous solution (although transient H-bonding interactions can be very strong); these interactions polarize the C₂=O moiety and downshift the C₂=O stretch. Hence, the C₂=O stretch monitors the distance between the oxygen of that key group and the essential active site histidine residue and mobile loop arginine; it is thought that this distance is a marker for reactivity. In fact, the frequency of the C₂=O stretch is a direct measure of the strength of the electrostatic interactions at the active site for a particular conformation and is highly correlated with the propensity toward the on-enzyme chemical reaction (production of lactate) of that conformation.¹⁷ The concentration of a specific conformation is proportional to the intensity of the IR band to a reasonable approximation. Hence, the IR band profile acts as a measure of the density of states per unit C₂=O stretch frequency. The C₂=O stretch frequency of a specific conformation of bound pyruvate within the LDH·NADH·pyruvate Michaelis complex is an excellent monitor of the protein’s ensemble nature because the stretch value is highly correlated with the propensity toward the on-enzyme chemical reaction (production of lactate) of that conformation.¹⁷ Thus, we have used the C₂=O stretch frequency as a quantitative measure of the energy landscape of the enzyme substrate complex compared to that found in solution. The results provide direct evidence of a restricted ensemble of more reactive conformational substates in the enzyme system.

Experimental Procedures

NAD⁺ and NADH were purchased from Roche. ¹⁵N-labeled ammonium chloride, uniformly ¹³C-labeled glucose, and ¹³C₂-labeled pyruvate were purchased from Cambridge Isotope Laboratories. ¹³C₂-labeled lactate was converted by the enzyme from ¹³C₂-labeled pyruvate. Typically, 15 mg of pyruvate and 100 mg of NADH were dissolved in 10 mL of deionized water without buffer. LDH was then added to the solution to start the reaction. HCl was added slowly during the reaction to maintain the pH of the reaction mixture. After the completion of the reaction, the reaction mixture solution was filtered with neutralized charcoal to remove NAD/NADH until no NAD could be detected by NMR. The lactate solution was then concentrated and desalted by being passed through a 20 cm × 1 cm Dowex50 column. Fractions with lactate are collected and lyophilized to powder for storage.

Pig heart LDH (phLDH) was purchased from Roche Diagnostics (Indianapolis, IN) and prepared as previously described.^20,21 The pig heart cDNA library was purchased from Zyagen. The pig heart LDH gene was obtained from this cDNA library by polymerase chain reaction (PCR) using forward primer CATGCCATGGGCCATCATCATCATCATCATGCAACTCTTAAGGAAAAACTG (with a six-residue His tag) and reverse primer CGGGATCCTCACAGGTCCTTCAGATCC. The LDH gene with the His tag was subcloned into pET14b plasmids from Novagen using restriction enzymes NcoI and BamHI with standard molecular biology procedures. The integrity of the gene was verified by sequencing. The plasmid was transformed into C43(DE3) competent Escherichia coli cells from OverExpress for LDH expression. The growth conditions of the cells and the purification procedures were otherwise the same as those published previously²² for Bacillus stearothermophilus LDH, except a 20 mL Ni column was used in the first protein purification step. The purity was estimated to be >95% using sodium dodecyl sulfate gels. Uniformly ¹⁵N- and ¹³C-labeled LDH was obtained by growing the C43(DE3) cells at 37 °C in minimal medium supplemented with 2 g of [¹³C]glucose and 0.5 g of ¹⁵N-labeled ammonium chloride per liter of culture medium. The expression of LDH was induced by the addition of IPTG to the culture medium to a final concentration of 0.5 mM when the cell density reached an OD of 0.8–1.2 at 600 nm. After 15 h, the cells were harvested, and the uniformly ¹⁵N- and ¹³C-labeled LDH was purified according to the same procedure as the unlabeled LDH. The D168N mutant plasmid was made by using PCR on the pET14b plasmid containing pig heart cDNA and the custom His tag in the presence of forward primer AGTGGATGTAACCTGAACTCTGCAAGG and reverse primer CCTTGCAGAGTTCAGGTTACATCCACT according to standard procedures. The uniformly ¹⁵N- and ¹³C-labeled D168N mutant enzyme was made using the same procedure described above.

The steady state k_cat was determined for the pig heart protein using 0.16 mM NADH or NADD ([4-²H]-pro-R-NADH), which is >100 times greater than the K_d value for NADH [in 100 mM phosphate (pH 8.0)]. NADH(D) concentrations were determined spectrophotometrically with a λ₃₄₀ of 6.22 mM^–1 cm^–1 and an A₂₆₀/A₃₄₀ of 2.3. The LDH concentration was determined using an extinction coefficient of 50 mM^–1 cm^–1 in terms of active sites (pig heart LDH is a homotetramer, and all protein concentrations in this paper are in terms of active sites). k_cat was determined by a loss of the absorbance maximum of NADH’s nicotinamide ring at 340 nm by titration of pyruvate at concentrations from 0.02 to 0.8 mM. NADD was synthesized and purified according to previously reported procedures.^23,24

Static FTIR spectroscopy was performed on a Magna 760 Fourier transform spectrometer (Nicolet Instrument Corp.) using an MCT detector.²⁵ We used a two-position sample shuttle to alternate between the unlabeled sample and labeled sample positions; this procedure substantially decreases the spectral contribution of residual water vapor after subtraction. Both LDH·NADH·[¹²C]pyruvate and LDH·NADH·[¹³C]pyruvate sample solutions were simultaneously loaded into a dual-cell shuttle accessory. CaF₂ windows with 6 μm Teflon spacers were used for the protein sample cell. The typical sample volume was 10 μL. Spectra were recorded in the range of 1100–4000 cm^–1 with 2 cm^–1 resolution. A Blackman–Harris three-term apodization and a Happ–Genzel apodization were applied. All samples were prepared in D₂O buffer with 100 mM phosphate (pH 7.2) (pH meter reading); measurements were taken at 295 K. The typical LDH reaction mixture was prepared at an initial LDH:NAD:lactate concentration ratio of 4:4:20 (where the LDH concentration refers to active sites). Under such conditions, approximately half of the NAD was converted to NADH, yielding an on-enzyme pyruvate concentration of ∼2 mM as determined by UV–vis measurements. Typically, two samples, prepared by using either ¹³C₂-labeled or unlabeled lactate, were loaded on a sample shuttle. Their spectra were measured alternatively five times with 128 scans each time for a total of 640 scans.

Results

Isotope-Edited Protein Amide Bands

Figure 2 shows the IR absorbance spectra of LDH (spectrum A) and [¹³C/¹⁵N]LDH (spectrum B) in the protein’s amide I region (a coupled mode containing a substantial amount of C=O stretch of the polypeptide chain). Note the amide I peak shifts ∼45 cm^–1, from 1650 to 1605 cm^–1, mostly because of the ¹³C label. Most of our studies were conducted using the labeled protein because this protein has a much reduced absorbance in the region of interest here, the C₂=O stretch of pyruvate, which lies at multiple frequencies but near 1680 cm^–1 (see Figure 3).

Figure 2.

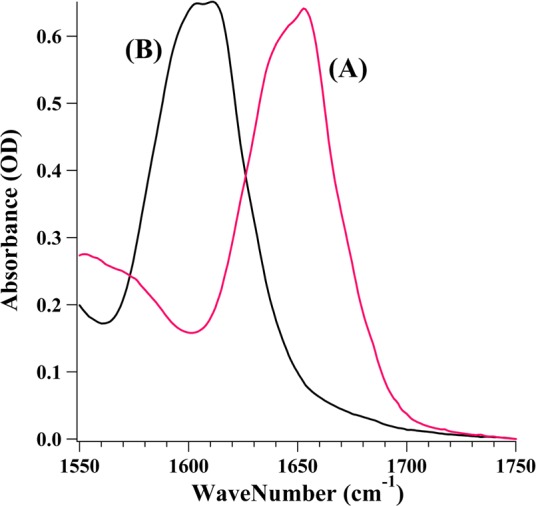
FTIR absorbance spectra of (A) LDH and (B) [¹³C/¹⁵N]LDH. The sample concentration was ∼4 mN in D₂O with 100 mM phosphate buffer (pH 7).

Figure 3.

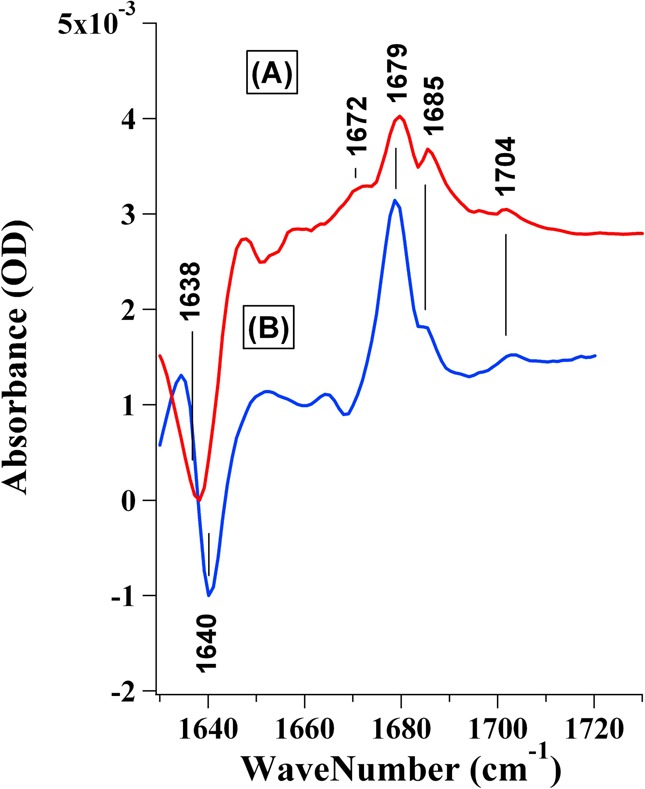
(A) Isotope-edited FTIR difference spectrum of the [¹³C/¹⁵N]LDH·NADH·[¹³C₂]pyruvate complex subtracted from that of the [¹³C/¹⁵N]LDH·NADH·[¹²C₂]pyruvate complex. (B) Isotope-edited FTIR difference spectrum of the LDH·NADH·[¹³C₂]pyruvate complex subtracted from that of the LDH·NADH·[¹²C₂]pyruvate complex. The samples were prepared from a 4:4:20 LDH/NAD/lactate mixture [initial concentration ratio (active sites for LDH)] in D₂O with 100 mM phosphate buffer (pH 7).

Isotope-Edited Static IR Spectrum of Bound Pyruvate

The bond vibrations associated with the C=O stretch of pyruvate are >1700 cm^–1 in solution but shift down when pyruvate is bound in LDH. Because the IR spectrum of a ligand bound to a protein is typically obscured by the many vibrations arising from the protein, an isotope-edited difference FTIR technique was used.^26,27 These studies were conducted by measuring the IR spectra for the sample where the C₂ atom of pyruvate is either with or without the ¹³C label. This highly controlled and precise comparison is required instead of simply a difference spectrum of ligand-bound versus free protein because ligand binding can perturb the vibrational modes of the protein, rendering interpretation of the resulting difference spectra difficult or impossible.

Figure 3 shows isotope-edited FTIR difference spectra of the LDH·NADH·pyruvate complex with LDH (spectrum A) or uniformly ¹³C- and ¹⁵N-labeled LDH (spectrum B). In these spectra, all IR bands unrelated to pyruvate C₂ should be subtracted out, leaving only IR bands that are affected by the ¹³C₂ labeling. The C₂=O stretch modes from unlabeled pyruvate appear as positive bands, and ¹³C-labeled pyruvate bands are negative. The major C₂=O stretch band at 1679 cm^–1 shifts down by ∼40 cm^–1 upon ¹³C₂ labeling, yielding the major negative band near 1640 cm^–1. This shift is expected via calculation of the shift from a local oscillator model of the C=O moiety and was used as one of the criteria in the subtraction procedure as described in detail previously.²² The pyruvate C₂=O band shifts ∼28 cm^–1 lower in the complex compared to its solution value [1708 cm^–1 (see spectrum D of Figure 5)], indicating the significantly polarized nature of the pyruvate C=O bond in the complex.

Figure 5.

(A) ¹²C₂=O spectral region for pyruvate in water. The pyruvate peak is at 1708 cm^–1 with a width (fwhm) of 22 cm^–1. (B) IR difference spectrum in the ¹²C₂=O spectral region for pyruvate in the [¹³C/¹⁵N](D168N)LDH·NADH·[¹²C₂]pyruvate complex. The data have been normalized such that the areas under the IR spectra of the three cases are equal. Using Gaussian functions, a minimum of four subcomponents was needed to fit to the IR spectrum with the position and bandwidth (fwhm) allowed to float. The following widths (relative areas) were found: 1674 cm^–1 (5.1 cm^–1, 1.2), 1679 cm^–1 (5.9 cm^–1, 7.9), and 1686 cm^–1 (4.7 cm^–1, 1.5). (C) IR difference spectrum in the ¹²C₂=O spectral region for pyruvate in the [¹³C/¹⁵N]LDH·NADH·[¹²C₂]pyruvate complex. The following peaks [widths (fwhm), relative areas] were found: 1674 cm^–1 (5.1 cm^–1, 1.2), 1679 cm^–1 (5.9 cm^–1, 7.9), 1686 cm^–1 (4.7 cm^–1, 1.5), and 1703 cm^–1 (5.7 cm^–1, 0.49). The protein samples were prepared from a LDH/NAD/lactate mixture with initial concentration ratios of 7:8:30 (wild type) and 3:3.3:14 (D168N mutant) in D₂O with 100 mM phosphate buffer (pH 7) at 20 °C. LDH brings about a rate of enhancement of 10¹⁴ M compared to the rate in a solution at pH 7 and a reactants concentration of 1 M. k_cat = 0.30 and a H/D KIE that is essentially negligible. Catalytic parameters for the (D168N)LDH mutant (B) and normal and labeled LDH (C and D, respectively) show essentially the same k_cat and K_d of 245 s^–1 (k_cat and K_d values of 235 s^–1 and 0.12 mM, respectively, for the unlabeled form and 242 s^–1 and 0.14 mM, respectively, for the labeled form) with a KIE of 1.4 for NADD/NADH.

Coupling between the Pyruvate C₂=O Stretch and the Reduced Nicotinamide Ring Stretch

In the unlabeled LDH complex, there is another prominent band at 1685 cm^–1 (Figure 3 A). This band intensity significantly decreases when LDH is labeled with ¹³C and ¹⁵N. Interestingly, no corresponding IR band near 1645 cm^–1 was observed when the pyruvate C₂ is labeled with ¹³C in the LDH complexes, suggesting that some other motion contributes to the 1685 cm^–1 band besides the pyruvate C₂=O stretch. We assign the 1685 cm^–1 band to the out-of-phase C=C stretch motions of the reduced nicotinamide moiety of bound NADH.²⁸ The isotope shift of this vibrational mode is due to coupling to the pyruvate C₂=O stretch motion due to strong interactions between NADH and pyruvate at the active site, despite the absence of a covalent bond between them.

To support this assignment, second-derivative analyses of the IR spectra of the LDH·NADH·pyruvate are shown in Figure 4. The second derivative narrows the band shape compared to the absorbance spectrum, and thus, it is more sensitive to small frequency shifts induced by a perturbation. Spectra A and B in Figure 4 show the second derivatives of FTIR absorbance spectra of LDH and the LDH·NADH complex, respectively, in the C=C and C=O stretch region. The band at 1685 cm^–1 in the second-derivative spectrum of the LDH·NADH complex (spectrum B) can be assigned to the out-of-phase C=C stretch mode of the reduced nicotinamide of NADH, based on its absence from the LDH spectrum (spectrum A). Spectra C and D in Figure 4 show the second derivatives of FTIR absorbance spectra of LDH·NADH·pyruvate and LDH·NADH·[¹³C₂]pyruvate complexes, respectively. The band at 1679 cm^–1 in the LDH·NADH·pyruvate complex is due to the major pyruvate C=O stretch, which is observed in the isotope-edited difference spectrum (Figure 3). In the LDH·NADH·[¹³C₂]pyruvate complex, this band shifts down to ∼1640 cm^–1; thus, it is absent in the frequency range shown in Figure 4. Remarkably, the band at 1685 cm^–1, which is due to the out-of-phase C=C stretch mode of the reduced nicotinamide of NADH, shifts down in energy by ∼1 cm^–1 when C₂ of pyruvate is labeled with ¹³C in the LDH·NADH·pyruvate complex, even though these groups are not covalently linked.

Figure 4.

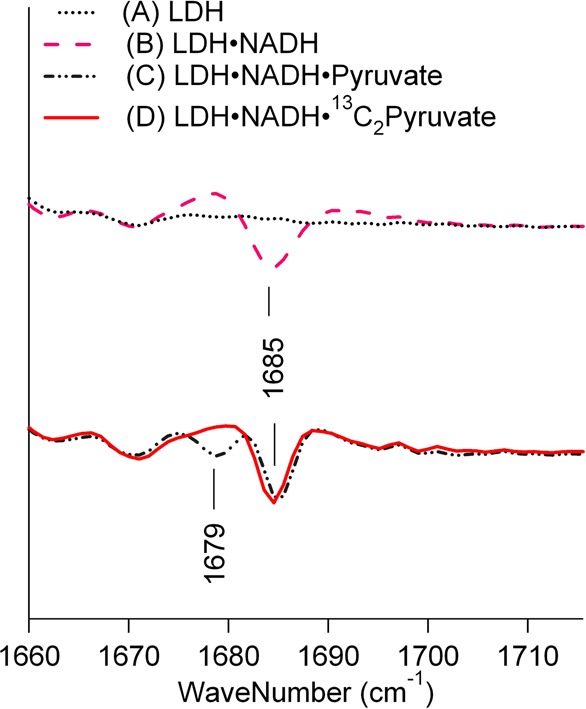
Second derivatives of IR spectra of (A) LDH and the (B) LDH·NADH, (C) LDH·NADH·[¹²C₂]pyruvate, and (D) LDH·NADH·[¹³C₂]pyruvate complexes in the C=O stretch region. Sample conditions are the same as those described in the legend of Figure 3.

The fact that the ¹³C labeling of the pyruvate C₂=O bond causes a small frequency shift of the nicotinamide ring mode of NADH suggests that the motions of these two groups at the active site in the LDH·NADH·pyruvate complex are synchronized and/or coupled to form a single, delocalized vibrational mode, which can happen only when they are in very close contact. This contact is close enough to allow some electronic orbital overlap between these two molecular groups. The simplest model is that in which the overlap is made through the C₄pro-R hydrogen of the reduced nicotinamide, which is transferred as a hydride to the C₂ atom of pyruvate in the chemical step. It is well established that the enzyme strongly restricts the orientation and conformation of the nicotinamide ring, such that any such close approach that allows direct vibrational coupling should be a reactive state given the very high fidelity of transfer of the pro-R hydrogen.²⁹

Determination of the Substate Population Distribution in the Michaelis Complex

The conformational distributions of the substrate pyruvate in the Michaelis complexes of the ¹³C- and ¹⁵N-labeled and unlabeled LDH are also different, as demonstrated by the intensity profiles of the pyruvate C=O stretches (see Figure 3). We have repeated the measurements of these LDH complexes more than 10 times, including some under different experimental conditions (e.g., different sample concentration ratios). The pyruvate C=O stretch intensity profiles show some variations under different conditions, but the following differences in ¹³C- and ¹⁵N-labeled and unlabeled LDH complexes are consistently observed. First, the main ¹³C=O stretch frequency of the ¹³C₂-labeled pyruvate is ∼ 2 cm^–1 lower in the unlabeled LDH complex. Second, the band intensities near 1685 and 1672 cm^–1 relative to that at 1680 cm^–1 are higher in the unlabeled LDH complex.

To quantitatively determine the pyruvate conformational distribution in the Michaelis complex, and how the distribution is affected by LDH isotope labeling and mutation, curve fitting procedures were used to simulate the observed intensity profile in the ¹²C=O region where protein interference is less pronounced. Figure 5 shows the C₂=O stretch bands (in the ¹²C=O region) of pyruvate in solution (A), in the [¹³C/¹⁵N](D168N)LDH·NADH·[¹²C₂]pyruvate complex (B), in the LDH·NADH·[¹²C₂]pyruvate complex (C), and in the [¹³C/¹⁵N]LDH·NADH·[¹²C₂]pyruvate complex (D) obtained by the isotope-edited difference methods. These pyruvate C=O stretch profiles can be typically fitted by four Gaussian curves as listed in Table 1. We assume each C=O band represents at least one distinct substate in the Michaelis complex, but with the caveat that the bands near 1685 cm^–1 also contain NADH band intensity. The relative populations of these substates as determined from the pyruvate C=O band intensities are also listed in Table 1. IR bands in the spectral region below ∼1665 cm^–1 contain contributions from ¹³C=O stretches, and they are excluded from the table.

Table 1. Curve Fitting Results for the Pyruvate C=O Stretch Profile in the LDH Michaelis Complexes^a.

	band (cm–1)	fwhm (cm–1)	intensity	population (%)	frequency average (cm–1)
pyruvate	1708	22	22	100	1708
[13C/15N](D168N)LDH·NADH·pyruvate	1683	5.2	2.2	17.9
	1691	7.2	6.7	54.5
	1701	13.2	3.4	27.6	1692.3
	1708	22	7.1	unbound
LDH·NADH·pyruvate	1673	5.7	6.5	33.3
	1679	5.0	4.7	24.1
	1686	7.9	5.7	29.2
	1699	13	2.6	13.3	1681.7
[13C/15N]LDH·NADH·pyruvate	1674	5.1	1.2	10.8
	1679	5.9	7.9	71.2
	1686	4.7	1.5	13.5
	1703	5.7	0.49	4.42	1680.5

^aBand represents the observed C=O stretch frequency. The resolution of the spectrometer was 2 cm^–1. The frequency errors for most bands are ±2 cm^–1 but for bands between 1670 and 1675 cm^–1 are ±3 cm^–1. fwhm denotes the full line width at the half-maximum. Intensity denotes the band intensity (arbitrary units). Population denotes the percentage of bound pyruvate at the given frequency. Frequency average denotes the population-weighted average frequency of all bound pyruvate bands.

As stated above, the frequency of the pyruvate C₂=O stretch is a direct measure of the electrostatic interactions that polarize the bond, and hence, it projects this feature of the reaction coordinate. The IR results of Figure 5 show directly the effects of active site electrostatic interactions believed to bring about an ∼10⁶-fold increase in rate from solution conditions to within the LDH Michaelis complex. The D168N mutant shows a steady state k_cat value of 0.30 s^–1 that is reduced by a factor of 820 from the wt protein k_cat value of 245 s^–1, and the corresponding active site electrostatic interactions on the pyruvate C₂=O bond are significantly weaker as indicated by the blue-shifted C=O stretch frequency profile (Figure 5). In a previous study on an analogue of the LDH Michaelis complex, an empirical correlation between bound pyruvate C=O frequencies and k_cat values for a number of LDH variants was suggested (see below).¹⁷ In the study presented here, our results show that the bound pyruvate has more than one frequency in the real Michaelis complex and the correlation must be reevaluated on the basis of the the population distribution of the substates. It is expected, every thing else being equal, that a substate with a lower C₂=O stretch will have a greater propensity toward on-enzyme chemistry.

Kinetic Isotope Effects

Steady state kinetics measurements of the LDH enzyme yielded a k_cat of 245 s^–1 with a KIE of 1.4 comparing enzyme loaded with NADD versus enzyme loaded with NADH.²⁰ This value for the H/D primary KIE is quite low; a value of ≥6 would be much more characteristic if the purely chemical step were rate-limiting. We can conclude that the chemical step is on a time scale similar to that of the various protein atomic rearrangements occurring within the phLDH·NADH·pyruvate Michaelis complex, such as loop closure, as well as other interconversions among the substate ensemble distribution. On the other hand, for (D168N)LDH, steady state k_cat (=0.30 s^–1) measurements yield an H/D KIE that is essentially negligible. This is an interesting observation because one explanation would be the chemical turnover rate in this mutant is reduced significantly more than the (partially) rate-limiting protein conformational motions. Currently, we are using an IR T-jump to study the interconversion kinetics among substates in the Michaelis complex to verify this possibility. All this is consistent, as shown in Figure 5, with a shift of the C₂=O stretch intensity profile in the (D168N)LDH·NADH·pyruvate complex ensemble toward conformations with much less propensity toward chemistry.

Binding Isotope Effects Due to ¹³C and ¹⁵N Labeling of LDH

Comparison between spectra A and B in Figure 3 reveals several interesting differences when pyruvate binds to unlabeled or ¹³C- and ¹⁵N-labeled LDH. For example, the main pyruvate C=O stretch frequencies (1679 cm^–1 bands) are different by <1 cm^–1 for the ¹²C pyruvate, but this difference increases to slightly more than 2 cm^–1 when C₂ is labeled with ¹³C (at 1640 and 1638 cm^–1, respectively). This result suggests the binding isotope effect due to pyruvate C₂ labeling may be somewhat different in ¹³C- and ¹⁵N-labeled LDH and unlabeled LDH. In addition, the most red-shifted pyruvate C=O stretch band intensity at 1674 cm^–1 has a significantly higher intensity in the unlabeled LDH (33% of bound pyruvate vs 11%), and the substate population distribution is also more evenly spread (Figure 5 and Table 1).

As discussed above, the IR intensity at 1686 cm^–1 in the isotope-edited difference spectra depends on the coupling of the pyruvate C₂=O stretch and the NADH ring stretch. The reduced relative intensity of this band in ¹³C- and ¹⁵N-labeled LDH [from 29 to 14% (Table 1)] suggests a reduced level of coupling of the two molecular groups, or a reduced electronic orbital overlap. Interestingly, while the D168N mutation significantly reduced the level of hydrogen bonding on the pyruvate C₂=O group, it did not affect the electronic orbital overlap of C₂=O with the reduced nicotinamide ring, as demonstrated by the unchanged IR intensity of the 1683 cm^–1 band upon mutation (Figure 5 and Table 1).

Discussion

There has been substantial interest in how atomic motion in proteins affects the functional properties of enzymes. Treatments of reaction rate theories typically depend on the time scale of the motions, with a separation between fast and slower motions of atoms.^30,31 For example, there has been much conjecture about the notion of so-called “promoting vibrations” (cf. ref (32)). These are femtosecond to picosecond vibrational-like motions of atoms located within the protein (as well as the bound substrate) that are part of the transition state coordinate, the bottleneck of the dynamical pathway of the actual chemical event. In contrast, we are interested here in the flux of the enzyme reaction system from the first step(s) of binding of the substrate to the enzyme to the formation of conformations poised for the actual chemical event. The focus of this study is atomic motions on time scales intermediate between vibrational times and the overall turnover of the enzyme, roughly motions from the subnanosecond to (more typically) microseconds to milliseconds. Events occurring slower than the time scale of the barrier crossing of the actual chemical event have been difficult to treat and characterize.

We have previously performed both static and dynamic studies of two well-characterized Michaelis mimics of the true Michaelis complex studied here. The results of those studies guided the design of our experiments. These Michaelis mimics are the so-called NAD–pyruvate adduct^17,33 (i.e., the LDH·NAD–pyruvate complex) and oxamate^25,34,35 (LDH·NADH·oxamate complex). Both are assumed to strongly resemble the LDH·NADH·pyruvate species with regard to general structure (K_d values and arrangement of active site contacts). However, at the sensitive level of structure that can be observed in isotope-edited IR studies, i.e., the C₂=O stretch profiles, the three complexes are quite different. The NAD–pyruvate adduct complex tends to show a carboxyl stretch more strongly shifted from its solution value. The oxamate complex shows a relatively less shifted C=O stretch along with a populated substate with no shift at all. In addition, kinetic IR T-jump studies show that the interconversion kinetics among the substates are very different. The substates of the LDH·NAD–pyruvate complex are virtually locked into place (very high free energy barriers to interconversion), and the substates of the LDH·NADH·oxamate complex interconvert on the submillisecond time scale. The entirety of the results suggests that the study of mimics yields substantial insights but also has substantial limitations for the questions being asked here.

As an organizing principle for understanding dynamical events on the slower time scales, we shall use the well-established notion that a protein exists as an ensemble of interconverting conformations. The dynamics of the system are then described well by the so-called energy landscape of the system. This multidimensional energy surface of the Michaelis complex describes how the system evolves from binding substrate to chemistry. For LDH, like apparently many proteins, the enzyme binds its substrate forming first a “loose” encounter complex whose structure is quite far from catalytic competence. From there, it is a good approximation that the system hunts, in a stochastic manner, through the various accessible conformations, arriving eventually at a reactive structure or, more likely, an array of reactive and relatively inactive structures. In this picture for enzymes, the phase space described by the energy landscape must be quite limited because enzymic catalysis occurs on typically short time scales; the system could not statistically sample all possible conformations that the protein complex could adopt in that little time. This can be likened to the protein folding problem and for many of the same reasons; the formation of reactive conformation(s) must be funneled with minimal frustration. We could call it the “catalysis landscape”.

We emphasize that this physical picture of the Michaelis complex is distinctly different and can be contrasted to the “standard” Eyring picture and evolved transition state concepts. In the literature on enzymes, bringing the two reacting molecules sufficiently close together and making them well oriented on the enzyme (and by extension the recruitment of crucial active site residues) to bring about the chemical event are typically understood as an enormous loss of entropy compared to the same system in solution⁵⁻⁷ (undoubtedly with stabilizing enthalpic contributions, as well⁹). The empirically determined free energy barrier to the chemical event is really an “effective” transition state free energy barrier, taking into account many components: those involved in bringing all the reacting groups together toward an ensemble of favorable to nonfavorable (propensity toward chemistry) structures and the actual barrier to the on-enzyme chemistry. Moreover, the Michaelis complex is typically depicted in a single conformation. The part of the effective transition state barrier attributed to bringing reactive groups together is probably the largest contribution to the reduction of the reaction barrier on LDH given previous work.¹²⁻¹⁴ This is also seen by the low primary H/D isotope effect on the overall k_cat; the search process for finding the active state(s) “dilutes” the H/D isotope effect that would be observed from the purely chemical event. Moreover, calculations of the ground state energy landscape of LDH strongly suggest that competent conformations within the Michaelis complex are actually rare;³⁶ ground state conformations that show slow direct turnover, but presumably fast conversion to productive conformations, substantially predominate.

Whether a specific ground state conformation within the LDH·NADH·pyruvate Michaelis complex ensemble is advanced along the reaction coordinate can be estimated by the distances from NADH’s C₄-H group to pyruvate’s C₂=O carbon and from pyruvate’s C₂=O group to the polarizing/proton donor groups at the active site (see Figure 1). These two distances are directly related to the hydride transfer and proton transfer that occur in the chemical step and, thus, are the major components of the reaction coordinate. In the studies presented here, we have shown that the isotope-edited difference FTIR techniques can potentially be used to evaluate both distances in the LDH·NADH·pyruvate Michaelis complex. The NADH C₄-H–pyruvate C₂=O carbon distance may be evaluated by the extent of coupling between the pyruvate C₂=O stretch and the out-of-phase C=C stretch of the reduced nicotinamide, although further studies are required to establish a quantitative correlation.

In previous studies, we were able to project out pyruvate’s C₂=O and the polarizing/proton donor groups distance and the strength of H-bond interactions because these directly show up in the (polarizing) downward shift of the C₂=O stretch, as discussed above. The larger the downward shift in frequency for a specific conformation, the closer the C₂=O group to the essential active site residues and the more that conformation is advanced toward chemistry. This is all in agreement with empirical studies that show the polarization of the C₂=O moiety,^12,14 and hence the C₂=O stretch,¹⁷ is highly correlated with chemical activity. Using the NAD–pyruvate analogue bound to bsLDH as a mimic for the Michaelis complex of the wt protein and a series of mutants, we found an empirical correlation for k_cat versus the shift in frequency of the C₂=O stretch from its solution value:

Sometimes, the C₂=O stretch shows up as heterogeneously broadened, so that the value at the average frequency was employed. Also, as mentioned above, the structure of the conformational substates is qualitatively different in the NAD–pyruvate adduct Michaelis mimic complex and in the actual Michaelis complex. Hence, while the rate of on-enzyme chemical conversion of a specific substate is clearly strongly dependent on the shift in the frequency of the C₂=O group, this correlation must be taken as semiquantitative. We are currently performing laser-induced T-jump IR studies of the LDH·NADH·pyruvate system to determine a kinetic model of the interconversion kinetics and thermodynamics among the substates and the rate of chemical conversion of a specific substate (M. Reddish, H.-L. Peng, H. Deng, K. S. Panwar, R. B. Dyer, and R. Callender, work in progress).

Figure 5 shows that the ensemble of conformations in solution produces a heterogeneously broadened C₂=O stretch band. This is expected because there is a distribution of water molecule conformations that surround the bond; each polarizes the C₂=O bond differently. In contrast, the LDH Michaelis complex shows a strongly downshifted IR profile. It, too, is heterogeneously broadened, but its character differs from that in solution, being composed of discrete substates, at least four as determined by the curve fitting results. According to the correlation between LDH k_cat and the bound pyruvate C=O frequency described above, we may assume that each of the substate populations has its corresponding degree of reactivity. The subpopulation of the ensemble showing a C₂=O stretch at lower frequencies, at, e.g., 1673 cm^–1 (Table 1), is more reactive toward forming the LDH·NAD⁺·lactate complex than that characterized by 1679 or 1686 cm^–1 and vastly more so than the species characterized by 1699 cm^–1 because, as stated above, pyruvate’s C₂=O stretch is a quantitative measure of C=O bond polarization, which is in turn correlated to the reactivity of the specific species; the larger the downshift in frequency, the greater the reactivity of the species.¹⁷ On the basis of substrate mimic kinetic studies, the substates appear to interconvert on time scales faster than k_cat.^22,25 Our preliminary data concerning laser-induced IR T-jump studies of the LDH·NADH·pyruvate system show that interconversion kinetics among the substates also proceed on the submillisecond time scale. Hence, whether the reaction proceeds through the more reactive but smaller-population 1673 cm^–1 substate (or even a less populated but more polarized substate) depends on (1) its reactivity relative to its small population, (2) whether the other less reactive substates can convert to it on time scales faster than the ∼1 ms catalytic event, and (3) the branching between the formation of the on-enzyme product relative to other substates within the Michaelis complex.

We can conclude that the process of binding NADH and pyruvate to the enzyme has indeed imposed an enormously reduced phase space on the reacting system compared to that in solution and strongly shifted toward reactive conformations. These conformations may include one or more of the structural features that are observed in our spectroscopic studies such as stronger hydrogen bonding to the pyruvate C₂=O group and closer contact between nicotinamide C4 and pyruvate C₂. The structure of the protein imposes an intermediate energy landscape in the case of the (D168N)LDH·NADH·pyruvate mutant system, as indicated by the C₂=O IR stretch band profile (Figure 5 and Table 1), resulting in intermediate catalytic efficacy. The nature of this mutant’s ensemble is characterized by a C₂=O IR stretch that is less shifted than that of the wt protein, but downshifted compared to the water spectrum; its IR profile is broader than that for the wt protein and even that of pyruvate in solution. This is strongly correlated with an intermediate catalysis rate (k_cat decreased by a factor of 820 from that of the wt protein). Interestingly, the k_cat and K_m parameters for the wild-type proteins are unaffected by the ¹³C and ¹⁵N labeling of the protein within our level of precision (235 s^–1 and 0.12 mM, respectively, for the unlabeled form and 242 s^–1 and 0.14 mM, respectively, for the labeled form) despite the fact that the labeling yields clear differences in the ensemble distribution. This may be due to numerous small changes between the two systems that have opposite and canceling effects on reactivity. The center C₂=O IR stretch frequency of the unlabeled protein distribution is comparatively slightly upshifted (Table 1), which suggests a slower relative k_cat. On the other hand, the NADH marker band intensity for catalytic competence at 1679 cm^–1 is larger for the unlabeled protein complex, suggesting a more competent substate population. In addition, the distribution profile of the unlabeled protein is broadened at both high and low C₂=O IR stretch frequency values compared to that of the labeled protein. If rare substates must be reached for effective catalysis, which seems likely, both labeled and unlabeled proteins have significant populations of low-C₂=O IR stretch frequency conformers. Clearly, there is much work to be performed to understand the dynamics quantitatively.

It is often stated that the nature of the chemistry occurring either in water or on the enzyme is largely the same.³⁷ What is clearly quite different is that an enzyme can impose a largely reduced and modified ensemble of conformational states and thereby direct the thermo-activated conformational sampling toward a small set of reactive substates. The value of k_cat reflects this conformational sampling as well as the actual time of the chemical event. The difference in chemical rate between solution and that catalyzed by LDH largely reflects the huge difference in the conformational sampling through ground state conformations.

Here we attempt to provide a quantitative analysis of the data for how the LDH reactivity may be affected by the pyruvate C=O stretch distribution observed in the Michaelis complex of the live reaction mixture. It is mostly based on a correlation between the bound pyruvate C=O frequency and LDH activity that was determined from the studies of a series of Michaelis complex analogues in which one C=O frequency can be associated with one activity value.¹⁷ Such analysis will provide some initial understanding of the energy landscape of the LDH Michaelis complex. The observed conformational substate distribution in the Michaelis complex and its associated structural features presented in this work provide additional opportunity to further characterize the energy landscape. For example, IR T-jump measurements^25,34 may be conducted to investigate how these substates interconvert kinetically among themselves, as well as their dynamic relationship to pyruvate binding and on-enzyme substrate turnover.

There has long been speculation that adaptation mechanisms and allostery involve a small tuning of an enzyme structure to affect its dynamical nature that in turn regulates key catalytic parameters. For LDH, for example, various isozymes all have the same active site architectures whether the isozymes are from psychrophiles, mesophiles, or hyperthermophiles, but their individual k_cat and K_m values appear to be tuned to operate properly at the respective temperatures.³⁸ The shifting of the energy landscape, that is, the shifting of the enzyme’s ensemble of microstates, as opposed to the evolution of specific active site structures, is postulated by many to account for the tuning (cf. ref (38)). The results presented here are consistent with this notion.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States