Variational Implicit Solvation with Poisson–Boltzmann Theory

Abstract

We incorporate the Poisson–Boltzmann (PB) theory of electrostatics into our variational implicit-solvent model (VISM) for the solvation of charged molecules in an aqueous solvent. In order to numerically relax the VISM free-energy functional by our level-set method, we develop highly accurate methods for solving the dielectric PB equation and for computing the dielectric boundary force. We also apply our VISM-PB theory to analyze the solvent potentials of mean force and the effect of charges on the hydrophobic hydration for some selected molecular systems. These include some single ions, two charged particles, two charged plates, and the host–guest system Cucurbit[7]uril and Bicyclo[2.2.2]octane. Our computational results show that VISM with PB theory can capture well the sensitive response of capillary evaporation to the charge in hydrophobic confinement and the polymodal hydration behavior and can provide accurate estimates of binding affinity of the host–guest system. We finally discuss several issues for further improvement of VISM.

I. Introduction

Aqueous solvent plays a significant role in dynamical processes of biological molecules, such as conformational changes, molecular recognition, and molecular assembly, that control cellular functions of underlying biological systems.^1,2 Implicit-solvent models are efficient descriptions of such dynamics of biomolecular interactions in an aqueous environment.³⁻⁵ In such a model, the solvent is treated implicitly as a continuum and the effect of individule solvent molecules are coarse grained. A large class of implicit-solvent models are based on dielectric boundaries that separate charged solutes from the solvent. Such description of a biomolecule in water using a dielectric solute–solvent interface is rather natural, as it has long been realized that there is indeed a vapor–liquid-like interface separating a biomolecule from the solvent.⁶⁻⁸ Moreover, electrostatic properties of biomolecules can presumably be accurately described by dielectric boundaries, as the dielectric environment of biomolecules is quite different from that of the aqueous solvent. Recent studies have shown that, with properly defined and estimated surface tension and other coarse-grained quantities, solute–solvent dielectric interfaces are crucial in the accurate description of biomolecular hydrophobic interactions.⁹⁻¹¹ It is therefore clear that, with an implicit solvent, dielectric solute–solvent interfaces are fundamental in the accurate and efficient prediction of biomolecular interfacial properties, electrostatic interactions, and solvation free energies. Providing such predictions by properly defining and precisely locating dielectric boundaries is one of the main goals of a recently developed variational implicit-solvent model (VISM).^12,13

The principle of VISM is to minimize a free-energy functional of all possible solute–solvent interfaces. Such a free-energy functional consists of the surface energy, solute–solvent van der Waals (vdW) interaction energy, and electrostatic interaction energy, all depending on the solute–solvent interface. The minimization of VISM free-energy functional determines stable equilibrium solute–solvent dielectric boundaries and solvation free energies. For years, we have developed a level-set method to numerically minimize such a VISM free-energy functional.¹⁴⁻²² With such a method, we begin with a large surface that encloses all the solute atoms and then evolve the surface in the direction of steepest descent of the VISM free energy. The surface evolution is tracked by solving numerically a partial differential equation of a level-set function that represents the surface. Our extensive computational results have demonstrated that the level-set VISM can capture polymodal hydration states, describe well the curvature and charge effect to the dry-wet transition, and provide accurate estimates of solvation free energies. We believe that VISM is the first implicit-solvent model that can capture multiple hydration states including hydrophobic cavities and dry-wet transitions of charged molecules in water that are important in protein–ligand binding.^2,17,23−26 Such pockets are hard to be described by traditional and popularly used, fixed-surface, implicit-solvent models, where a van der Waals surface (vdWS), solvent-excluded surface (SES), or solvent-accessible surface (SAS) is used as the dielectric boundary.²⁷⁻³¹

In this work, we incorporate the classical Poisson–Boltzmann (PB) theory of continuum electrostatics into our VISM formulation of the solvation free energy. This will improve our previous work using the Coulomb-field approximation (CFA) for electrostatics that does not describe the effect of ionic charges in the solvent.¹⁹⁻²¹ The PB theory is a well-established continuum description of electrostatic interactions of biomolecules in an aqueous solvent.³²⁻⁴² To couple the PB theory into VISM, here we develop robust numerical methods to solve the PB equation with arbitrarily shaped dielectric boundaries and to calculate the effective dielectric boundary force (DBF) that is the electrostatic part of total force as the negative variation of the VISM functional with respect to the location change of dielectric boundary.^39,43−47 The concept of DBF only arises in the variational approach to implicit solvation. In our previous work,^39,45 we derived the formula of DBF. Our numerical method generalizes the coupling interface method (CIM)⁴⁸ to have a compact discretization scheme. Our compact CIM (CCIM) has high accuracy for solving the PB equation and computing the DBF, required to evolve numerically the dielectric boundary during the relaxation dynamics.

We test the convergence and accuracy of our numerical algorithm by considering a single charged particle in ionic solvent for which analytical results are available. We then apply our level-set VISM with PB theory to several systems. First, we study the solvation of single ions and compare our level-set VISM results with experimental data. Second, we apply our VISM to study the potential of mean force of the solvent mediated interaction between two charged particles along their center-to-center distance. Third, we consider the hydrophobic interaction of two parallel plates in water with differently charge patterns and compare our VISM calculations with existing molecular dynamics (MD) simulations. Finally, we apply our level-set VISM with PB theory to the study of the hydration behavior, charge effect, and binding affinity of the host–guest system Cucurbit[7]uril and Bicyclo[2.2.2]octane.

Our extensive numerical calculations show that the level-set VISM with the PB theory is able to capture multiple local minimizers of the VISM free-energy functional that correspond to different hydration states. Moreover, we find that the electrostatic interaction has a strong influence on the conformation and solvation free energy of charged molecules in solvent. In particular, the PB description is more accurate than the CFA approximation of electrostatics. Our studies of the host–guest system also show that the VISM with PB theory can provide reasonably good estimates of the system solvation free energies.

We notice that other theories and models that are related to our VISM approach exist in literature.⁴⁹⁻⁵³ In some of these works, geometrical partial differential equations coupled with the PB equation are solved to determine equilibrium solute–solvent interfacial structures. Here, we relax our VISM functional to find stable equilibrium structures by computing the effective boundary force that includes the DBF. We also use our approach to analyze in detail some model systems in terms of the multimodal character of the potentials of mean force and the strong charge effect on hydration.

The rest of the paper is organized as follows. In section II, we present the VISM free-energy functional with the PB description of the electrostatic solvation free energy. In section III, we describe briefly the level-set method for minimizing the VISM free-energy functional, and numerical methods for solving the PB equation and computing the dielectric boundary force. In section IV, we apply our level-set VISM to the solvation of several charged molecular systems. Finally, in section V, we draw our conclusions.

II. Theory

A. Free-Energy Functional

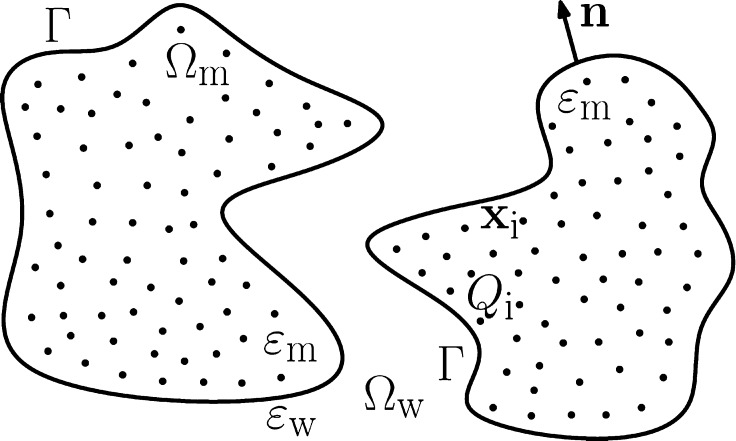
We consider the solvation of a charged solute molecule in an aqueous solvent that is treated implicitly as a continuum. We assume that the solute consists of N atoms that are located at x₁,...,x_N and carry partial charges Q₁,...,Q_N, respectively. We assume also that a solute–solvent interface Γ separates the solute region, Ω_m, from the solvent region, Ω_w, cf. Figure 1. In the variational implicit-solvent model (VISM),^12,13 one minimizes the solvation

free-energy functional

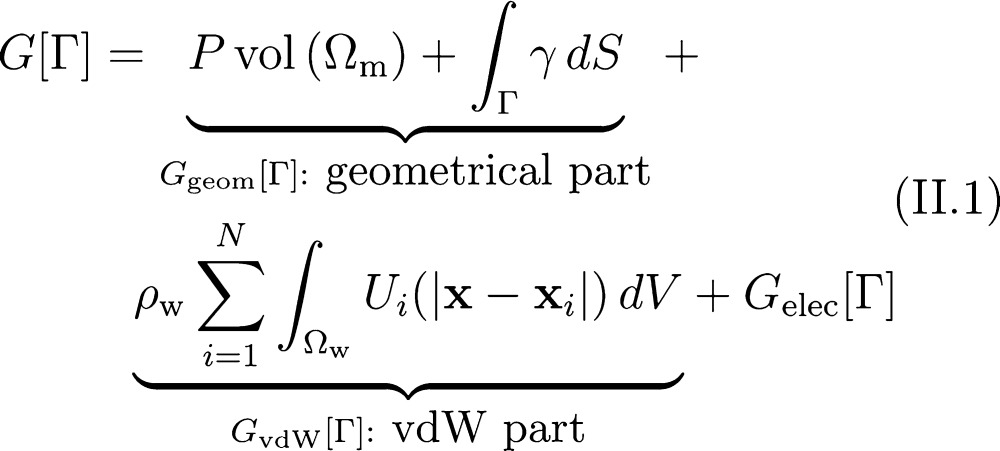II.1

among all possible solute–solvent interfaces Γ.

Figure 1.

Schematic view of a solvation system with an implicit solvent. A solute–solvent interface Γ separates the solvent region Ω_w from the solute region Ω_m that can have multiple components. The solute atoms are located at x₁,...,x_N and carry partial charges Q₁,...,Q_N, respectively. The dielectric coefficients of the solute and solvent regions are denoted by ε_m and ε_w, respectively.

The first term in eq II.1, proportional to the volume of solute region Ω_m, describes the work it takes to create a solute cavity in the solvent. P is the pressure difference between the solvent liquid and solute vapor. The second term is the surface energy, where γ is the surface tension. It is known that at the molecular scale the surface tension depends on local geometry of the surface.^54,55 Here, we use γ = γ₀(1 – 2τH), where γ₀ is the surface tension for a planar interface, τ is the curvature correction coefficient or the Tolman length, and H is the mean curvature defined as the average of the two principal curvatures.⁵⁴ We denote by G_geom[Γ] the sum of the first two terms in (II.1) and call it the geometrical part of the solvation free energy.

For each i (1 ≤ i ≤ N), U_i(|x – x_i|) in eq II.1 is the van der Waals (vdW) type interaction potential between the solute particle at x_i and a solvent molecule at x that is coarse grained. The summation term represents the vdW interaction between the solute and solvent, where ρ_w is the bulk density of the solvent. We define U_i to be the Lennard-Jones (LJ) potential

The parameters ε_i of energy and σ_i of length can vary with different solute atoms as in a conventional force field in molecular dynamics (MD) simulations. We denote by G_vdW[Γ] this summation term in (II.1), and call it the vdW part of the solvation free energy.

The last term G_elec[Γ] in (II.1) is the electrostatic part of the solvation free energy. It is given by^{32,34−36,39}

II.2

Here, ψ = ψ(x) is the electrostatic potential, ψ_reac = ψ – ψ_ref is the reaction field, and ψ_ref is the potential for the reference state

with ε₀ being the vacuum permittivity and ε_m the dielectric coefficient of solutes. We have assumed here that there are M ionic species in the solvent, with c_j^∞ and q_j being the bulk concentration and charge for the jth species. In eq II.2, β^–1 = k_BT with k_B the Boltzmann constant and T the absolute temperature. The first term in eq II.2 is the electrostatic potential energy corresponding to the fixed solute charges Q₁,...,Q_N, and the others terms in eq II.2 are the free energy of electrostatics due to the mobile ions in the solvent.

The potential ψ = ψ(x) solves the boundary-value problem of the Poisson–Boltzmann (PB) equation

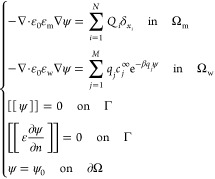II.3

Here, ε_w is the dielectric coefficient of solvent, [[u]] = u|_Ωw – u|_Ωm denotes the jump across Γ of a function u from Ω_m to Ω_w, ε = ε(x) takes the value ε_m in Ω_m and ε_w in Ω_w, respectively, the unit normal n at Γ points from Ω_m to Ω_w (cf. Figure 1), and ψ₀ is a given boundary value which is often given in practice by

where κ = (ε₀ε_wk_BT/Σ_j = 1^Mc_jq_j²)^1/2 is the inverse Debye length. In our numerical computations, we solve the following equations for the reaction field ψ_reac, instead of eq II.3 for ψ:

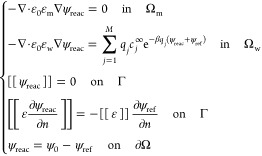II.4

B. Effective Boundary Force

We minimize the free-energy functional (eq II.1) by evolving an initial surface in the direction of steepest descent of the free energy. The evolution of the surface is therefore driven by the (normal component of the) effective boundary force, F_n, defined to be F_n = −δ_ΓG[Γ], the negative variational derivative of the free-energy functional G[Γ] with respect to the location change of the boundary Γ. With our convention that the unit normal vector n = n(x) for a point x on the boundary Γ points from the solute region Ω_m to the solvent region Ω_w, we have the effective boundary force^14,18,19

II.5

where K = K(x) is the Gaussian curvature, defined as the product of the two principal curvatures at a point x on Γ. Here F_n^elec(x) is the electrostatic part of the boundary force, the dielectric boundary force (DBF). It is given by⁴⁵

II.6

where I is the identity matrix. Note by eq II.3 that the normal component of the electric displacement ε∂ψ/∂n and the tangential component of the electric field (I – n ⊗ n)∇ψ are both continuous across Γ. Note also from eq II.6 that F_n^elec(x) < 0 for any point x on Γ, since in general ε_m < ε_w. This implies that the DBF always points from the solvent to the solute region.

C. A Shifted Dielectric Boundary

To compare with MD simulations, we use the LJ parameters in our solute–solvent vdW interactions the same as those in the MD simulations. Previously,^19,20,22 we found that an optimal VISM surface often corresponds to the surface with the first peak of water density determined using the position of oxygen atoms in water molecules. Such a surface is not necessary the best choice of dielectric boundary. This is because the center of charge of a polarized water molecule is displaced near a charged molecule, with the amount of displacement differing significantly between the two cases of positive and negative charges. This well-documented issue of charge asymmetry gives rise to the subtlety in defining a dielectric boundary.^{5,13,20,56−61} Our VISM does not explicitly treat the charge asymmetry. As a result, if we use a VISM surface as the dielectric boundary to calculate the electrostatic solvation energy, then the error can be sometimes significant.^19,20 Here we use an empirical method developed in our previous studies: after we obtain a VISM free-energy minimizing surface, we shift it in parallel toward the solute by ξ (in Å) and then use the shifted surface as the dielectric boundary to calculate the electrostatic solvation energy, cf. Figure 2. The parameter ξ should in principle depend on the local environment such as the sign of charges near the surface. However, to avoid being too complicated, we use a uniform value of shift and usually set it to be close to 1 Å.

Figure 2.

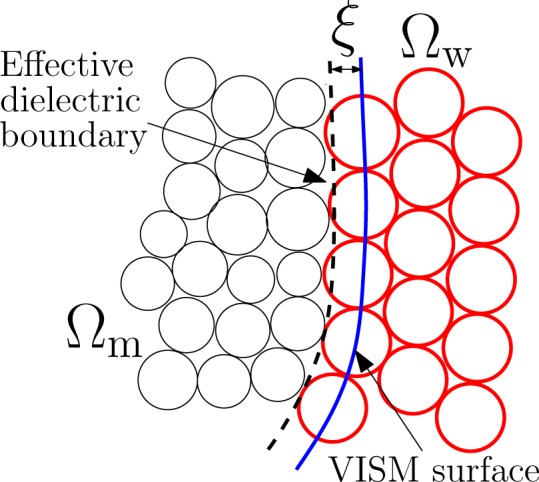
Effective dielectric boundary is obtained by shifting the VISM surface to the solute region by ξ in Å.

D. Potential of Mean Force

Consider the solvation of a solute that consists of two groups of atoms. One group of atoms are located at x₁,...,x_M and the other at x_M+1,...,x_N, respectively. We choose the distance d between the geometrical centers (Σ_i = 1^Mx_i)/M and (Σ_i = M+1x_i)/(N–M) of these two groups of atoms as a reaction coordinate. Also, we choose the system that two groups are infinitely far from each other as a reference state, that is, d_ref = ∞. For every fixed finite d, the minimization of the VISM solvation free-energy functional leads to a local minimizer, that is, a stable equilibrium solute–solvent interface Γ_d. We define the (total) potential of mean force as the sum of three contributions¹⁹

II.7

where

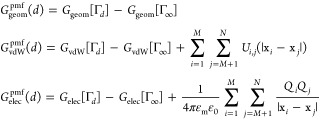Here, a quantity at ∞ is understood as the sum of two separate contributions

II.8

where Γ_I and Γ_II, both independent of d, correspond to the VISM equilibrium solute–solvent interfaces of those two solute groups that are treated individually. The quantity G in the above eq II.8 can be replaced by G_geom, or G_vdW, or G_elec. In the above definition of G_vdW^pmf(d), we include the contribution of the vdW interaction between the two solute groups. In the definition of G_elec(d), we include the Coulombic interaction between the two solute groups in the reference medium with the dielectric constant ε_m.

For a given reaction coordinate d, different initial conditions can result in multiple equilibrium interfaces, corresponding to different local minimizers of the VISM free-energy functional. The PMF therefore may have multiple branches along the reaction coordinate d, leading to a hysteresis. We call these branches equilibrium PMFs in contrast with the ensemble PMF that is the averaged PMF weighted with Boltzmann factors.

III. Numerical Methods

Numerically, we minimize the VISM free-energy functional II.1 by relaxing an initial surface that encloses all the solute atoms in the direction of steepest descent of free energy. We relax the surface by solving the level-set equation

III.1

Here, ϕ = ϕ(x,t) is a level-set function representing the evolving surface Γ = Γ(t) at time t; that is, Γ(t) consists exactly all the points x such that ϕ(x,t) = 0. The function F_n = F_n(x) is the effective boundary force given in eq II.5. This force is extended away from the surface so that the level-set eq III.1 can be solved in a finite computational box or a narrow band surrounding the surface Γ(t). Note that pseudo-time t here represents the optimization step.

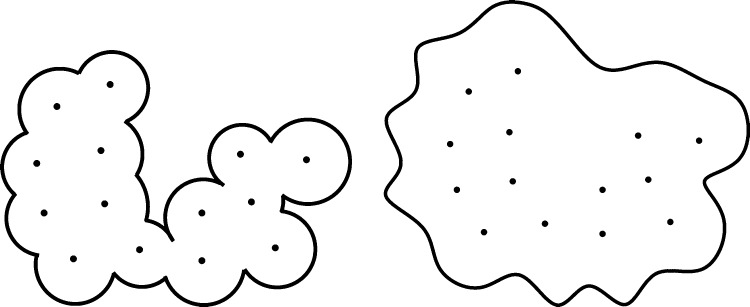
Due to the nonconvexity of the VISM free-energy functional, different initial surfaces can relax to different local minimizers with our steepest descent strategy. To capture different local minimizers, we usually start with two types of initial surfaces: a tight wrap that is a union of vdW spheres centered at solute atoms with reduced radii and a loose wrap that is a large surface loosely enclosing all the solute atoms. See Figure 3.

Figure 3.

Typical initial surfaces of the level-set VISM calculations. Left: A tight initial. Right: A loose initial.

To discretize the level-set eq III.1, we rewrite it as^14−16,18

where

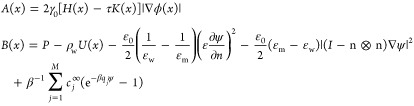The B|∇ϕ| is a hyperbolic term. We discretize it using an upwind scheme. In our implementation, we use a fifth-order WENO (weighted essential-no-oscillation) scheme. For the A term, we first linearize A = A(ϕ) at ϕ that is computed in the previous time step and adjust the parameter τ to enforce parabolicity of the linearized equation. We use the central differencing to discretize the derivatives in A with the adjusted τ.¹⁸

We use the forward Euler method to discretize the time derivative in the level-set eq III.1:

III.2

where φ^(k)(x) and F_n^(k)(x) are the approximations of ϕ(x,t_k) and F_n(x,t_k), respectively, at time t_k = kΔt (k = 1,2,...) and Δt is the time step size. We update the level-set equation ϕ by III.2 in a narrow band surrounding the surface. To satisfy the Courant–Friedrichs–Lewy condition, we choose

III.3

where h is the step size in space discretization, C = C(ϕ) is the matrix obtained in linearizing A(x) with respect to φ and is determined by A(ϕ) = γ₀C(ϕ):∇²ϕ, and

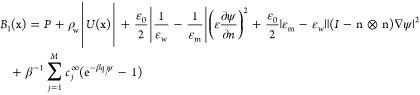The maximum in III.3 is taken over all the grid points in the band.^18,19

To solve eq II.4, we use Newton’s iteration

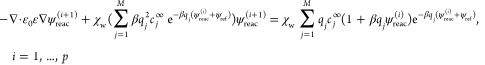III.4

where χ_w is the characteristic function of the solvent region Ω_w, that is, χ_w(x) = 1 in Ω_w and 0 otherwise, and the number of iteration p can vary from 1 to 30. In each iteration, we solve a linear partial differential equation with two jump conditions on Γ, cf. eq II.4 . We solve this linearized interface problem with a compact Coupling Interface Method (CIM) that is an improved version of CIM.^48,62 To compute the DBF (eq II.6) on the interface, we approximate ψ and ∇ψ by the interpolation of the potential at adjacent grid points.

IV. Test and Application

We use the TIP4P water model to determine the parameters for water and employ the Lorentz–Berthelot mixing rules for the LJ potentials of interaction between water and individual solute atoms. We also use k_BT for energy and Angström for length. Throughout our calculations, we fix T = 300 K, P = 0 bar, γ₀ = 0.1315 k_BT/Ų, ρ_w = 0.0331 Å^–3, ε_m = 1, ε_w = 78, and τ = 0.76 Å.

A. One Charged Particle

We consider a single particle with charge value Q centered at the origin. The VISM free-energy functional for this system reduces to a one-variable function of radius R:¹⁹

IV.1

This function can be numerically minimized with a very high accuracy. We use the LJ parameters ε = 0.3 k_BT and σ = 3.5 Å. We perform a series of test with different charge values: Q = 0.0 e, 0.5 e, 1.0 e, 1.5 e, 2.0 e. In our level-set calculations, we use a 120 × 120 × 120 computational grid to resolve a computational box (−4,4) × (−4,4) × (−4,4).

In Table 1, we show the result of our level-set calculations (labeled as level-set) and numerical minimization of (IV.1) (labeled as analytical). We compare the optimal radii, the nonpolar and polar solvation energies, and the total solvation energies for different values of Q. Clearly, the level-set relaxation gives very accurate results. Note that the optimal radius decreases as the charge value increases due to the strong dielectric boundary force acting on the solute–solvent interface. With a smaller radius, the reaction potential ψ_reac becomes larger and the system thus gains more electrostatic solvation energy. Meanwhile, the nonpolar part of the solvation energy also increases because of the rapidly increasing solute–solvent vdW interaction. Compared with the nonpolar part, the electrostatic part of the solvation energy becomes more and more dominant as the charge value increases.

Table 1. Solvation Free Energies (in k_BT) and VISM Optimal Radii (in Å) for a Spherical Particle with Different Charge Values Q (in e).

	optimal radii		nonpolar energy		polar energy		total energy
charge	level-set	analytical	level-set	analytical	level-set	analytical	level-set	analytical
0.0	3.167	3.157	4.845	4.836	0.0	0.0	4.845	4.836
0.5	3.040	3.030	5.216	5.273	–22.614	–22.686	–17.398	–17.412
1.0	2.810	2.801	9.406	9.660	–97.857	–98.144	–88.451	–88.484
1.5	2.610	2.605	20.977	21.285	–237.083	–237.455	–216.106	–216.170
2.0	2.459	2.453	40.512	41.304	–447.352	–448.281	–406.840	–406.977

We also apply our level-set VISM to the solvation of single ions K⁺, Na⁺, Cl^–, and F^–. We take the LJ parameters for these ions from the publication.⁶³ In our calculations, the dielectric boundary of the anion Cl^– or F^– is obtained by shifting the VISM equilibrium surface by ξ = 1 Å, which is the length of the water OH bond.^{13,19,20,57−59,64} In Table 2, we display the nonpolar and polar parts of the solvation free energy obtained by our level-set VISM calculations, and the experimental values of solvation free energy⁶⁵ for these ions. We see that our VISM result agrees well with experiment. Again, we observe that the polar part of solvation free energy contributes more than the nonpolar part.

Table 2. Solvation Free Energies (in k_BT) for Single Ions K⁺, Na⁺, Cl^–, and F^–: VISM Calculations vs Experiment⁶⁵.

ions	ε (kBT)	σ (Å)	nonpolar energy	polar energy	total energy	expt.
K+	0.008	3.85	16.5	–128.2	–111.7	–117.5
Na+	0.008	3.49	17.3	–147.8	–130.5	–145.4
Cl–	0.21	3.78	11.7	–137.8	–126.1	–135.4
F–	0.219	3.3	11.2	–182.8	–171.6	–185.2

B. Two Charged Particles

We consider a system of two ions K⁺ and Cl^– in water and in monovalent (1: 1) ionic solution with different bulk concentrations c_±1^∞ = 0.1 M, 0.5 M, and 0.8 M, respectively. The LJ parameters are ε_K = 0.2104 k_BT, ε_Cl = 0.2104 k_BT, ε_O = 0.2622 k_BT, σ_K = 3.250 Å, σ_Cl = 3.785 Å, and σ_O = 3.169 Å,⁶⁶ where O means the oxygen in water. When we calculate the electrostatic solvation energy, we employ a parallel shift of the equilibrium surface by ξ = 0.6 Å. This value is determined by trying several ξ-values. For each trial ξ-value, we compute the VISM solvation energy for each of the ions. We then compare the sum of these two computed energy values with the sum of the two experimental solvation energy values of the two ions, respectively. In other words, we determine the best uniform shift ξ = 0.6 Å for the two ions as they are infinitely separated from each other and use it for the system when the two ions are apart from each other with a finite distance. We choose the center-to-center distance of the two ions as the reaction coordinate and study the solvent-mediated PMF of the system. For each distance d, we minimize the VISM free-energy functional to get an equilibrium solute–solvent interface and compute each component of the solvation free energy with the obtained interface.

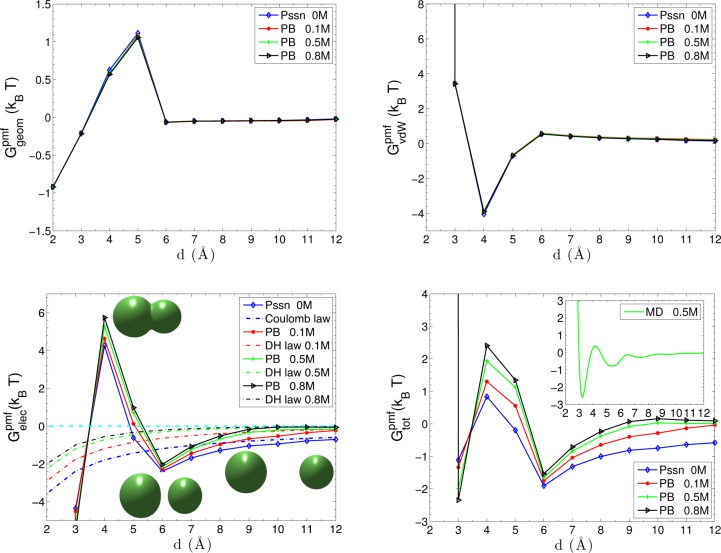
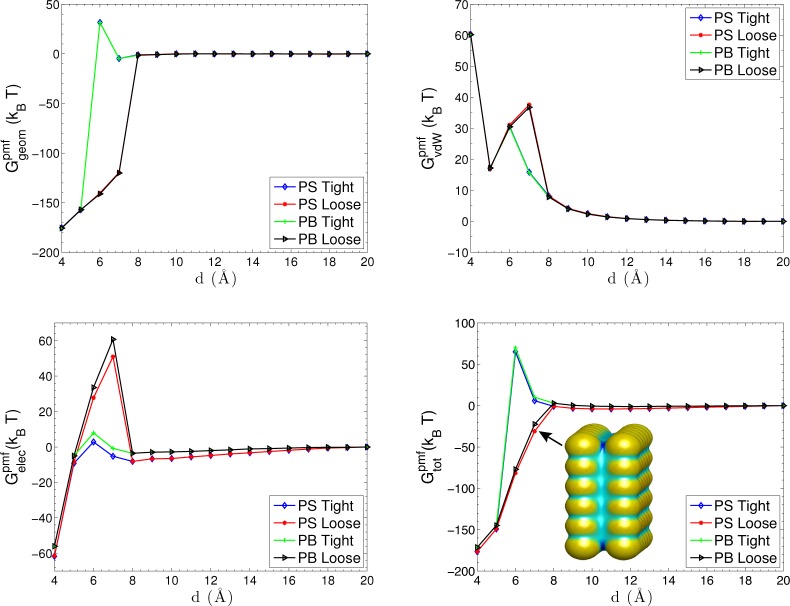
Figure 4 shows different contributions to the PMF. The geometric part of the PMF in the upper left of the figure shows a pronounced desolvation barrier at d = 5 Å, where the two VISM surface branches of charged particles start to merge together. The concavity of the merged solute–solvent interface accounts for the distortion of the water molecules in the overlapping hydration shells. At a small separation, the geometric part of PMF shows water-induced attraction due to less water-accessible area. The upper right of Figure 4 displays the vdW part of PMF with the solute–solute vdW interaction. It shows significant repulsions as the two objects merge together and peaks at d = 6 Å where the two objects begin to break.

Figure 4.

Different components of the PMF for the two-particle system of K⁺ and Cl^–. Upper left shows the geometrical part G_geom^pmf of the PMF. Upper right shows the vdW part G_vdW of the PMF. The solute–solute vdW interaction is included. Lower left shows the electrostatic part G_elec^pmf of the PMF. The Coulomb law and Debye–Hückel (DH) screening law for two-particle interactions are shown as references. Three inset figures are effective dielectric boundaries at d = 4 Å, d = 6 Å, and d = 10 Å, respectively. Lower right shows the total PMF G_tot in the mainframe and MD simulation results (with 0.5 M salt) in the inset.

In the lower left of Figure 4, we observe that the electrostatic part of the PMF varies with the ionic concentration. At a small separation d ≤ 3 Å, the attraction between two oppositely charged particles is greatly enhanced due to the short interaction distance and weak dielectric screening in the solute region. There is a high electrostatic desolvation barrier at d = 4 Å, due to the concave dielectric boundary. Such a barrier depicts the energy penalty of the steric depletion of polar water molecules that are originally attracted to the charged particles. In contrast, the favorable electrostatic interaction between water molecules and particles is only partially reduced at d = 5 Å. After two objects are completely solvated at d > 5 Å, the effect of solvent and ionic solution comes into play. Overall, the attractive interaction between the two particles is gradually screened, and the profiles converge asymptotically to the Coulomb law Q₁Q₂/4πε₀ε_wd and Debye–Hückel (DH) screening law (Q₁Q₂ e^–κd)/(4πε₀ε_wd). We see that after the two objects separate, the decay of electrostatic attraction as the separation increases is faster than that for the Coulomb or DH interaction. This is due to the solvent screening and the shape change of dielectric boundary. From the snapshots in the lower left of Figure 4, we can see that the dielectric boundary for the particles at the distance d = 6 Å are not perfect spheres. They are deformed slightly in the direction of the reaction coordinate, due to the strong electrostatic interaction between two particles. As the separation becomes larger, the electrostatic interaction becomes weaker and the shape of the dielectric boundary becomes more spherical. This indicates that the nonpolar and polar contributions affect each other via the equilibrium solute–solvent surface.

In the lower right of Figure 4, we show the PMF obtained by our VISM-PB in the mainframe and by MD simulation (for c_±1^∞ = 0.5 M) in the inset.⁶⁶ For d < 3 Å, both results show the repulsion that stems from the vdW interaction between the overlapping particles. Near d = 3 Å, both capture the significant electrostatic attraction due to the weak dielectric screening and short interaction distance. At a distance close to d = 4 Å, the two results show a desolvation barrier. For the distance between d = 5 Å and d = 6 Å, in which the solute–solvent surface of two particles breaks apart, both PMFs again show the attraction. The MD simulations show some oscillations for d > 6 Å while our mean-field VISM only predicts a monotonic PMF. Overall, however, there is a remarkable agreement between our VISM calculations and the MD simulations.

C. Two Parallel Charged Plates

We consider the solvation of a strong hydrophobic system of two parallel paraffin plates with different charge patterns,^19,67,68 and study the effect of charge pattern to the hydrophobic attraction, capillary evaporation between the plates, and the hysteresis of the PMF profiles. Each plate contains 6 × 6 fixed atoms with the LJ parameters ε = 0.265 k_BT and σ = 3.532 Å. The two plates are placed in pure water (labeled “PS”) or monovalent ionic solutions with 0.2 M bulk concentration (labeled “PB”). The plate–plate separation distance is chose to be the reaction coordinate to define the PMF.

We define five different charge patterns:

• •Pattern I: Each atom in the two plates carries a positive charge 0.2 e, cf. Figure 5 a.
• •Pattern II: One plate is positively charged and the other negatively charged. Each atom in the two plates is charged with the same charge value 0.2 e, cf. Figure 5a and b.
• •Pattern III: One plate is charged as shown in Figure 5c and the other plate is oppositely charged with the same value in corresponding positions.
• •Pattern IV: One plate is charged as shown in Figure 5d, and the other plate is oppositely charged with the same value in corresponding positions.
• •Pattern V: One plate is charged as shown in Figure 5e, and the other plate is oppositely charged with the same value in corresponding positions.

Figure 5.

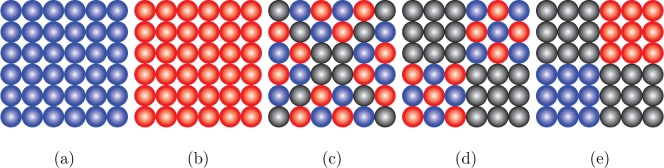
Homogeneously (a and b) and heterogeneously (c, d, and e) charged plates. Blue means a positive charge 0.2 e. Red means a negative charge −0.2 e. Gray means neutral.

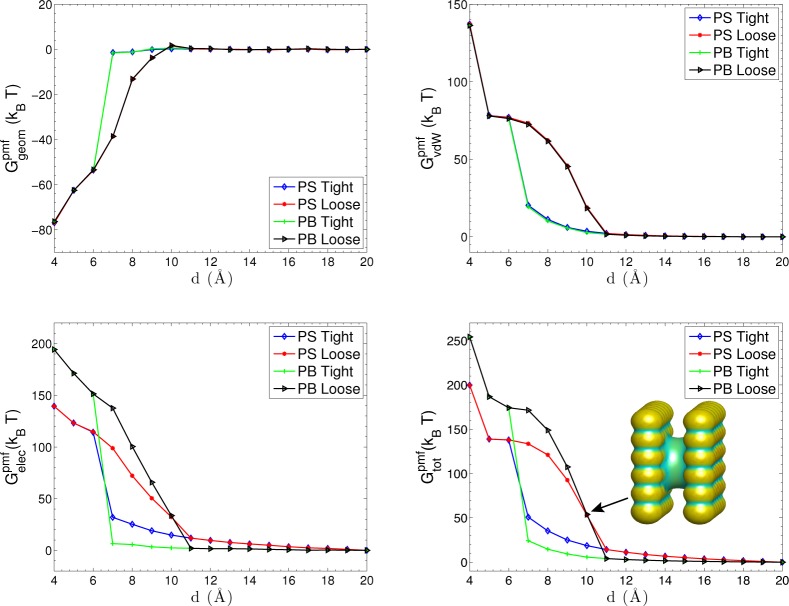
Figure 6 shows the total PMF and its different components for Pattern I. We observe the capillary evaporation when 6 Å < 11 Å. In this range of the plate–plate separation, there are in general two branches of the PMF. The lower one corresponds to the dry state and the upper one the wet state. We observe from the upper left and upper right of Figure 6 that, at a short plate–plate separation, the geometric part of PMF exhibits a strong attraction due to a small water-accessible area but the vdW part (including the solute–solute interaction) is repulsive. The dry state resulting from a loose initial leads to a higher vdW desolvation barrier. The electrostatic PMF is shown in the lower left part. The electrostatic repulsion results from the like-charge interaction. For a wet state, the electrostatic interaction is greatly screened at the distances d > 6 Å, due to the presence of solution between the plates. Clearly, a stronger screening occurs with ionic solution (PB). For a dry state, the electrostatic interaction gradually decreases as the separation increases where the solvent partially penetrates into the region between plates. The lower-right plot in Figure 6 displays the total PMF of the system, with a snapshot showing the solute–solvent surface of the dry state at d = 10 Å. We can see that the electrostatics attracts the solvent close to the charged atoms, pushing the solute–solvent surface deep into the middle regions of the two plates. We also observe that the total PMF profile is mainly determined by the electrostatic part with small nonpolar contributions at short separations.

Figure 6.

Total PMF and its different components vs the separation distance d between the two plates that are charged as Pattern I. PS denotes pure water and PB denotes ionic solutions. The inset snapshot shows the solute–solvent surface of the dry state at d = 10 Å. Color on the surface represents the mean curvature.

Figure 7 shows the total PMF and its components for Pattern II. We see that the capillary evaporation only occurs at shorter separations d < 8 Å, due to the strong electrostatic interaction between oppositely charged plates that drags polar water molecules and ions into the inter plate region. This can also be seen from the analytical formula II.6 of dielectric boundary force (DBF): a stronger electric field leads to a larger DBF. The nonpolar contributions, both G_geom^pmf and G_vdW, show a strong sensitivity to the local electrostatics, due to the very different solute–solvent surface geometries induced by different charge patterns. For the electrostatic part, there are obvious desolvation barriers when two solute–solvent surfaces of the plates begin to merge together, especially for a dry state. The polar water molecules between the charged plates are firmly attracted to the charged atoms by the strong electric field. However, they are sterically depleted away when two plates come closer than the critical distance, resulting a concave solute–solvent surface between the plates. The corresponding energy cost of the depletion is responsible for the high desolvation barriers in the electrostatic PMF. For a large distance, similar screening effects of the solvent and ionic solution can also be observed.

Figure 7.

Different components of the PMF vs separation distance d between the two plates that are charged as Pattern II. PS denotes pure water and PB denotes ionic solutions. The inset snapshot shows the solute–solvent surface of the dry state at d = 7 Å.

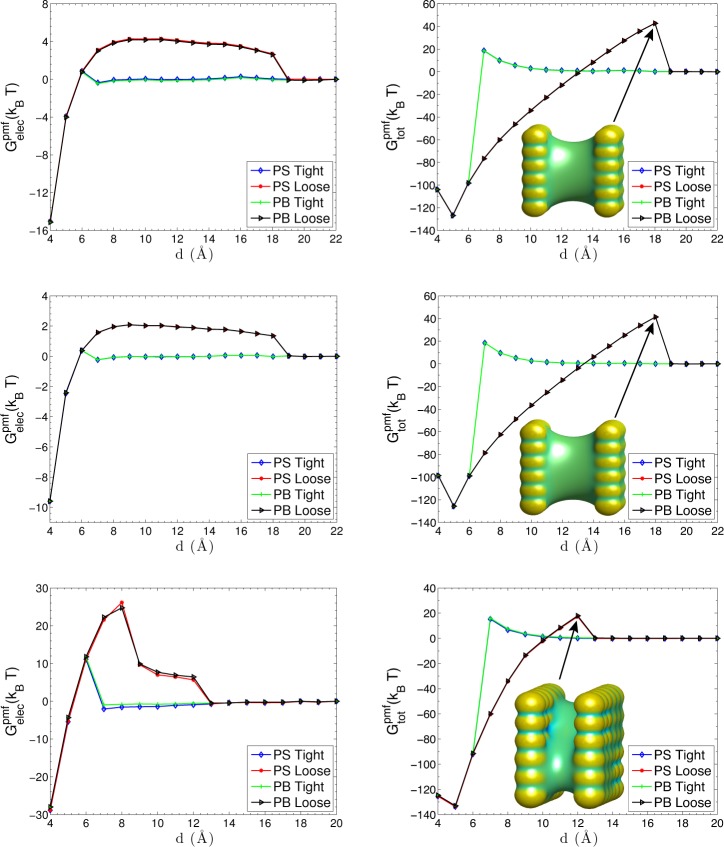
For two plates that are charged as Pattern III, IV, and V, we focus on the electrostatic part of the PMF and the total PMF, cf. Figure 8. We see that the largest distance of capillary evaporation for Patterns III and IV is increased to d = 18 Å This is because that the electrostatic interaction is reduced by the surrounding opposite charges. Again, we observe electrostatic desolvation barriers when water molecules between two plates evaporate. From the snapshots shown in Figure 8, we also see that the solute–solvent surfaces are concave between two plates when there are desolvation barriers. Compared with the results for Pattern I and Pattern II, the water molecules between the plates are easier to evaporate away from the charged plates, because of the weaker electrostatic interactions between the plates. The electrostatic desolvation barriers are therefore much lower. Since the electrostatic contribution is weak, the nonpolar contribution dominates and therefore the total PMFs for Pattern III and IV are very close to each other.

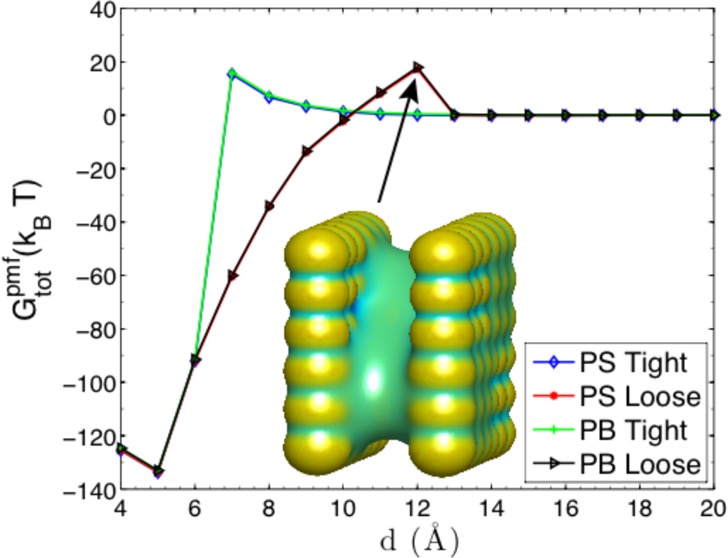
Figure 8.

Electrostatic part of the PMF and the total PMF. Top panel: Pattern III. The inset snapshot shows the solute–solvent surface of the dry state at d = 17 Å. Middle panel: Pattern IV. The inset snapshot shows the solute–solvent surface of the dry state at d = 17 Å. Bottom panel: Pattern V. The inset snapshot shows the solute–solvent surface of the dry state at d = 12 Å.

Pattern V is a rearrangement of III or IV, cf. Figure 5. Such a rearrangement increases largely the electrostatic contribution. We can see from the bottom panel of Figure 8 that the largest separation distance for capillary evaporation decreases down to d = 12 Å Remarkably, our VISM solute–solvent interface captures the stepwise cavitation for the dry state when the capillary evaporation takes place, cf. the snapshot of the solute–solvent surface in bottom-right plot of Figure 8, agreeing qualitatively with the MD simulations by Hua et al.⁶⁸ The electric field generated by the charged atoms at the two corners attracts polar solvent molecules, while the hydrophobic sites still keep dry. The desolvation barrier in the electrostatic PMF is consistent with this stepwise dewetting transition. For a distance between d = 9 Å and d = 12 Å, the desolvation barrier reaches its first plateau, because of the desolvation of water molecules near the hydrophobic, neutral atoms. When d < 9 Å, the desolvation barrier goes up further with a larger magnitude, since it costs larger energy penalties to desolve the water molecules near the hydrophilic, charged atoms. The total PMF shows another different type of hysteresis, induced by the different distribution of charged atoms in Pattern V. We can see that our level-set VISM has accurately captured the hydrophobic–hydrophilic coupling effects in this heterogeneously charged two-plate system.

Finally, we consider the water density between the plates, defined by

where ρ_w is the bulk water density, V_sol is the solvated volume between the plates, and V_tot is the total volume between the plates. Figure 9 displays the water density along the reaction coordinate for dry (loose initial) and wet (tight initial) states. The results predicted by tight initials do not show dewetting transitions. For loose initials, the region between the plates becomes solvated with the increasing separation for all the patterns except Pattern II where a complete solvation occurs suddenly when the separation increases from 7 Å to 8 Å. These dewetting transitions predicted by our VISM calculations have also been observed in MD simulations on similar two-plates systems.⁶⁸

Figure 9.

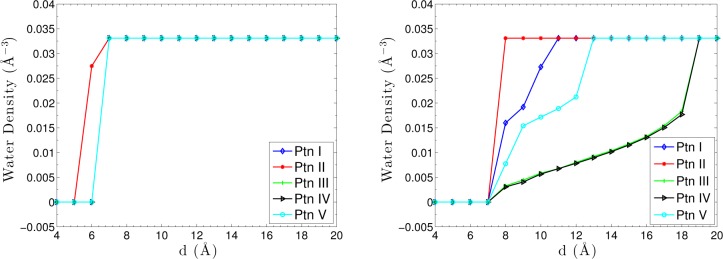
VISM estimate of water density between the two plates for different charge patterns (Ptn means Pattern). Left: Tight initials. Right: Loose initials.

D. Host–Guest System

We now apply our VISM with PB theory to the solvation of a host–guest system: a bicyclo[2.2.2]octane (B2) binding to a synthetic host cucurbit[7]uril (CB[7]). This host–guest system has wide applications in many fields, such as molecular machines, supramolecular polymers, gene transfection, and drug transport.⁶⁹⁻⁷⁴ Its ultrahigh binding affinity has attracted experimental and computational attention.⁷⁵⁻⁸¹ We studied this system in our recent work with a Coulomb-field approximation (CFA) of the electrostatics.²¹ Here, we use our VISM with PB theory to investigate the hydration behavior and the binding affinity of the host–guest system. We use a parallel shift of our VISM surface toward solute region by ξ = 1 Å when we calculate the electrostatic solvation energy. In our calculations, the host CB[7] and guest B2 are both modeled as rigid bodies. The force-field parameters and coordinates are taken from an MD study.⁸² To show the effect of electrostatics to the hydration and free energies, we study both charged and uncharged cases. The uncharged case is simply treated by setting the values of partial charges to be all zero. More details of parameters can be found in our recent work.²¹

1. Hydration Behavior of Isolated Host and Bound Host–Guest System

Figure 10 displays our VISM equilibrium surfaces of the isolated host with loose (upper panel) and tight (lower panel) initials. We observe both dry and wet states that result from loose and tight initials, respectively. Moreover, VISM equilibrium surfaces are tighter when charges are included. In such a case, the VISM surface with the PB description is tighter than that with the CFA of electrostatics.

Figure 10.

VISM equilibrium surfaces of the host CB[7] without and with charges. Left: No charges. Middle: With charges and the electrostatics is described by the CFA. Right: With charges and the electrostatics is described by the PB theory. Upper: Loose initials. Lower: Tight initials. The color on the surface represents the mean curvature being convex (red), flat (green), and concave (blue).

Table 3 displays individual contributions to the solvation free energy. We see that the electrostatic solvation energy is underestimated without the parallel shift of the VISM surface. Also, the electrostatics plays a dominant role in the solvation. Without charges, the solvation free energy of a dry state corresponding to a loose initial is lower than that of a wet state corresponding to a tight initial. However, with charges, the solvation free energy with a wet state is much lower. These conclusions are in line with recent explicit MD simulations of the identical nonpolar and polar systems.^21,82 Enhanced fluctuations are observed in MD simulations due to the toroidal confinement of the host cavity, and the host is mostly found in the wet state. Also, the average water density near solute atoms is much higher when the charges are included (cf. Figure 5 in ref (21)).

Table 3. Individual Contributions to the Charged and Uncharged Host–Guest Solvation Free Energy (in k_BT) predicted by Level-Set VISM with Different Initial Surfaces^a.

systems	electrostatics	initials	Ggeom[Γ]	GvdW[Γ]	Gelec[Γ]	total energy
CB[7]	uncharged	loose	91.5	–88.3	0.0	3.2
		tight	104.7	–97.6	0.0	7.1
	charged	loose	93.0	–81.8	–204.6(−96.9)	–193.4(−85.7)
		tight	103.5	–91.1	–216.2(−101.3)	–203.8 (−88.9)
B2	uncharged	loose	28.1	–18.6	0.0	9.5
		tight	28.1	–18.6	0.0	9.5
	charged	loose	27.8	–18.1	–20.6 (−3.5)	–10.9(6.2)
		tight	27.8	–18.1	–20.6 (−3.5)	–10.9(6.2)
CB[7]-B2	uncharged	loose	91.1	–93.4	0.0	–2.3
		tight	91.1	–93.4	0.0	–2.3
	charged	loose	91.2	–87.8	–212.6(−98.6)	–209.2(−95.2)
		tight	91.2	–87.8	–212.6(−98.6)	–209.2(−95.2)

^aThe values in parentheses denote the energies obtained without shifting the solute-solvent surface.

The VISM equilibrium surfaces for the bound host–guest system are shown in Figure 11. For the bound system, both the loose initials and tight initials give nearly the same equilibrium surfaces. The free energies listed in Table 3 also show this independence of the initial surfaces. Again, we can see that the electrostatic interaction pushes the equilibrium surface to be closer to the solute atoms, and the charge effect predicted by CFA is not as strong as that by the PB description. MD simulations also show that the water molecules distribute much closer to the charged atoms and water densities around atoms are much higher when charges are included.^21,82

Figure 11.

VISM equilibrium surfaces of the host–guest system CB[7]-B2. Left: No charges. Middle: With charges and the electrostatics is described by the CFA. Right: With charges and the electrostatics is described by the PB theory.

2. Binding Free Energies

The binding affinity is described by⁸³

where

is the difference between the total PMF (eq II.7) of the bound state and that of an unbound state, ΔG_TS is the entropy penalty upon binding, and ΔG_Val is the valence energy differences, including the energy changes of bond-stretch, angle-bend, dihedral, etc. The superscript R denotes the reference state.⁸³

Table 4 lists individual contributions computed with loose initials and tight initials. For comparison, reference results from the work⁸³ are also presented. Those results are obtained with a second-generation Mining Minima (M2) Algorithm,^79,84 in which free energies are estimated by the sum of the potential energies and implicit solvation energies at local energy wells. For the geometric contribution, both the loose and tight initials predict favorable binding energies because the water-accessible area is reduced after the host and guest are bound together. The tight initial, corresponding to a wet state of the host cavity, has a larger energy difference than the loose case, since more water-accessible area is lost upon binding. The vdW interaction between water and solutes disfavors binding, with an energy penalty of 12.1 k_BT for the loose initial and 21.4 k_BT for the tight initial. The reason for this energy penalty is that the favorable solute-water vdW interaction (cf. G_vdW[Γ] in Table 3) is reduced upon binding, especially for the tight case. The nonpolar part of the solvation favors the host–guest binding by −17.5 k_BT for the loose initial and −18.7 k_BT for the tight initial. This qualitatively agrees with the prediction of −4.4 k_BT in the work.⁸³

Table 4. Individual Contributions to the Host–Guest Binding Affinity^a.

contributions	loose initial	tight initial	M2 calculations83	expt.83
ΔGgeom[Γ]	–29.6	–40.1
ΔGvdW[Γ]	12.1	21.4
ΔGnp[Γ]	–17.5	–18.7	–4.4
ΔGelec[Γ]	12.6	24.2	24.5
ΔGelecR	–12.2	–12.2	–13.8
ΔGelecpmf	0.4	12.0	10.6
ΔGvdWR	–38.7	–38.7	–57.9
entropic penalty	(29.4)	(29.4)	29.4
valence energy	(2.0)	(2.0)	2.0
binding affinity	–24.4	–14.0	–20.3	–22.6

^a“Δ” means energy difference (in k_BT) between the bound and unbounded states. Unavailable data are blank cells. The numbers in parentheses are taken from ref (83). The last column presents the experimental data reported in ref (83). The energy difference of the nonpolar solvation energy is ΔG_np[Γ] = ΔG_vdW[Γ] + ΔG_geom[Γ]. ΔG_elec^R and ΔG_vdW are the energy differences of the Coulombic interaction and vdW interaction between the host and guest in the reference state, respectively. The energy difference of the electrostatic part of the PMF ΔG_elec^pmf = ΔG_elec[Γ] + ΔG_elec.

For the electrostatic part of the solvation (ΔG_elec[Γ]), both the loose initial and tight initial predict unfavorable energy differences. Remarkably, the tight initial, which corresponds to the wet state, predicts a 4.2 k_BT energy penalty, agreeing very well with 24.5 k_BT reported in ref (83). As a component of the electrostatic part of the PMF, the Coulombic interaction between the host and guest in the reference state has a favorable contribution −12.2 k_BT to the binding affinity. Such a contribution is independent of the solute–solvent interface. The electrostatic part of the PMF (i.e., ΔG_elec^pmf = ΔG_elec[Γ] + ΔG_elec) shows an unfavorable energy difference: 1.4 k_BT energy penalty for the loose case and 12.0 k_BT for the tight case, compared to 10.6 k_BT presented in the work.⁸³ These data indicate that the attractive Coulombic interaction in the reference state partially cancels the binding penalty from the electrostatic part of the solvation, leading to a relatively weak penalty of electrostatics to the binding.^76,77,83

The host–guest vdW interaction in the reference state strongly drives the binding with an attraction of −38.7 k_BT. In contrast, it is about −57.9 k_BT as reported in ref (83). The discrepancy can be attributed to the difference in the positional coordinates of the host and guest in the bound state. Since the two binding partners are treated as rigid bodies with a fixed relative orientation, we are unable to compute the entropy penalty and the valence energy changes upon binding. Here, we take these data, which are shown in parentheses in Table 4, from ref (83) to complete the computation of the binding affinity. In the last row of Table 4, we show the total binding affinity of the system given by loose initials and tight initials. We can see that both of them predict a favorable binding affinity, with −24.4 k_BT for the loose initial and −14.0 k_BT for the tight initial. They are in line with the calculation of −20.3 k_BT by the M2 algorithm and −22.6 k_BT of the experimental data.⁸³ Overall, VISM captures individual contributions to the binding affinity and predicts reasonably well binding free-energy values.

V. Conclusions

In this work, we introduce the Poisson–Boltzmann (PB) description of the electrostatics in the variational implicit-solvent model (VISM), and implement a level-set method to minimize the resulting VISM free-energy functional. Different types of initial surfaces in the free-energy minimization lead to different final stable equilibrium surfaces that describe multiple hydration states. One of our major efforts has been to design and implement a high-order Compact Coupling Interface Method (CCIM) for solving the PB equation to obtain the electrostatic potential and to compute the PB dielectric boundary force (DBF). We apply our theory and methods to a few charged systems that include single ions, two charged particles, two parallel plates, and a host–guest system.

Our extensive computational results with comparison with experiment and molecular dynamics (MD) simulations have demonstrated that VISM is able to capture multiple hydration states that lead to the hysteresis in the potential of mean force (PMF) and provide fairly accurate estimates of solvation free energies. It is clear that different components of the free energy all contribute to the relaxation of the system. In particular, the nonpolar parts (i.e., the geometrical and vdW parts) of interaction depends sensitively on the electrostatics via the solute–solvent interface. In fact, the analytical expression of the DBF and our numerical computations show clearly that the effective electrostatic force always pushes the solute–solvent interface into the solute region. The magnitude of such force predicted by the PB theory is larger than that by the Coulomb-field approximation, indicating that mobile ions enhance the charge effect. Even for the host–guest system CB[7]-B[2], our level-set VISM calculations reveal different hydration states that have been predicted by the MD simulations.

We now discuss several issues of our approach. First, our computational results show that the boundary shift of an optimal VISM surface works well for the final evaluation of electrostatic free energy. However, such a shift is inconsistent with the principle of free-energy minimization. One possible improvement of VISM is then to use two boundaries: one corresponding to a solute–solvent interface and the other to a dielectric boundary. With two boundaries in the VISM free-energy functional, we can relax them alternatively in numerical implementation. The difficulty is more analytical. At this point, we do not have a simple formulation of the VISM functional with these two bounaries and yet that is relatively simple to implement and efficient in computation. Another possible way is to redefine the LJ parameters in the solute–solvent interaction in the VISM description, so that the two boundaries can be unifined into one. We are now looking into these possible improvements. Second, solving the nonlinear PB equation in each step of level-set optimization is very costly. As typically the ionic concentrations are low in an aqueous solvent, it is reasonable to just use the linearized PB equation. Moreover, we can speed up our computations by use the CFA for electrostatics in the beginning of level-set iteration. Third, we have used mainly two types of initial surfaces, loose or tight initial surfaces, to relax our VISM functional. In some cases, the two corresponding relaxed VISM interfaces are different. They represent two local minima of the functional that are stable equilibrium conformations of an underlying molecular system. For a simple system, such as the two parallel plates, these are expected to be the only meaningful local minima. However, in general, we may not be able to capture all different kinds of local minima of the VISM functional by using only the loose and tight initial surfaces. There are two possible approaches to resolving this issue. A relatively simple one is to design different kinds of initial surfaces based on the solute atomic positions. A complicated one is to introduce fluctuations in the model to allow the system to jump from a local minimum to another. We will study these approaches in our future work. Finally, our current theory and methods do not provide a systematic way of computing the entropy of an underlying molecular system. Accurate predictions of enthalpy and entropy are, however, particularly important in understanding protein–ligand binding.² It is therefore our goal to develop a VISM compatible theory for such predictions.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States