Evidence that the Lombard effect is frequency-specific in humans

Abstract

Recent perspectives suggest that the Lombard effect is an increase in the suprasegmental speech parameters of vocal intensity, duration, and fundamental frequency in the presence of noise. It has been viewed as a non-specific response to ambient noise, but this assumption has not been thoroughly tested. Two experiments using healthy adults measured intensity, duration, and F0 changes in broadband (0.2–20 kHz) and notched noise (0.05–4 kHz removed) during a picture naming task. The pilot experiment showed that broadband noise containing speech-similar frequencies significantly increased intensity, duration, and F0 while notched noise, which removed the majority of speech-similar frequencies, had no effect. The main experiment added bandpass noise (0.05–4.0 kHz) which contained a major portion of speech-similar frequencies and was the mirror image of the notched noise. Broadband and notched noise results were replicated. Bandpass noise increased intensity and duration, but to a lesser degree than did broadband noise, and had no effect on F0. Findings show that the Lombard effect is sensitive to frequencies vital for speech and is not a general response to any competing sound in the environment. Implications for suprasegmental control of speech are discussed.

INTRODUCTION

Speech production involves coordination between the auditory and speech motor systems (Mottonen and Watkins, 2011). A key component of this coordination is self-monitoring which uses auditory feedback to detect speech errors (Ludlow and Cikoja, 1998), and is an important element in models of speech production (Levelt, 1989; Postma and Kolk, 1992). Auditory input such as background noise competes with verbal acoustic feedback and can be used to study self-monitoring because background noise can influence concurrent vocal responses (e.g., Postma and Kolk, 1992).

The Lombard effect has traditionally been conceptualized as an increase in vocal intensity that functions as a nonspecific response to noise (Lombard, 1911). Vocal intensity increases about 0.38 dB for every 1.0 dB increase in noise level above 55 dB sound pressure level (SPL) (Korn, 1954). More recent masking studies have identified other speech features that also change with background noise such as increased fundamental frequency (F0), increased duration, a shift in energy frequency bands and formant center frequencies, and spectral tilting (Junqua, 1996; Lane and Tranel, 1971; van Summers et al., 1988). The purpose of the Lombard effect in humans seems to be driven by both reflexive and communicative functions. Solitary speakers automatically increase intensity to aid in self-monitoring of their vocal output, but also increase intensity in company to ensure that the listener understands what they are saying (Garnier et al., 2010). These changes make Lombard speech more intelligible than speech that is produced in quiet (van Summers et al., 1988). The Lombard effect is modulated by high-level linguistic influences, as shown by greater durations of content words overall and higher F0 with agents versus function words (Patel and Schell, 2008). It is also found in many animals including non-human primates (Hage et al., 2006), birds (Cynx et al., 1998), cats (Nonaka et al., 1997), frogs (Lopez et al., 1988), and whales (Scheifele et al., 2005). Thus, the Lombard effect is not exclusive to humans, and therefore has general importance for regulating vocal output in a range of species.

Research of postlingually deaf cochlear implant users where the auditory input was blocked has shown similar results to that of background noise, and has provided important information about timing effects. Svirsky et al. (1992) tested three conditions (device-off condition, device off for 24 h, and device-on) and found significant changes in speaking intensity, fundamental frequency, vowel duration, and vowel formants across the three conditions. Although immediate effects in the short-term condition were seen, the largest effects occurred in the long-term auditory deprivation condition. Bharadwaj et al. (2006) found that word durations on fricatives (e.g., “she” versus “see”) significantly increased given a brief (15–20 s) acoustic deprivation of auditory feedback in half of the tested children and a quarter of the adults with cochlear implants. Taken together, these results suggest that measures of intensity, duration, and F0 generally increase in the presence of noise and with cochlear implant users when auditory input is blocked. Results also suggest that self-monitoring plays an important role in speech production temporally.

The frequencies produced by the speech motor system are matched to the differential sensitivity of the frequencies perceived by the auditory system. Within the range of human hearing, between 0.02 and 20 kHz, the most relevant speech signal frequencies are between 0.10 and 5 kHz (Bordon et al., 1994a). The human ear has different sensitivity thresholds for varying frequencies. The loudness level contours (Fletcher and Munson, 1933) are such that thresholds of frequencies in the speech range are lower than for frequencies outside the speech range. We postulated that there may be a relationship between the Lombard effect and the loudness level contours of human hearing. That is, the frequencies in which humans are most easily able to perceive may be the most influential on changing speech output when presented as a masker.

If the Lombard effect in humans indeed reflects the predispositions of the auditory system to self-monitor speech, then we predict this would constrain the properties of noise that are sufficient to elicit the Lombard effect. Garnier et al. (2010) have shown that when noise is similar to speech, as with cocktail party noise, it has greater effects on speech output parameters relative to broadband noise. This study takes the next step by more specifically testing the effects of noise frequency content on the Lombard effect by determining whether noise that covers a range of frequencies vital for speech (operationalized here as frequencies between 0.5–4.0 kHz) is necessary and sufficient to elicit the Lombard effect. If the Lombard effect is a non-specific response to noise then it would be present regardless of frequency content. We hypothesized that the Lombard effect is not a non-specific response to noise, but instead arises from masking of specific acoustic correlates of suprasegmental speech parameters. If true, then the effect should be maximized when speech frequencies are present in the noise, and absent when speech frequencies are not. We also predicted that these effects would increase linearly with exposure time to the masking stimuli due to the combined effects of sensory adaptation and masking. We further predicted that the changes among intensity, duration, and F0 would be strongly correlated with one another. Note that the term suprasegmental speech parameters refers to vocal intensity, duration, and F0 collectively, which are linguistic indices of prosody that vary over relatively long-term time scales (Perkell, 2012).

There are several other aspects of the present study that are novel relative to previous work. A picture naming task was used to precisely control the timing and content of vocalization. Next, multiple properties of vocal responses were measured (intensity, duration, F0), and the degree to which these suprasegmental speech parameters changed together in response to background noise were compared. Last, the potential influence of sensory adaptation to prolonged background noise was assessed by analyzing results over each trial block according to the first, middle, and last 1/3 of trials.

METHODS

The results from two experiments will be presented. The pilot experiment will be covered briefly as it was initially used to test whether or not the Lombard effect was influenced by the frequency content of masking noise. The main experiment used the same basic paradigm and replicated the results of the pilot experiment, but took a more analytical approach by using both notched and bandpass masking frequencies.

Participants

The pilot experiment tested sixteen healthy controls from the Tulane University and New Orleans communities (M/F = 8/8, age = 24.8 ± 5.7, range = 18–36 yrs). All participants were native English speakers, had normal pure tone thresholds (≤20 dB; 0.5, 1, 2, 3, 4, 6, 8 kHz), and reported no history of neurological, speech, or language disorders. Pure tone thresholds were measured with an audiometer. Participants were screened using the Peabody Picture Vocabulary Test (PPVT-4; Dunn and Dunn, 2007) and the Expressive Vocabulary Test (EVT-4; Williams, 2007) and scored within normal limits (mean standard score = 124 ± 10.8). Two participants from the pilot experiment were unable to complete the PPVT-4 and EVT-4 due to scheduling conflicts. All participants passed an informal screening to ensure normal articulation. The screening was performed by the first author who is a speech-language pathologist. These tests were administered to rule out any speech or language deficits. The main experiment tested a new cohort of sixteen participants from the Tulane University and New Orleans communities (M/F = 8/8; age = 21.5 ± 3.7, range = 18–30 yrs). All participants met the same criteria in the prior experiment, including scoring within normal limits on standardized language testing (mean standard score = 123 ± 6.8). Each participant in the experiments completed an informed consent document. The experiments were performed in accordance with a protocol approved by the Tulane University Institutional Review Board.

Research design

A picture naming task was used to measure vocal output in silence and in the presence of various continuous noise masks. The same pictures were presented in each condition, which controlled for any differences in syllables and naming durations among individual pictures. In the pilot experiment there were a total of five conditions—one quiet and four background noise conditions. The noise conditions had a 2 × 2 design, and varied by factors of intensity level (75, 90 dB) and noise frequency band (broadband 0.02–20 kHz, notched broadband attenuated from 0.5 to 4 kHz). In the main experiment, there were a total of seven conditions—one quiet and six background noise conditions. An additional level in the noise frequency band was added (bandpass, 0.5–4 kHz) making it a 2 × 3 design. Measures of speech output for both experiments included intensity, duration, and F0.

Stimuli

Target stimuli for both experiments were pictures (5 × 5 cm) of everyday objects displayed on a computer screen, which varied between one and four syllables. Masking stimuli for the pilot experiment consisted of two types of noise (broadband, notched). Broadband noise contained frequencies from 0.02 to 20 kHz, while notched noise was filtered from 0.5 to 4.0 kHz (Hanning filter, 48 dB/octave roll off) to attenuate frequencies in a range containing important cues for speech perception. The main experiment used the same broadband and notched noise from the pilot experiment, and added a bandpass noise mask (0.5–4.0 kHz; 48 dB/octave roll off), which is the inverse of the notched noise. The noise was generated using the software program Adobe Audition (Version 1.5, Adobe Systems Inc., 2005). Noise stimuli in both experiments were each presented at two intensity levels (75, 90 dB SPL). A sound level meter (Quest Technologies) was used to calibrate intensity level.

Procedure, data collection, and equipment

The experiments were conducted in a sound-attenuating booth. Participants sat in front of a computer monitor to view the target stimuli and wore headphones (Audio-Technica, ATH-M20) that delivered the background masking stimuli. Participants' speech outputs were collected using a microphone (Radio Shack, XLR-USB) placed ∼5 cm in front of their mouths. The frequency response curve for the headphones was 30–20 000 Hz and 15–15 000 Hz for the microphone. Participants viewed sequences of the same 24 pictures in five randomly constructed sequences (picture duration = 2 s, interstimulus interval = 5 s). Participants were instructed to remain still and to verbally name each picture when presented. Each of the noise conditions and the quiet condition were presented as a separate block with 24 trials. The order of blocks was counterbalanced across all participants for each experiment. Participant's speech outputs were sampled at 44.1 kHz and recorded using the program Stim2 (Version 4.0; Neuroscan Compumedics, 2003).

There were two differences in procedure between the experiments. In the pilot experiment, participants' distances from the microphone were measured before and then re-confirmed after each block. Participants remained still throughout the entire pilot, so in the main experiment, distances from the microphone were measured before the first block and re-confirmed at the end of the last block. The pilot experiment adjusted the intensity level for the background masking stimuli prior to each block using the sound level meter. The main experiment simplified this procedure by recording the correct location on the volume meter on the computer that represents the intensity level for each noise stimuli. The bar on the volume meter that corresponded to the correct intensity level was then adjusted prior to each condition.

To ensure that differences between the broadband and notched noise were not due to a perceived increase in loudness for the broadband noise four participants performed a forced choice loudness judgment task. Broadband and notched noise stimuli were presented as a pair for 4 s each with a 50 ms inter-stimulus interval. Stimulus pairs were presented at 75 and 90 dB. Intensity level and stimulus order were random. Participants were asked to judge whether the second stimulus was louder, softer, or the same as the first. Four out of four participants judged the broadband and notched noise stimuli to be equal in loudness.

Data and statistical analyses

All vocal responses for each participant were spliced in a row, and the onset and offset of the vocal response was visually determined from the waveform and marked by the first author. Inter-rater reliability for duration length of the vocal responses between the first author and an undergraduate data analyst for 10% of the total spliced productions was 0.98. The software package Multi-Speech 3700 (Version 3.2; Kaypentax, 2008) was used to compute F0 (Hz). Adobe Audition (Version 1.5; Adobe Systems Incorporated, 2005) was used to compute intensity (dB) and duration (ms). Intensity was computed using root mean square (RMS) normalized to the soundcard. The spliced whole-word vocal responses were used to calculate the change in the three measured suprasegmental speech parameters. Change in intensity, duration, and fundamental frequency were computed by subtracting the mean RMS level, duration, and fundamental frequency for each of the 24 vocal responses in the noise conditions from the mean RMS level, duration, and fundamental frequency, respectively, in the quiet condition.

Three statistical analyses were conducted. Statistical significance was defined as p < 0.05 except where noted. First, to calculate whether or not the Lombard effect was present, one-sample t-tests were conducted to determine if the change given each noise mask was significantly different from zero. Change was defined by subtracting values in the quiet condition from those in each noise condition with a precision to the hundredth decimal point. t-tests used a Bonferroni correction to define significance (p < 0.012). Second, to measure the effects of the background noises on the suprasegmental speech parameters, a repeated measures 2 (noise frequency band) × 2 (intensity level) × 3 (trial) multivariate analysis of variance (MANOVA) in which intensity level (90 dB, 75 dB), noise frequency band (broadband, notched), and trial (trials 1–8, trials 9–16, trials 17–24) were entered as within-groups independent variables. There were no significant effects of trial so this dependent variable was removed from the analysis. The dependent variables were intensity change (intensity noise–intensity quiet), duration change (duration noise–duration quiet), and F0 change (F0 noise–F0 quiet). To limit type 1 error, univariate comparisons were examined when statistical significance was seen first at the MANOVA level. Greenhouse-Geisser (alpha = 0.05) corrections are reported when sphericity was violated. Helmert contrasts to compare the significant effects between the noise levels were also calculated. The third analysis compared the relationship in the changes in the three suprasegmental speech parameters in noise using two-tailed Pearson correlations. The broadband 90 dB noise condition was chosen a posteriori for analysis because the Lombard effect was present in all three suprasegmental speech parameters.

The main experiment used the same data analysis procedures as the pilot experiment. Inter-rater reliability for duration length of the vocal responses between the first author and an undergraduate data analyst for 10% of the total spliced productions = 0.98. The statistical analysis was the same as in the pilot experiment but with bandpass noise added as a level in the noise frequency band factor. A Bonferroni correction of p < 0.008 was applied. As in the pilot, there were no significant effects of trial so this dependent variable was removed from the analysis.

RESULTS

Pilot experiment

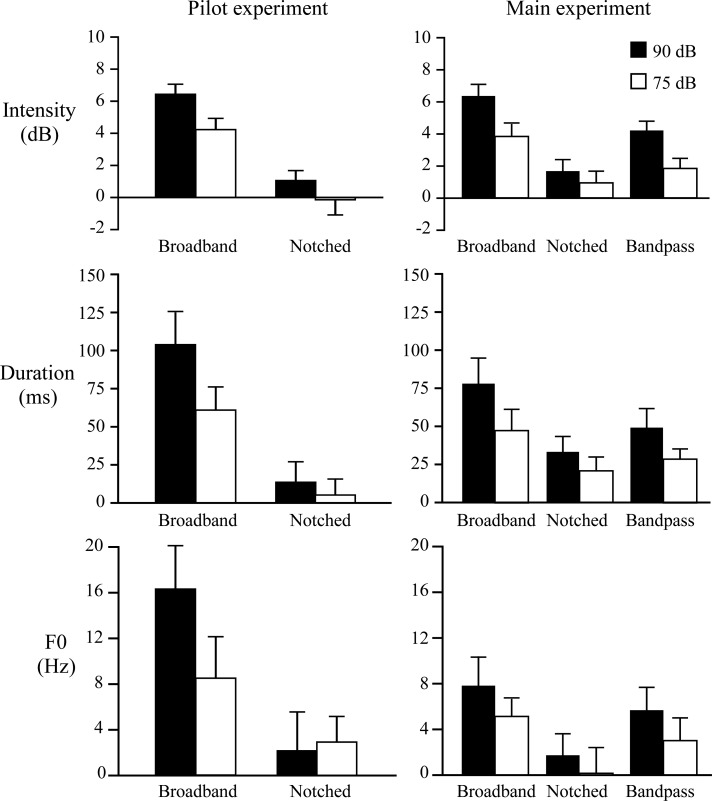
A summary of results from the initial pilot experiment is provided in the upper half of Table TABLE I.. The change in the suprasegmental speech parameters relative to the quiet condition were compared to zero using single sample t-tests to determine whether the Lombard effect was present (see Fig. 1). For broadband noise intensity was significantly greater than quiet at both 90 dB (t[15] = 6.71, p = 0.000) and 75 dB (t[15] = 7.34, p = 0.000). In contrast, intensity under notched noise did not significantly differ from quiet at either dB level. Similarly, duration was longer with broadband noise at 90 dB (t[15] = 5.19, p = 0.000) and 75 dB (t[15] = 4.21, p = 0.001) but did not significantly differ from quiet with notched noise at either dB level. F0 was greater with broadband noise at 90 dB (t[15] = 3.73, p = 0.002), but was not affected in the other three noise conditions.

TABLE I.

t-test and univariate results for conditions from the pilot and main experiments [independent variables are listed in the first row; results are listed under the dependent variables in the remaining columns (BB = broadband; N = notched; BP = bandpass; * = p < 0.05; ** = p < 0.01; *** = p <0.001; ns = not significant).

Pilot experiment:	Intensity	Duration	Frequency
BB 90 dB >Quiet	***	***	**
BB 75 dB > Quiet	***	**	ns
N 90 dB > Quiet	ns	ns	ns
N 75 dB > Quiet	ns	ns	ns
Intensity level effect: 90 > 75 dB	**	ns	ns
Noise frequency band effect: BB > N	***	***	***
Main experiment:	Intensity	Duration	Frequency
BB 90 dB > Quiet	***	***	**
BB 75 dB > Quiet	***	**	***
N 90 dB > Quiet	ns	ns	ns
N 75 dB > Quiet	ns	ns	ns
BP 90 dB > Quiet	***	**	ns
BP 75 dB > Quiet	**	**	ns
Intensity level effect: 90 > 75 dB	***	**	*
Noise frequency band effect:
(BB and BP) > N	***	**	*
BB > BP	**	*	ns

Figure 1.

Change from quiet in each suprasegmental speech parameter across noise conditions from the pilot and main experiments [dB change (top) = vocal intensity change; ms change (middle) = speaking duration change; Hz change (bottom) = fundamental frequency change].

The second analysis used a 2 (noise frequency band) × 2 (intensity level) MANOVA to compare the degree of change in intensity, duration, and F0 from quiet (see Fig. 1). There were significant main effects of noise frequency band (Wilk's Lambda = 0.155, F[3,13] = 23.65, p = 0.000) and intensity level (Wilk's Lambda = 0.485, F[3,13] = 4.60, p = 0.021) were present at the MANOVA level. Comparison of the noise conditions at the univariate level revealed a noise frequency band main effect on intensity change (F[1,15] = 68.72, p = 0.000), duration change (F[1,15] = 40.12, p = 0.000), and F0 change (F[1,15] = 30.80, p = 0.000). Each suprasegmental speech feature was significantly greater in broadband versus notched noise. The partial Eta squared effect sizes were 0.821 for intensity, 0.728 for duration and 0.672 for F0. Univariate comparisons also showed a main effect of intensity level on intensity change, with larger intensity increases in the 90 versus 75 dB condition (F[1,15] = 14.67, p = 0.002). The partial Eta squared effect size was 0.494. There were no changes between intensity levels in duration or F0.

The third analysis used Pearson correlations to describe the relationship of change among the suprasegmental speech features in broadband 90 dB noise. Results showed that intensity and duration change were strongly correlated (r[16] = 0.67, p = 0.004).

Main experiment

The pilot experiment showed that notched noise between 0.5 and 4 kHz does not elicit the Lombard effect. If speech-like frequencies between 0.5 and 4 kHz are crucial for self-monitoring then bandpass noise that includes only this frequency range should be sufficient to elicit a Lombard effect. The main experiment tested this prediction by adding another background noise condition (bandpass, 0.5–4.0 kHz) to those used in the pilot experiment.

A summary of results is provided in the lower half of Table TABLE I.. Analysis of intensity, duration, and F0 using single sample t-tests (p < 0.008) replicated the main results found in the pilot experiment for broadband and notched noise with one exception; F0 in this experiment was significantly higher in broadband 75 dB noise (t[15] = 5.22, p = 0.000). t-tests were conducted between the common measures of the pilot and main experiments. All were non-significant (p ≥ 0.10). This included direct comparison of F0 in broadband 75 dB noise, which was significantly higher in the main experiment but not the pilot. These results show reliability between the pilot and main experiment as the results were comparable. Turning to the new bandpass condition, intensity and duration were significantly longer at 90 dB (t[15] = 8.48, p = 0.000, t[15] = 3.93, p = 0.001, respectively) and 75 dB (t[15] = 3.34, p = 0.005, t[15] = 4.24, p = 0.001, respectively), while F0 did not at either intensity level (see Fig. 1).

MANOVA results from the pilot experiment that compared the effects of intensity level, and noise frequency band (including the new bandpass condition) were replicated (see Fig. 1).

There was a significant main effect of intensity level (Wilk's Lambda = 0.248 F[3,13] = 13.11, p = 0.000) and noise frequency band (Wilk's Lambda = 0.4219, F[6,10] = 5.93, p = 0.007). Comparison of the noise conditions at the univariate level replicated a noise frequency band main effect on intensity change (F[2,30] = 29.07, p = 0.000), duration change (F[2,30] = 6.94, p = 0.010), and F0 change (F[2,30] = 6.63, p = 0.004). Each suprasegmental speech parameter was significantly greater in broadband versus notched noise. The partial Eta squared effect sizes were 0.821 for intensity, 0.728 for duration and 0.672 for F0. Univariate comparisons also showed a replicated significant intensity level main effect on intensity change with larger intensity increases in the 90 versus 75 dB condition (F[1,15] = 37.06, p = 0.000). The partial Eta squared effect size was 0.494. There were two additional significant findings in this main experiment with regard to the intensity level main effect. Duration (F[1,15] = 9.65, p = 0.007) and F0 (F[1,15] = 7.36, p = 0.016) were also significantly greater in 90 versus 75 dB with partial Eta square effect sizes of 0.039 and 0.329, respectively. Helmert contrasts showed that intensity (F[1,15] = 38.68, p = 0.000), duration (F[1,15] = 7.55, p = 0.015), and F0 (F[1,15] = 9.52, p = 0.008) were significantly greater in broadband and bandpass noise collectively versus notched noise. Partial Eta square effect sizes were 0.721 for intensity, 0.335 for duration, and 0.388 for F0. Intensity (F[1,15] = 18.30, p = 0.001) and duration (F[1,15] = 6.26, p = 0.024) were significantly greater in broadband compared to bandpass noise with partial Eta square effect sizes of 0.557 and 0.295, respectively. F0 change in the noises was the same.

Pearson correlations comparing the relationships across suprasegmental speech measures in 90 dB broadband and bandpass noises showed that the only significant correlation was between intensity and F0 changes in bandpass noise (r[16] = 0.67, p = 0.005). The correlation between intensity and duration in the 90 dB broadband noise condition in the pilot experiment was not significant in the main experiment, however, the direction of the relationship was consistent and trended toward significance. When combining results from the broadband 90 dB noise condition in the pilot and main experiments, the relationship between intensity and duration was again strongly correlated (r[32] = 0.57, p = 0.001).

DISCUSSION

The primary objective of this study was to test the hypothesis that the Lombard effect is modulated by the frequency content of background noise. Suprasegmental speech parameter changes in intensity, duration, and F0 were measured in broadband, notched, and bandpass noise conditions. The bandpass and notched noise condition were mirror images of each other and contained mid-frequency bands with and without a major portion of speech-similar frequencies, respectively. Results showed that broadband noise significantly increased suprasegmental speech parameters, notched noise had no effect, and bandpass noise had decreased effects versus broadband on intensity and duration, and no effect on F0. This could be because some cues for intensity and duration are preserved outside the mid-frequency range of the bandpass noise, while information for F0 was adequate in this range. Taken together, these results support the idea that the Lombard effect is a selective response that depends on the spectral properties of ambient noise. This selectivity may be an indicator that in humans the Lombard effect is “tuned” to process speech-like sounds. The findings rule out the possibility that the Lombard effect is a nonspecific response to competing sounds in the environment during vocalization.

Loudness level contours demonstrate that humans do not perceive sound in a linear manner. That is, thresholds of frequencies in the speech range are lower than for frequencies outside the speech range. If auditory self-monitoring in humans has evolved to follow loudness level contours then noise containing speech frequencies would have greater effect on speech output than noise outside the speech spectrum. This view is supported by findings where the Lombard effect was largely absent with notched noise and present with bandpass filtered noise, when both are in the 0.5–4 kHz range. Thus, independent of loudness the frequencies having the greatest sensitivity in humans were also the most influential on changing vocal output when presented as a masker. Convergent evidence is provided by the animal literature which shows that it is necessary to include frequencies of a given species' vocal calls in the noise used to elicit the Lombard effect (Hage et al., 2006; Cynx et al., 1998; Nonaka et al., 1997; Lopez et al., 1988; Scheifele et al., 2005).

The suggestion that humans are selectively affected by speech-similar information in the environment consistent with the loudness level contours of the ear is not just another way of interpreting the Lombard effect. It is also an extension of how we understand the capabilities of our self-monitoring system at a basic level. Future research investigating this perspective could lead to a greater understanding of the capabilities of our self-monitoring system and perhaps new clinical and scientific use of the Lombard effect. For example, comparing the intelligibility scores between noise bands that contain speech-like frequencies versus notched noise bands with speech-like frequencies removed would further test the notion that humans selectively-adapt to speech-similar noise in the environment. Support would be garnered if intelligibility scores were significantly higher in the notched noise. In addition, the contribution by octave of noise frequencies in the speech range could be calculated to determine if the degree of speech output changes mirrors the form of loudness contour curves.

Previous work in monkeys found that mean firing rates of auditory cortical neurons are modulated during vocalizations (Eliades and Wang, 2003). Most neurons had reductions in mean firing rate during vocalization, but a subset of neurons showed reliable firing rate increases. When white noise masking was given the monkeys increased their vocal intensity, and vocal modulations of single-unit activity, both decreases and increases, were attenuated (Eliades and Wang, 2012). Although neural recording studies of the Lombard effect have not been done in humans, modulations of auditory cortical activity when speaking versus passive listening have been observed using intracranial field potentials (Greenlee et al., 2011), and EEG/MEG recordings (reviewed in Houde and Nagarajan, 2011). Taken together, the above findings suggest that auditory cortex activity is regulated during vocalization, potentially by feedforward information about vocal output provided by motor networks in the brain. The Lombard effect may be a way to reinstate the expected level of acoustic feedback when it is masked by noise that contains frequencies that overlap with vocal output.

The Lombard effect has been shown to vary by noise frequency band in at least two other studies. Egan (1972) found that mid band noise had the largest numerical increase, although statistical comparisons among specific noise bands were not performed. Lu and Cook (2009) found that high or low pass filtered noise with cutoffs of 1 or 2 kHz have effects on speech parameters that are comparable to broadband noise. The authors pointed out, some of the effects of low pass filtered noise may be due to the asymmetrical spread of masking into higher frequencies produced by the low-bandpass noise (Egan and Hake, 1950). Upward spread of masking may relate to why bandpass noise in the main experiment was nearly as effective as broadband noise at inducing the Lombard effect. However, upward spread of masking is inconsistent with the results in the pilot experiment that showed little to no Lombard effect when notched noise was used. If upward spread of masking was operative in the notched condition then spread from below the high pass cutoff of 0.05 kHz should have resulted in a measurable Lombard effect.

A secondary objective of this study was to compare the relationship of noise-induced changes among suprasegmental speech parameters. In the pilot experiment, vocal intensity and duration were strongly correlated in broadband noise, but neither was correlated with fundamental frequency. It is unclear why this pattern is seen among intensity, duration, and fundamental frequency. Previous findings show that vocal fundamental frequency is stable across the day (Nittrouer et al., 1990) and in noise (Vogel et al., 2011). We suspect that the smaller effects of noise on F0 could be due to it being a more stable acoustic parameter in general, while intensity and duration can be more dynamic. The tendency for F0 to rise with intensity level is a well-accepted phenomenon (Gramming et al., 1988). This coupling effect occurs because the increases in subglottic pressure that are necessary for increased intensity are accompanied by greater tension in the cricothyroid, and to a lesser degree suprahyoid, muscles, which also increases F0 (Bordon et al., 1994b). However, when background noise is present these measures are not strongly correlated, possibly due to a large degree of subject variability (Lindstrom et al., 2011). This may be due to the use of different techniques among speakers to increase these suprasegmental speech parameters. For example, a speaker can raise intensity but maintain F0 by relaxing either the cricothyroid or the thyroarytenoid muscle (Bordon et al., 1994b).

There are other possible reasons for the stronger association between intensity and duration. The pattern observed in this study may reflect the function of different neural pathways in our self-monitoring system for mediating F0 versus intensity and duration (Burnett et al., 1997). Another possibility is that the technique we used to measure change in F0 was not sensitive to the changes. F0 change here was measured as a linear change, not in terms of octave change or F0 range of the subject. As noted by one of the reviewers, the magnitude of F0 change may have been much greater if measured this way. We suspect that the association between intensity and duration is linked to the need for the speaker to understand their speech more clearly. The speaker may increase intensity and duration in the presence of the background noise in order to self-monitor his or her vocalizations better. The speaker avoids also increasing F0 to the same degree because there is no intelligibility payoff; one can be understood and understand oneself equally as well by speaking in a lower or a higher pitch. There are benefits to intelligibility if one's speech is louder and longer in duration. This notion is consistent with theories that the main benefit of the Lombard effect is intelligibility gains for the speaker and listeners (Garnier et al., 2010).

The relationship between intensity and duration trended towards significance in the main experiment. When data from both experiments were collapsed, the changes among intensity and duration were again significantly correlated. This suggests that the positively correlated relationship observed between intensity and duration is valid. For bandpass noise, only intensity and F0 change were correlated. We suspect that the variations are due to the typical tendency for intensity and F0 to rise in tandem. It is also possible that the relationship between the suprasegmental speech parameters differs by noise type. Further studies are warranted to determine the stability of the original pattern seen in broadband noise and the role of noise type on the pattern of change among the suprasegmental speech parameters.

This study also tested the stability of the Lombard effect over time. Although the effect occurs at noise onset and ceases when the noise stops (Lane and Tranel, 1971), this is the first study to our knowledge that measured the consistency of the effects during noise exposure. The current findings show that the degree of change in intensity, duration, and fundamental frequency to ambient noise was present at the beginning of each block and remained stable over the approximately three minute trials. Measures between separate trial blocks are known to be comparable (Egan, 1972). Therefore, the Lombard effect appears to be consistent across time and not subject to sensory adaptation. We note that sensory adaptation to pure tones is negatively associated with stimulus intensity, and shows little effect above approximately 40 dB SPL (Hellman et al., 1997). The intensity range where sensory adaptation diminishes is approximately the same intensity range where the Lombard effect first becomes evident (Egan, 1972). Future work would be needed to determine if there is a functional association with respect to the role of intensity in sensory adaptation and the Lombard effect.

CONCLUSION

The main result was that noise containing speech-similar frequencies elicited significant changes in several suprasegmental parameters of the speech output. We also observed that the Lombard effect was not present when noise within a large portion of speech-similar frequencies was removed. Thus, the Lombard effect is sensitive to the specific frequency content of competing noise, and is not a general response to ambient noise. Results also showed that vocal intensity and duration increases were strongly correlated, and that increases in all suprasegmental speech parameters measured were stable across different types of noise and over time. Findings bear on our understanding about the integration of the auditory and motor speech systems (Hickok, 2012), and suggest that monitoring of speech relative to competing environmental noises is selective for speech-similar frequencies.