Binaural detection with narrowband and wideband reproducible noise maskers. IV. Models using interaural time, level, and envelope differences

Abstract

The addition of out-of-phase tones to in-phase noises results in dynamic interaural level difference (ILD) and interaural time difference (ITD) cues for the dichotic tone-in-noise detection task. Several models have been used to predict listeners' detection performance based on ILD, ITD, or different combinations of the two cues. The models can be tested using detection performance from an ensemble of reproducible-noise maskers. Previous models cannot predict listeners' detection performance for reproducible-noise maskers without fitting the data. Here, two models were tested for narrowband and wideband reproducible-noise experiments. One model was a linear combination of ILD and ITD that included the generally ignored correlation between the two cues. The other model was based on a newly proposed cue, the slope of the interaural envelope difference (SIED). Predictions from both models explained a significant portion of listeners' performance for detection of a 500-Hz tone in wideband noise. Predictions based on the SIED approached the predictable variance in the wideband condition. The SIED represented a nonlinear combination of ILD and ITD, with the latter cue dominating. Listeners did not use a common strategy (cue) to detect tones in the narrowband condition and may use different single frequencies or different combinations of frequency channels.

INTRODUCTION

Tone-in-noise detection has been studied for decades; however, it is still not clear which cue or combination of cues can explain listeners' performance. Although model predictions based on a nonlinear combination of cues can explain a substantial amount of listeners' detection patterns in the diotic condition (Mao et al., 2013), no existing model can satisfactorily explain listeners' performance for the dichotic condition. In this study, two binaural models based on combinations of interaural level and time differences are proposed to predict listeners' dichotic performance. This work is part of an ongoing series of experimental and modeling studies of binaural detection (Evilsizer et al., 2002; Zheng et al., 2002; Davidson et al., 2006).

In early studies of binaural detection, random noise waveforms were generated in each trial for each listener (Blodgett et al., 1958; Blodgett et al., 1962; Dolan and Robinson, 1967), and detection performance was averaged across listeners and waveforms, described as “molar-level” performance by Green (1964). In order to test model predictions and compare the effectiveness of different cues, it is useful to consider detection performance on a waveform-by-waveform basis (molecular-level) for each listener (e.g., Schönfelder and Wichmann, 2013). Gilkey et al. (1985) and Gilkey and Robinson (1986) found that averaging detection performance across masker waveforms obscures the differences across individual waveforms and listeners, suggesting the utility of a more molecular-level approach. However, molecular-level predictions are difficult to obtain because of the unknown internal noise for each listener and the possible use of different cues by different listeners. The current study analyzed data from Evilsizer et al. (2002) and Isabelle (1995), plus three additional listeners tested with the same stimuli. In those studies, a “quasi-molecular” method was applied, in which the noise masker for each trial was randomly selected from a set of reproducible-noise waveforms. In the current study, model predictions were computed for the dichotic condition, in which identical noises are presented to the two ears with a target tone that is 180° out-of-phase to the two ears.

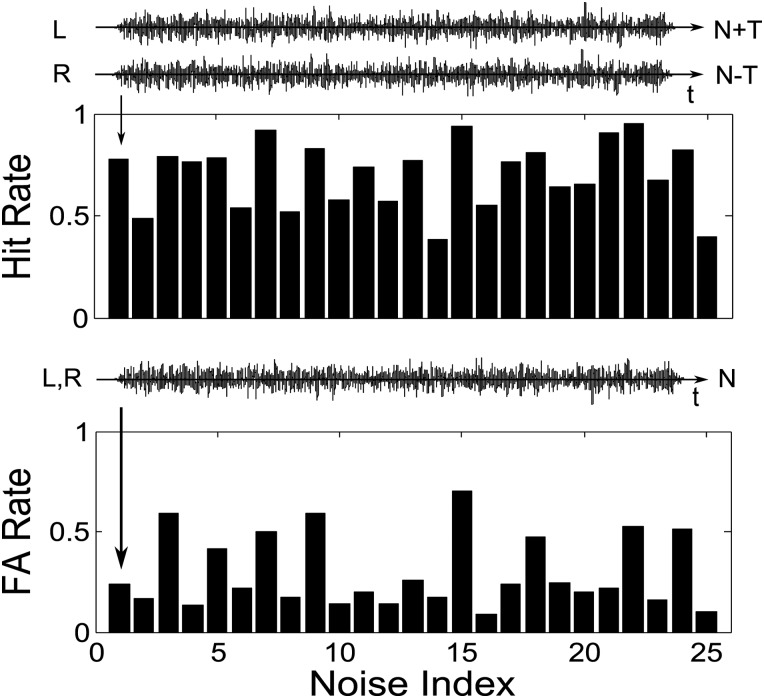
In each single-interval trial during the task, listeners responded “tone present” or “tone not present” for each binaural noise-alone or tone-plus-noise stimulus. Detection performance was described in terms of hit rates, the proportion of tone-plus-noise trials in which listeners correctly responded tone present, and false-alarm (FA) rates, the proportion of noise-alone trials in which listeners incorrectly responded tone present. The set of hit and FA rates for an ensemble of reproducible waveforms is referred to as the detection pattern (Fig. 1; Davidson et al., 2006).

In order to identify which cue or combination of cues listeners use in a dichotic tone-in-noise detection test, different models have been tested to predict detection patterns (Isabelle and Colburn, 1987; Isabelle, 1995; Goupell and Hartmann, 2007; Davidson et al., 2009a). For each model, a set of decision variables (DVs), each derived from a specific feature or combination of features of the waveforms, is compared with the detection patterns. Model predictions can be evaluated based on the amount of variance in the detection pattern that can be explained by calculating the squared correlation between DVs and detection patterns.

Several models based on binaural energy differences, interaural level difference (ILD), and interaural time difference (ITD) cues have been tested. Durlach (1963) proposed the equalization and cancellation model (EC), an energy-based model that subtracts the internal stimulus representation in one ear from that in the other ear after equalizing the masking waveforms in both ears. Isabelle (1995) tested the normalized interaural cross-correlation (NCC) model that computes the correlation of the waveforms at the two ears. The NCC model is related to the EC model because the DVs from both models are highly correlated to the energy of the noise-alone waveforms (Colburn et al., 1997). The NCC model is also related to ILD and ITD fluctuations (Bernstein et al., 1999). However, Isabelle (1995) showed that neither of these energy-related models could explain a significant amount of the variance in the dichotic detection patterns.

In addition to the energy-based cues, the combination of binaural out-of-phase tones with in-phase noises results in dynamic ILD and ITD cues. DVs computed from the sample standard deviation of the ILD (σ_ILD) and ITD (σ_ITD) have been used to predict detection patterns (Isabelle, 1995). Isabelle (1995) also calculated the peak deviation of ITD (M_β) by using the rare, large ITD magnitudes. The DV from the M_β model could be interpreted as the proportion of stimulus duration during which the instantaneous ITD magnitude exceeds a certain threshold β. Although some of these ILD- or ITD-based models could predict a significant amount of the variance in a few listeners' detection patterns, none of these models worked for all listeners (Isabelle, 1995; Davidson et al., 2009a).

Given that ILD and ITD represent different features of the waveform, it is reasonable to expect that the combination of these cues could capture more information about the waveform than either one alone. Isabelle and Colburn (1987) combined the two interaural difference cues by using a sum-of-squares model (SS). The DV was computed as a linear combination of the variance of ILDs and ITDs, and the weights were found by fitting the detection patterns (Isabelle and Colburn, 2004). Predictions from the SS model would be optimal if ILDs and ITDs were Gaussian-distributed and independent. However, it has been shown that the two cues are correlated (Zurek, 1991; Isabelle, 1995). Isabelle (1995) also combined ILD and ITD cues based on the deviation in lateral position (LP). The LP model was first used by Hafter (1971) to account for time-intensity trading in lateralization tests. The DV from the LP model was calculated as the mean magnitude of the lateralization position, in which ILDs and ITDs were combined through a trading ratio. The SS and LP models could not explain a significant proportion of variance of the listeners' detection patterns. More recently, Goupell and Hartmann (2007) proposed “independent-center” and “auditory-image” models that linearly combined ILDs and ITDs to predict listeners' performance for interaural correlation detection; the difference between these two models was the sequence of combining ILD and ITD information and integrating across time. Predictions from Goupell and Hartmann's models were significantly correlated with detection patterns for about half of the listeners (Davidson et al., 2009a). However, Davidson et al. (2009a) found by examining data from each listener that either ILDs or ITDs dominated in Goupell and Hartmann's linear combinations, suggesting that instead of combining ILDs and ITDs, in fact only the better of the two cues was used by the models.

The goal of the study presented here was to test the hypothesis that significantly better predictions of detection patterns could be obtained from models that combined ILD and ITD cues. Two models were tested for this hypothesis in the current study: A modified ILD-ITD combination model which takes into account the correlation between the two cues and a model based on the slope of the interaural envelope difference (SIED).

In the first model, a modified linear combination of ILD and ITD cues that weighted the two cues based on their covariance matrix (Oruç et al., 2003) was used to compute the DV. By computing weights from the covariance matrix of cue values, it is possible to avoid fitting the detection data as has been done in previous studies (Isabelle and Colburn, 1987; Goupell and Hartmann, 2007; Davidson et al., 2009b). In addition, waveforms were analyzed using multiple epochs, with each epoch weighted separately. Model predictions using this method of combining ILD and ITD cues were significantly better than previous dichotic model predictions.

In the second method, the interaural envelope difference was used to derive the DV. Predictions based on envelope cues from Richards (1992), Zhang (2004), Davidson et al. (2009a), and Mao et al. (2013) showed that the envelope-slope (ES) cue is robust and successful in predicting diotic detection patterns, which motivated the exploration of envelope cues in the dichotic condition. The ES cue focuses on changes in monaural envelope fluctuations, whereas binaural differences are key for dichotic detection. Thus modification of the diotic ES cue was required in order to consider the envelopes from both ears. A binaural envelope cue, the SIED, was proposed and tested in the second model of this study. Moreover, the SIED was shown to be related to both ILD and ITD information in a nonlinear manner. Predictions of the wideband detection patterns based on the SIED cue were significantly better than predictions using any single cue or any linear combination of ILD and ITD cues. In contrast, none of these cues provided significant predictions of the detection patterns for the narrowband condition, nor did the listeners employ a common strategy in that condition.

Given that there are no interaural differences in the noise-alone trials in a binaural-detection task, the prediction of FA rates in the dichotic condition is not possible with models based on interaural differences. Although internal noise is possibly an important factor to explain the FA rates, the statistical properties of internal noise are unknown. Furthermore, a simple additive noise would not explain the FA rates because such a noise would be averaged out in the “quasi-molecular” data sets analyzed here (because FA rates are computed by averaging multiple noise-alone trials), and a more complex noise model would thus be required. Model predictions for FA rates were not included in the current study.

DESCRIPTION OF DATA

The data analyzed in the current study were obtained from two previous experiments (Isabelle, 1995; Evilsizer et al., 2002). Three additional listeners were tested with the stimuli from Evilsizer et al. (2002), and one of them was also tested with the stimuli from Isabelle (1995). A total of six listeners were tested with wideband stimuli, and ten listeners were tested with narrowband stimuli.

In the Evilsizer et al. (2002) study, 4 listeners (S1–S4 in the current study) were tested with a set of 25 reproducible noise waveforms. Both narrowband (452–552 Hz) and wideband (100–3000 Hz) noise waveforms of 300-ms duration and a spectrum level of 40 dB sound pressure level (SPL) [e.g., approximately 75 dB SPL root-mean-square (rms) level for the wideband condition, and 60 dB SPL rms level for the narrowband condition] were tested. The spectral content of each narrowband waveform was matched to that of the corresponding frequency range of each wideband waveform. A 500-Hz sinusoidal target with 300-ms duration was used, and the tone level was set to equal the detection threshold of each listener. For the wideband condition, the tone level for the average listener was computed as the mean of the tone levels for all individual listeners. Three additional listeners (S5–S7) were tested with similar techniques, except that a two-down one-up tracking procedure (Levitt, 1971) replaced the fixed-level testing used by Evilsizer et al. (2002). Correct-answer feedback was provided after each trial. Listeners' detection thresholds were computed as the mean of the reversals (excluding the first six reversals) in all tracks. In each 100-trial track, trials within a 2-dB range of the detection threshold were used to create the detection patterns. Each listener's patterns were highly consistent over the course of the test.

In the experiment of Isabelle (1995), 3 listeners (S1–S3 in their study, referred to as S8–S10 in the current study) were tested with 10 narrowband (445–561 Hz) noises. The duration of the waveform was 300 ms, and the noise spectrum level was 54 dB SPL. A 500-Hz sinusoidal target with 300-ms duration was used, and the tone level was set to equal the detection threshold of each listener. One additional listener (S7) was tested with the same stimuli and similar techniques, except that a two-down one-up tracking procedure (Levitt, 1971) replaced the fixed-level testing used by Isabelle (1995). This listener's detection patterns were significantly consistent over the course of the test.

Listeners' detection patterns were described in terms of hit and FA rates, based on the probability that they responded tone present for each noise-alone or tone-plus-noise waveform (details of the experiments can be found in Evilsizer et al., 2002; Isabelle and Colburn, 1991; and Isabelle, 1995). Figure 1 shows the detection pattern of the average listener (i.e., the average detection pattern across six individual listeners who were tested using the Evilsizer et al. stimuli) for the wideband dichotic condition. The detection patterns were reliable, as each listener's detection pattern was highly consistent over the course of the experiment: The average Pearson product-moment correlation of seven listeners between the first-half and second-half of the trials was 0.70 for the Evilsizer et al. (2002) narrowband condition, and 0.81 for the six listeners tested with Evilsizer et al. (2002) wideband condition. The average Pearson product-moment correlation was not available for the Isabelle (1995) stimuli.

Figure 1.

A detection pattern for the average listener comprises hit and FA rates for each wideband (2900-Hz bandwidth) dichotic reproducible waveform averaged across six individual listeners. The x axis shows the index of the reproducible waveform. Insets show examples of the dichotic tone-plus-noise at left (N + T) and right (N − T) ears and the diotically presented noise-alone (N) waveforms for reproducible noise waveform number one (data from Evilsizer et al., 2002 and two listeners tested recently). The tone was added at the average threshold level of the six listeners, and the spectrum level of the noise was 40 dB SPL.

Table TABLE I. shows that the detection patterns were significantly correlated for all pairs of listeners for the wideband stimuli. Tables TABLE I. and TABLE I. show that detection patterns are significantly correlated for 6 out of 21 pairs of listeners for the narrowband stimuli from Evilsizer et al. (2002) (r = 0.40, p < 0.05 for the t-test), and for 1 out of 6 pairs of listeners for the stimuli from Isabelle (1995) (r = 0.63, p < 0.05 for the t-test). Note that the sign of the correlation varied across listeners for narrowband stimuli from both studies. Note also that the significance criterion differed for the Evilsizer et al. (2002) and Isabelle (1995) studies due to the different numbers of waveforms used in each study. Note that responses to only the first 10 reproducible waveforms in Isabelle's (1995, and Isabelle and Colburn, 1991) stimulus ensemble were analyzed here; these waveforms have similar statistics as those in the Evilsizer et al. (2002) study.

TABLE I.

Correlations between each pair of listeners in narrowband and wideband conditions (bold values indicate significant correlations).

(a) Pair-wise correlations of six listeners' hit rates for wideband stimuli from the Evilsizer et al. (2002) study.
	S2	S3	S4	S5	S6
S1	0.56	0.63	0.68	0.42	0.48
S2		0.62	0.51	0.58	0.64
S3			0.62	0.58	0.53
S4				0.71	0.69
S5					0.70

(b) Pair-wise correlations of seven listeners' hit rates for narrowband stimuli from the Evilsizer et al. (2002) study.
	S2	S3	S4	S5	S6	S7
S1	−0.59	0.50	−0.05	−0.40	−0.54	0.01
S2		−0.19	−0.32	0.20	0.34	0.16
S3			−0.18	−0.24	−0.49	0.08
S4				0.37	0.13	0.09
S5					0.70	0.19
S6						−0.04

(c) Pair-wise correlations of four listeners' hit rates for narrowband stimuli from the Isabelle (1995) study.
	S8	S9	S10
S7	−0.16	−0.22	0.07
S8		0.69	0.50
S9			0.54

There are a few differences between the two narrowband studies that are worth noting. The overall noise level was 15 dB higher for stimuli from Isabelle (1995) than for the narrowband stimuli from Evilsizer et al. (2002). In addition, for the narrowband waveforms, two out of seven listeners tested with the Evilsizer et al. (2002) stimuli had thresholds at a similar signal-to-noise ratio (SNR) as listeners from the study of Isabelle (1995), while the remaining listeners tested with the Evilsizer et al. (2002) stimuli had higher SNRs. In general, threshold SNRs were more variable across listeners in the narrowband condition, as compared to the wideband condition (Table TABLE II.).

TABLE II.

Listeners' threshold tone-levels (top, dB SPL) and SNRs1 (bottom italic, dB) for wideband and narrowband conditions. Noise spectrum level in Evilsizer et al. (2002) was 40 dB SPL (overall noise level was approximately 75 dB SPL for the wideband condition, and 60 dB SPL for the narrowband condition), and 54 dB SPL (overall noise level was 75 dB SPL) in Isabelle (1995).

	S1	S2	S3	S4	S5	S6	S7	S8	S9	S10
Evilsizer et al. (2002) wideband	45.0−30	43.0−32	50.0−25	46.0−29	47.5−27.5	44.7−30.0
Evilsizer et al. (2002) narrowband	39.0−21	49.0−11	47.0−13	39.0−21	53.6−6.4	49.8−10.2	44.4−15.6
Isabelle (1995) narrowband							57.8−17.2	55.0−20	55.0−20	55.0−20

For the wideband condition, detection patterns for an “average listener” were computed from the averaged patterns of the six individual listeners, all of whose patterns were significantly correlated [Table TABLE I.]. For the narrowband stimuli, an average listener was not used because listeners' detections patterns were not significantly correlated, in general, suggesting that they used different strategies in the detection test. Instead, only analyses of individual listeners are presented below for the narrowband condition.

METHODS

In this study, it was hypothesized that significantly better predictions of the dichotic detection patterns could be achieved using DVs that combined ILD and ITD cues. First, single-cue (ILD or ITD) DVs that combined information across time epochs are described. Next, DVs combining ILDs and ITDs across time epochs are presented. Finally, results for the envelope-related SIED model that includes a nonlinear combination of ILD and ITD information are described.

DVs that combine single-cue information across multiple time epochs

For both ILD- and ITD-based and SIED DVs, the 300-ms duration waveform was separated into several equal-duration time epochs, and local cue information was obtained from each time epoch. For the wideband condition, listeners were likely to use similar cues or combinations of cues for the detection test given that their detection patterns were significantly correlated. Thus, in order to select the duration of epochs for each cue, DVs for the average listener were computed for different durations of epochs that were divisors of 300 ms (e.g., 300, 150, and 100 ms, etc.). The Pearson product-moment correlation was calculated to quantitatively compare DVs from different durations of epochs to the detection pattern (hit rates, or percentage of correct identification of tone presence) of the average listener. For each cue, the number of epochs that yielded the highest correlation for the average listener was chosen and used for all listeners. For the narrowband condition, the same multiple-epoch scheme was tested for each individual listener since no average listener was used in this condition.

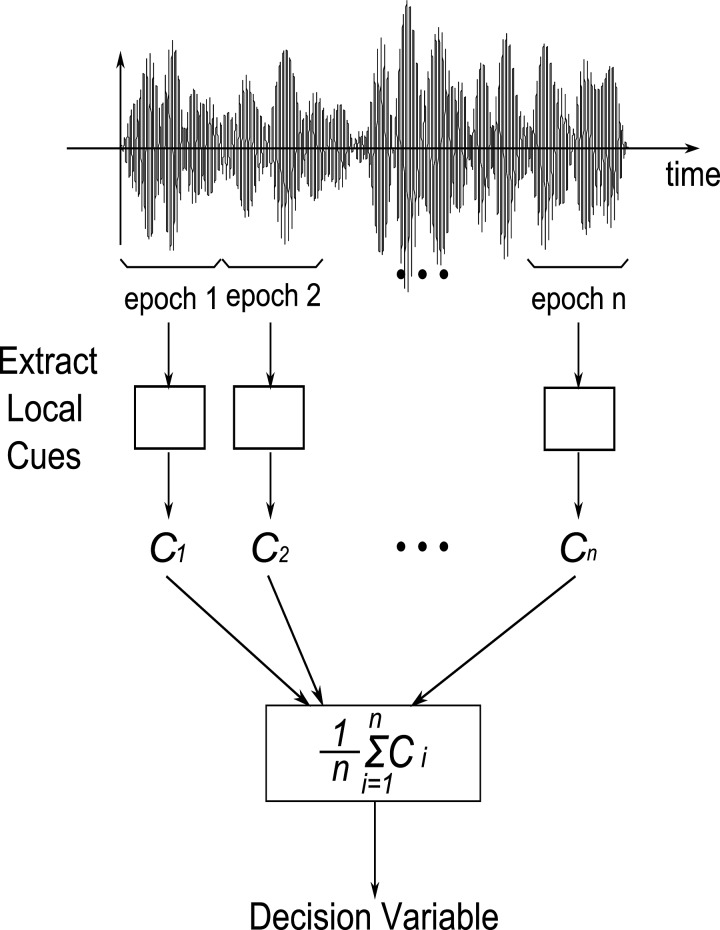
DVs were computed as the mean of local single-cue information across epochs. Figure 2 shows a schematic diagram of the single-cue multiple-epoch model, in which C_i represents the local cue value in the ith epoch and n is the number of epochs. For the ILD or ITD cue, the local cue is the sample standard deviation of ILD or ITD; for the SIED cue, the local cue is the DV from the SIED model. The analytical signal was used to obtain the ILD, ITD, and SIED cues. Both non-overlapping and half-overlapping windows were tested for the multiple-epoch scheme to investigate whether such details in computing local cues would affect model predictions. No difference in the results was observed between different overlap-window methods. The advantage of applying the multiple-epoch scheme is that a substantial value of the DV could be obtained when there were large variations of local cues only in certain epochs. However, in the single-epoch scheme, these large variations could be lost if the variation of the cue across the entire waveform were small.

Figure 2.

A schematic diagram illustrates a DV that was computed by combining local cue information across epochs for a single cue (ILD, ITD, or SIED). The waveform was separated into several equal-duration epochs along the time axis, and the local cues (C_i) were obtained. The DV was the mean value of the cue across epochs.

Note that DVs for the ILD, ITD, and SIED cues for the wideband condition were computed after applying a gammatone filter with center frequency at 500 Hz. For the narrowband condition, the gammatone filter was also used for the SIED cue, which allowed examination of different frequency channels (see below). In the narrowband condition, there were no significant differences between model predictions based on ILD or ITD cues with or without the gammatone filter. In order to match the narrowband ILD and ITD results in Davidson et al. (2006) and Isabelle (1995), in which no gammatone filter was used, results shown below for the narrowband ILD and ITD cues were computed without the gammatone filter.

DVs that combine ILD and ITD cues

As Isabelle and Colburn (1987) pointed out in their SS model, an optimal linear combination of the ILD and ITD cues could be achieved if these two cues were Gaussian-distributed and independent. In that ideal case, the optimal combination would yield the minimum variance of the combined cues by weighting each cue proportional to the inverse of its variance. Given that a cue with a smaller variance indicates a higher reliability, the optimal cue combination yielded the maximum reliability. However, ILD and ITD cues are correlated (Zurek, 1991; Isabelle 1995). Thus, consideration of the relationship between these two cues is necessary to obtain the optimal cue combination. By assigning weights w_i^ILD and w_i^ITD to the components in the $\overrightarrow{w}$ weight matrix, based on the product of the inverse of the covariance matrix Σ_ILD,ITD and a column vector e of all ones [Eq. 1], a modified linear cue combination was used that was optimal for correlated cues (Oruç et al., 2003). This combination yields a decision variable, D, with the minimum variance of the combined cue, and in turn, the maximum reliability:

$$D={\displaystyle \sum _i\left(w_i^{\text{ILD}}{S}_{\text{ILD}}\left(i\right)+w_i^{\text{ITD}}{S}_{\text{ITD}}\left(i\right)\right)},$$ (1)

where $\overrightarrow{w}=[w_i^{\text{ILD}},w_i^{\text{ITD}}]\hspace{0.17em}\mathrm{\mu }{\sum }_{\text{ILD},\text{ITD}}^{-1}e,e={[1,1,\mathrm{...},1]}^T$. $S_{\text{ILD}}$ and $S_{\text{ITD}}$ indicate the standard deviations of ILD and ITD cues in each time epoch.

DVs based on the SIED cue

In addition to the ILD and ITD cues, an envelope-related cue, the SIED, was tested for its ability to predict listeners' tone-in-noise detection patterns. A binaural envelope cue was investigated in this study because of the success and robustness of a monaural ES cue in predicting diotic detection patterns (Richards, 1992; Zhang, 2004; Davidson et al., 2009a; Mao et al., 2013). DVs for the diotic ES model were computed as the integral of the absolute value of the monaural envelope fluctuations across time. When a tone is added to narrowband noise, the envelope flattens and the ES DV decreases (Richards, 1992). An informal pilot study showed that this monaural ES cue predicted a significant amount of listeners' dichotic performance. In addition, the monaural ES model predictions of dichotic performance can be better than predictions based on ILD or ITD cues for most listeners in the narrowband and wideband conditions. Because the envelopes at the two ears are different for the dichotic condition, and the monaural ES cue can only reflect envelope fluctuations at one ear, the SIED model was developed to quantify the fluctuations of the interaural envelope difference.

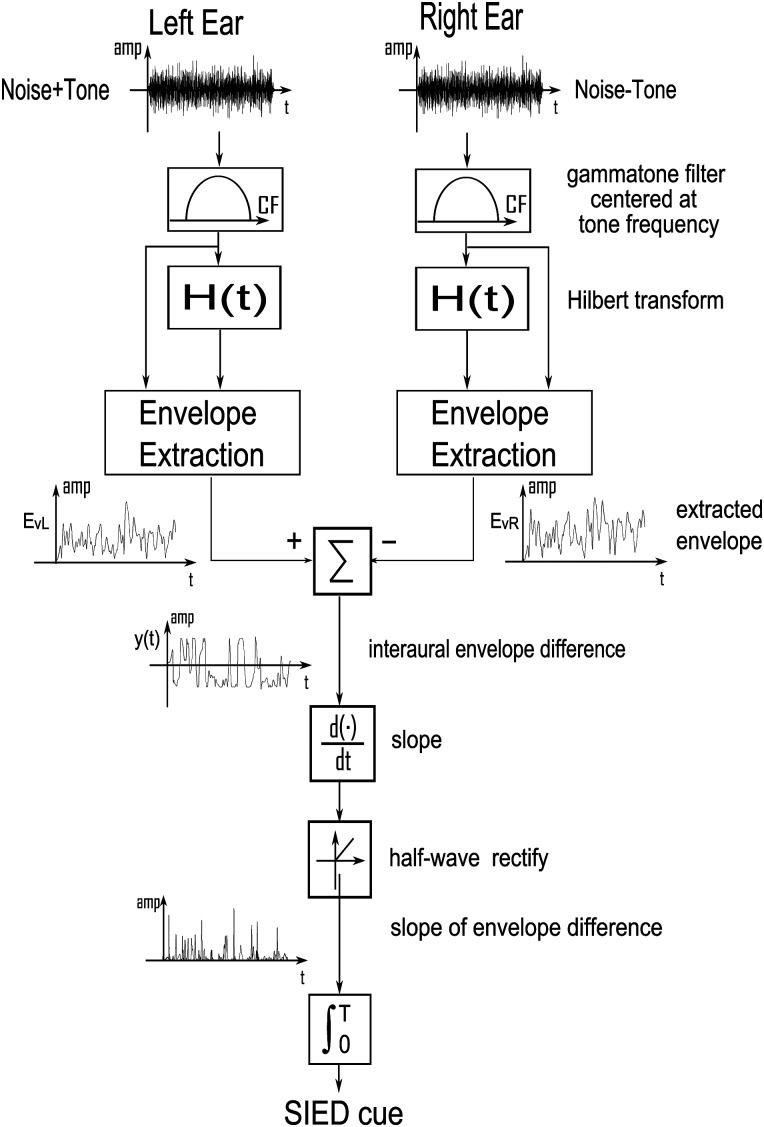
Figure 3 illustrates the SIED cue; the inset figures show the waveforms, monaural envelopes, and the interaural envelope difference. A fourth-order gammatone filter was used here; Johannesma et al. (1971), de Boer and de Jongh (1978), and Carney and Yin (1988) showed that the gammatone filter provides an excellent fit to both amplitude and phase properties of auditory-nerve responses. The SIED model was not intended to fully capture the auditory processing after basilar membrane filtering; rather, it was designed to be a mathematical (signal-processing type) model to test possible cues that listeners use for detection of tones in noise. The interaural envelope difference was calculated by taking the instantaneous difference between the monaural envelopes at the two ears. The instantaneous slope of the time-varying interaural envelope difference was then computed [Eq. 2],

$$y(t)=\frac{d}{\mathit{d}\mathit{t}}\left(E_{\mathit{v}\mathit{L}}(t)-E_{\mathit{v}\mathit{R}}(t)\right),$$ (2)

where E_vL and E_vR were the envelopes at the left and right ear, respectively. Finally, the half-wave rectified slope information was integrated over time to yield the DV for the SIED cue. The half-wave rectification was applied in order to better match the SIED model to physiological models; similar model performance was obtained with full-wave rectification (considering both positive and negative slopes) or using negative slopes only. Similar to the ILD and ITD cues, the SIED cue was based on the interaural differences resulting from the binaurally out-of-phase tones. The relationship between the SIED cue and ILD and ITD cues is analyzed in Sec. 4.

Figure 3.

A schematic illustration of the calculation of the SIED cue. Envelopes were extracted from the analytic signals, which were obtained using the Hilbert transform of the fourth-order gammatone filtered waveforms. The center frequency of the gammatone filter was set to the tone frequency of 500 Hz. The SIED was half-wave rectified and integrated over time to obtain the SIED DV.

Model predictions could be interpreted as the explainable proportion of variance in the listeners' performance across waveforms. In order to evaluate model predictions of listeners' detection patterns, a squared Pearson product-moment correlation (r²) was calculated between the DVs and the z-score of the detection patterns (Davidson et al., 2009a). The Pearson product-moment correlation (r) was compared to the significance level (p < 0.05 t-test), to test whether it was different from zero. The r² was also compared to the predictable variance to check the effectiveness of model predictions. For the wideband condition, the predictable variance was computed as the squared mean of the correlations between detection patterns of individuals and that of the average listener. Predictions based on the methods described above cannot explain the individual differences among listeners' detection patterns. In other words, a correlation value of one between model DVs and detection patterns for each individual cannot be achieved using a single model unless the listeners have identical detection patterns. However, when listeners' detection patterns are significantly correlated to each other, as in the wideband condition, the predictable variance is high and model predictions could potentially explain a large amount of the variance. Thus, for the wideband condition, the predictable variance was used as a benchmark to evaluate the overall quality of the model predictions. For the narrowband condition, detection patterns were not generally correlated across listeners, and thus neither an average listener nor the predictable variance was useful.

RESULTS

Model predictions based on the ILD, ITD, and SIED cues are shown in this section. Because dichotic cues rely on interaural differences, which are only available for the tone-plus-noise waveforms, predictions are only shown for hit rates. Model predictions were computed for each stimulus set for individual listeners for wideband and narrowband conditions and the average listener for the wideband condition.

Epoch duration for each cue

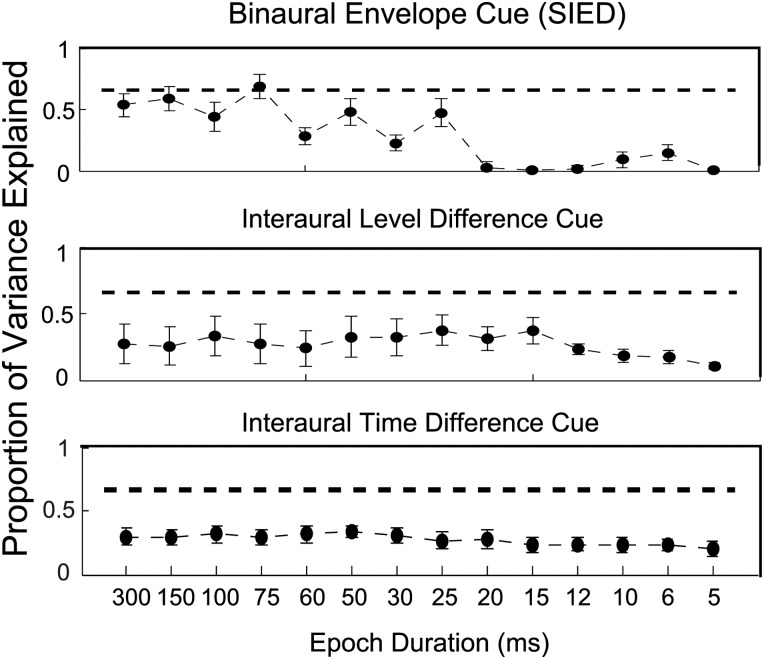
The epoch duration used for model predictions was chosen based on the average listener for the wideband condition and the individual listeners for the narrowband condition as described in Sec. 3. Model predictions of the average listener's hit rates in response to wideband stimuli from the Evilsizer et al. (2002) study using different epoch durations for each cue are shown in Fig. 4. The x axis shows different epoch durations, and the y axis shows the proportion of variance in the detection patterns that was explained by the model. The lengths of error bars indicate the standard deviation across the individual listeners. The circles indicate predictions for the wideband conditions; the dotted lines show the predictable variance for the wideband conditions. For all the cues, no significant differences in model predictions were observed using half-overlapping or non-overlapping windows; only the results from the non-overlapping windows are shown. For ILD and ITD cues, no significant differences (t-test, p < 0.05) in model predictions across epoch duration were observed. For the SIED cue, predictions using large epoch durations were significantly more correlated to listeners' detection patterns compared with predictions from small epoch durations ( < 75 ms), as expected due to the relatively long time course of envelope cues. In addition, model predictions based on the 75-ms epoch duration approached the predictable variance (squared mean of the correlations between detection patterns of individuals and that of the average listener, see below). Interestingly, the epoch length of 75 ms falls into the range of binaural integration windows (e.g., 50 to 200 ms) described by several studies of “binaural sluggishness” (Grantham and Wightman, 1979; Kollmeier and Gilkey, 1990; Culling and Colburn, 2000; Kolarik and Culling, 2009).

Figure 4.

Proportion of variance explained by the SIED (upper panel), ILD (middle panel), and ITD (bottom panel) cues for the average listener, based on all responses to the Evilsizer et al. (2002) stimuli, for wideband waveforms using different epoch durations. The dotted line shows the predictable variance for the wideband conditions. The x axis shows the epoch durations, and different filled circles represent predictions for wideband waveforms. The average listener was computed across six listeners for the wideband condition.

Model predictions of hit rates from the narrowband stimuli in the Evilsizer et al. (2002) and Isabelle (1995) studies with different epoch durations for the SIED, ILD, and ITD cues were also tested (results not shown). No significant differences of model predictions among different epoch durations were observed. For consistency, the epoch duration was fixed at 75 ms for ILD, ITD, and SIED cues for all datasets. For models that combined ILD and ITD cues, the epoch duration was also fixed at 75 ms for stimuli from both the Evilsizer et al. (2002) and Isabelle (1995) studies.

Model predictions for single- and multiple-epoch schemes

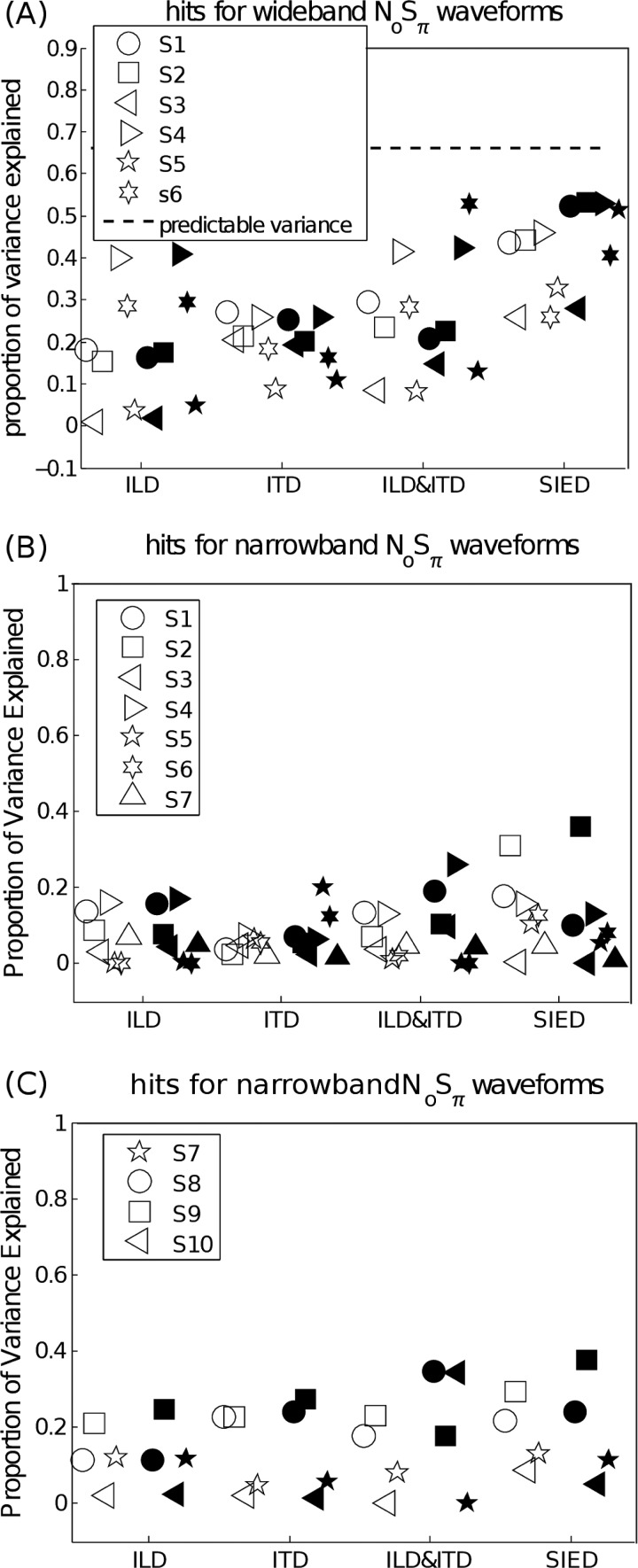
Model predictions of hit rates for individual listeners in response to the Evilsizer et al. stimuli [Figs. 5A, 5B] and individual listeners in response to Isabelle's stimuli [Fig. 5C] are shown. Predictions based on ILD, ITD, the combination of ILD and ITD, and SIED cues are shown in the four groups of symbols in each panel. For each group of symbols, the open symbols indicate the results of the single-epoch model, and the filled symbols show the results of the multiple-epoch model. The dotted line indicates the predictable variance for the wideband condition.

Figure 5.

The proportion of variance explained by several interaural difference cues (ILD, ITD, a combination of ILD and ITD, and SIED) predictions of hit rates for the individual listeners for waveforms of Evilsizer et al. (2002) study [(A) and (B)] and waveforms of Isabelle (1995) study [(C)]. The epoch duration was 75 ms for the multiple-epoch models (filled symbols). Different listeners were represented by different symbols.

As shown in each panel, model predictions based on the single-and multiple-epoch methods do not differ significantly for the ILD and ITD cues in any condition. For the combination of ILD and ITD cues based on the covariance matrix, multiple-epoch predictions were slightly, though not significantly, better than single-epoch predictions for some listeners. In addition, predictions based on the combination of ILD and ITD cues were also slightly better than predictions based on single ILD and ITD cues for some listeners in response to the Evilsizer et al. stimuli, but not for listeners in Isabelle's study. For the SIED cue, single- and multiple-epoch model predictions were not significantly different for most listeners, though predictions using the multiple-epoch model were slightly better than predictions using the single-epoch model for most listeners.

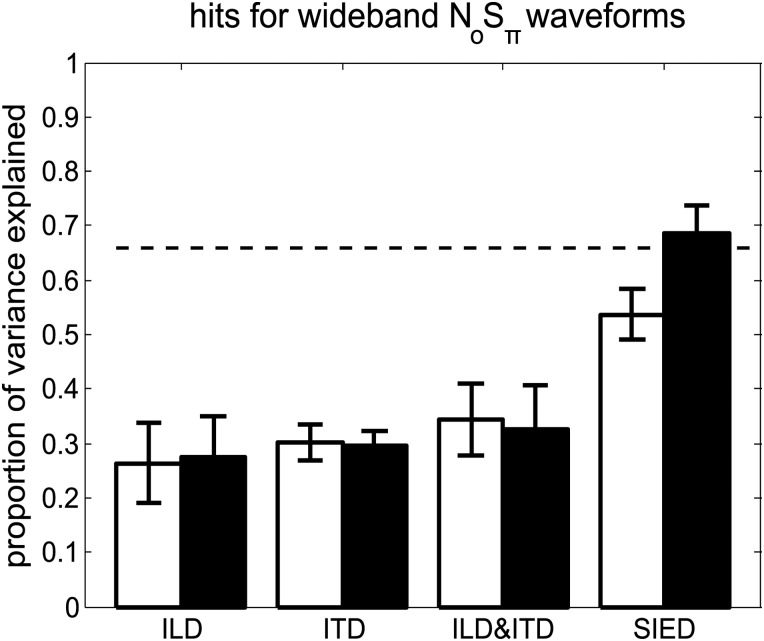
Model predictions of the ILD, ITD, a combination of ILD and ITD, and SIED cues for the average listener in the wideband condition are shown in Fig. 6. Model predictions using the ILD, ITD, and a combination of ILD and ITD cues were similar. The prediction based on the SIED cue was significantly better than the prediction using the other three cues and approached the predictable variance. Note that no average listener was used in the narrowband condition, because listeners' detection patterns were not significantly correlated in general.

Figure 6.

The proportion of variance explained by several interaural difference cues (ILD, ITD, a combination of ILD and ITD, and SIED) predictions of hit rates for the average listeners for the waveforms of the Evilsizer et al. study.

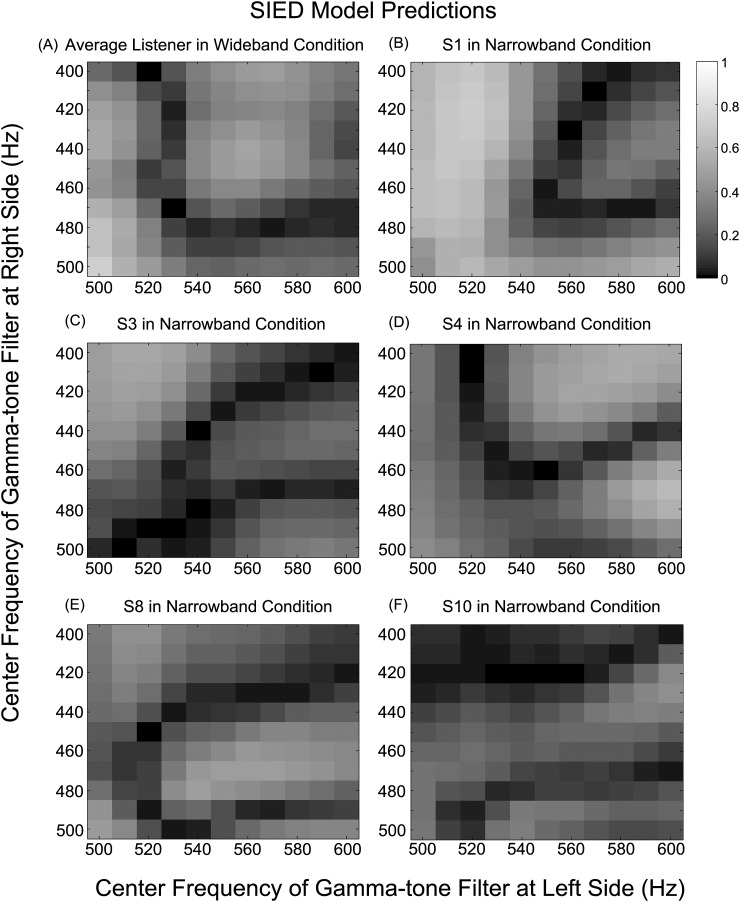
Joris et al. (2006) suggested that cochlear disparity is potentially important in determining the best delays observed in binaural ITD-sensitive neurons. Additional tests with the SIED cue were carried out using gammatone filters with mismatched center frequencies at the two ears. Predictions of listeners' detection patterns with pairs of filters having different center-frequencies for the two ears (x axis: Left ear, y axis: Right ear) are shown in Fig. 7. The gray scale values indicate the predicted variance in the listener's detection patterns.

Figure 7.

Predictions of listeners' detection patterns using mismatched center-frequency at two ears (x axis: Left ear, y axis: Right ear) for (A) average listener in wideband condition, (B)–(D) several individual listeners (S1, S3, and S4) in the narrowband condition from Evilsizer et al. (2002) and (E) and (F) several individual listeners (S8 and S10) from Isabelle (1995) studies.

For the wideband stimuli [Fig. 7A], only predictions from the average listener are shown. Trends in the predictions across different frequency channel combinations were similar across individual listeners in the wideband condition. The highest correlation was obtained from models with matched center frequencies at 500 Hz (bottom left corner). Listeners might also use the SIED from frequency channels away from the tone frequency, for example the region of frequency combinations centered on 440 and 550 Hz provides predictions that were significantly correlated to the average listener's detection pattern.

In contrast to the wideband case, for the narrowband stimuli [Figs. 7B, 7C, 7D, 7E, 7F], the center-frequency combinations that provided the best predictions of detection patterns differed qualitatively across listeners. Results from five individual listeners are shown, three from the Evilsizer et al. (2002) study and two from the Isabelle (1995) study. The across-subject differences in Figs. 7B, 7C, 7D, 7E, 7F may explain the low correlations of detection patterns between pairs of listeners. These results suggest that listeners might use different strategies, including different frequency channels or different combinations of frequency channels, for detecting tones in narrowband noise. Note that SIED results plotted in Fig. 5 were computed from the matched center frequencies at 500 Hz for narrowband and wideband conditions, though better predictions were observed for mismatched center frequencies for narrowband conditions [Figs. 7B, 7C, 7D, 7E, 7F].

Investigation of the SIED cue using binaurally modulated reproducible noises

Given the success of the SIED cue in predicting listeners' detection patterns, especially in the wideband condition, it is interesting to investigate how the SIED cue is related to the two classic dichotic cues: ILD and ITD. An initial inspection showed that SIED is not significantly correlated to ILD or ITD cues, though ILD and ITD cues were significantly correlated. van der Heijden and Joris (2010) proposed a method that used binaurally modulated stimuli to degrade ILD, ITD, or both, in order to determine the relative contributions of ILD and ITD cues in a binaural detection test. In the current study, binaural modulation was applied to the reproducible noise stimuli from both the Evilsizer et al. (2002) and Isabelle (1995) studies to test whether ILD, ITD, or both were related to the SIED cue. Different combinations of amplitude modulation (AM) and quasi-frequency modulation (QFM) were applied to the reproducible noises to introduce new ILDs, ITDs, or both. Then the effects of these manipulations on the SIED DV were examined to determine the contributions of each cue to the SIED.

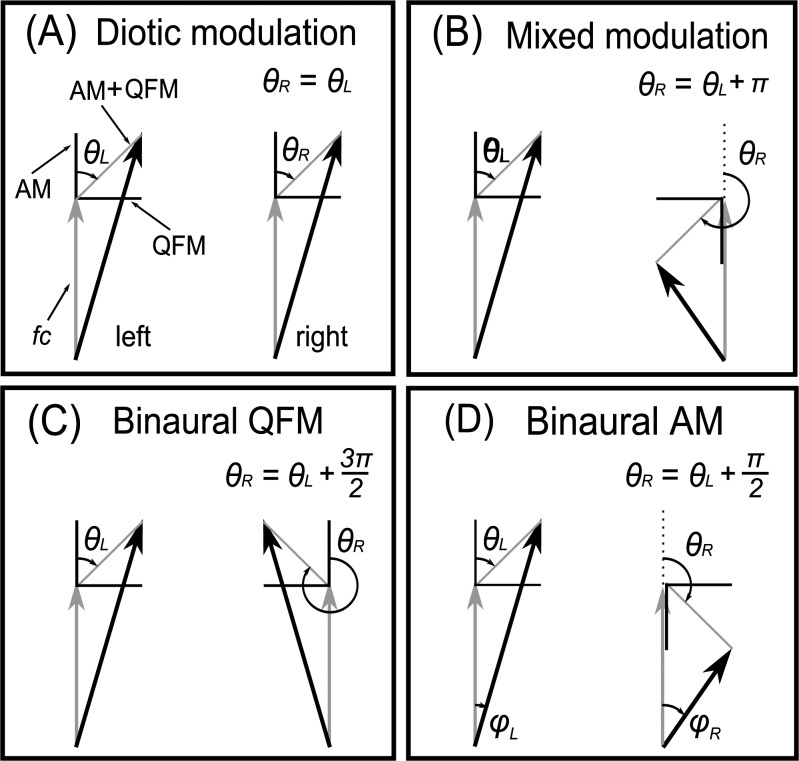
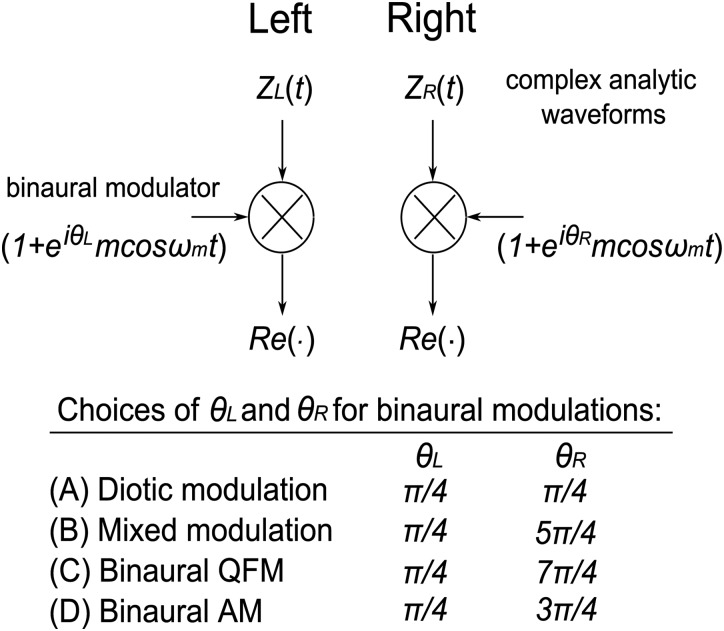
Figure 8 illustrates four different types of binaural modulations, showing the case of modulating a single tone, for simplicity. In each panel, a vector diagram represents the binaural modulations applied to the stimuli at the left and right ear: The solid gray vertical arrows show the carrier (fc); the solid black vertical lines indicate the AM component, which is parallel to the carrier; the solid black horizontal lines indicate the QFM component, which is perpendicular to the carrier; and the solid black arrows show the resulting modulated signal. The modulation depth (m) is represented by the length of the AM and QFM components. Because the modulation depths of the AM and QFM are equal, the two components have the same length, thus the sum of the two components (solid gray line) always forms an angle of π/4 radians with respect to the carrier.

Figure 8.

Four different binaural modulations used to separate ILD and ITD information: (A) Diotic modulation; (B) mixed modulation; (C) binaural QFM; (D) binaural AM (after van der Heijden and Joris, 2010).

For diotic modulation [Fig. 8A], identical modulations are applied to the left and right stimuli and no magnitude or phase differences between θ_L and θ_R exist, thus no new ILD or ITD cues are introduced. For mixed modulation [Fig. 8B], there is a phase difference of π radians between θ_L and θ_R; both magnitude and phase differences are observed between the solid black arrows for the two ears, thus new ILD and ITD cues are introduced by mixed modulation. For binaural QFM [Fig. 8C], there is a phase difference of 3π/2 radians between θ_L and θ_R; only phase differs between the solid black arrows for the two ears, thus a new ITD cue is introduced. For binaural AM [Fig. 8D], there is a phase difference of π/2 radians between θ_L and θ_R; the solid black arrows for the two ears differ primarily in terms of magnitude, with a small difference in phase between φ_L and φ_R, thus a new ILD cue with a small ITD cue is introduced.

In order to apply binaural modulation to reproducible noises, the carrier was the dichotic reproducible waveform [both narrowband and wideband waveforms from the Evilsizer et al. (2002) study and narrowband waveforms from the Isabelle (1995) study]. The modulation frequency, f_m, was 20 Hz (as in van der Heijden and Joris, 2010). Different binaural modulations were applied by varying the phase difference of the combination of AM and QFM at the two ears (θ_L, θ_R), as shown in Fig. 8. Given that the AM and QFM components differed by π/2 radians, the complex analytic waveform Z_L(t) or Z_R(t) obtained from the dichotic waveform was used to illustrate the mathematical implementation of binaural modulation (Fig. 9). After multiplying Z_L(t) or Z_R(t) with modulators for the two ears, the modulated waveforms were recovered by taking the real part of the complex signal. The effects on the SIED, ILD, and ITD cues after applying the binaural modulation to the reproducible noises are shown for a range of modulation depths, m (see Figs. 1011). The SIED DV was computed as shown in Fig. 3, using the binaurally modulated waveforms as inputs.

Figure 9.

The mathematical implementation of the binaural modulation of the dichotic waveforms for the left and right ears, where Z_L(t) or Z_R(t) represents the analytic waveform of noise-alone or tone-plus-noise stimuli and Re(·) indicates taking the real part of the complex signal.

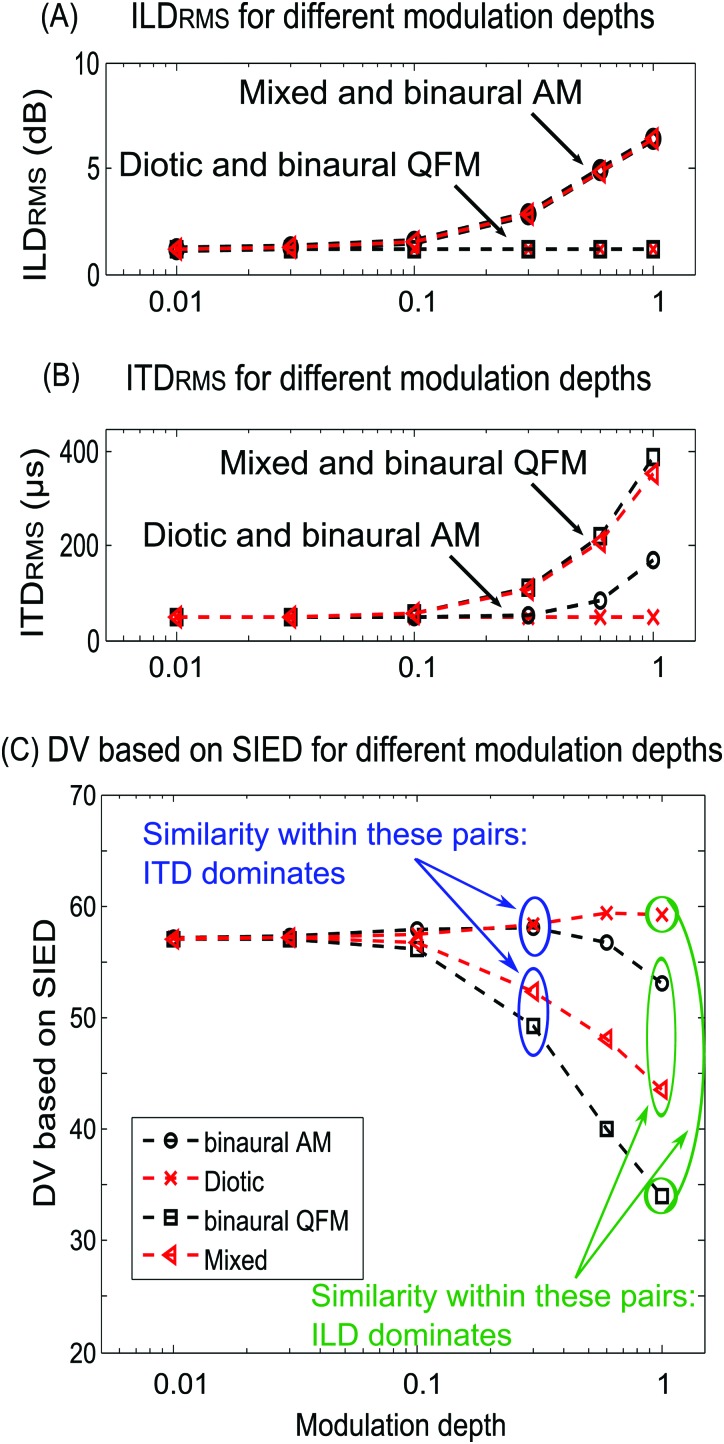
Figure 10.

ILD_rms, ITD_rms, and DV based on the SIED for binaurally modulated wideband and narrowband stimuli from Evilsizer et al. (2002). The x axis shows the modulation depth of the binaural modulator. Four different symbols are used to represent the four kinds of modulations: Black circles for binaural AM, red crosses for diotic, black squares for binaural QFM, and red triangles for mixed modulation. Relations between SIED and ILD, ITD cues are illustrated: If ITD dominates the SIED cue, then the pairs of symbols connected or circled by blue lines should overlap; if ILD dominates the SIED cue, then the pairs of symbols connected or circled by the green lines should overlap.

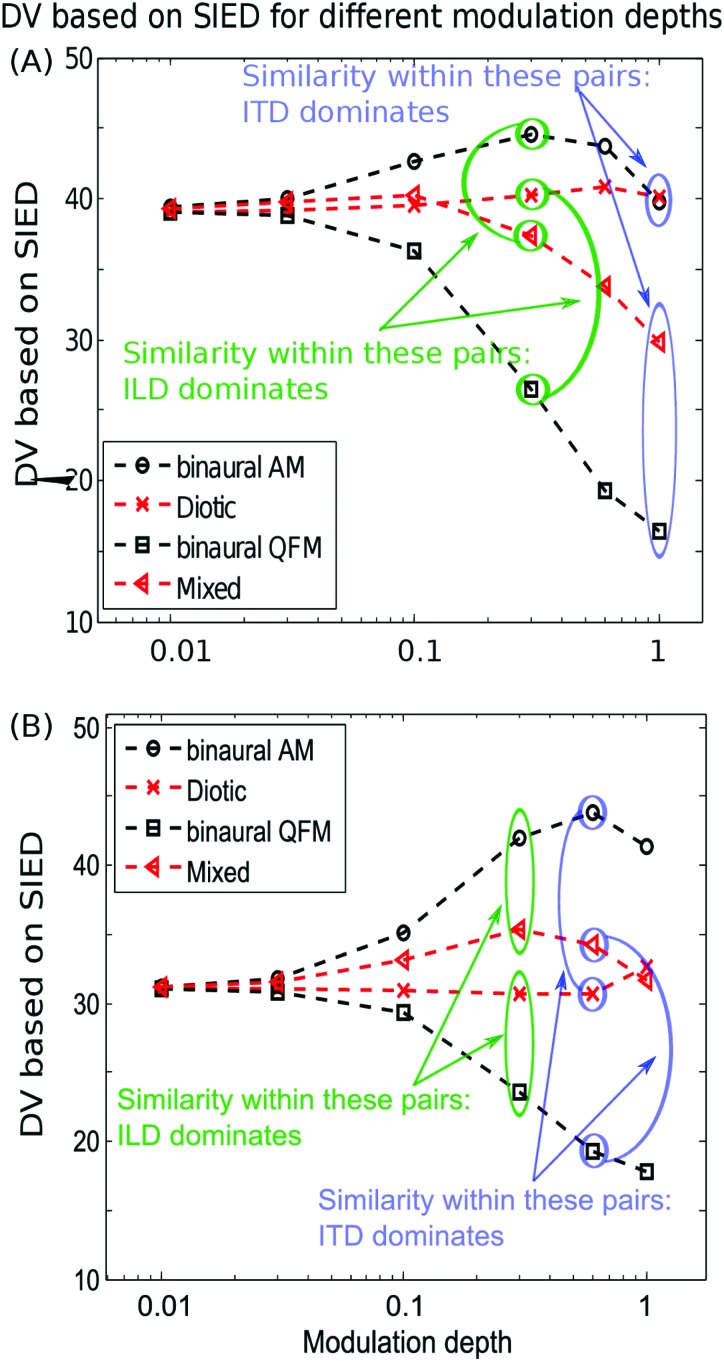
Figure 11.

The SIED DVs for binaurally modulated (A) narrowband stimuli from Evilsizer et al. (2002) and (B) narrowband stimuli from Isabelle (1995). The axes and symbols are the same as in Fig. 10C.

In order to verify that the newly introduced ILD and ITD information were separated by the binaural modulation, the rms values of ILD and ITD cues were computed from the four binaurally modulated dichotic reproducible noise waveforms. In Fig. 10A, there is no difference in ILD_rms for the diotic (crosses) and binaural QFM stimuli (squares), or for the mixed (triangles) and binaural AM (circles) stimuli at all modulation depths. In Fig. 10B, at small modulation depths (m≤ 0.3), no difference in ITD_rms was observed for the diotic (crosses) and binaural AM (circles) stimuli, or for the mixed (red triangles) and binaural QFM (squares) stimuli. However, when modulation depth increased, the diotic (crosses) and binaural AM (circles) stimuli had different ITD_rms, whereas ITD_rms for the mixed (triangles) and binaural QFM (squares) stimuli remained similar. The reason for the mismatch between ITD_rms for the diotic and ITD_rms for the binaural AM stimuli at large modulation depths is illustrated in Fig. 8D: When the modulation depth increases, the amplitude of the AM and QFM grow, and small phase differences of the solid black arrows between the two ears (φ_L, φ_R) are introduced as a by-product of the binaural AM. Note that ITD_rms and ILD_rms are all nonzero because of the binaural differences introduced by the original (un-modulated) dichotic waveforms at both ears. Figures 10A, 10B thus verified that the binaural modulation manipulated the ILD and ITD cues as intended, as least for m≤ 0.3.

The effects of the binaural modulations on the ILD and ITD cues were verified and interpreted as follows. If the SIED cues computed from the diotic modulation and binaural QFM stimuli were identical, then the ILD cue must dominate the SIED cue, because ILDs are the same for these two types of modulation, but ITDs differ. The similarity of ILD for these conditions is verified by the overlap of the cross (diotic stimuli) and square (binaural QFM stimuli) symbols in Fig. 10A. In contrast, this manipulation affects the ITDs, as indicated by the separation of the cross (diotic stimuli) and square (binaural QFM stimuli) symbols in Fig. 10B.

Similarly, if the SIED cues obtained from the diotic (cross) modulation and binaural AM (circle) stimuli were identical, then the ITD cue must dominate the SIED cue, because the ITDs are similar for these two types of modulation, indicated by the overlap of the cross and circle symbols at small modulation depths in Fig. 10B. In contrast, new ILDs are introduced by the binaural AM manipulation, as indicated by the separation of the cross and circle symbols in Fig. 10A. If neither condition were satisfied, then the SIED would be related to both ILD and ITD.

The effects of the ILD and ITD manipulations on the SIED DV can now be analyzed based on the results shown in Fig. 10C, which illustrates the SIED DV for binaurally modulated wideband reproducible noise waveforms. If the SIED DVs were identical for the mixed and binaural AM stimuli, and for the diotic and binaural QFM stimuli (green circled groups), respectively, then the SIED cue would be fully determined by the ILD cue [see Fig. 10A]. Similarly, if the SIED DVs were the same for the diotic and binaural AM stimuli, and for the mixed and binaural QFM stimuli (blue circled groups), respectively, then ITD would be the dominant cue [see Fig. 10B, for m≤ 0.3]. Also, it is possible that neither ILD nor ITD cue alone completely explains the SIED DV. In that case, both ILD and ITD cues would be related to the SIED cue.

The results of the binaural modulation test of the wideband SIED cue are as follows. At small modulation depths (m≤ 0.1), DVs from all four sets of stimuli are similar [Fig. 10C], as expected from Figs. 10A, 10B. When modulation depth increases, DVs from the binaural AM and diotic stimuli, and from the mixed and binaural QFM stimuli, diverge. Thus, neither ILD nor ITD completely dominates the DV associated with the SIED cue. Comparing the trends in the SIED DVs to ILD_rms and to ITD_rms, it is clear that at small modulation depths (m≤ 0.3), ITD dominates the SIED cue because the DVs for the diotic and binaural AM stimuli overlap in both Figs. 10B, 10C. However, when modulation depth increases further (m > 0.3), ILD contributes in addition to ITD, because DVs from both the diotic and binaural AM stimuli, and from the mixed and binaural QFM stimuli, no longer overlap. Thus, the results in Fig. 10 suggest that the SIED cue is dominated by ITD, with some contribution from ILD at high binaural modulation depths for the wideband stimuli in the Evilsizer et al. (2002) study.

The results of the binaural modulation test of the narrowband SIED cues are shown in Fig. 11A for the Evilsizer et al. (2002) stimuli and in Fig. 11B for the Isabelle (1995) stimuli. Figures of ILD_rms and ITD_rms for these two sets of stimuli are not shown, as these results are the same as in Figs. 10A, 10B. In Figs. 11A, 11B, the SIED DVs from the four sets of binaurally modulated narrowband stimuli start to diverge at small modulation depths (m< 0.1), unlike the results seen in Fig. 10C for the wideband stimuli. For the narrowband SIED cues from the Evilsizer et al. (2002) study, the trends are similar to the trends in Fig. 10C at large modulation depths: The SIED DVs fall into two pairs: DVs from the binaural AM stimuli and the diotic stimuli are one pair, and DVs from the binaural QFM stimuli and the mixed stimuli are another pair [Fig. 11A]. These results indicate that the SIED cue is dominated by ITD for this set of stimuli. However, for SIED cues from the Isabelle (1995) study, the trends are different from the trends in Fig. 10C. For these stimuli, DVs from all four sets of binaurally modulated stimuli separate at large modulation depths. The interpretation of the relationship between the SIED and ILD and ITD cues, and the different results of the SIED cue observed in Figs. 10C, 11A, 11B will be discussed below.

Although it is difficult to show that the SIED cue is based on a specific nonlinear combination of ILD and ITD cues, these results indicate that a linear combination of these two cues would not yield the SIED cue. As mentioned above, for the stimuli from the Evilsizer et al. (2002) study, the SIED DV is mainly determined by ITD at small modulation depths, because the differences of ILD_rms were similar between the diotic and binaural AM stimuli, and between the mixed and binaural QFM stimuli. If the SIED DVs were determined by a linear combination of ILD_rms and ITD_rms, then similar changes of the SIED cue would be observed between the diotic and binaural AM stimuli, and between the mixed and binaural QFM stimuli, at large modulation depths. However, at large modulation depths, smaller differences in the SIED DVs were observed between the diotic and binaural AM stimuli, as compared to the mixed and binaural QFM stimuli [Figs. 10C, 11A]. Thus, the SIED cue is related to a nonlinear combination of ILD and ITD, although other unidentified properties of the stimuli might also be related to the SIED cue. For the stimuli from the Isabelle (1995) study, it is difficult to identify whether ILD or ITD dominates the SIED cue. As mentioned above, a difference between the two narrowband studies is that both overall noise level and tone levels at listeners' thresholds are higher for the Isabelle (1995) stimuli (Table TABLE II.). This level difference would interact with the binaural modulations. Nevertheless, for both narrowband and wideband stimuli, the SIED cue is a nonlinear combination of ILD and ITD cues.

DISCUSSION

People with hearing loss find it difficult to discriminate sound sources or communicate in noisy backgrounds (Henry and Heinz, 2012), even when using hearing aids. Thus, it is useful to understand how those with normal hearing detect signals in noise, in order to help design more effective techniques for hearing-aid devices. Understanding tone-in-noise detection is a first step to finding cues that are important for the above goal.

In this study, predictions of hit rates across a set of reproducible noises were computed based on several binaural cues. Comparisons were made between predictions based on ILD, ITD, a linear combination of ILD and ITD, and an envelope-based SIED cue. The combined ILD and ITD model took into account the covariance between these two cues. For listeners tested with the Evilsizer et al. (2002) wideband stimuli, the combined ILD and ITD model and the SIED model both yielded significantly better predictions than previous models (Davidson et al., 2009a). In addition, wideband predictions based on the SIED cue approached the predictable variance.

For the narrowband stimuli in both Evilsizer et al. (2002) and Isabelle (1995), predictions based on the combined ILD and ITD model and the SIED model were not significantly better than the previous models of Isabelle (1995) and Davidson et al. (2009a). Further analysis of the correlations between ILD, ITD, and SIED cues for the narrowband and wideband conditions is shown in Table TABLE III.. All three cues were significantly correlated in these two conditions; however, listeners' detection patterns in these two conditions were not significantly correlated. Thus the observed difference of model predictions in these two conditions might be related to the different strategies used by the listeners across bandwidth conditions.

TABLE III.

Correlation of DVs for narrowband and wideband stimuli in Evilsizer et al. (2002). Note that S7 was only tested with the narrowband stimuli and is not listed here.

	S1	S2	S3	S4	S5	S6
ILD	0.43	0.52	048	045	0.62	0.56
ITD	0.39	0.47	0.62	0.42	0.56	0.53
SIED	0.77	0.70	0.67	0.76	0.52	0.68

Similar to previous studies (Isabelle, 1995; Davidson et al., 2009a), model predictions based on a single ILD or ITD cue did not explain a significant amount of the variance in listeners' narrowband detection patterns (Figs. 56). Similar to the method of Goupell and Hartmann (2007), analysis of the ITD cue was also computed by removing the large instantaneous phase changes when the envelope in either ear was small (Goupell and Hartmann, 2007), but significant model predictions were not observed for this modification of the ITD cue. Moreover, single-cue multiple-epoch methods did not yield significantly better predictions than single-epoch models for most listeners. However, model predictions that combined ILD and ITD across time epochs and took into account their covariance matrix yielded significantly better predictions of hit rates than those using single cue and single epoch for some listeners. Thus, these listeners may use a binaural integration strategy that combines ILD and ITD cues.

The dynamic variations of ILD and ITD cues are interrelated with the changes in the envelopes at both ears; thus the possibility that listeners use envelope cues was examined in this study. The success and robustness of the ES cue in predicting diotic detection patterns (Richards, 1992; Zhang, 2004; Davidson et al., 2009a; Mao et al., 2013) motivated the examination of a binaural envelope cue for the dichotic condition. The proposed SIED cue yielded better predictions of listeners' detection patterns for the wideband condition than any previous method. Further investigation showed that the SIED cue was related to both ILD and ITD in a nonlinear manner. The SIED cue is a simple description of a nonlinear combination of ITD and ILD cues. In addition, it was shown that the SIED is mainly determined by the ITD cue, though ILD contributes for stimuli with larger amplitude fluctuations. For most complex stimuli with time-varying amplitudes, the modulation depth also changes over time, thus both ILD and ITD cues will contribute to the SIED cue at different points within the stimulus. The dominance of ITD over ILD in predicting binaural detection results is consistent with the studies by van der Heijden and Joris (2010) and Webster (1951).

Further analysis was carried out to examine whether listeners rely on the slope or the energy of the envelope fluctuations to detect tones in noise. Computing the SIED cue using only the sharp slopes (e.g., max values in the slope) did not yield significant correlations to listeners' detection patterns. Instead of using the SIED cue, the energy of envelope fluctuations was also computed based on the energy of non-direct current (i.e., non-zero frequency) components in the modulation-frequency domain. The proportion of variance in listeners' detection patterns that was explained based on the envelope-energy model was significantly less than that explained by the SIED cue for all listeners in both the narrowband and wideband conditions. Thus, it was confirmed that the slope rather than the envelope energy yields a DV that is more consistent with observed detection patterns.

The binaural envelope cue has not previously been used to explain binaural detection and discrimination tests, and it is interesting to consider the ability of the SIED to explain the results from other dichotic studies. For instance, some listeners have a higher threshold for dichotic detection of a 500-Hz pure tone in low-noise noise (LNN) compared with Gaussian noise (Hall et al., 1998; Eddins and Barber, 1998; Goupell, 2012). LNN has less fluctuation in its envelope compared with Gaussian noise, because LNN is generated by manipulating the phases of each frequency component to reduce envelope fluctuations, whereas Gaussian noise has random phases for each frequency component. Goupell (2012) could predict a significant amount of several listeners' detection variance for just-noticeable-differences in interaural correlation for LNN stimuli using two models: A normalized cross-correlation model with envelope compression (Bernstein et al., 1999) and the independent-center model (Goupell and Hartmann, 2007). Although fitting is involved in these models, his results show that envelope fluctuation is a possible cue to explain some listeners' performance. In addition, Hall et al. (1998) suggested that these listeners could benefit from listening in the “dips” for the Gaussian noises that have larger fluctuations.

Another possible explanation for the difference in thresholds for LNN and Gaussian noise is related to differences in the size of the SIED cue, as a result of the increased envelope fluctuations for Gaussian noise. Inspection of the SIED cues from a set of random Gaussian noises and LNNs showed that, although mean DVs were similar for these two types of noises, at SNRs close to listeners' thresholds, the SIED cues from Gaussian noises were more variable across the maskers than for LNN (by approximately a factor of 2), as expected.

Henning (1973) tested two listeners for frequency-modulation and amplitude-modulation discrimination under both diotic and dichotic conditions. His results show that at low SNR, listeners have significantly lower discrimination thresholds under dichotic conditions than under diotic conditions; at high SNR, listeners have similar discrimination thresholds for the two conditions. Henning further demonstrated that results from the amplitude-modulation discrimination task could be predicted using Durlach's EC model (Durlach, 1963) and the Webster-Jeffress models (Webster, 1951). The SIED cue provides an alternative explanation for results from amplitude-modulation discrimination because envelope cues are available for the modulated stimuli. At low SNRs, the SIED cue was available for the dichotic condition, but not for the diotic condition; listeners' thresholds would be therefore lower for the dichotic than the diotic condition if they used the SIED cue. However, at high SNRs, the SIED cue would decrease for the dichotic condition because the tones would dominate the envelope; tone signals have flatter envelopes than noises, suggesting that the SIED would be less effective at high SNRs. Simulation results from amplitude- and frequency-modulated stimuli showed that the variance of the SIED cues decreased at low SNRs compared to SIED cues at high SNRs (by approximately one-half).

Because all three cues studied here (ILD, ITD, and SIED) depend on the interaural differences introduced by the addition of out-of-phase tones to in-phase noise, none of these cues exist for the noise-alone waveforms presented during the dichotic detection task. In order to predict FA rates, potential sources of binaural differences in response to noise-alone waveforms must be considered. One way to achieve this goal is to apply physiological models with realistic statistical properties, such as responses from model auditory-nerve fibers and central neurons, or to introduce multiplicative noises (Bernstein and Trahiotis, 2008; Ewert and Dau, 2004). In addition, convergence of model auditory-nerve fibers with mismatched center frequencies could also provide binaural differences in response to noise-alone waveforms (Joris et al., 2006). The analysis of narrowband detection results presented here suggests that an exploration of models that include combinations of different frequency channels deserves further study. Future studies will focus on physiological models, in which predictions of detection patterns for both hit and FA rates can be computed for the narrowband and wideband detection conditions.