Abstract
Accurate and fast evaluation of electrostatic interactions in molecular systems is one of the most challenging tasks in the rapidly advancing field of macromolecular chemistry and drug design. Electrostatic interactions are of crucial importance in biological systems. They are well represented by quantum mechanical methods; however, such calculations are computationally expensive. In this study, we have evaluated the University of Buffalo Pseudoatom Databank (UBDB)1,2 approach for approximation of electrostatic properties of macromolecules and their complexes. We selected the S663 and JSCH-20054 data sets (208 molecular complexes in total) for this study. These complexes represent a wide range of chemical and biological systems for which hydrogen bonding, electrostatic, and van der Waals interactions play important roles. Reference electrostatic energies were obtained directly from wave functions at the B3LYP/aug-cc-pVTZ level of theory using the SAPT (Symmetry-Adapted Perturbation Theory) scheme for calculation of electrostatic contributions to total intermolecular interaction energies. Electrostatic energies calculated on the basis of the UBDB were compared with corresponding reference results. Results were also compared with energies computed using a point charge model from popular force fields (AM1-BCC and RESP used in AMBER and CGenFF from CHARMM family). The energy trends are quite consistent (R2 ≈ 0.98) for the UBDB method as compared to the AMBER5 and CHARMM force field methods6(R2 ≈ 0.93 on average). The RSMEs do not exceed 3.2 kcal mol–1 for the UBDB and are in the range of 3.7–7.6 kcal mol–1 for the point charge models. We also investigated the discrepancies in electrostatic potentials and magnitudes of dipole moments among the tested methods. This study shows that estimation of electrostatic interaction energies using the UBDB databank is accurate and reasonably fast when compared to other known methods, which opens potential new applications to macromolecules.
1. Introduction
Electrostatic energy constitutes one of the most important components of the total intermolecular interaction energy and may substantially influence the overall interaction strength of the molecular species. This is especially true in the case of polar systems where electrostatic interactions are often the driving force for specific complex formation and stabilization. Therefore, electrostatics should be estimated with care and relatively high accuracy. On the other hand, it is difficult to achieve ab initio or DFT level results for macromolecules as such computations are extremely expensive and time consuming, if indeed feasible. In this view, it is not surprising that accurate and fast evaluation of electrostatic interactions in molecular systems is one of the most challenging tasks in the rapidly developing field of macromolecular chemistry, including molecular recognition, protein modeling, and drug design.
In the field of quantum chemistry, the intermolecular electrostatic energy represents the Coulombic interaction between two isolated molecular charge densities, ρtotA(r) and ρtot(r), not disturbed by the neighboring molecule(s) (molecular complex counterparts, solvent molecules, etc.).7
| 1 |
The effect of polarization of the molecular charge density by the electric field of the neighboring unperturbed charge densities is quantified in the form of induction energy. These two (electrostatic and induction), together with dispersion and exchange repulsion, constitute the most important components of the total interaction energy. For a small molecular system, they can be directly computed within the framework of perturbation theories, such as DFT-SAPT (Symmetry-Adapted Perturbation Theory based on the Density Functional Theory),8,9 for example.
Up to now, the most common approach to deal with the interactions in macromolecular systems is based on force fields. In classical force fields, there are only two nonbonded components of energy: electrostatics and van der Waals. The van der Waals component is usually computed with a Lennard–Jones potential and the electrostatic component with Coulomb’s law. To compute the electrostatic energy, the molecular charge distribution is commonly approximated by an appropriate set of atom-centered point charges. In more advanced force fields, higher levels of multipole expansion (dipoles, quadrupoles, etc.) are implemented or extra point charges (often representing lone pairs) are added to specific atoms. In classic additive force fields, the charges are fixed and often are not affected by the local electrostatic environment. Electronic polarization is accounted for in an average fashion for a specific environment (commonly water), and a cancellation of errors between the electrostatic and van der Waals contributions is commonly present. Considerable effort is devoted nowadays to develop next-generation polarizable force fields that incorporate in a direct way specific models for polarizability.10−17
The force field method is aimed at relatively good estimation of the total interaction energy and is not optimized to properly describe the individual components of energy. Indeed, in the case of the electrostatic component, for example, the point multipole expansion does not account for charge overlap effects and hence excludes the penetration energy.18,19 [Commonly, electrostatic interactions between molecules are described by point charge or point–multipole (distributed multipole) models. These models are computationally inexpensive and give accurate descriptions of interaction when the molecules are not very much close together. When molecules (atoms) are in close contact due to electron distribution overlap, these models gives an error called the penetration effect. This is the difference between the exact electrostatic interaction energy computed by integral over the continuous distributions of charge and electrostatic interaction energy computed from multipolar expansion approximation. Note that such defined penetration energy depends not only on the level of charge density overlap but also on the level at which multipole expansion is truncated.] Penetration is not taken directly into account in the classical force field approach, but it is compensated by a less repulsive van der Waals potential. As a consequence, electrostatic energies computed with Coulomb’s law from point charges come close to exact values only at large interatomic distances. In general, all interaction energy components in the force field exhibit rather large errors at typical vdW distances, which nevertheless tend to approximately cancel out in a systematic way. The performance of the force fields for various energy components has been recently tested against the DFT-SAPT results.20 There is ongoing research to develop more accurate, but still fast, methods for estimation of electrostatic properties that take directly into account both density asphericity and penetration.17,21−27
Among them there is the pseudoatom database approach that has its roots in crystallography. Up to now, there are three well-established databanks: generalized Experimental Library of Multipolar Atom Model (ELMAM/ELMAM2),26,28,29 theoretical Invariom database,25 and University of Buffalo Pseudoatom Databank (UBDB).1,2 The aforementioned databanks can be employed, besides being a source of aspherical scattering factors in an X-ray diffraction data refinement, to reconstruct the electron density distributions of macromolecules and, in turn, to derive the electrostatic properties of such complex systems.30−34 The following paper will focus on the UBDB.
Since its creation, the UBDB approach has been tested against quantum mechanical results computed for a small set of amino acids and similar molecules2,35 and for a more extensive set of nucleic acid bases.36 The test suggests that the UBDB approach leads to results of quality not much worse than from quantum mechanics, but still it is much faster. The question arises how this approach compares with the force fields methods. Does the quality of the electrostatic properties derived from the UBDB method more closely resemble the quantum mechanical or force field results? Does UBDB give more physical electrostatic properties than popular force fields, which for many systems are the only feasible source of information regarding electrostatic properties but were not designed to properly describe electrostatics. Hence, in the following paper, we present a thorough comparison of the recently extended UBDB with the AMBER and CHARMM force fields approach to electrostatics. A similar analysis has already been done in the case of the ELMAM2 database,26 in which the interactions in amino acid-based systems were compared to AMBER results. Here, we have chosen a larger and more diverse set of compounds that are widely used as a benchmark in many computational studies, that is, the S663 and JSCH-20054 biologically oriented training sets. All the derived electrostatic properties were then compared with DFT results. Such a strategy will serve as a comprehensive overview of the UBDB method performance and limitations and will indicate the reliability of its application.
2. Theory and Computation Methods
2.1. Pseudoatom Databank
The University of Buffalo Databank (UBDB)1,36 has been used together with the LSDB program2 to reconstruct electron density distributions of biological and organic molecules. The UBDB offers the possibility of structural refinement of X-ray diffraction data with the use of aspherical scattering factors computed from the transferable aspherical atom model (TAAM). Apart from X-ray data refinement, the UBDB can be applied for evaluation of electrostatic properties of molecular complexes using a reconstructed electron density distribution. The databank is based on isolated molecule charge densities computed in vacuum and therefore does not take into account intermolecular polarization effects. In addition to the previous databank version,36 the current version of the UBDB contains 253 atom definitions consisting of 21 hydrogen, 129 carbon, 33 nitrogen, 39 oxygen, 10 sulfur, 9 phosphorus, 2 chlorine, 4 fluorine, 2 bromine, and 3 boron atom types. For the purposes of this work, the database has been updated with seven new atom types commonly present in small organic molecules shown in Figure 1.
Figure 1.
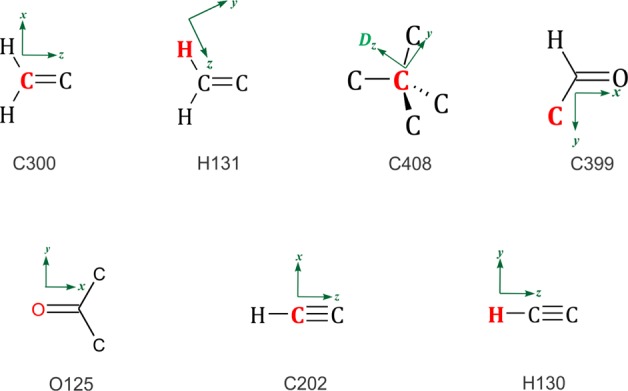
New atom types stored in the UBDB. The symbol D represents a dummy atom required for definition of the coordinate system.
The UBDB has been extended following the procedure applied in the previous version of the databank.36 Good quality experimental molecular geometries of model molecules were obtained from the Cambridge Structural Database (CSD).37 Hydrogen atom positions were corrected by extending X–H distances to their standard neutron diffraction values.38 Theoretical structure factors were obtained from single-point wave functions computed at the B3LYP/6-31G** level39−42 to which the Hansen and Coppens pseudoatom multipole model43 was fitted. In the pseudoatom model, individual atomic densities are described in terms of spherical core and valence densities with an expansion of atom-centered real spherical harmonic functions
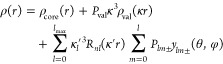 |
2 |
where ρcore and ρval are spherical and valence densities, respectively. The third term contains the sum of angular function ylm±(θ,ϕ) to take into account aspherical deformations. The coefficients Pval and Plm± are population for the spherical and multipole density, respectively. The κ and κ′ are scaling parameters that determine the expansion/contraction of spherical and multipolar valence densities, respectively. The derived multipole parameters were averaged for chemically similar atoms and together with atom type definitions were added to the UBDB.
2.2. Force Field Charge Assignment
For this analysis, the all atom additive General Amber Force Field (GAFF)5 and CHARMM General Force Field (CGenFF)6 were selected. To parametrize molecular complexes with the GAFF atom types, the Antechamber Toolkit44,45 was used, which typically only specifies bond and Lennard–Jones parameters. In addition, the program can calculate partial charges with different models and then generate an Amber force field model for an organic input molecule followed by atom type, bond, angle, and dihedrals. To obtain partial charges, two popular methods were employed: AM1-BCC46 and Restrained Electrostatic Potential fitting (RESP).47 The AM1-BCC methodology begins with the semi-empirical calculation of Mulliken (AM1) charges used to describe features of an electron distribution such as formal charge and delocalization, and in the final step, it generates bond charge corrections (BCCs) parametrized to reproduce ab initio (HF/6-31G*) electrostatic potentials. The RESP charges were computed from the molecular electrostatic potential using the Antechamber package. In our study, two sets of RESP partial charges were examined for each single molecule. The first set was obtained from the molecular electrostatic potential computed at the HF/6-31G* level in vacuum (here abbreviated simply as RESP). The second set comes from a molecular electrostatic potential computed at the same level but with a self-consistent reaction field (SCRF) method48 (hereafter, the set is abbreviated as RESP-SCRF), which was intended to mimic the solvated environment. The polarizable continuum model (PCM)48 with an external dielectric constant of 78.39 was used. The integral equation formalism method for PCM was used with the United Atom Topological Model (UA0) for the cavity, using the default parameters of Gaussian 03.49 It is known that the standard RESP methodology produces charges that are systematically overestimated by “approximately as much as the dipole is enhanced for a water molecule in the TIP3P50 or SPC51 models of water over its gas-phase value”.47
The RESP-SCRF method was used to understand to what extent highly polarized partial charges improve the quality of the molecular mechanics approximation, a phenomenon observed by some researchers.52
Conversely, the CGenFF program assigns atomic point charges by analogy53,54 with a set of model compounds, the charges on which were explicitly optimized for use in the CHARMM force field. It provides a wide range of atom types present in organic molecules, including heterocyclics,6 followed by generation of topology from CHARMM ver. 35b2.55
The water partial charges were taken from the TIP3P50 water model and used in all point charge methods tested.
2.3. Electrostatic Interaction Energy
To compute the electrostatic interaction energy (Ees), a variety of calculations were performed. In the UBDB approach, the molecular electron density was reproduced from the UBDB. The LSDB2 program was used to transfer the multipole populations from the UBDB to all structures. This transfer was based on the atomic connectivity and local symmetry recognition. The XDPROP module of the XD2006 package56 was used to calculate interaction energies from the derived charge density using the Exact Potential Multipole Method (EPMM).30,57 The EPMM evaluates the exact Coulomb integral in the inner region (≤4.5 Å) and combines it with a Buckingham-type multipole approximation for long-range interatomic interactions.58
In the case of the point charge methods, energies of nonbonded interactions were calculated between all pairs of atoms within a specified interatomic cutoff distance. A 999 Å cutoff was used for electrostatic interactions. The Ees was computed using a standard molecular mechanics force fields term
| 3 |
which corresponds to the Coulomb electrostatic
interaction in vacuum between a pair of atom-centered partial charges qi and qj, separated by a distance rij. The Ees term was computed separately for dimer (AB) and for each monomer
(A and B), and then the sum of Ees for
monomers was subtracted from the Ees for
the dimer. Such a procedure is equivalent to direct computation of
the intermolecular Ees by application
of the 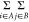 summation in eq 3.
summation in eq 3.
Such calculated energies were compared with the corresponding reference values (abbreviated as REF) obtained directly from wave functions computed for monomers in vacuum at the B3LYP/aug-cc-pVTZ level59 using GAUSSIAN03.49 The SPDFG60 program was used to calculate the exact Ees from the wave function. The numerical Rys quadrature is implemented in the SPDFG code for the computation of one- and two-electron Coulomb integrals.61,62 For details, refer to the Supporting Information. The Ees values obtained from SPDFG were taken as reference points as they have excellent agreement with EPol(1) obtained from the Symmetry-Adapted Perturbation Theory based on Density Function Theory (DFT-SAPT).8,9 The DFT-SAPT method gives directly all physical components of interaction energy: electrostatic EPol(1), induction, and dispersion (taking into account of overlap effects) and their exchange counterparts. [Induction interaction (also known as polarization) is the interaction between a permanent multipole on one molecule with an induced multipole on another. When a molecule is placed in the field of other molecules, moments will be induced on that molecule due to its polarizability. Whereas, dispersion interaction (also called London interactions) is an attractive component of the intermolecular interaction energy and acts between all type of molecules, polar or not. It arises due to the formation of a time variable instantaneous dipole of one system and the induced multipole of the second system.] The first-order SAPT energy (electrostatic+exchange) was computed with monomer densities and density matrices from the Kohn–Sham DFT. The second-order SAPT energy (induction, dispersion+exchange) from the (time-dependent) coupled perturbed theory utilized Kohn–Sham response functions. For the S66 data set, the correlation between EPol(1) from DFT-SAPT20 and Ees obtained from the SPDFG program was 0.99 and the RMSE was 0.5 kcal mol–1 (see the Supporting Information for details).
2.4. Electrostatic Potential Properties
To quantify the molecular electrostatic potential, we have calculated quantitative descriptors of the electrostatic potential mapped on the molecular van der Waals surface as proposed by Politzer and co-workers.63,64 The electrostatic potential (ri) of a single molecule was computed over a grid with ≈0.1 Å step size around the molecule with a 3.00 Å margin using the VMoPro module of the MoPro package.33,65 Statistical quantitative descriptors for electrostatic potential were evaluated at the van der Waals surface of thickness 0.3 Å. The reference electrostatic potential grids were calculated using GAUSSIAN03 at the B3LYP/aug-cc-pVTZ level. All quantitative notation used here is the same as in Politzer’s original papers. The descriptors were computed for each monomer and further averaged with the same molecules. This was done because some molecules (e.g., uracil) had slightly different geometries in different complexes.
2.5. Molecular Dipole Moments
Molecular dipole moments μ were computed only for isolated neutral molecules. To calculate dipole moments from the Hansen–Coppens representation of electron density, the MoPro package33,65 was used, applying the Buckingham approximation as described in the formula given by Spackman66 and Coppens67 at the molecular center of mass. Molecular dipole moments evaluated from atomic point charges were calculated in the MoPro package as well. The reference dipole moment magnitudes were directly obtained from the B3LYP/aug-cc-pVTZ wave functions computed in GAUSSIAN03. As with the electrostatic potential, dipoles were computed for each monomer and further averaged with the same molecules.
2.6. Molecular Geometries
In this study, we used molecular dimers taken from S663 and JSCH-20054 data sets. S66 is a benchmark data set characterized by well-balanced interaction energies for noncovalent interactions relevant to biological chemistry. It includes small organic molecules with a variety of interaction motifs and represents most typical noncovalent interactions. A total of 66 molecular complexes from the S66 data set can be divided in three subgroups: 23 complexes representing all possible types of of hydrogen bonding, 23 complexes representing dispersion-dominated interactions (π–π, aliphatic–aliphatic, and π–aliphatic), and in the remaining 20 complexes, the interactions consist of a combination of dispersion and electrostatic contributions. The JSCH-2005 data set is more focused on biological systems and contains almost exclusively nucleic acid bases, amino acids, and their derivatives. The set can be divided into four subgroups. Three subgroups contain nucleic acid bases divided according to the type of predominant noncovalent interaction: hydrogen-bonded base pairs (38 structures), interstrand base pairs (32 structures), and stacked base pairs (54 structures). The remaining fourth subgroup contains 19 amino acid complexes (see Supporting Information for details). One of the hydrogen-bonded base pairs (cytosine...protonated cytosine) was excluded from this study because it was previously reported to have two resonance structures,68 where a different nitrogen atom bears a +1 formal charge. Several force fields assign different charges when given either of two resonance structures of protonated cytosine, resulting in a high discrepancy in interaction energy. Equilibrium geometries of both data sets are taken from Hobza and co-workers.3,4
In addition to equilibrium geometries, we have also analyzed the S66 × 8 data set69 representing eight points along the dissociation curve for each complex from S66, altogether 528 dimers.
3. Results and Discussion
It has already been reported that electrostatic energies obtained from the combined method of UBDB and EPMM reproduce quite well the electrostatic energies obtained from quantum chemical calculations. The RMSE between UBDB+EPMM and ADF/B3LYP/TZP for 11 molecular dimers of α-glycine, N-acetylglycine, and L-(A)-lactic acid was 1.9 kcal mol–1.70 In another study of 10 amino acid dimers of glycine, serine, and leucine, the RMSE was 5 kcal mol–1 between UBDB+EPMM and ADF/B3LYP/TZP as compared to AMBER99, CHARMM27, MM3, and MMFF values ranging from 7 to 8 kcal mol–1.2 In a recent paper, the electrostatic energy was analyzed for nucleic acid base dimers, and the RMSE was 3.7 kcal mol–1 between UBDB+EPMM and GAUSSIAN03/B3LYP/6-31G**.36
3.1. The S66 Data Set
A good linear correlation between the UBDB+EPMM and the quantum chemical reference results was observed, with the slope close to unity (Table 1, Figure 2). The RMSE for UBDB+EPMM equals only 1.1 kcal mol–1.
Table 1. Statistics from Computed Electrostatic Energies for S66 Data Set Referred to the REF Resultsa.
| statistical descriptors | UBDB+EPMM | AM1-BCC | RESP | RESP-SCRF | CGenFF |
|---|---|---|---|---|---|
| R2 | 0.98 | 0.95 | 0.95 | 0.97 | 0.92 |
| slope | 0.97 | 1.52 | 1.41 | 1.03 | 1.56 |
| RMSE (kcal mol–1) | 1.1 | 4.2 | 3.7 | 1.9 | 4.4 |
| MAE (kcal mol–1) | 0.80 | 3.1 | 2.7 | 1.6 | 3.1 |
| ME (kcal mol–1) | –0.1 | –3.0 | –2.6 | –1.4 | –3.1 |
| % error | 4 | 62 | 56 | 43 | 65 |
R2 - correlation coefficient of linear regression fit inbetween reference and aproximated values, slope - the slope of the linear regression line, RMSE - root mean square error (RMSE = (∑t = 1n(fi – yi)2)2/1/n), MAE - mean absolute error (MAE = (1/n)∑t = 1| fi – yi|), ME - mean signed error (ME = ∑t = 1n(fi – yi)/n), % error - the error as a percent of the exact value (((fi – yi)/fi) × 100%), where fi and yi are the reference and approximated values, respectively.
Figure 2.
Comparison of electrostatic interaction energies computed from tested charge models with reference to theoretical results (B3LYP/aug-cc-pVTZ) for the S66 data set.
The AM1-BCC, RESP, and CGenFF results differ much more from the reference, with RMSEs equal to ≈4 kcal mol–1. The strength of electrostatic interactions is about 50% less favorable on average for all three point charge methods.
The quality of energies obtained from the AM1-BCC charges is nearly as good as that of the results that were obtained using RESP charges, despite the much simpler methodology applied in the latter case. A similar observation was reported by other authors.52 The RESP charges perform only slightly better than AM1-BCC, probably due to the fact that the empirical corrections used in AM1-BCC were parametrized to reproduce the RESP charges derived from HF/6-31G*. The smaller computational cost of computing the AM1-BCC charges, as compared to those obtained from DFT, make the AM1-BCC method more attractive.
One can wonder whether the RESP charges would perform better if a higher level of ab inito theory was used. The reason why it is recommended to derive charges at the HF/6-31G* level39 is that the always attractive three-body correlations could be accounted for in an average way. To achieve a more pronounced effect without relying on the deficiencies of the 6-31G* basis set only, a self-consistent reaction field (SCRF) method can be used to mimic the polarizable environment, which is an approach sometimes used in drug design. This particular choice of method hyperpolarizes the vacuum charges in a way that could be considered appropriate for condensed-phase simulation. We noticed a significant improvement in the quality of estimated energies calculated from point charges, which were obtained from the HF/6-31G* RESP combined with SCRF, with RMSE equal to 1.9 kcal mol–1.
The results based on CGenFF charges are almost as good as those obtained from the AM1-BCC method. The AM1-BCC method relies on calculations performed directly for particular molecules, and the CGenFF uses empirical (extended bond charge increment) rules to assign charges by analogy to a set of model compounds optimized to accurately interact with water. This charge assignment does not involve electronic structure calculations of any kind and is therefore much faster than the other methods.53 Taking into account the above facts, it maybe concluded that CGenFF performs quite well.
Considering the type of dominating interactions, the largest absolute errors in the Ees estimation were observed for the hydrogen-bonded complexes (Table 2). The values of Ees from UBDB+EPMM were the most similar to the REF among all tested methods (RMSE = 1.4 kcal mol–1). The AM1-BCC and CGenFF charges gave the largest discrepancies (RMSE = 6.3 and 6.8 kcal mol–1, respectively), and the RESP-SCRF charges were second close to the REF. The Ees for hydrogen bonding seems to be the most sensitive, on an absolute scale, to any simplifications in the electron density description. On the other hand, Ees in dispersion-dominated complexes seems to be least sensitive, on an absolute scale, to the method used for estimation (RMSE ≈ 2.5 kcal mol–1 for all point charge methods) with the exception for the UBDB+EPMM method, leading to energies evidently closer to the REF (RMSE = 0.9 kcal mol–1).
Table 2. Statistics from Computed Electrostatic Energy for Subgroups of the S66 Data Set.
| statistical descriptors | UBDB+EPMM | AM1-BCC | RESP | RESP-SCRF | CGenFF |
|---|---|---|---|---|---|
| H-bonded interaction (23 structures, average of referenceEes= −13.2 kcal mol–1) | |||||
| RMSE (kcal mol–1) | 1.4 | 6.3 | 5.5 | 2.1 | 6.8 |
| MAE (kcal mol–1) | 1.1 | 5.0 | 4.3 | 1.7 | 5.0 |
| ME (kcal mol–1) | –0.2 | –5.0 | –4.3 | –1.5 | –5.0 |
| % error | 2 | 36 | 30 | 11 | 33 |
| Dispersion dominated interaction (23 structures, average of referenceEes= −2.7 kcal mol–1) | |||||
| RMSE (kcal mol–1) | 0.9 | 2.4 | 2.5 | 2.2 | 2.7 |
| MAE (kcal mol–1) | 0.7 | 2.3 | 2.3 | 2.0 | 2.5 |
| ME (kcal mol–1) | –0.3 | –2.3 | –2.3 | –2.0 | –2.5 |
| % error | 16 | 98 | 99 | 96 | 107 |
| Mixed H-bonded and dispersion interactions (20 structures, average of referenceEes= −3.4 kcal mol–1) | |||||
| RMSE (kcal mol–1) | 0.8 | 2.0 | 1.4 | 1.1 | 2.0 |
| MAE (kcal mol–1) | 0.6 | 1.7 | 1.2 | 0.9 | 1.7 |
| ME (kcal mol–1) | 0.1 | –1.6 | –1.1 | –0.5 | –1.7 |
| % error | –7 | 50 | 36 | 18 | 54 |
However, when the error of estimation is related to the values of estimated energies (% error), it appears that these are dispersion-dominated complexes for which electrostatic energy is estimated as the worst on a relative scale. The AM1-BCC, RESP, RESP-SCRF, and CGenFF methods give rise to Ees in dispersion-dominated complexes that are too weak by about 100% and the UBDD+EPMM by 16%. Relatively, the results for hydrogen-bonded complexes are estimated as the best. The relative error was only 2% for UBDB+EPMM, 11% for RESP+SCRF, and around 33% for the remaining methods. The reason for the above behavior is undoubtedly related to fact that electrostatic contribution to interaction energies in dispersion-dominated systems are very small (here, −2.7 kcal mol–1 on average) at the limit of the tested method’s accuracy. On the other hand, hydrogen-bonding interactions are much stronger (here, 13.2 kcal mol–1 on average) and dominated by electrostatics that are very sensitive to the accurate description of anisotropy of interacting charge densities. It is clear that the UBDB+EPMM method is in very good agreement with the REF for estimating Ees in all types of interactions (hydrogen bonding, dispersion dominated, and mixed).
3.2. S66 × 8 Data Set
The accurate description of the entire potential energy surface is of great importance for any method that is applied to calculations for nonequilibrium geometries or molecular dynamics simulations. The Ees is one of the most important contributions to the intermolecular interaction energy, especially at long interatomic distances, where density overlap does not occur and the remaining contributions to energy (dispersion, induction, etc.) are negligible. Usually, at long distances, the point multipole approximation is good enough to compute accurate energies of electrostatic interactions. Proper estimation of electrostatics at short distances becomes an issue because here the electron density overlap appears and the multipole approximation becomes insufficient. The difference between the proper Ees and the Ees estimated from the point multipole approximation is referred to as the penetration electrostatic energy.
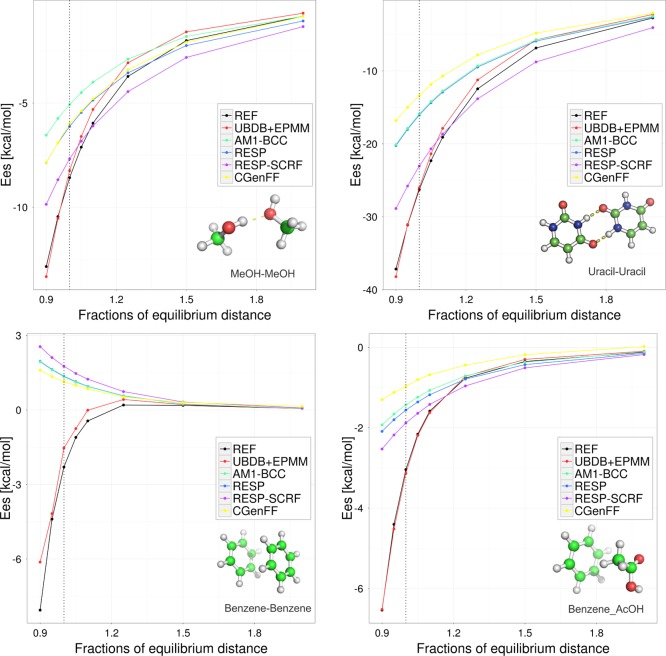
To study the performance of tested methods at both long- and short-range distances, we have analyzed S66 molecular complexes at eight scan points along the dissociation curve (seven different intermolecular distances from the equilibrium point and at equilibrium). Plots depicting the behavior of the estimated Ees depend on the distance for dimers, which represent examples of different subgroups, are given in Figure 3. Overall statistics are given in Table 3.
Figure 3.
Electrostatic interaction energy in kcal mol–1 computed by UBDB+EPMM and various point charge methods compared with the REF (B3LYP/aug-cc-pVTZ) energy. Dotted vertical lines along y axis correspond to the equilibrium distance. Top panels represent hydrogen-bonding-dominated interactions. Bottom left panel represents dispersion-dominated interactions. Bottom right panel represents mixed interactions.
Table 3. Statistics from Computed Electrostatic Energy for the S66 × 8 dataSet.
| statistical descriptors | UBDB+EPMM | AM1-BCC | RESP | RESP-SCRF | CGenFF |
|---|---|---|---|---|---|
| R2 | 0.98 | 0.91 | 0.91 | 0.91 | 0.89 |
| slope | 0.99 | 1.64 | 1.52 | 1.10 | 1.68 |
| RMSE kcal mol–1 | 1.1 | 4.1 | 3.7 | 2.4 | 4.3 |
| MAE kcal mol–1 | 0.8 | 2.4 | 2.1 | 1.6 | 2.5 |
| ME kcal mol–1 | –0.3 | –2.4 | –2.1 | –1.1 | –2.5 |
| % error | 12 | 57 | 53 | 38 | 55 |
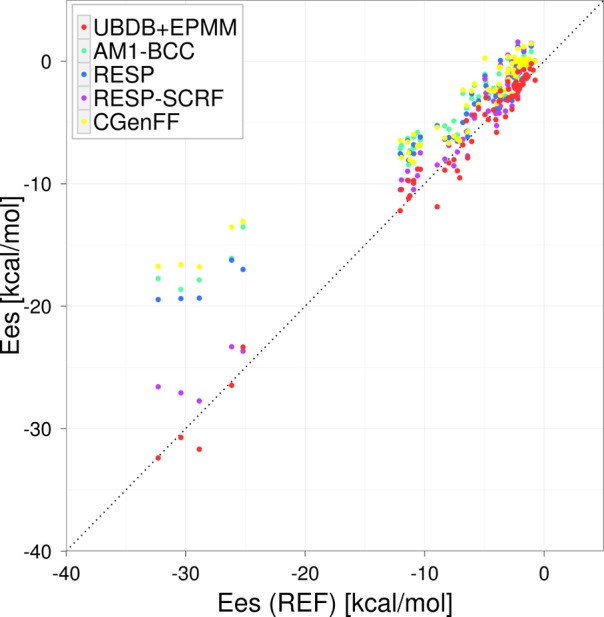
The values of Ees estimated by the UBDB+EPMM method quite nicely follow the reference ones. The error of Ees estimation in the case of UBDB+EPMM increases with decreasing distance; it starts from 0.4 kcal mol–1 and reaches a maximum of 1.9 kcal mol–1 at the shortest distances. The Ees obtained from point charges agrees well with the REF only at larger distances. The RMSE was usually below 1.0 kcal mol–1 for separations equal to 1.25 times the equilibrium distance or larger (Figure 4 and Table II of the Supporting Information). Interestingly, the RESP-SCRF method is the only one that overestimates the strength of the electrostatic interactions at longer distances, a phenomenon also reported by other authors.20 When molecules approach each other, the strength of electrostatic interactions become more and more severely underestimated, with RMSE up to ≈8 kcal mol–1 at 0.9 times the equilibrium distance. Indeed, the underestimation is already significant at equilibrium distances, as observed in the S66 data set. However, it should be noted that the vdW radii in force fields are chosen such that the interaction distances of hydrogen-bonded complexes are underestimated by about 0.2 Å with respect to the vacuum,71−73 as explained in the Introduction. In this light, the discrepancies in interaction energies will be compensated by the van der Waals term. The effect of such compensation would be comparable to about a 10% horizontal shift in Figure 3. Applying such a shift would bring the AM1-BCC, RESP, and CGenFF results in much better (albeit still not perfect) agreement with the reference and would lead to severe overestimation for RESP-SCRF. Therefore, the latter method may not be suitable for full force field calculations in which the interaction geometry is allowed to relax. Again, Ees estimated from polarized RESP charges (RESP-SCRF) were much closer to the reference values than those from vacuum RESP charges. This is especially true for ions and polar molecules, which is in agreement with the finding of other researchers.74,75
Figure 4.
Visualization of the differences in the RMSE (kcal mol–1) in Ees for S66 × 8 at different intermolecular distances.
The Ees scan nicely illustrates how neglecting the charge density overlap influences the values of Ees, while the interaction distance shortens. The scans also help to understand why the electrostatic energies in dispersion-dominated complexes are so badly estimated by the tested point charge models. In several dispersion-dominated dimers, the Ees computed from point charges become more and more positive with intermolecular distance shortening, as illustrated in Figure 3 for the benzene–benzene dimer. This is probably due to an insufficient level of multipole expansion. With atomic point charges only, unfavorable orientations of local dipole moments may lead to repulsive energies.
3.3. JSCH-2005 Data Set
The JSCH-2005 data set is composed of larger molecules, and the range of Ees is much larger than in the case of S66.
The range of Ees energies for hydrogen-bonded base pair complexes was from −7.9 to −49.5 kcal mol–1. In stacked complexes, the interaction energies were usually larger than −22.8 kcal mol–1 and reached 3.7 kcal mol–1. The Ees values of neutral amino acid complexes were below −8.6 kcal mol–1. The interaction energies of charged amino acid pairs were very negativ, and in the case of E49-K6(1BQ9), the Ees value reached −96.5 kcal mol–1. The Ees energy obtained from the UBDB+EPMM method was in good agreement with the REF with a correlation coefficient 0.98; the point charge methods deviated more from the REF (Table 4 and Figure 5).
Table 4. Statistics from Computed Electrostatic Energies for the JSCH-2005 Data Set with Reference to REF Results.
| statistical descriptors | UBDB+EPMM | AM1-BCC | RESP | RESP-SCRF | CGenFF |
|---|---|---|---|---|---|
| R2 | 0.97 | 0.93 | 0.94 | 0.96 | 0.91 |
| slope | 1.00 | 1.6 | 1.06 | 1.07 | 1.01 |
| RMSE kcal mol–1 | 3.2 | 7.4 | 6.7 | 4.7 | 7.6 |
| MAE kcal mol–1 | 2.0 | 5.4 | 4.9 | 3.7 | 5.3 |
| ME kcal mol–1 | –0.7 | –5.2 | –4.9 | –2.3 | 4.9 |
| % error | –7 | 49 | 49 | 22 | 48 |
Figure 5.
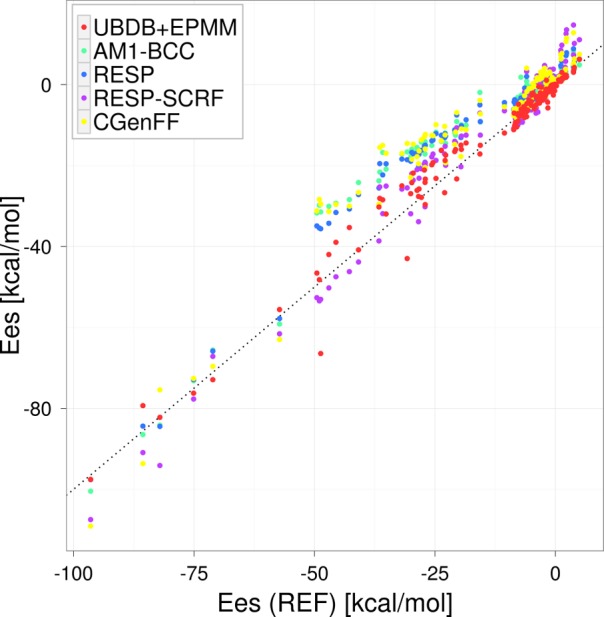
Comparison of electrostatic interaction energies with the REF values for the JSCH-2005 data set.
The overall statistics from electrostatic energies computed for the JSCH-2005 data set show a similar behavior to the S66 data set. All tested methods gave rise to the electrostatic interactions that were too weak on average. Again, the UBDB+EPMM method is the closest to the REF. The second closest is the RESP-SCRF method, and AM1-BCC, RESP, and CGenFF gave the largest discrepancies but were similar to each other. For each tested method, the absolute errors are larger than for the S66 data set, but the relative errors remain similar.
The JSCH-2005 data set was not as well characterized as the S66 set in terms of type of interactions dominated in molecular dimers and the size of molecules. Nonetheless, some trends observed in the case of the S66 subgroups are also visible here. In the planar subgroup, in which hydrogen bonding dominates, the RESP-SCRF is almost as close to the REF as UBDB+EPMM. In the stacked subgroup, in which dispersion interactions dominate, all point charge methods give similar absolute errors, although here the relative error is much smaller than it was for the similar subset of S66. The RMSE for UBDB+EMPMM ranged from 1.2 to 5.8 kcal mol–1, representing a significant improvement over point charge methods, which range from 1.0 to 13.4 kcal mol–1 (Table 5).
Table 5. Statistics from Computed Electrostatic Energies for Subgroups of the JSCH-2005 Data Set.
| statistical descriptors | UBDB+EPMM | AM1-BCC | RESP | RESP-SCRF | CGenFF |
|---|---|---|---|---|---|
| H-bonded base pairs (38 structures, average of referenceEes= −30.0 kcal mol–1) | |||||
| RMSE | 5.8 | 13.1 | 11.9 | 6.2 | 13.4 |
| MAE | 4.6 | 12.7 | 11.6 | 5.8 | 12.7 |
| ME | –2.5 | –12.7 | –11.6 | –3.8 | –12.7 |
| % error | 9 | 44 | 41 | 17 | 43 |
| Interstrand base pairs (32 structures, average of referenceEes= 0.0 kcal mol–1) | |||||
| RMSE | 1.2 | 1.0 | 1.2 | 2.5 | 1.4 |
| MAE | 0.7 | 0.7 | 0.9 | 1.9 | 1.0 |
| ME | 0.2 | –0.6 | –0.8 | –1.3 | –0.8 |
| % error | –1 | 18 | 29 | –11 | 60 |
| Stacked base pairs (54 structures, average of referenceEes= −5.2 kcal mol–1) | |||||
| RMSE | 1.5 | 4.6 | 4.2 | 4.6 | 4.5 |
| MAE | 1.1 | 4.2 | 3.8 | 3.6 | 3.6 |
| ME | –0.04 | –4.2 | –3.8 | –2.8 | –3.4 |
| % error | –10 | 62 | 54 | 19 | 30 |
| Amino acid complexes (19 structures, average of referenceEes= −26.6 kcal mol–1) | |||||
| RMSE | 2.0 | 2.7 | 2.4 | 4.5 | 4.5 |
| MAE | 1.4 | 2.3 | 2.5 | 3.3 | 3.4 |
| ME | –0.6 | –1.4 | –1.6 | 0.4 | –0.6 |
| % error | –38 | 77 | 84 | 95 | 84 |
3.4. Electrostatic Potential
Electrostatic potentials mapped on the van der Waals surfaces (MEPSs) in all examined models show positive or negative potential values characteristic for particular types of functional groups (Figures 6, 7, and 8). Politzer and co-workers have shown that quantitative information can be derived from the MEPS and used to predict several molecular properties.63,64 We used some of the MEPS descriptors proposed by them to do quantitative evaluation of electrostatic potentials computed from all tested methods. The charged molecules of the JSCH2005 data set were excluded for this study because of the undefined origin of formal charges. We focused our analysis on the average value of positive potential on the surface V+ and its variance σ+, the negative potential V– and its variance σ–, and on the average value of the total potential on the surface VTOT. It appears that all the tested methods (UBDB, AM1-BCC, RESP, and CGenFF) approximate average values of positive and negative potentials and their variance with similar errors. The statistics tends to be slightly more favorable for RESP and slightly poorer for CGenFF. Interestingly, V+ is much better approximated than V– in all tested methods: RMSEs ≈ 0.003 e/a0 and 0.006 e/a0 for V+ and V–, respectively. In the case of VTOT, some clear discrepancies between methods are visible. Although all tested methods lead to values of the overall potential on the van der Waals surface shifted toward negative values, compared to the reference (Figure 9), VTOT values from UBDB are much closer to the reference values (RMSD = 0.002 e/a0) and remain slightly positive for almost all molecules (Tables 6 and 7).
Figure 6.
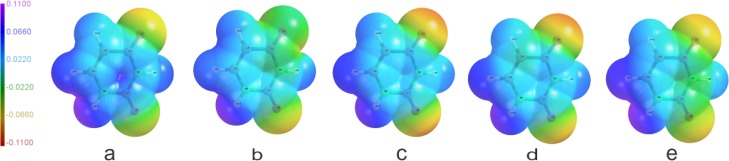
Isolated molecule electrostatic potential (ESP) of uracil mapped on the van der Waals surface for (a) REF, (b) UBDB, (c) AM1-BCC, (d) RESP, and (e) CGenFF models. The maximum negative and positive values of ESP correspond to the values −0.11 and 0.11 e/bohr, respectively.
Figure 7.
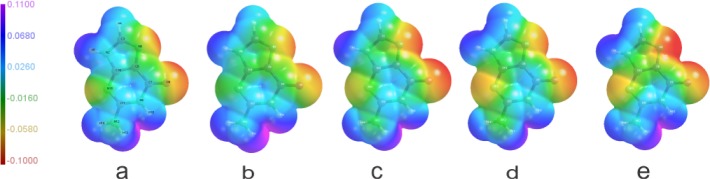
Isolated molecule electrostatic potential (ESP) of guanine mapped on the van der Waals surface for (a) REF, (b) UBDB, (c) AM1-BCC, (d) RESP, and (e) CGenFF models. The maximum negative and positive values of ESP correspond to the values −0.11 and 0.11 e/bohr, respectively.
Figure 8.
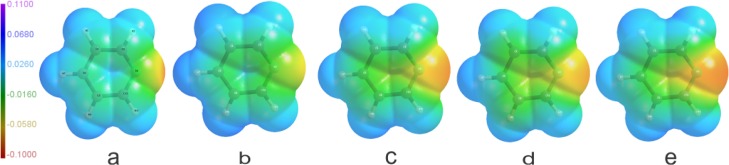
Isolated molecule electrostatic potential (esp) of pyridine mapped on the van der Waals surface for (a) REF, (b) UBDB, (c) AM1-BCC, (d) RESP, and (e) CGenFF models. The maximum negative and positive values of ESP correspond to the values −0.11 and 0.11 e/bohr, respectively.
Figure 9.
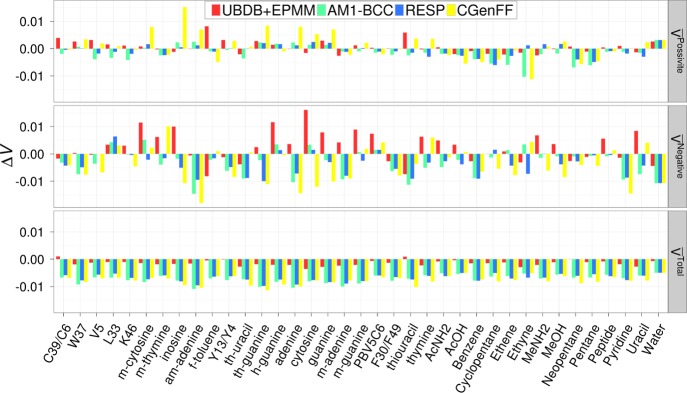
Visualization of the differences in the properties of isolated molecule electrostatic potential mapped on the van der Waals surface (e/bohr) between REF and the given model.
Table 6. Statistics from Computed MEPS Descriptors for Single Molecules from the S66 Data Set.
| statistical descriptors | UBDB | AM1-BCC | RESP | CGenFF |
|---|---|---|---|---|
| V+(Average of referenceV+= 0.025e/a0) | ||||
| R2 | 0.98 | 0.95 | 0.96 | 0.89 |
| RMSE (e/a0 × 103) | 1.5 | 4.7 | 3.1 | 4.5 |
| MAE (e/a0 × 103) | 1.3 | 3.8 | 2.7 | 3.5 |
| ME (e/a0 × 103) | 0.5 | 3.4 | 1.7 | 2.3 |
| % error | 5 | 30 | 19 | 21 |
| V–(Average of referenceV–= −0.024e/a0) | ||||
| R2 | 0.95 | 0.94 | 0.95 | 0.87 |
| RMSE (e/a0 × 103) | 3.9 | 3.2 | 5.4 | 6.8 |
| MAE (e/a0 × 103) | 3.3 | 3.9 | 4.3 | 5.7 |
| ME (e/a0 × 103) | –1.1 | 3.2 | 4.0 | 4.2 |
| % error | –13 | –24 | –27 | –72 |
| VTOT(Average of referenceVTOT= 0.0053e/a0) | ||||
| R2 | 0.81 | 0.73 | 0.77 | 0.37 |
| RMSE (e/a0 × 103) | 1.4 | 6.2 | 6.2 | 7.1 |
| MAE (e/a0 × 103) | 1.3 | 6.2 | 6.2 | 7.0 |
| ME (e/a0 × 103) | 1.3 | 6.2 | 6.2 | 7.0 |
| % error | 26 | 123 | 125 | 137 |
Table 7. Statistics from Computed MEPS Descriptors for Single Molecules from the JSCH-2005 Data Set.
| statistical descriptors | UBDB | AM1-BCC | RESP | CGenFF |
|---|---|---|---|---|
| V+(Average of referenceV+= 0.028e/a0) | ||||
| R2 | 0.86 | 0.94 | 0.96 | 0.85 |
| RMSE (e/a0 × 103) | 2.8 | 2.2 | 1.6 | 5.2 |
| MAE (e/a0 × 103) | 2.0 | 2.0 | 1.3 | 3.9 |
| ME (e/a0 × 103) | –1.2 | 0.07 | 0.03 | –2.8 |
| % error | –6 | 4 | 2 | –8 |
| V–(Average of referenceV–= −0.031e/a0) | ||||
| R2 | 0.70 | 0.75 | 0.85 | 0.60 |
| RMSE (e/a0 × 103) | 7.2 | 6.3 | 5.3 | 8.1 |
| MAE (e/a0 × 103) | 5.8 | 5.2 | 4.4 | 6.8 |
| ME (e/a0 × 103) | –3.7 | 3.7 | –3.5 | 4.0 |
| % error | 6 | –15 | –13 | –15 |
| VTOT(Average of referenceVTOT= 0.006e/a0) | ||||
| R2 | 0.84 | 0.92 | 0.89 | 0.75 |
| RMSE (e/a0 × 103) | 1.9 | 8.0 | 7.4 | 8.3 |
| MAE (e/a0 × 103) | 1.7 | 7.9 | 7.3 | 8.1 |
| ME (e/a0 × 103) | 1.5 | 7.9 | 7.3 | 8.1 |
| % errror | 33 | 180 | 162 | 177 |
3.5. Molecular Dipole Moment
The dipole moment μ is another important molecular property. It is used to characterize the overall charge distribution of a molecule. RESP was designed to accurately fit the electrostatic potential resulting from a quantum calculation, meaning that it should reproduce the dipole moment of the quantum mechanical charge distribution well, and this was the case (Table 8, Figure 10). The R2 for the RESP dipole for both S66 and JSCH-2005 data sets together was 0.99, and the lowest RMSE is observed for RESP. Slightly worse correlations are observed for UBDB and AM1-BCC, and the worst is CGenFF. Nonetheless, the magnitude of the RMS errors were in a similar range for all tested methods, with the lowest one being 0.46 D for RESP and the largest being 0.92 D for CGenFF. The performance of the CGenFF partial charges in the molecular dipole moment estimation is therefore satisfactory. It appears that the UBDB method is not better than point charge methods for molecular dipole moment magnitude approximation.
Table 8. Statistics from Computed Dipole Moment Magnitudes for Single Molecules from the S66 and JSCH-2005 Data Sets.
| statistical descriptors | UBDB | AM1-BCC | RESP | CGenFF |
|---|---|---|---|---|
| R2 | 0.94 | 0.93 | 0.99 | 0.88 |
| RMSE (Debye) | 0.56 | 0.68 | 0.46 | 0.92 |
| MAE (Debye) | 0.3 | 0.5 | 0.3 | 0.7 |
| ME (Debye) | 0.2 | 0.3 | 0.3 | 0.5 |
Figure 10.
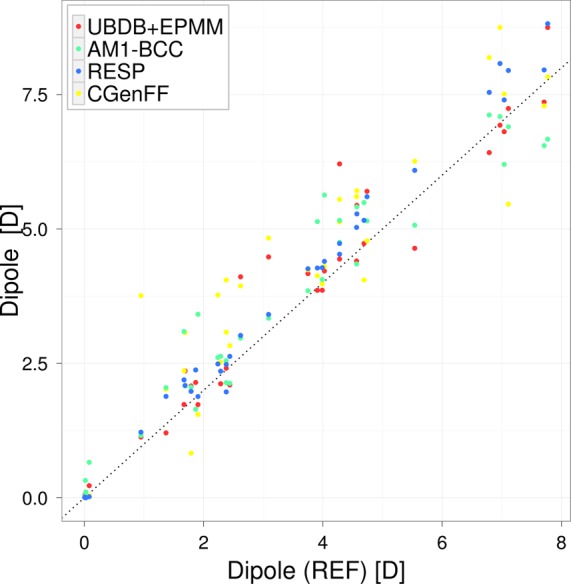
Isolated molecule dipole moments computed from tested methods are compared with those computed directly from the electronic wave function from B3LYP/aug-cc-pVTZ calculations (REF).
In the case of RESP dipole moment magnitudes, there is a small trend visible; with an increasing value of dipole moment magnitudes, RESP dipoles become more and more overestimated. This effect is much more pronounced for the RESP-SCRF dipole moments (see Supporting Information for details). The above trends illustrate the consequences of overestimated atomic charges derived from prepolarized charge densities. Application of a continuous solvent model with an external dielectric constant of 78.39 (RESP-SCRF charges) gives rise to quite a significant overestimation of molecular dipole moments (more than 30% in some cases) and brings values of Ees closer to the referential ones in a way that imitates some penetration effects. It is worth stressing here that the reference Ees does not contain any contribution from polarization effects and fully accounts for penetration effects. In fact, more proper reference values for Ees estimated from polarized charges would be a sum of electrostatic and induction energies.
4. Conclusions
The performance of the UBDB for electrostatic interaction energy (Ees) estimation was analyzed with the S66 and JSCH-2005 data sets. The results were compared with Ees estimated from various widely used molecular mechanics force fields and from quantum mechanical computation. For a total of 208 different molecular complexes, electrostatic energies were calculated at their equilibrium geometries as well as at shorter and longer distances. The energy obtained from UBDB+EPMM is in good agreement with reference energies obtained at the SPDFG/B3LYP/aug-cc-pVTZ level of theory (RMSE = 1.1 and 3.2 kcal mol–1 for S66 and JSCH-2005, respectively). The results clearly show that the UBDB+EPMM method much more closely resembles the reference quantum mechanical results in comparison to the point charge-based force field methods (AM1-BCC, RESP, and CGenFF; RMSE ≈ 4.0 and ≈7.0 kcal mol–1 for S66 and JSCH-2005, respectively). The discrepancies between energy estimated for point charge methods and REF were somewhat satisfactory at longer distances but increase when passing to shorter distances due to severe underestimation of electrostatic interaction strengths in that region. This is because the point charge approximation does not incorporate penetration effects arising at short distances and also because the point charges were parametrized for bulk-phase interaction distances, which are shorter than the vacuum-phase distances found in the S66 and JSCH-2005 data sets. It is assumed that these errors are compensated by stronger vdW interactions in the force fields being studied.
Along with electrostatic interaction energies, the following properties related to electron density distributions have been compared extensively: electrostatic potential and dipole moments. Here, the benefit of using UBDB-derived densities is only visible for the case of the average value of total electrostatic potential mapped on the molecular van der Waals surface. The UBDB seems to be more accurate than the point charge models. Other properties, including molecular dipole moment magnitudes, were quite well approximated by all tested methods including UBDB; those differences that were apparent suggest that RESP may be marginally the best one and CGenFF the worst.
All the results indicate that CGenFF point charges were almost as good as AM1-BCC. Bearing in mind that the latter were computed on demand for a particular molecule and the former assigns charges by analogy without involving electronic structure calculations, the CGenFF charges performed very well. Our results emphasize that the point charge model poorly represents the charge density distribution at equilibrium distances, which is a major drawback in electrostatic interaction energy estimation by force field methods. However, it should be emphasized that the force field charges are designed to mimic a condensed-phase environment in a mean field way, and often their deficiencies are compensated by cancellation of errors between electrostatic and vdW interaction such that a larger discrepancy with respect to the exact gas-phase target data is somewhat expected. The smaller difference between reference and UBDB+EPMM results strongly suggests that this is a better method for electrostatic energy estimation than the others. The strength of the UBDB+EPMM method most probably lies in the fact that for short distances exact evaluation of Ees is possible having access to UBDB-derived charge densities.
Acknowledgments
The authors thank Dr. Anatoliy Volkov for providing the SPDFG program. Support of this work by the Foundation of Polish Science through Grant POMOST No. POMOST/2010-2/3 (P.K., S.A.B., K.N.J, and P.M.D.) is gratefully acknowledged. K.N.J. also acknowledges the Foundation for Polish Science for financial support within the “START” programme. Additionally, this research is also supported by the Interdisciplinary Centre for Mathematical and Computational Modelling, Warsaw, Poland (Computation Grant No. G50-12/PMD). Molecular graphics were produced with help of the MolIso76 program. A.D.M.Jr. would like to thank the National Institutes of Health (NIH) (GM051501, GM070855) and NSF (CHE-0823198) for financial support.
Supporting Information Available
Table I and Figure 1 show the statistics and comparison for agreement of SPDFG energies with DFT-SAPT. Table II shows detailed information for statistics with the S66 × 8 data set at different fractions of equilibrium distance. Table III with a discrepancy factor shows the further statistics in dipole moments data for the S66 and JSCH-2205 data sets. Table IV shows the discrepancies in electrostatic potential with the REF. Table V shows the grid accuracy for electrostatic potential mapped on an isodensity surface. Figure 2 and Table VI show statistical detail for discrepancies in magnitude of dipole for the S66 data set and for the tested method including the RESP-SCRF point charge method. Tables VII and VIII contain the name and type of interactions present in molecular complexes of JSCH-2005 and S66, respectively. The UBDB and LSDB for automatic rebuilding of electron density are available at http://crystal.chem.uw.edu.pl. This material is available free of charge via the Internet at http://pubs.acs.org.
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- Messerschmidt M.; Volkov A.; Dominiak P. M.; Li X.; Coppens P. J. Chem. Theory Comput. 2007, 3, 232–247. [DOI] [PubMed] [Google Scholar]
- Volkov A.; Li X.; Koritsánszky T.; Coppens P. J. Phys. Chem. A 2004, 108, 4283–4300. [Google Scholar]
- Řezáč J.; Riley K. E.; Hobza P. J. Chem. Theory Comput. 2011, 7, 2427–2438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jurečka P.; Šponer J.; Cerný J.; Hobza P. Phys. Chem. Chem. Phys. 2006, 8, 1985–1993. [DOI] [PubMed] [Google Scholar]
- Wang J.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. J. Comput. Chem. 2004, 25, 1157–1174. [DOI] [PubMed] [Google Scholar]
- Vanommeslaeghe K.; Hatcher E.; Acharya C.; Kundu S.; Zhong S.; Shim J.; Darian E.; Guvench O.; Lopes P.; Vorobyov I.; Mackerell A. D. J. Comput. Chem. 2010, 31, 671–690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeziorski B.; Moszynski R.; Szalewicz K. Chem. Rev. 1994, 94, 1887–1930. [Google Scholar]
- Williams H. L.; Chabalowski C. F. J. Phys. Chem. A 2001, 105, 646–659. [Google Scholar]
- Jansen G.; Hesselmann A. J. Phys. Chem. A 2001, 105, 11156–11157. [Google Scholar]
- Stern H. A.; Kaminski G. A.; Banks J. L.; Zhou R.; Berne B. J.; Friesner R. A. J. Phys. Chem. B. 1999, 103, 4730–4737. [Google Scholar]
- Yu H. B.; Geerke D. P.; Liu H. Y.; van Gunsteren W. E. J. Comput. Chem. 2006, 27, 1494–504. [DOI] [PubMed] [Google Scholar]
- Jorgensen W. L.; Jensen K. P.; Alexandrova A. N. J. Chem. Theory Comput. 2007, 3, 1987–1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patel S.; Davis J. E.; Bauer B. A. J. Am. Chem. Soc. 2009, 109, 13890–13891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J.; Cieplak P.; Li J.; Wang J.; Cai Q.; Hsieh M.; Lei H.; Luo R.; Duan Y. J. Phys. Chem. B. 2011, 115, 3100–3111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren P.; Ponder J. W. J. Comput. Chem. 2002, 23, 1497–1506. [DOI] [PubMed] [Google Scholar]
- Lopes P. E. M.; Roux B.; MacKerell A. D. J. Theor. Chem. Acc. 2009, 124, 11–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopes P. E. M.; Huang J.; Shim J.; Luo Y.; Li H.; Roux B.; MacKerell A. D. J. J. Chem. Theory Comput. 2013, 9, 5430–5449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piela L.Ideas of Quantum Chemistry; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Stone A.The Theory of Intermolecular Forces, 2nd ed.; Oxford University Press: Oxford, U.K., 2013. [Google Scholar]
- Zgarbová M.; Otyepka M.; Sponer J.; Hobza P.; Jurećka P. Phys. Chem. Chem. Phys. 2010, 12, 10476–10493. [DOI] [PubMed] [Google Scholar]
- Gavezzotti A. J. Phys. Chem. B 2002, 106, 4145–4154. [Google Scholar]
- Wheatley R. J.; Mitchell J. B. O. J. Comput. Chem. 2004, 15, 1187–1198. [Google Scholar]
- Elking D. M.; Cisneros G. A.; Piquemal J.-P.; Darden T. A.; Pedersen L. G. J. Chem. Theory Comput. 2010, 6, 190–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gresh N.; Cisneros G. A.; Darden T. A.; Piquemal J.-P. J. Chem. Theory Comput. 2007, 3, 1960–1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dittrich B.; Hübschle C. B.; Luger P.; Spackman M. A. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2006, 62, 1325–1335. [DOI] [PubMed] [Google Scholar]
- Domagała S.; Fournier B.; Liebschner D.; Guillot B.; Jelsch C. Acta Crystallogr., Sect. A: Found. Crystallogr. 2012, 68, 337–351. [DOI] [PubMed] [Google Scholar]
- Ponder J. W.; Wu C.; Ren P.; Pande V. S.; Chodera J. D.; Schnieders M. J.; Haque I.; Mobley D. L.; Lambrecht D. S.; DiStasio R. A. J.; Head-Gordon M.; Clark G. N. I.; Johnson M. E.; Head-Gordon T. J. Phys. Chem. B 2007, 114, 2549–2564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pichon-Pesme V.; Lecomte C.; Lachekar H. J. Phys. Chem. 1995, 99, 6242–6250. [Google Scholar]
- Pichon-Pesme V G. B. L. C.; Christian J. Acta Crystallogr., Sect. A: Found. Crystallogr. 2004, 60, 204–208. [DOI] [PubMed] [Google Scholar]
- Volkov A.; King H. F.; Coppens P.; Farrugia L. J. Acta Crystallogr., Sect. A: Found. Crystallogr. 2006, A62, 400–408. [DOI] [PubMed] [Google Scholar]
- Li X.; Volkov A.; Szalewicz K.; Coppens P. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2006, 62, 639–647. [DOI] [PubMed] [Google Scholar]
- Dominiak P. M.; Volkov A.; Dominiak A.; Jarzembska K. N.; Coppens P. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2009, 65, 485–499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jelsch C.; Guillot B.; Lagoutte L.; Lecomte C. J. Appl. Crystallogr. 2005, 38, 38–54. [Google Scholar]
- Zarychta B.; Pichon-Pesme V.; Guillot B.; Lecomte C.; Jelsch C. Acta Crystallogr., Sect. A: Found. Crystallogr. 2007, 63, 108–125. [DOI] [PubMed] [Google Scholar]
- Bak J. M.; Domagała S.; Hübschlee C.; Jelsch C.; Dittrich B.; Dominiak P. M. Acta Cryst. A. 2009, 67, 141–153. [DOI] [PubMed] [Google Scholar]
- Jarzembska K. N.; Dominiak P. M. Acta Crystallogr., Sect. A: Found. Crystallogr. 2012, A68, 139–147. [DOI] [PubMed] [Google Scholar]
- Allen F. H. Acta Crystallogr., Sect. B: Struct. Sci. 2002, B58, 380–388. [DOI] [PubMed] [Google Scholar]
- Allen F. H.; Bruno I. J. Acta Crystallogr., Sect. B: Struct. Sci. 2010, 66, 380–386. [DOI] [PubMed] [Google Scholar]
- Krishnan R.; Binkley J. S.; Seeger R.; Pople J. A. J. Chem. Phys. 1980, 72, 650. [Google Scholar]
- Becke A. D. Phys. Rev. A 1988, 38, 3098–3100. [DOI] [PubMed] [Google Scholar]
- Perdew J. P. Phys. Rev. B 1986, 33, 8822–8824. [DOI] [PubMed] [Google Scholar]
- Lee C.; Yang W.; Parr R. G. Phys. Rev. B 1988, 37, 785–789. [DOI] [PubMed] [Google Scholar]
- Hansen N. K.; Coppens P. Acta Crystallogr., Sect. A: Found. Crystallogr. 1978, A34, 909–921. [Google Scholar]
- Wang J.; Wang W.; Kollman P. A.; Case D. A. J. Mol. Graphics Modell. 2006, 25, 247–260. [DOI] [PubMed] [Google Scholar]
- Pearlman D.; Case D.; Caldwell J.; Ross W.; Cheatham T.; DeBolt S.; Ferguson D.; Seibel G.; Kollman P. A. Comput. Phys. Commun. 1995, 91, 1–41. [Google Scholar]
- Jakalian A.; Jack D. B.; Bayly C. I. J. Comput. Chem. 2002, 23, 1623–1641. [DOI] [PubMed] [Google Scholar]
- Bayly C.; Cieplak P.; Cornell W.; Kollman P. J. Phys. Chem. 1993, 97, 10269–10280. [Google Scholar]
- Tomasi J.; Mennucci B.; Cammi R. Chem. Rev. 2005, 105, 2999–3094. [DOI] [PubMed] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Montgomery J. A. Jr.; Vreven T.; Kudin K. N.; Burant J. C.; Millam J. M.; Iyengar S. S.; Tomasi J.; Barone V.; Mennucci B.; Cossi M.; Scalmani G.; Rega N.; Petersson G. A.; Nakatsuji H.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Klene M.; Li X.; Knox J. E.; Hratchian H. P.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Ayala P. Y.; Morokuma K.; Voth G. A.; Salvador P.; Dannenberg J. J.; Zakrzewski V. G.; Dapprich S.; Daniels A. D.; Strain M. C.; Farkas O.; Malick D. K.; Rabuck A. D.; Raghavachari K.; Foresman J. B.; Ortiz J. V.; Cui Q.; Baboul A. G.; Clifford S.; Cioslowski J.; Stefanov B. B.; Liu G.; Liashenko A.; Piskorz P.; Komaromi I.; Martin R. L.; Fox D. J.; Keith T.; Al-Laham M. A.; Peng C. Y.; Nanayakkara A.; Challacombe M.; Gill P. M. W.; Johnson B.; Chen W.; Wong M. W.; Gonzalez C.; Pople J. A.. Gaussian 03, Revision C.02. Gaussian, Inc.: Wallingford, CT, 2004. [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar]
- Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; Hermans J. Intermol. Forces 1981, 331–342. [Google Scholar]
- Mobley D. L.; lise Dumont E.; Chodera J. D.; Dill K. A. J. Phys. Chem. B 2007, 111, 2242–2254. [DOI] [PubMed] [Google Scholar]
- Vanommeslaeghe K.; MacKerell A. D. J. J. Chem. Inf. Model. 2012, 52, 3144–3154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vanommeslaeghe K.; Raman E. P.; MacKerell A. D. J. J. Chem. Inf. Model. 2012, 52, 3155–3168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brooks B. R.; Bruccoleri R. E.; Olafson B. D.; States D. J.; Swaminathan S.; Karplus M. J. Comput. Chem. 1983, 4, 187–217. [Google Scholar]
- Volkov A.; Macchi P.; Farrugia L. J.; Gatti C.; Mallinson P.; Richter T.; Koritsánszky T.. XD2006 - A Computer Program for Multipole Refinement, Topological Analysis of Charge Densities and Evaluation of Intermolecular Energies from Experimental or Theoretical Structure Factors; University at Buffalo– The State University of New York, New York, 2006. [Google Scholar]
- Volkov A.; Koritsánszky T. S.; Coppens P. Chem. Phys. Lett. 2004, 391, 170–175. [Google Scholar]
- Buckingham A. D. Adv. Chem. Phys. 1967, 12, 107–142. [Google Scholar]
- Kendall R. A.; Dunning J. T. H.; Harrison R. J. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar]
- Volkov A.; King H. F.; Coppens P. J. Chem. Theory Comput. 2006, 2, 81–89. [DOI] [PubMed] [Google Scholar]
- Dupuis M.; Rys J.; King H. F. J. Chem. Phys. 1976, 65, 111–116. [Google Scholar]
- Rys J.; Dupuis M.; King H. F. J. Comput. Chem. 1983, 4, 154–157. [Google Scholar]
- Murray J. S.; Politzer P. J. Mol. Struct.: THEOCHEM 1998, 425, 107–114. [Google Scholar]
- Murray J. S.; Peralta-Inga Z.; Politzer P. Int. J. Quantum Chem. 2000, 80, 1216–1223. [Google Scholar]
- Guillot B.; Viry L.; Guillot R.; Lecomte C.; Jelsch C. J. Appl. Crystallogr. 2001, 34, 214–223. [Google Scholar]
- Spackman M. A. Chem. Rev. 1992, 92, 1769–1797. [Google Scholar]
- Coppens P.X-ray Charge Densities and Chemical Bonding; Oxford University Press: Oxford, U.K., 1997. [Google Scholar]
- Paton R. S.; Goodman J. M. J. Chem. Inf. Model. 2009, 49, 944–955. [DOI] [PubMed] [Google Scholar]
- Řezáč J.; Riley K. E.; Hobza P. J. Chem. Theory Comput. 2011, 7, 3466–3470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volkov A.; Koritsánszky T.; Coppens P. Chem. Phys. Lett. 2004, 391, 170–175. [Google Scholar]
- Jorgensen W. L. J. Phys. Chem. 1986, 90, 1276–1284. [Google Scholar]
- Jorgensen W. L.; Tirado-Rives J. J. Am. Chem. Soc. 1988, 110, 1657–1666. [DOI] [PubMed] [Google Scholar]
- MacKerell A. D. J.; Karplus M. J. Phys. Chem. 1991, 95, 10559–10560. [Google Scholar]
- Cieplak P.; Dupradeau F. Y.; Duan Y.; Wang J. J. Phys.: Condens. Matter 2009, 21, 333102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopes P. E. M.; Roux B.; MacKerell A. D. Theor. Chem. Acc. 2009, 124, 11–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hübschle C. B.; Luger P. J. Appl. Crystallogr. 2009, 39, 901–904. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.