Abstract
We report the parametrization of the approximate density functional tight binding method, DFTB3, for sulfur and phosphorus. The parametrization is done in a framework consistent with our previous 3OB set established for O, N, C, and H, thus the resulting parameters can be used to describe a broad set of organic and biologically relevant molecules. The 3d orbitals are included in the parametrization, and the electronic parameters are chosen to minimize errors in the atomization energies. The parameters are tested using a fairly diverse set of molecules of biological relevance, focusing on the geometries, reaction energies, proton affinities, and hydrogen bonding interactions of these molecules; vibrational frequencies are also examined, although less systematically. The results of DFTB3/3OB are compared to those from DFT (B3LYP and PBE), ab initio (MP2, G3B3), and several popular semiempirical methods (PM6 and PDDG), as well as predictions of DFTB3 with the older parametrization (the MIO set). In general, DFTB3/3OB is a major improvement over the previous parametrization (DFTB3/MIO), and for the majority cases tested here, it also outperforms PM6 and PDDG, especially for structural properties, vibrational frequencies, hydrogen bonding interactions, and proton affinities. For reaction energies, DFTB3/3OB exhibits major improvement over DFTB3/MIO, due mainly to significant reduction of errors in atomization energies; compared to PM6 and PDDG, DFTB3/3OB also generally performs better, although the magnitude of improvement is more modest. Compared to high-level calculations, DFTB3/3OB is most successful at predicting geometries; larger errors are found in the energies, although the results can be greatly improved by computing single point energies at a high level with DFTB3 geometries. There are several remaining issues with the DFTB3/3OB approach, most notably its difficulty in describing phosphate hydrolysis reactions involving a change in the coordination number of the phosphorus, for which a specific parametrization (3OB/OPhyd) is developed as a temporary solution; this suggests that the current DFTB3 methodology has limited transferability for complex phosphorus chemistry at the level of accuracy required for detailed mechanistic investigations. Therefore, fundamental improvements in the DFTB3 methodology are needed for a reliable method that describes phosphorus chemistry without ad hoc parameters. Nevertheless, DFTB3/3OB is expected to be a competitive QM method in QM/MM calculations for studying phosphorus/sulfur chemistry in condensed phase systems, especially as a low-level method that drives the sampling in a dual-level QM/MM framework.
Introduction
Phosphorus and sulfur are richly featured in chemistry and biology.1 Sulfur is part of amino acids Cys and Met and therefore involved in redox sensing; sulfur is the third most abundant mineral element in the human body. Sulfur is also part of many important biological cofactors such as iron–sulfur clusters, coenzyme A, and several vitamins. As another example, sulfonation states on heparan sulfate chains are known to govern crucial signaling pathways and molecular-recognition event.2 Sulfur is also involved in many chemical and materials applications. For example, sulfonic acids are used in many detergents. Nafion,3 a sulfonated tetrafluoroethylene based fluoropolymer-copolymer, is an important material used for the proton exchange membrane in fuel cells. Sulfur-containing heterocycles are broadly used in the field of organic electronics.4 Phosphorus is essential in biology because it is part of phospholipids, nucleic acids, and many vital small molecules such as various phosphates (e.g., ATP/GTP) as well as bone (hydroxyapatite). The phosphoryl transfer reaction, for example, arguably represents the most important chemical transformation in biology.1,5−7 Perturbations in phosphoryl transfer enzymes are involved in many serious human diseases such as cancer.8,9 Protein kinases and phosphatases are among the most important drug targets;10−15 there are ∼2000 protein kinases and ∼1000 phosphatases in the human genome, and these enzymes are essential to key cellular processes such as the control of cell cycles and division. In the chemical industry, phosphorus compounds are predominantly consumed as fertilizers, while organophosphorus compounds are also used in detergents, pesticides, and nerve agents.
To describe the rich (bio)chemistry that involve phosphorus and sulfur in complex condensed phase environments, computational studies in the framework of QM/MM methods are essential.16 Although ab initio based QM/MM simulations have become increasingly powerful thanks to developments in both computational hardware and theoretical algorithms,17−20 they remain computationally demanding and therefore not ideally suited when multiple reaction mechanisms need to be analyzed. This is particularly the case when sampling is critical, such as in the study of intrinsically flexible systems (e.g., signaling proteins)21,22 or enzymes that feature rather solvent-accessible active sites;23−25 adequate sampling is also important to processes that occur at the solid/liquid interface.26,27 Therefore, despite the tremendous progress in ab initio QM and QM/MM methods, it remains meaningful to explore further development of the semiempirical type of QM methods.28−31
In this context, the Self-Consistent Charge Density Functional Tight-Binding (SCC-DFTB) method proves to be a promising approach.32−34 It is an approximate Density Functional Theory (DFT) and is derived by expanding the DFT total energy functional up to second order around a reference charge density. The resulting perturbative series is further approximated by applying a minimal basis LCAO expansion of the Kohn–Sham orbitals, by using a monopole approximation for the charge density fluctuations in the second order terms and by approximating the zero-th order terms, which resemble the DFT double counting contributions for the reference density, with a sum of atomic pair potentials.32,35
The resulting approximate total energy terms have to be parametrized, and two classes of parameters can be distinguished: (i) the electronic parameters, which determine the atomic minimal basis set and the atomic reference densities as well as the chemical hardness values of the involved atoms—the determination of these parameters is quite straightforward; (ii) the repulsive energy parameters, which are necessary to determine the atomic pair potentials modeling the zero-th order contributions in the density expansion. Although these terms can in principle be computed based on DFT calculations, to achieve good general accuracy and partially compensate for approximations made in the other terms, an empirical fit to larger test sets is necessary, and therefore their determination is usually more involved.
SCC-DFTB has been parametrized for organic molecules containing O, N, C, and H, for which extensive tests have been performed,36−38 as well for molecules containing S,39 Zn,40−42 P,43 and a few other elements.44−48 The resulting parameter set is referred to as the “MIO” set and can be downloaded from the DFTB Web site: www.dftb.org.
To improve the description of hydrogen-bonded complexes and proton affinities, which are important to biological applications, DFTB has been extended to include third-order contributions and a modified second-order Coulomb scaling law,33,49,50 leading to the DFTB3 approach. In its first implementation, the “MIO” parameters, originally derived for the second-order method, were also used for DFTB3.43,50,51 Recently, two of us have reparametrized DFTB3 for O, N, C, and H, resulting in a parameter set called “3OB,”52 emphasizing the application to organic and biologically relevant molecules. The main goal was to improve heats of formation and reaction energies, as well as nonbonded interactions. As benchmark calculations indicated, DFTB3–3OB generally gives results comparable to the most successful semiempirical methods such as the OMx methods.30
In this work, motivated by the importance of P and S in (bio)chemistry, we extend the “3OB” parametrization to these elements. This is a worthwhile effort because our parametrization includes d orbitals, which have been known to be essential to the proper description of chemical species involving P and S, especially hypervalent compounds53 (see, for example, refs (54) and (55)). By contrast, many popular semiempirical methods such as PM356 and PDDG28,57 do not include d orbitals (PM658 does include d orbitals). We test the new parameters for P and S with a large set of biologically relevant molecules, focusing in particular on geometries, reaction energies, proton affinities, and hydrogen-bonding interactions. These results show that the 3OB set represents a notable overall improvement over the “MIO” set39,43 parameters for P/S containing compounds for both structural and energetic properties. For example, the deficiency concerning the S···N interaction as reported in ref (38) is removed. Moreover, due to major improvement in the atomization energies, reaction energies are generally better described with the 3OB parameters than the “MIO” parameters. For the majority S/P-containing compounds tested here, DFTB3/3OB also out-performs PM6 and PDDG, especially for structural properties, vibrational frequencies, hydrogen bonding energies, and proton affinities. Nevertheless, several limitations remain, such as too short hydrogen bonding distances for complexes that involve charged S/P species; problems also remain for the energetics of phosphoryl transfer reactions that involve changes in the coordination number of the phosphorus. Some of these limitations are likely due to the intrinsic deficiencies of the underlying functional (PBE59), while others might be alleviated via continuing development of the DFTB3 framework, such as including three-center terms and multipoles for the charge fluctuation.
Theory
The DFTB3 parametrization of sulfur and phosphorus follows the protocol we outlined previously52,60 and used to parametrize for C, H, N, and O.52 The theory of DFTB3 has been described in detail in ref (51); for a recent review, see ref (61). Here, we only briefly discuss the parameters that enter the DFTB3 total energy:
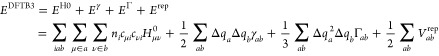 |
1 |
To determine the Hamilton matrix elements Hμv0, the atomic orbital basis functions ημ and the atomic reference densities ρa have to be determined. This is done by solving the Kohn–Sham equations for the atom in an additional harmonic potential with a confining radius rwf for the atomic basis set and a different radius rdens for the density. Since the d orbitals of S and P are unoccupied, we use another value for the confinement radius, denoted by rwfd. The off-diagonal matrix elements Hμv0 are then precomputed and tabulated using an exchange-correlation functional (PBE59), the atomic basis set consisting of Slater functions, and the initial atomic density. The diagonal elements Hμμ are equal to the atomic eigenvalues εx (x = s, p, or d orbital). Here, no confinement of the orbitals is used to ensure the proper dissociation limit. In the case of sulfur and phosphorus, however, we make an exception to this standard procedure and optimize εd as discussed in the following section. The Slater functions are defined by lmax as the highest angular momentum taken into account, nmax; another parameter that determines the size of the basis set; and α0, α1, ..., and α4, the exponents of the Slater functions.
For the second-order term of the energy Eγ, the atomic Hubbard parameters Ua are needed, which are calculated from DFT as the first derivative of the highest occupied orbital with respect to its occupation number. [Ua describes the electron interaction on-site of an atom and enters the γ function, which interpolates between the on-site and the long-range electron interaction of atom pairs. As a consequence of the form of the γ function in the interpolating region, which is well within the covalent and noncovalent bond distances (e.g., hydrogen bonds), the Hubbard parameter determines the size of the atom in an inverse relation. While this was found to be reasonable within one period of the system of elements, it is not for interactions between atoms of different periods. The most significant difference from the inverse relation was found for hydrogen.33 Therefore, the original γ function of DFTB232 is modified for DFTB350,51 (called γh in ref (51)) for all pairs that include at least one hydrogen atom. Essentially one additional parameter (called ζ) was introduced to damp the influence of the Hubbard parameter such that γ is closer to Coulomb behavior at short distances (see also Figure 3 of ref (51)) and therefore accounts for the small covalent radius of hydrogen. While the 3OB parameter set includes elements of the first (H) and second period (CNO), we now extend it to third period elements S and P. Naturally, the question arises as to whether one can improve performance by applying a similar modification to γ. Since the Hubbard parameters for S and P are larger than they should be to fulfill the inverse relation of second period elements, we would have to damp the γ function such that γ approximates the Coulomb behavior at larger distances. We have tested this idea but found insignificant improvement over the standard γ and therefore decided not to introduce additional complexity to our DFTB model. Note that an alternative to the γ function has been suggested that intrinsically contains such effects; however, it has not been applied and tested yet.62] For the third-order term EΓ, the derivative of the Hubbard parameter with respect to charge, Uad has to be determined. For CHNO it is calculated as the second derivative of the highest occupied orbital with respect to its occupation number. For P and S, as discussed below, we find a significant advantage in optimizing it.
The repulsive energy Erep is described as pair potentials. Their parametrization is done by fitting to a selected set of reference atomization energies, molecular geometries, vibrational frequencies, and barrier or reaction energies. A careful benchmark of a resulting fit is the most time-consuming part of the procedure, despite the progress of partially automatized fitting procedures.60,63
Specifically for the description of atomic energies and atomization energies (Eat), a further parameter was introduced, the spin-polarization energy Espin. Because the total energy of an atom is described in a spin-unpolarized manner in standard DFTB, the total energy is overestimated for open-shell atoms. Therefore, the energy difference between a restricted and an unrestricted spin DFT calculation, called Espin, is subtracted to yield the atomic energies at the DFT level. [Note that a spin-polarization corrected DFTB (sDFTB) has been proposed.64 In principle, sDFTB could also be used to calculate atomic energies; however, for calculation of atomization energies, it is not the standard. sDFTB uses parameters calculated for states with partial spin in the vicinity of spin-unpolarized atoms (as the Taylor-series suggests) and therefore is somewhat less accurate for single atoms than Espin. In contrast, for radical molecules, sDFTB is the method of choice.]
Parametrization of Sulfur and Phosphorus
Parameters for General Application
This section summarizes the choices of all parameters discussed in the previous section. We follow the search protocol established in refs (60) and (52) and divide the parameters into two parts, electronic and repulsive parameters.
The electronic parameters are given in Table 1. For the sake of completeness, we also include parameters that are calculated from DFT (U, Espin, εs/p) or are in line with the standard choice of the basis set (nmax, αi, i = 0–4); those parameters are not subject to optimization. We note that although l-dependent Hubbard parameters have been considered65 and being explored by us for improving the description of transition metals (Gaus and Cui, unpublished), the Hubbard parameter is taken to be l-independent for P and S. For all DFT calculated values, the PBE exchange correlation functional59 has been used. The following parameters have been optimized to improve the overall performance:
Table 1. Overview of Electronic Parameters (in Atomic Units if not Unitless)a.
| parameter | S | P |
|---|---|---|
| lmax | 2 | 2 |
| nmax | 2 | 2 |
| α0 | 0.50 | 0.50 |
| α1 | 1.19 | 1.17 |
| α2 | 2.83 | 2.74 |
| α3 | 6.73 | 6.41 |
| α4 | 16.00 | 15.00 |
| rwf | 3.8 | 3.6 |
| rwfd | 4.4 | 4.4 |
| rdens | 9.0 | 9.0 |
| εs | –0.63 000 872 | –0.51 063 909 |
| εp | –0.25 802 653 | –0.20 276 532 |
| εd | 0.32 140 766 | 0.52 019 087 |
| Espin | –0.03 121 074 | –0.06 868 820 |
| U | 0.3288 | 0.2894 |
| Ud | –0.11 | –0.14 |
As described in the text, U, Espin, εs,p, nmax, and αi are in line with the standard choices of DFTB parametrization and not subject to optimizations. By contrast, rwf, rwfd, rdens, εd, and Ud are adjusted based on properties of molecules in the fitting set.
• lmax: While a minimal basis has been used for H (s orbital only) and CNO (2s and 2p orbitals only), for S and P, we include 3s, 3p, and 3d orbitals, the latter being used as polarization functions, which are required to have a higher angular momentum than the valence orbitals. As already found previously for the “MIO” parameters for S and P, d orbitals are necessary to properly describe the diverse chemical environments of these elements.
• rwf: In DFTB, the atomic orbitals used as a basis set are confined using a harmonic confining potential characterized by this parameter. It essentially determines the spatial extension of the basis functions. Therefore, this parameter has influence on bonding properties as well as on noncovalent interactions (Pauli repulsion). For the H2S dimer, for example (also see discussions below), the intermolecular distance is found to be too short with our parametrization; this could be improved by using a larger rwf, but only at the cost of less accurate binding energy and angle of the hydrogen bond. For phosphorus, we have not tested dimer structures due to their rare appearance in biological systems; tests of other molecules indicate only a very subtle influence on the general performance of bond angles, bond lengths, and atomization energies. With a larger rwf, the angles improve, but for bond distances and Eat, slightly larger errors are found. With a smaller rwf, the opposite effects are observed: the description of angles worsens, while bond distances and Eat slightly improve.
• rwfd: Generally, this parameter has only a minor influence on the results. A larger rwfd tends to improve bond distances and worsens bond angles. Note that the quality of computed bond distances is to a large degree dependent on the repulsive potentials; however, for a higher degree of transferability to different chemical environments, it is also helpful to tune rwfd.
• rdens: The density compression has a large impact on the total electronic energy; however, the effect can be compensated by the repulsive potential without introducing substantial errors (as long as rdens is chosen within a reasonable range, e.g., rdens > 3.0 a0). Therefore, rdens is chosen such that the repulsive potentials smoothly interpolate to their cutoffs. Note that for hydrogen a very small density compression was chosen,52 causing the H–S and H–P potentials to be negative in the binding region while other potentials like O–S, O–P, N–S, and N–P are still significantly repulsive. Thus, the choice of rdens for S and P is a tradeoff between too negative and too repulsive potentials.
• εd: While all eigenvalues are usually calculated from atomic DFT calculations, an exception is made for the eigenvalues of the d orbitals since they are unoccupied in the ground state for atoms S and P, and therefore a change of εd does not affect the atomic total energy. Optimizing εd allows control of the d-orbital involvement in molecular bonding situations. This becomes particularly important for balancing energetics and geometries for the different oxides of S and P species. Generally, the calculated values of 0.02140766 au for S and 0.02019087 for P are too low; i.e., d orbitals are heavily involved in all types of bonding situations. Higher values reduce the excessive d-orbital participation. Empirically, we found that for C–S and C–P bonds a larger amount of d-orbital involvement decreased errors, while a rather small amount of d orbitals seemed more appropriate for O–S and O–P bonding situations.
• Ud: The Hubbard derivative appears in the third-order term EΓ (eq 1) and is usually calculated from DFT. In the case of S and P, the values are −0.0695 and −0.0701 au, respectively. For the mean absolute deviation (MAD) of eight proton affinities (PAs) for S containing species, however, we find a drop from 7.6 to 2.4 kcal/mol after optimizing Ud for sulfur. Similarly for P species, the MAD for 17 PAs is reduced from 9.1 to only 2.9 kcal/mol by optimizing Ud for P. The change of the Hubbard derivative only marginally affects other properties for systems with small charge fluctuations; however, for the highly oxidized phosphorus species, larger impacts are observed. Atomization energies become somewhat less accurate. P–P bond lengths are overestimated, and the P–O–P angle in diphosphoric acid is overestimated to be 141° instead of 116° for B3LYP/cc-pVTZ and 121° for DFTB3 using the calculated Hubbard derivative. Due to the importance of accurate PAs for many biochemistry applications, we choose to use the fitted Ud and list the values in Table 1.
Note that the spin-polarization constants that enter the sDFTB formalism have also been calculated and included in the Supporting Information.
For the repulsive potentials, first a fit for sulfur is carried out (including all electronic parameters), and subsequently phosphorus related parameters are optimized. Table 2 provides an overview of all reference systems and values that lead to the repulsive potentials related to S and P. For the solution of the linear equation system set up to determine the repulsive potentials, division points have to be selected. Further, additional equations can be chosen to better represent second derivatives. These parameters are specified in Table 2. The geometries are taken from the B3LYP/cc-pVTZ level of theory with the exception of [CH3–COO–PO3]2–, for which we use B3LYP/aug-cc-pVTZ. Atomization energies (Eat) are calculated from G3B3,66−68 barrier geometries and energetics (Ebar) from MP2/G3large. Additional equations for the fitting process (see ref (52)) are prepared using a few selected vibrational frequencies shown below as determined from BLYP/cc-pVTZ (unscaled) using the harmonic approximation. All reference structures can be found in the Supporting Information.
Table 2. Parameters Defining the Repulsive Potentialsa.
| molecules (weeq, wfeq if different than 1.0) and Eat (kcal/mol) | |||||
|---|---|---|---|---|---|
| SH2 (10.0, 1.0) | 181.9 | (CH3)3C–SH (0.0, 1.0) | HP=CH2 | 390.3 | |
| N2S | 248.2 | P2 | 116.6 | H3PO4 | 760.0 |
| H2SO4 | 592.5 | PH3 (2.0, 1.0) | 140.2 | P4O6 (0.1, 1.0) | 1056.2 |
| S2 | 84.7 | H2P–PH2 | 366.3 | P4O10 (0.1, 1.0) | 1595.9 |
| CH2S | 325.5 | N≡P (0.1, 0.1) | 147.8 | CH3S–P(=O)(OH)2 (0.0, 0.1) | |
| CH3SH | 472.5 | P(NH2)3 (0.1, 0.1) | 788.4 | H3PS4 (0.05, 0.05) | 527.2 |
| CH3S–SCH3 | 828.4 | CH3PH2 | 536.4 | [CH3COO–PO3]2– (0.0, 1.0) | |
| proton transfer reactions | rXX (Å) | Ebar (kcal/mol) |
|---|---|---|
| [H2S–H–SH2]+ | 3.4, 3.5, 3.6, 3.7 | 0.6, 1.9, 3.7, 6.1 |
| [HS–H–SH]− | 3.5, 3.6, 3.7, 3.8 | 2.5, 4.6, 7.2, 10.2 |
| potential | division points (a.u.) | additional equations (a.u.) |
|---|---|---|
| C–S | 2.8, 3.4, 4.0, 4.8 | V″(3.044) = 0.49 |
| H–S | 2.4, 2.9, 3.9, 4.3, 4.5 | V″(2.542) = 0.27 |
| N–S | 2.8, 3.2, 4.3, 5.5 | V″(3.007) = 0.55 |
| O–S | 2.6, 3.5, 4.7, 6.0, 6.2 | V″(3.986) = 0.00, V″(5.858) = 0.05 |
| S–S | 3.5, 4.2, 4.8, 5.4, 5.8 | V″(3.942) = 0.13 |
| C–P | 2.6, 3.0, 3.4, 3.8, 4.2, 4.6, 5.0 | V″(3.532) = 0.14, V‴(2.999) = −0.50 |
| H–P | 2.2, 2.4, 2.6, 3.2, 3.4, 3.6, 3.8, 4.0 | V″(2.685) = 0.20, V‴(2.685) = −0.64 |
| N–P | 2.7, 3.5, 4.0, 4.5, 5.0 | V″(2.812) = 0.84 |
| O–P | 2.6, 3.2, 4.6, 5.0, 5.4 | V″(2.782) = 0.77, V″(3.024) = 0.40 |
| P–P | 3.4, 4.0, 4.8, 5.0, 5.2 | V″(3.581) = 0.40 |
| P–S | 3.4, 3.8, 4.6, 5.6, 6.2, 6.7 | V″(3.659) = 0.27, V″(4.033) = 0.1 |
weeq and wfeq are the weighting factors for energy and force equations in 1/a.u. Reaction equations and additional equations are weighted with 1/a.u., for details see ref (52). rXX is the heavy atom distance.
Special Parametrization for Phosphate Hydrolysis Reactions
With the general parameter set outlined above, considerable errors are observed for phosphate hydrolysis reactions. The details are discussed in the benchmark sections. The bottom line is that the current DFTB3/3OB model still cannot properly describe the energetics of reactions where the phosphorus coordination changes from four to five/three oxygen atoms. This suggests that the current DFTB3 methodology has limited transferability for complex phosphorus chemistry with the required accuracy in energetics for mechanistic studies. As a temporary solution, we suggest a specific reaction parametrization69 of the O–P repulsive potential referred to as “OPhyd.” The need of this specific fit suggests that additional improvements in the DFTB3 methodology, such as the inclusion of three-center terms and better electrostatic models (e.g., multipoles for charge fluctuations62,70), are still needed and will be systematically analyzed in the future.
For “OPhyd,” we carry out the same fit for phosphorus as above with the inclusion of two reaction energies (the weight is 10/(kcal/mol)). The first one is a reaction of water with a dimethyl hydrogen phosphate, leading to a penta-coordinated intermediate (the geometries can be found in the Supporting Information, n_com1 → n_int1); the second reaction is the dissociation of methanol from the previous intermediate (n_int1 → n_com2). As reference energies, MP2/G3large values are calculated at B3LYP/6-31+G(d,p) geometries. This fit shifts the O–P repulsive potential by about −10 kcal/mol; i.e., overbinding for O–P bonds is introduced.
Benchmarks and Discussion
In this section, we discuss benchmark results for our 3OB parametrization for S and P in combination with the 3OB parameters52 for O, N, C, and H. [Note that in connection with 3OB as well as “MIO”, the hydrogen molecule is evaluated using the respective H–H-mod potential.71] Comparisons are made to MP2, DFT, popular semiempirical methods (PDDG28,57 and PM658), and the previous DFTB3/MIO parametrization (using the parameters as defined in ref (51): Ud = −0.23, −0.16, −0.13, −0.19, −0.14, −0.09 au for C, H, N, O, P, and S and ζ = 4.2). For PM6, it is worth noting that the choice of heat of formation for H2 and protons is essential to the computed hydrogenation reaction energies and proton affinities, respectively; we take the value of 0.0 and −54.0 kcal/mol for H2 and protons, respectively, as recommended by the MOPAC program (http://openmopac.net/manual/pm6_accuracy.html). We have not carried out any comparison to OMx methods despite their impressive performance for typical organic molecules30 because we are not aware of any systematic parametrization of OMx for P and S. Unless noted otherwise, energetics are given for geometries that are optimized at the respective level of theory. To compare directly the potential energy surfaces at different levels of theory, zero-point energies (ZPEs) are not included; the exception is for heat of formation calculations, in which vibrational contributions are included. As shown in the Supporting Information, the ZPEs calculated with DFTB3/3OB agree very well (within 1 kcal/mol) with higher-level calculations. For the calculation of noncovalent interactions, although we recognize the importance of including dispersion interactions in general, they are not included for most test cases here because these cases include small molecules and are dominated by hydrogen-bonding interactions (see Supporting Information, for explicit results); we explore explicitly the effect of dispersion to address a recently discussed caveat of DFTB in describing noncovalent interactions that involve sulfur.72 All DFTB calculations are carried out using our in-house DFTB code; for G3B3, MP2, B3LYP, BLYP, PBE, PM6, and PDDG/PM3, the Gaussian 03 and 09 software packages73,74 are used.
Sulfur
Atomization Energies and Geometries
The first test set consists of atomization energies and geometrical properties of 38 small neutral closed-shell molecules including sulfides, oxides, acids, thoils, sulfite, sulfate, sulfones, sulfoxides, etc. Table 3 summarizes the results; further details are included in the Supporting Information.
Table 3. Mean and Maximum Absolute Deviations from G3B3 Atomization Energies and Heats of Formations and B3LYP/cc-pVTZ Geometric Properties for Our Sulfur Test Set.
| propertya | Nb | MP2c | B3LYPd | PBEd | PM6 | PDDG | MIO | 3OB |
|---|---|---|---|---|---|---|---|---|
| Eat (kcal/mol) | 38 | 8.3 | 16.8 | 20.8 | 68.7 | 4.7 | ||
| Emaxat (kcal/mol) | 20.5 | 56.0 | 100.7 | 221.7 | 34.4 | |||
| ΔHf0 (kcal/mol) | 38 | 9.6e | 18.4 | 21.4 | 5.4 | 5.7 | 68.1 | 4.8 |
| ΔHf,max0 (kcal/mol) | 24.1e | 57.6 | 100.0 | 24.0 (1.5/12.5)f | 18.9 (3.8/15.7)f | 218.6 (1.1/12.0)f | 34.0 (0.4/1.8)f | |
| r (Å) | 124 | 0.008 | 0.007 | 0.014 | 0.015 | 0.027 | 0.014 | 0.008 |
| rmax (Å) | 0.037 | 0.019 | 0.041 | 0.079 | 0.121 | 0.224 | 0.042 | |
| a (deg) | 103 | 0.5 | 0.3 | 0.5 | 2.5 | 2.7 | 1.8 | 1.2 |
| amax (deg) | 3.7 | 1.6 | 3.2 | 31.6 | 14.8 | 11.4 | 9.6 | |
| d (deg) | 12 | 1.2 | 1.9 | 3.3 | 8.7 | 11.5 | 12.0 | 4.0 |
| dmax (deg) | 2.9 | 17.4 | 27.0 | 72.6 | 53.6 | 86.2 | 10.8 |
Bond lengths r, bond angles a, and dihedral angles d are compared to B3LYP/cc-pVTZ calculations; max stands for maximum absolute deviation.
Number of comparisons.
Basis set is cc-pVTZ.
Basis set is 6-31G(d).
Diphenylsulfoxide, -sulfone, and -sulfide have been excluded due to excessive computation time.
Single point G3B3 ΔHf0 computed at the structures optimized by semiempirical methods; the value before/after the slash is the mean/maximum absolute deviation from G3B3, which uses B3LYP/6-31G(d) structures.
DFTB3/3OB shows a very small MAD for atomization energies and clearly improves over DFTB3/MIO (4.7 vs 68.7 kcal/mol). [MIO reveals a strong overbinding that leads to large errors. Note that the overbindings of different bond pairs are balanced such that they cancel out for reaction energies.52 For S, however, additional drawbacks have been found especially for the S–O bond.38 We further discuss the consequences of the unbalanced overbinding within MIO for reaction energies below.] The largest deviations are found for SO3 and thiocyanates. For DFTB3, we have also carried out calculations for heats of formation following the standard approximations for the heat capacity corrections75 and using unscaled vibrational frequencies calculated with DFTB3. Encouragingly, DFTB3/3OB yields a small MAD of only 4.8 kcal/mol; it is 68.1 kcal/mol for DFTB3/MIO.
The poor performance of MP2 and DFT for atomization energies is in line with large errors for heats of formation as has been reported previously, e.g., in ref (76). A fit of atomic contributions reported in the same reference significantly reduces this error but has not been carried out in this study. PM6 and PDDG/PM3 are parametrized for directly yielding heats of formation and implicitly include corrections for heat capacity contributions. Therefore, the calculation of atomization energies with these methods is not straightforward. However, heats of formation have been reported to be in very good agreement with experiments for large test sets including very challenging cases such as cations, anions, and transition structures leading to a MAD of 6.5 and 6.4 kcal/mol for PM677 and PDDG,57 respectively. Note that those numbers were based on different test sets. Nevertheless, for our test set, we find similar results; the MADs of 5.4 and 5.7 kcal/mol (see Table 3) indicate very similar performances of PM6 and PDDG. This is quite remarkable as PDDG does not use d orbitals on sulfur atoms while PM6 does.
With a few exceptions, geometries are described very well for all semiempirical methods and particularly well for DFTB3/3OB; e.g., the MADs in bond distances are 0.008, 0.014, 0.027, and 0.015 Å respectively for DFTB3/3OB, DFTB3/MIO, PDDG, and PM6. The largest bond distance error for PDDG is found for the singlet state of C=S with a difference of 0.12 Å relative to B3LYP/cc-PVTZ. Other deviations are substantially smaller. DFTB3/MIO overestimates the N=S bond within N2S significantly by 0.22 Å. For the dihedral angle OSOH of sulfonic acid, large deviations to B3LYP/cc-pVTZ are found for almost all methods compared. Interestingly, this is not the case for ab initio methods using a triple-ζ basis; MP2 and B3LYP with the cc-pVTZ basis set deviate only about 2°. More statistics including mean absolute deviations for different bond types are given in the Supporting Information.
To demonstrate the superb performance of the semiempirical methods for structural properties, we have carried out single point heat of formation calculations with G3B3 at geometries of the respective level. The MADs of PM6, PDDG, DFTB3/MIO, and DFTB3/3OB are as low as 1.5, 3.8, 1.1, and 0.4 kcal/mol; the MAX values are 12.5, 15.7, 12.0, and 1.8 kcal/mol. These results again highlight the quality of DFTB3/3OB structures.
Vibrational Frequencies
The benchmark for vibrational frequencies is a cumbersome task since comparisons require matching the character of vibrational modes, which is not straightforward especially when comparing to experimental data for fairly large molecules. A rigorous comparison is out of the scope of this work. In Table 4, a few unscaled harmonic vibrational frequencies as calculated from semiempirical methods are compared to those from DFT calculations. For cases where an obvious assignment of the mode to experimental ones is possible, we have also listed the experimental values. Note that selected stretching frequencies are also used to determine the additional equations during the fitting (mainly for repulsive potentials), although the contributions from vibrational frequencies are rather limited.
Table 4. Selected Vibrational Frequencies in cm–1.
| molecule (point group) | irrep | description | exp | BLYPa | B3LYPa | PM6 | PDDG | MIO | 3OB |
|---|---|---|---|---|---|---|---|---|---|
| H2S (C2v) | A1 | bending | 1183 | 1176 | 1208 | 1055 | 1090 | 1042 | 1043 |
| A1 | stretch-sym | 2615 | 2601 | 2684 | 2689 | 1542 | 2728 | 2611 | |
| B2 | stretch-asy | 2626 | 2615 | 2698 | 2698 | 1588 | 2778 | 2665 | |
| S21 (D∞h) | Σg | S–S-stretch | 657 | 706 | 718 | 712 | 704 | 707 | |
| HSSH (C2) | A | S–S-stretch | 515 | 464 | 498 | 542 | 388 | 409 | 530 |
| dimethyldisulfide (C2) | A | S–S-stretch | 509 | 459 | 492 | 525 | 362 | 469 | 495 |
| thioformaldehyde (C2v) | A1 | C=S-stretch | 1059 | 1040 | 1087 | 1069 | 1076 | 1128 | 1052 |
| methanethiol (Cs) | A′ | C–S-stretch | 708 | 654 | 696 | 749 | 755 | 735 | 767 |
| A′ | H–S-stretch | 2597 | 2588 | 2674 | 2706 | 1556 | 2676 | 2595 | |
| dimethylsulfide (C2v) | A1 | CSC-bend | 282 | 250 | 258 | 257 | 256 | 255 | 255 |
| A1 | C–S-stretch-sym | 695 | 640 | 680 | 742 | 741 | 705 | 735 | |
| B2 | C–S-stretch-asy | 743 | 688 | 733 | 776 | 754 | 734 | 774 | |
| thiophene (C2v) | A1 | ring-sym | 608 | 594 | 615 | 559 | 628 | 609 | 621 |
| B2 | ring-asy | 751 | 716 | 751 | 678 | 692 | 783 | 776 | |
| A1 | ring-sym | 872 | 803 | 838 | 773 | 798 | 851 | 845 | |
| B2 | ring-asy | 903 | 850 | 879 | 853 | 907 | 912 | 903 | |
| 2,5-dihydrothiophene (C2v) | A1 | ring-sym | 506 | 491 | 512 | 470 | 524 | 499 | 520 |
| B2 | ring-asy | 665 | 592 | 632 | 628 | 639 | 642 | 675 | |
| A1 | ring-sym | 716 | 666 | 706 | 753 | 747 | 724 | 750 | |
| B2 | ring-asy | 824 | 797 | 826 | 806 | 848 | 851 | 860 | |
| tetrahydrothiophene (C2) | A | ring-sym | 472 | 457 | 475 | 442 | 495 | 472 | 485 |
| B | ring-asy | 684 | 631 | 669 | 724 | 729 | 691 | 723 | |
| A | ring-sym | 678 | 639 | 677 | 743 | 739 | 703 | 727 | |
| H2SO4 (C2) | A | S–O-stretch-sym | 831 | 706 | 794 | 773 | 723 | 700 | 805 |
| B | S–O-stretch-asy | 882 | 766 | 851 | 775 | 860 | 735 | 809 | |
| A | S=O-stretch-sym | 1136 | 1118 | 1196 | 1036 | 874 | 1166 | 1165 | |
| B | S=O-stretch-asy | 1452 | 1372 | 1445 | 1250 | 902 | 1397 | 1389 | |
| dimethyl sulfoxide (C2) | A′ | CSO-bend-sym | 264 | 278 | 269 | 359 | 266 | 262 | |
| A″ | CSO-bend-asy | 294 | 313 | 296 | 355 | 324 | 313 | ||
| A′ | S=O-stretch | 1102 | 1047 | 1097 | 1054 | 794 | 1162 | 1122 | |
| dimethylsulfone (C2v) | A1 | S=O-stretch-sym | 1121 | 1081 | 1145 | 1059 | 735 | 1131 | 1110 |
| B1 | S=O-stretch-asy | 1258 | 1258 | 1330 | 1170 | 816 | 1331 | 1312 | |
| MAD (δν/νexp%) | 5.6 | 2.6 | 6.6 | 15.1 | 5.1 | 3.8 | |||
| MAX (δν/νexp%) | 15.0 | 8.5 | 13.9 | 41.0 | 20.6 | 11.8 |
Basis set is cc-pVTZ.
Table 4 shows that the DFT methods are generally in good agreement with experiments, although BLYP tends to slightly underestimate the experimental values. DFTB3 with both parameter sets MIO and 3OB also performs quite well, and the deviations from experiments are similar to the ones for the DFT methods. For larger test sets, we expect a more consistent performance of BLYP and B3LYP than DFTB3.78,79 As to other semiempirical methods, PM6 reveals very satisfying results, with only S–O stretch frequencies consistently underestimated. By contrast, PDDG shows large errors of several hundreds of wavenumbers, specifically for S–H and S–O stretch frequencies (in H2S, H2SO4, and dimethylsulfone).
Reaction Energies
We mentioned earlier the overbinding tendency of DFTB3 with the MIO parameters.52 We have shown recently that for a set of reactions (with small stoichiometric coefficients) that include CHNO containing species, the overbinding of different bonds cancels out and leads to relatively small errors for reaction energies with exception of some species (e.g., N–O bond).52 During the MIO parametrization of sulfur, however, the parameters could not be adjusted in such a way that the overbinding approximately canceled out even for simple reactions. Table 5 shows the large deviations for DFTB3/MIO for a small set of selected reaction energies.
Table 5. Deviation for Reaction Energies of Neutral Closed Shell Sulfur Containing Molecules Compared to G3B3a.
| reaction | G3B3 | B3LYPb | PBEc | PM6d | PDDGd | MIO | 3OB |
|---|---|---|---|---|---|---|---|
| S2 + 2 H2 → 2 H2S | –59.3 | –3.6 | –0.1 | +4.9 | +11.1 | +33.0 | +1.5 |
| HSSH + H2 → 2 H2S | –15.6 | –0.2 | +2.5 | +10.5 | +7.9 | +19.7 | –3.7 |
| CH3SH + H2 → H2S + CH4 | –19.2 | –1.9 | +2.1 | +8.6 | +9.3 | +7.4 | +2.4 |
| CH3SH + H2O → H2S + CH3OH | 10.5 | –2.8 | –5.1 | –2.9 | –0.3 | +11.5 | +1.0 |
| CH3SH + NH3 → H2S + CH3NH2 | 7.0 | –1.1 | –1.8 | –4.6 | +3.4 | +8.7 | +2.2 |
| H2C=S + H2 → CH3SH | –37.1 | –1.8 | –2.3 | –3.9 | +3.7 | –0.1 | –3.7 |
| H2C=S + H2O → H2S + H2C=O | 1.2 | –5.5 | –10.1 | –6.9 | –5.6 | +14.8 | –8.0 |
| H2C=S + NH3 → H2S + H2C=NH | 2.0 | –3.2 | –3.0 | –11.1 | –1.2 | +11.1 | –3.1 |
| H2C=S + 2 H2 → H2S + CH4 | –56.4 | –3.5 | –0.1 | +4.8 | +13.2 | +7.4 | –1.2 |
| H2SO4 + 4 H2 → H2S + 4 H2O | –77.6 | –10.3 | +19.5 | +26.7 | +44.3 | +49.2 | –3.3 |
| O=S(OH)2 + 3 H2 → H2S + 3 H2O | –65.1 | –0.4 | +22.3 | +27.2 | +41.8 | +38.0 | –10.2 |
| HS(=O)2OH + 3 H2 → H2S + 3 H2O | –71.9 | –9.7 | +12.8 | +34.0 | +36.7 | +45.3 | –5.0 |
| SO2 + 3 H2 → H2S + 2 H2O | –60.6 | –5.8 | +14.2 | +13.3 | +11.9 | +35.4 | +0.6 |
| 2 SO2 → S21 + 2 O21 | 243.7 | –11.9 | –22.0 | +16.4 | –49.5 | +50.7 | –22.3 |
| 2 SO1 + O21 → 2 SO2 | –213.0 | +6.4 | +5.0 | +11.4 | +75.9 | –24.2 | +31.3 |
| 2 SO2 + O21 → 2 SO3 | –74.8 | +6.2 | +12.8 | –28.0 | +15.5 | –74.3 | –52.6 |
| SO3 + H2O → H2SO4 | –22.0 | +2.3 | +1.0 | +2.0 | –24.5 | +20.1 | +35.7 |
| SO2 + H2O → O=S(OH)2 | 4.5 | –5.5 | –8.1 | –13.9 | –29.8 | –2.6 | +10.8 |
| 2 O=S(OH)2 + O21 → 2 H2SO4 | –127.8 | +21.7 | +30.9 | +3.7 | +26.1 | –28.8 | –2.8 |
| O=S(OH)2 → HS(=O)2OH | 6.8 | +9.3 | +9.5 | –6.8 | +5.1 | –7.3 | –5.2 |
| MAD | 5.6 | 9.3 | 12.1 | 20.8 | 24.5 | 10.3 | |
| MAX | 21.7 | 30.9 | 34.0 | 75.9 | 74.3 | 52.6 |
Energies are calculated at 0 K excluding zero point energy and thermal corrections. All numbers are given in kcal/mol.
Basis set is cc-pVTZ.
Basis set is 6-31G(d).
Heats of formation for H2 are calculated as −26 and −22 kcal/mol for PM6 and PDDG. To correct for this exceptional error, this value is set to 0.0 kcal/mol. See main text.
By contrast, 3OB is parametrized to give reliable atomization energies (see discussions above). For reactions with small stoichiometric coefficients, it is expected that small errors in atomization energies lead to small errors for reaction energies as well. This is generally observed in Table 5. Together with an analysis of the atomization energies, there are a few species that show large errors and spoil the performance for the respective reactions; those are molecules SO (singlet), SO3, and O2 (singlet) with large atomization energy errors of +11.8, +34.4, and +11.9 kcal/mol, respectively. Reactions that do not include these outliers are in very good agreement with G3B3 and therefore demonstrate the strength of the 3OB parametrization protocol. By comparison, PDDG and PM6 are featured with larger MADs; PDDG has a MAD of 20.8 kcal/mol. In fact, even DFT calculations, especially PBE, may have large errors; the MAD for B3LYP/cc-PVTZ and PBE/6-31G(d) is 5.6 and 9.3 kcal/mol, respectively. [Because the reactions have been chosen somewhat arbitrarily, the overall MAD given in Table 4 has to be considered with care. As pointed out by Fishtik,80 one can in principle compile a set of chemical reactions that yield arbitrarily high or low overall errors for any kind of method by linearly combining the reactions. One can, however, transform the problem and assign species errors that are independent of a particular choice of linearlly independent reactions.80 Of course, for a meaningful analysis, one would still have to compile a set of reactions that include a representative set of species. Therefore, the test presented here serves as an illustration of the overbinding problematic for DFTB3/MIO only.]
Proton Affinities
One goal of the further development of DFTB2 toward DFTB3 was to improve the description of proton affinities, which are critical to the proper description of many biochemical reactions.16,34,81−83 This property is evaluated for sulfur-containing species in Table 6.
Table 6. Proton Affinities for Sulfur Containing Species in kcal/mol: Deviations in Comparison to G3B3a.
| system | G3B3 | B3LYPb | PBEc | PM6d | PDDG | MIO/calc | MIO | 3OB/calc | 3OB | G3B3//3OB |
|---|---|---|---|---|---|---|---|---|---|---|
| H3S+ | 174.1 | +0.3 | –0.3 | –13.7 | +8.6 | –5.4 | –7.5 | +1.2 | +0.8 | –1.5 |
| H2S | 355.7 | –1.1 | –3.6 | –16.4 | –12.1 | +0.4 | –2.1 | +6.9 | +0.5 | –0.6 |
| SH– | 498.4 | –1.1 | –4.8 | –3.3 | +12.2 | +18.1 | +15.2 | +24.6 | –2.8 | +0.1 |
| CH3SH2+ | 190.4 | +0.7 | –1.1 | +8.9 | –6.3 | –7.5 | –10.0 | –1.4 | –1.7 | –1.0 |
| CH3SH | 362.5 | –0.7 | –3.4 | –18.5 | –21.8 | –2.4 | –5.2 | +4.7 | +0.7 | –0.3 |
| H2SO4 | 317.6 | +0.7 | –2.0 | –4.1 | +6.1 | +19.9 | +15.8 | +7.8 | +5.1 | –1.0 |
| HSO4– | 454.3 | –0.1 | –2.8 | –9.3 | –2.9 | +24.3 | +17.2 | +6.3 | +2.2 | –0.1 |
| O=S(OH)2 | 330.3 | +2.0 | –1.9 | +3.8 | +7.3 | +17.5 | +13.7 | +18.4 | +17.5 | +3.7 |
| O=S(OH)O– | 471.5 | +0.6 | –2.1 | +7.4 | +7.3 | +35.5 | +29.1 | +28.9 | +27.7 | +2.6 |
| HS(=O)2OH | 318.2 | +2.4 | +0.9 | +11.2 | +16.8 | +19.7 | +15.7 | +7.7 | +5.5 | +1.2 |
| H3CS(=O)2OH | 323.5 | +2.9 | +1.4 | +6.1 | +8.3 | +14.1 | +10.0 | +4.0 | +2.0 | +0.8 |
| [H3CS(=O)(OH)2]+ | 186.3 | +4.0 | +2.3 | +13.0 | +14.3 | +5.2 | +2.1 | +4.7 | +3.2 | –2.0 |
| MAD | 1.4 | 2.2 | 9.6 | 10.3 | 14.2 | 11.0 | 9.7 | 5.8 | 1.2 | |
| MAX | 4.0 | 4.8 | 18.5 | 21.8 | 35.5 | 28.9 | 28.9 | 27.7 | 3.7 |
The molecules are given in the protonated form. The proton affinity is computed with the potential energies at 0 K without any zero-point energy correction (exception are PM6 and PDDG which calculate reaction enthalpies at 298 K). For the DFTB method, the deviation is given as the difference from the G3B3 method (Emethod – EG3B3).
Basis set is aug-cc-pVTZ.
Basis set is 6-31+G(d,p).
The energy of the proton in PM6 is in error by −54 kcal/mol, which has been accounted for by adding this number to the original result. See discussion at http://openmopac.net/manual/pm6_accuracy.html.
A difference between the 3OB and MIO parameters for CHNO is the use of calculated (3OB) and fitted (MIO) Hubbard derivative parameters. With the calculated Hubbard derivative for sulfur, the DFTB3/3OB proton affinities errors are quite large with a MAD of 9.7 kcal/mol (3OB/calc in Table 6). Therefore, we optimize Ud for sulfur and observe a significant reduction of errors for many species (the final 3OB-set). The overall MAD remains somewhat large (5.8 kcal/mol) due mainly to the significant errors for sulfurous acid and its anions; for the geometry of the anion [O2S–OH]−, the S–OH bond length is overestimated by about 0.14 Å in comparison to B3LYP/aug-cc-pVTZ. In general, nevertheless, the improvement of DFTB3/3OB over PM6 and PDDG is notable. It is also worth noting that a fit of Ud(S) for DFTB3/MIO does not substantially improve over the use of the calculated Ud(S) (MIO/calc), with a large MAD of 11.0 kcal/mol. Thus, the transferability of parameters has improved with the new 3OB parameter set. The comparison to PBE/6-31+G(d,p) shows that this set of proton affinities is well described by a standard density functional using a medium sized basis set; note that diffuse functions in the basis set are important for properly describing the anionic species. Finally, we note that G3B3 single points at DFTB3/3OB optimized structures lead to small errors in the proton affinities (a MAD of merely 1.2 kcal/mol) compared to the original G3B3, again highlighting the good quality of DFTB3/3OB structures.
Hydrogen Bonding Energies
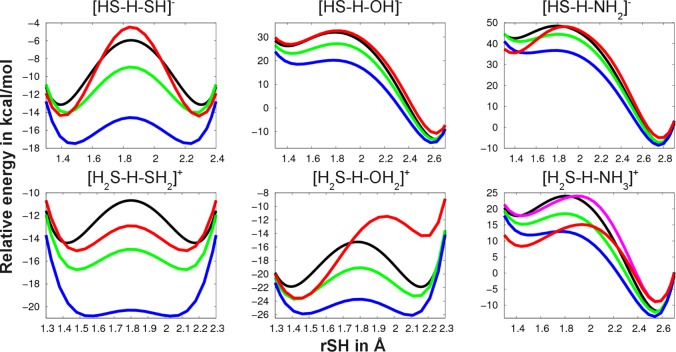
Hydrogen bonding energies are generally well described by DFTB3 as shown in Table 7 for neutral, protonated, and deprotonated dimers, except for two cases (see below); by comparison, PM6 and PDDG give less satisfactory results and sometimes very large errors. However, somewhat surprisingly, considerable errors are found for geometries with all semiempirical methods, including DFTB3 (Table 8). Besides the tremendous underestimation of the heavy atom distance, angles are also different than the counterpoise corrected MP2/G3large (MP2-CP) reference as shown for the most problematic cases in Figure 1. Note for example the different positions of the shared hydrogen between the monomers for DFTB3 and MP2-CP within [HS–H–SH]− and [H2S–H–SH2]+. This leads to the largest hydrogen bonding energy errors within the test set. Another obvious deficiency is that the shared hydrogen of [H2O–H–SH2]+ is covalently bound to sulfur rather than to oxygen. We will discuss this issue below in connection with the proton transfer barriers.
Table 7. Hydrogen Bonding Energies in kcal/mol: Deviations in Comparison to G3B3.
| G3B3 | MP2-CPa | MP2a | B3LYPb | PBEb | PM6 | PDDG | MIO | 3OB | |
|---|---|---|---|---|---|---|---|---|---|
| 2 H2S → (H2S)2 | –1.7 | +0.1 | –0.1 | +0.3 | –0.7 | 0.4 | 0.2 | –0.2 | +0.1 |
| SH– + H2S → HS-H–SH– | –11.7 | –1.3 | –2.3 | –3.1 | –8.4 | –6.3 | –18.6 | –9.9 | –11.1 |
| H3S+ + H2S → [H2S–H–SH2]+ | –13.6 | –0.4 | –1.5 | –4.3 | –9.4 | 4.0 | –8.1 | –7.5 | –9.3 |
| H2O + H2S → HS-H–OH2 | –2.4 | –0.1 | –0.6 | –0.9 | –1.8 | –3.1 | 0.5 | –1.6 | –0.9 |
| H2O + H2S → HO-H–SH2 | –3.0 | +0.4 | –0.1 | +0.0 | –0.9 | 0.1 | +1.0 | +1.2 | |
| H2O + SH– → HO-H–SH– | –14.8 | +0.5 | –0.3 | –0.6 | –2.4 | 0.0 | 1.6 | +0.2 | +0.3 |
| H3O+ + H2S → [H2O–H–SH2]+ | –23.5 | +0.4 | –0.8 | –2.9 | –6.7 | –12.0 | –25.4 | +4.1 | –2.0 |
| NH3 + H2S → HS-H–NH3 | –3.1 | –0.1 | –0.7 | –1.4 | –3.0 | –0.7 | 2.5 | –2.1 | –0.2 |
| NH3 + SH– → H2N–H–SH– | –8.2 | +0.3 | –0.2 | +0.1 | –1.4 | –3.2 | –2.2 | +1.6 | +1.0 |
| NH4+ + H2S → [H3N–H–SH2]+ | –12.8 | +0.2 | –0.4 | –0.8 | –2.8 | 2.4 | 2.9 | +0.7 | +1.3 |
| MAD | 0.4 | 0.7 | 1.4 | 3.7 | 3.6 | 6.2 | 2.9 | 2.7 | |
| MAX | 1.3 | 2.3 | 4.3 | 9.4 | 12.0 | 25.4 | 9.9 | 11.1 |
Basis set is G3large.
Basis set is 6-31+G(d,p), without counterpoise correction.
Table 8. Heavy Atom Distances in Å for Small Sulfur Containing Dimers: Deviations in Comparison to MP2-CP/G3large.
| dimer | MP2-CPa | MP2a | B3LYPb | B3LYPc | PBEc | PM6 | PDDG | MIO | 3OB |
|---|---|---|---|---|---|---|---|---|---|
| (H2S)2 | 4.180 | –0.066 | +0.007 | –0.004 | –0.163 | –0.098 | –0.275 | –0.372 | –0.329 |
| HS-H–SH– | 3.484 | –0.056 | –0.114 | –0.050 | –0.131 | –0.255 | –0.289 | –0.301 | –0.330 |
| [H2S–H–SH2]+ | 3.450 | –0.044 | –0.076 | –0.084 | –0.078 | –0.234 | –0.297 | –0.205 | –0.243 |
| HS-H–OH2 | 3.595 | –0.069 | –0.176 | –0.103 | –0.172 | –0.866 | –0.224 | –0.394 | –0.280 |
| HO-H–SH2 | 3.533 | –0.054 | +0.028 | –0.036 | –0.120 | –0.043 | –0.318 | –0.085 | |
| HO-H–SH– | 3.245 | –0.034 | +0.007 | –0.009 | –0.063 | –0.285 | –0.060 | –0.189 | –0.117 |
| [H2O–H–SH2]+ | 2.929 | –0.018 | –0.007 | –0.054 | –0.047 | –0.388 | 0.055 | –0.126 | +0.086 |
| HS-H–NH3 | 3.620 | –0.057 | –0.217 | –0.129 | –0.238 | –0.223 | 0.253 | –0.268 | –0.248 |
| H2N–H–SH– | 3.533 | –0.040 | +0.007 | +0.015 | –0.060 | –0.444 | –0.379 | –0.246 | –0.227 |
| [H3N–H–SH2]+ | 3.290 | –0.024 | –0.007 | –0.026 | –0.081 | –0.187 | 0.011 | –0.178 | –0.366 |
| MAD | 0.046 | 0.065 | 0.051 | 0.115 | 0.331 | 0.189 | 0.260 | 0.231 | |
| MAX | 0.069 | 0.217 | 0.129 | 0.238 | 0.866 | 0.379 | 0.394 | 0.366 |
Basis set is G3large. CP: counterpoise corrected calculation.
Basis set is 6-31G(d); this method is used within G3B3 for the geometry optimization.
Basis set is 6-31+G(d,p).
Figure 1.
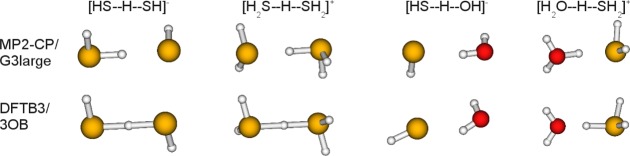
Problematic geometries for DFTB3/3OB with significant difference in angles or connectivity (i.e., the position of the hydrogen involved in hydrogen bonding) in comparison to counterpoise corrected MP2/G3large.
With an attempt to understand the significant errors in the hydrogen-bonding structures, we look further into the DFT results. Geometries calculated with B3LYP/6-31G(d) (which are used in G3B3) in comparison to the ones from MP2-CP differ also with respect to the bond lengths (Table 8); calculated hydrogen-bonding angles are quite similar to MP2-CP though. For [HS–H–SH]− and [H2S–H–SH2]+, similar to DFTB3/3OB, the shared hydrogen is halfway between the sulfur atoms. When going to larger basis sets (e.g., G3large or aug-cc-pVTZ), the structure of [H2S–H–SH2]+ becomes similar to the MP2-CP result shown in Figure 1; however, for [HS–H–SH]−, the shared hydrogen remains half way between the sulfur atoms. For PBE, the position of the hydrogen remains always halfway between the heavy atoms for both systems independent of the basis set. Therefore, these observations seem to suggest that the significant errors in the DFTB3/3OB structures are largely intrinsic to the DFT functional (PBE) used, although the errors in DFTB3/3OB are larger than those at the PBE level. Interestingly, despite the structural differences, the binding energies are comparable for G3B3 and MP2-CP, with a small MAD of 0.4 kcal/mol. Also, B3LYP and PBE with the 6-31+G(d,p) basis set show MADs of 1.4 and 3.7 kcal/mol, respectively, the latter being in fact larger than that for DFTB3/3OB. More details are provided in the Supporting Information.
The modified basis set in the 3OB-parametrization for CHNO leads to an improved O–O distance in the water dimer,52 which was too short with DFTB3/MIO. The larger wave function compression radius for oxygen in 3OB increases the Pauli repulsion, such that the underestimation of the O–O distance is reduced. For a proper binding energy, we then adjusted the parameter associated with the modified γ function for X–H pairs.33 In the case of sulfur, a larger rwf leads also to larger intermolecular distances as expected, however at the cost of larger errors for bond angles, which obviously limits the optimization. The current set is a compromise within the DFTB3 framework that uses the PBE functional.
Proton Transfer Barriers
To study proton transfer in molecules including sulfur atoms, we consider several simple model systems: [HS–H–SH]−, [H2S–H–SH2]+, [HS–H–OH]−, [H2S–H–OH2]+, [HS–H–NH2]−, and [H2S–H–NH3]+. For comparison with higher level methods, we fix the heavy atoms at four different interatomic distances. The shared hydrogen atom is moved on a straight line from the first heavy atom to the second one, and the total energy for each position is calculated after a relaxation of all other hydrogen atoms.
Figure 2 shows the potential energy curves for all model systems for one fixed heavy atom distance (all other graphs are shown in the Supporting Information). The energy is shown relative to the energy of two infinitely separated monomers; e.g., for [HS–H–OH]− the energy is shown relative to SH– and H2O. We compare DFTB3/3OB to MP2/G3large, B3LYP and PBE with the 6-31+G(d,p) basis set. While the relative energies vary by several kilocalories per mole between the methods due mainly to the difference in the binding energies, the barriers are overall consistent. For DFTB3/3OB, two major deficiencies are observed. First, the underestimation of the proton affinity of NH3 leads to too low a relative energy for the system [H2S–H–NH3]+. This drawback is already known and can be alleviated by applying a modified repulsive potential H–N-mod which improves the proton affinity (for details, see ref (52)). Second, for [H2S–H–OH2]+, the total energy of the SH2–H–OH2+ system is underestimated by almost 8 kcal/mol. The error does not stem from the differences in proton affinities for SH2 and H2O as their deviations from G3B3 are only +0.7 and +1.7 kcal/mol, respectively. However, the binding energy H2S + H3O+ → H2S–H3O+ is underestimated by ∼8 kcal/mol, whereas the binding energy of H2O + SH3+ → [SH3+–OH2] is only slightly overestimated by 2 kcal/mol.
Figure 2.
Proton transfer barriers. The energy is given relative to the energy of (SH– + XH) for the upper row, and relative to (SH2 + XH2+) for the lower row, where X = SH, OH, NH2. The vertical axes show the distance between sulfur and the shared hydrogen atom (rSH). The color code is black = MP2/G3large, green = B3LYP/6-31+G(d,p), blue = PBE/6-31+G(d,p), red = DFTB3/3OB, light red = DFTB3/3OB/H–N-mod; the heavy atom distance is 3.7, 3.6, and 3.8 Å for the upper row and 3.6, 3.2, and 3.6 Å for the lower row.
As a slightly larger example, we study a model proton transfer between a hydronium ion and sulfonic acid. Proton transfers involving sulfonic acids are implicated in proton conducting membrane materials used in fuel cells.3 The hydronium oxygen is fixed at a set of distances from the sulfur in the sulfonic acid, and the proton transfer is studied in a similar fashion as discussed above; the transferred proton is fixed for a set of distances along the S–O axis, while the remaining atoms are relaxed using DFTB3/3OB. The result for the O–S distance of 4.5 Å is shown in Figure 3 as an example. The DFTB3/3OB approach captures the exothermicity of the reactions rather well compared to B3LYP/aug-cc-pVTZ single point energies, while the barrier is substantially underestimated by almost 7 kcal/mol. The degree of underestimation is smaller at shorter O–O distances, but the result in Figure 3 underlines the fact that DFTB3 is developed based on PBE and therefore may underestimate proton transfer barriers at large donor–acceptor distances. Therefore, in applications where rates or proton conductance is of interest, it is likely important to calibrate/correct the computed barrier height based on high-level calculations.
Figure 3.
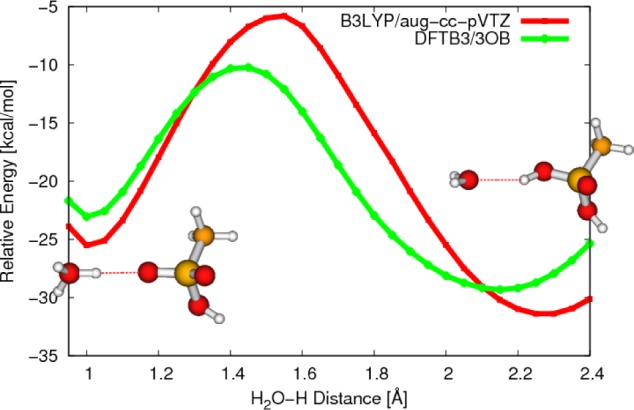
Potential energy curves for the proton transfer between a hydronium ion and a sulfonic acid calculated at DFTB3/3OB (red) and B3LYP/aug-cc-pVTZ (green) levels, respectively. The energies are relative to infinitely separated reactants.
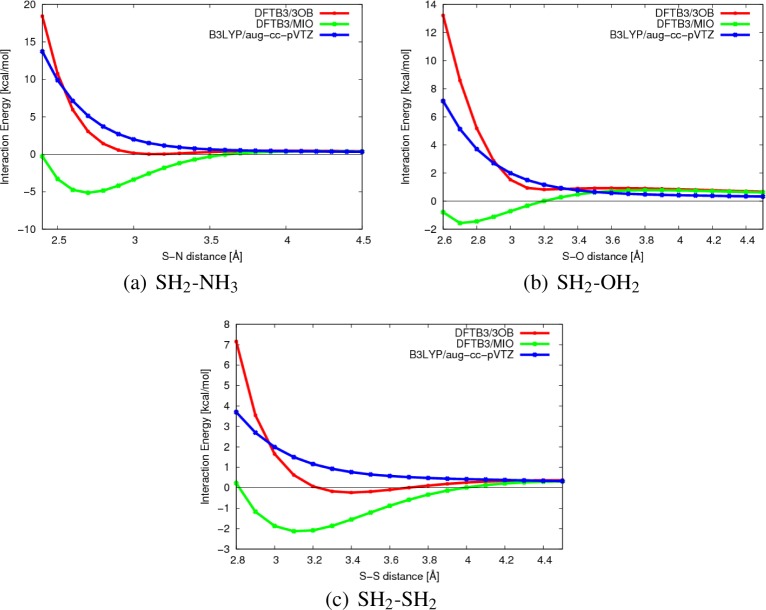
Noncovalent Interactions
In a recent study,72 it was pointed out that DFTB3/MIO leads to artificially favorable interactions involving sulfur atoms, thus spurious noncovalent binding for sulfur-containing compounds. Test calculations indicated that resolving the issue likely requires refitting the electronic parameters for sulfur. With the 3OB set of parameters, especially the new density compression radius (rdens), we see that the artificial binding discussed in ref (72) is significantly reduced; rather than a few kilocalories per mole, now the overbinding is on the order of 0.2 kcal/mol for the S–O/N interaction and 0.5 kcal/mol for the S–S interaction (Figure 4). We are unable to completely remove the attractive interactions within the framework of DFTB3 without affecting other properties discussed above, especially geometry and hydrogen-bonding interactions. For practical applications, however, we emphasize that when such weak overbinding effects need to be considered, explicit dispersion corrections are likely also important. In Figure 5, we compare optimized structures for antiparallel and parallel thiophene dimers, which were studied in ref (72), at different levels of theory. Without explicit dispersion, both DFTB3/MIO and DFTB3/3OB lead to structures considerably different from B3LYP including dispersion (B3LYP-D3BJ84); the S–S distance is longer with DFTB3/3OB, reflecting the weaker spurious interaction between the sulfur atoms compared to DFTB3/MIO. When the empirical dispersion85 is included, the DFTB3/3OB structures become in rather good agreement with B3LYP-D3BJ. The distance between the parallel thiophene monomers is underestimated; since the dispersion model used for DFTB3 here was developed in the framework of DFTB2,85 a more systematic refinement of the dispersion model together with DFTB3/3OB will likely further improve the result.
Figure 4.
Potential energy curves for selected noncovalent interactions involving sulfur atoms studied in ref (72). The format is similar to Figure 2 of ref (72). Although the artificially attractive interaction remains with DFTB3/3OB, the magnitude of interaction is significantly reduced compared to DFTB3/MIO.
Figure 5.
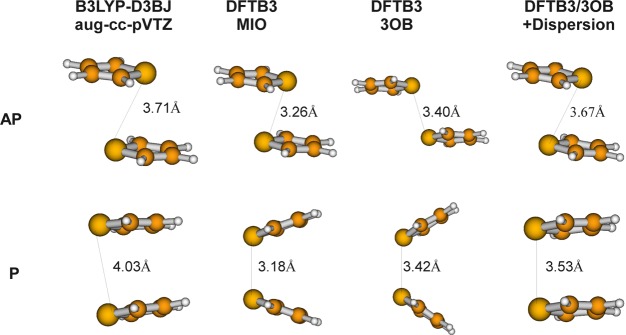
Optimized structures for antiparallel (AP) and parallel (P) thiophene dimers at different levels of theory. The S–S distance is given in Å.
Phosphorus
Atomization Energies and Geometries
Similar to what was done for sulfur, we have compiled a test set of small neutral closed-shell phosphorus-containing molecules. Among those are acids, oxides, phosphines, and thioesters with different oxidation states of phosphorus. Table 9 summarizes the results, and further details are given in the Supporting Information.
Table 9. Mean and Maximum Absolute Deviations for Small Neutral Closed-Shell Phosphorus Containing Moleculesa.
| property | Nb | MP2c | B3LYPd | PBEd | PM6 | PDDG | MIOe | 3OB | 3OB/OPhyd |
|---|---|---|---|---|---|---|---|---|---|
| Eat (kcal/mol) | 32 | 12.9 | 33.2 | 8.8 | 82.9 | 7.3 | 21.2 | ||
| Emaxat (kcal/mol) | 29.3 | 146.0 | 31.0 | 406.8 | 40.7 | 113.3 | |||
| ΔHf,0 (kcal/mol) | 32 | 14.3 | 34.3 | 8.8 | 15.3 | 15.0 | 82.4 | 7.2 | 21.5 |
| ΔHf,max0 (kcal/mol) | 32.7 | 146.8 | 30.8 | 57.3 (8.1/33.6)f | 43.1 (27.6/150.8)f | 405.3 (3.4/13.9)f | 40.5 (1.6/9.5)f | 114.3 (2.2/11.1)f | |
| r (Å) | 130 | 0.007 | 0.007 | 0.018 | 0.029 | 0.069 | 0.020 | 0.012 | 0.012 |
| rmax (Å) | 0.040 | 0.022 | 0.034 | 0.109 | 0.423 | 0.142 | 0.129 | 0.112 | |
| a (deg) | 130 | 0.6 | 0.6 | 1.2 | 4.3 | 5.4 | 3.8 | 3.3 | 3.0 |
| amax (deg) | 2.5 | 2.0 | 4.7 | 32.8 | 18.2 | 33.1 | 25.2 | 21.3 | |
| d (deg) | 42 | 1.7 | 2.9 | 4.4 | 29.9 | 39.4 | 21.4 | 17.5 | 16.4 |
| dmax (deg) | 6.5 | 17.5 | 25.5 | 139.0 | 152.3 | 70.0 | 101.4 | 119.5 |
Atomization energies are compared to G3B3 results; bond lengths r, bond angles a, and dihedral angles d are compared to B3LYP/cc-pVTZ calculations; max stands for maximum absolute deviation.
Number of comparisons.
Basis set is cc-pVTZ.
Basis set is 6-31G(d).
Trimethylmethylenephosphorane does not converge and is excluded from the statistics.
Single point G3B3 ΔHf0 computed at the structures optimized by semiempirical methods; the value before/after the slash is the mean/maximum absolute deviations from G3B3, which uses B3LYP/6-31G(d) structures.
Even though the MAD is dependent on the particular choice of the test set, 3OB for phosphorus seems overall less accurate than for sulfur (7.3 vs 4.7 kcal/mol). The largest deviations for atomization energies are found for the oxides P4O10 and P4O6 with an error of −40.7 and −33.9 kcal/mol, respectively. Again, the 3OB set is a major improvement over the MIO set, which shows large errors (MAD of 82.9 kcal/mol) due to overbinding. Even MP2 and B3LYP, without fitting atomic contributions, show large errors as discussed above for sulfur. The trends in the heats of formation also follow those for the atomization energies.
For geometries, 3OB also improves in comparison to MIO, although the magnitude of improvement is modest. However, some large errors remain; P–P bond lengths are overestimated, leading to the largest deviations of over 0.1 Å. Furthermore, the P–O–P angle in diphosphoric acid is overestimated by about 25°. Other large deviations for angles and dihedrals stem mainly from erroneous positions/orientations of a hydrogen atom. DFTB3/3OB also out-performs wave function based semiempirical methods for geometries. PDDG generally underestimates H–P and P–P bond lengths in comparison to B3LYP/cc-pVTZ or aug-cc-pVTZ; an exceptional outlier is found for the bond distance within P2 deviating by more than 0.4 Å. Considering that PDDG does not include d orbitals on phosphorus, the method performs remarkably well even though it is less accurate than PM6 and DFTB3.
For the purpose of representing also phosphate anions in our test sets, we have compiled nine model geometries that are important for many key biological processes (Table 10; for details, see the Supporting Information). The overall performance is similar to that for the neutral species. The largest deviations for bond lengths are found for P–O bonds in [CH3COO–PO3]2– and [HPO4]2–, which are underestimated by 0.127 and 0.044 Å, respectively. All other errors are smaller than 0.04 Å, demonstrating the excellent performance of DFTB3/3OB for bond lengths.
Table 10. Mean and Maximum Absolute Deviations for 9 Closed-Shell Phosphate Anions in Comparison to B3LYP/aug-cc-pVTZ Geometries.
| propertya | Nb | MP2c | B3LYPd | PBEd | PM6 | PDDGe | MIO | 3OB | 3OB/OPhyd |
|---|---|---|---|---|---|---|---|---|---|
| r (Å) | 53 | 0.004 | 0.007 | 0.019 | 0.024 | 0.031 | 0.017 | 0.013 | 0.013 |
| rmax (Å) | 0.027 | 0.025 | 0.056 | 0.180 | 0.111 | 0.173 | 0.127 | 0.116 | |
| a (deg) | 57 | 0.8 | 0.7 | 1.3 | 2.6 | 3.5 | 2.1 | 2.0 | 1.9 |
| amax (deg) | 4.5 | 6.3 | 10.2 | 8.1 | 14.5 | 11.8 | 10.3 | 9.5 | |
| d (deg) | 23 | 2.1 | 2.8 | 3.8 | 21.6 | 14.9 | 26.6 | 34.7 | 35.6 |
| dmax (deg) | 6.4 | 9.3 | 10.6 | 98.5 | 101.7 | 67.3 | 79.2 | 82.3 |
Bond lengths r, bond angles a, and dihedral angles d; max stands for maximum absolute deviation.
Number of comparisons.
Basis set is cc-pVTZ.
Basis set is 6-31G(d).
[CH3COO–PO3]2– dissociates during geometry optimization and is therefore excluded from the statistics.
The special parametrization 3OB/OPhyd based on phosphate hydrolysis reactions reveals a generally similar performance to that of 3OB (Tables 9 and 10); computed atomization energy and heat of formation are substantially worse due to the shift of the P–O repulsive potential by about −10 kcal/mol.
Finally, to compare the structures from semiempirical methods, we examine heats of formation using single point G3B3 energy calculations at structures determined by these methods. At DFTB3/MIO, DFTB3/3OB, and DFTB3/3OB/OPhyd geometries, we find MADs of 3.4, 1.6, and 2.2 kcal/mol in comparison to the reference G3B3 values (which uses B3LYP/6-31G(d) geometries). By contrast, G3B3 single point energetics with PM6 structures give a MAD of 8.1 kcal/mol. For PDDG, the considerable geometric inaccuracies cause the G3B3 single point energetics to deviate by as much as 27.6 kcal/mol on average. Clearly, the DFTB3 structures are considerably most reliable.
Vibrational Frequencies
A few selected unscaled harmonic vibrational frequencies calculated from DFT-based and semiempirical methods are compiled in Table 11. While stretching frequencies from B3LYP are consistently larger than those from BLYP, the differences are quite small (<60 cm–1). In general, DFTB3/3OB values are close to those predicted by DFT methods (only one exception for the N=P stretching frequency). PM6 shows more outliers; e.g., P–H stretching frequencies of PH3 are overestimated by about 400 cm–1 in comparison to B3LYP, whereas PDDG reproduces the overall trend quite well but also deviates substantially for the less typical bonding situations of N≡P and C=P.
Table 11. Selected Vibrational Frequencies in cm–1.
| molecule (point group) | irrep | description | BLYPa | B3LYPa | PM6 | PDDG | MIO | 3OB | 3OB/OPhyd |
|---|---|---|---|---|---|---|---|---|---|
| phosphine (C3v) | A1 | sym. bending | 998 | 1018 | 994 | 861 | 929 | 931 | 931 |
| E | asy. bending | 1106 | 1038 | 1135 | 1046 | 1028 | 1033 | 1033 | |
| A1 | sym. stretch | 2305 | 2386 | 2760 | 2190 | 2407 | 2313 | 2313 | |
| E | asy. stretch | 2314 | 2394 | 2756 | 2302 | 2446 | 2354 | 2354 | |
| diphosphorus (D∞h) | A1g | P–P stretch | 758 | 806 | 835 | 891 | 774 | 796 | 796 |
| H2P=PH2 (C2) | B | P–P stretch | 388 | 419 | 648 | 477 | 412 | 412 | 412 |
| methylphosphine (Cs) | A′ | C–P stretch | 632 | 666 | 768 | 674 | 713 | 679 | 679 |
| methylenephosphine (Cs) | A′ | C=P stretch | 961 | 1004 | 1095 | 1192 | 1046 | 1065 | 1065 |
| N≡P (C∞v) | A1 | N–P stretch | 1322 | 1402 | 1496 | 1627 | 1453 | 1331 | 1331 |
| H2N=PH2 (C1) | A | N=P stretch | 780 | 813 | 828 | 788 | 811 | 1027 | 1027 |
| H3PO4 (C3) | A | sym. P–O stretch | 772 | 831 | 772 | 785 | 932 | 861 | 833 |
| E | asy. P–O stretch | 863 | 919 | 834 | 812 | 1027 | 956 | 850 | |
| A | sym. P=O stretch | 1259 | 1318 | 1310 | 1348 | 1338 | 1289 | 1260 | |
| H3PS4 (C3) | A | sym. P–S stretch | 348 | 379 | 452 | 362 | 325 | 391 | 391 |
| E | asy. P–S stretch | 447 | 489 | 586 | 415 | 377 | 461 | 461 | |
| A | P=S stretch | 647 | 673 | 638 | 536 | 567 | 655 | 655 | |
| MAD (δν/νB3LYP%) | 5.4 | 12.2 | 9.4 | 7.0 | 4.8 | 5.0 | |||
| MAX (δν/νB3LYP%) | 8.6 | 54.7 | 20.4 | 22.9 | 26.3 | 26.3 |
Basis set is cc-pVTZ.
Reaction Energies
Table 12 shows a few simple reactions that are compiled to evaluate the performance for certain bond breaking and forming processes. As this set of reactions is arbitrarily chosen, the MAD should be interpreted with caution. However, it is obvious that B3LYP performs quite well despite its poor description for atomization energies; the effect of the basis set is also small. Within DFTB3/MIO, the overbinding is not balanced between different bond types; thus large errors are observed (see also discussion for reactions containing sulfur above). DFTB3/3OB performs well overall but has outliers for particular species, HP=O, hypodiphosphoric acid, and also P(OH)5. Note that the latter indicates already the underlying problem for hydrolysis reaction barriers where the transition state contains pentavalent phosphorus. Specifically, the last reaction in Table 12 that changes the P coordination from 4 to 5 oxygen is reasonably well described by 3OB/OPhyd. By construction, all other reactions involving P–O bond forming or breaking deviate significantly for 3OB/OPhyd in comparison to the G3B3 method. The performance of PM6 and PDDG is less satisfying than DFTB3/3OB, with almost doubled MADs.
Table 12. Deviations for 16 Reaction Energies of Neutral Closed Shell Phosphorus Containing Molecules Compared to G3B3a.
| reaction | G3B3 | B3LYPb | B3LYPc | PBEc | PM6d | PDDGd | MIO | 3OB | 3OB/OPhyd |
|---|---|---|---|---|---|---|---|---|---|
| PH3 + H2O → H2P–OH + H2 | 9.4 | –0.0 | –2.4 | –2.7 | –7.5 | –5.5 | –27.2 | –0.5 | –10.9 |
| PH3 + H2O → HP=O + 2H2 | 40.1 | +2.5 | –2.4 | –2.3 | –2.3 | –11.7 | –39.6 | –10.3 | –18.5 |
| PH3 + CH4 → H3C–PH2 + H2 | 13.7 | +2.5 | +2.2 | +0.5 | –11.6 | –13.4 | –8.7 | –4.4 | –4.4 |
| PH3 + C2H6 → H3C–PH2 + CH4 | –4.6 | +0.7 | +1.2 | +0.9 | –2.1 | –8.9 | –7.5 | –2.8 | –2.8 |
| (CH3)2P=O + 2H2O → HP(=O)(OH)2 + 2CH4 | –36.0 | –4.0 | –9.8 | –7.2 | +22.5 | +12.1 | –41.5 | +3.3 | –16.1 |
| PH3 + 4H2O → H3PO4 + 4H2 | –31.5 | +9.3 | –4.5 | –7.6 | +4.3 | –17.4 | –92.7 | –2.1 | –39.0 |
| H2P(=O)OH + H2O → HP(=O)(OH)2 + H2 | –16.0 | +1.9 | –1.6 | –2.2 | –1.9 | –0.7 | –24.2 | +2.7 | –6.8 |
| HP(=O)(OH)2 + H2O → H3PO4 + H2 | –12.1 | +2.3 | –1.1 | –1.5 | –3.2 | +0.7 | –32.3 | –5.8 | –15.1 |
| P(OH)3 + H2O → H3PO4 + H2 | –24.1 | +8.3 | +3.1 | +2.1 | +14.6 | +4.0 | –18.7 | –7.2 | –13.2 |
| (HO)2(O=)P–P(=O)(OH)2 + 2H2O → 2H3PO4 + H2 | –29.5 | –0.3 | –3.7 | +0.8 | –6.3 | +16.3 | –60.8 | –21.8 | –39.7 |
| 2PH3 → H2P–PH2 + H2 | 4.3 | +2.0 | +2.0 | –0.3 | –18.0 | –37.9 | –21.2 | –8.1 | –8.1 |
| PH3 + NH3 → NP + 3H2 | 59.8 | +8.7 | +2.9 | +4.0 | –4.2 | –35.8 | –12.3 | –6.4 | –6.4 |
| PH3 + NH3 → HN–PH + 2H2 | 48.3 | +4.0 | +1.7 | +1.1 | –8.4 | –20.1 | –2.5 | –1.5 | –1.5 |
| PH3 + NH3 → H2N–PH2 + H2 | 11.4 | +1.7 | +0.6 | –0.0 | –14.0 | –11.3 | +3.9 | +1.2 | +1.2 |
| P(NH2)3 + 3H2O → P(OH)3 + 3NH3 | –20.2 | –6.5 | –11.1 | –9.3 | +20.4 | +4.2 | –92.7 | –8.6 | –39.6 |
| H3PO4 + H2O → P(OH)5 | 0.4 | +0.7 | –4.8 | –8.8 | –18.4 | +16.1 | –3.6 | +19.3 | +4.8 |
| MAD | 3.5 | 3.4 | 3.2 | 10.0 | 13.5 | 30.6 | 6.6 | 14.3 | |
| MAX | 9.3 | 11.1 | 9.3 | 22.5 | 37.9 | 92.7 | 21.8 | 39.7 |
Energies are calculated at 0 K excluding zero point energy and thermal corrections. All numbers are given in kcal/mol.
Basis set is cc-pVTZ.
Basis set is 6-31G(d).
Heats of formation for H2 are calculated as −26 and −22 kcal/mol for PM6 and PDDG. To correct for this exceptional error, this value is set to 0.0 kcal/mol.
Proton Affinities and Hydrogen Bonding Energies
For a test on proton affinities, we use one of our earlier compilations from ref (43). Similar to the situation for sulfur, we find that when using the calculated Hubbard derivative, proton affinities in the gas phase are overestimated (for both MIO/calc and 3OB/calc, see Table 13). The fit of the phosphorus Hubbard drivative eliminates this systematic deviation with both MIO and 3OB parameters, except for certain cases that still have error on the order of 5–10 kcal/mol. The special parametrization 3OB/OPhyd, which uses the same Hubbard parameter, also performs very well. This is not surprising as the binding situation of P–O bonds does not alter significantly for the calculation of proton affinities.
Table 13. 18 Proton Affinities for Phosphorus Containing Molecules in kcal/mol: Deviation of DFTB in Comparison to G3B3a.
| moleculeb | G3B3 | B3LYPc | PBEc | PM6d | PDDG | MIO/calc | MIO | 3OB/calc | 3OB | 3OB/OPhyd |
|---|---|---|---|---|---|---|---|---|---|---|
| H3PO4 | 334.0 | –2.4 | –4.3 | –18.0 | –2.9 | +18.3 | +5.5 | +11.5 | +4.2 | +3.4 |
| H2PO4– | 464.5 | –3.3 | –5.8 | –17.8 | +12.1 | +17.2 | –4.3 | +10.4 | –1.7 | –2.0 |
| DMPHe | 336.3 | –1.3 | –4.4 | –13.2 | –6.4 | +15.9 | +4.8 | +10.6 | +4.5 | +3.8 |
| MMPe | 336.7 | –2.0 | –4.5 | –16.6 | –6.0 | +15.8 | +3.8 | +9.8 | +3.1 | +2.4 |
| MMP–e | 460.5 | –3.0 | –6.0 | –12.7 | +11.0 | +18.3 | –1.2 | +12.0 | +1.3 | +1.0 |
| PH3OH+ | 201.6 | +3.0 | –0.1 | +13.0 | +13.6 | +4.8 | –0.0 | +0.7 | –1.5 | –0.4 |
| PH2OHOH+ | 201.6 | +1.5 | –0.7 | +2.2 | +7.3 | +8.2 | +2.1 | +3.1 | –0.1 | +0.2 |
| PHOHOHOH+ | 200.8 | –0.0 | –2.5 | –5.6 | +4.0 | +13.6 | +6.2 | +8.5 | +3.7 | +3.4 |
| PH2(OH)=O | 336.6 | +1.4 | –0.9 | +2.3 | +21.6 | +12.2 | +3.3 | +7.9 | +3.3 | +4.2 |
| PH(OH)(OH)=O | 334.7 | –0.4 | –2.6 | –6.5 | +12.8 | +16.0 | +5.3 | +10.2 | +4.4 | +4.4 |
| P(O)(OH)(−O–CH2CH2–O−) | 336.3 | –2.2 | –5.0 | –13.9 | –7.3 | +13.4 | +2.4 | +8.3 | +2.1 | +1.5 |
| P(OH)(OH)(−O–CH2CH2–O−)(OH*) | 359.0 | –2.8 | –7.7 | –18.3 | –16.4 | +12.9 | +0.3 | +5.9 | –0.3 | –1.0 |
| P(OH*)(OH)(−O–CH2CH2–O−)(OH) | 350.4 | –2.9 | –6.7 | –18.1 | –17.2 | +11.0 | –0.4 | +3.1 | –2.9 | –3.6 |
| P(OH*)(OH)(−O–CH2CH2–O−)(OCH3) | 351.2 | –2.7 | –6.5 | –17.7 | –20.9 | +8.9 | –1.4 | —f | –3.6 | –4.0 |
| P(OH)(OCH3)(−O–CH2CH2–O−)(OH*) | 359.6 | –2.7 | —g | –17.6 | –18.9 | +3.3 | +0.1h | –4.1 | –9.6 | –10.2 |
| P(OH*)(OCH3)(−O–CH2CH2–O−)(OH) | 352.9 | –2.4 | –6.4 | –19.1 | –19.5 | +10.1 | –0.5 | +2.6 | –2.9 | –3.5 |
| P(OH)(OH)(OH)(OH*)(OH)_ax | 357.3 | –2.2 | –6.4 | –18.8 | –9.0 | +14.2 | –1.2 | +6.8 | –0.9 | –1.6 |
| P(OH)(OH)(OH)(OH*)(OH)_eq | 347.0 | –3.5 | –7.1 | –17.1 | –8.3 | —i | –0.0 | —i | —i | –3.1 |
| MAD | 2.2 | 4.3 | 13.8 | 12.0 | 12.6 | 2.4 | 7.2 | 2.9 | 3.0 | |
| MSE | –1.6 | –4.3 | –11.9 | –2.8 | +12.6 | +1.4 | 6.7 | 0.2 | –0.3 | |
| MAX | 3.5 | 7.7 | 19.1 | 21.6 | 18.3 | 6.2 | 12.0 | 9.6 | 10.2 |
The proton affinity is computed using potential energies at 0 K without any zero-point energy correction.
The molecules are given in the protonated form.
Basis set is 6-31+G(d,p).
The energy of the proton in PM6 is in error by −54 kcal/mol, which has been accounted for by adding this number to the original result. See discussion at http://openmopac.net/manual/pm6_accuracy.html.
“DMPH” refers to dimethyl hydrogen phosphate, “MMP” to P(O)(OH)(OH)(OCH3), and “MMP–” to P(O)(O)(OH)(OCH3)−.
One ligand dissociates.
Converges to a slightly different minima and is excluded from the statistics.
This value is different from the one we reported in ref (51), where the molecule was erroneously optimized to a different local minimum. Here, we stay as close to the conformation of the high-level optimized one as possible.
Molecule dissociates, forming H2O, and has been excluded from the statistics. Depending on the basis set, this dissociation also occurs for the DFT functionals PBE and B3LYP, e.g., dissociation for basis set 6-311G(2d,2p), no dissociation for basis set cc-pVTZ.
A few model systems for hydrogen bonding energies between water and phosphate esters in the gas phase are compiled in Table 14. In comparison to G3B3, DFTB3 slightly underestimates the binding; PM6 and PDDG generally have larger errors. Note that hydrogen bond lengths are underestimated with B3LYP/6-31G(d) (the geometry used for G3B3) in comparison to B3LYP/aug-cc-pVTZ by almost 0.04 Å on average. DFTB3/3OB predicts even shorter hydrogen bonds, the mean signed error (MSE) is −0.06 Å; for MIO it is −0.10 Å. PM6 often leads to very different structures (which is why only single point energies on PDDG structures are shown in Table 14), and PDDG is also featured with substantially larger errors with a MAD of 0.226 Å (Table 15). More details are summarized in the Supporting Information.
Table 14. Hydrogen Bonding Energies for Phosphates in kcal/mol: Deviations in Comparison to G3B3a.
| moleculeb | G3B3 | MP2c | B3LYPc | B3LYPd | PBEd | PM6-SPe | PDDG | MIO | 3OB | 3OB/OPhyd |
|---|---|---|---|---|---|---|---|---|---|---|
| MMPH–OH2 | 13.3 | +0.2 | –1.9 | –0.4 | +1.0 | –5.4 | –2.8 | –2.0 | –2.7 | –2.7 |
| MMP–1–H2O | 17.9 | –0.4 | –2.7 | –1.1 | –0.3 | –5.2 | –3.1 | –0.6 | –1.1 | –1.3 |
| MMP–1–OH2 | 17.4 | +0.1 | –2.0 | –1.0 | +0.6 | –4.8 | –3.5 | –1.3 | –2.0 | –2.1 |
| MMP–2–H2O | 32.3 | –0.4 | –3.2 | –0.9 | +0.5 | –4.5 | +2.4 | –0.5 | –0.6 | –0.7 |
| DMPH–OH2 | 14.4 | +0.0 | –2.1 | –0.5 | +0.8 | –5.3 | –3.2 | –2.9 | –3.7 | –3.8 |
| DMP–1–H2O | 18.1 | –0.6 | –2.9 | –1.3 | –0.6 | –5.2 | –3.0 | –1.0 | –1.4 | –1.6 |
| MAD | 0.3 | 2.5 | 0.9 | 0.6 | 5.1 | 3.0 | 1.4 | 1.9 | 2.0 | |
| MAX | 0.6 | 3.2 | 1.3 | 1.0 | 5.4 | 3.5 | 2.9 | 3.7 | 3.8 |
The binding energy is computed with the potential energies at 0 K without any zero-point energy correction.
MMPH: dihydrogenated monomethylphosphate. MMP–1: monohydrogenated momomethylphosphate. MMP–2: dehydrogenated monomethylphosphate, respectively for DMP: dimethylphosphate; coordinates are given in the Supporting Information.
Basis set is aug-cc-pVTZ.
Basis set is 6-31+G(d,p).
During the geometry optimization using PM6, the hydrogen bonds relaxe to substantially different minima. Therefore, single-point calculations have been used for comparison.
Table 15. Hydrogen Bonding Distances in Å for Small Phosphorus Containing Systems: Deviations in Comparison to B3LYP/aug-cc-pVTZ.
| system | H-bond | B3LYPa | MP2a | B3LYPb | B3LYPc | PBEc | PDDGd | MIO | 3OB |
|---|---|---|---|---|---|---|---|---|---|
| DMPH–OH2 | HOH–O | 1.892 | –0.028 | –0.004 | +0.025 | –0.029 | –0.219 | –0.062 | –0.010 |
| DMPH–OH2 | H–OH2 | 1.776 | –0.031 | –0.055 | –0.009 | –0.081 | –0.090 | +0.018 | +0.075 |
| DMP–1–H2O | HOH–O1 | 2.052 | –0.036 | –0.028 | –0.004 | –0.031 | –0.322 | –0.170 | –0.125 |
| DMP–1–H2O | HOH–O2 | 2.093 | –0.060 | –0.031 | +0.009 | –0.023 | –0.360 | –0.191 | –0.144 |
| MMPH–OH2 | H–OH2 | 1.773 | –0.031 | –0.054 | –0.015 | –0.087 | –0.084 | +0.020 | +0.072 |
| MMPH–OH2 | O–HOH | 1.916 | –0.034 | –0.015 | +0.024 | –0.037 | –0.239 | –0.091 | –0.034 |
| MMP–1–H2O | HOH–O1 | 2.064 | –0.046 | –0.040 | –0.002 | –0.034 | –0.329 | –0.183 | –0.140 |
| MMP–1–H2O | HOH–O2 | 2.073 | –0.043 | –0.031 | +0.008 | –0.024 | –0.335 | –0.178 | –0.127 |
| MMP–1–OH2 | H–OH2 | 2.113 | –0.063 | –0.136 | –0.019 | –0.125 | –0.346 | –0.205 | –0.102 |
| MMP–1–OH2 | O–HOH | 1.638 | –0.009 | +0.093 | +0.008 | –0.030 | 0.003 | +0.029 | +0.001 |
| MMP–2–H2O | HOH–O1 | 1.862 | –0.040 | –0.007 | +0.009 | –0.026 | –0.193 | –0.113 | –0.115 |
| MMP–2–H2O | HOH–O2 | 1.861 | –0.040 | –0.007 | +0.009 | –0.026 | –0.192 | –0.112 | –0.114 |
| MAD | 0.038 | 0.042 | 0.012 | 0.046 | 0.226 | 0.114 | 0.088 | ||
| MAX | 0.063 | 0.136 | 0.025 | 0.125 | 0.360 | 0.205 | 0.142 |
Basis set is aug-cc-pVTZ.
Basis set is 6-31G(d); this method is used within G3B3 for the geometry optimization.
Basis set is 6-31+G(d,p).
Optimization using PM6 often leads to very different geometries; thus only PDDG results are reported. See Supporting Information.
Hydrolysis Reactions
Phosphorus parameters have been benchmarked and used to study phosphate hydrolysis reactions.21,43,86,87 We have adopted the compilation of elementary steps of these reactions and show results for our new parametrization in Table 16.
Table 16. Deviations of Exothermicities and Barrier Heights in Comparison to MP2/G3Large Single Point Calculations at B3LYP/6-31+G(d,p) Relaxed Geometries for 37 Elementary Steps in the Hydrolysis of MMP and DMPa.
| method | MP2 | B3LYP | PBEb | PM6 | PDDG | MIO | 3OB | 3OB/OPhyd | 3OB | 3OB/OPhyd | MP2 | MP2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| at geometry optimized by | B3LYP | B3LYP | B3LYP | B3LYP | B3LYP | B3LYP | B3LYP | B3LYP | 3OB | 3OB/OPhyd | 3OB | 3OB/OPhyd |
| com1 → ts1 (MMP,B) | 31.0 | –1.7 | –6.1 | –14.5 | +12.3 | –7.2 | +11.4 | –0.8 | –0.8 | +0.5 | ||
| com1 → int1 (MMP,E) | 30.6 | –1.4 | –5.7 | –16.4 | +14.8 | –7.0 | +12.9 | –0.8 | –1.5 | +0.6 | ||
| com1 → ts1_2 (MMP,B) | 41.5 | –2.1 | –7.4 | –11.9 | +9.4 | –3.3 | +9.7 | +1.1 | +9.8 | +1.8 | +1.8 | +1.1 |
| com1 → int1_2 (MMP,E) | 31.0 | –1.1 | –5.1 | –17.8 | +15.6 | –5.9 | +15.4 | +0.5 | +14.5 | –0.2 | +0.8 | +0.7 |
| int1_2 → ts2_0 (MMP,B) | 11.9 | –2.0 | –3.3 | +7.4 | –7.2 | +2.7 | –4.9 | +1.6 | –4.9 | +0.3 | –2.1 | +3.0 |
| int1_2 → ts2 (MMP,B) | 3.6 | +0.1 | –0.4 | +4.3 | +0.4 | –1.1 | –2.7 | –0.2 | +2.3 | +2.3 | +6.6 | +6.4 |
| int1_2 → com2 (MMP,E) | –28.8 | –0.9 | +3.4 | +20.4 | –17.6 | +4.4 | –16.6 | –1.8 | –15.7 | –0.9 | –1.8 | –1.8 |
| com1 → diss_tsa (MMP,B) | 36.8 | –4.2 | –10.2 | –6.2 | +11.8 | +4.9 | –2.8 | –2.2 | –7.8 | –6.0 | –2.0 | +0.4 |
| com1 → diss_int (MMP,E) | 19.6 | –6.5 | –7.5 | –4.6 | –14.8 | +0.3 | –23.1 | –10.5 | –22.5 | –10.0 | –1.0 | –1.4 |
| com1_w2 → ts1_2_w2 (MMP,B) | 39.9 | –2.1 | –8.5 | –24.0 | +10.0 | –12.7 | +5.3 | –4.8 | +6.2 | –3.1 | –1.5 | +1.9 |
| com1_w2 → int1_2a_w2 (MMP,E) | 28.0 | –0.5 | –4.4 | –21.6 | +16.4 | –7.9 | +12.8 | –2.1 | +11.9 | –2.8 | +0.2 | –0.1 |
| int1_2a_w2 → int1_2_w2 (MMP,E) | 0.4 | +0.8 | +0.5 | +4.0 | +1.3 | +2.5 | +2.9 | +3.0 | +2.7 | +2.7 | +1.1 | +1.1 |
| int1_2_w2 → ts2_0_w2 (MMP,B) | 11.4 | –1.8 | –3.7 | +1.4 | –0.2 | –5.4 | –9.0 | –3.5 | –7.7 | –2.1 | –4.2 | +0.0 |
| com1_da → ts1_da (MMP,B) | 55.0 | –3.1 | –6.8 | –7.7 | –11.1 | –0.2 | +2.0 | –0.7 | +4.2 | –0.3 | +7.4 | +1.0 |
| com1_da → int_da (MMP,E) | 4.5 | –2.0 | –1.8 | +1.4 | +4.0 | –2.0 | –1.9 | –1.9 | –1.7 | –1.6 | –0.2 | –0.4 |
| com1 → ts1 (DMP,B) | 38.6 | –1.4 | –5.9 | –15.0 | +5.8 | –7.3 | +9.4 | –0.5 | +9.9 | –0.9 | +0.6 | +0.5 |
| com1 → int1 (DMP,E) | 35.4 | –0.2 | –4.4 | –19.4 | +11.8 | –7.6 | +13.8 | –0.9 | +12.9 | –1.6 | +1.8 | +1.4 |
| int1 → int1_2 (DMP,E) | 1.3 | –0.7 | –1.3 | +1.9 | +1.6 | +1.3 | +1.3 | +2.1 | +0.7 | +0.8 | +0.1 | +0.3 |
| int1_2 → ts2 (DMP,B) | 0.6 | –0.5 | –0.5 | +3.1 | –2.4 | +1.2 | –0.8 | +1.5 | –0.4 | +3.4 | –0.1 | –0.4 |
| int1_2 → com2 (DMP,E) | –35.2 | –0.7 | +4.3 | +21.2 | –15.2 | +6.0 | –15.0 | –1.0 | –13.5 | +1.0 | –1.8 | –1.7 |
| n_com1 → n_ts3 (DMP,B) | 33.6 | –1.4 | –8.1 | –11.0 | +28.5 | +0.2 | +16.5 | +4.4 | +12.2 | +0.8 | +2.3 | +1.2 |
| n_com1 → n_int1 (DMP,E) | 13.2 | +0.4 | –3.2 | –15.6 | +21.8 | –4.9 | +18.2 | +3.6 | +17.7 | +3.1 | +0.8 | +1.1 |
| n_int1 → n_ts4 (DMP,B) | 22.9 | –1.6 | –5.4 | +8.0 | +13.4 | +5.1 | +0.6 | +1.2 | –3.6 | –1.4 | +0.2 | +0.8 |
| n_int1 → n_com2 (DMP,E) | –15.8 | –1.9 | +0.9 | +23.2 | –14.9 | +3.7 | –18.7 | –4.2 | –18.9 | –4.2 | –0.6 | –1.0 |
| DMP_P → diss_ts (DMP,B) | 40.9 | –2.9 | –9.1 | –2.3 | +11.2 | +8.8 | +0.2 | –0.7 | –2.2 | –3.2 | –0.6 | –1.5 |
| DMP_P → diss_prod (DMP,E) | 28.2 | –3.8 | –6.7 | –12.6 | –0.9 | –0.9 | –6.1 | –5.2 | –18.7 | –7.3 | +5.6 | +4.0 |
| diss_prod2 → diss_ts2 (DMP,B) | 13.5 | +0.7 | –2.5 | +12.1 | +18.3 | +10.4 | +8.9 | +5.1 | +16.9 | +4.7 | –2.8 | –1.2 |
| diss_prod2 → MMP_P (DMP,E) | –29.8 | +3.6 | +6.7 | +18.4 | +12.3 | +0.6 | +8.1 | +5.1 | +19.6 | +8.1 | –2.2 | –1.2 |
| diss_w_reac → diss_w_ts (DMP,B) | 20.9 | –2.3 | –7.4 | –8.0 | +10.8 | +0.7 | +1.3 | +0.7 | +2.1 | +1.5 | +1.0 | +0.8 |
| diss_w_reac → diss_w_prod (DMP,E) | 18.4 | –2.6 | –5.6 | –6.5 | +1.0 | +0.3 | –2.5 | –2.9 | –12.9 | –2.9 | +12.0 | +0.0 |
| diss_w_prod2 → diss_w_ts2 (DMP,B) | 1.9 | +0.2 | –1.6 | +0.9 | +10.9 | +0.3 | +3.3 | +2.8 | +16.6 | +3.4 | –8.2 | –0.1 |
| diss_w_prod2 → diss_w_reac2 (DMP,E) | –21.0 | +2.8 | +6.2 | +14.5 | +7.7 | –0.7 | +2.2 | +2.3 | +14.7 | +2.0 | –8.3 | +0.1 |
| n_w_com1 → n_w_ts3 (DMP,B) | 28.2 | –1.8 | –10.1 | –24.3 | +32.4 | –8.9 | +13.7 | +0.2 | +10.6 | –0.2 | –0.2 | +0.2 |
| n_w_com1 → n_w_int1 (DMP,E) | 13.1 | +1.0 | –3.1 | –15.7 | +22.2 | –5.8 | +17.5 | +2.8 | +17.3 | +2.7 | +0.6 | +0.7 |
| n_w_int1 → n_w_int2 (DMP,E) | –0.5 | +0.5 | +0.4 | –0.0 | +0.8 | +0.6 | +1.0 | +1.0 | +0.6 | +0.6 | +0.4 | +0.4 |
| n_w_int2 → n_w_ts4 (DMP,B) | 15.1 | –2.3 | –6.2 | –2.6 | +17.2 | –3.1 | –2.9 | –2.7 | –0.9 | –1.1 | +4.2 | +2.1 |
| n_w_int2 → n_w_com2 (DMP,E) | –13.0 | –2.0 | +1.3 | +23.8 | –14.8 | +4.1 | –19.0 | –4.4 | ||||
| MAD | 1.8 | 4.7 | 11.5 | 11.4 | 4.1 | 8.5 | 2.5 | 9.8 | 2.5 | 2.5 | 1.1 | |
| MAX | 6.5 | 10.3 | 24.3 | 32.4 | 12.7 | 23.1 | 10.5 | 22.5 | 10.0 | 12.0 | 6.4 |
Compilation from ref (43); no zero-point corrections are included in either exothermicity or barrier heights. All quantities are given in kcal/mol. The processes are labeled in the notation of ref (43); “E” stands for “Exothermicity,” “B” for “Barrier;” coordinates are listed in the Supporting Information.
Basis set is 6-31+G(d,p).
In ref (43), transition and intermediate states, reactants, and products have been optimized using B3LYP/6-31+G(d,p). First, we compare the single point energetics at those structures. DFTB3/3OB shows a rather poor performance with a MAD of 8.5 kcal/mol, although slightly better than PM6 and PDDG, which have MADs beyond 10 kcal/mol. A closer look reveals that the poor performance is systematically found for reactions where pentavalent phosphorus structures are involved, whereas the performance for reactions that include only tri- and tetravalent structures (i.e., all reactions that follow a dissociative pathway, abbreviated as “diss” in Table 16) are overall in reasonably good agreement with the MP2 reference. Along this line, we have to distinguish even further. Some structures are trivalent, i.e., a PO3 unit is (almost) trigonal-planar; however one water is still axially coordinated to the phosphorus. The P–water distance lies within the P–O repulsive potential; that is, the P–water distance is smaller than the cutoff of the P–O repulsive potential. Only for the geometry named diss_int, however, where no axial water is included, is any P–water distance beyond the cutoff of the repulsive potential; thus, in the reaction, phosphorus reacts from a four-coordinated to a three-coordinated complex. Specifically for that reaction, a large error is found. In other words, the 3OB parameters seem to work well as long as P is coordinated by exactly four oxygen atoms. For coordinations with three and five oxygens, large errors are obtained indicating a deficiency in properly describing different hybridization states. We have attempted tuning the s-orbital eigenvalue to achieve a more appropriate balance for different hybridized systems (similar to tuning the s-orbital eigenvalue of nitrogen88); however by doing so we could not identify an overall well-performing parameter set. This indicates that the current DFTB3 methodology has limited transferability for complex phosphorus chemistry at the level of accuracy in energetics required for detailed mechanistic studies due to the small basis set, the lack of three-center integrals, or multipole moments of the charge fluctuation.61 We emphasize that even for these challenging cases, as discussed below, the 3OB structures are rather reliable and MP2 single point energies at these structures have a rather small MAD of 2.5 kcal/mol compared to MP2 at B3LYP structures.
As a temporary and ad hoc solution to this problem, we suggest the special parametrization OPhyd that reduces these errors as follows. In the first two reactions in Table 16 a fifth oxygen is bound to a phosphorus atom. Both the transition state (ts1) and the intermediate state (int1) are overestimated in energy by about 10 kcal/mol. Therefore, we shift the O–P repulsive potential by about 10 kcal/mol to be more attractive. While this introduces an overbinding for all P–O bonds, the energy difference between tetra- and pentavalent phosphorus is compensated. Note that for the reaction from a tetra- to trivalent P (com1 → diss_int), a considerable error of about 10 kcal/mol remains. Due to the dominance of tetra- and pentavalent phosphorus models in our compilation, the MAD drops down to only 2.5 kcal/mol.
As a second comparison, we optimize all structures at the DFTB3 level. Transition states are found using the nudged elastic band technique.89 The results for DFTB3/3OB/OPhyd are impressive, with the MAD in comparison to MP2/G3large at B3LYP/6-31+G(d,p) geometries staying at 2.5 kcal/mol. However, a few structural problems appear. Hydrogen bonds are often too short by about 0.1 Å. P–O coordinations of leaving groups are too long, most severely for the structures diss_prod and diss_prod2 with deviations of over 0.4 Å. The geometry n_w_com2 relaxes to a different minimum with a different type of hydrogen bonding network; therefore it is excluded from the statistics. For the standard 3OB parameters, additionally the fifth ligand of int1_mmp dissociates, and this structure is therefore also excluded from the statistics.
In a third comparison, we calculate MP2/G3large single-point energies at DFTB3 geometries. For DFTB3/3OB, the MAD drops down to only 2.5 kcal/mol; for comparison, PBE/6-31+G(d,p) single points at B3LYP structures have a MAD of 4.7 kcal/mol (see Table 16). Thus, even though the energetics for tri- and pentavalent structures are inaccurate, DFTB3/3OB can be corrected using higher level methods to yield very good energetics. For the special parametrization, 3OB/OPhyd results are excellent; the MAD is only 1.1 kcal/mol, showing that the geometrical differences between B3LYP/6-31+G(d,p) and 3OB/OPhyd are of minor relevance, or from a different perspective, the potential energy surface seems very shallow and leads to similar energies.
Conclusion
Considering the importance of phosphorus and sulfur in (bio)chemistry, we extend the parametrization of the approximate density functional tight binding approach, DFTB3, to these elements. The parametrization is carried out in a framework consistent with the DFTB3/3OB set52 for O, N, C, and H; thus the resulting parameters can be used to describe a broad set of organic and biologically relevant P/S-containing molecules. The 3d orbitals, which are known to be polarization functions essential to the proper description of structure and energetics of P/S-containing molecules, are included in the parametrization, in contrast to a few popular wave function based semiempirical methods such as PM3/PDDG. Compared to the previous parametrizations of DFTB2 and DFTB3 (the “MIO” set), the electronic parameters of the current 3OB parametrization were chosen with the goal of minimizing errors in atomization energies. As a result, systematic overbinding of covalent interactions is avoided, leading to generally more reliable reaction energies. The parameters are available for download from www.dftb.org.
The parameters are tested with a fairly diverse set of molecules of chemical and biological relevance. We focus on the geometries, reaction energies, proton affinities, and hydrogen bonding interactions of these molecules; vibrational frequencies are also examined, although less systematically. These properties calculated at the DFTB3/3OB level are compared to results of DFT (B3LYP and PBE), ab initio (MP2, G3B3), and several popular semiempirical methods (PM6 and PDDG), as well as predictions of DFTB3 with the older parametrization (the MIO set). In general, DFTB3/3OB is a major improvement over the previous parametrization (DFTB3/MIO), and for the majority of cases tested here, it also outperforms PM6 and PDDG, especially for structural properties, vibrational frequencies, hydrogen bonding interactions, and proton affinities. For reaction energies, DFTB3/3OB exhibits major improvement over DFTB3/MIO, due mainly to significant reduction of errors in atomization energies; compared to PM6 and PDDG, DFTB3/3OB also generally performs better, although the magnitude of improvement is more modest. Compared to high-level calculations, DFTB3/3OB is most successful at predicting geometries; the energetics are largely on par with results of DFT (especially PBE, which is the functional used in DFTB3 for deriving the relevant matrix elements) using a medium basis set (e.g., 6-31G(d)), although larger errors are seen more often with DFTB3. We note that since we focus on molecules of biological interest, our test cases here do not feature a large number of radical species.
The extensive tests also indicate that there are remaining cases for which the current DFTB3 methodology has trouble properly making a description. For example, SO (singlet) and SO3 have large errors (11.8 and 34.4 kcal/mol, respectively) in atomization energies; thus reactions involving these species are generally not well described by DFTB3/3OB. Another example involves a substantial underestimation of hydrogen-bonding distances for many (especially charged) sulfur-containing species; the comparison to DFT calculations using different functionals and basis sets suggest that the errors are likely due in part to the intrinsic limitations of the PBE functional and also to the minimal basis set used in DFTB3. It is worth noting that the computed hydrogen bonding energies, nevertheless, are generally fairly reliable and even slightly better than PBE/6-31+G(d,p). Finally, another remaining limitation is that DFTB3/3OB is still incapable of providing reliable energetics for phosphate hydrolysis reactions that involve a change in the coordination number of the phosphorus. Thus, the current DFTB3 model has limited transferability for complex phosphorus chemistry at the level of accuracy in energetics required for detailed mechanistic investigations. As a temporary solution, we develop a specific parametrization, 3OB/OPhyd, where an overbinding is introduced to O–P interactions to empirically minimize the errors for a set of reference reactions. Although this is clearly not a satisfactory solution for the long-term, the 3OB/OPhyd can serve as a useful tool for exploring the energy landscape of phosphoryl transfer reactions in biological systems, especially for structural properties. Alternatively, the 3OB structures remain reliable for these challenging cases, and one may still use the standard 3OB parameters to obtain structures and improve energetics with higher level methods.
Due to computational efficiency and general robustness for structural property predictions, QM/MM calculations using DFTB3/3OB as the QM level will be an effective computational approach for the analysis of condensed phase systems. The energetic properties from such calculations should be taken as semiquantitative in nature and can be improved by combining with ab initio QM/MM calculations. For example, the fact that single point high-level calculations using DFTB3/3OB geometries often exhibit small errors suggests that, for example, DFTB3/3OB is likely effective as the low-level QM approach that drives the sampling for reliable free energy simulations in the framework of dual-level QM/MM calculations.20,24,90−93 Along this line, for the phosphate hydrolysis reaction, the closer agreement between 3OB/OPhyd and higher level methods in energies makes 3OB/OPhyd better suited for dual-level QM/MM free energy calculations than the standard 3OB set. Since many reactions that involve phosphorus/sulfur chemistry implicate metal ions, a pressing need is to extend the DFTB3/3OB parametrization to these ions, such as the alkali metal ions, zinc and copper; this will be reported in separate work in the near future. Along this line, we note that although there is currently an impressive effort to develop DFTB parameters for the entire periodic table in a largely automated fashion,94 developing parameters appropriate for many (bio)chemical applications would require careful calibration and refinement as we have done here for sulfur and phosphorus. Finally, the remaining limitations highlight that it is also worthwhile continuing to improve the DFTB3 methodology, such as by including multipole terms for the charge fluctuation and better description of polarization and short-range repulsions.
Acknowledgments
The work on the parametrization of DFTB3/3OB has been supported by NIH grant R01-GM084028 and continued with R01-GM106443. Computational resources from the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by NSF grant number OCI-1053575, are greatly appreciated; computations are also supported in part by National Science Foundation through a major instrumentation grant (CHE-0840494).
Supporting Information Available
Excel file for additional MP2/DFT/DFTB/PM6/PDDG results, additional statistics and molecular geometries (xyz structures), the comparison of zero-point energies, and the effect of dispersion. This material is available free of charge via the Internet at http://pubs.acs.org.
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- Alberts B.; Bray D.; Lewis J.; Raff M.; Roberts K.; Watson J. D.. Molecular Biology of the Cell; Garland Publishing, Inc.: New York, 1994. [Google Scholar]
- Hanson S. R.; Best M. D.; Wong C. H. Sulfatase: structure, mechanism, biological activity, inhibition and synthetic utility. Angew. Chem., Int. Ed. 2004, 43, 5736–5763. [DOI] [PubMed] [Google Scholar]
- Mauritz K. A.; Moore R. B. State of understanding of Nafion. Chem. Rev. 2004, 104, 4535–4585. [DOI] [PubMed] [Google Scholar]
- Anthony J. E. Functionalized acenes and heteroacenes for organic electronics. Chem. Rev. 2006, 106, 5028–5048. [DOI] [PubMed] [Google Scholar]
- Westheimer F. H. Why nature chose phosphates. Science 1987, 235, 1173–1178. [DOI] [PubMed] [Google Scholar]
- Knowles J. R. Enzyme catalyzed phosphoryl transfer reactions. Annu. Rev. Biochem. 1980, 49, 877–919. [DOI] [PubMed] [Google Scholar]
- Cleland W. W.; Hengge A. C. Enzymatic mechanisms of phosphate and sulfate transfer. Chem. Rev. 2006, 106, 3252–3278. [DOI] [PubMed] [Google Scholar]
- Kiaris H.; Spandidos D. A. Mutations of Ras Genes in Human Tumors. Int. J. Oncol. 1995, 7, 413–421. [PubMed] [Google Scholar]
- Roberts P. J.; Der C. J. Targeting the Raf-MEK-ERK mitogen-activated protein kinase cascade for the treatment of cancer. Oncogene 2007, 26, 3291–3310. [DOI] [PubMed] [Google Scholar]
- Cohen P. Protein kinases - the major drug targets of the twenty-first century?. Nat. Rev. Drug Discovery 2002, 1, 309–315. [DOI] [PubMed] [Google Scholar]
- Davies S. P.; Reddy H.; Caivano M.; Cohen P. Specificity and mechanism of action of some commonly used protein kinase inhibitors. Biochem. J. 2000, 351, 95–105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garber K. Rapamycin’s resurrection: A new way to target the cancer cell cycle. J. Natl. Cancer Inst. 2001, 93, 1517–1519. [DOI] [PubMed] [Google Scholar]
- Collins I.; Workman P. Design and development of signal transduction inhibitors for cancer treatment: Experience and challenges with kinase targets. Curr. Signal Transduction Ther. 2006, 1, 13–23. [Google Scholar]
- Robertson J. G. Enzymes as a special class of therapeutic target: clinical drugs and modes of action. Curr. Opin. Struct. Biol. 2007, 17, 674–679. [DOI] [PubMed] [Google Scholar]
- Zhang Z. Y. Protein tyrosine phosphatases: Structure and function, substrate specificity, and inhibitor development. Annu. Rev. Pharmacol. Toxicol. 2002, 42, 209–234. [DOI] [PubMed] [Google Scholar]
- Kamerlin S. C. L.; Sharma P. K.; Prasad R. B.; Warshel A. Why nature really chose phosphate. Q. Rev. Biophys. 2013, 46, 1–132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y. Pseudobond ab initio QM/MM approach and its applications to enzyme reactions. Theor. Chem. Acc. 2006, 116, 43–50. [Google Scholar]
- Hu H.; Yang W. T. Free Energies of Chemical Reactions in Solution and in Enzymes with Ab Initio Quantum Mechanics/Molecular Mechanics Methods. Annu. Rev. Phys. Chem. 2008, 59, 573–601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Senn H. M.; Thiel W. QM/MM methods for biomolecular systems. Angew. Chem., Int. Ed. 2009, 48, 1198–1229. [DOI] [PubMed] [Google Scholar]
- Plotnikov N. V.; Kamerlin S. C. L.; Warshel A. Paradynamics: An Effective and Reliable Model for Ab lnitio QM/MM Free-Energy Calculations and Related Tasks. J. Phys. Chem. B 2011, 115, 7950–7962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Y.; Yu H.; Cui Q. Extensive Conformational Transitions Are Required to Turn On ATP Hydrolysis in Myosin. J. Mol. Biol. 2008, 381, 1407–1420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wong K. Y.; Lee T. S.; York D. M. Active Participation of the Mg2+ Ion in the Reaction Coordinate of RNA Self-Cleavage Catalyzed by the Hammerhead Ribozyme. J. Chem. Theory Comput. 2011, 7, 1–3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hou G. H.; Cui Q. QM/MM analysis suggests that Alkaline Phosphatase (AP) and Nucleotide pyrophosphatase/phosphodiesterase (NPP) slightly tighten the transition state for phosphate diester hydrolysis relative to solution: implication for catalytic promiscuity in the AP superfamily. J. Am. Chem. Soc. 2012, 134, 229–246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hou G. H.; Cui Q. Stabilization of Different Types of Transition States in a Single Enzyme Active Site: QM/MM Analysis of Enzymes in the Alkaline Phosphatase Superfamily. J. Am. Chem. Soc. 2013, 135, 10457–10469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duarte F.; Amrein B. A.; Kamerlin S. C. L. Modeling catalytic promiscuity in the alkaline phosphatase superfamily. Phys. Chem. Chem. Phys. 2013, 15, 11160–11177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y. L.; Köppen S.; Frauenheim T. An SCC-DFTB/MD Study of the Adsorption of Zwitterionic Glycine on a Geminal Hydroxylated Silica Surface in an Explicit Water Environment. J. Phys. Chem. C 2011, 115, 9615–9621. [Google Scholar]
- Mori T.; Hamers R. J.; Pedersen J. A.; Cui Q.. An Explicit Consideration of Desolvation is Critical to Binding Free Energy Calculations of Charged Molecules at Ionic Surfaces. J. Chem. Theory Comput. 2013, 9, in press. [DOI] [PubMed] [Google Scholar]
- Repasky M. P.; Chandrasekhar J.; Jorgensen W. L. PDDG/PM3 and PDDG/MNDO: Improved semiempirical methods. J. Comput. Chem. 2002, 23, 1601–1622. [DOI] [PubMed] [Google Scholar]
- Winget P.; Selçuki C.; Horn A. H. C.; Martin B.; Clark T. Towards a “next generation” neglect of diatomic differential overlap based semiempirical molecular orbital technique. Theor. Chem. Acc. 2003, 110, 254–266. [Google Scholar]
- Korth M.; Thiel W. Benchmarking semiempirical methods for thermochemistry, kinetics, and noncovalent interactions: OMx methods are almost as accurate and robust as DFT-GGA methods for organic molecules. J. Chem. Theory Comput. 2011, 7, 2929–2936. [DOI] [PubMed] [Google Scholar]
- Giese T. J.; York D. M. Density-functional expansion methods: Grand challenges. Theor. Chem. Acc. 2012, 131, 1145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elstner M.; Porezag D.; Jungnickel G.; Elsner J.; Haugk M.; Frauenheim T.; Suhai S.; Seifert G. Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 1998, 58, 7260–7268. [Google Scholar]
- Elstner M. The SCC-DFTB method and its application to biological systems. Theor. Chem. Acc. 2006, 116, 316–325. [Google Scholar]
- Riccardi D.; Schaefer P.; Yang Y.; Yu H.; Ghosh N.; Prat-Resina X.; König P.; Li G.; Xu D.; Guo H.; Elstner M.; Cui Q. Development of effective quantum mechanical/molecular mechanical (QM/MM) methods for complex biological processes. J. Phys. Chem. B 2006, 110, 6458–6469. [DOI] [PubMed] [Google Scholar]
- Porezag D.; Frauenheim T.; Köhler T.; Seifert G.; Kaschner R. Construction of tight-binding-like potentials on the basis of density-functional theory: Application to carbon. Phys. Rev. B 1995, 51, 12947–12957. [DOI] [PubMed] [Google Scholar]
- Krüger T.; Elstner M.; Schiffels P.; Frauenheim T. Validation of the density-functional based tight-binding approximation method for the calculation of reaction energies and other data. J. Chem. Phys. 2005, 122, 114110. [DOI] [PubMed] [Google Scholar]
- Otte N.; Scholten M.; Thiel W. Looking at self-consistent-charge density functional tight binding from a semiempirical perspective. J. Phys. Chem. A 2007, 111, 5751–5755. [DOI] [PubMed] [Google Scholar]
- Sattelmeyer K. W.; Tirado-Rives J.; Jorgensen W. L. Comparison of SCC-DFTB and NDDO-based semiempirical molecular orbital methods for organic molecules. J. Phys. Chem. A 2006, 110, 13551–13559. [DOI] [PubMed] [Google Scholar]
- Niehaus T. A.; Elstner M.; Frauenheim T.; Suhai S. Application of an approximate density-functional method to sulfur containing compounds. J. Mol. Struct.: THEOCHEM 2001, 541, 185–194. [Google Scholar]
- Elstner M.; Cui Q.; Munih P.; Kaxiras E.; Frauenheim T.; Karplus M. Modeling zinc in biomolecules with the self consistent charge-density functional tight binding (SCC-DFTB) method: Applications to structural and energetic analysis. J. Comput. Chem. 2003, 24, 565–581. [DOI] [PubMed] [Google Scholar]
- Moreira N. H.; Dolgonos G.; Aradi B.; da Rosa A. L.; Frauenheim T. Toward an Accurate Density-Functional Tight-Binding Description of Zinc-Containing Compounds. J. Chem. Theory Comput. 2009, 5, 605–614. [DOI] [PubMed] [Google Scholar]
- Saha S.; Pal S.; Sarkar P.; Rosa A. L.; Frauenheim T. A Complete Set of Self-Consistent Charge Density-Functional Tight-Binding Parametrization of Zinc Chalcogenides (ZnX; X=O, S, Se, and Te). J. Comput. Chem. 2012, 33, 1165–1178. [DOI] [PubMed] [Google Scholar]
- Yang Y.; Yu H.; York D.; Elstner M.; Cui Q. Description of phosphate hydrolysis reactions with the Self-Consistent-charge Density-Functional-Tight-Binding (SCC-DFTB) theory. 1. Parameterization. J. Chem. Theory Comput. 2008, 4, 2067–2084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai Z.; Lopez P.; Reimers J. R.; Cui Q.; Elstner M. Application of the computationally efficient self-consistent-charge density-functional tight-binding method to magnesium-containing molecules. J. Phys. Chem. A 2007, 111, 5743–5750. [DOI] [PubMed] [Google Scholar]
- Kubar T.; Bodrog Z.; Gaus M.; Aradi B.; Frauenheim T.; Elstner M. Parametrization of the SCC-DFTB Method for Halogens. J. Chem. Theory Comput. 2013, 9, 2939–2949. [DOI] [PubMed] [Google Scholar]
- Zheng G. S.; Witek H. A.; Bobadova-Parvanova P.; Irle S.; Musaev D. G.; Prabhakar R.; Morokuma K. Parameter calibration of transition-metal elements for the spin-polarized self-consistent-charge density-functional tight-binding (DFTB) method: Sc, Ti, Fe, Co, and Ni. J. Chem. Theory Comput. 2007, 3, 1349–1367. [DOI] [PubMed] [Google Scholar]
- Dolgonos G.; Aradi B.; Moreira N. H.; Frauenheim T. An Improved Self-Consistent-Charge Density-Functional Tight-Binding (SCC-DFTB) Set of Parameters for Simulation of Bulk and Molecular Systems Involving Titanium. J. Chem. Theory Comput. 2010, 6, 266–278. [DOI] [PubMed] [Google Scholar]
- Grundkotter-Stock B.; Bezugly V.; Kunstmann J.; Cuniberti G.; Frauenheim T.; Niehaus T. A. SCC-DFTB Parametrization for Boron and Boranes. J. Chem. Theory Comput. 2012, 8, 1153–1163. [DOI] [PubMed] [Google Scholar]
- Elstner M. SCC-DFTB: What is the proper degree of self-consistency. J. Phys. Chem. A 2007, 111, 5614–5621. [DOI] [PubMed] [Google Scholar]
- Yang Y.; Yu H.; York D.; Cui Q.; Elstner M. Extension of the self-consistent-charge density-functional tight-binding method: Third-order expansion of the density functional theory total energy and introduction of a modified effective coulomb interaction. J. Phys. Chem. A 2007, 111, 10861–10873. [DOI] [PubMed] [Google Scholar]
- Gaus M.; Cui Q.; Elstner M. DFTB3: Extension of the Self-Consistent-Charge Density-Functional Tight-Binding Method (SCC-DFTB). J. Chem. Theory Comput. 2011, 7, 931–948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaus M.; Goez A.; Elstner M. Parametrization and Benchmark of DFTB3 for Organic Molecules. J. Chem. Theory Comput. 2013, 9, 338–354. [DOI] [PubMed] [Google Scholar]
- Thiel W.; Voityuk A. A. Extension of MNDO to d orbitals: Parameters and results for the second-row elements and for the zinc group. J. Phys. Chem. 1996, 100, 616–626. [Google Scholar]
- Reed A. E.; Schleyer P. v. R. Chemical bonding in hypervalent molecules – the dominance of ionic bonding and negative hyperconjugation over d-orbital participation. J. Am. Chem. Soc. 1990, 112, 1434–1445. [Google Scholar]
- Dobado J. A.; Martinez-Garcia H.; Molina J. M.; Sundberg M. R. Chemical bonding in hypervalent molecules revised. Application of the Atoms in Molecules Theory to Y-3 X and Y-3 XZ (Y = H or CH3; X = N, P or As; Z = O or S) compounds. J. Am. Chem. Soc. 1998, 120, 8461–8471. [Google Scholar]
- Stewart J. J. P.Encyclopedia of Computational Chemistry; Wiley: Hoboken, NJ, 1998; Chapter PM3. [Google Scholar]
- Tubert-Brohman I.; Guimarães C. R. W.; Jorgensen W. L. Extension of the PDDG/PM3 Semiempirical Molecular Orbital Method to Sulfur, Silicon, and Phosphorus. J. Chem. Theory Comput. 2005, 1, 817–823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stewart J. J. P. Optimization of parameters for semiempirical methods V: Modification of NDDO approximations and application to 70 elements. J. Mol. Model. 2007, 13, 1173–1213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [DOI] [PubMed] [Google Scholar]
- Gaus M.; Chou C.-P.; Witek H.; Elstner M. Automatized parametrization of SCC-DFTB repulsive potentials: Application to hydrocarbons. J. Phys. Chem. A 2009, 113, 11866–11881. [DOI] [PubMed] [Google Scholar]
- Gaus M.; Cui Q.; Elstner M.. Density Functional Tight Binding (DFTB): Application to organic an biological molecules. WIREs Comput. Mol. Sci. 2013, in press
- Bodrog Z.; Aradi B. Possible improvements to the self-consistent-charges density-functional tight-binding method within the second order. Phys. Status Solidi B 2012, 249, 259–269. [Google Scholar]
- Bodrog Z.; Aradi B.; Frauenheim T. Automated repulsive parametrization for the DFTB method. J. Chem. Theory Comput. 2011, 7, 2654–2664. [DOI] [PubMed] [Google Scholar]
- Köhler C.; Frauenheim T.; Hourahine B.; Seifert G.; Sternberg M. Treatment of collinear and noncollinear electron spin within an approximate density functional based method. J. Phys. Chem. A 2007, 111, 5622–5629. [DOI] [PubMed] [Google Scholar]
- Kohler C.; Seifert G.; Frauenheim T. Density functional based calculations for Fe-n (n < = 32). Chem. Phys. 2005, 309, 23–31. [Google Scholar]
- Curtiss L. A.; Raghavachari K.; Redfern P. C.; Rassolov V.; Pople J. A. Gaussian-3 (G3) theory for molecules containing first and second-row atoms. J. Chem. Phys. 1998, 109, 7764–7776. [Google Scholar]
- Curtiss L. A.; Raghavachari K.; Redfern P. C.; Pople J. A. Assessment of Gaussian-3 and density functional theories for a larger experimental test set. J. Chem. Phys. 2000, 112, 7374–7383. [DOI] [PubMed] [Google Scholar]
- Curtiss L. A.; Redfern P. C.; Raghavachari K. Assessment of Gaussian-3 and density-functional theories on the G3/05 test set of experimental energies. J. Chem. Phys. 2005, 123, 124107. [DOI] [PubMed] [Google Scholar]
- Gonzalez-Lafont A.; Truong T. N.; Truhlar D. G. Direct dynamics calculations with NDDO (neglect of diatomic differential overlap) molecular orbital theory with specific reaction parameters. J. Phys. Chem. 1991, 95, 4618–4627. [Google Scholar]
- Giese T. J.; Chen H. Y.; Dissanayake T.; Giambasu G. M.; Heldenbrand H.; Huang M.; Kuechler E. R.; Lee T. S.; Panteva M. T.; Radak B. K.; York D. M. A Variational Linear-Scaling Framework to Build Practical, Efficient Next-Generation Orbital-Based Quantum Force Fields. J. Chem. Theory Comput. 2013, 9, 1417–1427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DFTB - Density Functional based Tight Binding. http://www.dftb.org (accessed on July 20th, 2012).
- Petraglia R.; Corminboeuf C. A Caveat on SCC-DFTB and Noncovalent Interactions Involving Sulfur Atoms. J. Chem. Theory Comput. 2013, 9, 3020–3025. [DOI] [PubMed] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Montgomery J. A. Jr.; Vreven T.; Kudin K. N.; Burant J. C.; Millam J. M.; Iyengar S. S.; Tomasi J.; Barone V.; Mennucci B.; Cossi M.; Scalmani G.; Rega N.; Petersson G. A.; Nakatsuji H.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Klene M.; Li X.; Knox J. E.; Hratchian H. P.; Cross J. B.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Ayala P. Y.; Morokuma K.; Voth G. A.; Salvador P.; Dannenberg J. J.; Zakrzewski V. G.; Dapprich S.; Daniels A. D.; Strain M. C.; Farkas O.; Malick D. K.; Rabuck A. D.; Raghavachari K.; Foresman J. B.; Ortiz J. V.; Cui Q.; Baboul A. G.; Clifford S.; Cioslowski J.; Stefanov B. B.; Liu G.; Liashenko A.; Piskorz P.; Komaromi I.; Martin R. L.; Fox D. J.; Keith T.; Al-Laham M. A.; Peng C. Y.; Nanayakkara A.; Challacombe M.; Gill P. M. W.; Johnson B.; Chen W.; Wong M. W.; Gonzalez C.; Pople J. A.. Gaussian 03, revision C.02; Gaussian, Inc.: Wallingford, CT, 2004. [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H. P.; Izmaylov A. F.; Bloino J.; Zheng G.; Sonnenberg J. L.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Rega N.; Millam N. J.; Klene M.; Knox J. E.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Martin R. L.; Morokuma K.; Zakrzewski V. G.; Voth G. A.; Salvador P.; Dannenberg J. J.; Dapprich S.; Daniels A. D.; Farkas Ö.; Foresman J. B.; Ortiz J. V.; Cioslowski J.; Fox D. J.. Gaussian 09, Revision A.1; Gaussian, Inc.: Wallingford, CT, 2009. [Google Scholar]
- Curtiss L. A.; Raghavachari K.; Redfern P. C.; Pople J. A. Assessment of Gaussian-2 and density functional theories for the computation of enthalpies of formation. J. Chem. Phys. 1997, 106, 1063–1079. [Google Scholar]
- Tirado-Rives J.; Jorgensen W. L. Performance of B3LYP density functional methods for a large set of organic molecules. J. Chem. Theory Comput. 2008, 4, 297–306. [DOI] [PubMed] [Google Scholar]
- Stewart J. J. P. Optimization of parameters for semiempirical methods V: Modification of NDDO approximations and application to 70 elements. J. Mol. Model. 2007, 13, 1173–1213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witek H. A.; Morokuma K.; Stradomska A. Modeling vibrational spectra using the self-consistent charge density-functional tight-binding method II. Infrared spectra. J. Chem. Theory Comput. 2005, 4, 639–655. [DOI] [PubMed] [Google Scholar]
- Małolepsza E.; Witek H. A.; Morokuma K. Accurate vibrational frequencies using the self-consistent-charge density-functional tight-binding method. Chem. Phys. Lett. 2005, 412, 237–243. [Google Scholar]
- Fishtik I. Unique Stoichiometric Representation for Computational Thermochemistry. J. Phys. Chem. A 2012, 116, 1854–1863. [DOI] [PubMed] [Google Scholar]
- Range K.; Riccardi D.; Cui Q.; Elstner M.; York D. M. Benchmark calculations of proton affinities and gas-phase basicities of molecules important in the study of biological phosphoryl transfer. Phys. Chem. Chem. Phys. 2005, 7, 3070–3079. [DOI] [PubMed] [Google Scholar]
- Riccardi D.; Yang S.; Cui Q. Proton transfer function of carbonic anhydrase: Insights from QM/MM simulations. Biochim. Biophys. Acta 2010, 1804, 342–351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goyal P.; Ghosh N.; Phatak P.; Clemens M.; Gaus M.; Elstner M.; Cui Q. Proton storage site in bacteriorhodopsin: new insights from QM/MM simulations of microscopic pKa and infrared spectra. J. Am. Chem. Soc. 2011, 133, 14981–14997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grimme S.; Ehrlich S.; Goerigk L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [DOI] [PubMed] [Google Scholar]
- Elstner M.; Hobza P.; Frauenheim T.; Suhai S.; Kaxiras E. Hydrogen bonding and stacking interactions of nucleic acid base pairs: A density functional-theory based treatment. J. Chem. Phys. 2001, 114, 5149–5155. [Google Scholar]
- Yang Y.; Cui Q. The hydrolysis activity of adenosine triphosphate in myosin: a theoretical analysis of anomeric effects and the nature of the transition state. J. Phys. Chem. A 2009, 113, 12439–12446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Y.; Cui Q. Does water relay play an important role in phosphoryl transfer reactions? Insights from theoretical study of a model reaction in water and tert-butanol. J. Phys. Chem. B 2009, 113, 4930–4939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaus M.Extension and Parametrization of an Approximate Density Functional Method for Organic and Biomolecules. Ph.D. thesis, Karlsruhe Institute of Technology, Karlsruhe, Germany, 2011. Publicly available at www.bibliothek.kit.edu (accessed May 31, 2012). [Google Scholar]
- Jónsson H.; Mills G.; Jacobsen K. W. In Classical and Quantum Dynamics in Condensed Phase Simulations; Berne B., Cicotti G., Coke D., Eds.; World Scientific: Singapore, 1998; p 385. [Google Scholar]
- Marti S.; Moliner V.; Tuñón I. Improving the QM/MM description of chemical processes: A dual level strategy to explore the potential energy surface in very large systems. J. Chem. Theory Comput. 2005, 1, 1008–1016. [DOI] [PubMed] [Google Scholar]
- Claeyssens F.; Harvey J. N.; Manby F. R.; Mata R. A.; Mulholland A. J.; Ranaghan K. E.; Schutz M.; Thiel S.; Thiel W.; Werner H. J. High-accuracy computation of reaction barriers in enzymes. Angew. Chem., Int. Ed. 2006, 45, 6856–6859. [DOI] [PubMed] [Google Scholar]
- Retegan M.; Martins-Costa M.; Ruiz-Lopez M. F. Free energy calculations using dual-level Born–Oppenheimer molecular dynamics. J. Chem. Phys. 2010, 133, 064103. [DOI] [PubMed] [Google Scholar]
- Polyak I.; Benighaus T.; Boulanger E.; Thiel W. Quantum mechanics/molecular mechanics dual Hamiltonian free energy perturbation. J. Chem. Phys. 2013, 139, 064105. [DOI] [PubMed] [Google Scholar]
- Wahiduzzaman M.; Oliveira A. F.; Philipsen P.; Zhechkov L.; van Lenthe E.; Witek H. A.; Heine T. DFTB Parameters for the Periodic Table: Part 1, Electronic Structure. J. Chem. Theory Comput. 2013, 9, 4006–4017. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.