Extension and Limits of the Network of Coupled Motions Correlated to Hydride Transfer in Dihydrofolate Reductase

Abstract

Enzyme catalysis has been studied extensively, but the role of enzyme dynamics in the catalyzed chemical conversion is still an enigma. The enzyme dihydrofolate reductase (DHFR) is often used as a model system to assess a network of coupled motions across the protein that may affect the catalyzed chemical transformation. Molecular dynamics simulations, quantum mechanical/molecular mechanical studies, and bioinformatics studies have suggested the presence of a “global dynamic network” of residues in DHFR. Earlier studies of two DHFR distal mutants, G121V and M42W, indicated that these residues affect the chemical step synergistically. While this finding was in accordance with the concept of a network of functional motions across the protein, two residues do not constitute a network. To better define the extent and limits of the proposed network, the current work studied two remote residues predicted to be part of the same network: W133 and F125. The effect of mutations in these residues on the nature of the chemical step was examined via measurements of the temperature-dependence of the intrinsic kinetic isotope effects (KIEs) and other kinetic parameters, and double mutants were used to tie the findings to G121 and M42. The findings indicate that residue F125, which was implicated by both calculations and bioinformatic methods, is a part of the same global dynamic network as G121 and M42, while W133, implicated only by bioinformatics, is not. These findings extend our understanding of the proposed network and the relations between functional and genomic couplings. Delineating that network illuminates the need to consider remote residues and protein structural dynamics in the rational design of drugs and of biomimetic catalysts.

Introduction

It is broadly acknowledged that enzyme motions on a wide range of time scales can play an important role in various aspects of enzyme function: for instance, substrate binding, product release, protein rearrangements, shifts in pK_a and protonation of various functional groups, and catalyzed chemical conversion.¹ While structural data on soluble proteins has established clear links between active site structure and enzymatic function,² it has become apparent that motions of the protein as a whole, as well as motions of the associated substrate and solvent environments, must be considered if we are to understand the factors influencing the rates of enzyme-catalyzed reactions.³⁻⁸ Such an understanding of the interplay between enzyme function, structure, dynamics, coupled motion, and hydrogen tunneling in covalent bond activation could eventually permit improved de novo construction of artificial biocatalysts and will significantly advance our understanding and ability to manipulate enzyme catalysis.

The enzyme dihydrofolate reductase (DHFR) has become a benchmark system for investigations into the correlation between enzyme structure-motion and enzyme-catalyzed activation of chemical bonds.^9,10 This enzyme is a short monomer of 18 kDa, classified as an NADPH-dependent oxidoreductase that catalyzes the conversion of 7,8-dihydrofolate (DHF) to S-5,6,7,8-tetrahydrofolate (THF) via hydride transfer from C4 of NADPH to C6 of DHF. It has been extensively characterized by a range of biophysical techniques.¹⁰⁻¹² Early crystallographic data emphasized the greater mobility of certain loop regions of DHFR in response to ligand-binding at the active site;¹³ later, both crystallographic and NMR experiments revealed that the M20 loop in particular assumes various conformations relative to the active site as the catalytic cycle progresses, and suggested that the movement of this loop might modulate the turnover rate by limiting the rate of product dissociation.^11,14−16 In another study of DHFR, ensemble kinetics and single-molecule fluorescence microscopy were used to study conformational transitions associated with enzyme catalysis.¹⁷ Recently, Hecht, Benkovic, and co-workers examined functional motions of the enzyme by introducing two pyrenylalanine chromophores into DHFR, which lead to excimer formation at the reactive state.¹⁸ NMR relaxation experiments have indicated that complexes of DHFR with various ligands generate dynamic changes across the protein, and that these can be correlated with kinetic events along the catalytic cycle.¹⁹

Molecular dynamics (MD) simulations, quantum mechanical/molecular mechanical (QM/MM), and bioinformatics analysis (denoted as genomic coupling or coevolution^10,20) studies have supported the presence of a “global dynamic network” of residues in DHFR.²¹⁻²⁴ These theoretical studies were instrumental in the selection of mutational targets for kinetic experiments undertaken to more directly measure the extent, nature, and effects of the hypothesized dynamic network in DHFR. Two remote residues in particular, G121 and M42 (19 and 15 Å from the active site, respectively), were identified as influencing the dynamic motions across the enzyme.²⁵ Kinetic analyses of mutants of these residues revealed synergistic behavior: for example, single mutations at these sites resulted in single-turnover rate changes that were smaller in magnitude than the change produced by the corresponding double mutants.^26,27

In accordance with the experimental work of Benkovic and co-workers,²⁷ Hammes-Schiffer and co-workers²¹ identified G121 and M42 as residues whose motion is not only coupled to each other, but is also correlated with the reaction coordinate. This prediction was tested by measuring the temperature dependence of intrinsic kinetic isotope effects (KIEs) for both the wild-type enzyme and a series of remote mutants (G121V, M42W and G121V-M42W DHFR), between 5 and 45 °C.^25,28−30 The results were interpreted within the framework of the phenomenological Marcus-like models.^3,6,31−35 According to these models, an increase in the temperature dependence of KIEs arises from broader distribution of the distances between the H-donor and acceptor (donor–acceptor distances, DADs) when the reaction coordinate reaches the transition state (TS) or the tunneling ready state (TRS): the quantum-mechanical delocalized TS.^5,6 In the wild-type enzyme KIEs are temperature-independent; this is not true of the DHFR mutants, which indicates that these remote mutations directly affect the dynamic distribution of DADs in the active site.³⁰

It should be noted that the proposed coupling of protein motions to the reaction coordinate in DHFR is not received without controversy. Recently, Allemann, Moliner, and their co-workers conducted experimental and computational studies on isotopically labeled “heavy” forms of ecDHFR and its dynamically altered mutant N23PP,^36,37 where findings from single turnover rate measurements did not detect any significant effects of altered protein dynamics on the enzyme’s activity. However, these single turnover rates have been shown to reflect a complex combination of microscopic rate constants rather than the hydride transfer step itself.³⁸ Interestingly, the QM/MM studies in the same paper³⁷ are not consistent with the findings of the single turnover measurements, and do indicate a significant effect of the mutation in question there (N23PP of ecDHFR) on the hydride transfer step, and more generally the role of enzyme motions in the hydride transfer reaction. Actually, the calculations in ref (37) agree very well with different QM/MM calculations by Hammes-Schiffer³⁹ and with our published experimental findings regarding the effect of N23PP ecDHFR mutant on the catalyzed hydride transfer reaction.³⁸ By exposing the chemical step through measurements of intrinsic KIEs as carried out in the current and previous studies of the enzyme,^25,28,29,40 the hydride transfer step can be evaluated without complications arising from the kinetic complexity associated with single-turnover measurements.

This study is a critical extension of the network examined in the past,²⁵ as it examines two new residues that have been predicted to be part of the network: F125^10,41,42 and W133 (Figure 1).¹⁰ The choice of residues was based on QM/MM analysis and genomic coupling analysis. Of these methods, only QM/MM analysis^41,42 specifically examined motion of the protein along the reaction coordinate. Residues identified by genomic coupling analysis,^10,20 on the other hand, might very well be coupled to each other for a wide variety of reasons (folding, ligand binding, solubility, etc.) other than catalyzing the chemical step. Our findings confirmed that residue F125 is indeed another component of the proposed dynamic network, but indicated that W133, while affecting several kinetic steps in the catalytic cascade, does not participate in the network that affects C–H bond activation. The identification of a third residue (125) that is remote from the active site and from the two previously identified residues (121 and 42), and which synergistically affects the catalyzed hydride transfer, further supports the existence of and defines the network of motions that are globally distributed across the protein. The finding that residue 133 is not part of that network provides an important control, assuring that only specific residues comprise that network. In other words, not every remote mutation has a synergistic effect on the chemical step.

Figure 1.

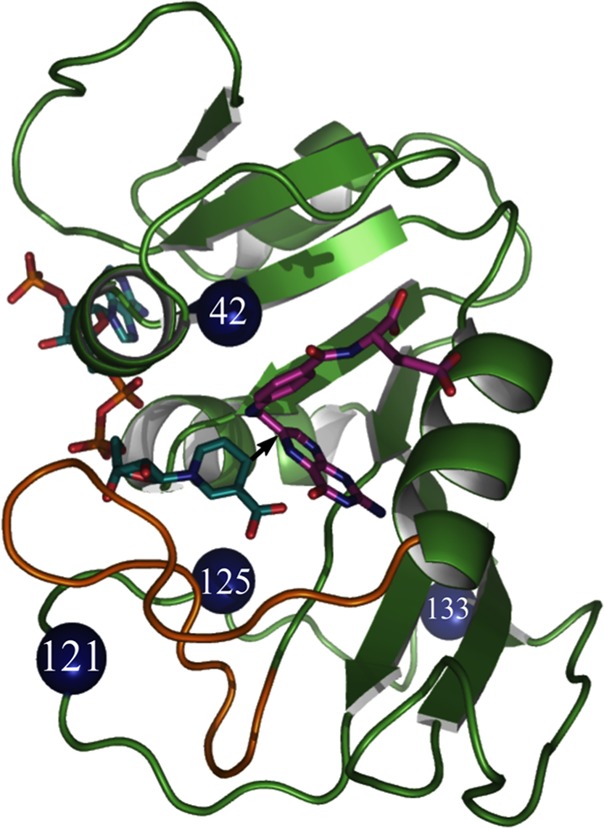
Structure of WT-ecDHFR (PDB code 1RX2), with folate in magenta and NADP in light blue. A black arrow marks the hydride’s path from C4 of the nicotinamide to C6 of the folate, and the residues studied here are marked as blue spheres.

Experimental Section

Chemicals

All chemicals were reagent grade and used as purchased from Sigma Aldrich (St. Louis, MO) unless otherwise indicated. [Ad-¹⁴C]-NAD⁺ and ³H-glucose were purchased from Perkin-Elmer. [Ad-¹⁴C]-NADPH, 4R-[Ad-¹⁴C, 4-²H]-NADPH, 4R-³H-NADPH, and 7,8-dihydrofolate were synthesized and stored as per previously published protocols.^27,43,44 Glucose dehydrogenase from Bacillus megaterium (GluDH) was purchased from Affymetrix/USB.

Construction of Expression Vector, Protein Expression, and Purification

The sequence of the mutagenic, forward primer (W133F-forward) is 5′-GAG CCG GAT GAC TTC GAA TCG GTA TTC-3′, and the sequence of the mutagenic, reverse primer (W133F-reverse) is 5′-GAA TAC CGA TTC GAA GTC ATC CGG CTC-3′. The sequence of the mutagenic, forward primer (F125M-forward) is 5′-GAC ACC CAT ATG CCG GAT TAC GAG-3′, and the sequence of the mutagenic, reverse primer (F125M-reverse) is 5′-CTC GTA ATC CGG CAT ATG GGT GTC-3′. The sequence of the mutagenic, forward primer (G121V-F125M-forward) is 5′-GAG GTG GAA GTA GAC ACC CAT-3′, and the sequence of the mutagenic, reverse primer (G121V-F125M-reverse) is 5′-ATG GGT GTC TAC TTC CAC CTC-3′. The sequence of the mutagenic, forward primer (M42W-F125M-forward) is 5′-GTG ATT TGG GGC CGC CAT ACC-3′, and the sequence of the mutagenic, reverse primer (M42W-F125M-reverse) is 5′-GGT ATG GCG GCC CAT AAT CAC-3.

PCR reaction was completed using pET22b-DHFR as a template for single mutants and pET-22b-F125M as a template for double mutants. The original template was digested with the DpnI restriction enzyme, and the PCR product was transformed into DH5α cells. Plasmid was extracted from the overnight culture, and the sequence was verified by automated DNA sequencing by the University of Iowa DNA facility. Primers were purchased from Integrated DNA Technologies. E.coli ΔfolA BL21(DE3) cells were transformed with the pET-22b-derived expression plasmid prior to expression and purification. F125M, W133F, G121V-F125M, and M42W-F125M DHFR mutants for single turnover and KIE measurements were expressed, purified, and stored using methods discussed elsewhere.^23,43,44

Synthesis of Labeled Cofactors for Primary KIEs

[Ad-¹⁴C]-NADPH, (R)-[Ad-¹⁴C, 4-²H]-NADPH, and (R)-[4-³H]-NADPH were synthesized according to previously published procedures.⁴⁵⁻⁴⁹ Briefly, for [Ad-¹⁴C]-NADPH and 4R-[Ad-¹⁴C, 4-²H]-NADPH synthesis, [Ad-¹⁴C]-NAD⁺ was used as a starting material and was phosphorylated into NADP⁺ using the enzyme NAD⁺ kinase (NADK) from chicken liver. In the case of [Ad-¹⁴C]-NADPH synthesis, [Ad-¹⁴C]-NADP⁺ was subsequently reduced with glucose using GluDH.⁴⁷ (R)-[Ad-¹⁴C, 4-²H]-NADPH was synthesized from [Ad-¹⁴C]-NADP⁺ by reduction with deuterated isopropanol and alcohol dehydrogenase from Thermoanaerobium brockii (tbADH).⁵⁰ (R)-[4-³H]-NADPH was synthesized by reduction of NADP⁺ with 2-deoxy-d-glucose-³H using GluDH, followed by oxidation of the resulting (S)-[4-³H]-NADPH with acetone using tbADH, and finally reduced using GluDH and unlabeled glucose, as described previously.⁴⁸ All synthesized cofactors were purified by semipreparative reverse-phase HPLC on a Supelco column and stored at −80 °C prior to use.⁴⁶

Competitive KIE Experiments

(4R)-[Ad-¹⁴C,4-²H]-NADPH or [Ad-¹⁴C]-NADPH and (4R)-[4-³H]-NADPH were combined in a 1:6 DPM ratio of ¹⁴C:³H (to compensate for the lower efficiency of ³H scintillation counting), for primary D/T or H/T KIE experiments, and copurified using reverse-phase HPLC to remove impurities. The copurified radiolabeled NADPH was divided into aliquots containing 300 000 DPM of ¹⁴C, and flash frozen for short-term storage (up to 3 weeks) at −80 °C. All experiments were performed in MTEN buffer (50 mM MES, 25 mM Tris, 25 mM ethanolamine and 100 mM NaCl) at pH 9.0, across the temperature range 5–45 °C. DHF was added to a final concentration of 0.85 mM, which is approximately 200-fold excess over NADPH (final concentration of 4 μM). Enzyme was added to initiate the reaction, and at different time intervals the reaction was quenched by adding an excess of methotrexate (K_d =1 nM), and stored on dry ice until HPLC analysis. The quenched reaction was bubbled with oxygen to completely oxidize tetrahydrofolate. The samples were separated by reverse phase HPLC.⁴⁶ The fractional conversion (f) of NADPH was determined as per the following equation, from the ratio of ¹⁴C in the product to the total amount of ¹⁴C in the product and reactant peaks:

1

The observed KIEs were calculated according to the following equation:

2

Here R_t is the ³H:¹⁴C ratio in products at fractional conversion f, and R_∞ is that ratio at 100% conversion. The intrinsic KIEs were extracted from the respective observed values by using the modified Northrop equation^32,51,52

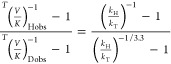3

where ^T(V/K)_Dobs and ^T(V/K)_Hobs are the observed competitive D/T and H/T KIE values, respectively, and k_H/k_T represents intrinsic H/T KIE. The intrinsic KIEs were calculated numerically from all the possible combinations of observed H/T and D/T values. The equations were numerically solved using a program that is freely available on our website under tools: https://chem.uiowa.edu/kohen-research-group/calculation-intrinsic-isotope-effects. All intrinsic values were fitted to the Arrhenius equation in order to determine the isotope effect on the Arrhenius pre-exponential factors as well as the temperature dependence of the KIEs.

Calculation of Kinetic Complexity

The observed KIEs were measured under irreversible reaction conditions; the reverse commitment to catalysis is negligible, and thus, the observed KIE is deflated from the intrinsic value according to eq 4(51,53,54)

4

where KIE_obs is the observed KIE on the second-order rate constant k_cat/K_M, KIE_int is the intrinsic KIE, and C_f is the forward commitment to catalysis for hydrogen transfer, which is the sum of the ratios between the rate of the forward, isotopically sensitive hydride-transfer step and each of the rates of the preceding backward, isotopically insensitive steps.

Single Turnover Rates

The single turnover rates of the mutant variants of DHFR were measured by monitoring NADPH fluorescence at 450 nm using an Applied Photophysics SX20 stopped-flow spectrophotometer as described previously.^12,40 Briefly, a 20 μM solution of DHFR was incubated with 15 μM NADPH at 25 °C. The solution was then rapidly mixed with 100 μM dihydrofolate, and the fluorescence decay was monitored at 450 nm using a 400 nm cutoff filter. The excitation wavelength was 340 nm, and all experiments were carried out in 50 mM MTEN buffer at pH 7.0. The data were fit to a single exponential function and are reported as the average of three independent measurements.

Results and Discussion

Temperature Dependence of Intrinsic KIEs

Competitive primary H/T and D/T KIEs on the second-order rate constant k_cat/K_M were measured for F125M, W133F, G121V-F125M, and M42W-F125M DHFR at temperatures ranging from 5 to 45 °C. The methods employed were the same as those used to study WT DHFR and G121V, M42W and G121V-M42W DHFR.^25,28−30 Intrinsic KIE values were then calculated from the observed values by methods described in previous publications.^25,40,49 Figure 2 shows the Arrhenius plots of the intrinsic KIEs for the mutants and the WT enzyme. These data were fitted to the Arrhenius equation in order to obtain isotope effects on the activation energy (ΔE_a(T-H)) and on the Arrhenius pre-exponential factor (A_H/A_T), where H and T refer to protium and tritium isotopologues, respectively. All the observed and intrinsic KIEs, their standard deviations, and the Arrhenius plots for the new mutants examined here are listed in Supporting Information Tables S1–S4 and Figure S1–S4.

Figure 2.

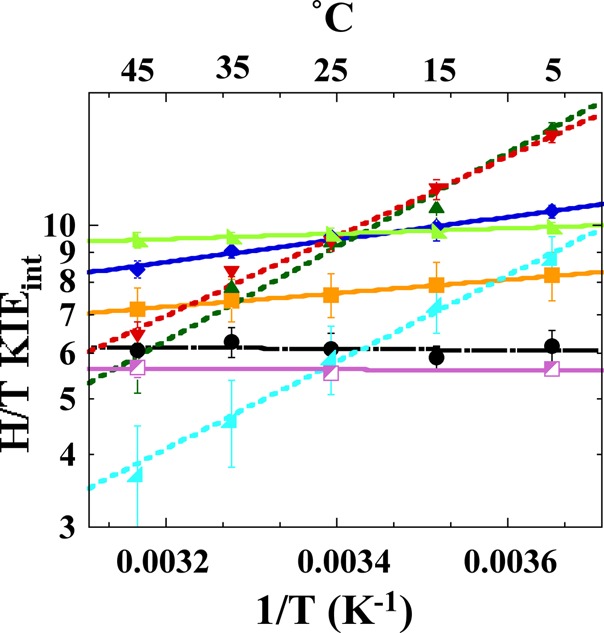
Comparison of Arrhenius plots of intrinsic H/T KIEs of WT (black; ref (30)) and distal DHFR mutants: W133F (magenta), M42W (orange; ref (28)), G121V (light green; ref (29)), F125M (dark blue), M42W-F125M (dark green), G121V-F125M (red), M42W-G121V (light blue; ref (25)). The lines represent the nonlinear regression to Arrhenius equation; dashed lines are used for WT, solid lines for single mutants and dotted lines for the double mutants. The error bars represent standard deviation.

As is evident in Figure 2 and Table 1, the intrinsic H/T KIE values for F125M were greater in magnitude than those of the WT enzyme, and showed steeper temperature dependence than did any of the other DHFR single-distal mutants for which data are available (i.e., G121V, M42W, or W133F). Additionally, ΔE_a(T-H) values are larger than zero but less than 1 kcal/mol for F125M, as was the case for both G121V and M42W (Table 1). F125M also showed A_H/A_T values greater than the upper limiting semiclassical value, as did G121V and M42W.^28,29 Such an isotope effect on the Arrhenius pre-exponential factors (A_H/A_T) indicates that semiclassical models cannot explain the findings with or without tunneling correction.³² These features (inflated KIE values, a moderate temperature dependence of the intrinsic KIEs relative to the wild-type enzyme, and A_H/A_T above the semiclassical limits) have been interpreted previously as an indication that this residue is of importance in the dynamic modulation of the DAD (donor–acceptor distance) for hydride-transfer at the TRS.^5−7,25 In addition, the slope of the Arrhenius plot (ΔE_a(T-H)) is a meaningful indicator of the nature of the hydride transfer. A slope close to zero indicates narrow DAD distribution, and greater slope indicates broader distribution.

Table 1. Comparative Kinetic Parameters from Arrhenius Plot and Single Turnover Rates of Distal Mutants and Wild Type E. coli DHFR.

DHFR	khyd(S-1)a	kwt/kmut	AH/ATb	ΔEa(T-H)b (kcal/mol)	ΔΔEa(T-H)c
WT	228 ± 8d		7.0 ± 1.5d	–0.1 ± 0.2d
W133F	88 ± 1	3 ± 0.1	5.8 ± 0.8	–0.01 ± 0.08
G121V	1.4 ± 0.2e	163 ± 24	7.4 ± 1.6e	0.23 ± 0.03e
M42W	5.6 ± 0.4f	41 ± 3	2.8 ± 0.2f	0.58 ± 0.04f
F125M	5.44 ± 0.03	42 ± 2	1.9 ± 0.3	0.96 ± 0.09
G121V-F125M	3.76 ± 0.04	61 ± 2	0.03 ± 0.004	3.4 ± 0.1	2.2 ± 0.1
M42W-G121V	0.03 ± 0.01g	7600 ± 1300	0.1 ± 0.1g	3.6 ± 0.3g	2.8 ± 0.3
M42W-F125M	0.45 ± 0.02	512 ± 31	0.01 ± 0.003	4.0 ± 0.2	2.5 ± 0.4

^aPre-steady-state rates of H transfer at 25 °C and pH 7.

^bSimilar trends were observed for H/D and D/T (data not shown).

^cΔΔE_a(T-H) = ΔE_{a(T-H)mutant1–2} – (ΔE_{a(T-H)mutant1} + ΔE_{a(T-H)mutant2}).

^dReference (30)

^eReference (29).

^fReference (28).

^gReference (25).

The double mutants G121V-F125M and M42W-F125M were used to investigate whether F125 is a component of the same proposed global dynamic network that G121 and M42 are part of, according to studies of their double mutant G121V-M42W.²⁵ The findings presented in Figure 2 and Table 1 show that both G121V-F125M and M42W-F125M have intrinsic KIEs with steep temperature dependence; in other words, ΔE_a(T-H) ≫ 1 relative to their respective single mutants (0 < ΔE_a(T-H) < 1) and the WT (ΔE_a(T-H) ≈ 0). The double mutants also presented A_H/A_T ratios below the lower semiclassical limit of 0.3,³² while their respective single mutants and the WT presented A_H/A_T > 1. In terms of Marcus-like models,^6,8,35 these findings imply that, at its TRS, the average DAD for the WT is optimal for hydride transfer and has a narrow distribution around the average. The single mutants are similar to WT, but their average DAD is longer, resulting in larger KIEs.³⁰ The DAD ensemble is also somewhat broader, leading to some temperature dependence of their KIEs. The DAD’s distribution is broadest for the double mutants, leading to very steep temperature dependence of their KIEs. These results implicate F125 as a third residue involved in the network-coupled motions in ecDHFR.

Intrinsic KIEs of W133F

Bioinformatics analysis predicted that W133 might participate in the same proposed dynamic network as G121, M42, and F125.¹⁰ However, our experiments reveal no significant changes in either single-turnover rate or intrinsic KIEs when the size of that residue is reduced from tryptophan to phenylalanine. Single turnover rate, k_hyd, is only 3-fold slower for W133F, and its intrinsic KIEs are similar in magnitude to those of WT across a temperature range 5–45 °C. These results do not support the participation of W133 in the network of coupled motions that G121, M42, and, we suggest, F125 are part of. The fact that W133F has no effect on the intrinsic KIEs and their temperature dependence is an important result, because if every remote mutation tested were to alter the nature of the hydride transfer, it would not support the existence of a discrete/distinct “network”, and would suggest a more globally uniform role of all residues in catalysis. Moreover, W133 might very well be coupled to other residues, affecting other protein functions such as folding or solubility, but not to the network affecting the chemical step.

Comparison between Active Site Mutants and Distal Mutants

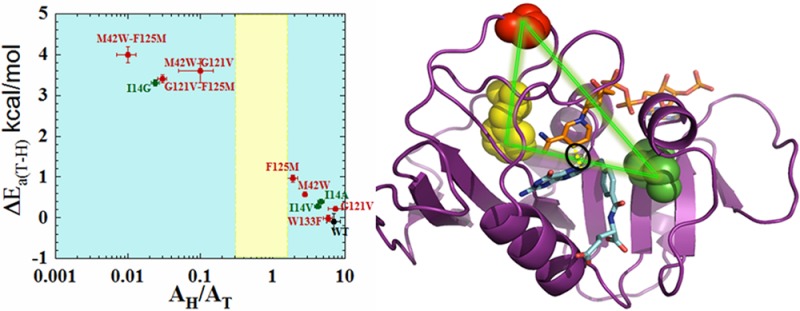
Since it is easier to understand the effect of local mutants on the DAD, the effects of the remote mutants studied here can be evaluated and described by comparison with the function of the well-characterized active site residue I14.⁴⁰ The bulky and hydrophobic I14 is located behind the nicotinamide ring and appears to hold the H-donor close to the H-acceptor.⁴⁰ In ref (40) we systematically reduced the size of the side chain of I14 to generate I14V, I14A, and I14G mutants. As indicated in Figure 3, moderate reductions of the side chain (I14V and I14A) were found to result in A_H/A_T and ΔE_a(T-H) values similar to those found for the remote single mutants (F125M, G121V, and M42W). Further reduction in the size of the side chain of I14 (i.e., I14G), however, results in A_H/A_T values below the semiclassical limit and steeply temperature-dependent KIEs,⁴⁰ with values similar to those for all the remote double mutants under study. MD calculations for the active site mutants indicated that I14 modulates the DAD for hydride transfer by “holding” the nicotinamide ring (H-donor) close to the folate (H-acceptor), and restricts the DAD to a narrow and well-reorganized ensemble for efficient H tunneling.⁶ Reducing the side chain of this residue thus results in a proportionally less-reorganized TRS with broader thermal sampling of the DAD, which is manifested in more steeply temperature dependent KIEs.⁵⁵ The correlation between the results of the distal mutants and those obtained for the I14 mutants is graphically summarized in Figure 3. The parameters obtained from the Arrhenius plots of the single mutants are clustered around the I14A and I14V mutants, whereas those of the double mutants are clustered around I14G. Consequently, one can envision the effect of the remote mutants on the structure and dynamics of the active site as being similar to that of the active site mutation, causing similar perturbation of the intrinsic KIEs and their temperature dependence. The single remote mutants have moderate but significant effects on the DAD distribution and average length, as I14V and I14A do, whereas the double mutants cause much more dramatic changes that are analogous to those seen in MD simulations with I14G.⁴⁰ The similarities between the effects of active site and remote mutants provide a valuable benchmark for assessing the effects of remote mutants on the dynamics associated with H-tunneling. These may allow us to understand the kinetic findings on a molecular level, by analogy to the active-site mutants that are easier to apprehend from a structural perspective.

Figure 3.

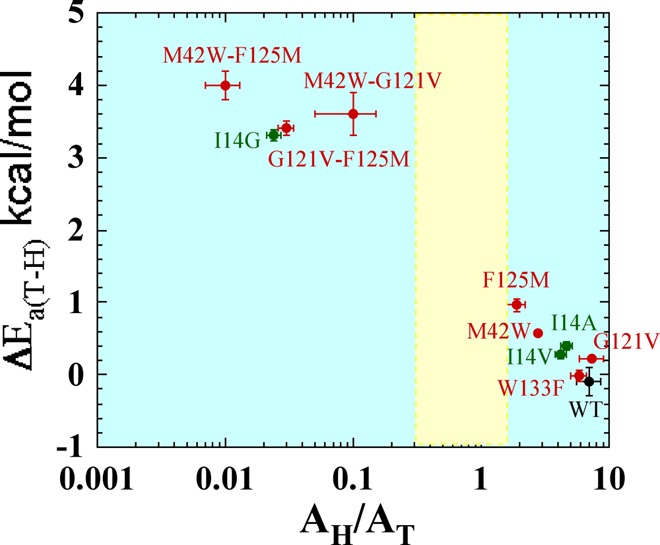
Correlation of temperature dependence parameters of WT (black), distal (red), and local (green) mutants of DHFR, where error bars represent standard deviation. Yellow block represents semiclassical range of Arrhenius pre-exponential factor (0.3–1.7).³²

Fitting the Temperature Dependence of Intrinsic KIEs to a Phenomenological Model

The above discussion used isotope effects on Arrhenius parameters (A and E_a) to assess the effect of mutations on the catalyzed chemical conversion (C–H→C hydride transfer). The intrinsic KIEs and their temperature dependence can also be fitted via nonlinear regression to a simple phenomenological model with two alternative parameters. Rather than the entropy and enthalpy parameters that result from of the Arrhenius or Eyring equations, a regression to the Marcus-like model results in an average DAD₀ and its distribution (f, the force constant).⁵⁵ In this fitting procedure, in the case of very steep KIE temperature dependence (ΔE_a > 1 kcal/mol), a single DAD’s population model cannot fit the data. Two populations of DADs are needed, one from which H tunnels and one that is already over the energy barrier.⁵⁵ In the latter case the two regression parameters are the average DAD of the population at longer distances (DAD_long) and the energy difference between these two populations (ΔG). Either of these two parameters (from these two regressions to Marcus-like models) is potentially more useful in understanding the effect of mutation on the enzyme at the molecular level than the isotope effects on entropy and enthalpy that result from the traditional fit to the Arrhenius equation. All of the DHFR single remote mutants studied so far had ΔE_a < 1 and thus were fitted using the single-population model, while all the double mutants (ΔE_a >1) were fitted using a two-population model. Please note that the two-population model can be fitted to any set of data, but is less informative than the one population model as DAD_long and ΔG are less direct probes for the distribution of DADs at the TRS than are f and DAD₀. The fitted parameters are listed in Table 2 and graphically presented in Figure 4.

Table 2. Fitting Parameters of 1 Population and 2 Populations of Distal Mutants and Wild Type E. coli DHFR.

	1 population		2 populations
DHFR	DAD0 (Å)	f (kcal/mol/Å2)	DADL (Å)	ΔG (kcal/mol)
WT	3.06 ± 0.06a	>250a,b	3.06 ± 0.004a	>2.5a,b
W133F	3.06 ± 0.00003	>250b	3.05 ± 0.0002	>2.9b
G121V	3.08 ± 0.001a	390a	3.07 ± 0.0002a	2.86 ± 0.06a
M42W	3.12 ± 0.006a	80 ± 7a	3.07 ± 0.001a	1.87 ± 0.05a
F125M	3.24 ± 0.05	26.9 ± 8	3.09 ± 0.005	1.69 ± 0.07
G121V-F125M			3.29 ± 0.006	3.73 ± 0.1
M42W-G121V			3.34 ± 0.02a	4.39 ± 0.3a
M42W-F125M			3.33 ± 0.005	4.51 ± 0.09

^aReference (55).

^bIn case of temperature independent KIEs, i.e., whenever the trend in values with temperature is smaller than the experimental error, the regression gives a value that represents the experimental error as the upper limit of the parameter’s value (f or ΔG). This value is not an indication of a trend in KIEs vs temperature, just of the experimental confidence in the limiting value.

Figure 4.

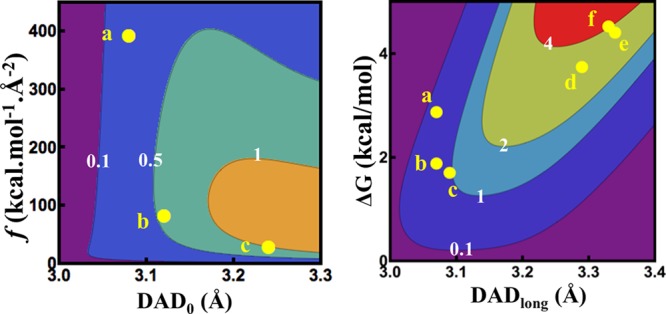
Contour plots of ΔE_a in kcal/mol (values in white digits) as a function of (left) average DAD (DAD₀) and force constant (f) and (right) DAD of the long population (DAD_long) and the difference in free energy between the two populations (ΔG). The yellow dots represent the different mutants and are labeled as follows: a, G121V; b, M42W; c, F125M; d, G121V-F125M; e, M42W-G121V; f, M42W-F125M (errors for all the points are smaller than the dot representing the data).

As is apparent in Figure 4, right panel, in the double mutants the dominant tunneling-population at the TRS is centered at a longer DAD, where the probability of tunneling is much higher with the lighter protium than with the heavier deuterium or tritium. The ΔG values of the double mutants indicate that a significantly smaller population is centered at a shorter DAD, where the zero point energy (ZPE) is above the energy barrier for all isotopes of H. With increasing temperature, the population at shorter DAD grows, resulting in smaller KIE values, thus leading to steep temperature dependence of the KIEs. All the single mutants have a narrower distribution of DADs with shorter average DAD than their respective double mutants’, in accordance with their weaker temperature dependence than the double mutants’ (Figure 4).

Apparently, F125M has a longer average DAD₀ and a lower force constant (f), indicating broader DAD distribution at the TRS,⁵⁵ or a more poorly reorganized TRS than any other single distal DHFR mutants have. F125M is also associated with a larger ΔE_a than the other single mutants are. As illustrated in Figure 4, the single distal mutants G121V, M42W, and F125M have smaller temperature dependence of KIEs than their respective double mutants do. The observation that single mutants have little effect on the nature of hydride transfer while the double mutants have a much more pronounced effect has been interpreted as a synergistic effect consistent with these two residues’ functioning as part of the same global network.^10,25 As is apparent from Tables 1 and 2, W133F’s KIEs and their temperature dependence are not significantly different than the WT’s (within experimental errors), indicating no involvement of that residue in the C–H → C transfer process. The last outcome is not trivial, as k_hyd for W133F is one-third the rate of the WT’s, and its kinetic complexity is reduced (see below), indicating effects on other kinetic stapes but the chemical one.

Single Turnover Rates

Single turnover rates were measured for all the mutants. These measurements were made using the procedures described previously,²⁷ and the rates are summarized in Table 1. Both G121V-F125 M and M42W-F125M show dramatic changes in both KIEs and single turnover rates.

The single turnover rate includes several microscopic kinetic steps occurring between the formation of the ternary reactants complex and the hydride transfer step. Those may include the closing of the M20 loop, flipping of the nicotinamide ring into the active site, and protonation of the reactant (N5). It is interesting to note that the F125M-G121V is somewhat faster than G121V, while the other DHFR double mutants were slower than the associated single mutants; nevertheless, it is not unprecedented in enzymology for a second mutation to correct the perturbation caused by the first one. The fact that k_hyd for F125M-G121V is faster than it is for G121V, while the temperature dependence of its intrinsic KIEs is steeper, indicates that the F125M mutation corrected the disturbance caused by G121V for steps that precede the activation of the C–H bond of the hydride donor, but that the chemical conversion (C–H → C transfer) per se was dramatically disrupted as it was in the two other double mutants. This is not unexpected as the preactivation steps occur at the ms time scale and the chemical conversion occurs at the ps–fs time scale. This interpretation is also in accordance with a similar observation made for another distal mutant of DHFR (N23PP), where the M20 loop dynamics are slower than the WT’s; this mutant had to explore a much broader set of conformational changes across the protein, going from ground state to TS for the hydride transfer.⁵⁶

Kinetic Complexity

In most enzymatic and organic reactions, the experimentally observed KIE is smaller than the intrinsic KIE, which is explained by a “kinetic complexity” that is masking the intrinsic effect. In reactions with significant kinetic complexity, isotopically insensitive steps mask the isotope effect on the chemical step, making the observed KIE smaller than the intrinsic KIE. Hence the observed KIE will be smaller than intrinsic KIE by an amount depending on the “commitment to catalysis” (see eq 4 under Experimental Section).⁵²

The Arrhenius plot of wild type and all DHFR mutants on their commitment to catalysis on k_cat/K_M for H-transfer (C_f in Supporting Information eq S4) is illustrated in Supporting Information Figure S5. At physiological temperature W133F has lower commitment than the WT (Supporting Information Figure S5), but its commitment has two phases, as does the commitment in the WT, suggesting similar behavior for both enzymes. Unlike WT and W133F, all other mutants demonstrate a continuous, almost linear trend of commitment with temperature, which could indicate that a single step is responsible for most of the commitments throughout the temperature range.

Conclusions

According to Marcus-like phenomenological models, the temperature dependence of intrinsic KIEs arises from thermally activated conformational sampling, which brings the donor and acceptor partners to a tunneling ready state (TRS).^6,25 Like most native enzymes with their natural substrates under physiological conditions, WT DHFR accurately reorganizes the H-donor and acceptor into a narrowly distributed TRS, and thus exhibits temperature independent intrinsic KIEs. W133F, while 3-fold slower than the WT, retains that behavior, indicating that while W133 might very well be coevolving with G121, M42, and F125,¹⁰ this residue does not affect the chemical step and is not part of the dynamic network correlated with the C–H activation. In contrast, the temperature dependence of the intrinsic KIEs for F125M (8 Å from the active site) indicates that the mutation disrupts the ability of the enzyme to perfectly reorganize the TRS, and the much steeper temperature dependence of the intrinsic KIEs of its double mutants with G121V and M42W indicates that it is a part of the network predicted in refs (10 and 25,41).

The results presented herein strongly validate calculations predicting that F125, G121, and M42 are part of the same network of dynamic motions that is correlated with the hydride transfer step.^21,22,57,58 Interestingly, all the residues discussed here (42, 121, 125, 133) were also predicted to be coevolving by bioinformatics analysis of DHFR genes from many organisms.¹⁰ The finding that not all of those coevolving residues¹⁰ are part of the dynamic network that affects the chemical step suggests that some coevolution might be related to other protein functions, such as folding, solubility, etc. These results implicate an effect of the whole protein structure and dynamics on the catalyzed chemistry and provide a rationale for why enzymes are so much larger than their active sites as well as why there are conserved and coevolved distal residues far from the active site.

Supporting Information Available

Arrhenius plot for observed and intrinsic KIE for each mutant, forward commitment plot for all the mutants, and observed and intrinsic KIE values. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Present Address

^† Institute of Pharmaceutical Science, King’s College London, Franklin-Wilkins Building, 150 Stamford Street, London SE1 9NH, United Kingdom.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States