External and middle ear sound pressure distribution and acoustic coupling to the tympanic membrane

Abstract

Sound energy is conveyed to the inner ear by the diaphanous, cone-shaped tympanic membrane (TM). The TM moves in a complex manner and transmits sound signals to the inner ear with high fidelity, pressure gain, and a short delay. Miniaturized sensors allowing high spatial resolution in small spaces and sensitivity to high frequencies were used to explore how pressure drives the TM. Salient findings are: (1) A substantial pressure drop exists across the TM, and varies in frequency from ∼10 to 30 dB. It thus appears reasonable to approximate the drive to the TM as being defined solely by the pressure in the ear canal (EC) close to the TM. (2) Within the middle ear cavity (MEC), spatial variations in sound pressure could vary by more than 20 dB, and the MEC pressure at certain locations/frequencies was as large as in the EC. (3) Spatial variations in pressure along the TM surface on the EC-side were typically less than 5 dB up to 50 kHz. Larger surface variations were observed on the MEC-side.

INTRODUCTION

As sound propagates along the ear canal (EC), the tympanic membrane and ossicles (together comprising the middle ear) are set into motion and provide an efficient path for energy flow into the inner ear. While there has been extensive study of the middle ear, precisely how the sound pressure drives the tympanic membrane (TM) is still not well understood, particularly at higher frequencies. The TM displays a complex pattern of motion above several kHz (Khanna and Tonndorf, 1972; Decraemer et al., 1989; Furlong et al., 2009; Rosowski et al., 2013; Cheng et al., 2013), a feature that likely is related to the middle ear's remarkable performance (Fay et al., 2006). In gerbil, the species studied here, forward transmission is broadband (i.e., spectrally flat transmission to the inner ear) with a passive gain of 20–30 dB and a delay of ∼25 μs (Olson, 1998; Dong and Olson, 2006). A recent empirical study (de La Rochefoucauld and Olson, 2010) suggested that TM motion is comprised of a superposition of two modes of motion, one that is “piston-like” and another that is “wave-like.” However, to what extent each of these modes contributes to sound propagation through the middle ear is still an open question. Another study (Puria and Allen, 1998) posited that the wave-like component can be explained by describing the TM as a lossless transmission-line that supports traveling waves.

Three further physical aspects of the middle ear bear consideration. The first deals with the acoustics of the middle ear cavity (MEC).1 At frequencies below several kHz, lumped element formulations can be employed and have been used extensively to study middle ear function [e.g., Zwislocki (1962); Lynch et al. (1994)]. However at higher frequencies, more complex acoustical effects are present in the MEC and may affect middle ear transmission. For example, one theoretical model (Rabbitt, 1990) showed that reflections off the bullar wall could enhance the pressure drive to the TM. The second is to what extent the TM absorbs incident energy as opposed to reflecting it. Numerous studies have examined spatial variations in EC sound pressure to characterize reflectance off the TM [e.g., Stinson et al. (1982); Stinson and Khanna (1989); Ravicz et al. (2007)]. Indeed, reflectance off the TM measured in the EC forms a foundation for basic clinical tools (i.e., tympanometry) and has been developed in a number of other novel audiological applications [e.g., Keefe et al. (1992); Feeney and Keefe (1999); Keefe et al. (2010)]. One study suggested that the mechanical load upon the TM (in particular the cochlea acting as a resistive load) greatly affects the degree of reflectance (Puria and Allen, 1998). A third important aspect of the middle ear (not explored in the present study) is how it operates in the reverse direction, specifically how energy generated as otoacoustic emissions (OAEs) in the inner ear makes it out to the EC where it can be measured with an external microphone. Various studies have examined the validity of the middle ear acting in a reciprocal fashion [e.g. Shera and Zweig (1992); Puria (2003); Voss and Shera (2004); Dong and Olson (2006); Dalhoff et al. (2011); Dong et al. (2012)], a consideration relating back to modeling the middle ear as a two-port network.

The goal of the present study is to explore how sound pressure effectively drives the TM and thereby conveys acoustic energy to the inner ear, particularly at higher frequencies (1–60 kHz). Our approach is to use micro-sized pressure transducers (Olson, 1998) to map out the sound pressure distribution in both the external and middle ear cavities. Several specific questions this experimental study aims to address are:

• (1)What is the pressure ratio directly across the TM?
• (2)How does the pressure vary along the TM surface (on both sides)? Do spatial variations exist that relate to the wave-like motion of the TM?
• (3)What is the spatial dependence of sound pressure in the MEC? Is there evidence for reflections from the bony back wall that could in turn affect TM motion?
• (4)How does the physiological state of the TM (removal of pars flaccida and/or pars tensa, overt drying) affect sound pressure distribution in the EC and MEC? What effect does ossicular disruption (i.e., removing the cochlear load) have?

To address these questions, we focus here on gerbil (Meriones unguiculatus), due to the relatively large MEC and the fact that there has been extensive study on both middle and inner ear function in this species.

METHODS

Geometric reference

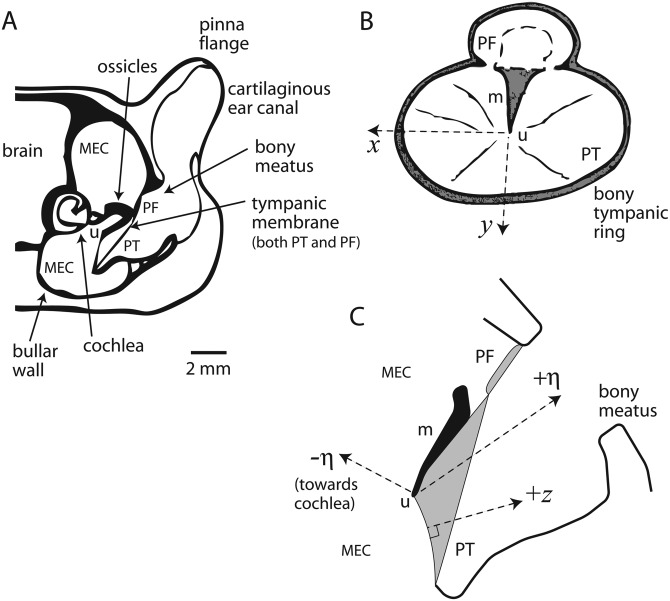
It is useful to define a geometric framework indicating the spatial orientation of our measurements and thereby provide a structure for discussing the physical interpretation. Based upon the experimental approach, we chose to use the TM surface as the reference and describe Euclidian space via a pair of curvilinear coordinates (x and y) and one linear coordinate (z).

The origin of the coordinate system is the umbo (Fig. 1). Curvilinear axes x and y both point away from the umbo along the surface of the TM: x points in a direction orthogonal to the manubrium while y in a direction parallel to the manubrium [see Fig. 1B]. Thus, any point along the surface can be described by a given coordinate pair (x, y), all referenced relative to the umbo. Since both axes extend along the curved TM surface, they are not straight lines. z is the distance from a point (x, y) on the TM surface in the direction orthogonal to the surface at that point.2z = 0 at the TM surface, z > 0 into the canal, and z < 0 into the MEC. We also define +η, which points along a straight line from the umbo toward the bony meatus roughly parallel to the manubrium [see Fig. 1C]. Typically, η ∈ [0, 3.5] mm spanned the distance from the umbo to the plane of the bony meatus. On the MEC side, −η points toward the bony cochlear bulge. For positions very close to the umbo [i.e., (x, y, z) ∼ (0, 0, ±40 μm)], we will use the shorthand notation z (or η) ∼ 0^±. Also note that as schematized in Fig. 6, we define a dimension z′ where the sensor path moves back toward the bullar wall, but that path is not necessarily orthogonal to the TM surface for the given (x, y) starting point.

Figure 1.

(A) Schematic of general anatomy of gerbil auditory periphery [adapted from Ravicz et al. (1992) with permission from the author]. (B) Indicates coordinate system for describing measurements. The umbo (u) is used as a reference for the origin. The view is looking into the residual ear canal at the TM through the bony meatus [adapted from Rosowski et al. (1999) with permission of the author]. Dashed arrows indicate the x- and +y-axes, which are orthogonal to one another and referenced relative to the manubrium (m). These two axes trace out the inner surface of the TM (i.e., they are not straight due to the curvature of the TM). The two regions of the TM are indicated: pars tensa (PT) and pars flaccida (PF). (C) The +z axis points into the EC from the TM for any point (x, y) along the surface. Similarly, −z points away from the TM into the MEC. The +η-axis points from the umbo outward toward the center of the meatus; −η-axis points from the umbo inward toward the bony bulge of the cochlea.

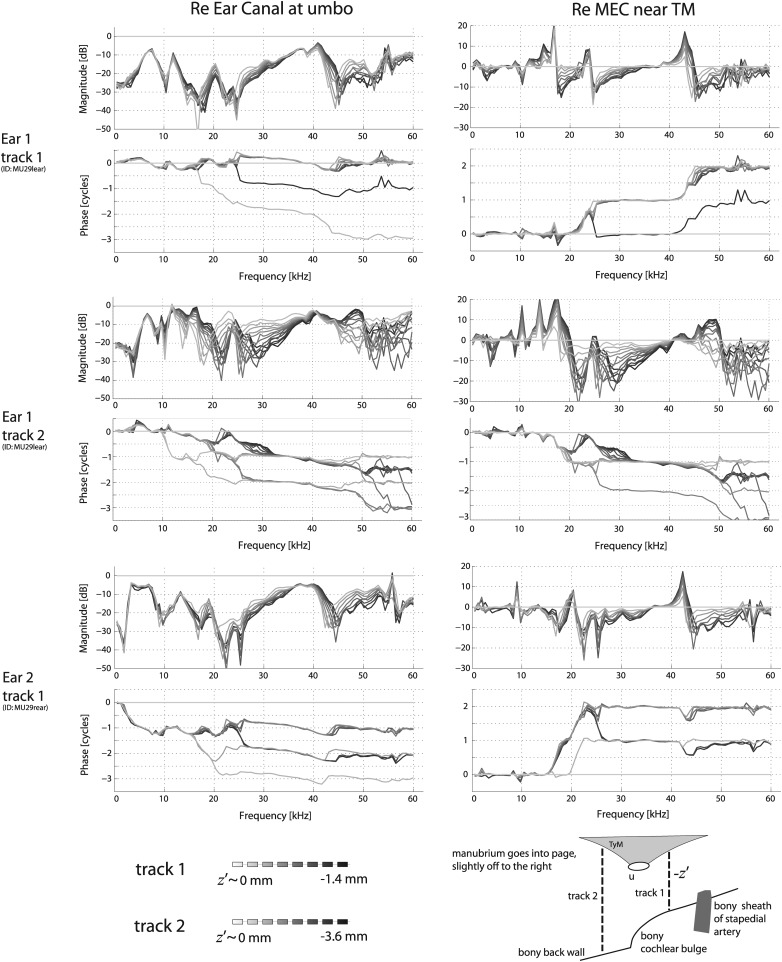
Figure 6.

Variations in pressure in the MEC as the sensor was moved from close to the TM toward the back bony wall [P_MEC(−z′)] for different placements along (x, y) as indicated in the bottom panel. The left column shows the response for a given z′ track relative to the EC-side pressure at the umbo {i.e., $\mathbf{[}{\mathbf{P}}_{\text{MEC}}(z^{\prime })]/[{\mathbf{P}}_{\text{EC}}(\eta \sim 0^{+})]$} while the right-hand column is relative to the MEC-side pressure closest to the TM {i.e., $\mathbf{[}{\mathbf{P}}_{\text{MEC}}(z^{\prime })]/[{\mathbf{P}}_{\text{MEC}}(z^{\prime }=0)]$}. Darker curves indicate locations further away from the TM (closer to the back bony wall). Note that for these runs, the starting point was close to the TM but not right at the umbo (lower right schematic). Two different z′ tracks for one ear are shown here (thick lines in bottom schematic), while only one is shown for a second ear.

Definition of variables

The key variables relevant to the study are summarized in Table TABLE I. and are expressed as Fourier coefficients (measured in steady-state) throughout the manuscript. Typically, we directly measured P_EC(x, y, z) and P_MEC(x, y, z) while controlling P_stim, the sound pressure measured close to the speaker outlet by a probe microphone. The middle ear input impedance, Z_input, is the complex ratio of pressure at umbo on the EC-side [P_EC(η ∼ 0⁺)] to volume velocity at the TM, V_tym (Ravicz et al., 1992).

TABLE I.

Definition of basic physical quantities described in paper. All bold quantities listed are the (complex) Fourier coefficients, and thus are functions of frequency.

Variable	Description
PEC(x, y, z)	pressure in ear canal (EC)
PMEC(x, y, z)	pressure in middle ear cavity
Pstim	external stimulus pressure
${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}$	complex ratio of pressures across TM [Eq. 1]
HΔTM	pressure difference ratio across TM [Eq. 2]
Zinput	middle ear input impedance
ZMEC	impedance associated with MEC
Zc	characteristic impedance of air (at room or body temperature)

P_EC and P_MEC are spatially dependent and are shaped by their acoustic environment, including the dynamics of the TM. As the TM has been previously noted to exhibit multiple modes of motion, consistent with a sum of both “piston-like” and “wave-like” motions (de La Rochefoucauld and Olson, 2010), we further clarify terminology that will be returned to later. Because the TM is not a rigid object and must undergo elastic deformation when a force is applied to it, we will avoid the term “piston” here. However, the basic concept remains unchanged (and is similar to the dynamics of a simple circular/flat membrane): for lower frequency stimuli, when the whole TM moves in phase in a simple in/out fashion this motion can be described as uni-phasic. At higher frequencies, the motion becomes more complicated and the motion can be described as multi-phasic.3 The multi-phasic case may stem from standing waves and/or traveling waves along the TM surface.

Sound pressure measurements

Sound pressure was measured in two ways. First, a probe tube microphone (Leonard, 1964; Sokolich, 1977) was used that consisted of a 1/2 in. Brüel & Kjær microphone (type 4134, with a post amplifier type 2804) coupled with a custom cover that allowed for connection of a ∼2.3 cm probe tube with outer and inner diameters of 1.4 and 1.1 mm, respectively. This assembly was calibrated via a custom enclosure that allowed for a comparison to a separate 1/4 in. Brüel & Kjær microphone with known calibration and frequency response. The factory-calibration of the 1/4 in. Brüel & Kjær microphone (type 4938) was confirmed using a Brüel & Kjær pistonphone at 1 kHz. Second, fiber-optic pressure sensors were used (Olson, 1998) that allowed for insertion into relatively small spaces given their dimensions (∼100 μm diameter). Each pressure sensor was calibrated relative to the probe tube microphone both before and after each experiment to ensure stability.4 A drawback of the sensors was their sensitivity, as their noise floor (with a 1 Hz bandwidth) is typically 50–60 dB sound pressure level (SPL), flat across frequency. The sensor was positioned using both a manual and motor-controlled micro-manipulator. The latter allowed for steps as small as 1 μm, although ∼12 μm steps were generally used. Placement very close to the TM (within 10–20 μm) could be achieved by advancing the sensor until it “tapped” the surface, then drawing back one or two steps. This process did not damage the TM or change the sensor sensitivity. The angle of incidence of the sensor relative to the TM had no apparent effect upon the measured pressure. Microphone signals were bandpass filtered (PARC EG&G amplifier) between 0.01 and 300 kHz.

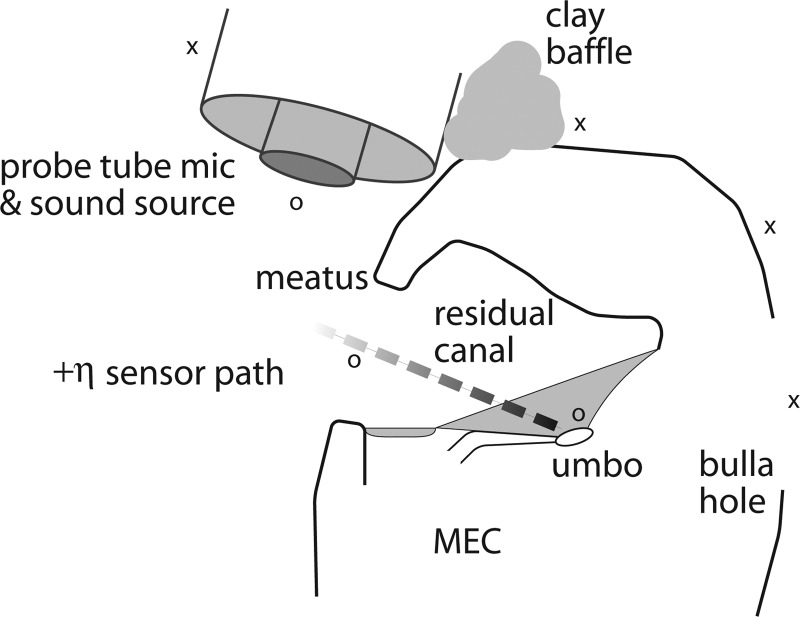
In order to make pressure measurements in the MEC, it was necessary to open up the bulla cavity to some extent. Additionally, for in vivo experiments, this was crucial to allow a vent and thereby prevent a buildup of static pressure in the MEC (presumably due to closure of the Eustachian tube under anesthesia). While these holes were made as small as possible, in some cases they needed to be substantial (e.g., 1 × 2 mm rectangle) to allow for sensor placement over a sufficient range of locations. An acoustic baffle (via clay) was placed between the acoustic assembly and the bullar hole (see Fig. 2). This issue is discussed in more detail in Sec. 3G.

Figure 2.

Schematic to show placement of sound source and probe tube microphone relative to residual (bony) meatus. Also note the path indicated for +η (see Sec. 2), which shows the shading scheme used in subsequent figures (e.g., Fig. 7) for measuring P_EC(η). The x and o symbols are discussed in results Sec. 3G.

Acoustic stimulation

The majority of stimuli were presented in open-field, as this allowed visual placement (via a surgical microscope) of the sensor tip at various locations in the EC and MEC. The acoustic source was a modified Radio Shack “Super-Tweeter” speaker. The speaker was coupled to the probe tube microphone via a short/flexible plastic tube and a custom brass coupler such that the speaker and microphone ports were at approximately the same location (see Fig. 2). The acoustic assembly was typically placed ∼1–2 mm lateral to the meatus. The stimulus sound level was calibrated in situ at the start and end of each experiment using flat-spectrum random-phase noise. A variety of stimulus types were used for the pressure measurements: single tones, chirps, and noise. For the broadband stimuli, levels at the probe tube microphone typically ranged from 50 to 90 dB SPL, while for narrowband stimuli, 100 dB SPL tones were used to ensure responses above the sensor noise floor. P_stim was typically measured precisely via the probe tube microphone (see Fig. 2), which could also be independently verified via the pressure sensor placed close to the microphone port. The sound pressure at the plane of the meatus [i.e., P_EC(η ∼ 3.5 mm)] was approximately P_stim − 10 dB. The speaker response was linear with respect to driving voltage over the range used (70–110 dB SPL). Although broadband and narrowband stimuli led to similar results, the majority of data reported here are for tone stimuli so to maximize the signal-to-noise ratio. A sampling rate of 195 kHz was used. The uncertainty across the averaging period for a given measurement (e.g., individual curves comprising Fig. 3) was small in that responses could be repeated with typically less than 1–2 dB change.

Figure 3.

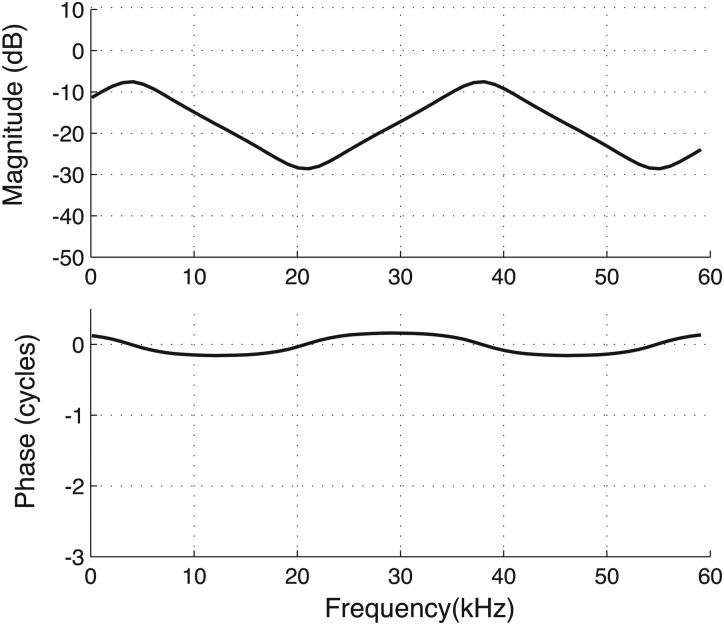
Transfer function indicating the pressure change across the TM. (A) Schematic to show sensor placement (thick black lines) used to measure ${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}$, placed within ∼40 μm of the umbo on either side of the TM. Only a single sensor was used, and it was placed sequentially between these two locations while all other physical aspects remained unchanged. The microphone is at the tip of the sensor, close to u. (B) ${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}$, the complex ratio of the MEC pressure relative to the EC pressure, P_MEC/P_EC). Each thin curve represents data from a unique ear (13 unique animals) and the thick curve for the magnitude is a locally weighted regression curve to emphasize the trend. In all measurements, a hole was made to the MEC as described in the Methods. (C) Same data, but plotted as H_ΔTM (see text). (D) Same as panel (C), except a linear frequency axis is shown.

Animals

Measurements were made both in vivo and postmortem. In some cases, postmortem measurements were necessary to allow experimental access (e.g., exposure of the medial side of the bulla wall). In other cases, postmortem measurements were continued after the animal had been euthanized with pentobarbital to examine changes in physiological state. Based on our own experience, as long as the tissues remain fresh and moist there is no apparent change in middle ear transmission for many hours postmortem [e.g., de La Rochefoucauld et al. (2008, 2010)]. The importance of keeping the middle ear tissues moist is well known from the temporal bone literature [e.g., Nakajima et al. (2005)].

Thirty female adult gerbils (Meriones unguiculatus) were used, some of these postmortem from other experiments. For in vivo measurements, animals were dosed first with ketamine to quiet the animal and then with sodium pentobarbital, with redosing as needed based on toe pinch response. Buprenorphine was administered as analgesic. Under anesthesia the middle ear reflex is absent in gerbil (Schmiedt and Zwislocki, 1977), so the middle ear muscles were left intact. Following in vivo measurements, the animal was overdosed with sodium pentobarbital. For postmortem data, measurements were made either within several hours following death, or the tissue was refrigerated in a moist paper towel and used on a subsequent day. In those cases, the tissue was allowed to come to room temperature and kept moist unless noted otherwise. Unless noted otherwise, for all postmortem data the ear was freshly exposed just prior to the start of the experiment (i.e., the pinna was removed, tissue removed around the meatus and bulla, and MEC opened). The pars tensa (parsT) and ossicles were left intact, except for experiments where these were purposely manipulated. In some experiments pars flaccida (parsF) was removed by penetrating and retracting it with an insect pin that was bent at its tip. For disarticulation (i.e., interruption of the incuo-stapedial joint), a fine needle was inserted through the bulla hole to displace the ossicles. Care was taken not to touch any other structure or put significant tension upon the TM. Unless noted otherwise, all data shown here are from temporal bones that were still embedded in the head (i.e., not extracted). Animal use was approved by the Columbia University IACUC.

Numerical simulations

Model computations were performed using Matlab, with sufficient spectral resolution to identify notch depth visually.

RESULTS

Middle ear transmission

Several experiments were made early in the study to characterize middle ear transmission (i.e., pressure just inside the scala vestibuli near the stapes footplate relative to pressure in the EC near the umbo) in order to verify reproducibility of that reported previously (Olson, 1998). While not shown here, these experiments were consistent with that previous report, even for tissue that was several days postmortem. This observation supported the use of postmortem tissue in the present study, provided that the tissue was kept sufficiently hydrated. As discussed in Sec. 3E, significant changes in pressure were observed upon drying out of postmortem tissue.

Trans-TM pressure $\left({\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}\right)$

The pressure change across the TM was computed as the (dimension-less) complex ratio of the response at the umbo in the MEC relative to the EC (${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}$), i.e.,

$${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}\equiv \frac{{\mathbf{P}}_{\text{MEC}}(\eta \sim 0^{-})}{{\mathbf{P}}_{\text{EC}}(\eta \sim 0^{+})}.$$ (1)

Data from 13 different ears are plotted in Fig. 3. A significant magnitude change is apparent, varying with frequency. Although there is variation between ears, the general level and shape of the curve emerges robustly from the grouped responses. Aside from jumps in the phase, some phase accumulation is apparent and suggestive of a short delay. These values were not much affected by making the measurements at different locations across the surface of the TM, as is described further in Fig. 5. Thus, ${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}$ does not exhibit a strong dependence upon x or y for small $|z|$. Also shown in Fig. 3 are the same data, plotted as the pressure difference ratio (H_ΔTM) [e.g., Pinder and Palmer (1983), Fig. 3(B) in Voss et al. (2001)], defined as

$${\mathbf{H}}_{\Delta \text{TM}}=\frac{{\mathbf{P}}_{\text{EC}}(\eta \sim 0^{+})-{\mathbf{P}}_{\text{MEC}}(\eta \sim 0^{-})}{{\mathbf{P}}_{\text{EC}}(\eta \sim 0^{+})}.$$ (2)

Figure 5.

Further analysis of pressure measured across the TM surface from Fig. 4 [panels (A) and (C)]. (A) Pressure data close to the TM presented as “snapshots” at nine times in the stimulus cycle. This presentation helps to visualize uni-phasic and multi-phasic (wave-like) components of the pressure pattern. The dashed curve in each panel is the time when the average pressure (over space) was greatest. (B) Spatial average of the pressure at instant in cycle when average amplitude was greatest [time of dashed curves in panel (A)]. Units for solid lines are Pascals, while the dashed/dotted lines show the unitless ratio. (C) Quantifying spatial pressure variation via the ratio of the spatial standard deviation and spatial mean at the time in the cycle when the average was greatest [time of dashed curves in panel (A)].

Near-TM surface pressure

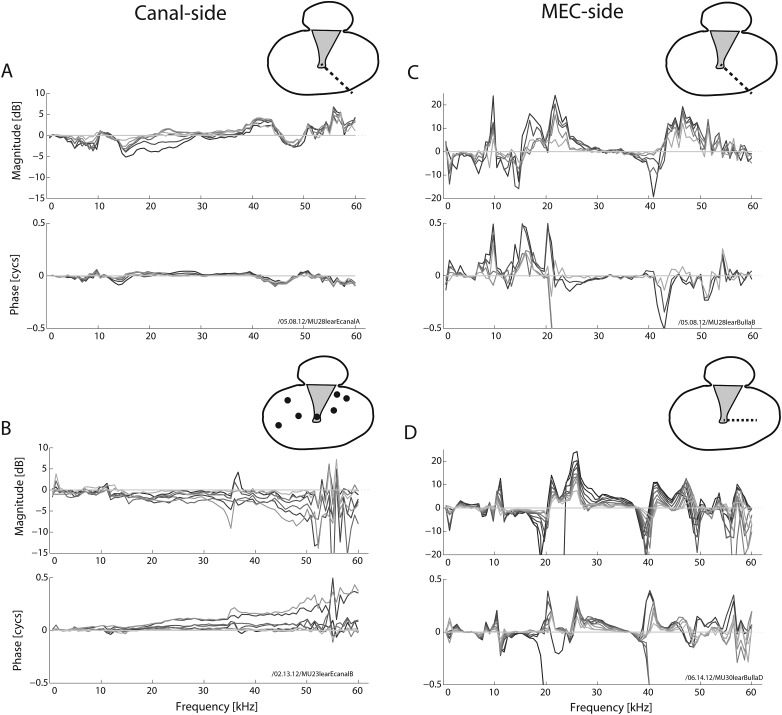
Because TM motion is known to exhibit substantial phase differences across its surface, we explored whether these multi-phasic motions were producing multi-phasic pressure patterns. To this end, we measured P_EC and P_MEC across the surface of the TM along both straight and more random paths outward from the umbo (insets in Fig. 4). As shown in Fig. 4, the pressure close to the TM exhibited significant spatial dependence on the MEC side, and relatively little variation on the EC side. On the EC-side the pressure was approximately in phase across the spatial extent of measurement, consistent with a previous study (Ravicz et al., 2007).

Figure 4.

Relative spatial differences in pressure very close to the TM, panels (A) and (B) for the EC-side, panels (C) and (D) for the MEC-side. Individual curves show responses normalized to the pressure at the umbo, i.e., the complex ratio for the EC-side of $\mathbf{[}{\mathbf{P}}_{\text{EC}}(x,y,z\sim 0^{+})]/[{\mathbf{P}}_{\text{EC}}(\eta \sim 0^{+})]$ [panels (A) and (B)] or the MEC-side $\mathbf{[}{\mathbf{P}}_{\text{MEC}}(x,y,z\sim 0^{-})]/[{\mathbf{P}}_{\text{MEC}}(\eta \sim 0^{-})]$. Darker indicates further away from the umbo. As for Fig. 3, sensor placement was typically within 40 μm of the TM (i.e., $|z|\sim 0$). To map out along x and y [see Fig. 1C], the sensor was moved away from the umbo while trying to keep z constant (and relatively small). Inset (view looking at TM through meatus) for each panel shows sensor path taken. For panels (A) and (C), the data are from the same ear and for roughly the same direction, just different sides of the TM. The sensor was moved radially away from the umbo in ∼0.24 mm steps. For panel B, the sensor was placed in a variety of locations (each indicated via •) across the EC-side surface of parsT. For panel (D), the sensor was moved radially away from the umbo in ∼0.06 mm steps. Note the difference in magnitude scales between EC- and MEC-side measures. For the EC-side, there is relatively little spatial variation, in either magnitude or phase, compared to the MEC side.

Further analysis of these data was done via a series of “snapshots,” as shown in Fig. 5A. From the amplitude (A) and phase data (ϕ) of Figs. 4A, 4C, spatial patterns were computed as A cos (ωt + ϕ) over nine times (i.e., snapshots) within a cycle. This “stroboscopic” illustration of the motion is shown for frequencies of 5, 10, 15, 20, and 40 kHz. In each panel of Fig. 5A, the dashed curve indicates the time for which the computed pressure was a maximum when averaged over all spatial positions. The pressure on the EC-side was relatively uniform in space, whereas on the MEC-side there was significant spatial variation. In an extreme case, a node appeared at 20 kHz at the location 0.6 mm from the umbo. At 15 and 40 kHz, the variations in MEC pressure were less extreme than at 20 kHz and can be described as a multi-phasic pattern superimposed on a uni-phasic pattern. At 10 and 5 kHz the uni-phasic pattern was dominant. Panels (B) and (C) of Fig. 5 show a further analysis of the spatial variations. Panel (B) is the spatial average of A cos (ωt + ϕ) at the times identified by the dashed curves in (A) (when the overall motion was largest at each stimulus frequency). The MEC-side pressure was smaller than the EC-side. These data provide a verification of Fig. 3, which were taken from point measurements at the umbo (EC and MEC-side), in that the same trend of ${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}$ is seen when different spatial locations across the TM surface are considered. The two other curves in Fig. 5B reinforce this point: the dashed line indicates the ratio of MEC to EC pressure, and the dotted line is the average curve from Fig. 3. Both curves show similar trends: a pressure drop of at least 10 dB (gray line) across the TM at most frequencies. Figure 5C quantifies the degree of spatial variation by using the results from the dashed curves in the upper panels and showing the spatial average [as in Fig. 5B] and the spatial standard deviation of the data in each dashed curve from A. The ratio of that standard deviation to the spatial average is shown. For the MEC-side, the ratio could be greater than one: the standard deviation was larger than the average at some frequencies. This is reasonable, considering results such as those in Fig. 5A at 20 kHz. On the MEC-side the ratio was greater than 0.5 at many frequencies, and on the EC side was close to 0.1, confirming the pictorial representation of the degree of spatial variation seen in panel (A).

MEC spatial pressure variations

Figure 6 explores the spatial variation in the MEC from locations close to the TM to locations close to the bony back wall. Two tracks were explored: the first traversed the relatively short distance between the TM and the cochlear wall (total distance ∼1.4 mm, step size 0.175 mm) while the second was anterior to the cochlea (total distance from the TM to the bulla wall ∼4 mm). For this latter track, measurements were made from a location close to the TM to a location 3.6 mm distant in steps of 0.3 mm, but measurements right at the bulla wall were not made due to positioning constraints. The plotted data were referenced to either (left) the umbo on the EC-side [P_EC(η ∼ 0⁺)] or (right) the measurement location closest to the TM in the MEC (z ∼ 0⁻). The left plots are useful for considering the pressure drop across the TM and the right plots are useful for considering the MEC spatial variation. The data from two animals were quite similar, indicating good reproducibility. The spatial pressure variation observed along the longer track was substantial, with clear interference notches and accompanying half cycle phase shifts. Along the shorter track the spatial pressure variation was relatively small.

Canal spatial pressure variations and changes with condition

As the sensor was advanced into the residual EC (i.e., decreasing η), variations in P_EC were observed (Fig. 7). These measurements provide an estimate of reflectance off the TM, as pressure reflected back will cause spatially dependent notches due to destructive interference. We noted above that along directions orthogonal to η, P_EC exhibited relatively little spatial dependence in the EC, consistent with Ravicz et al. (2007). Thus in the EC the (1-D tube) approximation P_EC(x, y, z) ∼ P_EC(η) is reasonable.

Figure 7.

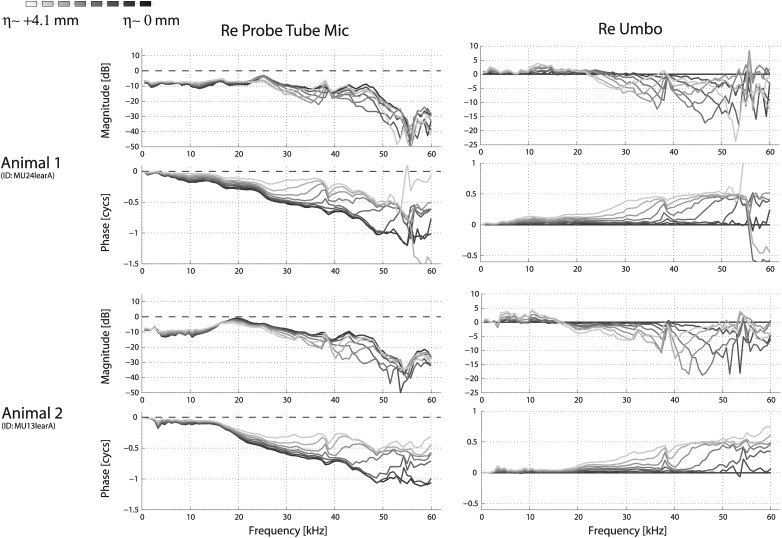
Spatial variations in EC pressure as the pressure sensor was advanced from the meatus toward the umbo [P_EC(η⁺)] (see Fig. 2). Data are shown from two representative animals (top and bottom sets of four panels), and indicate the degree of variability observed across ears. For each animal, the same data are plotted in the left column as referenced to the probe tube microphone $\{[{\mathbf{P}}_{\text{EC}}(\eta )]/{\mathbf{P}}_{\text{stim}}\}$ and on the right as referenced to the measurement made closest to the umbo $\{[{\mathbf{P}}_{\text{EC}}(\eta )]/[{\mathbf{P}}_{\text{EC}}(\eta \sim 0^{+})]\}$. The schematic on the top indicates that the darker curves correspond to positions closer to the umbo. The sensor was advanced approximately 0.59 mm for each successive measurement. Stimuli were 100 dB SPL tones, as measured at the probe tube microphone placed externally nearly the meatus, approximately 2 mm away. Sensor absolute calibration was not well characterized in animal 2 and thus the pressure values re: P_stim are approximate, but this does not affect the spatial variations.

The effects of disarticulation upon sound pressure in the EC are shown in Fig. 8. Data from two animals are shown. In both cases, the MEC was opened via a small hole (1–2 mm diameter) to allow access of a small pick into the MEC for the disarticulation. The data from these two animals are representative in that they demonstrate the variation that we observed in the four animals in which these measurements were made: In two animals the disarticulation increased reflectance in the EC, judging by the increase in the depth of interference notches (as in Animal 2), while in two others there was not a noticeable change in the pressure (as in Animal 1). Animal 1 was several hours postmortem at the time of the data collection while Animal 2 was in vivo. For Animal 2, following euthanasia and overnight refrigeration, the temporal bone was extracted and the measurements were repeated. There was very little change compared to the disarticulated case shown in Fig. 8 (bottom right), so the different observations are not due to pre-versus-postmortem condition.

Figure 8.

Changes in spatial variation in EC pressure [P_EC(η⁺)] due to ossicular interruption. Data from two different animals are shown, both before and after disarticulation of the incuo-stapedial joint. Similar to Fig. 7, the sensor was advanced from the meatus toward the center of the umbo. All responses were referenced to the measurements closest to the umbo $\{[{\mathbf{P}}_{\text{EC}}(\eta )]/[{\mathbf{P}}_{\text{EC}}(\eta \sim 0^{+})]\}$, with the darker shading indicating responses closer to the umbo. The spatial tracks taken along the EC were similar, but not identical, between the before and after disarticulation conditions. The sensor was advanced approximately 0.59 mm for each successive measurement. Stimuli were 100 dB SPL tones, as measured at the probe tube microphone placed externally nearly the meatus, approximately 2 mm away.

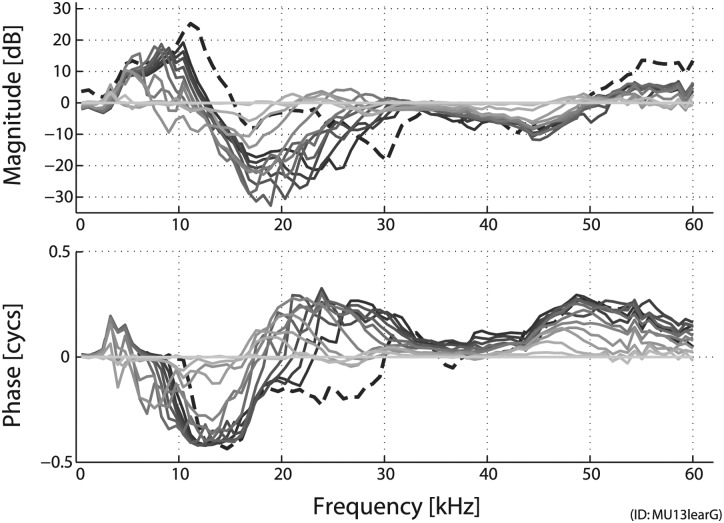
Several experiments were carried out to examine how the physiological and physical state of the preparation affected the various measurements, particularly the acoustic responses in the EC. The changes that occurred when a postmortem preparation was not maintained in a hydrated state are collectively lumped together into the term dry-out. Likely locations for change include: cochlear load (due to the fluids of the inner ear disappearing), material properties of the TM (due to desiccation), and the tension of the ligaments supporting the ossicles. As shown in Fig. 9, the pressure at a fixed location in the EC can vary significantly (±25 dB) with dry-out. In this particular case, the pressure at the umbo increased from 3 to 12 kHz, but decreased from 12 to 30 kHz (as if a notch developed, whose frequency shifted upward with time). This effect evolved smoothly as time progressed. Thus, the physiological state of the TM had a strong effect upon the pressure in the canal.

Figure 9.

Changes in EC pressure close to the umbo [P_EC(η ∼ 0⁺)] due to changes in condition upon dry-out. Data are from an extracted temporal bone (ID: MU13lear, same ear as Animal 2 shown in Fig. 7). The preparation was removed from the refrigerator and allowed to come to room temperature (while in a moist container) just prior to recording. The positioning of the setup (i.e., sound source, sensor, temporal bone) was unchanged throughout, the only change was time. Measurements were made approximately every 20 min and are referenced to the initial measurement (darker indicating later in time). A final measurement was made 15 h later (dashed line), presumably indicating a fully dried out condition. Stimuli were 100 dB SPL tones. MEC cavity was vented via a small hole in the bullar wall.

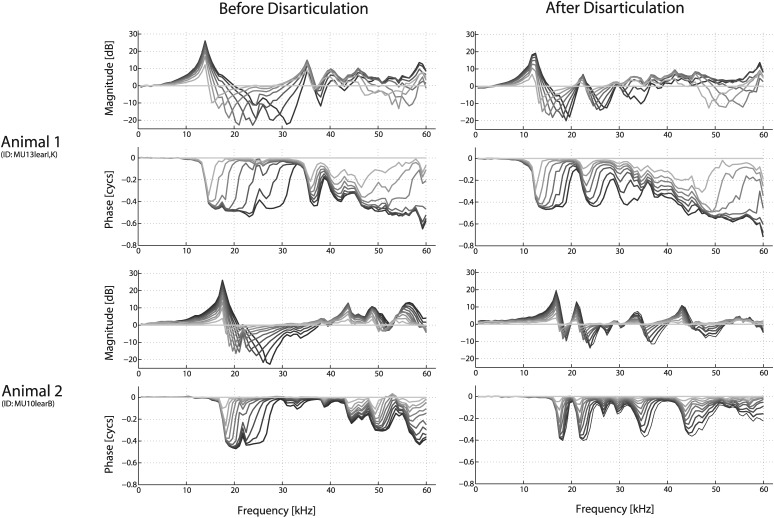
To better understand how changes in material properties could affect the acoustical responses, further postmortem experiments examined the effects due to dry-out after a suitably long amount of time had passed to allow for responses to stabilize. A period of 24 h at room temperature appeared sufficient to attain a reasonably fully dried out state. In such a state, there was relatively little change in $\left|{\mathbf{P}}_{\text{MEC}}(\eta \sim 0^{-})\right|$ above 10 kHz before and after removal of the TM. The effect of changes in the EC spatial profile were measured (Fig. 10, left column), as was the subsequent effect of ossicular disruption (right column). Compared to the viable condition (Fig. 8), not only is the overall profile substantially different in the dried-out condition, but so is the effect of disarticulation, such that the patterns of reflected sound changed substantially upon removal of the cochlear/ossicular load.

Figure 10.

Changes in spatial variation in EC pressure [P_EC(η⁺)] of extracted temporal bones after dry out, both before and after ossicular interruption. Data collected in a fashion similar to that described in the legends of Figs. 78. Data are referenced to the probe tube mic $\{[{\mathbf{P}}_{\text{EC}}(\eta )]/{\mathbf{P}}_{\text{stim}}\}$, with the darker shading indicating responses closer to the umbo (approximately 0.59 mm for each successive measurement).

Pars flaccida removal

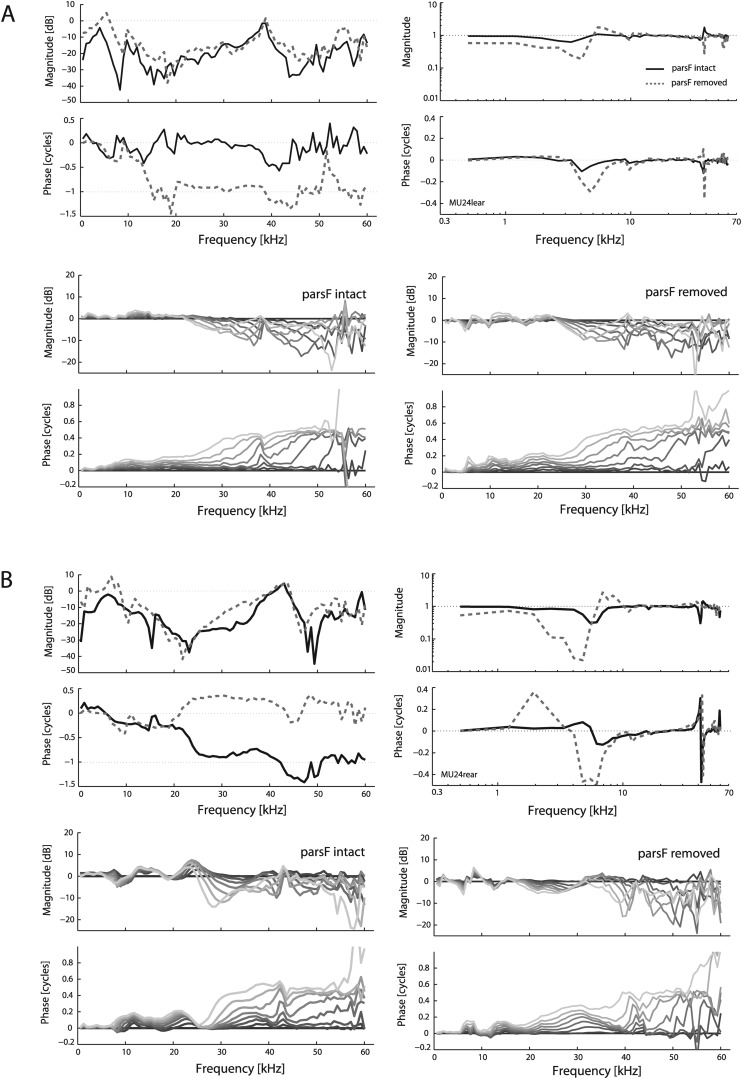
Given that several previous studies have removed the parsF [e.g., de La Rochefoucauld and Olson (2010)], typically to allow access to the stapes or cochlea, we explored how such an opening affected the pressure at the TM. In the top panels of Fig. 11 we show data similar to that of Fig. 3, on the left as the ratio ${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}$ and on the right the pressure difference ratio H_ΔTM. Results from two preparations are shown [Figs. 3A, 3B]. Both exhibit a 5–10 dB increase in ${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}$ at frequencies below ∼20 kHz, with relatively random variations at higher frequencies (left upper panels). However, the phases of P_MEC and P_stim tend to be different, so the pressure difference remains substantial even when these magnitudes are similar. This can be seen in the right panels, where H_ΔTM remains close to 1 following removal of parsF (right upper panels). In preparation A the removal caused ∼4 dB decrease in the pressure difference ratio up to 2.5 kHz, and then a slightly larger dip at ∼4 kHz. Above 6 kHz, there was no significant difference in H_ΔTM before and after removal of parsF. The preparation of panel B showed a larger decrease in the H_ΔTM at frequencies from 2 to 6 kHz, but like the preparation of panel A, above 6 kHz the changes were small. The bottom plots of panels (A) and (B) of Fig. 11 show that parsF removal had relatively little effect upon the reflectance, in that the depth of interference notches did not change substantially or systematically.

Figure 11.

Effects of removing pars flaccida (parsF). Results are shown for two different ears, one in vivo (A) and the other postmortem that had been refrigerated for two weeks (B). For each ear, four panels are shown. In the top two, the trans-TM pressure is shown in a fashion similar to that in Figs. 3A, 3B, ${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}$ on the left and H_ΔTM on the right, with intact-parsF case indicated via a solid line and removed-parsF shown by the dashed line. The bottom sets of panels show the spatial variation in canal pressure (similar to Fig. 7, referenced to the umbo), the left for intact-parsF and the right for the parsF removed. Darker shading indicates closer to the umbo.

Additional observations

Pars tensa removal and reverse TM stimulation via bullar hole

An important control question was to what extent opening the MEC cavity created an additional sound pathway: Was the TM also being significantly driven from the MEC-side by P_stim due to the bulla hole? Such a question was particularly relevant for experiments where the MEC had to be opened sufficiently to allow for sensor placement at a variety of locations in the MEC (∼1 × 2 mm rectangular hole). This question was explored in a number of ways, including: (1) Adding in/removing the clay baffle (see Fig. 2), (2) Sealing the hole with clay (both for the sensor inside and outside the bulla), (3) Mapping out the pressure distribution (with the sensor) as it was moved away from the source around the bulla toward the hole, (4) Mapping the pressure in the bulla as the sensor was pulled out of the hole, (5) Observing the change in the bulla pressure as the meatus (EC opening) and or sound source was plugged/unplugged, (6) Observing the effect upon both canal and bulla pressure when the TM (both parsF and parsT) was removed, and (7) Making smaller holes to the MEC wall.5

These manipulations led to the following observations: First, upon plugging the bulla hole with clay, P_EC was little affected for frequencies above 5 kHz except for occasional small frequency shifts in the peaks/valleys.6 However in one case where these measurements were made following disarticulation, there was a slight downward shift and accentuation of spectral structure for frequencies below about 7 kHz only (no effect at higher frequencies). Second, thoroughly plugging the meatus had a drastic effect upon the MEC pressure (P_MEC) and caused the response to drop down into the noise floor above 10 kHz. Third, the effect of adding or removing a clay baffle (Fig. 2) had relatively little effect upon ${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}$. Fourth, the sound pressure distribution measured at various locations about the preparation (see Fig. 2) indicate that the sound field falls off steeply away from the source (x symbols) but is relatively uniform about the meatus and into the EC close to the umbo (o symbols). Thus it appears that most of the relevant acoustic stimulus energy enters into the EC rather than leaking back around through the bullar wall hole. In fact, what little sound pressure was measurable just outside the hole appeared to be coming from the MEC (i.e., through the EC and TM) and radiating outward from the hole. Last, while the sound pressure was fairly uniform throughout the residual EC when the TM was in its normal physiological state, removal of the TM drastically changed P_EC, in particular, producing large notches. Large holes in parsT (but umbo/manubrium still in place) produced similar effects as total TM removal. When placed close to where the umbo had been, P_EC(η ∼ 0⁺) appeared highly similar to P_MEC(η ∼ 0⁻) for the intact condition. P_MEC was relatively little changed upon TM removal, such that $|{\mathbf{H}}_{\Delta \text{TM}}|$ became vanishingly small (which was to be expected in the absence of the TM).

Modifying ear canal shape

Aside from the frequency/spatial-dependent notch apparent for many (but not all) ears, the pressure was fairly uniform in the EC as the sensor was advanced from the meatus toward the umbo [i.e., P_EC(η⁺) as shown in Fig. 7]. One question was whether this depended crucially upon the geometry of the EC. To test this, a small amount of clay was carefully placed along the bony wall opposite the TM (where the curved shape shown in panel C of Fig. 1 suggests focusing) leaving enough room to advance the sensor along the path toward the umbo unimpeded. The clay modified the shape of the EC (taking up ≈30% of the volume), but did not touch the TM. When the clay was in place the location of various peaks and valleys shifted downward with frequency by as much as 10 kHz, but otherwise the change was small.7

DISCUSSION

This paper explores several questions aimed at better understanding how sound pressure sets the TM into motion and thereby efficiently delivers energy to the inner ear. We concentrate the discussion upon several salient observations emerging from the data, initially providing a brief overview of the relevant anatomy.

Overview of gerbil middle ear anatomy

Several previous reports provide detailed descriptions and schematics of the gerbil external and middle ear morphology and mechanics (Ravicz et al., 1992; Rosowski et al., 1999; Ravicz et al., 2007). We note several features relevant to the discussion. First, the EC (upon removal of the pinna and soft tissue about the external auditory meatus) is a cavity in which the TM is not simply the termination of the end of a tube. Instead, the TM covers a substantial fraction of the EC's surface area along one side, the other side tapering down (see Fig. 1) so to perhaps focus sound pressure at the TM surface along its semi-conical shape. Second, it should be noted that there are considerable differences in the morphology of the external ears of humans and gerbils (e.g., EC length and shape, relative size of parsF versus parsT). Thus, one needs to be careful when considering the present results in the context of human hearing. Lastly, the TM itself appears as an extremely light and fragile structure, giving rise to an expectation that it will undergo significant motion when driven with pressure and thereby generate substantial pressure on the MEC side (Rabbitt, 1990).

Spatial variations along ear canal

Figures 78 show the spatial variation of P_EC and indicate the existence of spatially dependent notches (i.e., areas of destructive interference between forward- and reverse-traveling waves). These data can be directly related to previous studies such as Stinson (1985) and Ravicz et al. (2007). The latter study reported interference notches at frequencies above about 30 kHz, with dips that varied from 10 to 25 dB. Some preparations showed deeper notches (indicating greater reflection) and the variability across ears was apparent in the factor of three range in power reflectance [see Fig. 13 of Ravicz et al. (2007)]. The notches reported here are reasonably similar to the results of Ravicz et al. (2007), but some preparations exhibited relatively shallow notches (e.g., less than 10 dB up to 45 kHz, Fig. 8 upper left). It is not known why the results of the two studies differ somewhat in P_EC notch depth—Ravicz et al. (2007) used both probe tube microphones and micro-pressure sensors similar to those in the current report, and studied both pre- and post-mortem ears. It is possible that the fairly small number of preparations in both reports simply was not enough to fully characterize the range of reflectance values across different gerbil ears.

Pressure ratio across TM (${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}$)

Our results for ${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}$ indicate a significant drop in pressure across the TM. These results are consistent with previous studies [e.g., Rosowski and Saunders (1980); Pinder and Palmer (1983); Voss et al. (2001)], which reported that $|{\mathbf{H}}_{\Delta TM}|\approx 1$ (especially above 1 kHz). While Fig. 3 shows this ratio can be smaller at certain frequencies (e.g., 5, 40, and 55 kHz) and that individual curves can depart significantly from the trend (e.g., ${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}$ being close to or greater than 1 in several cases), $|{\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}|$ when averaged across animals was always at least 7 dB down. Figure 5 shows that the $|{\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}|$ averaged over several locations on the TM in a single preparation similarly was always less than one and usually down by a factor of three or more. While most measurements of ${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}$ were made across the umbo, the general features were little changed when measuring across the TM for different locations along parsT.

The frequency-dependent features of $|{\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}|$ (Fig. 3) do not match the relatively flat middle ear transmission found with intracochlear pressure measurements [e.g., Olson (1998); Dong and Olson (2006)]. However, the pressure difference across the TM is the quantity driving the TM, not the pressure ratio and H_ΔTM [Figs. 3C, 3D] is the more important quantity to consider in this regard. H_ΔTM it is quite flat with frequency, which does match the relatively flat transmission observed in other studies. These observations underscore that the relatively large value of $|{\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}|$ indicates that the pressure drive to the TM is well approximated by P_EC(η ∼ 0⁺).

The phase data shown in Fig. 3 are suggestive of a delay between P_MEC and P_EC. The ${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}$ phase does not impact transmission in an obvious way, since as noted above, to a good approximation the drive to the TM is P_EC(η ∼ 0⁺). Nevertheless, it is interesting that the delay between P_MEC and P_EC is on the order of tens of microseconds, similar to that of the documented TM transmission: in gerbil the lag of intracochlear pressure (just inside the stapes footplate) relative to P_EC is ∼25–30 μs, independent of frequency [e.g., Olson (1998); Dong and Olson (2006)]. While a fraction of the forward transmission delay appears attributable to the ossicles (de La Rochefoucauld et al., 2010), the majority may arise at the TM. The source of TM delay has been explored in previous work, but a clear understanding has yet to emerge (Puria and Allen, 1998; Fay et al., 2006; Parent and Allen, 2007; de La Rochefoucauld and Olson, 2010; Goll and Dalhoff, 2011). For example, delays could arise via (relatively) slow-moving inward-traveling waves that carry energy from the outer edges in toward the center where the umbo attaches to the TM (although delays measured along the gerbil manubrium indicated motion propagation outward from the umbo to the lateral process of the malleus [de La Rochefoucauld et al. (2010)]. TM traveling waves may be present in other types of tympanums such as those of frogs, where middle ear transmission delays can be substantially longer than those of mammals [0.7 ms; van Dijk et al. (2011)]. A recent theoretical study examined a relationship between delays associated with both transmission and TM surface waves and suggested the two could be independent of one another (Goll and Dalhoff, 2011). Section 1 of modeling Sec. 4G attempts to provide an explanation concerning several aspects of ${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}$.

Pressure distribution along TM surface

Previous studies have demonstrated complicated spatial variations in displacement across the TM surface of mammals (Khanna and Tonndorf, 1972; Decraemer et al., 1989; Furlong et al., 2009; Rosowski et al., 2013), as well as non-mammals [Pinder and Palmer (1983); Manley (1972)]. It has been suggested that this motion is a combination of uni- and multi-phasic motion patterns (de La Rochefoucauld and Olson, 2010). While TM velocity was not measured in the current study, pressure variations close to the surface were examined on both sides of the TM. By and large, the spatial variation on the EC-side was small, indicating that multi-phasic motion of the TM did not influence the pressure field very much, even as close as 40 μm to the TM. Apparently the pressure produced by the multi-phasic motion of the TM was only a small perturbation to the stimulating pressure. These results are consistent with previous measurements made by Ravicz et al. (2007).

In contrast, significant spatial variations in pressure were apparent along the TM surface on the MEC-side, and wave-like spatial pressure patterns are illustrated in Fig. 5. The pressure in the MEC is produced by the motion of the TM, which has a prominent multi-phasic component. Therefore, it was not surprising that the P_MEC(x, y, z ∼ 0⁻) also would have a multi-phasic character. Recognizing that motion of the TM will produce MEC pressure, a further question was whether reflection of this pressure off the back cavity walls was large enough to significantly modify the MEC pressure at the TM, and thus augment or diminish the pressure difference across the TM that drives its motion. This question is addressed in the next section.

MEC acoustics

Rabbitt (1990) hypothesized that reflections in the MEC provide an additional drive to TM motion and thus extend high frequency sensitivity, and our observations of MEC pressure variations speak to this notion. For track 1 in Fig. 6, standing wave patterns (i.e., pressure minima accompanied by half-cycle phase shifts) were not in evidence. While there are regions where notches appeared, the degree of the associated phase shifts were variable in size. One likely explanation is that given the distance of 1.4 mm corresponds to a quarter wave of frequency 61 kHz, standing waves would not be observed over the relatively short track 1. It also must be considered that because the MEC is not a simple 1-D tube, but a more complex 3-D cavity, the “classic” standing wave expectation may be too simple [e.g., consider an arbitrary position in/track through a spherical 3-D geometry, Russell (2010)].

Track 2 expands upon these reasonings: with a total distance of 5 mm, quarter-wave standing wave patterns would emerge at a frequency of ∼17 kHz and indeed, half cycle phase shifts and interference notches were apparent, especially in regions from ∼17–30 kHz and ∼45–55 kHz. At many frequencies, especially between 10 and 20 kHz and above 35 kHz, there were locations along track 2 where the pressure within the MEC was within 3 dB (factor of 0.9) of P_EC. Moreover, there were broad regions where the MEC pressure well away from the TM was larger than that close to it. In these regions, the reflecting pressure from the back walls of the bulla appeared to be interfering with the pressure traveling forward from the TM, thereby effectively reducing the pressure P_MEC(z ∼ 0⁻). Such has the effect of enhancing the pressure ratio ${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}$ across the TM. Thus, it is possible that reflecting pressures within the MEC contribute to producing the large pressure drop across the TM.

Reflection requires a transit time of ∼1 cm/340 m/s= 30 μs, and it seems this delay would diminish transmission fidelity of short duration stimuli and perhaps lead to problematic reverberation. On the other hand, the well-known “quarter-wave-resonance” of the human EC boosts transmission in the 2 kHz frequency region and this is due to a much longer reflection delay. At this point it is unclear whether pressure reflected off the back bullar plays a significant role in driving TM motion. Further modeling, coupled to the data presented here, would be useful to address this question. To date, most middle ear models have not incorporated reflection in the MEC. For example, the MEC is considered to be at atmospheric pressure [i.e., H_ΔTM(f) = 1] in many middle ear models [e.g., Gan et al. (2004)] and as a radiation load in others [e.g., Puria and Allen (1998); Fay et al. (2006)].

Changes in condition of middle ear

We explored the effects of several manipulations on P_MEC and P_EC. The effect of parsF removal was explored because this manipulation had been performed in previous studies for purposes of experimental access. Disarticulation was explored because its effect tests a theory of middle ear transmission. We also explored the effect of drying, because studies that work with extracted temporal bones pay careful attention to maintaining hydration [e.g., Nakajima et al. (2005)]. To summarize the findings, at frequencies 6 kHz and above parsF removal did not change the driving pressure across the TM, the results of disarticulation on P_EC were mixed, and P_EC was significantly affected by drying out of the preparation.

Several previous studies have opened parsF to provide access to the stapes [e.g., de La Rochefoucauld et al. (2008, 2010)]. Based on control measurements, the removal caused little change in transmission to the cochlea (de La Rochefoucauld et al., 2008). The data in Fig. 11 show that up to ∼6 kHz, removal of parsF caused a decrease in the pressure difference ratio, H_ΔTM, but that little change was observed above 6 kHz. Changes in compound action potential and stapes velocity have been reported to be almost undetectable following PF removal de La Rochefoucauld et al. (2008), and our H_ΔTM findings at frequencies above 6 kHz are consistent those results. At frequencies below 6 kHz, it is possible that the smaller changes of the preparation in panel A of Fig. 11 are more typical. Although the methodology was somewhat different, our results can also be compared to those of Teoh et al. (1997): Our data agree with those in their Fig. 11, showing that opening parsF caused an increase in ${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}$ of ∼10 dB up to 10 kHz (where their measurements stopped). A recent study (Maftoon et al., 2013) examined TM motion in gerbil (≤10 kHz), comparing between parsF intact versus retracted (the MEC being closed), and reported a slight decrease in umbo velocity upon retraction.

This study also explored the change in P_EC due to ossicular disarticulation. The ossicles connect the TM to the cochlea and thereby contribute to the load impedance. Because the cochlea absorbs power, one would expect that removing that load via disarticulation would lead to an increased reflection. Indeed, Puria and Allen (1998) found an increase in notch depth following disarticulation in cats, and that observation supported the study's model of the TM as a wave-supporting, impedance matched transmission line. However, another study had found only small changes in middle ear input impedance following disarticulation (Lynch, 1981) and a recent study (Chang et al., 2013) reported that ossicular interruption (as well as stapes footplate fixation) had relatively little effect upon TM motion. Our data are variable in this regard: Fig. 8 shows that in one animal (top) disarticulation had little effect upon reflectance (as indicated in the depth of interference notches) while the other (bottom) exhibited relatively large changes. This variability in change with disarticulation, along with the variability in notch depth in P_EC without disarticulation (Sec. 3B), suggests that the TM itself can absorb or shunt acoustic energy (thus avoiding reflections). In our auditory physiology studies of gerbil, it is extremely rare for an animal to possess an apparent conductive hearing loss. Thus it is unlikely that the variability in TM reflection is due to middle ear pathology.

Upon dry-out, ossicular interruption had a substantial effect on P_EC of both preparations studied in this manner (Fig. 10), causing the existence of a new set of notches. When the TM was in its normal, hydrated physiological state, its dynamics were less affected by changes to its load. Section 3G2 attempts to provide an explanation concerning some aspects of dry out.

1-D model to examine several observations

We describe here two different theoretical considerations based upon a simple 1-D framework for the acoustics of the external and middle ear spaces. The purpose is to demonstrate that such can, to first approximation, capture several basic features observed in the reported data and also provide explanatory power. For reference, several basic acoustical concepts are outlined in the Appendix.

${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}$

The phase of ${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}$ [Fig. 3B] exhibited ripples of ∼ ± 1/4 cycle (note curves hovering around zero), as well as larger shifts that resulted in nearly full cycle shifts. At the frequencies for which ripples occurred, $|{\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}|$ showed maxima and minima. Some of these features of ${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}$ can be predicted by considering the acoustic impedances in a quasi-lumped element formulation [e.g., Zwislocki (1962)]. Although the multi-phasic P_MEC pressure apparent in Fig. 5 argues against a 1-D model, a strong uni-phasic component is also present at most frequencies, allowing this 1-D approximation of the system. P_EC drives the TM motion (and thereby the ossicular chain and cochlea), as well as the air in the MEC. Thus, the mechanical impedance of TM/ossicles/cochlea is in series with the MEC acoustical impedance, Z_MEC (defined at the MEC side of the TM). Their sum is the middle ear input impedance, Z_input. Therefore, ${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}$= P_MEC/P_EC = Z_MEC/Z_input.

Z_input of gerbil has been measured (Ravicz et al., 1992) and above ≈1 kHz it is primarily resistive (i.e., Z_input is chiefly real and positive). Using the high frequency asymptote (≥1 kHz) of the middle ear input impedance from Ravicz et al. (1996), the magnitude of Z_input is slightly larger than the characteristic impedance of a tube with diameter that of the EC, $Z_c/A_{\mathrm{EC}}$, where Z_c is the characteristic impedance of air and A_EC is the cross-sectional area of the EC. For simplicity, we assume ${\mathbf{Z}}_{\text{input}}=2\mathbf{(}{\mathbf{Z}}_c/A_{\text{EC}})(\ge 1\hspace{0.17em}\text{kHz})$.

Z_MEC was assumed that of a 1-D cavity. The depth of the cavity (L) was taken as 5 mm, a reasonable anatomical value. This depth ultimately determines the frequency spacing of the predicted ${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}$ ripples. Because the MEC widens out compared to the EC, we assumed the MEC area is A_MEC = 4A_EC. This seemingly large factor is necessary in order that on-average a substantial pressure drop occurred across the model TM, as was observed in ${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}$. The terminating impedance at L is Z_L, and is unknown. Z_MEC can be determined analytically by considering incident and reflecting waves within the cavity (Hall, 1993), with the result

$${\mathbf{Z}}_{\text{MEC}}(\omega )=\frac{{\mathbf{Z}}_c}{A_{\text{MEC}}}\left[\frac{\frac{Z_L}{{\mathbf{Z}}_c}+i\hspace{0.17em}\tan (\mathit{kL})}{1+i\left(\frac{Z_L}{{\mathbf{Z}}_c}\tan (\mathit{kL})\right)}\right].$$ (3)

There are two free parameters: the real and imaginary parts of $Z_L/{\mathbf{Z}}_c=a+\mathit{ib}$. If a is infinite and b = 0, the cavity is perfectly reflecting closed tube; if a = b = 0, it is a perfectly reflecting open tube. Large b with a = 1 also gives rise to substantial reflection. These conditions produce steep maxima and minima in the amplitude of ${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}$. On the other extreme, for a = 1 and b = 0, the cavity is perfectly absorbing (no reflection). A plot with a = b = 1.5 is shown in Fig. 12. The model exhibits ∼±1/4 cycle ripples that appear at frequencies for which the amplitude ratio has maxima and minima. The size and spacing of the maxima and minima are similar to what was observed. Thus, several aspects of the data can emerge from a simple 1-D model for the MEC impedance.

Figure 12.

Simple model prediction of ${\mathcal{R}}_{{\mathbf{P}}_{\text{TM}}}$ [compare to Fig. 3B] found with the input impedance of the middle ear and the acoustic impedance of the MEC. The input impedance is known from previous experimental studies, and the MEC acoustic impedance was based on a model of a cavity with complex termination.

The analysis of Fig. 12 was based on reflections from the back wall of the MEC cavity and these reflections also would produce spatial pressure variations within the MEC. The standing wave ratio (the ratio of the maximum to the minimum pressure at different locations, and one frequency) is set by the terminating impedance. With the a and b parameter values used here, the predicted standing wave ratio within the MEC was 3.4, or 11 dB. These predicted spatial variations are not as large as those measured in the MEC (Fig. 6), where the standing wave ratio could be greater than 30 dB. Although useful for some basic understanding, the 1-D model is far from a complete description.

Dry out and disarticulation

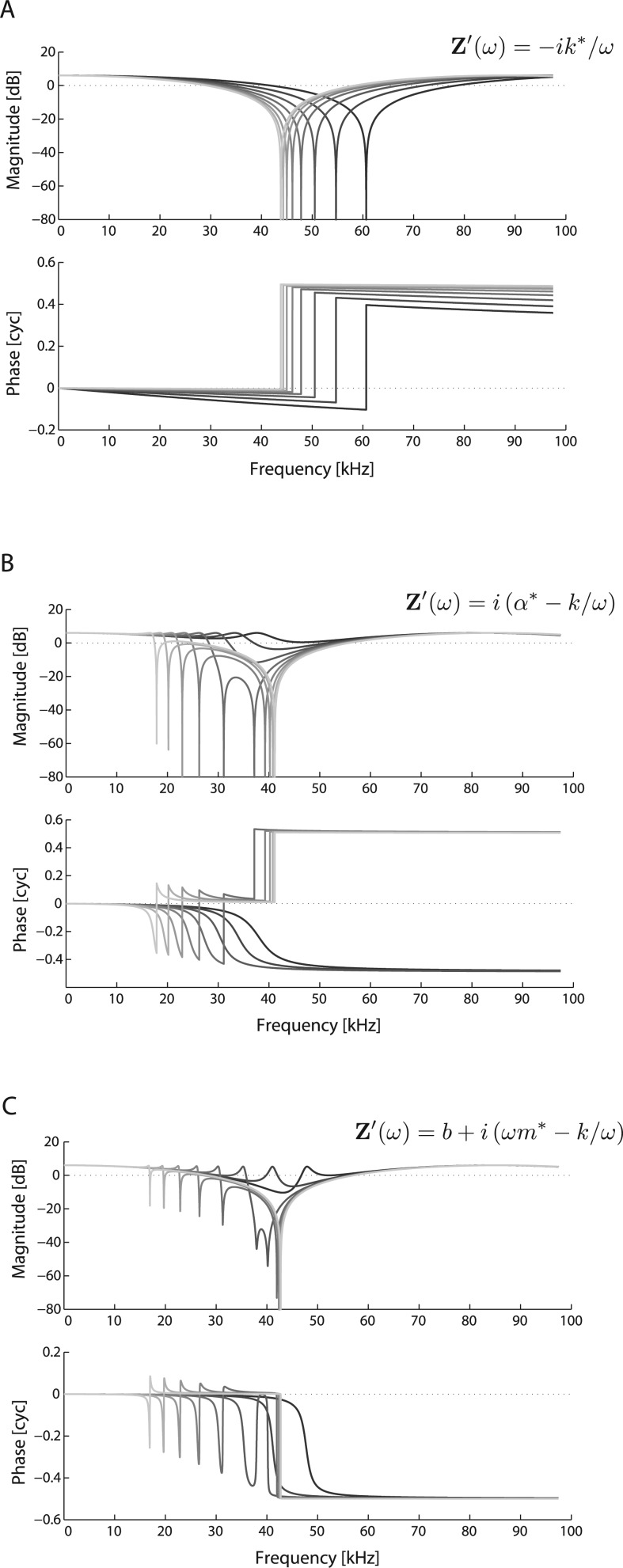
We expand our analysis from Sec. 1 to examine the EC pressure in more detail. Similar to Z_MEC above, we treat the canal simply as a 1-D tube with variable terminating impedance Z′. First, by assuming the TM acts as a stiffness only [i.e., Z′(ω) = −is/ω], the spatial location of a notch will occur at

$$x(\omega ,s)=\frac{c}{2\omega }\left[\pi -\arctan \left(\frac{2s\omega }{{\omega }^2-s^2}\right)\right].$$ (4)

This expression indicates that the position of a pressure null can vary with the stiffness of the terminating load. In the limit of very high stiffness (i.e., a rigid boundary), the quantity

$$\left(\frac{2s\omega }{{\omega }^2-s^2}\right)\to 0.$$

Considering principal values only, we obtain

$$x=\frac{c}{4f},$$ (5)

where f = ω/(2π). This is just the characteristic quarter wavelength known for rigid tubes.

Computational results from this model are shown in Fig. 13 for comparison to Fig. 9A, i.e., measurement location is fixed. Figure 13A shows the effect of the stiffness being incrementally changed. For the stiffest case, the notch frequency is close to the quarter-wave resonance location with a rigid boundary. As the stiffness decreases, the notch moves upward in frequency. Note that the phase-gradient also increases with decreasing stiffness, consistent with the notion of a delay due to the spatial separation between x and the (fixed) measurement location. While this model is too simple to describe the EC acoustics, it demonstrates a mechanism consistent with the nature of the data shown in Fig. 9. Furthermore, the analysis indicates that if such a simple model were to apply, the effective stiffness of the TM decreased with dry-out.

Figure 13.

Simulations showing the magnitude and phase of the sum of an incident and reflected wave for a 1-D tube [Eq. A3] with changes in terminating impedance Z′. Inset equations indicated chosen form of impedance, the superscript * identifying the parameter varied. Measurement location was taken as 2 mm away from termination and c = 343 m/s. (A) Impedance is an acoustic stiffness only [Eq. A5], varied in log-spaced steps from s = 8 × 10⁶ (lighter) to 5 × 10⁵ N/m³ (darker). (B) α from Eq. 6 varied from 12.5 (lighter) to 27.5 N/s m³ (darker). Stiffness was 3 × 10⁶ N/m³. (C) Harmonic oscillator-like [Eq. 7], with the acoustic mass m varied from 0.1 (lighter) to 0.8 (darker) mN s²/m³. Stiffness was 9 × 10⁶ N/m³ and damping 0.1 N/s m³.

We can modify the terminating impedance in other ways to describe more complex conditions. Heuristically, consider

$${\mathbf{Z}}^{\prime }(\omega )=i(\alpha -s\mathrm{/}\omega \mathrm{),}$$ (6)

where $\alpha \in ℝ$. The extra reactive term due to α is neither a stiffness or mass (due to lack of dependence upon ω).8 Such an expression for the impedance leads to the existence of a second notch [Fig. 13B], noting that both notches can disappear altogether depending upon the relative values of α and s. Such may help explain observations of changes due to disarticulation in the dried out state (Fig. 10), where an additional notch manifests. We can also consider the terminating impedance as that of a harmonic oscillator (Rabbitt, 1990), given by

$${\mathbf{Z}}^{\prime }\left(\omega \right)=b+i(m\omega -k/\omega ).$$ (7)

As shown in Fig. 13C, varying the mass while holding the damping and stiffness constant causes a second notch to manifest when the resonant frequency is near (but below) the quarter wave resonance frequency. While these 1-D models are too simple to fully explain the observed data, they are useful to help understand the basis for the changes in P_EC upon dry-out and disarticulation.

SUMMARY

Our study has experimentally examined the acoustics throughout the gerbil (residual) external and middle ear spaces, focusing chiefly on higher frequencies (1–60 kHz). Returning to the questions initially posed at the outset, we have found that:

• (1)There is a significant pressure drop across the TM at most frequencies. Thus, the external-stimulus-induced EC-side sound pressure at the TM can be considered the drive to the TM (and ultimately the cochlea).
• (2)On the EC-side, variations in the pressure along the TM surface are relatively small, indicative of a uniform driving pressure. However on the MEC-side, these surface variations are significant. This is likely because the multi-phasic TM motion is able to more significantly affect the (relatively smaller) pressure on the MEC side.
• (3)Significant spatial variations in MEC pressure exist, presumably due to interference stemming from reflections throughout the bony cavity. In some frequency regions these reflections appear to be large enough to shape the pressure difference that drives TM motion.
• (4)The physiological state of the TM has a significant effect upon external and middle ear acoustics. In a dried out state, changes in ossicular coupling are accentuated, whereas in vivo changes due to disarticulation are less drastic. Opening of parsF has a relatively small effect upon the acoustics about the TM, despite a direct path for sound energy into the MEC. However, opening of parsT caused substantial spatial variations in EC acoustics.

We employed a simple 1-D modeling framework to interpret some of the findings. Beyond that, these experimental results should prove useful to more detailed theoretical models for the mammalian external/middle ear [e.g., Funnell et al. (1987); Rabbitt (1990); Ravicz et al. (1992); Puria and Allen (1998); Gan et al. (2006); Fay et al. (2006); Parent and Allen (2007); Goll and Dalhoff (2011)] to better elucidate the dynamic role of the TM.

APPENDIX

We describe here some basic acoustical concepts relevant for Sec. 4G. Consider a 1-D tube whose longitudinal axis is described by the spatial dimension x and is filled with some medium(s) whose specific acoustic impedance is Z = ρc where ρ is the medium's density [kg/m³] and c the speed of sound in the medium. The incident pressure wave (p_i) propagates in the +x direction, the “reflected” wave (p_r) along −x. Each wave also has an associated particle velocity (v_i and v_r). All bold quantities can be described by their respective Fourier coefficients,

$$p(x,\omega ,t)=p_i+p_r={\mathbf{P}}_i(\omega )e^{i\omega (t-x/c)}\mathrm{+}{\mathbf{P}}_r(\omega )e^{i\omega (t+x/c)}.$$ (A1)

Consider two adjacent mediums inside the tube, each with their own characteristic acoustic impedances (for example, Z₁ = ρ₁c₁ and Z₂ = ρ₂c₂), their interface at x = 0 being the discontinuous boundary condition. The impedances away from the boundary are given by

$$\frac{{\mathbf{P}}_i}{{\mathbf{V}}_i}={\mathbf{Z}}_1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{{\mathbf{P}}_r}{{\mathbf{V}}_r}=-{\mathbf{Z}}_1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{{\mathbf{P}}_t}{{\mathbf{V}}_t}={\mathbf{Z}}_2,$$

where the subscript t indicates the transmitted component. The reflectance is defined as $\mathbf{R}\equiv {\mathbf{P}}_r/{\mathbf{P}}_i$ and can be expressed as

$$\mathbf{R}(\omega )\mathrm{=}\frac{{\mathbf{Z}}^{\prime }-1}{{\mathbf{Z}}^{\prime }+1},$$ (A2)

where ${\mathbf{Z}}^{\prime }\equiv {\mathbf{Z}}_2/{\mathbf{Z}}_1$. From Eq. A2, the reflectance explicitly depends upon the (normalized) impedance (Z′) the incident wave is subject to at the interface. That is, the terminating load directly affects the properties of the reflected wave and thereby interference between P_i and P_r. Such is apparent if we rewite Eq. A1 as

$$p(x,\omega )\sim {\mathbf{P}}_i(\omega )[e^{-i\omega x/c}\mathrm{+}\mathbf{R}(\omega )e^{i\omega x/c}].$$ (A3)

Consider a maximal null, that is, a spatial location where the two waves fully cancel one another out due to destructive interference. From Eq. A3, two conditions must be met for such a null

$$|e^{-i\omega x/c}|=|\mathbf{R}(\omega )e^{i\omega x/c}|,$$

$$-\omega x/c=\omega x/c+\theta +\pi ,$$

where $\theta \equiv \angle \mathbf{R}=\angle [({\mathbf{Z}}^{\prime }-1)/({\mathbf{Z}}^{\prime }\mathrm{+1})]$. The first equation simply indicates that $|\mathbf{R}|=1$. The second equation indicates that the phase difference must be a half cycle. Rearranging, we have

$$x=\frac{c}{2\omega }(\mp \pi -\theta )$$ (A4)

(the ∓ comes from the phase wrapping ambiguity). Even in the case of a null where the two waves do not fully cancel out (i.e., $|\mathbf{R}|<1$), Eq. A4 still needs to be satisfied.

Consider the case where the terminating load can be described simply by a stiffness

$${\mathbf{Z}}^{\prime }(\omega )=-is/\omega ,$$ (A5)

where s is the stiffness coefficient. Then from Eq. A2, we have

$${\mathbf{R}}_s(\omega )=\frac{is+\omega }{is-\omega },$$ (A6)

where the subscript indicates a stiffness only. Solving for the phase leads to

$$\angle {\mathbf{R}}_s=\theta ={\tan }^{-1}\left(\frac{2s\omega }{{\omega }^2-s^2}\right).$$

Plugging this back into Eq. A4 (and ignoring the phase wrapping ambiguity) leads to Eq. 4.