Sensitivity to envelope-based interaural delays at high frequencies: Center frequency affects the envelope rate-limitation

Abstract

Sensitivity to ongoing interaural temporal disparities (ITDs) was measured using bandpass-filtered pulse trains centered at 4600, 6500, or 9200 Hz. Save for minor differences in the exact center frequencies, those target stimuli were those employed by Majdak and Laback [J. Acoust. Soc. Am. 125, 3903–3913 (2009)]. At each center frequency, threshold ITD was measured for pulse repetition rates ranging from 64 to 609 Hz. The results and quantitative predictions by a cross-correlation-based model indicated that (1) at most pulse repetition rates, threshold ITD increased with center frequency, (2) the cutoff frequency of the putative envelope low-pass filter that determines sensitivity to ITD at high envelope rates appears to be inversely related to center frequency, and (3) both outcomes were accounted for by assuming that, independent of the center frequency, the listeners' decision variable was a constant criterion change in interaural correlation of the stimuli as processed internally. The finding of an inverse relation between center frequency and the envelope rate limitation, while consistent with much prior literature, runs counter to the conclusion reached by Majdak and Laback.

INTRODUCTION

The ability to perceive changes of ongoing interaural temporal disparities (ITDs) imposed on high-frequency complex stimuli has long been recognized as being mediated by the envelopes of such stimuli. Furthermore, the efficiency of such ITD processing has been shown to be dependent on the rate of fluctuation of the envelope (see Henning and Ashton 1981; McFadden and Pasanen, 1976; Nuetzel and Hafter, 1981; Bernstein and Trahiotis 1994, 2002). Specifically, as the rate of envelope fluctuation increases beyond some upper limit (typically between 250 and 500 Hz), threshold ITDs increase rapidly. The research reported herein concerns whether that upper limit is related to the center frequency of the stimulus.

Bernstein and Trahiotis (1994) measured sensitivity to ongoing ITDs conveyed by SAM tones and by two-tone complexes as a function of rate of modulation. They employed carrier frequencies of 4 and 8 kHz. Bernstein and Trahiotis found that the rate of modulation above which threshold ITDs increase was substantially lower for stimuli centered at 8 kHz than for stimuli centered at 4 kHz. That result ran counter to what one would expect if attenuation of spectral sidebands via peripheral auditory filtering and, thus reduced depth of modulation of the envelope, were responsible for the loss of sensitivity to ITD with increases in the rate of modulation. This is so because the auditory filter centered at 8 kHz is roughly twice as wide as the one centered at 4 kHz. Therefore all other things being equal, the rate of modulation (and the resulting spectral separation of the sideband components composing the stimulus complex) at 8 kHz could be twice that at 4 kHz before the same relative attenuation of the sidebands would occur.

In a later study, Bernstein and Trahiotis (2002) measured threshold ITDs for SAM tones and transposed tones centered at 4, 6, or 10 kHz while varying rate of modulation. In agreement with their previous results, the rate of modulation above which threshold ITDs increased appeared to be inversely related to center frequency. Despite this observed relation, Bernstein and Trahiotis showed that the data obtained at all three center frequencies could be reasonably well accounted for by a cross-correlation-based model that included a 150-Hz low-pass envelope filter, like the one described by Kohlrausch et al. (2000) and Ewert and Dau (2000).

Recently, Majdak and Laback (2009) reported the results of an experiment designed explicitly to measure effects of center frequency and rate of fluctuation of the envelope on threshold ITDs. The stimuli they employed were 1500, 2121, and 3000 Hz-wide bandpass filtered click trains centered near 4600, 6500, or 9200 Hz, respectively. In our judgment, such stimuli appear to be particularly useful because the temporal signatures of their filtered envelopes have especially steep slopes that would be expected to facilitate sensitivity to ITD (Bernstein and Trahiotis, 2009; Klein-Hennig, et al., 2011; Laback et al., 2011). An increased sensitivity to ITD might help to reveal differences across center frequency by increasing the “dynamic range” of the data. Majdak and Laback concluded that (1) overall, sensitivity to changes in ITD decreased with center frequency and (2) the cutoff frequency of the envelope low-pass filter did not change with center frequency.

Majdak and Laback's conclusion concerning the cutoff frequency of the envelope low-pass filter appears to be inconsistent with the aforementioned findings and interpretations of Bernstein and Trahiotis (1994, 2002). Close scrutiny of the experimental procedures of Majdak and Laback (2009) revealed what could be important differences between their procedures and those employed by Bernstein and Trahiotis (1994, 2002). Perhaps the most salient difference was the nature of the “background noise” commonly used to preclude listeners' use of ITD-information conveyed by low-frequency distortion products. While Majdak and Laback employed a continuous, interaurally uncorrelated, broadband noise (50 Hz to 20 kHz) presented at a spectrum level of about 9 dB, Bernstein and Trahiotis employed a continuous, diotic, noise low-passed at 1300 Hz and presented at a spectrum level equivalent to 30 dB SPL.

It seemed plausible that the choice of background noise by Majdak and Laback (2009) may have, unintentionally, affected the processing of ITDs by their listeners in two distinct manners. First, the spectral extent of Majdak and Laback's interaurally uncorrelated background noise overlapped the spectral regions of the “target” stimuli that conveyed the ITD. Therefore the addition of that interaurally uncorrelated noise to the target stimulus could have degraded the fidelity of the ITD-information to be detected. Second, the quite low spectrum level of their background noise may not have precluded listeners' use of ITDs conveyed by the low-frequency fine-structures of distortion products. Indeed the use of ITDs conveyed by low-frequency distortion products might account for the very low threshold ITDs (about 50 μs or less) obtained from their listeners NH2, NH7, and NH8 at a pulse rate of 200 Hz and a center frequency of 9.2 kHz. Such thresholds are atypically small for envelope-based ITDs conveyed by stimuli at such a high center frequency.

In light of these differences, we decided to measure threshold ITDs using the target stimuli of Majdak and Laback (2009) in our laboratory while employing either the background noise employed by Bernstein and Trahiotis (1994, 2002) or the (different) background noise employed by Majdak and Laback.

EXPERIMENT

Procedure

Save for minor differences in the exact center frequencies used, the set of stimuli employed were essentially those of Majdak and Laback (2009). They consisted of filtered pulse trains. The duration of each pulse was 10.4 μs, the inverse of the sampling rate of 96 kHz. The trains of pulses were filtered via eighth-order Butterworth filters having center frequencies of 4600, 6500, or 9200 Hz and, respectively, constant-percentage (33%) bandwidths of 1500, 2121, or 3000 Hz. Data were obtained for a complimentary set of stimuli having constant bandwidth by collecting additional data for stimuli centered at 6500 and 9200 Hz and a bandwidth of 1500 Hz. The rates of repetition of the pulses employed spanned the range from 64 to 609 Hz in half-octave steps. Each particular stimulus was generated digitally as a 4-s-long buffer. Ongoing ITDs were imposed by applying linear phase shifts to the representation of the targets in the frequency domain and then transforming them to the time domain. Prior to presentation, a 300-ms-long segment of the stimuli destined for each ear was chosen randomly from the buffer, after which coincident 10-ms cos² rise/decay ramps were applied. Finally, the target stimuli were converted to analog voltages (TDT AP2) and were presented via Etymotic ER-2 insert earphones at a level of 66 dB SPL. For the 33% constant-percentage bandwidth conditions, two different background noises were ultimately employed to preclude listeners' use of low-frequency distortion products arising from normal, non-linear peripheral auditory processing. The first was a continuous diotic noise, low-passed at 1.3 kHz (spectrum level equivalent to 30 dB SPL). This type of noise has commonly been employed in similar experiments conducted over decades in several different laboratories, including our own (e.g., Nuetzel and Hafter, 1976, 1981; Bernstein and Trahiotis, 1994, 2002, 2009; Dietz et al., 2013). The second background noise was that employed by Majdak and Laback (2009). It was a continuous, broadband (50 Hz to 20 kHz), interaurally uncorrelated, Gaussian noise presented at a spectrum level equivalent to 9.2 dB SPL. For the constant bandwidth conditions, only the diotic noise low-passed at 1.3 kHz was employed as a background.

Threshold ITDs were measured using a two-cue, two-alternative, forced choice, adaptive task. Each trial consisted of a warning interval (500 ms) and four 300-ms observation intervals separated by 400 ms. Each interval was marked visually by a computer monitor. Feedback was provided for approximately 400 ms after the listener responded. The stimuli in the first and fourth intervals were diotic. The listener's task was to detect the presence of an ongoing ITD (left-ear leading) that was presented with equal a priori probability in either the second or the third interval. The remaining interval, like the first and fourth intervals, contained diotic stimuli. The ITD for a particular trial was determined adaptively to estimate 70.7% correct (Levitt, 1971). The initial step size for the adaptive track corresponded to a factor of 1.584 (equivalent to a 2 dB change of ITD) and was reduced to a factor of 1.122 (equivalent to a 0.5 dB change of ITD) after two reversals. A run was terminated after 12 reversals and threshold was defined as the geometric mean of the ITD across the last ten reversals.

For data obtained with the 1.3 kHz, low-pass, diotic background noise, four normal-hearing adults (ranging in age between 32 and 54 yr) served as listeners and all were tested using the same ordering of the stimuli.1 Beginning with the center frequency/bandwidth combination of 4600 Hz/1500 Hz, three estimates of threshold ITD were first obtained for a pulse rate of 64 Hz, and then successive triplets of estimates of threshold ITD were obtained for increasing pulse rates taken in half-octave steps. Testing at the center-frequency/bandwidth combination was terminated when a pulse rate was reached such that (1) estimates of threshold ITD could not be obtained via the adaptive tracking procedure or (2) estimates of threshold ITD exceeded one quarter-period of the repetition rate of the pulses. One quarter-period represents the ITD that produces maximal lateralization for ITDs conveyed by either the fine structures (e.g., Elpern and Naunton, 1964; Sayers, 1964; Domnitz and Colburn, 1977) or the envelopes (Bernstein, 1984) of stimuli. Larger ITDs have been shown to produce a “reversal” in that the corresponding intracranial images are perceived to be closer to midline. This procedure was repeated for the center frequency/bandwidth combination of 6500 Hz/2121 Hz and then for the center frequency/bandwidth combination of 9200 Hz/3000 Hz. Considering all three center frequency/bandwidth combinations, the pulse repetition rate at which listeners could not effectively perform the task was, for the majority of cases, highly repeatable and unambiguous.

The next step was to gather, for each listener, three new estimates of threshold ITD by visiting all of the conditions in reverse order, beginning, for each center frequency/bandwidth combination with the pulse repetition rate found earlier to be too high to yield valid threshold ITDs. For the constant-bandwidth condition, the same procedure described in the preceding text was repeated using the center-frequency/bandwidth combinations of 6500 Hz/1500 Hz and 9200 Hz/1500 Hz. After collection of data was completed in the constant-percentage and constant bandwidth conditions in which the 1.3 kHz low-pass background noise was employed, three of the four listeners were retested in the 33% constant-percentage bandwidth conditions using the continuous background noise employed by Majdak and Laback (2009).

For some conditions, the six estimates of threshold ITD obtained included values that exceeded one quarter-period of the repetition rate of the pulses. If at least four of the six values did not exceed one quarter-period, the “invalid” thresholds were discarded, and the remaining four thresholds were used in the subsequent calculation of the final threshold for that particular listener and condition. If a majority of the estimates of threshold failed to meet that criterion, the condition was judged as “not possible” for the particular listener. In the rare event that the ratio of the median to the interquartile range of the valid thresholds to be used in the calculation of a final threshold fell below 1.5, three new estimates of threshold were obtained, and the process described in the preceding text was carried out for the most recent six estimates. Threshold ITD for each listener and stimulus condition was computed by taking the log of each of the four to six individual estimates and then taking the anti-log of their median.

Results

Constant 33%-bandwidth across CF, 1.3 kHz low-pass background noise

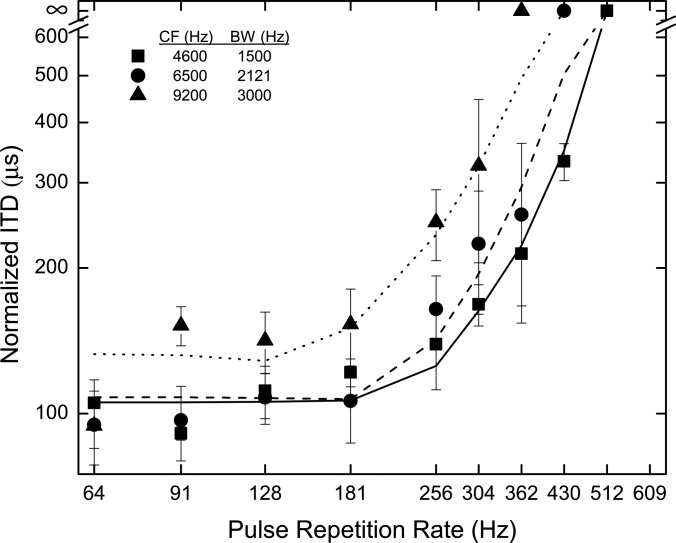
Figure 1 displays mean normalized threshold ITDs plotted as a function of the pulse repetition rate of the stimuli. Normalization was employed to remove inter-listener differences in sensitivity to ITD. The normalization was accomplished, separately for each listener by (1) computing a “reference value,” which was defined as the geometric mean of the threshold ITDs obtained at pulse repetition rates of 64, 91, and 128 Hz in the 4600 Hz/1500 Hz condition, (2) dividing the threshold ITD obtained in each and every stimulus condition for that listener by that reference value. The reference values used for normalization were 40, 94, 151, and 189 μs for listeners DN, BT, RS, and RH, respectively. Mean normalized thresholds were obtained by computing the geometric mean of the normalized thresholds obtained across the four listeners in each stimulus condition. Finally, those normalized thresholds were transformed back into normalized threshold ITDs by multiplying them by the geometric mean of the four reference values used for normalization. In this fashion, we transformed dimensionless normalized thresholds into normalized threshold ITDs, which were scaled in μs. Error bars represent ±1 standard error of the normalized means. The lines represent predictions from a generalized cross-correlation model and will be discussed in the following text.

Figure 1.

Normalized threshold ITD as a function of pulse repetition rate. Symbols represent the data averaged across the four listeners; lines represent predictions of them via a cross-correlation-based model (see text). Points plotted above the break in the ordinate represent conditions for which thresholds exceeded the limit of one-quarter of the period of the pulse repetition rate. The parameter of the plot is the center frequency of the filtered pulse train. Error bars indicate ±1 standard error of the mean. Data were obtained employing a continuous, diotic background noise low-passed at 1.3 kHz.

For the relatively rare stimulus combinations for which not all of the listeners could perform the task, normalized mean threshold ITD was defined in the following way. If valid thresholds were obtained from only three of the listeners, only their data were used. If valid thresholds could be obtained from only two of the listeners, then that particular stimulus combination was deemed “not possible.” Such cases are indicated in Fig. 1 by points plotted above the break in the ordinate. This procedure was employed because it yielded what we judged to be a patterning of the averaged data that was most representative of the data obtained from each individual listener. Only the six lowest values of pulse repetition rate yielded valid threshold ITDs at all three center frequencies of the stimuli. This type of outcome was expected based on our prior research (Bernstein and Trahiotis, 1994, 2002). Those studies showed that there were envelope rates above which valid threshold ITDs could not be obtained and that those envelope rates decreased as the center frequency of the stimulus was increased.

Visual inspection of the data reveals that threshold ITDs generally increased with increases in center frequency. In addition, threshold ITDs increased dramatically as pulse repetition rate was increased beyond 181 Hz. These general outcomes are consistent with data reported by us (Bernstein and Trahiotis, 1994, 2002) and by Majdak and Laback (2009).

The data in Fig. 1 were subjected to a two-factor (three center frequencies × six values of pulse repetition rate), within-subjects analysis of variance (ANOVA). The dependent variable within the analysis was the log of the ITD values shown. Within the ANOVA, the error terms for the main effects and for the interaction were the interaction of the particular main effect (or the interaction) with the subject “factor” (Keppel, 1991). In addition to testing for significant effects, the proportions of variance accounted for (ω²) were determined for each significant main effect and interaction (Hays, 1973).

Overall, the statistical analysis revealed that 59% of the variability in the data was accounted for by the stimulus variables. Each of the two main effects was significant (assuming an α of 0.05) and, in aggregate, they accounted for 51% of the variance: (1) pulse repetition rate [F(5,15) = 10.9, p < 0.001], accounting for 38% of the variance; (2) center frequency [F(2,6) = 7.4, p = 0.02], accounting for 13% of the variance. The interaction between pulse rate and center frequency fell just short of significance at the 0.05 level [F(10,30) = 2.1, p = 0.055] accounting for 8% of the variance.

The ANOVA, performed on the truncated set of data, is a very conservative test of the main effects and their potential interactions for three reasons. First, the analysis does not incorporate, for the pulse repetition rates that had to be omitted, effects that are consistent with the notion that the envelope rate above which threshold ITDs increase is inversely related to center frequency. Second, an inverse relation between center frequency and the envelope rate above which threshold ITDs increase would be expected to manifest itself as a divergence of the data obtained across center frequency only at high pulse-repetition rates. Because the ANOVA is computed across the entire range of values of pulse-repetition rate tested, the lack of a significant interaction between the factors center frequency and pulse-repetition rate is not diagnostic. Third, the patterning of the data is, as was expected, curvilinear, thereby not fulfilling the assumptions concerning linearity inherent in the typical ANOVA. In fact, the normalized threshold ITDs at each of the three center frequencies were extremely well fit by exponential functions of the form

$${\text{ITD}}_{\text{norm}}=a\ast e^{(b\ast \text{PF})},$$ (1)

where ITD_norm is the normalized ITD and PF is the pulse repetition rate. Fitting the data with functions of the form of Eq. 1, the values of r² were 0.93, 0.96, and 0.94, for center frequencies of 4600, 6500, and 9200 Hz, respectively. Thus recognizing that the data are curvilinear reveals that about 95% of the variability among them is attributable to the stimulus variables and that the data contain much less error variance than one might infer from the ANOVA.

The lines in Fig. 1 represent predictions made via a cross-correlation based model of binaural processing (e.g., Bernstein and Trahiotis, 2002, 2009). Specifically, the model incorporates an initial stage of gammatone-based bandpass filtering at the center-frequency of the stimulus (implemented via Dr. Michael Akeroyd's “Binaural Toolbox” for matlab®, also see Slaney, 1993; Patterson et al., 1995), envelope compression (exponent = 0.23), square-law rectification, and fourth-order low-pass filtering at 425 Hz to capture the loss of neural synchrony to the fine-structure of the stimuli that occurs as the center frequency is increased (see Weiss and Rose, 1988; Bernstein and Trahiotis, 1996). The model also includes a second-order (12 dB/octave) Butterworth low-pass filter designed to attenuate spectral components of the envelope above a specific cutoff frequency.

Normalized interaural correlations were measured through the model as a function of ITD separately for each particular stimulus condition (i.e., combination of center frequency, bandwidth, and pulse repetition rate). Separate sets of such measures were made when the cutoff frequency of the model's low-pass filter was varied from 10 to 1000 Hz, in 5-Hz steps. To allow for interpolation, spline functions were fit (matlab®) to the paired, discrete values of normalized interaural correlation and ITD using a least-squares criterion.

The next step was to determine the single value of change in normalized interaural correlation and the three cutoff frequencies of the envelope low-pass filter (one for each center frequency) that maximized the variance accounted for between the predictions of the model and the experimentally obtained values of normalized threshold ITD plotted in Fig. 1. This was accomplished via the “fminbnd” minimization procedure within matlab®.

These analyses resulted in a criterion change in normalized interaural correlation of 0.003 and envelope low-pass filter cutoffs of 300 Hz for the stimuli centered at 4600 Hz, 195 Hz for the stimuli centered at 6500 Hz, and 125 Hz for the stimuli centered at 9200 Hz. The amount of variance accounted for over the entire set of valid threshold ITDs was 91% and was 95%, 92%, and 85% for the valid thresholds obtained at 4600, 6500, and 9200 Hz, respectively. Notably, those amounts of variance accounted for were determined using a metric sensitive to rms differences between predicted and obtained values and were not calculated as the less stringent r² index, which is often used to evaluate the strength of the relations between predicted and obtained values.2

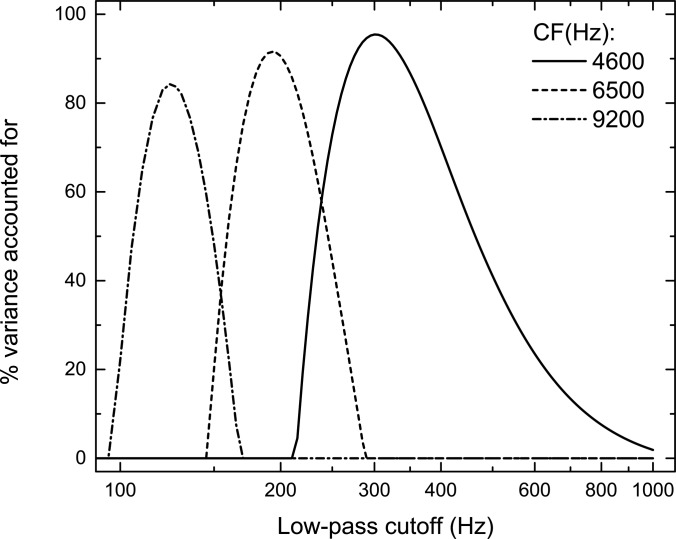
To assess the sensitivity of the precision of fits at each center frequency to changes in the assumed cutoff of the envelope low-pass filter, we re-computed the variance accounted for at each center frequency while varying the cutoff of the low-pass envelope filter within the model. The results of those computations are plotted in Fig. 2. The peaked nature of the curves attests to the precision of the fits in that at each center frequency, relatively small changes in the low-pass cutoff of the envelope filter lead to substantial changes in the amounts of variance accounted for. The curves reveal that if one makes predictions of the data obtained at any one of the three center frequencies by using the best-fitting low-pass filter cutoff for the data obtained at either of the other two center frequencies, then the amounts of variance accounted for fall to zero.

Figure 2.

Percentages of variance accounted for by predictions of the data obtained with the constant 33%-bandwidth stimuli (plotted in Fig. 1). Percentages are plotted as a function of the cutoff frequency of the envelope low-pass filter included within the model.

The success and relatively precise nature of the predictions across center frequency notwithstanding, we wondered whether the assignment of a single best-fitting value of criterion change in normalized correlation at all center frequencies could have affected the validity of the analysis. Therefore we conducted separate calculations in which the best-fitting change in correlation and best-fitting low-pass cutoff frequency were determined independently for the data obtained at each center frequency. That analysis yielded values of change in correlation that were essentially identical to each other and to the value of 0.003 determined in the first analysis. Furthermore, the low-pass filter cutoff frequencies determined using this type of analysis were very close to those determined in the initial analysis, being 320 vs 300 Hz, 180 vs 195 Hz, and 120 vs 125 Hz for the data obtained at 4600, 6500, and 9200 Hz, respectively. In addition, the amounts of variance accounted for obtained at each center frequency were within 1% of those calculated from the initial analysis.

We obtained yet another set of predictions after applying a three-point moving average to the data obtained at each center frequency. This was done to determine if the values of criterion interaural correlation, the derived filter cutoffs, and the amounts of variance accounted for could have been inadvertently influenced by local pulse-rate-to-pulse-rate variability in the measured threshold ITDs. The results of the analysis on the smoothed data yielded a criterion change in interaural correlation virtually identical to that found earlier. The low-pass filter cutoffs were identical to those found earlier for the 6500 and 9200 Hz center frequencies and differed by only 5 Hz for the 4600-Hz center frequency. The associated amounts of variance accounted for were within 3% of those calculated for the “non-smoothed” data.

Finally, at the suggestion of one of the reviewers, we determined the amount of variance in the data plotted in Fig. 1 that could be accounted for by finding the best-fitting single value of the cutoff of the envelope low-pass filter while allowing the criterion change in interaural correlation to vary at each center frequency. This “fixed low-pass filter/variable correlation criterion” analysis resulted in a low-pass cutoff of 205 Hz and criterion changes in correlation of 0.001 for the stimuli centered at 4600 Hz, 0.003 for the stimuli centered at 6500 Hz, and 0.008 for the stimuli centered at 9200 Hz. The amount of variance accounted for over the entire set of valid threshold ITDs was 70% and was 71%, 90%, and 42% for the valid thresholds obtained at 4600, 6500, and 9200 Hz, respectively. Recall that the corresponding values of variance accounted for by the “variable low-pass filter/fixed correlation criterion” analysis reported in the preceding text were substantially higher, being 91%, 95%, 92%, and 85%, respectively. Thus the predictions yielded by the fixed low-pass filter/variable correlation criterion analysis are substantially poorer than those yielded by the variable low-pass filter/fixed correlation criterion analysis.

One other observation seems worthy of mention. Bernstein and Trahiotis (2002) measured threshold ITDs for SAM tones and transposed tones centered at 4, 6, or 10 kHz while varying rate of modulation, albeit with a much coarser sampling than in the present study. Assuming the operation of an envelope low-pass filter having a cutoff of 150 Hz, as suggested by Kohlrausch et al. (2000) and Ewert and Dau (2000), Bernstein and Trahiotis performed a fixed low-pass filter/variable correlation criterion analysis. The results of that analysis, like the present one, showed that the data obtained across center frequency could be reasonably well accounted for when the criterion change in interaural correlation increased with center-frequency. In that respect both studies are in agreement. The new, more comprehensive set of data, however, appear to more strongly support the notion that, for high-frequency, complex waveforms, the criterion change in interaural correlation is essentially constant across center frequency while the cutoff of the envelope low-pass filter decreases with center frequency.

The consistencies among the outcomes of all four quantitative analyses discussed in the preceding text appear to support strongly the following conclusions: (1) a single criterion change in normalized interaural correlation underlies performance at all three center frequencies tested; (2) the cutoff frequency of the envelope low-pass filter that determines sensitivity to ITD at high envelope rates is inversely related to center frequency; (3) the vertical separations between the curves in Fig. 1 indicate losses in sensitivity to ITD as center frequency is increased. Those losses are accounted for by the model under the assumption that the decision variable used by the listeners is a constant criterion change in interaural correlation of the stimuli as processed internally.

Constant 33%-bandwidth across CF, broadband background noise

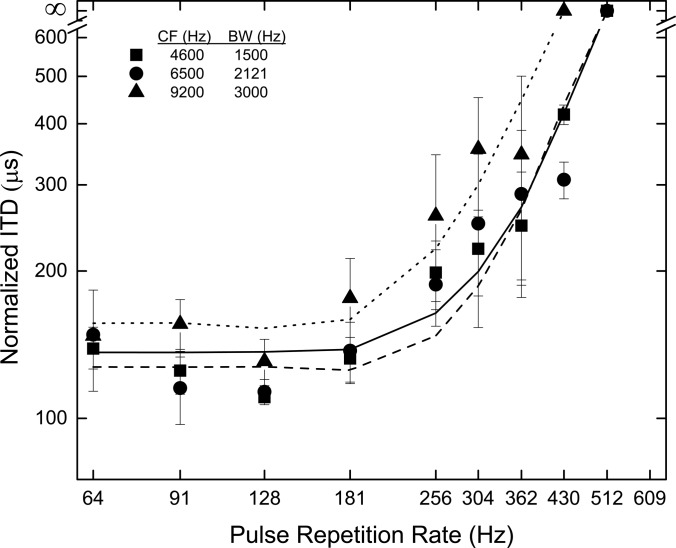
The data obtained with three of the original listeners and the same type of background noise as that employed by Majdak and Laback (2009) are plotted in Fig. 3. All details concerning the presentation of the data and their analysis are identical to those described in the preceding text for the data presented in Fig. 1. Visual comparisons across the two figures reveal very similar patterning of the two sets of data. Quantitative analyses identical to those described for the data in Fig. 1 resulted in a criterion change in normalized interaural correlation of 0.005 and envelope low-pass filter cutoffs of 320 Hz for the stimuli centered at 4600 Hz, 240 Hz for the stimuli centered at 6500 Hz, and 150 Hz for the stimuli centered at 9200 Hz. The amount of variance accounted for over the entire set of valid threshold ITDs was 84% and was 92%, 71%, and 85% for the valid thresholds obtained at 4600, 6500, and 9200 Hz, respectively. Most importantly, the cutoff frequencies derived from this second set of data are remarkably similar to the ones (300, 195, and 125 Hz, respectively) obtained when the background noise was low-passed at 1.3 kHz and when one additional listener's data were also available. In our view, this attests to the robust nature of the findings and reinforces the consistencies in the relation between target center-frequency and envelope low-pass cutoff frequency found in this and in previous experiments conducted in our laboratory (Bernstein and Trahiotis, 1994, 2002).

Figure 3.

Like Fig. 1. Data were obtained employing a continuous, interaurally uncorrelated background noise bandpassed between 50 Hz and 20 kHz.

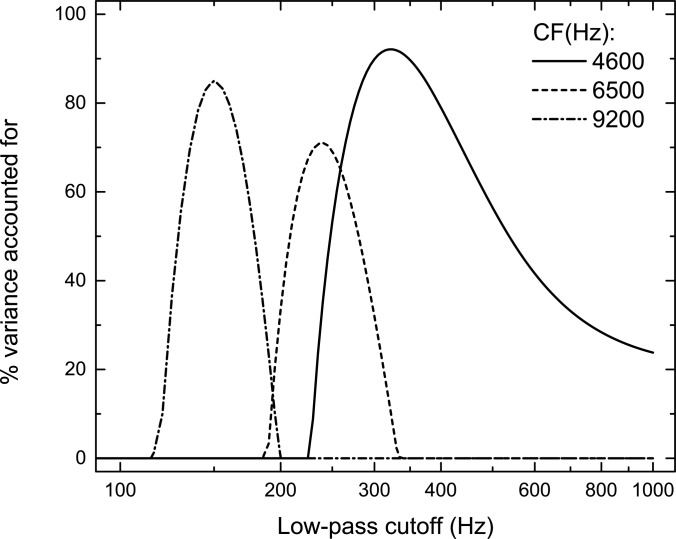
As was done for the data in Fig. 1, to assess the sensitivity of the precision of fits at each center frequency to changes in the assumed cutoff of the envelope low-pass filter, we re-computed the variance accounted for at each center frequency while varying the cutoff of the low-pass envelope filter within the model. The results of those computations are plotted in Fig. 4. Once again, the peaked nature of the curves attests to the precision of the fits in that at each center frequency, relatively small changes in the low-pass cutoff of the envelope filter lead to substantial changes in the amounts of variance accounted for. Furthermore, once again, the curves reveal that if one makes predictions of the data obtained at any one of the three center frequencies by using the best-fitting low-pass filter cutoff for the data obtained at either of the other two center frequencies, then the amounts of variance accounted for fall to zero. In summary, the data and their respective analyses appear to support strongly an inverse ordinal relation between the center frequency of the target stimulus and low-pass filter cutoff that, via mathematical analyses, best fits the data.

Figure 4.

Like Fig. 2 but for the data plotted in Fig. 3

Constant 1500-Hz-bandwidth across CF, 1.3 kHz low-pass background noise

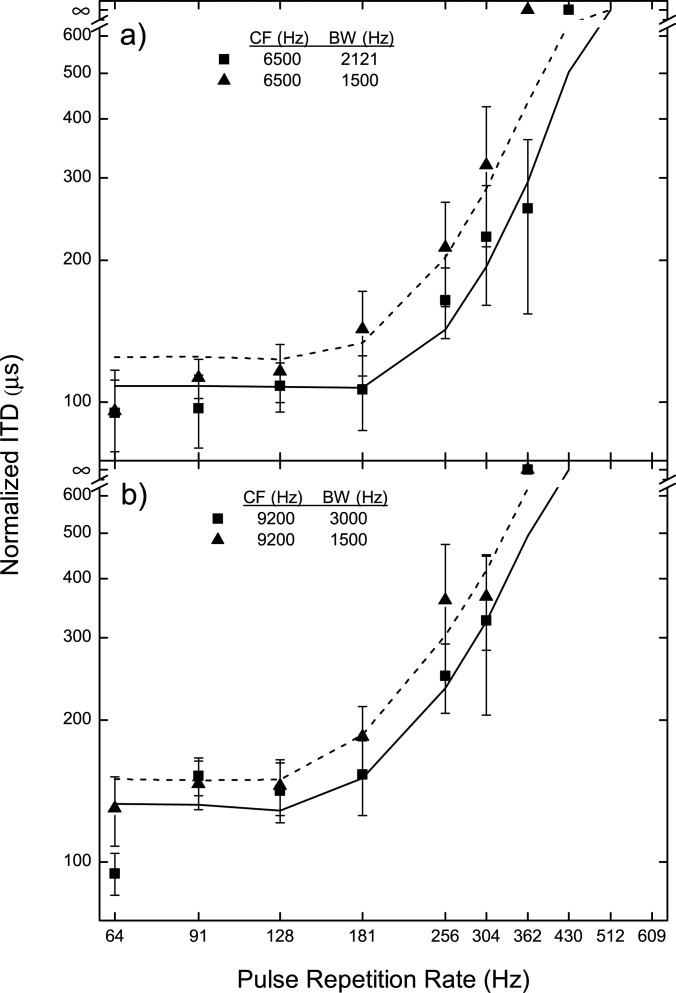
Panels (a) and (b) of Fig. 5 contain normalized threshold ITDs obtained at center frequencies of 6500 and 9200 Hz, respectively. The normalization factors were the same as those described earlier and employed for the data in Fig. 1. Within each panel, the solid squares represent threshold ITDs replotted from Fig. 1 for data obtained in the 33%-bandwidth paradigm. The solid triangles within each panel represent threshold ITDs obtained when the bandwidth was held constant at 1500 Hz. As before, the lines in each panel represent predictions from the model.

Figure 5.

Like Fig. 1, for the data obtained with the stimuli centered at 6500 Hz (a) and 9200 Hz (b). Solid squares within each panel represent normalized threshold ITDs replotted from Fig. 1 for data obtained in the 33%-bandwidth paradigm. Solid triangles within each panel represent normalized threshold ITDs obtained when the bandwidth was held constant at 1500 Hz. The lines in each panel represent predictions from the model.

The data obtained at each center frequency indicate that at most pulse repetition rates, reducing the bandwidth to 1500 Hz produced elevations in threshold ITD. Those elevations appear to be understandable on the basis of earlier findings showing that sensitivity to changes in ITDs varies directly with the relative peakedness/sharpness of the shapes of the envelopes of stimuli centered at high frequencies (Bernstein and Trahiotis, 2009; Klein-Hennig, et al., 2011; Laback et al., 2011). That outcome is relevant to the data in Fig. 5 because, when the bandwidths of the pulsatile stimuli centered at 6500 Hz and 9200 Hz were reduced, the peaks of their envelopes became broader as did the corresponding peaks of their interaural correlation functions. Therefore, in order to produce a given criterion change in interaural correlation, an ITD of greater magnitude would be required (see Bernstein and Trahiotis, 2009).

The predictions from the model for data obtained with the 1500-Hz bandwidth were made by employing the same criterion change in normalized interaural correlation that was found to maximize the model's fits to the data in Fig. 1. Assuming that criterion change in correlation, the procedure sought, at each center frequency, the cutoff frequency of the envelope low-pass filter that produced the most accurate predictions. The dashed lines in each panel represent the fits to the data obtained with a constant bandwidth of 1500 Hz. The solid lines in both panels represent the same predictions that were shown in Fig. 1 for the 33%-bandwidth conditions.

The best-fitting cutoff frequencies of the envelope low-pass filters for the 1500-Hz, constant-bandwidth conditions were 160 Hz for the 6500-Hz center frequency and 125 Hz for the 9200-Hz center frequency. The amounts of variance accounted for were 90% and 94% for the data obtained at the center frequencies of 6500 and 9200 Hz, respectively. The reader is reminded that the low-pass cutoff frequencies for these two center frequencies for the 33%-bandwidth conditions were 195 and 125 Hz, respectively. Thus at the center frequency of 6500 Hz, reducing the bandwidth to 1500 Hz affected both overall sensitivity to ITD and the apparent cutoff of the low-pass envelope filter. At the center frequency of 9200 Hz, however, reducing the bandwidth to 1500 Hz affected only overall sensitivity to ITD.

In order to help interpret the different outcomes vis a vis changes in the cutoff of the envelope low-pass filter at the two center frequencies, we used the model in an attempt to fit the data obtained at 6500 Hz while employing a low-pass cutoff of 180 Hz, a value intermediate between the estimates of 195 and 160 Hz obtained for the 2121 and 1500 Hz bandwidths, respectively. The amounts of variance accounted for remained substantial, being 87% and 78% for the 2121 and 1500 Hz bandwidths, respectively. Consequently, at this juncture, the change in the frequency of the low-pass cutoff found at the center frequency of 6500 Hz should be considered suggestive rather than definitive.

DISCUSSION AND CONCLUSIONS

This study was motivated by apparent differences in conclusions reached by Majdak and Laback (2009) and by Bernstein and Trahiotis (1994, 2002) concerning whether the cutoff of the putative envelope low-pass filter influencing sensitivity to changes in envelope-based ITD varies with the center frequency of the stimulus. The studies from the two laboratories differed in several ways, including two which appeared to be especially salient. One potentially important difference concerned the stimuli [filtered pulse trains (Majdak and Laback) vs SAM tones, transposed tones, and two-tone complexes (Bernstein and Trahiotis)]. A second, potentially important difference concerned the properties of broadband noise, the addition of which, in both studies, was intended to preclude listeners' use of ITDs conveyed by low-frequency distortion products. Majdak and Laback employed a continuous, interaurally uncorrelated, broadband noise (50 Hz to 20 kHz) presented at a spectrum level of about 9 dB; Bernstein and Trahiotis employed a continuous, diotic, noise low-passed at 1300 Hz and presented at a spectrum level equivalent to 30 dB SPL. Other differences among the studies were, in the context of general knowledge concerning binaural information processing, judged by us to be of little consequence.

The experiment reported herein employed Majdak and Laback's filtered pulse train stimuli and both types of background noise. The data obtained with both types of background noise and quantitative analyses of them strongly support Bernstein and Trahiotis’ earlier findings indicating that the cutoff of the putative envelope low-pass filter becomes lower as the center frequency of the stimuli is increased, in this case from 4600 to 6500 to 9200 Hz. Therefore, it appears that the properties of the high-frequency stimuli conveying the envelope-based ITDs were not responsible for the differing conclusions reached by us and by Majdak and Laback. Said differently, it appears that there exists an ordinal relation between the cutoff frequency of the putative envelope low-pass filter and the center frequency of stimuli including two-tone complexes, SAM tones, transposed tones, and filtered pulse trains.

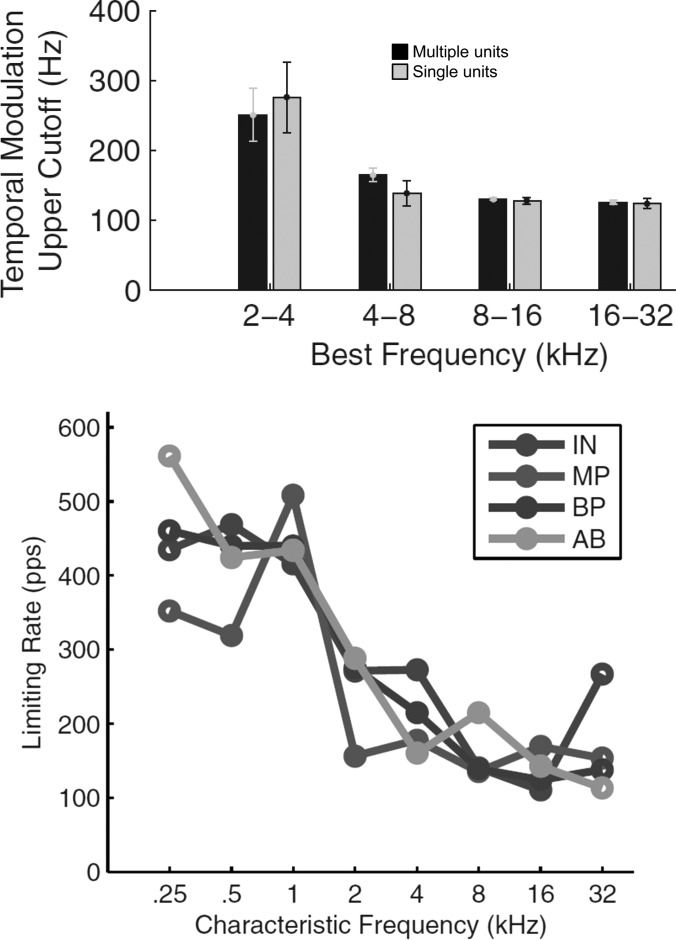
In our view, some recent neurophysiological findings appear to provide consensual validation of our behavioral and theoretical results (Rodríguez et al., 2010; Middlebrooks and Snyder, 2010). Both sets of investigators measured responses of neural units within the inferior colliculus (IC) of cats. Rodríguez et al. stimulated acoustically with spectrally and temporally dynamically changing “ripple” stimuli. Middlebrooks and Snyder (2010) stimulated the auditory nerve electrically using pulsatile stimuli. Figure 6 displays some representative data from each physiological study that pertain directly to the data obtained in the current behavioral study. The results of both neurophysiological studies indicate that the rates of fluctuation beyond which envelope coding degrades systematically decrease with increases in the frequency to which the unit is best tuned. For our purposes, it is especially interesting to observe this trend in responses obtained from neural units having “best” or “characteristic” frequencies of 2 kHz and higher. This is so because it is those neural responses that are best synchronized to the envelope, as opposed to the fine-structure of the stimulus.3 In both studies, those rates (between about 100 and 250 Hz) are remarkably similar to the ones derived behaviorally (Fig. 1).

Figure 6.

Neurophysiological data obtained from the inferior colliculi of cats. Upper panel: Upper cutoff of temporal modulation rate as a function of center frequency obtained via measures of single or multiple units. Adapted from Rodríguez et al. (2010) with permission from APS pending. Lower panel: The limiting rate of phase-locking to pulsatile stimuli as a function of center frequency. The legend refers to four different types of electrodes used to obtain the measurements. They are IN, intraneural; MP, monopolar intrascalar; BP, bipolar intrascalar; AB, apical ball. Adapted from Middlebrooks and Snyder (2010) with permission from SFN.

In summary, the preponderance of behavioral data obtained both recently and in the past in experiments concerning sensitivity to envelope-based ITDs conveyed by a variety of high-frequency, complex stimuli and with two types of background noise indicate that there exists an inverse relation between the center frequency of the target stimulus conveying the ITD and the putative envelope low-pass filter cutoff that limits sensitivity to ITD for relatively high rates of fluctuation of the envelope. This conclusion is bolstered by recent neurophysiological data obtained from units in the inferior colliculus.