Statistical intensity variation analysis for rapid volumetric imaging of capillary network flux

Abstract

We present a novel optical coherence tomography (OCT)-based technique for rapid volumetric imaging of red blood cell (RBC) flux in capillary networks. Previously we reported that OCT can capture individual RBC passage within a capillary, where the OCT intensity signal at a voxel fluctuates when an RBC passes the voxel. Based on this finding, we defined a metric of statistical intensity variation (SIV) and validated that the mean SIV is proportional to the RBC flux [RBC/s] through simulations and measurements. From rapidly scanned volume data, we used Hessian matrix analysis to vectorize a segment path of each capillary and estimate its flux from the mean of the SIVs gathered along the path. Repeating this process led to a 3D flux map of the capillary network. The present technique enabled us to trace the RBC flux changes over hundreds of capillaries with a temporal resolution of ~1 s during functional activation.

1. Introduction

Optical coherence tomography (OCT) has enabled quantification of blood flow in arteries and veins [1], and visualization of the microvasculature [2]. For quantifying blood flow properties with the microvasculature, we must recall that capillaries have different flow characteristics than arteries and veins. Most importantly, red blood cells (RBCs) flow one by one in capillaries with sometimes large separations, and the hematocrit or linear RBC density significantly varies across segments in capillary networks [3]. Due to this discrete nature of capillary RBC flow and varying hematocrit, it is common to consider RBC flux in units of RBC/s. The flux quantifies the number of RBCs passing per unit time and is directly related to oxygen delivery.

Doppler OCT has been widely used to quantify blood flow speed in arteries and veins [1, 4], but its application in capillaries is challenging owing to the discrete nature of capillary RBC flow and the fact that many capillaries lie nearly along the transverse direction. Several decorrelation-based methods have been proposed to image the speed or flow even in the transverse direction, either explicitly producing a speed map [5–7] or indirectly presenting a decorrelation map [8, 9]. These approaches have been validated in large vessels or glass pipes whose diameters are larger than 100 μm [7, 9–11]. Cerebral capillaries are ~8 μm in diameter so that RBCs only can pass one by one, often with a large separation between RBCs. While the previously described decorrelation metrics can still be applied in capillaries, it is necessary to properly interpret the relation between the decorrelation metric and the RBC flow properties.

A second issue in quantifying capillary flow properties is the varying hematocrit. While arteries and veins have a relatively constant hematocrit equal to the systematically measured one, the hematocrit or RBC linear density is known to vary significantly across segments in capillary networks [3, 12]. Many of the Doppler and decorrelation-based methods validated their measurements of the RBC speed using blood samples with a constant hematocrit, but the signal decorrelation rate will generally depend on the hematocrit. For instance, the metrics used in [9, 10, 13] were shown to be linearly related to the flow speed; however, the slope of the linear relations will also be a function of the hematocrit [14], and this was not validated in those papers.

Techniques based on identification of individual RBC passage will be relatively free from the above issues of the discrete RBC flow speed and varying hematocrit, and will be able to quantify the RBC flux. Two-photon microscopy line scanning methods [3] and fluorescence video microscopy methods [15] identify individual RBC passage. However, those methods monitor only one or a few capillaries at a time that locate within the scan line or a thin focal depth, while capillaries are known to exhibit highly diverse responses to functional activation [16]. Thus, in order to characterize capillary network flow dynamics with sufficiently high statistical power, one should be able to measure blood flow properties over hundreds of capillaries at the same time and with high temporal resolution of ~1 s during functional activation. As OCT obtains axial information over a generally large focal depth, it would be able to monitor more capillaries across different depths as long as OCT can identify individual RBCs. Recently, we found that dynamic OCT imaging can capture individual RBCs passing through capillaries and demonstrated the use of this finding to obtain 3D maps of capillary RBC speed, flux, and linear density [12]. Although this technique is faster than previous techniques, it still requires hundreds of seconds to obtain a map over a capillary network consisting of hundreds of capillaries.

In this paper, we present a novel method to quantify capillary RBC flux with higher temporal resolution from rapid volumetric imaging data where only two scans are repeated for each plane. To achieve this, we utilize a metric of statistical intensity variation (SIV). After briefly reviewing our previously published approach of measuring RBC passage [12], we then utilize it to validate that the SIV metric provides a measure of RBC flux in capillaries. To obtain sufficient ensemble averaging of the SIV metric, we average the metric over each capillary segment. Finally, we demonstrate the utilization of this SIV method to measure dynamic changes in RBC flux over hundreds of capillaries in the rodent cerebral cortex during somatosensory activation.

2. Materials and methods

2.1 Animal preparation

Sprague Dawley rats (250-300 g, n = 2) were initially anesthetized with isofluorane (1.5-2.5%, v/v), and ventilated with a mixture of air and oxygen during surgical procedures. Tracheotomy and cannulation of the femoral artery and vein were done. Following this, the head was fixed in a stereotaxic frame, and the scalp retracted. A craniotomy was performed using a saline-cooled dental drill and a 3 mm x 3 mm area over the somatosensory cortex was exposed. The dura was carefully removed, and the brain surface was covered with agarose gel in artificial cerebrospinal fluid and a glass cover slip and sealed with dental acrylic cement. After surgery, rats were anesthetized with Alpha Chloralose (40 mg/kg intravenous bolus followed by 40-50 mg/kg/hr, i.v.) and moved to our OCT system for experiment. Physiological signs such as heart rate, body temperature and blood pressure were continuously monitored during surgery and during the experiment. All animal experimental procedures were reviewed and approved by the Massachusetts General Hospital Subcommittee on Research Animal Care.

2.2 Spectral-domain optical coherence tomography system

We optimized a spectral-domain OCT (SD-OCT) system (Thorlabs, Inc., Newton, New Jersey, USA) for dynamic in vivo imaging of the rodent cerebral cortex as described in a previous publication [17]. We employed a large-bandwidth NIR light source (1310-nm center wavelength with 170-nm bandwidth) for a large imaging depth (up to 1 mm in brain tissue) and high axial resolution (3.5 μm). The transverse resolution is 3.5 μm with our 10x objectives (NA = 0.26). Note that the transverse resolution is identical to the axial one for isotropic voxels. The system sensitivity was 105 dB with the power of 4 mW. The scanning speed is 47,000 A-scan/s. We used 400 A-scans per B-scan (91 frame/s, 11-ms time gap) in the experiments for the present technique, while we previously used 96 A-scans per B-scan (250 frame/s, 4-ms time gap) for the previous technique introduced in Figs. 1 and 2 . We used scanning and stimulation protocols similar to widely used ones in literature [18].

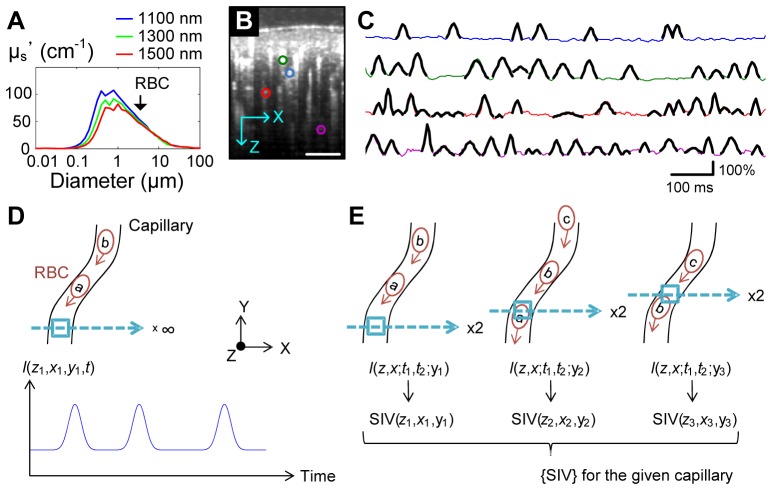
Fig. 1.

(A) Mie scattering calculation. The reduced scattering coefficient (μ_s’) is presented as a function of the scatterer diameter. The black arrow indicates the diameter of RBCs (~6.5 μm). The refractive index of medium, the refractive index of scatterers and the volume fraction of scatterers in medium were assumed to be 1.33, 1.57 and 0.05, respectively. (B) Cross-sectional OCT angiogram of the rodent cerebral cortex. Scale bar, 100 μm. (C) RBC passage captured in OCT intensity time courses. Each line presents the time course of relative changes in the OCT intensity at the center of each capillary indicted by the color circles in (B). Each peak (overlaid black pieces) represents single RBC passage. The peaks were localized with a spatial extent consistent with RBC size and peaks moved through a capillary when the scanning line was aligned to the capillary (data shown in [12]). Reprinted from the authors’ previous publication [12]. (D) A schematic of the dynamic OCT imaging sequence to capture individual RBC passage as in (C). (E) A schematic of the scanning sequence for SIV imaging. Only two B-scans were repeated for each Y-position, and SIV values will be gathered along the capillary segment path.

Fig. 2.

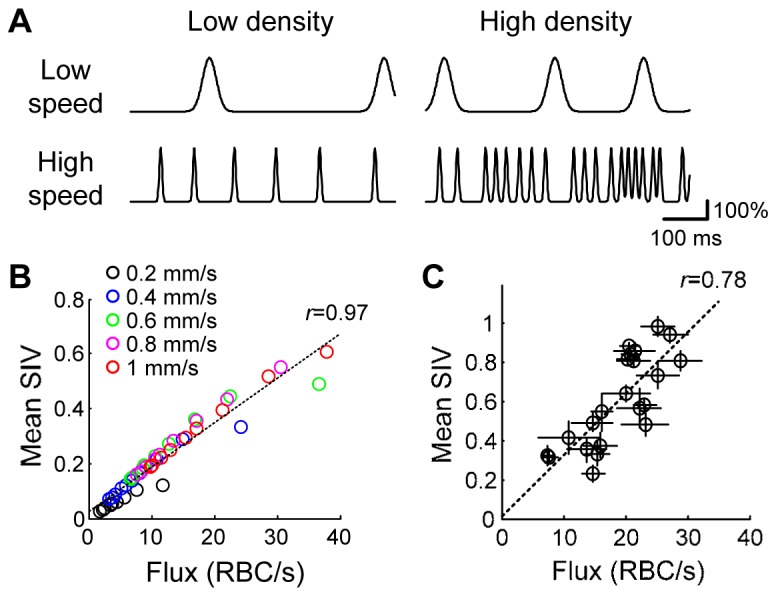
Numerical simulation and experimental validation of the SIV relation to the RBC flux. (A) Examples of the synthesized time courses for various RBC speeds and densities. (B) Numerical simulation result. (C) Experiment result. 22 capillaries were analyzed. Data are presented as mean ± SD.

3. Results

3.1 OCT intensity fluctuates when RBC passes

The intensity of the OCT signal at a voxel basically represents the amplitude of light backscattered from the voxel. According to the Mie scattering theory, 1-μm wavelength light is supposed to be largely scattered by particles of 0.1-10 μm in diameter (Fig. 1(A)). Therefore, we can expect that within capillaries, RBCs (~6.5 μm in diameter) will result in large OCT signals compared to blood plasma. If this is true, the OCT signal at a given voxel located in a capillary should go up and come back down when an RBC passes.

This idea has been validated in our previous publication [12]. Also, the OCT identification of individual RBC passage was used for quantifying the flow properties of RBCs such as the flux [RBC/s], speed [mm/s], and linear density [RBC/mm]. For example, when repeating B-scans at a fixed cross-sectional plane of the cortex and analyzing the 3D data of I(z,x,t), the time courses at the centers of several capillaries exhibited asynchronous peaks representing individual RBC passage through each capillary (Fig. 1(C)). As slower RBC flow will result in a broader peak, the RBC speed was estimated from the mean width of the peaks while the flux is estimated from the number of the peaks. Therefore, by repeating the acquisition and analysis at many Y-positions, our previous technique enabled us to obtain 3D maps of capillary RBC flux, speed, and density [12].

Unfortunately this technique was not fast enough to trace hemodynamic responses whose time constant is ~1 s. The reason is that it should anchor B-scans for a moment (generally longer than a few seconds [12]) to capture the RBC passages (see Fig. 1(D) for conceptual illustration). Here, we developed another technique that enables much faster estimation of capillary RBC flux.

3.2 Statistical intensity variation (SIV) measurement of capillary RBC flux: Concept

Whereas our previous technique repeated B-scans hundreds of times at one Y-position, the present technique repeats only two B-scans at each Y-position for rapid volumetric imaging. We first defined a metric quantifying the intensity variation between the two consecutive B-scans,

$$SIV\left(z,x,y\right)\equiv \frac{E\left[{\left\{I\left(z,x,t_2;y\right)-I\left(z,x,t_1;y\right)\right\}}^2\right]}{E\left[\frac{1}{2}\left\{I^2\left(z,x,t_2;y\right)+I^2\left(z,x,t_1;y\right)\right\}\right]}$$ (1)

where I(z,x,t ₁;y) and I(z,x,t ₂;y) are the first and second B-scans at a given Y-position, respectively, and E[ ] denotes ensemble averaging. The ensemble averaging can be implemented by averaging over neighboring voxels and/or repeated volumes. This ensemble averaging will minimize the stochastic speckle effect in the OCT intensity.

A single SIV value would not quantify RBC flow properties because the value will depend on the space and time of its acquisition. For instance, SIV(z₁,x₁,y₁) in Fig. 1(E) will be zero in principle as no RBC passes, but SIV(z₂,x₂,y₂) will be larger than zero. Here, our basic idea is that gathering and analyzing many SIV values from a given capillary segment will enable us to estimate RBC flow properties, under the reasonable assumption that the properties are approximately constant along the non-branched single capillary segment (see Fig. 1(E) for conceptual illustration).

In more detail, if one gathers SIVs at random moments while fixing the Y-position, it will be conceptually identical to a random sampling of SIVs from the time course embedding the peaks (Fig. 1(D), for example). Then, the mean SIV will increase as the speed increases (i.e., sharper peaks), but it will also increase as the density increases (i.e., more peaks for unit time). Thus, we hypothesized that the mean SIV will be a function of the RBC flux, because (Flux) = (Density) × (Speed). This estimation will still work when moving the scanning Y-position and gathering SIV values along the given capillary segment as illustrated in Fig. 1(E), since it will similarly randomly sample SIVs from the RBC peak train traveling along the capillary segment.

One may be concerned with a possible ‘lock-in’ between the B-scan swipe and the traveling RBC train; however, such a lock-in would appear very rarely or its effect, if any, would be negligible in practice. The reason is that (i) the B-scan swipe speed (0.08 mm/s with our Δt = t ₂ – t ₁ = 11 ms and Nyquist spatial sampling frequency) was lower than the typical range of capillary RBC speed (0.2-2 mm/s); and (ii) SIVs were obtained with the ensemble averaging across volumes as well.

3.3 SIV measurement of capillary RBC flux: Validation

We performed numerical simulations and experimental measurements to test the hypothesis that the mean SIV will be a function of the RBC flux. First, we numerically synthesized OCT time courses embedding RBC passage peaks, for various flow speeds and mean RBC separations. The spatial separation between adjacent RBCs, which is related to the linear density, were distributed as w _RBC + x, where w _RBC is the RBC size (6.5 μm) and x follows the Gamma distribution x^{k −1}e^{- x / θ} with the shape k = 5 and the scale θ = (mean separation) / k. Each RBC peak’s width was a function of the RBC speed v, (w _RBC ² + w _voxel ²)^1/2 / v [12], where we used the OCT voxel size w _voxel = 3.5 μm.

We synthesized 50 time courses for the RBC speeds of 0.2, 0.4, 0.6, 0.8 and 1 mm/s and mean RBC separations of 10, 20, 30, …, and 100 μm. Each time course was 10 s in length. Figure 2(A) shows several examples of the synthesized time courses, where higher density exhibits more peaks and higher speed leads to sharper peaks. The RBC flux was determined by (Flux) = (Density) × (Speed). From each time course, we sampled a set of SIV values with the time gap equal to the one that will be used in experiments (11 ms). Then, we averaged the set of SIV values into a mean value and compared it to an RBC flux obtained by counting the RBC passage peaks in the time course. As a result, we found that the mean SIV was proportional to the RBC flux regardless of various speeds and densities as hypothesized (r = 0.97, Fig. 2(B)). When we compared the mean SIV with the known RBC speed, no simple relation was found because the relation also depended on the RBC density as we expected.

We also experimentally investigated the relation of SIV to RBC flux. We obtained OCT intensity time courses of capillary centers (4 s in length, n = 22) that exhibited individual RBC passage as in Fig. 1(C). For each time course, we split it into four 1-s pieces; for each piece, we counted the number of peaks for true RBC flux values and obtained the mean of randomly sampled SIVs; and then presented their mean and standard deviation (SD) as a single data point in Fig. 2(C). We found that the mean SIV was linearly related with the RBC flux (r = 0.78). The slope and intersect will depend on the measurement system and scanning protocol including the time gap (Δt). The slope was slightly larger in the experiment, likely because the experimental data had non-zero fluctuations even when no RBC passes. The empirical relation with our system and Δt = 11 ms was (SIV) = 0.012 + 0.032 × (Flux). As isotropic voxels were used, this relation is independent in principle of the direction of RBC flow or the angle between the capillary axis and the scanning plane.

3.4. Hessian matrix analysis-based vectorization of capillaries

In order to gather SIV values along capillary segment paths, we need to know the position vectors of the capillaries. Here, we vectorized each capillary using a method based on Hessian matrix analysis similarly to the prior works [19, 20].

We performed SIV imaging of the rodent cerebral cortex in the cranial window preparation (Fig. 4(A)), producing 3D SIV volume data (400 × 432 × 512 voxels in X-Y-Z axes over the FOV of 350 μm × 360 μm; the volume rate was 0.1 vol/s). Ten volumes were used for building one SIV volume, where the ensemble averaging was performed by convolving with a 3D Gaussian kernel (FWHM = 4 μm) and averaging over ten volumes (see Fig. 3 for overall data processing procedures). Figures 4(B) and 4(C) show the en face maximum projections of exemplary volume data of the OCT angiogram and SIV, respectively. The angiogram and SIV volume were obtained from the same raw data where two B-scans were repeated for each Y-position.

Fig. 3.

A diagram of data processing.

Fig. 4.

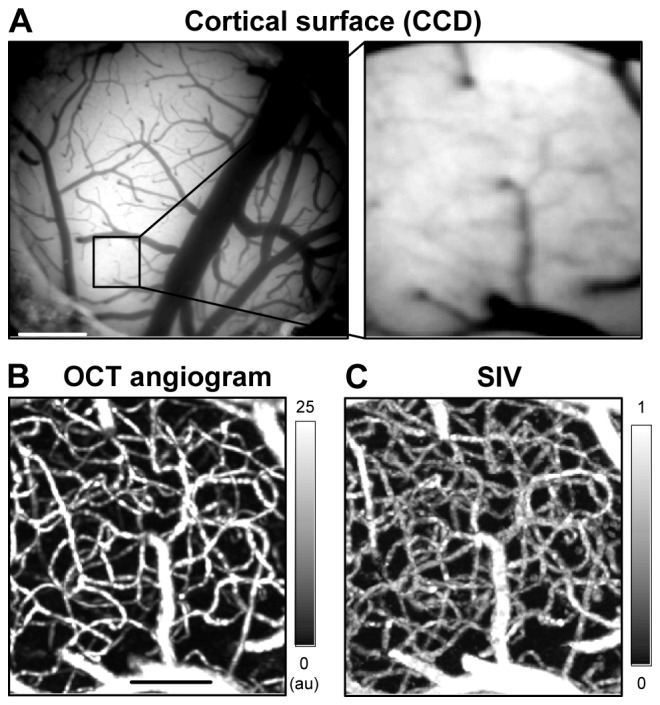
Volumetric SIV imaging. (A) CCD image of the brain cortex through the cranial window. (B) En face maximum intensity projection (MIP) of the OCT angiogram. Ten volumes were averaged. (C) En face MIP of the SIV volume data.

From the OCT angiogram and SIV volume data, we developed an algorithm to automatically identify and vectorize individual capillaries, enabling us to collect SIVs along each capillary segment. We first re-sampled the 3D angiogram data so that the axial sampling frequency becomes two times that of the lateral axis. Taking into account the fact that the vertical cross-section of capillaries typically results in a vertically long ellipse due to multiple scattering in OCT, the re-sampling made the cross-section of capillaries closer to a circle, which was more beneficial for the following Hessian matrix-based processing.

At every voxel in the volume data, the Hessian matrix and its eigenvalues and eigenvectors were obtained. As eigenvalues of the Hessian matrix represent the second-order derivatives of the neighboring spatial pattern along the corresponding eigenvectors, the eigenvalues have generally been used for enhancing the contrast of vessels in volumetric image data [19, 20]. As described in [19], when the neighboring spatial pattern is close to an ellipsoid, the eigenvalues (λ₁, λ₂ and λ₃) are related to the widths of the ellipsoid along the corresponding eigenvectors (i.e., principal axes). Here we used the eignevalues to define a 'tubeness' at every voxel quantifying how the neighboring structure looks like a tube,

$$T=\{\begin{array}{c}\left|{\lambda }_3\right|{\left(\frac{{\lambda }_2}{{\lambda }_3}\right)}^{{\gamma }_{23}}{\left(1+\frac{{\lambda }_1}{\left|{\lambda }_2\right|}\right)}^{{\gamma }_{12}},{\lambda }_3<{\lambda }_2<{\lambda }_1\le 0\\ \left|{\lambda }_3\right|{\left(\frac{{\lambda }_2}{{\lambda }_3}\right)}^{{\gamma }_{23}}{\left(1-\alpha \frac{{\lambda }_1}{\left|{\lambda }_2\right|}\right)}^{{\gamma }_{12}},{\lambda }_3<{\lambda }_2<0<{\lambda }_1<\frac{\left|{\lambda }_2\right|}{\alpha }\\ \begin{array}{l}\\ 0,\text{otherwise}.\end{array}\end{array}$$ (2)

where α, γ ₁₂, and γ ₂₃ are processing parameters. We found that the use of α = 0.25, γ ₁₂ = 0.5, and γ ₂₃ = 0.5 produced good results with our data, similar to those suggested in the literature [19]. In practice, the tubeness was obtained over several sizes of the Hessian matrix calculation (i.e., the size of the neighboring space to be tested) for covering various diameters of vessels, and then the largest tubeness and corresponding eigenvectors were chosen. Figure 5(A) presents the en face projection of the obtained tubeness volume.

Fig. 5.

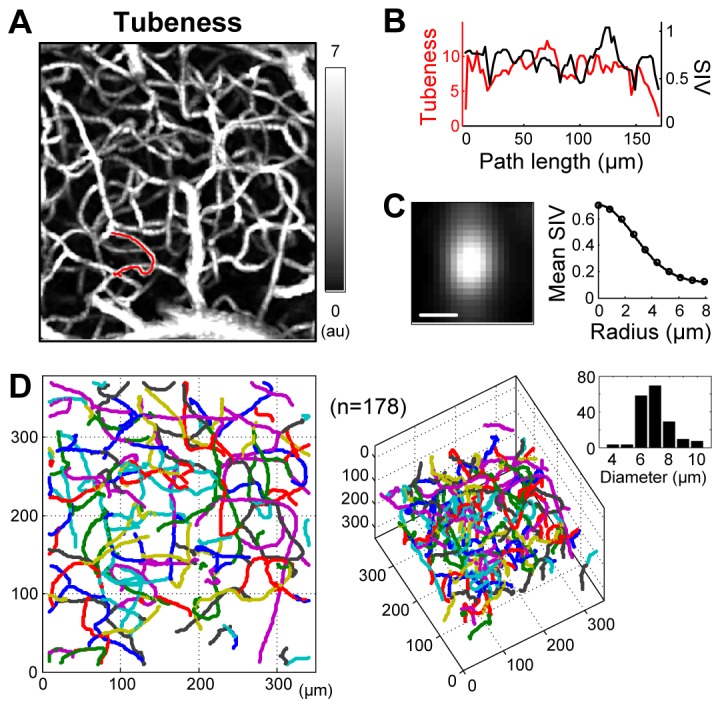
Vectorization of capillary segments. (A) En face MIP of the tubeness. (B) For an example of vectorization indicated by the red curve in (A), the tubeness and SIV are plotted versus the path length. This segment consisted of 75 points and its length was 169 μm. The tubeness exhibited relatively smaller values at the branch while the SIV did not. (C) For all 75 points of the exemplary segment, slices of the SIV map were obtained over the cross-sectional planes normal to the capillary direction and then averaged (left). The diameter of the capillary segment can be estimated from the mean cross-section, where the mean SIV as a function of the distance from the center (i.e., radius) was fit with a Gaussian function (right). The diameter of this segment was 6.3 μm. Scale bar, 5 μm. (D) En face and inclined views of the vectorized capillary segments with random color (n = 178). The bar graph in the right side presents the histogram of the diameter.

Our algorithm traced vessels using the tubeness and the eigenvectors (direction vectors of the ‘tube’). The tubeness was high at the centerline of vessels and became lower at the branch of vessels since the branch is less close to a tube in morphology. Therefore, our algorithm stopped tracing when the tubeness became smaller than a predefined threshold (Fig. 5(B), for example). By repeating this step, the algorithm properly traced a number of capillary segments so that the cross-sections averaged through the segment paths were close to 2D Gaussian patterns even when the paths were highly tortuous (see Fig. 5(C) for example). With this ‘raw’ vectorization, we performed a simple manual inspection to refine the selection of capillary segments, taking into account the fact that cerebral capillaries have a diameter less than 10 μm. Following this procedure, hundreds of capillaries were identified and vectorized as shown in Fig. 5(D).

3.5. SIV imaging of capillary network RBC flux

Using the vectorized capillary segment paths and the SIV volume data, the RBC flux of each capillary segment was obtained from the mean SIV averaged along its path. Consequently, the present technique enabled us to measure the RBC flux over hundreds of capillaries, leading to a 3D flux map of the capillary network as shown in Fig. 6 .

Fig. 6.

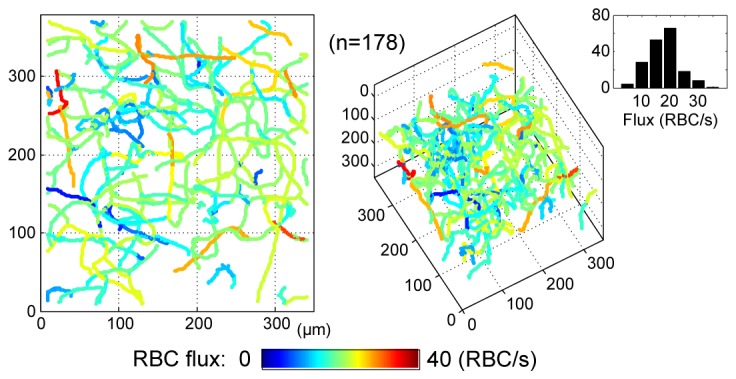
3D flux map of the capillary network. The bar graph in the right side presents the RBC flux histogram of the identified 178 capillaries.

3.6. Rapid volumetric imaging of capillary network flux responses to functional activation

As an exemplary application, we used the present technique to quantify how the RBC flux varies with functional activation across hundreds of capillaries. In order to achieve the desired temporal resolution enough to trace fast hemodynamic responses whose time constant is typically ~1 s, we split the ROI into nine sub-ROIs and repeated SIV imaging over ten runs of forepaw stimulation for each sub-ROI (Fig. 7 ). Merging these data resulted in a temporal series of 20 consecutive SIV volumes with a temporal sampling frequency of 1.3 s (ΔT = T_{n +1} – T_n), where each SIV volume was obtained by averaging over ten runs while being aligned to the stimulation onset.

Fig. 7.

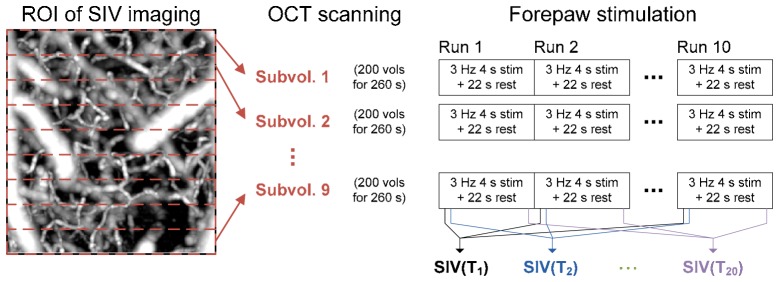
Scanning and stimulation protocols for SIV imaging of capillary network flux response to functional activation. For each sub-volume, ten runs of electrical stimulation (3 Hz for 4 s in the middle of a 22-s resting period) were applied to the contralateral forepaw while SIV imaging was repeated 220 volumes.

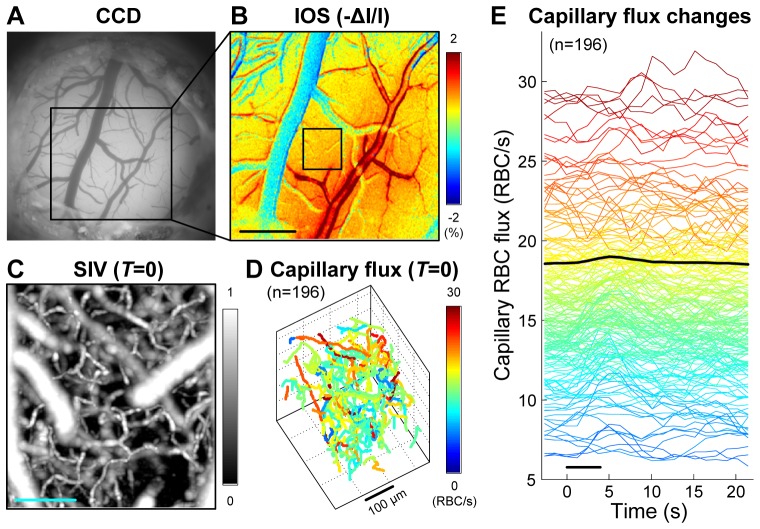
This dynamic SIV imaging was performed over an ROI near the center of functional activation in the somatosensory cortex corresponding to forepaw stimulation. The activation center was identified with intrinsic optical signal (IOS) imaging (Fig. 8(B) ). One of the temporal series of 20 SIV volumes is presented in Fig. 8(C). We identified 196 capillary segments from a representative angiogram volume that was obtained by averaging over ten runs and 20 temporal volumes, and then used the series of SIV volumes to estimate the RBC flux, for each capillary segment, and at each time. This analysis led to a temporal series of 20 capillary network flux maps, one of which is in Fig. 8(D). This means that the present technique enabled us to trace how the RBC flux varies with activation over 196 capillaries as shown in Fig. 8(E).

Fig. 8.

SIV imaging of capillary network flux responses. (A) A CCD image of the rodent somatosensory cortex. (B) IOS imaging of the hemodynamic response of the cortical surface. As we used 570-nm illumination, a decrease in the CCD intensity (red color) represents an increase in the blood volume. Scale bar, 500 μm. (C) En face MIP of SIV at T = 0 s. A temporal series of 20 SIV volumes like this were obtained. We located the OCT focus at a slightly deeper area to include the capillaries near the neurons of the somatosensory cortex. Scale bar, 100 μm. (D) Capillary network flux map at T = 0 s. A temporal series of 20 flux maps like this were obtained. (E) Time courses of RBC flux changes of the 196 capillaries during functional activation. A change in the mean flux averaged across capillaries is presented by the thick black curve. The peak change was 2.2% and highly significant (p < 10⁻⁸). The black bar in the bottom indicates the duration of forepaw stimulation (3 Hz for T = 0 – 4 s).

As can be seen in Fig. 8(E), some capillaries exhibited early flux increases while some exhibited late increases or even decreases. This diversity in the capillary response, which differs from the well-known arteriolar hemodynamic response, has been observed in the literature, but over only less than 20 capillaries using methods that measure one capillary at a time [16].

4. Discussion and conclusion

Capillary RBC flow exhibits the characteristic discrete nature and varying hematocrit [3]. These characteristics should be carefully considered when measuring RBC flow properties in capillaries. Also, they shed light on the importance of the flow property of RBC flux in oxygenating neighboring tissue. The RBC flux is closely related to the oxygenation since it directly represents how many oxygen sources pass the tissue per unit time.

As mentioned in the Introduction, existing phase- or decorrelation-based methods are not suitable for measuring capillary RBC flux, and even their speed measurement in capillaries will be contaminated by the discrete nature and/or varying capillary hematocrit. Traditional Doppler OCT measures the axial component of blood flow velocity [1, 4] and is thus difficult to apply to capillaries which often are tangential to the optical axis. Variations of Doppler OCT [9, 21] permit estimation of transverse velocity, and other methods [9, 13, 22], some of which use similar metrics to our SIV, have been proposed to more directly measure the transverse velocity; but those methods seem to have limited sensitivity in small vessels [23]. Although another method [8] has been suggested for better sensitivity in capillaries, speed measurements of the method and the above described ones will be inaccurate due to the discrete nature of capillary RBC flow, and due to the varying capillary hematocrit as described below.

Many of those methods validated their measurement of the speed using either solid phantoms or blood samples with a constant hematocrit; however, the signal decorrelation rate will generally depend on the hematocrit or the scatterer density. For instance, the metrics used in [13, 22] that are conceptually similar to our SIV were shown to be linearly related to the flow speed, but we believe that the slope of the linear relations will also be a function of the hematocrit or scatterer density, but this was not varied in those papers. Our simulation also showed that the mean SIV is proportional to the RBC speed, but with different slopes depending on the density (data not presented). This hematocrit issue will be less critical in measuring arterial and venous flow as they have a relatively constant hematocrit equal to the systemically measured hematocrit, but it can be problematic in quantifying capillary flow as the hematocrit or RBC linear density is known to vary significantly across capillary segments [3, 12]. Consequently, many of the existing decorrelation-based methods might not be suitable for accurately quantifying capillary blood flow when taking into account the above described discrete nature of RBC flow and the varying hematocrit.

The SIV technique described here is based on the finding that OCT intensity fluctuates in response to individual discrete RBC passage in capillaries. Figure 8 demonstrates the ability of the present SIV technique for imaging RBC flux dynamics over a reasonably large capillary network with high temporal resolution. To our knowledge, no technique thus far has enabled such high-throughput monitoring of capillary RBC flux dynamics as shown in Fig. 8(E). This ability will be used for a study of how capillary network blood flow patterns respond to functional activation in healthy and disordered brains. As OCT is widely used for in situ and clinical studies, the present technique is applicable to such studies including human ophthalmology.

One of the limitations of the present technique is that it currently measures the RBC flux only. How to extract information about speed and density from a set of SIV values gathered along a capillary segment path will be further investigated.

The dynamic range of the measurable RBC flux is a function of the time gap (Δt = t ₂ – t ₁; 11 ms in our implementation). A larger dynamic range will be achieved if one obtains different time gaps in a single volume scan in a similar way proposed in [24, 25]. Combining information of SIVs with different time gaps will lead to an extended dynamic range and possibly more accurate and precise estimation. The upper limit in the measured capillary RBC fluxes in this study was relatively lower than those in the literature. Some of the literature reported that 70-80% of capillaries exhibited lower than 40-45 RBC/s [16, 26], while others reported that 80% of capillaries exhibited lower than 80 RBC/s [3]. This high variability across the literature might be attributed to the animal species, anesthesia and physiology including the blood pressure at the moment of measurement. The animals used in this study exhibited relatively low blood pressures of ~70 mmHg during the experiments. Nevertheless, we believe that this paper provides the proof of concept of the SIV technique.

Finally, one could switch the B-scan swipe direction across repeated volume scans in order to minimize the effect of a possible ‘lock-in’ between the B-scan swipe and traveling RBCs. As described in section 3.2, the used B-scan swipe speed was 0.08 mm/s, lower than the typical range of capillary RBC speed. If one uses a faster scanning protocol so that the B-scan swipe speed lies within the speed range to be measured, it will be worth considering a dual-direction swipe approach.

In conclusion, this paper describes the development of the SIV technique for rapid volumetric imaging of capillary network flow dynamics in the rodent cerebral cortex. As a future work, the present technique will be used for studying how the brain capillary network flow pattern differs across young, aged, and pathological brains such as in Alzheimer’s disease.