Multiple-object geometric deformable model for segmentation of macular OCT

Abstract

Optical coherence tomography (OCT) is the de facto standard imaging modality for ophthalmological assessment of retinal eye disease, and is of increasing importance in the study of neurological disorders. Quantification of the thicknesses of various retinal layers within the macular cube provides unique diagnostic insights for many diseases, but the capability for automatic segmentation and quantification remains quite limited. While manual segmentation has been used for many scientific studies, it is extremely time consuming and is subject to intra- and inter-rater variation. This paper presents a new computational domain, referred to as flat space, and a segmentation method for specific retinal layers in the macular cube using a recently developed deformable model approach for multiple objects. The framework maintains object relationships and topology while preventing overlaps and gaps. The algorithm segments eight retinal layers over the whole macular cube, where each boundary is defined with subvoxel precision. Evaluation of the method on single-eye OCT scans from 37 subjects, each with manual ground truth, shows improvement over a state-of-the-art method.

1. Introduction

Optical coherence tomography (OCT) is an interferometric technique that detects reflected or back-scattered light from tissue. An OCT system probes the retina with a beam of light and lets the reflection interfere with a reference beam originating from the same light source. The resultant interfered signal describes the reflectivity profile along the beam axis; this one-dimensional depth scan is referred to as an A-scan. Multiple adjacent A-scans are used to create two-dimensional (B-scans) and three-dimensional image volumes. OCT has allowed for in vivo microscopic imaging of the human retina, enabling the unprecedented study of ocular diseases. OCT as a modality has provided increased access to the inner workings of the retinal substructures, allowing for detailed cohort analyses of multiple sclerosis (MS) with respect to the macular retinal layers [1–3]. MS is an inflammatory demyelinating disorder of the central nervous system, with neuronal loss in the retina being a primary vector of MS, which is independent of any axonal injury [2, 4]. Though unmyelinated, it is very common to observe inflammation and neuronal loss in the retina of MS patients. The retinal nerve fiber (RNFL) principally consists of axons of ganglion cell neurons, with these axons joining together at the optic disc to form the optic nerve. MS is clinically manifested in the optic nerves as optic neuritis, it can also be observed through the degeneration of axons in the optic nerves, resulting in the atrophy of various [5, 6]. For approximately 95% of MS patients there is no visibly pathological corruption of the OCT images as a result of MS, the remaining 5% have microcystic macular edema (MME) [3]. MS subjects with MME were excluded from our cohort. OCT has also contributed to the study of more traditional ophthalmological conditions such as glaucoma [7–10] and myopia [11], as well as to retinal vasculature [12, 13], and to the exploration of more obliquely related conditions such as Alzheimer’s disease (AD) [14–16] and diabetes [17, 18]. The study of such a wide assortment of pathologies necessitates automated processing, which in the case of macular retinal OCT starts with segmentation of the various retinal cellular layers.

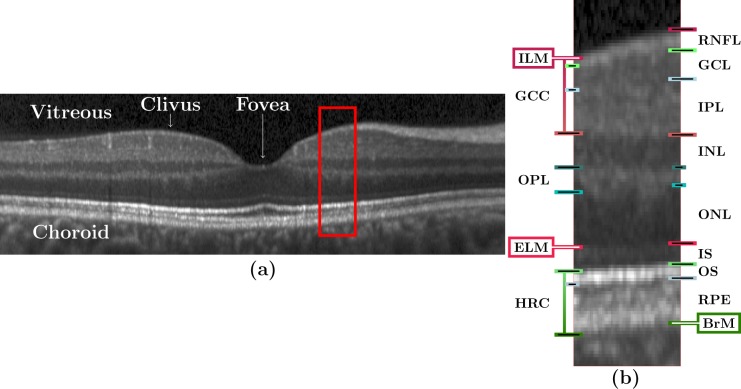
Figure 1 shows a spectral domain OCT image of the macula along with definitions of various regions and layers. In particular, Fig. 1(a) shows a B-scan image through the fovea while Fig. 1(b) shows a zoomed portion with definitions of the various retinal layers and boundaries. It is apparent from these images that the boundary between the GCL and IPL is hard to discern, which is often the case in OCT images. As a result, it is common for OCT layer segmentation methods to treat these two layers as one, which we refer to as the GCIP. The layers our automated algorithm segments (in order from the vitreous to the choroid) are the RNFL, GCIP, INL, OPL, ONL, IS, OS, and RPE. These eight layers (and their associated nine boundaries) are the maximal set that are typically segmented from OCT of the macular retina.

Fig. 1.

(a) A B-scan from a subject in our cohort with annotations indicating the locations of the vitreous, choroid, clivus, and fovea. (The image has been rescaled by a factor of three along each A-scan for display purposes.) The red boxed region is shown magnified (×3) in (b) with markings to denote various layers and boundaries. The layers are: RNFL; ganglion cell (GCL); inner plexiform (IPL); inner nuclear (INL); outer plexiform (OPL); outer nuclear (ONL), inner segment (IS); outer segment (OS); retinal pigment epithelium (RPE). The named boundaries are: inner limiting membrane (ILM); external limiting membrane (ELM); Bruch’s Membrane (BrM). The OS and RPE are collectively referred to as the hyper-reflectivity complex (HRC), and the ganglion cell complex (GCC) comprises the RNFL, GCL, and IPL.

There has been a large body of work on macular retinal OCT layer segmentation [19–35]. A diverse array of approaches have been investigated including methods based on active contours [19, 20], machine learning [23–25], graphs [24–30, 36, 37], dynamic programming [28], texture analysis [21], simple image gradients [31], registration [34], and level sets [35]. None of these methods, with the exception of the the active contours [19, 20] method of Ghorbel et al. and the “loosely coupled level sets” (LCLC) method of Novosel et al. [35], define boundaries between retinal layers in a subvoxel manner. This voxel level limit in precision manifests itself in layers that are forced to be at least one voxel thick even if they are very thin or absent (which is the case for some layers at the fovea). The thickness constraints can be controlled in the graph-based methods [24–30, 36, 37], allowing for layers of zero thickness which would enable the segmented surfaces to overlap. However, those methods that do allow a hard constraint of a zero thickness layer are still not reflecting the true thickness of the layer, which is somewhere between zero and one pixel thick. Upsampling could be seen as a way to increase the resolution of the data enabling sufficient samples between layers. Upsampling, however, has several drawbacks the first of which is its failure to address the underlying problem. As layers are still required to be a certain voxel thickness at the operating resolution used by any of the algorithms. Secondly, upsampling can introduce various spurious artifacts such as ringing due to Gibbs phenomenon [38] which would hamper the ability to correctly identify layer boundaries.

The active contour work of Ghorbel et al. [19, 20] generates segmentations on all the layers in a tight window around the fovea (between the clivi) of a B-scan that itself must also pass through the fovea. Hence, this work is limited in its scope and impact. The LCLS method partially addresses the lack of subvoxel precision. Level set methods are inherently capable of subvoxel precision, but since LCLS incorporates a “proper ordering” constraint on pairs of adjacent level sets, it becomes necessary for the zero crossings of these pairs to be separated by at least one voxel position. Therefore, although the thickness of a specific layer can be arbitrarily small at a given voxel position, the thickness of layers adjacent to this one must be at least one voxel thick. As in LCLS, our method also uses a level set approach, but we employ three significant extensions. First, we segment all retinal layers simultaneously using a multiple-object geometric deformable model (MGDM) approach [39]. Second, Our method distinguishes itself by operating on the complete 3D volume in concert, unlike many other methods which use the adjoining B-scans to simply smooth out the estimated boundaries [36]. Third, our method uses a geometric transformation of the raw data prior to running MGDM in order to surmount the voxel precision restrictions that are present in LCLS and in the graph based methods. As MGDM does not allow gaps or overlap of objects, we can create a complete segmentation of the retinal image. In addition, the output MGDM level sets can be considered to represent a partial volume model of the tissues, which is a capability that is not available with current graph based methods.

2. Methods

Our method builds upon our random forest (RF) [40] based segmentation of the macula [24] and also provides for a new computational domain which we refer to as flat space. First, as is common in the literature, we estimate the boundaries of the vitreous and choroid with the retina. From these estimated boundaries, we apply a mapping that was learned by regression on a collection of manual segmentations, which maps the retinal space between the vitreous and choroid to a domain in which each of the layers is approximately flat, referred to as flat space. In the original space, we use the random forest layer boundary estimation [24] to compute probabilities for the boundaries of each layer and then map them to flat space. These probabilities are then used to drive MGDM [39], providing a segmentation in flat space which is then mapped back to the original space. Detailed descriptions of these steps are provided below.

2.1. Preprocessing

We use several of the preprocessing steps outlined in Lang et al. [24], which we briefly describe here. The first step is intensity normalization, which is necessary because of automatic intensity rescaling and automatic real-time averaging performed by the scanner, both of which lead to differences in the dynamic ranges of B-scans. Intensity normalization is achieved by computing a robust maximum I_m and linearly rescaling intensities from the range [0, I_m] to the range [0, 1], with values greater than I_m being clamped at 1. The robust maximum, I_m, is found by first median filtering each individual A-scan within the same B-scan using a kernel size of 15 pixels. The robust maximum is set to a value that is 5% larger than the maximum intensity of the entire median-filtered image. Next, the macular retina is detected by estimating the ILM and the BrM (providing initial estimates that are updated later). Vertical derivatives of a Gaussian smoothed image (σ = 3 pixels) are computed and the largest positive derivative is associated with the ILM while the largest negative derivative below the ILM is associated with the BrM. We thus have two collections of gradient extrema, positive and negative, each associated with a boundary, the ILM and BrM respectively. These two collections are crude estimators of these boundaries and contain errors, the correction of which is accomplished by comparing the estimated boundaries to the boundary given by independently median filtering the two collections. Points that are more than 15 voxels from the median filtered curve are removed as outliers and an interpolated point replaces it in the collection.

2.2. Flat space

We now introduce the concept of our new computational domain, which we refer to as flat space. We geometrically transform each subject image to a space in which all retina layers of the subject are approximately flat. To learn this transformation, we took OCT scans from 37 subjects comprising a mix of controls and MS patients and manually delineated all retinal layers. We then converted the positions of the boundaries between the manually delineated retinal layers into proportional distances between the BrM (which is given a distance of zero) and the ILM (which is given a distance of one). We then estimated the foveal centers of all scans based on the minimum distance between the ILM and BrM within a small search window about the center of the macula, and then aligned all subjects by placing their foveas at the origin. For each aligned A-scan, we then computed the interquartile mean of the proportional positions of each of the seven retinal layer boundaries between the ILM and BrM.

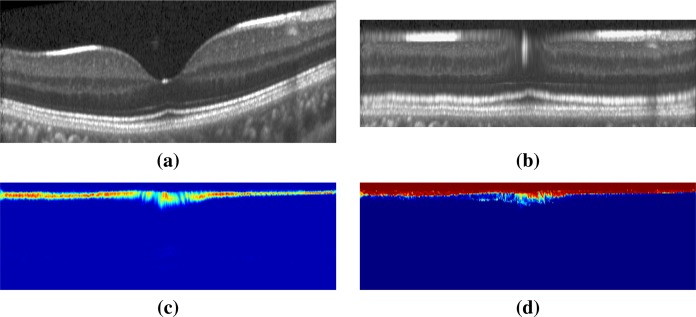
To place OCT data from a new subject into flat space, we first estimate the ILM and BrM boundaries and the foveal center from the subject’s OCT data as outlined above, in Section 2.1. We then estimate the positions of seven internal boundaries for each A-scan based on the mean proportional positions learned above. Each A-scan is then resampled by linearly interpolating new values at the estimated boundary positions and at ten equally spaced vertices between these boundary positions. The pixel intensities between the BrM and ILM are interpolated to have 89 pixel values between these two boundaries. The 89 pixels are computed on the A-scan distributed such that there is a pixel on the estimated boundaries position based on the flat space mapping, with ten additional pixels placed between each of the boundary estimates. In this way, each A-scan is represented by 89 values from the BrM to the ILM, which we put together into a three-dimensional volume that represents an approximately flat subject macula. An additional ten pixels are added above the ILM and another ten below the BrM. These additional pixels allow for errors in our initial estimates of these two boundaries. Resulting in a flat space in which each vertical column has exactly 109 pixels. Figure 2(a) shows a B-scan and Fig. 2(b) shows its flat space mapping.

Fig. 2.

Shown is (a) the original image in native space. In flat space are (b) the original image, (c) a heat map of the probabilities for one of the boundaries (ILM), and (d) the y-component of the GVF field for that same boundary. The color scale in (c) represents zero as blue and one as red.

2.3. RF boundary estimate

We estimate probabilities for the locations of nine boundaries within each OCT image using a RF method previously reported [24]. This method trains a RF using a set of image features and corresponding manual delineations derived from a training set of OCT images. The trained RF can be applied to the image features derived from a new OCT image and used to estimate the probabilities of the locations of nine retinal boundaries within the new OCT image. There are 27 features used in RF training and classifying. The first three are the relative location and signed distance of the voxel from the fovea. The next nine are the voxel values in a 3 × 3 neighborhood in the B-scan around the voxel. The last fifteen are various directional derivatives (first and second order) taken after oriented anisotropic Gaussian smoothing at different orientations and scales. The first twelve of which are generated by using the signed value of the first and magnitude of the second derivatives on six images corresponding to two scales and three orientations. The two scales for Gaussian smoothing are σ_x,y = {5, 1} pixels and σ_x,y = {10, 2} pixels while the three orientations are at −10, 0, and 10 degrees from the horizontal. The final three features are the average vertical gradients in an 11 × 11 neighborhood located at 15, 25, and 35 pixels below the current pixel, calculated using a Sobel kernel on the unsmoothed data. Rather than labeling the layers, the RF is trained to label each boundary.

Given a new image, the RF classifier is applied to all of the voxels, producing for each voxel the probability that the voxel belongs to each boundary. Since the RF classification is carried out on the original OCT image, the boundary probabilities are assigned to the voxels of the original OCT image. The RF training data and validation have all been previously completed in each subjects native space, for this reason we have kept the probability estimation from the RF in the subjects own native space. Examples showing these nine probability maps are shown in [24]. Here, we add an additional step to this process: transforming the estimated boundary probability maps to flat space. This allows us to carry out segmentation in flat space while utilizing features (and probabilities) developed on the original images. A probability map for the ILM boundary is shown in flat space in Fig. 2(c).

2.4. MGDM segmentation in flat space

We use MGDM to improve our estimates of the nine boundaries based on the probability maps generated by the RF classifiers. The recently developed MGDM [39] framework allows control over the movement of the boundaries of our ten retinal objects (eight retinal layers plus the choroid and sclea complex, and the vitreous) in order to achieve the final segmentation in flat space. MGDM is a multi-object extension to the conventional geometric level set formulation of active contours [41]. It uses a decomposition of the signed distance functions (SDFs) of all objects that enables efficient contour evolution while preventing object overlaps and gaps from forming. We consider N objects O ₁, O ₂, ..., O_N that cover a domain Ω with no overlaps or gaps. Let ϕ_i, be the signed distance function for O_i defined as

$${\varphi }_i(x)=\{\begin{array}{cc}-d_x(O_i),& x\in O_i,\\ d_x(O_i),& x\notin O_i,\end{array}$$ (1)

where

$$d_x(O_i)=\underset{y\in O_i}{\text{min}}\Vert x-y\Vert$$ (2)

is the shortest distance from point x ∈ Ω to O_i. In a conventional multi-object segmentation formulation, each object is moved according to a speed function f_i(x) defined for each object using the standard PDE for level set evolution,

$$\frac{\partial {\varphi }_i(x)}{\partial t}=f_i(x)\left|\nabla {\varphi }_i(x)\right|.$$ (3)

MGDM uses a special representation of the objects and their level set functions to remove the requirement to store all these level set functions. The new representation also enables a convenient capability for boundary-specific speed functions.

We define a set of label functions that give the object at x and all successively nearest neighboring objects

$$\begin{array}{c}\hfill L_0(x)=i\iff x\in O_i\hfill \\ \hfill L_1(x)\underset{j\ne L_0(x)}{=\text{argmin}}{d}_x(O_j)\hfill \\ \hfill L_2(x)=\underset{j\ne \{L_0(x),L_1(x)\}}{\text{argmin}}{d}_x(O_j)\hfill \\ \hfill ⋮\hfill \\ \hfill L_{N-1}(x)=\underset{j\ne {\left\{L_k(x)\right\}}_{k=0,\dots ,N-2}}{\text{argmin}}{d}_x(O_j).\hfill \end{array}$$ (4)

We then define functions that give the distance to each successively distant object

$$\begin{array}{c}{\phi }_0(x)=d_x(L_1(x))\\ {\phi }_1(x)=d_x(L_2(x))-d_x(L_1(x))\\ {\phi }_2(x)=d_x(L_3(x))-d_x(L_2(x))\\ ⋮\\ {\phi }_{N-2}(x)=d_x(L_{N-1}(x))-d_x(L_{N-2}(x))\end{array}$$ (5)

Together, these functions describe a local “object environment” at each point x. It can be shown that the SDFs at x for all objects can be reconstructed from these functions [39].

The first computational savings of MGDM comes about by realizing that approximations to the SDFs of the closest objects can be computed from just three label functions and three distance functions:

$$\widehat{{\varphi }_i}(x)=\{\begin{array}{ll}-{\phi }_0(x),\hfill & i=L_0(x)\hfill \\ {\phi }_0(x),\hfill & i=L_1(x)\hfill \\ {\phi }_0(x)+{\phi }_1(x),\hfill & i=L_2(x)\hfill \\ {\phi }_0(x)+{\phi }_1(x)+{\phi }_2(x),\hfill & i\ne L_{0,1,2}(x),\hfill \end{array}$$ (6)

where the notation i ≠ L _0,1(x) means i ≠ L ₀(x) and i ≠ L ₁(x) while i ≠ L _0,1,2(x) means i ≠ L ₀(x) and i ≠ L ₁(x) and i ≠ L ₂(x). These are level set functions sharing the same zero level sets as the true signed distance functions; they give a valid representation of the boundary structure of all the objects–details and conditions of the stability of this approximation are in Bogovic et al. [39]. Therefore, storing just these six functions (three label functions and three distance functions) is sufficient to describe the local object environment of every point in the domain.

The second computational savings of MGDM comes about by realizing that the evolution equations Eq. (3) can be carried over by updating the distance functions instead of the signed distance functions, as follows

$$\frac{\partial {\psi }_k(x)}{\partial t}=\frac{1}{2}\left(f_{L_k}(x)-f_{L_{k+1}}(x)\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}k=2,1,0,$$ (7)

for all k in the narrow band (voxels near the boundaries). Evolving these distance functions must be carried out by starting with ψ ₂, then ψ ₁, and finally ψ ₀; any changes to the ordering of object neighbors during this process is reflected by changes in the associated label functions. Reconstruction of the actual objects themselves need not be carried out until after the very last iteration of the evolution. To accomplish this, an isosurface algorithm is run on on each level set function $\widehat{{\varphi }_i}(x)$, and the object boundaries will have subvoxel resolution by virtue of the level sets.

Since MGDM keeps track of both the object label and its nearest neighbor at each x, the update Eq. (7) is very fast to carry out. Furthermore, it can use both object-specific and boundary-specific speed functions. Given the index of the object and its neighbor stored at each x, a simple index into a lookup table gives the appropriate speed functions to use for that object and particular boundary. This aspect of MGDM is used in the OCT implementation described in this paper.

We use two speed functions to drive MGDM. The first speed function is the inner product of a gradient vector flow (GVF) [42] field computed from a specific boundary probability map with the gradient of the associated signed distance function. Nine GVF fields are computed, one for each retinal boundary, which ensures a large capture range—i.e., the entire computational domain—for each boundary that MGDM must identify. The second speed function that is used in MGDM is a conventional curvature speed term [41]. Since the curvature speed term encourages flat surfaces, this is a perfect regularizer to use in flat space.

MGDM segments all retinal layers (plus the vitreous and choroid) at once. Like the topology preserving geometry deformable model (TGDM) [43], which maintains single-object topology using the simple point concept, MGDM is capable of preserving multiple object relationships using the digital homeomorphism concept, which is an extension of the simple point concept to multiple objects [44]. We therefore use the digital homeomorphism constraint in MGDM to maintain proper layer ordering. For the simple object arrangement in the retina (i.e., ordered layers), this constraint amounts to the same constraint used in LCLS [35]. As MGDM is operating in flat space, it does not come with the same one voxel layer thickness limitation on the final boundary segmentation.

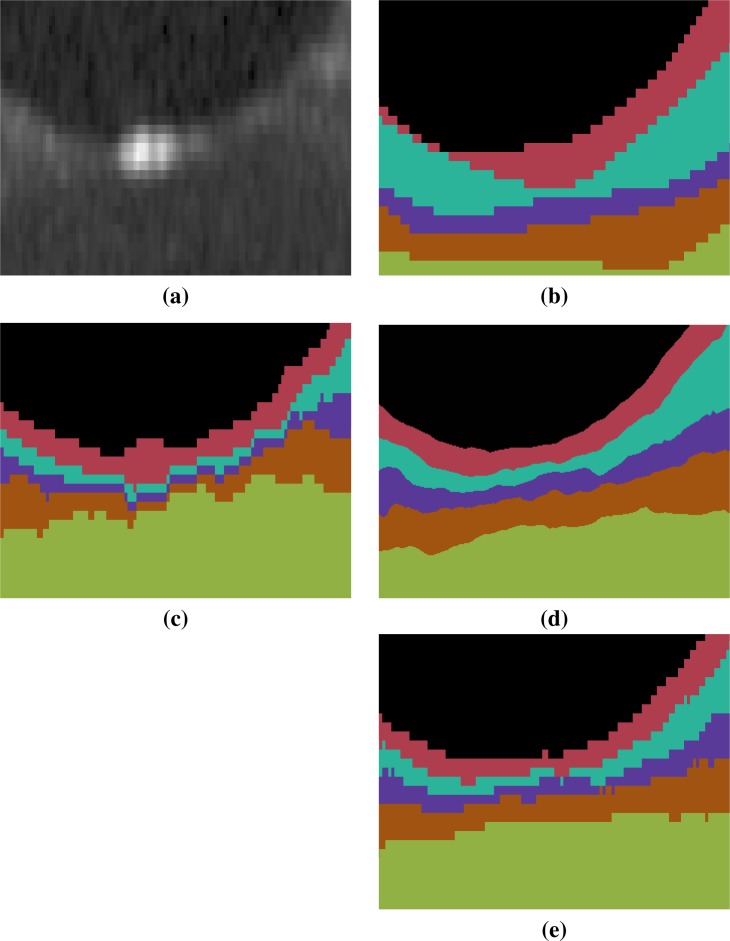
MGDM uses the two forces together with topology control to move the retinal layers in flat space until convergence, see Fig. 3(b). The flat space segmentation is then mapped back into the subject’s native space, see Fig. 3(d). Using MGDM in flat space has several computational advantages. First, the curvature force is a natural choice since all the layers are nominally flat. Second, flat space allows for greater precision of surface definition since mapping the MGDM result back to the native space can put surfaces much closer together than one voxel. Third, flat space is a smaller digital image domain than native space since there are only 109 vertices per A-scan by construction. This leads to a reduced computational burden. An example of an MGDM initialization in flat space is shown in Fig. 3(a) and the result for the same subject is shown in flat space in Fig. 3(b). The MGDM result mapped back to native space is shown in Fig. 3(d).

Fig. 3.

Shown in flat space are (a) the MGDM initialization, and (b) the MGDM result. The MGDM result mapped back to the native space of the subject is shown in (d) and for comparison the manual segmentation of the same subject is shown in (c). The same color map is used in this figure and in Fig. 4.

3. Experiments and results

3.1. Data

Data from the right eyes of 37 subjects (a mixture of 16 healthy controls and 21 MS patients) were obtained using a Spectralis OCT system (Heidelberg Engineering, Heidelberg, Germany). Seven subjects from the cohort were picked at random and used to train the RF boundary classifier. The RF classifier has been previous [24] shown to be robust and independent of the training data and thus should not have introduced any bias in the results. The research protocol was approved by the local Institutional Review Board, and written informed consent was obtained from all participants. All scans were screened and found to be free of microcystic macular edema, which is sometimes found in a small percentage of MS subjects [3].

All scans were acquired using the Spectralis scanner’s automatic real-time function in order to improve image quality by averaging 12 images of the same location (ART setting was fixed at 12). The resulting scans had signal-to-noise ratios (SNR) of between 20 dB and 38 dB, with a mean SNR of 30.6 dB. Macular raster scans (20° × 20°) were acquired with 49 B-scans, each B-scan having 1024 A-scans with 496 voxels per A-scan. The B-scan resolution varied slightly between subjects and averaged 5.8 μm laterally and 3.9 μm axially. The through-plane distance (slice separation) averaged 123.6 μm between images, resulting in an imaging area of approximately 6 × 6 mm. We note that our data is of a higher resolution and better SNR than many other recent publications. The nine layer boundaries were manually delineated on all B-scans for all subjects by a single rater using an internally developed protocol and software tool. The manual delineations were performed by clicking on approximately 20–50 points along each layer border followed by interpolation between the points using a cubic B-spline. Visual feedback was used to move points to ensure a correct boundary.

3.2. Results

We compared our multi-object geometric deformable models based approach to our previous work (RF+Graph) [24] on all 37 subjects. In terms of computational performance, we are currently not competitive with RF+Graph, which takes only four minutes on a 3D volume of 49 B-scans. However, our MGDM implementation is written in a generic framework and an optimized method based on a GPU framework could offer 10 to 20 fold speed up [45]. To compare the two methods, we computed the Dice coefficient [46] of the automatically segmented layers against manual delineations. The Dice coefficient is a measure of how much the two segmentations agree with each other. It has a range of [0, 1], with a score of 0 meaning complete contradiction between the two, while 1 represents complete concurrence.

The resulting Dice coefficients are shown in Table 1. It is observed that the mean Dice coefficient is larger for MGDM than RF+Graph in all layers. Further, we used a paired Wilcoxon rank sum test to compare the distributions of the Dice coefficients. The resulting p-values in Table 1 show that six of the eight layers reach significance (α level of 0.001). Therefore, MGDM is statistically better than RF+Graph in six of the eight layers. The two remaining layers (INL and OPL) lack statistical significance because of the large variance.

Table 1.

Mean (and standard deviations) of the Dice Coefficient across the eight retinal layers. A paired Wilcoxon rank sum test was used to test the significance of any improvement between RF+Graph [24] and our method, with strong significance (an α level of 0.001) in six of the eight layers.

Layer	Dice Coefficient		P-Value
	RF+Graph [24]	MGDM
RNFL	0.877 (±0.0533)	0.903 (±0.0279)	< 0.001
GCIP	0.892 (±0.0529)	0.911 (±0.0290)	< 0.001
INL	0.806 (±0.0261)	0.811 (±0.0339)	0.238
OPL	0.855 (±0.0164)	0.860 (±0.0250)	0.294
ONL	0.909 (±0.0186)	0.926 (±0.0163)	< 0.001
IS	0.751 (±0.0295)	0.805 (±0.0225)	< 0.001
OS	0.816 (±0.0323)	0.846 (±0.0301)	< 0.001
RPE	0.884 (±0.0227)	0.900 (±0.0268)	< 0.001

An example of the manual delineations as well as the result of our method on the same subject are shown in Fig. 3, with a magnified region about the fovea in Fig. 4. Table 2 includes the absolute boundary error for the nine boundaries we approximate; these errors are measured along the A-scans in comparison to the same manual rater. We, again, used a paired Wilcoxon rank sum test to compute p-values between the two methods for the absolute distance error, six of the nine boundaries reach significance (α level of 0.001).

Fig. 4.

Shown is a magnified (×18) region around the fovea for each of (a) the original image, (b) the manual delineation, and automated segmentations generated by (c) RF+Graph [24] and (d) our method. The result in (d) is generated from the continuous representation of the level sets in the subjects native space, shown in (e) is the voxelated equivalent for our method. The RF+Graph method has to keep each layer at least one voxel thick (the GCIP and INL in this case). We also observe the voxelated nature of the the RF+Graph result, whereas our approach has a continuous representation due to its use of levelsets shown in (d) but can also be converted a voxelated format (e). The same color map is used in this figure and in Fig. 3.

Table 2.

Mean absolute errors (and standard deviation) in microns for our method (MGDM) in comparison to RF+Graph [24] on the nine estimated boundaries. A paired Wilcoxon rank sum test was used to compute p-values between the two methods with strong significance (an α level of 0.001) in six of the nine boundaries.

Boundary	Absolute Errors		P-Value
	RF+Graph [24]	MGDM
ILM	4.318 (±1.1089)	3.478 (±0.8084)	< 0.001
RNFL-GCL	6.192 (±2.1597)	5.339 (±1.8408)	< 0.001
IPL-INL	6.319 (±1.1818)	6.289 (±2.0463)	0.141
INL-OPL	5.464 (±2.8283)	4.467 (±0.4669)	< 0.05
OPL-ONL	4.657 (±1.1318)	4.129 (±1.2162)	< 0.001
ELM	5.229 (±0.9822)	4.031 (±0.9623)	< 0.001
IS-OS	4.108 (±1.2415)	3.309 (±1.0028)	< 0.001
OS-RPE	4.944 (±1.3937)	4.437 (±1.5522)	< 0.001
BrM	4.291 (±0.8959)	3.739 (±2.4001)	0.411
Overall	4.947 (±1.4558)	4.468 (±1.9830)	< 0.001

4. Discussion and conclusion

The Dice coefficient and absolute boundary error in conjunction with the comparison to RF+GC suggest that our method has very good performance characteristics. In comparison to the state-of-the-art methods, Song et al. [27] reports mean unsigned boundary error of 5.14μm (±0.99) while Dufour et al. [26] reports 3.03μm (±0.54). Our results on the surface appear to be in between these two recent methods. However, the comparison is inherently flawed as the data used in both of these methods is of differing quality to our own, and was acquired on a different scanner with different parameters. The fact that we used a larger cohort than either of these two methods may account for our larger variance. In terms of specific boundaries, again with the caveat of different data and noting that layer definitions seem to vary somewhat by group and scanner used, we compare for the ILM and BrM. Song et al. reports unchanged results from their earlier work [30] which had an unsigned boundary error of 2.85μm (±0.32), with Dufour et al. reporting 2.28μm (±0.48); clearly for this boundary we have room for improvement. For BrM, Song et al. reports unchanged results from their prior work which reported 8.47μm (±2.29), and Dufour et al. reported 2.63μm (±0.59). Our approach is better than that of Song et al., and not as good as that of Dufour et al. However, Song et al. and Dufour et al. segment six and seven boundaries respectively, whereas our method identifies nine boundaries. There are only a few methods that are able to accurately segment nine or more boundaries [20, 21, 33]. The data used in our study is of a very high quality for OCT data, with a mean SNR of 30.6 dB, which might be part of the reason for the improved accuracy of our results. An obvious criticism of our approach is the use of the same 37 subjects for developing our regression mapping to flat space and for the validation study. Our current study involved healthy controls and MS subjects with essentially normal appearing eyes, a future area of work will be in exploring cases of more pronounced pathology were the flat mapping may fail or the forces driving MGDM may be insufficient. From a computation standpoint, the MGDM process is computationally expensive, and currently takes 2 hours and 9 minutes (±4 minutes) to process a full 3D OCT macular cube, lagging behind the state-of-the-art methods [24, 26] which can run in less than a minute. A GPU based implementation of MGDM [45] would offer a 10 to 20 fold speed up, taking the run time to the five minute range.

In this paper, a fully automated algorithm for segmenting nine layer boundaries in OCT retinal images has been presented. The algorithm uses a multi-object geometric deformable model of the retinal layers in a unique computational domain, which we refer to as flat space. The forces used for each layer were built from the same principles. These could be refined or modified on a per-layer basis to help improve the results.