The influence of material anisotropy on vibration at onset in a three-dimensional vocal fold model

Abstract

Although vocal folds are known to be anisotropic, the influence of material anisotropy on vocal fold vibration remains largely unknown. Using a linear stability analysis, phonation onset characteristics were investigated in a three-dimensional anisotropic vocal fold model. The results showed that isotropic models had a tendency to vibrate in a swing-like motion, with vibration primarily along the superior-inferior direction. Anterior-posterior (AP) out-of-phase motion was also observed and large vocal fold vibration was confined to the middle third region along the AP length. In contrast, increasing anisotropy or increasing AP-transverse stiffness ratio suppressed this swing-like motion and allowed the vocal fold to vibrate in a more wave-like motion with strong medial-lateral motion over the entire medial surface. Increasing anisotropy also suppressed the AP out-of-phase motion, allowing the vocal fold to vibrate in phase along the entire AP length. Results also showed that such improvement in vibration pattern was the most effective with large anisotropy in the cover layer alone. These numerical predictions were consistent with previous experimental observations using self-oscillating physical models. It was further hypothesized that these differences may facilitate complete glottal closure in finite-amplitude vibration of anisotropic models as observed in recent experiments.

INTRODUCTION

An important feature of normal phonation is that the glottis remains closed for a considerable portion of one oscillation cycle. The glottal closure pattern (e.g., the speed, extent, and duration of glottal closure) is essential to the production of normal voice with harmonics at frequencies well above the oscillation frequency of the vocal folds (Stevens, 1998). Incomplete closure in the membranous glottis is well known to result in change in voice quality as occurs in voice disorders (Isshiki, 1989). Therefore, understanding the underlying physiological mechanisms responsible for complete glottal closure during vibration and its control has both theoretical and clinical importance.

In humans, it is often assumed that geometric approximation of the vocal folds through arytenoid adduction is sufficient to achieve complete glottal closure during phonation. However, recent experiments using self-oscillating silicone-based physical models (Zhang et al., 2006, 2009; Mendelsohn and Zhang, 2011; Zhang, 2011) showed that isotropic (i.e., the material properties are the same along different directions) physical models often vibrated with incomplete glottal closure although the two vocal folds were in full contact with each other at rest. The isotropic models also exhibited other vibration features noticeably different from humans, including one-mass-like motion, excessively large vertical (superior-inferior) vibration amplitude, and anterior-posterior (AP) out-of-phase motion within each vocal fold (i.e., different portions of the vocal fold along the AP direction vibrated out-of-phase with each other). Stiffening the body layer in an isotropic model reduced the mean glottal opening but also led to strong excitation of AP out-of-phase motion, which further prevented complete glottal closure during vibration (Mendelsohn and Zhang, 2011; Zhang, 2011).

Complete glottal closure during vibration was achieved in a recent study by either embedding synthetic fibers aligned along the AP direction in locations close to the vocal fold surface or adding a relatively stiffer outer epithelium layer (Xuan and Zhang, 2014). The presence of embedded fibers also suppressed the AP out-of-phase motion. Xuan and Zhang (2014) further showed that the fibers were the most effective when embedded in the cover layer close to the surface, and had minimum effects when they were embedded in the body layer. Although this study demonstrated the importance of material anisotropy (due to the embedded fibers) and inhomogeneity (due to the presence of an epithelium layer) on vocal fold vibration, the exact underlying physical mechanisms responsible for the observed improvement in the glottal closure pattern have not been studied. Understanding why isotropic models are unable to vibrate with complete glottal closure and why anisotropic models are able to vibrate with complete glottal closure will provide insight into similar physiological and physical mechanisms present in human phonation and their role in voice control, which cannot be studied in human subjects.

Understanding such mechanisms also has important implications for modeling of voice production. Despite the anisotropic nature of the vocal folds (due to the presence of muscle fibers in the muscle layer and collagen and elastin in the lamina propria; Hirano and Kakita, 1985), and the fact that stiffness conditions in different layers of the vocal fold critically determine the resulting vocal fold vibration pattern (van den Berg and Tan, 1959; Hirano, 1974; Titze and Talkin, 1979; Hirano and Kakita, 1985), vocal fold material properties in previous studies were often collectively referred to as vocal fold stiffness, with no clear differentiation among its values along different directions. Early models of phonation (e.g., the two-mass model in Ishizaka and Flanagan, 1972, and its many variants) simplified the vocal folds into lumped masses and springs that had no clear correspondence to the physiological anisotropic stiffness conditions in realistic vocal folds. Although three-dimensional continuum models of phonation were developed in previous studies (Titze and Talkin, 1979; Berry et al., 1994; Alipour et al., 2000; Xue et al., 2012; Zheng et al., 2011; Sidlof et al., 2013), high computational costs associated with modeling the three-dimensional fluid-structure interaction prevented systematic investigations of the effects of vocal fold material anisotropy on phonation. Systematic numerical studies so far have been largely limited to two-dimensional models with isotropic plane-strain material models, which considered parametric variations in vocal fold stiffness in the transverse (coronal) plane only. An important feature that is missing in two-dimensional models is vocal fold stiffness along the AP direction. The AP stiffness is important because, while vibration occurs largely in the transverse plane (the plane perpendicular to the AP direction), control of vibration is achieved mainly by adjusting the stiffness and tension of the vocal fold along the AP direction through laryngeal muscle activation. Understanding the effects of vocal fold anisotropy on vocal fold vibration would provide a better understanding of the limitations and relevance of these simplified models of phonation.

The goal of this study was to provide a theoretical understanding of vibration in a three-dimensional anisotropic vocal fold, based on which the above experimental observations can be better interpreted, and the possible influence of vocal fold anisotropy, due to the presence of collagen and elastin, can be better understood. Because of the high computational costs in modeling the three-dimensional fluid-structure interaction and the need for a systematic investigation, a linear stability analysis approach as in previous studies (Zhang et al., 2007; Zhang, 2009; Zhang and Luu, 2012) was used in this study. Focusing on the stability of the coupled vocal fold-airflow system when subjected to disturbances of infinitesimal amplitude and using a simplified glottal flow model, this approach is computationally efficient and thus ideal for parametric investigations. Despite simplifications in both the flow and solid domains, this linear stability approach has been very successful in predicting or explaining experimental observations in physical model experiments regarding the dependence of phonation threshold pressure on vocal fold geometry and stiffness (Mendelsohn and Zhang, 2011; Zhang, 2010) and left-right difference in vibration amplitude and phase in left-right asymmetric vocal fold conditions (Zhang and Luu, 2012).

In addition to its computational efficiency, the linear stability analysis approach is appealing also because it allows us to focus on vocal fold eigenmodes and eigenmode synchronization, a central feature of the phonation process. Previous studies using both lumped-element models and continuum models (Ishizaka, 1981; Zhang et al., 2007; Zhang, 2010, 2011) have shown that phonation onset results from synchronization of two vocal fold eigenmodes by the glottal flow. Synchronization of two modes at the same frequency but different phases establishes a flow pressure field that is at least partially in-phase with vocal fold surface velocity, allowing cross-mode interaction to establish a net energy flow from airflow into the vocal fold tissue (Zhang et al., 2007). Synchronization of two modes of qualitatively distinct vibration pattern also leads to a vertical phase difference or a wave-like motion along the medial surface, a feature that is often considered essential to normal phonation (Titze, 1988). The details of the synchronization pattern (i.e., which eigenmodes are synchronized and how much flow pressure is required for this to occur) critically determine the resulting vocal fold vibration pattern and phonation frequency. Changes in the eigenmode synchronization pattern (due to changes in either geometry or material properties) may lead to abrupt changes in phonation frequency and a qualitatively different vibration pattern (Berry et al., 1994, 2006; Steinecke and Herzel, 1995; Neubauer et al., 2001; Tokuda et al., 2007; Zhang, 2009; Zhang and Luu, 2012). Thus, focusing on this concept of vocal fold eigenmodes and how they are synchronized provides a theoretical framework based on which the effects of vocal fold anisotropy on vocal fold vibration can be systematically investigated and understood.

The linear stability analysis in previous studies used a two-dimensional vocal fold model, which, by design, was not able to predict variations in vibration pattern along the AP direction or any influence of material anisotropy. In this study, this linear stability model was first extended to a three-dimensional vocal fold model in Sec. 2. In Sec. 3B we will show that this computational model was able to predict many important observations in previous experiments using isotropic vocal fold models. The more realistic anisotropic conditions are considered in Secs. 3C, 3D in which we will show that increasing anisotropy or increasing the ratio between the AP stiffness and the transverse stiffness led to a continuously-changing vertical phase difference in vocal fold motion along the medial surface, an increased amplitude of the medial-lateral motion with respect to the superior-inferior motion, and a more in-phase vibration pattern along the AP length. These changes in vocal fold vibration may lead to more efficient flow modulation and facilitate complete glottal closure during vibration as observed in our recent experiments.

METHOD

Linear stability analysis

The numerical vocal fold model and the linear stability analysis were similar to those in previous studies (Zhang et al., 2007; Zhang, 2009; Zhang and Luu, 2012). The reader is referred to these previous studies for details of the model and equation derivation. The following focuses on model modifications made to extend the analysis to a three-dimensional vocal fold model.

The following assumptions were made to simplify the analysis. First, the static prephonatory deformation of the vocal folds when subjected to the subglottal pressure was neglected. That is, the vocal fold geometry was assumed to remain unchanged as the subglottal pressure was increased. This assumption is generally valid for high-pitch or high intensity phonation in which the vocal folds are stiffened due to muscle activation, but the prephonatory deformation can be large for low-pitch low intensity phonation. Second, the glottal flow was assumed to be a one-dimensional potential flow until it separated from the glottal wall at a location downstream of the minimum glottal constriction where the glottal area was 1.2 times of the minimum glottal area. Although this one-dimensional flow model is only a rough approximation of the complex flow field observed in phonation (Neubauer et al., 2007; Sciamarella and Le Quere, 2008; Mihaescu et al., 2010; Sidlof et al., 2011; Zheng et al., 2011), our previous analysis using this simplified flow model was able to qualitatively predict experimental observations in both symmetric and asymmetric vocal fold conditions (Mendelsohn and Zhang, 2011; Zhang and Luu, 2012), and thus this flow model was considered adequate for qualitative analysis in this study. Third, left-right symmetry in vocal fold geometry and vibration along the glottal midline was imposed. Extension of the analysis procedure to left-right asymmetric conditions is straightforward as in Zhang and Luu (2012). Finally, as in previous studies (Zhang et al., 2007; Zhang, 2009), no supra- or sub-glottal tracts were included in this study to avoid possible source-tract coupling. A constant flow rate was imposed at the glottal entrance, and downstream of the glottis the jet flow was discharged into free space (Zhang et al., 2007).

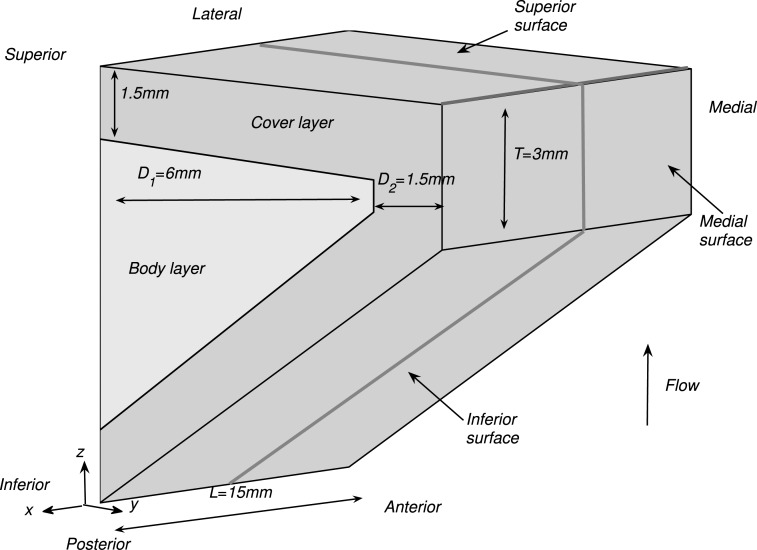
Figure 1 shows the three-dimensional vocal fold model used in this study. A body-cover idealization as suggested by Hirano (1974) was used. For simplicity, the vocal fold model was assumed to have a uniform cross-sectional geometry along the AP direction. The cross-sectional geometry of the vocal fold model was defined similarly as in previous studies (Zhang, 2009, Fig. 2). The vocal fold model was fixed at the lateral surface and the two side surfaces at the anterior and posterior ends.

Figure 1.

(Color online) The three-dimensional vocal fold model. The flow direction is along the positive z axis. The coupled vocal folds-flow system was assumed to be symmetric about the glottal channel centerline so that only one vocal fold was considered in this study. The two solid lines indicate the location along which results were shown in Figs. 3, 5, 6910.

For isotropic conditions, the material properties of each layer were characterized by the Young's modulus E_i, the vocal fold density, and a constant Poisson's ratio of 0.4995. For anisotropic conditions, each layer of the vocal fold was modeled as a transversely isotropic, nearly incompressible, linear material with a plane of isotropy perpendicular to the AP direction, as in previous studies (Itskov and Askel, 2002; Cook et al., 2008; Zhang, 2011). The material control parameters for the transversely isotropic vocal fold included the transverse Young's modulus E_t, the AP Young's modulus E_ap, the AP shear modulus G_ap, and density for each of the two layers. The longitudinal Poisson's ratio was assumed to be 0.495. To reduce the number of conditions to be investigated, E_ap = 4G_ap was further assumed in this study. Because the transversely isotropic conditions were the only anisotropic conditions considered in this study, the words anisotropic and transversely isotropic were used interchangeably below.

The x-component (AP direction), y-component (medial-lateral direction), and z-component (superior-inferior direction) of vocal fold displacement [u, v, w] were approximated as linear superposition of the in vacuo eigenmodes of the vocal folds

$$u(x,y,z,t)={\displaystyle \sum _{i=1}^N{q}_i{\phi }_{i,x};\hspace{1em}v(x,y,z,t)={\displaystyle \sum _{i=1}^N{q}_i{\phi }_{i,z};w(x,y,z,t)={\displaystyle \sum _{i=1}^N{q}_i{\phi }_{i,z},}}}$$ (1)

where [φ_i,x, φ_i,z, φ_i,z] are the displacement of the ith in vacuo eigenmode of the vocal fold, q_i is the ith generalized coordinate, and N is the number of eigenmodes included in the numerical simulation. In this study, N = 20 was used. Assuming infinitesimal displacement of the vocal fold, the change in glottal opening area due to vocal fold displacement was calculated by integrating the medial-lateral displacement v along the vocal fold surface contour l(z) at different superior-inferior location z,

$$g(z,t)=-2{\displaystyle {\int }_{l(z)}v(x,y,z,t)dl.}$$ (2)

The factor of 2 appears due to the imposed left-right symmetry in vocal fold vibration.

Phonation onset was investigated by examining how the eigenmodes and eigenvalues of the coupled airflow-vocal fold system vary as the subglottal pressure is increased from zero (Zhang et al., 2007). Phonation onset occurs when the growth rate (real part of the eigenvalue) of one of the eigenmodes (the critical eigenmode) first becomes positive, indicating the coupled system becomes linearly unstable. The governing equations of the eigenvalue problem were derived from Lagrange's equations (Zhang et al., 2007), as

$$M\ddot{q}+C\dot{q}+Kq=Q,$$ (3)

where M, C, K are the mass, damping, and stiffness matrices of the vocal fold structure, respectively, and Q is the generalized force vector associated with the fluctuating intraglottal pressure due to vocal fold vibration. The mass and stiffness matrices M and K were defined as

$$M_{\mathit{i}\mathit{j}}=\frac{\partial }{\partial {\ddot{q}}_j}\left(\frac{d}{\mathit{d}\mathit{t}}\left(\frac{\partial L}{\partial {\dot{q}}_i}\right)\right);\hspace{1em}{K}_{\mathit{i}\mathit{j}}=\frac{\partial }{\partial q_j}\left(-\frac{\partial L}{\partial q_i}\right),$$ (4)

where Lagrangian L = V − U. The associated kinetic energy V and potential energy U of the vocal fold structure were defined similarly to that in Zhang et al. (2007). The corresponding generalized force Q was calculated as

$$Q_k=-{\displaystyle {\int }_{S_{\text{FSI}}}\left(p\frac{\partial u}{\partial q_k}{n}_x+p\frac{\partial v}{\partial q_k}{n}_y+p\frac{\partial w}{\partial q_k}{n}_z\right)}ds,k=1,2,\hspace{0.17em}\dots ,\hspace{0.17em}N,$$ (5)

where S_FSI denotes the fluid-structure interface of the vocal fold with the normal vector n pointing outward from the vocal fold volume, and p is the fluctuating flow pressure on the fluid-structure interface due to the fluctuating glottal area g, which was obtained by solving the linearized Bernoulli's equation and the one-dimensional continuity equation (Zhang et al., 2007).

In this study, a constant loss factor σ of 0.4 was used, which relates the mass and damping matrices as follows:

$$C=\sigma \hspace{0.17em}\omega \hspace{0.17em}M,$$ (6)

where ω is the angular frequency.

Equation 3 was solved as an eigenvalue problem by assuming a solution form of q = q₀e^st, where s is the eigenvalue and q₀ is the corresponding eigenvector. The subglottal pressure was gradually increased until phonation onset was detected. The phonation threshold pressure would then be the subglottal pressure at onset, and the phonation onset frequency would then be given by the imaginary part of the corresponding eigenvalue. The vibratory pattern at onset can be calculated from the corresponding eigenvector using Eq. 1.

Simulation conditions

The different stiffness conditions considered in this study were summarized in Table TABLE I.. Also listed are five specific cases that are discussed and compared in detail in the text below. To qualitatively validate the three-dimensional model, phonation onset characteristics in an isotropic one-layer vocal fold model (case 1) and an isotropic two-layer model (case 2) were first discussed and compared to previous experimental observations. The effect of material anisotropy on phonation onset was then illustrated by comparing a transversely isotropic one-layer model (case 3) to the isotropic models. The last two cases, cases 4 and 5, considered two extreme conditions of a more general two-layer transversely isotropic model in which the degrees of anisotropy in the body and cover layers were individually varied.

TABLE I.

Material property conditions investigated in this study. The subscripts b and c denote the body and the cover layer, respectively, in two-layer models. For all conditions, the vocal fold density was 1.2 kg/mm³, and the minimum glottal half-width at rest was 0.2 mm.

Model	Model parameters and values
Isotropic one-layer	Case 1: Ei = 4 kPa; v = 0.4995
Isotropic two-layer	Ei,c = 4 kPa; Ei,b = [4–200] kPa; v = 0.4995
	Case 2: Ei,b = 120 kPa
Transversely isotropic one-layer	Et = 4 kPa; vap = 0.495; Eap = 4Gap
	Gap = [1–50] kPa
	Case 3: Gap = 50 kPa
Transversely isotropic two-layer	Et = 4 kPa; vap = 0.495
	Eap,b = 4Gap,b; Eap,c = 4Gap,c
	Case 4: Gap,b = 30 kPa; Gap,c = 1 kPa
	Case 5: Gap,b = 1 kPa; Gap,c = 30 kPa

RESULTS

In vacuo eigenmodes

As observed in Zhang (2011), one major difference between isotropic and transversely isotropic models is that many of the low-order modes in isotropic models exhibited out-of-phase motion along the AP length, i.e., different regions of the vocal fold surface along the AP direction vibrated at different phases. Such modes are referred to as AP modes in the following. Two types of AP modes can be further differentiated, depending on whether the surface motion produces a non-zero medial-lateral displacement when integrated over the vocal fold surface, i.e., whether the surface motion produces non-zero net flow modulation. For the vocal fold geometry in Fig. 1, AP modes with medial-lateral motion that is symmetric along the middle coronal cross-section are flow modulating (FM) modes, whereas AP modes that are antisymmetric along the coronal cross-section are non-FM modes. The non-AP modes are by definition also FM modes. The AP modes, both FM and non-FM, for cases 1 and 3 are labeled in Table TABLE II.. For the isotropic model in case 1, AP out-of-phase motion occurred in modes as low as the second in vacuo mode, and both the second and third in vacuo modes were non-FM AP modes. For the transversely isotropic model in case 3, only the tenth in vacuo mode exhibited AP out-of-phase motion. Differentiation between FM and non-FM modes is important because the non-FM modes generally do not participate in the eigenmode synchronization process, as demonstrated by the zero percentage energy weights of these modes in the critical eigenmode at onset in Table TABLE II., and thus have minimum effects on vocal fold vibration. The FM AP modes, however, do modulate flow and thus can be excited during phonation. When excited, these modes are likely to induce AP phase difference in vocal fold vibration.

TABLE II.

Energy percentages of the first seven in vacuo modes contributing to the critical eigenmode at onset.

in vacuo mode No.	Isotropic one-layer (case 1)	Transversely isotropic one-layer (case 3)
1	58.55	36.12
2	0 a	52.27
3	0 a	6.86
4	11.93	0.12
5	12.12	0.93
6	0 a	0.83
7	16.83 b	0.95

^aAP non-flow modulating modes.

^bAP flow-modulating modes.

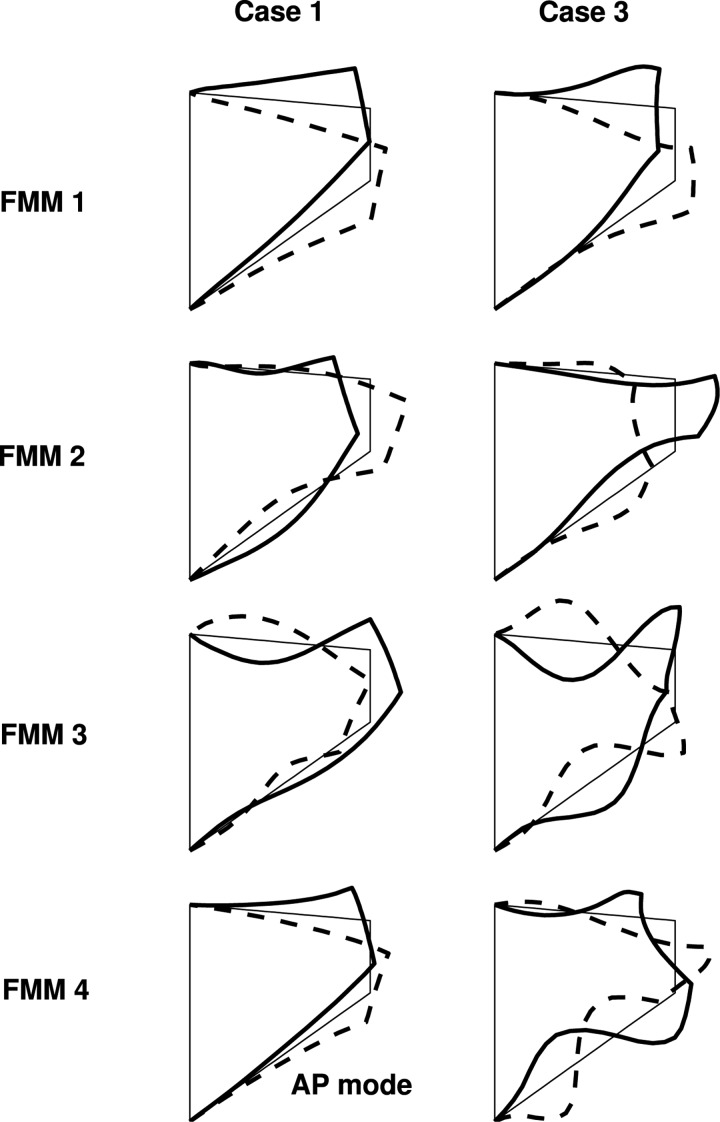
Figure 2 compares vocal fold surface motion in the middle cross-section for the first four in vacuo FM modes between cases 1 and 3. For the isotropic model in case 1, the first, second, and fourth FM modes all exhibited a qualitatively similar swing-like in-phase motion, with the medial-lateral and superior-inferior motion synchronized with a 180° phase difference: the vocal fold swung upward and laterally with a divergent medial surface shape and swung downward and medially with a convergent medial surface shape. The third in vacuo FM mode showed similarly swing-like motion, but with the medial-lateral and superior-inferior component synchronized in phase, instead of the 180° out-of-phase as in the other three FM modes. Synchronization of these modes of similar motion is likely to lead to a similarly in-phase swing-like motion during phonation. More importantly, all four FM modes had a strong superior-inferior component, in particular the first in vacuo mode which exhibited dominantly vertical motion in the superior-inferior direction. Due to the strong coupling between the medial-lateral and superior-inferior motions in all four modes, excitation of the medial-lateral motion, which is required for flow modulation and sound production, in the isotropic model will be always accompanied by a much stronger superior-inferior motion, particularly if the first in vacuo mode is strongly excited.

Figure 2.

The first four in vacuo FM modes of the vocal fold model in cases 1 and 3. In each plot, the thick solid line and the dashed line indicate extreme positions of the corresponding mode, spaced 180° apart in a vibratory cycle, and the thin solid line indicates equilibrium positions. The AP modes indicate modes exhibiting out-of-phase medial-lateral motion along the AP length.

In contrast, the first few in vacuo FM modes of the transversely isotropic model in case 3 exhibited qualitatively distinct motion: while the first FM mode was still a combination of medial-lateral and superior-inferior motion of roughly equal amplitude, the second FM mode was dominantly medial-lateral. Thus, large medial-lateral motion can be achieved without an equally strong superior-inferior component in the anisotropic vocal fold by a strong excitation of the second mode. The qualitatively distinct motion in the first few modes also indicates that these modes can be synchronized to produce complex vibration patterns that are distinctly different from those in the in vacuo modes.

Vibration at isotropic conditions and comparison to experiments

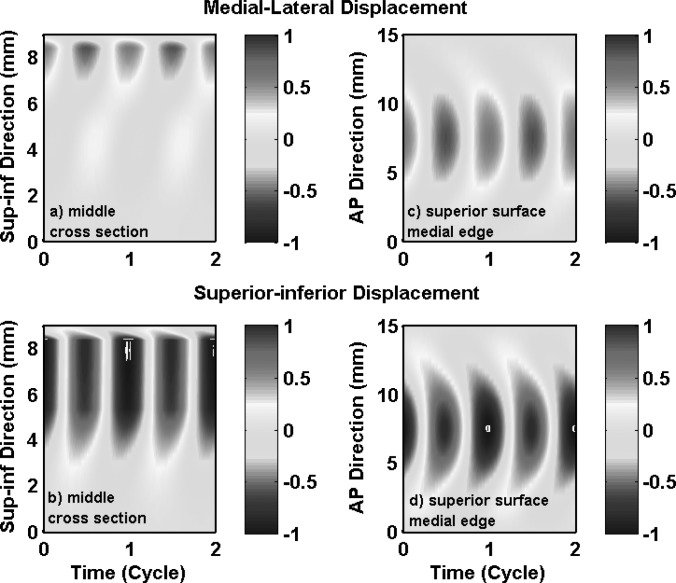
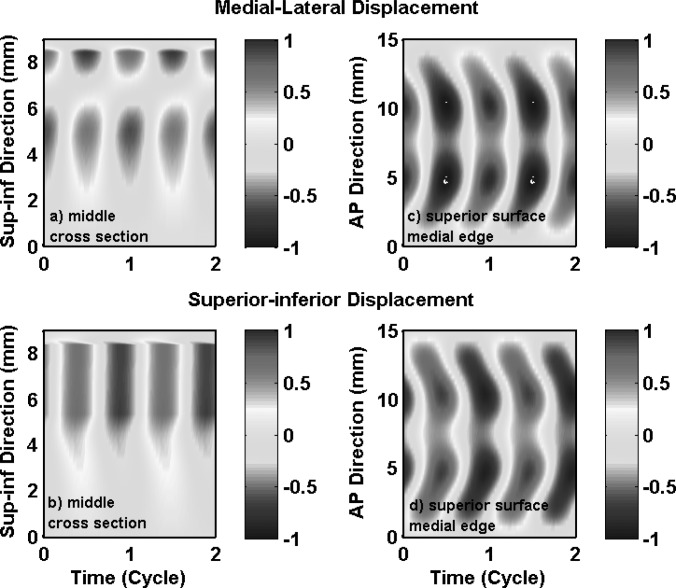
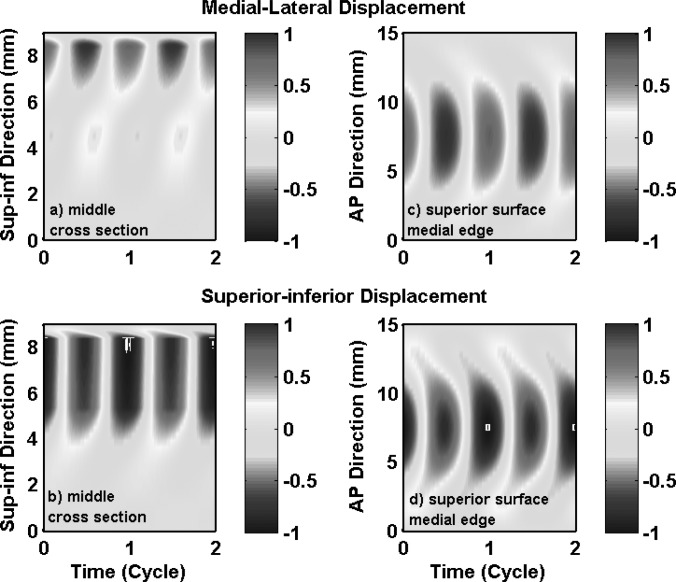
Phonation onset in the one-layer isotropic model in case 1 was due to the synchronization of the first two in vacuo FM modes of the vocal folds. Vocal fold vibration at onset had significant contributions from the first four FM modes (Table TABLE II.), with a 59% energy contribution from the first in vacuo mode. Because of this strong excitation of the first in vacuo mode, vocal fold vibration in case 1 had a dominant superior-inferior component, as shown in Figs. 3a, 3b which show the medial-lateral and superior-inferior displacements along vocal fold surface in the middle cross-section as a function of the superior-inferior location and time. Thus, although the isotropic model was able to self-oscillate when coupled with airflow, it was unable to produce the large medial-lateral motion required for efficient flow modulation because only a small portion of the vibrational energy was spent on the medial-lateral motion.

Figure 3.

(Color online) Case 1: one-layer isotropic model. Spatiotemporal plot of the medial-lateral (a) and superior-inferior (b) components of the vocal fold surface displacement in the middle cross-section as a function of the vertical location along the superior-inferior direction and time, and the spatiotemporal plot of the medial-lateral (c) and superior-inferior (d) components of the vocal fold surface displacement along the superior edge of the medial surface as a function of the AP location and time. The displacements were normalized by the maximum value of the two components (medial-lateral and superior-inferior) along the entire vocal fold surface. The origin of the superior-inferior coordinate corresponds to the inferior edge of the vocal fold or inlet to the glottis.

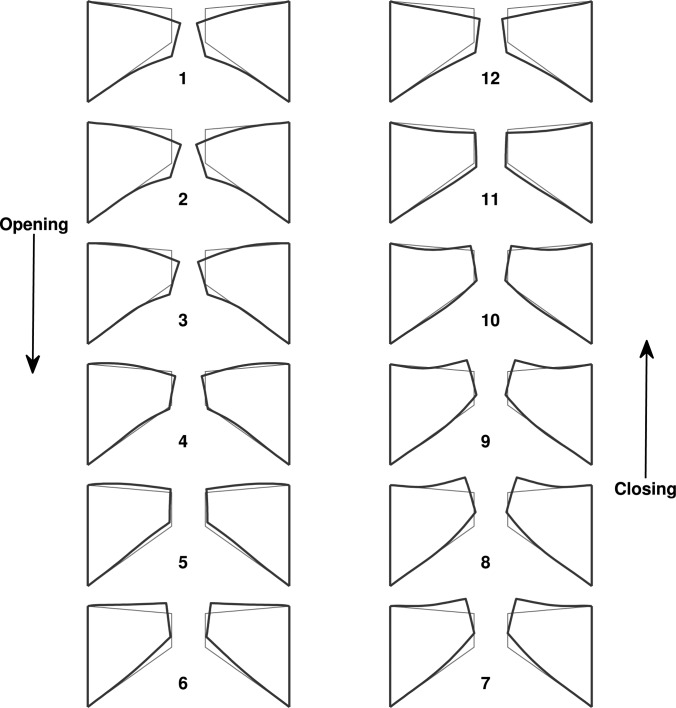
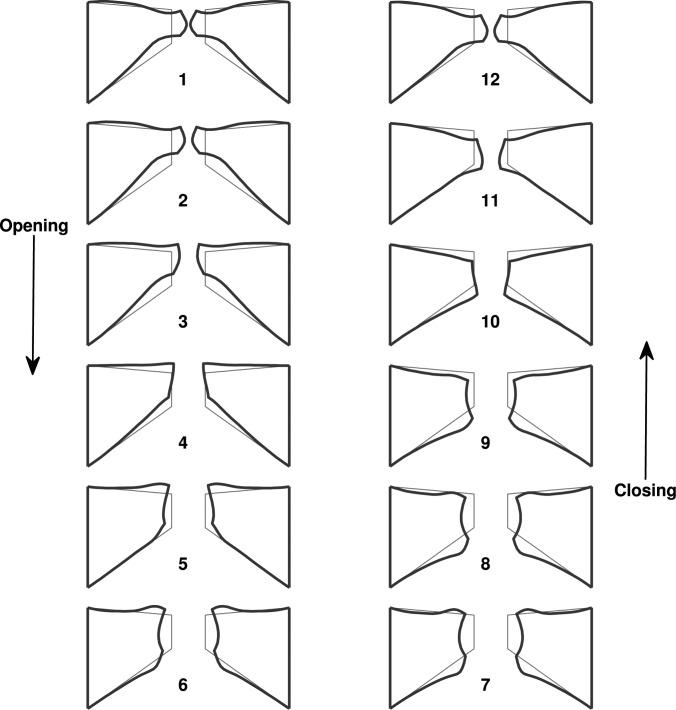
Because of the high similarity in the motion of the first few in vacuo FM modes, the isotropic model exhibited a similar one-mass swing-like motion: the entire medial surface (except for the lower margin) vibrated in-phase along the medial-lateral direction and the vibration amplitude decayed rapidly from the upper margin towards the lower margin [Fig. 3a, Fig. 4], similar to that in the first in vacuo mode of the vocal fold. Note that the medial surface corresponded to the region with a superior-inferior location between 5.3 and 8.3 mm in Fig. 3. There was a nodal line at the lower part of the medial surface at which the medial-lateral vibration amplitude was constantly zero. Further inferior to this nodal line, the lower margin of the medial surface and the inferior surface vibrated 180° out of phase from the medial surface, but with a much reduced vibration amplitude. The swing-like motion is better illustrated in Fig. 4, which shows the vocal fold surface profile in the middle cross-section during one oscillation cycle. Note that the first frame corresponds to the instant when the middle point of the medial surface was at its maximum medial excursion (thus approximately the beginning of the opening phase). Due to this swing-like motion and the rapidly reduced vibration amplitude from the upper margin towards the lower margin, the vocal fold opened with a convergent medial surface shape (Fig. 4), changed to straight as the vocal fold upper margin returned to neutral position, then gradually changed to a divergent medial surface as the vocal fold continued to open. This vibration pattern was reversed in the closing phase: the vocal fold remained divergent during the first part of the closing phase then transitioned to a convergent profile in the middle of the closing phase. Because of the relatively fixed (almost 180°) phase difference between the medial-lateral motion and the superior-inferior motion [Figs. 3a, 3b], the vocal fold reached the highest and lowest positions at instants of maximum and minimum glottal opening, respectively.

Figure 4.

(Color online) The middle cross-section of the isotropic vocal fold model (case 1) during one oscillation cycle. The thin lines correspond to the undeformed vocal fold geometry. The first frame corresponds to the instant when the middle point of the medial surface was at its maximum medial excursion (thus approximately the beginning of the opening phase).

Figures 3c, 3d also show vocal fold vibration at the superior edge of the medial surface as a function of the AP location and time, again for case 1. Large vocal fold motion, in both the medial-lateral and superior-inferior directions, was confined to the middle third region along the AP direction, and decayed rapidly towards the anterior and posterior ends. Figure 3 also shows that there was a noticeable phase difference along the AP direction in both the medial-lateral and superior-inferior motion, with the middle region leading the off-center regions. This AP phase difference was due to strong excitation of the fourth FM mode (with a percentage energy weight of 16.85%; Table TABLE II.) which was an AP mode.

These observations in Figs. 34 were consistent with previous experimental observations in isotropic physical models, which include one-mass-like motion of the vocal fold (Zhang et al., 2006), excessively large vertical motion (Zhang et al., 2006), concentration of large vocal fold motion along the middle region along the AP direction, and AP out-of-phase motion (Mendelsohn and Zhang, 2011; Zhang, 2011).

Increasing the body-layer stiffness in a two-layer isotropic vocal fold model did not yield a qualitative change in the swing-like vibration pattern in the middle cross-section, except for an increased medial-lateral vibration amplitude on the inferior surface which is not quite efficient in flow modulation, as shown in Figs. 5a, 5b for case 2. However, increasing body-cover stiffness ratio did lead to AP out-of-phase motion in the first few in vacuo eigenmodes of the vocal fold (Zhang, 2011). As a result, vocal fold vibration in case 2 demonstrated a strong AP out-of-phase motion in both the medial-lateral and superior-inferior motion. Unlike that in case 1, large vibration in case 2 was not confined to the middle third of the vocal fold along the AP direction, and maximum vibration amplitude occurred at the one third and two thirds location along the AP length, as shown in Figs. 5c, 5d. This AP out-of-phase vibration pattern was consistent with the experimental observation in Mendelsohn and Zhang (2011; Fig. 3) and Zhang (2011; Fig. 6). Large AP phase differences are general undesirable because the out-of-phase regions may cancel out each other and reduce effective flow modulation and energy transfer, thus decreasing the overall voice production efficiency.

Figure 5.

(Color online) Case 2: two-layer isotropic model. Spatiotemporal plot of the medial-lateral (a) and superior-inferior (b) components of the vocal fold surface displacement in the middle cross-section as a function of the vertical location along the superior-inferior direction and time, and the spatiotemporal plot of the medial-lateral (c) and superior-inferior (d) components of the vocal fold surface displacement along the superior edge of the medial surface as a function of the AP location and time. The displacements were normalized by the maximum value of the two components (medial-lateral and superior-inferior) along the entire vocal fold surface.

In summary, despite of the many simplifications, the linear stability model of this study was able to qualitatively predict major observations from previous experiments. With this qualitative validation, the method was then applied to vocal folds of transversely isotropic material properties, and the results are discussed below.

Transversely isotropic one-layer models

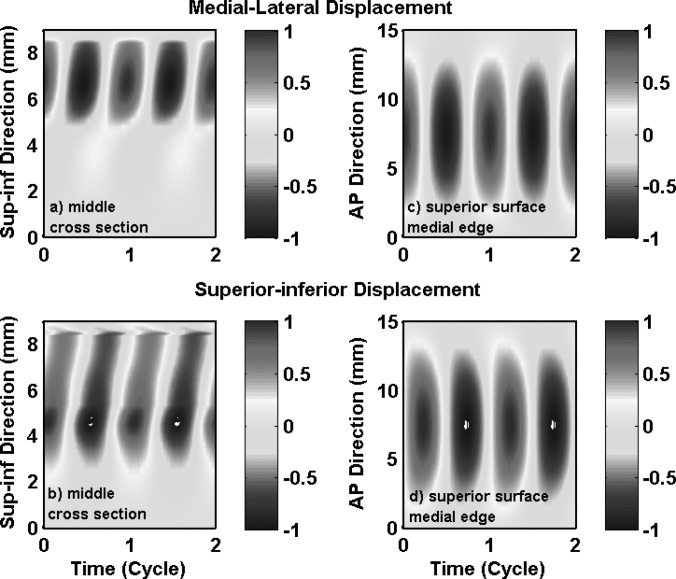
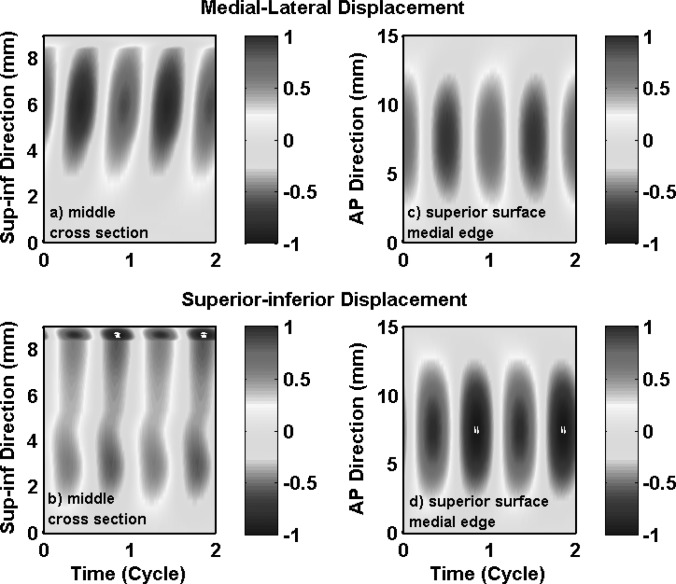
For the transversely isotropic model in case 3, phonation onset occurred again as the first two in vacuo eigenmodes were synchronized. The first two in vacuo modes contributed about 88% to the total energy in vocal fold vibration at onset (Table TABLE II.). Note that the second in vacuo mode, which exhibited primarily medial-lateral motion, was the most dominant mode and contributed about 52% of the total energy. Because the strong medial-lateral motion in these two in vacuo modes, particularly the second in vacuo mode, the resulting vibration at onset exhibited strong medial-lateral motion, as shown in Fig. 6a. Unlike case 1 in which the medial-lateral vibration amplitude decayed rapidly towards the inferior direction, the medial-lateral vibration amplitude in case 3 was more uniformly distributed along the entire medial surface. In addition, a clear wave-like motion can be observed along the medial surface, as demonstrated by a continuously changing phase along the medial surface in both the medial-lateral and superior-inferior motion in Figs. 6a, 6b. Because the first few in vacuo modes were all non-AP modes, the AP out-of-phase motion observed in isotropic conditions (cases 1 and 2) was suppressed and the entire length of the vocal fold vibrated in phase [Figs. 6c, 6d]. Large vocal fold motion, in both the medial-lateral and superior-inferior directions, now spread over a much larger region along the AP length, in contrast to the middle third region in case 1.

Figure 6.

(Color online) Case 3: one-layer transversely isotropic model. Spatiotemporal plot of the medial-lateral (a) and superior-inferior (b) components of the vocal fold surface displacement in the middle cross-section as a function of the vertical location along the superior-inferior direction and time, and the spatiotemporal plot of the medial-lateral (c) and superior-inferior (d) components of the vocal fold surface displacement along the superior edge of the medial surface as a function of the AP location and time. The displacements were normalized by the maximum value of the two components (medial-lateral and superior-inferior) along the entire vocal fold surface.

Figure 7 shows the vocal fold surface profile in the middle cross-section during one oscillation cycle in case 3. The vocal fold vibration clearly had a much larger medial-lateral motion (in relative to the superior-inferior motion) compared with case 1. Because of the vertical phase difference in both the medial-lateral and the superior-inferior motion, the vocal fold surface had a much wavy shape compared with that in case 1. Vocal fold opening started as the lower margin started to move away from the glottal midline. The vocal fold medial surface gradually took over a slightly convergent medial surface shape, and was able to maintain the convergent shape all the way until the end of the opening phase when the upper and lower margins started to move in opposite directions as the lower margin started to move towards the glottal midline. Similarly in the closing phase, the vocal fold was able to maintain a divergent medial surface shape for the entire closing phase except for the end when the lower margin started to move away from the glottal midline. Unlike case 1 in which the medial-lateral and superior-inferior extremes were reached at the same time, the phase difference between the medial-lateral and the superior-inferior motion varied along the medial surface so that maximum glottal opening did not correspond to the highest vertical position of the vocal fold.

Figure 7.

(Color online) The middle cross-section of the transversely isotropic one-layer vocal fold model (case 3) during one oscillation cycle. The thin lines correspond to the undeformed vocal fold geometry. The first frame corresponds to the instant when the middle point of the medial surface was at its maximum medial excursion (thus approximately the beginning of the opening phase).

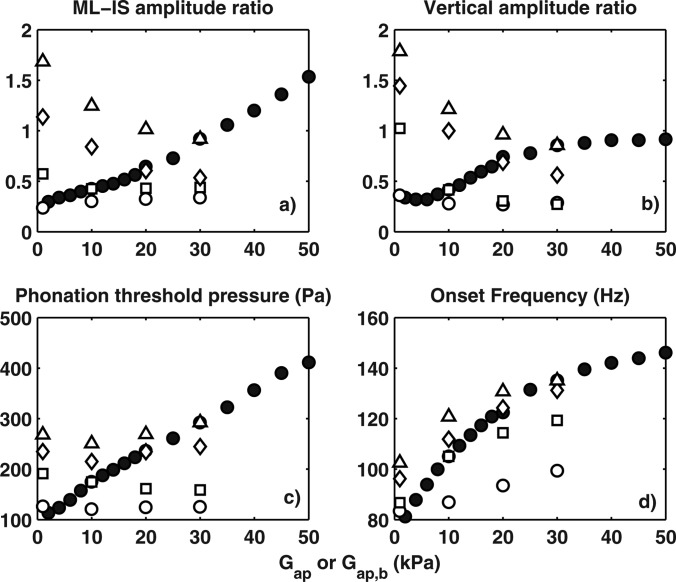
The effects of increasing material anisotropy in the one-layer transversely isotropic model were further quantified as a function of increasing AP shear modulus while keeping the transverse stiffness constant. Figure 8a (solid circles) shows the vibration amplitude ratio between the medial-lateral and superior-inferior motion (evaluated at the middle point of the medial surface in the middle cross-section), and Fig. 8b shows the vertical amplitude ratio or the amplitude ratio of the medial-lateral motion between the lower and upper margins of the medial surface. Both measures increased with increasing AP stiffness, indicating enhanced medial-lateral motion with respect to the superior-inferior motion and a more uniform medial-lateral vibration amplitude along the medial surface. Increasing AP-transverse stiffness ratio also suppressed AP out-of-phase motion and a more uniform distribution of large vocal fold motion along the AP length (not shown in the figure). Also shown in Fig. 8 are the phonation threshold pressure and onset frequency, both of which increased with increasing AP stiffness.

Figure 8.

(a) The vibration amplitude ratio between the medial-lateral motion and the superior-inferior motion, evaluated at the middle point of the medial surface in the middle cross-section; (b) the medial-lateral vibration amplitude ratio between the lower and upper margins of the medial surface; (c) phonation threshold pressure; and (d) phonation onset frequency in the one-layer transversely isotropic model (●) and the two-layer transversely isotropic model (○: G_ap,c = 1 kPa; ◻: G_ap,c = 10 kPa; ◇: G_ap,c = 20 kPa; △: G_ap,c = 30 kPa).

Transversely isotropic two-layer models

It has been shown that the degree of anisotropy can be controlled through activation of the laryngeal muscles, particularly the thyroarytenoid and the cricothyroid muscles (Yin and Zhang, 2013). The effects of the degrees of anisotropy of the body and cover layers on vibration in a two-layer transversely isotropic vocal fold are also shown in Fig. 8 (open symbols). In general, increasing anisotropy (or AP-transverse stiffness ratio) of the cover layer led to significant enhancement of the medial-lateral motion, both in relative vibration amplitude and its distribution along the medial surface. Increasing anisotropy in the body layer however was much less effective and, for conditions of strong anisotropy in the cover layer, it even reduced the relative medial-lateral vibration amplitude. Figures 910 show the vibration pattern at onset for two extreme cases of the two-layer transversely isotropic models. Case 4 had large anisotropy in the body layer but was almost isotropic in the cover layer, and its vibration (Fig. 9) was quite similar to that in case 1, with weak in-phase medial-lateral motion along the medial surface and out-of-phase motion along the AP length. Case 5 had large anisotropy in the cover layer but was almost isotropic in the body layer. Vocal fold vibration in this case had the largest vibration amplitude ratio between the medial-lateral and superior-inferior motion and an in-phase motion along the AP length. This observation is consistent with the experimental observation in Xuan and Zhang (2014), which showed that embedded fibers facilitated complete glottal closure, presumably through enhanced medial-lateral motion, only when the fibers were embedded in the cover layer close to the vocal fold surface. Embedding fibers in the body layer did not lead to any noticeable difference in vocal fold vibration, with still incomplete glottal closure and noticeable AP out-of-phase motion.

Figure 9.

(Color online) Case 4: two-layer transversely isotropic model with strong anisotropy in the body layer. Spatiotemporal plot of the medial-lateral (a) and superior-inferior (b) components of the vocal fold surface displacement in the middle cross-section as a function of the vertical location along the superior-inferior direction and time, and the spatiotemporal plot of the medial-lateral (c) and superior-inferior (d) components of the vocal fold surface displacement along the superior edge of the medial surface as a function of the AP location and time. The displacements were normalized by the maximum value of the two components (medial-lateral and superior-inferior) along the entire vocal fold surface.

Figure 10.

(Color online) Case 5: two-layer transversely isotropic model with strong anisotropy in the cover layer. Spatiotemporal plot of the medial-lateral (a) and superior-inferior (b) components of the vocal fold surface displacement in the middle cross-section as a function of the vertical location along the superior-inferior direction and time, and the spatiotemporal plot of the medial-lateral (c) and superior-inferior (d) components of the vocal fold surface displacement along the superior edge of the medial surface as a function of the AP location and time. The displacements were normalized by the maximum value of the two components (medial-lateral and superior-inferior) along the entire vocal fold surface.

It is interesting to note that, while increasing anisotropy in both layers increased phonation onset frequency [Fig. 8d], the phonation threshold pressure increased significantly only with increasing anisotropy in the cover layer [Fig. 8c]. Increasing anisotropy in the body layer did not produce noticeable change in phonation threshold pressure.

DISCUSSION AND CONCLUSIONS

Summary of results

This study showed that the isotropic model had a tendency to exhibit a vertical swing-like motion, probably due to the less constrained boundary conditions in the superior-inferior direction. This tendency was so strong that the first few in vacuo modes all exhibited a swing-like motion with the medial-lateral and superior-inferior components coupled with similar phase relationship. Synchronization of modes of similar vibration pattern will necessarily lead to qualitatively the same vibration pattern, in this case a swing-like in-phase motion. Due to the strong superior-inferior motion in the first few in vacuo modes, particularly the first in vacuo mode, vocal fold vibration at onset was dominantly along the superior-inferior direction. The isotropic model also had AP out-of-phase motion in the first few in vacuo modes, resulting in AP out-of-phase vocal fold vibration and confinement of large vibration to the middle third region along the AP length.

Increasing vocal fold anisotropy, specifically the ratio between the AP and transverse stiffnesses, decoupled the medial-lateral motion and the superior-inferior motion in the in vacuo modes and made it possible to excite a large medial-lateral motion without proportional excitation of the superior-inferior motion. The first few in vacuo modes also exhibited qualitatively distinct vibration patterns so that these modes can be synchronized to produce vibration patterns qualitatively distinct from those in the in vacuo modes. As a result, the transversely isotropic model vibrated with a continuously changing vertical phase difference in vocal fold motion along the medial surface, and with a large medial-lateral vibration amplitude uniformly distributed along the entire medial surface. Stiffening the vocal fold along the longitudinal direction also suppressed the AP out-of-phase motion and caused large medial-lateral motion to spread to a larger region along the AP length.

Implications on phonation

How do these vibratory differences affect voice production? Increased medial-lateral vibration amplitude (which modulates airflow) with respect to the superior-inferior motion (which does not modulate airflow directly) indicates that more energy can be used for flow modulation, thus increasing flow modulation efficiency. Similarly, a more uniform vibration pattern along the AP length would also increase flow modulation efficiency. Furthermore, a vertical phase difference is likely to produce a glottal flow waveform that deviates from a sinusoid wave form, which facilitates production of high-order harmonics in the produced sound spectrum.

As the linear stability analysis is valid only for infinitesimal vibration amplitude at onset, this study did not provide a direct and conclusive explanation regarding why isotropic models often do not achieve complete glottal closure during vibration as observed in previous experiments (Zhang et al., 2006; Mendelsohn and Zhang, 2011; Zhang, 2011), and why embedding fibers to the cover layer facilitates complete glottal closure (Xuan and Zhang, 2014). However, it is reasonable to expect qualitatively similar differences in vibration pattern between isotropic models and the transversely isotropic models may also occur in finite-amplitude vibrations. Thus, the isotropic models vibrate with incomplete glottal closure probably because most of the energy transfer from airflow is spent on the vertical motion rather than the medial-lateral motion and thus unable to produce large enough medial-lateral vibration amplitude to close the glottis. The AP out-of-phase motion and confinement of large medial-lateral motion to the middle region may further prevent complete glottal closure, as shown in Fig. 6 of Xuan and Zhang (2014). Complete glottal closure is more likely to be achieved in transversely isotropic models (e.g., with embedded fibers) with enhanced medial-lateral motion with respect to the superior-inferior motion and the suppression of the AP out-of-phase motion. This study also showed that such improvement in the glottal closure pattern was the most effective with large anisotropy in the cover layer alone and the least effective with large anisotropy in the body layer. This may explain the observation in Xuan and Zhang (2014) that improvement in the glottal closure pattern was more effective when the fibers were embedded in locations close to the vocal fold surface. In addition to the mechanisms explored in this study, Zhang (2011) showed that transversely isotropic models are able to better maintain adductory position, meaning that the prephonatory static deformation of the vocal folds is smaller and the prephonatory medial surface is less divergent, compared with isotropic models. This reduced prephonatory opening and glottal divergence may further facilitate complete glottal closure.

The importance of material anisotropy in affecting vocal fold vibration, particularly the glottal closure pattern, indicates that it may play an important role in the regulation of voice quality. In humans, the degree of vocal fold anisotropy can be regulated through activation of laryngeal muscles, particularly the thyroarytenoid and the cricothyroid muscles (Yin and Zhang, 2013). Vocal fold anisotropy is also expected to vary with age or due to vocal pathologies, due to structural changes of the extracellular matrix. Understanding changes in vocal fold anisotropy due to these factors may provide insights into mechanisms underlying voice control and voice changes. On the other hand, the importance of material anisotropy as demonstrated in this study implies that phonation is essentially a three-dimensional process and thus three-dimensional models, at least on the structure side, are preferred if the goal were to understand such voice control processes.

Limitations of this study

As discussed above, one major simplification of this study was that the static prephonatory deformation of the vocal fold was neglected. This is not always valid, especially when the vocal folds are at a relaxed condition (Zhang, 2011). Thus, one direction of future work is to take this static deformation into consideration. Another aspect of the fluid-structure interaction that may be oversimplified in this study is the use of a one-dimensional flow model. More realistic flow models need to be used so that the effects of realistic flow features (e.g., flow curvature effects, asymmetric flow pressure, and vortex shedding; Erath and Plesniak, 2006; Neubauer et al., 2007; Khosla et al., 2007) can be considered. For example, it is possible that non-FM modes may participate in synchronization if a non-uniform flow pressure distribution along the AP direction is allowed, which may happen in realistic phonation. On the other hand, vocal fold vibration critically depends on the eigenmode synchronization pattern, which again depends on vocal fold geometry and material properties (Zhang, 2010). Particularly, it is possible that isotropic vocal folds with a drastically different geometry may have distinct vibration patterns in the first few in vacuo modes and thus produce a vibration pattern similar to the transversely isotropic model of this study. Finally, the importance of vocal fold anisotropy points to the need for a better characterization of vocal fold anisotropy at different normal and pathological voice conditions, which remains essentially unknown.