Abstract
Ultrasound contrast agents (UCAs) can be employed to nucleate cavitation to achieve desired bioeffects, such as thrombolysis, in therapeutic ultrasound applications. Effective methods of enhancing thrombolysis with ultrasound have been examined at low frequencies (<1 MHz) and low amplitudes (<0.5 MPa). The objective of this study was to determine cavitation thresholds for two UCAs exposed to 120-kHz ultrasound. A commercial ultrasound contrast agent (Definity®) and echogenic liposomes were investigated to determine the acoustic pressure threshold for ultraharmonic (UH) and broadband (BB) generation using an in vitro flow model perfused with human plasma. Cavitation emissions were detected using two passive receivers over a narrow frequency bandwidth (540–900 kHz) and a broad frequency bandwidth (0.54–1.74 MHz). UH and BB cavitation thresholds occurred at the same acoustic pressure (0.3 ± 0.1 MPa, peak to peak) and were found to depend on the sensitivity of the cavitation detector but not on the nucleating contrast agent or ultrasound duty cycle.
INTRODUCTION
Stroke is the fourth leading cause of mortality in the United States (Hoyert and Xu, 2012). Despite the need for therapies, the only Federal Drug Administration-approved thrombolytic, recombinant tissue plasminogen activator (rt-PA), is administered in less than 5% of ischemic stroke patients due to strict usage guidelines (California Acute Stroke Pilot Registry CASPR Investigators, 2005). Novel treatments to improve stroke therapy are aimed at shortening the time to recanalization and reducing the risk of intracerebral hemorrhage, and could broaden the range of patients receiving rt-PA treatment.
Ultrasound-enhanced thrombolysis (UET) is under development as an adjuvant to rt-PA (Akiyama et al., 1998; Shaw et al., 2008, 2009). Ultrasound contrast agents (UCAs) are stabilized microbubbles that can be injected into the bloodstream and have previously been used to nucleate acoustic cavitation (Rota et al., 2006; Sboros, 2008). Initial studies have demonstrated the efficacy of UET in the presence of UCAs (Molina et al., 2006; Datta et al., 2008; Hitchcock et al., 2011). These studies demonstrated UET when acoustic emissions characteristic of stable cavitation, ultraharmonics (UHs) (Ilyichev et al., 1989; Datta et al., 2008) and the subharmonic (Neppiras, 1969), were present. Conversely, broadband emissions, which are characteristic of inertial cavitation (Apfel, 1982), correlated with a reduction of thrombolysis enhancement (Datta et al., 2008).
Ultrasound frequencies between 100 and 800 kHz penetrate the skull efficiently (Ammi et al., 2008; Fry and Barger, 1978). This frequency range is well below that intended for the use of UCAs [2–8 MHz (Klibanov, 2002)]. Little is known about the threshold for bubble activity nucleated by UCAs exposed to pulsed ultrasound with center frequencies below 1 MHz for the development of UET.
The current study was performed to determine the threshold for cavitation activity in an in vitro human clot model with an UCA in flow exposed 120-kHz pulsed or continuous wave ultrasound. Two UCAs were used to nucleate cavitation, Definity® and echogenic liposomes (ELIP). Definity®, a commercially available UCA, has been shown previously to nucleate stable cavitation and enhance thrombolysis (Datta et al., 2008; Brown et al., 2011; Hitchcock et al., 2011). ELIP are potential theragnostic agents for the treatment of stroke (Huang et al., 2009; Radhakrishnan et al., 2012; Kopechek et al., 2013) with the ability to encapsulate and release rt-PA upon exposure to ultrasound. The liposomes are composed of phospholipid bilayers encapsulating a liquid core and gas pocket. The exact location and size of the gas pockets within the liposome is unknown, but these pockets most likely exist on the hydrophobic side of the lipid or within a lipid monolayer in the aqueous compartment (Unger et al., 1998). Lipid monolayers surround and stabilize the gas within the fluid-filled liposomes (Huang et al., 2009).
MATERIALS AND METHODS
The thresholds for cavitation emissions nucleated by Definity® or ELIP exposed to 120-kHz pulsed ultrasound were determined over a range of duty cycles (10% to 100%). To mimic in vivo UET, the cavitation thresholds were measured using a flow model in the presence of a blood clot. Cavitation emissions were measured from these UCAs with two passive cavitation detectors (PCDs), over different frequency bands (0.54–0.90 MHz and 0.54–1.74 MHz). The thresholds for both UH emissions (characteristic of stable cavitation) and broadband (BB) emissions (characteristic of inertial cavitation) were compared statistically.
Human plasma and clots
Human fresh-frozen plasma (HFFP) was procured from a blood bank (Hoxworth Blood Center, Cincinnati, OH) in 180–300 ml units. The frozen units were thawed to room temperature, aliquoted into 30 ml samples, refrozen, and stored at −80 °C. These aliquots were thawed for each experiment and allowed to reach atmospheric gas equilibrium at 37 °C in an open container for 2 h.
Human clots were manufactured around silk sutures following the protocol developed by Shaw et al. (2008). Following local institutional review board approval, and written informed consent, human whole blood was drawn from a pool of volunteers. Aliquots of 0.5 ml were transferred to sterile glass tubes containing small borosilicate glass micropipettes (1.12 mm inner diameter, World Precision Instruments, Inc.), pre-threaded with 7-0 silk sutures (Ethicon Industries, Cornelia, GA). The blood was drawn into the micropipette and over the suture by capillary action. The blood was allowed to clot around the silk suture at 37 °C for 3 h. Following clot formation, the tubes were stored at 5 °C for a minimum of 3 days to allow for full clot retraction. Each clot was used within 14 days. Preparation in this manner has been shown to generate reproducible, retracted clots that are easy to remove from the micropipette (Cheng et al., 2005). The clots were 700–800 μm in diameter.
Definity®
Definity® vials were activated at room temperature using the VialmixTM agent activator (Lantheus Medical Imaging, Billerica, MA) according to the manufacturer's instructions. After a 45-s activation cycle, the vials were allowed to return to room temperature over 60 min. The agent was diluted by a factor of 150 by volume in the plasma to achieve a number density of approximately 8 × 107 UCA/ml. This number density is higher than the manufacturers recommended dose for LVO.
Echogenic liposomes
Echogenic liposomes were prepared at the University of Texas Health Science Center at Houston as described by Buchanan et al. (2008). The molar ratio of lipids was 27:42:8:8:15 of l-a-phosphatidylcholine (chicken egg; EPC), 1,2-dipalmitoyl-sn-glycero-3-phosphocholine, 1,2-dipalmitoyl- sn-glycero-3-[phosphor-rac-1-glycerol], 1,2-dipalmitoyl-sn- glycero-3-phos-phoethanolamine (Avanti Polar Lipids, Alabaster, AL) and cholesterol (Sigma Aldrich, St. Louis, MO).
Liposomes were shipped to the University of Cincinnati as a lyophilized powder and stored at 4 °C until use. Each 6 mg vial of liposomes was reconstituted with 600 μl filtered, deionized water (NANOPure, Barnstead International, Dubuque, IA) prior to experiments. The agent was diluted by a factor of 66 by volume in HFFP for a final lipid concentration of 0.152 mg/ml [1.2 × 109 liposomes/ml (Kopechek et al., 2011)].
In vitro flow apparatus
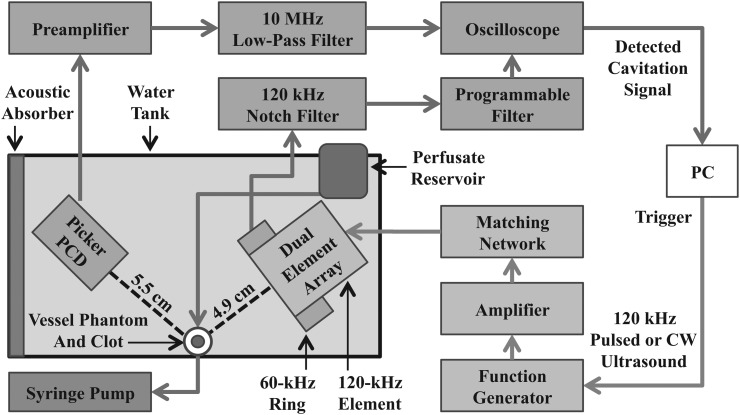
The exposure system used to measure cavitation thresholds is represented schematically in Fig. 1. Experiments were performed in an acrylic tank (16 cm × 33 cm × 9 cm) filled with preheated, degassed water. Water temperature (37.3 ± 0.3 °C) and gas saturation (20 ± 5% dissolved oxygen at 37 °C) were maintained throughout the duration of the experiment using a recirculation system.
Figure 1.
(Color online) Diagram of experimental in vitro setup.
After reaching dissolved gas and temperature equilibration, plasma was transferred to a reservoir submerged within the tank. The regulated water temperature ensured the plasma and UCAs remained at physiologic temperature throughout the experiment. A flow loop consisting of low-density polyethylene tubing (inner diameter-1.6 mm, outer diameter-3.2 mm, part 1 J-109-10, Freelin Wade Co., McMinnville, OR) directed the plasma (with or without UCAs) from the bottom of the reservoir through the region of insonification. Flow was maintained at 1 ml/min with a programmable syringe pump (model 44, Harvard Apparatus, South Natick, MA) in continuous withdrawal mode.
The flow system consists of a 2.15 mm inner-diameter glass micropipette (5-000-2200, Drummond Scientific Co., Broomall, PA) with a 0.3 mm wall thickness. The acoustic pressure attenuation by the micropipette was previously found to be less than 1% of signal at 120 kHz (Cheng et al., 2005). The clot was inserted through the micropipette and held into place by latex tubing tightly fitted over the micropipette, thereby suspending the clot along the axis of the capillary tube.
Ultrasound exposure and cavitation detection
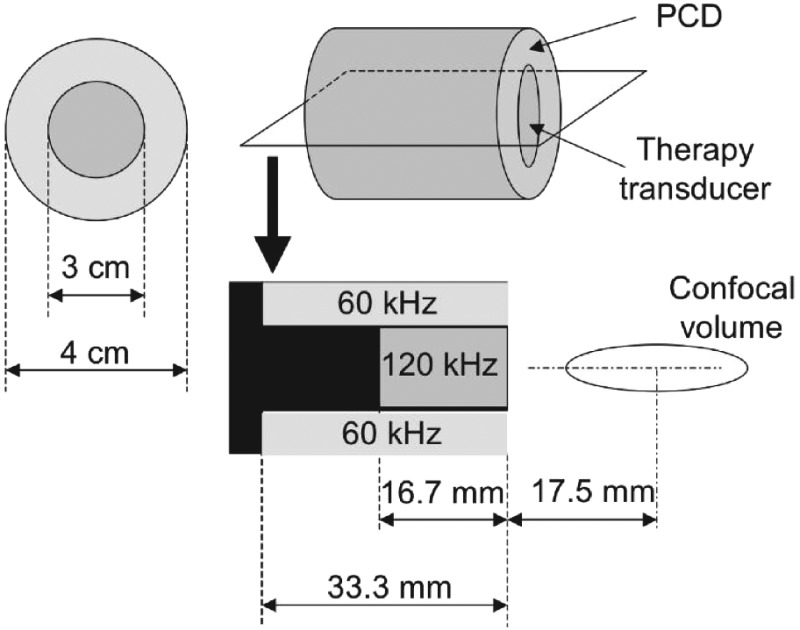
A dual element annular array (DA) (Fig. 2) was designed and built (H160, Sonic Concepts, Inc. Woodburn, WA). The unfocused central 120-kHz element was used to insonify the flow phantom and was driven at its resonant frequency. Impedance matching was provided with a custom-built matching network. The duty cycle (DC) of the acoustic excitation varied between 10% and 100%. The pulse duration was chosen at 10% DC to be 20 acoustic cycles. This pulse duration was the minimum pulse duration required to achieve sufficient frequency resolution of UH emissions. Larger DCs increased the pulse duration but retained the same quiescent period (1.5 ms). Details of the acoustic excitations are shown in Table TABLE I..
Figure 2.
Schematic of dual element annular array for 120 kHz insonation and 60 kHz passive cavitation detection.
TABLE I.
Ultrasound pulse settings used for 120-kHz insonation.
| Duty cycle (%) | Number of cycles | Off time (ms) | PRF (Hz) |
|---|---|---|---|
| 10 | 20 | 1.5 | 600 |
| 20 | 45 | 1.5 | 533 |
| 40 | 120 | 1.5 | 400 |
| 80 | 720 | 1.5 | 133 |
| 100 | - | - | - |
The unfocused ring element of the DA was used for passive cavitation detection. The fundamental resonance of the ring was designed to be 60 kHz, the subharmonic of the excitation element, and has lower sensitivity at UHs of 120 kHz. However, preliminary experiments indicated a high noise level at 60 kHz, the subharmonic frequency. Low signal to noise ratio at the subharmonic frequency was also reported by McDannold et al. (2006) during cavitation experiments at 260 kHz. Therefore the ring element was used to detect BB and UH activity over the 540–900 kHz range with a SNR of 3–10 dB. The signal from the ring element was filtered by a 120-kHz notch filter (Sonic Concepts) and a 250–1000 kHz fourth-order Butterworth band-pass filter (3945, Krohn-Hite Co., Brockton, MA) with 20 dB input gain (Fig. 1). A second PCD was aligned confocally with the blood clot sample in flow phantom. This secondary PCD, a focused 2.25-MHz transducer (595516C, Picker Roentgen GmbH, Espelkamp, Germany), has previously been utilized to detect cavitation at 120 kHz (Hitchcock et al., 2011). The PCD aperture is 1.9 cm and the focal length is 5.5 cm. The received signal from the Picker was filtered by a 10-MHz low-pass filter (J73E, TTE Inc., Los Angeles, CA) to reduce aliasing from radio frequency interference and amplified with a wideband low-noise amplifier (CLC100, Comlinear Corp., Fort Collins, CO).
The acoustic fields of the central element and annular ring element were mapped in situ with a PVDF hydrophone (TC4038, Reson, Goleta, CA) mounted on a computer-controlled micropositioning system. The blood clot within the flow phantom was positioned at the maximum of the 120-kHz beam near the bottom of the tank and oriented such that the cylindrical axis of the flow phantom was orthogonal to the beam axis.
Experimental protocol
Samples (plasma and UCA or plasma alone) were exposed to 1-s insonations at a peak-to-peak acoustic pressure between 0.08 and 0.62 MPa. For continuous wave exposure (100% DC), the maximum pressure was limited to 0.52 MPa to avoid overheating the matching network (as specified by the manufacturer). A 10-ms waveform from each of the two PCDs was digitized at 25 MHz using a digital oscilloscope (Lecroy Wave Runner LT372, Chestnut Ridge, NY) and transferred to a computer (2.3 GHz, MacBook Pro, Apple Inc., Cupertino, CA) for analysis offline. After each insonation, the ultrasound exposure was suspended for 6 s to allow fresh media to flow into the sample chamber. Acoustic pressures (0.08–0.62 MPa in 17 evenly spaced increments, 0.08–0.52 MPa in 14 steps for 100% DC) were cycled through ten times, randomizing the order of excitation pressures at the beginning of each cycle, yielding ten excitations at each acoustic pressure per data set. This experimental protocol was repeated with fresh media five times for each UCA and DC, resulting in 50 measurements per exposure parameter (UCA, DC, acoustic pressure).
Passive cavitation detection signal processing
Primary scattering in the tank dominated the signal of the received ring PCD. To reduce the acoustic clutter, received signals from degassed water (without a clot) were subtracted from cavitation signals in the time domain. The MATLAB function “alignsignals” was used to ensure the degassed and cavitation waveforms were in phase before subtraction.
For continuous wave insonation, a Hann window was applied to each 10-ms waveform, and the power spectrum was computed in MATLAB (MathWorks Inc., Natick, MA). For pulsed insonations, the power spectra of each pulse of the 10-ms waveform were summed. Thus the total cavitation emissions were computed for a total 10-ms duration for both pulsed and continuous wave insonations. The use of a fixed 10-ms duration allowed comparison of total cavitation emissions across all ultrasound exposure schemes. Prior to computing the power spectrum of each pulse, a Hann window was applied, and the pulse was zero padded symmetrically to 10 ms. To eliminate scattering from formed elements in the plasma, power spectra from plasma controls were subtracted from UCA power spectra in the frequency domain for both PCDs.
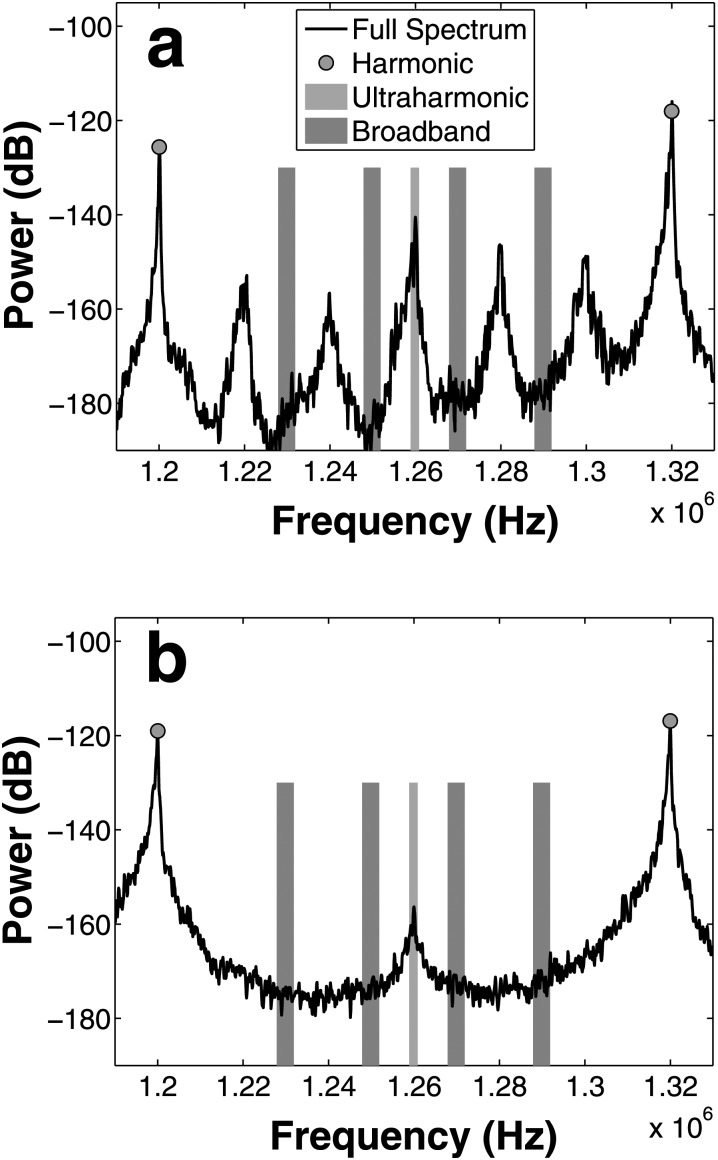
The UH bands of the power spectrum, [, where m is an integer and f0 is 120 kHz], were summed over a 2-kHz bandwidth [Figs. 3a, 3b], centered around each UH. BB bands of the power spectrum were defined as the average power for frequency bands centered at each UH ±10 kHz and ±30 kHz and within a bandwidth of 4 kHz. These bands were chosen to exclude the f0/6 UHs present in ELIP spectra [Fig. 3a].
Figure 3.
(Color online) Power spectrum for ELIP (a) and Definity (b) indicating frequency bands used to quantify ultraharmonic (light shading, or lavendar online) and broadband (dark shading, or red online) energy. Broadband bins were chosen to minimize the contribution of f0/6 energy present in ELIP spectra (a).
Spectra were windowed in the frequency domain to include only UHs with a sufficient signal-to-noise ratio (SNR). The SNR for a particular UH band was defined following Santin et al. (2008) as the ratio of average UH power spectral density in the presence of Definity® to the average UH power spectral density in the presence of degassed water (i.e., without microbubbles). A conservative choice of 3 dB was used as a threshold for the choice of UH bands used in the analysis. Using this criterion, only UH bands within 540 and 900 kHz were analyzed for the ring PCD. Similarly, only UH bands within 540 and 1740 kHz for the Picker PCD were assessed. The average SNR for the ring PCD was greater than 10 dB for DCs 40% and greater. However, the SNR was between 3 and 10 dB for the 10% and 20% DC exposures. The average SNR for the Picker PCD was greater than 20 dB for all DCs.
Determination of cavitation threshold
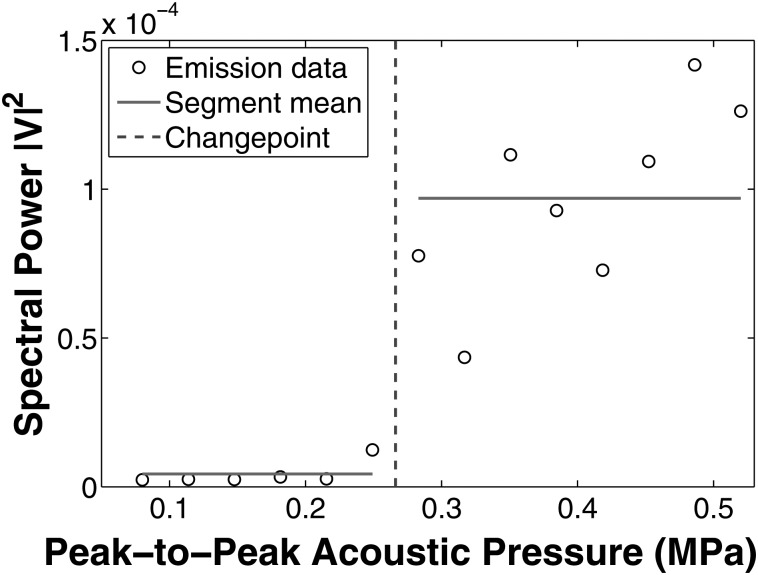
UH and BB cavitation thresholds were determined using the software package changepoint (Killick and Eckley, 2013) in R (version 2.15.2, The R Foundation for Statistical Computing, Vienna, Austria). The algorithm applies a neighborhood segmentation method (Auger and Lawrence, 1989) that determines the pressure change point via maximum-likelihood estimation. For a given DC and UCA, the change point algorithm was applied to determine the acoustic pressure that best segmented the spectral power measurements (either UH or BB) into two groups with similar means and variances (Fig. 4). The change point method was applied to each data set (UCA type and DC) to determine thresholds for UH and BB emissions for both PCDs.
Figure 4.
(Color online) An example of changepoint analysis method for determination of acoustic threshold. Horizontal lines indicate neighborhoods with similar mean and variance. The change point (dashed line) is the transition point from one segment to the other.
Statistical treatment of the threshold data
The statistical difference between the UH and BB thresholds was compared using MATLAB for each combination of UCA, DC, and PCD using a two-way unbalanced Student's t-test. For each combination of emission type (UH or BB), PCD, and DC, the thresholds for the two UCAs were compared using Student's t-test. The cavitation thresholds were analyzed as a function of DC using a one-way unbalanced analysis of variance (ANOVA) in MATLAB (MathWorks Inc., Natick, MA). For each UCA, PCD, and emission type, cavitation data were tested for equal mean across DC groups.
RESULTS
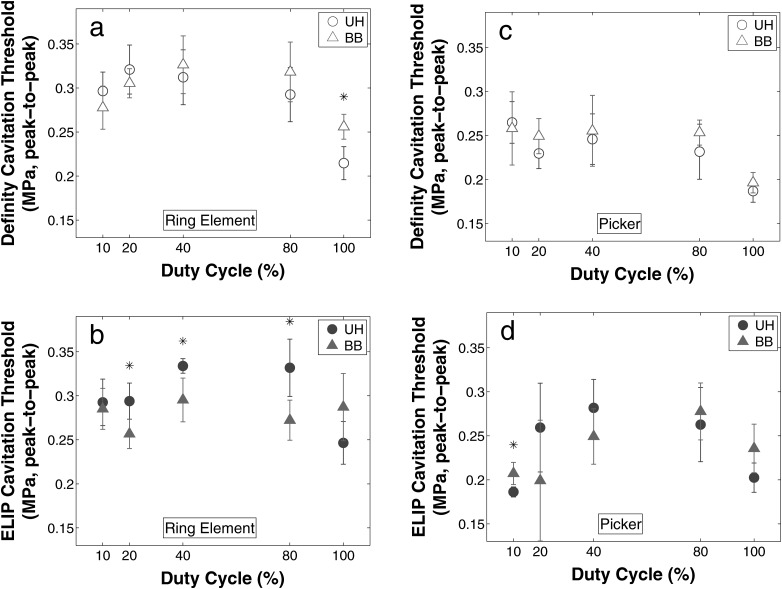
Figure 5 shows the thresholds for UH and BB emissions nucleated by Definity® or ELIP. Figures 5a, 5b show thresholds detected by the ring PCD, and Figs. 5c, 5d show thresholds detected by the Picker PCD.
Figure 5.
(Color online) Ultraharmonic (circle) and broadband (triangle) thresholds for Definity (open marker) and ELIP (filled marker) cavitation thresholds were determined using a 60 kHz ring element [(a) and (b)] and 2.25 MHz circular single-element transducer [(c) and (d)] as PCDs. Each point represents the mean, and each error bar indicates the standard deviation of five trials for each duty cycle and UCA combination. Stars (*) indicate significant differences in the mean peak-to-peak acoustic pressure threshold (α = 0.05).
The acoustic pressure thresholds for UH and BB emissions were statistically different in five of 20 cases, four of which were measured with the ring PCD. However, the absolute value of the difference in pressure thresholds was only on the order of 0.11 MPa peak-to-peak. The cavitation thresholds measured with the ring PCD were consistently higher (0.15 MPa, on average) in comparison to equivalent thresholds measured using the Picker PCD. Also the type of nucleation agent, ELIP versus Definity®, did not affect the cavitation thresholds.
Upon comparison of a single experimental configuration across all DCs, all cases were significant using a one-way unbalanced ANOVA (α < 0.05) except the BB threshold for ELIP using the DA as PCD (p = 0.14). In all but one case, however, the 20%, 40%, and 80% DCs were not statistically different. Generally, the 100% and 10% DCs occurred at statistically lower acoustic pressures than the other DCs regardless of emission type.
DISCUSSION
Comparison of UH and BB thresholds
The thresholds for UH and BB cavitation activity occur at nearly the same acoustic pressure (approximately 0.3 MPa, peak to peak). Hence BB emissions from inertial cavitation and UH emissions from stable cavitation will occur simultaneously at 120 kHz. The findings of this study suggest that an intermittent ultrasound pulsing scheme that triggers a quiescent period when bubble activity ceases to allow influx of fresh nuclei could help promote sustained bubble activity.
In addition, other investigators have used the presence of harmonics (as opposed to UH or BB) to indicate the onset of bubble activity (Arvenitis et al. 2012). This scheme, however, relies on the assessment of nonlinear propagation and inclusion in the signal processing of the PCD. This finding is consistent with previous investigators using UCAs to nucleate cavitation at 120 kHz. Hitchcock et al. (2011) applied continuous-wave 120 kHz ultrasound and Definity® in an ex vivo porcine carotid artery model. They found that a maximal amount of UH energy was delivered over 30 min at an acoustic pressure of 0.44 MPa (peak to peak). However, both UH and BB emissions were present at this pressure. Threshold measurements for Definity® around a human clot model (Datta et al., 2008) without plasma flow exposed to pulsed ultrasound (80% DC, 1667 Hz pulse repetition frequency) produced no acoustic pressure that yielded only UH emissions.
These findings suggest that the UH and BB thresholds for UCA may overlap when excited at 120 kHz. Arvanitis et al. (2012) insonified microbubbles at 220 kHz and also found the presence of concomitant UH and BB emissions. Similarly, O'Reilly and Hynynen (2012) found that UH emissions could not be detected without the presence of BB emissions at 550 kHz in the presence of microbubbles. Other investigators (Biagi et al., 2007; Hitchcock et al., 2011) reported that at higher frequencies, closer to the UCA resonance (1–5 MHz), they found a marked separation between the onset of UH and BB emissions. This separation of cavitation thresholds was not observed in this study at 120 kHz. Other types of acoustic emissions may be needed to indicate acoustically activated microbubbles below the stable and inertial cavitation thresholds for low frequency (<1 MHz) ultrasound exposure of UCAs (McDannold et al., 2012). These investigators noted a lack of deleterious bioeffects in brains infused with an UCA and exposed to intermittent 220 kHz ultrasound below the stable and inertial cavitation thresholds.
Nucleation of cavitation has been shown to occur via the rupture of the shell of the UCA (Yeh and Su, 2008), thereby liberating the gas. Previous calculations have predicted that resonant-sized UCAs will rupture before the detection of subharmonic emissions (Bader and Holland, 2013). The largest peak in the volume-weighted size distribution for Definity and ELIP is 6 and 2 μm, respectively (Faez et al., 2012; Raymond et al., 2013). The encapsulated gas pockets that are available to nucleate cavitation from Definity or ELIP are much smaller than the resonant size at 120 kHz [approximately 50 μm (Marmottant et al., 2005)]. The threshold pressure for contrast agent shell rupture increases below resonance (Bader and Holland, 2013). Thus the inertial and stable cavitation thresholds were similar probably because once the contrast agent rupture threshold was reached, both cavitation thresholds pressures had been surpassed for the liberated bubbles.
Definity vs ELIP cavitation thresholds
The pressure thresholds for the two UCAs were statistically different in only four of the 20 combinations of PCD, emission, and DC. These differences occurred in three of the four cases at the two lowest DCs. The pressure threshold for Definity® was higher in all cases when there was a significant difference between the UCAs. If rupture is required to nucleate cavitation, this increased threshold suggests Definity® is more resistant to rupture than ELIP.
Comparison of PCDs
Both the UH and BB thresholds determined with the 60 kHz ring PCD were higher than the thresholds determined with the 2.25 MHz Picker PCD. The difference in sensitivity of the two transducers likely contributes to this variation. The 60 kHz ring PCD was designed to be sensitive at the subharmonic of the fundamental, 60 kHz. However, the SNR was too limited at frequencies below 250 kHz to detect bubble activity. Because of low-frequency noise, cavitation emissions detected by the 60 kHz ring PCD were analyzed at higher-frequency UH bands (540–900 kHz). A low SNR below the fundamental for PZT type receivers was also observed by McDannold et al. (2006). These authors found that it was not possible to detect subharmonic emission using a similar array (260 kHz center element with concentric PCD ring of 10 piezoelectric elements, each with a center frequency of 670 kHz) during in vivo experiments of blood-brain barrier disruption due to the low SNR below the fundamental. Future experiments using 120-kHz insonation should incorporate PCD elements that are designed to detect UHs above 250 kHz to avoid this low-frequency noise.
DC dependence
Both UH and BB thresholds were not statistically significantly different for DCs of 20%, 40%, and 80%. The UH and BB thresholds at 10% and 100% were statistically lower than the other DCs. The statistically lower thresholds at 10% DC are likely due to reduced SNR for both detectors. Both detectors had the best SNR at 100% DC, which may explain the statistically lower thresholds at this DC. In addition, Fowlkes and Crum (1988) posited that gas will passively dissolve into solution primarily during the “off” phase of pulsed ultrasound. Thus, the absence of an off period in the 100% case would allow sufficient emissions from cavitation events to surpass the sensitivity limit of the detector.
Cavitation thresholds for UCAs have been shown to decrease with an increase in ultrasound pulse duration for pulses of 10 or fewer cycles (Atchley et al., 1988; Chen et al., 2003). However, Giesecke and Hynynen (2003) showed no change in the inertial cavitation thresholds for longer pulse durations (20–100 ms). Chen et al. (2003) found that insonifying Optison® with 1.1 MHz ultrasound at a 3 MPa peak-to-peak pressure amplitude produced inertial cavitation that increased rapidly with pulse duration but saturated after 100 cycles. These results suggest that lowering the cavitation threshold by increasing the pulse duration becomes nonproductive after a certain number of cycles. The current study had a minimum of 20 cycles, and the threshold did not vary appreciably with DC (typically less than 50 kPa peak to peak). Thus our data suggest that the threshold for UH and BB bubble activity is invariant for pulse duration longer than 20 cycles at 120 kHz.
Limitations of the study
Each insonifying pulse of ultrasound had a duration of at least 20 cycles to facilitate determination of the threshold in the frequency domain. Ideally, the shortest pulse observed would have been a single-cycle pulse. However, preliminary experiments indicated that a minimum of 20 cycles was required to achieve sufficient frequency resolution for cavitation measurement.
The experiments in this study were performed at atmospheric pressure. Attempts were made to perform experiments at mean arterial pressure of 100 mmHg. However, changes in dissolved gas saturation complicated threshold measurements by precipitation of bubbles from oversaturated HFFP or loss of ELIP echogenicity by gas dissolution into under saturated HFFP. While this relatively small change in static pressure is not expected to have a substantial effect on the BB thresholds (Bader et al., 2012), Dave et al. (2013) found subharmonic emissions decreased linearly with increasing ambient pressure. Ganor et al. (2005) concluded that this change in subharmonic emission was due in part to the reduction in steady-state bubble radius as a result of a higher compression force. UH emissions have also been found to decrease with increasing static pressure (Sun et al., 2012) although the strength of the dependence varies with insonifying frequency.
CONCLUSIONS
Acoustic cavitation thresholds were measured at 120 kHz for two lipid-shelled agents, Definity® and ELIP, over a range of ultrasound DCs. UH and BB thresholds for Definity® and ELIP occurred at approximately the same acoustic pressure amplitude (0.2–0.35 MPa, peak to peak) for all DCs and for pulses longer than 20 cycles. The simultaneous onset of UH and BB activity suggests that nucleation of cavitation occurs via rupture of the UCAs, which were driven off resonance. The thresholds for UH or BB activity were within two standard deviations for all ultrasound pulse settings used in this study. Thus an acoustic pressure will initiate both stable and inertial bubble activity in flow with an ultrasound contrast agent exposed to ultrasound with a frequency band far from the agent's resonance.
ACKNOWLEDGMENT
The authors acknowledge Shaoling Huang, MD, Ph.D., who manufactured the echogenic liposomes. We also acknowledge helpful discussions with the members of the Image-Guided Ultrasound Therapeutics Laboratories at the University of Cincinnati. This work is supported by NIH Grant Nos. NS047603 and HL059586.
References
- Akiyama, M., Ishibashi, T., Yamada, T., and Furuhata, H. (1998). “ Low-frequency ultrasound penetrates the cranium and enhances thrombolysis in vitro,” Neurosurgery 43, 828–832. 10.1097/00006123-199810000-00062 [DOI] [PubMed] [Google Scholar]
- Ammi, A., Mast, T., Huang, I.-H., Abruzzo, T., Coussios, C.-C., Shaw, G., and Holland, C. (2008). “ Characterization of ultrasound propagation through ex vivo human temporal bone,” Ultrasound Med. Biol. 34, 1578–1589. 10.1016/j.ultrasmedbio.2008.02.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Apfel, R. (1982). “ Acoustic cavitation: A possible consequence of biomedical uses of ultrasound,” Br. J. Cancer Supple. 45(5 ), 140–146. [PMC free article] [PubMed] [Google Scholar]
- Arvanitis, C. D., Livingstone, M. S., Vykhodtseva, N., and McDannold, N. (2012). “ Controlled ultrasound-induced blood-brain barrier disruption using passive acoustic emissions monitoring,” PLoS ONE 7(9 ), e45783 10.1371/journal.pone.0045783.t001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atchley, A., Frizzell, L., Apfel, R., Holland, C., Madanshetty, S., and Roy, R. (1988). “ Thresholds for cavitation produced in water by pulsed ultrasound,” Ultrasonics 26, 280–285. 10.1016/0041-624X(88)90018-2 [DOI] [PubMed] [Google Scholar]
- Auger, I. E., and Lawrence, C. E. (1989). “ Algorithms for the optimal identification of segment neighborhoods,” Bull. Math. Biol. 51, 39–54. [DOI] [PubMed] [Google Scholar]
- Bader, K. B., and Holland, C. K. (2013). “ Gauging the likelihood of stable cavitation from ultrasound contrast agents,” Phys.Med.Biol 58, 127–144 10.1088/0031-9155/58/1/127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bader, K. B., Mobley, J., Church, C. C., and Gaitan, D. F. (2012). “ The effect of static pressure on the strength of inertial cavitation events,” J. Acoust. Soc. Am. 132, 2286. 10.1121/1.4750494 [DOI] [PubMed] [Google Scholar]
- Biagi, E., Breschi, L., Vannacci, E., and Masotti, L. (2007). “ Stable and transient subharmonic emissions from isolated contrast agent microbubbles,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 54, 480–497 10.1109/TUFFC.2007.272. [DOI] [PubMed] [Google Scholar]
- Brown, A. T., Flores, R., Hamilton, E., Roberson, P. K., Borrelli, M. J., and Culp, W. C. (2011). “ Microbubbles improve sonothrombolysis in vitro and decrease hemorrhage in vivo in a rabbit stroke model,” Invest. Radiol. 46, 202–207 10.1097/RLI.0b013e318200757a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buchanan, K. D. K., Huang, S. S., Kim, H. H., Macdonald, R. C. R., and McPherson, D. D. D. (2008). “ Echogenic liposome compositions for increased retention of ultrasound reflectivity at physiologic temperature,” J. Pharmacol. Sci. 97, 2242–2249 10.1002/jps.21173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- California Acute Stroke Pilot Registry CASPR Investigators (2005). “ Prioritizing interventions to improve rates of thrombolysis for ischemic stroke,” Neurology, 64, 654–659 10.1212/01.WNL.0000151850.39648.51. [DOI] [PubMed] [Google Scholar]
- Chen, W.-S., Brayman, A. A., Matula, T. J., Crum, L. A., and Miller, M. W. (2003). “ The pulse length-dependence of inertial cavitation dose and hemolysis,” Ultrasound Med. Biol. 29, 739–748 10.1016/S0301-5629(03)00029-2. [DOI] [PubMed] [Google Scholar]
- Cheng, J., Shaw, G., and Holland, C. (2005). “ In vitro microscopic imaging of enhanced thrombolysis with 120-kHz ultrasound in a human clot model,” Acoust. Res. Lett. Online, 6, 25–29. 10.1121/1.1815039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Datta, S., Coussios, C.-C., Ammi, A., Mast, T., de Courten-Myers, G., and Holland, C. (2008). “ Ultrasound-enhanced thombolysis using Definity as a cavitation nucleation agent,” Ultrasound Med. Biol. 34, 1421–1433. 10.1016/j.ultrasmedbio.2008.01.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dave, J. K., Halldorsdottir, V. G., Eisenbrey, J. R., Merton, D. A., Liu, J. B., Machado, P., Zhao, H., Park, S., Dianis, S., Chalek, C. L., Thomenius K. E., Brown, D. B., and Forsberg, F. (2013). “ On the implementation of an automated acoustic output optimization algorithm for subharmonic aided pressure estimation,” Ultrasonics 53, 880–888 10.1016/j.ultras.2012.12.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faez, T., Skachkov, I., Versluis, M., Kooiman, K., and de Jong, N. (2012). “ In vivo characterization of ultrasound contrast agents: Microbubble spectroscopy in a chicken embryo,” Ultrasound Med. Biol. 38, 1608–1617 10.1016/j.ultrasmedbio.2012.05.014. [DOI] [PubMed] [Google Scholar]
- Fowlkes, J. B., and Crum, L. A. (1988). “ Cavitation threshold measurements for microsecond length pulses of ultrasound,” J. Acoust. Soc. Am. 83, 2190–2201. 10.1121/1.396347 [DOI] [PubMed] [Google Scholar]
- Fry, F., and Barger, J. (1978). “ Acoustical properties of the human skull,” J. Acoust. Soc. Am. 63, 1576. 10.1121/1.381852 [DOI] [PubMed] [Google Scholar]
- Ganor, Y., Adam, D., and Kimmel, E. (2005). “ Time and pressure dependence of acoustic signals radiated from microbubbles,” Ultrasound Med. Biol. 31, 1367–1374 10.1016/j.ultrasmedbio.2005.06.014. [DOI] [PubMed] [Google Scholar]
- Giesecke, T., and Hynynen, K. (2003). “ Ultrasound-mediated cavitation thresholds of liquid perfluorocarbon droplets in vitro,” Ultrasound Med. Biol. 29, 1359–1365. 10.1016/S0301-5629(03)00980-3 [DOI] [PubMed] [Google Scholar]
- Hitchcock, K. E., Ivancevich, N. M., Haworth, K. J., Stamper, D. N. C., Vela, D. C., Sutton, J. T., Pyne-Geithman, G. J., and Holland, C. K. (2011). “ Ultrasound-enhanced rt-PA thrombolysis in an ex vivo porcine carotid artery model,” Ultrasound Med. Biol. 37, 12 10.1016/j.ultrasmedbio.2011.05.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoyert, D. L., and Xu, J. (2012). “ Deaths: Preliminary data for 2011,” Natl. Vital Stat. Rep. 61(6 ), 1–65. http://stacks.cdc.gov (Last viewed 07/23/2012). [PubMed] [Google Scholar]
- Huang, S.-L., Kee, P. H., Kim, H., Moody, M. R., Chrzanowski, S. M., MacDonald, R. C., and Mcpherson, D. D. (2009). “ Nitric oxide-loaded echogenic liposomes for nitric oxide delivery and inhibition of intimal hyperplasia,” J. Am. Coll. Cardiol. 54(7 ), 652–659 10.1016/j.jacc.2009.04.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ilyichev, V. I. V., Koretz, V. L. V., and Melnikov, N. P. N. (1989). “ Spectral characteristics of acoustic cavitation,” Ultrasonics 27, 357–361. 10.1016/0041-624X(89)90034-6 [DOI] [PubMed] [Google Scholar]
- Killick, R., and Eckley, I. A. (2013). “ changepoint: An R package for changepoint analysis,” retrieved from http://CRAN.R-project.org/package=changepoint (Last viewed 07/23/2012).
- Klibanov, A. L. (2002). “ Ultrasound contrast agents: Development of the Field and current status,” Top. Curr. Chem. 222, 73–106 10.1007/3-540-46009-8_3. [DOI] [Google Scholar]
- Kopechek, J. A., Haworth, K. J., Radhakrishnan, K., Huang, S.-L., Klegerman, M. E., Mcpherson, D. D., and Holland, C. K. (2013). “ The impact of bubbles on measurement of drug release from echogenic liposomes,” Ultrason. Sonochem. 20, 1121–1130 10.1016/j.ultsonch.2012.12.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kopechek, J. A., Haworth, K. J., Raymond, J. L., Douglas Mast, T., Perrin, S. R., Klegerman, M. E., Huang, S., McPherson, D. D., and Holland, C. K. (2011). “ Acoustic characterization of echogenic liposomes: Frequency-dependent attenuation and backscatter,” J. Acoust. Soc. Am. 130, 3472–3481. 10.1121/1.3626124 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marmottant, P., van der Meer, S., Emmer, M., Versluis, M., de Jong, N., Hilgenfeldt, S., and Lohse, D. (2005). “ A model for large amplitude oscillations of coated bubbles accounting for buckling and rupture,” J. Acoust. Soc. Am. 118, 3499–3505. 10.1121/1.2109427 [DOI] [Google Scholar]
- McDannold, N., Arvanitis, C. D., Vykhodtseva, N., and Livingstone, M. S. (2012). “ Temporary disruption of the blood-brain barrier by use of ultrasound and microbubbles: Safety and efficacy evaluation in rhesus macaques,” Cancer Res. 72(14 ), 3652–3663 10.1158/0008-5472.CAN-12-0128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDannold, N. N., Vykhodtseva, N. N., and Hynynen, K. K. (2006). “ Targeted disruption of the blood-brain barrier with focused ultrasound: Association with cavitation activity,” Phys. Med. Biol. 51, 793–807 10.1088/0031-9155/51/4/003. [DOI] [PubMed] [Google Scholar]
- Molina, C., Ribo, M., Rubiera, M., Montaner, J., Santamarina, E., Delgado-Mederos, R., Arenillas, J., Huertas, R., Purroy, F., Delgado, P., and Alvarez-Sabin, J. (2006). “ Microbubble administration accelerates clot lysis during continuous 2-MHz ultrasound monitoring in stroke patients treated with intravenous tissue plasminogen activator,” Stroke 37, 425–429. 10.1161/01.STR.0000199064.94588.39 [DOI] [PubMed] [Google Scholar]
- Neppiras, E. (1969). “ Subharmonic and other low-frequency emission from bubbles in sound-irradiated liquids,” J. Acoust. Soc. Am. 46, 567–601. [Google Scholar]
- Oreilly, M. A., and Hynynen, K. (2012). “ Blood-brain barrier: Real-time feedback-controlled focused ultrasound disruption by using an acoustic emissions-based controller,” Radiology 263(1 ), 96–106 10.1148/radiol.11111417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Radhakrishnan, K., Haworth, K. J., Huang, S.-L., Klegerman, M. E., Mcpherson, D. D., and Holland, C. K. (2012). “ Stability of echogenic liposomes as a blood pool ultrasound contrast agent in a physiologic flow phantom,” Ultrasound Med. Biol. 38, 1970–1981 10.1016/j.ultrasmedbio.2012.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raymond, J. L., Haworth, K. J., Bader, K. B., Radhakrishnan, K., Griffin, J. K., Huang, S.-L., McPherson, D. D., and Holland, C. K. (2013). “Broadband attenuation measurements of phospholipid-shelled ultrasound contrast agents,” Ultrasound Med. Biol. (in press). 10.1016/j.ultrasmedbio.2013.09.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rota, C., Raeman, C. H., Child, S. Z., and Dalecki, D. (2006). “ Detection of acoustic cavitation in the heart with microbubble contrast agents in vivo: A mechanism for ultrasound- induced arrhythmias,” J. Acoust. Soc. Am. 120, 2958–2964. 10.1121/1.2346132 [DOI] [PubMed] [Google Scholar]
- Santin, M., Bridal, S. L., Haak, A., and O'Brien, W. D. (2008). “ Spectral and temporal signal modifications occuring between stable and transient inertial cavitation,” The 2008 IEEE Ultrasonics Symposium (IUS), pp. 989–992. 10.1109/ULTSYM.2008.0239 [DOI]
- Sboros, V. (2008). “ Response of contrast agents to ultrasound,” Adv. Drug Deliv. Rev. 60, 1117–1136 10.1016/j.addr.2008.03.011. [DOI] [PubMed] [Google Scholar]
- Shaw, G., Meunier, J., Huang, S.-L., Lindsell, C., McPherson, D., and Holland, C. (2009). “ Ultrasound-enhanced thrombolysis with tPA-loaded echogenic liposomes,” Thombosis Res. 124, 306–310. 10.1016/j.thromres.2009.01.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaw, G. J., Meunier, J. M., Lindsell, C. J., and Holland, C. K. (2008). “ Tissue plasminogen activator concentration dependence of 120 kHz ultrasound-enhanced thrombolysis,” Ultrasound Med. Biol. 34, 1783–1792 10.1016/j.ultrasmedbio.2008.03.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun, T., Jia, N., Zhang, D., and Xu, D. (2012). “ Ambient pressure dependence of the ultra-harmonic response from contrast microbubbles,” J. Acoust. Soc. Am. 131, 4358–4364. 10.1121/1.4707512 [DOI] [PubMed] [Google Scholar]
- Unger, E., McCreery, T., Sweitzer, R., Shen, D., and Wu, G. (1998). “ In vitro studies of a new thrombus-specific ultrasound contrast agent,” Am. J. Cardiol. 81, 58G–61G. 10.1016/S0002-9149(98)00055-1 [DOI] [PubMed] [Google Scholar]
- Yeh, C.-K., and Su, S.-Y. (2008). “ Effects of acoustic insonation parameters on ultrasound contrast agent destruction,” Ultrasound Med. Biol. 34, 1281–1291 10.1016/j.ultrasmedbio.2007.12.020. [DOI] [PubMed] [Google Scholar]