Citrate bridges between mineral platelets in bone

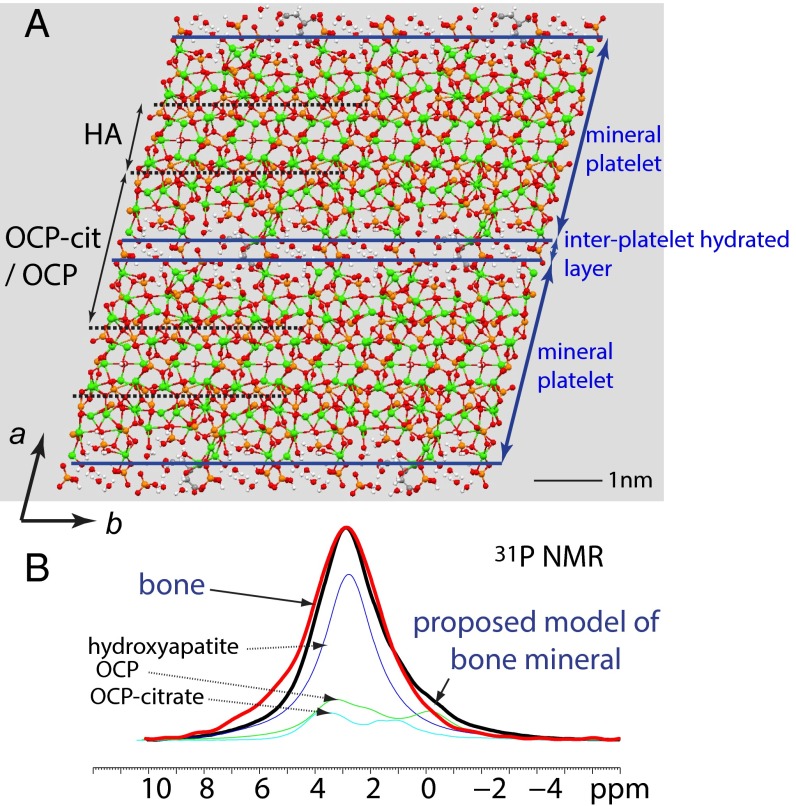
Significance

Bone contains ∼2% wt citrate; however, its role in bone remains a much-debated question. We propose a new structure for bone mineral in which citrate in hydrated layers forms bridges between mineral platelets, which can explain a number of observations at odds with previous models. The incorporation of citrate between mineral platelets can explain the flat, plate-like morphology of bone mineral platelets and may be important in controlling the crystallinity of bone mineral, which in turn, is highly relevant to the mechanical properties of bone.

Abstract

We provide evidence that citrate anions bridge between mineral platelets in bone and hypothesize that their presence acts to maintain separate platelets with disordered regions between them rather than gradual transformations into larger, more ordered blocks of mineral. To assess this hypothesis, we take as a model for a citrate bridging between layers of calcium phosphate mineral a double salt octacalcium phosphate citrate (OCP-citrate). We use a combination of multinuclear solid-state NMR spectroscopy, powder X-ray diffraction, and first principles electronic structure calculations to propose a quantitative structure for this material, in which citrate anions reside in a hydrated layer, bridging between apatitic layers. To assess the relevance of such a structure in native bone mineral, we present for the first time, to our knowledge, ¹⁷O NMR data on bone and compare them with ¹⁷O NMR data for OCP-citrate and other calcium phosphate minerals relevant to bone. The proposed structural model that we deduce from this work for bone mineral is a layered structure with thin apatitic platelets sandwiched between OCP-citrate–like hydrated layers. Such a structure can explain a number of known structural features of bone mineral: the thin, plate-like morphology of mature bone mineral crystals, the presence of significant quantities of strongly bound water molecules, and the relatively high concentration of hydrogen phosphate as well as the maintenance of a disordered region between mineral platelets.

Bone is a complex organic–inorganic composite material (1), in which calcium phosphate nanoparticles are held within a primarily collagen protein matrix. The mineral component is a poorly crystalline phase, closely related to hydroxyapatite. The currently accepted model of bone mineral is ∼50- to 150-nm-thick stacks of very closely packed apatitic platelets, each of order 2.5–4 nm in thickness (1–4), arranged so that their large (100) faces are parallel to each other and their c axes are strongly ordered (parallel to collagen fibrils) (5). NMR studies show that, in addition to the largely ordered but nonstoichiometric apatitic phase, there is a substantial, highly hydrated, disordered phase containing up to 55% of the bone mineral phosphatic ions (6, 7) but in the form of hydrogen phosphate or phosphate strongly hydrogen-bonded to water rather than apatitic orthophosphate (8). This phase has been assigned as a surface phase, but whether the surface in question is that of individual mineral platelets or the surface of the overall structure formed by a stack of such platelets is not yet clear. There is, however, significant experimental evidence that is not explained by this model as it stands. First, there has never been any observation of an isolated mineral platelet in mature bone, even in preparations in which there have been attempts to disperse the mineral structures (9). This feature suggests that the mineral platelets are not independent structures—indeed, their ordered aggregation has recently been described as a strongly bound continuum structure (2). Therefore, one must ask the question: what drives and maintains their stacked arrangement? Second, up to 28% of the water associated with bone mineral is highly organized and very strongly bound to mineral, with water hydrogens of the order of ∼2.3–2.55 Å from mineral phosphorus atoms (10). This finding is in sharp contrast with <15% of such a water population for synthetic nanoscopic, carbonated apatite models of bone mineral (10), suggesting that bone mineral somehow has an extra capacity for strongly bound water compared with synthetic apatitic models. Moreover, there is significant NMR evidence for two distinct sites for structural water in bone mineral (11). It is worth noting here that heating at 225 °C only removes 63% of the water in hydrated bone; clearly, there is a significant population of water molecules that is very difficult to remove (11). One suggestion has been that this tightly bound water occupies hydroxyl sites in the core apatitic structure (6). Although hydroxyl groups have been found to be present in bone mineral at only ∼20% of the concentration expected for hydroxyapatite (12, 13), it is difficult to see how such a model could incorporate sufficient water molecules while retaining an apatitic structure—certainly, no such synthetic material has been made. Another fact to be rationalized is that NMR shows that the hydrogen phosphate groups in bone mineral, proposed to be in highly hydrated, labile surface layers, are, in fact, relatively immobile: the ³¹P chemical shift anisotropies of these groups are comparable with those measured for mineral brushite, for instance (14), in which the hydrogen phosphate groups are static; if the hydrogen phosphate groups in bone mineral are highly mobile, their effective ³¹P chemical shift anisotropy should be significantly smaller than that for static hydrogen phosphate groups. This feature, in turn, is not consistent with the idea that the majority of hydrogen phosphate groups exist in a loosely bound, mobile hydrated surface layer. Some of the apatitic core phosphate sites are almost certain to be substituted with hydrogen phosphate, and these are likely to be relatively immobile; however, this possibility cannot account for the NMR evidence, indicating that the majority of hydrogen phosphate groups are in disordered environments, close to water, and relatively immobile. All of these data are, however, consistent with the bone mineral platelets being tightly bound to each other in their ordered parallel arrays through a more solid-like layer than previously thought, in which water (in particular) is trapped between the mineral platelets. Such a view would be consistent with the most recent evidence that water is critical for ordering mineral platelets in bone (15) as well as the notion that bone mineral is essentially a continuum structure that remains, for instance, even when the surrounding organic matrix is removed (2).

Another factor that needs to be taken into account is the presence of citrate in bone. Its presence in bone is an accepted fact, but until 2010, there was no attempt to rationalize its presence within a structural model of bone mineral. In 2010, the association of citrate with bone mineral was shown by NMR, and it was proposed that citrate was bound to the surface of bone mineral particles (16). Given the very close spacing of the mineral platelets in bone [below the resolution of even the highest resolution transmission electron microscopy (TEM) studies], there is the distinct possibility that, in fact, citrate binds between the surfaces of mineral platelets, helping perhaps to establish the continuum of platelet structures of which bone mineral is observed to consist. Critically, such a structure has the potential to explain the trapping of extra structured water in bone mineral.

With this possibility in mind, we propose here a new model for bone mineral, in which disordered citrate ions bridge between the surfaces of apatitic mineral layers or platelets in hydrated layers sandwiched between the mineral platelets. In our model, water molecules in these interplatelet hydrated layers are within 2.3–2.55 Å of mineral phosphorus atoms, which model the presence of extra structured water in bone mineral compared with model carbonated apatites (10). In our model, these hydrated layers are lined with hydrogen phosphate groups (inherently disordered because of the disordered citrate anions among them), which would account for the high proportion of such species in bone mineral. To provide a model for such a composite structure, we explore, in detail, the characteristics of a double salt octacalcium phosphate-citrate (OCP-citrate), in which citrate resides in hydrated layers, bridging between apatitic layers; to our knowledge, we propose for the first time a quantitative structure for this material using a combination of solid-state NMR spectral parameters, powder X-ray diffraction data, and first principles electronic structure calculations. The resulting structure is inherently disordered in the vicinity of the citrate ions; the ability of the citrate anion to coordinate to surrounding calcium ions through any or all of its one hydroxyl and three carboxylate groups allows it to adopt many possible orientations in the hydrated layer, with concomitant adjustments of the surrounding structure, leading to a disordered structure in and around the citrate-containing hydrated layer.

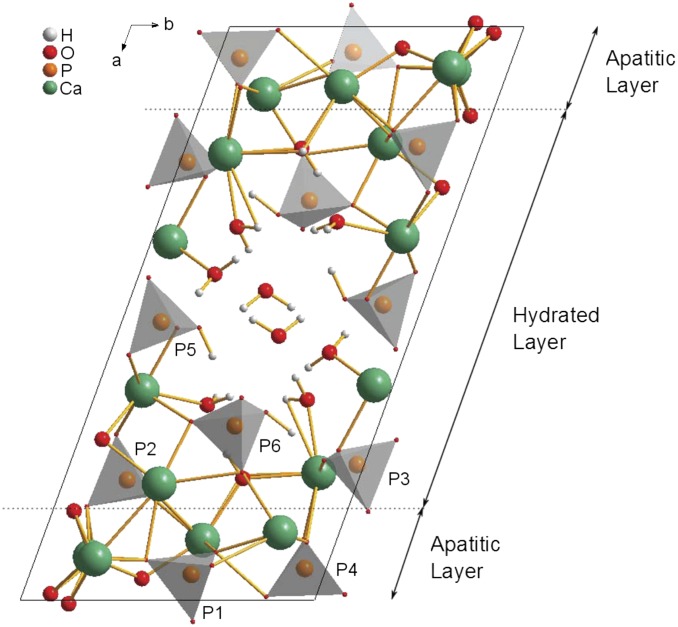
The existence of OCP-dicarboxylic acid and OCP-tricarboxylic acid double salts (the nomenclature double salt is used here in line with how these materials have been referred to in the literature previously) was first shown in 1983 (17–19), with a structural formula of Ca₁₆(HPO₄)_2.8(PO₄)₈(CIT)_0.8.16.4 H₂O, where CIT corresponds to the 3− anion, proposed for the OCP-citrate double salt on the basis of chemical analysis, with similar formulae for all other double salts characterized, albeit with varying water contents (20). Subsequently, these double salt compounds were shown to have crystallographic structures similar to the parent OCP structure (Fig. 1) by powder X-ray diffraction (XRD) (20, 21); in all cases, the unit cell of the double salt was shown to be expanded along the a axis, whereas the b and c unit cell dimensions remained largely unchanged, leading to the proposal that the organic acid anions were incorporated into the (100) plane/hydrated layer. According to the compositional formula, the organic acid anion replaces one of the hydrogen phosphate sites in the OCP structure [i.e., one of the P5 or P6 sites in the OCP structure (22) shown in Fig. 1]. Studies of the double salt structures by FTIR spectroscopy led to the conclusion that it is one of the P5 hydrogen phosphate sites that is replaced by the organic acid anion (20), a conclusion borne out by a recent detailed, multinuclear NMR study on the OCP-succinate double salt (23).

Fig. 1.

Unit cell of OCP (22) showing the numbering of the phosphate groups used here and with the regions commonly described as the hydrated layer and apatitic layers indicated. The hydrated layer contains both of the hydrogen phosphate groups (P5 and P6) and two of the orthophosphate groups (P2 and P3), whereas the remaining orthophosphate groups (P1 and P4) are found within the apatitic layer. The unit cell has close to P symmetry (i.e., centrosymmetric with no other symmetry elements).

However, despite this previous work, no quantitative structure has yet been proposed for any of the OCP double salts. In the case of the OCP-citrate structure, this state of affairs is primarily because from its powder XRD pattern, it is poorly crystalline and from IR and Raman vibrational spectroscopy, the citrate anion is disordered (20). These features are precisely what make OCP-citrate interesting from the point of view of a potential model for bone mineral, because as described above, bone mineral is poorly crystalline and contains significant atomic disorder in the surface regions of the mineral platelets (i.e., the hydrated layer between the mineral platelets in our model, where the disordered citrate ensures a disordered surface structure between mineral platelets). The lack of crystallinity in bone mineral is important—there are many biomechanical studies (24–27) that show that the degree of crystallinity of the mineral phase is of critical importance to the strength of the bone tissue, with increases in crystallinity associated with impairment in mechanical function (24). If a feature is important in a biological structure, there is generally a mechanism that has evolved to control it; here, we suggest that the presence of citrate ensures atomic disordering of the surface regions between mineral platelets, maintains a water layer between them, and prevents platelets from combining over time into larger single crystals.

To explore the potential of OCP-citrate as a model for bone mineral platelet stacks, we need to develop a structural model for the OCP-citrate double salt that takes account of its structural disorder. We then examine how well the citrate bridging, hydrated layer of OCP-citrate models the water layer between mineral platelets in bone and finally, what implications the structure of such a model has for the mechanical properties of bone.

Results and Discussion

To develop a quantitative structure for OCP-citrate, we began from the OCP structure, because all previous work and our own work shows that the OCP-citrate structure is strongly related to that of OCP. Multinuclear solid-state NMR spectroscopy was used to glean information about the environment of the phosphatic and citrate anions in the structure, which we then used to build a series of possible structural models. These models were geometry-optimized using first principles electronic structure calculations through the Cambridge Serial Total Energy Package (CASTEP) software (28–30) and the calculated NMR parameters and powder XRD patterns for the resulting optimized structures compared with experimental data to determine the plausibility of each structure (i.e., the degree to which the NMR parameters and powder XRD pattern calculated for a model structure agree with the experimental data). The true structure, because of its inherent disorder, is best described as the coexistence of a set of structures in this approach, and our ultimate goal here is to find a set of structures that defines the range of structural disorder within OCP-citrate.

Thus, we begin our discussion here with an analysis of the NMR and powder XRD structural characterization of OCP-citrate that we used to derive possible structural models for geometry optimization.

Characterization of OCP-Citrate.

OCP-citrate was synthesized and its identity was confirmed as described in Materials and Methods and SI Materials and Methods. Microanalysis of our OCP-citrate samples gave a carbon content of 3.49 ± 0.16 wt% and energy-dispersive X-ray spectroscopy gave a Ca/P ratio of 2.01 ± 0.55 (these broad compositional ranges are typical for OCP-di-/tricarboxylic acid double salts) (20, 21, 31) and a compositional formula of Ca₁₆(PO₄)₈(HPO₄)₃(HCIT).(11 ± 1)H₂O; all are in agreement with the stoichiometric approximation to the structural equation (20, 31), with one citrate anion per unit cell.

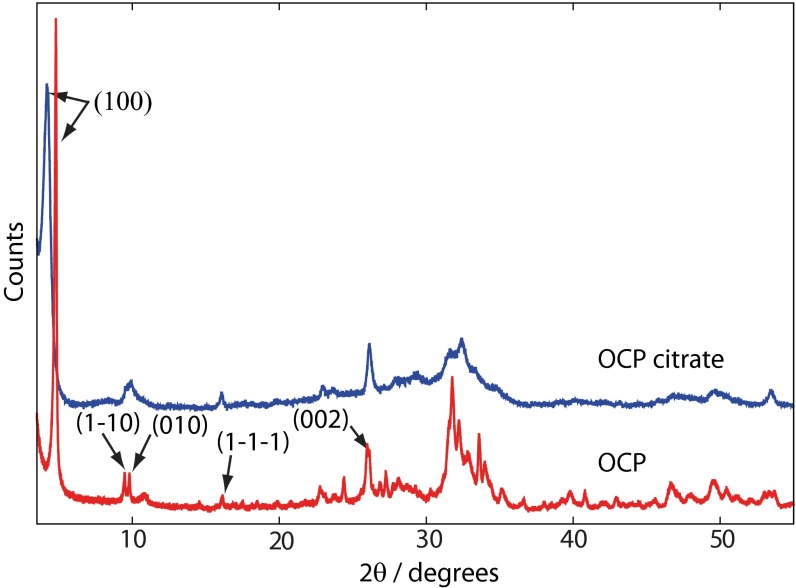
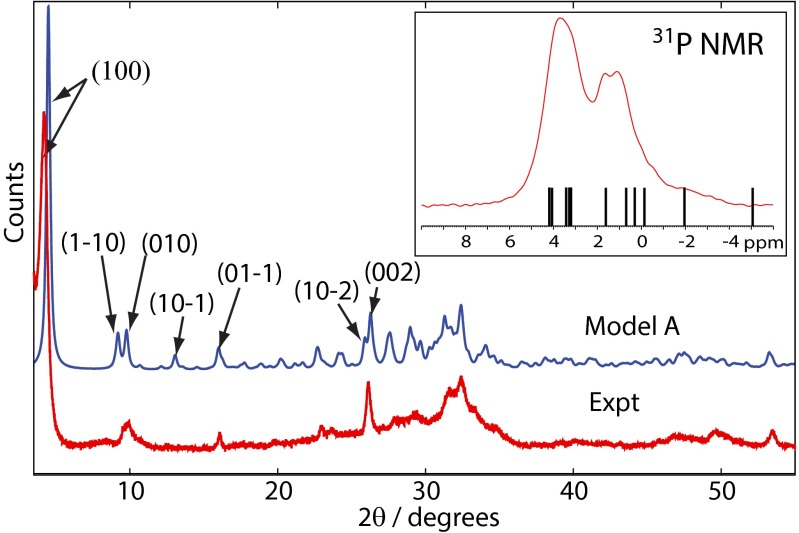
SEM and TEM (Fig. S1) show that OCP-citrate crystallizes into well-formed crystals of constant morphology (typical dimensions are 790 ± 100 nm × 100 ± 30 nm × ∼20–50 nm). The powder XRD pattern for freshly synthesized OCP-citrate is shown in Fig. 2; as found in previous work (20, 23), there is a significant shift in the scattering angle associated with the (100) reflection on inclusion of citrate: 4.85° in OCP compared with 4.09° in OCP-citrate, indicating the expansion of the OCP unit cell along the a axis to accommodate the citrate anions (d₁₀₀ = 2.16 nm for OCP-citrate; d₁₀₀ = 1.97 nm for OCP) in the (100) plane/hydrated layer of the unit cell structure. Otherwise, the powder XRD pattern of OCP-citrate is similar to that of OCP, although most of the reflections are significantly broadened compared with those for OCP, which was also found in previous work, because of poor crystallinity (20) and the thinness of the crystals. The fact that some reflections remain sharp while others are broad is most likely because of the flat, plate-like morphology of the OCP-citrate crystals, whereas differences in intensity of some of those sharp reflections compared with the equivalent ones for OCP [e.g., (002)] are most likely because the plate-like morphology of the OCP-citrate crystals prevents an isotropic distribution of crystal orientations in the powder. Indeed, selected area electron diffraction (Fig. S1) shows arcs in the Debye–Scherrer rings indicative of a nonisotropic crystal orientation distribution. Such a situation was found previously for OCP-succinate (23), where it was determined that the large flat face of those crystals corresponded to the (100) plane. The fact that there is restricted growth of the OCP-citrate crystals in the [100] direction is consistent with incorporation of citrate in the (100) plane/hydrated layer, leading to slower growth along this direction.

Fig. 2.

Powder XRD diffractograms of OCP (red) and OCP-citrate (blue). The shift of the (100) reflection from 4.85° to 4.09° between OCP and OCP-citrate, respectively, is indicative of the expansion of the OCP unit cell along the a axis resulting from incorporation of the citrate within the hydrated layer of OCP in the latter compound. The principle reflections for OCP are labeled; other signals consist of a superposition of several reflections.

It is clear from previous work and the information described above that OCP-citrate contains significant disorder. Solid-state NMR spectroscopy is an excellent technique for studying disordered materials and has previously been used to gain atomic-level insights into the structure of OCP-succinate (23), but there have been no reports of solid-state NMR spectra of OCP-citrate. The NMR spectra presented in this section are therefore shown, where appropriate, with comparable spectra of OCP.

The ¹H NMR spectrum of OCP-citrate (Fig. S2) is dominated by a broad signal centered at ∼5.5 ppm because of the water in the structure (32) and (presumably) overlies signals from citrate ¹H as well. The water ¹H signal in OCP is motionally narrowed because of the mobility of the water molecules in that structure (22, 32, 33). The 5.5-ppm signal because of water in OCP-citrate is significantly broader than the water ¹H signal of OCP (Fig. S2), indicating that the water molecules in OCP-citrate are reorienting more slowly or through a smaller amplitude (or both) compared with OCP. These findings suggest that the inclusion of citrate within the structure interferes with the water channel, which is along the crystallographic c axis in the so-called hydrated layer of OCP (Fig. 1). This conclusion is consistent with the citrate anion replacing one of the hydrogen phosphate ions that lines the water channels (17, 20) and the citrate anion protruding into the water channel.

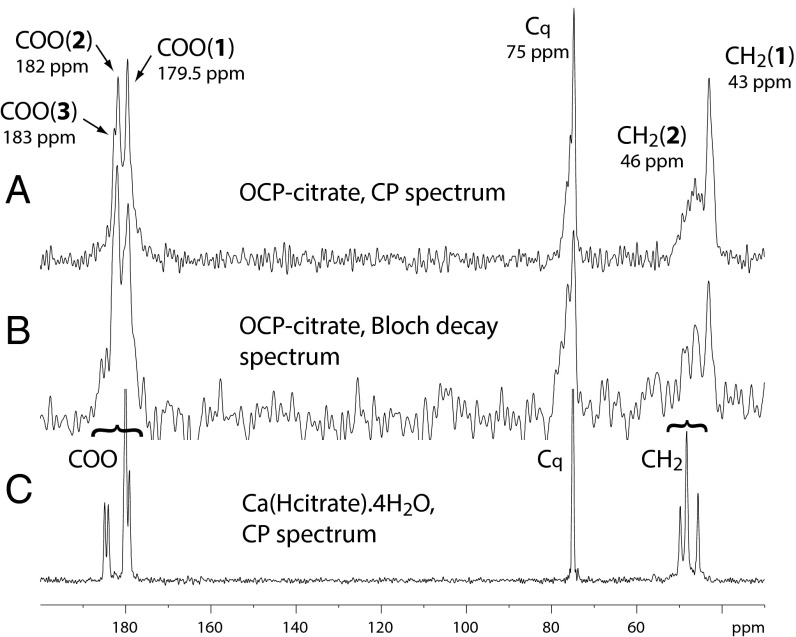
The environment and structure of the citrate anion in OCP-citrate are both readily probed by ¹³C Bloch decay (BD) and cross-polarization (CP) NMR spectra of the material (Fig. 3). The carboxylate carbons give three signals: two well-resolved signals at 179.5 and 182 ppm [labeled COO(1) and COO(2), respectively] (Fig. 3) and a shoulder at ∼183 ppm [labeled COO(3)]. The quaternary carbon (C_q) gives a signal with maximum intensity that is at 75 ppm, with a broader tail of shoulders to high frequency, whereas the methylene carbons give two signals, a sharper one centered at 43 ppm [labeled CH₂(1)] and a broader one centered at 46 ppm [CH₂(2)]. Analysis of the integrated intensities in the (quantitative) BD ¹³C NMR spectrum gives the ratio of COO:Cq:CH₂ signal intensities as ∼3:1:2, as expected given the chemical formula of citrate [C_q(OH)(COO⁻)(CH₂COO⁻)₂]. Deconvolution of the three carboxylate signals shows that they have close to equal intensity within the limits of error, and therefore, they can be assigned to the three carboxylate groups of a single citrate environment. The signals are, however, broader than one would expect for a highly ordered environment (the ¹³C spectrum of crystalline calcium citrate is shown in Fig. 3 as an example of linewidths expected for highly ordered environments); thus, it seems likely that there is some disorder or heterogeneity in these three carboxylate environments.

Fig. 3.

(A) The ¹³C CP spectrum (contact time of 1 ms) and (B) the ¹³C BD spectrum of OCP-citrate. (C) The ¹³C CP spectrum of Ca(Hcitrate).4H₂O (contact time of 3 ms) is included for comparison. The signals are labeled as discussed in the text and with the chemical shift at the maximum intensity of the signal.

The two methylene signals, CH₂(1) and CH₂(2), also have equal intensities and therefore, can be assigned to the two methylene carbons of a single citrate environment, as for the carboxylate signals. Clearly, the two methylene groups of the single citrate environment in the structure are inequivalent, which is not surprising given that the OCP unit cell and the citrate anion have incompatible symmetries: the OCP unit cell structure lacks any symmetry except a center of symmetry, and citrate is not centrosymmetric.

The disorder of the citrate anion may be static or dynamic. We investigated the possibility of dynamic disorder by cooling a sample of OCP-citrate to 200 K and rerecording ¹³C CP magic angle spinning NMR spectra. Cooling the sample to 200 K does not change the relative intensities of the CH₂(1) and CH₂(2) signals (Fig. S3), which remain 1:1 in the quantitative direct polarization ¹³C spectrum, but it significantly increases the resolution in the CP ¹³C spectrum (Fig. S3), with the broad CH₂(2) signal (46 ppm) beginning to resolve into sharper components. This observation is consistent with the citrate CH₂(2)COO(H) branch undergoing reorientational motion at room temperature and that motion being slowed by lowering the temperature so that signals from individual conformers are better resolved at the lower temperature. The fact that the CH₂(2)COO(H) branch is able to reorient dynamically strongly suggests that it is not coordinated to calcium (or any other species) but is relatively free to rotate. Because the citrate anion is contained in the hydrated layer of the OCP structure (Fig. 1), the most likely orientation of the CH₂(2)COO branch that permits relatively facile reorientation is for it to be protruding into the water layer itself. This feature will be used when constructing possible models of the OCP-citrate unit cell structure for subsequent geometry optimization. The resolution of the sharper CH₂(1) methylene signal also increases at 200 K, with a shoulder resolving on its low-frequency side, suggesting that this methylene group also has more than one possible conformation or orientation.

Lowering the temperature to 200 K (note: lowering the temperature below 200 K led to the formation of ice crystals on the sample, suggestive of water loss from the sample and thus, possible transformations of the crystal structure) also markedly increases the CP efficiency of the broad CH₂(2) (46 ppm) methylene signal (Fig. S3), the high-frequency tail of the quaternary carbon signal (75 ppm), and the low-frequency tail of the COO(1) carboxylate signal (179.5 ppm) relative to the other signals in their respective spectral regions. This finding is consistent with there being room temperature molecular motions affecting all of these carbon environments. (Molecular motion partially averages the ¹H-¹³C dipolar coupling that mediates CP and thus, reduces the CP spectral intensity; lowering the temperature reduces the amplitude of the motion and thus, the degree to which the ¹H-¹³C is reduced by the motion, resulting in larger CP intensities.) Thus, we tentatively assign the CH₂(2) and COO(1) sites as being in the same (dynamic) CH₂COO(H) branch [i.e., the COO(1) signal comes from the uncoordinated CH₂(2)COO(H) branch protruding into the hydrated layer].

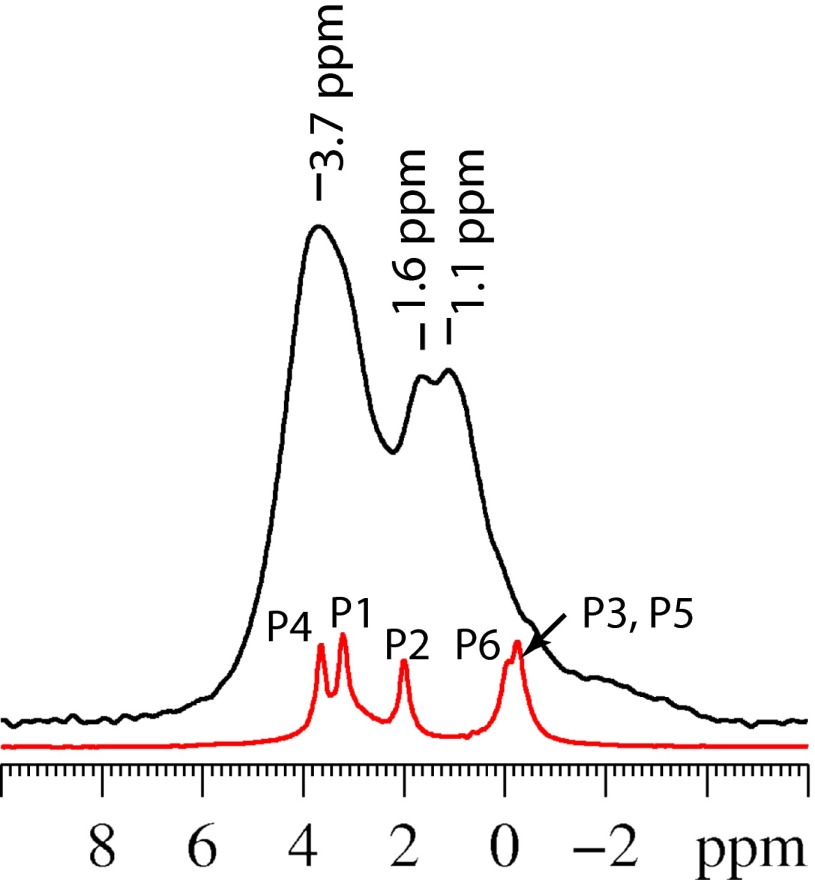
The nature of the phosphate sites in OCP-citrate and how their environment differs from that in the parent OCP compound are readily assessed by ³¹P NMR. The ³¹P NMR BD spectrum of OCP-citrate (Fig. 4) shows significantly broader lines than the corresponding spectrum for the parent OCP compound (also shown in Fig. 4 for comparison). Some reduction in the resolution of the ³¹P NMR spectrum is expected because of the lack of symmetry within the crystallographic unit cell after citrate is incorporated—it is impossible to substitute citrate into any of the phosphate sites of OCP without violating the centrosymmetric condition of the OCP unit cell, because citrate itself does not contain a center of symmetry. As a result, instead of 12 pairwise equivalent ³¹P environments giving rise to a total of five distinct ³¹P signals as in OCP, the OCP-citrate system has 11 distinct ³¹P environments within the unit cell. Nevertheless, in a highly crystalline compound, one would still expect to resolve some of the 11 expected signals or observe them as shoulders on other signals, but such resolution is lacking, indicating some disorder of the phosphate sites. Some structural disorder of phosphate sites close to the citrate anion is likely to be imposed by the conformational disorder of the dynamic CH₂COO(H) branch of the citrate; the ³¹P chemical shift is known to correlate strongly with P-O bond length (34) and is sensitive to O-P-O bond angle (35), and a small distribution of both O-P-O–bond angles and P-O–bond lengths would be expected if the neighboring citrate anion has a range of conformations. In turn, a distribution of phosphate structures/orientations close to the citrate anion will have a knockon effect for the phosphate sites more remote from the citrate, leading to some degree of line broadening for all ³¹P signals. Another source of line broadening in NMR spectra is inefficient ¹H decoupling arising from mobile ¹H; we will return to this point later.

Fig. 4.

(Black line) ³¹P BD magic angle spinning NMR spectrum of OCP-citrate. (Red line) BD NMR spectrum of OCP for comparison with assignments as previously determined (22) using the nomenclature given in Fig. 1.

Comparing the ³¹P signal frequencies between OCP and OCP-citrate in Fig. 4, there is a clear shift of the signals in the low-frequency part of the spectrum, such that the P3, P5, and P6 signals of OCP seem to have been shifted to higher frequency in OCP-citrate (Fig. 4 shows signal assignment). As described in the Introduction, the citrate anion is hypothesized to substitute for one of the P5 hydrogen phosphate sites in the OCP structure. As such, one might expect the presence of the citrate anion to perturb the ³¹P signals from the nearby P3 (formally orthophosphate hydrogen bonded to water) and P6 (hydrogen phosphate) sites that neighbor and indeed, are hydrogen bonded to the P5 sites in the OCP structure. The low chemical shifts of the P3, P5, and P6 ³¹P signals for OCP (P6, −0.1 ppm; P3 and P5, −0.3 ppm) (22) result from the strong hydrogen-bonded network that extends between all six of these groups in the OCP structure and the water molecules between them. In the OCP-citrate compound, only a small broad signal remains in the spectral region below 0 ppm, with two new, broad, overlapping signals at higher frequency (centered at 1.1 and 1.6 ppm) largely replacing the low-frequency OCP signals. Thus, we conclude that the incorporation of citrate anions into the OCP structure has, for the most part, destroyed the cooperative hydrogen bonding between the phosphatic sites of the hydrated layer that led to the low-frequency signals for those groups in OCP.

The question remains as to the assignment of the ³¹P signals at 1.1 and 1.6 ppm in OCP-citrate. ¹H-³¹P 2D heteronuclear correlation (HETCOR) spectra allow assignment of the ³¹P signals by indicating which ¹H and ³¹P sites are close in space, and ¹H-³¹P 2D HETCOR spectra for OCP-citrate (Fig. S4) show that the overlapping signals 1.1 and 1.6 ppm are correlated with both water and hydrogen phosphate ¹H signals at short mixing times (500 μs), indicating that these signals are caused by (at least in part) hydrogen phosphate sites.

The apatitic orthophosphate sites (P1 and P4) (Fig. 1) in OCP-citrate give the broad signal centered at 3.7 ppm (compared with 3.2 and 3.6 ppm in OCP for P1 and P4, respectively). The 2D ¹H-³¹P HETCOR spectrum of OCP-citrate shows a correlation between the apatitic orthophosphate sites and water ¹H, even at short mixing times, indicating that there is significant dipolar coupling between water ¹H and the ³¹P nuclei associated with these sites. We note that, given this situation, mobility of the water molecules dipolar coupled to the orthophosphate sites will affect the ¹H decoupling process for the ³¹P signals from these sites, rendering the ¹H decoupling less effective, and will undoubtedly contribute to the line broadening of their signals.

Also of interest in the 2D ¹H-³¹P HETCOR spectrum at long mixing times (10 ms) (Fig. S4) is the ¹H signal at 2.7 ppm, which we can assign to citrate methylene ¹H—useful when comparing NMR parameters calculated for trial OCP-citrate structures with experimental data later.

To complete the characterization of OCP-citrate, we determined that both water and citrate can be extracted from OCP-citrate (the latter under relatively mild conditions as described in SI Materials and Methods and Figs. S5–S7).

Constructing Structural Models of OCP-Citrate.

Our next step was to use the structural information gleaned from the NMR data discussed above, along with that from powder XRD and FTIR spectroscopy (20), to construct possible models for the unit cell structure of OCP-citrate that we then geometry-optimized.

Specifically, the structural information used in constructing possible unit cell structures is listed below.

• There is only sufficient carbon content for one citrate per unit cell.

• Citrate replaces a hydrogen phosphate site, and therefore, citrate was mainly included in the trial structures as a singly protonated 2− anion, denoted HCIT²⁻, to achieve charge balance (although 3− citrate anions were included in some models) (Table S1).

• The citrate is most likely to replace a P5 hydrogen phosphate anion [FTIR data (20)], and therefore, one (or more) P5 hydrogen phosphate anion was removed from the OCP structure.

• The hydrogen phosphate sites that can be substituted for citrate are all in the hydrated layer of the OCP structure (Fig. 1), and therefore, the citrate anion was placed in the hydrated layer in all trial structures.

• Incorporation of citrate expands the unit cell along the a axis (powder XRD).

• The OCP-citrate chemical composition has been determined here to be close to Ca₁₆(PO₄)₈(HPO₄)₃(HCIT).(11 ± 1)H₂O, although the water content is demonstrably variable.

• One CH₂COO(H) branch of the citrate (at least) is conformationally disordered and likely to be protruding uncoordinated into the water layer.

Ten possible models were geometry-optimized using first principles electronic structure calculations as implemented in CASTEP (28, 36, 37), and the NMR parameters and powder XRD patterns associated with the resulting structures were calculated; Table S1 details the eight geometry-optimized structures that give NMR parameters that are, in some way, comparable with experiment, while bearing in mind that the calculated NMR chemical shifts are those for 0 K, whereas experimental values are determined at room temperature. In addition, we took into account that the accuracy of the ¹³C chemical shifts in these calculations is ∼1–2% of the chemical shift range of ¹³C [i.e., ±(2–4) ppm] (28).

In evaluating the geometry-optimized models of OCP-citrate, a number of trends became apparent.

• NMR calculations on seven of our models showed a significant separation of the two ¹³C NMR methylene signals (∼2–12 ppm difference in chemical shift depending on the structural model) in agreement with ¹³C NMR experiments.

• In general, the CASTEP calculations indicated that the ¹³C COO⁻ signals at higher frequency are likely to correspond to Cq-COOH or Cq-COO⁻ environments rather than –CH₂COOH, consistent with reports of solution-state NMR of metal–citrate complexes (38, 39).

• To predict the effect of hydration level on the ¹³C chemical shifts, the geometry of two of the models (models A and B in Table S1) were reoptimized after inclusion of additional water molecules, and the NMR parameters were recalculated. With a single exception, the ¹³C chemical shift of all of the CH₂ and Cq environments moved to lower frequency on addition of water [Δδ(CH₂) ∼ −(3–5) ppm, Δδ(Cq) ∼ −(1, 2) ppm], and the ¹³C chemical shifts of the ¹³Cq-COO⁻ and ¹³COO_t sites moved to higher frequency [Δδ(Cq-COO) ∼ +(2–5) ppm, Δδ(CtOO) ∼ +(1–3) ppm], consistent with the experimental ¹³C NMR spectrum of the dehydrated compared with the hydrated material (SI Materials and Methods and Fig. S6).

• Structures in which one or more of the structural criteria outlined previously were ignored did not give powder XRD and NMR data consistent with experiment.

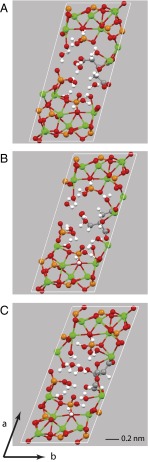
The lowest energy structure (structure A below) that fits experimental data is shown in Fig. 5A. The citrate anion in this structure has one CH₂-COOH branch dangling in the water channel of the OCP-citrate structure that is not coordinated to calcium ions but surrounded by water. This CH₂-COOH branch is primarily constrained by the presence of the (mobile) water molecules and thus, can be expected to have a distribution of rotational conformers at room temperature, giving disorder in the unit cell structure and a distribution of chemical shifts for the associated ¹³C methylene carbon signal and the quaternary carbon signal as observed experimentally. Moreover, a glance at Fig. 5A shows that the citrate anion has space around it to rock within the hydrated layer—this feature is discussed further when this model structure is compared with bone mineral.

Fig. 5.

(A) The unit cell of the model with the lowest energy structure for OCP-citrate (model A) fitting experimental ¹³C NMR and powder XRD data and with composition Ca₁₆(PO₄)₈(HPO₄)₃(HCIT).10H₂O (HCIT, HOOC.CH₂.C(OH)(COO⁻)CH₂COO⁻). Note that one of the CH₂-CtOOH⁻ branches is dangling into the water channel and not coordinated to any calcium ions. (B) Unit cell of a structure of the same composition that is 29 kJ mol⁻¹ higher in internal energy than model A (model B), in which the whole citrate anion has been rotated ∼180° with respect to the b axis (details in Table S1). (C) Unit cell of a structure of the same atomic composition but with the chemical formula Ca₁₆(PO₄)₈(HPO₄)₂(H₂PO₄)(CIT).10H₂O (model C; 83 kJ mol⁻¹ higher in internal energy than model A) (additional details in Table S1).

The calculated and experimental ¹³C chemical shifts for this structural model are compared in Table 1. Agreement between experimental and calculated chemical shifts is good, especially when one takes into account the fact that the ¹³C chemical shifts are calculated for a single 0 K structure, whereas the experimental measurement is made at room temperature, where there is, most likely, a distribution of citrate conformers and/or orientations, because the citrate anion is known from NMR to be dynamic. In particular, the lowest frequency carboxylate ¹³C chemical shift calculated, 178.6 ppm, comes from the (protonated) carboxylate group of the dangling, uncoordinated CH₂COOH branch of the citrate, and the highest frequency methylene signal calculated, 45.6 ppm from the methylene group of that same branch in structure A, both assignments as determined experimentally.

Table 1.

Comparison of the experimental ¹³C chemical shifts for OCP-citrate and those calculated for structure A

	COOH(1)	COO(2)	COO(3)	Cq	CH2(1)	CH2(2)
Experimental	179.5	182	183	75–77	42–44	44–49
Calculated	178.6	181.7	184.7	79.8	37.8	45.6

For the experimental data, the observed ranges of chemical shifts are given for the broader signals. All values are given in parts per million. The calculated chemical shifts for COOH(1) and CH₂(2) correspond to the uncoordinated CH₂COOH branch of the citrate anion in structure A.

The calculated ³¹P chemical shifts are plotted in Fig. 6, Inset with respect to the experimental ³¹P BD NMR spectrum and exhibit a distribution consistent with the experimental data. There is one outlier calculated at −5.1 ppm, which is to be expected, because this signal arises from the remaining P5 hydrogen phosphate anion in the hydrated layer that is involved in strong hydrogen bonds to surrounding water molecules. At 0 K, the temperature for which the structure and NMR spectrum are calculated, the proton in the POH group is strongly bound into the HPO₄²⁻ anion. However, at room temperature, the HPO₄²⁻ proton is exchanging with surrounding water molecules, and the P5 anion is, on average, some intermediate in structure between an HPO₄²⁻ anion and a hydrated orthophosphate (PO₄³⁻) anion; therefore, the observed room temperature signal will be a time average of a HPO₄²⁻ signal (∼−5 ppm) and a hydrated orthophosphate (∼2 ppm). A similar phenomenon was observed in the parent OCP structure (22) with respect to the ³¹P chemical shifts of hydrogen phosphate and orthophosphate groups strongly hydrogen bonded to water. The ranges of ¹H chemical shifts for each hydrogen environment for the structural model in Fig. 5A is given in Table S2 and are consistent with those ranges expected (38, 39), although lack of resolution in the ¹H spectrum precludes detailed comparison; we note, however, that the citrate methylene ¹H chemical shift (average) is calculated to be 2.9 ppm (±0.4 ppm SD), which compares well with the experimental value of 2.7 ppm found from the ¹H-³¹P HETCOR experiments (Fig. S4).

Fig. 6.

Experimental powder XRD diffractogram of OCP-citrate (red) and calculated powder XRD pattern (blue) for model A (Fig. 5A) assuming a preferred crystal orientation of (100). Selected reflections are labeled; remaining signals are superpositions of several reflections. (Inset) Calculated ³¹P chemical shifts for the OCP-citrate model A structure are shown marked with lines relative to the experimental ³¹P BD NMR spectrum.

Comparison of the powder XRD pattern for structural model A is shown in Fig. 6 and agrees well with the experimental pattern, except that the (100) reflection in the calculated pattern seems at higher 2θ than in the experimental pattern (i.e., the a unit cell parameter is smaller in structural model A than in the experimental structure). This discrepancy is to be expected, because model A is a structure calculated at 0 K, whereas the experimental XRD measurement is at room temperature, and we would expect some unit cell expansion between 0 K and room temperature. There are some other discrepancies, but they are small, especially in view of the uncoordinated CH₂COOH branch of the citrate anion being conformationally disordered at room temperature, and each of those conformations is likely to be associated with a different spatial distribution of surrounding phosphate and calcium ions—in other words, the room temperature structure is, in fact, a dynamic combination of multiple structures.

Interestingly, a second structure (structure B) (Fig. 5B) with the same chemical composition as A and only a slightly less favorable internal energy (by 29 kJ mol⁻¹), in which the citrate anion is flipped ∼180° with respect to the b axis relative to structure A, also yields calculated ¹³C chemical shifts consistent with experiment, indicating that the citrate disorder may involve a set of quite different citrate orientations as well as librations and changes of conformation. A third structure (structure C) (Fig. 5C), 83 kJ mol⁻¹ higher in energy than A with the same atomic composition but the chemical formula Ca₁₆(PO₄)₈(HPO₄)₂(H₂PO₄)(CIT).10H₂O, gives ¹³C NMR chemical shifts for the citrate anion that are consistent with those shifts observed experimentally for partially dehydrated OCP-citrate. Structure C is a much more compressed structure; the hydrated layer is partially collapsed so that the citrate anion is wedged between the apatitic layers. This sort of structural collapse is a plausible model for a structure undergoing removal of water from the hydrated layer and likely to be typical of the citrate environment found in the dehydrated material.

Evidence for an OCP-Citrate–Like Phase in Bone Mineral.

The association of citrate with the mineral component of bone was previously shown with NMR by a ¹³C{³¹P} Rotational Echo DOuble Resonance (REDOR) NMR experiment (16). This experiment identifies the carbon species in close spatial proximity to phosphorus, and because the vast majority of phosphorus in bone is in the mineral component, the experiment effectively identifies the organic species in closest proximity to the mineral.

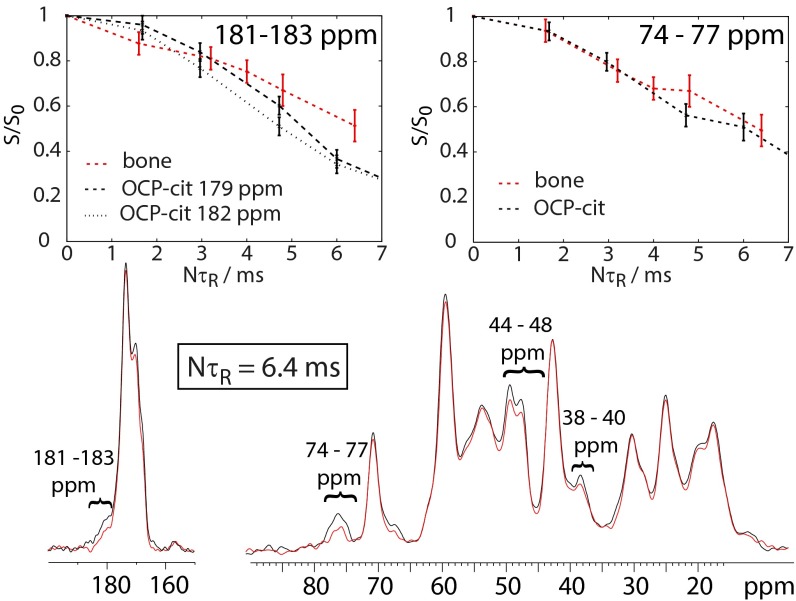
Fig. 7 shows the ¹³C{³¹P} REDOR behavior of adult horse limb bone. In such spectra, signals in the REDOR spectrum (red) that are dephased (reduced in intensity) relative to the reference spectrum (black) are caused by ¹³C sites close in space to ³¹P (i.e., mineral). For the bone sample, there is, as observed previously by us and others (16, 40, 41), clear dephasing in the 180- to 183-, 73- to 77-, 44- to 48-, and 38- to 40-ppm regions (Fig. 7) of the spectrum, which corresponds closely to the signal frequencies for citrate in OCP-citrate. [The other signals that show (small) dephasing for bone can all be assigned to lysine and hydroxylysine, which in bone collagen, are glycosylated with galactosyl and glucosyl galactosyl. These sugar species, and others, also contribute to the signal in the 74- to 77-ppm region of the spectrum and presumably account for the stronger dephasing of this signal than the signals assigned to citrate methylene carbons.] Fig. 7 also compares the extent of REDOR dephasing in OCP-citrate with that for the spectral regions in bone where citrate signals are expected. Exact correspondence cannot be expected, because the citrate signals in bone are overlaid with signals from other bone components that are unlikely to be as close to bone mineral as the citrate, and the REDOR dephasing curves (Fig. 7, Upper) are the sum of such curves over all ¹³C sites giving signals in the specified frequency range. Nevertheless, these comparisons show that it is plausible that the citrate environment in bone is similar to that in OCP-citrate. Comparison of REDOR dephasing curves for the lowest energy structural models of OCP-citrate is shown in Fig. S8 for completeness (along with an assessment of how citrate mobility might affect REDOR dephasing).

Fig. 7.

(Lower) ¹³C{³¹P} REDOR spectrum of adult horse limb bone for a 6.4-ms REDOR dephasing time. Signals reduced in intensity (dephased) in the REDOR spectrum (red) with respect to the reference spectrum (black) are caused by ¹³C carbons close in space to phosphorus (i.e., bone mineral). The spectral regions that suffer significant dephasing and are referred to in the text are indicated. (Upper) REDOR dephasing curves as a function of dephasing time (Nτ_R) for equine bone and OCP-citrate for the signals indicated. S, REDOR spectral intensity; S₀, reference spectral intensity (each integrated over the spectral frequency range given in the top right in each plot).

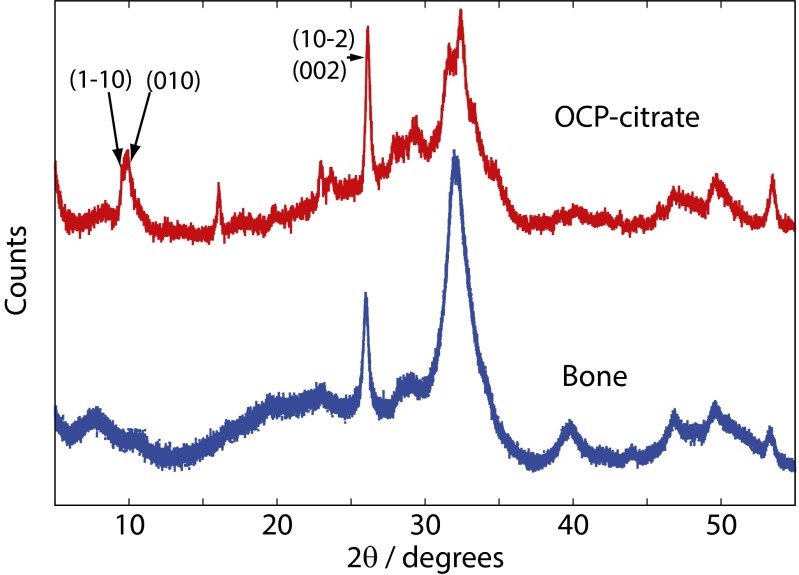
Additional evidence for an OCP-citrate–like structural arrangement in bone comes from powder XRD. Fig. 8 compares the powder XRD patterns for OCP-citrate and bone (fresh rabbit bone); there are clear similarities between the two powder patterns and that for OCP-citrate, mirroring all of the main features of the bone powder XRD pattern.

Fig. 8.

Comparison of the experimental powder XRD diffractograms of OCP-citrate (red) with fresh rabbit limb bone (natively hydrated; blue).

How could an OCP-citrate structure be incorporated into bone mineral? Bone mineral consists of stacks of very closely spaced mineral platelets. The spacing between mineral platelets in their stacks in bone is difficult to determine, because it is below the resolution of even high-resolution TEM imaging. A recent study (3) quoted it as being less than 0.1 nm, although this value too is below the resolution of that study (0.18–0.34 nm). OCP-citrate mirrors the bone mineral structure of very closely spaced mineral platelets; in OCP-citrate, the apatitic layers are separated by only a thin hydrated layer (of order of ∼5 Å, depending on exactly how the boundaries of the hydrated layer are defined), a gap small enough that citrate can bridge across it. In fact, in model structure A, the P5 HPO₄²⁻ anion also bridges across the hydrated layer, and therefore, the hydrated layer of OCP-citrate models well what has been observed by high-resolution TEM in terms of the lack of separation between mineral platelets. However, bone mineral undeniably has a significant component with a structure related to hydroxyapatite (albeit with many substitutions), and although OCP-citrate has an apatitic layer, it is not large enough to account for the amount of apatitic mineral in bone. It is well-known that hydroxyapatite and OCP can form an epitaxial interface with the minimum of interfacial energy (42, 43) between the (200) plane of hydroxyapatite and the (100) plane of OCP. Hydroxyapatite layers could be incorporated within the apatitic layers of OCP-citrate in a similar manner to form thicker mineral platelets. The thickness of bone mineral platelets has been previously estimated by NMR to be ∼2.5 nm (44). The thickness of the mineral layer in OCP-citrate between its hydrated layers is 1.2–1.4 nm. Adding one unit cell of hydroxyapatite to the (100) plane of OCP-citrate (i.e., intersecting the OCP-citrate structure with a unit cell of hydroxyapatite, which has a thickness of 0.95 nm along its a dimension) would create mineral platelets with a thickness, of ∼2.2 nm. The most recent measurements of bone mineral platelet thickness by a combination of TEM methods (3) suggest average platelet thickness is ∼5 ± 2 nm, which agrees with previous measurements of ∼4 nm (4). Thicker mineral platelets could be formed in our model simply by addition of more unit cells of hydroxyapatite into the OCP-citrate structure; for instance, addition of a four-unit cells layer of hydroxyapatite to the (100) plane of OCP-citrate would give a platelet thickness close to 5 nm.

The structure of such a model with addition of a one-unit cell layer of hydroxyapatite to the (100) plane of OCP-citrate is shown in Fig. 9 based on the known citrate content of bone (SI Materials and Methods), which suggests that there will be of order one citrate anion per three unit cells of hydroxyapatite. Thus, in the structural model of Fig. 9, with just a single layer of hydroxyapatite unit cells added into the OCP-citrate structure, only one-third of the OCP-citrate unit cells have citrate in them, and the remaining two-thirds of the hydrated interface between the mineral platelets are being modeled with an OCP-like structure, elongated to match the OCP-citrate unit cell dimensions (i.e., OCP-citrate without citrate). Fig. 9 also shows what the ³¹P NMR spectrum of the proposed hydroxyapatite-OCP-citrate material might look like based on experimental ³¹P NMR spectra for its pure components [i.e., hydroxyapatite, OCP-citrate, and (disordered) OCP; note that a thicker layer of hydroxyapatite inserted into the OCP-citrate structure would result in a greater proportion of the OCP-citrate unit cells containing citrate and less OCP-like structure being present] and shows a closely similar chemical shift distribution to that of bone mineral. [Note: the calculated ³¹P NMR spectrum does not take account of the many ionic substitutions in bone mineral (in particular, carbonate) that affect the ³¹P NMR spectrum (45) or the fact that the interface regions between the hydroxyapatite, OCP, and OCP-citrate unit cells will have modified structures from the pure compounds and thus, different ³¹P chemical shift distributions from the pure compounds used to produce the hypothetical ³¹P NMR spectrum for our proposed bone mineral model.]

Fig. 9.

(A) The model proposed for bone mineral consisting of unit cells of OCP-citrate split along (200) and sandwiching unit cells of hydroxyapatite (HA), resulting in a parallel arrangement of mineral platelets alternating with hydrated layers (the hydrated layers of the OCP-citrate cells). Only one in three of the OCP-citrate cells contains citrate; remaining ones are modeled here with OCP with a unit cell expanded to match that of OCP-citrate. Blue lines indicate the surfaces of the mineral platelets (defined so that all calcium ions are contained within the mineral platelets), which are bridged by citrate anions. In practice, the position and orientation of the citrate anions in the hydrated layers will be disordered. (B) Comparison of the ³¹P NMR spectra of bone (red) and the proposed model of bone mineral described in A (black) formed by summing the experimental ³¹P NMR spectra for pure hydroxyapatite (dark blue), OCP-citrate (green), and OCP (light blue) in the total intensity ratio of 3:1:2. The experimental spectra of hydroxyapatite and OCP have 200 Hz Gaussian line broadening applied to simulate disorder in the model structure.

A model of bone mineral consisting of closely packed mineral layers bridged by citrate and separated by water (and hydrogen phosphate ions) naturally explains a number of significant observations: that there is extra structured water in bone mineral compared with synthetic models of bone mineral, that bone mineral contains substantial amounts of relatively immobile but disordered hydrogen phosphate, and that bone mineral is deficient in hydroxyl groups compared with a purely apatitic structure. Most importantly, it can provide an explanation for the platelet morphology of bone mineral crystals, for which there has previously been no satisfactory explanation (46). In OCP-citrate, the presence of citrate anions in the (100) plane of the structure inhibits growth of the mineral in the a direction, which leads to the flat platelet morphology of the OCP-citrate crystals. In the same way, binding citrate anions between the (100) faces of bone mineral crystals would inhibit growth of those crystals in the a direction and lead to the (100) faces being the large face of the platelets, which is, indeed, observed (5). Furthermore, the presence of citrate between the mineral platelets would maintain segregation between mineral platelets if only through a disordering of the atomic structure in their vicinity. If it were not the case, loss of water from between the mineral platelets would allow transformation over time, whereby neighboring platelets combine to form a larger single crystal, which in turn, could have disastrous consequences for the mechanical properties of bone. As discussed in the Introduction, the mechanical properties of bone depend on the crystallinity of the mineral component, with greater crystallinity and larger mineral crystals associated with greater fragility. In this model, the incorporation of citrate naturally restricts the degree of crystallinity and size of the mineral particles, and indeed, it could be the biological mechanism for controlling the crystallinity. One last point to mention is that the presence of citrate binding between mineral platelets could explain why, although TEM and SEM reveal apparently separate mineral platelets, those mineral platelets form a continuum of structure, robust enough to withstand removal of the surrounding protein matrix, grinding, and sonication (9).

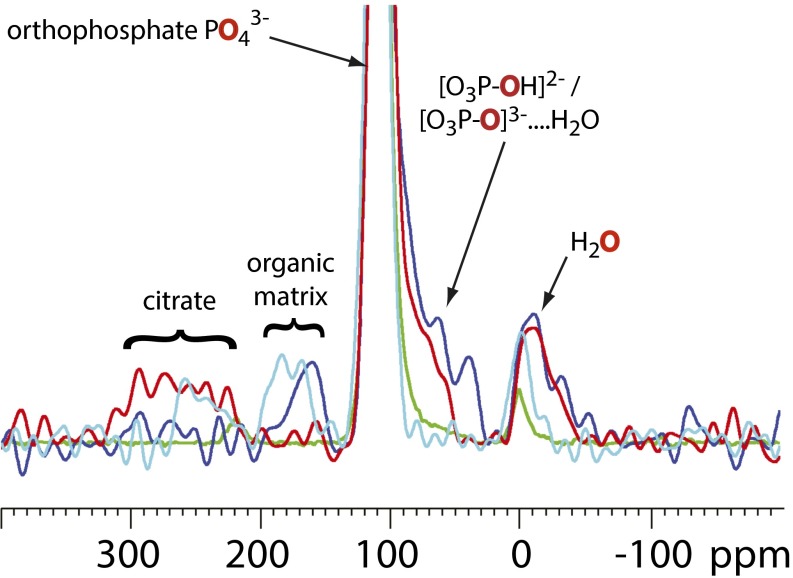
Finally, there is an abundant atomic species in bone mineral that, to the best of our knowledge, has yet to be used in the study of bone mineral structure, namely oxygen; ¹⁷O is the only NMR-active isotope of oxygen, and it is a quadrupolar nucleus (I = 7/2) with low natural abundance, but its NMR spectra are accessible at high field. ¹⁷O NMR is a potentially valuable tool, because the mineral phosphate oxygens are likely to be highly sensitive reporters of the phosphatic environment. To this end, Fig. 10 compares ¹⁷O double frequency sweep NMR spectra for bone with those of (5% ¹⁷O-enriched) hydroxyapatite, bone mineral soaked in citric acid, and OCP-citrate. Apatitic orthophosphate signals are expected in the 90- to 120-ppm range, whereas hydrogen phosphate OH ¹⁷O will be much lower, around 60–90 ppm, and hydrated orthophosphate will be somewhere between these two regions. It is clear that neither hydroxyapatite nor citrated bone mineral gives spectra comparable with bone in this crucial region of the spectrum (crucial because it is the presence of acidic and hydrated phosphate groups in bone mineral that distinguishes it from pure hydroxyapatite mineral). OCP-citrate, however, provides a far better match to the ¹⁷O NMR spectrum of bone.

Fig. 10.

¹⁷O Double frequency sweep NMR spectra of (fresh) sheep bone (blue), OCP-citrate (red), 5% ¹⁷O-enriched hydroxyapatite (green), and bone mineral soaked in aqueous citric acid (cyan). The individual spectra have been scaled so that the magnitude of the apatitic orthophosphate peak (truncated) is equal to that from bone to compare the relative nonapatitic phosphate populations. The oxygen site giving rise to each signal is highlighted in red. The signals below 0 ppm are caused by water, and those signals above 150 ppm are caused by organic compounds (the organic matrix in the bone samples and citrate in OCP-citrate and the bone soaked in aqueous citrate) as indicated.

Conclusions

We have proposed a new model for bone mineral, in which citrate ions are incorporated into the mineral structure in hydrated layers, binding between mineral platelets in a manner akin to the model compound OCP-citrate. The binding of citrate ions between bone mineral platelets can account for many well-known structural features of bone mineral, such as the presence of significant quantities of both strongly bound structural water and disordered but relatively immobile hydrogen phosphate ions in addition to the expected orthophosphate of pure hydroxyapatite. It can account for why the stack of mineral platelets in bone forms a continuum of structure that remains even when the surrounding protein matrix is removed and the mineral is subjected to sonication.

Critically, incorporation of citrate into the hydrated layer of an OCP-like structure in the model compound OCP-citrate acts to restrict the growth of the mineral crystals in the a direction and therefore, produce a flat, plate-like morphology; a similar process with citrate binding between the surfaces of mineral platelets in bone can account for the similar flat platelet morphology of bone mineral crystals as well as their propensity to form stacks. The conformation and/or spatial orientation of citrate in the model mineral structure is disordered, and a similar situation in bone mineral would ensure that the atomic structure around the citrate ions, namely the surfaces of the mineral platelets, is also disordered, which in turn, ensures a gap of disordered (and hydrated) material between mineral platelets and prevents the formation of large single crystals that would be detrimental to bone mechanical properties. The degree of incorporation of citrate into bone mineral could be important in explaining the changes to bone mineral crystallinity in metabolic diseases (25) and understanding the mechanical properties of bone at a molecular level.

Materials and Methods

Synthesis.

OCP-citrate was prepared using a previously published synthetic procedure (31) starting from α-tricalcium phosphate [Ca₃(PO₄)₂]. Full details (including synthesis of OCP) are given in SI Materials and Methods.

Bone Samples.

Rabbit bone.

Sample was taken from the femur bone of a female rabbit approximately 6 mo old. Before cryomilling, sample was stored in liquid nitrogen.

Adult horse bone.

Horse limb cortical bone was taken from an adult horse used for general purpose exercise that was euthanized for humanitarian reasons unconnected with this work.

All bone samples were cryomilled before being packed into NMR rotors. Before cryomilling, samples were stored at −80 °C.

Density Functional Theory Calculations.

Working models of the OCP-CIT structure were created using the PyMOL Molecular Graphics System, version 1.3 (Schrödinger, LLC). These models were then geometry-optimized using CASTEP, version 5.502 (conditions as per optimization of OCP) (22).

Details of physical measurements are contained in SI Materials and Methods.