Polydispersity-driven topological defects as order-restoring excitations

Significance

Defects play an essential role in many aspects of materials. To actively introduce defects and to understand their roles in affecting the crystallinity constitutes fundamental problems in materials science. In this paper we report the introduction of topological defects by size polydispersity. Size polydispersity is usually an inevitable feature of a variety of real systems. It is important in several research fields to know how size polydispersity affects the degree of crystallinity and enhances mechanical properties of materials. In this study, the defects are found to be order-restoring excitations protecting the crystalline order. Moreover, they are shown to be crucial for the attraction of impurity particles. The disclosed mechanism may lead to engineering defects by size polydispersity.

Abstract

The engineering of defects in crystalline matter has been extensively exploited to modify the mechanical and electrical properties of many materials. Recent experiments on manipulating extended defects in graphene, for example, show that defects direct the flow of electric charges. The fascinating possibilities offered by defects in two dimensions, known as topological defects, to control material properties provide great motivation to perform fundamental investigations to uncover their role in various systems. Previous studies mostly focus on topological defects in 2D crystals on curved surfaces. On flat geometries, topological defects can be introduced via density inhomogeneities. We investigate here topological defects due to size polydispersity on flat surfaces. Size polydispersity is usually an inevitable feature of a large variety of systems. In this work, simulations show well-organized induced topological defects around an impurity particle of a wrong size. These patterns are not found in systems of identical particles. Our work demonstrates that in polydispersed systems topological defects play the role of restoring order. The simulations show a perfect hexagonal lattice beyond a small defective region around the impurity particle. Elasticity theory has demonstrated an analogy between the elementary topological defects named disclinations to electric charges by associating a charge to a disclination, whose sign depends on the number of its nearest neighbors. Size polydispersity is shown numerically here to be an essential ingredient to understand short-range attractions between like-charge disclinations. Our study suggests that size polydispersity has a promising potential to engineer defects in various systems including nanoparticles and colloidal crystals.

The curiosity of human beings regarding crystals can be traced back to Ancient Greece when Theophrastus, a student of Aristotle, adapted the idea of atoms developed by Democritus et al., to explain the formation of crystals in his treatise, On Stones (1). The inquiry into the remarkable ability of interacting elementary units to spontaneously form regular structures, the mechanism of crystallization, has lasted until now (2–4). In the past decades, much effort has been directed to 2D crystals on spatially curved surfaces and such systems have exhibited features not found in the corresponding phase for planar or flat space systems (4, 5). The richest confluence of theoretical and experimental ideas in the area of 2D crystals has significantly enhanced our understanding of crystallization (3, 6). Specifically, topological defects have been identified as an essential ingredient to impair regular crystalline order (4, 5, 7), and they are found to be highly involved in many physical processes, notably in 2D crystal melting (8–10). The elementary topological defects in 2D hexagonal lattices are disclinations, which are vertices surrounded by n nearest neighbors with 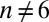. The disclinations disrupt the local order of sixfold rotational symmetry and appear as points of local n-fold symmetry. Elasticity theory has demonstrated an analogy of the interaction between disclinations to the interaction between electric charges by associating a charge 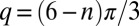to a disclination, which is positive if 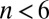and negative if 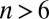, with attraction between oppositely charged disclinations and repulsion among like-charge disclinations. Disclinations are building blocks for a variety of defect motifs such as dislocations (5, 7), scars (11), and pleats (12). Recently, crystalline colloidal arrays confined on capillary bridges with variable Gaussian curvatures have been studied experimentally and theoretically (12–14). The fascinating particle fractionalization event is observed where an interstitial is fissioned into two dislocations (topological dipoles composed of a pair of oppositely charged disclinations) that are later absorbed by other defects; in this event the role of defects switches from order disrupting to order restoring (14). Moreover, the practical application of defects in 2D materials is well exemplified by a previous study where extended defects are introduced into the graphene lattice to control the charge distribution serving as a metallic wire; such wires might be potential building blocks for atomic-scale, all-carbon electronics (15).

Previous studies mainly focus on the curvature-driven defects in 2D crystals where the interacting particles are identical and evenly distributed on curved surfaces (4, 5, 11, 12). Recent work shows that even on flat geometries topological defects can be introduced via the long-range interaction-driven density inhomogeneity in the otherwise regular particle arrays (16), suggesting the intimate relation between the topological defects and the spatial variation of the distance between neighboring particles. We are therefore led to using size polydispersity to introduce density inhomogeneity and thus the topological defects; this routine is more direct and easier to manipulate in comparison with using long-range potentials. Nonuniform size of particles in contact naturally introduces the spatial variation of density. It is straightforward to see that in the condensation of particles to form 2D crystals, the coordination number of larger particles surrounded by identical smaller particles tends to exceed six, destroying the regular hexagonal crystalline lattice. Practically, size polydispersity is an important, usually inevitable feature of a variety of real systems such as granular materials (17), nanoparticles (18), and colloidal crystals (19). It can significantly influence the physics in many aspects including crystallization (20), granular dynamics (21), and adsorption (22), and may even kinetically inhibit the formation of regular phases (18).

The fabrication of soft particles including colloids and nanoparticles with functionalized surfaces (23–25), nanogel-colloids (26–28), as well as the extensive use of micelles and amphiphilic self-assembled fibers (29) to create materials with unique properties, has opened new fundamental questions regarding topological defects and polydispersity effects in systems with soft potential interactions. An ideal deterministic hard-disk model with controllable amount of particles with the “wrong” size has been proposed to study topological defects in polydispersed systems; the geometric rule organizes the growth of the cluster of hard disks during which topological defects are developed (30). The softening of the hard-sphere potential creates richer energy landscapes that allow the system to explore various energy basins. It is of interest to study the effect of such a relaxation on topological defect structure. Indeed, soft particles represent an important class of materials used to generate several non–close-packed crystalline structures inaccessible via the excluded volume interaction (31).

In this work, we study the topological defect structures in a 2D model system of soft spherical particle arrays. Through a simulated annealing Metropolis Monte Carlo simulation procedure (32), we observe the transition of the stress distribution around the impurity particle from an isotropic to a branched pattern. To release the accumulated stress, topological defects finally proliferate when the size of the impurity particle exceeds some critical value. With further expansion of the impurity particle, the defect motif evolves from neutral quadrupole to trapped disclination at the site of the impurity. In polydispersed particle systems, we identify a distinct screening mode from that in identical particle arrays on curved surfaces (33). This screening scenario is phenomenologically similar to the screening of electrically charged entities by counterions in electrolyte solutions. By pushing this analogy further, we find the short-range attraction between trapped like-charge disclinations mediated by the nearby topological charges. Moreover, we demonstrate that size polydispersity is able to transform a square lattice to a hexagonal lattice; the featured screening mode is also found in the resulting defective hexagonal lattice. Our study suggests the utility of size polydispersity to precisely control the locations of disclinations and the implications to realizing flexible engineering of defects in 2D systems that can find potential applications in relevant contexts.

Results and Discussion

The model system is composed of elastic spherical particles confined on a flat surface. According to classical elasticity theory (31, 34), the elastic energy penalty associated with an axial compression of two deformable spheres conforms to a power law whose exponent is 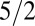, i.e., the Hertz potential:

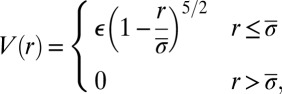where 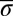is the average diameter of the two contact particles, r is the interparticle distance, and the energy scale ϵ is set to be unity in simulations. The Hertzian model has been used to disclose rich phases in the packing of soft particles confined on interfaces (31). To highlight the topological defects solely induced by impurity particles, we prepare a stress-free and defect-free initial state where all of the particles with a uniform diameter 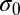sit on the lattice sites of a 2D hexagonal or square crystal whose lattice constant is 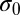, i.e., any particle is mutually circumscribed with its nearest neighbors. To introduce size polydispersity, we pick up a particle from the constructed crystal patch and change its size to 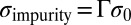. For each given Γ, we perform annealing Monte Carlo simulation to identify the low-energy configuration. The technical details of the algorithm are presented in SI Text. In simulations, the particles are confined within the hexagonal or square walls. Note that an impurity particle only modifies the arrangement of nearby particles as observed in simulations; the regular crystalline lattice beyond a modest distance from the impurity particle is observed to be well protected by the induced topological defects. The boundary effect is therefore negligible for all crystal patches analyzed in this work considering that the particles near the boundary are immobile in the energy relaxation processes (the underlying reason is presented in the discussion of Fig. 2). To further confirm that the influence of the boundary on the response of the system to impurity particles can be excluded, we perform simulations using the alternative periodic boundary condition and the key results are reported in SI Text. Therefore, the behaviors of the system are critically controlled by the parameter Γ and are independent of the total number of particles N. In small crystal patches, the boundary may interact with the impurity particles. Although of intrinsic interest as a boundary-driven phenomenon, it is not our primary focus in this work.

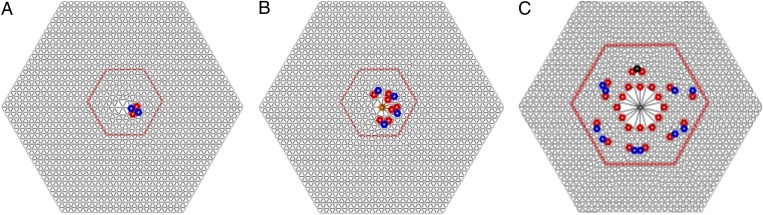
Fig. 2.

Growing impurity particle size leads to the emergence of topological defects. The vertices in the plot represent the centers of particles, and the disclinations are indicated by colored dots; red for fivefold disclination, blue for sevenfold disclination, black for eightfold disclination, and orange for ninefold disclination. These topological defects impose confinement on the propagation of the defective region and thus protect the larger hexagonal lattice beyond the red boxes. (A) 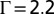, (B) , and (C) 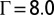. The topological charges at the central impurity particles are (A) 0, (B) 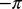, and (C) 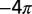, respectively. The number of particles is .

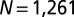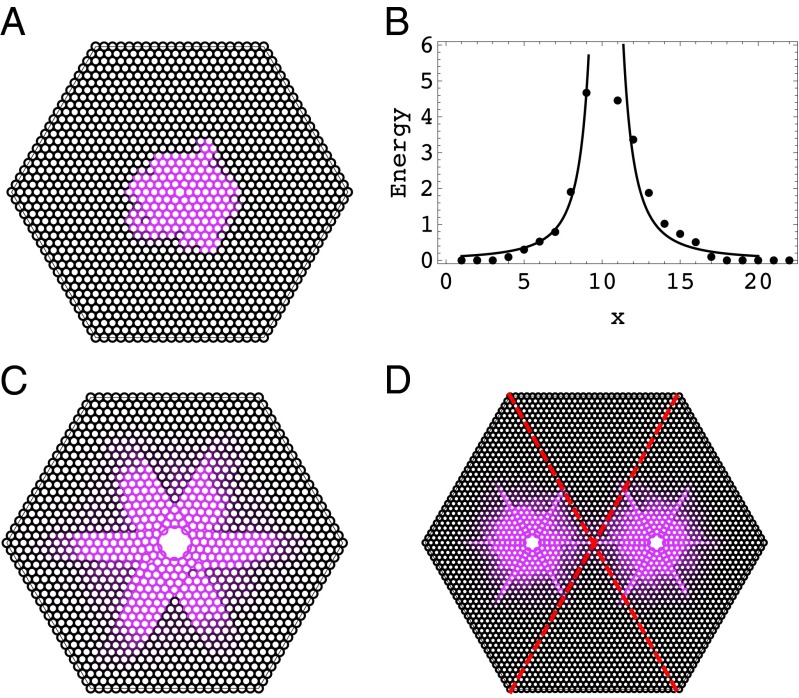
Simulations indicate that in response to the increase of the size of the central impurity particle, the hexagonal lattice system experiences elastic and plastic deformations in sequence, characterized by the appearance of topological defects. The distribution of the strain energy is almost isotropic for 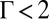. Fig. 1A shows the stressed region (purple) for 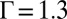. The angularity and protrusions in the pattern may be attributed to the discreteness of the system. Fig. 1B shows the energy of individual particles on the horizontal line passing through the impurity particle in Fig. 1A, where the impurity particle is located at 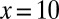. The spatial variation of the particle energy is well fitted by the power law 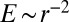, where r is the distance from the central impurity particle. The total energy versus the system size therefore follows a logarithm law. According to the continuum elasticity theory, the elastic energy created by dislocations also conforms to the logarithm law, suggesting that the effect of the impurity particle in our system is similar to that of dislocations (4). In contrast, the elastic energy of a disclination increases with the system size in a square law (4).

Fig. 1.

Impurity particles represented by circles of larger sizes induce stresses on surrounding particles which are colored. The branching of the stressed colored region occurs as Γ increases from 1.3 (A) to 4.0 (C). The decay of the particle energy away from the central impurity particle is plotted in B for the system A, where 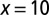prescribes the location of the impurity particle. The energy, which is measured in the unit of ϵ defined in the expression for the Hertz potential, is rescaled by a factor of 10⁴, and the x axis is in the unit of 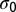. The two curves conform to a power law. The branched structures around two impurity particles are shown in D for 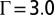. The number of particles is 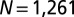(A and C) an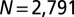d (D).

As the value for Γ exceeds about 2.5, we find an obviously branched stressed region with the sixfold symmetry; this is a solution beyond the isotropic solution in continuum elasticity theory (34). Fig. 1C shows the case of 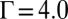. We notice that the stress almost vanishes at the tips of the arms. The influence of the boundary on the stressed region is therefore negligible. These symmetric branched patterns are also found in systems whose size ranges from N = 331 to N = 2,791. In addition, we introduce two impurity particles, as shown in Fig. 1D, and find that the associated branched patterns surrounding each impurity particle are almost uncorrelated beyond a modest distance. The two rhombic patches separated by the dashed lines in Fig. 1D can therefore be regarded as independent crystals. The orientation and symmetry of the pattern is preserved in both hexagonal and rhombic boundary shapes regardless of the position of the impurity particle. These numerical observations indicate the robustness of the symmetric branched structure. The sixfold symmetry of the branched pattern seems to originate from the local hexagonal arrangement of particles around the impurity particle; in simulations of square lattices we observe stressed regions of fourfold symmetry.

The growing central impurity particle finally leads to irregular rearrangement of nearby particles, as shown in Fig. 2 A–C where the connected dots represent the centers of particles. These irregularities are analyzed in terms of topological defects by introducing the Delaunay triangulation (35). The appearance of topological defects signifies the occurrence of plastic deformations. Fig. 2 A–C shows that an impurity particle locally disturbs the lattice; the red hexagonal boxes in Fig. 2 separate the defective and the unaffected regions. This confined perturbation can be attributed to the topological charge neutrality within these red hexagonal boxes, as required by the topological constraint (4). In contrast, in 1D systems the stress from an impurity particle can always be propagated to the boundary. This is an interesting observation in the sense that the induced topological defects protect the order of the larger perfect hexagonal lattice at the price of sacrificing the order in the region of limited size near the impurity particle. This is in sharp contrast with the conventional order-disrupting role of defects in many physical processes like 2D crystal melting (8–10).

As in crystalline particle arrays on curved geometries where the variation of curvature induces the evolution of defect patterns (12, 13, 36), increasing the parameter Γ in our planar system can generate rich defect motifs, including those not observed on curved surfaces. Neutral topological defects start to emerge as Γ reaches 2.2 in the hexagonal system (Fig. 2A); this is a quadrupole with vanishing Burger’s vector (Fig. 2A) that has little effect on its surrounding environment (4). To show this point, in simulations for the hexagonal system of 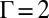we find three almost-degenerate states with no defects, one quadrupole, and two separated quadrupoles, respectively. Their energy difference is as slight as below 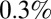. As Γ increases to 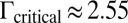, the central impurity particle possesses a negative topological charge that is screened by bounding topological defects, including the three compound 5-7-5 topological charges (scars of net topological charge 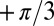) (Fig. 2B). This observation conforms to the topological constraint that the total topological charge of a topologically planar triangulated cluster is always 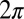regardless of its shape (4). The six 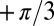disclinations are located at the six corners of the hexagonal lattice, so the total topological charge of interior disclinations is zero, as demonstrated in Fig. 2. Note that the topological charge of a boundary vertex is defined by 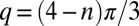, where n is the number of nearest neighbors (4). The “charging” of the central impurity particle is energetically favored; the squeezed-out topological charges make the dip in the energy profile as shown in Fig. 3A. Topological defects are also found in simulations of hard disks in ref. 30, where the arrays of hard disks are generated via a deterministic packing algorithm; successive particles are brought into contact with a growing cluster such that they are as close as possible to the center of the seed configuration. Based on the numerical observation that hard-sphere arrays are often relaxed by imposing a softer potential, it is conjectured in ref. 30 that topological defects might annihilate each other (or move to the boundary) by softening the potential. Our simulations show that the softening of the potential does facilitate the annihilation of defects. Consequently, the softening of the potential significantly delays the appearance of quadrupoles and the trapped central disclination until 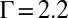(in comparison with 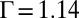in hard-particle systems) and 2.55 ( 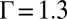in hard-particle systems), respectively. This delay in the appearance of the trapped disclination due to the softened potential is also observed in the system where the impurity particle is smaller than other particles. In simulations, we observe the trapped positive disclination for 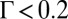in a slightly prestressed system in contrast with 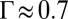in hard-particle systems.

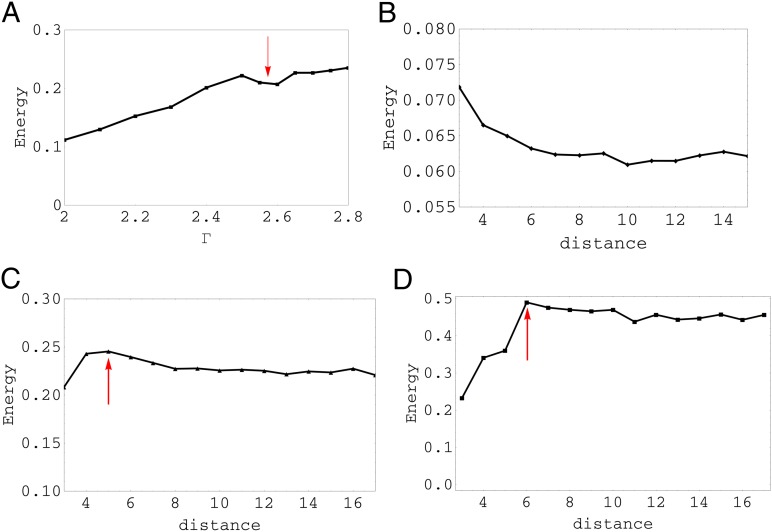
Fig. 3.

Dependence of the energy on the size of the impurity particles as well as their separation. (A) The energy vs. the size of the impurity particle Γ, where the dip of the energy profile at about 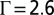signifies the emergence of the trapped disclination at the impurity. (B–D) The energy vs. the distance between two impurity particles. (B) 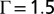, (C) 2.0, and (D) 2.5. The distance is measured in the unit of 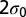. The energy is measured in the unit of ϵ defined in the expression for the Hertz potential.

Microscopically, the reduction of the system energy results from a series of instability events through which particles near the center of the system are inevitably squeezed to approach the growing impurity particle, as observed in simulations. These events increase the neighbors of the impurity particle and it therefore gains a negative topological charge. Note that the mechanism of impurity-driven defects is similar to that of curvature-controlled proliferation of defects. Both impurity particles and the curvature appear as sources in the biharmonic equation for the Airy stress function, whereas the emergence of topological defects is to reduce the stress (37). Geometrically, a positive (negative) disclination can be intuitively understood by removing (inserting) a wedge from a flat lattice (4). An isolated disclination in a flat 2D system is therefore highly energetically unfavored and screening mechanisms should follow to reduce the energy of the system. As a well-established screening mechanism by experiment (11, 38), theory (5), and simulation (33), a cloud of radiating grain boundaries emerges in response to an isolated disclination on both positively and negatively curved surfaces.

Our simulations disclose a fundamentally different screening mode in polydispersed systems in the sense that this mode is highly energetically unfavored to exist in systems of identical particles. In this distinct screening scenario, a multivalent disclination of topological charge 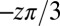trapped at the site of the impurity particle is bounded by z oppositely charged topological compounds (scars) (e.g., see Fig. 2B at 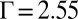) or isolated disclinations (e.g., see Fig. 2C at 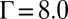); the net topological charge remains zero. The principal stress generated by the disclination is screened by these surrounding topological charges. Further away from the central disclination, we find scattered neutral compound defects and isolated dislocations screening the residue stress; they proliferate with the growing impurity particle, without contributing to the total topological charge within the hexagonal boxes in Fig. 2 A–C. These plastic deformations effectively inhibit the propagation of the irregularity in the particle arrangement near the large impurity particle, and the regular hexagonal structure beyond the red hexagonal boxes (in Fig. 2 A–C) is well protected.

Systematic simulations for system size ranging from N = 331 to N = 2,791 indicate that this basic screening scenario composed of bounding disclinations (or scars) and scattered neutral defects is preserved in a wide range of the values for the parameter Γ. On the basis of this observation, we speculate that the true ground state also possesses such a basic screening mode. Note the phenomenological similarity of the distribution of bounding and scattered topological charges around a multivalent disclination and that of counterions around a charged object in electrolyte solutions, despite the difference in their respective system dimensions. Qualitatively, the binding of topological charges to the trapped large disclination is like the condensation of counterions on charged macromolecules in solutions (39).

The similarity of the screened large disclination and the screened charged sphere in solution may be pushed further to explore the role of topological defects. In particular, like-charge attractions mediated by counterions have been observed in strongly charged polyelectrolyte solutions (40, 41) due to short-range correlations of electrostatic origin (42–45). The elasticity theory of topological defects has revealed that, similar to electric charges, disclinations of like sign repel and those of unlike sign attract (4). It is therefore natural to ask if two disclinations of the same sign can also attract under some conditions. Fig. 3 B–D shows the variation of the system energy with the separation of two large impurity particles for 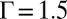(Fig. 3B), 2 (Fig. 3C), and 2.5 (Fig. 3D), respectively. With the reduction of the distance, the energy profile falls beyond a slight barrier in Fig. 3 C and D, indicating a short-range attraction between the two like-charge disclinations. 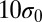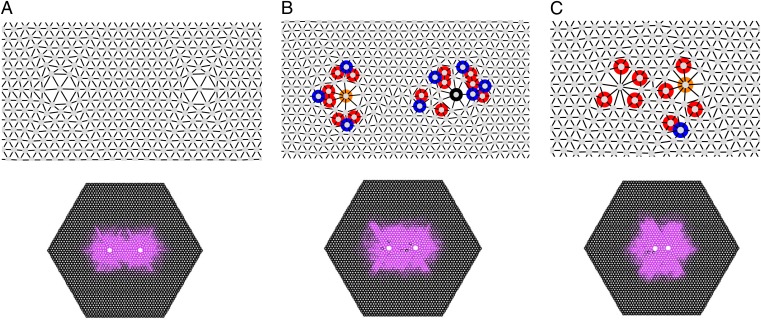In simulations, we notice that both impurity particles are topologically charged and induced defects proliferate around when their separation d is less than and 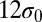, respectively. These critical separations exactly correspond to the maximum energies as indicated by the vertical arrows in Fig. 3 C and D. Fig. 4 shows the evolution of the defect pattern as well as the stressed region when the two impurity particles approach from 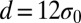(Fig. 4A), 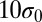(Fig. 4B) to 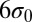(Fig. 4C) for 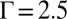. In the range of parameters in Fig. 3 B–D, the stressed region never reaches the boundary, so the influence of the boundary can be excluded to account for the attraction. Therefore, the short-range attraction of the two impurity particles can be attributed to the mediation of induced defects, whereas their appearance is in response to the accumulated and enhanced stress around the impurity particles with their approach. The critical stress for the emergence of defects relies on the interaction between particles according to simulations of the single impurity systems. The short-range attraction that is accompanied by the proliferation of topological defects is also numerically observed in systems of multiple impurities, as reported in SI Text. These results further confirm the scenario of defects-mediated short-range attraction between like-charge disclinations.

Fig. 4.

Evolution of topological defect motifs and the stress patterns with the approach of the two impurity particles. The vertices in the plot represent the centers of particles. (Upper) Arrangement of nearby particles around the impurity particles. Disclinations of different types are distinguished by colors; red for fivefold disclination, blue for sevenfold disclination, black for eightfold disclination, and orange for ninefold disclination. (Lower) The corresponding stressed regions. The energy of the system is reduced from A to B with the mediation of defects. (A) 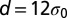, (B) 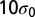, and (C) . .

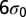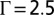Note that although like-charge attraction is observed in both systems of electric charges and topological defects, the underlying physics is distinct. Besides the quantitatively different interaction potentials between charges in these two systems (4), the anomalous like-charge attraction in solutions is due to the correlation induced by counterions (42–44), whereas the reduction of energy in the approach of disclinations originates from the release of the accumulated stress via the induced defects. Another fundamental difference between these two systems is that the number of topological charges is generically not conserved whereas the electric charges in solutions are conserved. To observe the attraction of impurity particles, the parameter Γ has a lower bound value below which the system is free of defects and no attraction occurs as shown in Fig. 3B for 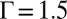. Indeed, several simulations for varying Γ and N suggest that to make two impurity particles attractive at short separations they must be topologically charged. On the other hand, the preexistent defects when the two impurity particles approach may obscure the short-range attraction, as has been seen in the system of 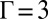, which is larger than the critical value 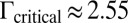. Simulations estimate a window of 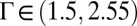to observe the short-range attraction of impurity particles.

We proceed to explore the effect of growing impurity particle size in square lattices where the initial state is also stress-free. Fig. 5A shows the variation of the energy with the growth of the impurity particle centered at a square lattice. The sudden fall of the energy profile at 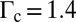signifies a transition from the square lattice to the hexagonal lattice. The cross-like stress distribution in the square lattice as illustrated in Fig. 5A (Inset) is completely released in the lattice transition at the price of the proliferation of topological defects. The phenomenon of sudden release of stress via proliferation of defects is also found in several distinct contexts, including the dislocation theory on the mechanism of earthquakes, which involves the appearance of dislocations under the prevailing stress in the earth’s shell (46, 47). Note that in a prestressed system where the diameter of the particles 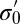is larger than 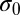, the diameter at which the particles are mutually circumscribed, a slight expansion of the impurity particle by can trigger the square to hexagonal transition, as has been tested in systems with 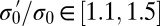. Fig. 5B shows the preservation of the featured screening mode in the collapsed state. The defects along the boundary are due to the edge effect. Note that the cross-like stressed region does not need to reach the boundary of the crystal patch to trigger the lattice transition. It suggests that an impurity particle can even induce the transformation of an infinitely large square lattice. The collapse of a larger square lattice of 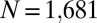at the same critical value 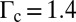has been numerically observed, where isolated dislocations are connected to form long grain boundaries extending to the boundary of the crystal that divide the whole system into several domains. Fig. 5A shows that with the increase of the size of the impurity particle beyond 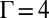, the system regains stress.

Fig. 5.

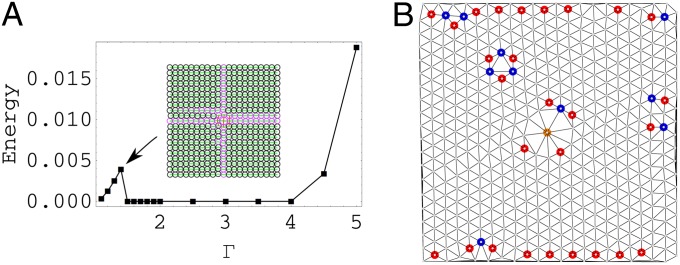
Size polydispersity drives the transformation from a square lattice to a hexagonal lattice. (A) The plot of energy vs. Γ. The kink at 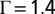signifies the transition from the square lattice (Inset; the green horizontal lines are to indicate the regularity of the square lattice) to the hexagonal lattice. The energy is measured in the unit of ϵ defined in the expression for the Hertz potential. (B) The defective hexagonal lattice at 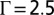, where the featured screening mode is preserved. The number of particles is .

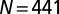Concluding Remarks

In this work, we study the topological defect structure underlying the frustrated particle arrangement around impurity particles. The geometric incompatibility of impurity particles and the remaining particles leads to the characteristic organization of topological defects in the screening mode identified in simulations. These induced topological defects play the role of order restoring; the larger perfect hexagonal lattice beyond the defective region of limited size is well protected. Moreover, topological defects are involved in the short-range attraction of disclinations of the same sign, which are observed numerically. This work may have implications to understanding various size polydispersity-related effects. For example, in heterogeneous crystallization, with the involvement of topological defects, the geometry of the impurity seed particle can significantly influence the kinetic pathway (48, 49). Furthermore, in metallurgy, impurity atoms of different sizes have been introduced into metals to improve their mechanical properties; these impurity particles can annihilate the stress around preexistent dislocations that increases the metal strength and reduces plasticity (7).