Shape matters in protein mobility within membranes

Significance

Lateral Brownian diffusion of proteins in lipid membranes has been predicted by Saffman and Delbrück to depend only on protein size and on the viscosity of the membrane and of the surrounding medium. Using a single-molecule tracking technique on two transmembrane proteins that bend the membrane differently and are reconstituted in giant unilamellar vesicles, we show that the mobility of a membrane protein is crucially dependent on the local membrane deformation self-generated around the protein, which can be tuned by adjusting membrane tension. The feedback between membrane shaping and mobility is well explained by analytical and numerical models that include the friction of the deformed membrane patch with the surrounding medium and the friction internal to the bilayer.

Abstract

The lateral mobility of proteins within cell membranes is usually thought to be dependent on their size and modulated by local heterogeneities of the membrane. Experiments using single-particle tracking on reconstituted membranes demonstrate that protein diffusion is significantly influenced by the interplay of membrane curvature, membrane tension, and protein shape. We find that the curvature-coupled voltage-gated potassium channel (KvAP) undergoes a significant increase in protein mobility under tension, whereas the mobility of the curvature-neutral water channel aquaporin 0 (AQP0) is insensitive to it. Such observations are well explained in terms of an effective friction coefficient of the protein induced by the local membrane deformation.

Brownian motion plays an essential role in biological processes. Since the pioneering experiments of Perrin (1), the observation of diffusing objects has emerged as a mean to extract the rheological properties of the surrounding medium or the probe particle size. The theoretical investigation of diffusion of proteins within membranes has been studied widely going back to P. G. Saffman and M. Delbrück (SD). They investigated the hydrodynamic drag acting on a membrane inclusion when the membrane is described as a 2D fluid sheet of viscosity 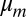embedded within a less viscous fluid of viscosity η (2). In this theory, the diffusion coefficient D₀ in the limit of a large viscosity contrast between the membrane and bulk fluid is given by:

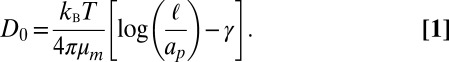The length 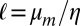is the length scale over which flow is generated within the bilayer by the inclusion, k_BT is the thermal energy, and γ is Euler’s constant. This model predicts a logarithmic dependence of D₀ on the protein radius a_p, which has been confirmed for some in vitro experiments on membranes containing transmembrane proteins (see ref. 3 and references therein). In contrast, the experiments of Gambin et al. (4) showed significant deviations from the SD theory.

A possible origin for the discrepancy observed by Gambin et al. (4) is the significant local membrane deformation due to the interaction between the inclusion and the lipid bilayer (5). Naji et al. suggested in ref. 6 that inclusions experience additional dissipation, either due to internal flows within the membrane or to additional fluid flows produced by the deformed membrane. This work triggered a number of theoretical studies investigating the coupling of inclusion proteins with the membrane that had been pioneered by the Seifert’s group (see ref. 7 and references therein). Such studies have systematically gone beyond the SD model by including additional effects (8–12). So far, a thorough verification of these ideas has not been attempted. To investigate the effect of the protein–lipid coupling on the protein mobility, we study its dependence on membrane tension, because this parameter affects the local membrane deformation.

In this work, we compare the mobility of two transmembrane proteins with the same lateral size, aquaporin 0 (AQP0) and a voltage-gated potassium channel (KvAP), reconstituted in giant unilamellar vesicles (GUVs). Whereas AQP0 does not deform locally the bilayer, KvAP locally bends the membrane (13). Using single-particle tracking (SPT), we demonstrate that the curvature-coupled protein KvAP undergoes a significant increase in mobility under tension, whereas the mobility of the curvature-neutral water channel AQP0 is insensitive to it. This difference, which goes beyond the SD model, is explained by an approach that includes the interplay between membrane deformation and friction with the surrounding medium and within the bilayer. This is compelling evidence that the Brownian motion of a shaping-membrane protein is not simply dependent on the inclusion size but also related to the lateral extension of the deformed membrane patch, which depends on tension.

Results

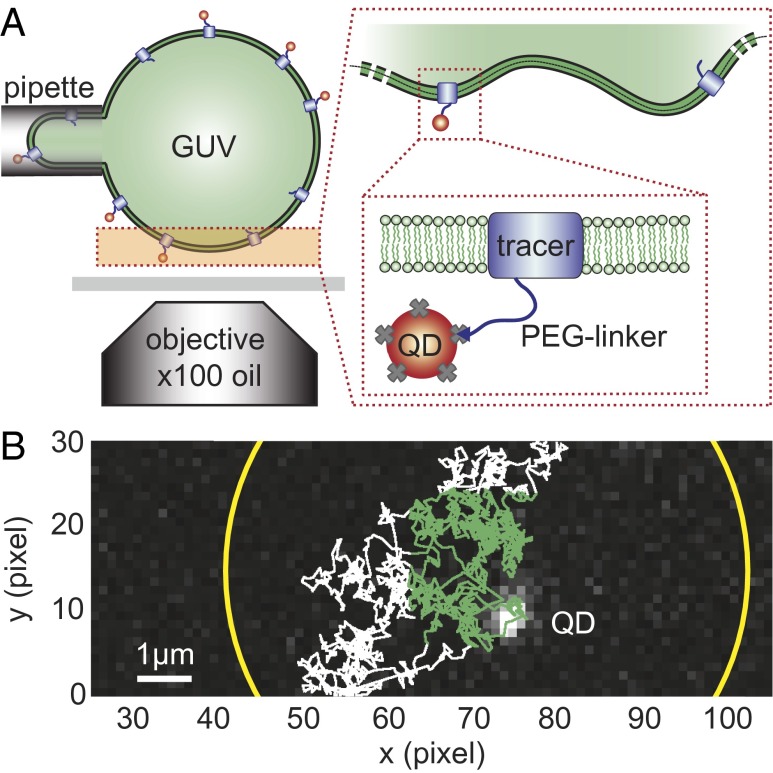
The membrane inclusions are two tetrameric transmembrane proteins of size a_p = 4 nm: (i) AQP0, a water channel abundant in the eye lens (14), and (ii) an archeabacterial voltage-gated potassium channel (KvAP) (15). KvAP has been shown to have a strong affinity for curved membranes and thus inducing bending of the membrane. The inclusion ability to curve membranes is generally quantified by its spontaneous curvature C_p, which reflects the preferred value of local membrane curvature. For KvAP, we have measured 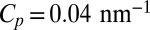(13). In contrast, AQP0 does not exhibit any preference for curved membranes, and thus has a zero spontaneous curvature (13). To investigate the lateral mobility of these proteins in membranes, they were reconstituted at low density (∼40 inclusions per μm²) in fluid phase GUVs, and a small protein fraction was then labeled with quantum dots (QDs). Although both protein insertions are present in the GUV, only one insertion was labeled with the QDs (13). Micropipette aspiration was then used to hold the GUV in place and to control its membrane tension Σ (16) (Fig. 1A). To measure protein displacements, the QD position was detected with SPT near the bottom of the vesicle using epifluorescence microscopy equipped with a fast and sensitive camera (17). We limited our analysis to a small rectangular membrane area (Fig. 1B). We find that the mean-square displacement (MSD) of the proteins exhibits a linear time dependence at short time and a crossover to a constant value dependent on the size of the observation window at larger time (Materials and Methods and Fig. S1). Details of our protocols and analysis are described in the Supporting Information.

Fig. 1.

Experimental approach to diffusion measurements in fluctuating membrane. (A) Schematic of experimental setup: a GUV containing tracer molecule (lipid, AQP0, or KvAP) labeled with a QD is aspirated in a micropipette. In a typical sequence, 100–1,000 individual QDs explore the bottom pole of the GUV. Single QD displacements are measured as a function of the applied membrane tension Σ. (B) Example of QD trajectory. The truncated circle corresponds to the boundary of the area explored by QDs within the depth of field of the microscope. Only the green part of the trajectory contained in a centered square region of interest is considered for the single-QD tracking analysis. One pixel is 160 nm.

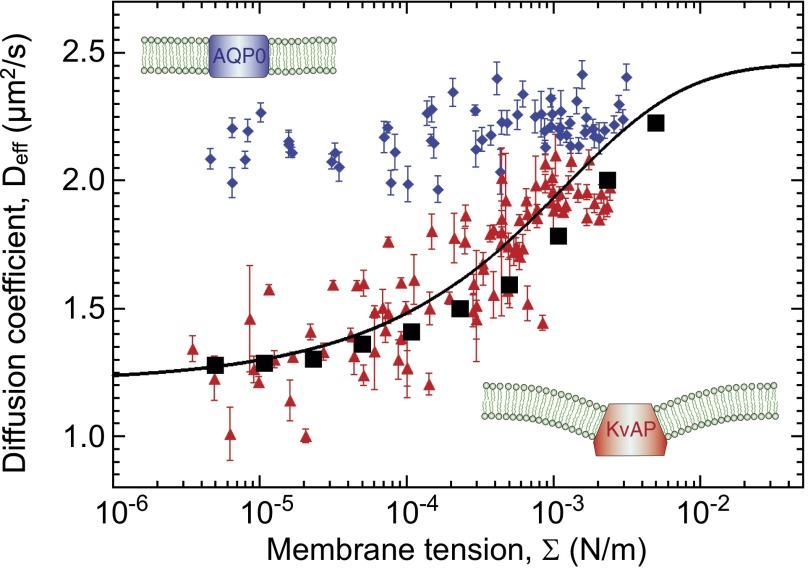
We determined the diffusion coefficient D_eff for each applied membrane tension (Fig. 2 and Fig. S2). In the high-tension limit, the diffusion coefficients of AQP0 and KvAP are comparable and correspond to the value predicted by the SD model (Eq. 1), namely 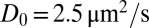for a_p = 4 nm. When the tension drops from 10⁻³ to 10⁻⁶ N/m, less than a 5% variation of D_eff is found for AQP0, whereas a drastic decrease of about 40% is revealed for KvAP. In any case, such a tension dependence is incompatible with the standard SD approach.

Fig. 2.

Protein lateral mobility in fluctuating membranes. Semilogarithmic plot of the diffusion coefficients (D_eff) as a function of the membrane tension Σ, for AQP0 and KvAP labeled with streptavidin QDs. Each point represents a median diffusion coefficient obtained from hundreds of individual trajectories for a GUV at a given tension; the error bars correspond to SE. KvAP data adjusted by Eq. 3 (solid line) yields a protein coupling coefficient 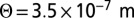considering 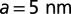, 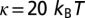and . 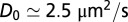Simulations of the protein diffusion on a membrane subject to thermal fluctuations agree well with the experimental data and theory. (Insets) Sketches of membrane deformation near proteins.

To address this issue, we have developed an analytical model and numerical simulations. SD theory implicitly assumes that the protein diffuses in a membrane that remains flat and unaffected by the presence of the protein. In contrast, we take into account that the protein strongly affects its environment. The back action on the diffusing object, translates into a modified drag force. This phenomenon is general in physics and is known as polaron effect (18). A polaron is a charge carrier that deforms a surrounding lattice and moves in it with an induced polarization field. Similarly in liquids, an isolated ion recruits nearby counterions in a process that affects its mobility. Here, we consider a single protein diffusing on a membrane patch of size 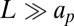described by a height function 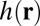. We use the modified Helfrich Hamiltonian:

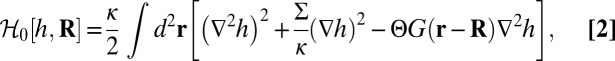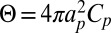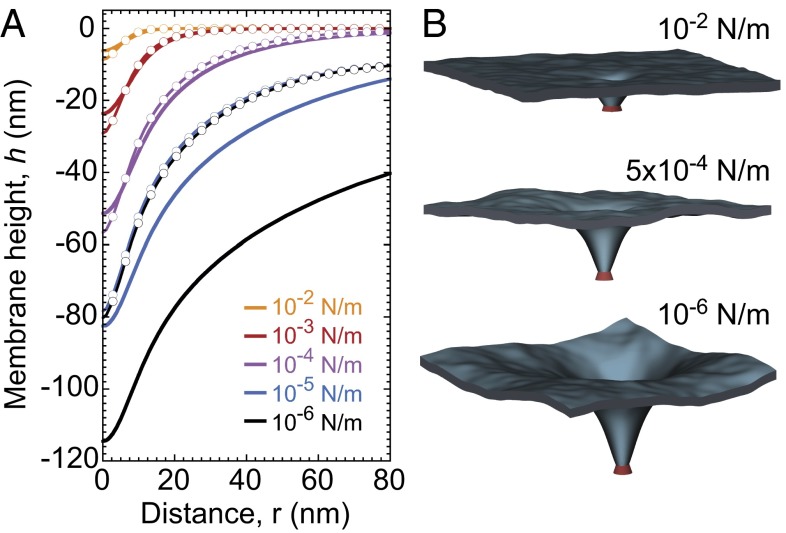
where the first two terms represent the energy of elastic bending of the bilayer with modulus κ and tension Σ, and the last term models the membrane curvature induced at the location of the protein R, which is time dependent. The strength of the induced curvature scales linearly with the protein spontaneous curvature C_p, , similarly to refs. 6 and 8. The range of influence of the protein on the membrane is modeled by the weight function G, which is normalized to 1 and is nonzero over a distance of the order of a_p. This Hamiltonian carries with it a cutoff length a, which corresponds to the bilayer thickness (∼5 nm). From this approach, we obtain the membrane profile around the inclusion given in Eq. S37. The lateral characteristic width of this membrane profile is the crossover length between the tension and the bending regime for the fluctuations, namely , whereas the characteristic height of the membrane deformation at zero tension scales as Θ (Eq. S31). The geometry of the local deformation from the membrane midplane induced by KvAP when subjected to various tensions is shown in Fig. 3 (Fig. S3). Using the method of refs. 6, 8, and 10, we have carried out simulations (with parameters shown in Fig. S4), which also confirm the expected theoretical membrane profile as shown in Fig. 3.

Fig. 3.

Membrane shape as a function of the tension. (A) Profile calculated from Eq. S37 with , κ = 20 k_BT, and a_p = 4 nm (solid lines). Profile calculated from the numerical energy minimum shape using simulation (dashed line). The height value far away from the inclusion is chosen to be zero. Discrepancy at low tension originates from the finite size of the membrane L² used in the simulations (Supporting Information). (B) Three-dimensional membrane profiles obtained from numerical simulations for three different tensions (see also Movies S1 and S2).

Below, we investigate the implications of this local membrane deformation for the mobility of the protein. The model assumes that the dynamics of the membrane is controlled by hydrodynamics in the surrounding fluid of viscosity η. The corresponding timescale is much faster than the diffusion time of the inclusion, justifying the use of an adiabatic approximation to derive an effective dynamics for the protein. Using the framework developed by Démery and co-worker in ref. 9, the effective drag force exerted on the inclusion, namely, 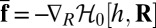, can be obtained analytically at fixed inclusion velocity v. To leading order in v, this leads to a friction coefficient λ given by 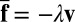. We find that 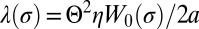, where 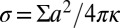is a reduced tension and 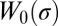is a function given in Eq. S27. The diffusion coefficient D_eff is obtained from the effective drag coefficient using the Einstein relation:

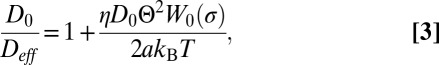where D₀ represents the bare diffusion coefficient of the inclusion in a flat tense membrane, given by Eq. 1. The tension dependence of D_eff is shown in Fig. 2 and Fig. S5. The same dependence was found in simulations (Fig. 2 and Movies S1 and S2), in which the protein diffusivity was directly computed from the MSD of stochastic trajectories. Moreover, it is important to appreciate that the friction coefficient λ is independent of temperature, which shows that the thermal fluctuations of the membrane do not contribute to this effect within the adiabatic approximation. An extended description of the theory and simulations is proposed in the Supporting Information.

Discussion

We next test our model against the KvAP experiments. We find that theory and simulations fit very well the experimental results for D_eff versus Σ using a coupling coefficient 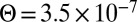m. This proves that the mechanical coupling between the proteins and the membrane can strongly affect protein mobility. At high tension, the experimental data of AQP0 and KvAP converge to the same plateau value, consistently with the SD limit because they have about the same steric radius. As a control, we measured the diffusion coefficient of pure lipids, and confirmed that it is independent of tension as found for AQP0 (Fig. S6). The corresponding constant value for D₀ agrees with the prediction of the SD model, using a lipid size 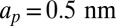. At lower tension, Fig. 2 shows that the KvAP data start to deviate significantly from the plateau at 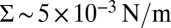, which corresponds to the point at which the lateral characteristic length ξ is of the order of the protein size as expected from our theory.

An additional outcome of this approach concerns the dependence of D_eff with the protein radius a_p, which can be obtained from the following scaling argument. Because the protein makes a fixed angle with respect to the membrane, 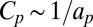. Given the relation 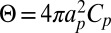, this implies 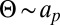. Below the crossover to the SD regime, the local membrane deformation is much larger than the protein size 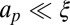, and the drag is dominated by the contribution due to the membrane deformation. Therefore, using Eq. 3, one finds 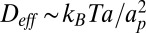, in agreement with ref. 9. Note that such a result is also compatible with the Stokes–Einstein scaling law in obtained in ref. 6, because in this reference only one characteristic length for the protein is used; thus, .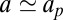

Contribution of an Advected Lipid Layer.

Despite a good agreement between model and data, the physical interpretation of the coupling coefficient Θ requires a more detailed discussion. Indeed, the spontaneous curvature deduced from this coupling coefficient via a fit of the data is significantly larger than that obtained from thermodynamic measurements, based on the preferential sorting at equilibrium of the proteins between GUV and highly curved membrane nanotubes (13). One possible interpretation for this discrepancy is that, in dynamic measurements, the basic relevant object, namely, the association of the moving protein with the deformed membrane around it, may have a size larger than a_p. Such an enhancement of the size could describe physically a layer of lipids dragged by the motion of the protein as considered in ref. 11. Given the value of the coupling coefficient Θ, we obtain an effective area of the protein of the order of 2,200 nm². This is equivalent to an effective radius of 47 nm, a rather large value with respect to the lipid and protein sizes (0.5 and 4 nm, respectively).

Additional Contribution Due to Interleaflet Friction.

At this point, we propose an alternate explanation for the discrepancy between the dynamic measurement and the thermodynamic one. In the approach outlined so far, the dissipation only originates in the fluid displaced by the “bump” in the membrane. However, as pointed out in ref. 6, other dissipation mechanisms in the membrane are possible and likely to be dominant in highly viscous membranes. As a consequence of the curvature induced in the bilayer near the protein, a difference of lipid density between the leaflets is built up, which either relaxes after the protein has passed or is carried by the protein. In any case, there is locally a difference of velocity between each leaflet, which is responsible for further dissipation from intermonolayer slip as the inclusion moves.

A simplified internal structure can be given to the membrane by decorating both leaflets with additional fields representing lipid density deviations from the equilibrium density, 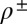(19). A neutral surface is defined for each leaflet by the property that bending and stretching are decoupled in energy when deformations are defined with respect to it. The neutral surfaces of each monolayer are located at a distance d from the overall neutral surface of the bilayer. Deviations from the equilibrium density for each layer can be accounted for with the Hamiltonian:

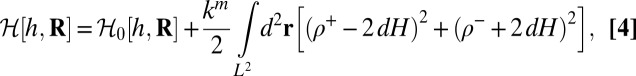where H represents the mean curvature of the membrane, and k^m is the elastic compression modulus of the 2D fluid within each monolayer.

As far as the dynamics is concerned, we introduce two additional parameters, namely, the shear viscosity of each lipid monolayer, 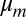, and the friction coefficient between the two leaflets, b. We find with this improved model the same stationary membrane profile but a modified drag coefficient of the form:

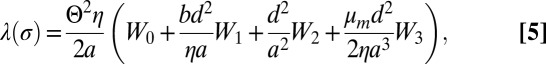where W_i are functions dependent on the reduced tension σ, defined in the Supporting Information (Eq. S46).

This drag friction coefficient reflects three dissipation sources: (i) the dissipation in the bulk fluid, which is proportional to η and corresponds to the W₀ term discussed above in Eq. 3 with a correction given by the W₂ term, (ii) the interleaflet dissipation, which is proportional to b and appears in the W₁ term, and (iii) the dissipation due to the shear viscosity of a single monolayer, which is proportional to and is given by the W₃ term. One can evaluate the relative importance of these contributions in Eq. 5 using the following bilayer parameters 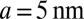, 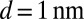(19), 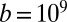J⋅s⋅m⁻⁴ (20–22) and 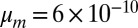J⋅s⋅m⁻² (23), from which one finds the dimensionless factors 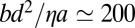, , 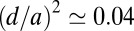and 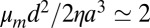. It follows from such estimates that the monolayer friction should play the largest role in the effective friction of the protein (Eq. 5). As a result, it should also be the case for the effective diffusion coefficient corresponding to this drag coefficient :

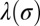With the inclusion of dissipative mechanisms internal to the membrane, we can still account for the dependence of D_eff versus Σ (Fig. S6) and Eq. 6, but with a lower a coupling coefficient 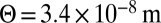, corresponding to a C_p = 0.16 nm⁻¹. This value is then much more compatible with the thermodynamic measurements previously reported in ref. 13.

In this paper, we provide compelling evidence that the effective mobility of a protein is controlled not only by its intrinsic geometric size as in the SD model, but by an effective size that depends on dissipation mechanisms present in the surrounding fluid and in the membrane. An additional outcome of our study is that it is possible to extract from this type of experiment a measurement of the spontaneous curvature of the protein and of the interleaflet friction at the single-molecule level. All these parameters depend on the local environment and on the shape of the protein, in a way that needs to be investigated more systematically in future experiments.

In cell membranes, the local environment of proteins is heterogeneous and dynamic. A more realistic approach to such a situation would require further studies on (i) the diffusion of a protein in a membrane that may be driven out of equilibrium (24), or (ii) the diffusion of a protein that can be activated, such as voltage-gating channels, mechanosensitive channels, G-protein–coupled receptors or light-activated rhodopsins. The strong dependence of the protein mobility on its local environment should lead to a more complex kinetics of clustering of membrane receptors and of association of membrane receptors to ligands. More generally, such effects can contribute to the lateral organization of cell membranes and to the formation of dynamical heterogeneities.

Materials and Methods

Detailed protocols are given in SI Materials and Methods.

Protein Reconstitution in GUVs and Micromanipulation.

Archeabacterial voltage-gated potassium channels (KvAP) or native AQP0 were reconstituted in GUVs using the electroformation method on platinum wires (13, 25, 26). The final protein-to-lipid mass ratio is estimated to 1:200, corresponding approximately to 40 proteins per μm². Before the SPT experiments, biotinylated proteins were labeled with QD655–streptavidin conjugate (Life Technologies). QD-labeled GUVs were then transferred to the microscopy observation chamber. They were aspirated in a glass micropipette and the membrane tension Σ was adjusted by changing the difference of hydrostatic pressure (16). For each vesicle, the membrane was prestressed at 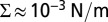during 2 min and then Σ was decreased to the lowest value before diffusion measurement.

QD Imaging and Analysis.

Micromanipulated GUV was positioned so that the bottom pole could sit within the depth of field of the optical Nikon Eclipse Ti microscope (Fig. 1A). The high-speed imaging of single QDs attached to tracer molecules was made using an epifluorescence microscope equipped with an electron-multiplying CCD camera (iXon DU-897; Andor Technology). The membrane tension was then increased step by step and for each membrane tension, two sequences of 30,000 images were recorded with 2-ms exposure time. In a typical sequence, 100–1,000 individual QDs explore a membrane surface of 3- to 5-μm width in the focal plane (Fig. 1B). Detection and tracking of individual QDs was performed with MATLAB routines (SPTrack, version 4). QD centroid positions were determined with a spatial resolution of 10 nm. Trajectories were built by connecting the fluorescence peaks that could be unequivocally assigned to individual QD using a modified routine of the Multiple-Target Tracing (MTT) software developed by Sergé et al. (27), based on Bayesian inference methods. To avoid geometrical artifacts related to the projection of these 3D trajectories on the focal plane, we limited our analysis to a square region of interest (ROI) around the GUV bottom pole. Only trajectories that were at least 30 points long in ROI were kept for further analysis.

For each vesicle at a given membrane tension, we recorded between 50–1,000 trajectories in ROI. The diffusion coefficient of the tracer is extracted from the analysis of the MSD, 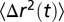defined in Eq. S1. Although the MSD appears linear with respect to time at short time, a saturation at larger time is typically observed. We interpret this saturation illustrated in Fig. S1 as a consequence of the truncation of the trajectories, which leave the observation window (the ROI). A theory based on the solution of the diffusion equation in a finite 2D domain of size 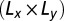, developed in the Supporting Information, gives the conditional MSD to remain in this window: 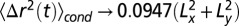, for 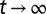. This explains the crossover between a linear behavior of the MSD at short times to a plateau at long times. In all experiments, we have carefully checked that we were far from the crossover regime when measuring the effective mobility. We particularly thank M. Lomholt (MEMPHYS, Odense, Denmark) for insightful discussions on this issue.

This diffusion coefficient was obtained from the short time behavior of the MSD with , where b is a variable offset reflecting the spot localization accuracy (28). From this analysis, we obtained a distribution of diffusion coefficients corresponding to one vesicle at one tension from which we extracted the median value and the SE of the diffusion coefficient reported in Fig. 2.

Computational Methods.

The computational methods follow closely the algorithms developed in ref. 10. The membrane–protein system were thermalized by introducing stochastic driving fields for both the proteins and membrane. The stochastic dynamic equations were integrated in time using the Euler–Maruyama method (29). The membrane profiles were extracted from our computational model by allowing for the membrane mechanics to relax to equilibrium for a fixed protein and taking a cross-section through the protein location. To obtain statistics, we used a straightforward Monte Carlo approach, where independent trajectories were realized for the protein diffusion subjected to membrane thermal fluctuations. The tension dependence of the diffusivity was determined from simulations of the membrane–protein system started with a flat membrane and letting the system equilibrate. After equilibration, the MSD was computed and the diffusivity statistics determined by generating several simulation trajectories for each reported tension value. In this manner, both the energy minimizing shape profiles and stochastic protein dynamics were obtained from the computational model.