Mathematical approaches to modeling development and reprogramming

Abstract

Induced pluripotent stem cells (iPSCs) are created by the reprogramming of somatic cells via overexpression of certain transcription factors, such as the originally described Yamanaka factors: Oct4, Sox2, Klf4, and c-Myc (OSKM). Here we discuss recent advancements in iPSC reprogramming and introduce mathematical approaches to help map the landscape between cell states during reprogramming. Our modelization indicates that OSKM expression diminishes and/or changes potential barriers between cell states and that epigenetic remodeling facilitate these transitions. From a practical perspective, the modeling approaches outlined here allow us to predict the time necessary to create a given number of iPSC colonies or the number of reprogrammed cells generated in a given time. Additional investigations will help to further refine modeling strategies, rendering them applicable toward the study of the development and stability of cancer cells or even other reprogramming processes such as lineage conversion. Ultimately, a quantitative understanding of cell state transitions might facilitate the establishment of regenerative medicine strategies and enhance the translation of reprogramming technologies into the clinic.

In a landmark representation of cell differentiation, Waddington depicted a developmental landscape where pluripotent cells were positioned at the top of a hill progressively losing differentiation potential while going downhill into different valleys representing irreversible differentiated states (1). This metaphor implied the presence of two different types of barriers. On one hand, barriers that separate stable adjacent differentiated cell lineages and on the other hand the existence of a vertical hierarchy of barriers separating the different transient progenitor states from stable differentiated cells., Differentiated cells at the bottom of the hill would represent an energetically favored state, as cells would tend to “fall down” during differentiation, whereas reversion to pluripotency would imply the need for energy expenditure to overcome barriers. Although the Waddington landscape lacked a rigorous quantization, it resonated intuitively because it provided a framework for understanding why some cell states are stable, whereas some others, the progenitor states, transit toward more differentiated stable states. Additionally, the Waddington landscape allowed for the modeling of a complex network of molecular barriers governing cell fate transitions. In practice, the number of possible molecular barriers is large, and the term is used to describe nearly any intracellular factor that mitigates or impedes cellular reprogramming. In the Waddington model (1), however, the complexities of these molecular barriers are reduced into an effective energy landscape, and cell transitions are represented as flows from one energy state to another.

In 2006, Takahashi and Yamanaka demonstrated that differentiated cells could be induced back to pluripotency [induced pluripotent stem cells (iPSCs)] by a specific set of transcription factors, including OCT4/POU class 5 homeobox 1 (POU5F1), sex determining region Y (SRY) box 2 (SOX2), KLF4, and c-MYC (OSKM; the so-called Yamanaka factors) (2, 3). These experiments demonstrated that differentiated cell identity was not a fixed and irreversible state and that somatic cells could be experimentally reverted to a pluripotent state. By analogy with developmental processes, reprogramming to pluripotency can be interpreted as cells being pushed back uphill in Waddington’s landscape. The fact that reversion to pluripotency is not a naturally occurring process, together with the slow kinetics and efficiencies of iPSC generation (2–8), contributed to the idea that cells needed to surpass energetic barriers during reprogramming. Further investigations have indicated that reprogramming to pluripotency implies the “removal of molecular barriers” (a term generally used through the literature; yet, from a mathematical point of view, barriers might be removed, diminished, or simply change in their nature for allowing cells to proceed to a pluripotent state) present in differentiated cells. These findings have opened the question as to whether only an elite subset of cells is able to overcome these limitations and become fully reprogrammed (9). Arguing against this possibility, Hanna et al. showed that virtually all cells have the ability to be reprogrammed given sufficient time and suggested that reprogramming was largely ruled by stochastic cellular transitions (10). From this study, it was clear that accelerating the kinetics of reprogramming, mainly by accelerating cell division rates, contributed to enhanced efficiencies at a given analyzed time point. Additionally, it was shown that, whereas certain populations are seemingly refractory to reprogramming, the ability to generate iPSCs is intrinsic to any cell inside the global population given sufficient time and the appropriate “reprogramming push,” whether by additional expression of the Yamanaka factors, the use of additional reprogramming factors, the use of chemicals, or even by direct modification of epigenetic components. Thus, Hanna et al. concluded that reprogramming did not proceed by favoring an elite model in which only some cells have the ability to generate iPSCs (10–12). More recently, the Hanna group has reported on a critical epigenetic component whose manipulation greatly enhances and accelerates reprogramming to iPSCs (12). Specifically, down-regulation of methyl CpG-binding domain 3 (MBD3) levels were reported to enhance reprogramming to efficiencies nearing 100%, therefore bringing about the possibility that reprogramming proceeds, at least under these conditions, as a deterministic process (12).

Waddington Landscape: A Platform for Modeling Differentiation Landscapes?

Notwithstanding all these observations or the myriad known roadblocks to pluripotency that have been reported thus far, including cell proliferation and epigenetic remodeling (13–19), it is still unclear how best to represent reprogramming in a mathematical framework or even whether a complete mathematical framework can exist for reprogramming processes. The question remains as to what is the best way to incorporate differentiation, that is, the developmental processes exemplified by the Waddington landscape, and dedifferentiation, the process of reprogramming to iPSCs into a rigorous, quantifiable theory. One option for such mathematical models is to focus on landscapes describing differences in free energy between possible cellular states. Thus, an understanding of the landscape governing the reprogramming would allow one to make quantitative predictions for reprogramming kinetics and the best clinical methodologies to shepherd cells from one state into another. Mapping such a landscape can be done in different ways, usually using measurements of cell state transition times or by derivation from first principles using kinematic biochemical models.

In the last few years, much progress has been made toward the establishment of a mathematical framework describing development, which is the differentiation of cells into specialized cell lineages. Recent reports have evaluated and mapped sections of the developmental Waddington landscape by leveraging on statistical physics (20–24). Building on their work with nonequilibrium network circuits (20, 21, 24), Wang et al. were able to map a small segment of the Waddington landscape pertaining to the transition of the multipotent myeloid progenitor cell into either a myeloid or erythroid (24). As was anticipated by Waddington, they observed that the initial multipotent cell starts in a metastable state and flows into one of two attractor basins corresponding to the final differentiated cell states. Most noticeably, they also compute the most probable paths between the initial and final states of the cells during development. Interestingly they observe a hysteresis effect where the most probable differentiation path was not equal to the most probable dedifferentiation path (24). Therefore, implying that transitions through different cell states might require more than a simple scalar energy field, like an additional force field that will push the cells as they travel from one state to the next. Similar effects were also observed following extensions to a larger network of 52 genes related to stem cell differentiation (25). Noticeably, the forces necessary to transit through different cellular states can represent intrinsic cellular factors, such as the use of reprogramming factors, environmental and cell interaction signals, such as those driving differentiation and development, and media conditions for driving the differentiation, or dedifferentiation, of one cellular state to another.

Regardless of the actual forces underlying the conversion of one cellular state to another one, these observations bring about the question of whether reprogramming to iPSCs effectively follows the same pathways observed during the development of an organism in a reverse manner or whether different paths are followed during the dedifferentiation of somatic cells to iPSCs. If reprogramming follows an inverse developmental path, this would imply that partially reprogrammed cells could represent intermediate multipotent states similar to those observed during development and open new venues for the generation of specific cell types in absence of full reprogramming to pluripotency. On the contrary, if reprogramming to iPSCs proceeds through alternative paths to those followed during development and cell differentiation, partially reprogrammed cells might them represent a somewhat artificial state with no real natural counterpart. Noticeably, this does not necessarily exclude the possibility of generating intermediate multipotent progenitor cells (26). Several different reports have argued in favor of these possibilities (27, 28). First, Polo et al. analyzed in a systematic manner the process of dedifferentiation to iPSCs from an epigenetic and genomic perspective and speculated that the process could inversely recapitulate development (27). Although this interesting possibility was raised based on the sequence of molecular remodeling events observed during the course of reprogramming, actual comparisons with the intermediate cell states naturally occurring during development and cell differentiation remained unreported. Regardless of whether reprogramming proceeds as an inverse “developmental process” and natural progenitor states arise during iPSCs generation, several recent reports have elaborated on the possibility of exploiting partial reprogramming, or dedifferentiation, for lineage conversion approaches: that is, the generation of specific cell types in the absence of iPSC generation. Lineage conversion has received increased attention over the years as a complementary approach to iPSC generation, and excellent recent reviews have been published. Lineage conversion can be accomplished in the absence of cell dedifferentiation by forcefully establishing gene signatures typical of the target somatic cell type [e.g., overexpression of MYOD, a transcription factor (TF) typical of differentiated muscle cells, suffices for the conversion of fibroblasts into muscle-like cells] (26, 29, 30). Alternatively, several other publications have reported on the use of reprogramming factors commonly used during iPSC generation for the partial dedifferentiation of somatic lineages to an intermediate, yet largely undefined, cellular state, with multipotent differentiation properties (26, 30–35). The possibility to drive lineage conversion processes based on partial reprogramming argues that, at least during the initial phases of reprogramming, the use of the Yamanaka factors or others related to the acquisition of pluripotency first erases differentiated cell identity and that such epigenetic modifications allow for cell respecification into appropriate lineages on exposure to extracellular and/or additional intracellular clues. Indeed, erasure of the epigenome during iPSC reprogramming has been largely documented, with iPSC reprogramming factors acting as pioneer TFs, i.e., factors whose initial activities rely on the modification of the epigenome to allow for the necessary chromatin modifications permitting and guiding subsequent access to specific gene promoters during the initial steps of reprogramming (29, 36–38).

Quantifying Pluripotent States and Population Heterogeneity

Mapping reprogramming landscapes, whether during iPSC generation or even in lineage conversion processes, can provide detailed insights on the process if the specific gene networks regulating the process are well established (Fig. 1). However, this approach has some inherent limitations. For one, cell states are represented in the space of gene expression, meaning that for complicated processes the networks can be large, as in the case of the 52-gene network recently studied by Li and Wang. Comprehensive studies on the gene networks underlying reprogramming to iPSCs are of outmost importance because despite recent reports highlighting more precise gene networks underlying reprogramming (27, 39–41), there is always uncertainty in the completeness of the gene network. Despite this uncertainty, recent insights on the molecular mechanisms driving reprogramming to iPSCs have indicated the existence of two distinct waves of molecular events, regardless of whether single cells or whole populations were analyzed during the initial reprogramming steps (27, 42). During the early phase (up to 3 d) of reprogramming, epigenetic remodeling appears to take place at the chromatin level in line with a recent report suggesting that the reprogramming factors act as pioneers TFs (37). Accompanying chromatin remodeling, transcriptome changes result in the down-regulation of markers characteristic of the initial somatic cell population while contributing to the activation of cell cycle and mesenchymal-to-epithelial transition genes. From days 9 to 12, a second major wave of events is observed, where epigenetic remodeling occurs at the methylome level, accompanying the up-regulation of genes related to the establishment and maintenance of pluripotency. Thus, from the second wave onward, the reprogramming could proceed in the absence of exogenous reprogramming factor expression. These observations follow a previous report describing a first phase of stochastic effects preceding the hierarchical activation of multiple transcription factors orchestrating reprogramming to iPSCs (39). These reports converge on the idea that once endogenous pluripotency factors, including Sox2 (38), Oct4, and Nanog homeobox (Nanog), are activated, cells will ultimately progress to iPSCs (27, 28).

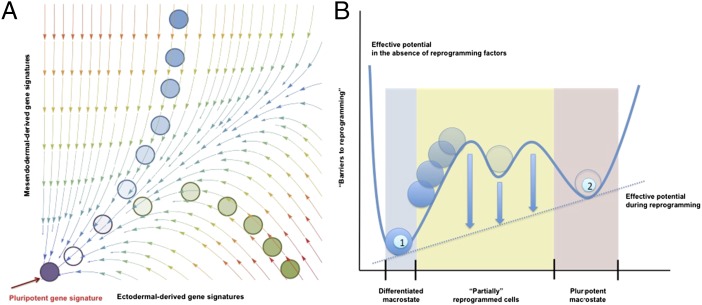
Fig. 1.

Comparison of mathematical models derived from single-cell and population-level analyses. (A) Schematic representation of a probability landscape as determined from gene network analysis at the single-cell level. The planar axes represent gene expression levels for two different genes G1 and G2; a vertical component would represent the probability of a given cell to express the defining genes (G1 and G2) at a specific level. The arrows represent the curl flux forces, and the colors represent the magnitudes of the potential. The motion of a cell in this space is governed by both the curl flux and the shape of the potential landscape. For simplification, reprogramming has been depicted as the changes in gene expression from mesendodermal- and ectodermal-derived somatic lineages (e.g., cardiomyocytes and hepatocytes serve as a representative mesendodermal-derived lineages, whereas neurons would represent and ectodermal origin). (B) Effective potential landscape determined from population-level analyses. This potential landscape reduces many of the complexities at the single-cell level into a 1D effective potential energy function in cell state space. Higher potential energies are represented by larger heights. The numbers refer to the differentiated somatic cell state (1) and the pluripotent state (2). Note that population approaches consider variable macrostates in which different individual gene signatures are equally represented.

However, high-dimensional spaces are difficult to analyze because we are inherently restricted to small (two- or three-) dimensional visualizations. Therefore, it may be easy to overlook, for instance, subpopulations of partially reprogrammed cells that are apparently refractory to reprogramming as seen in some dedifferentiation experiments. One potential explanation is that these refractory cells may have fallen into local, false metastable minima in the cell state space, and it is not clear that these false minima will represent natural intermediate progenitor states such as those arising during development as discussed above. Whether reprogramming to iPSCs faithfully recapitulates developmental programs in an inverse manner could be investigated, for example, by comparing intermediate dedifferentiated cells, such as those generated during lineage conversion processes driven by iPSC-reprogramming factors, to the intermediate cellular states emerging by differentiation during development. From the standpoint of physical experiments, this means that it may be possible to reproducibly achieve a refractory subpopulation of partially reprogrammed cells that seem homogeneous in physical characteristics but are extremely heterogeneous—or even dynamically changing—in their gene expression profiles. This discrepancy between experiments and models represents a potential pitfall that must be considered when working with landscapes derived from gene regulatory networks or any mathematical space where the dimensions might not coincide identically with physically measurable characteristics.

An alternative to studying reprogramming dynamics at the gene network level is to study the cells at the population level (Fig. 1). Population-level studies have the advantage that they are built in the space of phenotypes rather than a more abstract space. However, this advantage is in itself a challenge because it is inherently limited by the necessary assumption that pluripotency represents a qualitative functional state while obviating intraclone variability at the single cell level, the precise feature that gene network analyses for modeling might actually overlook. As such, population-level approaches would have to consider different macrostates, for example, the initial differentiated somatic cell and the final pluripotent state as marked by functional characteristics or defined pluripotent marker expression. A prime example of population level macrostates comes from the cancer biology field. Indeed, whereas pluripotent cells represent an individual cell identity with exactly identical gene and protein expression signatures remains largely unknown and a matter of intense research, this is not the case in certain cancers. Indeed, multiple different cancer stem cell populations have been described for a given cancer type (e.g., glioblastoma), despite presenting different gene and protein expression signatures. As such, the field has recently pointed out the necessity to characterize cancer stem cells not based on marker expression but instead at the functional level, while considering the possibility of multiple different populations at the genetic and protein level (42–45). These observations led to the idea that cancer cells might interconvert across different states and raised the possibility that populations of cancer stem cells arise by reversion of more differentiated cancer cells. Such a model of reversibility, or cancer cell reprogramming, has been recently presented by Gupta et al. (46) and, more recently, has been experimentally corroborated by the Weinberg laboratory in breast cancer cells.

In terms of pluripotent cells, recent reports seem to indicate that iPSCs represent a functional state presenting a high degree of variability when comparing different clones or even at the single-cell level (47–49). However, whereas single-cell variability undoubtedly occurs as a consequence of different epigenetic signatures and/or the presence of differential genomic aberrations, the actual causes of these population-wide differences remains unclear. As discussed by Liang and Zhang (50), epigenetic and genetic aberrancies leading to interclone variability in terms of gene expression might arise as a result of two different processes. First, the acquisition of such aberrations might confer cells with growing advantages and result in the positive selection of defined epigenetic and genetic patterns in an analogous manner to models of cancer progression. Second, heterogeneity in the initial somatic cell population might be translated through to the final iPSC clones rather than being completely washed out by the reprogramming process. However, how does intraclone variability arise at the single-cell level? One possibility is merely due to spontaneous mutation rates. Even when clonal iPSC colonies have been established, the continuous growth and proliferation of the cells might contribute to the spontaneous acquisition of mutation, ultimately affecting gene expression and providing a level of intraclone variability, a phenomenon observed in embryonic stem cells (ESCs) independently of experimental reprogramming (48). Another possibility deals with the actual nature of pluripotent cells. Overall, pluripotent cells represent a highly variable cell type, and dynamic expression of not only so-called pluripotent markers but also of early lineage markers can be readily observed in culture (50, 51).

These observations pose the question of whether pluripotency represents a discrete cellular identity and therefore whether specific epigenetic and genetic signatures should be observed despite the variability expected in normal distributions typically observed in biological processes. Another possibility is that pluripotency represents a dynamic functional state that, whereas presenting certain differences in terms of gene and protein expression, can be largely ascribed to the functional ability to generate all different somatic cell lineages on differentiation. Whether pluripotency represents a discrete cellular identity or rather a functional metastate is a major and controversial question that remains largely unsolved and would certainly determine whether gene network mathematical approaches are more suitable for the modeling of reprogramming than population-level studies or vice versa. In support of the notion that pluripotency might represent a functional state, we and others have recently reported on the reprogramming of somatic cells to iPSCs by substituting so-called pluripotency factors with lineage-specific genes (51, 52). By balancing counteracting differentiation forces, reprogramming to a pluripotent state could be achieved, thus implying the establishment of a fine-tuned equilibrium as discussed by MacArthur and Lemischka (47). Most noticeably, whereas OCT4 has been traditionally considered the master regulator of pluripotency and irreplaceable for the reprogramming of human cells to iPSCs, genes associated to mesendodermal lineage specification were able to substitute for OCT4 during the reprogramming of murine and human fibroblasts to a pluripotent state (51, 52). Together, these observations highlight pluripotency as a functional state rather than a discrete cellular identity characterized by well-defined and static gene networks and highlights pluripotency as a statistical property resembling a macrostate in statistical physics as proposed and thoroughly discussed by MacArthur and Lemischka (47). If this macrostate identity is correct, it would again create a challenge to representing pluripotent states in a gene expression landscape, as the gene expression signature for a pluripotent cell may be dynamic or nonunique.

Mathematical Approaches to Cell Reprogramming

Given these challenges for representing pluripotent cells in a mathematical framework, it is important to dissociate those cellular characteristics that are fundamental to pluripotent cells from those that are merely ornamental. By leveraging on detailed long-term studies, population-level models that are extensive enough to provide meaningful predictions for the clinic can be constructed by considering the space of observable cellular phenotypes.

The first model of reprogramming at the population level was presented by Hanna et al. (10). By monitoring NANOG-GFP expression, a pluripotent-related gene up-regulated in cells poised them to become iPSCs (27), Hanna et al. previously found that given enough time, virtually any cell could eventually give rise to pluripotent cells, in line with the abovementioned reports (10). The results were comparable under p53-null conditions, albeit with faster kinetics, supporting the notion that reduced cell proliferation represents one of the barriers to iPSCs and that increased proliferation contributes to reprogramming (13). Because the reprogramming times for the population were distributed broadly instead of very narrowly, Hanna et al. indicated that the data were more consistent with the hypothesis that reprogramming happens stochastically rather than in a manner with deterministic timing. It may be possible that the process is in fact deterministic, and the distribution of reprogramming times results solely from hitherto uninvestigated heterogeneities in the initial populations. This type of hidden variables hypothesis could perhaps be tested by comparing the reprogramming times of multiple preparations of similar somatic populations. During the preparation of this article, the Hanna laboratory reported on the efficient reprogramming of somatic cells to iPSCs with efficiencies nearly reaching 100% in just 7 d. By modulating the expression of the Mbd3/NuRD complex genes, components responsible for the remodeling of the chromatin, Rais et al. were able to demonstrate that chromatin remodeling acts as a major factor preventing synchronized reprogramming to iPSCs and established that MBD3 inhibition, in combination with exogenous Yamanaka factor expression in a permissive growth environment, sufficed for the conversion of a largely inefficient process into a highly efficient one, in which cells progressively undergo dedifferentiation toward pluripotency in an uninterrupted manner (12). Although the full reprogramming process took less than 1 wk compared with up to 18 wk in their original study, there is still noticeable structure in the latency data. Rais et al. found a relatively poor fit when modeling the process as an infinitely sharp step function and instead found the best fit to the data to be a phase type distribution, which results from the sequential action of one or more Poisson-type processes (12).

There is significant agreement between their model and their data when considering the cumulative distribution functions (CDFs), However, the probability distribution functions (PDFs) of the data reveal deviations from model predictions for the short-time dynamics. Specifically, abrupt, noise-assisted single barrier crossings are incompatible with the data. A simple elaboration of this model is to fit both the CDFs and the PDFs of the data and consider the observed latencies as the distribution of first passage times (DFPTs) from the differentiated state to the iPSC state. By fitting this distribution and appealing to the Fokker-Plank formalism, it is possible to infer the shape of an effective potential governing the reprogramming process. Such an approach could provide a means for the mathematical modeling of reprogramming events. In such an scenario, the distributions of latencies reported by Hanna et al. (10) are better modeled by an inverse Gaussian distribution rather than an exponential distribution, regardless of the cell lines analyzed (10) (Fig. 2 and Table 1). In contrast to the abrupt single transitions implied by an exponential distribution, first passage times that are inverse Gaussian distributed correspond to a uniform diffusion in cell state space aided by a linear drift, meaning the initial population undergoes progressive changes toward a final state. A linear drift diffusion model represents a solution to the Fokker-Planck equation when the potential landscape is a flat, sloping incline. Hence, one possibility is that the potential barriers between the two cell states, somatic and pluripotent, are effectively diminished and/or changed during reprogramming in a manner that allows cells to be pushed toward the pluripotent state. Due to diffusion, some cells may intermittently travel away from pluripotency, but the drift, or overall push, ensures that the cells will not in general transit back and forth between states. Although the problem of finding the potential that produces a distribution of first passage times that best fits the data is formally noninvertible, it is still possible to find a solution by globally searching the parameter space. In principle, it is intuitive to imagine that the transition from somatic cell to pluripotent cell in the presence of exogenous transcription factor expression occurs as a two-state transition model. We found, however, that of all of the potentials considered, the best fit for the experimental data was a flat landscape with a shallow slope, as shown in Fig. 3. We note that our findings and approach are in the same spirit as the Langevin-based analysis used by Sisan et al. (53) to model GFP expression heterogeneity in clonal fibroblasts. These approaches differ radically from constructing the landscape directly from the regulating gene network because it does not require a priori knowledge of the gene circuitry and it reduces the high-dimensional problem down to a single-dimensional effective potential, as in the original Waddington landscape. However, such population-level approaches are not exclusive but rather complement gene network-based modeling studies, such as those presents by Buganim et al. in a recent publication (39, 54).

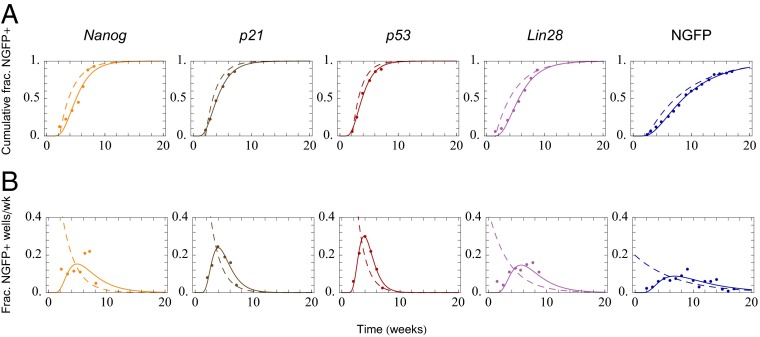
Fig. 2.

Comparison of analytic fits for an intermediate-barrier model (dashed lines) and a linear drift-diffusion model (solid lines) for cumulative and differential iPSC reprogramming data. Analytical fits for Nanog GFP (NGFP)-Nanog overexpressing cells, NGFP-p21 knockdown (KD), NGFP-p53KD, NGFP-Lin28OE, and NGFP cells are shown, respectively. (A) Cumulative distributions are plotted with respect to time. (B) Fraction of NGFP-positive cells over time.

Table 1.

Goodness-of-fit statistics

Comparative fit of cumulative data	Nanog OE	p21 KD	p53 KD	Lin28 OE	NGFP WT
Cumulative fraction IG, wk	0.982	0.999	0.998	0.994	0.999
Cumulative fraction Exp, wk	0.9	0.962	0.974	0.893	0.983
Cumulative fraction IG, rescaled time	0.971	0.995	0.998	0.989	0.996
Cumulative fraction Exp, rescaled time	0.649	0.745	0.677	0.874	0.983
Fraction NGFP+ per week IG	0.794	0.975	0.991	0.93	0.9

For each of the comparative fits—cumulative fraction of NGFP⁺ cells measured in weeks, cumulative fraction of NGFP⁺ cells measured in population rescaled time (data not shown), and the differential fraction of NGFP⁺ wells per week—we calculated R² values for the exponential distribution (Exp) and inverse Gaussian distribution curve (IG) fits. We found that in all cases the inverse Gaussian distribution provided a better R² to the fit. These R² values are shown in the table (note that R² values for the exponential model fitting the fraction of NGFP⁺ per week were not included because, being the result of a nonlinear fit, they were generically negative). OE, overexpression; KD, knockdown; WT, wild type.

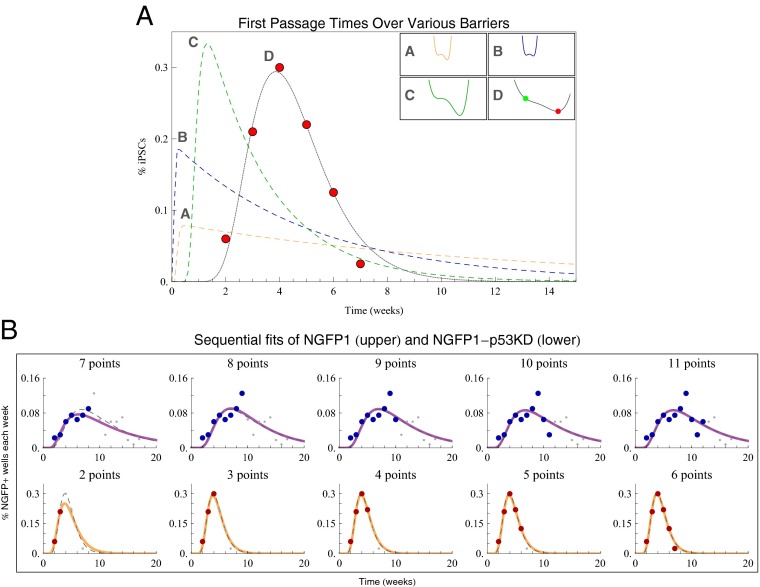
Fig. 3.

Dedifferentiation to pluripotency is a gradual barrier-free process. (A) Prototypical two-state intermediate barrier potentials and their numerically calculated distributions when varying height and width. The potential in 2D closely approximates the best-fit linear and progressive dedifferentiation and provides excellent agreement with the data. (B) Practical exemplification of the underlying distribution of reprogrammed cells when fit with a subset of the data. From left to right, we increase the number of data points (red and blue, respectively) that are used to fit the drift-diffusion model (orange and purple solid lines, respectively) to the measurements. Data points omitted from the fit are shown in gray; the dashed gray lines show the fits using all time points. Effectively, once the peak in the reprogramming rate had been observed, one can make accurate predictions for the future time course of the reprogramming process.

Finally, by comparing the fitted inverse Gaussian parameters for each cell type studied by Hanna and colleagues, a consistent interpretation for the action of MBD3 abrogation can be found based on the acceleration of the drift speed driving reprogramming (Tables 1 and 2). This remarkable increase in drift speed can be interpreted in cell state space as a much sharper potential incline and in gene expression space could correspond to either a steeper landscape or a dramatic change in the curl flux along the path of dedifferentiation. Because each cell line analyzed encountered its own set of molecular barriers, there was no a priori guarantee that the fitted inverse Gaussian parameters would be correlated. However, because OSKM mitigated these barriers, we found that the fit parameters provide a coherent picture of the physical process even when the latencies are drastically different. We emphasize, however, that one major implication remains regardless of how the latency data are modeled: the fact that all cells can become iPSCs given sufficient time (10, 12, 27).

Table 2.

Fits to gamma distributions

Cell type analyzed	R2	a	b
Nanog OE	0.831	5.135	0.797
p21 KD	0.981	7.516	1.571
p53 KD	0.996	9.993	2.283
Lin28 OE	0.9496	5.667	0.795
NGFP WT	0.9116	3.799	0.378

The table includes the goodness-of-fit parameters, the shape parameters, a, and the rate parameters, b, for gamma distributions fit to the differential fractions of NGFP⁺ wells per week for each cell line observed. Note that the R² values are comparable to those for the inverse Gaussian fits, and the shape parameters range from roughly 4 to 10. OE, overexpression; KD, knockdown; WT, wild type.

Conclusions and Perspectives

The observation that all cells have the potential for reprogramming and that this process is accomplished by the action of reprogramming factors effectively modifying existing barriers that normally prevent the spontaneous transition to a pluripotent state is an important insight into the nature of reprogramming process. Quantitative characterization of the reprogramming process brings closer the goal of defining reprogramming methodologies for boosting reprogramming efficiencies in terms of time and number of generated iPSCs. It is important to point out that, although the cell population approaches presented here were based on quantitative measurements obtained under continuous ectopic OSKM expression (10), they also account for the measurements by Polo et al. obtained using transient ectopic OSKM expression (12, 27) and are in agreement with the “stabilization phase” recently reported by Golipour et al. (40). According to a drift-diffusion model, these barriers disappear, whether by flattening or by being effectively modified during reprogramming, allowing cells to drift-diffuse toward pluripotency, a process that can be further synchronized and accelerated on inhibition of key chromatin remodeling components such as MBD3. In those situations where chromatin remodeling is not experimentally manipulated, a small fraction of cells in the presence of exogenous OSKM will be fast enough or sufficiently primed to be able to pass both barriers within the initial days of reprogramming. Accordingly, when exogenous OSKM expression is turned off, the original barriers return, and these cells become trapped between the two barriers as “partially reprogrammed cells.” In support of these observations, Polo et al. found that these trapped cells could be rescued by further OSKM expression, which in our model corresponds to a second removal of the barriers, allowing the refractory population to proceed again via the drift-diffusion process (27). Additionally, the recent data from Hanna and colleagues indicate that experimental removal of chromatin remodeling barriers results in the acceleration of the reprogramming process, and the majority of the cells are able to rapidly progress toward the acquisition of a pluripotent state. Therefore, it is tempting to speculate that these biological observations of the reprogramming process can all be reconciled in a single theoretical framework by postulating that the effective action of OSKM expression—be it exogenous or endogenous—is to eliminate effective potential barriers, allowing all cells to gradually dedifferentiate toward pluripotency via a drift-diffusion mechanism as observed by Hanna and colleagues (10, 12).

In summary, recent findings have started to elucidate the nature of the pluripotent state and shed new light into the causes accounting for pluripotent cell variability in terms of their epigenetic and genetic signatures at the single-cell level. The observations that pluripotent cells represent dynamic cellular states has led to the establishment of an equilibrium model suitable for statistical modeling of pluripotency as discussed by MacArthur and Lemischka and experimentally implied by two recent publications (47, 51, 52). Our understanding of the nature of pluripotency has matured alongside our understanding of the gene interactions at the heart of the reprogramming process. These advances have facilitated models of the reprogramming landscape both at the single-cell level and the population level. Approaches at both levels are complementary representations of the same problem and will both be important in quantifying the reprogramming process. One of the main applications for models of reprogramming is that they could allow for the prediction of entire distributions of reprogramming times with just a few initial data points or from knowledge of the gene regulatory network. Such practical implications will ultimately allow for the estimation of defined experimental outcomes. By leveraging on mathematical models, experimental parameters such as the most suitable somatic cell source for reprogramming or the time necessary to obtain a given number of reprogrammed colonies can then be estimated, thus saving time and the associated expenses and eventually facilitating the use of reprogramming approaches in the clinic. By mapping the reprogramming landscape in terms of gene expressions, it may also be possible to create novel reprogramming methodologies that otherwise would not have been apparent from standard molecular studies. Altogether, as more and more reprogramming data are collected, predictive mathematical models of development and dedifferentiation will have an increasingly important role in clinical and drug discovery applications based on reprogramming approaches.

Materials and Methods

For all numerical and analytical analysis, we used Mathematica version 8 for both Mac OS X and Windows. All kinetics data, population data, and exponential model parameters used herein are taken from figure 4 in Hanna et al. (10).

Numerical Solutions Based on the Fokker-Planck Equation.

To calculate the latencies h(t) numerically for a given metastable two-state potential we first calculated the underlying probability density function f(x,t) using NDSolve to solve the Fokker-Planck equation

We set the initial distribution f(x,t) = 0 to be a narrow normal distribution (width of 0.05) centered on the higher of the two potential minima. We removed restrictions on the maximum number of steps NDSolve could take by setting 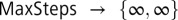. We imposed boundary conditions that the probability distribution should go to zero both at the second (lower) minima and at 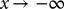(numerically implemented as a point sufficiently anterior to the initial distribution to be effectively inaccessible). We systematically varied these implementations for boundary conditions at 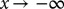and found that they have minimal effect on the final outcome. We also studied variations of the initial and boundary conditions by varying the mean of the initial distribution and position of the right-hand barrier by 10% of their initial value.

Once the probability density f(x,t) was computed numerically, we then computed the conditional probability of finding the particle having not passed over the second potential minimum (located at b) at time t: 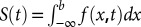(55). The latency distribution is then a negative derivative of S(t): 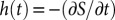. Thus, to evaluate h(t) at a given time point, t, we evaluated the derivative of f(x,s) with respect to s, integrated f(x,s) from 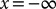to x = b, and then evaluated the result at s = t. The above mentioned computational calculations were done for all t between t = 0 and t = 20 in steps of 0.1. Integrations were done using NIntegrate with the default method options.

To compare fits of cumulative data the cumulative distribution functions for both the inverse Gaussian and gamma distributions were obtained in Mathematica via CDF[InverseGaussianDistribution[a, b], t] and CDF[GammaDistribution[a, b], t]—although these expressions were also checked for consistency by hand.

Range of Two-State Potentials Studied.

The potential functions 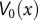to be analyzed using the Fokker-Planck equation were selected in two steps. First, prototypical two-state quartic potentials were found by hand using Locators in a DynamicModule coupled to the five coefficients of a quartic polynomial. These potentials were chosen for their relative and absolute positions of their minima. The parameters for each starting potential were then varied from 1/5 of their initial value to five times their initial value (in steps of 1/10 of the initial value), and their subsequent DFPTs were calculated. All different DFPT calculations were repeated several hundred times, and results were tested for their congruence with the reported latency data.

In another systematic study of potentials, several data points defining the positions of the minima, the height and width of the intermediate barrier, and the shape of the potential at infinity were varied and subsequently fit to a quartic polynomial using the built-in function Fit. Data points influencing the vertical positions of the minima were varied from 0 to −200 and 0 to −400, respectively (with the left minima always being greater than the right). Data points influencing the horizontal positions of the minima were varied from −100 to 0 and 0 to 100, respectively. Points influencing the barrier height were varied from 0 to 100. For each potential, we calculated the latency distribution using a logarithmic distribution of diffusion constants ranging between 10⁻² and 10². All variations were done independently.

For the specific potentials referenced in Fig. 3A, the parameters for potentials A, B, and C, respectively, were as follows: V₀(x) = 4x⁴ − 9.3x³ − 5.5x² + 5.8x, D = 1, f(x,0) = 7.9788e^{−200(0.5711 + x)2}, f(−2.0,t) = f(1.9971,t) = 0; V₀(x) = 5.8x⁴ − 9.3x³ − 5.5x² + 5.8x, D = 2.1, f(x,0) = 7.9788e^{−200(0.5388 + x)2}, f(−2.0,t) = f(1.4129,t) = 0; and V₀(x) = 0.2x⁴ − 1.5x³ + 0.4x, D = 0.605, f(x,0) = 7.9788e^{−200(0.2907 + x)2}, f(−2.0,t) = f(5.6091,t) = 0.

The interior of potential D was modeled to match the best fit inverse Gaussian parameters; the parameters were as follows: V₀(x) = 0.0046x⁴ − 0.0942x³ + 0.5951x² − 2.8301x − 0.2170, D = 1.45, f(x,0) = 7.979e^−200(x)2, f(−10.0,t) = f(10.81,t) = 0.

Please refer to Tables 1 and 2 for exact R² values of the analyzed distributions.