Development of a Magnetic Nanoparticle Susceptibility Magnitude Imaging Array

Abstract

There are several emerging diagnostic and therapeutic applications of magnetic nanoparticles (mNPs) in medicine. This study examines the potential for developing an mNP imager that meets these emerging clinical needs with a low cost imaging solution that uses arrays of digitally controlled drive coils in a multiple-frequency, continuous-wave operating mode and compensated fluxgate magnetometers. The design approach is described and a mathematical model is developed to support measurement and imaging. A prototype is used to demonstrate active compensation of up to 185 times the primary applied magnetic field, depth sensitivity up to 2.5 cm (p < 0.01), and linearity over 5 dilutions (R² > 0.98, p <0.001). System frequency responses show distinguishable readouts for iron oxide mNPs with single magnetic domain core diameters of 10 nm and 40 nm, and multi-domain mNPs with a hydrodynamic diameter of 100 nm. Tomographic images show a contrast-to-noise ratio of 23 for 0.5 ml of 12.5 mg Fe/ml mNPs at 1 cm depth. A demonstration involving the injection of mNPs into pork sausage shows the potential for use in biological systems. These results indicate that the proposed mNP imaging approach can potentially be extended to a larger array system with higher-resolution.

1. Introduction

The use of magnetic nanoparticles (mNPs) to treat and diagnose cancer is an active area of research with several different treatments and platforms being explored. One of the potentially promising approaches is hyperthermia cancer therapy with mNPs (Day, Morton et al. 2009; Pankhurst, Thanh et al. 2009). The use of high-strength alternating magnetic fields (AMFs) to heat magnetic particles for localized hyperthermia treatment of cancers was first reported in 1957 (Gilchrist, Medal et al. 1957). Two clinical trials using mNPs for cancer hyperthermia therapy have recently been reported (Day, Morton et al. 2009). One study enrolled 10 patients with recurrent prostate cancer (Johannsen, Gneueckow et al. 2007), and the other study enrolled 66 patients with recurrent glioblastoma multiforme (Maier-Hauff, Ulrich et al. 2011). The high concentrations of nanoparticles used in these clinical trials enabled the use of computed tomography (CT) for mNP imaging. In both studies the injected nanofluid contained 112 mg Fe from magnetite per ml of solution. The median volume of injected nanofluid in the prostate cancer trial was 11.4 ml into a median target volume of 15.8 ml. This median injected volume was 4.5 ml in the glioblastoma multiforme trial.

Magnetic nanoparticles are also used as contrast agents in conventional and experimental techniques of cancer imaging and in other imaging applications. Currently available mNP imaging technologies are magnetic resonance imaging (MRI) (Choi, Choi et al. 2004; Corot, Robert et al. 2006; Sun, Lee et al. 2008), CT (Johannsen, Gneveckow et al. 2007; Maier-Hauff, Ulrich et al. 2011) and ultrasound (US) (Dayton and Ferrara 2002; Yang, Li et al. 2009). There are also a number of different research approaches to mNP imaging including saturation methods (Gleich and Weizenecker 2005; Nikitin, Vetoshko et al. 2007; Ferguson, Minard et al. 2009; Goodwill, Scott et al. 2009; Nikitin, Vetoshko et al. 2009; Rauwerdink, Giustini et al. 2010; Rauwerdink and Weaver 2011; Croft, Goodwill et al. 2012; Goodwill, Saritas et al. 2012; Rahmer, Weizenecker et al. 2012; Saritas, Goodwill et al. 2013; Tu, Klein et al. 2013), relaxometry (Romanus, Huckel et al. 2002; Chung, Hoffmann et al. 2004; Flynn and Bryant 2005; Ludwig, Heim et al. 2005; Astalan, Jonasson et al. 2007; Fornara, Johansson et al. 2008; Sarangi, Tan et al. 2009; Adolphi, Huber et al. 2010; Denoual, Saez et al. 2010; Richter, Kettering et al. 2010; Yoshida, Ogawa et al. 2010; Sarangi, Tan et al. 2011; Bhuiya, Asai et al. 2012; Coene, Crevecoeur et al. 2012; Crevecoeur, Baumgarten et al. 2012; Johnson, Adolphi et al. 2012), alternating current (AC) methods (Yang, Abe et al. 2004; Hong, Wu et al. 2006; Chen, Sanchez et al. 2008; Enpuku, Nabekura et al. 2009; Janosek, Ripka et al. 2009; Chieh and Hong 2011; Dieckhoff, Yoshida et al. 2012) and remanence measurements (Carvalho, Bruno et al. 2007; Ge, Shi et al. 2009; Carvalho and Bruno 2011). These research methods have used a variety of sensors for these applications. Super conducting quantum interference devices (SQUIDs) are particularly used in AC and relaxometry methods (Flynn and Bryant 2005; Enpuku, Nabekura et al. 2009; Richter, Kettering et al. 2010; Chieh and Hong 2011). A study that is particularly relevant to the present one but using magnetic relaxometry and an array of SQUID sensors and drive coils has recently been published (Steinhoff, Liebl et al. 2012). Pickup coils are primarily used for high frequency saturation methods (Gleich and Weizenecker 2005; Nikitin, Vetoshko et al. 2009; Goodwill, Saritas et al. 2012). Magnetoresistive sensors are effective in AC and Brownian relaxation methods for cell labeling (Denoual, Saez et al. 2010; Enpuku, Tamai et al. 2010; Yoshida, Ogawa et al. 2010). Fluxgate magnetometers have been used in a number of methods (Dieckhoff, Schilling et al. 2011; Dieckhoff, Schilling et al. 2012; Yoshida, Enpuku et al. 2012), including in miniature arrays (Janosek, Ripka et al. 2009). Another interesting sensor is miniature atomic magnetometers used in relaxometry methods (Johnson, Adolphi et al. 2012). Magnetic nanoparticles can also be used to detect tumors using either targeted or untargeted mNPs. This approach has been demonstrated in preclinical trials of cancer detection in lymph nodes (Anninga, Ahmed et al. 2013).

In the present study, we have applied a needs based, lean design approach to developing an mNP imaging system. Our starting point is that the susceptibility imaging system must be portable, use low magnetic field strengths, and operate outside of a magnetically shielded environment. Costs should be been kept low by purchasing off the shelf electronics components when possible, and the instrument footprint should be small enough for integration into the bedside clinical environment. If successful, future studies will focus on meeting clinical needs for temporal and spatial resolutions.

Our technical approach is to use an array of digitally controlled drive coils and compensated fluxgate magnetometers. Applying lean principles to the design process, we developed a prototype with the minimal functionality to test the feasibility of the proposed approach. Our bench top prototype consists of three applied field coils and two fluxgates. The coils generate frequency-encoded applied magnetic fields that are geometrically and actively nulled at the sensors. Continuous readouts of magnetization fields are used to resolve the spatial locations and concentrations of mNP samples.

Sensitivity to mNPs in our approach is based on continuous wave (CW) AC susceptibility measurement. When a magnetically susceptible material is subjected to an external applied magnetic field, the induced magnetic field produced by that material will be B = μ₀ (H + M), where μ₀ is the magnetic permeability in a vacuum, B is the magnetic induction or B-field, H is the magnetic field strength, and M is the magnetization field. The magnetization field arises from the magnetically susceptible material as M = Hχ_v where χ_v is the volume magnetic susceptibility. Diamagnetic materials are defined as having χ_v < 0 and paramagnetic as having χ_v > 0. Although the M-field only exists inside of the magnetic material, it gives rise to additional external B-field that contributes to the magnetic field detected by a sensor such as a fluxgate magnetometer. Studying this additional B-field requires that it be distinguished from the directly coupled applied magnetic field and from background noise.

Mathematical models for magnetic susceptibility imaging have been developed previously. The magnetic inverse problem has been described in detail (Lima, Irimia et al. 2006). Two-dimensional magnetic susceptibility tomography (MST) methods have been developed for use on samples of uniform thickness (Thomas, Ma et al. 1993). Three-dimensional methods of MST have not been implemented, but the analytical groundwork for the method have been developed (Wikswo 1980; Wikswo, Opfer et al. 1980). Further developments of MST for biological imaging (Thomas, Sepulveda et al. 1993), non-destructive evaluation (NDE) (Wikswo, Ma et al. 1993), dia-magnetic and para-magnetic objects (Sepulveda, Thomas et al. 1994) and in a non-uniform magnetic field (Parente Ribeiro, Wikswo et al. 2000) have also been reported. Models including a system of voxels containing magnetically susceptible material, an array of excitation coils, and an array of sensors have been developed for magnetic relaxometry (Crevecoeur, Baumgarten et al. 2012) and brain hemodynamics (Burke and Diamond 2012). The susceptibility-imaging model presented in this study relies empirically upon calibration data rather than models of field theory. This empirical approach is necessary for our approach to digital magnetic field compensation and is tolerant of imprecise knowledge of model elements such as coil and sensor geometry. The model presented in this work also incorporates AC susceptibility effects and accounts for the delays that result from electrical components such as inductors and capacitors. This is done by capturing all of the delays and gains resulting from the physical implementation of the hardware without individually specifying each element in the physical system.

In this study, we present a method for susceptibly imaging with mNPs. We show experimental results that demonstrate digital compensation, distance sensitivity to 2 cm, and concentration sensitivity in the range of 1 to 10 mg Fe/ml. We also demonstrate that our system can distinguish between mNPs with single magnetic domain core diameters of 10 nm and 40 nm, and multiple domain mNPs with a 100 nm hydrodynamic diameter. Finally we present results for tomographic line imaging of 4 and 6 voxels at a 1 Hz frame rate for depths of 0.5 and 1 cm. We also present results of injecting the 100 nm mNPs into pork sausage as a means of demonstrating the potential of imaging in biological systems.

2. Methods

2.1. Hardware

2.1.1. Coil and Sensor Configuration

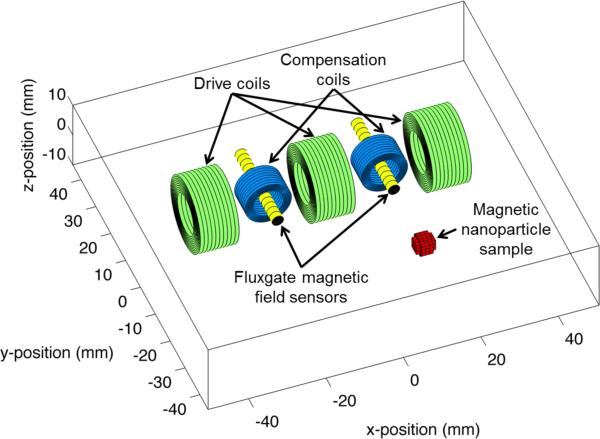
In the proposed coil and sensor configuration (figure 1), the applied field and compensation electromagnets (green and blue coils) generate H, the magnetically susceptible nanoparticles generate M, and the fluxgate sensors (yellow) measure B, which results from the directly coupled fields from the coils and the induced magnetization of the mNPs. Due to the proximity of the drive coils to the fluxgate sensors in our system configuration, compensation of the directly coupled magnetic fields from the drive coils to the fluxgate sensor array is required so that the induced magnetization field is not swamped by the drive coil fields. In order to be effective, the digital and geometric compensation must be sufficient to lower the directly coupled magnetic fields to within the dynamic range of the sensors and analog-to-digital converter (ADC) without injecting noise into the measurements. This requirement limits the applied fields that can be achieved before the compensation methods start to increase the noise measured by the sensors. These applied field limits can be extended by using higher performance hardware such as ADCs and digital to analog converters (DACs) with larger dynamic range.

Figure 1.

Diagram of the experimental setup. The driving coils are arranged orthogonally to the fluxgates. The compensation coils are aligned with the fluxgates. A nanoparticle sample is placed some distance away in front of the apparatus.

The configuration shown has geometric compensation and active compensation. The geometric compensation results from arranging the measurement axes of the fluxgate sensors orthogonally to the principle direction of field generation from the drive coils. The effectiveness of geometric compensation is limited in practice by geometric inaccuracies in the coil and sensor construction, and by inaccuracies in the alignment of coils and sensors in a constructed array. Residual direct coupling from the drive coils to the sensor array is actively compensated by tuning the compensation coil gains to simultaneously null the directly coupled magnetic fields from all drive coils to all fluxgate sensors. The active compensation algorithm that was developed for this purpose is introduced in section 2.2.

One of the central questions in the configuration of the coils and sensors is whether the applied fields will induce magnetization fields in mNP samples that are measurable along the measurement axes of the fluxgate sensors. A secondary question is whether the strength of the cross fields on the fluxgates will exceed their operating range. These questions were examined using a previously developed simulation (Burke and Diamond 2012) that was adapted to the proposed coil-sensor configuration. The model relates magnetic fields detected by the fluxgates to variations in magnetic susceptibility throughout the imaging volume. To obtain this model, the applied fields from drive coils were modeled by integrating the Biot-Savart law around the loops of the coils, approximating the wire as an infinitely thin conductor, and multiple loops were summed by superposition. The resulting field has a closed form solution (Smythe 1967). The imaging volume was then divided into rectilinear elements (voxels) and the applied magnetic field strength was determined at the centroid of each voxel. This applied field was then used to calculate the magnetic induction field due to a unit change in magnetic susceptibility in the voxel. This induced field was then projected from all voxels to the sensor locations where the magnetic field at the fluxgate sensors results in a measured signal. This relationship between the susceptibility in the voxels and the measurements from the fluxgates is the forward model that is needed for tomographic imaging.

2.1.2. Analog and Digital Systems

The prototype design used three drive coils, two sensors and two compensation coils (figure 1). The drive coils (Jantzen-1258, 0.3 mm diameter wire, 5 mH, 10.1 Ω at DC, 15 mm inner diameter × 15 mm height × 25 mm outer diameter, Jantzen, Praestoe, Denmark) were arranged orthogonally to the fluxgate axes to create a higher condition number for matrix inversion while still producing magnetic fields at the sample that produced a magnetization field that resulted in a signal above the noise floor when measured by the sensor. To measure the magnetic field, FLC-100 fluxgate magnetometers (Stefan-Mayer Instruments, Dinslaken, Germany) were used. This fluxgate has an on-axis sensing range of ±100 μT, a cross field operating range of ±1 mT, a cutoff frequency of 1 kHz, noise specification <50 pT/√Hz at 10 Hz, and size of 44 mm × 14 mm × 5.5 mm. Compensation coils (Jantzen-1814, 0.3 mm diameter wire, 0.15 mH, 1.3 Ω at DC, 15 mm inner diameter × 8 mm height × 18 mm outer diameter) were aligned on a common axis with the fluxgates.

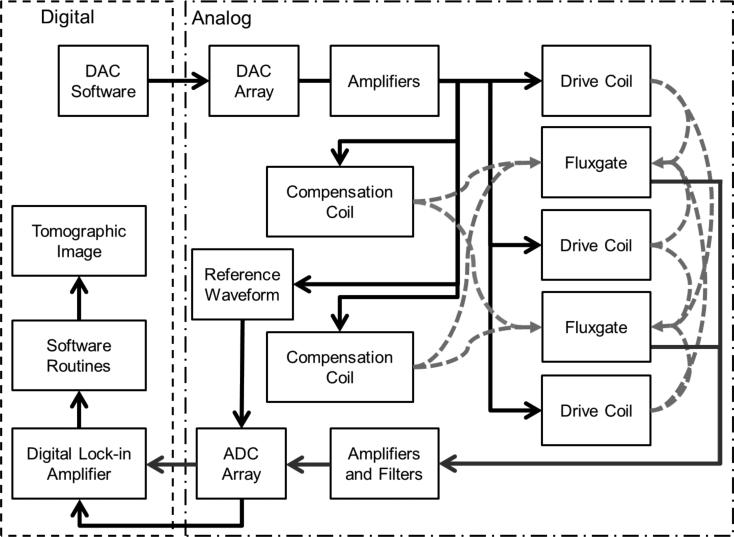
As shown in figure 2, a software controlled DAC array (CS4334, Cirrus Logic Inc., Austin, TX, USA) was used to produce AC currents at frequencies between 500–950 Hz for control of the drive and compensation coils. The DAC array was controlled by a general purpose controller (NIUSB 6289, National Instruments, Austin, TX, USA). Operational amplifiers (LM 412, Texas Instruments, Dallas, TX, USA) were then used to amplify to current amplitudes of 30 mA peak-to-peak. The applied fields from the drive coils at this current produce magnetic fields of 10 μT at a sample point 0.5 cm in front of a fluxgate sensor. In addition, the DAC also produced a reference current for each frequency being used. Each fluxgate field measurement was then amplified and low pass filtered by a 4th order analog Butterworth filter with a cutoff frequency of 3.3 kHz. Data was acquired at 20 kS/s with an 18-bit analog to ADC (NI-USB 6289, National Instruments, Austin, TX, USA).

Figure 2.

Flowchart of the system. The DAC produces a current that is amplified and used to generate magnetic fields with the coils. This field interacts with the mNPs and the resulting magnetic induction field along with any uncompensated field is detected by the fluxgates. This field is amplified and sampled by an ADC. A digital lock-in amplifier determines the in-phase and out-of-phase field components for subsequent imaging algorithms.

To help orient the reader to the prototype in a completed form, figure 3 shows a photograph of the working prototype.

Figure 3.

A photograph of the prototype. The fluxgates, drive coils, compensation coils, mNP samples and imaging grid are labeled.

2.2. Measurement and Imaging Models

The compensation and imaging methods presented in this section are based on empirical measurements that can be made with an imager. This approach avoids the need for precise modeling or mechanical calibration of the coils and sensor geometry and also the captures the gains and phase lags in the electronics without additional work. One of the field theory-based approaches cited in the introduction may also be used for imaging if all of the geometric factors and electronic components are precisely modeled.

2.2.1. Compensation Algorithm

The compensation algorithm is based on a mathematical model of the magnetic fields that are directly coupled from each drive and compensation coil to the fluxgate sensors. The compensation is performed separately at each reference frequency. Typically the drive coils are modulated at unique frequencies so the compensation is performed separately for each drive coil. At a given reference frequency f₀, the scalar magnetic field strength B measured by the kth uniaxial fluxgate sensor S is the sum of fields from drive coils D and compensation coils C

$$B_{S_k}=\sum _i{B}_{D_i{S}_k}+\sum _j{B}_{C_j{S}_k}.$$ (1)

In practice, the measurement from a drive or compensation coil to a sensor passes through analog circuitry as shown in figure 2. The magnetic field from the ith drive coil modulated at frequency f₀ and measured by the kth fluxgate sensor is modeled as

$$B_{D_i{S}_k}=G_{D_i{S}_k}\left[A_{D_i}^{″}\sin (2\pi f_{0}t+{\varphi }_{D_i{S}_k})+A_{D_i}^{\prime }\cos (2\pi f_{0}t+{\varphi }_{D_i{S}_k})\right],$$ (2)

where the A_D values indicate the amplitudes commanded with the DAC for sine (A″) and cosine (A′) reference components of the modulated signals. Geometric gain factors G account for coupling between the drive or compensation coils and the fluxgate sensors, and the phase angles ϕ account for unknown but constant lags between the commanded reference signals from the DAC and the sensor signals recorded by the ADC. These gain and phase factors account for the characteristics of the analog circuitry as well as geometric factors in the sensor design. Similarly, the field strength measured by the kth sensor from the jth compensation coil is modeled as

$$B_{C_j{S}_k}=G_{C_j{S}_k}\left[A_{C_j}^{″}\sin (2\pi f_{0}t+{\varphi }_{C_j{S}_k})+A_{C_j}^{\prime }\cos (2\pi f_{0}t+{\varphi }_{C_j{S}_k})\right].$$ (3)

Sine and cosine reference signals R at reference frequency f₀ are generated by the DAC to control the drive and compensation coils and are also recorded concurrently with the fluxgate data file using the ADC

$$R^{″}=\sin \left(2\pi f_{0}t\right),$$ (4)

$$R^{\prime }=\cos \left(2\pi f_{0}t\right).$$ (5)

Substituting the reference signals R″ and R′ into (2) and (3), the phase terms can be expressed as coefficients of the reference signals, which is a convenient mathematical form for understanding the compensation algorithm

$$B_{D_i{S}_k}=G_{D_i{S}_k}\left[A_{D_i}^{″}\left(R^{″}\cos \left({\varphi }_{D_i{S}_k}\right)+R^{\prime }\sin \left({\varphi }_{D_i{S}_k}\right)\right)+A_{D_i}^{\prime }\left(R^{\prime }\cos \left({\varphi }_{D_i{S}_k}\right)-R^{″}\sin \left({\varphi }_{D_i{S}_k}\right)\right)\right],$$ (6)

$$B_{C_j{S}_k}=G_{C_j{S}_k}\left[A_{C_j}^{″}\left(R^{″}\cos \left({\varphi }_{C_j{S}_k}\right)+R^{\prime }\sin \left({\varphi }_{C_j{S}_k}\right)\right)+A_{C_j}^{\prime }\left(R^{\prime }\cos \left({\varphi }_{C_j{S}_k}\right)-R^{″}\sin \left({\varphi }_{C_j{S}_k}\right)\right)\right].$$ (7)

To simplify the notation, it is convenient to define G in terms in-phase and out-of-phase components

$$\begin{array}{cc}\hfill G^{″}=& G\sin \left(\theta \right),\hfill \\ \hfill G^{\prime }=& G\cos \left(\theta \right).\hfill \end{array}$$ (8)

Such that (6) and (7) can be simplified to

$$B_{D_i{S}_k}=A_{D_i}^{″}\left(G_{D_i{S}_k}^{\prime }{R}^{″}+G_{D_i{S}_k}^{″}{R}^{\prime }\right)+A_{D_i}^{\prime }\left(G_{D_i{S}_k}^{\prime }{R}^{\prime }-G_{D_i{S}_k}^{″}{R}^{″}\right)$$ (9)

and

$$B_{C_j{S}_k}=A_{C_j}^{″}\left(G_{C_j{S}_k}^{\prime }{R}^{″}+G_{C_j{S}_k}^{″}{R}^{\prime }\right)+A_{C_j}^{\prime }\left(G_{C_j{S}_k}^{\prime }{R}^{\prime }-G_{C_j{S}_k}^{″}{R}^{″}\right).$$ (10)

To compensate for the residual magnetic field from the drive coil fields at the sensor, the sum of the magnetic fields from the compensation coils must be equal and opposite to the magnetic field from the drive coils

$$\sum _j{B}_{C_j{S}_k}=-B_{D_i{S}_k}$$ (11)

for each sensor k from 1 to K. The compensation balance expression in (11) can also be rewritten in terms of G and A

$$\sum _j{A}_{C_j}^{″}\left(G_{C_j{S}_k}^{\prime }{R}^{″}+G_{C_j{S}_k}^{″}{R}^{\prime }\right)+A_{C_j}^{\prime }\left(G_{C_j{S}_k}^{\prime }{R}^{\prime }-G_{C_j{S}_k}^{″}{R}^{″}\right)=A_{D_i}^{″}\left(G_{D_i{S}_k}^{\prime }{R}^{″}+G_{D_i{S}_k}^{″}{R}^{\prime }\right)+A_{D_i}^{\prime }\left(G_{D_i{S}_k}^{\prime }{R}^{\prime }-G_{D_i{S}_k}^{″}{R}^{″}\right)$$ (12)

for each sensor k from 1 to K. When multiplied by R′ or R″ and time averaged, reference terms $\overline{R^{\prime }{R}^{″}}$ tend to zeros while square terms $\overline{R^{\prime 2}}$ and $\overline{R^{″2}}$ tend to 2. This simplifies (12) into two expressions

$$\begin{array}{cc}\hfill 2\sum _j{A}_{C_j}^{″}{G}_{C_j{S}_k}^{″}+A_{C_j}^{\prime }{G}_{C_j{S}_k}^{\prime }=& -2\left(A_{D_i}^{″}{G}_{D_i{S}_k}^{″}+A_{D_i}^{\prime }{G}_{D_i{S}_k}^{\prime }\right),\hfill \\ \hfill 2\sum _j{A}_{C_j}^{″}{G}_{C_j{S}_k}^{\prime }-A_{C_j}^{\prime }{G}_{C_j{S}_k}^{″}=& -2\left(A_{D_i}^{″}{G}_{D_i{S}_k}^{\prime }-A_{D_i}^{\prime }{G}_{D_i{S}_k}^{″}\right).\hfill \end{array}$$ (13)

The duration of the time averaging window in (12) defines the measurement rate and subsequent imaging rate. To measure the G′ and G″ terms in the above equations, the compensation algorithm requires a series of calibration measurements. This is done by selectively turning on amplitudes at a reference level A₀ for only the sine or cosine component of a single drive or compensation coil while maintaining all other commanded amplitudes at zero. For example, with a single drive coil and two sensors, the calibration measurements from drive coil 1 are measured from sensors 1 and 2

$$\begin{array}{cc}\hfill B_{0,D_1{S}_1}=& A_{0,D_1}^{″}\left(G_{D_1{S}_1}^{\prime }{R}^{″}+G_{D_1{S}_1}^{″}{R}^{\prime }\right),\hfill \\ \hfill B_{0,D_1{S}_2}=& A_{0,D_1}^{″}\left(G_{D_1{S}_2}^{\prime }{R}^{″}+G_{D_1{S}_2}^{″}{R}^{\prime }\right).\hfill \end{array}$$ (14)

The measurements from compensation coils 1 and 2 coupled to fluxgates sensors 1 and 2 are

$$\begin{array}{cc}\hfill B_{0,C_1{S}_1,A^{″}}=& A_{0,C_1}^{″}\left(G_{C_1{S}_1}^{\prime }{R}^{″}+G_{C_1{S}_1}^{″}{R}^{\prime }\right),\hfill \\ \hfill B_{0,C_1{S}_1,A^{\prime }}=& A_{0,C_1}^{\prime }\left(G_{C_1{S}_1}^{\prime }{R}^{\prime }-G_{C_1{S}_1}^{″}{R}^{″}\right),\hfill \\ \hfill B_{0,C_1{S}_2,A^{″}}=& A_{0,C_1}^{″}\left(G_{C_1{S}_2}^{\prime }{R}^{″}+G_{C_1{S}_2}^{″}{R}^{\prime }\right),\hfill \\ \hfill B_{0,C_1{S}_2,A^{\prime }}=& A_{0,C_1}^{\prime }\left(G_{C_1{S}_2}^{\prime }{R}^{\prime }-G_{C_1{S}_2}^{″}{R}^{″}\right),\hfill \\ \hfill B_{0,C_2{S}_1,A^{″}}=& A_{0,C_2}^{″}\left(G_{C_2{S}_1}^{\prime }{R}^{″}+G_{C_2{S}_1}^{″}{R}^{\prime }\right),\hfill \\ \hfill B_{0,C_2{S}_1,A^{\prime }}=& A_{0,C_2}^{\prime }\left(G_{C_2{S}_1}^{\prime }{R}^{\prime }-G_{C_2{S}_1}^{″}{R}^{″}\right),\hfill \\ \hfill B_{0,C_2{S}_2,A^{″}}=& A_{0,C_2}^{″}\left(G_{C_2{S}_2}^{\prime }{R}^{″}+G_{C_2{S}_2}^{″}{R}^{\prime }\right),\hfill \\ \hfill B_{0,C_2{S}_2,A^{\prime }}=& A_{0,C_2}^{\prime }\left(G_{C_2{S}_2}^{\prime }{R}^{\prime }-G_{C_2{S}_2}^{″}{R}^{″}\right).\hfill \end{array}$$ (15)

The next step in the calibration algorithm is to mix the calibration measurements with either the sine or cosine reference signals and then average the results over time. In this example, we mix the two measurements of (14) and (15) with R″ and then with R′ and divide through by A₀ to isolate the G terms

$${\mathrm{G}}_{CS}=2\left[\begin{array}{cccc}\hfill \frac{\overline{B_{0,C_1{S}_1,A^{″}}{R}^{″}}}{A_{0,C_1}^{″}}\hfill & \hfill \frac{\overline{-B_{0,C_1{S}_1,A^{\prime }}{R}^{″}}}{A_{0,C_1}^{\prime }}\hfill & \hfill \frac{\overline{B_{0,C_2{S}_1,A^{″}}{R}^{″}}}{A_{0,C_2}^{″}}\hfill & \hfill \frac{\overline{-B_{0,C_2{S}_1,A^{\prime }}{R}^{″}}}{A_{0,C_2}^{\prime }}\hfill \\ \hfill \frac{\overline{B_{0,C_1{S}_1,A^{″}}{R}^{\prime }}}{A_{0,C_1}^{″}}\hfill & \hfill \frac{\overline{B_{0,C_1{S}_1,A^{\prime }}{R}^{\prime }}}{A_{0,C_1}^{\prime }}\hfill & \hfill \frac{\overline{B_{0,C_2{S}_1,A^{″}}{R}^{\prime }}}{A_{0,C_2}^{″}}\hfill & \hfill \frac{\overline{B_{0,C_2{S}_1,A^{\prime }}{R}^{\prime }}}{A_{0,C_2}^{\prime }}\hfill \\ \hfill \frac{\overline{B_{0,C_1{S}_2,A^{″}}{R}^{″}}}{A_{0,C_1}^{″}}\hfill & \hfill \frac{\overline{-B_{0,C_1{S}_2,A^{\prime }}{R}^{″}}}{A_{0,C_1}^{\prime }}\hfill & \hfill \frac{\overline{B_{0,C_2{S}_2,A^{″}}{R}^{″}}}{A_{0,C_2}^{″}}\hfill & \hfill \frac{\overline{-B_{0,C_2{S}_2,A^{\prime }}{R}^{″}}}{A_{0,C_2}^{\prime }}\hfill \\ \hfill \frac{\overline{B_{0,C_1{S}_2,A^{″}}{R}^{\prime }}}{A_{0,C_1}^{″}}\hfill & \hfill \frac{\overline{B_{0,C_1{S}_2,A^{\prime }}{R}^{\prime }}}{A_{0,C_1}^{\prime }}\hfill & \hfill \frac{\overline{B_{0,C_2{S}_2,A^{″}}{R}^{\prime }}}{A_{0,C_2}^{″}}\hfill & \hfill \frac{\overline{B_{0,C_2{S}_2,A^{\prime }}{R}^{\prime }}}{A_{0,C_2}^{\prime }}\hfill \end{array}\right],$$

$${\mathrm{G}}_{D_{1}S}=2\left[\begin{array}{c}\hfill \frac{\overline{B_{0,D_1{S}_1,A^{″}}{R}^{″}}}{A_{0,D_1}^{″}}\hfill \\ \hfill \frac{\overline{B_{0,D_1{S}_1,A^{″}}{R}^{\prime }}}{A_{0,D_1}^{″}}\hfill \\ \hfill \frac{\overline{B_{0,D_1{S}_1,A^{″}}{R}^{″}}}{A_{0,D_1}^{″}}\hfill \\ \hfill \frac{\overline{B_{0,D_1{S}_2,A^{″}}{R}^{\prime }}}{A_{0,D_1}^{″}}\hfill \end{array}\right].$$

We also define a vector A_CS of amplitudes that must be commanded by the DAC to the compensation coils

$${\mathbf{A}}_{CS}=\left[\begin{array}{c}\hfill A_{C_1}^{″}\hfill \\ \hfill A_{C_1}^{\prime }\hfill \\ \hfill A_{C_2}^{″}\hfill \\ \hfill A_{C_2}^{\prime }\hfill \end{array}\right].$$

It is then possible to solve for A_CS by applying a matrix inversion

$${\mathbf{A}}_{CS}=-{\mathbf{G}}_{CS}^{-1}{\mathbf{G}}_{DS}{A}_{D_1}^{″}.$$ (16)

The compensation measurements and calibration calculations are then performed at the reference frequencies used for the remaining drive coils to create field free measurements at the fluxgate locations at all AC modulation frequencies simultaneously. These field free measurements allow many coils and frequencies to be applied simultaneously without saturating the fluxgate sensors.

2.2.2. Coil-to-Sensor Phase Lags and Geometric Gains

The compensation algorithm described in the prior section does not require explicit calculations of the phase lags between the drive coils or compensation coils and the fluxgate sensors. It also does not require calculation of the geometric gains between the coils and sensors. This phase lag and gain information is implicit in the compensation data set and solution. However, calculation of the phase lags and gains is useful information for monitoring the stability of the system over time and for obtaining calibrated estimates of the magnetic susceptibility of a sample. It should be noted that these phase lags and gains result from the practical implementation of the system model, which is from digital input to digital output and encompasses all of the hardware and geometric conditions in between.

The phase delays between the drive coils and fluxgate sensors can be calculated using measurement data obtained using data driven by the sine amplitude calibration data

$${\varphi }_{D_i{S}_k}={\tan }^{-1}\left(\frac{\overline{B_{0,D_i{S}_k{A}^{″}}{R}^{\prime }}}{\overline{B_{0,D_i{S}_k{A}^{″}}{R}^{″}}}\right)$$ (17)

or equivalently from the cosine amplitude calibration data

$${\varphi }_{D_i{S}_k}={\tan }^{-1}\left(\frac{\overline{B_{0,D_i{S}_k{A}^{\prime }}{R}^{″}}}{\overline{B_{0,D_i{S}_k{A}^{\prime }}{R}^{\prime }}}\right).$$ (18)

The geometric gains between the drive coils and fluxgates are similarly obtained from the magnitude of the sine calibration data

$$G_{D_i{S}_k}=\frac{2}{A_{0,D_1}}\sqrt{{\left(\overline{B_{0,D_i{S}_k{A}^{″}}{R}^{″}}\right)}^2+{\left(\overline{B_{0,D_i{S}_k{A}^{″}}{R}^{\prime }}\right)}^2}$$ (19)

or the cosine calibration data

$$G_{D_i{S}_k}=\frac{2}{A_{0,D_i}}\sqrt{{\left(\overline{B_{0,D_i{S}_k{A}^{\prime }}{R}^{″}}\right)}^2+{\left(\overline{B_{0,D_i{S}_k{A}^{\prime }}{R}^{\prime }}\right)}^2}.$$ (20)

The phase lags and gains relating the compensation coils to the fluxgate sensors are obtained in the same manner as the calculations above. An alternative to this measurement-based approach is to precisely model the fields of the drive and compensation coils and model the circuitry to obtain models of the generated fields and phase lags, and to use the relative positions, orientations and system characteristics of the fluxgate sensors to obtain the geometric gains and the phase lag contributions from the sensors.

2.2.3. Measurement of Induced Fields

The magnetic field strength at the nth sample volume V of mNPs is the sum of contributions from drive coils and compensation coils

$$H_{DC,V_n}=\sum _i{H}_{D_i{V}_n}+\sum _j{H}_{C_j{V}_n}.$$ (21)

At reference frequency f₀, the field strength at the nth voxel from the ith drive coil is

$$H_{D_{i}C,V_n}=G_{D_i{V}_n}\left(A_{D_i}^{″}\sin (2\pi f_{0}t+{\varphi }_{D_i{S}_k})+A_{D_i}^{\prime }\cos (2\pi f_{0}t+{\varphi }_{D_i{S}_k})\right)+\sum _j{G}_{C_j{V}_n}\left(A_{C_i}^{″}\sin (2\pi f_{0}t+{\varphi }_{C_j{S}_k})+A_{C_j}^{\prime }\cos (2\pi f_{0}t+{\varphi }_{C_j{S}_k})\right),$$ (22)

where H_Di,Vn and H_Cj,Vn are the geometric gains between a drive or compensation coil respectively and a given voxel. The magnetic induction per unit volume V of the sample combines the influences of the applied field and the concentration of nth sample volume. The magnetic induction field from the sample as measured at the fluxgate sensors S includes a geometric gain G_VnSk relating the nth sample volume to the kth sensor along its measurement axis

$$B_{D_{i}C,V_n,S_k}=G_{V_n{S}_k}{\left[mNP\right]}_n{H}_{D_{i}C,V_n},$$ (23)

where [mNP]_n is the concentration of mNPs in the nth location. Substituting (22) for H_DiC,Vn and assuming an mNP related phase shift associated the AC susceptibility response from each voxel to each sensor ϕ_VnSk we obtain an expression for the measured magnetic field

$$B_{D_{i}C,V_n,S_k}=G_{V_n{S}_k}{\left[mNP\right]}_n\left\{G_{D_i{V}_n}\left[A_{D_i}^{″}\left(\sin (2\pi f_{0}t+{\varphi }_{D_i{V}_n}+{\varphi }_{V_i{S}_k})\right)+A_{D_i}^{\prime }\left(\cos (2\pi f_{0}t+{\varphi }_{D_i{V}_n}+{\varphi }_{V_n{S}_k})\right)\right]+\sum _j{G}_{C_j{V}_n}\left[A_{C_i}^{″}\left(\sin (2\pi f_{0}t+{\varphi }_{C_j{V}_n}+{\varphi }_{V_n{S}_k})\right)+A_{C_j}^{\prime }\left(\cos (2\pi f_{0}t+{\varphi }_{C_j{V}_n}+{\varphi }_{V_n{S}_k})\right)\right]\right\}.$$ (24)

Expanding (24) and substituting (4) and (5) for the reference sine and cosine terms we obtain

$$B_{D_{i}C,V_n,S_k}=G_{V_n{S}_k}{\left[mNP\right]}_n\left\{G_{D_i{V}_n}[A_{D_i}^{″}\left(\sin ({\varphi }_{D_i{V}_n}+{\varphi }_{V_n{S}_k})R^{\prime }+\cos ({\varphi }_{D_i{V}_n}+{\varphi }_{V_n{S}_k})R^{″}\right)+\sum _j{G}_{C_j{V}_n}\left[A_{C_i}^{″}\left(\sin ({\varphi }_{C_j{V}_n}+{\varphi }_{V_n{S}_k})R^{\prime }+\cos ({\varphi }_{C_j{V}_n}+{\varphi }_{V_n{S}_k})R^{″}\right)+A_{C_j}^{\prime }\left(-\sin ({\varphi }_{C_j{V}_n}+{\varphi }_{V_n{S}_k})R^{″}+\cos ({\varphi }_{C_j{V}_n}+{\varphi }_{V_n{S}_k})R^{\prime }\right)\right]\phantom{]}\right\}.$$ (25)

The measured field expression (25) can be condensed by defining 3-point geometric gains and phases that account for the coupling from a drive coil to a sample volume and from a sample volume to a fluxgate sensor

$$\begin{array}{cc}\hfill G_{D_i{V}_n{S}_k}=& G_{D_i{V}_n}{G}_{V_n{S}_k},\hfill \\ \hfill {\varphi }_{D_i{V}_n{S}_k}=& {\varphi }_{D_i{V}_n}+{\varphi }_{V_n{S}_k}.\hfill \end{array}$$ (26)

Similar 3-point gain and phase terms are defined for the compensation coils

$$\begin{array}{cc}\hfill G_{C_j{V}_n{S}_k}=& G_{C_j{V}_n}{G}_{V_n{S}_k},\hfill \\ \hfill {\varphi }_{C_j{V}_n{S}_k}=& {\varphi }_{C_j{V}_n}+{\varphi }_{V_n{S}_k}.\hfill \end{array}$$ (27)

Further defining sine components and cosine components of the gains and phases

$$\begin{array}{cc}\hfill G_{D_i{V}_n{S}_k}^{″}=& G_{D_i{V}_n{S}_k}\sin \left({\varphi }_{D_i{V}_n{S}_k}\right),\hfill \\ \hfill G_{D_i{V}_n{S}_k}^{\prime }=& G_{D_i{V}_n{S}_k}\cos \left({\varphi }_{D_i{V}_n{S}_k}\right),\hfill \end{array}$$ (28)

and

$$\begin{array}{cc}\hfill G_{C_j{V}_n{S}_k}^{″}=& G_{C_j{V}_n{S}_k}\sin \left({\varphi }_{C_j{V}_n{S}_k}\right),\hfill \\ \hfill G_{C_j{V}_n{S}_k}^{\prime }=& G_{C_j{V}_n{S}_k}\cos \left({\varphi }_{C_j{V}_n{S}_k}\right),\hfill \end{array}$$ (29)

it is possible to rewrite (25) as

$$B_{D_{i}C,V_n,S_k}={\left[mNP\right]}_n\left\{[A_{D_i}^{″}\left(G_{D_i{V}_n{S}_k}^{″}{R}^{\prime }+G_{D_i{V}_n{S}_k}^{\prime }{R}^{″}\right)+\sum _j\left[A_{C_i}^{″}\left(G_{C_j{V}_n{S}_k}^{″}{R}^{\prime }+G_{C_j{V}_n{S}_k}^{\prime }{R}^{″}\right)+A_{C_j}^{\prime }\left(G_{C_j{V}_n{S}_k}^{″}{R}^{″}+G_{C_j{V}_n{S}_k}^{″}{R}^{″}\right)\right]\phantom{]}\right\}.$$ (30)

Mixing the model of the measured induction field with the reference sine and averaging over time converges to the scalar quantity

$$\overline{B_{D_{i}C,V_n,S_k}{R}^{″}}={\left[mNP\right]}_n\left\{A_{D_i}^{″}{G}_{D_i{V}_n{S}_k}^{\prime }+\sum _j\left(A_{C_j}^{″}{G}_{C_j{V}_n{S}_k}^{\prime }+A_{C_j}^{\prime }{G}_{C_j{V}_n{S}_k}^{″}\right)\right\}.$$ (31)

Alternatively mixing the measured induction field with a reference cosine and time averaging converges to

$$\overline{B_{D_{i}C,V_n,S_k}{R}^{\prime }}={\left[mNP\right]}_n\left\{A_{D_i}^{″}{G}_{D_i{V}_n{S}_k}^{″}+\sum _j\left(A_{C_j}^{\prime }{G}_{C_j{V}_n{S}_k}^{\prime }+A_{C_j}^{″}{G}_{C_j{V}_n{S}_k}^{″}\right)\right\}.$$ (32)

2.2.4. Coil-to-Voxel-to-Sensor Geometric Gains

The 3-point geometric gains that relate the drive or compensation coils to the sample volumes and then to the sensors can be obtained from additional empirical calibration measurements or by theoretical modeling of the generated, induced, and measured fields. The empirical approach entails turning on the sine or cosine of a drive or compensation coil and mixing with a reference signal and averaging to obtain the following approach calibration measurements

$$\begin{array}{cc}\hfill G_{D_i{V}_n{S}_k}^{\prime }=& \frac{\overline{B_{0,D_i,V_n,S_k}{R}^{″}}}{{\left[mNP\right]}_{0,n}{A}_{0,D_i}^{″}},\hfill \\ \hfill G_{D_i{V}_n{S}_k}^{″}=& \frac{\overline{B_{0,D_i,V_n,S_k}{R}^{\prime }}}{{\left[mNP\right]}_{0,n}{A}_{0,D_i}^{″}},\hfill \\ \hfill G_{C_j{V}_n{S}_k}^{\prime }=& \frac{\overline{B_{0,C_j,V_n,S_k}{R}^{″}}}{{\left[mNP\right]}_{0,n}{A}_{0,C_j}^{″}},\hfill \\ \hfill G_{C_j{V}_n{S}_k}^{″}=& \frac{\overline{B_{0,C_j,V_n,S_k}{R}^{\prime }}}{{\left[mNP\right]}_{0,n}{A}_{0,C_j}^{″}}.\hfill \end{array}$$ (33)

Three-point geometric gains are needed to reconstruct tomographic images of the magnetic susceptibility in multiple volumes (a.k.a. voxels) that comprise the imaging field of view. In a system with I drive coils, J compensation coils and K sensors, N voxels, there are 2(I + J)KN scalar 3-point gains.

2.2.5. Tomographic Imaging

The challenge of working with arrays of drive coils, fluxgate sensors, and sample volumes is that there is mixing of the induced fields from magnetically susceptible material in the measurements. The benefit of the array measurement approach is that the information contained in these mixed measurements can be inverted to form spatial images. Solving this inverse problem is referred to as tomographic imaging.

When multiple sample volumes are present, the magnetic induction field associated with the ith drive coil and measured by the kth fluxgate sensor results from the sum of the induction fields from all of the sample volumes, which are indexed by n in the expression

$$B_{D_{i}C,V,S_k}=\sum _n{G}_{V_n{S}_k}{\left[mNP\right]}_n{H}_{D_{i}C,V_n}.$$ (34)

Mixing the fluxgate measurements with the sine and cosine reference signals and averaging over time yields the sum of contributions from all sample volumes

$$\left[\begin{array}{c}\hfill \overline{B_{D_{i}C,V,S_k}{R}^{″}}\hfill \\ \hfill \overline{B_{D_{i}C,V,S_k}{R}^{\prime }}\hfill \end{array}\right]=\sum _n\left(\left[\begin{array}{c}\hfill A_{D_i}^{″}{G}_{D_i{V}_n{S}_k}^{\prime }+\sum _j\left(A_{C_j}^{″}{G}_{C_j{V}_n{S}_k}^{\prime }+A_{C_j}^{\prime }{G}_{C_j{V}_n{S}_k}^{″}\right)\hfill \\ \hfill A_{D_i}^{″}{G}_{D_i{V}_n{S}_k}^{″}+\sum _j\left(A_{C_j}^{\prime }{G}_{C_j{V}_n{S}_k}^{\prime }+A_{C_j}^{″}{G}_{C_j{V}_n{S}_k}^{″}\right)\hfill \end{array}\right]{\left[mNP\right]}_n\right)$$ (35)

This can be simplified by introducing combined gain terms from the ith drive coil, nth voxel, and kth sensor

$$\begin{array}{cc}\hfill K_{D_{i}C,V_n{S}_k}^{″}=& A_{D_i}^{″}{G}_{D_i{V}_n{S}_k}^{\prime }+\sum _j\left(A_C^{″}{G}_{C{V}_n{S}_k}^{\prime }+A_C^{\prime }{G}_{C{V}_n{S}_k}^{″}\right),\hfill \\ \hfill K_{D_{i}C,V_n{S}_k}^{\prime }=& A_{D_i}^{″}{G}_{D_i{V}_n{S}_k}^{″}+\sum _j\left(A_C^{\prime }{G}_{C{V}_n{S}_k}^{\prime }+A_C^{″}{G}_{C{V}_n{S}_k}^{″}\right).\hfill \end{array}$$ (36)

This results in a concise linear equation relating mNP concentrations to the measured fields.

$$\left[\begin{array}{c}\hfill \overline{B_{D_{i}C,V,S_k}{R}^{″}}\hfill \\ \hfill \overline{B_{D_{i}C,V,S_k}{R}^{\prime }}\hfill \end{array}\right]=\sum _n\left(\left[\begin{array}{c}\hfill K_{D_{i}C,V_n{S}_k}^{″}\hfill \\ \hfill K_{D_{i}C,V_n{S}_k}^{\prime }\hfill \end{array}\right]{\left[m\mathrm{NP}\right]}_n\right)$$ (37)

If the product of the number of drive coils and sensors equals the number of sample volumes, then the above summation can be arranged into a matrix-form linear model that can be inverted to solve for the sample concentrations. In our system with 3 drive coils, 2 sensors and 6 voxels, the system model is

$$\mathbf{B}=\mathbf{KC},$$ (38)

where

$$\left[\begin{array}{c}\hfill \overline{B_{D_{1}C,V,S_1}{R}^{″}}\hfill \\ \hfill \overline{B_{D_{1}C,V,S_1}{R}^{\prime }}\hfill \\ \hfill \overline{B_{D_{1}C,V,S_2}{R}^{″}}\hfill \\ \hfill \overline{B_{D_{1}C,V,S_2}{R}^{\prime }}\hfill \\ \hfill \overline{B_{D_{2}C,V,S_1}{R}^{″}}\hfill \\ \hfill \overline{B_{D_{2}C,V,S_1}{R}^{\prime }}\hfill \\ \hfill \overline{B_{D_{2}C,V,S_2}{R}^{″}}\hfill \\ \hfill \overline{B_{D_{2}C,V,S_2}{R}^{\prime }}\hfill \\ \hfill \overline{B_{D_{3}C,V,S_1}{R}^{″}}\hfill \\ \hfill \overline{B_{D_{3}C,V,S_1}{R}^{\prime }}\hfill \\ \hfill \overline{B_{D_{3}C,V,S_2}{R}^{″}}\hfill \\ \hfill \overline{B_{D_{1}C,V,S_1}{R}^{\prime }}\hfill \end{array}\right]=\left[\begin{array}{cccccc}\hfill K_{D_{1}C{V}_1{S}_1}^{″}\hfill & \hfill K_{D_{1}C{V}_2{S}_1}^{″}\hfill & \hfill K_{D_{1}C{V}_3{S}_1}^{″}\hfill & \hfill K_{D_{1}C{V}_4{S}_1}^{″}\hfill & \hfill K_{D_{1}C{V}_3{S}_1}^{″}\hfill & \hfill K_{D_{1}C{V}_6{S}_1}^{″}\hfill \\ \hfill K_{D_{1}C{V}_1{S}_1}^{\prime }\hfill & \hfill K_{D_{1}C{V}_2{S}_1}^{\prime }\hfill & \hfill K_{D_{1}C{V}_3{S}_1}^{\prime }\hfill & \hfill K_{D_{1}C{V}_4{S}_1}^{\prime }\hfill & \hfill K_{D_{1}C{V}_5{S}_1}^{\prime }\hfill & \hfill K_{D_{1}C{V}_6{S}_1}^{\prime }\hfill \\ \hfill K_{D_{1}C{V}_1{S}_2}^{″}\hfill & \hfill K_{D_{1}C{V}_2{S}_2}^{″}\hfill & \hfill K_{D_{1}C{V}_3{S}_2}^{″}\hfill & \hfill K_{D_{1}C{V}_4{S}_2}^{″}\hfill & \hfill K_{D_{1}C{V}_5{S}_2}^{″}\hfill & \hfill K_{D_{1}C{V}_6{S}_2}^{″}\hfill \\ \hfill K_{D_{1}C{V}_1{S}_2}^{\prime }\hfill & \hfill K_{D_{1}C{V}_2{S}_2}^{\prime }\hfill & \hfill K_{D_{1}C{V}_3{S}_2}^{\prime }\hfill & \hfill K_{D_{1}C{V}_4{S}_2}^{\prime }\hfill & \hfill K_{D_{1}C{V}_5{S}_2}^{\prime }\hfill & \hfill K_{D_{1}C{V}_6{S}_2}^{\prime }\hfill \\ \hfill K_{D_{2}C{V}_1{S}_1}^{″}\hfill & \hfill K_{D_{2}C{V}_2{S}_1}^{″}\hfill & \hfill K_{D_{2}C{V}_3{S}_1}^{″}\hfill & \hfill K_{D_{2}C{V}_4{S}_1}^{″}\hfill & \hfill K_{D_{2}C{V}_5{S}_1}^{″}\hfill & \hfill K_{D_{2}C{V}_6{S}_1}^{″}\hfill \\ \hfill K_{D_{2}C{V}_1{S}_1}^{\prime }\hfill & \hfill K_{D_{2}C{V}_2{S}_1}^{\prime }\hfill & \hfill K_{D_{2}C{V}_3{S}_1}^{\prime }\hfill & \hfill K_{D_{2}C{V}_4{S}_1}^{\prime }\hfill & \hfill K_{D_{2}C{V}_5{S}_1}^{\prime }\hfill & \hfill K_{D_{2}C{V}_6{S}_1}^{\prime }\hfill \\ \hfill K_{D_{2}C{V}_1{S}_2}^{″}\hfill & \hfill K_{D_{2}C{V}_2{S}_2}^{″}\hfill & \hfill K_{D_{2}C{V}_3{S}_2}^{″}\hfill & \hfill K_{D_{2}C{V}_4{S}_2}^{″}\hfill & \hfill K_{D_{2}C{V}_5{S}_2}^{″}\hfill & \hfill K_{D_{2}C{V}_6{S}_2}^{″}\hfill \\ \hfill K_{D_{2}C{V}_1{S}_2}^{\prime }\hfill & \hfill K_{D_{2}C{V}_2{S}_2}^{\prime }\hfill & \hfill K_{D_{2}C{V}_3{S}_2}^{\prime }\hfill & \hfill K_{D_{2}C{V}_4{S}_2}^{\prime }\hfill & \hfill K_{D_{2}C{V}_5{S}_2}^{\prime }\hfill & \hfill K_{D_{2}C{V}_6{S}_2}^{\prime }\hfill \\ \hfill K_{D_{3}C{V}_1{S}_1}^{″}\hfill & \hfill K_{D_{3}C{V}_2{S}_1}^{″}\hfill & \hfill K_{D_{3}C{V}_3{S}_1}^{″}\hfill & \hfill K_{D_{3}C{V}_4{S}_1}^{″}\hfill & \hfill K_{D_{3}C{V}_5{S}_1}^{″}\hfill & \hfill K_{D_{3}C{V}_6{S}_1}^{″}\hfill \\ \hfill K_{D_{3}C{V}_1{S}_1}^{\prime }\hfill & \hfill K_{D_{3}C{V}_2{S}_1}^{\prime }\hfill & \hfill K_{D_{3}C{V}_3{S}_1}^{\prime }\hfill & \hfill K_{D_{3}C{V}_4{S}_1}^{\prime }\hfill & \hfill K_{D_{3}C{V}_5{S}_1}^{\prime }\hfill & \hfill K_{D_{3}C{V}_6{S}_1}^{\prime }\hfill \\ \hfill K_{D_{3}C{V}_1{S}_2}^{″}\hfill & \hfill K_{D_{3}C{V}_2{S}_2}^{″}\hfill & \hfill K_{D_{3}C{V}_3{S}_2}^{″}\hfill & \hfill K_{D_{3}C{V}_4{S}_2}^{″}\hfill & \hfill K_{D_{3}C{V}_5{S}_2}^{″}\hfill & \hfill K_{D_{3}C{V}_6{S}_2}^{″}\hfill \\ \hfill K_{D_{3}C{V}_1{S}_2}^{\prime }\hfill & \hfill K_{D_{3}C{V}_2{S}_2}^{\prime }\hfill & \hfill K_{D_{3}C{V}_3{S}_2}^{\prime }\hfill & \hfill K_{D_{3}C{V}_4{S}_2}^{\prime }\hfill & \hfill K_{D_{3}C{V}_5{S}_2}^{\prime }\hfill & \hfill K_{D_{3}C{V}_6{S}_2}^{\prime }\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\left[mNP\right]}_1\hfill \\ \hfill {\left[mNP\right]}_2\hfill \\ \hfill {\left[mNP\right]}_3\hfill \\ \hfill {\left[mNP\right]}_4\hfill \\ \hfill {\left[mNP\right]}_5\hfill \\ \hfill {\left[mNP\right]}_6\hfill \end{array}\right]$$

The concentrations can be calculated using a Moore-Penrose pseudo-inversion

$$\mathbf{C}={\left({\mathbf{K}}^T\mathbf{K}\right)}^{-1}{\mathbf{K}}^T\mathbf{B}.$$ (39)

In this image reconstruction, we have twice as many gain terms as needed for a normal matrix inversion. This apparent redundancy arises from separately calculating in-phase and the out-of-phase components of the mNPs response. The pseudo-inversion operation in (39) recombines these components into a single image.

2.3. Nanoparticles

Testing was performed using mNPs of three different sizes. The largest mNPs had a hydrodynamic diameter of 100 nm Fe₃O₄ and were starch-coated nanoparticles (10-00-102, micromod Partikeltechnologie GmbH, Rostock, Germany). These mNPs were diluted to 12.5 mg Fe/ml and placed in 0.5 ml Eppendorf tubes. The AC magnetic susceptibility properties of these mNPs have previously been reported (Gruttner, Muller et al. 2007; Dennis, Jackson et al. 2009). The intermediate size mNPs had a core of 40 nm diameter Fe₃O₄ with 10 nm polyethylene glycol (PEG) coatings (SHP-40, Ocean NanoTech LLC, Springdale, AR, USA). The smallest sized mNPs were also from Ocean Nanotech and had a 10 nm core diameter with 10 nm PEG coatings (SHP-10). Both of the Ocean Nanotech mNPs were concentrated at 5 mg Fe/ml and also placed in 0.5 ml Eppendorf tubes.

2.4. Experimental Procedures

To test the performance and feasibility of our prototype, we performed a series of experiments. These experiments were also intended to demonstrate the feasibility of expansion to a larger imaging array.

2.4.1. Noise Testing

A question central to the feasibility of this approach is measurement of the system noise and the ability to compensate the residual magnetic field at the fluxgate sensors. Noise was assessed with and without active field compensation to determine if noise was injected into the measured magnetic fields due to the compensation coils. The Welch method was used to plot the noise power spectrum with and without a compensation field. This was done using a Blackman window of 2¹⁸ data points, a Fourier transform of 2²⁰ data points and a sampling rate of 20 kHz.

2.4.2. Compensation Testing

The compensation algorithm was tested by comparing the magnetic fields prior to and during active compensation. This test measures the effectiveness of digital compensation across fluxgates and drive coils. A 10 s measurement was made at 1 Hz without compensation on all six channels and then repeated with compensation. To measure the compensation, three frequencies (625, 725 and 825 Hz) were chosen for the drive coils. Each drive coil was turned on for 20 s with a single frequency and each compensator coil was turned on for 20 s at all three frequencies. The gain terms for active compensation were calculated as described in section 2.2.

2.4.3. Distance Sensitivity and Concentration Linearity

Distance sensitivity was assessed with a 12.5 mg Fe/ml sample of 100 nm mNPs in a 0.5 mL Eppendorf tube that was moved away from the sensor in increments of 0.5 cm. The sample was initially placed 0.5 cm from the sensor and moved to a distance of 3 cm. The sample was held in each position for 30 s with an initial 30 s used to determine the residual field at the sensor. By subtracting the residual field amplitude from each measurement it was possible to determine the induced field amplitude at each of the 6 positions. Since the magnetic field amplitude is proportional to a complex geometric factor based on distance, the logarithm of the data was taken to show the sensitivity of the induced magnetic field with respect to distance.

Concentration linearity was assessed using a serial dilution of 100 nm particles in 0.5 ml tubes. Five samples were prepared, starting at 12.5 mg Fe/ml down to 0.782 mg Fe/ml. These samples were used to test the sensitivity of the prototype at a depth of 0.5 cm. Each sample was held in position for 30 s with an initial 30 s used to find the residual magnetic field at the sensor. Using the measured field amplitude it is possible to compute the induced field by subtracting the residual field from each of the measurements. Measurements were computed at 10 Hz and fit to a line to evaluate the linearity of the system with respect to concentration.

2.4.4. System mNP Response

To show that our approach is not limited to functioning with a single size of mNP or a single operating frequency, three different nanoparticles were measured at several frequencies. The system was designed to operate in the frequency range between 500–950 Hz so the induced field of the nanoparticles was measured between 525–925 Hz at 100 Hz intervals. A single drive coil was used to create all five frequencies simultaneously and the induced field was measured with a single fluxgate sensor. The residual field was measured for 30 s and then the nanoparticle sample was placed 0.5 cm from the sample for 30 s. Each sample was 0.25 ml of mNP solution in a 0.5 ml tube. The 100 nm Micromod mNP sample had a concentration of 25 mg Fe/ml while the 10 nm and 40 nm Ocean NanoTech mNPs had concentrations of 5 mg Fe/ml. The in-phase and outof-phase fields were computed using a digital lock-in amplifier. This was done for each of the three mNP samples. This measurement does not isolate the frequency response of the mNPs from the imager electronics so it is referred to as a system frequency response for the mNP samples. To facilitate comparisons between samples, the system frequency responses were normalized by the respective mNP concentrations.

2.4.5. Tomographic Imaging

Tomographic imaging was performed using a 100 nm samples concentrated at 12.5 mg Fe/ml and 6.25 mg Fe/ml. Line imaging was performed perpendicular to the fluxgate sensors at distances of 0.5 cm and 1 cm. Six imaging positions were used, spaced 1 cm from each other and spanning the distance between each of the fluxgate sensors. Calibration was first performed with AC currents at either 625, 725 or 825 Hz and running the compensation algorithm to minimize the residual field at each of the sensors. The imaging calibration procedure involved placing the 12.5 mg Fe/ml in each of the six imaging position for 20 s and determining the gain coefficients described in section 2.2.5. Once the gain coefficients were determined, tomographic imaging was performed on new data by placing the sample in an imaging position for 20 s before being moved to the next position. Several imaging tests were performed. The 12.5 mg Fe/ml was imaged at 0.5 cm and at 1 cm and the 6.25 mg Fe/ml sample was imaged at 0.5 cm. Due to the limited induced field at 1 cm, a 4-voxel image was also constructed to show the performance when the largest distance between drive coil and sensor is reduced. To demonstrate de-mixing of multiple mNP samples imaged simultaneously, a 12.5 mg Fe/ml and a 6.25 mg Fe/ml sample were simultaneously placed in different voxels at a depth of 0.5 cm. One of the samples was then moved to a new voxel location every 20 s for 120 s.

2.4.6 Biological Demonstration

To demonstrate that mNP imaging can be performed in a biological sample, an approximately 28 g uncooked pork sausage (Product code 2378, McKenzie Maple Breakfast Link Sausage, Burlington, VT, USA) was used as a background medium. The side of the sausage was located a distance of 0.5 cm from the sensor and contained in a 2 cm wide × 2 cm deep × 10.5 cm long plastic holder. Four wells were created in the sausage corresponding approximately to each of the four middle voxel locations spaced by 1 cm. The distance from the sensor to each of these wells was approximately 1 cm. The sausage and samples for injection were allowed to equilibrate to room temperature. A calibration run was then performed using 0.25 ml of 12.5 mg Fe/ml mNPs in an Eppendorf tube by placing the tube in each of the four wells of the sausage. Eppendorf tubes were not used during the subsequent imaging experiment. During the imaging experiment, direct injections of 0.2 ml of 100 nm mNPs concentrated at 12.5 mg Fe/ml or 0.2 ml of saline were alternately delivered into each of the four wells in the sausage at 40 s intervals. The sequence of injections was to inject saline into well 1 and wait 40 s, then inject mNP into well 2 and wait another 40 s and then repeat for wells 3 and 4.

3. Results

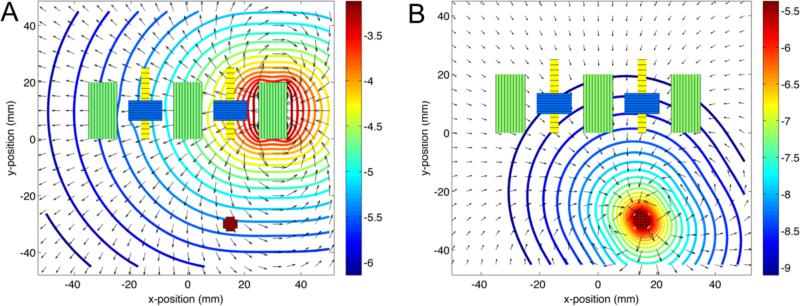
The simulator allows for visualization of the magnetic field components from the drive and compensation coils and the mNPs (figure 4). The fluxgates are only sensitive to field components along the y-axis, which spatially averages to zero at the fluxgates due to field nulling by the compensation coils. The cross field on the fluxgate from the adjacent drive coil was approximately 100 μT, which is within the 1 mT operating range of the chosen fluxgate sensor (model FLC-100). The simulated applied field was 1 mT at the center of the drive coil, 10 μT at the mNP sample located at 2 cm depth. Assuming χ_v = 1.97 (MKS units corresponding to 100 nm Fe₃O₄ magnetite core Micromod nanoparticles). The mNP signal level near the fluxgates was approximately 10 nT.

Figure 4.

Top view of the simulation setup with magnetic field magnitudes indicated by the contours in log₁₀(T) and the field directions indicated by the arrows. A: Field from 30 mA in the right drive coil (450 turns) with both compensation coils on. B: Magnetic induction field from the mNP sample centered at a distance of 30 mm from the nearest fluxgate.

The approximate costs of the prototype components are provided in table 1. In addition the table was extended to include estimated component costs of a 64-voxel and 1024-voxel imaging system based on extending the costs of the existing prototype.

Table 1.

Cost of materials (USD) for the 6-voxel prototype and estimated costs for larger 64-voxel and 1024-voxel imaging systems.

Components	6-voxel prototype ($)	64-voxel imager ($)	1024-voxel imager ($)
Sensors, coils	428	1705	6820
Amplifiers, DAC, ADC*	2833	411	1644
Resistors, capacitors	59	263	1052
Adapters, boards, power supply, misc.	285	634	2536
Controller*	2775	46	234
Total	6380	3059	12286

^*Lower cost chip-based ADC and controller components are specified for the 64-voxel and 1024-voxel systems instead of the more costly general purpose NI-USB 6289 used in the current 6-voxel prototype.

3.1. Noise Spectra

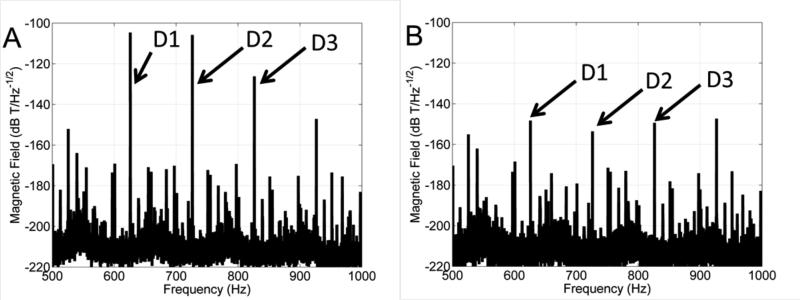
The noise power spectrum is shown with and without compensation (figure 5). The noise power does not change with and without compensation for the field strengths used with this prototype. It is also possible to see the effects of 60 Hz power line harmonic noise. Despite this, it is possible to select frequencies that have minimal interference from 60 Hz noise. For experimental imaging, the frequencies chosen were 625, 725 and 825 Hz. The noise power at these frequencies was 66, 36 and 26 pT RMS respectively.

Figure 5.

Noise spectral density calculated using the Welch method. The noise spectrum is plotted without active compensation (A) and with active compensation (B). The spectral lines corresponding to the three drive coils are indicated by the arrows. The noise amplitude is 66, 36 and 26 pT RMS at 625, 725 and 825 Hz respectively.

3.2. Compensation Efficacy

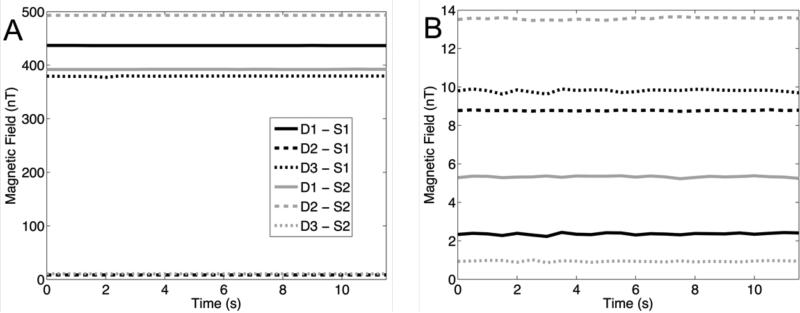
The residual fields at the sensors prior to and during active compensation are shown in figure 6. Before compensation, 4 channels have field amplitudes between 350–500 nT while the other two channels have field amplitudes less than 30 nT. The strong interactions are due to sensor and drive coils being in close proximity or geometric alignment. After compensation each of the channels have residual field amplitudes less than 15 nT. Compensation effectiveness measured as the uncompensated to compensated magnetic field ratios are as high as 185 (D1-S1=185, D2-S1=0.940, D3-S1=38.7, D1-S2=73.6, D2-S2=36.4, D3-S2=11.2).

Figure 6.

Compensation results. A: Uncompensated magnetic fields from each of the drive coils D to each of the sensors S. B: Compensated magnetic fields. In all cases the compensated fields were reduced to below 15 nT.

3.3 Concentration and Distance Sensitivity Results

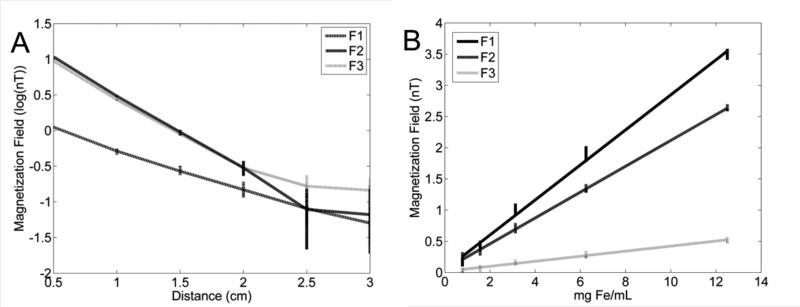
Distance sensitivity to the 100 nm mNPs is shown in figure 7A. The measurements are from one fluxgate at three frequencies (F1 = 625 Hz, F2 = 725 Hz, F3 = 825 Hz), each applied to a different drive coil. The magnetic induction fields are plotted on a log scale to linearize the expected geometric fall off rate of the measurements. The readouts in figure 7A appear to remain linear until the 2–2.5 cm distance range. Readouts in the 2.5–3 cm range appear to be effected by noise. From previous measurements of the noise spectrum, the noise floor should be between 30–50 nT, which is between –1.3 to –1.5 on a log scale. To quantify the distance sensitivity threshold, a two-sided t-test was performed on data at adjacent positions. Measured means were found to be significantly different (p < 0.01) until the 2–2.5 cm distances but not beyond.

Figure 7.

A: Illustration of depth sensitivity. The sample was initially placed at 0.5 cm and moved 0.5 cm every 30 s. The data is plotted as log₁₀ for all three drive coils and one fluxgate sensor. Differences in the magnetization field are significantly different until 2.5 cm. B: Concentration linearity. Samples were serially diluted and placed 0.5 cm from the sensor for 30 s. Linear regressions were performed on measurements and in all three cases R² > 0.98 and p < 0.001.

Concentration measurements are shown in figure 7B. The first and second frequencies (F1 and F2) correspond to drive coils situated next to the fluxgate sensor and induce a strong response from the nanoparticles. The third frequency (F3) was used on the drive coil situated several centimeters from the fluxgate sensor and therefore has a much weaker field at the nanoparticle sample. This reduced the response, but it was still above the noise floor. All three channels have a linear response (R² > 0.98, p<0.001)

3.4. System mNP Responses

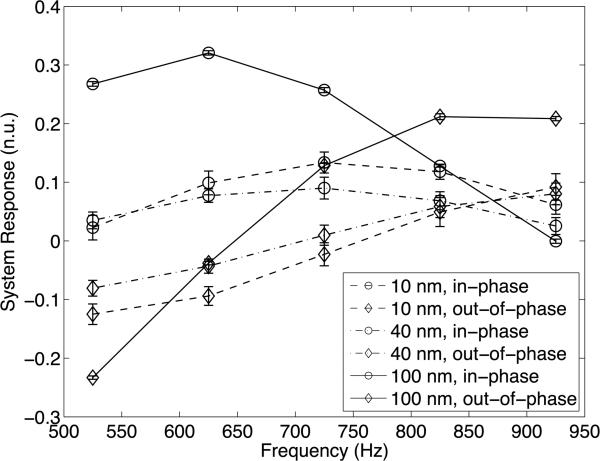
Figure 8 shows the system responses to the mNP samples. The figure shows the in-phase and outof-phase responses of these nanoparticles with respect to the reference signal. In order to properly compare the results, the responses were normalized by the mNP concentrations. From the results, it is apparent that all three mNP samples are detectable by our system. The 100 nm nanoparticles have a stronger response but all three are on the same order of magnitude. In addition, the 100 nm mNPs have a very different shape to their response. The 10 and 40 nm nanoparticles have more similar but still distinguishable responses across the tested frequency range. Error bars are indicated on the plot are standard deviations of the measured responses computed at 1 Hz.

Figure 8.

System frequency responses for different sizes of mNPs. The frequency response of the system to mNP samples is shown over the frequencies from 525–925 Hz. The in-phase and outof-phase components are plotted separately for each of the mNPs. Error bars show the standard deviations of the measurements from 30 s readings processed at 1 Hz.

3.5. Tomographic Imaging Results

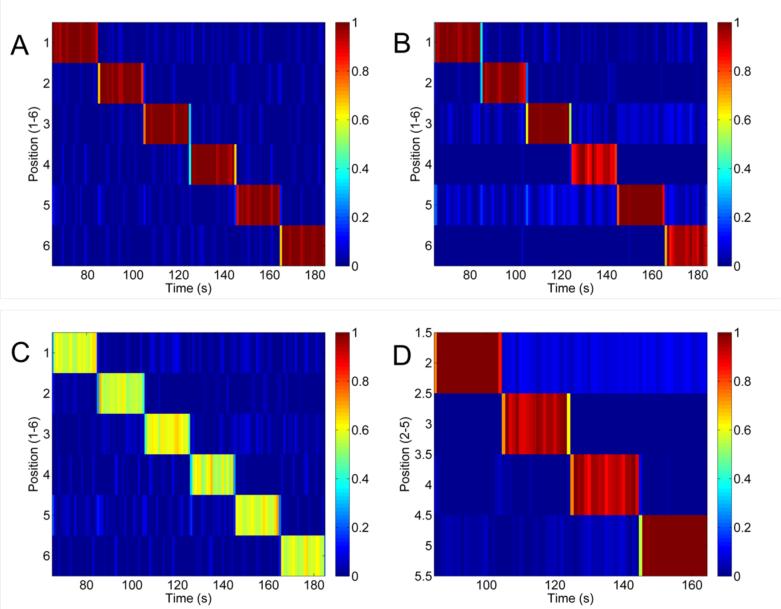
Figure 9A shows the calibration image that is produced after solving for all of the gain terms as described in section 2.2.5 and then solving for the mNP concentrations in the voxels using the calibration data as the input. The imaging contrast to noise (CNR) was computed using the mean of the mNP concentrations in the correct locations divided by the standard deviation of the other positions in the image. In figure 9A, the CNR is 30. Figure 9B is an image produced at 0.5 cm with the same gain terms but a new data set so that the training and test data are not identical. In this case the CNR was reduced to 16. Figure 9C shows line images produced by using a 100 nm sample with approximately half the concentration as the calibration sample. CNR for this image was 14. In Figure 9D the samples were placed at a distance of 1 cm. In this experiment a new calibration was produced at 1 cm. Using the gain terms from the 1 cm calibration, new data was collected with the sample placed in the middle 4 positions. The image at 1 cm was reduced to 4 voxels because the interactions between far coils and the nanoparticle sample are weaker at that distance and make the image significantly noisier than at 0.5 cm. However, the middle 4 voxels have strong interactions and it is possible to produce a clear image. In this image the CNR was found to be 23.

Figure 9.

Tomographic line images for evaluation of imaging CNR. A: Calibration image from data used to create the 6-voxel line image from a 12.5 mg Fe/ml mNP sample at 0.5 cm depth (CNR = 30). B: Line imaging with new test data at 12.5 mg Fe/ml (CNR = 16). C: Test sample concentration reduced to 50% of the calibration sample (CNR = 14). D: 4-voxel images at 1 cm depth using a 12.5 mg Fe/ml mNP sample (CNR = 23).

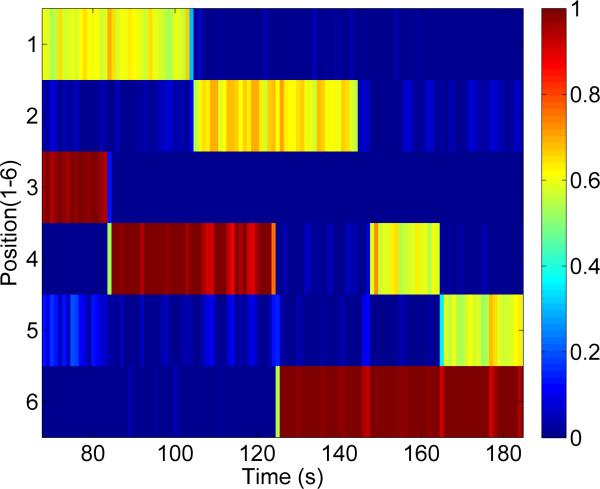
Figure 10 shows a tomographic image of two samples reconstructed at the same time. In this image a full concentration sample and a half concentration sample were imaged at a depth of 0.5 cm. In this image, one of samples was moved to a new voxel every 20 s for a total of 120 s of imaging time.

Figure 10.

Dual mNP imaging. Two mNP samples were imaged simultaneously. One mNP sample was at full concentration and the second was at approximately half concentration. The imaging pattern randomly moves one of the samples to a new location every 20 s.

3.6. Biological Demonstration

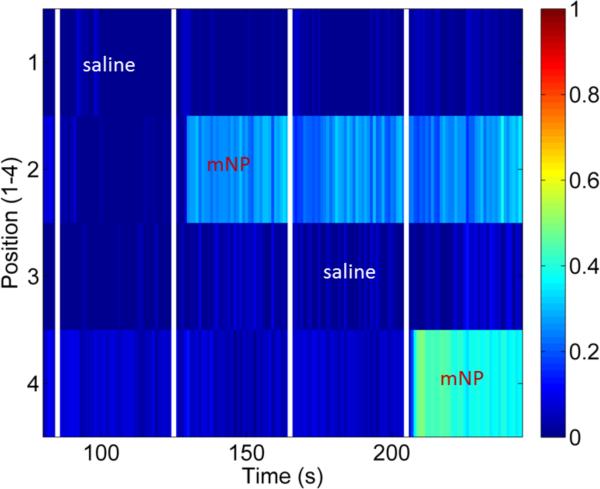
Figure 11 shows the results of alternately injecting pork sausage with approximately 0.2 ml 100 nm mNPs or approximately 0.2 ml of saline in four pre-defined positions with 1 cm spacing. The saline injections had no discernable effect on the sausage image whereas the mNPs injections are clearly distinguishable.

Figure 11.

Injection of mNP and saline into a sausage. Approximately 0.2 ml of saline or 12.5 mg Fe/ml mNP was injected into the sausage at each of the positions in intervals of 40 s. Injections at the times indicated on the figure. The injection positions were approximately 1 cm from the sensor and spaced by 1 cm along the sausage.

4. Discussion and Conclusion

We have developed a bench top prototype for mNP imaging. The prototype met several performance goals that indicate its feasibility to expand into a larger imaging array. The system was built using primarily low cost, off the shelf electronics at a total cost of approximately 6380 USD (most of this cost was in two general purpose NI-USB 6289 devices used in the DAC and ADC arrays). The system was able to measure multiple AC frequencies and reconstruct images at 1 Hz. Digital compensation and a calibration algorithm were found to be effective and reduced directly coupled magnetic fields by up to a factor of 185 from drive coils to fluxgates. An empirical measurement model was developed that uses a series of calibration measurements to account for system gains and phases and geometric factors that are needed for both image reconstruction and magnetic field compensation. Sensitivity was demonstrated up to a depth of 2.5 cm (p < 0.01) and sensitivity to concentration was found to be linear (R² > 0.98, p<0.001). The system frequency responses showed distinguishable features for 10, 40 and 100 nm diameter mNPs. Tomographic line images were reconstructed at 1 Hz at depths of 0.5 and 1 cm with CNR values ranging from 14–23. Finally, we injected mNPs and saline into a pork sausage approximately following the imaging grid to demonstrate the feasibility of mNP imaging in a biological medium.

Our development approach focused on meeting important performance targets to motivate further development into a clinical tool with a minimally complex prototype. One of our goals was to produce an imager with relatively low cost off the shelf electronic components. We have succeeded in this with the current prototype by producing a prototype for about 6380 USD. Even in an expanded imaging array, we are confident that off shelf electronics components can be used. An expanded 64-voxel imaging array is expected to cost about 3000 USD with cost savings coming from cheaper ADC and controller hardware. Even at 1024 voxels, the hardware costs are expected to be about 12 000 USD. This would make the cost of a clinical mNP imaging system more similar to an ultrasound system rather than an MRI system. The prototype is also light and small, and should remain so in future design iterations. The magnetic field strengths used in this system are also low, roughly 10-100 μT in the imaging field of view, leading to low power consumption. Even in an expanded array, magnetic fields will remain low leading to manageable power consumption. This is important for the development of a portable mNP imaging system that may need to be integrated with other clinical equipment.

One of the important uncertainties addressed by this prototype was about the effectiveness of the digital compensation scheme. Compensation was able to reduce the directly coupled fields by a factor ranging of up to 185. Overall the compensation was sufficient to reduce the directly coupled fields to less than 15 nT on all channels simultaneously. This level of compensation indicates that it is possible to increase the field strength at 0.5 cm depth from 10 μT to 100 μT and to substantially increase the number of drive coils. For example, if 30 drive coils were used at 10 times the applied field then the compensated field at the sensor is expected to be 15 nT × 10 × 30 = 4.5 μT, which is still within the operating range of the fluxgates. This provides confidence that the proposed scheme of geometric and active compensation can work in a larger imaging array.

Three different sizes of mNPs were tested with our prototype at frequencies from 525–925 Hz to characterize the system response to each of the mNPs. In all three cases a strong response from the mNP was measured. These measurements show that the proposed method is not limited to a narrow mNP size range. It was also found that the in-phase and out-of-phase responses of these mNPs are distinguishable within the standard deviation of the measurements. Further testing will be needed to determine the limits of distinguishability between different mNP sizes.

The imaging goal for this prototype was to produce line images with less than 10 mg Fe at 0.5 cm depth with a frame rate of 1 Hz. This was achieved with 6-voxel imaging of 6.25 mg Fe. Four-voxel imaging of 6.25 mg Fe at 1 cm depth was also demonstrated. The reduction to 4 voxels at 1 cm depth was due to weak interactions of the drive coil fields with the sample at longer distances, a concern that can be addressed with a more compact design.

A couple of factors are likely to have limited the noise floor in the current prototype. The coils and sensors were not rigidly clamped or glued together in the apparatus. This could result in mechanical instability where small vibrations or relative displacements cause large deviations in the residual magnetic field and contribute to poor image quality. Future designs will secure the coils more rigidly. Another limitation was that the magnetic field in the present prototype was 10 μT at 0.5 cm because current in the coils was limited to 30 mA. Drive coil currents could be increased with alternative standard components that have higher current ratings. These two design modifications would increase coil-sample-sensor signal levels and help improve imaging quality at greater depths.

In this study the magnetic field at the mNP location was estimated to be less than 10 μT and therefore the magnetization of the mNPs remained linear. If the magnetic field had been increased beyond 1 mT then the mNP response might have become nonlinear. With the current imaging model, a nonlinear response would have produced imaging distortion. For future expansion into a larger imaging array, it is important that the total magnetic field remain less than 1 mT in order to avoid causing distortions due to nonlinear magnetic susceptibility effects.

Our 6-voxel imager is extendable to a larger array. The electronics and mechanical structure can be modified to fit more drive coils and fluxgate sensors, and even extended into a two-dimensional array. The array can also be made more compact by reducing the distance between drive coils and fluxgates to reduce voxel size. In an expanded array, more channels in the frequency space between 500 – 900 Hz would be used. From the noise characterization data, the fluxgate has reasonably low noise in this region but interference could result from 60 Hz harmonics. In order to expand the number of frequencies used for imaging, some considerations will need to be made to avoid these power line harmonics. It may ultimately be necessary to actively compensate for 60 Hz noise or to use gradiometers rather than magnetometers.

To demonstrate that the system can acquire mNP contrast in a biological system, mNPs were injected into pork sausage. The sausage contained a mixture a fat, muscle, connective tissue and water. It was expected that some contrast would be obtained from biological tissue and from the diamagnetic properties of water. This contrast was noticed in preliminary testing by placing and removing the sausage from in front of the sensors. As the imaging demonstration showed, a differential measurement can be made with biological tissue. By measuring the susceptibility response before and after injection of mNPs, it is possible to isolate the response due to mNPs.

Our objectives at this phase of development were to document the system design and the measurement and imaging methods. Experimentally we aimed to demonstrate compensation at levels that would allow for a ten-fold expansion of the imaging array. We also aimed to illustrate distance sensitivity of at least 2 cm, and concentration sensitivity in the range of 1 to 10 mg Fe/ml for relevance to clinical mNP imaging. In a clinical breast cancer hyperthermia application for instance, tumors are primarily expected to be found at depths of 1 – 5 cm from the surface (Hagness, Taflove et al. 1999) and mNP concentrations for brain cancer clinical trials have been as high as 112 mg Fe/ml (Maier-Hauff, Ulrich et al. 2011). In addition, we aimed to show that measured responses iron oxide mNPs with single magnetic domain core diameters of 10 nm and 40 nm, and a multi-domain mNPs with a hydrodynamic diameter of 100 nm have clearly distinguishable frequency responses. Finally, we aimed to achieve temporal resolution of 1 Hz for 6-voxel imaging of less than 10 mg Fe at a depth of 0.5 cm. For a portable handheld system, a frame rate of 1 Hz was important because both the patient and the clinician would need to hold steady while the measurement was being made. For clinical use, a resolution of 3 mm would be comparable to conventional imaging modalities. Our objective was 10 mm resolution in the current prototype and 5 mm resolution in the next generation of prototype. In the clinical hyperthermia, mNPs can migrate as far as 5 cm after several hours and so an imaging system that can measure a 10 cm region with 5 mm resolution might be useful in this setting. In the clinical context, imaging could be performed prior to or interleaved with hyperthermia heating due to the potential for interference from other applied magnetic fields. We believe that our demonstrated level of functionality is a reasonable baseline for continued development of a clinical mNP imager.

Overall, the prototype met our design objectives for this phase of development. The prototype is also low cost with minimal hardware complexity. Several improvements can be incorporated into future designs to improve imaging resolution and quality. Given the present experimental results, the proposed approach for multiple-frequency, continuous-wave mNP imaging appears extendable into a larger imaging array. This work could ultimately provide a solution to the challenging problem of real time intraoperative mNP image guidance.