Skip to main content
PMC home page
The Review of Scientific Instruments logoLink to The Review of Scientific Instruments
. 2014 Mar 14;85(3):033703. doi: 10.1063/1.4865116

Synchronous digitization for high dynamic range lock-in amplification in beam-scanning microscopy

Ryan D Muir 1, Shane Z Sullivan 1, Robert A Oglesbee 1, Garth J Simpson 1,a)
PMCID: PMC3987178  PMID: 24689588

Abstract

Digital lock-in amplification (LIA) with synchronous digitization (SD) is shown to provide significant signal to noise (S/N) and linear dynamic range advantages in beam-scanning microscopy measurements using pulsed laser sources. Direct comparisons between SD-LIA and conventional LIA in homodyne second harmonic generation measurements resulted in S/N enhancements consistent with theoretical models. SD-LIA provided notably larger S/N enhancements in the limit of low light intensities, through the smooth transition between photon counting and signal averaging developed in previous work. Rapid beam scanning instrumentation with up to video rate acquisition speeds minimized photo-induced sample damage. The corresponding increased allowance for higher laser power without sample damage is advantageous for increasing the observed signal content.

INTRODUCTION

The S/N of a nonlinear optical measurement is one of the critical defining properties dictating the available scope of use of emerging nonlinear optical microscopy techniques. Several strategies have been adapted to optimize S/N in regard to the imaging approach. In beam-scanning instruments, fast imaging techniques minimize the single-pass pixel dwell times of the laser, which raises the laser intensity damage threshold and allows higher incident powers.1 In nonlinear optical and multi-photon techniques that scale quadratic or higher with laser power, increases in the damage threshold offer substantial potential increases in S/N with increased laser power.1, 2 From the perspective of the sample, fast imaging can reduce image degradation in vivo from pulsation of local blood vessels, respiration, or physical movement by the subject.3 High S/N is essential for high speed (video rate) beam-scanning imaging, where each focal volume is often measured for only a few laser shots.3, 4

In regard to the signal measured by the optical sensor, two general measurement strategies have emerged for obtaining high S/N images, depending on the nature of the nonlinear interaction (Figure 1). In the case of trace-light detection (e.g., by coherent anti-Stokes Raman scattering (CARS), second harmonic generation (SHG), and TPEF), time-gated photon counting and signal averaging strategies are often used. Both of these strategies seek to directly quantify the observed intensity. For stimulated Raman scattering (SRS), transient absorption, and related methods relying on the detection of weak modulation of large signals, lock-in detection recovers the amplitude of modulation by extracting and measuring the signal level within a narrow frequency band.15 Several lock-in amplification (LIA) systems have been custom built in-lab while questing for faster (video-rate) measurements and higher levels of S/N.4, 5

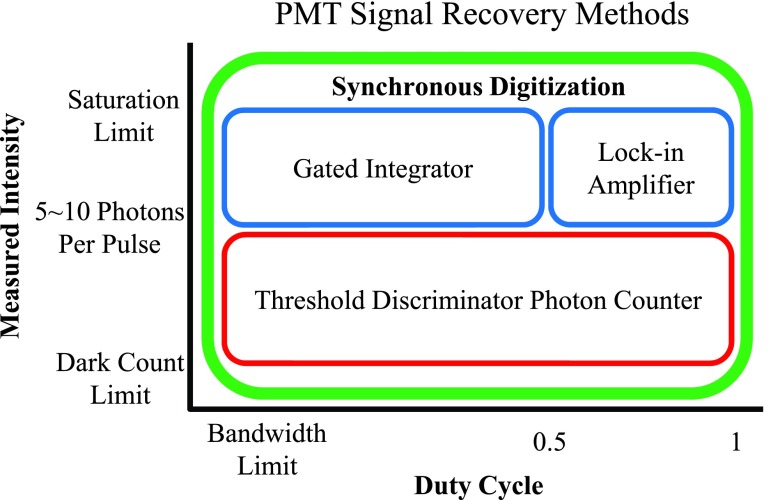
Figure 1.

Figure 1

Open in a new tab

A visual representation of the main signal recovery methods and the conditions under which they are optimized.15 Discrimination-based photon-counting generally provides higher S/N under low intensity conditions, but suffers from relatively low linear dynamic range. For bright optical signals confined to a short duty cycle, gated integration typically provide a S/N advantage. Otherwise, for techniques with a 50% duty cycle, LIA is typically advantageous.

Gated integration and LIA are often described as being time domain and frequency domain techniques, respectively. For optical signals, LIA typically provides a S/N advantage with a 50% duty cycle (e.g., a modulated signal with equal time spent in peaks and troughs). Duty cycle for optical signals is defined here as the fraction of time that the signal spends in an active (non-zero) state. Under these conditions of a high duty cycle, the signal strength of the locked-in frequency component is maximized. In the other extreme of a low duty cycle, a time-gated integrator can be set to observe the signal only during its relatively brief active state, neglecting the noisy and nearly information-less off-duty content. For systems where the majority of the signal is confined to a relatively short amount of time, such as in pulsed systems at low repetition rates, gated integration usually provides a S/N advantage over LIA. However, gated integrators are unable to perform repeated measurements at MHz rates, and the time-gating benefits are often lost in such cases.

LIA and gated integration are not mutually exclusive in their method of signal recovery. Lock-in detection works by temporally mixing (multiplying) a modulated signal by a reference modulated waveform, and integrating the resulting DC product waveform over a period of time. Alternatively, gated integration can be intuited as lock-in amplification using a pulsed reference waveform with pulses equal to the gate width. While in principle gated integration and LIA can be intuitively connected, in practice the instrumentation for each has become highly specialized.

Both techniques suffer performance losses relative to the shot-noise limit for detection at low light levels, where a S/N advantage arises from photon counting. In LIA, most conventional instruments are optimized for detection of low modulation amplitudes on large signals well outside the photon-counting regime and suffer significantly in the limit of low optical flux. For both conventional LIA and gated integration, the intrinsic variance in the one-photon peak height distribution yields an additional noise source above the shot-noise limit from single photon counting in this regime. Software LIA algorithms can be subsequently applied to counting data to determine the modulation amplitude, but using fundamentally different instrumentation that is typically incompatible with analogous measurements at high photon flux.6, 7, 8, 9

The discrete timing of the signal arrival in pulsed laser systems has the potential to provide practical advantages in S/N enhancement for time-domain measurements not routinely exploited in conventional LIA measurements. In a previous publication,10 clocking a set of oscilloscope cards synchronously with the laser at 80 MHz was found to be an efficient means of recovering the complete histogram of voltage transients through flash analog to digital conversion (ADC), which in turn could be either processed in real-time or stored for later analysis. Using this synchronous digitization (SD) approach, the signal was recorded only at its most information-rich points in time, rejecting the noise content at other times. Werley et al. have also recently implemented a SD technique at a kHz sampling rate to perform pump-probe THz spectroscopy,11, 12 and found it superior to conventional LIA for signal recovery in their system. SD has also been performed by Evans et al. in their video-rate CARS system.13 While reasonably successful within those application spaces, these previous architectures were not amenable to analysis of low light levels.

In the present work, SD is coupled with real-time statistical data analysis to extend the linear dynamic range of modulated signal detection seamlessly across the photon counting and signal averaging regimes.10 In this manner, the broader area indicated in the outermost box in Figure 1 can be spanned with a single measurement platform for modulated pulsed light detection with repetition rates exceeding 100 MHz. Preliminary efforts centered on homodyned SHG imaging, in which the signals were modulated through polarization modulation. Homodyne detection is defined here as the interference of the SHG signal with a local oscillator reference at the same optical frequency.14 Rapid beam scanning allowed for image acquisition at 15 frames per second (fps) with 512 × 512 pixel resolution in up to four channels of simultaneous detection, with longer exposures created by discontinuous pooling of multiple frames of raw data prior to digital lock-in analysis.

USING SD FOR SIMULTANEOUS LOCK-IN DETECTION OF MULTIPLE FREQUENCY COMPONENTS

In many optical spectroscopy or microscopy applications, the amplitude of modulation within optical sensor data is proportional to the measurement of interest (e.g., stimulated Raman gain/loss spectroscopy, some forms of two-photon absorption imaging, photothermal imaging, etc.). For systems utilizing a pulsed laser source and fast optical detection, a train of transient signal events was initially transduced by the optical sensor. This time domain signal can be intuitively converted to a frequency domain signal through common Fourier transform relationships (Figure 2), with the end result being modulation frequency sidebands about every laser firing frequency harmonic. The conventional LIA with a sinusoidal reference is able to only recover one of these signal sidebands; for recovering signal content in a pulsed laser system, the single-frequency selectivity of LIA can become a hindrance to high S/N measurements instead of a boon.

Figure 2.

Figure 2

Open in a new tab

(a) The expected time domain signal from an 80 MHz lasing system as observed by the detector: t1 is the pulse width of the ultrafast pulses, t2 is the time between pulses, and t3 is the period of the sinusoidal modulation. (b) Separation of the time domain signal into its time domain components. (c) The Fourier transform of each of the time domain components into their frequency domain counterparts. (d) Recombining the frequency domain counterparts gives the overall frequency domain content as observed by the detector. LIA with a sinusoidal reference tuned to the modulation frequency is only able to recover the signal's fundamental frequency contribution, f3, and misses the contributions from the higher frequency doublets.

The SD technique can be used to recover the full signal content at all of the harmonics within the intrinsic bandwidth of the instrument. In the SD technique,10 only the peak voltage of every signal transient is captured by flash ADC, and a software lock-in algorithm can be applied to the captured data. Flash ADC returns information that is highly analogous to that retrieved by boxcar integration, though is compatible with up to GHz sampling rates. In software, the processed data points are temporally multiplied by a sine wave, and the resulting product is integrated over a period of time. Since the SD technique only samples at discrete points in time, the software multiplication of discretely sampled data could be temporally reconstructed as a train of sinusoidally patterned discrete values (Figure 3c). The Fourier transform of this waveform gives a continuum of doublets at every harmonic, and the frequency of every doublet is locked-in and combined with the final result.

Figure 3.

Figure 3

Open in a new tab

(a) Conventional lock-in multiplies the signal in time by a reference cosine wave, which corresponds to convolving the signal's frequency content by a reference doublet in the frequency domain. This doublet matches only the fundamental frequency of the modulation content from the signal shown in (b). (c) SD samples only the signal peaks and then multiplies the binned and analyzed data by a reference cosine. This transforms into a train of doublets in frequency space, which matches the fundamental and higher frequency modulation content of the signal shown in (b). Comparing reference waveforms (a) and (c) in the time domain, the sharp pulse train in (b) is more closely approximated by the comb of transients in (c) compared to the pure sinusoid of (a).

The advantages of SD-LIA are most pronounced for low intensity light of less than an average of ∼0.5 photons/pulse, in which photon counting offers a S/N advantage. In this regime, conventional LIA and gated integration techniques suffer when compared to photon counting techniques. Depending upon the measured intensity, either counting or averaging data may be selectively preserved at each pixel in the image to maintain optimal S/N across the entire dynamic range of the photomultiplier tube (PMT).10, 16 SD data processed in this way can subsequently be processed with a software LIA algorithm to recover the amplitude of modulation with S/N approaching the shot noise limit across the entire intrinsic linear dynamic range of the detector. This binned analysis is particularly advantageous for quantitative image analysis where the distribution of pixel intensities may span a dynamic range of several decades.

EXPERIMENTAL METHODS

High speed SD imaging

High speed SD lock-in imaging was performed in a homodyned SHG microscopy system (Figure 4). The polarization of an ∼800 nm Ti:sapphire laser beam (Spectra-Physics, Mountain View, CA) was passively modulated by doubling the laser's firing rate from 80 MHz to 160 MHz using two polarizing beam splitters and a 6.25 ns delay stage. The resulting train of pulses produced two orthogonally interleaved linear polarizations per shot. This beam was directed into an in-house built microscope, in which the beam was scanned across a crystalline urea sample surface by an 8 kHz resonant mirror/galvanometer mirror pair (EOPC PLD1S/Cambridge Technology 6210H). The horizontally (H) and vertically (V) polarized components of SHG were collected in transmission (Hamamatsu H10721-01), with bandpass filters (HQ 400/20m-2p; Chroma Technology, Bellows Falls, VT) to reject the incident beam. Unpolarized SHG was also collected in the return, or epi, direction (Hamamatsu E990-501). Laser transmittance of the fundamental laser beam was also collected by a photodiode (Thorlabs DET10A). Microcrystalline cellobiose samples (Sigma-Aldrich) were prepared by sonication of the stock crystals in acetone and deposition of the suspended material on a 0.5 mm z-cut quartz slide. After drying, the crystals were immersed in refractive index matching oil (Cargille Formula 1248) and topped with a glass coverslip.

Figure 4.

Figure 4

Open in a new tab

The polarization of the laser beam was passively modulated by doubling an 80 MHz Ti:sapphire laser to 160 MHz using two polarizing beam splitters and a 6.25 ns delay stage. The resulting 160 MHz train of light pulses produced orthogonally interleaved polarizations, with modulation at 80 MHz. The laser served as the master clock for all electronics. The laser was galvanometer/sample scanned across the sample, and the resulting SHG was separated and detected as H and V polarizations. When the LIA was used for measurements, its DC output was recorded with the same digitizer.

Two flash digitizers (AlazarTech ATS-9462) with a total of four digitization channels were used to directly capture data from all four sensors synchronously with the laser. The digitizer's onboard 10 MHz phase-locked-loop was clocked by the laser's 80 MHz photodiode signal after passing through a divide-by-8 frequency division circuit built in-house, and the digitizer's master clock set in software to digitize at 160 MHz synchronously with the doubled laser. A second in-house built circuit controlled the galvanometer mirror by incrementing the galvanometer angle for every digital pulse received. Two digital output ports on the digitizer provided an ∼8 kHz clock generated as an integer division of 160 MHz, as well as a “capture-in-progress” digital flag. The 8 kHz clock synchronously clocked the resonant mirror and galvanometer (one resonant mirror sweep per galvanometer step), and the “capture-in-progress” flag forced the galvanometer to a zero position when not active. All digitizer control and subsequent data processing was performed with MATLAB. Dwell time per pixel was approximately 50 ns per sweep, or 8 laser shots at 160 MHz.

Conventional LIA and SD-LIA imaging comparison

For imaging comparison of SD-LIA to conventional LIA, the trans-H SHG intensity was directly measured by a 200 MHz SR844 lock-in amplifier (Stanford Research Systems, Sunnyvale, CA), with the X- and Y-channels subsequently recorded by the digitizer. The LIA was set for 100 μs time constant, 12 dB/octave filter, low noise wide and closed reserves, and 50 Ω input impedance. The 100 μs time constant was chosen as the shortest well-defined and reproducible time constant available in the 200 MHz LIA settings. Although a faster “filterless” option was also available, the time constant was not precisely known, but estimated to be 10–20 μs in the user manual. A pixel dwell time of 100 μs per pixel was created by disabling the resonant mirror and performing galvanometer/sample scanning (Prior Scientific Proscan), where the galvanometer angle was stepped every 100 μs. The trans-H SHG sensor was subsequently measured by SD-LIA under these conditions for direct comparison to conventional LIA.

Conventional LIA and SD-LIA S/N comparison

The polarization of an ultrafast fiber laser beam (170 fs, 1060 nm, ∼1 W, Fianium, Southampton, United Kingdom) was passively modulated by doubling the laser's firing rate from 50 MHz to 100 MHz using two polarizing beam splitters and a 10 ns delay stage.17 A 2 cm lens focused the beam into a z-cut quartz slide, and the unpolarized SHG was detected in the return direction (Hamamatsu H10721-01). The PMT gain was reduced to prevent sensor damage at high signal intensity, and the lost gain was recovered with a 10× fixed gain amplifier (Texas Instruments THS4303EVM) to maintain the photon-counting threshold above the Johnson noise. For the conventional LIA, the amplified sensor output was measured and locked in by a SR844 lock-in amplifier (Stanford Research Systems, Sunnyvale, CA), with the X- and Y-channels subsequently recorded by the digitizer (AlazarTech ATS-9350). The LIA was set for 100 μs time constant, 12 dB/octave filter, normal wide reserve, low noise closed reserve, and 50 Ω input impedance. The sensor was subsequently measured by SD-LIA under these conditions for direct comparison to conventional LIA.

RESULTS AND DISCUSSION

LIA and SD-LIA imaging speeds

Images from the LIA and SD-LIA techniques are shown in Figure 5, using a Nikon 10×/0.3NA objective. The gray background shows a reference signal from the z-cut quartz, where the black and white particles on the surface arise from the constructive and deconstructive interference of the homodyned signal from the cellobiose crystals. 6.25 ns between laser shots along with ∼3 ns signal transients creates a near 50% duty cycle, which Figure 1 shows to be the optimal measurement conditions for LIA. All of the images provide qualitatively similar information content. However, the sharp edges in the SD images appear to be blurred along the fast axis of the LIA image, as shown in the blow up insets in Figure 5. The hysteresis from the preceding pixel value is attributed to the 100 μs RC time constant of the LIA. For an instantaneous change in AC amplitude, LIA requires five time constants to lose memory of the preceding pixel value to within 99%.18 For pixel dwell times equal to the LIA time constant, the amplitude from the previous pixel has only charged/discharged by ∼63%, significantly biasing the result in the adjacent pixel and effectively acting as a low-pass filter along the fast scan axis.

Figure 5.

Figure 5

Open in a new tab

SHG microscopy images from cellobiose deposited on and homodyned with z-cut quartz, detected with a SR844 200 MHz LIA (left), or SD-LIA (right). The particles appear to be elongated in the direction of the fast axis (vertical) in the LIA image compared to the SD-LIA image (inset).

The 100 μs time constant of the LIA set the minimum pixel dwell time for the images shown in Figure 5 and correspondingly the maximum frame-rate. A measurement with a 100 μs dwell time per pixel requires at least 26 s for a 512 × 512 pixel image. Using the “filterless” mode of the LIA would have increased the available scanning speed by 5–10 times, at the cost of ambiguity in the measurement time-constant that was desired to allow quantitative comparisons. With the SD technique, the minimum dwell time was reduced to the sampling speed of the ADC, and the resonant mirror scan speed became the new speed limiting factor in this setup. Using an 8 kHz resonant mirror and galvanometer mirror, a 512 × 512 pixel image can be acquired in 65 ms, or a video can be recorded at 15 fps.

From two incident polarizations and four channels of detection, eight videos were simultaneously captured and processed in real-time (Multimedia view, encoded with H.264 codec) at 15 fps, single frames of which are shown in Figure 6. Incident laser intensity measured before the objective was 100 mW. Two PMT detectors were placed in the transposition, measuring the vertical and horizontal components of the SHG signal. One PMT detector was placed in the return direction, measuring unpolarized SHG signal. A photodiode was placed in the transdirection to measure the intensity of the vertical component of the transmitted fundamental laser wavelength. Laser transmittance provides information similar to monochrome bright-field imaging, with the advantage of perfect spatial and temporal registry with the nonlinear optical images. Birefringence provides additional selectivity for crystal detection.

Figure 6.

Download video file (11.2MB, wmv)
Download video file (9.5MB, mov)
Open in a new tab

A single frame of the SHG videos of cellobiose deposited on z-cut quartz immersed in oil, acquired simultaneously by four detectors with the SD technique in 65 ms. SD-LIA is also generated at 15 frames per second and shown in the bottom row of images. The local oscillator is much weaker in the return direction, leading to much smaller modulation signal content. (Multimedia view) .

The implications of increased measurement speed are favorable for imaging non-static samples, such as biological or kinetic systems, which result in blurred or distorted images if the acquisition time period is not sufficiently short. Additionally, fast beam-scanning techniques minimize the pixel dwell times of the laser, which raises the laser intensity damage threshold from local heating. In conventional LIAs, the imaging speed is intimately linked to the analog integrator time constant, which also results in hysteresis effects. Since the ADC samples each laser shot without hysteresis, SD-LIA can be achieved with a minimum of two laser shots, and the absolute information of the individual modulation states can be simultaneously preserved.

Conventional LIA and SD-LIA S/N comparison

The performance of SD-LIA was evaluated against conventional LIA by measuring the SHG signal from z-cut quartz in the return (epi) direction, as described in Sec. 3. The time constant of the LIA was set to 100 μs, which is the amount of time required to discharge the previous value by ∼63%. As specified in the SR844 user manual for the LIA settings used, five time constants of integration time are required for the LIA to reach 99% of its final value, giving a total integration time of ∼500 μs for 1% residual bias with a 100 μs time constant.18 For this experiment, the output of the conventional LIA was sampled in 500 μs time intervals in accordance with this integration time. SD-LIA was performed with data acquisition over 500 μs time intervals. At each power setting, the S/N of SD-LIA was optimized by selecting between binomial photon counting versus signal averaging as described in previous work.10 The duty cycle of the signal was approximately 30%, which is near the optimal conditions for conventional LIA as illustrated in Figure 1.

The measured S/N is plotted as a function of the incident laser power as shown in Figure 7 for both SD-LIA and LIA. Laser power was measured immediately after the z-cut quartz sample and ranged from 16 mW to 500 mW. For optical interactions scaling linearly with light intensity, the S/N depends on the square root of the intensity in the shot noise limit.5 Due to the quadratic dependence of SHG on the incident intensity, a slope of one is consistent with shot noise limited S/N in SHG detection. Incidentally, a slope of unity is not in itself sufficient to assume a S/N ratio at the shot-noise limit defined by Poisson statistics, as there can be an additional negative vertical offset in S/N due to the inherent peak-height variance of the detector response.10, 16 It was also shown that threshold binomial counting techniques approach the shot-noise limit in the limit of low signal intensities, since the intrinsic PMT detector noise is rejected in the thresholding approach.10, 16 As described in Figure 1, counting and integrating techniques retrieve the highest S/N in the low and high intensity limits, respectively. In the present study, SD-LIA measurements at 500 mW intensity were determined to be in the integrating range, and all other data points were within the binomial counting range.10

Figure 7.

Figure 7

Open in a new tab

S/N comparison of SD-LIA and LIA as a function of incident laser power (log-log scale) along with linear fits of the data points. Two different sensitivity ranges were used on the LIA to span the wide dynamic range with high S/N. Even under dynamic range and duty cycle conditions well-suited for LIA, 500 μs SD-LIA provided superior S/N compared to LIA.

Linear fits were applied to the data with equal weighting for all data points in Figure 7, which illustrates how the fitted line of S/N from the high intensity signal regime deviates slightly from the S/N measured at the low intensity signal regime. The slopes of the fitted lines were 1.178 (±0.12), 1.273 (±0.13), and 1.588 (±0.25) for the SD-LIA, 10 mV sensitivity LIA, and 100 mV sensitivity LIA lines respectively. Two different sensitivity ranges were required on the LIA to span the wide dynamic range of modulation amplitudes. The departure toward lower S/N in LIA is also predicted (Figure 1) to occur as noise sources dominate the integrated signal content.10, 16 Interestingly, even under near ideal duty cycle and high intensity conditions for the LIA described in Figure 1, SD-LIA provides superior S/N compared to LIA.

The departure toward higher S/N in the SD-LIA measurements performed at low incident power are reproducible and not due to uncertainty in the measured S/N ratio. At these low powers, binomial photon counting provides an additional S/N advantage by removing noise from the intrinsic variance in the peak voltage per photon generated by the detector.10, 16 SD-LIA maintained between Poisson-limited and detector-noise-limited performance across the entire range without requiring hardware adjustments (e.g., sensitivity).

In practice, high dynamic range of the measurement is common in nonlinear imaging, where the >6 orders of magnitude linear dynamic range of the PMT sensor can be accessed within a single image. Conventional LIAs recover signal most efficiently when the measured signal spans the full input dynamic range of the LIA. It is impractical to adjust the LIA's input dynamic range to match the dynamic range of the measurement at every pixel, so the LIA dynamic range is typically set to either favor bright signals or weak signals. In contrast, SD-LIA avoids these limitations by automatically transitioning between threshold-based photon counting for weak signals and signal averaging for bright signals.10

IMPLICATIONS FOR BEAM-SCANNING MODULATION-BASED MICROSCOPY MEASUREMENTS

SD-LIA was found to produce S/N exceeding that of LIA, even under conditions typically considered optimal for measurement with LIA. Through this combination, a single measurement platform was demonstrated to simultaneously support multiple measurements positioned at opposing locations within the space of duty cycle and intensity range illustrated in Figure 1. The SD system presented here was able to preserve the data from every laser shot at 16 bit resolution up to 160 MHz with four simultaneous channels of acquisition, and was used to produce eight 512 × 512 pixel movies of raw data simultaneously at video rate, corresponding to different polarization-dependent combinations. High scan speeds reduce damage to fragile samples, and allow the user to increase the laser intensity before damage occurs. In visible-detected SHG imaging, both counting and averaging techniques were performed to achieve high S/N, high dynamic range images. By selecting between photon counting and signal averaging on a pixel-by-pixel basis, the vertical axis of Figure 1 was spanned with a single measurement platform. Additional S/N gains of SD-LIA over conventional LIA are reasonably expected with decreasing rep-rate and duty cycle, spanning the horizontal axis in Figure 1. Furthermore, high speed imaging allows higher laser power before the onset of sample damage from local heating, which is particularly advantageous for nonlinear optical microscopy for which the signal scales nonlinearly with the total incident intensity.

The hardware/software coupling demonstrated in this work also offers the promise to enable new and unique imaging approaches from this same data acquisition platform. The implemented SD hardware and software is highly accessible, with the core component being a commercial data acquisition card interfaced with MATLAB. Customized SD-LIA algorithms could be developed, such as arbitrary waveform lock-in for systems that provide non-sinusoidal signal in time, or discontinuous lock-in for scanning trajectories that sample pixels non-uniformally. In both previous work and in the present study, SD coupled with statistical methods also enabled S/N optimization in high dynamic range measurements spanning the photon counting and signal averaging regimes. In nonlinear optical imaging, this general analysis could be applied to broad classes of modulation-based spectroscopies, over wide ranges of duty cycles and photon fluxes.

ACKNOWLEDGMENTS

The authors gratefully acknowledge support from the NIH Grant No. R01GM-103401 and support from Eli Lilly and Co. from the Lilly Research Awards Program. The authors also acknowledge Nigel Ferdinand, Muneeb Khalid, and Bing Tom of AlazarTech for their help in developing software to control the digitizer cards, supplying new firmware features on request, expanding the clocking abilities of their digitizers, as well as their general technical support. We also thank the Ji-Xin Cheng group at Purdue for use of a SR-844 200 MHz LIA.

References

  1. Boyd R. W., Nonlinear Optics (Academic Press, San Diego, CA, 2003). [Google Scholar]
  2. Verbiest T., Clays K., and Rodriguez V., Second-Order Nonlinear Optical Characterization Techniques: An Introduction (CRC Press, Boca Raton, 2009), p. 185. [Google Scholar]
  3. Suhalim J. L., Boik J. C., Tromberg B. J., and Potma E. O., “The need for speed,” J. Biophoton. 5, 387–395 (2012). 10.1002/jbio.201200002 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Saar B. G., Freudiger C. W., Reichman J., Stanley C. M., Holtom G. R., and Xie X. S., “Video-rate molecular imaging in vivo with stimulated Raman scattering,” Science 330, 1368–1370 (2010). 10.1126/science.1197236 [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Slipchenko M. N., Oglesbee R. A., Zhang D., Wu W., and Cheng J. X., “Heterodyne detected nonlinear optical imaging in a lock-in free manner,” J. Biophoton. 5, 801 (2012). 10.1002/jbio.201200005 [DOI] [PubMed] [Google Scholar]
  6. Stanford Research Systems, Signal Recovery with PMTs (Sunnyvale, CA, 2004). [Google Scholar]
  7. Cova S., Longoni A., and Freitas I., “Versatile digital lock-in detection technique: Application to spectrofluorometry and other fields,” Rev. Sci. Instrum. 50, 296–301 (1979). 10.1063/1.1135819 [DOI] [PubMed] [Google Scholar]
  8. Wang T., Zhao H., Wang Z., Hou S., and Gao F., “Multi-channel photon counting DOT system based on digital lock-in detection technique,” Proc. SPIE 7896, 789612 (2011). 10.1117/12.871779 [DOI] [Google Scholar]
  9. Wang X., Zhang G., Chen R., Gao Y., Xiao L., and Jia S., “Detection efficiency enhancement of single-photon detector at 1.55-μm by using of single photons lock-in and optimal threshold,” Opt. Laser Technol. 44, 1773 (2012). 10.1016/j.optlastec.2012.01.010 [DOI] [Google Scholar]
  10. Muir R. D., Kissick D. J., and Simpson G. J., “Statistical connection of binomial photon counting and photon averaging in high dynamic range beam-scanning microscopy,” Opt. Exp. 20, 10406–10415 (2012). 10.1364/OE.20.010406 [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Werley C. A., Fan K., Strikwerda A. C., Teo S. M., Zhang X., Averitt R. D., and Nelson K. A., “Time-resolved imaging of near-fields in THz antennas and direct quantitative measurement of field enhancements,” Opt. Exp. 20, 8551–8567 (2012). 10.1364/OE.20.008551 [DOI] [PubMed] [Google Scholar]
  12. Werley C. A., Teo S. M., and Nelson K. A., “Pulsed laser noise analysis and pump-probe signal detection with a data acquisition card,” Rev. Sci. Instrum. 82, 123108 (2011). 10.1063/1.3669783 [DOI] [PubMed] [Google Scholar]
  13. Evans C. L., Potma E. O., Puoris'haag M., Cote D., Lin C. P., and Xie X. S., “Chemical imaging of tissue in vivo with video-rate coherent anti-Stokes Raman scattering microscopy,” Proc. Natl. Acad. Sci. U.S.A. 102, 16807–16812 (2005). 10.1073/pnas.0508282102 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Dadap J., Shan J., Weling A., Misewich J., and Heinz T., “Homodyne detection of second-harmonic generation as a probe of electric fields,” Appl. Phys. B 68, 333–341 (1999). 10.1007/s003400050628 [DOI] [Google Scholar]
  15. SRS, Signal Recovery with PMTs (Sunnyvale, CA, 2004). [Google Scholar]
  16. Kissick D. J., Muir R. D., and Simpson G. J., “Statistical treatment of photon/electron counting; extending the linear dynamic range from the dark count rate to saturation,” Anal. Chem. 82, 10129 (2010). 10.1021/ac102219c [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. S. G.EvangelidesJr., Mollenauer L. F., Gordon J. P., and Bergano N. S., “Polarization multiplexing with solitons,” Lightwave Technol. J. 10, 28–35 (1992). 10.1109/50.108732 [DOI] [Google Scholar]
  18. SRS, Stanford Research Systems Model SR844 RF Lock-in Amplifier User's Manual (Sunnyvale, CA, 2007). [Google Scholar]

Articles from The Review of Scientific Instruments are provided here courtesy of American Institute of Physics

RESOURCES