The statistics of local motion signals in naturalistic movies

Abstract

Extraction of motion from visual input plays an important role in many visual tasks, such as separation of figure from ground and navigation through space. Several kinds of local motion signals have been distinguished based on mathematical and computational considerations (e.g., motion based on spatiotemporal correlation of luminance, and motion based on spatiotemporal correlation of flicker), but little is known about the prevalence of these different kinds of signals in the real world. To address this question, we first note that different kinds of local motion signals (e.g., Fourier, non-Fourier, and glider) are characterized by second- and higher-order correlations in slanted spatiotemporal regions. The prevalence of local motion signals in natural scenes can thus be estimated by measuring the extent to which each of these correlations are present in space-time patches and whether they are coherent across spatiotemporal scales. We apply this technique to several popular movies. The results show that all three kinds of local motion signals are present in natural movies. While the balance of the different kinds of motion signals varies from segment to segment during the course of each movie, the overall pattern of prevalence of the different kinds of motion and their subtypes, and the correlations between them, is strikingly similar across movies (but is absent from white noise movies). In sum, naturalistic movies contain a diversity of local motion signals that occur with a consistent prevalence and pattern of covariation, indicating a substantial regularity of their high-order spatiotemporal image statistics.

Introduction

Extraction of motion from visual input is crucial to making use of the visual input for a variety of purposes, including separation of figure from ground (Grossberg, 1994), navigation through space (Ullman, 1979b), and collision avoidance. Neural processing of visual motion is usually considered to consist of two stages: first, the extraction of local motion signals, and second, a stage in which these local signals are combined.

Local motion signals are typically classified according to their mathematical properties (Chubb & Sperling, 1988; Lu & Sperling, 2001; Reichardt, 1961). This has led to an important insight: There are two kinds of cues with distinct mathematical properties (Fourier and non-Fourier; see below) that can lead to the perception of visual motion. But it is unclear how these mathematical distinctions relate to the kinds of motion signals that are present outside of the laboratory. This is the question we address here: Specifically, do naturalistic spatiotemporal stimuli contain different kinds of local motion signals? If so, how do they covary? These questions have important functional implications. For example, if different kinds of local motion signals are strongly correlated, extraction of only one kind of motion signal could suffice from a functional point of view, and sensitivity to the other kinds of local motion might just be a byproduct of neural computations, useful to investigators for uncovering their nature. Alternatively, if the complement of motion signals depends on context (e.g., object motion vs. self-motion), then there might be selective pressure for separate extraction of multiple kinds of local motion signals. This would enable higher-level modules for action, object recognition, etc. to be separately linked to the appropriate kinds of local motion signals.

Approaching this question requires quantifying and characterizing the different kinds of motion signals that are present in natural contexts, and doing this in a way so that they can be compared on an equal footing. This is not as straightforward as it might at first seem because motion types have been defined in very different manners. Specifically, Fourier (F) motion is typically defined by the presence of a pairwise spatiotemporal correlation (Adelson & Bergen, 1985; Reichardt, 1961) of luminance. (The reason that the term Fourier motion is used is that the set of pairwise correlations—the autocorrelation function—is the Fourier transform of the power spectrum, as is well known [Bracewell, 1999].) In contrast, other kinds of motion signals have been defined on the basis of perceptual phenomena that occur in the absence of such correlations. The best-known examples of this are often called non-Fourier (NF) motion (Chubb & Sperling, 1988; Fleet & Langley, 1994), in which there is pairwise spatiotemporal correlation of a feature (e.g., a spatial edge or a temporal flicker edge). Moreover, motion perception can also occur in the absence of pairwise correlations of luminance (F motion) or of local features (NF motion), a phenomenon known as glider (G) motion (Fitzgerald, Katsov, Clandinin, & Schnitzer, 2011; Hu & Victor, 2010). However, the extent to which these mathematically distinct signals are present in naturalistic inputs is unknown. To address this question, a necessary first step is to formalize the notions of F, NF, and G motion signals (and their subtypes) in terms of specific mathematical transformations so that they can be compared on equal footing.

Here, we develop such measures and apply them to naturalistic movies (several popular films). The data show that all kinds of motion signals that we analyzed coexist in moving visual images. The proportions of motions are relatively constant across movies, and there are consistent correlations between the different kinds of motion signals. However, within individual movie segments, one or another kind of motion signal may predominate, indicating that these correlations are only partial; that is, the different motion types provide nonredundant information.

Materials and methods

Data

The movie database was assembled by J. E. Cutting (www.cinemetrics.lv) and included hand annotations of the boundaries between continuous camera segments (i.e., “shots”). We used these boundaries (with fades and similar transitions excluded, and a five-frame additional margin) to define the analysis segments. All movies had similar characteristics: 24 frames per second, with each frame provided at a resolution of 256×256 pixels to respect copyright concerns. Most analyses made use of this resolution, though some (as indicated below) were carried out after further downsampling these pixels in blocks by averaging. We use the term check to represent the analysis unit (i.e., either a single pixel or a block of pixels that have been averaged). Since the original films had a landscape aspect ratio, each pixel in the database represented a rectangular region of the original film, larger in the horizontal direction than the vertical. Specific movies that were selected were The 39 Steps (1935), A Night at the Opera (1935), Anna Karenina (1935), and Mr. and Mrs. Smith (2005). In designating check position, we used matrix convention in which the X-coordinate increases from top to bottom and the Y-coordinate increases from left to right. The analyses in the main text concern the YT plane (i.e., horizontal motion); parallel analyses in the XT plane (vertical motion) are in Supplement S1.

Quantification of motion signals

Our goal was to quantify different kinds of local motion signals (F, standard NF, and G) in a segment of a naturalistic movie. We did this by first measuring each kind of motion signal based on the luminance correlations within the appropriate spatiotemporal template (Figure 1) to obtain local motion scores, and then, for each kind of motion, we combined these scores across space in different ways.

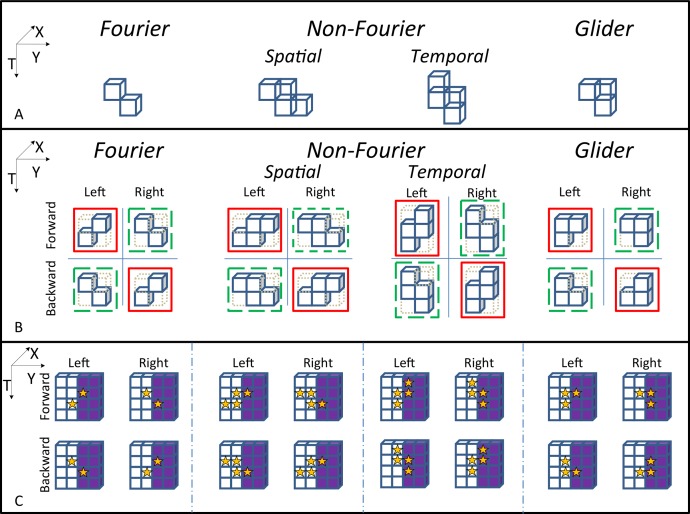
Figure 1.

A summary of calculation of the basic local motion scores. (A) The templates used to quantify each kind of local motion. (B) Details of the various motion score calculations. First, Weber contrast values in the solid-bordered checks are multiplied together. These products are then summed in an opponent fashion (scores from red-outlined configurations are added; scores from green-outlined configurations are subtracted) to generate a local score motion signal (see text for details). (C) How opponency removes spurious signals due to static luminance edges. Each subpanel diagrams the result of a computation of the local motion score when the template (stars) is positioned near a luminance edge. The four components of each subpanel correspond to the four components of the subpanels in B. For F and NF templates, left-oriented and right-oriented placements of the template each include the same number of dark and light checks. Thus, the left and right components of the calculation result in cancellation by their opponency. In contrast, for the G template, the left-oriented placement of the template contains one dark check, while the right-oriented placement contains two dark checks. Thus, the left-versus-right opponency does not result in cancellation. However, forward and backward placements of the template are matched in terms of the luminances of the checks that they contain, and therefore the forward-versus-backward opponency properly cancels the spurious motion signal. Note that for the F and NF templates, this second explicit stage of opponency has no effect. This is because of their symmetry: A left-to-right flip of the template is the same as a forward-to-backward flip (B).

We began by motivating the definition of each kind of motion signal. Typically, F motion is defined by pairwise spatiotemporal correlation of the luminance values in the image (Van Santen & Sperling, 1985). NF motion denotes the motion of a local feature, such as an edge or flicker, in the absence of pairwise spatiotemporal correlation of luminance. An example of NF motion is an object that is flickering randomly—thus eliminating pairwise correlations—while moving across a background of equal mean luminance (Chubb & Sperling, 1988). However, although several models for NF motion extraction have been proposed (Chubb & Sperling, 1988; Fleet & Langley, 1994), there is no single mathematical quantity (analogous to spatiotemporal correlation used for F motion) that is recognized as defining its strength. As will be shown later and in Supplement S3, our approach is able to capture the motion signals in these stimuli. Finally, G motion (Hu & Victor, 2010) encompasses third- or higher-order correlation in slanted spatiotemporal regions and occurs in the absence of pairwise spatiotemporal correlation of luminance (F motion) or simple features (NF motion).

These motion types have a fundamental similarity: They all depend on correlations within a slanted spatiotemporal region (Figure 1). For F motion, the correlation is pairwise, and the region consists of two checks, offset in space and time. For NF motion, the region consists of four checks, and the shape of the region depends on the subtype of NF motion. For NF motion of a spatial feature (NF-S), the region is a parallelogram consisting of two pairs of checks, and the pairs are in adjacent time-slices. Each pair of checks effectively detects the spatial feature (match vs. mismatch), and the combination of the two pairs detects whether this feature moves. For NF motion of a temporal feature (NF-T), the same region is rotated to interchange the roles of space and time. Each pair of checks detects whether there is local flicker, and the combination of the two pairs detects whether the feature moves. For the G motion types considered here, the region is a triplet of checks. Depending on the orientation of the triangle formed by the three checks, the region corresponds to either expansion or contraction over time. Thus, in all cases, the local motion signal corresponds to the correlations among a group of checks in a specific shape, i.e., the template (Figure 1). The templates shown in Figure 1A correspond to motion to the right; flipping them across the Y-axis corresponds to motion to the left.

To quantify the correlations within these templates, we calculated the product of the luminance values in their checks (after subtracting the mean luminance of each shot separately). To implement this for color movies, we first converted the color inputs to gray levels using Matlab's (The MathWorks, Inc., Natick, MA) rgb2gray function. (The numeric range of luminance is irrelevant because we later normalized our calculations by a parallel computation for a movie with spatial correlations removed; see next section for details.)

Following Reichardt (1961) and many others, we noted that the raw correlation value (i.e., the product of the luminance contrasts) will contain spurious motion signals when a static spatial edge is present. As is standard for F motion, we removed this spurious signal by an opponent process in which correlations from left-facing and right-facing templates were subtracted (Figure 1). This strategy suffices for NF motion as well, but is insufficient for G motion (Figure 1). To eliminate this signal for G motion, we added a second opponent stage in which signals from forward- and backward-facing templates were subtracted. Fundamentally, this second opponent stage is needed because the glider for G motion lacks the symmetry of the templates for F and NF motion—for F and NF templates, left-versus-right spatial opponency is equivalent to forward-versus-backward temporal opponency. In other words, because of this symmetry for F and NF templates, the standard single-opponent calculation (space only) is equivalent to a double-opponent calculation (space and time), but for G templates, these two opponencies must be explicit. (Note that had we included only the forward-versus-backward opponency for G templates, then we also would not have eliminated spurious motion signals due to full-field flicker.)

Formally, the calculation of the local motion score is as follows. A motion type corresponds to a template, B, which is a set of spatiotemporal voxels in a specific relative position. We represent a template as a set of triplets [(x₁,y₁,t₁), (x₂,y₂,t₂), …, (x_n,y_n,t_n)], in which each of the x_i, y_i, and t_i are integers and n is the number of elements in the template. Since the template is determined by the relative positions of its voxels, we require that min(x_i) = min(y_i) = min(t_i) = 0, where i = 1, …, n.

A template that is reversed along the X-dimension, which we denote as B^X, is the template in which each triplet (x_i,y_i,t_i) of B is replaced by [L_X(B)−x_i,y_i,t_i], where L_X(B) is the length of the template in the X-dimension, namely, max(x_i). Reversals along the Y and T dimensions are similarly defined. B^YT, for example, denotes a template that has been reversed along the Y dimension and then along the T dimension.

The raw correlation value for the glider B at the position (x,y,t) is defined as a product that involves all offsets contained in the glider:

where I(x,y,t) is the luminance of the image at the position (x,y,t) and Ī_shot is the median luminance across the shot. Finally, the local motion score at position (x,y,t) for motion type B in direction Z is defined by the double-opponent calculation:

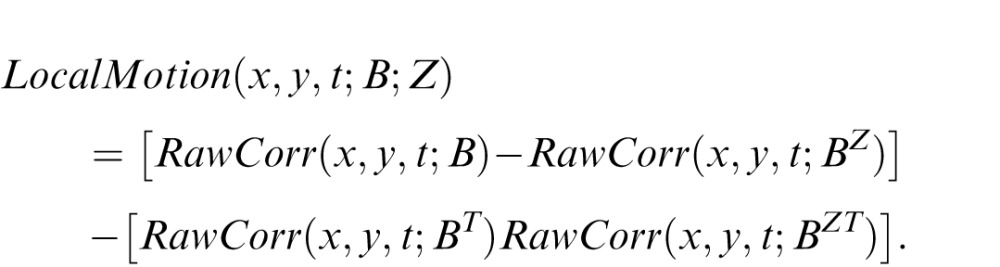Note that although our approach aims to capture specific types and kinds of local motion signals (F, NF-S, NF-T, and G), it can be easily modified to capture motion signals carried by correlations in other spatiotemporal configurations (e.g., Hu & Victor, 2010) by using the appropriate templates.

Combining local motion signals within a shot

Once the local motion scores were calculated as described above, the next step was to quantify motion signals within a movie “shot” (i.e., a sequence of frames that correspond to an individual scene). We used two kinds of strategies: a first kind that simply aggregates the local motion signals, and a second kind that is sensitive to whether these local motion signals are spatially coherent. Each of these strategies was applied separately to the three kinds of templates (F, NF, and G).

In the first kind of strategy, we simply computed the sum of the squares of the local motion signals for all placements of a particular kind of template within the shot. We normalized this quantity by dividing it by the results of a parallel computation applied to the same shots but in which the checks within each frame were scrambled. For the computation of the normalizing quantity, local correlations were determined by subtracting the global mean rather than the shot mean to avoid normalizations requiring division by quantities near zero. This allows for a meaningful comparison of the different motion types, independent of the size and shape of their templates. We call these quantities (computed separately for F, NF-S, NF-T, and G motions) the “simple motion” (SM) scores.

In formal terms, to derive the SM score from local motion scores, we proceeded as follows. First, for normalization purposes, we defined the local motion of a random movie:

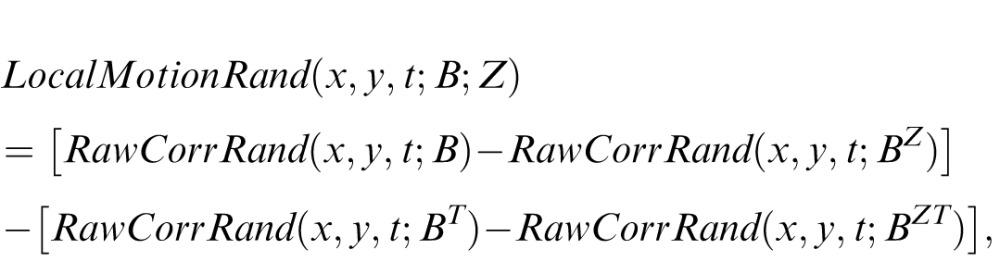where

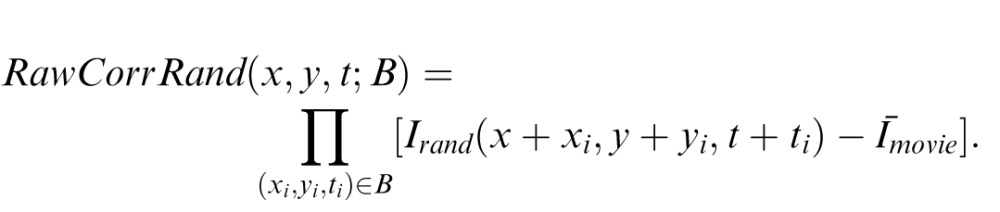Here, I_rand is a movie in which checks are randomly permuted within a shot, and Ī_movie is the median luminance across the movie. The SM score for a shot, for motion type B in direction Z, is the local motion score, averaged over the shot, normalized by the corresponding quantity for a random movie:

The above average is taken over all positions (x, y, t) of the template within the shot.

We note that there is an important caveat that arises when this approach is applied to synthetic stimuli (in contrast to digitized naturalistic movies, considered here). Specifically, the grid used for motion analysis and the grid used for stimulus synthesis are separate grids, and must be considered as such. That is, when the motion scores are computed, the template must be placed in generic positions on the stimulus and not just in register with the grid used for stimulus generation. This detail is critical. Without it, the present approach might fail to detect the motion signal in some of the drift-balanced stimuli of Chubb and Sperling (1988), but with it, the approach captures the motion in all of them. This is illustrated and further discussed in Supplement S3 (Figure S13).

The second kind of strategy, which is designed to be sensitive to whether the local motion signals are spatially coherent, generalizes the use of a Reichardt model output to quantify the strength of standard F motion signals. In these strategies, the luminances in the “region of interest” (ROI) of 16 checks (either 1×4×4 or 4×1×4; [X, Y, T]) are considered together. Each ROI is then scored to indicate to what extent there was a coherent F, NF, or G motion signal throughout the patch. To simplify the process of defining and computing these scores, we first binarized the luminance values in each check—we replaced each luminance by +1(black) or −1 (white), depending on how it compared with the median luminance within the shot. (Parallel analyses in Supplement S1 show that the results were robust with respect to the threshold used for binarization [Figures S7, S8 and S11] and that similar results were found for analysis in the XT plane [Figures S5 and S6]. Results in the main text are for the YT plane.) Note that this binarization can be considered as a form of dimension reduction. Prior to binarization, there are 256¹⁶ possibilities for the ways that a 16-check ROI can be colored; after binarization, there are only 2¹⁶ such combinations. Thus, binarization dramatically simplifies the process of defining, and then computing, a mapping from all of the possible ROI to a motion score; this is our motivation for it.

Formally, binarization corresponds to replacing each intensity I(x, y, t) by I^binarized(x, y, t), where I^binarized(x, y, t) is +1 or −1, according to whether I(x, y, t) is above or below a threshold (here, the median luminance within the shot). All of the above quantities can then be calculated from the binarized movie. We denote such quantities by RawCorr^binarized(x, y, t; B), RawCorrRand^binarized(x, y, t; B) etc. Once binarization replaces each luminance value with +1 or −1, the product of luminance values within a template reduces to determining whether there is an even or an odd number of checks of each color. All of the colorings that yield a product of +1 contribute positively to a rightward motion signal, and all of the colorings that yield a product of −1 contribute negatively. Thus, the configurations that contribute positively to the motion score can be enumerated in a library. This is shown in Figure 2A, using the four-check NF-S template as an example. Since all of the colorings in the library yield a product of +1, they have an even number of white and black checks distributed among its four positions (two checks at one time step and two checks at the next). Thus, if a coloring has a spatial edge at one time step (one black and one white check), it must have a spatial edge at the next; if it lacks a spatial edge at one time step (two blacks or two whites), it must lack a spatial edge at the next. These relationships capture the notion that NF-S corresponds to spatiotemporal correlation of the presence or absence of an edge.

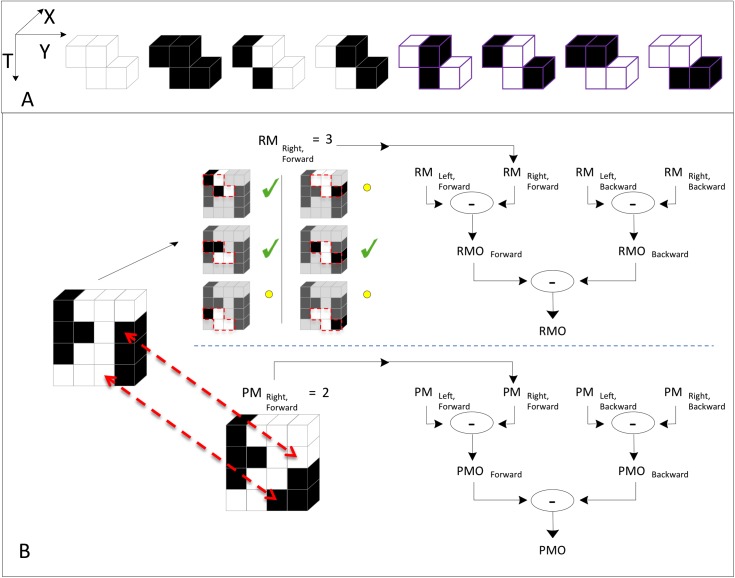
Figure 2.

A summary of calculation of the RMO and PMO local scores in a spatiotemporal ROI, using NF-S motion as an example; further details are in the text. (A) The library of eight template colorings consistent with NF-S motion. Note that all colorings have an even number of black checks. (The four rightmost colorings, marked in purple, are the templates used for pure NF-S, as the two-check F templates that they contain are inconsistent with F motion.) (B) Calculation of RMO and PMO scores for a 1×4×4 spatiotemporal ROI. For the RMO method (top), we consider all placements of the template within the ROI. There are six such placements (red dashes), and we tally the placements that yield colorings contained in the library of panel A, as these are the placements in which the black and white checks are consistent with NF-S motion. Checkmarks indicate the placements that result in colorings that are within the library; circles indicate the placements that result in colorings that are not in the library. Tallying the number of placements in the library yields a unidirectional RM motion score (in this case, right forward). Analogous scores are calculated by reversing the NF-S template in space (left forward) and time (right backward, left backward). These four unidirectional RM scores are combined in an opponent calculation to yield the RMO score for the ROI. For the PMO method (bottom) the entire ROI is treated as a whole. We determine the fewest number of checks that must be changed so that every placement of the template within the ROI yields a coloring that is in the library of panel A. In this case, changing two checks suffices: When these two checks are flipped in contrast (dashed arrows), all glider placements are in the library, and the resulting ROI is entirely consistent with NF-S motion. The tally of these changes yields the right, forward unidirectional PM signal. These four unidirectional PM signals are combined by an opponent computation to yield the PMO score for the ROI.

Based on these libraries, each ROI can be analyzed in terms of the configurations it contains to yield a score that quantifies the amount of each kind of coherent motion. We used two complementary approaches (but as we show below, the conclusions are largely similar).

The first approach (Figure 2B, top left) considers all of the placements of the template within the ROI and tallies the number that contributes positively to the motion signal. This yields a set of “rule match” (RM) scores—one for each orientation of the template (right forward, left forward, right backward, left backward). These components are then compared to form a final “rule match opponent” (RMO) score for the ROI.

The second approach, “pattern match” (PM), treats the ROI in a more holistic fashion. To compute the PM measure (Figure 2B, bottom left), we determine the minimum number of checks that must be changed so that the ROI is made up entirely of template colorings within the library (i.e., that all have the relevant motion signal). As is the case for the RM approach, the four separate scores for each orientation of the template are then combined to yield a final “pattern match opponent” (PMO) score for the ROI.

The formal definition of the RMO and PMO scores are as follows. These scores are defined for any template B and any slab-like ROI that can contain the template along either the X or Y dimension, and has its other spatial dimension equal to one. Since the RMO score is an opponent score, we first define its components: the RM score RM(B; Z; ROI). This is given by the total number of displacements (x_i, y_i, t_i) of the template within the ROI for which RawCorr^binarized(x + x_i, y + y_i, t + t_i; B) = 1, and thus is effectively a sum of RawCorr^binarized scores within the ROI. The RMO score, RMO(B; Z; ROI), is then

To define the PM score (PMO), we use the Hamming distance, a standard way of comparing two sets of binary numbers. Specifically, the Hamming distance between an ROI and another region K of the same size is given by

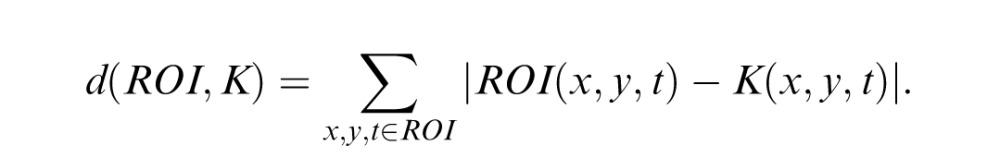The PM score PM(B; Z; ROI) is the minimum Hamming distance from the ROI to any region K for which every placement of the template in K yields a local motion score of +1. This minimum takes into account all possible colorings of K; this is one reason why the dimensionality reduction is important. Finally, the PMO score is given by

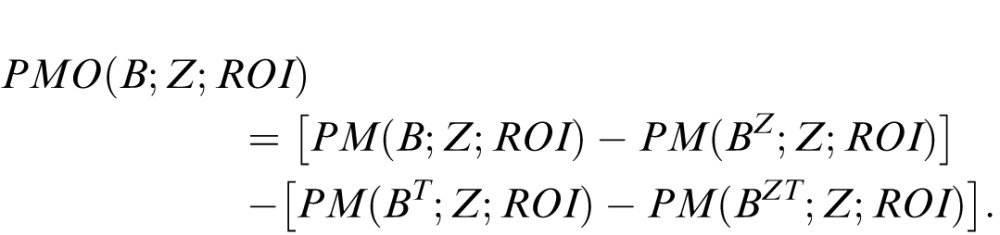Analogous RMO and PMO calculations were carried out for the other motion types (F, NF-T, and G) based on libraries that consisted of all colorings of the corresponding templates (Figure 1) that yielded a product of +1. For G motion, the procedure is asymmetric with respect to bright and dark: The resulting library includes three black checks but not three white ones, so it captures expansion and contraction of dark regions but not of light ones. We therefore designated this library G-K (black glider) and, in parallel, carried out computations based on a library G-W (white glider) containing the complementary colorings. Further, we also calculated RMO and PMO scores for the “pure NF-S” and “pure NF-T” signals. These were based on libraries that consisted of the NF-S or NF-T library, from which the libraries that contained F motion signals were removed (purple-outlined templates on the right in Figure 2).

Once RMO and PMO scores were calculated within each ROI, they were pooled within each shot by summing their squares. As is the case for the SM scores, we normalized this quantity by dividing it by the results of a parallel computation applied to random movie segments.

Note that for F motion, the RMO score is exactly the output of a special case of a Reichardt detector (one with spatial inputs that are point-like and closely spaced, and has a pure delay of one frame prior to the multiplication step) operating on a binary image. For the PMO score, the correspondence is close but not exact (see Supplement 2, Figure S12 for further details). These correspondences were expected because the RMO and PMO scores were intended to generalize the Reichardt model in a manner that would be sensitive to local coherence.

Results

Our results concern the prevalence of different kinds of local motion signals in naturalistic scenes and how they covary. As described above, we considered three basic kinds of motion: F, NF, and G. F motion is equivalent to pairwise spatiotemporal correlation of luminance. NF motion (Chubb & Sperling, 1988; Fleet & Langley, 1994) is spatiotemporal correlation of a feature, and we identified two subtypes: spatiotemporal correlation of a spatial feature (NF-S) or a temporal feature (NF-T). The G motion considered here is characterized by expansion or contraction of either white or black patches, which can occur in the absence of pairwise spatiotemporal correlation of luminance, flicker, or edge (Hu & Victor, 2010). We begin with an analysis of the prevalence of each kind of motion in four popular movies, using a simple measure of local motion signals (SM) and two measures that are sensitive to whether these signals are locally coherent (RMO and PMO; see Materials and methods for details on how these measures are defined). Then, using the various subtypes of motion signals that emerge from the RMO and PMO procedure, we consider how the different kinds of motion signals covary across movie segments (shots).

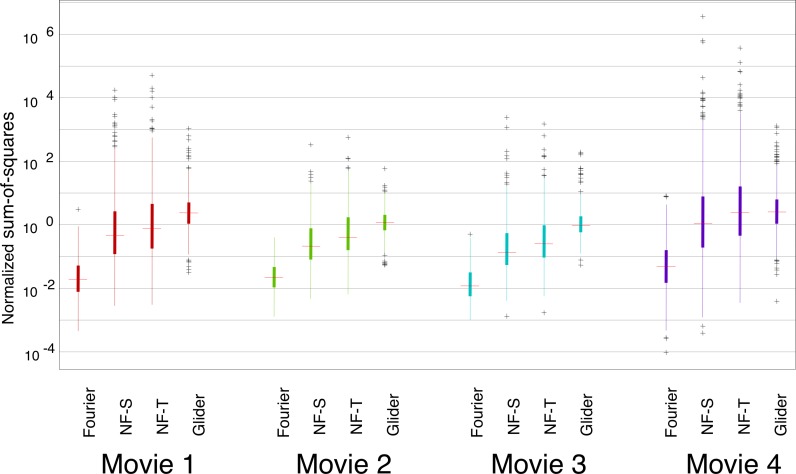
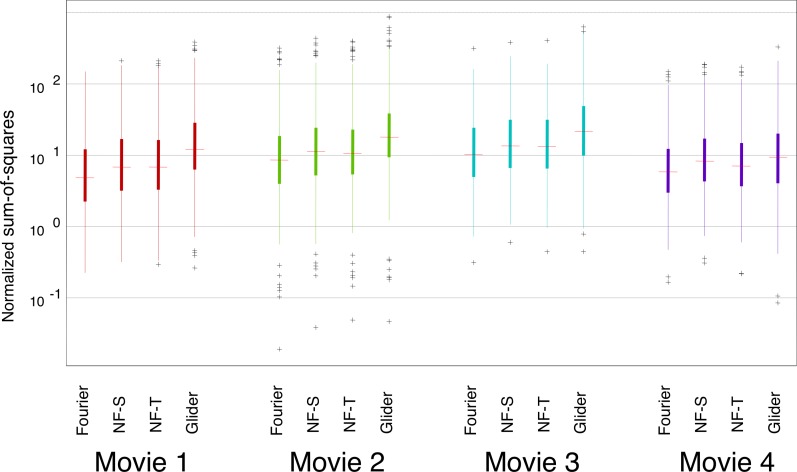
Results for the SM scores are shown in Figure 3. Overall, F motion strengths are the weakest, NF motion strengths are approximately 10 times stronger, and G motion strengths are intermediate between those two. There is a slight difference between spatial and temporal subtypes of NF motion: NF-S is slightly stronger than NF-T. Importantly, this pattern of relative strengths of the different kinds of motion signals is preserved across movies. The consistency of motion signals across movies holds across spatial scales. In Figure 3, the full available movie resolution was used (each analysis check consisted of a single movie pixel of the 256×256-pixel frame in the database); Figure 4 shows the results of an analysis in which each analysis check contains the average across a 16×16 block of pixels. With this coarse-grained analysis, F motion strength remains much weaker than NF and G strengths, and there is a modest change in the behavior of the NF and G signals. Specifically, while the tails for NF motions remain larger than the tails for G motion (as was the case at the fine scale), the median for G motion is now larger than the median for NF motion. This shift, as well as the overall pattern of motion strengths at each scale, is consistent across movies. An extended analysis of motion strengths at intermediate scales is shown in Supplement S1, Figures S1 and S2.

Figure 3.

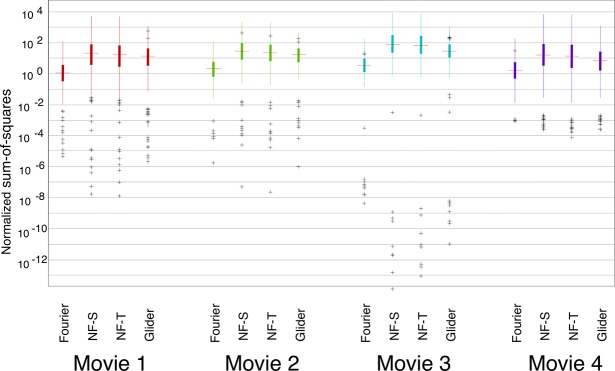
Prevalence of different kinds of motion signals is similar across movies. For each movie, SM scores (see Materials and methods) were calculated for each movie segment, and the distribution is summarized by the median (horizontal line), the interquartile range (heavy vertical line), the “whiskers” (thin vertical line, covering four times the interquartile range), and the outliers (individual symbols, outside the range of the whiskers). Values are normalized by SM motion scores obtained from movies of random pixels of similar segment length. Each motion was calculated with respect to its relevant template shape (see Figure 1A) in the YT plane (i.e., horizontal motion); each check corresponded to a single pixel in the discretization of the movie (256×256 pixels per frame, 24 frames per second). Movies were (1) The 39 Steps (1935), (2) Anna Karenina (1935), (3) A Night at the Opera (1935), and (4) Mr. and Mrs. Smith (2005).

Figure 4.

Prevalence of different kinds of motion signals, analyzed at a coarse spatial scale, is similar across movies. For each movie, SM scores were calculated after downsampling each 16×16 block of pixels in the original movie to a single check. For other details see Figure 3.

The above analyses quantify the strength of each kind of motion signal in each movie segment (shot), but do so via an SM measure that is insensitive to whether the motion signals are locally coherent. We next carry out parallel analyses with two measures (RMO and PMO; see Materials and methods) that are designed to be sensitive to coherence of motion signals within 16-check ROIs. A key step in the construction of these measures is binarization of the movie to reduce the dimensionality of the problem (see Materials and methods). Thus, as a preliminary step, we first examined the effects of binarization itself.

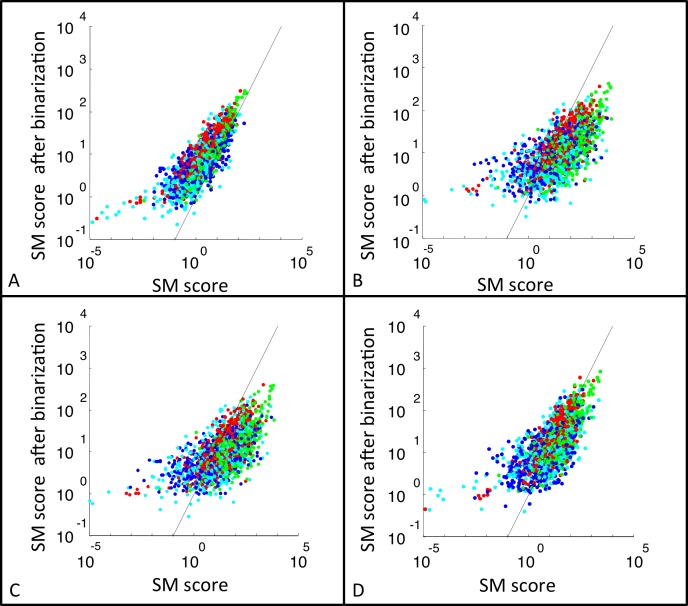
Figure 5 directly compares measures of motion strength on a shot-by-shot basis calculated with and without binarization. For all motion types, binarization compresses the range of the motion scores from approximately a factor of 10⁶ (without binarization) to 10³ (with binarization to +1 and −1). Most of this compression is due to an increase in the lowest motion scores since binarization eliminates the possibility of multiplication by values near zero. But the upper ends of the distribution are also affected by binarization: Thresholding substantially reduces highest values for NF-S and NF-T (Figure 5B and C) and slightly reduces the highest values for G (Figure 5D). The likely reason for this is that the NF scores reflect products of four values (since the templates have four checks) and the G scores reflect products of three values (since the templates have three checks). Hence, binarization results in a moderate reduction in the extreme high values that result from products of three luminance values (G) and a more severe reduction in the extreme high values that result from products of four values (NF). In line with the increasing range compression as the number of checks in the template increase, correlations of the log-scaled SM scores with and without binarization are largest for F motion (0.79), next-largest for G motion (0.69), and smallest for NF-S and NF-T motion (0.62 and 0.63, respectively; p < 0.001 in all cases).

Figure 5.

The effect of binarization on local motion scores for (A) F, (B) NF-S, (C) NF-T, and (D) G motions. SM scores were calculated for each movie segment based on raw luminance values (abscissa), and also following binarization with the threshold set at the overall shot median luminance (ordinate). No spatial downsampling was applied. A random sample of 500 shots from each movie is presented here. Movies were color coded as follows: (red) The 39 Steps, (blue) Anna Karenina, (green) A Night at the Opera, and (cyan) Mr. and Mrs. Smith (2005). The black line is the line of identity.

We note that when applied to binary movies, the local motion score for F motion coincides exactly with the output of a Reichardt detector because the SM score computes exactly the same product as the Reichardt detector, and the binarization step has no effect on a movie that has already been binarized. See Supplement S2, Figure S12 for further details and for the relationship of the RMO and SMO scores to the Reichardt detector for binary and gray-level movies.

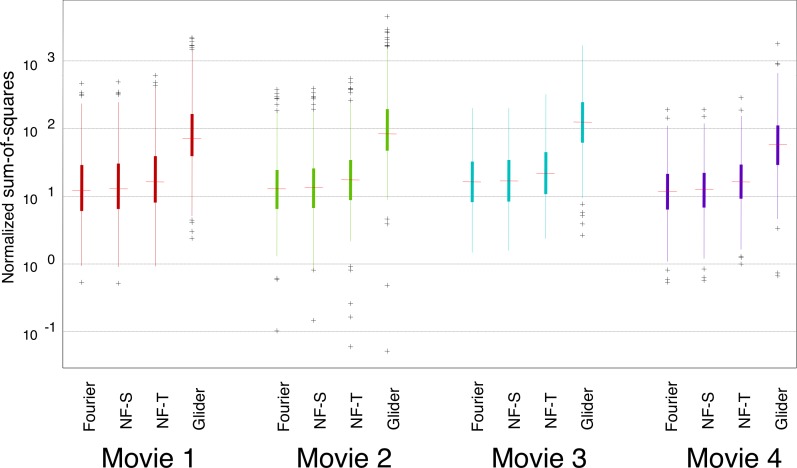
The effects of binarization on the shot-by-shot distributions of SM scores are shown in Figure 6 (analyzed at a fine spatial scale) and Figure 7 (analyzed after 16×16 downsampling). An extended analysis of motion strengths at intermediate scales is shown in Supplement S1, Figures S1 and S2. As expected from Figure 5, the distributions are more compact than the corresponding distributions shown in Figures 3 and 4. F motion remains the smallest signal and G motion is the largest, as the upper tail of the NF motion distributions is most severely affected by the binarization. As is the case for the analysis without binarization, the pattern of motion strengths is similar across movies at each spatial scale.

Figure 6.

Prevalence of different kinds of motion signals is similar across binarized movies. For each movie, data were first converted to −1 or +1 using a threshold equal to the median overall luminance value within each shot, and SM scores were then calculated. For other details, see Figure 3.

Figure 7.

Prevalence of different kinds of motion signals, analyzed at a coarse spatial scale, is similar across binarized movies. For each movie, SM scores were calculated after downsampling each 16×16 block of pixels in the original movie to a single check, and then binarization. For other details see Figure 4.

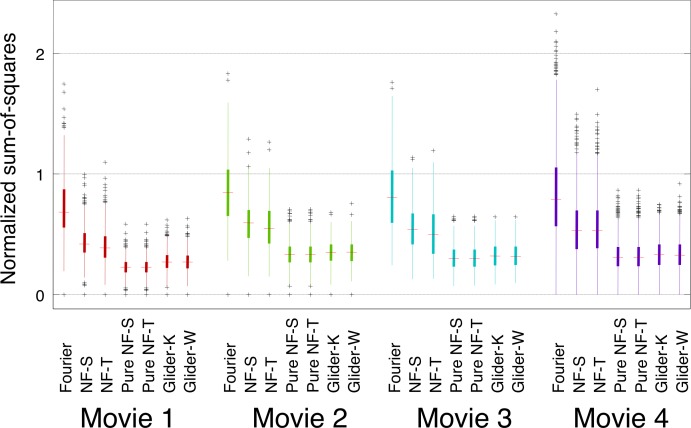
We now turn to the indices that examine the strength of coherent motion of each type. Briefly (see Materials and methods for further details), the indices were calculated as follows. First, correlations of the binarized movies were calculated within slanted spatiotemporal templates corresponding to each motion type (Figure 1). Since the movies are binarized, calculation of the correlations (the products of the luminances in each check) reduces to determining whether each template's coloring is present in a library (shown in Figure 2 for NF-S). Second (Figure 2B), correlations were combined within a spatiotemporal ROI. Two variants were used for this pooling process: one in which the local correlations were simply summed (RMO) and one in which they were treated holistically (PMO). Third, signals in opposite directions were compared to determine a net motion signal for each ROI. Finally, the sum of the squares of these local signals within each shot were normalized by the results of a similar calculation applied to random movie segments. Results for the PMO index are shown in Figure 8. Overall, F motion strengths were the largest, NF motion strengths were 50% to 70% as large, and the other kinds of motion (pure NF and G) were somewhat smaller. There was virtually no difference between spatial and temporal subtypes of NF motion and virtually no difference between white and black subtypes of G motion. As with all previous analyses, the pattern of relative strengths of the different kinds of motion signals was preserved across movies.

Figure 8.

Prevalence of different kinds of motion signals is similar across movies, as measured by the PMO score. The ROI consisted of a 4×4 block of checks in the YT plane (i.e., horizontal motion); each check corresponded to a single pixel in the discretization of the movie (256×256 pixels per frame, 24 frames per second). For other details see Figure 3.

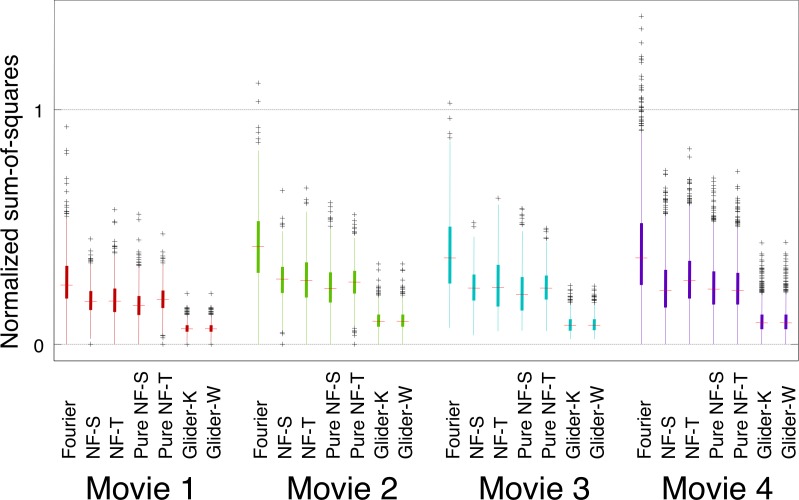
Parallel results for the RMO index are shown in Figure 9. Overall values of motion strength are smaller than for the PMO index (Figure 8), and the RMO index shows a larger difference between the NF motion strengths and the G motion strengths than the PMO index. However, the basic findings obtained with the two kinds of ROI indices are similar: F motion strengths are largest, followed by NF motion, and then by G motion, and the relative sizes of the motion signals are consistent across movies.

Figure 9.

Prevalence of different kinds of motion signals is similar across movies, as measured by the RMO score. The ROI consisted of a 4×4 block of checks in the YT (horizontal motion) plane. For other details see Figure 8.

The analyses in Figures 8 and 9 were performed with ROI oriented parallel to the YT plane and for a single resolution (each check used in the analysis corresponded to one pixel in the database's digitization of the movie); the results hold for other resolutions (Supplement S1, Figures S3 and S4) and orientations (Supplement S1, Figures S5 and S6). In addition, Supplement 1, Figures S7 and S8 show parallel results for binarization at the global midgray level rather than the median for each shot.

In sum, when motion signals are measured in a purely local manner (SM score), F signals are weaker than NF or G signals (Figures 3, 4, 6, and 7). But when spatial coherence is taken into account (via either the PMO index [Figure 8] or the RMO index [Figure 9]), F signals dominate. This shift, as well as the pattern of motion strengths captured by each index, is similar across analysis scales and movies.

Covariation of motion signals

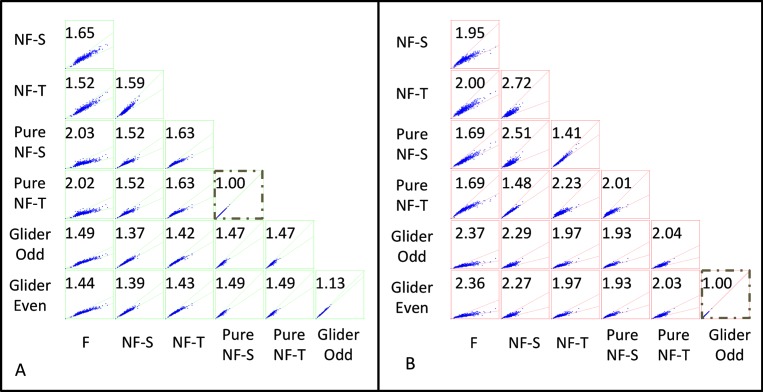
The distributions shown in Figures 8 and 9 indicate a substantial variation in the amount of motion signals present in each shot. We now focus on this variability and examine how the different kinds of motion signals covary with one another. One possibility is that the different kinds of motion signals are tightly correlated—that some segments have low levels of all motion signals and others have high levels, with the amount of one signal determining the amount of the others. Alternatively, the motion signals may be somewhat independent, present in ratios that depend on the characteristics of the individual shots. With this motivation in mind, we determined the pattern of covariation of the several kinds of motion signals.

Results are shown in Figure 10 (panel A for PMO and panel B for RMO). While it is clear that there are strong correlations between motion signals of each type with every other type, it is also clear that they are not completely redundant (except for the specific pairs of motion scores that are guaranteed to be identical; see Supplement S2). That is, given the size of one kind of motion signal, the size of another kind can vary by a factor of two or more. The extent to which one motion signal determines the other depends on the specific pair of signals. For example, considering the PMO indices (Figure 10A), an F signal is only a weak determinant of a pure NF-T signal (their ratios can vary by more than a factor of two), but the G and the NF-S signals are strongly correlated (their ratios vary by less than 40%). With the RMO index (Figure 10B), the patterns of covariation are in general similar, though there is somewhat less correlation overall between the motion indices. Supplement S1, Figure S9 shows a corresponding analysis for a second movie; the pattern of covariation for each kind of index (PMO and RMO) is very similar to that of Figure 10. This shared pattern of covariation across movies is a consequence of the statistical structure of the movies themselves, not of the way that the indices are calculated (e.g., that they are determined from overlapping sets of templates). This is shown in Supplement S1, Figure S10, when a similar analysis is applied to random movies. In this case, the different kinds of motion signals are largely uncorrelated. Supplement 1, Figure S11 shows parallel results for binarization at the global midgray level rather than the median for each shot for one movie.

Figure 10.

Covariance patterns of motion scores: (A) PMO and (B) RMO. Within each scattergram, each point represents a pair of normalized motion scores determined from a single movie segment (“shot”). Axes range from 0 to 2 (PMO) and 0 to 1 (RMO). The number in each plot indicates the average ratio between the pair of motion scores; the two sloping lines in each plot indicate the wedge that contains 95% of the values. Large values of one motion score typically occur with large values of the other scores, but the ratios between a pair of scores can vary by up to a factor of two. (Pure NF-S and NF-T PMO scores are identical, and the two G motion RMO scores are identical; see Supplement S2.) Analysis was carried out in the YT plane (horizontal motion) at the maximum resolution of the database for The 39 Steps.

Discussion

Identifying the presence of moving objects and determining their velocity begins with neural computations that analyze restricted patches of the visual input in order to extract local motion signals.

Based on their mathematical properties, several types of local motion signals have been recognized. The simplest is pairwise spatiotemporal correlation of the luminance pattern (Adelson & Bergen, 1985; Reichardt, 1961); this is known as F motion since the presence of pairwise spatiotemporal correlation can be identified from the Fourier amplitudes of the stimulus. Subsequently, it was recognized that pairwise spatiotemporal correlation is not necessary to produce a percept of visual motion (Chubb & Sperling, 1988; Fleet & Langley, 1994; Hu & Victor, 2010). A percept of motion can be produced by spatiotemporal correlation of a local feature rather than of the luminance pattern itself—a phenomenon typically called NF motion (Chubb & Sperling, 1988) to emphasize that the correlations cannot be identified from the Fourier amplitudes. A percept of motion can also be produced by spatiotemporal correlations among three points, a phenomenon known as G motion (Hu & Victor, 2010), even when spatiotemporal correlations of simple features are not present. Note that both NF motion and G motion each encompass multiple distinct subtypes of local motion signals—for NF motion the subtype is determined by the choice of local feature (e.g., edge or flicker), and for G motion the subtype is determined by the geometry of the three spatiotemporal points that are correlated (although here we consider only one specific configuration: a right triangle whose legs are aligned with space and time axes).

Although each of these kinds of motion signals is mathematically distinct and separately available to perception, their occurrence in the natural environment is poorly characterized. We therefore developed several ways to quantify the strengths of different kinds of local motion signals so that they could be compared on an equal footing.

This step was necessary because of the way that the different kinds of motion signals are usually defined: F motion signals are defined in terms of a computational model that is applicable to any stimulus (Adelson & Bergen, 1985; Reichardt, 1961), while NF motion and G motion are defined in terms of specific exemplars, along with the absence of an F signal. The key consideration that enabled a comparable measure that is applicable to the different kinds of motion signals is that each kind of motion corresponds to a correlation in a spatiotemporal region with a specific geometry (i.e., within a specific template; see Materials and methods). For standard (F) motion, this template is a pair of checks on a space-time diagonal. For NF motion, the template is a set of four checks, forming a parallelogram in space-time. For G motion, the template is a set of three checks in a triangle. As expected, when applied to standard (F) motion, this method yields results that are consistent with computations based on standard spatiotemporal correlation (i.e., the Reichardt detector; Adelson & Bergen, 1985; Reichardt, 1961, 1987; Van Santen & Sperling, 1985): For gray-level movies, results are strongly correlated, and for binary movies, they coincide (Supplement S2, Figure S12).

For NF motion, the development of a motion score is less straightforward, as different exemplars of NF motion can have qualitatively different natures. For example, NF motion stimuli can be constructed based on beats, contrast modulation, transparency, or occlusion. Fleet and Langley (1994) observed that the motion signals in all of these stimuli have a common aspect that is manifest in the power spectrum: Power is concentrated in spatiotemporal planes that do not include the origin. Since calculation of the power spectrum requires inspection of a wide region of space, this observation does not directly translate into a measure of a local NF motion signal. However, it is closely linked to the rationale for our approach. As Fleet and Langley (1994) observe, power in a spatiotemporal plane away from the origin corresponds to pairwise spatiotemporal correlation of a feature; this pairwise correlation, in turn, can be detected by a local nonlinearity. This is exactly the approach taken here. Each of the two kinds of features considered—spatial and temporal edges—are identified based on whether the values within a pair of checks match or mismatch (a local nonlinearity). Then, multiplication (or the parity rule) within the four-check template computes the pairwise spatiotemporal correlation of these two-check features. However, the actual computations used by the visual system to extract NF motion are unknown. Thus, despite the grounding of the approach in a common mathematical feature of NF motion (Fleet & Langley, 1994), we used multiple variants of the basic correlation measure to ensure the robustness of our results: measures with and without a binarizing nonlinearity, and measures that used different kinds of spatial pooling (SM, RMO, PMO).

An advantage of this approach to measuring NF motion strength is that it extends to G motion simply by changing the shape of the template. Moreover, by changing the template and the rules for scoring its colorings, this approach can be extended to deal with further types of features, such as temporal correlation of orientation (Dong & Atick, 1995; Fleet & Langley, 1994; Kayser, Einhäuser, & König, 2003).

Since many studies have been devoted to understanding the correlation structure of natural scenes (Field, 1987; Reinagel & Zador, 1999; van Hateren & van der Schaaf, 1998)—including their temporal aspects (Cutting, DeLong, & Brunick, 2011; Dong & Atick, 1995; Kayser et al., 2003)—it may appear surprising that relatively little is known about the local motion signals that they contain. The basic reason is that the focus of most studies has been on the second-order statistics of natural scenes. While F motion signals can be determined from second-order statistics, G motion and NF motion require, respectively, knowledge of third- and fourth-order statistics. Thus, studies of the spatiotemporal power spectrum (Dong & Atick, 1995) cannot characterize NF motion and G motion completely, as the spectrum is a characterization only of pairwise correlations. On the other hand, it is difficult to carry out an exhaustive characterization of high-order statistics of natural scenes because of the dimensional explosion that results. Thus, in order to carry out an analysis that suffices to identify G motion and NF motion, we are necessarily selective about the high-order image statistics that are analyzed.

Once the motion-related high-order statistics were identified, we used two methods to pool them within each ROI (see Materials and methods): RMO and PMO. The RMO score simply compares the number of template positions in which the local motion signal is present and the number of positions in which it is absent; it is thus linear and is as local as possible, as it adds no further spatial interactions. In contrast, the PMO score determines the closest match of the ROI to an exemplar ROI in which the local motion signal is present in every template position. Therefore, the PMO score is nonlinear—it is strongly sensitive to whether the motion is coherent throughout the ROI—and, consequently, is somewhat less local than the RMO score. Neither score is necessarily larger than the other: For specific ROI colorings, the RMO score may be higher than, equal to, or lower than the PMO score. Thus, the two scores provide different ways to measure the strength of each kind of motion signal. Nevertheless, as emphasized above, our basic conclusion holds in either case (Figures 8, 9, and 10) and across scales of analysis and binarization strategies (Supplement S1). That is, each kind of motion signal (F, two varieties of NF, and two varieties of G) is present in natural movies. Across movies they are present in approximately similar amounts, and at the level of individual movie segments there is substantial variation in the proportion of each kind of motion signal but a similar pattern of covariation.

The level of consistency across movies is perhaps surprising, given the finding of Cutting et al. (Cutting, Brunick, DeLong, Iricinschi, & Candan, 2011; Cutting, DeLong, et al., 2011) that the general amount of visual change in movie shots increased significantly over the period that the movies span (1935–2000). Our approach, though, is different, as it is specifically sensitive to different kinds of local motion rather than overall amount of visual change. Further, the similarity of the strengths of local motion signals appears to hold over a range of shot lengths, which vary over a twofold range (8.96 s, 9.6 s, and 9.16 s in the 1935 films but 4.15 s in the 2005 film, also reflecting a trend in movie making; Cutting, Brunick, et al., 2011; Cutting, DeLong, et al., 2011).

The segment-to-segment variation in the relative strength of the different kinds of motion signals (Figure 10) also deserves comment. As is evident from these scattergrams, different kinds of motion signals tend to occur in combination. This is very different from most artificial stimuli used to study motion in the laboratory, as such stimuli are typically designed with the goal of isolating a single kind of cue. Moreover, the fact that there are correlations between different kinds of motion signals in the natural environment has implications for understanding the design of neural circuits that detect motion. If high-order motion cues coexist with F motion cues, then they can be exploited (Fitzgerald et al., 2011) to improve on the performance of a standard Reichardt detector (Reichardt, 1961). As we show here, this coexistence is characteristic of motion signals in naturalistic movies (Figure 10 and Supplement S1, Figure S9), so these theoretical considerations (Fitzgerald et al., 2011) are relevant to natural vision.

Although there are correlations between different kinds of motion signals, they are not redundant. Specifically, given the level of one motion signal (e.g., F motion) in a movie segment, one can estimate the level of another (e.g., G motion), but the estimate holds only within a factor of two.

This diversity in the complement of motion cues that are present in a given movie segment may have implications for how motion is analyzed at later processing stages. In central visual processing, motion is used for many different purposes, such as navigation, collision avoidance, extraction of object structure (Ullman, 1979a; Vaina, Lemay, Bienfang, Choi, & Nakayama, 1990), and the analysis of biological motion (Ahlstrom, Randolph, & Ahlstrom, 1997; Beintema & Lappe, 2002; Burr & Thompson, 2011; Fox & McDaniel, 1982; Grill-Spector & Malach, 2004; Grossberg, 1994; Johansson, 1973; Koenderink & Van Doorn, 1991; Nakayama, 1985; Ullman, 1979a), each of which is carried out in distinct networks of brain areas (Grill-Spector & Malach, 2004; Grossman et al., 2000; Smith, Greenlee, Singh, Kraemer, & Hennig, 1998; Vaina et al., 1990).

Some aspects of the different kinds of low-level motion signals suggest that they may be selectively important in these different contexts, or for different purposes. One example of this potential for selectivity is that, as Fleet and Langley (1994) point out, NF motion signals can arise from occlusion. When an untextured object moves across the visual field in front of a textured background, it progressively occludes and then reveals spatial features of the background, generating a spatial NF motion signal. A similar NF motion phenomenon occurs if the foreground object is semitransparent: The features are not eliminated, but their contrast is modulated. Another way in which a specific kind of motion signal may arise in a specific context is that G motion signals can arise from looming—that is, the motion of an object toward the observer. This is because the basic element of G motion is correlation in a three-point spatiotemporal configuration of checks (Hu & Victor, 2010). For three points arranged in a right triangle with one side aligned with the temporal axis—the case considered here—this corresponds to an expanding or contracting region.

Since different kinds of local motion signals can arise in different contexts, it is reasonable to speculate that brain areas that make use of motion for different purposes (e.g., segmentation vs. navigation) receive inputs from local motion detectors with appropriately matched properties. This would enable the parallel high-level analyses of motion in central visual areas to focus on the kinds of low-level signals that are the most relevant to their separate functions.