A novel electron gun for inline MRI-linac configurations

Abstract

Purpose: This work introduces a new electron gun geometry capable of robust functioning in the presence of a high strength external magnetic field for axisymmetric magnetic resonance imaging (MRI)-linac configurations. This allows an inline MRI-linac to operate without the need to isolate the linear accelerator (linac) using a magnetic shield. This MRI-linac integration approach not only leaves the magnet homogeneity unchanged but also provides the linac flexibility to move along the magnet axis of symmetry if the source to target distance needs to be adjusted.

Methods: Simple electron gun geometry modifications of a Varian 600C electron gun are considered and solved in the presence of an external magnetic field in order to determine a set of design principles for the new geometry. Based on these results, a new gun geometry is proposed and optimized in the fringe field of a 0.5 T open bore MRI magnet (GE Signa SP). A computer model for the 6 MeV Varian 600C linac is used to determine the capture efficiency of the new electron gun-linac system in the presence of the fringe field of the same MRI scanner. The behavior of the new electron gun plus the linac system is also studied in the fringe fields of two other magnets, a 1.0 T prototype open bore magnet and a 1.5 T GE Conquest scanner.

Results: Simple geometrical modifications of the original electron gun geometry do not provide feasible solutions. However, these tests show that a smaller transverse cathode diameter with a flat surface and a slightly larger anode diameter could alleviate the current loss due to beam interactions with the anode in the presence of magnetic fields. Based on these findings, an initial geometry resembling a parallel plate capacitor with a hole in the anode is proposed. The optimization procedure finds a cathode-anode distance of 5 mm, a focusing electrode angle of 5°, and an anode drift tube length of 17.1 mm. Also, the linac can be displaced with ±15 cm along the axis of the 0.5 T magnet without capture efficiency reduction below the experimental value in zero field. In this range of linac displacements, the electron beam generated by the new gun geometry is more effectively injected into the linac in the presence of an external magnetic field, resulting in approximately 20% increase of the target current compared to the original gun geometry behavior at zero field. The new gun geometry can generate and accelerate electron beams in external magnetic fields without current loss for fields higher than 0.11 T. The new electron-gun geometry is robust enough to function in the fringe fields of the other two magnets with a target current loss of no more than 16% with respect to the current obtained with no external magnetic fields.

Conclusions: In this work, a specially designed electron gun was presented which can operate in the presence of axisymmetric strong magnetic fringe fields of MRI magnets. Computer simulations show that the electron gun can produce high quality beams which can be injected into a straight through linac such as Varian 600C and accelerated with more efficiency in the presence of the external magnetic fields. Also, the new configuration allows linac displacements along the magnet axis in a range equal to the diameter of the imaging spherical volume of the magnet under consideration. The new electron gun-linac system can function in the fringe field of a MRI magnet if the field strength at the cathode position is higher than 0.11 T. The capture efficiency of the linac depends on the magnetic field strength and the field gradient. The higher the gradient the better the capture efficiency. The capture efficiency does not degrade more than 16%.

INTRODUCTION

The ideal image guidance strategy in radiation therapy is to have real-time volumetric and position information of the tumor and surrounding healthy tissue during the treatment itself. One compelling approach is to use magnetic resonance imaging (MRI) which is a noninvasive technique that not only allows real time volumetric imaging, but provides exquisite soft tissue contrast to differentiate cancerous from healthy tissue. To date two base MRI-linac configurations have been proposed, i.e., the inline^{1, 2, 3} and the perpendicular^{4, 5} configurations, which are defined by the relative orientation of the linac with respect to the main magnetic field of the MRI scanner. All these configurations assume a fixed position of the linac with respect to the MRI scanner.

In Ref. 2, it was shown that relatively small transverse magnetic fields of 0.01 T strongly deflect the electron beam inside the electron gun with no current being injected inside the linac. Therefore, for a perpendicular MRI-linac configuration there must exist magnetic shielding for the linac to avoid electron beam deflection inside the electron gun and linac by the transverse magnetic field of the MRI scanner. For an inline configuration, shown in Fig. 1, the field lines are parallel with the flow of electrons and a big fraction of the current generated by the electron gun cathode will manage to exit the anode as shown in Ref. 2 especially at strong magnetic fields, i.e., above 0.1 T.

Figure 1.

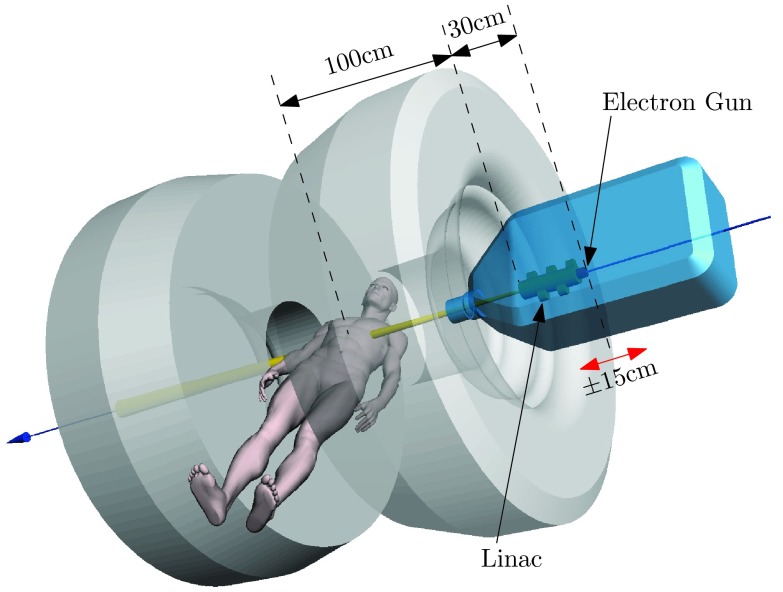
Schematic representation of the inline MRI-linac apparatus. The treatment beam is inline with the main magnetic field of the MRI magnet. The patient is positioned between the poles of the open bore MRI magnet in a perpendicular position with respect to the main magnetic field and the treatment beam. The x-ray source is placed 100 cm from the system isocenter, which defines the standard configuration of the MRI-linac system. Hence, for the standard configuration, the electron gun cathode position is approximately 130 cm from the MRI-linac isocenter. The linac is allowed to move along the system axis of symmetry with ±15 cm around the standard configuration position.

The first and obvious solution to mitigate current loss in the electron gun for an inline MRI-linac is to employ a magnetic shield. Another solution would be to modify the electron gun geometry to allow its operation in the fringe field of the MR scanner as first proposed in Ref. 2, thus removing the need of a magnetic shield for the linac.

The advantages and disadvantages of having a magnetic shield are numerous. The most important ones are related to design and operation of the MRI-linac system. The presence of a magnetic shield for the linac will not only involve the design of the shield itself but also the design of the magnet to accept the shield in its close proximity. Also, the presence of a magnetic shield will limit the ability to move the linac with respect to the MR scanner if this is required. There are radiotherapy procedures, e.g., stereotactic radiosurgery, for which it is desired to have the tumor positioned in the radiotherapy machine isocenter during treatment and this is achieved by moving the system couch. For a MRI-linac, the range of motion for a patient inside the MRI scanner is limited, and the only option to achieve an optimum distance between the tumor and the linac is to move the linac.

The absence of a magnetic shield involves the redesign of one component only, the electron gun, leaving the other essential components such as the magnet and the linac unchanged. To avoid the redesign of other elements, e.g., the tungsten target, the new electron gun should generate an electron beam with characteristics as close as possible to the zero field electron beam. Also, the range of motion for the linac will be greater compared to the case with a magnetic shield and it will be constrained only by the geometries of the linac and the magnet. However, the absence of a magnetic shield will require the replacement of all the magnetic parts in the linac construction with nonmagnetic parts.

The main focus of this paper is to design a robust electron gun capable of functioning in the fringe field of several MRI scanners for the inline MRI-linac configuration without magnetic shielding. Also, the ability to move the linac along the axis of symmetry of the magnet is investigated and characterized. This MRI-linac configuration for which the linac can be moved relative to the MRI scanner so it can track the tumor position was first presented in Ref. 6 and was called robotic linac adaptation (RLA) configuration. The RLA configuration is in a sense a generalization of the inline MRI-linac configuration with no magnetic shielding, and the basic principle which allows a RLA configuration to work is the magnetic confinement of the electron beam along the magnet axis in the presence of the axially symmetric fringe field of the MRI magnet. To perform a consistent study, it is necessary to simulate not only the modified electron gun but also the corresponding linac to ensure proper electron beam capture and acceleration when magnetic fringe fields are present. In this paper, we consider the Varian 600C linac for which there are published linac and electron gun models.^{7, 8}

METHODS AND MATERIALS

The magnetic fields

In this work, we consider the magnetic fringe fields corresponding to three magnets of different strengths, i.e., 0.5 T GE Signa SP open bore magnet, 1.0 T open bore prototype magnet, and 1.5 T GE Conquest magnet. The magnetic field map measurement of the 0.5 T GE (Pewaukee, WI) magnet was previously reported in Ref. 2. The magnetic field for the 1.0 T magnet is representative of an actively shielded open bore magnet being built by Agilent (Oxford, UK) technologies for The University of Sydney MRI-linac program. Also, the fringe field map of the 1.5 T GE (Pewaukee, WI) magnet was provided by the magnet manufacturer as a representative field map. To simplify field manipulations, we have used analytical approximations for the field components.

Because the magnetic fields have cylindrical symmetry and the regions in space where all the simulations were performed are free from currents and close to the axis of symmetry, the fields components can be approximated⁹ as functions of the field axial component along the axis of symmetry, B_z(0, z), its derivatives and the radial coordinate r

$$B_z(r,z)=B_z(0,z)-\frac{r^2}{4}\frac{{\partial }^2{B}_z(0,z)}{\partial z^2}+\cdots ,$$ (1a)

$$B_r(r,z)=-\frac{r}{2}\frac{\partial B_z(0,z)}{\partial z}+\frac{r^3}{16}\frac{{\partial }^3{B}_z(0,z)}{\partial z^3}+\cdots .$$ (1b)

The axial component of the fringe field B_z(0, z) was approximated by a 9° polynomial between 0.8 and 3.0, 0.8 and 1.6, and 0.8 and 1.8 m for the 0.5, 1.0, and 1.5 T magnets, respectively. The differences in the spatial domains were due to limited availability of field map data for each magnet. The fields computed with Eq. 1 were compared against the corresponding magnet fields maps for radial coordinates less than 0.1 m. The field derivation approach based on Eq. 1 has simplified the computation procedure and it has reduced the computation time necessary to derive the field maps for the electron gun finite element models. The new electron gun geometry optimization was performed in the fringe field of the 0.5 T magnet, and the solution was tested in the fringe fields of all the three magnets to characterize its robustness and performance limits.

Simple modifications of the zero field gun geometry

The electron gun redesign procedure involved two steps. The first step considered simple modifications of the zero field electron gun geometry model originally presented in Ref. 10. The behavior of the altered electron gun geometry at zero field and in the presence of 0.06, 0.12, and 0.18 T external magnetic fields was characterized. The original geometry has a 2 mm diameter anode drift tube and a 4.62 mm cathode transverse diameter. The geometry alterations comprised a set of four distinct cases corresponding to: (i) a 4.4 mm cathode transverse diameter, (ii) a 150° conical cathode with 4.62 mm base diameter, (iii) a 150° with a 2 mm base diameter, and (iv) a geometry with 3.4 mm transverse diameter cathode and a 3.4 mm anode drift tube diameter. The behavior of each electrode geometry was characterized by the root mean square (rms) emittance ε_rms of the beam, the beam diameter, and the gun current which is defined as the beam current at the anode exit. Similarly, the target current is defined as the beam current at the target position. The rms emittance is a figure of merit which characterizes beam laminarity. A smaller rms emittance corresponds to a better beam laminarity and it is generally correlated with an increased linac beam capture efficiency. The capture efficiency is defined as the ratio between the target current and the gun current. For the Varian 600C series linac, it was determined in Ref. 10 that the gun current, the target current, and implicitly the capture efficiency are 0.360 A, 0.134 A, and 37%, respectively. In the paraxial approximation, the rms emittance can be defined based on phase space information as¹¹

$${\varepsilon }_{x,\text{rms}}=\sqrt{⟨x^2⟩⟨x^{\prime 2}⟩-{⟨x{x}^{\prime }⟩}^2},$$ (2)

where $x_i^{\prime }=d{x}_i/d{z}_i$ is the angle in the XZ-plane a particle makes with the beam axis of symmetry, i.e., Z-axis.

Optimization of the new gun geometry

The second step is based on the observations gathered from the first step described in Sec. 2B. A new electron gun geometry shown in Fig. 2 was proposed and optimized to work at 0.19 T in the fringe field of the 0.5 T GE Signa SP magnet. The value of the magnetic field of 0.19 T corresponds to the value of the magnetic field of the 0.5 T magnet 1.3 m away from the MRI scanner isocenter. Since, the distance between the electron gun cathode, i.e., the electron emitting surface, and the linac tungsten target is ≈0.3 m, this means that a 1.3 m distance between cathode and the MRI-linac isocenter places the linac target button at the standard distance of 1.0 m away from the isocenter.

Figure 2.

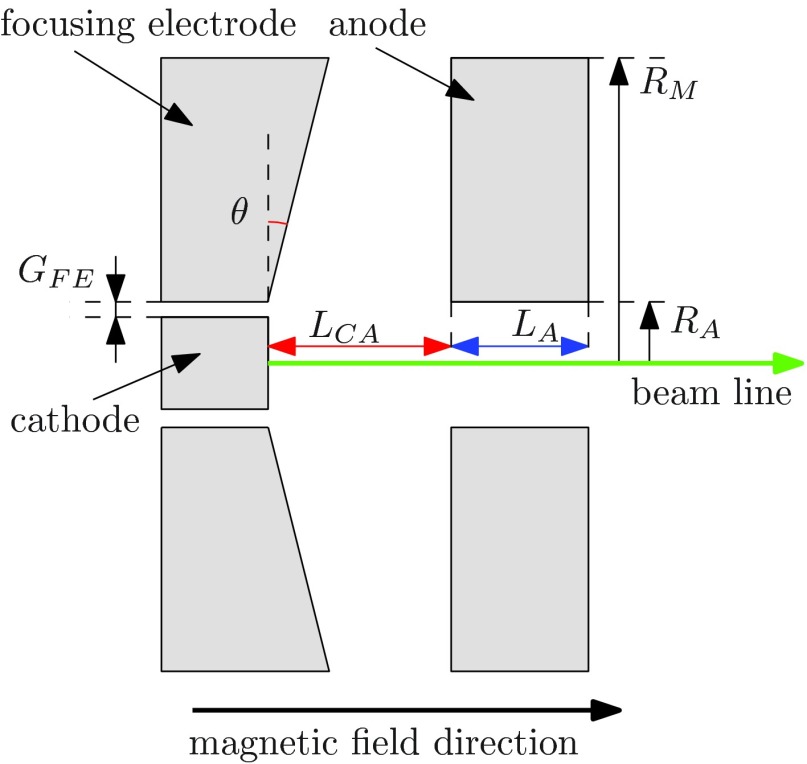
Axial cross section of the new electron gun geometry.

The starting point geometry resembled a parallel plate capacitor with a hole in the anode. The starting and end values for the geometry parameters, as well as the individual interval steps values used in the optimization process are presented in Table 1.

Table 1.

The range of values used in the optimization procedure for the geometrical parameters. Also, these parameters are listed in the order that they were optimized.

Parameter	Start value	End value	Step size
Model radius (RM) [mm]	20	12	−1
Anode radius (RA) [mm]	1	3	0.1
Focusing electrode angle (θ) [deg]	0	10	1
Cathode-anode distance (LCA) [mm]	3	10	1
Focusing electrode gap (GFE) [mm]	0.1	1	0.1
Anode length (LA) [mm]	20	…	…

The optimization procedure aimed at reducing the rms emittance at the electron gun exit. Besides the focusing electrode angle θ and the cathode-anode distance L_CA, all the other parameters were considered independent of each other. The model radius R_M controls the size of the finite element model which is proportional to the solution time. There is a limit for R_M above which the solution in the electron beam region does not change. To reduce the simulation time, the R_M threshold value was determined by decreasing its value from 20 to 10 mm in steps of 1 mm. For consistency, after each subsequent optimization step a check procedure ensured that the solution did not change if the model radius was increased back to 20 mm. Next, the anode drift tube radius R_A was increased to allow all the current to pass without any collisions inside the anode drift tube. The optimization for the focusing electrode angle θ and the cathode-anode distance L_CA was performed on a rectangular grid described by the parameters in Table 1. Also, the influence on the solution of the gap between the cathode and the focusing electrode G_FE was considered.

Finally, to achieve linac capture efficiency above the experimental value¹⁰ of 37% for cathode positions of 1.15, 1.3, and 1.45 m in the fringe field of the 0.5 T magnet, the anode drift tube length L_A was adjusted. As mentioned before, the 1.3 m cathode position would correspond to a distance of 1.0 m between the x-ray source and the MRI-linac isocenter. Hence, the cathode positions of 1.15 and 1.45 m would allow treatment of tumors positions displaced from the isocenter along the axis of symmetry, and located inside an imaging spherical domain with a 0.3 m diameter. To achieve this, for each of the three solutions the rms emittance together with the other two Twiss parameters α and β defined as¹¹

$${\alpha }_x=-\frac{⟨x{x}^{\prime }⟩}{{\varepsilon }_{x,\text{rms}}},$$ (3a)

$${\beta }_x=\frac{⟨x^2⟩}{{\varepsilon }_{x,\text{rms}}},$$ (3b)

were computed for various positions along the beam axis. The Twiss parameters change with the axial position. Since the Twiss parameters at the gun exit depend on the anode drift tube length L_A, the linac capture efficiency depends on L_A. The values of the Twiss parameters were used to transport the electrons through the linac in the presence of the corresponding magnetic fields. The capture efficiency was determined as a function of axial position and an optimum value for L_A was found.

The new gun geometry behavior in arbitrary magnetic fields

The normal operation mode of the newly designed electron gun corresponds to a situation where the beam does not collide with the gun electrodes. However, as the field strength decreases so does the magnetic confinement of the electron beam. Therefore, the gun current will decrease due to beam collision with the inside of the anode drift tube. Hence, it is important to determine the magnetic field range for which the gun performs optimally.

Two tests were performed in the fringe fields of the three magnets in order to quantify the behavior of the new electron gun. The first test derived the gun current for magnetic fields less than 0.12 T to establish the magnetic field strength threshold above which no current is lost due to beam collision inside the anode drift tube. The magnetic fields were decreased from 0.12 T in steps of 0.005 T down to the minimum allowed field value.

The second test aimed at characterizing the electron gun-linac system behavior above the magnetic field strength threshold found in the first step. The field was increased from the threshold value in steps of 0.01 T up to the maximum allowed value for each magnet and the linac capture efficiency was determined. The field upper limit corresponds to a field value at approximately 1.1 m from the MRI-linac isocenter. This corresponds to the cathode position when the x-ray source is 0.8 m from the MRI-linac isocenter, i.e., the tungsten button is located at the minimum value considered for the axial coordinate of the spatial domain of the field maps.

Software packages used in simulations

The software tools used in this work can be catalogued in three distinct groups. First, the magnetic field maps for the three magnets were generated with Matlab ver. R2012b (Ref. ¹²) and the comparisons between exiting field maps and the maps provided by Eq. 1 were performed with Matlab and COMSOL Multiphysics ver. 4.3b.¹³ Also the fit procedure for the axial component B_z(0, z) was done with Matlab.

Second, the electron gun geometry optimization procedure was simulated with SCALA ver. 14.0 (Ref. ¹⁴) (Vector Fields Ltd., OPERA-3d) which is a full three-dimensional (3D) space charge solver. The thermionic emission model used to generate electrons from the cathode surface for the new electron gun geometry optimization was based on the Langmuir-Fry law.^{15, 16} This thermionic model is realistic enough to match experimental data according to Ref. 17 and at the same time it is not too computationally intensive. This allowed for a good balance between the simulation realism and the computation time. However, Child's law¹⁸ thermionic model was used for the first step of the analysis, i.e., for the simple modification study of the zero field geometry, to remain consistent with the original simulations performed in Ref. 10 with EGN2w (Ref. ¹⁹) (Stanford Linear Accelerator, CA). The same sampling distance of 3 × 10⁻⁴ m was considered for both thermionic models. The electron beam transport in SCALA is simulated using macroparticles which are defined as assemblages of many physical particles of the same type, e.g., electrons, which are treated as single units. The electron beam phase space was obtained by recording the individual contributions of any macroparticle which crosses a plane perpendicular to the gun axis located at the gun exit position. The phase space information of these macroparticles allowed the computation of the electron beam emittance and beam Twiss parameters as defined in Eqs. 2, 3, respectively. These parameters characterize the statistical properties of the electron beam at the gun exit, i.e., at the linac entry point.

Third, the linac simulations were performed with PARMELA (Ref. ²⁰) with a procedure identical to the one described in Ref. 7. The input for PARMELA used the Twiss parameters at the electron gun exit and corresponding magnetic field maps to simulate the electron beam injection and acceleration along the linac from 30.7 keV to 6 MeV. These simulations allowed the computation of the linac capture efficiency, which was then used to determine the optimum length of the anode drift tube L_A in Fig. 2 and characterize the behavior of the electron gun plus linac system for various magnetic field strengths and gradients.

RESULTS AND DISCUSSION

The magnetic fields

Each of the three fringe fields used in this paper were approximated by a 9 degrees polynomial as a function of axial coordinate

$$B_z(0,z)=\sum _{i=0}^9{A}_i{z}^i,$$ (4)

where the numerical values for coefficients A_i are presented in Table 2. These polynomials interpolate the data for B_z(0, z) with R-square values of 0.99999 for all three magnets.

Table 2.

Fringe field fit polynomial coefficients corresponding to each magnet.

Magnet	A0	A1	A2	A3	A4	A5	A6	A7	A8	A9
0.5 T	−0.799	8.715	−20.495	24.187	−17.236	7.905	−2.360	0.445	−0.048	0.002
1.0 T	18.806	−157.431	596.808	−1264.408	1649.740	−1388.907	761.337	−263.686	52.579	−4.611
1.5 T	78.251	−629.503	2227.702	−4458.866	5574.510	−4539.852	2420.476	−817.785	159.317	−13.663

The relative errors of the field components given by Eq. 1 with respect to the experimental field maps were computed in the domain of interest, and their maximum values are reported in Table 3. The relative errors were below 0.2% and 0.7% for the axial and the radial field components, respectively.

Table 3.

Maximum relative errors for the field components and the spatial domains where these values were computed.

Magnet	ΔBz [%]	ΔBr [%]	z [m]	r [m]
0.5 T	0.04	0.50	[0.8; 3.0]	[0; 0.1]
1.0 T	0.17	0.70	[0.8; 1.6]	[0; 0.1]
1.5 T	0.09	0.55	[0.8; 1.8]	[0; 0.1]

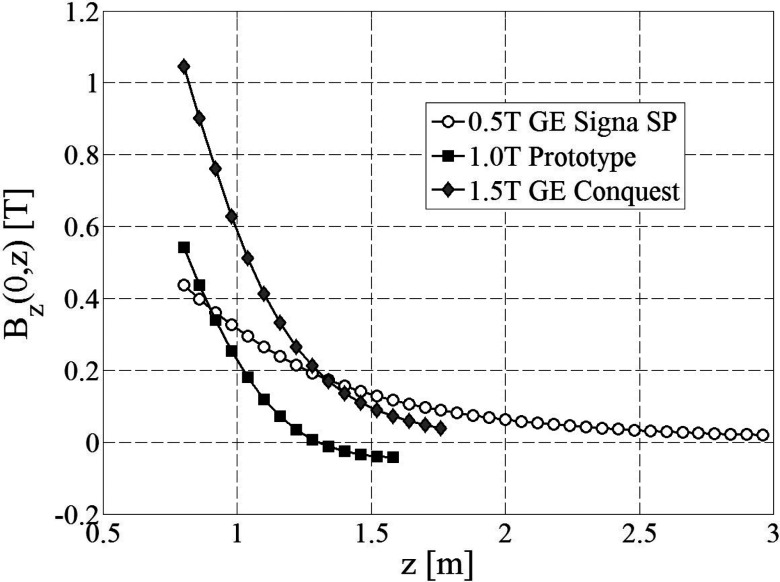
The fit values of the fringe fields axial components along the magnet axis, B_z(0, z), corresponding to the three magnets used in the simulations are shown in Fig. 3. It is interesting to note that the active shielding of the 1 T magnet is designed such that the field vanishes 1.3 m away from its isocenter, which causes a change of sign in the axial component of the magnetic field.

Figure 3.

Axial component of the magnetic fields along the axis of symmetry as a function of axial coordinate.

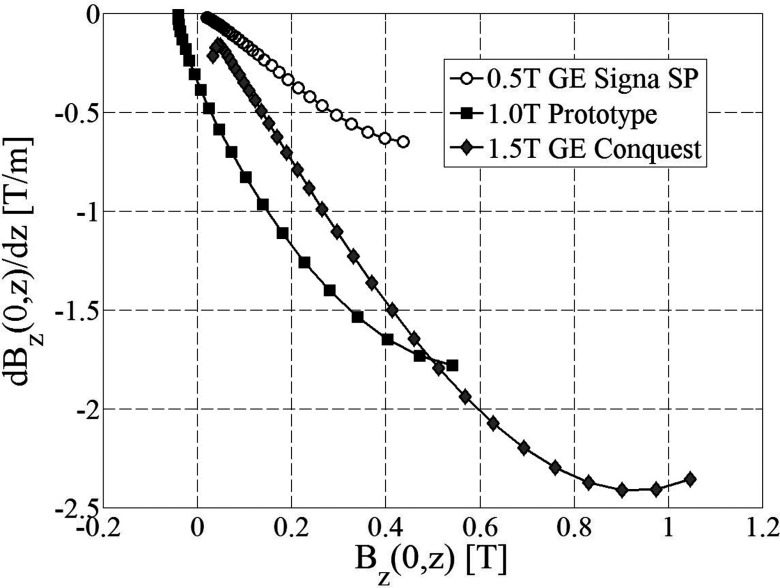
To quantify the gradient differences of the three magnets, the first derivative of the field with respect to the axial coordinate was plotted in Fig. 4 against the corresponding field value.

Figure 4.

First derivative of the axial component of the magnetic fields along the axis of symmetry as a function of the corresponding axial field value.

It is found that the 1.0 T prototype magnet has the steepest gradient, followed by the 1.5 T GE Conquest and the 0.5 T GE Signa SP.

Simple modifications of the zero field gun geometry

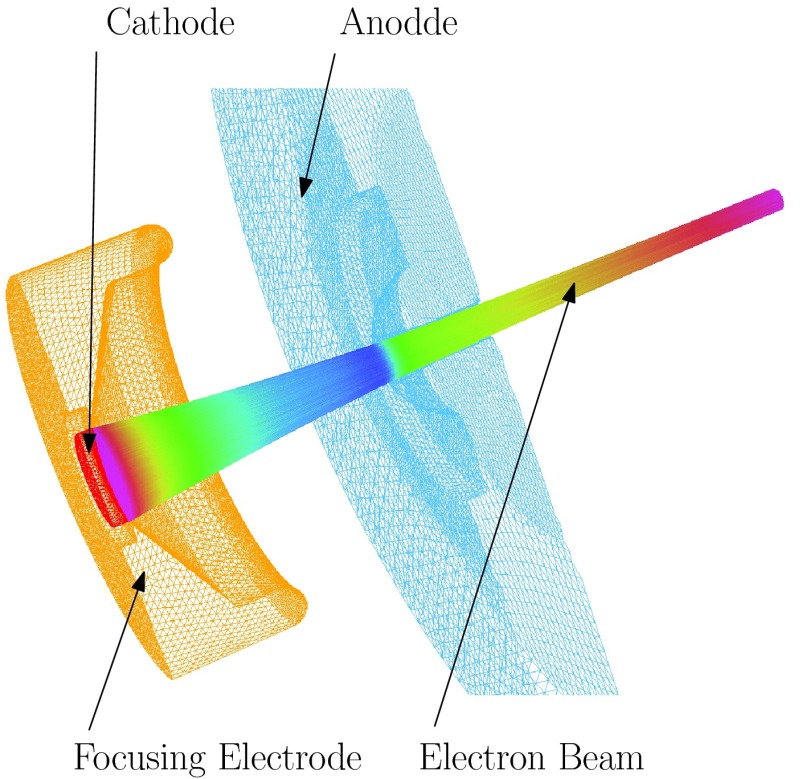
To generate design principles for the new electrode geometry and based on previous observations of the gun behavior in external magnetic fields,¹ a set of simulations with simple modifications of the original gun geometry were performed. The space charge simulation result of the beam together with the zero field geometry is presented in Fig. 5.

Figure 5.

Original gun geometry with the electron beam obtained from a space charge simulation.

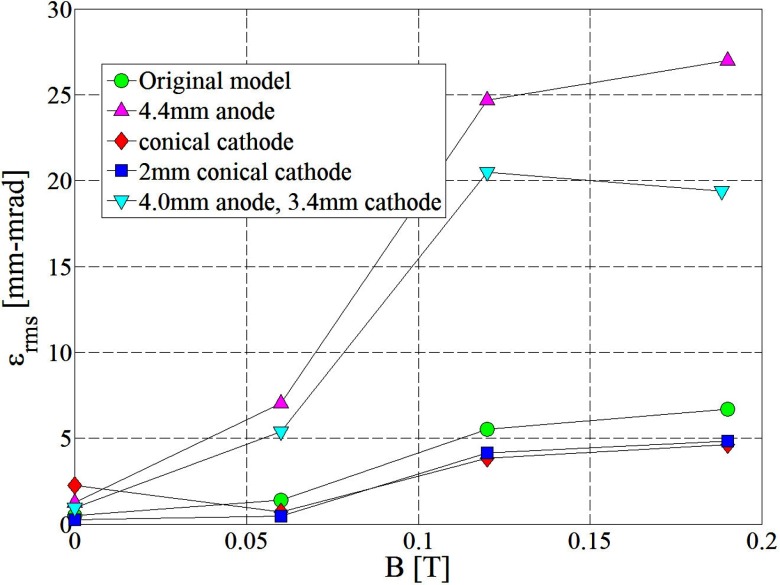
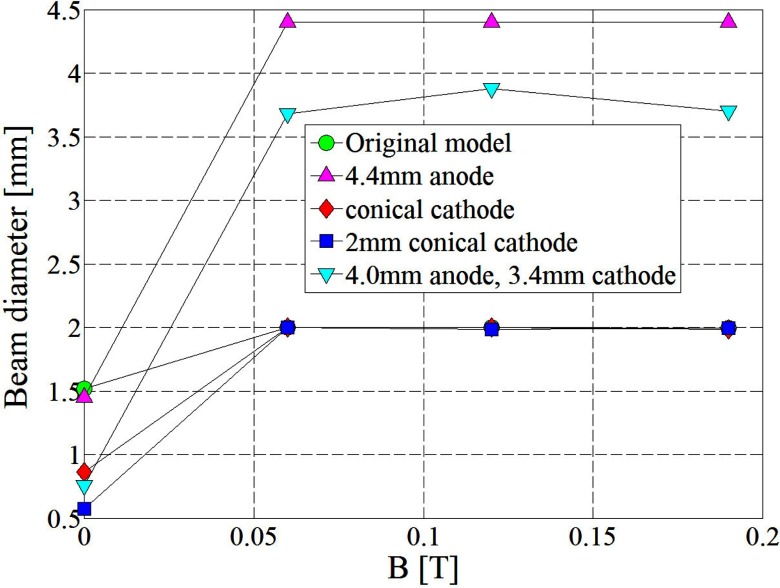
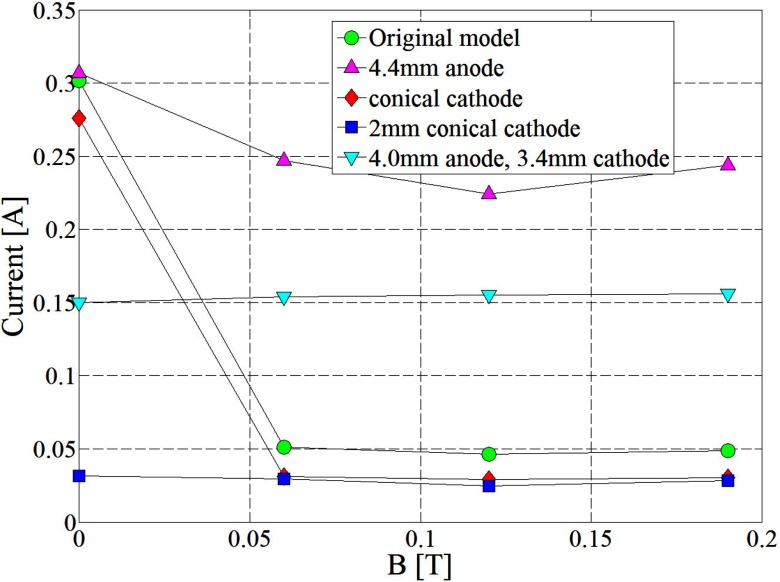
The rms beam emittance, the beam diameter, and the gun current were computed at various field strengths for the original geometry and the four slightly modified gun geometries and the results are reported in Figs. 678, respectively.

Figure 6.

Simple modifications of zero field gun geometry: beam emittance at gun exit for various external field strengths and various gun geometries.

Figure 7.

Simple modifications of zero field gun geometry: beam diameter at gun exit for various external field strengths and various gun geometries.

Figure 8.

Simple modifications of zero field gun geometry: gun current for various external field strengths and various gun geometries.

As shown in Fig. 6 the emittance increases in all cases. To alleviate the increase of the beam emittance the electrons will have to be generated and accelerated along the field lines of the magnetic field. This constrains the cathode surface to coincide with the equisurfaces of the magnetic field which in this case are almost flat surfaces at the cathode location.

Second, in Fig. 7 the beam diameter increases for all the cases which is not desired as this leads to current loss due to beam interaction with the anode drift tube walls.¹

However, in Fig. 8 a smaller cathode produces a larger current than the anode opening which indicates less current loss inside the anode drift tube. This is a good indication that the size of the anode drift tube diameter and the cathode transverse diameter have to be carefully chosen. It was determined from simulations that a Type-M cathode,²¹ which has a work function of 1.8 eV, with a transverse diameter of 1.7 mm will generate 0.361 A at a temperature of 1189 K which is exactly the gun current at zero field. This means the cathode workload will be of about 4 A/cm² allowing a cathode lifetime of several years.²¹ The cathode working temperature was determined in a preliminary study which looked at the emitted cathode current as a function of temperature. Also, throughout the optimization study the value of the cathode temperature and implicitly the emitted cathode current did not change.

Optimization of the new gun geometry

Based on the result from Sec. 3B a geometry resembling a parallel plate capacitor with a hole in the anode plate was proposed as a starting point. In what follows we provide the optimization procedure steps as described in Sec. 2C. First, it was determined that below a model radius R_M of 12 mm the solution, as described by the relative error of beam rms emittance 2 and the Twiss parameters 3 at gun exit, deviates more than 0.2% when compared to the solution with R_M equal to 20 mm.

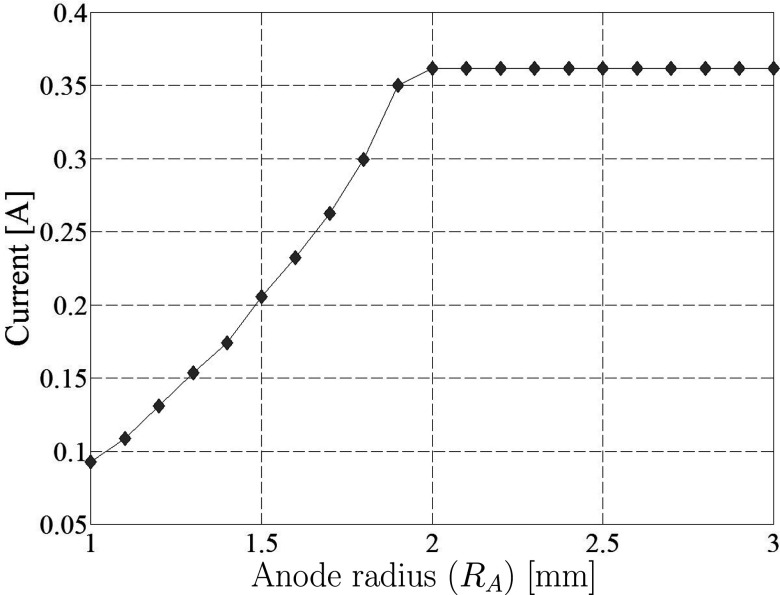
Next, the anode radius R_A was increased to determine the value for which the beam no longer collides with the inner walls of the anode drift tube. In Fig. 9, the gun current reaches its designed value of 0.361 A for an anode drift tube radius of 2.0 mm. To ensure no beam collisions with the anode drift tube in the real situation where a less laminar beam is expected due to cathode surface morphology, a final design value of 2.2 mm, i.e., 10% larger than the minimum saturation value, was considered.

Figure 9.

New electron gun geometry: gun current as a function of anode drift tube radius.

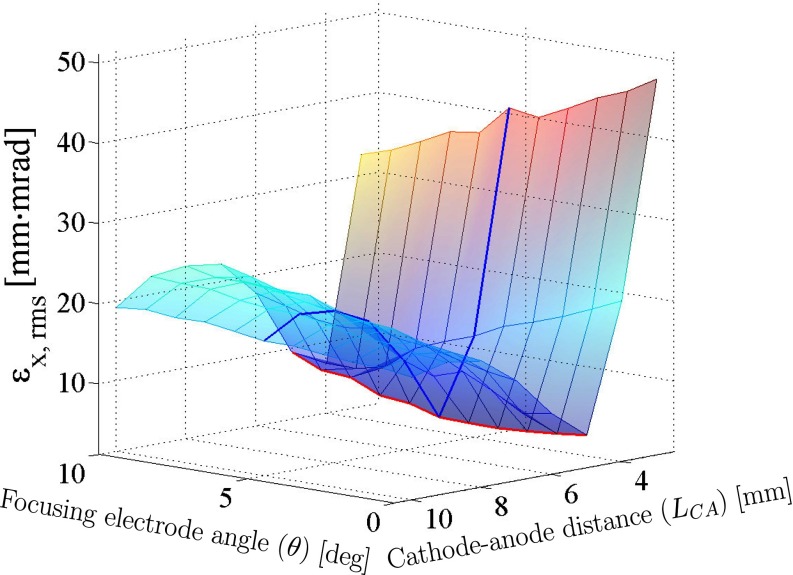
The electric field in the beam vicinity is influenced by the cathode anode distance L_CA and the shape of the focusing electrode characterized here by the focusing electrode angle θ. The rms beam emittance at gun exit as a function of these two geometrical parameters is presented in Fig. 10 and a minimum of 4.4 mm mrad is achieved for a focusing electrode angle of 5° and a cathode-anode distance of 5 mm.

Figure 10.

New electron gun geometry: transverse beam rms emittance at gun exit as a function of focusing electrode angle θ and cathode-anode distance L_CA. The coordinates curves on the mesh specify the rms emittance minimum position.

The study related to the gap between the cathode and the focusing electrode, G_FE, has showed a slight increase of the emittance at the gun exit with the gap dimension but it left the linac capture efficiency virtually unchanged. For this reason, the initial gap value of 0.1 mm was used as the value for all the subsequent studies.

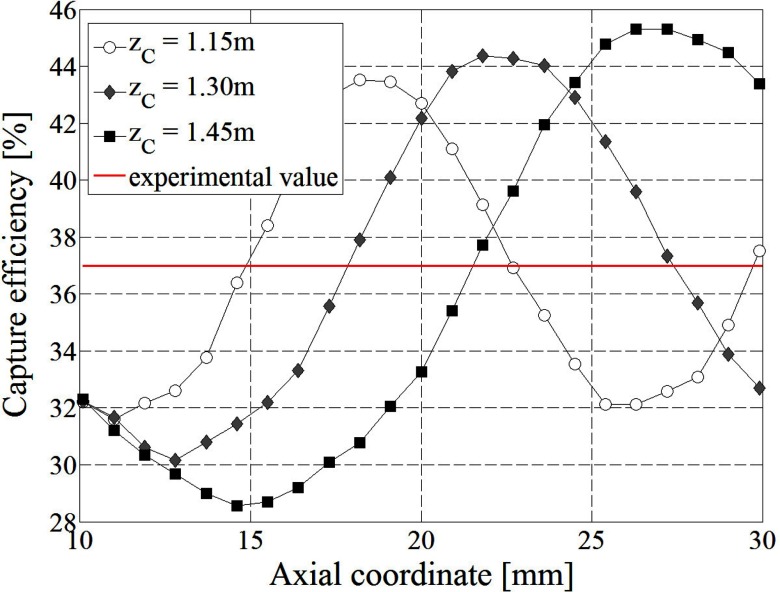
To determine the optimum injection point, i.e., the length of the anode drift tube L_A, the linac capture efficiency was determined as a function of the axial coordinate along the gun axis for three cathode positions. In Fig. 11, both the experimental capture efficiency at zero magnetic field and the capture efficiency of the linac for the three considered positions are shown. The axial coordinate in Fig. 11 refers to the sum of the cathode anode distance L_CA, which is constant and equal to 5 mm, and the anode drift tube length L_A.

Figure 11.

New electron gun geometry: linac capture efficiency as a function of electron gun axial coordinate L_CA + L_A, i.e., anode drift tube end coordinate, for three cathode positions with respect to the magnet isocenter. The cathode position, z_C, is located in origin and the axial coordinate increases toward the electron gun exit.

It was determined that for an axial coordinate of 22.1 mm, i.e., an anode drift tube length of 17.1 mm, the linac capture efficiency is higher than the experimental capture efficiency at zero magnetic field for any linac displacements inside a range of ± 0.15 m around the central cathode position located 1.3 m from the MRI-linac isocenter. In this range of displacements for the linac, the maximum capture efficiency of 44% is achieved for the central cathode position. This corresponds to a target current of 0.162 A which is 20% more than the zero magnetic field case.

The new gun geometry behavior in arbitrary magnetic fields

As mentioned before, this electron gun geometry works in conjunction with magnetic beam confinement. Below a certain magnetic field strength threshold the magnetic beam confinement ceases to be effective. This breakdown is shown in Fig. 12 where the gun current starts to decrease for a field value below 0.11 T due to beam collision inside anode drift tube.

Figure 12.

New electron gun geometry test: gun current for various field strengths.

Hence, the new electron gun geometry is capable of producing electron beams without any beam collisions with the anode if the magnetic field strength is above 0.11 T regardless of the MRI magnet. There are some small differences between various magnets regarding the magnetic field strength limit at which the breakdown occurs and they are correlated to the field gradient shown in Fig. 4. A steeper field gradient corresponds to a smaller breakdown field value limit. It is interesting to note that the minimum current of 0.176 A occurs at small field strengths, i.e., below 0.02 T, which is approximately 50% of the current saturation value of 0.36 A.

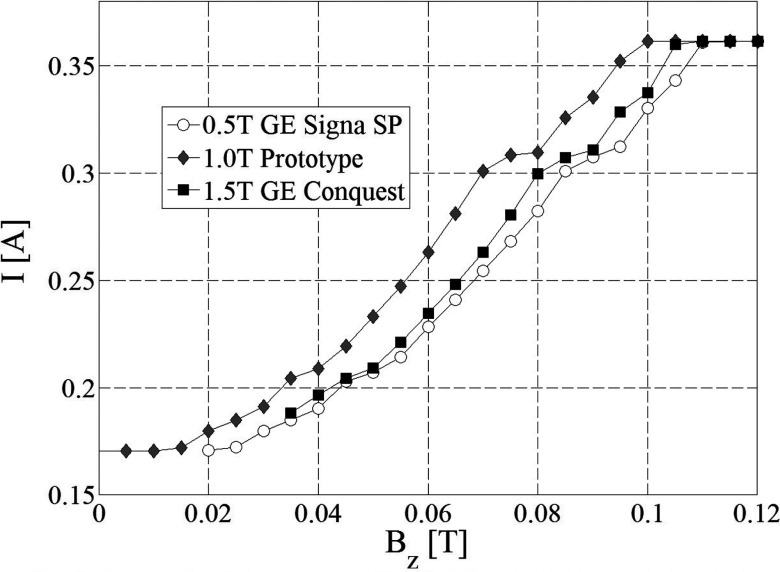
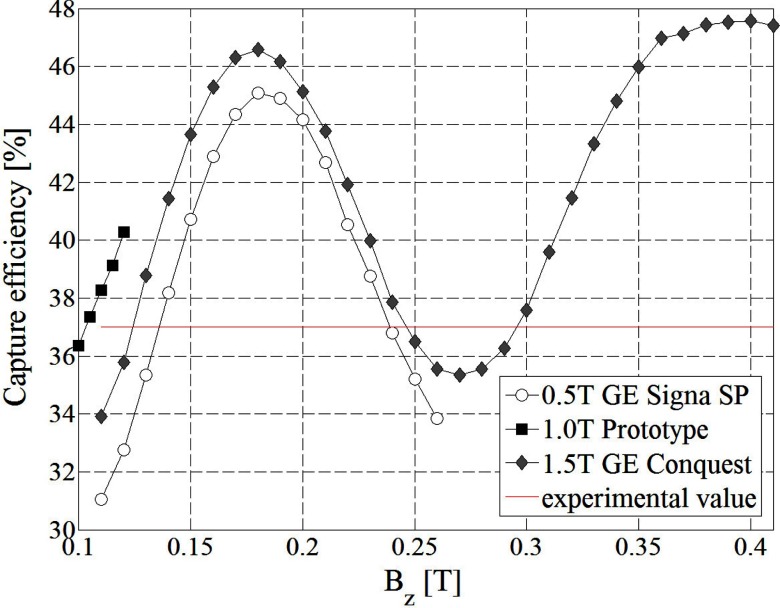
Although the fact that the geometry was optimized for the 0.5 T magnet fringe field it can be seen from Fig. 13 that the same electron gun geometry can perform very well in the fringe field of the other magnets.

Figure 13.

New electron gun geometry test: linac capture efficiency for various field strengths.

It is interesting to note that the linac capture efficiency increases as the fringe field gradient gets steeper. Also the linac capture efficiency does not decrease dramatically with the minimum of 31% occurring for the 0.5 T magnet at 0.11 T. This decrease in capture efficiency will produce smaller dose rates, i.e., slightly longer treatment times. The worst case scenario corresponds to a reduction of the target current to 0.124 A which is 16% less than the zero magnetic field case. In other words, the new electron gun-linac system can robustly function for fields strengths higher than 0.11 T.

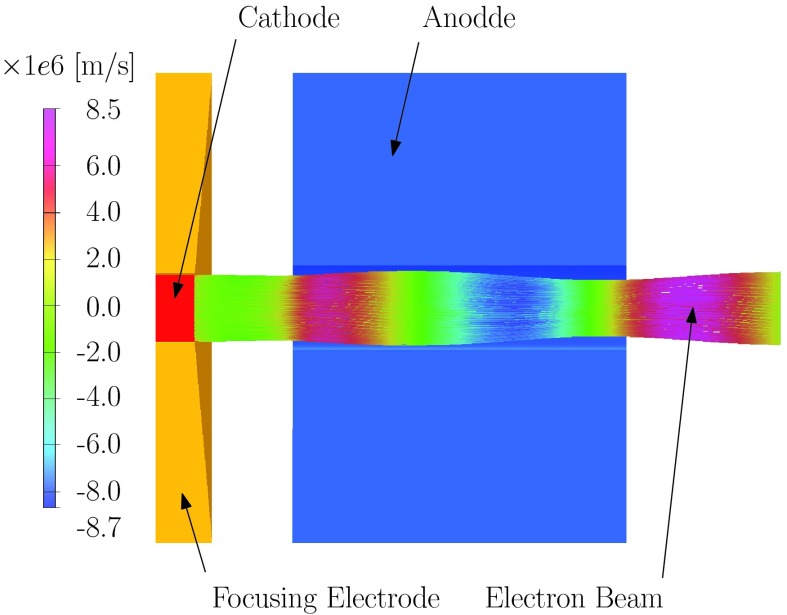
The newly designed electron gun and its corresponding space charge solution at the optimum position are presented in Fig. 14. The optimum position corresponds to a cathode positioned at 1.3 m from the isocenter of the 0.5 T magnet. At that position, the electrons in the beam are experiencing a magnetic field strength of B = 0.19 T. The magnetic beam confinement shown in Fig. 14 is a direct consequence of Bush's theorem²² which is valid only for axially symmetric configurations. The axial symmetry of the inline MRI-linac is the fundamental principle which allows for the new electron gun geometry to function in external magnetic fields without the need for decoupling the physics of the MRI scanner and the linac using a magnetic shield. Figure 14 also shows that the beam at the electron gun exit is divergent and the beam diameter is close to its minimum.

Figure 14.

Optimized electron gun geometry with SCALA 3D space charge solution in the fringe field of the 0.5 T magnet. The gun cathode was positioned 1.3 m away from the 0.5 T magnet isocenter which correspond to a mean field strength of 0.19 T. The scale bar represents the radial velocity of the electrons.

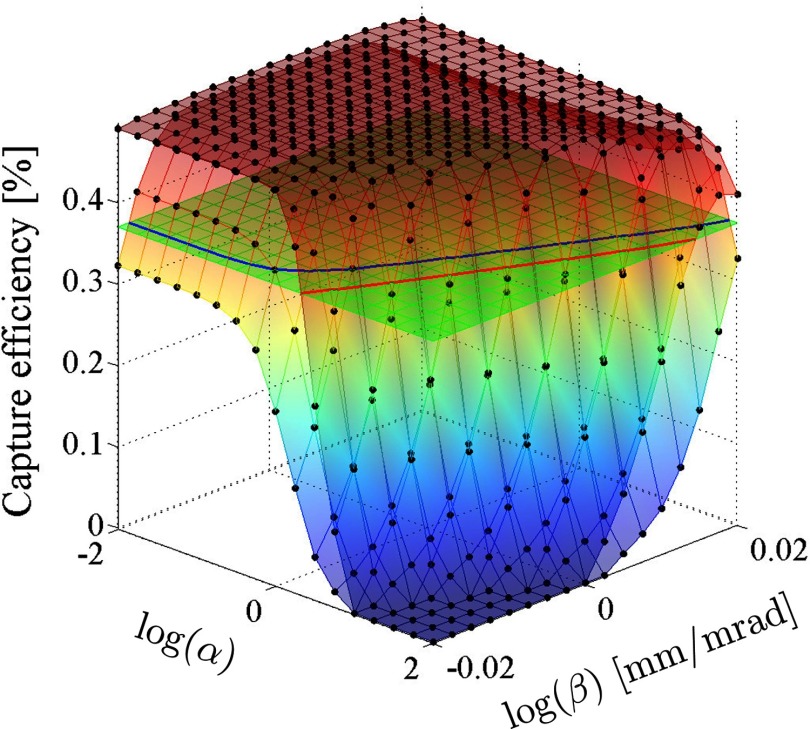
The new electron gun geometry proposed in this study not only alleviates the problem of current loss through the beam collision with the anode, but it also improves the capture efficiency of the linac in the presence of the external magnetic field. To illustrate this property, Fig. 15 presents the linac capture efficiency in the presence and absence of a magnetic shield as functions of the Twiss parameters α and β for a rms emittance of 0.4 mm mrad. This is the rms emittance value of the electron beam at the gun exit for the original zero field gun geometry. Also, the range values for α and β were chosen around their zero field values. The magnetic beam confinement renders more efficient beam acceleration for the same set of Twiss parameters. This results in a higher target current which is equivalent to a higher dose rate, which translates to shorter treatment times.

Figure 15.

Capture efficiency as a function of Twiss parameters α and β for a fixed emittance value (ε = 0.4 mm mrad) in the absence (lower surface) and presence (upper surface) of external magnetic field. The horizontal plane is located at the experimental value and the curves represent the intersection lines between this plane and the two surfaces for the zero and nonzero external magnetic fields.

The electron gun geometry considered in this study does not involve more complex geometries and configurations, e.g., a grid in front of the cathode and a focusing electrode kept at a different electric potential than the cathode. However, the more complex designs of electron guns which work in external magnetic fields can use the present electron gun characteristics as a starting point in the design procedure. Also, the design procedure presented in this work for the electron gun can be reproduced for any combination of MRI magnet, linac, and its corresponding electron gun, assuming complete experimental information is available for all three systems.

CONCLUSIONS

In this work, a new electron gun geometry was designed and optimized to work in the fringe fields of a 0.5 T open bore split MRI magnet. The electron gun is capable of generating and accelerating electron beams in the presence of external magnetic fields without current loss. The beam characteristics have been proved to be suitable for injection into the Varian 600C linac and it was determined that the capture efficiency of the linac increases in the presence of external magnetic field. Also the electron gun-linac system can be displaced ±0.15 m along the MRI-linac axis of symmetry around a cathode central position located 1.3 m from the MRI-linac isocenter without decrease in linac capture efficiency.

It was verified that the new electron gun-linac system can robustly function in the fringe fields of a 1.0 T and 1.5 T magnets if the fields strength at cathode position is higher than 0.1 T. The decrease of the target current is no more than 16% in the worst case scenario.

The simulation outcomes of the new electron gun geometry show that an inline MRI-linac configuration without magnetic shielding is possible. Also, it was shown that such an electron gun can be used in MRI-linac configurations where the linac can be displaced along the system axis of symmetry relative to the MRI-linac isocenter, which is a particular case of the RLA MRI-linac configuration.