Abstract
Purpose: For interstitial photodynamic therapy (iPDT) of bulky tumors, careful treatment planning is required in order to ensure that a therapeutic dose is delivered to the tumor, while minimizing damage to surrounding normal tissue. In clinical contexts, iPDT has typically been performed with either flat cleaved or cylindrical diffusing optical fibers as light sources. Here, the authors directly compare these two source geometries in terms of the number of fibers and duration of treatment required to deliver a prescribed light dose to a tumor volume.
Methods: Treatment planning software for iPDT was developed based on graphics processing unit enhanced Monte Carlo simulations. This software was used to optimize the number of fibers, total energy delivered by each fiber, and the position of individual fibers in order to deliver a target light dose (D90) to 90% of the tumor volume. Treatment plans were developed using both flat cleaved and cylindrical diffusing fibers, based on tissue volumes derived from CT data from a head and neck cancer patient. Plans were created for four cases: fixed energy per fiber, fixed number of fibers, and in cases where both or neither of these factors were fixed.
Results: When the number of source fibers was fixed at eight, treatment plans based on flat cleaved fibers required each to deliver 7180–8080 J in order to deposit 90 J/cm2 in 90% of the tumor volume. For diffusers, each fiber was required to deliver 2270–2350 J (333–1178 J/cm) in order to achieve this same result. For the case of fibers delivering a fixed 900 J, 13 diffusers or 19 flat cleaved fibers at a spacing of 1 cm were required to deliver the desired dose. With energy per fiber fixed at 2400 J and the number of fibers fixed at eight, diffuser fibers delivered the desired dose to 93% of the tumor volume, while flat cleaved fibers delivered this dose to 79%. With both energy and number of fibers allowed to vary, six diffusers delivering 3485–3600 J were required, compared to ten flat cleaved fibers delivering 2780–3600 J.
Conclusions: For the same number of fibers, cylindrical diffusers allow for a shorter treatment duration compared to flat cleaved fibers. For the same energy delivered per fiber, diffusers allow for the insertion of fewer fibers in order to deliver the same light dose to a target volume.
Keywords: photodynamic therapy, treatment planning, optical fiber, Monte Carlo simulation, spectroscopy
INTRODUCTION
Photodynamic therapy (PDT) is a therapeutic procedure that relies on the combination of photosensitizer, molecular oxygen, and targeted illumination in order to create cytotoxic effects.1 PDT is approved by the US Food and Drug Administration for the treatment of esophageal and nonsmall cell lung cancer, actinic keratoses, Barrett's esophagus, and macular degeneration.2 For tumors that are either deep within the body or too bulky to be penetrated by surface illumination, optical fibers are inserted directly into the tumor volume in order to deliver treatment light.3 This is known as interstitial photodynamic therapy (iPDT).
For iPDT, treatment light is typically delivered by cylindrical diffusing fibers or flat cleaved optical fibers. Cylindrical diffusers are optical fibers in which the distal portion emits light radially from the fiber core, in order to deliver light to regions perpendicular to the fiber axis. Diffusers have been used as treatment fibers for iPDT of prostate cancer,4 tongue base carcinoma,5 and cholangiocarcinoma,6 among other treatment sites. Flat cleaved fibers are cleaved and polished optical fibers that emit light into a known range of angles centered on the fiber axis. In the context of iPDT, these fibers have been used predominantly in the treatment of prostate cancer,7 with some applications in the treatment of large skin,8 esophageal, duodenal, and colorectal tumors.9
Since iPDT does not allow for direction visualization of the treatment light and is often performed in proximity to healthy tissue, careful treatment planning is required to ensure that a therapeutic dose is delivered to the tumor while minimizing damage to surrounding healthy tissue. This dose is a combination of photosensitizer concentration (drug dose) and fluence (light dose). Depending on the wavelength of treatment light, optical properties can vary between patients and tissue types,10 resulting in differing light dose distributions. Determination of patient optical properties is therefore typically considered a crucial component in the creation of treatment plans, with this commonly being done using isotropic sources and detectors11 or dedicated spectroscopy instruments.12
Due to the risk of undesirable side effects from other treatment modalities, iPDT has been identified as a good alternative for the treatment of prostate cancer.3 Therefore, a number of research groups have focused their efforts on treatment planning in this context. Altschuler et al.13 demonstrated optimization of diffuser position, length, and fluence in order to create treatment plans for iPDT of the prostate. In that study, optical properties for treatment planning were measured using the treatment diffusers as sources for spectroscopy, with separate optical fibers inserted into the prostate to serve as detectors. Davidson et al.14 also demonstrated a treatment planning system for iPDT of the prostate using diffuser sources, based on ultrasound imaging and a diffusion approximation for light propagation. This technique again required the insertion of separate detector fibers in order to determine optical properties. In order to eliminate the insertion of additional spectroscopy fibers, Swartling et al.7 utilized flat cleaved fibers as treatment sources and spectroscopy fibers. This system used a fiber switch in order to control whether fibers delivered treatment light or performed spectroscopy for recovery of optical properties. This system has been used extensively by researchers at Lund University,8, 15, 16 and has been commercialized (IDOSE®, SpectraCure AB, Magistratsvägen, Sweden).
In the current study, we compare flat cleaved and cylindrical diffusing fibers as sources for iPDT. The two source geometries are compared on the basis of the number of fibers and duration of illumination required to deliver a 90 J/cm2 light dose to 90% of a tumor volume (D90) derived from patient CT data. Since flat cleaved fibers are used to facilitate interstitial spectroscopy, the goal is to determine the consequences of their use as treatment sources.
METHODS
Patient data
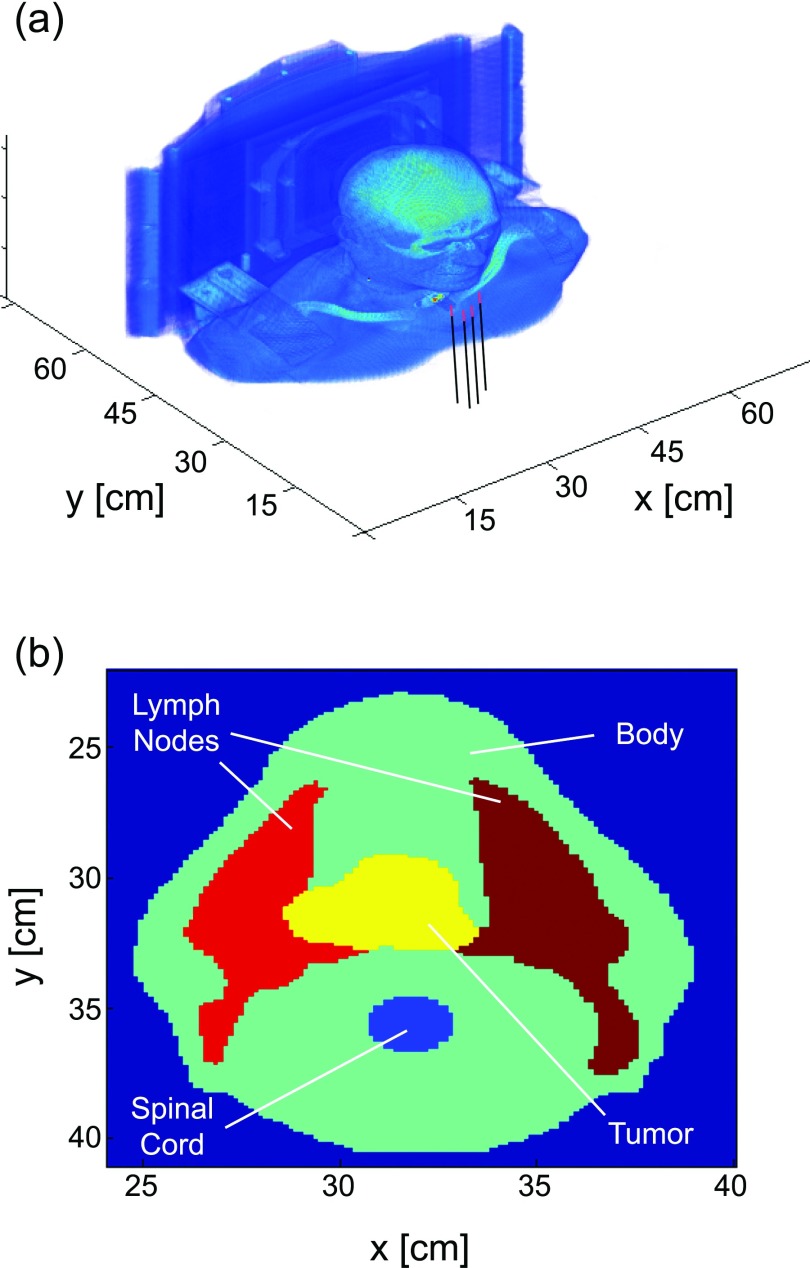
All treatment planning was performed on an anonymized CT dataset obtained from a head and neck cancer patient that was treated with ionizing radiation at Roswell Park Cancer Institute in Buffalo, NY. The patient had a tumor with maximum dimensions of 6.1 × 7.5 × 7 cm located at the tongue base. Tumor and healthy tissues were identified and demarcated by a physician as part of the planning process for the patient's radiotherapy. A 3D rendering of the patient dataset is shown in Fig. 1a, with the insertion of four diffusers shown for reference. A cut at the midplane of the tumor volume is shown in Fig. 1b, with the tumor and healthy tissues identified.
Figure 1.
(a) 3D rendering of the patient CT dataset, illustrating the insertion of cylindrical diffusing fibers for iPDT. (b) Cut through CT dataset at the midplane of the tumor volume, showing tumor and surrounding healthy tissues.
This dataset was used as a model treatment planning environment, in order to design the treatment this patient would have been given if they had received iPDT. Each voxel in the CT dataset corresponded with a voxel in the treatment planning simulation space. Voxels were identified by the tissue type and corresponding optical properties. In this case, uniform optical properties were assumed for all tissue types. The coordinate system was set so that treatment fibers were inserted along the z-axis. We also refer to the z coordinate of the fiber as the fiber's axial position.
Treatment planning software
The treatment planning software is based on a graphics processing unit (GPU) enhanced Monte Carlo (MC) simulation framework for light propagation through complex, 3D tissue volumes. This MC framework is used for simulating light distributions from individual treatment sources and for calculating final dose metrics after optimization. The treatment planning algorithm consists of three major components: (1) initial reference simulation, (2) optimization of source positioning and treatment time, and (3) performance of full MC simulation for optimal source characteristics. The algorithm is displayed schematically in Fig. 2.
Figure 2.
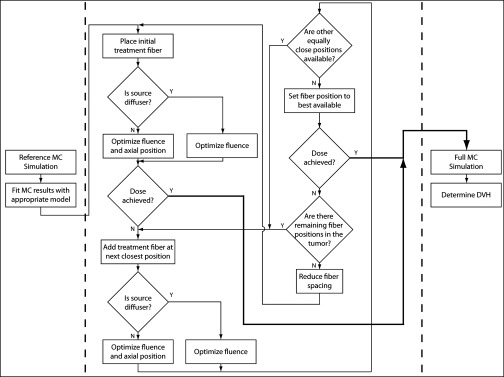
Block diagram illustrating the treatment planning algorithm. The three major components of the process are separated by dotted lines, and the thick black lines represent satisfactory treatment plans.
For the initial reference simulation, MC is performed with the desired source model embedded in an infinite tissue volume with uniform optical properties. For diffuser sources, the model described in Baran and Foster17 was used. For flat cleaved fibers, initial photon position was selected randomly on the face of a 400 μm optical fiber and launched within its 0.22 numerical aperture (NA = n sin θ), with the range of possible launch angles corrected for the tissue refractive index (n = 1.4). For all cases considered in this paper, typical optical properties of μa = 0.2 cm−1 and μs′ = 5 cm−1 were used,18 and 106 photon packets were launched per simulation, with run-times of 1–2 min per fiber. Voxel dimensions were 0.013 × 0.013 × 0.025 cm. After simulation, the fluence distribution generated by a single source was condensed by fitting with an appropriate model. For diffuser sources, the radial distribution of fluence from the diffuser axis was fit with a zeroth order modified Bessel function of the second kind, which was assumed to be uniform over the diffuser length. For flat cleaved fiber sources, the fluence distribution was fit with a diffusion point source located one transport mean free path from the fiber face. These fits allowed for concise representations of fluence distributions from individual sources in the optimization process, while still utilizing the accuracy of a full MC simulation.
For optimization of sources, both the number of fibers and energy per fiber can be fixed or allowed to vary. All treatment planning was performed under the assumption that fibers will be inserted using a standard brachytherapy template with hole spacings of 5 mm. The template was positioned so that the first fiber placed was roughly in the center of the tumor mass. Subsequent fibers were added one at a time, with the fiber spacing initially set to 1 cm. If an adequate treatment plan could not be created with this spacing and the other constraints, fiber spacing was reduced to 5 mm.
Whenever a fiber was added to the treatment plan, the possible positions were restricted to available holes in the grid template, starting from those positions closest to the center. At each available fiber position, the total energy delivered by the fiber was optimized using a constrained, nonlinear optimization algorithm (fmincon, MATLAB, Mathworks, Natick, MA) with energy constrained to be positive. For diffuser fibers, the diffuser length and axial position were selected to match the axial length of the tumor at the given fiber position, as determined from the region of interest (ROI) information in the patient dataset. Diffuser lengths were constrained to integers, in cm, in order to match commercially available fibers. For flat cleaved fibers, the axial position was also optimized, with the position constrained to be within the tumor volume. In both cases, the metric to be minimized in the optimization was given by
| (1) |
where Tthresh is the number of voxels in the tumor volume with a deposited dose equal to or greater than the prescribed light dose and T is the number of voxels in the tumor. Since the main goal of this paper is to compare the two types of source fibers, a relatively simple constraint condition was used. In a more realistic treatment planning scheme, constraints on the dose delivered to healthy tissue would also need to be incorporated.
For a given combination of fiber positions and energies delivered, the distribution of light dose in the patient volume was determined by summing the contributions of each fiber. This was done by placing scaled versions of the dose distribution from the reference simulation at the location of each source, with each fiber fixed at its optimal position. It was assumed that delivered light dose scaled linearly with the energy delivered by the source fiber. The drug dose was assumed to be uniform, so that the efficacy of the treatment plan depended only on the light dose.
After all of the closest available fiber positions were evaluated for coverage of the tumor volume, the position that yielded the minimum value of Eq. 1 was selected as the next fiber position. This process was repeated until the desired dose distribution was achieved. If the desired dose distribution could not be achieved with the maximum energy per fiber and the largest number of fibers allowable by the tumor size and fiber spacing, the fiber spacing was reduced and the optimization rerun. If the desired dose could not be achieved with fiber spacings of 5 mm, the case that returned the dose closest to that prescribed was specified as the treatment plan. This was not encountered in the current study.
Once the optimum fiber positions and energies were determined, a full MC simulation using this information and the patient volume was run in order to accurately determine the fluence distribution. The results of this were used to generate a dose volume histogram (DVH) for each tissue type present in the patient volume.
Treatment planning scenarios
For all treatment planning scenarios described in this paper, the target light dose to the tumor volume was 100 J/cm2. The goal was to deliver 90% of this target dose to 90% of the tumor volume (D90 = 90 J/cm2), as is commonly the case in treatment planning for brachytherapy19 and some cases of iPDT.14 The maximum energy delivered by a single fiber was restricted to 3600 J, corresponding to the delivery of 1 W of laser power for 60 min.
As mentioned previously, the energy per fiber and number of fibers could be fixed or allowed to vary as free parameters. Here, we performed treatment planning for the cases of fixing one, both, or neither of these factors. In Case 1, the number of fibers was fixed at eight, and the energy per fiber was allowed to fluctuate. This case was designed to simulate a scenario in which the number of fibers is limited due to clinical complexity or intervening anatomy, while the length of treatment time is of lesser importance. In Case 2, the energy per fiber was fixed at 900 J (1 W of laser power for 15 min) and the number of fibers was allowed to change. This was meant to represent a situation in which the total energy delivered by any one fiber is limited either by available laser power or maximum treatment time. For Case 3, the number of fibers was set to eight and the energy per fiber was set to 2400 J (1 W of laser power for 40 min). The goal here was to compare outcomes for an identical number of treatment fibers and energy delivered per fiber. Case 4 allowed both the number of fibers and energy per fiber to fluctuate, in order to replicate a scenario in which neither treatment time nor number of fibers are limiting factors. The results of different treatment plans were compared on the basis of the number of fibers required, the total energy delivered by each fiber, the percentage of the tumor volume that received the desired light dose, and DVH.
RESULTS
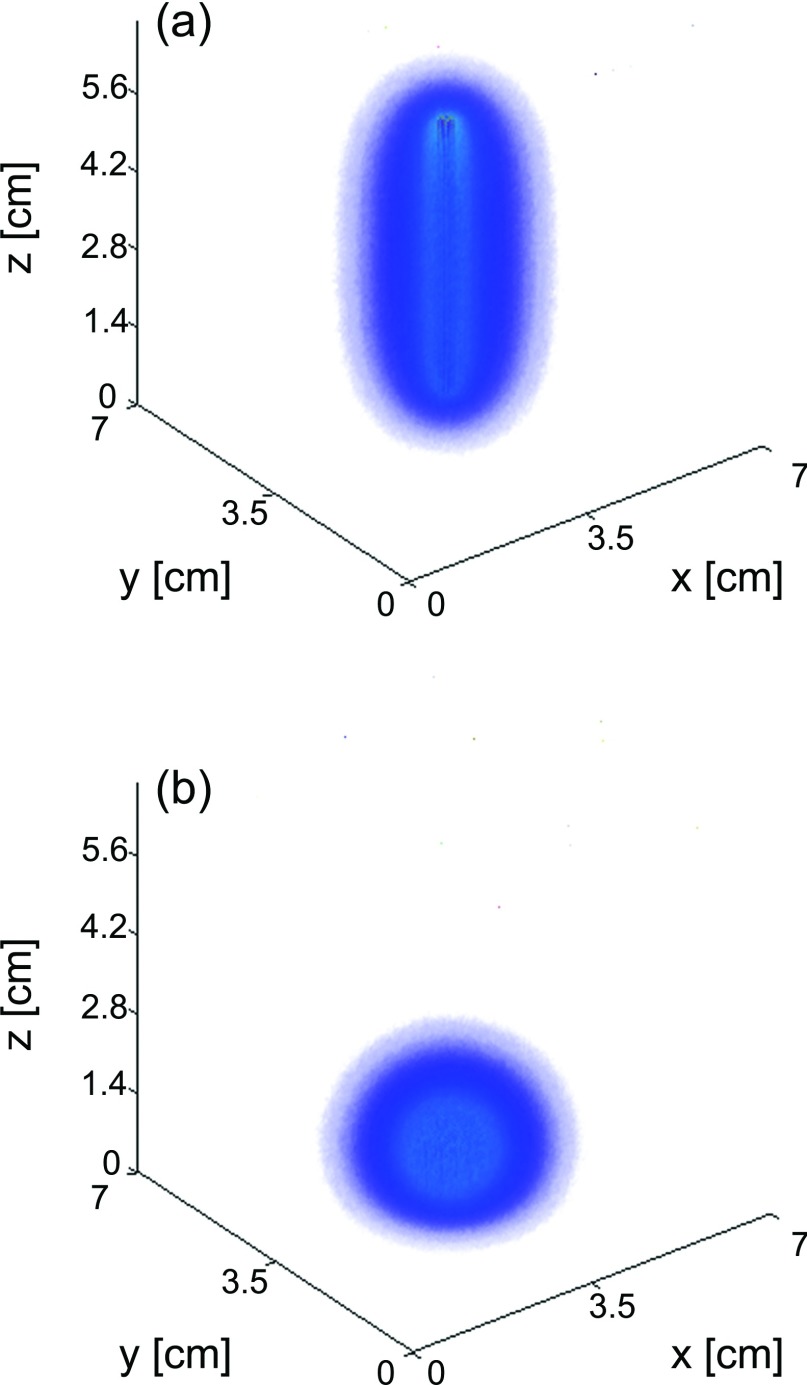
Typical fluence distributions in a homogeneous medium from diffuser and flat-cleaved fibers are shown in Fig. 3. In this case, each fiber delivered a total of 1000 J to the sample. Fluence is shown on the same scale for both fiber types.
Figure 3.
(a) Fluence deposited in a homogeneous sample by a 5 cm diffuser and (b) flat cleaved fiber. Both fibers delivered a total of 1000 J to a tissue volume with μa = 0.2 cm−1 and μs′ = 5 cm−1. The fluence scale is the same for both (a) and (b).
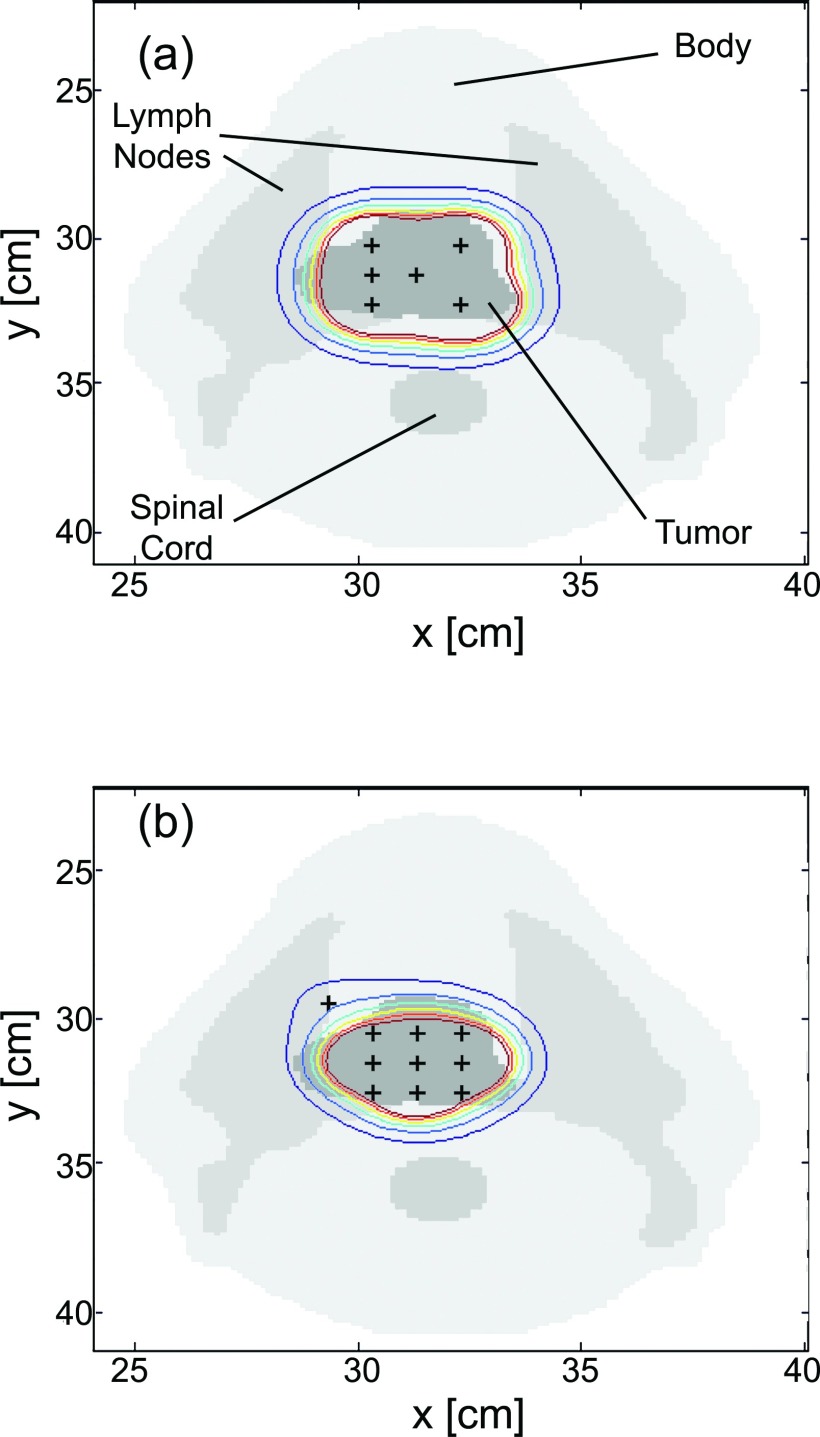
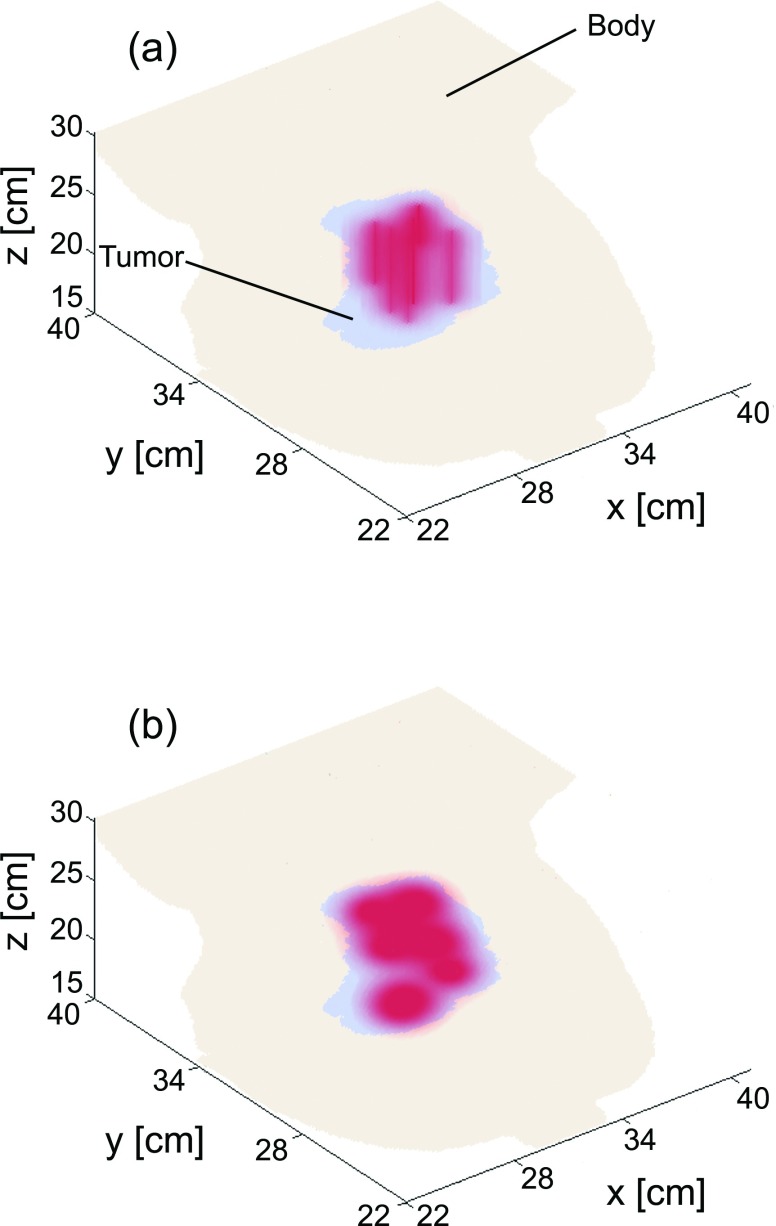
The optimized fiber positions for Case 4 are shown in Fig. 4. The cross-section shown is from a CT slice at the midplane of the tumor volume, as shown in Fig. 1b. As can be seen, the treatment plan using cylindrical diffusing fibers required six diffusers, while the flat cleaved plan required ten fibers to achieve a D90 of 90 J/cm2. The overlaid contours represent isodose lines, with the outermost contour corresponding to a light dose of 50 J/cm2 and subsequent lines representing dose increments of 50 J/cm2. Note in Fig. 4b that the fiber which appears to be outside the tumor volume is in fact within the tumor at that fiber's axial position. These plots illustrate the capability of diffusers to cover a larger volume for the same incident optical power and treatment time, and the more localized treatment field that can be obtained with flat cleaved fibers. 3D renderings of these light dose distributions are shown in Fig. 5.
Figure 4.
Cuts through the patient CT data showing the placement of source fibers (+) after treatment planning for (a) cylindrical diffuser fibers and (b) flat cleaved fibers. The contours shown are isodose lines, with the outermost contour corresponding to 50 J/cm2 and subsequent contours representing dose increments of 50 J/cm2. Note that the flat cleaved fiber in (b) is actually in the tumor volume at the fiber's axial position.
Figure 5.
3D renderings of fluence deposited in tissue after treatment planning for (a) cylindrical diffusing fibers and (b) flat cleaved fibers. The anatomical data shown correspond to an enlarged version of Fig. 1, with only the tumor and bulk body tissue shown.
The results of the four treatment planning cases are summarized in Table 1. Diffuser lengths required varied between 3 and 7 cm. The values given for diffuser fibers are total energy (J), rather than energy per length (J/cm) as is commonly reported.
Table 1.
Summary of the results of the four treatment planning scenarios simulated. In Case 1, the number of fibers was fixed at eight. For Case 2, the energy per fiber was fixed at 900 J. In Case 3, the number of fibers was fixed at eight and the energy per fiber was set to 2400 J. In Case 4, both the number of fibers and energy per fiber were allowed to fluctuate.
| Cylindrical diffusing fibers |
Flat cleaved fibers |
|||||
|---|---|---|---|---|---|---|
| Treatment planning | Energy/fiber | Tumor coverage | Energy/fiber | Tumor coverage | ||
| case | # fibers | (J) | (%) | # fibers | (J) | (%) |
| 1 | 8 | 2270–2350 | 93.0 | 8 | 7180–8080 | 93.0 |
| 2 | 13 | 900 | 90.4 | 19 | 900 | 90.1 |
| 3 | 8 | 2400 | 93.2 | 8 | 2400 | 79.0 |
| 4 | 6 | 3485–3600 | 90.1 | 10 | 2780–3600 | 91.0 |
As can be seen, when the number of fibers was fixed, diffusers required the delivery of approximately 70% less energy per fiber than flat cleaved fibers in order to deliver the same light dose to the tumor volume. Assuming the same optical power per fiber is used in both cases, this translates to a 70% reduction in treatment time for the diffuser case. With the treatment time and laser power fixed, 13 diffusers versus 19 flat cleaved fibers were required. When treatment time, laser power, and number of treatment fibers were fixed, cylindrical diffusers delivered the desired light dose to 93.2% of the tumor volume, compared to 79% for flat cleaved fibers. With the number of fibers and energy both left free, six diffusers delivering 3485–3600 J or ten bare fibers delivering 2780–3600 J were required to achieve the desired dose. The results shown in Table 1 are for a specific combination of optical properties (μa = 0.2 cm−1 and μs′ = 5 cm−1). The exact values would scale with varying optical properties, but the general trends would remain the same.
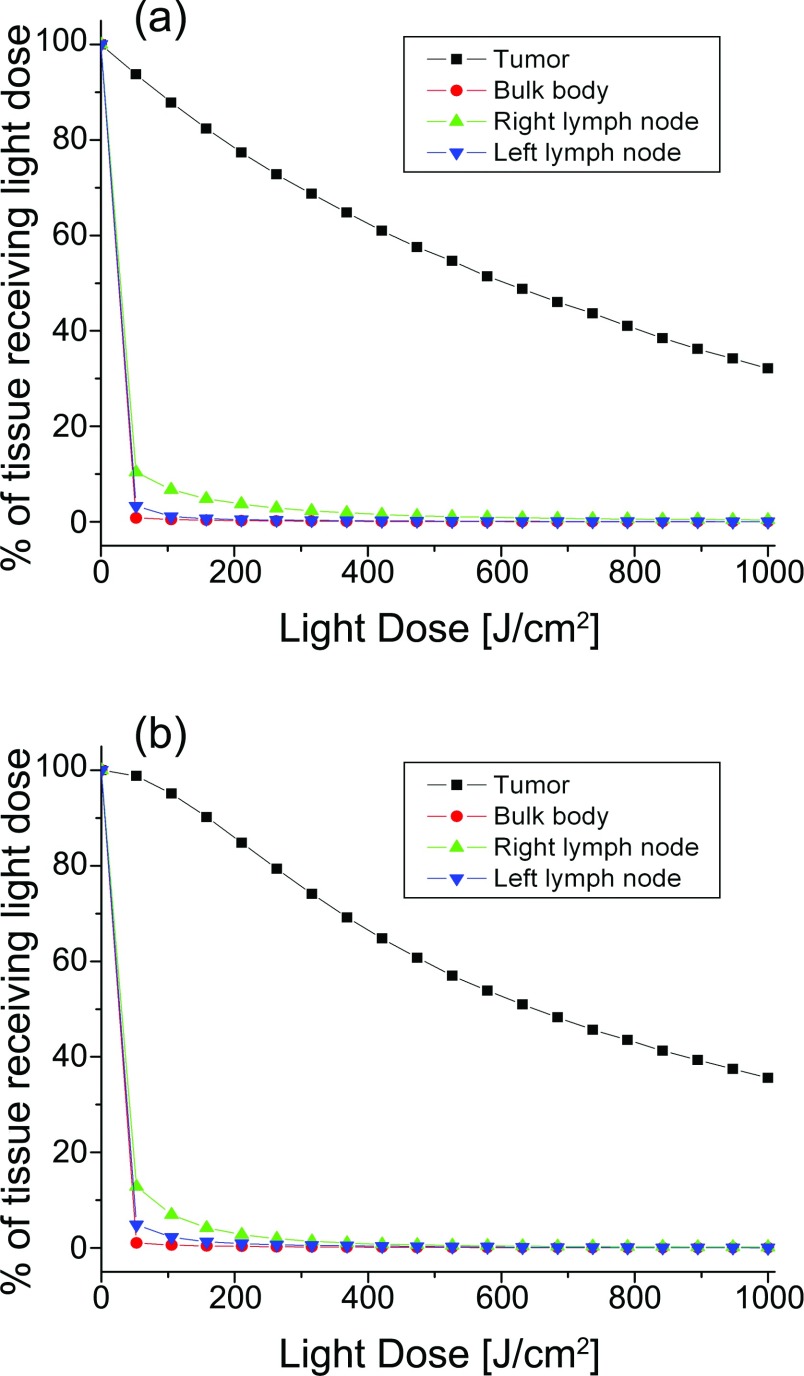
Dose volume histograms were generated for all treatment plans created. Representative DVHs are presented for Case 4 in Fig. 6. For both types of source fiber, 90%–91% of the tumor volume received the threshold light dose or higher, while healthy tissues received comparatively lower doses. It should be noted that large portions of the tumor volume received greater than the threshold light dose, due to the relative simplicity of the optimization metric given by Eq. 1. For the case of PDT, this overdosing of tumor tissue is not of significant concern. The tissue types shown in Fig. 6 were the only regions of the patient that received any appreciable dose.
Figure 6.
Dose volume histograms for the results of treatment planning with both the number of fibers and energy per fiber allowed to vary for (a) cylindrical diffusing fibers and (b) flat cleaved fibers. Six diffusers delivering 3485–3600 J or ten bare fibers delivering 2780–3600 J were required for this treatment plan. All other tissue types received negligible light dose.
DISCUSSION
In terms of reducing the number of treatment fibers and the duration of treatment, cylindrical diffusers were superior to flat cleaved fibers in each scenario that was simulated. Diffusers required fewer treatment fibers and less treatment time per fiber in order to deposit the same light dose in the tumor volume. The basis for this efficiency is illustrated in Fig. 3, which depicts the volumes of tissue illuminated by these two source geometries. Flat cleaved fibers are used in iPDT because of the simplicity with which they can be used to perform spectroscopic determination of optical properties. At typical optical properties and fiber separations, flat cleaved fibers can be represented as diffusion point sources,20 which allows for relatively simple diffusion techniques to be used for recovery of optical properties during iPDT. For this reason, they have been used extensively by researchers at Lund University.7, 8, 15, 16
Given their limitations as treatment sources, however, it is interesting to consider alternatives. For example, whereas flat cleaved fibers can be represented as a single diffusion point source, diffusers can be represented as sums of diffusion point sources over the diffusing length. If the local optical properties are assumed to be homogeneous, this can be used with isotropic detector fibers in order to determine optical properties. The use of cylindrical diffusers as spectroscopy sources has been demonstrated by researchers at the University of Pennsylvania in clinical studies of prostate iPDT.13, 21 This has also been described for the case of heterogenous optical properties by Dimofte et al.22 In this method, the diffuser fiber was again modeled as a sum of diffusion point sources, with isotropic spherical diffusers used as detectors. In this case, the isotropic detector is translated within the catheter, and the optical properties are binned by location. The measured fluence rate at any particular detector position therefore depends on a weighted average of the optical properties between the source and detector. By solving for the binned values simultaneously at all detector positions, locally heterogenous optical properties can be recovered using a single diffuser and isotropic detector.
In most cases of clinical iPDT, calibrated isotropic detectors are present in the tissue volume in order to measure the light dose at various locations. This is also true when flat cleaved fibers are used as treatment and spectroscopy fibers.7 The spectroscopy scheme described by Dimofte et al.22 therefore does not require the insertion of additional fibers relative to current treatment conditions, but would necessitate scanning of the detector fibers for optical property recovery. As cylindrical diffusing fibers are better suited for treating large tumor volumes, a spectroscopy scheme using treatment diffusers as spectroscopy sources and detectors would be highly advantageous.
As shown in Fig. 3, the fluence deposited by flat cleaved fibers falls off much more quickly in three dimensions with distance from the source. While this means that these fibers cannot treat as large a volume for the same laser power and treatment time, it does mean that they can be used when rapid fall-off is desirable. For example, in the case of vulnerable healthy structures bordering the tumor, flat cleaved fibers could be used to deliver a locally lethal dose to the tumor volume, while delivering a subthreshold dose to the healthy tissue. A similar method has been used in brachytherapy, where shorter radioactive sources are placed close to the tumor periphery.23 Further examination of treatment plans combining diffusers and flat cleaved fibers could lead to light dose distributions that are more closely tailored to the tumor volume.
It should be noted that the treatment planning scheme presented in this paper assumes that therapeutic response is determined entirely by photosensitizer concentration and fluence, as has been done by other researchers.7, 13, 14 Since the photosensitizer concentration is assumed to be homogeneous, fluence is the only factor that influences outcome. In reality, response will also depend on oxygen dynamics, local photosensitizer concentration, and photobleaching of the sensitizer. Incorporation of these factors into the treatment planning process, using interstitial spectroscopy, would likely improve the accuracy of the treatment plans generated. The effects of these factors could be different for the two fiber types, due to the higher fluence rates near the tips of flat-cleaved fibers. For certain photosensitizers, the rate of photobleaching and eventual tumor response is related to the fluence rate.24 In this case, the choice of treatment fiber could have further consequences on outcome.
CONCLUSIONS
Cylindrical diffusers and flat cleaved fibers are both suitable for delivery of treatment light in iPDT. In bulky tumors, diffusers can deliver a prescribed light dose with fewer fibers inserted and shorted treatment times. Flat cleaved fibers allow for spectroscopy to be performed with the treatment fibers and can help reduce dose to vulnerable healthy structures at the expense of the insertion of more fibers. This spectroscopy advantage may be diminished as the use of diffusers as light sources for spectroscopy becomes more widespread.
ACKNOWLEDGMENTS
The authors would like to thank Dr. Daryl Nazareth of the Department of Radiation Medicine at Roswell Park Cancer Institute for providing the anonymized CT dataset used for creating the treatment plans shown in this paper. This work was supported by NIH Grant Nos. CA68409 and CA55791.
References
- Agostinis P., Berg K., Cengel K. A., Foster T. H., Girotti A. W., Gollnick S. O., Hahn S. M., Hamblin M. R., Juzeniene A., Kessel D., Korbelik M., Moan J., Mroz P., Nowis D., Piette J., Wilson B. C., and Golab J., “Photodynamic therapy of cancer: An update,” CA Cancer J. Clin. 61, 250–281 (2011). 10.3322/caac.20114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allison R. R., Mota H. C., and Sibata C. H., “Clinical PD/PDT in North America: An historical review,” Photodiagnosis Photodyn. Ther. 1, 263–277 (2004). 10.1016/S1572-1000(04)00084-5 [DOI] [PubMed] [Google Scholar]
- Svanberg K., Bendsoe N., Axelsson J., Andersson-Engels S., and Svanberg S., “Photodynamic therapy: Superficial and interstitial illumination,” J. Biomed. Opt. 15, 041502 (2010). 10.1117/1.3466579 [DOI] [PubMed] [Google Scholar]
- Patel H., Mick R., Finlay J., Zhu T. C., Rickter E., Cengel K. A., Malkowicz S. B., Hahn S. M., and Busch T. M., “Motexafin lutetium-photodynamic therapy of prostate cancer: Short- and long-term effects on prostate-specific antigen,” Clin. Cancer Res. 14, 4869–4876 (2008). 10.1158/1078-0432.CCR-08-0317 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jerjes W., Upile T., Hamdoon Z., Abbas S., Akram S., Mosse C. A., Morley S., and Hopper C., “Photodynamic therapy: The minimally invasive surgical intervention for advanced and/or recurrent tongue base carcinoma,” Lasers Surg. Med. 43, 283–292 (2011). 10.1002/lsm.21048 [DOI] [PubMed] [Google Scholar]
- Ortner M.-A., “Photodynamic therapy for cholangiocarcinoma,” Lasers Surg. Med. 43, 776–780 (2011). 10.1002/lsm.21106 [DOI] [PubMed] [Google Scholar]
- Swartling J., Axelsson J., Ahlgren G., Kälkner K. M., Nilsson S., Svanberg S., Svanberg K., and Andersson-Engels S., “System for interstitial photodynamic therapy with online dosimetry: First clinical experiences of prostate cancer,” J. Biomed. Opt. 15, 058003 (2010). 10.1117/1.3495720 [DOI] [PubMed] [Google Scholar]
- Johansson A., Johansson T., Thompson M. S., Bendsoe N., Svanberg K., Svanberg S., and Andersson-Engels S., “In vivo measurement of parameters of dosimetric importance during interstitial photodynamic therapy of thick skin tumors,” J. Biomed. Opt. 11, 034029 (2006). 10.1117/1.2204027 [DOI] [PubMed] [Google Scholar]
- Regula J., MacRobert A. J., Gorchein A., Buonaccorsi G. A., Thorpe S. M., Spencer G. M., Hatfield A. R. W., and Bown S. G., “Photosensitisation and photodynamic therapy of oesophageal, duodenal, and colorectal tumours using 5 aminolaevulinic acid induced protoporphyrin IX: A pilot study,” Gut 36, 67–75 (1995). 10.1136/gut.36.1.67 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheong W.-F., Prahl S. A., and Welch A. J., “A review of the optical properties of biological tissues,” IEEE J. Quantum Electron. 26, 2166–2185 (1990). 10.1109/3.64354 [DOI] [Google Scholar]
- Zhu T. C., Finlay J. C., and Hahn S. M., “Determination of the distribution of light, optical properties, drug concentration, and tissue oxygenation in-vivo in human prostate during motexafin lutetium-mediated photodynamic therapy,” J. Photochem. Photobiol. B 79, 231–241 (2005). 10.1016/j.jphotobiol.2004.09.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baran T. M., Fenn M. C., and Foster T. H., “Determination of optical properties by interstitial white light spectroscopy using a custom fiber optic probe,” J. Biomed. Opt. 18, 107007 (2013). 10.1117/1.JBO.18.10.107007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altschuler M. D., Zhu T. C., Li J., and Hahn S. M., “Optimized interstitial PDT prostate treatment planning with the Cimmino feasibility algorithm,” Med. Phys. 32, 3524–3536 (2005). 10.1118/1.2107047 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davidson S. R. H., Weersink R. A., Haider M. A., Gertner M. R., Bogaards A., Giewercer D., Scherz A., Sherar M. D., Elhilali M., Chin J. L., Trachtenberg J., and Wilson B. C., “Treatment planning and dose analysis for interstitial photodynamic therapy of prostate cancer,” Phys. Med. Biol. 54, 2293–2313 (2009). 10.1088/0031-9155/54/8/003 [DOI] [PubMed] [Google Scholar]
- Thompson M. S., Johansson A., Johansson T., Andersson-Engels S., Svanberg S., Bendsoe N., and Svanberg K., “Clinical system for interstitial photodynamic therapy with combined on-line dosimetry measurements,” Appl. Opt. 44, 4023–4031 (2005). 10.1364/AO.44.004023 [DOI] [PubMed] [Google Scholar]
- Johansson A., Axelsson J., Andersson-Engels S., and Swartling J., “Realtime light dosimetry software tools for interstitial photodynamic therapy of the human prostate,” Med. Phys. 34, 4309–4321 (2007). 10.1118/1.2790585 [DOI] [PubMed] [Google Scholar]
- Baran T. M. and Foster T. H., “New Monte Carlo model of cylindrical diffusing fibers illustrates axially heterogeneous fluorescence detection: Simulation and experimental validation,” J. Biomed. Opt. 16, 085003 (2011). 10.1117/1.3613920 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson D. J., Karakullukçu M. B., Kruijt B., Kanick S. C., Veen R. P. L. V., Amelink A., Sterenborg H. J. C. M., Witjes M. J. H., and Tan I. B., “Optical spectroscopy to guide photodynamic therapy of head and neck tumors,” IEEE J. Sel. Top. Quantum Electron 16, 854–862 (2010). 10.1109/JSTQE.2009.2035930 [DOI] [Google Scholar]
- Potters L., Cao Y., Calugaru E., Torre T., Fearn P., and Wang X.-H., “A comprehensive review of CT-based dosimetry parameters and biochemical control in patients treated with permanent prostate brachytherapy,” Int. J. Radiat. Oncol., Biol., Phys. 50, 605–614 (2001). 10.1016/S0360-3016(01)01473-0 [DOI] [PubMed] [Google Scholar]
- Jacques S. L. and Pogue B. W., “Tutorial on diffuse light transport,” J. Biomed. Opt. 13, 041302 (2008). 10.1117/1.2967535 [DOI] [PubMed] [Google Scholar]
- Li J., Altschuler M. D., Hahn S. M., and Zhu T. C., “Optimization of light source parameters in the photodynamic therapy of heterogeneous prostate,” Phys. Med. Biol. 53, 4107–4121 (2008). 10.1088/0031-9155/53/15/007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dimofte A., Finlay J. C., Liang X., and Zhu T. C., “Determination of optical properties in heterogeneous turbid media using a cylindrical diffusing fiber,” Phys. Med. Biol. 57, 6025–6046 (2012). 10.1088/0031-9155/57/19/6025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khan F. M., The Physics of Radiation Therapy, 4th ed. (Lippincott, Philadelphia, PA, 2010). [Google Scholar]
- Robinson D. J., Bruijn H. S. D., Veen N. V. D., Stringer M. R., Brown S. B., and Star W. M., “Fluorescence photobleaching of ALA-induced protoporphyrin IX during photodynamic therapy of normal hairless mouse skin: The effect of light dose and irradiance and the resulting biological effect,” Photochem. Photobiol. 67, 140–149 (1998). 10.1111/j.1751-1097.1998.tb05177.x [DOI] [PubMed] [Google Scholar]