Abstract
BACKGROUND AND PURPOSE:
The auditory radiation crosses other white matter tracts and cannot reliably be delineated or quantitatively assessed with DTI fiber tracking. This study investigates whether HARDI fiber tracking can be used to robustly delineate the full extent of the tract.
MATERIALS AND METHODS:
HARDI (64-direction, b=3000 s/mm2) and DTI (30-direction, b=1000 s/mm2) were acquired from 25 control participants between 8 and 26 years old. Probabilistic HARDI and DTI fiber tracking of the auditory radiation was performed with starting and filter regions automatically generated from the FreeSurfer white matter parcellation. DTI fiber tracking was performed with both the 64-direction and the 30-direction datasets. Fiber-tracking trials demonstrating connectivity from the Heschl gyrus to the medial geniculate nucleus were considered successful.
RESULTS:
The HARDI fiber tracking success rate was 98% and was significantly higher than the 64-direction DTI rate of 50% or the 30-direction DTI rate of 42% (P < .001). The success rates of HARDI fiber tracking for the left and right auditory radiations were not significantly different. In contrast, the left auditory radiation was successfully delineated with DTI fiber tracking at a higher rate than the right auditory radiation.
CONCLUSIONS:
HARDI can discriminate the complex white matter pathways at the junction of the auditory radiation and the ILF. HARDI fiber tracking can reliably delineate the auditory radiation.
Diffusion MR fiber tracking uses the random motion of water to determine the orientation of coherent axonal bundles.1,2 In particular, fiber tracking follows the estimated fiber orientation voxel to voxel in 3D to delineate specific white matter pathways.3–6 DTI fiber tracking has become a standard tool to analyze white matter tract geometry and microstructure. DTI fiber tracking software is readily available from research groups and MR scanner manufacturers. Accordingly, there has been a surge in the number of publications using DTI fiber tracking to delineate specific tracts for qualitative or quantitative purposes. A limitation, however, is that the diffusion tensor model fails to accurately represent the complex architecture of crossing white matter fibers. For this reason, DTI fiber tracking fails to accurately follow white matter pathways through tract intersections.
HARDI is capable of discriminating multiple fiber populations crossing within the same voxel. HARDI requires the acquisition of more than 50 gradient directions at high b-value, whereas DTI only requires 6 directions at lower b-values. The higher angular resolution provides a more accurate representation of the 3D pattern of water diffusion within a voxel. Numerous methods exist to reconstruct the architecture of brain tissue from HARDI data.7–12 All methods have in common the ability to provide the orientation of multiple white matter tracts within each voxel. Fiber tracking with HARDI can follow white matter tracts through regions of crossing fibers, whereas DTI fiber tracking would terminate or provide erroneous results in these same areas.13–16
The auditory radiations are an important sensory pathway that relays acoustic information from the medial geniculate nucleus of the thalamus to the primary AC. The auditory radiation crosses the ILF, a major anteroposterior white matter tract. Thus, DTI fiber tracking cannot consistently delineate the auditory radiation. In a prior study, probabilistic DTI fiber tracking was capable of following the acoustic pathway from the cortex to the inferior colliculus in only 50% of trials.17 Our study compares the performance of probabilistic HARDI with probabilistic DTI fiber tracking of the auditory radiation. The goal of our study was to develop a robust framework for studying a primary sensory pathway that is often difficult to identify by traditional quantitative measurement methods.
Materials and Methods
MR Imaging
MR imaging was performed with a 3T Verio (Siemens, Erlangen, Germany) scanner on 25 children and adults between 8 and 26 years old (mean age, 16.4 years). All participants were healthy volunteers and had no abnormal findings on MR imaging. Informed consent was obtained from each participant or his or her guardian as applicable according to our institution's regulations. The whole-brain HARDI acquisition included 64 gradient directions at b=3000 s/mm2; TR, 14.8 s; TE, 111 ms; voxel size, 2 × 2 × 2 mm; and matrix, 128 × 128. Two b=0 s/mm2 volumes were included in the HARDI acquisition. An additional DTI acquisition used 30 diffusion gradient directions at b=1000 s/mm2; 1 b=0 s/mm2 volume; TR, 11 s; TE, 76 ms; voxel size, 2 × 2 × 2 mm; and matrix, 128 × 128. The 30-direction diffusion sequence is the routine clinical DTI sequence used at our institution. The HARDI acquisition was approximately 18 minutes in duration and the DTI acquisition 6 minutes in duration. Both HARDI and DTI acquisitions used a Stejskal-Tanner monopolar, spin-echo echo- planar sequence, a 32-channel head coil, maximal gradient strength of 45 mT/m, and a parallel acceleration factor of 2 with generalized autocalibrating partially parallel acquisition (Siemens). Diffusion volumes were corrected for eddy current distortion with the Functional MR Imaging of the Brain Diffusion Toolbox in FSL (http://www.fmrib.ox.ac.uk/fsl).18 Anatomic T1-weighted magnetization-prepared rapid acquisition with gradient echo volumes were also acquired from each participant. Parameters were TR, 2000 ms and TE, 3.71 ms, with 1-mm isotropic voxels and full head coverage.
Diffusion MR Fiber Tracking
The solid-angle q-ball reconstruction of the HARDI data were used with a probabilistic fiber-tracking algorithm.8,13 The HARDI fiber-tracking algorithm uses the residual bootstrap to estimate the uncertainty in the q-ball fiber orientation estimates. The range of probable fiber orientations is probed with a Monte Carlo strategy as each voxel is visited many times by independent tracts. The total number of fiber trajectories passing through each voxel provides a confidence level of that voxel's inclusion in the tract of interest. For comparison, probabilistic DTI fiber tracking was performed with both the 64-diffusion gradient direction HARDI acquisition and the 30-direction standard DTI acquisition. The DTI fiber-tracking algorithm uses the residual bootstrap to estimate uncertainty in the primary eigenvector orientation.19 The DTI and HARDI fiber-tracking probabilistic algorithms use similar statistical methods to estimate uncertainty and propagate fiber trajectories. A Monte Carlo strategy probes the range of possible propagation directions, and trajectories are based on fiber assignment by continuous tracking.4 Both HARDI and DTI fiber tracking were implemented with in-house software written in Interactive Data Language (Exelis Visual Solutions, Boulder, Colorado).
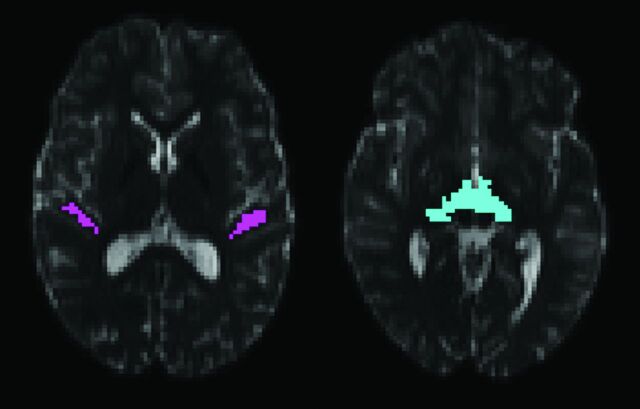
Volume segmentation and white matter parcellation was performed with FreeSurfer (http://surfer.nmr.mgh.harvard.edu) on each participant's T1-weighted image and used to generate regions of interest for fiber tracking.20 The T1-weighted volume was registered with the Functional MR Imaging of the Brain Linear Image Registration Tool (FLIRT) to the echo-planar volumes without diffusion weighting (b=0) from the 30-direction and 64-direction diffusion acquisitions.21 The 2 b=0 volumes from the 64-direction acquisition were averaged before registration. All registrations were visually examined to ensure correct placement of the major sulci and ventricles. The FreeSurfer parcellation map was then mapped into the coordinate space of each diffusion acquisition. The white matter of the transverse temporal gyrus was used to launch fiber tracks. A target region including the medial geniculate nucleus was generated with custom-built software operating on the FreeSurfer parcellations. The thalamus and ventral diencephalon segmentations were first dilated with a 2 × 2 × 2 voxel structuring element. The intersection of the 2 dilated segmentations is on the inferior surface of the thalamus and is retained as the target region of interest. Fig 1 shows the starting and target regions. A set of regions of interest outside the auditory radiation were used to eliminate common patterns of errant fiber trajectories. These additional regions included the medial orbitofrontal white matter, corpus callosum, isthmus of the cingulated gyrus, precentral gyrus, supramarginal gyrus, putamen, and palladium. Fiber tracks passing through the starting and target regions, but not through the exclusion regions, were retained as the auditory radiation.
Fig 1.
The starting region of interest for fiber tracking within the Heschl gyrus is shown on the left. The target region of interest on the inferior surface of the thalamus is shown on the right. The regions are shown overlaid on axial sections through the b=0 s/mm2 echo-planar volume from the 64-direction HARDI acquisition.
HARDI and DTI fiber tracking were each performed with an FA threshold of 0.125, an angle threshold of 70°, and 128 starting points per voxel. A low FA threshold was chosen because HARDI can detect fiber architecture in voxels where the diffusion tensor model produces low FA. The relatively high angle threshold reflects the ability of HARDI to detect crossing fibers. Tractography was performed at the native 2 × 2 × 2-mm image resolution.
Successful fiber tracking was defined as the presence of at least 1 trajectory connecting the Heschl gyrus to the medial geniculate nucleus. To further examine performance, the number of trajectories produced by each fiber-tracking method was compared by adjustment of the threshold for successful fiber tracking. Left and right side auditory radiations were examined separately. Comparisons between rates of success were performed with the McNemar χ2 test.
Results
Figure 2 shows an example set of HARDI fiber tracks (red streamlines), following the auditory radiation from the AC to the thalamus. The q-ball orientation distribution functions show the anteroposterior ILF (green peaks) crossing the smaller left-right peaks of the auditory radiation. The HARDI fiber tracking follows the auditory radiation through the crossing, whereas DTI fiber tracking fails. Fig 3 shows DTI fiber tracks emerging from the Heschl gyrus and incorrectly following the dominant anteroposterior coursing the ILF.
Fig 2.
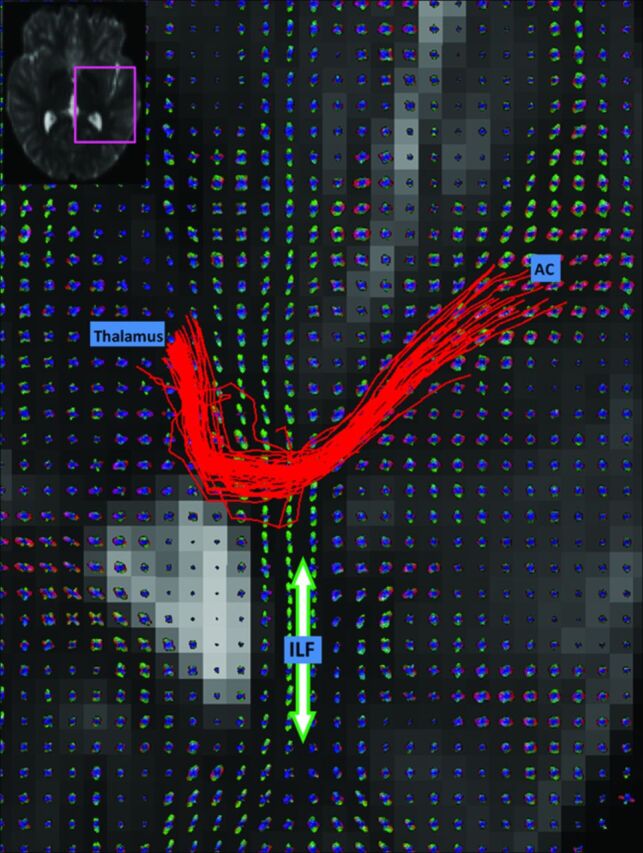
Q-ball reconstructions of the HARDI data are shown for each voxel on an axial section. HARDI fiber tracks (red streamlines) course from the AC to the thalamus. The ILF (green fiber peaks and orientation indicated with arrow) intersects the auditory radiation.
Fig 3.
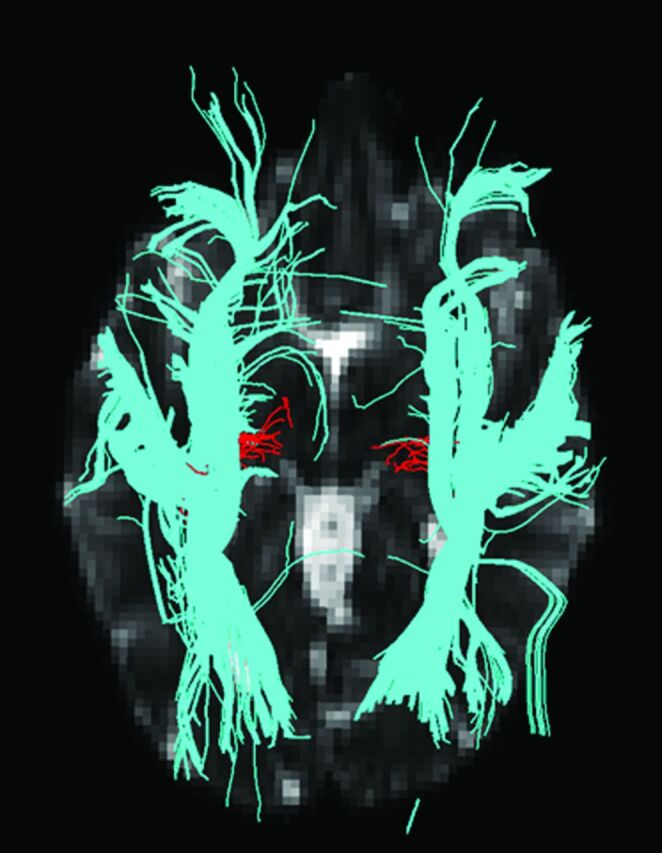
HARDI fiber tracks (red) and DTI fiber tracks (blue) are visualized in the left and right hemispheres. DTI fiber tracks are from the 64-direction dataset. The left hemisphere is on the left side of the figure. Both HARDI and DTI fiber tracks were launched from the same starting regions in the Heschl gyrus. The HARDI fiber tracks reaching the thalamic target regions are retained. For this figure, all DTI fiber tracks are retained regardless of destination. The DTI fiber tracks emerge from the Heschl gyrus and follow the ILF in either the anterior or posterior direction. No DTI fiber tracks cross the ILF to reach the thalamus in the right hemisphere.
At a threshold of 1 trajectory (Fig 4), the success rate of HARDI fiber tracking was 98%; 64-direction DTI, 50%; and 30-direction DTI, 42%. HARDI fiber tracking successfully delineated the auditory radiation at a significantly higher rate than either DTI fiber tracking method (McNemar χ2 test with Bonferroni correction, P < .001 each; Table). The success rate of 30-direction low-b-value and 64-direction high-b-value DTI fiber tracking was not significantly different. Age did not correlate with fiber-tracking success for any fiber-tracking method (logistic regression, P > .4 for each).
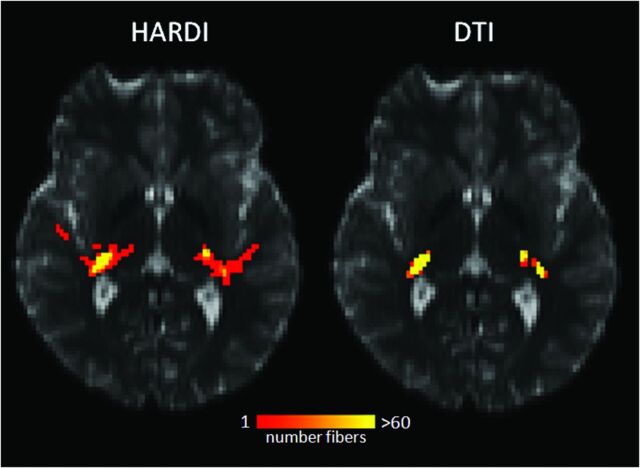
Fig 4.
HARDI and DTI fiber tracks connecting the AC to the thalamic target region are shown in a case where both methods were successful in each hemisphere. The number of fiber trajectories passing through each voxel is encoded with the overlay color. The yellow voxels have the highest probability of being within the auditory radiation.
Comparison of DTI and HARDI auditory fiber-tracking results. Successful connections contained 1 or more fiber trajectories
| Successful |
Unsuccessful |
|||||
|---|---|---|---|---|---|---|
| Left | Right | Total | Left | Right | Total | |
| DTI - 30 Directions | 16 | 5 | 21 | 9 | 20 | 29 |
| DTI - 64 Directions | 18 | 7 | 25 | 7 | 18 | 25 |
| HARDI - 64 Directions | 24 | 25 | 49 | 1 | 0 | 1 |
The success rates of HARDI fiber tracking for the left and right auditory radiations were not significantly different. In contrast, the left auditory radiation was successfully delineated with DTI fiber tracking at a higher rate than that of the right auditory radiation. This hemisphere difference was significant for both 30-direction and 64-direction DTI fiber tracking (P < .003 each, McNemar χ2 test with Bonferroni correction, Table).
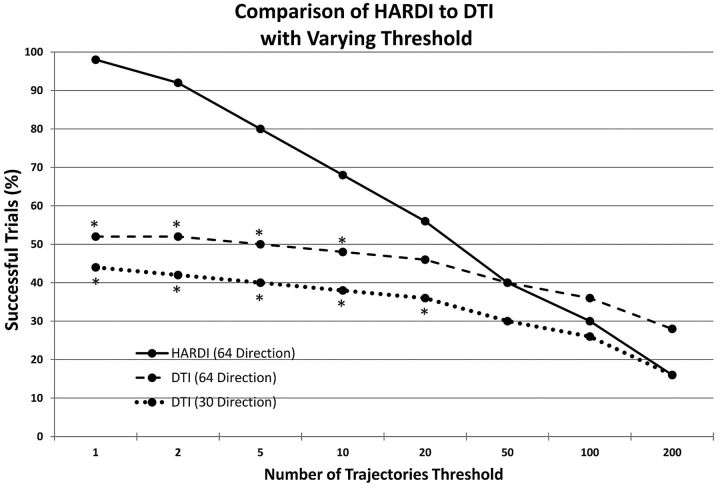
Fig 5 examines fiber-tracking results, as the number of trajectory thresholds varies from 1 to 200. DTI and HARDI rates of success decrease as the threshold is increased. However, the HARDI rate of success is significantly higher than that of the 30-direction DTI success rate through a threshold of 10 and the 64-direction DTI success rate through a threshold of 20 (P < .01 each, McNemar χ2 test).
Fig 5.
The threshold for successful fiber-tracking is varied between 1 and 200 trajectories connecting the AC to the thalamus. The percentage of successful HARDI and DTI fiber-tracking trials is shown at each threshold. An asterisk indicates that the HARDI rate of success is significantly higher than the respective DTI fiber-tracking rate of success (P < .01).
Discussion
This study demonstrates the advantage of HARDI for performing fiber tracking of the auditory radiation. HARDI can reliably resolve crossing white matter tracts at the intersection of the auditory radiation and the ILF. In contrast, the diffusion tensor model often fails to accurately represent the microstructure at this junction and only depicts the orientation of the dominant ILF tract. The DTI fiber-tracking success rate observed in this study is consistent with the results from Crippa et al.17 DTI fiber-tracking performance with the 64-direction (b=3000 s/mm2) diffusion data was not significantly different from that of the 30-direction (b=1000 s/mm2) data, with neither being robustly successful. Thus, our present results indicate that an improved signal-to-noise ratio or increased number of directions cannot improve DTI fiber-tracking performance.
The HARDI acquisition is longer than a traditional DTI acquisition. However, it has been successfully included in our pediatric and adult research protocols. In implementation of HARDI, the primary differences between a DTI and HARDI acquisition are the number of directions and the b-value. Changing these parameters is straightforward on many scanners. However, higher b-values produce images with a lower signal-to-noise ratio. High-field strength and high specification gradients are necessary to improve signal-to-noise ratio at high b-values. A current limitation is that HARDI postprocessing is not a feature available on most scanners. However, as HARDI is translated into a clinical tool, the availability of HARDI reconstruction algorithms and fiber-tracking tools is expected to improve.
Diffusion MR and tractography provide an estimate of white matter microstructure and connectivity.22,23 Tractography operates with the assumption that white matter fiber orientation can be inferred from the random movement of water. The choice of image acquisition parameters and tractography algorithm determines the accuracy of tractography results. Image noise, low spatial resolution, and a low number of diffusion gradient directions are imaging factors that limit the accuracy of calculated fiber orientations. When incorrect HARDI or DTI fiber orientations are used for tractography, errors propagate along the trajectories. A noninvasive reference standard for the subcortical position of the auditory radiation does not exist. However, prior knowledge of neuroanatomy can be added by the user to delineate a specific tract. This study used multiple atlas-based starting, target, and filter regions of interest to constrain the fiber tracks to the auditory radiation.
Probabilistic algorithms attempt to compensate for noise and inherent inaccuracies of the HARDI and DTI methods by probing multiple possible propagation directions. Deterministic fiber- tracking algorithms are common, but they do not account for the uncertainty inherent in all diffusion MR imaging experiments. The probabilistic fiber-tracking algorithms used in our study estimate the uncertainty in the HARDI and DTI fiber orientations with the bootstrap method.13,19,23,24 The residual bootstrap technique is a method to determine the probability distribution of fiber orientations from 1 diffusion MR acquisition. It is necessary to launch a large number of trajectories from the starting region to probe the range of possible fiber orientations along the tract. The number of fiber trajectories passing through a voxel provides a relative assessment of that voxel's likelihood of inclusion in the tract of interest. However, there is no way to translate the number of trajectories to an absolute metric of probability. The number of trajectories generated is related to the size of the starting region and the density of starting points. As seen in Fig 5, HARDI ceased to perform better than DTI at a threshold of 20 trajectories. However, this threshold level is directly related to the number of starting points.
Prior quantitative studies of the auditory radiation have relied on region-of-interest measurements within the tract. Lutz et al25 placed regions of interest in the Heschl gyrus and the acoustic radiation adjacent to the thalamus to study the effect of aging on the auditory system. Roberts et al26 used regions of interest in the Heschl gyrus to measure the correlation of diffusion anisotropy (on the basis of DTI) to magnetoencephalography-detected electrophysiologic auditory-evoked superior temporal gyrus responses. Manually placed regions of interest are restricted to points within the auditory radiation near known landmarks. Hand-drawn region-of-interest measurements have higher variability than measures originating from 3D regions of interest defined by fiber tracking.27 In addition, white matter tracts have heterogeneous geometry and microstructure as they course through different regions of the cerebrum. Regions of interest that only outline a small portion of the tract may not be representative of the entire tract and may be insensitive to microstructural changes occurring elsewhere along the tract. As shown in our study, HARDI fiber tracking extends the localization of auditory radiation tracts beyond the landmarks used as starting and target regions. Thus, our work provides the framework for quantitative studies of the entire auditory radiation.
DTI fiber tracking was more successful in delineating the left auditory radiation than the right. This asymmetry may be attributed to the structural and functional asymmetries of the language and auditory systems.28–31 Greater left hemispheric cortical activity and white matter volumes in language networks may be related to a larger and more compact auditory radiation. In addition, diffusion fiber-tracking studies have shown structural asymmetry in the ILF.32,33 These factors reduce DTI partial voluming and increase diffusion anisotropy. These structural differences may result in an improved success rate of DTI fiber tracking of the left auditory radiation. However, HARDI fiber tracking demonstrated no asymmetry in performance because of its ability to discriminate crossing fibers in both hemispheres.
The auditory radiation is a primary sensory pathway and is important for language comprehension. Auditory dysfunction measured with magnetoencephalography has been associated with autism spectrum disorders.34 Abnormal morphologic patterns and diffusion parameters in the Heschl gyrus have been identified in schizophrenia.35,36 Further studies are needed to investigate the microstructure of the auditory radiation in these neuropsychiatric disorders. The findings in our study indicate that more detailed and robust measures of the auditory radiation can be obtained by HARDI fiber tracking. Unlike other primary sensory pathways such as the somatosensory and optic radiations, HARDI is necessary for study of the acoustic radiation because traditional DTI fiber-tracking analysis is not reliable in this tract. HARDI metrics that describe tract-specific microstructure are still under development. In the future, these HARDI metrics may be combined with HARDI fiber tracking to perform microstructural assessment of the auditory radiation in clinical studies.
Conclusions
HARDI fiber tracking of the auditory radiation performs significantly better than DTI fiber tracking, with HARDI easily discriminating the complex white matter pathways at the junction of the auditory radiation and the ILF. Thus, HARDI is a necessary component of clinical studies seeking to assess the entire auditory radiation with diffusion MR imaging.
Acknowledgment
The authors thank Thorsten Feiweier of Siemens for providing the diffusion works in progress pulse sequence used in this study. Dr. Roberts thanks the Oberkircher family for the Oberkircher Family Chair in Pediatric Radiology.
ABBREVIATIONS:
- AC
auditory cortex
- FA
fractional anisotropy
- HARDI
high angular resolution diffusion imaging
- ILF
inferior longitudinal fasciculus
Footnotes
Disclosures: Jeffrey Berman—RELATED: Grant: NIH K01; American Society of Neuroradiology Foundation Scientist Award. *Lisa Blaskey—RELATED: Grant: Nancy Lurie Marks Foundation,*Comments: Salary paid by a grant from the Nancy Lurie Marks Family Foundation and Autism Speaks–both of which partially supported this study. Timothy Roberts—RELATED: Grant: NIH, *Comments: R01-DC008871; UNRELATED: Consultancy, Stock Options: Prism Clinical Imaging, Comments: Consulting/MAB arrangement. Stock options only. No overlap with this study. (*Money paid to institution.)
This study was supported in part by National Institutes of Health (NIH) grant R01DC008871 (T.R.), NIH grant R01DC008871-02S1, NIH grant K01MH096091 (J.I.B.), NIH grant K08 MH085100 (J.C.E.), and Award P30HD026979 from the Eunice Kennedy Shriver National Institute of Child Health & Human Development of the NIH. Additional grants were from the Research Scientist Award of the Foundation for the American Society of Neuroradiology, the Nancy Lurie Marks Family Foundation, and Autism Speaks. This research has been funded in part by a grant from the Pennsylvania Department of Health. The Pennsylvania Department of Health specifically disclaims responsibility for any analyses, interpretations, or conclusions.
Previously presented in part as an abstract at International society for Magnetic Resonance in Medicine, 2011, Montreal, Canada.
REFERENCES
- 1. Basser PJ, Mattiello J, LeBihan D. Estimation of the effective self-diffusion tensor from the NMR spin echo. J Magn Reson B 1994;103:247–54 [DOI] [PubMed] [Google Scholar]
- 2. Beaulieu C. The basis of anisotropic water diffusion in the nervous system—a technical review. NMR Biomed 2002;15:435–55 [DOI] [PubMed] [Google Scholar]
- 3. Conturo TE, Lori NF, Cull TS, et al. Tracking neuronal fiber pathways in the living human brain. Proc Natl Acad Sci U S A 1999;96:10422–27 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Mori S, Crain BJ, Chacko VP, et al. Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Ann Neurol 1999;45:265–69 [DOI] [PubMed] [Google Scholar]
- 5. Mori S, van Zijl PC. Fiber tracking: principles and strategies—a technical review. NMR Biomed 2002;15:468–80 [DOI] [PubMed] [Google Scholar]
- 6. Basser PJ, Pajevic S, Pierpaoli C, et al. In vivo fiber tractography using DT-MRI data. Magn Reson Med 2000;44:625–32 [DOI] [PubMed] [Google Scholar]
- 7. Tuch DS. Q-ball imaging. Magn Reson Med 2004;52:1358–72 [DOI] [PubMed] [Google Scholar]
- 8. Aganj I, Lenglet C, Sapiro G, et al. Reconstruction of the orientation distribution function in single- and multiple-shell Q-ball imaging within constant solid angle. Magn Reson Med 2010;64:554–66 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Tournier JD, Yeh CH, Calamante F, et al. Resolving crossing fibres using constrained spherical deconvolution: validation using diffusion-weighted imaging phantom data. Neuroimage 2008;42:617–25 [DOI] [PubMed] [Google Scholar]
- 10. Hess CP, Mukherjee P, Han ET, et al. Q-ball reconstruction of multimodal fiber orientations using the spherical harmonic basis. Magn Reson Med 2006;56:104–17 [DOI] [PubMed] [Google Scholar]
- 11. Tournier JD, Calamante F, Gadian DG, et al. Direct estimation of the fiber orientation density function from diffusion-weighted MRI data using spherical deconvolution. Neuroimage 2004;23:1176–85 [DOI] [PubMed] [Google Scholar]
- 12. Ozarslan E, Shepherd TM, Vemuri BC, et al. Resolution of complex tissue microarchitecture using the diffusion orientation transform (DOT). Neuroimage 2006;31:1086–103 [DOI] [PubMed] [Google Scholar]
- 13. Berman JI, Chung S, Mukherjee P, et al. Probabilistic streamline Q-ball tractography using the residual bootstrap. Neuroimage 2008;39:215–22 [DOI] [PubMed] [Google Scholar]
- 14. Perrin M, Poupon C, Cointepas Y, et al. Fiber tracking in Q-ball fields using regularized particle trajectories. Inf Process Med Imaging 2005;19:52–63 [DOI] [PubMed] [Google Scholar]
- 15. Campbell JS, Siddiqi K, Rymar VV, et al. Flow-based fiber tracking with diffusion tensor and Q-ball data: validation and comparison to principal diffusion direction techniques. Neuroimage 2005;27:725–36 [DOI] [PubMed] [Google Scholar]
- 16. Behrens TE, Berg HJ, Jbabdi S, et al. Probabilistic diffusion tractography with multiple fibre orientations: What can we gain? Neuroimage 2007;34:144–55 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Crippa A, Lanting CP, van Dijk P, et al. A diffusion tensor imaging study on the auditory system and tinnitus. Open Neuroimag J 2010;4:16–25 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Smith SM, Jenkinson M, Woolrich MW, et al. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage 2004;23 Suppl 1:S208–19 [DOI] [PubMed] [Google Scholar]
- 19. Chung S, Lu Y, Henry RG. Comparison of bootstrap approaches for estimation of uncertainties of DTI parameters. Neuroimage 2006;33:531–41 [DOI] [PubMed] [Google Scholar]
- 20. Fischl B, Sereno MI, Tootell RB, et al. High-resolution intersubject averaging and a coordinate system for the cortical surface. Hum Brain Mapp 1999;8:272–84 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Jenkinson M, Smith S. A global optimisation method for robust affine registration of brain images. Med Image Anal 2001;5:143–56 [DOI] [PubMed] [Google Scholar]
- 22. Chung HW, Chou MC, Chen CY. Principles and limitations of computational algorithms in clinical diffusion tensor MR tractography. AJNR Am J Neuroradiol 2011;32:3–13 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Jones DK, Pierpaoli C. Confidence mapping in diffusion tensor magnetic resonance imaging tractography using a bootstrap approach. Magn Reson Med 2005;53:1143–49 [DOI] [PubMed] [Google Scholar]
- 24. Jeurissen B, Leemans A, Jones DK, et al. Probabilistic fiber tracking using the residual bootstrap with constrained spherical deconvolution. Hum Brain Mapp 2011;32:461–79 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Lutz J, Hemminger F, Stahl R, et al. Evidence of subcortical and cortical aging of the acoustic pathway: a diffusion tensor imaging (DTI) study. Acad Radiol 2007;14:692–700 [DOI] [PubMed] [Google Scholar]
- 26. Roberts TP, Khan SY, Blaskey L, et al. Developmental correlation of diffusion anisotropy with auditory-evoked response. Neuroreport 2009;20:1586–91 [DOI] [PubMed] [Google Scholar]
- 27. Partridge SC, Vigneron DB, Charlton NN, et al. Pyramidal tract maturation after brain injury in newborns with heart disease. Ann Neurol 2006;59:640–51 [DOI] [PubMed] [Google Scholar]
- 28. Morillon B, Lehongre K, Frackowiak RS, et al. Neurophysiological origin of human brain asymmetry for speech and language. Proc Natl Acad Sci U S A 2010;107:18688–93 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Devlin JT, Raley J, Tunbridge E, et al. Functional asymmetry for auditory processing in human primary auditory cortex. J Neurosci 2003;23:11516–22 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Ackermann H, Hertrich I, Mathiak K, et al. Contralaterality of cortical auditory processing at the level of the M50/M100 complex and the mismatch field: a whole-head magnetoencephalography study. Neuroreport 2001;12:1683–87 [DOI] [PubMed] [Google Scholar]
- 31. Geschwind N, Levitsky W. Human brain: left-right asymmetries in temporal speech region. Science 1968;161:186–87 [DOI] [PubMed] [Google Scholar]
- 32. Wakana S, Caprihan A, Panzenboeck MM, et al. Reproducibility of quantitative tractography methods applied to cerebral white matter. Neuroimage 2007;36:630–44 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Thiebaut de Schotten M, Ffytche DH, Bizzi A, et al. Atlasing location, asymmetry and inter-subject variability of white matter tracts in the human brain with MR diffusion tractography. Neuroimage 2011;54:49–59 [DOI] [PubMed] [Google Scholar]
- 34. Roberts TP, Khan SY, Rey M, et al. MEG detection of delayed auditory evoked responses in autism spectrum disorders: towards an imaging biomarker for autism. Autism Res 2010;3:8–18 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Douaud G, Smith S, Jenkinson M, et al. Anatomically related grey and white matter abnormalities in adolescent-onset schizophrenia. Brain 2007;130:2375–86 [DOI] [PubMed] [Google Scholar]
- 36. Lee K, Yoshida T, Kubicki M, et al. Increased diffusivity in superior temporal gyrus in patients with schizophrenia: a diffusion tensor imaging study. Schizophr Res 2009;108:33–40 [DOI] [PMC free article] [PubMed] [Google Scholar]