Receptor Tyrosine Kinases Fall into Distinct Classes Based on Their Inferred Signaling Networks

Abstract

Although many anticancer drugs that target receptor tyrosine kinases (RTKs) provide clinical benefit, their long-term use is limited by resistance that is often attributed to increased abundance or activation of another RTK that compensates for the inhibited receptor. To uncover common and unique features in the signaling networks of RTKs, we measured time-dependent signaling in six isogenic cell lines, each expressing a different RTK as downstream proteins were systematically perturbed by RNA interference. Network models inferred from the data revealed a conserved set of signaling pathways and RTK-specific features that grouped the RTKs into three distinct classes: (i) an EGFR/FGFR1/c-Met class constituting epidermal growth factor receptor, fibroblast growth factor receptor 1, and the hepatocyte growth factor receptor c-Met; (ii) an IGF-1R/NTRK2 class constituting insulin-like growth factor 1 receptor and neurotrophic tyrosine receptor kinase 2; and (iii) a PDGFRβ class constituting platelet-derived growth factor receptor β. Analysis of cancer cell line data showed that many RTKs of the same class were coexpressed and that increased abundance of an RTK or its cognate ligand frequently correlated with resistance to a drug targeting another RTK of the same class. In contrast, abundance of an RTK or ligand of one class generally did not affect sensitivity to a drug targeting an RTK of a different class. Thus, classifying RTKs by their inferred networks and then therapeutically targeting multiple receptors within a class may delay or prevent the onset of resistance.

INTRODUCTION

Receptor tyrosine kinases (RTKs) are critical effectors of cell fate and are expressed ubiquitously during development and throughout the adult body. Fifty-eight RTKs are encoded within the human genome, belonging to 20 subfamilies as defined by genetic phylogeny (1). RTKs initiate intracellular signaling events that elicit diverse cellular responses such as survival, proliferation, differentiation, and motility (2). Dysregulation of RTK-activated pathways, often a consequence of receptor overexpression, gene amplification, or genetic mutation, is a causal factor underlying numerous cancers. Thus, an increasing number of U.S. Food and Drug Administration–approved RTK-targeted therapies are emerging (1).

Since the introduction of RTK-directed therapeutics, it has become clear that multiple RTKs are active in cancer cells. This limits the efficacy of these drugs (3) and can serve as a mechanism of intrinsic or acquired resistance (4–6). Stimulation of tumor cells with certain RTK ligands can overcome inhibition of other RTKs (7, 8). Therefore, it seems that certain RTKs have sufficient signaling redundancy to compensate for each other upon targeted inhibition. To elucidate exactly which RTKs exhibit this redundancy and why, we used a set of engineered isogenic cell lines to measure the dynamic signaling networks of six RTKs while simultaneously perturbing 38 different signaling nodes singly or in combination using RNA interference (RNAi). Using multiple computational network inference approaches, we found that specific groups of RTKs exhibited functional redundancy because they induced similar downstream signaling networks. The six RTKs studied here fall into three classes based on their inferred networks, and these classes are consistent with clinically observed modes of resistance to RTK-targeted therapies.

RESULTS

A systematic perturbation-based approach uncovers RTK-specific signaling networks

Reverse engineering of biological networks from gene expression or signal transduction data using computational network inference algorithms is a method for identifying network structure (9). Although these approaches often uncover important regulatory interactions, spurious correlations in gene expression or protein activity make it difficult to isolate direct, causal interactions. To circumvent this limitation, targeted perturbations (10), in conjunction with dynamic measurements (11, 12), can be used to constrain network topology and infer directionality between nodes.

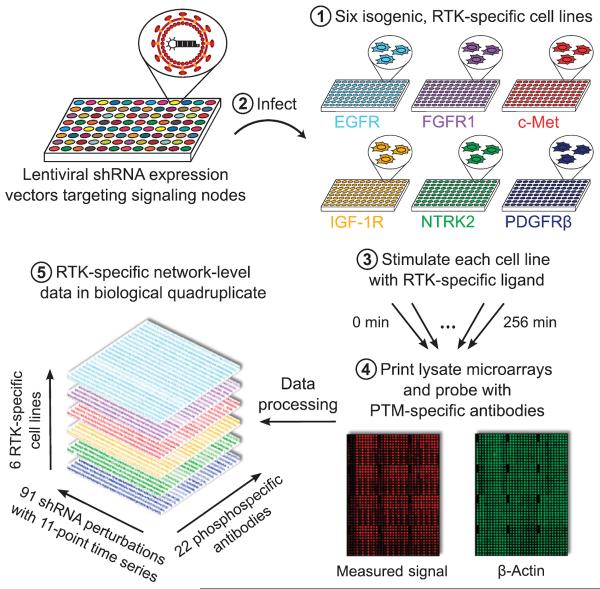
We used a perturbation strategy to infer the topology of RTK-activated signaling networks. We systematically perturbed network nodes using RNAi and measured time-dependent changes in phosphorylation status under each perturbation condition using high-throughput lysate microar-rays (Fig. 1). We focused on a representative subset of six phylogenetically diverse RTKs: epidermal growth factor receptor (EGFR or ErbB1), fibro-blast growth factor receptor 1 (FGFR1), insulin-like growth factor 1 receptor (IGF-1R), hepatocyte growth factor (HGF) receptor (c-Met), neurotrophic tyrosine receptor kinase type 2 (NTRK2 or TrkB), and platelet-derived growth factor receptor β (PDGFRβ). To isolate the unique features of each RTK from potentially confounding differences across diverse cell lines, we used a set of six otherwise isogenic cell lines, with comparable amounts of one of the six RTKs in each, and in which downstream signaling can be activated by treatment with cognate ligand (13). Thirty-eight proteins within these cell lines were systematically perturbed by lentivirus-mediated RNAi (14), individually (table S1) or in pools (table S2), using a total of 88 short hairpin RNA (shRNA) interventions with a median average of 77% knockdown efficiency. To account for possible off-target reactivity of the RNAi reagents, two different shRNA clones that target different regions of the same transcript were used for each gene.

Fig. 1. Schematic of perturbation-based profiling for analysis of RTK-specific signaling networks.

Six isogenic cell lines expressing EGFR, FGFR1, c-Met, IGF-1R, NTRK2, or PDGFRβ were treated with lentiviral shRNA expression vectors to modulate the abundance of 38 downstream signaling proteins. Upon stimulation with RTK-specific ligands, time-dependent signaling events were monitored by probing for changes in the phosphorylation [post-translational modification (PTM)] of specific sites in downstream proteins using high-throughput lysate microarrays. The resulting compendium of signaling measurements, constituting more than half a million individual data points, served as a starting point for network inference.

The targeted proteins function in various pathways downstream of RTKs, notably the phosphatidylinositol 3-kinase (PI3K) to Akt pathway, the Ras to MAPK (mitogen-activated protein kinase) pathway, and the phospholipase C–γ (PLC-γ) to protein kinase C (PKC) or Ca²⁺ signaling pathway (15). We also targeted phosphatases, cytoskeletal components, and receptor-proximal adaptor proteins. For each cell line and each RNAi intervention, we tracked RTK signaling activity by treating the cell lines with cognate ligands for 10 different durations ranging from 1 to 256 min (including a zero time point control for each) for four biological replicates of each experiment. We used “reverse-phase” protein arrays (16) with previously validated antibodies and methods (17) to quantify the relative phosphorylation of 22 sites on 21 signaling proteins in each of the lysates (table S3). Collectively, these data provide a measure of the state of signaling at the receptor and adaptor layer, the activity of the MAPK, Akt, PKC, and calcium signaling cascades, and the activity of various transcription factors (see tables S4 and S5 for processed raw data and discretized median data).

RNAi perturbations reveal conserved Akt, MAPK, and PKC pathways across six RTKs

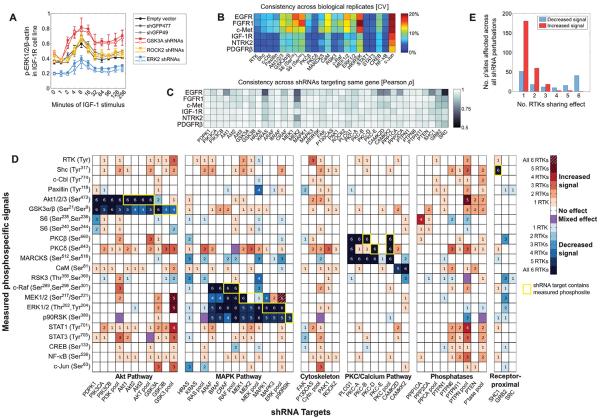
To assess the effect of each RNAi intervention on the phosphorylation status of the 21 signaling proteins, we quantified the effects of all 88 shRNAs relative to 3 control shRNAs [two shRNA vectors targeting green fluorescent protein (GFP) and one non–shRNA-expressing empty vector control]. For every shRNA perturbation, we calculated the area under the curve (AUC) from graphs of the amount of phosphorylated protein (herein called the signal) across the 11 time points for each RTK-specific cell line, phosphorylation site, and biological replicate. A targeted shRNA was considered to affect a signal only if its AUC was significantly greater than or less than the AUC of all three shRNA controls [based on a 1% false discovery rate (FDR), two-sample t test]. The effects of knocking down GSK3A (glycogen synthase kinase 3α), ROCK2 (Rho-associated kinase 2), or ERK2 (extracellular signal–regulated protein kinase 2) on the amount of phosphorylated ERK1 and ERK2 (ERK1/2) in IGF-1–stimulated cells illustrate how the data were plotted for AUC analysis and indicated that GSK3A functioned as a negative regulator of IGF-1–stimulated ERK1/2 phosphorylation, whereas ROCK2 did not appear involved in this pathway (Fig. 2A).

Fig. 2. Perturbations reveal specificity in RTK-induced signal transduction.

(A) Time courses showing examples of shRNA perturbations that affect the phosphorylation of ERK1/2 in the IGF-1R cell line. Values shown are means ± SD of four biological replicates at each time point. Solid and empty squares of the same color represent data from two different shRNAs. (B) The CV across four biological replicates was calculated at each time point under each shRNA perturbation for each of the indicated phosphorylated proteins or sites (along the bottom). The first column, RTK, indicates the phosphorylation of the respective receptor (along the side). The median of the resultant CV values is shown. (C) Pearson correlation between measured signals resulting from two shRNAs targeting the same gene, when considering all signals and time points together. Values approaching 1 are highly consistent. (D) Conservative summary of network-wide shRNA effects, showing only significant effects (against 1% FDR) that were observed consistently with both hairpin clones. The phosphorylation of sites in network proteins (rows) after knocking down downstream RTK target proteins (columns) was categorized as increased (red shades) or decreased (blue shades) relative to shRNA controls. Yellow outlines denote conditions where a phosphosite was measured on a protein that was targeted by a shRNA, such as Akt1-Ser⁴⁷³ by Akt1 shRNA. (E) Number of RTK-specific cell lines in which the phosphorylation of target sites is affected similarly by shRNA-mediated knockdown of network proteins.

Biological replicates were consistent: 75% of RTK–phosphorylation site pairs had a coefficient of variation (CV) <10% (Fig. 2B). To assess the consistency in signaling responses between pairs of shRNAs targeting the same gene, we combined data from a single shRNA for all phosphorylation sites and time points (see Materials and Methods), calculated the Pearson correlation coefficients between these values for each shRNA pair, and found that it exceeded 0.85 for 95% of the targeted genes across the six cell lines (Fig. 2C). The effects of each individual shRNA on the phosphorylation status of each target in each RTK-specific cell line are shown, represented as an increase or decrease in phosphorylation site status (fig. S1) or represented as the log₂ value (fig. S2).

Tallying the number of RTK-specific cell lines exhibiting significant perturbation effects revealed that network connections within the Akt, MAPK, and PKC pathways were conserved across the RTKs (Fig. 2D). Although there were some isoform-specific differences observed in the various RTK-expressing cell lines, perturbations within each of these pathways, specifically (i) PI3K→PDPK1 (3-phosphoinositide–dependent protein kinase-1)→Akt→GSK3, (ii) Raf→MEK (mitogen- and extracellular signal–regulated protein kinase kinase)→ERK→p90RSK (p90 ribosomal S6 kinase), and (iii) PLCgγPKCβ/δ→MARCKS (myristoylated alanine-rich C kinase substrate), decreased phosphorylation of proteins within these pathways in most of the cases across all six RTK-expressing cell lines (Fig. 2D). In contrast, most other perturbation effects occurred only across subsets of the RTK-expressing cell lines. For example, knocking down CAMKK2 (calcium/calmodulin kinase kinase 2) reduced RSK3 phosphorylation in only three of the six RTK-expressing cell lines and increased phosphorylation of ERK1/2 in one cell line.

The directionality of relationships between signaling nodes—whether an shRNA caused an increase or decrease in signal at a specific phosphorylation site (phosphosite)—was highly conserved across RTKs, as indicated by few phosphorylation sites that exhibited a mixed effect (purple boxes in Fig. 2D). Considering only those significant effects (1% Storey FDR) that were consistent in response to both shRNAs (excluding shRNA pools), all (107 of 107) effects observed in at least two cell lines affected the signal in the same direction (either increased or decreased) across cell lines (Fig. 2D). When effects from shRNA pools were also included, more than 96% (184 of 191) of shRNA-induced effects showed consistent directional effects (Fig. 2D) Nevertheless, even when pairs of shRNA clones that were not consistent with each other were included, 92% (565 of 612) of shRNA-induced effects were directionally consistent (fig. S1). These results indicate that perturbation sensitivities across RTK-activated signaling networks, if they are present, are generally conserved and that RTKs use distinct subsets of the global signaling network that underlies all RTKs.

In contrast to the many reduced phosphorylation site signals observed across all six RTK-expressing cell lines, the phosphorylation sites that exhibited increased signals after shRNA-mediated perturbations tended to be conserved across fewer RTKs (Fig. 2, D and E). Only one increased signal was observed across all six RTKs [the phosphorylation of MEK1 and MEK2 (MEK1/2) in response to ERK pooled shRNA knockdown], and only three increases were observed across five RTKs (the phosphorylation of MEK1/2 and ERK1/2 in response to GSK3 pooled shRNA knockdown, and the phosphorylation of Akt in response to PTPN pooled shRNA knockdown). Although feedback within the MAPK pathway and cross talk between the Akt and MAPK pathways have previously been observed—for example, negative feedback from ERK to SOS (son of sevenless) and from ERK to c-Raf (18) could explain the effect of ERK knockdown on MEK1/2 phosphorylation, and negative regulation of the MEK-ERK pathway by GSK3 (19) could explain the effect of GSK3 knockdown on phosphorylation of these two MAPK components—the extent to which they are conserved across RTKs was not previously appreciated. Knockdowns resulting in increased signals across five or six RTK-expressing cell lines were observed only with shRNA pools but not with single shRNAs (Fig. 2D), suggesting that isoform-specific roles within RTK signaling networks can be overcome by concurrently perturbing multiple isoforms.

Quantification of the specificity of the shRNA effects showed that most perturbations affected only one to three RTK-expressing cell lines and that shared effects (affecting five or six RTK-expressing cell lines) were mostly decreased signals (Fig. 2E) that occurred on proteins within the MAPK, Akt, and PKC pathways (Fig. 2D). Knockdowns affecting one to three RTKs more frequently resulted in signal increases than signal decreases, suggesting that regulatory relationships that have inhibitory effects may play a greater role in conferring RTK signaling specificity than do relationships with activating effects. The separate distributions of observed positive and negative regulatory effects, considered across RTKs or across the measured signals, were significant relative to a model that assumes positive and negative shRNA effects occur randomly (fig. S3). Thus, although the RTKs shared many of the same pathways, they exhibited RTK-specific effects to targeted perturbations.

Changes in phosphorylation signals after shRNA perturbations can arise from one or more of the following phenomena: (i) reduction in the concentration of a kinase or phosphatase that directly affects the concentration of its phosphorylated substrate; (ii) transcriptional, translational, or posttranslational feedback or compensation in the network; and (iii) modulation of scaffold or protein complex stoichiometries (20), including decreases in the concentrations of proteins to which phosphatases dock. We expected that the nonspecific effect of lentiviral infection itself was minimal because, rather than being dominated by a possible “infection signal,” many shRNAs exhibited different effects on the signaling network than those of the empty vector and GFP-targeted control shRNAs.

Posttranslational feedback in the network may function through feedback reactions [such as ERK phosphorylating inhibitory sites on c-Raf or Raf-1 (18)] or through indirect effects, such as retroactivity, which is a process by which changes in substrate concentration affect the output of the kinase (21). For example, if a kinase has multiple substrates, reducing the concentration of one substrate may increase phosphorylation of its other substrates. Similarly, if a phosphatase has multiple substrates, reducing the concentration of one may increase the dephosphorylation of its others. Altered substrate availability has been considered theoretically in the context of kinase inhibitors (22), where inhibiting a kinase can turn on a quiescent parallel pathway by increasing the availability of an upstream kinase shared by the inhibited kinase and the parallel pathway. Thus, some of the shRNA perturbation effects may result from direct or less intuitive indirect processes.

The observed shRNA effects were not just a function of which proteins are phosphorylated by a kinase (or dephosphorylated by a phosphatase), but rather which residues are phosphorylated or dephosphorylated. Thus, the absence of an shRNA effect at a particular phosphosite may imply that (i) the two proteins (the shRNA target and the phosphorylated protein) are not functionally related; (ii) the proteins are functionally related through the measured phosphosite, but there was insufficient knockdown of the shRNA target to observe an effect; or (iii) the proteins are functionally related, but not through the measured phosphosite. These issues must be considered when inferring network topology.

Data-driven network inference reveals three RTK classes

To better understand the signaling network topology and dynamics underlying these perturbation-induced effects, we performed network inference using each RTK-expressing cell line's data separately. The 0-min time point was separated to represent the basal, unstimulated network state, and the remaining 10 time points were grouped into three time scales based on k-means clustering of the temporal data across all RTKs. Although the algorithm did not require it, the resulting four time scales contained only contiguous time points: basal (0 min), early (1 and 2 min), intermediate (4, 8, and 16 min), and late (32, 64, 96, 128, and 256 min).

The premise of network inference is to quantify relationships between signals using some metric, which varies from one algorithm to another. Some methods use continuous input data to capture linear or nonlinear but monotonic signal-signal relationships. Other methods bin the continuous data into discrete states in an attempt to capture nonmonotonic nonlinear relationships. The use of complementary network inference methods can improve confidence by circumventing the biases inherent in any single algorithm (23). Therefore, we used five different network inference algorithms: Bayesian network analysis (24), mutual information, and context likelihood of relatedness (CLR), which use discrete input (25, 26); Spearman correlation, which uses continuous input that is nonlinear and monotonic; and Pearson correlation, which uses continuous input that is linear and monotonic. Among these methods, only Bayesian network analysis estimates causality (upstream-downstream–type relationships), which is done by scoring the degree to which fluctuations in signal values for putative upstream nodes are transmitted to putative downstream nodes in a nonrandom fashion. Moreover, only Bayesian network analysis quantifies higher-order parent-child relationships (in our implementation, up to three parents influencing one child node). All four other methods only quantify pairwise relationships.

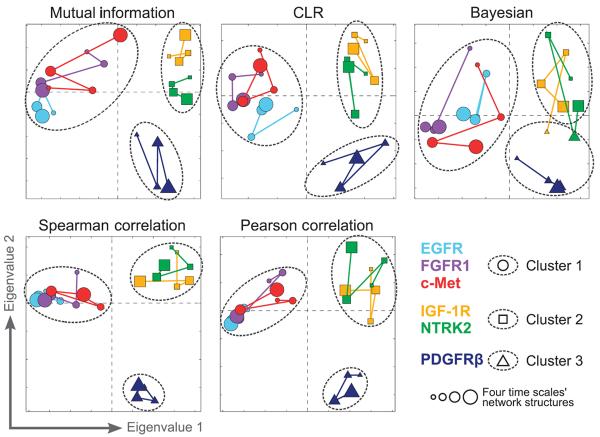
We applied each of these five methods to the 24 different data subsets across the six RTKs and four time scales, yielding 24 different network states per method. To visualize differences in the inferred network structures across RTKs and time scales, adjacency matrices describing the topology of the inferred networks were analyzed using multidimensional scaling (MDS) (27) (Fig. 3). Remarkably, the five inference methods consistently revealed three distinct RTK classes: an EGFR/FGFR1/c-Met class, an IGF-1R/NTRK2 class, and a PDGFRβ class, regardless of the time scale. These three RTK classes were robust because they were maintained across a wide range of thresholds used to define the presence or absence of edges in the network models (fig. S4).

Fig. 3. Clustering RTK-specific network models reveals three RTK classes.

Connectivities of RTK signaling networks were derived from large-scale signaling data using five different network inference algorithms. Relationships between RTK-specific networks were visualized in two dimensions using MDS. Marker color denotes receptor cell line. Marker size denotes the four time scales from basal (0 min; smallest markers) to late (32 to 256 min; largest markers). Marker shape and dashed outlines represent k-means clustering assignments.

Because of the limited availability of highly selective antibodies, we only measured one phosphosite for each receptor. Because these sites may have different biological functions, we repeated the network inference procedure while excluding the receptor phosphosite data. The same network classes were identified (fig. S5), indicating that the identified three network classes are not sensitive to the specific receptor phosphosites that we measured on the arrays.

Consensus across inference methods reveals RTK class–specific signaling

To determine which relationships (edges) accounted for the differences in network topology across the three observed RTK classes, we developed a consensus network for each RTK using the 20 networks that resulted from applying all five inference methods to data from all four time scales. We then compared these RTK-specific consensus networks to identify edges consistently observed within one, two, or all three RTK classes (see Materials and Methods, fig. S6). For example, the c-Cbl–CaM (calmodulin) edge appeared in 17, 17, 16, 0, 0, and 2 networks for the EGFR, FGFR1, c-Met, IGF-1R, NTRK2, and PDGFRβ receptors, respectively. Hence, the c-Cbl–CaM edge was considered to be specific to the EGFR/FGFR1/c-Met class but absent from the IGF-1R/NTRK2 and PDGFRβ classes. Because variation in network structure arose primarily from different RTKs rather than different time scales, this consensus approach highlighted RTK class–specific relationships conserved across most time scales.

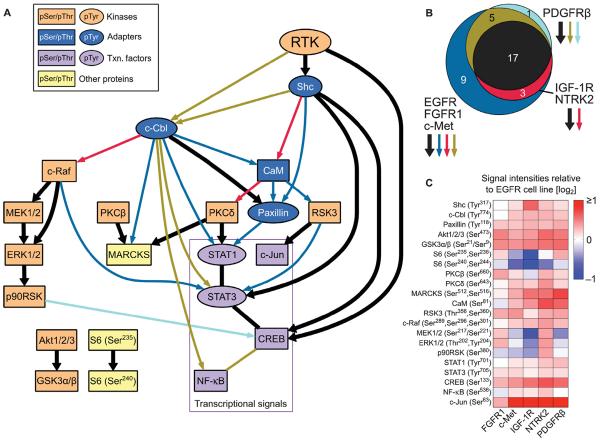
The consensus network analysis revealed an RTK signaling core shared by all six RTKs, along with sets of RTK class–specific edges (Fig. 4A). The IGF-1R/NTRK2 and PDGFRβ networks both contained fewer edges than the EGFR/FGFR1/c-Met network; all edges in the IGF-1R/NTRK2 network and all except one edge in the PDGFRβ network were also present in the EGFR/FGFR1/c-Met network (Fig. 4B). This indicates that, among the measured phosphosites, the EGFR/FGFR1/c-Met network has a greater number of highly correlated signal-signal relationships compared to the sparser IGF-1R/NTRK2 and PDGFRβ networks. In biological terms, this may correspond to a greater degree of coordination in activating downstream proteins (for example, by receptor-proximal scaffolding proteins). As found with the direct analysis of shRNA-induced effects, the shared RTK backbone (black edges in Fig. 4A) identified through our network inference approach contained the conserved MAPK, Akt, and PKC pathways, as well as various other conserved directional edges. Most of the RTK class–specific edges resulted from class-specific changes in the phosphorylation status of c-Cbl, Shc, paxillin, and CaM, suggesting that these receptor-proximal signaling events may play a central role in mediating RTK class–specific responses.

Fig. 4. A consensus model for the six RTKs reveals a core signaling backbone and RTK class-specific interactions.

(A) RTK backbone edges (relationships) are shown in thick black lines, whereas class-specific relationships are colored and correspond to (B). Nodes are colored according to their approximate biological function, and tyrosine- and serine/threonine-containing phosphorylation epitopes are shown as ovals and boxes, respectively (noted in insert; Txn, transcription). (B) Venn diagram showing shared and class-specific edges across the three RTK classes. All IGF-1R/NTRK2 edges and all but one of the PDGFRβ edges are present in the EGFR/FGFR1/c-Met network. (C) Median signal values (across all time points, shRNA conditions, and biological replicates) for each phosphosite in each cell line relative to the EGFR cell line.

Some nodes in the RTK class network models had no inputs and thus had no directed path from the activated, phosphorylated receptor (RTK in Fig. 4A) to the node. This can occur across all RTKs (for example, Akt had no inputs in any of the RTK class models) or within an RTK class (for example, the MAPK cascade beginning with c-Raf had no inputs in the PDGFRβ class network but had c-Cbl as an input in the other RTK classes' networks). Lack of an input does not necessarily imply that the node is not regulated or not phosphorylated in the class-specific RTK network that lacks the relationship. For example, the median phosphorylation signal of c-Raf in the PDGFRβ cell line was similar or higher than those in the other cell lines (Fig. 4C). Instead, nodes lacking inputs for some or all RTK classes are likely under the influence of unmeasured signals (termed hidden nodes) or under the influence of measured signals, but in a complex way that was not captured in the inferred network.

To determine whether clustering the raw data directly could recapitulate the network classes, the raw data were clustered using (i) median signal values across all time points (fig. S7A), (ii) signal values from all time points (fig. S7B), (iii) signal values from each time scale (fig. S7C), or (iv) signal values from each time point (fig. S7D). Data from all shRNA perturbations were used in each case. The three inferred network classes were recapitulated using the raw data in only 2 of 16 clustering scenarios (late time scale and 256 min). The IGF-1R/NTRK2 class was recapitulated when the data from the basal state (time 0) or 2-min data were clustered (fig. S7, C and D). The EGFR/FGFR1/c-Met class was recapitulated when the 4-min data were clustered (fig. S7D). That all five network inference methods highlighted the same three RTK classes, but clustering of the raw data generally did not, suggests that inferred network topologies contain information not accessible by clustering the raw data directly.

To explore this notion further, we generated synthetic data from networks with four different predefined topologies (fig. S8A, see Materials and Methods). We simulated five sample data sets per network (fig. S8B) and then attempted to classify the resulting 20 data sets according to their underlying network using either the raw data or the network topologies inferred from the raw data (fig. S8C). The inferred topologies clearly segregated according to their underlying network, whereas the raw data did not. This further supports the notion that inferred network topologies, in which relationships between measured signals are explicitly quantified, provide insight into the multivariate structures underlying raw data beyond what can be observed by clustering the raw data directly. This strengthens our case for using the inferred RTK network classes as relevant indicators of signaling network differences among the six RTKs.

Given that the six cell lines differ predominantly by a single variable—the identity of the expressed RTK—we speculate that it may be receptor-intrinsic biophysical properties causing the RTKs to group into the three identified network classes. To this end, we compared the sequences of the six RTKs' cytoplasmic and kinase domains. We also compared previously published data about kinase inhibitors' binding affinities for these receptors (28), hypothesizing that using small molecule binding profiles as a proxy for kinase substrate specificity may provide an explanation for the observed RTK classes. None of these three properties, however, produced clusters identical to the network models (fig. S9). The inhibitor profile clusters did match the kinase domain clusters, however, suggesting that the kinase domain sequence largely explains the RTKs' differential sensitivities to kinase inhibitors.

RTKs and ligands are coexpressed in cancer cell lines and enriched in certain solid tumor types

To determine the expression of the genes that encode the six RTKs and ligands used in this study in relevant cancer cell lines, we analyzed the Cancer Cell Line Encyclopedia (CCLE) data set, which includes mRNA expression values for ~19,000 genes in 967 cancer cell lines (29). We defined expressed genes as those with expression values exceeding five on an RMA (robust multichip average) scale because of the bimodal distribution of RMAvalues across all genes in the CCLE (fig. S10). EGFR, FGFR1, MET, and IGF1R were widely expressed (97, 96, 81, and 95% of cell lines, respectively), whereas PDGFRB and NTRK2 were only expressed in 23 and 4% of cell lines, respectively.

The degree of coexpression for RTK- and ligand-encoding gene pairs varied across the six RTKs (Fig. 5A). Because of the CCLE experimental design, gene expression represents that of the tumor cells and not of the stromal cells. Therefore, we used coexpression of the genes encoding receptor and ligand as an indicator of potential autocrine activation of these RTKs. The low coexpression of some receptors and the ligands used in our study may be because some receptors can be activated by multiple ligands. Including genes encoding additional ligands that can activate EGFR (30), FGFR1 (31), NTRK2 (32), and PDGFRβ (33) in the analysis revealed that most cell lines expressing an RTK gene also express at least one cognate ligand gene (Fig. 5B). As a first approximation, we assume that the signaling networks induced by these other family ligands would be similar to those induced by the ligands used in our study. For the other RTKs, c-Met is only known to be activated by HGF, and data for IGF2 (the gene encoding another ligand for IGF-1R) and NTF4 (the gene encoding another ligand for NTRK2) were not available in the CCLE.

Fig. 5. RTK and ligand expression in CCLE cell lines.

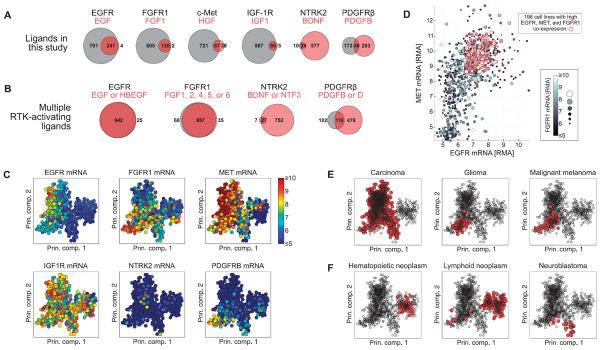
(A) Number of cell lines expressing a given receptor but no ligand (value displayed inside or to left of gray circle), a given ligand but no receptor (value displayed inside or to right of light red circle), or coexpressing receptor and ligand (value displayed inside dark red overlapping region) across 967 cell lines in the CCLE. (B) Including additional cognate ligands increases the number of cell lines in the CCLE that coexpress receptor and at least one ligand. (C) Gene expression values of the six RTKs displayed in principal component (Prin. comp.) space. Each circle represents a cell line, and the color represents the abundance of the indicated mRNA. (D) mRNA abundance expressed as RMA for EGFR (x axis), MET (y axis), and FGFR1 (gray scale) plotted against one another. Red circles indicate cell lines with greater than median expression of each of the three RTKs. (E and F) Tumor histologies enriched (E) or depleted (F) for coexpression of EGFR, FGFR1, and MET. Red markers indicate cell lines derived from the indicated tumor histology type. Significance of enrichment or depletion by hypergeometric test: P = 8.7 × 10⁻²⁶, P = 3.0 × 10⁻⁶, P = 1.9 × 10⁻³ for carcinoma, glioma, and melanoma, respectively (E); P = 2.0 × 10⁻³⁰, P = 1.7 × 10⁻²⁴, and P = 7.8 × 10⁻³ for hematopoietic neoplasm, lymphoid neoplasm, and neuroblastoma, respectively (F). The PCA results plotted in (C), (E), and (F) represent the first two components of the PCA coefficients, or loadings.

Some receptor- and ligand-encoding genes may exhibit low coexpression because these receptors are more commonly activated in a paracrine or endocrine manner; we would therefore not expect high receptor gene and ligand gene coexpression in tumor cells alone. For example, IGF-1R is often activated by IGF-1 secreted by the liver, and c-Met is often activated by HGF secreted from stromal cells (34) or activated in a ligand-independent manner (35). Nevertheless, the genes encoding the RTKs used in this study and those encoding one or more of their cognate ligands were coexpressed across many cell lines in the CCLE, and a similar extent of coexpression was detected using RMA thresholds from >4 to >6 (fig. S11).

To determine whether specific subsets of cancer cell lines coexpressed the genes encoding the RTKs analyzed in our study, we first used principal components analysis (PCA) to provide a two-dimensional visual representation of the data that segregated the cell lines according to global differences in their gene expression patterns (Fig. 5C). In this representation, principal components 1 and 2 (PC1 and PC2) explain 8.1 and 4.6% of the variance across cell lines, respectively, indicating that not all variation in the data is captured in these views. Nevertheless, it is clear from these images that the mRNAs for multiple RTKs were present and abundant in many cancer cell lines. Further, these data show that IGF1R is highly expressed in nearly all cell types; MET, FGFR1, and EGFR show the next broadest expression; and PDGFRB and NTRK2 are expressed in smaller subsets of cell lines.

Given that many cell lines coexpressed EGFR, FGFR1, and MET and given the similarities of the inferred EGFR, FGFR1, and c-Met networks, we sought to identify which tumor types coexpressed the genes encoding these three RTKs. Plotting the mRNA expression data of these three RTKs on the same axes indicated that in CCLE, there are 196 cell lines with high expression (exceeding median expression) for EGFR, FGFR1, and MET (Fig. 5D). Using information in the CCLE about the original tumor histology of each cell line, we calculated which tumor histologies had greater or less EGFR, FGFR1, and MET coexpression than that expected by chance. Carcinoma, glioma, and melanoma cell lines were significantly enriched for EGFR, FGFR1, and MET coexpression (Fig. 5E), whereas hematopoietic neoplasm, lymphoid neoplasm, and neuroblastoma showed a significant lack of coexpression of these RTKs (Fig. 5F). These results were robust to the RMA threshold used to define the coexpression signature (fig. S12), with the exception of the melanoma cell lines for which, at lower expression thresholds, there was significant coexpression, and at higher expression thresholds, there was significant lack of coexpression, suggesting that the three RTK-encoding genes were not all highly expressed in the same melanoma cell lines. Overall, these results indicate that specific patterns of RTK gene coexpression (for example, EGFR/FGFR1/MET) are overrepresented in certain tumor types.

RTK network class genes are correlated with responses to RTK-targeted therapies

Given these results, we hypothesized that preexisting coexpression of multiple RTK-encoding genes in the same network class mediates primary (intrinsic) resistance to RTK-targeted inhibitors. This redundancy in RTK networks may also contribute to the development of acquired resistance to RTK inhibition, through selection of subpopulations of cells with higher abundance of compensatory RTKs or feedback within the inhibited cells that increases the abundance of compensatory RTKs. To test our hypothesis, we used the CCLE data set to assess whether the abundance of RTKs or their ligands correlates with resistance to therapies targeting RTKs in the same class. For example, we predicted that resistance to EGFR inhibitors may be mediated more effectively by FGFR1 and c-Met than by IGF-1R, NTRK2, or PDGFRβ, and thus, the abundance of FGFR1 or c-Met was more likely to correlate with resistance than was the abundance of RTKs in the other classes.

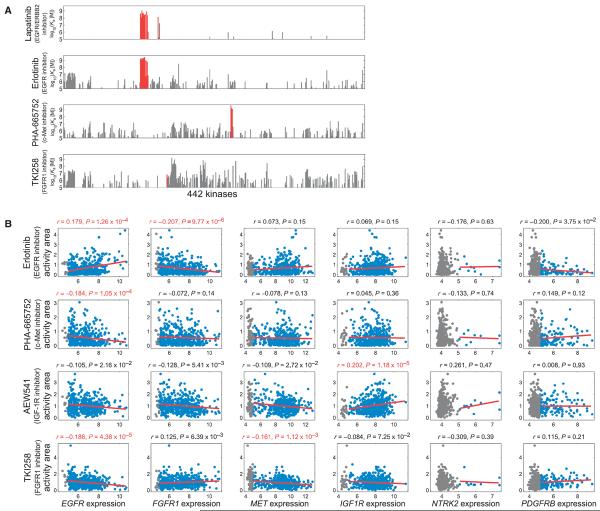
In addition to gene expression data, the CCLE contains cell growth inhibition data across ~500 cell lines for 24 anticancer compounds, including erlotinib (an EGFR inhibitor), TKI258 (an inhibitor of several kinases, including FGFR1), PHA-665752 (a c-Met inhibitor), and AEW541 (an IGF-1R inhibitor). There are caveats associated with using the CCLE data to assess drug resistance mechanisms. The off-target effects of the kinase inhibitor may complicate interpretation of these resistance profiles (28). Plotting the affinity of each drug for 442 kinases in the human genome showed that erlotinib, PHA-665752, and TKI258 were likely to have many off-target effects compared to, for example, lapatinib, which inhibits the EGFR family member HER2 (also known as ErbB2) more selectively (Fig. 6A). These off-target effects may induce resistance mechanisms that act in concert with the resistance mechanisms for each compound's primary target(s). Regarding TKI258, it binds 18 kinases with greater affinity than it binds FGFR1; however, many of these other genes were poorly expressed in the CCLE cell lines, with the exception of TBK1 (TANK binding kinase 1), MAP4K4 (mitogen-activated protein kinase kinase kinase kinase 4), and IRAK1 (interleukin-1 receptor–associated kinase 1) (fig. S13). A second caveat is that receptors and their ligands are not always coexpressed, as noted in Fig. 5, so ligand-mediated receptor activation is less likely for some receptors.

Fig. 6. RTK expression correlates with decreased sensitivity to same-class RTK-directed drugs.

(A) Affinity and specificity of kinase inhibitors lapatinib, erlotinib, PHA-665752, and TKI258 for 442 kinases [data from (28)]. On-target effects are shown in red. (B) Correlating RTK gene expression with responses to EGFR, FGFR1, c-Met, and IGF-1R inhibitors across hun dreds of cancer cell lines. Cell lines with RMA expression values >5 or <5 are shown in blue or gray, respectively. Red lines indicate linear fits to the data. Values above subplots are Spearman correlation coefficients and P values, shown in red for genes that significantly correlated (1% FDR) with drug response.

With these caveats in mind, we quantified the relationship between gene expression and cellular response to erlotinib, TKI258, PHA-665752, or AEW541 by calculating the Spearman correlation coefficient between each gene's expression values and the activity area for that drug in each drug-treated cell line. Activity area is a metric for growth inhibition: Greater activity area implies greater growth inhibition and thus increased sensitivity to the drug. Gene expression values that positively correlate with activity area thus denote sensitivity to the drug, whereas negative correlations denote resistance. This correlation analysis captures how the quantitative magnitude of gene expression influences drug sensitivity, rather than only considering the effect of the presence or absence of an RTK.

As anticipated, we found that EGFR and IGF1R expression correlates with sensitivity to EGFR and IGF-1R inhibitors, respectively. Consistent with our hypothesis that resistance to an inhibitor targeting an RTK of one class may be mediated more effectively by another RTK of the same class, EGFR expression correlated with resistance to inhibitors targeting c-Met and FGFR1, FGFR1 expression correlated with resistance to the inhibitor targeting EGFR, and MET expression correlated with resistance to the inhibitor targeting FGFR1. In contrast, NTRK2 and PDGFRB expression was not significantly correlated with responses to any of those four inhibitors (Fig. 6B). Among the six cognate ligands, the expression of BDNF (which encodes the ligand for NTRK2) correlated with resistance to the inhibitor targeting IGF-1R (an RTK of the same class). The expression of IGF1, however, correlated with resistance to the inhibitor targeting EGFR, an RTK of a different class, and none of the other ligands (EGF, FGF1, HGF, and PDGFB) significantly correlated with responses to any of the four inhibitors (Fig. 7).

Fig. 7. Relationships between ligand gene expression and response to RTK-directed drugs.

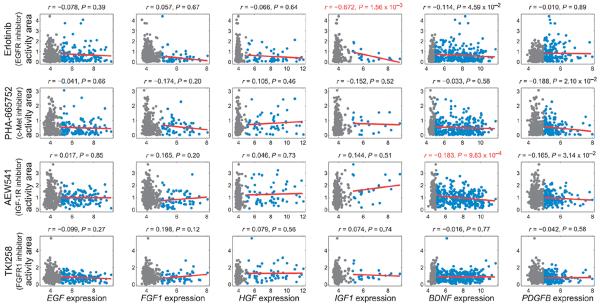
Correlations between ligand gene expression and responses to EGFR, FGFR1, c-Met, or IGF-1R inhibitors were determined across hundreds of cancer cell lines. Cell lines with RMA expression values >5 or <5 are shown in blue or gray, respectively. Red lines indicate linear fits to the data. Values above subplots are Spearman correlation coefficients and P values, shown in red for genes that significantly correlated (1% FDR) with drug response.

Our analyses were designed to consider the relationship between gene expression and drug response only among cell lines that expressed a gene of interest. The above correlations (Figs. 6B and 7) were computed using the threshold RMA >5 to define expressed genes. Because we cannot determine a priori the RMA level at which a gene should be considered “expressed,” we recalculated the correlation between gene expression and drug response using a range of alternative RMA thresholds (>0, 4, 4.5, 5.5, and 6) for both receptors and ligands (fig. S14). All of the drug-receptor gene expression correlations that were detected using a threshold of >5 were also detected at lower thresholds (RMA >0, 4, and 4.5), whereas only the erlotinib-EGFR and AEW541-IGF1R correlations were observed at higher thresholds (RMA >5.5 and 6). Additionally, at low thresholds, MET expression correlated with resistance to the c-Met inhibitor (RMA >0 and 4), and PDGFRB expression correlated with resistance to EGFR inhibitor (RMA >0, 4, and 4.5). Compared to the RMA >5 threshold, additional ligand-drug correlations were detected at lower thresholds, although the AEW541-BDNF correlation was maintained at all low thresholds (RMA >0, 4, and 4.5), and no ligand gene expression significantly correlated with drug responses for RMA >5.5 or >6.

It is likely that fewer significant correlations were detected at higher RMA thresholds because not all genes are highly expressed across many cell lines. This was especially true for the ligand-encoding genes, several of which are weakly expressed compared to the receptor-encoding genes. It is also possible that the highest RMA thresholds (>5.5 and 6) are too stringent, excluding cell lines from the gene expression–drug response correlation calculation that nevertheless contain biologically meaningful information. Conversely, it is possible that the lowest RMA thresholds (>0, 4, and 4.5) are too permissive, allowing cell lines to be included in the correlation calculation that do not express a given gene at biologically meaningful levels.

Thus, despite the caveats associated with our analysis of the CCLE data, the RMA >5 threshold revealed several cases in which same-class RTK-encoding expression correlated with resistance (EGFR with the c-Met or FGFR1 inhibitors, FGFR1 with the EGFR inhibitor, METwith the FGFR1 inhibitor, and BDNF with the IGF-1R inhibitor), and only one case in which expression of a ligand of a different class correlated with resistance (IGF1 with the EGFR inhibitor). This supports the notion that coexpression of same-class RTKs may contribute to resistance to RTK-targeted therapies.

DISCUSSION

Here, we integrated pathway-level phosphorylation measurements using lysate microarray technology after systematic RNAi perturbations with computational network inference to quantify signaling network specificity across six RTKs. The shRNA perturbations revealed a core set of Akt, MAPK, and PKC pathways conserved across all six RTKs, which were recapitulated in RTK-specific network inference models, along with additional RTK-specific signaling relationships. The six RTK network models clustered into three classes: EGFR/FGFR1/c-Met, IGF-1R/NTRK2, and PDGFRβ. Using gene expression data from the CCLE, we showed coexpression of RTK and ligand pairs across many cancer cell lines, along with enrichment for EGFR, FGFR1, and MET coexpression in carcinoma, glioma, and malignant melanoma cell types. Using corresponding anticancer drug response data from the CCLE, we found evidence for same-class RTK- or ligand-mediated resistance mechanisms prevailing over resistance mechanisms mediated by RTKs or ligands from different classes. We propose that RTKs within the same network class are more capable of promoting resistance to therapies targeting RTKs in that class than are RTKs in a different class.

There is extensive literature evidence consistent with the notion of intraclass drug resistance mechanisms among the six RTKs studied here. The most comprehensive evidence comes from two recent studies that measured the ability of different growth factors to rescue cells from various RTK inhibitors (7, 8). Harbinski et al. (7) observed that (i) EGF family ligands and FGF family ligands rescue c-Met–dependent cell lines from c-Met inhibition; (ii) EGF family ligands and HGF rescue FGFR2- and FGFR3-amplified cell lines from FGFR inhibition; and (iii) synergistic growth inhibition was observed in response to combined FGFR1 and c-Met inhibition both in vitro and in vivo. Wilson et al. (8) observed that (i) FGF2 (FGF-basic) and HGF each partially rescue EGFR mutant cell lines from erlotinib-induced cytotoxicity; (ii) EGF, NRG1 (neuregulin 1), and FGF2 each partially rescue MET-amplified cell lines from cytotoxicity induced by crizotinib, a c-Met inhibitor; and (iii) EGF, NRG1, and HGF each partially rescue FGFR-amplified cell lines from FGFR inhibition. In Wilson's study, PDGF-AB ligand did not rescue any cell line from any drug, and IGF-1 only partially rescued 3 of the 41 tested cancer cell lines from any drug. Although our study used PDGF-BB and FGF1 (FGF-acidic) ligands, these results nonetheless indicate that the rescue potential of growth factors mimics the RTK classes extracted from our network models: HGF and ligands of the EGF or FGF families have generally similar rescue potential across cell types, whereas IGF-1 and PDGF family ligands have sparse to nonexistent rescue potential among the inhibitors tested by Harbinski et al. and Wilson et al.

The link between EGFR and c-Met is well established: c-Met can compensate after anti-EGFR therapy (4); conversely, EGFR can compensate after anti–c-Met therapy (5, 36). Additional evidence linking FGFR1 and EGFR signaling also exists. Combining EGFR and FGFR family kinase inhibitors has been shown to exhibit additive (37) or synergistic (38) growth inhibition, and combining dominant-negative forms of both EGFR and FGFR1 resulted in synergistic increases in cell death (38). Additionally, FGFR1/FGF2 autocrine signaling has been observed in non–small cell lung cancer (NSCLC) cell lines that do not respond to gefitinib (39), and the induction of FGFR2 and FGFR3 expression has been observed in response to gefitinib in gefitinib-sensitive NSCLC and head and neck squamous cell carcinoma cell lines (40).

There is also evidence for resistance to EGFR inhibitors by the EGFR inhibitor–induced derepression of IGF-1R signaling (41); however, IGF-1R compensates poorly for EGFR loss because IGF-1R only strongly maintains activation of the Akt pathway, whereas c-Met activates both the Akt and the MAPK pathways (4). Consistent with these reports, IGF-1R had the lowest median phosphorylation of MEK, ERK, and p90RSK among the six RTKs in our study, whereas c-Met exhibited similar activity to EGFR (Fig. 4C). These observations are consistent with the weak rescue potential of IGF-1 noted above. All non-EGFR cell lines exhibited comparable phosphorylation of Akt and GSK3 and were actually higher than that observed in the EGFR cell line, suggesting that activation of Akt is not a distinguishing feature among these six RTKs, at least in the context of saturating doses of growth factor in our isogenic system.

The evidence is less clear for therapies against IGF-1R, NTRK2, and PDGFRb, in part because there are fewer studies of targeted therapies against these RTKs. EGFR is cited as a reason for primary, but not acquired, resistance to anti-IGF-1R therapy (42), whereas others suggest that the insulin receptor is the primary driver of resistance to anti-IGF-1R therapy (43). Resistance to anti-PDGFRβ therapy (in the form of imatinib, which targets Abl, c-Kit, and PDGFRα/β) seems to involve mutations of the targeted proteins and amplification of Src family kinases, rather than compensation by other RTKs (44). To our knowledge, no studies have addressed resistance to any anti-NTRK2 therapies; our results, however, suggest that IGF-1R signaling may compensate after NTRK2 inhibition.

In addition to RTK network phenocopying, there may be other mechanisms mediating coactivation of particular RTKs, especially chromosomal structure processes (45). Notably, EGFR and MET are both present on chromosome 7, and all genes on chromosome 7 are significantly amplified in sets of glioma and lung tumors (46). Further, MET is located at a fragile site on chromosome 7, which makes it prone to amplification (47). Literature evidence that other RTKs are present at fragile sites was not found. Thus, amplification of MET may be an especially prevalent mechanism for resistance to EGFR inhibitors because not only does c-Met phenocopy the EGFR/FGFR1 network, it is also prone to co-amplification with EGFR.

Although RTKs of the same class have similar network models and are capable of inducing resistance to inhibition of other RTKs in that class, these same-class RTKs are not fully redundant. Simply inspecting the RTK-specific shRNA effects shows that, although there were similarities, the effects of downstream protein knockdown across RTKs of the same class were not identical (figs. S1 and S2). Further, it may be that if we observed or perturbed different or additional signaling nodes beyond those studied here, we would see that the network models of RTKs within the same class diverge from one another. Thus, although the network models we developed here are sufficient to classify drug resistance patterns, the similarity of same-class RTKs is a relative concept.

The evidence for the importance of RTK network phenocopying in drug resistance is strong, but the exact mechanism enabling this behavior is unclear. Some previous work has explored the notion that receptor recruitment interactions define specificity in receptor-activated signaling. Using chimeric EGF and insulin receptors, early work showed that RTK cytoplasmic domains encode kinase specificity, mitogenic and transforming potential, and receptor routing (48). Others have shown in yeast that kinase domains encode limited intrinsic discriminatory specificity and that the functional identity of a kinase is instead largely determined by its recruitment interactions (49). These observations are consistent with our results showing that RTK-proximal signaling relationships in the network models tended to be RTK-specific, whereas downstream relationships tended to be conserved across all RTKs. Thus, although we are not certain how these three RTK clusters emerged, it was unlikely to be driven purely by their kinase specificity and instead was likely to emerge from specificity in receptor-proximal protein recruitment.

In conclusion, the RTK signaling classes identified in this study are consistent with clinically observed mechanisms of resistance to targeted therapies in cancer. The limited efficacy of single-agent RTK-directed therapies may therefore result in part from preexisting coexpression of same-class RTKs across a diverse spectrum of tumor types. In this scenario, these tumors are primed to compensate for the loss of RTK function after therapy. We submit that classifying RTKs by their inferred networks and then therapeutically targeting same-class receptors, either in combination or sequentially, may provide clinical benefit by delaying or preventing the onset of resistance.

MATERIALS AND METHODS

Cell culture

Isogenic human embryonic kidney (HEK) 293 cells expressing EGFR, FGFR1, IGF-1R, c-Met, NTRK2, or PDGFRβ were described previously (13). All cell lines were cultured in Dulbecco's modified Eagle's medium (DMEM; Mediatech) supplemented with 10% fetal bovine serum (HyClone), 2 mM glutamine, penicillin (100 IU/ml), and streptomycin (100 μg/ml) (Mediatech), and hygromycin B (150 μg/ml) (Invitrogen).

Lentiviral shRNA expression vectors were produced with a three plasmid system as described previously (14, 50). Briefly, HEK293T cells were cotransfected with plasmid pLKO.1 containing the shRNA expression cassette of interest, as well as packaging plasmids pCMV-dR8.91 (containing HIV gag, pol, and rev genes) and pMD2.G [coding for VSVG (vesicular stomatitis virus glycoprotein) envelope protein]. Medium was replaced after 24 hours with medium supplemented with 1% (w/v) bovine serum albumin (BSA), and viral supernatants were harvested 48 and 72 hours after transfection. Viral stocks were centrifuged and decanted to remove cellular debris, and stored in aliquots at −80°C. Relative virus titers were determined by transducing A549 lung carcinoma cells at low multiplicity of infection (MOI), selecting for viral integrants with puromycin (Invitrogen), and measuring relative cell densities by resazurin viability assay. Viral pools were generated by mixing equal volumes of the titer-normalized component viruses. The total viral titer of each pool thus matched the average titer of the component viruses. A complete list of all 76 individual shRNA constructs used in this study is given in table S1, and a list of all 12 shRNA pools used in this study is given in table S2.

For gene knockdown experiments, RTK-expressing HEK293 cells were first plated onto D-lysine–coated 96-well plates (BD Biosciences) at a density of 20,000 cells/cm². After 24 hours, medium was replaced with medium containing lentiviral particles and polybrene (10 μg/ml) (Sigma-Aldrich), and plates were centrifuged at 1178g for 30 min at 37°C for enhanced infection efficiency. The average MOI for the individually tested shRNAs was about 10 integrants per cell, whereas the average MOI for the pools ranged from about 1 to 5 integrants per cell per shRNA component of the pool. Thus, for the shRNA pool infections, most cells received one or more integrants of each constituent shRNA, although it should be noted that the two pools with more than three shRNAs may have greater variability between cells in the number of RNAi perturbations introduced. For single and pooled shRNAs targeting signaling proteins, cells were infected in biological quadruplicates per cell line and time point. Cells were also treated in parallel with nontargeting shRNA vectors (control shRNAs) shGFP49 (shRNA ID TRCN0000072192; 8 replicates), shGFP477 (shRNA ID TRCN0000072201; 8 replicates), or pLKO.1 empty vector (TRCN0000204879; 4 replicates). Twenty-four hours after infection, medium was replaced with medium containing puromycin (1.5 μg/ml) (Invitrogen) to select for virally infected cells. We observed complete cell death of mock-infected cultures within 24 hours of selection, and no cell death was detectable in any virally infected cultures. Ninety-six hours after infection, at 70 to 80% confluency, cells were washed once with phosphate-buffered saline (PBS) and incubated in serum-free medium for an additional 24 hours. To initiate RTK signaling, cells were stimulated with the cognate ligand of each RTK: EGF (EGFR), FGF1/FGF-acidic (FGFR1), IGF-1 (IGF-1R), HGF (c-Met), BDNF (NTRK2), and PDGF-BB (PDGFRβ) (PeproTech). After 1, 2, 4, 8, 16, 32, 64, 96, 128, or 256 min, cells were washed with ice-cold PBS and lysed in 2% SDS buffer as described previously (51, 52). Lysates of cells not treated with RTK ligands served as the “0” time point. Cell ly-sates were cleared by filtration through 0.2-μm filter plates (Pall Corporation) and stored at −80°C until microarraying.

Microarray fabrication

Custom lysate microarrays were printed by Aushon Biosystems on 11.5-cm × 7.5-cm single-pad nitrocellulose-coated glass slides. Slides were custom-manufactured and were a gift from Grace Bio-Labs. Lysates were arrayed at a spot-to-spot spacing of 400 μm using eight depositions with solid 110-μm pins, which resulted in an average feature diameter of 180 μm when visualizing spot protein content. Each lysate in our experiment, including lysates of cells treated with control shRNAs and lysates of mock-infected cells, was initially spotted once on each microarray slide. A small number of microarray source plates were then reprinted onto the same slides in cases where spots were missed because of instrument errors, as assessed visually under a microscope. Each microarray ultimately contained a total of 26,496 microarray features, 25,344 of which represented biologically unique lysates. After microarray printing, slides were stored dry, in the dark, and at room temperature until further processing.

Microarray probing

To remove the buffer and detergent contained in each microarray spot, slides were washed three times for 5 min each with 1× PBS/0.1% Tween 20 (PBST), incubated in tris-HCl (pH 9) for 72 hours with daily replenishment, washed again with PBST, and centrifuged dry. Slides were then blocked with 5% BSA/PBST for 1 hour at 4°C. Microarrays were incubated in a pool of 1:1000 anti–β-actin antibody (Sigma-Aldrich) and 1:1000 phosphospecific antibody (table S3) in 5% BSA/PBSTat 4°C for 24 hours. After washing, slides were incubated in a pool of 1:1000 680-nm dye-labeled anti-rabbit and 1:1000 800-nm dye-labeled anti-mouse antibodies (LI-COR) in 5% BSA/PBST for 24 hours at 4°C. Slides were washed again three times for 5 min each with 1× PBSTand centrifuged dry. Microarrays were scanned in the 680- and 800-nm channels using the Odyssey Imaging System (LI-COR) at 21-μm resolution.

Extraction of microarray data

Slides were visually inspected, and initial feature finding and spot centering were performed with the Array-Pro software package (Media Cybernetics). Spots with morphological defects, notably spots of noncircular shape, spots affected by lint or scratches, and spots overlapping with neighboring spots, were manually flagged and excluded from our data set. We then used custom-built code for MATLAB 7.4 (MathWorks) to refine the positioning of the circular areas over which the Array-Pro software would integrate the microarray spots to derive signal intensities. Signal intensities from both target proteins and β-actin were then integrated accordingly, and target protein signals were normalized to their respective β-actin signal intensities to account for any differences in lysate concentration or spotting. Normalized signal was used in all subsequent data analysis steps.

Data preprocessing

To remove data outliers that were not detected by visual inspection of the microarrays, a smoothing window approach was applied. For a time point t_i within a time course from a particular phosphosite, RTK cell line, and shRNA condition, the data from the three time points t_i–1, t_i, and t_i+1 across all biological replicates were grouped together in a vector X. An upper bound was defined as Q3(X) + 1.5IQR(X), and a lower bound was defined as Q1(X) − 1.5IQR(X), where IQR(X) is the interquartile range of X, and Q1(X) and Q3(X) are the first and third quartile of X, respectively. Any data replicates at time t_i that were above the upper bound or below the lower bound were flagged. This procedure was applied to time points sequentially, starting with the first time point in each time series. When applied to the first time point in each time series, only the first and second time points were used. When applied to the last time point in each time series, only the penultimate and last time points were used. This time window approach allowed us to take advantage of the temporal dependence of the data, because phosphorylation values at adjacent time points were expected to be approximately similar. Data for a given time point could only be flagged by smoothing if there were at least three replicate data points initially present in the vector X.

In total, less than 2.1% (11,644 of 564,960) of all collected data points were flagged either because of poor spot morphology or using the smoothing window approach. After flagging outliers, the flagged data point(s) at t_i (for a given RTK, phosphosite, and shRNA condition) was replaced with the mean value of the remaining data replicates at time t_i.

Each test shRNA had four biological replicates associated with each RTK, phosphosite, and time point. Because a small number of microarray source plates were printed more than once onto each slide, additional technical replicates were available in some instances. In addition, several control shRNAs had 8 or 12 biological replicates associated with each RTK, phosphosite, and time point. In these cases, every fourth replicate was averaged together to condense the replicates into only four replicates per shRNA, RTK, phosphosite, and time point. For example, if there were 12 replicate data points, they would be condensed into four data points based on the following scheme: {1, 5, 9}, {2, 6, 10}, {3, 7, 11}, and {4, 8, 12}. This condensing step was done after any individual replicate was replaced in the flagging step. The processed replicate data for all RTKs, phosphosites, time points, and shRNA conditions are available in table S4.

Quantifying the consistency of biological replicates and shRNA pairs

To quantify the consistency across biological replicate measurements for each phosphosite in each RTK cell line, the CV across the four biological replicates at each time point (across 11 time points) in each shRNA time course (across 91 shRNA conditions) was calculated, producing 91 × 11 = 1001 CV values. For each of the six RTKs and 22 phosphosites, the median of those 1001 values is shown in Fig. 2B.

To quantify the consistency in signaling network responses across pairs of shRNAs directed at the same gene, we compared the median phosphorylation signal values (calculated across the four biological replicates) across all phosphosites and all time points for each pair of shRNAs targeting one of the 38 unique genes. Thus, for each shRNA pair, the Pearson correlation coefficient between two vectors, each containing 22 phosphosites × 11 time points = 242 median data values, was calculated. These correlation values across the six RTKs and 38 unique genes are shown in Fig. 2C.

Quantifying shRNA effects

To quantify shRNA-induced effects on measured signals, AUC values were compared between time courses of test shRNAs (shRNAs targeting signaling proteins) and control shRNAs (pLKO.1empty, shGFP477, and shGFP49). We first assembled four time series vectors for each phosphosite, RTK cell line, and shRNA by randomly assigning each of the four replicate measurements at each time point into one of the four time series vectors. We then calculated the four AUC values associated with each of the time series by the trapezoidal method (using the “trapz” function in MATLAB R2009a), accounting for the nonuniform intervals between time points in the time series. Thus, each replicate time series was represented by a single AUC value.

For each test shRNA, we then compared its four AUC values to the four AUC values of each of the three control shRNAs in turn. Using a two-tailed, two-sample t test assuming equal sample variances, this yields P values P_pLKO, P_GFP477, and P_GFP49. Performing this procedure on all 88 test shRNAs, 22 phosphosites, and six RTKs generated three lists of 11,616 P values. Using each list of P values separately, we used the Storey method (53) to determine significance levels for each of the three control shRNAs. At a 1% FDR, the significance levels were calculated to be α_pLKO = 0.02871, α_GFP477 = 0.01625, and α_GFP49 = 0.02515.

shRNA-induced effects on measured phosphosites were considered significant only if all three P values were below the FDR-corrected levels of significance (that is, P_pLKO < α_pLKO, P_GFP477 < α_GFP477, and P_GFP49 < α_GFP49), and if the shRNA-induced change in AUC value was either an increase over all three control shRNAs or a decrease over all three control shRNAs. To impose additional stringency, only instances where a measured signal was significantly affected (as defined above) by both shRNAs targeting each gene are shown in Fig. 2D. Using the alternative Benjamini method (54) to calculate levels of significance, we obtained α_pLKO = 0.00399, α_GFP477 = 0.00315, and α_GFP49 = 0.00377.

Simulations of shRNA effects

Simulations to determine whether the observed pattern of shRNA-induced effects was consistent with a model of random distribution across RTKs or across phosphosites were performed by first computing the total number of significantly decreased and increased signal effects across the six RTKs, 22 phosphosites, and 88 test shRNAs [11,616 cases in total: 1346 (11.6%) decreased and 1232 (10.6%) increased] using the 1% Storey FDR method as described above, with the exception that we did not require that the same significant effect be observed for both test shRNAs for a gene of interest. Next, these same numbers of increased and decreased signals were randomly distributed in silico among the 11,616 total RTK-phosphositeshRNA combinations. We then tallied the total number of RTKs (0 to 6) or phosphosites (0 to 22) exhibiting a signal effect for each phosphosite-shRNA pair or RTK-shRNA, respectively, to assess shRNA effect distribution across the cell lines or phosphosites, respectively. This simulation was repeated for 2500 different random assignments of the signal effects.

To corroborate the simulation, we then derived analytical estimates of the expected distribution of shRNA-induced effects across RTKs and across phosphosites when assuming a random hypergeometric distribution (using the “hygepdf” function in MATLAB R2009a). For the distribution across RTKs, we assumed drawings of 6 of 11,616 samples at a time, and for the distribution across phosphosites, we assumed drawings of 22 of 11,616 samples at a time, where, again, the samples represented the 11,616 possible RTK-phosphosite-shRNA combinations.

The significance of this comparison was measured using a χ² goodness-of-fit test. In the tests, we compared the number of increases or decreases in signal observed across zero to six RTKs with that expected by chance. In both cases, the distribution of observed effects was significantly different than the distribution of random effects (P = 0, using 3 degrees of freedom given seven bins and three parameters in the hypergeometric distribution). Similarly, we compared the number of observed increases or decreases in signal observed across 0 to 22 phosphosites with that expected by chance. In both cases, the distribution of observed effects was significantly different than the distribution of random effects (P = 0, using 19 degrees of freedom given 23 bins and three parameters in the hypergeometric distribution).

Identifying signaling time scales

To facilitate analysis of dynamic changes in signaling network structure, we wished to aggregate the 11 time points in our data set into broader time scales representing “basal,” “early,” “intermediate,” and “late” signaling events. The data at time zero were taken to represent the basal network state. To determine which of the remaining 10 time points in our data set corresponded to early, intermediate, and late time scales, we subjected our data to k-means clustering (k = 3) in MATLAB using the squared Euclidean distance metric and 200 replicates of each cluster assignment (using the “kmeans” function). For each time point, data were first compiled across all six RTKs, 22 phosphosites, 91 shRNAs (88 test shRNAs + 3 control shRNAs), and four biological replicates into a vector of 6 × 22 × 91 × 4 = 48,048 data points. The input for the clustering algorithm consisted of a matrix of 10 time points × 48,048 data points. This pan-RTK approach identified time scales that were indicative of signaling dynamics across all RTKs.

Data discretization

The Bayesian network, mutual information, and CLR algorithms we used in our study require discrete data as their input. Because our experimental phosphorylation data were continuous in nature, we discretized all time course data into four levels, with 1 indicating the lowest phosphorylation values and 4 indicating the highest phosphorylation values. To further increase data robustness, the median data value was calculated across the biological replicates at each time point (for each RTK, phosphosite, and shRNA condition), following the previously described data preprocessing step. The median data were subsequently discretized. For each phosphosite, data were discretized separately for each RTK and time scale. Within each data subset (for a particular phosphosite, RTK, and time scale), the z scores of the raw data were calculated. Those data points with z > 4 were set to discrete value 4. Those data points with z < −4 were set to discrete value 1. The remaining data points were discretized according to four-level k-means clustering in MATLAB using the squared Euclidean distance metric and 100 replicates of each cluster assignment (using the kmeans function). The ordinality of the discrete data was always maintained, such that 1 and 4 consistently represented the low and high raw signal values, respectively. The discrete data for all RTKs, phosphosites, and shRNA conditions are available in table S5.

Network inference algorithms

The core Bayesian network inference algorithm was implemented as previously described (55), using a modified version of the Bayesian network structure learning toolbox in MATLAB R2009a (56) based on the algorithm of Koivisto and Sood (24). Here, the equivalent sample size (ESS) in the Dirichlet parameter prior was varied for each time scale to help normalize for varying sample size across time scales. ESS values of 20, 1, 1, and 3.4 × 10⁻⁴ were used for the basal, early, intermediate, and late time scales, respectively. shRNA perturbations were modeled as perfect interventions. That is, when a measured phosphosite (for example, PKCβ Ser⁶⁶⁰) was present on the protein product of a transcript targeted by an individual shRNA (PKCB) or shRNA pool (PKC pool), then these phosphosite data were considered to be under the influence of that shRNA intervention. In such cases, the discrete data were not modified from their previously determined values, but the network scoring function was modified to take the intervention into account.

It should be noted that the c-Raf signal (inclusive of Ser²⁸⁹, Ser²⁹⁶, Ser³⁰¹) was considered to be under the influence of not only the CRAF shRNAs and the RAF shRNA pool but also the ARAF and BRAF shRNAs, because ARAF and BRAF shRNAs significantly decreased the c-Raf (Ser²⁸⁹, Ser²⁹⁶, Ser³⁰¹) signal for all six RTKs (1% Storey FDR) and even significantly decreased the c-Raf (Ser²⁸⁹, Ser²⁹⁶, Ser³⁰¹) signal for four of the six RTKs using the more conservative 1% Benjamini FDR. This suggests that the c-Raf (Ser²⁸⁹, Ser²⁹⁶, Ser³⁰¹) antibody detected phosphorylation of the A-Raf and B-Raf isoforms, so we considered the c-Raf (Ser²⁸⁹, Ser²⁹⁶, Ser³⁰¹) signal to be under the influence of ARAF, BRAF, CRAF, and RAF pool shRNAs.

Previous knowledge was used to restrict viable Bayesian network structures. RTK phosphosites were not allowed to have any parent nodes (meaning, no incoming edges), and transcription factor sites [c-Jun, NF-kB (nuclear factor kB), STAT1 (signal transducer and activator of transcription 1), and STAT3] were not allowed to have any child nodes (meaning, no outgoing edges), except if those child nodes were other transcription factor sites. Nodes were restricted to a maximum of three parents. That is, when computing the posterior edge probabilities, consensus networks containing all possible one-, two-, and three-parent node-node interactions were considered. Higher-order parent-child relationships, beyond three-parent interactions, were not considered.

The directionality of the edges (Fig. 4) was based on the consensus directionality observed in the 24 Bayesian networks inferred across the six RTKs and four time scales, along with the previous knowledge assumptions. Because the RTK phosphosite was assumed in the prior knowledge to be a root node, all nodes connected to it were required to be child nodes. Similarly, because the phosphosites on transcription factors were required to have no children nodes, except for other transcription factor phosphosites, all nodes connected to transcription factor sites were required to be parents of the transcription factor nodes. Edges inferred between transcription factor phosphosites were left undirected, under the assumption that an edge between two transcription factors likely represented mutual coordination by an unmeasured node(s), rather than the action of one phosphosite on another. The edges from the CaM phosphosite were the most uncertain in the consensus directionality analysis. Hence, the directions of these three edges (to PKC, paxillin, and RSK3) are least confident.

CLR was implemented in MATLAB R2009a using code provided by Faith et al., with z scores (edge weights) calculated using the “plos” method (26). The mutual information matrix was calculated using a simple histogram method within the CLR code. Spearman and Pearson correlation networks were calculated using the median data (median across the biological replicates) and the “corr” function in MATLAB R2009a. For the CLR, mutual information, Spearman, and Pearson networks, all 22 measured phosphosites were used as input for the algorithms. Because of algorithmic memory constraints, we were able to use only 20 of the 22 measured phosphosites [p-S6 (Ser²⁴⁰, Ser²⁴⁴) and p-CREB (Ser¹³³) were left out] for Bayesian network inference. However, the same discretized data for the 20 nodes in the Bayesian network inference were used for those 20 of 22 nodes present in the other algorithms.

Comparison of RTKs' inferred network structures using dimensionality reduction

To compare inferred network structures across RTKs, MDS was used as a dimensionality reduction technique. To enable comparisons across different network inference methods, first, each network structure's adjacency matrix was converted into a binary vector describing the presence or absence of each edge. For each network inference method, pairwise distances between all 24 networks' binary vectors were calculated using the “pdist” function in MATLAB with the Jaccard distance metric, which considers binary features, but it does not consider cases where two observations (networks) both have a value of zero (are both missing a particular edge). The Jaccard distance matrices were then used as input for classical MDS using the “cmdscale” function in MATLAB. If the Euclidean distance metric were used instead of the Jaccard distance metric, then the MDS procedure would be identical to PCA.

All of the resultant MDS eigenvalue features were then clustered using k-means clustering (k = 3) to identify groups of similar network structures. For all four network inference methods, clustering was performed in MATLAB using the squared Euclidean distance metric and 200 replicates of each cluster assignment (using the kmeans function).

For the Bayesian networks, the MDS input networks had an edge weight threshold of >0.1 applied. For the CLR and mutual information (MI) networks, the MDS input networks had an edge weight threshold of z > 1 and MI > 0.3 applied, respectively. For the Spearman and Pearson correlation networks, the 60th percentile of the absolute value of the correlation coefficients was calculated across the 24 correlation networks, corresponding to |correlation coefficient| >0.35 and |correlation coefficient| >0.30, respectively. For the Bayesian networks, the adjacency matrix vectors contained 400 directed edge features (although self-edges were not allowed by the algorithm). For the four undirected network inference methods, the adjacency matrix vectors contained 231 undirected edge features (again excluding self-edges).

Network model edge weight threshold robustness

To determine the robustness of the network model clusters (EGFR/FGFR1/ c-Met, IGF-1R/NTRK2, and PDGFRβ) to the edge weight threshold applied to each network inference method's result, the edge weight threshold was varied over a range of values and then clustering was repeated at each value. The range was based on the 10th to 90th percentile of the edge weight values, at 10-percentile increments. For the case of Spearman and Pearson correlations, the percentile was calculated using the absolute values of the correlation coefficients. The other three inference methods (mutual information, CLR, and Bayesian) have strictly nonnegative edge weights, so no absolute value was needed. For the Bayesian network edge weights, to increase the dynamic range of the sensitivity analysis, edge weights <0.02 and >0.98 were removed before calculating the 10-percentile increments, because, by the algorithm's design, most of the resultant edge weights are near zero and several are unity.

Generating receptor class–specific consensus networks across inference methods

The frequency of each edge in the five inference methods and four time scales was calculated for each RTK. The same edge thresholds used for the dimensionality reduction results shown in Fig. 3 were applied. To directly compare the five inference methods, the Bayesian networks were converted to an undirected form. Further, because the Bayesian networks included only 20 of 22 measured nodes, whereas the four other inference methods contained all 22 nodes, edges were normalized to the total number of instances they were considered across the five inference methods (4 time scales × 5 inference methods = 20, versus 4 time scales × 4 inference methods = 16 for the edges connecting nodes excluded from the Bayesian networks). This provided a scale between 0 and 1 for each edge, representing that edge's frequency within a particular RTK across four or five inference methods and four time scales.

To generate class-specific networks, it was required that an edge appeared with a frequency ≥0.5 for each RTK within an RTK set and ≤0.25 for each RTK outside the RTK set. RTK sets included (i) each individual RTK class, (ii) two of the three RTK classes, and (iii) all three RTK classes. Pan-RTK backbone edges were required to have a frequency ≥0.5 across all six RTKs.

Clustering the raw data

When clustering the median signal values, first, each signal's median value was calculated across all biological replicates, shRNA perturbations, and time points. This gave an indication of the typical magnitude of phosphorylation for each phosphosite in each RTK cell line. The resulting matrix of 22 phosphosites by six RTKs was then mean-centered and unit variance–scaled across each phosphosite. This matrix was then clustered in MATLAB using k = 3 and 100 replicates with random initial centroid assignments.

When clustering signals from all time points together, data matrices representing the data for each RTK and all 22 phosphosites were first constructed (representing a matrix with 22 rows and 11 time points × 91 shRNAs × 4 biological replicates = 4004 columns). The data were then mean-centered and unit variance–scaled for each signal separately (across rows). This process was repeated for all six RTKs. These normalized matrices were then converted into vectors to form a new matrix of six rows (one per RTK) and 22 × 4004 = 88,088 columns. This matrix was then clustered using the “kmeans” function in MATLAB as described above.

A similar approach was taken to cluster signals from each time scale and signals from each time point. In each case, signals from the relevant time point(s) were first mean-centered and unit variance–scaled for each RTK separately, and then the resultant matrices were converted to vectors and compiled into a multi-RTK matrix. This matrix was then clustered using the kmeans function in MATLAB as described above.

Generating synthetic data for network inference

Directed acyclic networks were randomly generated, allowing only one parent node per child node and containing only one root node (source signal). The signal values for the root node were 200 points randomly sampled from a uniform distribution between values 1 and 6. The signal values for all downstream nodes were specified on the basis of the signal value of its input parent node, namely, y_output = y_input.

Data were simulated in a stepwise fashion, such that the only input to the simulation process was the signal values of the root node. Then, at each step in the simulation from parent to child node, heritable variation was added to each node's data. This variation was drawn from a random normal distribution with mean zero and a 10% CV. This variation-added signal was then used as input for the node's child node in the network. Heritable variation was also added to the terminal nodes in the network, even though they have no child nodes. Once all nodes were simulated, then nonheritable variation was added to the simulated data. This variation was drawn from a uniform distribution over the range ± 1, and this variation was added independently for each node.

As an example, in the simple case of a two-node network A→B, the 200 signal values for A are drawn from a uniform distribution, and then those values have random normally distributed heritable variation added to them. The subsequent values, A′, are then used as input for node B. The values of node B are then based directly on its input node, so the values for B are equal to A′. Then, random normally distributed heritable variation is added, creating B′. After the simulation, random uniformly distributed noise is added independently to both A′ and B′, creating A″ and B″, which are the final output from the simulation. To generate the results in fig. S8, four synthetic networks were generated, each containing 22 nodes. This is the same number of nodes measured in our experimental signaling data. For each network, five independent data sets were simulated. Because the input values and heritable and nonheritable variation are all stochastic, this generated five different data sets per network.

To analyze the data by PCA, for each of the 20 data sets, the matrix of 22 nodes × 200 conditions was converted into a vector, providing a final input matrix for PCA of 20 data sets × 4400 data points. In the case of the normalized raw data, data for each node were first mean-centered and unit variance–scaled before putting the data set into vector format. Spearman correlation was used to represent inferred network topologies. For the binary case, a threshold of the 60th percentile correlation value (>0.8198) was used (the same correlation percentile used in Fig. 3). The percentile was calculated on the basis of the correlation values across all 20 data sets. PCA was used for the raw data, normalized raw data, and continuous correlation values, whereas MDS was used for the binary correlation values.

CCLE mRNA expression PCA

CCLE mRNA data were downloaded at the CCLE Web site (http://www.broadinstitute.org/ccle) from the file CCLE_Expression_Entrez_2012-04-06.gct. The data were analyzed using PCA (“princomp” function) in MATLAB. The input matrix for this function was 18,926 genes' RMA gene expression values in 967 cell lines. The matrix was entered such that the genes were considered “observations” and the cell lines were considered “variables.” Before PCA was applied, the gene expression values were mean-centered and unit variance–scaled for each gene across all cell lines. Cell lines with greater than median expression of EGFR, MET, and FGFR1 were used to define “high” expression as shown in Fig. 5D (RMA >6.53, >8.63, and >6.88, respectively).

Tumor histology enrichment and depletion

Enrichment and depletion of EGFR, FGFR1, and MET mRNA coexpression, in particular tumor histologies, were assessed using the information provided by Barretina et al. (29) in 967 cell lines and quantified using the hypergeometric test (“hygepdf” function) in MATLAB R2009a. First, coexpression of EGFR, FGFR1, and MET was determined given a particular RMA threshold defining expressed genes. Next, it was determined if cell lines originally derived from tumors of particular histologies exhibited EGFR, FGFR1, and MET coexpression either more or less often than expected by chance, given the total number of cell lines coexpressing these genes, the total number of cell lines of each histology, and the overlap of the two sets. The probability of observing as many or more cases of overlap (N) between EGFR/FGFR1/MET coexpressing cells and cells of a given histology was obtained by summing the probability density function from the number of cell lines with overlap N to the total number of cell lines. Conversely, the probability of observing as many or fewer cases of overlap N was obtained by summing the probability density function from zero cases to N cases. Cell lines with histology “other” or with no histology information provided were not considered for enrichment. For each RMA threshold and each histology type, the lower P value between enrichment versus depletion was selected. Given the 20 histologies and 11 tested RMA thresholds, this provided a list of 20 × 11 = 220 P values. Applying the Benjamini method with a 5% FDR to this list of P values denoted all P < 0.0191 to be significant.

Correlating gene expression and drug activity area

Pharmacological profiling data were downloaded at the CCLE Web site (http://www.broadinstitute.org/ccle) from the file CCLE_NP24.2009_profiling_2012.02.20.csv. Spearman correlation was calculated between gene expression values and drug activity area. The six RTKs and six cognate ligands used in this study were considered together for multiple hypothesis correction. That is, at each RMA threshold, the Spearman correlation and associated P values were calculated across the 12 genes (six RTKs and six ligands) and four drugs, providing 48 P values. These P values were then corrected for a 1% FDR using the Benjamini method. The 1% FDR significance levels for the >0, 4, 4.5, 5, 5.5, and 6 RMA thresholds were P < 5.93 × 10⁻³, 3.72 × 10⁻³, 5.93 × 10⁻³, 5.41 × 10⁻³, 3.76 × 10⁻³, and 2.80 × 10⁻³, respectively. At each respective RMA threshold, all enrichment or depletion observations with P values below these levels were considered significant. Cell lines with values of zero for the measured activity area were not included in the correlation calculations because there was no indication of how insensitive a cell line with zero activity area may be to a drug.

Comparison of receptor-intrinsic properties using dimensionality reduction

To compare different receptor-specific intrinsic properties, MDS and PCA were used as dimensionality reduction techniques. We extracted K_d (dissociation constant) values describing the affinities between 72 kinase inhibitor drugs and our six RTKs from Davis et al. (28). Of the 72 inhibitors, 61 bound to at least one RTK with K_d < 10 μM. The K_d values were converted to log₁₀(K_a) values, and, to ensure that inhibitor-receptor interactions not reported by Davis et al. (because they either were not detected in an initial 10-μM screen or had K_d > 10 μM) would not numerically dominate the clustering results, those interactions were set to log₁₀(K_a) = 3. That is, nonmeasurable or nonexistent interactions were set to have affinity K_d = 1 mM. This matrix of 6 RTKs × 61 inhibitor compounds was then used as input for PCA.

The amino acids constituting the cytoplasmic domains of the six RTKs were defined as follows: EGFR (amino acids 669 to 1210), FGFR1 (amino acids 398 to 822), IGF-1R (amino acids 960 to 1367), c-Met (amino acids 956 to 1390), NTRK2 (amino acids 455 to 822), and PDGFRβ (amino acids 557 to 1106). The amino acids constituting the kinase domains of the six RTKs were defined as follows: EGFR (amino acids 712 to 979), FGFR1 (amino acids 478 to 767), IGF-1R (amino acids 999 to 1274), c-Met (amino acids 1078 to 1345), NTRK2 (amino acids 538 to 807), and PDGFRβ (amino acids 600 to 962). For both the kinase and cytoplasmic domains, in each case, the domains were aligned across RTKs using the “multialign” function in MATLAB R2009a with the Gonnet scoring matrix. Pairwise distances between all aligned sequences were then calculated using the “seqpdist” function in MATLAB R2009a, also using the Gonnet scoring matrix. This distance matrix was then used as input for classical MDS using the “cmdscale” function in MATLAB R2009a.

For the kinase inhibitor data, kinase domain sequences, and cytoplasmic domain sequences, all five eigenvalues resulting from MDS were used for subsequent k-means clustering. For all receptor-intrinsic properties, k-means clustering was performed with the city block distance metric and 200 replicates of each cluster assignment.