Abstract
Partially clustered designs, where clustering occurs in some conditions and not others, are common in psychology, particularly in prevention and intervention trials. This paper reports results from a simulation comparing five approaches for analyzing partially clustered data, including Type I errors, parameter bias, efficiency, and power. Results indicate that multilevel models adapted for partially clustered data are relatively unbiased and efficient and consistently maintain the nominal Type I error rate when using appropriate degrees of freedom. To attain sufficient power in partially clustered designs, researchers should attend primarily to the number of clusters in the study. An illustration is provided using data from a partially clustered eating disorder prevention trial.
Keywords: Partially clustered data, multilevel models, intraclass correlation, intervention studies
Clustered designs are common in psychological research. A design can be considered clustered whenever there is nesting of one set of units within another, such as psychotherapy patients nested within therapy groups or students nested within classrooms. Clustered designs are often described as hierarchical and include at least two levels: (a) the cluster level and (b) the individual level, where individuals are nested within clusters. Ignoring the hierarchical nature of clustered designs can create critical problems for inferences about the effects of predictors. In this paper, we discuss a specific type of clustered design, namely designs that are partially clustered (Bauer, Sterba, & Hallfors, 2008).
It is important to differentiate between fully and partially clustered designs. In a fully clustered design, clustering occurs in all study conditions. Examples include school-based research where each student is clustered within a school, or studies comparing group-administered interventions. In contrast, in partially clustered designs some study conditions involve clustering and others do not. For instance, a study might compare married individuals (clustered within dyads) to single individuals (unclustered), or individuals working on a task with others (clustered within teams) versus individuals working on a task alone (unclustered). Partially clustered designs are also common in intervention research. One example is the comparison of individual therapy versus bibliotherapy. In the individual therapy condition, patients are clustered within therapists. In the bibliotherapy condition, patients are unclustered as they do not interact with a therapist. Another example is a trial comparing a group-administered treatment (participants clustered within groups) to no treatment (participants unclustered).
Partially clustered designs characteristically give rise to two sets of participants—those who are clustered within groups and those who are not. In some cases, fully clustered designs can produce superficially similar data, wherein some individuals are the sole members of their clusters. For example, if a researcher sampled families and then collected data on all siblings, there would be some families with only one child. Conceptually, however, only children can still be regarded as clustered within the family. That is, the observations made on only children will still contain unique variance associated with the family as well as unique variance associated with the child, even if we cannot statistically separate these two variance components based on the observations of only children alone. The variance structure for all observations is parallel. In contrast, in partially clustered designs the variance structure is not parallel because the cluster effect only affects the clustered condition(s). It is not theoretically sensible to estimate cluster-level variance for unclustered participants.
Clustered data of any kind complicate statistical analyses. In particular, it is critical to account for clustering to maintain the nominal Type I error rate (α = .05) for the fixed effects (e.g., the intervention effect). If the observations within clusters are incorrectly assumed to be uncorrelated (i.e., independent), the probability of a Type I error usually increases, which is especially true for between-cluster effects (Crits-Christoph & Mintz, 1991; Kenny & Judd, 1986; Kenny, Kashy, & Bolger, 1998; Murray, 1998; Wampold & Serlin, 2000). In partially clustered designs, it is often reasonable to assume that observations in the unclustered condition are independent. However, in the clustered condition, observations will often be correlated, meaning that individuals within a cluster are more similar to one another than individuals from different clusters.
For example, consider a study where therapy groups are the cluster. Because group members interact with one another throughout the course of the intervention, group members’ observations can be correlated (Baldwin, Stice, & Rohde, 2008; Herzog et al., 2002; Imel, Baldwin, Bonus, & Macoon, 2008). These within-cluster correlations could arise from a number of sources within the group including degree of cohesion, attendance patterns, attrition, the presence of a domineering group member, skill of the group leader, and degree of engagement in the treatment. Within-cluster correlations are not limited to group-administered interventions, but can also occur when participants interact with the same therapist (Crits-Christoph et al., 1991; Wampold & Serlin, 2000) or in school-based interventions where students are clustered within schools, classrooms, or teachers (Nye, Konstantopoulos, & Hedges, 2004). In addition to being important for Type I error rates, within-cluster correlations may also be substantively interesting because they may reflect group, therapist, or teacher effects (e.g., Imel et al., 2008; Nye et al., 2004; Wampold & Brown, 2005).
Very few studies that have used partially clustered designs have accounted for the clustering in their statistical analysis. Although methods for accounting for clustering in fully clustered designs in intervention trials have been discussed extensively (e.g., Baldwin, Murray, & Shadish, 2005; Baldwin et al., 2008; Crits-Christoph & Mintz, 1991; Martindale, 1978; Murray, 1998; Wampold & Serlin, 2000), partially clustered designs have received much less methodological attention. Consequently, researchers have not had adequate options for analyzing their partially clustered data. Five papers have documented methods for estimating intervention effects in partially clustered designs (Bauer et al., 2008; Hoover, 2002; Lee & Thompson, 2005; Myers, DiCecco, & Lorch, 1981; Roberts & Roberts, 2005). Myers et al. (1981) discussed a quasi-F test for accommodating partially clustered data and Hoover (2002) discussed an adjustment to an independent samples t-test. The other more recent methodological work has focused on multilevel (or mixed) models that provide researchers with a flexible approach for estimating intervention effects. Like this prior research, we shall focus especially on the estimation of intervention effects in partially nested designs, although the issues we describe are equally relevant to other effects in partially clustered designs.
The existing methodological work on analysis of partially clustered designs has five limitations. First, previous work has not thoroughly evaluated the performance of the various analysis approaches to partially clustered designs. Roberts and Roberts (2005) report a small simulation study that suggests that multilevel models may perform well, but their simulation was limited with respect to number of clusters, cluster size, and total sample size. Second, previous work has not evaluated different methods for computing degrees of freedom for the test of the intervention effect. Bauer et al. (2008) recommend using the Kenward and Roger’s (1997) adjustment for degrees of freedom, but acknowledge that the importance of this adjustment for partially clustered designs is unknown. Additionally, comparing methods for calculating degrees of freedom is important because some software programs only use one method for calculating degrees of freedom (e.g., HLM, SPSS) or use a z-distribution (e.g., Stata, Mplus) and without evidence regarding the performance of the degrees of freedom methods, researchers are likely to use the default degrees of freedom reported by their software of choice. Third, previous work has not evaluated analytic approaches that ignore clustering or that treat cluster as a fixed effect. Fourth, previous research has not evaluated whether the various analytic approaches are unbiased and efficient with respect to the intervention effect and variance components. Fifth, the discussion of power in partially clustered designs has been either limited to large sample formulae and has not addressed degrees of freedom (Moerbeek & Wong, 2008) or only briefly mentions power in small samples but does not provide data regarding power (Roberts & Roberts, 2005). Consequently, power for analyses that use appropriate degrees of freedom in finite samples has not been fully evaluated.
In this paper, we address each of the limitations of previous research directly. First, we evaluate the performance of multilevel models with respect to Type I error rates under a variety of realistic design situations—varying number of clusters, cluster size, magnitude of within-cluster correlation, and degree of heteroscedasticity. Second, we compare the performance of three methods for computing degrees of freedom for treatment effects in multilevel models—the “between and within” method, the Satterthwaite method, and the Kenward-Roger method. Third, we evaluate analytic approaches to partially clustered data that ignore clustering and that treat cluster as a fixed effect. Fourth, we evaluate the bias and efficiency of the analytic approaches with respect to the intervention effect and variance components. Fifth, we present data on power for tests of intervention effects in partially clustered designs that incorporate degrees of freedom for reasonable sample sizes. Finally, although not a limitation of previous work per se, the use of multilevel models for partially clustered data is rare outside of the methodological literature. Consequently, to increase the likelihood that researchers adopt these methods, we synthesize the existing methodological work on partially clustered designs and provide a substantive example using an existing data set including annotated SAS syntax for estimating intervention effects (see online supplemental material).
Approaches to Modeling Partially Clustered Data
Before presenting the simulation results, we introduce four models for analyzing partially clustered data: our preferred approach as well as three other approaches that are, in our view, less optimal. In particular, we consider the assumptions each model makes regarding the variance structure of the data. Specifying the variance structure correctly is critical for making inferences about cluster effects and for obtaining efficient and unbiased standard errors for the fixed effects (e.g., tests of intervention effects).
For instance, consider the case where one wishes to compare a group-administered treatment to an unclustered control condition. Let us represent the participant by i and cluster by j. Considering first just the unclustered participants, we might posit the following model:
| (1) |
where μ0 is the mean value of Y for the control condition, and e0i captures residual variation around the mean (and E(e0i) = 0). Next, we might represent the scores of the clustered participants as
| (2) |
where μ1 is mean value of Y for the treatment condition, uj captures cluster-level variation about the mean, and e1ij captures individual-level variation about the mean (and E(uj) = 0, E(e1ij) = 0). The intervention effect is μ1 − μ0.
Note that, due to the non-parallel nesting structure, there is one source of variation in Equation (1), person-to-person differences, whereas there are two sources of variation in Equation (2), cluster-to-cluster differences as well as person-to-person differences. The condition-specific variances are therefore:
| (3) |
| (4) |
where is the person-to-person variance in the unclustered condition, is the person-to-person variance in the clustered condition, and is the cluster-to-cluster variance. Dependence between observations exists only in the clustered condition, where the intraclass correlation (ρ) is implied to be
| (5) |
and can range from zero to one. The ρ within the unclustered condition is zero.
Let us now consider how well each modeling approach captures these characteristics of partially clustered data.
Ignoring Clustering
The most common approach to analyzing partially clustered data is to ignore the clusters and assume that all individuals are independent (Bauer et al., 2008). These models can take many forms—for example, ANCOVA, repeated measures ANOVA, growth curve models, or survival models. For the simple example given above, one such model might be
| (6) |
where the intervention is represented by a dummy variable, Xi (1 for the intervention condition and 0 for the comparison). The parameter β0 then represents μ0, and the parameter β1 represents the intervention effect, μ1 − μ0.
Note that this model, like others that ignore clustering, does not separate cluster-to-cluster variability from person-to-person variability. That is, the variance structure is implied to be
which is inconsistent with Equations (3) and (4). Although it may sometimes be true that the variance within the treatment and control conditions is equal, here the variance in the treatment condition is pooled into a single term reflecting only person-to-person variation. By implication, ρ is incorrectly assumed to be zero in both conditions. Consequently, standard errors for the fixed effects will be incorrect, usually elevating the Type I error rate for the test of the intervention effect. Moreover, because only person-to-person variance is specified, these models provide no insight into conceptually interesting clustering effects (e.g., the effects of groups, therapists, or classrooms).
Including Cluster as a Fixed Effect
A second approach to modeling partially clustered data is to include cluster as a fixed effect. Suppose that for our simple example the treated participants were divided among four clusters (e.g., group or therapist). Dependence due to cluster membership is accounted for by regressing the dependent variable on dummy variables representing each cluster and a dummy variable for the control condition. A fixed-effects model for this design is:
| (7) |
where Cluster1–Cluster4 are dummy variables representing membership in treatment clusters 1–4. The overall model intercept is not estimated so that we can estimate a coefficient for the control group and each cluster. The coefficients for Cluster1–Cluster4 correspond to cluster-specific means. The intervention effect can therefore be evaluated by performing a contrast of the combined mean of the treatment clusters with the mean for the control group. In our example, if an equal number of participants were in each treatment group, the contrast coefficients would be −1 for Control and .25 for Clusters 1–4. The significance test for the contrast provides a test of the intervention effect.
With this model, the between-cluster variance in Equation (4) is accounted for through differences among the cluster means, or the coefficients β1 through β4, leaving only person-to-person variability. This can be seen in the variance equations for the two conditions:
where J is the total number of groups in the clustered condition (for our example, J = 4), pj is the proportion of participants from the clustered condition within group j, and β̄ is the grand mean of the groups, computed as
In effect, the term βj − β̄ represents uj from Equation (2) and represents from Equation (4).
This approach mimics the correct variance structure for the two conditions when in Equations (3) and (4). Nevertheless, there are several disadvantages to absorbing cluster differences through fixed effects. First, cluster-to-cluster differences contribute to explained variance in the model, whereas the source of these differences is actually unknown. The Type I error rate for the test of the intervention effect is therefore only accurate when inferences are restricted to the specific clusters in the study (e.g., treatment groups 1 to 4; Serlin, Wampold, & Levin, 2003; Siemer & Joorman, 2003a, 2003b). In contrast, we generally seek to make inferences to the broader population of clusters (e.g., all possible treatment groups, not simply those in the study). For such inferences, the mean-square-error of the model, , fails to fully represent the unexplained variance, as cluster-to-cluster variance has been excluded. As with ignoring clustering, the consequence is that the test of the intervention effect will have a higher than desired Type I error rate.
Model Data as if Fully Clustered
A third approach to modeling partially clustered data is to conduct the analysis as if the design was fully clustered. Each participant in the unclustered condition is assigned a unique cluster ID (value for j) and considered to be the sole member of their cluster (i.e., a singleton). For instance, for our simple example, the Level-1 (i.e., individual level) equation for the model would be:
| (8) |
where Yij is the post-test value of the outcome for person i in cluster j, and “clusters” now include singletons from the control condition. Likewise, the coefficients β0j and β1j represent the intercept and intervention effect for cluster j. The Level-2 (i.e., cluster-level) equations specify how these coefficients vary across clusters:
| (9) |
| (10) |
Note that the intercept varies across clusters through the inclusion of the term u0j, permitting cluster-to-cluster variability in the outcome variable. The slope for the intervention effect is assumed to be constant. Finally, a combined model can be obtained by substituting Equations (9) and (10) into Equation (8):
| (11) |
Conventionally, it is assumed that the individual- and cluster-level residuals are independent and normally distributed:
| (12) |
| (13) |
With this model, γ00 represents μ0, γ00 + γ10 represents μ0 and γ10 is the intervention effect, μ1 − μ0. The variance structure is
| (14) |
| (15) |
Note that the variance of the outcome is equivalently decomposed into between- and within-cluster variance in both conditions. That is, the fully clustered model assumes that the variance in both conditions is due to differences among clusters and differences among individuals within clusters. This assumption is untenable in the unclustered condition as there cannot be variability due to clusters. The exclusively person-to-person variance that exists within the unclustered condition is thus artificially partitioned to conform to the between- and within-cluster components that exist within the clustered condition.
For both conditions, ρ is implied to be
| (16) |
A non-zero ρ for the unclustered condition is not theoretically plausible. Because each control “cluster” is a singleton, however, the non-zero ρ for unclustered participants is immaterial for estimation. Therefore, under the special circumstance that the variance within the two conditions is equal [as implied by Equations (14) and (15)], the fully nested model will produce accurate standard errors for fixed effects (e.g., intervention effect) and accurate estimates of the two variance components in Equation (4). It does not produce a direct estimate of the single variance in Equation (3), but this can be inferred by summing the two variance components. If, however, the variance is not equal across conditions, this model will not produce accurate standard errors for testing the fixed effects, as we will see in our simulation results.
Although it is conventional to do so, we need not assume that the Level 1 residual variance is constant across conditions in fully clustered models. If we modify the model to allow for heteroscedasticity across conditions, we arrive at the variance structure
| (17) |
| (18) |
Although this modified model retains the non-sensical decomposition of between- and within-cluster variance for the unclustered condition, it now conforms completely to the underlying variance structure of the data. The two variance components in Equation (18) equal the corresponding quantities in Equation (4). For the unclustered condition, however, interpretation of the variance components is not straightforward—the term does not represent the same quantity in Equation (17) as in Equation (3). In Equation (3), is the total variance within the unclustered condition. In contrast, in Equation (17), is what remains after subtracting from the total variance within this condition. In some cases, this artificial decomposition of variance in Equation (17) can be problematic. For instance, if the between-cluster variance is large, then for Equation (17) to hold the implied value of may approach zero or even be negative, resulting in computational problems or inadmissible estimates.
Adapt Multilevel Model to Partially Clustered Data
A fourth approach is to adapt the multilevel model to match the non-parallel data structure of partially clustered data (Bauer et al., 2008; Lee & Thompson, 2005; Roberts & Roberts, 2005). Each individual within the clustered condition is again considered to be the single member of his or her own cluster. The Level-1 (i.e., individual-level) equation for the adapted model is similar to the fully clustered model:
| (19) |
However, the Level-2 equations are altered to match the structure of the partially clustered data:
| (20) |
| (21) |
Here γ00 and γ10 are interpreted in the same way as in the fully clustered model. The term u1j allows for between-cluster variability in outcome levels solely within the intervention condition. Note that we did not include the cluster-level residual u0j for β0j because the control condition consists only of unclustered individuals, which makes it impossible (and non-sensical) to separate cluster- and individual-level variability. Because the parameterization of this model reflects the partial clustering of the data, we refer to this as the partially clustered model.
A combined model can be obtained by substituting Equations (20)–(21) into Equation (19):
| (22) |
The partially clustered model assumes that the individual- and cluster-level residuals are independent and normally distributed as:
| (23) |
| (24) |
where and are the variances of the individual- and cluster-level variances, respectively. The implied variance structure of the model is thus
| (25) |
| (26) |
which matches the variance structure in Equations (3) and (4) so long as the person-to-person variation is equal in magnitude across conditions. Alternatively, a heteroscedastic version of this model can be specified where
| (27) |
| (28) |
permitting differences in person-to-person variability across conditions and conforming exactly to Equations (3) and (4). The ρ for the clustered condition implied by either Equation (26) or (28) will equal the ρ in Equation (5) and ρ for the unclustered condition is appropriately implied to be zero by either Equation (25) or (27).
It is worth noting that the heteroscedastic partially clustered model and the heteroscedastic fully clustered model are likelihood equivalent. In both cases, three unique variance components are estimated, the total variance is permitted to differ across conditions, and the variance in the clustered condition is appropriately partitioned into between- and within-cluster components. The fully clustered model inappropriately partitions the variance in the unclustered condition, but this is of little consequence as the implied non-zero ρ does not come into play in estimation (as all “clusters” are singletons in this condition). The two models can therefore be considered alternative parmaterizations (though this is not the case for the homoscedastic versions of these models). We favor the partially clustered model, however, because all of the parameters are directly interpretable, the decomposition of variance is sensible for both clustered and unclustered conditions, and the partially clustered model is not vulnerable to estimation problems if the between-cluster variance is large.
In sum, the partially clustered model fully matches the structure of the data. It allows researchers to explore how both individuals and clusters are related to outcomes, it provides interpretable estimates of variance components, and it should produce accurate standard errors for fixed effect estimates. Little research has yet been done, however, to verify that partially clustered models maintain the nominal Type I error rate under circumstances likely to be encountered in intervention studies. Nor has the performance of the partially clustered model been compared to the three other analytic approaches described previously with respect to Type I errors or parameter bias and efficiency. We use simulation methods to speak to these issues, but first we discuss methods for determining degrees of freedom for tests of fixed effects in partially clustered designs.
Degrees of Freedom
In multilevel models test statistics for fixed effects estimates are only normally distributed in large samples; for small-sample inference an approximation using the t-distribution is preferable. Unfortunately, the degrees of freedom for the t-distribution are not clear, as is the case with partially clustered designs (Bauer et al., 2008). We evaluated three methods for computing degrees of freedom in multilevel models: (a) the between-within method, (b) the Satterthwaite (1946) approximation, and (c) the Kenward-Roger method (Kenward & Roger, 1997).1
The between-within method is based on a loose analogy to repeated measures ANOVA and separates the degrees of freedom into two parts—between-clusters degrees of freedom and within-clusters degrees of freedom. Effects of predictors that only vary between-clusters, such as an intervention effect, are assigned between-clusters degrees of freedom. Predictors that vary within-clusters, such as individual-level covariates, are assigned the within-clusters degrees of freedom. This method for computing degrees of freedom was used by Singer (1998) in her influential paper on fitting multilevel models using the MIXED procedure in SAS. The between-within method is, however, likely to provide a poor approximation for models fit to partially clustered data because it is not sensitive to the complexities of the data inherent in partially clustered designs. For example, the between-within method is not sensitive to the fact that partially clustered data have a complex variance structure. In contrast, both the Satterthwaite and Kenward-Roger methods can be expected to perform better, as the optimal degrees of freedom for the t-distribution for both methods explicitly take into account the variance structure of the data. In each case, a method of moments approach is taken to arrive at the degrees of freedom that produce the best approximation to the test distribution, based on information available from the sample. The Kenward-Roger method first inflates the variance-covariance matrix of the fixed and random effects to correct for small sample bias and uncertainty. Satterthwaite degrees of freedom are available in SAS and are the only degrees of freedom currently provided by the SPSS MIXED procedure. Kenward-Roger degrees of freedom are available in SAS.
Performance of Models for Partially Clustered Designs
We used Monte Carlo simulations to evaluate the models described above. Monte Carlo simulations can be contrasted with typical data analyses (Morgan-Lopez & Fals-Stewart, 2008). In typical data analyses, we estimate parameters (i.e., treatment effects) using data collected from participants. However, the true value of any parameter is unknown and we never know exactly how close our sample estimate is to the actual population value. In contrast, in Monte Carlo studies, we estimate parameters using many simulated datasets where the true value of the population parameter is known. Thus, we can determine whether sample results are close to the population value. Common uses of Monte Carlo simulations include investigating bias in parameter estimates (whether the models consistently under- or over-estimate the population parameter), determining whether models maintain the desired Type I error rate, and determining statistical power.
Simulation Design
Data were generated to simulate a partially clustered intervention study including both a clustered (Xij = 1) and unclustered (Xij = 0) condition (cf. Roberts & Roberts, 2005). The intervention effect was set to zero and the total variance in the outcome within the clustered condition was set to one. Data in the clustered condition were thus generated according to the following model:
| (29) |
where
| (30) |
| (31) |
The data in the unclustered condition were generated according to the following model:
| (32) |
where
and θ is the ratio of the residual variance in the unclustered condition to the clustered condition:
| (33) |
When θ = 1 there is a common residual variance across conditions, .
We chose values for the simulation parameters that reflect partially clustered studies reported in the literature. We set the number of clusters (c) equal to 2, 4, 8, or 16. Cluster size (m) was set to 5, 15, or 30. We focused on relatively small cluster sizes because those will be most common in partially clustered designs. Cluster size in fully clustered designs reported in the literature vary from small (2 or 3) to large (300+). In contrast, most partially clustered studies that we have been able to locate typically use relatively small clusters (30 or less). We suspect that this occurs because when large clusters are used in a study, the unit of assignment to condition is typically clusters (e.g., assigning communities to intervention versus control). It would be unusual to assign several communities to an intervention and compare those communities to an unclustered group of individuals. In contrast, when clusters are small, the unit of assignment is sometimes clusters and sometimes individuals. When the unit of assignment is individuals, clustering is usually introduced by the intervention (e.g., participants are placed in therapy groups). When clustering is introduced by the intervention, it is often logical to use a comparison condition that does not involving clustering. The sample size in the unclustered condition (n) was equal to c × m.
We set ρ to be 0, .05, .1, .15, or .30, which represents the range of ρ’s observed in the intervention literature (cf. Baldwin et al., 2008; Bauer et al., 2008; Crits-Christoph et al., 1991; Herzog et al., 2002; Imel et al., 2008; Kim, Wampold, & Bolt, 2006; Lutz, Leon, Martinovich, Lyons, & Stiles, 2007; Wampold & Brown, 2005). Including a ρ = 0 condition allowed us to examine the performance of the models when the data are actually independent in the clustered condition (i.e., clustering is superfluous). Because relatively few ρ’s have been reported, it is difficult to say where in the range of 0 to .30 most ρ’s will fall, though we suspect that most will fall at or below .15.
Finally, it is noteworthy that the clustered and unclustered conditions have unequal variances because the clustered condition includes the between-cluster variance. There may be additional heteroscedasticity because the residual variances differ across conditions (e.g., interventions may decrease or increase within-cluster variability). To explore the impact of heteroscedascitity of the residual variances, we set the ratio of the residual variance in the unclustered condition to the clustered condition (θ) equal to .5, 1, or 2. The total difference between the condition-specific variances is largest when θ = .5 and smallest when θ = 2. Thus, models that assume equal variances across conditions should perform worst when θ = .5. Almost no information regarding the ratio of residual variances in clustered and unclustered conditions has been reported. However, we believe that most studies will fall within our range of θ values.
For each combination of c, m, ρ, and θ we generated and analyzed 10,000 samples of data. We chose 10,000 replications to minimize the standard error of our simulation estimates (e.g., the Type I error rate). After generating the data, we estimated treatment effects with five models: (a) an ANOVA that ignored clusters, (b) the fixed effects approach described above, (c) the homoscedastic fully clustered model, (d) the homoscedastic partially clustered model, and (e) the heteroscedastic partially clustered model. We estimated but do not report detailed results for the heteroscedastic fully clustered model because it is likelihood equivalent to the heteroscedastic partially clustered model and thus the results are generally redundant. The only difference in the results for the heteroscedastic fully clustered model was its poor convergence rate (problems in up to 20.3% of replications).
Additionally, for the multilevel models, we used three methods for calculating degrees of freedom: (a) the between-within method, (b) the Satterthwaite method, and (c) the Kenward-Roger method. The Satterthwaite and Kenward-Roger results were virtually identical. Consequently, we only report the Satterthwaite results to conserve space. For each combination of θ and analysis type we present the Type I error rate, which is equal to the proportion of significant intervention effects across the replications, as well as the bias and variability of the estimates of the treatment effect and of the cluster variance. Bias was defined as the difference between the average estimate for a given parameter across the replications and the population value. Variability in estimates was indexed with the mean squared error (MSE), which is defined as the average squared deviation between an estimate of a given parameter and the population value. To quantify the effect of the variables in the simulation on Type I error rate, bias, and variability of the estimates, we estimated an ANOVA model with error rate, bias, or variability as the outcome and the simulation variables as the factors. Because effect sizes for the interactions (two-way and above) were small, we report effect sizes (η2) for main effects only. Data were generated and models were fit using SAS 9.2. The multilevel models were estimated with restricted maximum likelihood (REML) estimation.
Type I Errors
ANOVA and Fixed Effects
Table 1 presents summary information about Type I errors across the simulation conditions. Type I error rates were roughly equivalent for the fixed effects models as compared to ANOVA and neither performed well. For both the ANOVA and fixed effect models, the magnitude of ρ had the largest effect on Type I error rate (η2 = .55) followed by m (η2 = .25). When ρ was 0 both models maintained the nominal Type I error rate across values of c and m. However, when ρ was .05 or greater, Type I error rates were inflated. The inflation was relatively small when m and ρ were small. However, Type I error rates increased as ρ increased and as m increased. These variables are important because as both increase the variance in clustered condition increases by a factor of 1+(m − 1)ρ (also know as the variance inflation factor or design effect; Donner, Birkett, & Buck, 1981). In order to maintain the Type I error rate, this additional variance needs to be included in the standard error of the intervention effect. Because the ANOVA model ignores clusters, the additional variance is not included. Although fixed effects models explicitly include a cluster variance, they do not perform well because the additional variance in the clustered condition is incorrectly treated as “explained” variance and removed form the mean-squared-error used to test the intervention effect. Mean differences between the intervention clusters and control condition that are due to cluster sampling variability may then appear to be statistically significant (Zucker, 1990).
Table 1.
Monte Carlo Type I Error Rates for Partially Clustered Designs
| θ = .5 | θ = 1 | θ = 2 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Range | Mean | SD | Range | Mean | SD | Range | |
| ANOVA | .18 | .13 | .05 – .50 | .15 | .11 | .05 – .46 | .13 | .09 | .05 – .38 |
| Fixed Effects | .19 | .14 | .05 – .53 | .17 | .12 | .05 – .48 | .13 | .10 | .05 – .40 |
| Fully Clustered Models | |||||||||
| Between-Within Homoscedastic | .11 | .07 | .03 – . 36 | .08 | .04 | .03 – .25 | .03 | .01 | .01 – .07 |
| Satterthwaite Homoscedastic | .11 | .07 | .04 – .33 | .07 | .03 | .03 – .18 | .02 | .01 | .01 – .06 |
| Partially Clustered Models | |||||||||
| Between-Within Homoscedastic | .07 | .04 | .03 – .23 | .07 | .03 | .03 – .21 | .07 | .03 | .03 – .19 |
| Satterthwaite Homoscedastic | .05 | .02 | .03 – .12 | .05 | .02 | .03 – .12 | .06 | .01 | .04 – .12 |
| Between-Within Heteroscedastic | .07 | .04 | .03 – .23 | .07 | .03 | .03 – .21 | .06 | .03 | .03 – .18 |
| Satterthwaite Heteroscedastic | .05 | .02 | .03 – .12 | .05 | .02 | .03 – .12 | .05 | .01 | .03 – .12 |
Both the ANOVA and fixed effects approaches assumed equal variance across conditions. Consequently, Type I error rates were highest when heteroscedasticity was largest (i.e., θ = .5; η2 = .03). This occurred in the ANOVA analyses because both cluster variability and extra residual variability in the clustered condition are ignored and some of this additional variability gets falsely associated with intervention condition, which produces a Type I error. Error rates were inflated with the fixed effects analyses because, as before, cluster variance is treated as known and the extra residual variability is ignored.
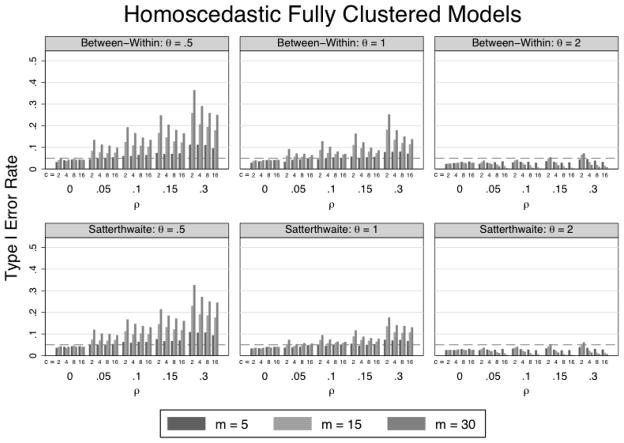
Fully Clustered Model
Figure 1 presents the Type I error rates for the homoscedastic fully clustered model. Type I error rates for the fully clustered model ranged from .01 to .36 (see Table 1) and were affected by all variables in the simulations. Error rates increased with increases in ρ (η2 = .21) and in m (η2 = .08) and decreased with increases in c (η2 = .05). The Satterthwaite degrees of freedom had smaller error rates than between-within degrees of freedom (η2 = .01). We discuss this result in more detail when reporting the results of the partially clustered models. Additionally, θ influenced the Type I error rate (η2 = .18). As expected, error rates exceeded 5% when θ = .5 but were below 5% when θ = 2.
Figure 1.
Type I error rates (y-axis) for tests of the intervention effect for the homoscedastic fully clustered model. Error rates are presented for various combinations of cluster size (m), clusters in the clustered condition (c), intraclass correlation (ρ), ratio of unclustered residual variance to clustered residual variance (θ), and degrees of freedom method.
Partially Clustered Model
Figures 2 and 3 display the Type-I error rates for the homoscedastic and heteroscedastic partially clustered models, respectively. Type I error rates for the partially clustered models ranged from .03 to .23 (see Table 1). Type I error rates were affected by ρ (η2 = .26), c (η2 = .14), m (η2 = .12), and degrees of freedom method (η2 = .08) but not whether the model assumed homoscedastic versus heteroscedastic residuals (η2 = 0) nor θ (η2 = 0). However, the effects of ρ, c, and m had little influence in the Satterthwaite models as compared to the between-within models.
Figure 2.
Type I error rates (y-axis) for tests of the intervention effect for the random coefficient model assuming homoscedastic Level-1 residuals. Error rates are presented for various combinations of cluster size (m), clusters in the clustered condition (c), intraclass correlation (ρ), ratio of unclustered residual variance to clustered residual variance (θ), and degrees of freedom method.
Figure 3.
Type I error rates (y-axis) for tests of the intervention effect for the heteroscedastic partially clustered model. Error rates are presented for various combinations of cluster size (m), clusters in the clustered condition (c), intraclass correlation (ρ), ratio of unclustered residual variance to clustered residual variance (θ), and degrees of freedom method.
Five conclusions can be drawn from the results of the partially clustered simulations. First, the partially clustered models provided superior results to the ANOVA (ignoring clustering), fixed-effects, and fully clustered models. Second, the difference between homoscedastic and heteroscedastic models was small and not critical to Type I errors. Third, Type I error rates were slightly depressed when the population ρ was 0, which is a consequence of the non-negativity constraint on variance components (Murray, Hannan, & Baker, 1996). We can relax this constraint by modeling within-cluster correlations as a covariance instead of variance (cf. Kenny, Mannetti, Pierro, Livi, & Kashy, 2002). To test whether modeling within-cluster correlation as a covariance brought the Type I error rate up to .05, we ran a simulation using Satterthwaite degrees of freedom where c = 4, m = 15, ρ = 0, and θ = 1. As expected the Type I error rate was .05. Fourth, the multilevel models did not perform well when there were only two clusters. This is not too surprising given that estimating the cluster-level variance with only two clusters is tenuous at best. Further, maximum likelihood methods often do not perform well when sample sizes are small. Trials occasionally use two to three clusters per condition (e.g., Beck, Coffey, Foy, Keane, & Blanchard, 2009) and some researchers have suggested that three clusters, though perhaps not optimal, can be sufficient (Ost, 2008). Our results suggest that at least 8 or preferably 16 clusters are needed to consistently maintain the Type I error rate.
The fifth conclusion is that the Satterthwaite method for computing degrees of freedom outperformed the between-within method (η2 = .08). Given that both the Satterthwaite and between-within methods used identical standard errors for fixed effects, the only difference between them is the degrees of freedom. The between-within method generated inflated Type I error rates when the number of clusters was low or when cluster size was relatively large. The Type I error rates for the between-within method also increased as ρ increased. In contrast, the Satterthwaite method maintained Type I error rates at or near α = .05 except when there were only two clusters. The Type I error rates were relatively constant across the number of clusters and cluster size. Likewise, the Type I error rates were not systematically affected by the magnitude of ρ as they were with the between-within method. This difference between the Satterthwaite and between-within methods is due to the fact that Satterthwaite degrees of freedom take into account the magnitude of the between-cluster variance when calculating degrees of freedom and thus will be appropriately adjusted as this variance increases. In contrast, the between-within method does not take into account the between-cluster variance and only uses the number of clusters, cluster size, and number of fixed effects estimated to calculate degrees of freedom.
Bias and Efficiency
Intervention Effect
Across models and conditions in the simulation, bias in the estimate of the intervention effect was negligible, with bias never exceeding |.02|. The variability in the estimates was also relatively small (mean MSE < .1 and maximum MSE < .4). The MSE increased as m (η2 = .20) and c (η2 = .52) decreased and as ρ (η2 = .07) increased. Thus, all five model types produced unbiased and reasonably efficient estimates of the treatment effect.
Variance Components
We limited our analysis of bias and efficiency of variance components to the fully and partially clustered models because they estimate the cluster and residual variances directly. Table 2 presents the mean values for bias and MSE across models, stratified by θ and averaged over m, c, and ρ. Across models variability in the estimates of the variance components was typically small, except when θ = 2 and when m and c were small. Across models bias in was most affected by θ (η2 = .17) followed by ρ (η2 = .04), whether heteroscedasticity in the residuals was modeled (η2 = .04), and whether the partially clustered model was used (η2 = .02). Neither c or m had an effect (η2 = 0).
Table 2.
Bias and variability in the variance components.
| θ = .5 | θ = 1 | θ = 2 | ||||
|---|---|---|---|---|---|---|
|
| ||||||
| Bias | MSE | Bias | MSE | Bias | MSE | |
| Fully Clustered Homoscedastic | ||||||
| −0.07 | 0.01 | −0.02 | 0.02 | 0.44 | 0.42 | |
| −0.23 | 0.07 | −0.05 | 0.03 | 0.12 | 0.10 | |
| 0.21 | 0.06 | −0.05 | 0.03 | −0.76 | 0.65 | |
| Partially Clustered Homoscedastic | ||||||
| 0.03 | 0.04 | 0.02 | 0.04 | −0.01 | 0.04 | |
| −0.23 | 0.04 | −0.01 | 0.02 | 0.45 | 0.25 | |
| 0.21 | 0.06 | −0.01 | 0.02 | −0.43 | 0.24 | |
| Partially Clustered Heteroscedastic | ||||||
| 0.02 | 0.04 | 0.02 | 0.04 | 0.02 | 0.04 | |
| −0.01 | 0.04 | 0.01 | 0.04 | −0.01 | 0.04 | |
| 0.00 | 0.01 | 0.00 | 0.04 | 0.00 | 0.16 | |
Note. MSE = mean square error; θ = ratio of the unclustered to clustered variance
The homoscedastic fully clustered model led to biases in , which is due to the misspecification of the variance structure (see Figure 4). In contrast, was relatively unbiased for the partially clustered models. In the partially clustered models, bias was highest when m, c, and ρ were small, was always less than |.2|, and did not consistently impact the Type I error rate. To the extent that is of substantive interest, the partially clustered models will consistently provide unbiased and interpretable estimates.
Figure 4.

Bias in , and for the homoscedastic fully clustered model across values of the intraclass correlation (ρ) and ratio of unclustered residual variance to clustered residual variance (θ). Cluster size was m = 30 and the number of clusters was c = 16. Results were similar with other values of m and c.
Across models bias in and was most affected by θ (η2 = .40 and .44, respectively) followed by whether the partially clustered model was used (η2 = .03 and .05, respectively) and whether heteroscedasticity in the residuals was modeled (η2 = .01 and .02, respectively). Across models ρ, c, and m did not have an effect on bias (all η2 = 0). Bias in the and was evident in the fully clustered model (see Figure 4) and the homoscedastic partially clustered model but not the heteroscedastic partially clustered model. In the homoscedastic fully clustered model and homoscedastic partially clustered model, the direction of the bias depended upon θ. When θ = .5 (i.e., ), constraining the residual variances to be equal produced a negative bias in and positive bias in . Just the opposite was true when θ = 2. Although bias in the Level-1 residual variance does not dramatically impact Type I error rates for the test of the intervention effect, it will impact the estimate of ρ, which is often of substantive interest.
In sum, although all models were unbiased and efficient when estimating treatment effects, only the heteroscedastic partially clustered model was consistently unbiased and efficient for both treatment effects and variance components because this model matches the structure of the data in partially clustered designs. Thus, heteroscedastic partially clustered models using Satterthwaite degrees of freedom appear to be the model of choice for analyzing partially clustered data.
Power
Both partially and fully clustered designs require larger sample sizes than designs that do not involve nesting. Consequently, it is essential to use power calculations that account for the structure of the data when planning studies. Moerbeek and Wong (2008) provide large sample formulae for partially clustered designs that do not address degrees of freedom and that will overestimate power when sample sizes are limited. Roberts and Roberts (2005) briefly discuss power in small samples but do not provide data. Additionally, Roberts (2008) has written a power program called cluspower for Stata that can accommodate two-sample partially clustered designs.
A flexible alternative to large sample power formulae and cluspower is to use Monte Carlo simulation to establish power. In power simulations, we set a population intervention effect size and then simulate data for realistic sample sizes, eliminating the need to assume large samples. Power is computed as the proportion of replications in the simulation where a statistically significant intervention effect was observed. In addition to determining power in finite samples, power simulation is also flexible in that it can easily accommodate many design variations (e.g., multiple intervention conditions, complex variance/covariance structures, multiple outcomes) and can be more accurate than analytic formulae (Littell, Milliken, Stroup, Wolfinger, & Schabenberger, 2006).
We used Monte Carlo simulation to determine power for the test of the intervention effect in partially clustered designs for sample sizes observed in the literature. We set the intervention effect to be equal to one-half of the pooled standard deviation of the outcome. We used the same values of c, m, ICC, and θ as in the previous simulations as they represent values observed in the literature. We generated 10,000 data sets for each cell in the simulation design and fit both the homoscedastic and heteroscedastic partially clustered models to each data set. Because the between-within method for calculating degrees of freedom resulted in inflated Type I error rates and because the Kenward-Roger and Satterthwaite degrees of freedom produced essentially identical results, we only used the Satterthwaite degrees of freedom.
Figure 5 presents the results of the power simulations. The pattern of results is similar to what is seen in fully clustered designs (Murray, 1998). As ρ increases, power decreases. Further, increasing the number of clusters has a bigger impact on power than increasing cluster size, although both improve power. For some studies, there may be natural limits to cluster size, such as when evaluating group psychotherapy where increasing group size beyond 8–10 individuals may be clinically problematic. Consequently, it may only be appropriate to increase the number of groups. In contrast, in school-based research, it may be feasible to increase both the number of classrooms and the number of students per classroom sampled. The heteroscedastic models had nearly identical power to the homoscedastic models, even when θ = 1. Given that the heteroscedastic models are the least biased with respect to the intervention effect and the variance components and that there is no penalty with respect to power even when the residuals are actually homoscedastic, the heteroscedastic models appear to be the model of choice.
Figure 5.
Power (y-axis) for tests of the intervention effect for multilevel models using the Satterthwaite method for computing degrees of freedom. The intervention effect was one-half of the pooled standard deviation difference between the clustered and unclustered conditions. Power values are presented for various combinations of cluster size (m), clusters in the clustered condition (c), intraclass correlation (ρ), ratio of unclustered residual variance to clustered residual variance (θ), and degrees of freedom method.
One problem with recommending the partially clustered models as the de facto standard for partially clustered data is that they assume that ICC >0 . However, when ICC = 0, fitting the partially clustered model may unnecessarily reduce power. In our simulations, when ICC = 0 power was consistently over 80% if c = 8 or 16 and m = 15 or 30. In fact, when c = 4 and m = 30, power was over 80%. As a follow-up to these observations, we fit a one-way ANOVA model to the simulated data where ICC = 0 and compared it to the results of the heteroscedastic partially clustered model. Results were nearly identical when using the homoscedastic partially clustered model. Because θ had little impact on power, we limited these analyses to the simulated data where θ = 1. When c = 8 or 16, the partially clustered had slightly less power or equivalent power to the ANOVA model. When c = 2 or 4, the partially clustered model had consistently less power than the ANOVA model. This is to be expected given that the available degrees of freedom will be low when c = 2 or 4. Across levels of c power is reduced because of the non-negativity constraint on , which biases the estimate of upward and thereby reduces power. The difference in power should be reduced by allowing negative within-cluster correlations. Regardless, mistakenly using a partially clustered model is only a problem when c is small (cf. Kenny et al., 1998).
Roberts and Roberts (2005) recommended allocating more participants to clustered conditions than unclustered conditions to maximize power (see also Moerbeek and Wong, 2008). For a given total sample size, differential allocation can be done by changing the number of clusters but keeping cluster size constant, changing cluster size but keeping the number of clusters constant, or a combination of both. We simulated a partially clustered study to investigate the benefits of the first two approaches to differential allocation. We did not investigate combining approaches because the number of possible combinations is very large and makes simulation prohibitive.
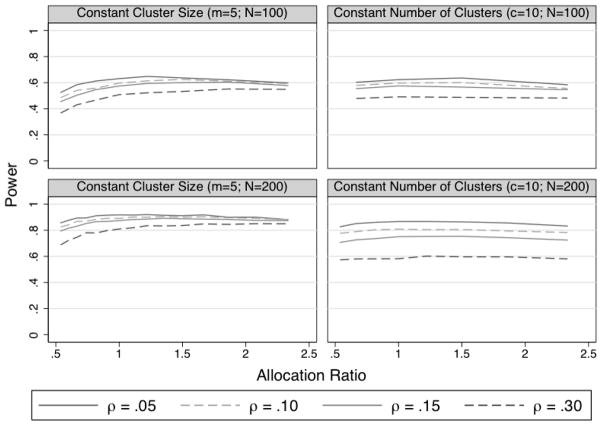
We calculated power to detect a difference of one-half of the pooled standard deviation between a clustered and unclustered condition for a study with either N = 100 or N = 200 participants. In the simulations, the allocation ratio represents the number of participants in the clustered condition compared to the unclustered condition. We compared the power of studies with allocation ratios of approximately .5 to approximately 2.5. For the simulations where we changed the number of clusters but kept cluster size constant, we set cluster size to m = 5. When N = 100, the smallest allocation ratio was 35/65 (.54), the next smallest was 40/60 (.67), and so on up to the largest allocation ratio which was 70/30 (2.33). When N = 200, the smallest allocation was 70/130 (0.54), the next smallest was 75/125 (.6), and so on up to the largest allocation ratio which was 140/60 (2.33). For simulations where we changed cluster size but kept the number of clusters constant, we set the number of clusters to c = 10. In these simulations, when the allocation ratio is less than one, clusters are smaller than when the allocation ratio is greater than one. When N = 100, the smallest allocation ratio was 40/60 (.67), the next smallest was 50/50 (1), and so on up to the largest allocation ratio which was 70/30 (2.33). When N = 200, the smallest allocation ratio was 70/130 (0.54), the next smallest was 80/120 (0.67), and so on up to the largest allocation ratio which was 140/60 (2.3). We also compared four ρ values (.05, .10, .15, .30), set the Level-1 residual variance equal across conditions, and used Satterthwaite degrees of freedom. We did not evaluate an ρ = 0 condition because there would be no need for differential allocation in that situation.
Four conclusions can be drawn from these simulations (see Figure 6). First, allocating more participants to the clustered condition by increasing the number of clusters provides a small increase in power as compared to equal allocation. Second, allocating more participants to the clustered condition by increasing cluster size has almost no impact on power because the benefit of additional observations per cluster is balanced out by the increased variance inflation that accompanies increased cluster sizes for a given ρ. Third, allocating more participants to the unclustered condition reduces power and thus is not recommended. Fourth, given the small increase in power due to unequal allocation, the decision to use equal allocation will likely depend on other issues besides power. For example, in a study comparing a group-based treatment to no treatment, it may be beneficial to allocate more people to the treatment condition to increase the number of participants treated (Roberts & Roberts, 2005).
Figure 6.
Power (y-axis) for tests of the intervention effect across a range of allocation ratios of participants to the clustered and unclustered conditions. The intervention effect was one-half of the pooled standard deviation difference between the clustered and unclustered conditions. Power values are presented across a range of allocation ratios, intraclass correlations (ρ), and total sample size (N).
Roberts and Roberts (2005) provided a formula for optimal allocation of individuals in large studies that use a partially clustered design:
| (34) |
where m is the cluster size in the clustered condition and ρ is the intraclass correlation. The ratio is the ratio of the sample size in clustered condition as compared to the unclustered condition. They note that in small studies the optimal allocation ratio will be larger than the value produced by Equation (34). Our results are consistent with this. Equation (34) assumes a constant cluster size and thus we can compare the left-hand panels of Figure 6 to Equation (34). For example, when ρ = .10 and m = 5, Equation (34) suggests that the optimal allocation ratio is 1.18 whereas Figure 6 suggests that optimal allocation is closer to 1.5. This is true regardless of sample size, although the difference between Equation (34) and the simulation results is smaller when N = 200. Thus, researchers can use simulation methods to accurately determine the optimal allocation of participants to condition when designing partially clustered studies.
The power simulations highlight the need to account for any clustering during the planning stage of an intervention study. If researchers do not plan for clustering, they may end up in a difficult situation with no good options for analyzing and interpreting their results. For example, consider a partially clustered intervention with one clustered and one unclustered condition. The clustered condition includes 40 participants, divided evenly among four clusters. The unclustered condition also includes 40 participants. We could use a multilevel model with Satterthwaite degrees of freedom to estimate the intervention effect. The multilevel model maintains the nominal Type I error rate, but the power to detect an intervention effect of d = .5 will be low (Power < 0.4). Although the multilevel model in principle allows for generalizations beyond the clusters included in the study, the quality of those generalizations will be suspect given that there are only four clusters. As discussed above, alternatively incorporating cluster as a fixed effect is problematic because (a) it limits the results of the analysis to the specific clusters included in the study and (b) if there is variation among clusters in the population, it increases the rate of Type I errors for the intervention effect if one attempts to make inferences beyond the specific clusters in the study. Finally, whatever the modeling strategy, if the design includes few clusters, it is difficult to learn about differences among clusters.
Substantive Example: The Body Project
To illustrate the multilevel model for partially clustered data, we reanalyzed data from Stice, Shaw, Burton, and Wade (2006), which evaluated the Body Project, a dissonance based eating disorder prevention intervention. Female adolescents (N = 480) were randomly assigned to one of four conditions: a dissonance intervention (n = 114), healthy-weight management program (n = 117), an expressive writing control condition (n = 123), and an assessment-only control condition (n = 126). The dissonance intervention was delivered in 17 groups (average m = 6.7) and the healthy weight program was delivered in 18 groups (average m = 6.5). The expressive writing and assessment-only conditions were unclustered. We focus our discussion on one of the primary outcomes: Thin-Ideal Internalization (TII), which was measured with the Ideal-Body Stereotype Scale-Revised (Stice, 2001). See Stice et al. (2006) for a complete description of the intervention, participants, procedures, and outcomes.
The Level-1 and Level-2 equations for the Body Project data are similar to Equations (19)–(21) but need to be expanded to incorporate the four conditions and a baseline value of TII.2 Specifically, the Level-1 equation for the Body Project is as follows:
| (35) |
TIIPOSTij is the post-test value of TII for person i in group j. DISij, HWij, and EWij are indicator (dummy) variables for the dissonance, healthy weight, and expressive writing conditions, respectively. The assessment only condition was the reference category. The regression coefficients for the indicators are β1j, β2j, and β3j and they capture differences relative to the assessment-only control condition. TIIPREij is the baseline value of TII and β4j is the regression coefficient for TIIPRE. Finally, eij represents the individual-level residual.
The Level-2 equations are:
| (36) |
| (37) |
| (38) |
| (39) |
| (40) |
where γ00 is the average intercept and represents the mean of the reference condition (i.e., assessment only) when the baseline value of TII is zero. We centered TIIPRE around its grand mean to make the zero value more interpretable. The parameters γ10, γ20, and γ30 are interpreted, respectively, as the mean difference between the DIS, HW, and EW conditions relative to the assessment only condition, controlling for TIIPRE. The u1j and u2j terms are cluster-level disturbances that allow the intervention effects for DIS and HW to vary across cluster. We did not include cluster-level disturbance terms for γ00 or γ30 because both the EW and assessment only conditions were unclustered.
A composite model can be obtained by substituting Equations (36)–(40) into Equation (35):
| (41) |
Note that there are only cluster-level residuals associated with the two grouped conditions. This model assumes that individual- and cluster-level residuals are independent and normally distributed as:
| (42) |
| (43) |
| (44) |
ρ for the dissonance condition is:
| (45) |
ρ for the healthy weight condition is:
| (46) |
We conducted two multilevel analyses using the Body Project data. In the first analysis, we assumed that the Level-1 residuals were homoscedastic and thus constrained the residual variances to be equal. In the second analysis, we allowed the Level-1 residual variances to differ across all four intervention conditions. In addition to estimating an overall intervention effect, we also used contrasts to test three hypotheses described in the original Body Project report (see Stice et al., 2006, p. 264). Specifically we tested (a) whether the dissonance and healthy weight conditions differed from the expressive writing and assessment only conditions, (b) whether the dissonance condition differed from the healthy weight condition, and (c) whether the healthy weight condition differed from the expressive writing and assessment only conditions. All models were estimated using the SAS MIXED procedure and used the Satterthwaite method for computing degrees of freedom. The online supplemental material provides annotated SAS code for estimating this model.
Table 3 presents the results of the analyses. In the homoscedastic model, the overall intervention effect was significant, F(3, 71.7) = 10.44, p < .01, indicating differences among the treatment conditions. The contrasts indicated that the dissonance and healthy weight conditions significantly reduced TII as compared to expressive writing and assessment only conditions, t(64) = −4.97, p < .01. Further, the healthy weight condition significantly reduced TII as compared to the expressive writing and assessment only condition, t(26.4) = −2.44, p < .05. The dissonance condition resulted in lower TII but this difference was not statistically significant, t(32.4) = −1.99, p = .06. The cluster-level variances for the dissonance and healthy weight conditions were 0.04 and 0.06, respectively, indicating some variability in TII across clusters (i.e., intervention groups). Estimates of ρ for the dissonance and healthy weight conditions were 0.13 and 0.18, respectively, indicating that 13% and 18% of the variance in dissonance and healthy weight conditions was associated with group membership.
Table 3.
Intervention effects for thin-ideal internalization from the Body Project
| Fixed Effects | Homoscedastic Residuals | Heteroscedastic Residuals | ||||
|---|---|---|---|---|---|---|
| Estimate | Test | Estimate | Test | |||
| γ00 | Intercept | 3.55 | t(473) = 2.53** | 3.55 | t(432) = 2.10* | |
| γ10 | DIS | −0.44 | t(28.6) = −5.25** | −0.44 | t(23.2) = −5.51** | |
| γ20 | HW | −0.24 | t(35.1) = −2.65* | −0.24 | t(30.7) = −2.74** | |
| γ30 | EW | −0.07 | t(443) = −1.02 | −0.07 | t(239) = −1.12 | |
| γ40 | Baseline TII | 0.83 | t(474) = 17.27** | 0.85 | t(445) = 18.21** | |
| Random Effects
| ||||||
|
|
DIS | 0.04 | z = 1.28 | 0.03 | z = 0.93 | |
| HW | 0.06 | z = 1.77* | 0.05 | z = 1.56# | ||
|
|
DIS | 0.27a | z = 14.88** | 0.34 | z = 6.84** | |
| HW | 0.27a | z = 14.88** | 0.33 | z = 7.12** | ||
| EW | 0.27a | z = 14.88** | 0.25 | z = 7.78** | ||
| AO | 0.27a | z = 14.88** | 0.20 | z = 7.87** | ||
| ρDIS | 0.13 | 0.08 | ||||
| ρHW | 0.18 | 0.13 | ||||
| Intervention Effects
| ||||||
| Overall | F(3,71.7) = 10.44** | F(3,62.3) = 11.32** | ||||
| DIS + HW vs EW + AO | −0.30 | t(64) = −4.97** | −0.31 | t(57.3) = −5.10** | ||
| DIS vs HW | −0.21 | t(32.4) = −1.99# | −0.21 | t(32.1) = −1.99# | ||
| HW vs EW + AO | −0.20 | t(26.4) = −2.44* | −0.20 | t(25.5) = −2.47* | ||
Note.
p = 0.06;
p ≤ .05;
p ≤ .01;
= These residual variances were constrained to be equal; DIS = Dissonance; HW = Healthy Weight; EW = Expressive Writing; AO = Assessment Only
The heteroscedastic model significantly improved model fit, as evidenced by a likelihood-ratio test, χ2(3) = 8.8, p = .03. The cluster-level variances in the dissonance and healthy weight conditions were similar to the homoscedastic models (see Table 3). In contrast, the Level-1 residual variances changed substantially as compared to the homoscedastic models. In the heteroscedastic models the Level-1 residual variances were larger for the clustered conditions and smaller for the unclustered conditions as compared to the homoscedastic models. The increased Level-1 variance in the clustered conditions suggests that the group-based interventions increased the differences among the participants as compared to the control conditions. The differentiation may occur because some participants are well suited to a group-based intervention and others not as much. Thus, variability may increase in the clustered conditions as compared to the unclustered conditions because some participants respond well (or poorly) to the group environment.
Regardless of the reason, these changes in the random effects reduced ρs in the heteroscedastic models to 0.08 and 0.13 in the dissonance and healthy weight conditions, respectively. These changes in the random effects can impact the standard errors for fixed effects, such as the intervention effect. In our case, the intervention effects were not substantially affected. However, in other studies such differences could be more impactful and thus the degree of heteroscedasticity should be tested.
Conclusions
Despite the fact that partially clustered trials are as common as fully clustered trials (Bauer et al., 2008), methodological work on partially clustered intervention trials has only recently begun. Several recent papers, including the present paper, have outlined a flexible multilevel modeling approach for analyzing partially clustered data. The new simulation results presented here indicate that a multilevel model adapted to match the partially clustered design improves upon models that ignore clustering, treat clusters as a fixed effect, or treat the design as if it is fully clustered. Further, random coefficient multilevel models maintain the nominal Type I error rate when Satterthwaite or Kenward-Roger degrees of freedom are used. This information is valuable as some software programs only use one method for calculating degrees of freedom or use a z-distribution.
Addressing the methodological issues associated with partially clustered designs is not as simple as just applying the multilevel model because most partially clustered studies do not include a sufficient number of clusters to have adequate power. Generally speaking, sample sizes in partially clustered designs should increase, especially with respect to the number of clusters. At a fixed total sample size, allocating more participants to the clustered condition by increasing the number of clusters provides a small benefit in this regard. Regardless, it is strongly recommended that researchers evaluating interventions in partially clustered designs carefully consider the methodological issues outlined in this paper when designing their studies and analyzing the resulting data.
Supplementary Material
Acknowledgments
This research was supported by National Institutes of Health (NIH) Research Grant MH/DK6195.
Footnotes
Faes et al. (2009) describe a fourth method based on what they term the “effective sample size,” which they define as: “the sample size one would need in an independent sample to equal the amount of information in the actual correlated sample” (p. 389). The Satterthwaite and Kenward-Roger degrees of freedom perform as well as this new methodology for Gaussian outcomes (Faes et al., 2009), which we focus on in this article. Consequently, we did not include this method in our simulations.
Additionally, as noted above, some software packages assume infinite degrees of freedom and use a z-test instead of a t-test. Although we do not include this approach in our simulations, we expect it to perform worse than any of the other methods we describe because assuming infinite degrees of freedom makes no adjustment for the finite, and often small, number of clusters included in the analysis.
An alternative to adjusting for baseline values of the dependent variable is to use a repeated measures approach, where the baseline value is part of the outcome vector. In randomized trials, adjusting for baseline values will typically be the most powerful analysis. However, the adjustment for baseline approach is often not appropriate in quasi-experiments or observational studies because the assumption of equal distribution of the baseline values across conditions is not plausible (Fitzmaurice, Laird, & Ware, 2004). In those cases, we recommend using a repeated measures approach or the equivalent approach of change scores to analyzing partially clustered data.
Contributor Information
Scott A. Baldwin, Brigham Young University
Daniel J. Bauer, University of North Carolina at Chapel Hill
Eric Stice, Oregon Research Institute.
Paul Rohde, Oregon Research Institute.
References
- Baldwin SA, Murray DM, Shadish W. Empirically supported treatments or type I errors? Problems with the analysis of data from group-administered treatments. Journal of Consulting and Clinical Psychology. 2005;73:924–935. doi: 10.1037/0022-006X.73.5.924. [DOI] [PubMed] [Google Scholar]
- Baldwin SA, Stice E, Rohde P. Statistical analysis of group-administered intervention data: Reanalysis of two randomized trials. Psychotherapy Research. 2008;18:365–376. doi: 10.1080/10503300701796992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bauer DJ, Sterba SK, Hallfors DD. Evaluating group-based interventions when control participants are ungrouped. Multivariate Behavioral Research. 2008;43:210–236. doi: 10.1080/00273170802034810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beck JG, Coffey SF, Foy DW, Keane TM, Blanchard EB. Group cognitive behavior therapy for chronic posttraumatic stress disorder: An initial randomized pilot study. Behavior Therapy. 2009;40:82–92. doi: 10.1016/j.beth.2008.01.003s. [DOI] [PubMed] [Google Scholar]
- Crits-Christoph P, Baranackie K, Kurcias JS, Beck AT, Carroll K, Perry K, Zitrin C. Meta-analysis of therapist effects in psychotherapy outcome studies. Psychotherapy Research. 1991;1:81–91. [Google Scholar]
- Crits-Christoph P, Mintz J. Implications of therapist effects for the design and analysis of comparative studies of psychotherapies. Journal of Consulting and Clinical Psychology. 1991;59:20–26. doi: 10.1037//0022-006x.59.1.20. [DOI] [PubMed] [Google Scholar]
- Donner A, Birkett N, Buck C. Randomization by cluster: Sample size requirements and analysis. American Journal of Epidemiology. 1981;14:322–326. doi: 10.1093/oxfordjournals.aje.a113261. [DOI] [PubMed] [Google Scholar]
- Fitzmaurice GM, Laird NM, Ware JH. Applied longitudinal data analysis. Hoboken, NJ: Wiley; 2004. [Google Scholar]
- Herzog TA, Lazev AB, Irvin JE, Juliano LM, Greenbaum PE, Brandon TH. Testing for group membership effects during and after treatment: The example of group therapy for smoking cessation. Behavior Therapy. 2002;33:29–43. doi: 10.1016/S0005-7894(02)80004-1. [DOI] [Google Scholar]
- Hoover DR. Clinical trials of behavioural interventions with heterogeneous teaching subgroup effects. Statistics in Medicine. 2002;21:1351–1364. doi: 10.1002/sim.1139s. [DOI] [PubMed] [Google Scholar]
- Imel ZE, Baldwin SA, Bonus K, Macoon D. Beyond the individual: Group effects in mindfulness-based stress reduction. Psychotherapy Research. 2008;18:735–742. doi: 10.1080/10503300802326038. [DOI] [PubMed] [Google Scholar]
- Kenny DA, Judd CM. Consequences of violating the independence assumption in analysis of variance. Psychological Bulletin. 1986;99:422–431. [Google Scholar]
- Kenny DA, Kashy DA, Bolger N. Data analysis in social psychology. In: Gilbert DT, Fiske ST, Lindzey G, editors. The Handbook of Social Psychology. 4. I. New York: Oxford University Press; 1998. pp. 233–265. [Google Scholar]
- Kenny DA, Mannetti L, Pierro A, Livi S, Kashy DA. The statistical analysis of data from small groups. Journal of Personality and Social Psychology. 2002;83:126–137. doi: 10.1037//0022-3514.83.1.126. [DOI] [PubMed] [Google Scholar]
- Kenward M, Roger J. Small sample inference for fixed effects from restricted maximum likelihood. Biometrics. 1997;53:983–997. [PubMed] [Google Scholar]
- Kim DM, Wampold BE, Bolt DM. Therapist effects in psychotherapy: A random-effects modeling of the National Institute of Mental Health Treatment of Depression Collaborative Research Program data. Psychotherapy Research. 2006;16:161–172. doi: 10.1080/10503300500264911. [DOI] [Google Scholar]
- Lee KJ, Thompson SG. The use of random effects models to allow for clustering in individually randomized trials. Clinical Trials. 2005;2:163–173. doi: 10.1191/1740774505cn082oa. [DOI] [PubMed] [Google Scholar]
- Littell RC, Milliken GA, Stroup WW, Wolfinger RD, Schabenberger O. SAS for mixed models. 2. Cary, NC: SAS Institute; 2006. [Google Scholar]
- Lutz W, Leon S, Martinovich Z, Lyons JS, Stiles WB. Therapist effects in outpatient psychotherapy: A three-level growth curve approach. Journal of Counseling Psychology. 2007;54:32–39. doi: 10.1037/0022-0167.54.1.32. [DOI] [Google Scholar]
- Martindale C. The therapist-as-fixed-effect fallacy in psychotherapy research. Journal of Consulting and Clinical Psychology. 1978;46:1526–1530. doi: 10.1037//0022-006x.46.6.1526. [DOI] [PubMed] [Google Scholar]
- Moerbeek M, Wong WK. Sample size formulae for trials comparing group and individual treatments in a multilevel model. Statistics in Medicine. 2008;27:2850–2864. doi: 10.1002/sim.3115. [DOI] [PubMed] [Google Scholar]
- Morgan-Lopez AA, Fals-Stewart W. Consequences of misspecifying the number of latent treatment attendance classes in modeling group membership turnover within ecologically valid behavioral treatment trials. Journal of Substance Abuse Treatment. 2008;35:396–409. doi: 10.1016/j.jsat.2008.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray DM. Design and analysis of group-randomized trials. New York: Oxford University Press; 1998. [Google Scholar]
- Murray DM, Hannan PJ, Baker WL. A Monte Carlo study of alternative responses to intraclass correlation in community trials: Is it ever possible to avoid Cornfield’s penalities? Evaluation Review. 1996;20:313–337. doi: 10.1177/0193841X9602000305. [DOI] [PubMed] [Google Scholar]
- Myers JL, DiCecco JV, Lorch RF. Group dynamics and individual performances: Pseudogroup and quasi-F analyses. Journal of Personality and Social Psychology. 1981;40:86–98. [Google Scholar]
- Nye B, Konstantopoulos S, Hedges LV. How large are teacher effects? Educational Evaluation and Policy Analysis. 2004;26:237–257. [Google Scholar]
- Ost LG. Efficacy of the third wave of behavioral therapies: A systematic review and meta-analysis. Behaviour Research and Therapy. 2008;46:296–321. doi: 10.1016/j.brat.2007.12.005. [DOI] [PubMed] [Google Scholar]
- Roberts C. cluspower [Computer software and manual] 2008 Retrieved from http://personalpages.manchester.ac.uk/staff/chris.roberts/
- Roberts C, Roberts SA. Design and analysis of clinical trials with clustering effects due to treatment. Clinical Trials. 2005;2:153–162. doi: 10.1191/1740774505cnO76oas. [DOI] [PubMed] [Google Scholar]
- Satterthwaite FW. An approximate distribution of estimates of variance components. Biometrics Bulletin. 1946;2:110–140. [PubMed] [Google Scholar]
- Serlin RC, Wampold BE, Levin JR. Should providers of treatment be regarded as a random factor? If it ain’t broke, don’t “fix” it: A comment on Siemer and Joorman (2003) Psychological Methods. 2003;8:524–534. doi: 10.1037/1082-989X.8.4.524w. [DOI] [PubMed] [Google Scholar]
- Siemer M, Joorman J. Assumptions and consequences of treating providers in therapy studies as fixed versus random effects: Reply to Crits-Christoph, Tu, and Gallop (2003) and Serline, Wampold, and Levin (2003) Psychological Methods. 2003a;8:535–544. doi: 10.1037/1082-989X.8.4.535. [DOI] [PubMed] [Google Scholar]
- Siemer M, Joorman J. Power and measures of effect size in analysis of variance with fixed versus random nested factors. Psychological Methods. 2003b;5:425–433. doi: 10.1037/1082-989X.8.4.524s. [DOI] [PubMed] [Google Scholar]
- Singer JD. Using SAS PROC MIXED to fit multilevel models, hierarchical models, and individual growth models. Journal of Educational and Behavioral Statistics. 1998;24:323–355. [Google Scholar]
- Stice E. A prospective test of the dual pathway model of bulimic pathology: Mediating effects of dieting and negative affect. Journal of Abnormal Psychology. 2001;110:124–135. doi: 10.1037//0021-843x.110.1.124. [DOI] [PubMed] [Google Scholar]
- Stice E, Shaw H, Burton E, Wade E. Dissonance and healthy weight eating disorder prevention programs: A randomized efficacy trial. Journal of Consulting and Clinical Psychology. 2006;74:263–275. doi: 10.1037/0022-006X.74.2.263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wampold BE, Brown GS. Estimating variability in outcomes attributable to therapists: A naturalistic study of outcomes in managed care. Journal of Consulting and Clinical Psychology. 2005;73:914–923. doi: 10.1037/0022-006X.73.5.914. [DOI] [PubMed] [Google Scholar]
- Wampold BE, Serlin RC. The consequences of ignoring a nested factor on measures of effect size in analysis of variance. Psychological Methods. 2000;5:425–433. doi: 10.i037//1082-989x.5.4.425. [DOI] [PubMed] [Google Scholar]
- Zucker DM. An analysis of variance pitfall: The fixed effects analysis in a nested design. Educational and Psychological Measurement. 1990;50:731–738. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.