Abstract
Designing a plastic scintillation detector for proton radiation therapy requires careful consideration. Most plastic scintillators should not perturb a proton beam if they are sufficiently small but may exhibit some energy dependence due to quenching effect. In this work, we studied the factors that would affect the performance of such scintillation detectors.
We performed Monte Carlo simulations of proton beams with energies between 50 and 250 MeV to study signal amplitude, water equivalence, spatial resolution, and quenching of light output. Implementation of the quenching effect in the Monte Carlo simulations was then compared with prior experimental data for validation.
The signal amplitude of a plastic scintillating fiber detector was on the order of 300 photons per MeV of energy deposited in the detector, corresponding to a power of about 30 pW at a proton dose rate of 100 cGy/min. The signal amplitude could be increased by up to a factor of 2 with reflective coating. We also found that Cerenkov light was not a significant source of noise. Dose deposited in the plastic scintillator was within 2% of the dose deposited in a similar volume of water throughout the whole depth-dose curve for protons with energies higher than 50 MeV. A scintillation detector with a radius of 0.5 mm offers a sufficient spatial resolution for use with a proton beam of 100 MeV or more. The main disadvantage of plastic scintillators when irradiated by protons was the quenching effect, which reduced the amount of scintillation and resulted in dose underestimation by close to 30% at the Bragg peak for beams of 150 MeV or more. However, the level of quenching was nearly constant throughout the proximal half of the depth-dose curve for all proton energies considered.
We therefore conclude that it is possible to construct an effective detector to overcome the problems traditionally encountered in proton dosimetry. Scintillation detectors could be used for surface or shallow measurements with a single calibration for a specific beam energy. For deeper measurements, Monte Carlo simulations can be used to generate depth-dependent correction factors.
Keywords: Proton therapy, plastic scintillators, dosimetry, Monte Carlo
1. Introduction
As in all forms of radiation therapy, proton therapy must be precisely planned and delivered for the treatment to be successful. However, proton dose measurement is a delicate process. Rapid dose fall-off at the end of the proton range creates a high dose gradient in the axial direction of pristine Bragg peak and therefore requires excellent spatial resolution. This is also true of spread-out Bragg peak (SOBP), which are a superposition of pristine Bragg peak of different energies weighted in a way that results in a uniform dose distribution at the distal part of the depth dose curve. Because the proton range is highly sensitive to variations in density, the detector is likely to affect the surrounding dose distribution. Consequently, any detector could create perturbations, especially at the end of the proton range. It is important to ensure that detector characteristics, such as water equivalence, are preserved for all proton energies.
Torrisi examined the use of plastic scintillator dosimeters in proton therapy (Torrisi 2000), but plastic scintillators have never been used extensively for proton dose measurements. The main disadvantage of using scintillation detectors in proton therapy is the well-known quenching of scintillators. Quenching is an under-response of the irradiated scintillator as a function of incident LET, which means that the output of the plastic scintillator (i.e. number of scintillation photon produced per MeV deposited) will vary as a function of the proton energy. Nonetheless, proton therapy could benefit from advantages exhibited by plastic scintillator dosimeters in photon and electron radiation therapy, such as high spatial resolution and water equivalence (Beddar, et al. 1992a, 1992b).
Previous studies have looked at point-like scintillation detectors in proton therapy. Safai et al developed a small inorganic scintillator dosimeter and demonstrated the advantages of a small inorganic scintillator rather than a larger detector in proton therapy, such as a high spatial resolution (Safai, et al. 2004). However, inorganic scintillators are not water equivalent, which leads to dose perturbations. Torrisi characterized the quenching in plastic scintillators used in proton therapy but only studied protons of energy equal to or lower than 60 MeV (Torrisi 2000). While a proton beam of 60 MeV might be used to treat an ocular melanoma, a proton beam of 250 MeV may be required to treat a prostate. Our study thus aimed at further improving our knowledge of the feasibility of applying miniature plastic scintillation detectors to proton therapy and identifying the factors that may affect their performance during treatment. We studied the properties of plastic scintillators over the whole range of clinical proton energies (i.e. 50 MeV to 250 MeV) for pristine Bragg peak and for SOBP. First we estimated the total signal produced by the scintillation detectors. Then we determined whether advantages of plastic scintillators seen in photon and electron therapy (e.g., high spatial resolution and water equivalence) also hold in proton therapy. Finally we considered quenching and identified specific applications where plastic scintillation detectors may be useful in the clinical setting.
2. Materials and methods
Plastic-based scintillators are commonly found in one of two shapes: as simple piece of plastic (most commonly polyvinyl toluene, PVT) containing scintillating solutes or as a scintillating fiber, which is a piece of polystyrene containing scintillating solutes and surrounded with a non-scintillating plastic cladding in the same manner as an optical fiber. Polystyrene is usually used in commercial scintillating fiber because polystyrene has better light transmission than PVT. We henceforth use the term “plastic scintillator” to refer to the form of plastic scintillator without a cladding and “scintillating fiber” to refer the form of plastic scintillator possessing a non-scintillating cladding. Moreover, we use the term “plastic scintillation detector” to refer to a dose detector made with any of the two shapes of plastic-based scintillators.
Monte Carlo simulations were used to study scintillation detectors in a large number of experimental situations without requiring an actual access to the often limited research time of a clinical proton facility. In addition to simulations, experimental measurements were used to study the quenching effect in plastic scintillators. (Beddar and Siebers 1995).
2.1. Monte Carlo simulations
The Monte Carlo simulations were based on the GEANT4 (GEometry ANd Tracking) simulation toolkit version 4.7p2 (Agostinelli et al. 2003; Allison et al. 2006). GEANT4 can track most physical particles, from neutrinos to heavy ions, and has therefore been a valuable tool in hadron and proton therapy. In addition to tracking ionizing particles, GEANT4 can also produce and track optical photons (see Figure 1 a and b) (Levin and Moisan 1996). The use of GEANT4 to simulate clinical proton facilities have rendered results that were all in good agreement with experimental measurements (Cirrone et al. 2005; Aso et al. 2005; Paganetti et al. 2004) and thus justify this approach.
Figure 1.
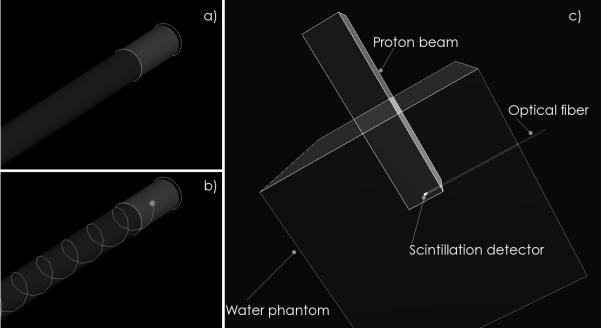
Monte Carlo simulations of a) a scintillating fiber detector consisting of a small scintillating fiber coupled to a long optical fiber; b) production of optical photons in the scintillating fiber and capture by the optical fiber through total internal reflection; c) a typical simulation setup where a scintillating fiber detector is placed inside a cubic water phantom and irradiated by a non-diverging proton beam.
In Geant4, the user has to choose from a list of possible physics processes to handle electromagnetic and hadronic interactions (Geant4 Physics Reference Manual). Different models are offered for most interactions. Those models can be either data-driven, parameterization-driven or theory driven. When available, the data-driven models are usually preferred. Moreover, for all electromagnetic processes, the user can choose between a standard package that covers energies down to 10 keV and a low-energy package that covers energies down to 250 eV. The low energy package was used in this work. This package uses data from publicly distributed evaluated data libraries: EPDL97, EEDL and EADL. For proton elastic scattering processes, we used the default parameterization based on the International Commission on Radiation Units and Measurements (ICRU) report no. 49 (ICRU 1993). For the inelastic scattering processes we used the theory-driven precompound model and the default parameterization-based low-energy inelastic model . We chose those models based on previous work by Paganetti et al, (Paganetti, et al. 2004; Paganetti and Gottschalk 2003).
Unless otherwise specified, the plastic scintillation detector was modeled as either a cylindrical PVT-based plastic scintillator or a cylindrical scintillating fiber of a given length and radius (which were varied) coupled to an optical fiber of the same radius with a length of 1 m. The material used for the plastic scintillator was based on the commercial BC-408 (Saint-Gobain Crystals, Paris, France). The scintillating fiber and the optical fiber was based on the commercial single-clad BCF-12 and BCF-98 (Saint-Gobain Crystals, Paris, France), respectively. The single-clad BCF-12 scintillating fiber consists of a scintillating polystyrene core surrounded by a non-scintillating polymethylmethacrylate (PMMA) cladding. The purpose of the cladding is to increase light collection through total-internal reflection.
In Geant4, a scintillator is characterized by its light yield, its photon emission spectrum and by the exponential decay of its time spectrum. The wavelength spectrum of the scintillation photons in Monte Carlo simulations was set according to values that we measured previously. (Archambault et al. 2005). The other parameters were obtained from the manufacturer of plastic scintillator and scintillating fibers. Geant4 uses this information to compute the probability that a scintillation photon of wavelength λ be emitted every time an ionizing particle deposit energy inside the scintillating material. The coupling efficiency between the scintillating fiber and the optical fiber was accounted for by giving a certain probability based on experimental values (Ayotte et al. 2006) to absorb a photon crossing the interface. Attenuation of the scintillation photons as a function of their wavelength inside the plastic scintillation detector and the optical fiber was based on the manufacturer’s attenuation spectrum in dB/m. This attenuation spectrum was used in the Monte Carlo simulation to attenuate the optical photons propagating in the plastic scintillation detector and the optical fiber in a realistic manner.
Two types of optical photons were produced and tracked by the simulation. The first type is the above-described scintillation light that is produced exclusively in the scintillating material. The second type of optical photon is Cerenkov light from a theory-driven model in Geant4. Cerenkov light can be produced in every material for which a refractive index value has been assigned. In our case, Cerenkov light was produced in the scintillating material as well as in the optical fiber. Cerenkov light was not produced inside the water phantom because plastic scintillation detector are usually shielded from external source of light.
2.1.1. Signal amplitude
The detector signal amplitude determines a plastic scintillation detector’s sensitivity and the reproducibility of its data. Signal amplitude can be optimized within a plastic scintillation detector to improve both these features (for instance by cladding, as noted above). Thus, in tests of signal amplitude we examined the effects of both beam (that is, proton fluence) and detector. We therefore simulated plastic scintillation detectors exposed to different fluences of proton. Simulations were done in water, in the middle of the plateau region. The plastic scintillation detector was 2 mm in length and 1 mm in diameter and it was were placed perpendicular to the beam direction as illustrated in Figure 1c. The amount of scintillation light reaching the proximal end of the optical fiber (i.e. the end closer to the photodetector) was recorded as a function of dose deposited inside the plastic scintillation detector. The power of the signal at the proximal end of the plastic scintillation detector was obtained in two steps. First, the number of photons collected at the proximal end of the detector per unit of dose deposited in the plastic scintillation detector was converted to an energy value according to the wavelength of each photon. Then, this energy value was converted to a power value by using different dose rates that are commonly used in the clinic. The amount of Cerenkov light produced in the simulation was also recorded because it is a well-known source of noise in other application of plastic scintillation detectors (Beddar, et al, 1992). We then compared the single-clad BCF-12 scintillating fiber described above with a multi-clad BCF-12 scintillating fiber. Multi-clad scintillating fibers possess a second cladding for better light collection. We also compared scintillating fiber with a plastic scintillator (i.e. no cladding). Our simulations of signal amplitude also included a comparison of different types of coating applied on the exterior of the plastic scintillation detector. We examined the following cases: no coating, a coating made from a Lambertian reflector, and a coating made from a specular reflector. In the simulations, coatings were infinitely thin and therefore had no impact on the dose distribution.
2.1.2. Water equivalence
Water equivalence of plastic scintillation detector was characterized over the whole range of clinical proton energies. Primary protons were incident on the water phantom as a non-diverging square field. The simulated dose deposited inside the phantom was recorded in tallies 0.1 mm thick with and without the presence of a plastic scintillation detector 2 mm in length and 1 mm in diameter placed perpendicular to the beam direction. We recorded the dose deposited in the plastic scintillation detector and the dose deposited in water in the absence of the plastic scintillation detector in a cylinder at the same position and of the same dimension as the scintillator. The ratio between those to dose was then evaluated for all proton energies at five different depths of the Bragg peak: on the surface of the water phantom, 10 mm anterior to the Bragg peak, 5 mm anterior to the Bragg peak, centered on the Bragg peak, and 3 mm posterior to the Bragg peak. An example of the setup used in the Monte Carlo simulations is shown in Figure 1-c.
2.1.3. Spatial resolution
Because of the sharp dose fall-off at the end of a pristine Bragg peak or SOBP, spatial resolution in the axial direction is more important in proton than in photon or electron therapy (Vatnitsky et al. 1999). The finite size of the detector produces dose averaging that can result in unrealistic dose measurements in regions of high dose gradients. To evaluate the impact of the detector size on dose measurements, we first simulated depth-dose curves for protons of energies between 50 MeV and 250 MeV. Then, dose at the Bragg peak was recorded as an average dose throughout a cylinder to represent dose-averaging occurring in detectors of different sizes. The length of the plastic scintillation detectors was 2 mm placed perpendicular to the beam direction. Radii between 0.25 mm and 5 mm were used.
2.2. Quenching
A radiation beam incident on a plastic scintillation detector produces excited molecule (i.e. excitons) and damaged molecules through excitation or ionization. The excitons can lead to the production of scintillation when they return to a normal state. Two mechanisms are responsible for quenching, one fast and the other more slowly. In the first mechanism the damaged molecules act as traps for excitons that could otherwise produce scintillation. The second mechanism is a mutual quenching between two excited molecules (Voltz et al. 1966; Michaelian and Menchaca-Rocha 1994).
Several mathematical models of various complexities can be used to describe quenching. The first model for quenching was proposed by Birks (Birks 1951) and is still used today (Torrisi 2000). To account for quenching in Monte Carlo simulations, we used a refined version of the Birk model that is sometimes referred to as the Chou-Birks model:
| (1) |
where dS/dX represents the scintillation light produced per unit length and dE/dX is the stopping power. AdE/dX represents the number of excitons per unit path length and kBdE/dX represents the probability that a damaged molecule captures an exciton. C(dE/dX)2 accounts for quenching effects with various modes and degrees of excitation, which in turn depends upon the initial energy loss of the irradiating particle (Chou 1952). A, C, and kB are to be fit experimentally and can be found in the literature (Craun and Smith 1970).
While equation (1) is not the most refined description of quenching, it is an intuitive model that yields relatively accurate measurements in most situations. Moreover, due to its widespread use, it is easy to find values for the experimental parameters that are required to fit the Birk model in the literature. Therefore, equation (1) was implemented inside the Monte Carlo simulations so that the production of scintillation light could exhibit quenching. Quenching should only be affected by the stopping power of the beam and not by the actual dose rate.
First, the validity of the quenching model was established by comparison with experimental measurements. Then simulations of depth-dose curves were performed with and without quenching. In those simulations, we looked at three parameters: the initial quenching (i.e. the amount of quenching at the surface of the water phantom), the quenching at the Bragg peak, and the depth of agreement. We defined the depth of agreement as the fraction of the proton range for which the quenching does not differ by more than 2% from its initial value. Both the initial quenching and the quenching at the Bragg peak were computed as the difference between the dose simulated in the absence of quenching and the dose simulated in the presence of quenching normalized by the dose simulated in the absence of quenching.
3. Results
3.1. Signal amplitude
In the first set of simulations, the plastic scintillation detectors described in section 2.1 were exposed to protons of different fluences. Table 1 shows the dose deposited in these detectors according to the types of cladding and coating on the detector; it also shows the signal power reaching the proximal end of the plastic scintillation detector for photon beams administered at two different dose rates, 100 cGy/min and 500 cGy/min. A dose rate of 100 cGy/min is similar to the overall dose rate used in synchrotron-based proton therapy, while 500 cGy/min is on the order of the dose rate of synchrotron-based proton therapy during a single pulse. The values presented in Table 1 are independent of proton energy, but this is only because quenching was not included in this simulation. The statistical uncertainties in these values were all less than 0.2%.
Table 1.
Photon collection and signal power for different types of miniature scintillation probes.
| Cladding | Coating |
Photons
collected |
Signal power (pW) | |
|---|---|---|---|---|
| 100 cGy/min | 500 cGy/min | |||
| (MeV−1) | ||||
| None | None | 146 | 13 | 65 |
| None | Lambertian | 600 | 54 | 269 |
| None | Specular | 628 | 56 | 281 |
| Single-clad | None | 327 | 29 | 146 |
| Single-clad | Lambertian | 754 | 67 | 337 |
| Single-clad | Specular | 627 | 56 | 280 |
| Multi-clad | None | 329 | 29 | 147 |
While Cerenkov radiation is an important source of noise in measurements of signal amplitude for application of plastic scintillation detector in photon and electron therapy (Beddar, et al. 1992), our simulation of proton irradiations showed that the amount of Cerenkov light produced by a proton beam in the plastic scintillation detector is low. Table 2 shows the relative fraction of Cerenkov light for different proton energies as a function of the length of irradiated optical fiber. The number of Cerenkov photons is low because the protons themselves are not relativistic and the electrons that they put in motion have low energies. For comparison, note that the signal amplitude coming from Cerenkov light represents 1% of the total signal (i.e. scintillation and Cerenkov lights) per centimeter of optical fiber irradiated (Archambault et al. 2006).
Table 2.
Cerenkov light amplitude relative to the scintillation signal.
| Proton energy |
Cerenkov light per
length of irradiated optical fiber |
|---|---|
| (MeV) | (%/cm) |
| 50 | <0.001 |
| 100 | 0.002 |
| 150 | 0.01 |
| 200 | 0.03 |
| 250 | 0.04 |
3.2. Water equivalence
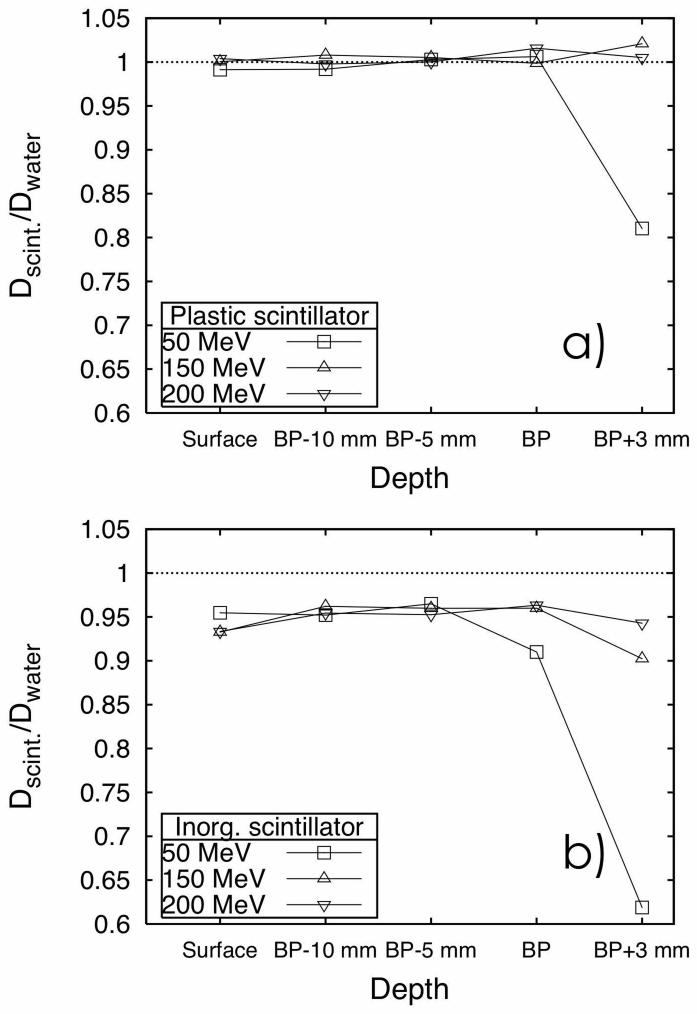
Water equivalence was assessed by simulating the dose deposited in plastic scintillation detector with radii of 1 mm positioned at five locations. Results were normalized to the dose deposited in the same volume of water without the detector. Figure 2-a shows the results for three proton energies. Dose deposited in the plastic scintillator was always within 2% of the dose deposited in water, except for 50-MeV protons at a location 3 mm beyond the Bragg peak. For comparison, the same Monte Carlo simulation was run using inorganic scintillators such as those used by Safai et al (Safai, et al. 2004) (see Figure 2-b). It is notable that inorganic scintillators had responses between 5% and 11% lower than that of water, except for 50-MeV photons beyond the Bragg peak. This greater reduction in response was due to the chemical composition and higher density of the inorganic scintillators.
Figure 2.
Ratio between the dose deposited in a scintillation detector (Dscint.; 1 mm radius and 2 mm long) inside a water phantom and the dose deposited in a similar volume of water in the absence of scintillation detector (Dwater) according to the depth of the detector reltative to the Bragg peak (BP). In a) the scintillation detector is made of a plastic scintillating fiber; in b) the scintillation detector is made of an inorganic scintillator. The depth of the Bragg peak were 2.2 cm, 15.6 cm and 25.6 cm for the beams of 50 MeV, 150 MeV and 200 MeV respectively.
3.3. Spatial resolution
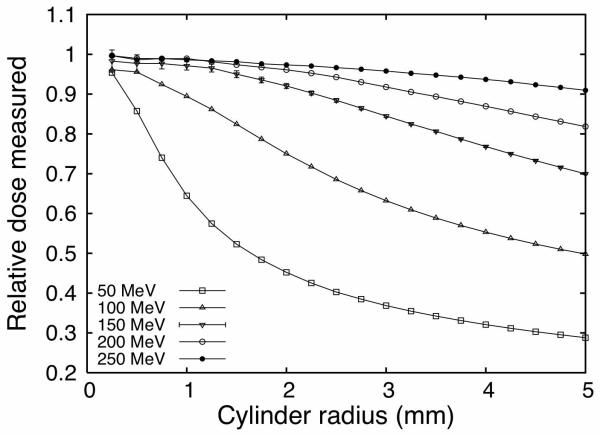
Geometric averaging of dose inside the plastic scintillation detector could lead to a reduction in spatial resolution. Figure 3 shows the dose measured at the Bragg peak for detector radii ranging from 0.25 mm to 5 mm normalized to the dose deposited in a region 0.1 mm thick centered on the Bragg peak. Simulation of measurements centered at the Bragg peak is a stringent but important test for the detector because the Bragg peak is the part of the dose deposition curve where dose underestimation due to averaging inside the sensitive volume of the detector is largest. Therefore, Figure 3 represents the maximum dose underestimation that can happen at a given proton energy.
Figure 3.
Simulation of the dose measured by a cylindrical detector centered on the Bragg peak normalized by the point-dose at the Bragg peak as a function of the radius of the detector. Error bars shown at 150 MeV represents the uncertainty in the Monte Carlo simulations (one standard deviation) and are representative of the uncertainties of all energies.
3.4. Quenching
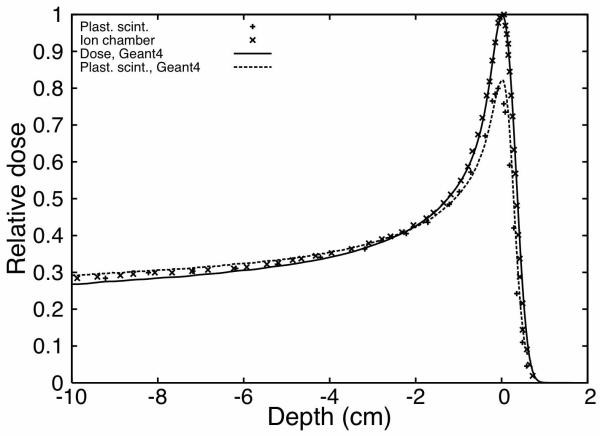
To verify that the implementation of equation (1) in the Monte Carlo simulations was accurate, we compared the simulated values to experimental measurements taken in an ion chamber in a previous analysis (Beddar and Siebers 1995). The scintillation detector used was similar to the one described in the literature (Beddar et al. 1992a). This scintillation detector includes a background optical fiber to subtract spurious light that can be created by Cerenkov or luminescence. Two simulations were performed. In the first, dose deposited in a water phantom by a proton beam of 155 MeV was recorded as a function of depth. The second simulation used the same setup, but equation (1) was applied every time a proton deposited energy in the phantom. Therefore, this second simulation was equivalent to a depth-dose curve measured with a plastic scintillation detector subject to quenching. In this second simulation, we implicitly assumed that the plastic scintillation detector had perfect water equivalence and as shown in Figure 2, this assumption is not far from reality. The results of these simulations and previous data are presented in Figure 4. In Figure 4, the ion chamber and the scintillation measurements were normalized in the plateau region. Therefore the initial quenching is not seen.
Figure 4.
Impact of scintillation quenching on a 155-MeV Bragg peak. Plastic scintillator measurements are compared to ion-chamber measurements to illustrate the quenching effect. Comparison is also made with Monte Carlo simulation. “Dose, Geant4” shows the simulation of dose deposition in water and “Plast. scint., Geant4” shows the simulation of the quenched response of a scintillation detector.
Table 3 summarizes three parameters used in the study of quenching (the initial quenching, the quenching at the Bragg peak, and the depth of agreement) at different proton energies.
Table 3.
Characterization of quenching.
| Energy |
Initial
quenching |
Quenching at
the Bragg peak |
Depth of
agreement |
|---|---|---|---|
| (MeV) | (%) | (%) | (%) |
| 50 | 16 | 42 | 55 |
| 100 | 14 | 39 | 70 |
| 155 | 13 | 30 | 83 |
| 200 | 13 | 29 | 89 |
| 250 | 13 | 27 | 93 |
4. Discussion
The overall signal amplitude (i.e. scintillation light) collected at the proximal end of a plastic scintillation detector is a key parameter to determine its sensitivity and reproducibility. Our data clearly show the advantage of coating the plastic scintillation detector with a reflective material. A reflector can increase signal amplitude by a factor of 4 for a plastic scintillator and a factor of 2 for a plastic scintillating fiber. However, in practice, a real plastic scintillation detector might not be as perfectly coated as in the simulation. Therefore, the increase in signal amplitude observed in plastic scintillation detectors with reflective coatings represents the maximum possible increase in signal amplitude resulting from the application of a reflective coating. Reflective coating should be sufficiently thin to avoid causing additional perturbation of the proton beam. In addition, the composition of such coating should also be selected to avoid materials with high atomic numbers because of their relatively high potential for interactions that would cause beam perturbations. The data in Table 1 can be used to select a photodetector with a suitable sensitivity. To maximize the overall signal amplitude, one should limit dose readings to the time that the proton beam is actually “on,” which can be achieved by gating data acquisition with the pulse signal from the treatment machine.
Our finding of a low amount of Cerenkov light indicates that in proton therapy a plastic scintillation detector can be used without any of the filtration methods necessary for photon and electron radiation therapy (Fontbonne et al. 2002; Archambault et al. 2006). However, even if Cerenkov light is unlikely to affect a plastic scintillation detector in proton therapy, undesired noise may still result from the luminescence of clear optical fibers. Measurements have proven that such luminescence is not a concern for photon and electron applications (Beddar et al. 1992), but measurements have never been conducted for protons.
Our finding that dose deposited in plastic scintillator was generally within 2% of the dose deposited in water in the absence of a plastic scintillation detector is explained, in part, by the similarity between cross-sections in water and the cross-sections in PVT for protons with energies between 50 MeV and 250 MeV. Over this energy range, the stopping powers for PVT were 99% of the stopping powers for water. The difference for protons at 50 MeV beyond the Bragg peak can be explained by the small difference in density between the two materials (1.03 g/cm3 for PVT versus 1.0 g/cm3 for water). Because protons are sensitive to small variations in density, a dosimetry system without any heterogeneity would be useful. One option is to design a dosimetry system with PVT-based plastic scintillator detector embedded in a PVT phantom. Because both phantom and detectors would be of the same material, no heterogeneities would affect the dose distribution.
In proton therapy, the rapid dose fall-off of the beam in the axial direction requires detectors with high spatial resolution. We showed that measuring a Bragg peak accurately requires a detector radius of 0.5 mm or smaller for proton beams of 100 MeV or higher. For lower proton energies, the radius of the detector should be no more than 0.25 mm, the typical lower limit for commercial plastic scintillating fibers. Increasing the spatial resolution by decreasing the radius also decreases the overall signal produced by the detector proportional to the square of the radius. Thus, for small plastic scintillation detectors, a reflective coating might be necessary to achieve a signal of sufficient amplitude. To achieve better depth dose resolution, it could be possible to alter the shape of the scintillation detector. For example, a thin rectangular slab of 0.25 mm or less in thickness and millimeter-sized width could be used. However, achieving a good light coupling between this thin slab and an optical fiber would be difficult. Detector response at the Bragg peak is important considering the advent of intensity-modulated proton therapy administered with scanning beams. In such intensity-modulated proton therapy, the target volume is covered with a series of mono-energetic pencil beams. It is therefore important to ensure that the detector does not underestimate the dose because of averaging inside the sensitive volume.
Quenching cannot be avoided in plastic scintillation detectors. However, for a given beam energy, we found that the relative amount of quenching does not vary by more than 2% in at least the first half of the proton range. For the highest energy considered, 250 MeV, the depth of agreement went beyond 90%. Plastic scintillation detectors are therefore well suited to superficial dose measurements. They could be used to measure precisely the entrance dose at the skin. Because quenching is stable in the proximal part of the depth-dose curve, using plastic scintillation detectors as surface detectors would require only one energy-specific calibration to account for the initial quenching of a given beam energy. Even with a relatively simple quenching model, it was possible to predict quenching accurately. Monte Carlo simulations could therefore be used to determine depth-dependent correction factors for all beam energies. Those correction factors could then be used to extend the use of plastic scintillation detectors beyond the depth of agreement.
5. Conclusion
Protons used for therapy have properties that distinguish them from more common photon and electron therapies. Those properties may complicate dose measurements in proton therapy. In photon and electron therapy, plastic scintillation dosimeters are among the most promising new detectors. Their high sensitivity, good spatial resolution, and water equivalence make them ideal for measuring complex dose patterns. Proton therapy could also benefit from the use of such detectors. In this study, we used Monte Carlo simulations to characterize the behavior of plastic scintillation detectors irradiated with proton beams with a wide range of proton energies.
We have quantified the amplitude of light collected at the proximal end of the plastic scintillation detector for materials with various types of cladding and coating. Those signal amplitude values can be used to select a photodetector with the appropriate sensitivity. Two of the main advantages of plastic scintillation detector, such as water equivalence and high spatial resolution, were preserved for most of the clinical energy range. However, at the lowest proton energy (50 MeV), we did observe some discrepancies. To minimize the impact of the detector in cases of irradiation by low-energy protons, one should use a detector diameter of 0.25 mm or smaller. A PVT-based phantom and PVT-based scintillation detector, such as the detectors using scintillating fibers, could be used to prevent all fluence perturbation by the plastic scintillation detector. The main disadvantage of plastic scintillation detectors is the quenching effect, which becomes more important as the beam energy decreases. Our Monte Carlo simulations have shown, however, that quenching is a major problem only close to the Bragg peak, making plastic scintillation detectors well suited for surface dose measurements. For deeper measurements, Monte Carlo calculations could be used to compute correction factors for quenching in proton beams of known energy.
At present, proton therapy typically consists of two- or three-field treatments administered by passively scattered SOBP. Those treatments are simple compared to other modalities, such as intensity-modulated photon therapy. However, more complex proton treatments, such as scanning beam intensity-modulated proton therapy, are gaining in popularity. Like intensity-modulated radiation therapy, intensity-modulated proton therapy will require new dose detectors to perform fast and accurate quality assurance. Miniature plastic scintillation detectors have been shown to be water equivalent and are capable of providing high spatial resolution. These properties are desirable for dosimetry applications in intensity-modulated proton therapy. For such applications, quenching, which is the main disadvantage of plastic scintillation detectors, could be corrected by depth-dependent correction factors obtained from Monte Carlo simulations.
Acknowledgments
This work was supported in part by the National Cancer Institute (NCI) (1R01CA120198-01A2). One author, LA was supported in part by the Odyssey program and the Houston Endowment, Inc. Award for Scientific Achievement at The University of Texas M. D. Anderson Cancer Center.
Footnotes
Classification numbers: 87.10.Rt, 87.53.Jw, 87.53.Kn, 87.55.K-, 87.55.tg, 29.40.Mc
REFERENCES
- Agostinelli S, et al. G4--a simulation toolkit. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 2003;506(no. 3):250–303. [Google Scholar]
- Allison J, et al. Geant4 developments and applications. Nuclear Science, IEEE Transactions. 2006;53(no. 1):270–278. [Google Scholar]
- Archambault L, Arsenault J, Gingras L, Beddar S, Roy R, Beaulieu L. Plastic scintillation dosimetry: optimal selection of scintillating fibers and scintillators. Medical physics. 2005;32(no. 7):2271–8. doi: 10.1118/1.1943807. [DOI] [PubMed] [Google Scholar]
- Archambault L, Beddar S, Gingras L, Roy R, Beaulieu L. Measurement accuracy and cerenkov removal for high performance, high spatial resolution scintillation dosimetry. Medical physics. 2006;33(no. 1):128–35. doi: 10.1118/1.2138010. [DOI] [PubMed] [Google Scholar]
- Aso T, et al. Verification of the Dose Distributions With GEANT4 Simulation for Proton Therapy. Nuclear Science, IEEE Transactions. 2005;52(no. 4):896–901. [Google Scholar]
- Ayotte G, Archambault L, Gingras L, Lacroix F, Beddar S, Beaulieu L. Surface preparation and coupling in plastic scintillator dosimetry. Medical physics. 2006;33(no. 9):3519–25. doi: 10.1118/1.2256300. [DOI] [PubMed] [Google Scholar]
- Beddar AS, Mackie TR, Attix FH. Water-equivalent plastic scintillation detectors for high-energy beam dosimetry: I. Physical characteristics and theoretical consideration. Physics in medicine and biology. 1992a;37(no. 10):1883–900. doi: 10.1088/0031-9155/37/10/006. [DOI] [PubMed] [Google Scholar]
- Beddar AS, Mackie TR, Attix FH. Water-equivalent plastic scintillation detectors for high-energy beam dosimetry: II. Properties and measurements. Physics in medicine and biology. 1992b;37(no. 10):1901–13. doi: 10.1088/0031-9155/37/10/007. [DOI] [PubMed] [Google Scholar]
- Beddar AS, Siebers JV. Application of miniature plastic scintillation detectors to proton therapy beam dosimetry. Radiotherapy and Oncology. 1995;37:S44. [Google Scholar]
- Beddar AS, Mackie TR, Attix FH. Cerenkov light generated in optical fibres and other light pipes irradiated by electron beams. Physics in Medicine and Biology. 1992;37:925–935. [Google Scholar]
- Birks JB. Scintillations from Organic Crystals: Specific Fluorescence and Relative Response to Different Radiations. Proceedings of the Physical Society A. 1951;64:874–877. [Google Scholar]
- Chou CN. The Nature of the Saturation Effect of Fluorescent Scintillators. Physical Review. 1952;87(no. 5):904. [Google Scholar]
- Cirrone GAP, et al. Implementation of a new Monte Carlo-GEANT4 Simulation tool for the development of a proton therapy beam line and verification of the related dose distributions. Nuclear Science, IEEE Transactions. 2005;52(no. 1):262–265. [Google Scholar]
- Craun RL, Smith DL. Analysis of response data for several organic scintillators. Nuclear Instruments and Methods. 1970;80:239. [Google Scholar]
- Fontbonne JM, et al. Scintillating fiber dosimeter for radiation therapy accelerator. Nuclear Science, IEEE Transactions. 2002;49(no. 5):2223–2227. [Google Scholar]
- [Accessed September 24, 2007];Geant 4 Physics Reference Manual. http://geant4.web.cern.ch/geant4/UserDocumentation/UsersGuides/PhysicsReferenceManual/html/index.html.
- ICRU 49 . Stopping Powers and Ranges for Protons and Alpha Particles. Bethesda, MD: 1993. [PubMed] [Google Scholar]
- Levin A, Moisan C. A more physical approach to model the surface treatment of scintillation counters and its implementation into DETECT. Nuclear Science Symposium, 1996. Conference Record., 1996 IEEE; 1996. pp. 702–706. vol.2. [Google Scholar]
- Michaelian K, Menchaca-Rocha A. Model of ion-induced luminescence based on energy deposition by secondary electrons. Physical Review B. 1994;49(no. 22):15550. doi: 10.1103/physrevb.49.15550. [DOI] [PubMed] [Google Scholar]
- Paganetti H, Gottschalk B. Test of GEANT3 and GEANT4 nuclear models for 160 MeV protons stopping in CH2. Medical physics. 2003;30(no. 7):1926–31. doi: 10.1118/1.1586454. [DOI] [PubMed] [Google Scholar]
- Paganetti H, Jiang H, Lee S-Y, Kooy HM. Accurate Monte Carlo simulations for nozzle design, commissioning and quality assurance for a proton radiation therapy facility. Medical Physics. 2004;31(no. 7):2107–2118. doi: 10.1118/1.1762792. [DOI] [PubMed] [Google Scholar]
- Safai, Sairos, Lin Shixiong, Pedroni Eros. Development of an inorganic scintillating mixture for proton beam verification dosimetry. Physics in medicine and biology. 2004;49(no. 19):4637–55. doi: 10.1088/0031-9155/49/19/013. [DOI] [PubMed] [Google Scholar]
- Torrisi L. Plastic scintillator investigations for relative dosimetry in proton-therapy. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms. 2000;170(no. 3-4):523–530. [Google Scholar]
- Vatnitsky S, et al. Proton dosimetry intercomparison based on the ICRU report 59 protocol. Radiotherapy and oncology : journal of the European Society for Therapeutic Radiology and Oncology. 1999;51(no. 3):273–9. doi: 10.1016/s0167-8140(99)00060-2. [DOI] [PubMed] [Google Scholar]
- Voltz R, Lopes da Silva J, Laustriat G, Coche A. Influence of the Nature of Ionizing Particles on the Specific Luminescence of Organic Scintillators. The Journal of Chemical Physics. 1966;45(no. 9):3306–3311. [Google Scholar]