Higher critical plaque wall stress in patients who died of coronary artery disease compared with those who died of other causes: a 3D FSI study based on ex vivo MRI of coronary plaques

Abstract

Mechanical forces play an important role in the rupture of vulnerable plaques. This process is often associated with cardiovascular syndromes, such as heart attack and stroke. In this study, magnetic resonance imaging (MRI)-based models were used to investigate the association between plaque wall stress (PWS) and coronary artery disease (CAD).

Ex vivo MRI data of coronary plaques from 12 patients were used to construct 12 three-dimensional (3D) fluid-structure interaction (FSI) computational models. Six of the patients had died from CAD and six had died from non-CAD causes. PWS was assessed using all nodal points on the lumen surface of each plaque. The maximum PWS from all possible vulnerable sites of each plaque was defined as the 3D critical plaque wall stress (CPWS).

Mean 3D CPWS in the CAD group was 94.3% higher than that in the non-CAD group (265.6 vs. 136.7 kPa, P=0.0029). There was no statistically significant difference in global maximum plaque wall stress (GMPWS) between the two groups (P=0.347). There was also no statistically significant difference in plaque burden between the CAD group (84.4 ± 5%) and the non-CAD group (82.0 ± 8%, P=0.552). The results indicate that plaques from patients who died from CAD were associated with higher CPWS compared with those from patients who died from non-CAD causes. With further validation, analysis of CPWS may prove to be an important component in assessment of plaque vulnerability.

1. Introduction

Cardiovascular disease is the leading cause of death in the developed world. Most acute cardiac syndromes, including heart attack and stroke, are associated with plaque rupture, which often occurs without warning. Mechanical forces, such as critical plaque wall stress (CPWS) and flow shear stress, may be associated with plaque rupture (Bluestein et al., 2008; Cheng et al., 2006; Gijsen et al., 2013; Groen et al., 2007; Melek et al., 1999; Tang et al., 2005; Tang et al., 2009); however, this association is not well established. Medical imaging technologies, including magnetic resonance imaging (MRI), intravascular ultrasound (IVUS), angiography, and computed tomography (CT), have been developed for patient screening and diagnosis. The severity of plaque stenosis is still widely used as a guide in decisions about revascularization. There is increasing evidence to indicate that luminal stenosis alone is probably not the best criterion for stratification of disease severity (Barnett et al., 1998; Rothwell et al., 2003; Underhill et al., 2010). For example, in the European Carotid Surgery Trial, 44% of the 3,018 trial participants with symptomatic carotid disease had less than 30% stenosis (Rothwell et al., 2003); and in the North American Symptomatic Carotid Endarterectomy Trial (NASCET), 61% of the 2226 recently symptomatic subjects had less than 50% carotid stenosis (Barnett et al., 1998). Finding biomarkers that can be used for more accurate assessment of plaque vulnerability and for early prediction of possible rupture and clinical events is of great importance to the research community and public health.

Mechanical forces play an important role in the rupture of vulnerable plaques: plaque rupture occurs when the mechanical forces acting on the plaque cap exceed its material strength; therefore, mechanical forces should be considered during plaque assessment. Image-based computational models for mechanical analysis enable a more accurate assessment of the risk of plaque rupture (Bluestein et al., 2008; Cheng et al., 1993; Leach et al., 2010; Li et al., 2007; Tang et al., 2004; Tang et al., 2009;). Cheng et al. (1993) analyzed 24 stable/unstable coronary artery lesions using two-dimensional (2D) solid models and suggested that concentrations of circumferential tensile stress in the atherosclerotic plaque may play an important role in plaque rupture and myocardial infarction. Based on in vivo MRI data from the carotid bifurcation, Li et al. (2007) found that plaque stress in asymptomatic patients was lower than that in symptomatic patients. Tang et al. (2004) introduced a three-dimensional (3D) multi-component fluid-structure interactions (FSI) model for image-based mechanical analysis of plaque to obtain more accurate and complete mechanical data, including both structural and flow stresses. Thin fibrous caps and large lipid-rich necrotic cores were shown to be associated with extreme stress and may correlate with plaque instability. Mechanical analysis using the FSI model has since gained popularity as it provides more complete results compared with other methods. Bluestein et al. (2008) investigated the effect of microcalcifications on vulnerable plaque and observed that microcalcifications may increase plaque vulnerability. In a small study based on in vivo MRI data, Tang et al. (2009) compared ruptured plaques with non-ruptured plaques using FSI models and showed that plaques with prior ruptures are associated with higher critical stress conditions than those with no prior rupture. In another study, Leach et al. (2010) compared carotid atheroma rupture observed in vivo and plaque stress distribution from FSI analysis based on pre-rupture medical imaging. They found a region of pronounced elevation in stress within the fibrous plaque layer of the lesion with a location and extent corresponding to that of the observed site of plaque rupture.

There are few modelling studies for coronary plaques because it is difficult to obtain in vivo data non-invasively. Yang et al. (2009) introduced an IVUS-based coronary plaque model with FSI, cyclic bending (secondary to heart motion) and anisotropic vessel properties and showed that cyclic bending has considerable impact on predictions of plaque stress. In a follow-up IVUS study, Samady et al. (2011) indicated that coronary flow shear stress is associated with progression and transformation of atherosclerotic plaque and arterial remodelling in patients with coronary artery disease (CAD). In a large-scale, one-year follow-up study, Stone et al. (2012) found that large plaque burden and low endothelial shear stress were predictors of increase in plaque area and worsening of clinically-relevant luminal obstructions. The latter two studies focussed on flow and did not include structural stress analysis.

The current 3D FSI study was conducted using ex vivo MRI coronary plaque data to investigate the association between mechanical forces and CAD.

2. Methods

2.1 MRI Data Acquisition

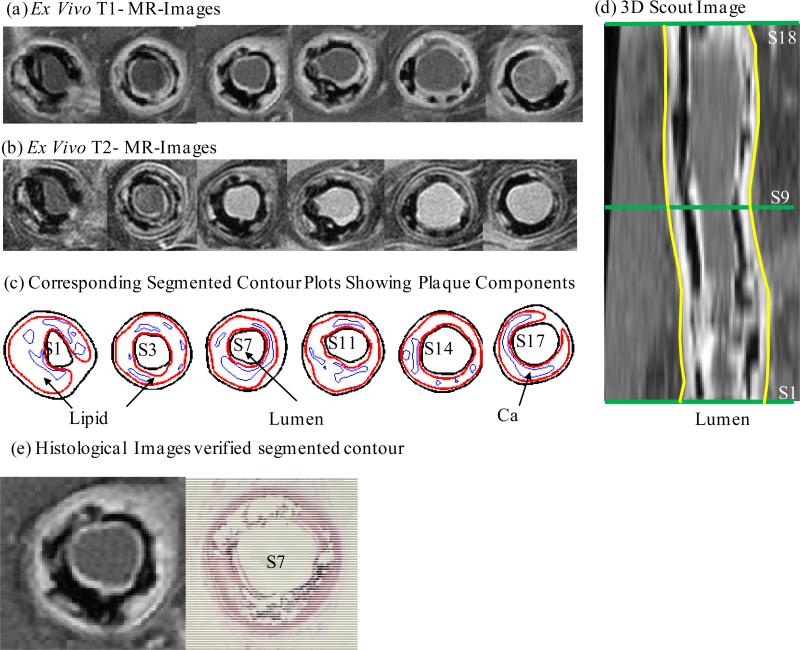
In this study, 3D ex vivo MRI data were obtained from 12 human coronary plaques (11 male; mean age 60 years; consent obtained) using multi-contrast MRI techniques with high resolution (Tang et al., 2005). The whole heart was fixed before dissection. A piece of heart tissue containing the coronary artery was dissected from each heart and these specimens were fixed in a 10% buffered formalin solution and placed in a polyethylene tube. Fixation maintained the vessel shape, curvature, tortuosity and size under zero pressure for MRI scans. The specimen was stored at 4°C within 12 hours after removal from the heart. All imaging procedures were performed on a 3-T Siemens Allegra clinical system (Siemens Medical Solutions, Malvern, PA). A single-loop volume coil (Nova Medical, Inc, Wilmington, MA) with a diameter of 3.5 cm was used as a transmitter and receiver. Initially, 3D gradient-echo images with a slice thickness of 0.5 mm were used to define the orientation of the coronary artery vessel axis. Multi-contrast (T1, T2, proton density-weighting, and gradient-echo) MRI imaging was conducted to better differentiate the components in the plaque (Figure 1). The first three imaging contrasts were obtained using a multi-slice 2D spin-echo sequence with different repetition time (TR) and echo time (TE) values. Data were acquired perpendicular to the vessel axis with a slice thickness of 1 mm. The fourth imaging contrast was obtained using a 3D gradient-echo sequence with the same slice location and thickness as the spin-echo sequence. Field of view was 25 × 19 mm², matrix was 256 × 192, and slice thickness was 1 mm. Image resolution was 0.1×0.1×1.0 mm³. With machine interpolation, the segmented data had resolution of 0.05×0.05×1.0 mm³. After completion of the MRI study, 10 μm transverse sections were taken from each specimen at 1 mm intervals, embedded in paraffin and stained with haematoxylin and eosin (H&E), Masson's trichrome and elastin van Gieson's (EVG) stains to identify the following major plaque components: calcification (Ca), lipid-rich necrotic core (LRNC), and fibrotic plaques (FP). Plaque vulnerability of these samples was assessed pathologically to provide a benchmark to validate computational findings. The 3D ex vivo MRI data were read by a self-developed software package, Atherosclerotic Plaque Imaging Analysis (APIA) written in Matlab (Math Works, MATLAB, Natick, MA), and also validated by histological analysis (Figure 1 (e)).

Figure 1.

a) Selected ex vivo T1-MRI images of a human coronary plaque sample (Patient #4) (CAD group); b) Selected ex vivo T2-MRI images of the plaque in a); c) Segmented contour plots showing plaque components; d) 3D Scout MR image; e) Histological image of selected slice.

2.2 3D FSI Computational Model

A 3D multi-component FSI model was constructed for each plaque based on ex vivo MRI data to obtain mechanical stress/strain and flow shear stress for analysis. Blood flow was assumed to be laminar, Newtonian, viscous and incompressible. The blood vessel was extended on both inlet and outlet sides to make it fully developed. The incompressible Navier-Stokes equations with arbitrary Lagrangian-Eulerian (ALE) formulation were used as the governing equations. Both the artery wall and plaque components were assumed to be hyperelastic, isotropic, incompressible and homogeneous. The modified Mooney-Rivlin model was used to describe the material property of each component in the plaque (Bathe 2002; Yang et al., 2007; Tang et al., 2008).

$$W=c_1(I_1-3)+c_2(I_2-3)+D_1[e^{D_2(I_1-3)}-1],$$ (1)

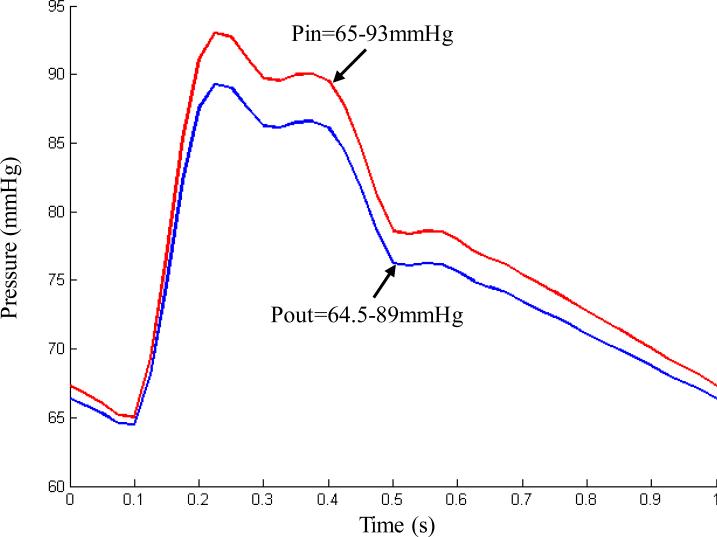
where $I_1=\sum C_{ii}$ and $I_2=\frac{1}{2}(I_1^2-C_{ij}{C}_{ij})$ are the first and second strain invariants, respectively, C = [C_ij] = X^T X is the right Cauchy-Green deformation tensor, X = [X_ij] = [∂x_i / ∂a_j] , {x_i} is the current position, {a_i} is the original position, and c_i and D_i are material parameters chosen to match experimental measurement (Yang et al., 2007; Tang et al., 2008). In this paper, the following parameter values were chosen: vessel/fibrous cap, c₁=36.8 kPa, D₁=14.4 kPa, D₂=2; clacification, c₁=368 kPa, D₁=144 kPa, D₂=2.0; lipid-rich necrotic core, c₁=2 kPa, D₁=2 kPa, D₂=1.5; c₂=0 was set for all materials. A no-slip condition between all interfaces was assumed. The fluid and structure models were coupled through their interface. The conditions of traction equilibrium and compatibility of displacements/velocities were imposed along the structure-fluid interfaces. Pulsating pressure conditions were imposed at both inlet and outlet in the numerical simulations (Tang et al., 2004). Figure 2 shows a typical cardiac pressure profile scaled to 65-93 mmHg. This was used as upstream pressure for the plaque sample shown in Figure 1, based on patient-specific systolic and diastolic arm pressure from the last hospital admission. The downstream pressure was set (64.5-89 mmHg) according to the upstream pressure, so that the flow rate was within physiological range.

Figure 2.

A typical cardiac pressure profile scaled with patient-specific systolic (93 mmHg) and diastolic (65 mmHg) arm pressure from the last hospital admission and used as upstream pressure condition (Pin) for the computational simulations of the plaque sample shown in Figure 1.

2.3 Mesh Generation

A Volume Component-Fitting Method (VCFM) was developed to generate mesh for these models. Using this technique, the 3D plaque geometry was divided into thousands of small “volumes” to curve-fit the very irregular plaque. Details are published in our earlier paper (Huang et al., 2012). The computational mesh was created in ADINA (ADINA R & D, Inc., Watertown, MA, USA) computing environment. Each plaque model required about 2000 small volumes to fit the complex solid plaque morphology and 600 small volumes to fit the fluid domain. There were around 20,000 8-node brick 3D elements and 30,000 4-node tetra 3D elements generated for each solid plaque and fluid domain.

2.4 Solution Method

The coupled FSI plaque models were solved by ADINA, which uses unstructured finite element methods for both fluid and solid models. Non-linear incremental iterative procedures were used to handle FSI. The governing finite element equations for both the solid and fluid models were solved by the Newton-Raphson iteration method. Mesh analysis was performed for each model by reducing the mesh density in each dimension by 10% until differences between solutions from two consecutive meshes were negligible (less than 1% in L₂-norm). Further details of the models and methods can be found in papers by Bathe (2002) and Tang et al. (2003).

2.5 Stress Data Extraction

As stress is a tensor, maximum principal stress at each node was chosen as a representative scalar value and was called plaque wall stress (PWS). Data for PWS were extracted from 3D FSI solutions for all integral nodes on lumen surfaces of 12 plaque models. The maximum value of PWS from all integral nodes was determined for each plaque as global maximum plaque wall stress (GMPWS).

Critical PWS analysis was conducted using a critical site selection method and critical stress approach (Tang et al., 2005). Vulnerable sites were defined as those where a thin cap covered a plaque component. All possible vulnerable sites for each plaque were determined for every 2D slice that matched an MRI slice position.

The maximum PWS value from all vulnerable sites for each slice was determined as its 2D critical plaque wall stress (2D CPWS). Healthy regions where there were no plaque components were excluded from the critical PWS analysis, even if a high stress concentration occurred there. The 3D critical plaque wall stress (3D CPWS) was defined as the maximum of all 2D CPWS values of the plaque.

2.6 Plaque Burden

Plaque burden was calculated for each plaque to assess the difference in severity of stenosis between the CAD group (in which patients had died from CAD) and the non-CAD group (in which patients had died from non-CAD causes). Plaque burden is a common measure of stenosis severity by area and is defined as:

$$\text{Plaque burden}=\text{Vessel area}∕(\text{vessel area}+\text{lumen area}),$$ (2)

where vessel area is the area bounded by the out-boundary and lumen contour. Plaque burden was calculated for each slice and the maximum value from all the 2D slices was defined as the plaque burden for the plaque.

2.7 Statistical Analysis

Normality of the data was assessed using the Shapiro–Wilk test. The Independent-Samples t-test was used for statistical analysis to compare the difference in CPWS and plaque burden between the CAD and non-CAD groups. P<0.05 was established as the level of statistical significance. All statistical analysis was performed with SPSS 17.0 (SPSS Inc, Chicago, Ill).

3. Results

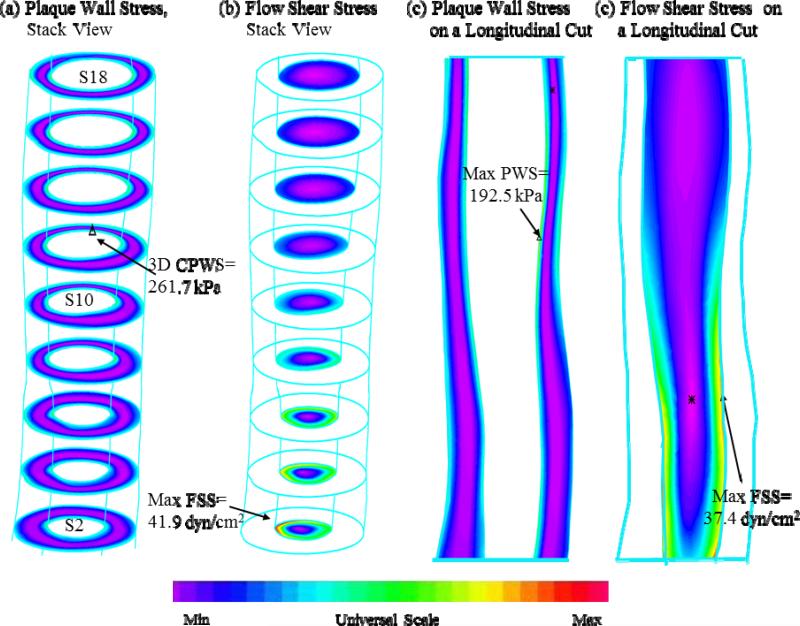
Demographic and clinical characteristics of the 12 patients are shown in Table 1 and plaque characteristics are shown in Table 2. An overview of 3D FSI solution behaviours based on MR images of the plaque sample (shown in Figure 1) are shown in Figure 3. CPWS, GMPWS and plaque burden data were obtained from the 12 full 3D FSI models and reported in Table 2. Comparisons of these data between the CAD and non-CAD groups are given below.

Table 1.

Demographic and Clinical Characteristics of the Study population (n=12).

	CAD	Non-CAD	P value
Age (years)	64 (50-72)	53 (45-67)
Male, n (%)	5 (83)	6 (100)
Black, n (%)	4 (67)	4 (67)
Body mass index, kg/m2	29 (23-40)	35 (24-47)
Systolic Blood Pressure (mmHg)	129 (93-150)	144 (102-175)	0.387
Diastolic Blood Pressure (mmHg)	81 (65-91)	72 (62-104)	0.393
Baseline Lipid Profile
Total Cholesterol, mg/dL	132 (81-182)	179 (76-260)	0.259
Triglycerides, mg/dL	140 (74-196)	114 (54-180)	0.477
High-density lipoprotein, mg/dL	41 (12-60)	51 (26-72)	0.411
Low-density lipoprotein, mg/dL	64 (33-86)	105 (29-177)	0.207

CAD represents the group of patients who died from coronary artery disease (CAD), non-CAD represents the group of patients who died from non-coronary artery disease causes (non-CAD). P values are for CAD vs non-CAD comparisons.

Table 2.

Summary of 3D critical plaque wall stress (3D CPWS), global maximum plaque wall stress (GMPWS), and plaque burden in the CAD and non-CAD groups.

Case		3D CPWS (kPa)		3D GMPWS (kPa)		Plaque Burden
CAD	Non-CAD	CAD	Non-CAD	CAD	Non-CAD	CAD	Non-CAD
P1	P7	307.1	162.3	359	320	0.868	0.868
P2	P8	227.2	153.9	345	1250	0.811	0.878
P3	P9	226	141.7	404	667	0.849	0.679
P4	P10	261.7	141.8	262	465	0.891	0.786
P5	P11	387	98.9	391	143	0.876	0.891
P6	P12	184.8	121.8	326	265	0.767	0.819
Mean value		265.6±72	136.7±23	348±51	518±401	0.844±0.05	0.82±0.08
P value		0.002		0.347		0.552

Figure 3.

Overview of 3D FSI solution behaviours based on MR images of the plaque sample shown in Figure 1. a) plaque wall stress, stack view; b) flow shear stress, stack view; c) plaque wall stress on a longitudinal cut surface; d) flow shear stress on a longitudinal cut surface.

3.1 3D CPWS in the CAD group was significantly higher than that in the non-CAD group

The 3D CPWS values from the six plaques in the CAD group were: 307.1, 227.2, 226.0, 261.7, 387.0, and 184.8 kPa, with a mean of 265.6 ±72.2 kPa. The 3D CPWS values from the six plaques in the non-CAD group were: 162.3, 153.9, 141.7, 141.8, 98.9, and 121.8 kPa, with a mean of 136.7 ± 23.0 kPa. The mean 3D CPWS from the CAD group is 94.3% higher than that in the non-CAD Group (P=0.0029, Figure 4(a)).

Figure 4.

Comparison of the mechanical conditions (plaque wall stress) and plaque burden between the CAD group (patients who died from CAD disease) and non-CAD group (patients who died from non-CAD causes).

3.2 2D CPWS in the CAD group was significantly higher than that in the non-CAD group

2D CPWS values were also compared between the two groups. There were 176 2D slices: 87 in the CAD group and 89 in the non-CAD group. The mean 2D CPWS in the CAD group was 139.8 ± 63.9 kPa, which was 54.3 % higher than that in the non-CAD group (90.6 ± 44.8 kPa, P<0.0001, Figure 4 (b)).

3.3 No statistically significant difference in GMPWS between the two groups

There was no statistically significant difference in GMPWS between the two groups (P=0.347, Figure 4(c)). Furthermore, the mean GMPWS in the non-CAD Group was 49.2% higher than that in the CAD group (518.3 vs. 347.5 kPa).

3.4 No statistically significant difference in plaque burden between the two groups

The mean plaque burden from the CAD group was 84.4 ±5 %, which is only 3% higher than that in the non-CAD group (82.0 ± 8 %, P=0.552). The difference was not statistically significant (Figure 4(d)).

4. Discussion

4.1 3D CPWS may be a good indicator for plaque vulnerability

Mechanical forces are generally thought to play an important role in the rupture of vulnerable plaque; however, there is a paucity of solid evidence to support the hypothesis that mechanical forces may be used for more accurate assessment of plaque vulnerability because there is no gold standard or clinical data, such as actual plaque rupture observed from in vivo data. The use of samples from patients who died of CAD and 3D FSI models is our first attempt to investigate the possible link between death from CAD and 3D coronary CPWS. In the current study, 3D CPWS is the only indicator that showed a statistically significant difference between the CAD and non-CAD groups; the other two indicators, GMPWS and plaque burden, showed no statistically significance difference. These findings support the hypothesis that localized 3D CPWS may be a better indicator than GMPWS or plaque burden for assessment of plaque vulnerability.

There is a general consensus that a threshold critical stress value of 300 kPa and cap thickness of 65 μm may be linked to plaque rupture (Virmani et al., 2006; Finet et al., 2004); however, model stress predictions are heavily dependent on the data used by those models and validation using in vivo data with plaque rupture is difficult (Tang et al., 2009). Histology-based models have the best resolution and often gave high stress predictions, whereas models based on in vivo data (where resolution is limited to 200-600 μm) often have lower stress predictions. Teng et al. (2009) conducted ultimate strength tests, where tissue samples were stretched until they broke, for human carotid artery samples (n=73) and found that the ultimate axial and circumferential strength for media sections were 519 ± 270 kPa and 1230 ± 533 kPa, respectively.

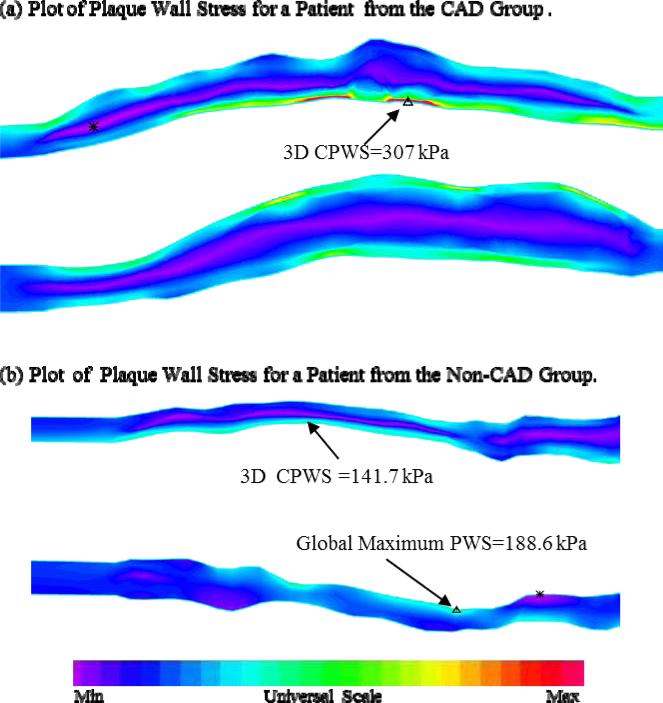
Interestingly, mean GMPWS in the non-CAD group was 49.2% higher than that in the CAD group (P=0.347). This is because GMPWS may occur at a healthy site where either the vessel wall is very thin or vessel curvature is considerable. Indeed, stress distributions in plaque are affected by many factors including, but not limited to, vessel and plaque geometry, plaque structure, and blood pressure. The combination of these factors determines GMPWS and its location. Figure 5 gives PWS plots from two plaques, one from each group. Figure 5(a) presents a band plot of PWS for a plaque from the CAD group: the 3D GMPWS occurred at the critical site. Figure 5(b) presents the band plots of PWS for a plaque from the non-CAD group: the 3D GMPWS occurred at a healthy site and was 33.1% higher than 3D CPWS.

Figure 5.

Plots of Plaque Wall Stress (PWS) for plaque samples selected from the two groups showing that the global maximum plaque wall stress (GMPWS) may occur at a healthy site (marked on (b)) and may be higher than 3D critical plaque wall stress (3D CPWS).

4.2 Limitations

There were several limitations to this study, as follows: 1) only a small number of patients (n=12) was included in this study, human coronary plaque samples are hard to obtain and the 3D FSI model construction is very time consuming. This is the first time that a potential link between death from CAD and PWS has been investigated: the results will be validated when further data become available; 2) this is an ex vivo study and the MRI data were taken after the blood vessels were fixed with formalin. Models based on in vivo data would have better vessel morphologies and be associated with more accurate stress/strain predictions; 3) isotropic models were used for vessel and plaque material properties in this paper – this could be improved by using anisotropic models in the future; 4) the bending of the vessel was not considered because this is an ex vivo study and bending data were not available. Cyclic bending could be considered when in vivo data become available. Models from both groups generally had the same limitations in this study, so any differences between the groups should be considered statistically meaningful; 5) arm systole and diastole pressures were used in the simulations because pressure conditions at the location of the plaque were not available.

5. Conclusions

In this study, a possible relationship between PWS and death from CAD was investigated using 3D FSI models based on ex vivo MRI data from 12 patients, where six had died of CAD and six had died of non-CAD causes. The CPWS in the CAD group was found to be statistically significantly higher than that in the non-CAD group. There were no statistically significant differences in plaque burden and GMPWS between the two groups. These results indicate that CPWS conditions may lead to more accurate assessment of plaque vulnerability. Large-scale studies are needed to validate these findings.