Exploring the genetic architecture of alcohol dependence in African-Americans via analysis of a genomewide set of common variants

Abstract

Alcohol dependence (AD) is a complex psychiatric disorder that affects about 12.5% of US adults. Genetic factors play a major role in the development of AD.

We conducted a genome-wide association study in 2875 African Americans (AA) including 1719 AD cases and 1156 controls. We used the Illumina Omni 1-Quad microarray, which yielded 769,498 single-nucleotide polymorphisms (SNPs) after quality control. To explore the genetic architecture of AD, we estimated the variance that could be explained by all SNPs and subsets of SNPs using two different approaches to genome partitioning.

We found that 23.9% (s.e. 9.3%) of the phenotypic variance could be explained by using all of the common SNPs on the array. We also found a significant linear relationship between the proportion of the top SNPs used and the phenotypic variance explained by them. Based on genome partitioning of common variants, we also observed a significant linear relationship between the variance explained by a chromosome and its length. Chromosome 4, known to contain several AD risk genes, accounted for excess risk in proportion to its length. By functional partitioning, we found that the genetic variants within 20 kb of genes explained 17.5% (s.e. 11.4%) of the phenotypic variance. Our findings are consistent with the generally accepted view that AD is a highly polygenic trait, i.e., the genetic risk in AD appears to be conferred by multiple variants, each of which may have a small or moderate effect.

1 Introduction

AD is a substance use disorder that affects about 12.5% of American adults at some time in their lives [9]. Alcohol misuse leads to physical and mental harm and serious social problems and contributes to the high cost of medical care.

Much progress has been made in our understanding of the genetic basis of AD. About 50-60% of the phenotypic variance of AD can be accounted for by genetic factors [8,24]. In recent years, millions of SNPs have been genotyped in genome-wide association studies (GWAS) to identify loci that underlie AD [6,3]. Because a million or more statistical tests are performed in GWAS, a stringent statistical significance threshold (e.g., 5 × 10⁻⁸) must be used in GWAS to control the false positive rate. Despite this stringent criterion, several loci have been implicated as contributing to the etiology of AD. To name a few, two closely linked intergenic SNPs (rs7590720, P = 9.72×10⁻⁹ and rs1344694, P = 1.69 × 10⁻⁸) located on chromosomal region 2q35 were genome-wide significant in a German population [28]. From a GWAS in Japanese, a cluster of 12 SNPs in the ALDH2 gene were significantly associated with AD [25]. The strong effect of ALDH2 on AD risk in Asian populations has been confirmed by meta-analysis [14] and by a recent GWAS conducted by us in a Chinese population [22].

Despite this progress, the identified susceptibility loci explain only a small fraction (approximately, < 2%) of the AD heritability [1]. This phenomenon is known as “missing heritability” [17]. Therefore, many genetic variants that influence risk for AD remain undiscovered [7]. In fact, many variants of small effect are unlikely to be identified individually given the relatively small samples that are available and the stringent significance threshold that is required. In this study, we explored the genetic architecture of AD in African-Americans via analysis of a genomewide set of common variants, adopting the framework proposed by Yang et al. [31,33].

2 Methods

2.1 Data collection

A total of 3318 African Americans (AAs) were recruited for studies of the genetics of drug or alcohol dependence at five US sites: Yale University School of Medicine, the University of Connecticut Health Center, the University of Pennsylvania School of Medicine, the Medical University of South Carolina, and McLean Hospital (Harvard Medical School). The samples consisted of small nuclear families (SNFs) originally collected for linkage studies, and, mostly, unrelated individuals. All subjects were interviewed using an electronic version of the Semi-Structured Assessment for Drug Dependence and Alcoholism (SSADDA) [19] to derive diagnoses for major psychiatric traits according to DSM-IV criteria. Subjects gave written informed consent as approved by the institutional review board at each site, and certificates of confidentiality were obtained from NIDA and NIAAA.

2.2 Genotyping and Quality control

All DNA samples were genotyped on the Illumina HumanOmni1-Quad v1.0 microarray containing 988,306 autosomal SNPs. Genotyping was conducted at the Center for Inherited Disease Research (CIDR) and the Yale Center for Genome Analysis (YCGA). SNP genotypes were called using GenomeStudio software V2011.1 and genotyping module version 1.8.4 (Illumina, San Diego, CA, USA).

For quality control, we removed SNPs with a missing rate > 0.01. We tested for consistency with Hardy-Weinberg Equilibrium expectations and excluded SNPs with P-value < 0.0001. SNPs with minor allele frequency (MAF) < 5% were also removed to focus on the analysis of common variants. Genetic relationships were examined in the family-based sample by calculating pairwise identity by descent (IBD) proportion estimates using PLINK [21]. Thirty-six subjects with missing phenotypes were excluded in our analysis. In addition, 407 subjects with alcohol abuse were removed because their affection status was uncertain. After all data cleaning and quality control (QC) was completed, there were 2875 individuals and 769,498 SNPs for analysis. Finally, our AD sample consists of 1156 controls (405 males and 706 females) and 1719 cases (1004 males and 715 females). Among the 1156 AD controls, there are 178 and 612 cases of opioid dependence and cocaine dependence, respectively.

2.3 Statistical analysis

2.3.1 Estimation of variance explained by all genotyped SNPs

We used the linear mixed model (LMM)-based approach to estimate the variance components. We note two key assumptions under this modeling framework when we interpret the results. First, the model assumes additive genetic effects. As a result, the estimated variance should be less than the total variance that can be explained by all genetic factors, e.g., dominance effects and epistasis are excluded. Second, the estimation is based on the genotyped markers. However, information from non-genotyped markers may be partially captured in this estimation due to linkage disequilibrium. For convenience, the estimated variance is referred to as “chip heritability” (see ref. [26] for a more detailed discussion of heritability estimation).

We used recently developed statistical methods [12, 31] to estimate the variance explained by all autosomal markers. Specifically, we considered the following linear mixed model

$$\begin{array}{lll}\mathbf{y}& =& \mathbf{X}\mathit{\beta }+\mathbf{Wu}+\mathbf{e},\\ \mathbf{u}& ~& N(0,{\sigma }_u^2\mathbf{I}),\\ \mathbf{e}& ~& N(0,{\sigma }_e^2\mathbf{I}),\end{array}$$ (1)

where y ∈ ℝ^n×1 is the response vector; X ∈ ℝ^n×c is the design matrix of fixed effects including the intercept and other covariates such as age, sex and principal components, β is the vector for regression coefficients of the covariates; W = [w_im] ∈ ℝ^n×M is the standardized genotype matrix given by

$$w_{\mathit{im}}=\frac{(g_{\mathit{im}}-p_m)}{\sqrt{2p_m(1-p_m)}},$$ (2)

where g_im ∈ {0, 1, 2} is the number of copies of the reference allele for the SNP of the individual and p_m is the frequency of the reference allele; u is the random effect from, $N(0,{\sigma }_u^2\mathbf{I})$, and e is the residual error with variance ${\sigma }_e^2$. Here n is the sample size, c is the number of fixed effects and M is the number of random effects. After integrating out u and e, we have

$$\mathbf{y}~N(\mathbf{X}\mathit{\beta },{\mathbf{WW}}^T{\sigma }_u^2+{\sigma }_e^2\mathbf{I}).$$ (3)

The genetic relationship matrix (GRM) is defined as $\mathbf{A}=\frac{{\mathbf{WW}}^T}{M}$ and the proportion of the phenotype variance explained by the genotyped markers in W, is given by $h^2=\frac{M{\sigma }_u^2}{M{\sigma }_u^2+{\sigma }_e^2}$. For case-control studies, the estimated heritability (h²) is transformed on the liability scale [12].

Since the AA population is admixed, standardization of the genotype matrix based on Equation (2) does not consider the different admixed proportions of different individuals. Recently, an estimator of genetic relationship matrix named REAP was proposed to adjust the allele frequency in the admixed population [27]. Specifically, instead of using a single allele frequency for all individuals, an individual-specific allele frequency is used to standardize the genotype matrix

$$w_{\mathit{im}}=\frac{(g_{\mathit{im}}-p_{\mathit{im}})}{\sqrt{2p_{\mathit{im}}(1-p_{\mathit{im}})}},$$ (4)

where p_im is the expected allele frequency of individual i at the m-th marker. Let ${\mathbf{q}}_m={[q_m^1,\dots ,q_m^K]}^T$ denote the vector of K ancestral population-specific allele frequencies of the m-th marker, and ${\mathbf{a}}_i={[a_i^1,\dots ,a_i^K]}^T$ denote the proportion of ancestry for individual i. The expect allele frequency for individual i at the m-th marker is given by $p_{\mathit{im}}={\mathbf{a}}_i^T{\mathbf{q}}_m$. For our data analysis, q_m and a_i were inferred using the ADMIXTURE software [2], with YRI and CEU data from HapMap used as the reference panel.

To reduce the effect of common environmental factors shared by related individuals, the genetic relationship matrix A = [A_ij] for all samples was calculated first. If A_ij was larger than a specified threshold, either individual i or j was excluded in the analysis. In our first approach, we chose a threshold of 0.025, which implied that the individuals more closely related than second cousins are excluded in our analysis. Ultimately, we retained 1,838 unrelated individuals. We included age, sex and five principal components as fixed effects. Then we estimated the variance parameters ${\sigma }_u^2$ and ${\sigma }_e^2$ using the Restricted maximum likelihood method (REML) [12,32].

Although the above approach can reduce the effect of shared environment, it may exclude many samples and substantially reduce statistical power. To maximize the use of the collected samples, we considered a second approach suggested by Do et al [4], in which a common variance component is used to account for the impact of shared environment. Specifically, we considered the following linear mixed model

$$\begin{array}{lll}\mathbf{y}& =& \mathbf{X}\mathit{\beta }+\mathbf{Wu}+\mathbf{Cv}+\mathbf{e},\\ \mathbf{u}& ~& N(0,{\sigma }_u^2\mathbf{I}),\\ \mathbf{v}& ~& N(0,{\sigma }_{\upsilon }^2\mathbf{I}),\\ \mathbf{e}& ~& N(0,{\sigma }_e^2\mathbf{I}),\end{array}$$ (5)

where v is the random effect accounting for the shared environment, C = [c_ij] ∈ ℝ^n×F is its design matrix, and F is the number of families. The design matrix C is an incidence matrix, i.e., c_ij = 1 if the i-th individual belongs to the j-th family, otherwise c_ij = 0. Under this model setting, it is assumed that, the family members within the j-th family share the same environmental factor captured by the random effect v_j and these random effects share a common variance component ${\sigma }_{\upsilon }^2$. The advantage of this model is that it makes full use of the collected samples, but its estimation may be an approximation because the individuals within a family may not have the same environmental impact.

2.3.2 Estimation of variance explained by top ranking SNPs

To explore further the genetic architecture of AD, we estimated the variance explained by the top ranking SNPs based on different P-value thresholds. To minimize the effect of the “winners curse” [35], we used the following strategy:

• Step 1: We randomly partitioned the entire data set into two halves, denoted as D⁽¹⁾ and D⁽²⁾.

• Step 2: We used the first half of the data, D⁽¹⁾, to perform the association test and calculate the P-values. To account simultaneously for the confounding effects of population structure, family structure, and cryptic relatedness, we used LMM [11,34], which is capable of correcting for these confounding effects [20,23]. Specifically, we used the GEMMA program [34] to calculate the P-values based on D⁽¹⁾.

• We selected the top ranking SNPs based on their P-values using nine different P-value thresholds [0.5, 0.4, 0.3, 0.2, 0.1, 0.05, 0.01, 0.005, 0.001], and used the samples in D⁽²⁾ to fit LMM for chip-heritability estimation, as described in the previous section.

• Step 4: We repeated Steps 1-3 B times. Here we chose B to be 50.

2.3.3 Variance estimation in genome partitioning

When the entire genome is partitioned in K parts, a multiple variance components model can be used to jointly estimate the variance components [33],

$$\begin{array}{lll}\mathbf{y}& =& \mathbf{X}\mathit{\beta }+\sum _{k=1}^{k=K}{\mathbf{W}}_k\mathbf{u}+\mathbf{Cv}+\mathbf{e},\\ {\mathbf{u}}_k& ~& N(0,{\sigma }_{u_k}^2\mathbf{I}),\\ \mathbf{v}& ~& N(0,{\sigma }_{\upsilon }^2\mathbf{I}),\\ \mathbf{e}& ~& N(0,{\sigma }_e^2\mathbf{I}),\end{array}$$ (6)

where W_k is the standardized genotype matrix corresponding to the k-th part of the genome, and ${\sigma }_{u_k}^2$ is the corresponding variance component. Similarly, the proportion of variance explained by the k-th part is given by $h_k^2=\frac{M_k{\sigma }_{u_k}^2}{{\sum }_k{M}_k{\sigma }_{u_k}^2+{\sigma }_e^2}$, where M_k is the number of markers in the k-th part. In this study, we used two approaches:

• Partitioning the genome into chromosomes.

• Partitioning the genome into genic and intergenic regions.

3 Results

3.1 Variance explained by all autosomal SNPs

Assuming the prevalence of AD to be 10%, we estimated that 22.1% (s.e. 17.7%) of the phenotypic variance could be explained by the common SNPs using the first approach.

With the second approach, the estimated proportion of variance explained by genetic variation and shared environmental factors was 23.9 % (s.e. 9.3%) and 3.9% (s.e. 1.5%), respectively.

The estimates obtained from the two approaches differed by less than 2%, thus, they appear to have been robust to the different analytical approaches. The standard error for the estimate from the second approach was smaller, presumably because it made use of all available samples in the analysis.

3.2 Variance explained by the top ranking SNPs

The left panel of Figure 1 shows that, as expected, more SNPs were selected as the P-value threshold became less stringent. The proportion of selected SNPs was almost identical to the P-value threshold, indicating that the P-values obtained in the association test were not inflated. SNPs with P ≤ 0.001 explained only 0.68% of the phenotypic variance (the median value based on 50 random partitions, the right panel of Figure 1). As the P-value threshold became less stringent, the explanatory value of the sets of SNPs increased and then plateaued; about 17.6% of the phenotypic variance could be explained by SNPs with P ≤ 0.1. This indicates that most of the chip-heritability can be attributed to SNPs with P ≤ 0.1. We further checked the linear relationship between the proportion of SNPs and their explained variance based on 50 random partitions; the obtained R² = 19.8%(P = 1.62 × 10⁻¹⁴), reflecting a highly significant association between the proportion of SNPs and their explained variance.

Fig. 1.

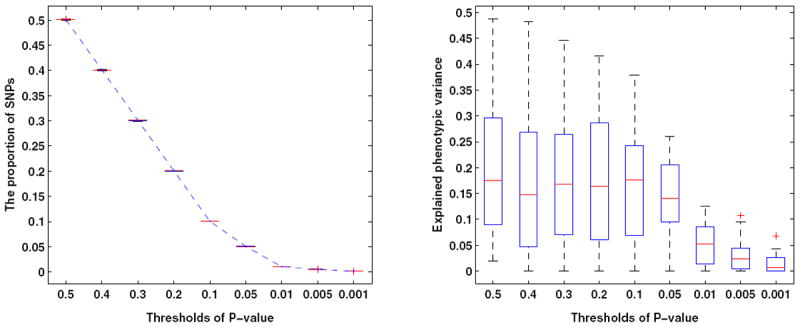
Left panel: The proportion of SNPs selected using different P-value thresholds. Right panel: Variance explained by top ranking SNPs based on different P-value thresholds. The results were obtained based on 50 random partitions of the entire data set to avoid winner’s curse.

3.3 Genome partition of common genetic variants

3.3.1 Partitioning the genome by chromosome

We first estimated the genetic relationship matrix based on SNPs on each autosome using all individuals. Next we fitted a linear regression to explore the relationship between the number of known genes in a chromosome and its explained variance. This result is shown in the left panel of Figure 2. The R² was 0.14% (P-value= 0.8685), indicating that there is no significant association between them. When we considered the relationship between the length of a chromosome and its explained variance, we observed a significant linear relationship between them (R² = 20.75%, P-value= 0.033), as shown in the right panel of Figure 2.

Fig. 2.

Variance explained by each individual chromosome. Left panel: number of genes vs. explained variance. The R² is 0.14% (P-value= 0.8685), which shows no significant association between the number of genes and the explained variance. Right panel: chromosome length vs. explained variance. The R² is 21.2% (P-value=0.031), which reflects a significant association between chromosome length and explained variance.

3.3.2 Partitioning the genome into genic and intergenic regions

Based on information available from the UCSC Genome Browser hg19 assembly [18], we used ANNOVAR [30] to annotate all the SNPs. We mapped all SNPs to the following four regions: exon, intron, intergenic, and other regions (e.g., downstream, upstream, splicing). For simplicity, we then partitioned the entire genome into genic and intergenic regions. With d as the smallest distance between a SNP and all genes, a SNP was assigned to the intergenic region if d ≥ τ (the distance threshold). For example, when τ = 10 kb, a SNP is not within 10 kb of any gene and would be assigned to the intergenic region. This resulted in 9% of SNPs in the intergenic region being assigned to the genic region. The partitioning shown in the left panel of Figure 3 corresponds to τ = 10 kb. Clearly, more SNPs were assigned to the genic region as the threshold τ increased. In the following analysis, we increased τ from 0 kb to 50 kb.

Fig. 3.

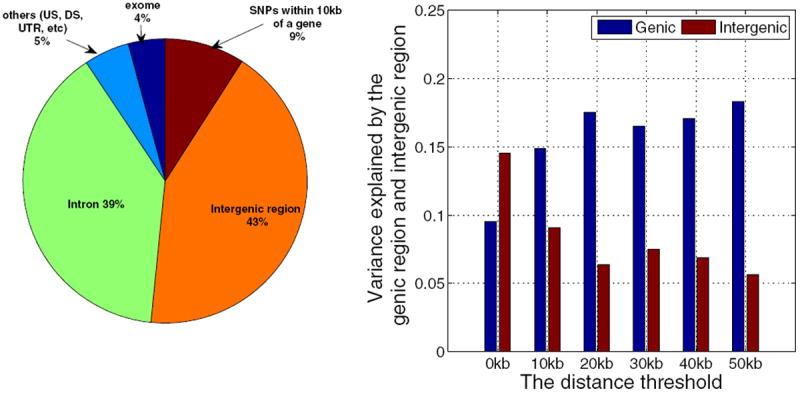
Variance explained by the genic and intergenic regions. Left panel: functional partition of all SNPs. The entire genome was divided into four categories – exons (4%), introns (39%), intergenic regions, and others (e.g., downstream (DS), upstream (US) and untranslated region (UTR)). We defined the intergenic region based on the minimal distance d between a SNP and all genes. A SNP was assigned to the intergenic region if d ≥ τ (the distance threshold), otherwise it was assigned to the genic region. Given τ = 0 kb, the proportion of SNPs in each category is shown in the figure, i.e., 52% of the SNPs were in the intergenic region and the remaining SNPs were in the genic region. Given τ = 10 kb, about 9% of SNPs were partitioned to the genic region, and thus the intergenic region was reduced to 43%. Right panel: Variance explained by the genic and intergenic regions. As the distance threshold increased, more SNPs were partitioned into the genic region. The variance explained by the genic region increased quickly when τ increased from 0 kb to 20 kb, and remained almost the same when τ increased from 20 kb to 50 kb.

For a given threshold τ, we calculated two GRMs based on SNPs in the genic and intergenic regions, and then fitted an LMM to estimate how much variance could be explained by these two parts. The results are shown in the right panel of Figure 3. For τ = 0 kb, the genic region, composed of 48% of all SNPs, explained only about 9.5% (s.e. 11.9%) of the phenotypic variance, while the intergenic region, composed of 52% of SNPs, explained 14.5% (s.e. 12.2%) of the phenotypic variance. As the threshold increased to 10 kb, the variance explained by the genic region quickly increased to 14.9% (s.e. 11.7%). After that, the variance explained by the genic region increased slowly. When the threshold increased to 20 kb, the explained variance increased to 17.5% (s.e. 11.4%). For the intergenic region, the explained variance dropped quickly when the threshold increased to 20 kb and then remained almost the same. These findings indicate that most AD-associated common genetic variants are likely to be distributed within 10-20 kb of a gene.

4 Discussion

The present study provides insight into the nature of the contribution of common genetic variation to AD risk. The most important implication of this study is that the estimated chip-heritability can account for about half of the broad-sense heritability of AD. Interestingly, a recent study [29] reported the chip-heritability of AD to be 21%, based on 7,188 Caucasian participants. This evidence suggests that about half of the “missing” heritability is not actually missing but jointly accounted for by small or moderate effects of common variants.

We were able to explore the genetic architecture of AD through genome partitioning. We found that the variance explained by each chromosome is proportional to chromosome length rather than the number of genes. We also found that the genetic variants within 10-20 kb of all genes make an important contribution to the phenotypic variance.

Interestingly, our partition-by-chromosome provided evidence for a greater proportional contribution to AD risk in AAs of common variants mapped to chromosome 4. Numerous known AD risk genes map to chromosome 4, most notably those that encode a set of alcohol dehydrogenase genes (e.g., [15]) and a set of GABA receptor subunits, most notably GABRA2 [5]. Although most published evidence obtains from European-ancestry populations (and Asian-ancestry populations for ADH1B [13]), several investigators have provided evidence directly relevant to African-ancestry populations as well [10,16]. This result, we believe, adds credence to the findings overall.

In summary, we explored the genetic architecture of AD in the AA population via the analysis of common variants. Our results support the notion that AD is a highly polygenic trait, i.e., there exist many risk variants conferring small or moderate effects. The limited sample size is a major issue with respect to the goal of identifying the causal variants. However, sample recruitment is expensive and time-consuming. Some alternative ways to boost statistical power of GWAS data analysis can be considered. First, accumulating evidence suggests that different complex human traits are genetically correlated, i.e., multiple traits share common genetic bases, which is known as pleiotropy. It is a promising direction to exploit the pleiotropy between AD and other psychiatric disorders by combining multiple GWAS sets, because the sample size can be effectively increased. Our findings also show that, as would reasonably have been predicted, SNPs do not equally contribute to the AD risk (nor do chromosome or functional units; chromosome 4 (physical region) and regions within 20kb of genes (functional region) contribute more). Thus, incorporating biologically relevant information could be an effective way to prioritize SNPs. Other examples of this general strategic approach include use of eQTLs related to brain function, or regulatory regions annotated from ENCODE data. We expect that more genetic risk variants can be identified by simultaneously integrating multiple GWAS data sets and multiple sources of biological relevant information.