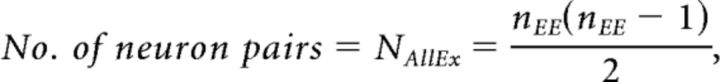Long-Term Recordings Improve the Detection of Weak Excitatory–Excitatory Connections in Rat Prefrontal Cortex

Abstract

Characterization of synaptic connectivity is essential to understanding neural circuit dynamics. For extracellularly recorded spike trains, indirect evidence for connectivity can be inferred from short-latency peaks in the correlogram between two neurons. Despite their predominance in cortex, however, significant interactions between excitatory neurons (E) have been hard to detect because of their intrinsic weakness. By taking advantage of long duration recordings, up to 25 h, from rat prefrontal cortex, we found that 7.6% of the recorded pyramidal neurons are connected. This corresponds to ∼70% of the local E–E connection probability that has been reported by paired intracellular recordings (11.6%). This value is significantly higher than previous reports from extracellular recordings, but still a substantial underestimate. Our analysis showed that long recording times and strict significance thresholds are necessary to detect weak connections while avoiding false-positive results, but will likely still leave many excitatory connections undetected. In addition, we found that hyper-reciprocity of connections in prefrontal cortex that was shown previously by paired intracellular recordings was only present in short-distance, but not in long distance (∼300 micrometers or more) interactions. As hyper-reciprocity is restricted to local clusters, it might be a minicolumnar effect. Given the current surge of interest in very high-density neural spike recording (e.g., NIH BRAIN Project) it is of paramount importance that we have statistically reliable methods for estimating connectivity from cross-correlation analysis available. We provide an important step in this direction.

Introduction

Characterization of synaptic interactions on a large scale is essential to understand information processing in neural circuits. In an attempt to characterize local circuit dynamics, combined electrophysiological and imaging techniques have started to map out neocortical circuits (Bock et al., 2011; Ko et al., 2011). With recent developments in multielectrode recording technology, it has also become possible to monitor large numbers of neurons simultaneously with high temporal resolution (McNaughton et al., 1983; Csicsvari et al., 2003; Buzsaki, 2004). Even though this number is still small relative to the total number of neurons, one advantage of ensemble recordings is that it can greatly facilitate the study of spike-train interactions, because the number of neuron pairs increases as the square of the number of units recorded. The obtained spike trains are often analyzed by cross-correlations to infer synaptic interactions (Alonso and Martinez, 1998; Ostojic et al., 2009). The cross-correlogram, a well established technique to investigate temporal relationships between neural spikes, describes the covariance between the binned spike trains of two neurons at various time lags (Perkel et al., 1967b; Kirkwood, 1979; Aertsen and Gerstein, 1985; Brown et al., 2004). A plausible argument for synaptic connectivity can be made from the presence of short-latency peaks in the correlogram within the range of central glutamatergic EPSP and GABAergic IPSP rise times (Csicsvari et al., 1998; Barthó et al., 2004; Fujisawa et al., 2008).

Despite the potential usefulness of the cross-correlation method, the detection of excitatory interactions between pyramidal neurons (E–E interaction) has been difficult (Barthó et al., 2004; Fujisawa et al., 2008), because these interactions are generally weak (McNaughton, 1980; Mason et al., 1991; Deuchars et al., 1994; Markram et al., 1997; Thomson and Deuchars, 1997; Reyes and Sakmann, 1999; Thomson et al., 2002). Excitatory synaptic strength of intracellularly measured cortical connections has been shown to follow a lognormal distribution (Song et al., 2005), suggesting that a very small number of strong connections are embedded in a large number of weak connections. In addition, the duration of typical ensemble recordings is not long (up to a few hours). The consequence is a limited sampling of spike occurrences and also a poor sampling of the possible state-space occupancy distribution (Perkel et al., 1967a,b). Cells are tuned to respond to a given set of input vectors and some vectors in the set may never occur during the sampling epoch. Thus, for some connected cells in the sample, the input which brings them close enough to threshold to allow synaptic interaction may not occur during the sampling period. In other words, the effective contribution of cell A to the firing of cell B is not independent of the activity of other cells in the network. Hence, some connections may not be visible in spike cross-correlograms from a given sample epoch.

To explore these issues, we analyzed neural ensembles from rat prefrontal cortex and estimated the asymptotic detection probability of excitatory connections and investigated the nature of the distribution of the detected excitatory connections.

Materials and Methods

Recording experiment.

Twenty-five hour continuous, multineuron recording datasets were collected from three adult male Brown Norway/Fischer 344 hybrid rats that were trained to run a spatial sequence task (Euston et al., 2007) and were also subjected to a novel object exposure procedure (Tatsuno et al., 2006). The recording sessions were divided into two 12 h sleep/rest sessions interrupted by 1 h behavior, which was either the sequence task or the novel object exposure, to yield a total recording duration of 25 h per recording session. The animals were implanted with a hyperdrive with 12 independently movable tetrodes (Gothard et al., 1996; <1 MΩ impedance) in the left medial prefrontal cortex (3.2 mm AP, 1.3 mm ML relative to bregma) to record from dorsal anterior cingulate cortex and prelimbic cortex. The tetrodes were used to record extracellular single units. The anatomical positions of the tetrodes were confirmed histologically.

Two additional probes were placed 4–5 mm deep in the medial prefrontal cortex to record a differential reference signal. The animal's position was tracked at 60 frames/s using LEDs mounted on the headstage that were detected by a color camera that was mounted on the ceiling of the recording room (∼0.33 cm/pixel). The thresholded signals were recorded with a Cheetah Data Acquisition System (Neuralynx), digitized at 32 kHz and bandpass filtered between 600 Hz and 6 kHz. Local field potential data were filtered between 1 and 475 Hz and sampled at 2 kHz.

Animal care and surgeries were conducted in accordance with National Institutes of Health guidelines and approved Institutional Animal Care and Use Committee protocols. After surgery, rats were administered 26 mg of acetaminophen (children's Tylenol, McNeil) and also received 2.7 mg/ml acetaminophen in the drinking water for 1–2 d after surgery. In addition, they were given oral ampicillin on a 10 d on/off regimen for the duration of the experiment.

Spike sorting.

Spiking activity was analyzed offline using an automated spike-sorting algorithm (KlustaKwik by K.D. Harris, University College London, London, UK) to isolate units and separate them from noise. The resulting clusters were manually refined using cluster cutting software (MClust 3.0 by A.D. Redish, University of Minnesota, Minneapolis, MN, with customizations by P. Lipa, University of Arizona, Tucson, AZ, S. L. Cowen, University of Arizona, Tucson, AZ, and D. Euston, University of Lethbridge, Canada) in a multiparameter space including features, such as energy (area under the waveform), peak to trough distance, principal component, time (to control for stability of the recording of the unit over the entire recording duration), and cross correlograms. In addition, all units were verified by waveform visualization software (WaveformCutter 1.0 by S. Cowen). Only units with <0.3% interspike intervals falling within 2 ms refractory period were accepted.

During long recording times, the position of the electrode can shift and, consequently, the shape of the recorded waveform can change. This can lead to errors in spike sorting and can cause false temporal firing relationships between neuron pairs. For this reason, we only included neurons that show good isolation and little variance in their waveforms and Z-scored peak amplitudes over the entire length of recordings (Fig. 1a). As a measure for the stability of the neurons, we calculated the fractional change of firing rate between the first and last 4 h periods. We found that the fractional change for the majority (95%) of the neurons that were selected by the first criteria was <80%, suggesting that the neurons were stable for the 25 h period of recordings.

Figure 1.

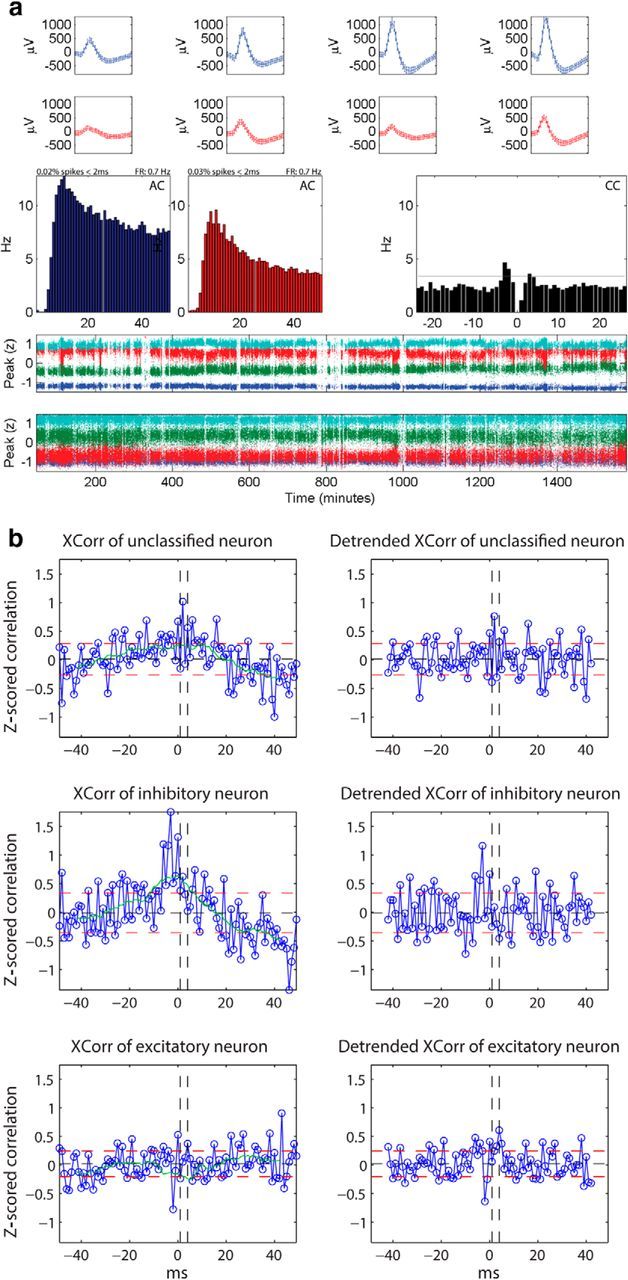
a, Stability of neurons and cleanness of clusters recorded on the same tetrode. Average waveforms (top rows), autocorrelograms (AC, middle left rows), cross correlogram (CC, middle right rows), and time plots (two bottom rows) of two excitatory neurons recorded on the same tetrode are depicted. The percentage of spikes within 2 ms of refractory period included in the cluster and the firing rate are indicated above the autocorrelograms. Both clusters show distinct waveforms (each waveform is depicted for a 1 ms window) and have clean refractory periods (0.02 and 0.03%, respectively, spikes within 2 ms of refractory period). Their cross correlogram is reciprocally significant (EE2) at a significance threshold of α = 10⁻⁵ (gray horizontal line). b, Classification of neurons. In the left column, the average Z-scored cross-correlations of three different neurons, without the detrending procedure, are depicted in blue. Right, The corresponding detrended average Z-scored cross-correlations are plotted. The black horizontal dashed line depicts the mean, the red horizontal dashed lines depict one SD above and below the mean, respectively, and the green line is the moving average of the Z-scored cross-correlation computed with a moving window of 15 ms. The vertical black dashed lines represent the limits of the window of interest between 1 and 4 ms, within which short-latency peaks or troughs are assessed for classification. The top row represents an unclassified neuron that, without detrending, would have been classified possibly falsely as excitatory. The middle row shows an inhibitory neuron that without detrending, would have been classified as excitatory. The last row represents an excitatory neuron that would have been left unclassified without detrending.

In addition, inspired by the recent finding by Mizuseki and Buzsaki (2013) that the distribution of firing rates follows a lognormal distribution in the hippocampal formation, we also calculated the distribution of firing rate of our data. Figure 2c shows the firing rate distribution during the first and last 4 h of recording. We found that not only does the firing rate follow a lognormal distribution, but also the shape of the distribution did not change between the two periods. We also confirmed that the firing rate calculated of the entire recording follows a lognormal distribution.

Figure 2.

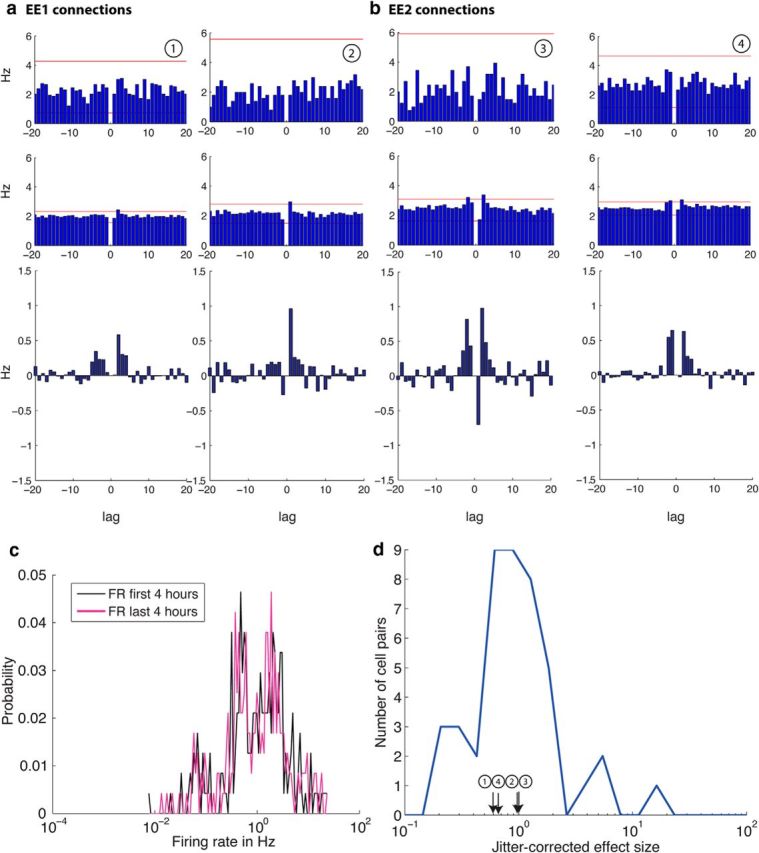
Examples of cross correlograms between two putative pyramidal neurons that are unidirectionally connected (a, EE1 connections) or reciprocally connected (b, EE2 connections).Top, Cross-correlations for 1 h spike trains and in the second row, cross-correlations for the same neurons pairs for 25 h spike trains are shown with a window size of 20 ms and a bin size of 1 ms. The red horizontal lines depict the significance level (α = abs) determined by 1000 spike-jittered cross-correlations. Note the improved signal-to-noise ratio in the 25 h cross correlograms (middle row), which enables the detection of small, short latency peaks. The bottom row shows the jitter corrected correlograms for 25 h obtained by subtracting the mean of the jittered cross correlograms of each cell pair from the original cross correlogram (middle row). c, The distribution of firing rate probability among all neurons for the first 4 h (black) and last 4 h (pink) of recording. The firing rate distribution for both recording intervals is lognormal. Note the log scale on the x-axis. d, The distribution of the jitter corrected effect size for EE1 and EE2 connections. The distribution of the jitter corrected peaks of the significant cross-correlations is lognormal as previously shown by Mizuseki and Buzsaki (2013). The peaks of the neuron pairs shown in a and b are indicated in the plot.

Neuron classification.

Neurons are classified into excitatory, inhibitory, or unclassified based on statistical dependency with other neurons. First, for each reference neuron, cross-correlations against all other neurons were calculated with a bin size of 1 ms and a window size of ±50 ms. Second, each cross-correlation was converted to a Z-score with its mean and SD. This alleviated the problem of spike rate differences. Next, we calculated the moving average (window size: 15 ms) of the Z-scored cross-correlations and subtracted it from the original signal to obtain a detrended Z-scored cross-correlation. This procedure removed modulations in intermediate temporal ranges that are slower than monosynaptic interactions. Correlations that showed putative common input (measured as a peak or trough encompassing lag [−1:1]) were excluded from further cell classification analysis. Cross-correlation pairs that did not contain relevant information were also removed [if none of the Z-scored correlation values within [−4, 4] exceeded 2 or −2, the pair was removed]. Finally, the average cross-correlation of the remaining pairs was calculated (Fig. 1b). Mean and 1 SD of the average cross-correlation for the bins outside of [−4, 4] ms were used as a threshold to determine whether a bin within [1, 4] ms has a relevant correlation signal for cell classification; if at least one bin exceeded the upper threshold (mean + 1 SD) and no bin undershot the lower threshold (mean − 1 SD), the reference neuron was classified as a putative excitatory neuron. If at least one bin undershot the lower threshold (mean − 1 SD) and no bin exceeded the upper threshold (mean + 1 SD), the reference neuron was classified as a putative inhibitory neuron. Otherwise, the reference neuron was left unclassified. We also inspected all individual cross-correlations visually to verify whether the decision of the algorithm we applied on the average detrended Z-scored cross-correlations was consistent with the judgment made by human observers. In summary, this procedure aims at classifying a reference neuron based on the average statistical influence of the reference neuron to all possible postsynaptic target neurons.

Cross-correlation analysis.

All simultaneously recorded neurons from each animal were cross correlated with each other with a bin size of 1 ms. The cross-correlation values were normalized by the firing rate of the reference neuron. This procedure resulted in n·(n − 1)/2 correlation pairs (n = number of recorded units; self-correlation was excluded). For each neuron pair, the spikes of one spike train were jittered randomly within an interval of [−5, 5] ms to break up the short-latency relationships between spikes. The bin size and jitter interval were chosen based on synaptic integration times in frontal cortex neurons in vivo (Léger et al., 2005). Then, the jittered spike trains were cross-correlated with a bin size of 1 ms. This procedure was repeated 1000 times to compute a surrogate dataset of cross-correlations. Various significance thresholds (α levels) were computed from the distribution of jittered data to detect peaks or troughs with short latency and duration (≤2 ms) in the cell pair correlations (Barthó et al., 2004; Fujisawa et al., 2008): α levels used are 0.5, 0.2, 0.1, 0.05, 0.02, 0.01, 5 × 10⁻³, 2 × 10⁻³, 1 × 10⁻³, 5 × 10⁻⁴, 2 × 10⁻⁴, 1 × 10⁻⁴, 5 × 10⁻⁵, 2 × 10⁻⁵, 1 × 10⁻³, and the global min/max value (referred to as absolute limit: abs) which corresponds to the overall maximum and minimum values of all bins in the surrogate dataset. If a single bin exceeded the significance level within the first 4 ms before or after lag 0, the correlation was scored as significant excitation and the pair was considered monosynaptically connected. Similarly, if two neighboring bins undershot the significance level within the first 4 ms before or after lag 0, the connection was scored as significant inhibition (Barthó et al., 2004). This way, significance was tested for both possible directions of interaction between the two neurons. To verify our method and temporal window within which we assess significance of the short-latency peaks, we repeated the same analysis as described above for 4 ms windows ∼±25 ms and ±50 ms.

The length of the recording period used for the cross correlogram calculation was varied from 1 to 25 h with 1 h increments. First, for each hour segment and for a given significance level α, we constructed a matrix of significant cross-correlations for all possible nonoverlapping blocks (i.e., 25 blocks for 1 h segments, 12 blocks for 2 h segments, etc.). This resulted in a matrix with an entry for each significant correlation type EE1, EE2, EI1, EI2, IE1, II1, EU1, and IU1 (EE1 represents unidirectional excitation between two excitatory neurons; EE2 represents reciprocal excitation between excitatory neurons; EI1 represents unidirectional excitation from an excitatory neuron onto an inhibitory neuron; EI2 represents reciprocal connection between an inhibitory and an excitatory neuron; IE1 represents unidirectional inhibition from an inhibitory neuron onto an excitatory neuron; II1 represents unidirectional inhibition between two inhibitory neurons; EU1 represents unidirectional excitation from an excitatory neuron onto an unclassified neuron; IU1 represents unidirectional inhibition from an inhibitory neuron onto an unclassified neuron). Because swapping reference- and target-neurons results in the mirror image of the original cross correlogram, only the upper triangle of the result matrix was considered. We then summed the number of significant correlations for each correlation type. To estimate the distribution of the number of detected correlations for each hour segment, we used bootstrapping with replacement (Mooney and Duval, 1993; Hoffman and McNaughton, 2002). The matrix was randomly resampled with replacement as many times as needed to obtain 1000 samples for each hour segment. For instance, for the 1 h segment, each upper triangle of the 25 result matrices was resampled 40 times. For the 25 h segment, only one result matrix was obtained and was therefore resampled 1000 times. The median, 84^th and 16^th percentile were calculated to characterize the distribution. For the tetrode-wise analysis, the connection matrix of each tetrode was resampled with replacement 1000 times. The result was summed across tetrodes and datasets. Again, the median, 84^th and 16^th percentile of the bootstrapped sample distribution were calculated.

The experimentally derived detection probability of excitatory connections p_αⁿ for the significance level α and the recording length of n hours was defined as follows:

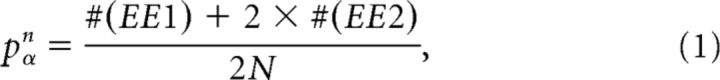where #(EE1) is the number of significant unidirectionally connected pairs, #(EE2) is the number of significant reciprocally connected pairs, and N is the total number of neuron pairs.

Extrapolation by fitting the statistical power function using simulated annealing.

To investigate how the experimentally derived detection probability of weak E–E connections p_αⁿ may improve beyond the recording duration of 25 h, we applied curve fitting based on statistical power. To obtain a reasonable estimate, we used a framework for the case that both the data from the alternative hypothesis and the data from the null hypothesis follow the normal distribution with a known SD. The statistical power function, defined as the probability of rejecting the null hypothesis when the alternative is true, is written as follows:

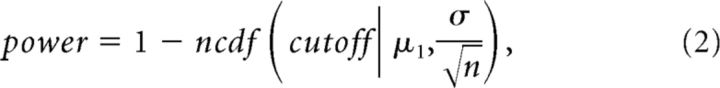where the cutoff is the threshold value for rejecting the null hypothesis. When the alternative is true, μ₁ is the mean of the alternative hypothesis (the mean peak cross-correlation value within −4 to +4 ms excluding 0), σ is the SD of the null and alternative hypotheses, n is the sample size (the length of recording in hours), and:

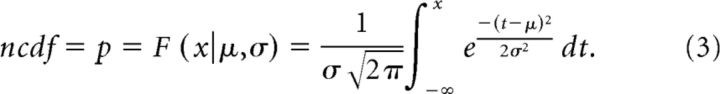Using the significance level α, the cutoff is written as follows:

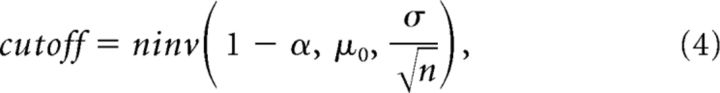where μ₀ is the mean of the null hypothesis (chance-level cross-correlation value estimated by spike-jittering) and:

Plugging Equation 4 into Equation 2 yields the following:

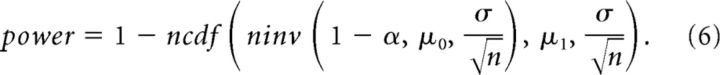We conjectured that the probability of detecting a significant cross-correlation between two neurons, if a connection exists and the conditions for its making a contribution to postsynaptic spiking are realized, follows the same form of statistical power. The fitted detection probability of excitatory connections C_αⁿ for the significance level α and the recording length of n hours can be obtained as follows:

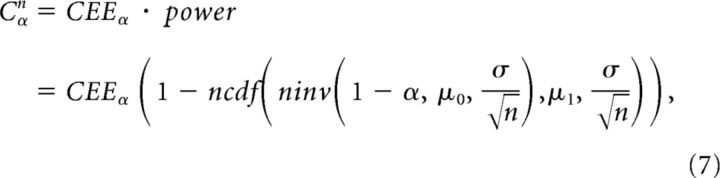where CEE_α is the asymptotic detection probability of excitatory connections p_αⁿ at the significance level α. Finally, to obtain a better fit, the significance level α and the SD σ in the right hand side in Equation 7 were treated as fitting parameters α_param and σ_param, respectively. This gives the final fitting equation as follows:

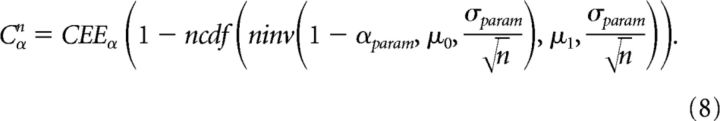In summary, CEE_α, α_param, and σ_param in Equation 8 were optimized to fit the data of the experimentally derived detection probability of weak E–E connections p_αⁿ. This yields the fitted detection probability of excitatory connections C_αⁿ. Note that in a standard testing of a normal mean with a known standard distribution, α and α_param are identical and they represent the significance level of the test. Similarly, σ and σ_param are identical and they represent the standard distribution of the null and alternative hypotheses. In this study, however, α_param was separated from α and σ_param was separated from σ, and they were treated as fitting parameters. This distinction was necessary to obtain a good fit to our experimental data. We speculate that it might be partly due to the fact that μ₁ follows a skewed continuous distribution rather than a normal distribution. Given the fact that many different fitting functions were indeed able to fit our experimental data almost equally well, but would produce greatly different asymptotes, we chose a fitting function that is based on statistical power.

Actual curve fitting was conducted by simulated annealing (Metropolis et al., 1953; Kirkpatrick et al., 1983) using MATLAB Global Optimization Toolbox (MathWorks). Simulated annealing is a well established, general optimization method that has been used as a powerful optimizer for n-body problems including the classic traveling salesman problem (Metropolis et al., 1953; Kirkpatrick et al., 1983). The method can be pictured as the physical process of first heating a material and then lowering the temperature slowly, which corresponds to minimizing the system's energy. More precisely, at a sufficiently high temperature, the system is slightly perturbed and the change of energy, ΔE, is calculated. The new state is accepted if ΔE is negative. If the energy increases, the new state is accepted under a certain probability (p = exp [− ΔE⧸(k_BT)], where k_B = Boltzmann constant and T = temperature) to avoid that the system gets stuck in local minima. This process is repeated many times at the current temperature. The temperature is slowly decremented until the system is frozen (Kirkpatrick et al., 1983). The method may not find the optimum solution but is most likely to find one of the near-optimum solutions. We ran 1000 optimization trials to select the best parameter values that would give the least sum of squares. See Table 2 for optimization results for all α levels. The r-squares, R²_AllEx and R²_AllExTT, were computed to estimate the goodness of fit of the optimized function to the data.

Table 2.

Optimization results for fitting the statistical power function (Eq. 8) to the experimental data p_αⁿ for all investigated α levels

α	CEEα, AllExTT	αparam, AllExTT	μ0	μ1	σparam, AllExTT	LSSAllExTT	R2AllExTT
0.5	46.29	0.415	1.83	2.2	0.267	62.649	0.36
0.2	39.18	0.470	1.83	2.2	1.042	20.919	0.94
0.1	30.09	0.271	1.83	2.2	0.691	10.824	0.98
0.05	24.73	0.166	1.83	2.2	0.631	8.583	0.98
0.02	21.39	0.090	1.83	2.19	0.612	6.378	0.99
0.01	19.01	0.060	1.83	2.2	0.582	4.222	0.99
5 × 10−3	18.13	0.040	1.83	2.2	0.572	3.806	0.99
2 × 10−3	17.43	0.032	1.83	2.2	0.606	4.147	0.99
1 × 10−3	16.74	0.026	1.83	2.2	0.617	3.488	0.99
5 × 10−4	14.70	0.020	1.83	2.2	0.578	2.834	0.99
2 × 10−4	11.63	0.014	1.83	2.2	0.508	3.092	0.99
1 × 10−4	10.73	0.012	1.83	2.2	0.507	2.555	0.99
5 × 10−5	10.20	0.009	1.83	2.2	0.487	3.307	0.98
2 × 10−5	9.45	0.010	1.83	2.2	0.506	2.507	0.98
1 × 10−5	8.85	0.009	1.83	2.2	0.489	2.952	0.98
abs	8.56	0.007	1.83	2.2	0.470	3.056	0.98

α	CEEα, AllEx	αparam, AllEx	μ0	μ1	σparam, AllEx	LSSAllEx	R2AllEx
0.5	57.02	0.7	1.83	2.2	0.804	4.706	0.97
0.2	37.85	0.49	1.83	2.2	0.913	5.264	0.98
0.1	25.53	0.35	1.83	2.2	0.864	2.539	0.99
0.05	17.00	0.22	1.83	2.2	0.741	1.858	0.99
0.02	10.94	0.11	1.83	2.19	0.649	1.577	0.99
0.01	8.06	0.06	1.83	2.2	0.577	1.383	0.98
5 × 10−3	8.02	0.06	1.83	2.2	0.573	1.739	0.98
2 × 10−3	5.34	0.02	1.83	2.2	0.583	0.478	0.99
1 × 10−3	4.76	0.02	1.83	2.2	0.629	0.214	0.99
5 × 10−4	4.21	0.02	1.83	2.2	0.637	0.189	0.99
2 × 10−4	3.27	0.02	1.83	2.2	0.603	0.102	0.99
1 × 10−4	2.65	0.02	1.83	2.2	0.603	0.056	0.99
5 × 10−5	2.53	0.01	1.83	2.2	0.554	0.063	0.99
2 × 10−5	2.18	0.01	1.83	2.2	0.529	0.083	0.99
1 × 10−5	2.15	0.01	1.83	2.2	0.535	0.076	0.99
abs	1.97	0	1.83	2.2	0.455	0.112	0.99

Top, The table shows the optimization results for all 16 α levels using simulated annealing for fitting the data p_αⁿ normalized by the number of excitatory neuron pairs per tetrode (N_AllExTT). The left column represents the significance thresholds (α) that were applied to count the number of significant cross-correlations. The parameter CEE_α,AllExTT (the asymptotic detection probability of excitatory connections p_αⁿ), α_{param,AllExTT} as well as σ_{param,AllExTT} were optimized using simulated annealing. μ₀ and μ₁ were estimated from the data; μ₀ is the mean of the jittered cross-correlations of all EE pairs. μ₁ is the mean of the peaks within the window [−4;4] of all significant EE cross-correlations. LSS (least sum of squares)_AllExTT shows the smallest LSS that was used to select the best fit out of the 1000 optimization trials. R²_AllExTT provides a measure for the goodness of the optimization result. Bottom, The table shows the simulated annealing optimization results for all 16 α levels for fitting the data normalized by the total number of excitatory neuron pairs (N_AllEx). CEE_α,AllEx, α_param,AllEx, and σ_param,AllEx were optimized using simulated annealing. The columns for α, μ₀, μ₁, LSS, and R_AllEx² are as described in the top.

Calculation of the effect size, h.

To compare the size of the short-latency peak across neuron pairs, we introduced the effect size h, which was defined as the normalized significant peak as follows:

where h_peak is the height of the maximum peak in the cross correlogram in [−4,−1] ms and [1,4] ms (i.e., the maximum peak taken of this 8 ms window) for unidirectional excitatory connections (EE1) and the height of the maximum peaks in the cross correlogram in [−4,−1] ms and [1,4] ms for reciprocal excitatory connections (EE2; i.e., the maximum peak taken of each 4 ms window), and μ_jitter and σ_jitter are the mean and SD of the jittered data for the corresponding cross-correlation, respectively (Fujisawa et al., 2008).

Results

Long-term recordings of 25 h length were analyzed using cross-correlations to identify excitatory connections between prefrontal putative pyramidal neurons. Six datasets obtained from three rats that were subjected to both a repeated sequence running task and novel object experience, were analyzed (two novel-object datasets were described previously; Tatsuno et al., 2006). Table 1 shows the number of neuron pairs in each session. In total, we analyzed 237 neurons and 4787 correlation pairs. An example of units included in the analysis is shown in Figure 1a. We classified the neurons into excitatory (54%), inhibitory (8%), and unclassified neurons (38%) based on their overall short-latency effects on postsynaptic neurons (see Materials and Methods; Fig. 1b), as the different classes were not unambiguously differentiable based on their waveform characteristics. This may be due to our recording parameters, e.g., using a rather tight bandpass filter between 600 Hz and 6 kHz, which affects the shape of the recorded spikes.

Table 1.

The number of neuron pairs, significant excitatory connections, and the experimentally derived detection probability of excitatory connection pairs p_αⁿ in our data counted in three different ways for comparison with intracellular and extracellular recording studies

Datasets	Counting method
	Song et al. (2005)	Present study	Fujisawa et al., (2008)
Rat 1
Novel
No. neuron pairs	36	276	820*
No. EE1 connections	5	6	6
No. EE2 connections	1	1	1
No. unconnected pairs	30	269	813*
pαn (connectivity)**	0.10	0.01	0.00
Sequence
No. neuron pairs	22	210	528*
No. EE1 connections	9	12	12
No. EE2 connections	2	3	3
No. unconnected pairs	11	195	513*
pαn (connectivity)**	0.30	0.04	0.02
Rat 2
Novel
No. neuron pairs	26	153	780*
No. EE1 connections	2	2	2
No. EE2 connections	1	1	1
No. unconnected pairs	23	150	777*
pαn(connectivity)**	0.08	0.01	0.00
Sequence
No. neuron pairs	5	55	325*
No. EE1 connections	1	1	1
No. EE2 connections	0	0	0
No. unconnected pairs	4	54	324*
pαn (connectivity)**	0.10	0.01	0.00
Rat 3
Novel
No. neuron pairs	77	253	903*
No. EE1 connections	4	4	4
No. EE2 connections	0	0	0
No. unconnected pairs	73	249	899*
pαn (connectivity)**	0.03	0.01	0.00
Sequence
No. neuron pairs	109	496	1431*
No. EE1 connections	6	10	10
No. EE2 connections	9	3	3
No. unconnected pairs	100	483	1418*
pαn (connectivity)**	0.11	0.02	0.01
Total No. neuron pairs	275	1443	4787*

*Includes inhibitory and unclassified neurons as well as excitatory neurons, whereas all other counts contain excitatory neurons only;

**α = abs, n = 25.

The number of neuron pairs, the number of unidirectional excitatory connections (EE1), the number of reciprocal excitatory connections (EE2), and the number of unconnected neuron pairs (NO), as well as the connection probability (detection probability of excitatory connections, p_α²⁵, Eq. 1) for the 25 h recordings are reported in three different ways in order to compare them to intracellular recording studies (Song et al., 2005) and to extracellular recordings (Fujisawa et al., 2008 and the counting method in this paper, in which we only consider excitatory neurons across all tetrodes). Therefore, all three columns contain our data, simply reported according to three different counting methods, which are detailed below.

Formula for calculating the number of neuron pairs for Song et al. (2005) criteria:

where n_EE,i is the total number of excitatory neurons within tetrode i and N_TT is the total number of tetrodes.

Formula for calculating the number of neuron pairs for our criteria:

where n_EE is the total number of excitatory neurons.

Formula for calculating the number of neuron pairs for Fujisawa et al. (2008) criteria:

where n_all is the total number of all recorded neurons, including inhibitory and unclassified neurons.

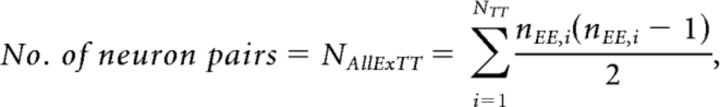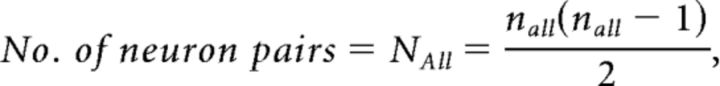The formula for calculating the connection probability of excitatory neuron pairs p_αⁿ was provided by Equation 1.

Changes of detection probability over various lengths of recordings

Significant excitatory connections between neuron pairs were detected by using a spike train jitter method (Barthó et al., 2004; Fujisawa et al., 2008). As the threshold for significant interactions is chosen somewhat arbitrarily by the experimenter and influences the size of the type I error (false-positives), we investigated a wide range of significance levels; 16 different α levels ranging from 0.5 to absolute limit (abs). The absolute limit is derived from the absolute maximum value of all bins in the jittered data for each neuron pair and represents the strictest α level. Note that it is not much smaller than 10⁻⁵ (the smallest used before abs).

Figure 2a,b shows four examples of cross correlograms between two putative pyramidal neurons with the absolute limit. Although no significant short-latency peak was detected with a 1 h recording (Fig. 2a,b, top row), it was detected with a 25 h recording (Fig. 2a,b, middle row). The reduced fluctuations in the correlogram reflect the improved signal-to-noise ratio and enable the detection of small peaks. As expected, longer recording times increase the chance of detecting weak excitatory connections. In addition, we also calculated the jitter-corrected cross-correlograms (Fig. 2a,b, bottom row; Hirabayashi et al., 2013; Mizuseki and Buzsaki, 2013). This is obtained by subtracting the mean jittered cross-correlations for each bin from the original cross-correlation. The results show that the significant peaks clearly stand out. The firing rate distribution of the analyzed dataset follows a lognormal distribution as previously shown (Mizuseki and Buzsaki, 2013) and does not change between the first and last 4 h of recordings (Fig. 2c). The distribution of the jitter corrected significant peaks follows a lognormal distribution as well (Fig. 2d), which is also consistent with previous findings (Mizuseki and Buzsaki, 2013).

The experimentally derived detection probability of excitatory connections p_αⁿ for the significance level α and the recording length of n hours was given by Equation 1. To make the results comparable to paired intracellular recordings between pyramidal neurons (Song et al., 2005), N was taken as the total number of possible excitatory neuron pairs (N_AllEx = 1443; Table 1). In addition, because intracellular recordings are typically done in slices and are limited to a smaller volume of tissue, we also calculated N as the number of possible excitatory neuron pairs per tetrode (N_AllExTT = 275; Table 1). Although the results for both N_AllEx and N_AllExTT are presented, we consider that N_AllExTT is more directly comparable to previous intracellular recordings (Song et al., 2005). The results of detection probabilities normalized by all recorded neuron pairs (Barthó et al., 2004; Fujisawa et al., 2008; N_All = 4787), including connection types other than excitatory interactions are shown in Figure 9.

Figure 9.

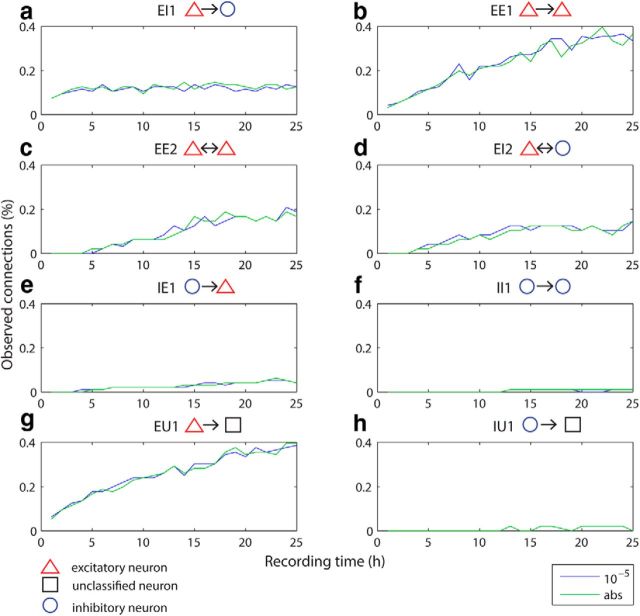
Detection probabilities over different hour segments for different categories of connection types. Significance thresholds (α 10⁻⁵ and abs) are color coded and indicated at the bottom right of the figure panel. The median of the bootstrapped detection probabilities, normalized by the total number of neuron pairs (4787) including excitatory, inhibitory and unclassified neurons for 1 to 25 h are plotted for the two different significance thresholds for eight different types of connections: (a) unidirectional excitation from an excitatory neuron onto an inhibitory neuron, EI1; (b) unidirectional excitation between two excitatory neurons, EE1; (c) reciprocal excitation between excitatory neurons, EE2; (d) reciprocal connection between an inhibitory and an excitatory neuron, EI2; (e) unidirectional inhibition from an inhibitory neuron onto an excitatory neuron, IE1; (f) unidirectional inhibition between two inhibitory neurons, II1; (g) unidirectional excitation from an excitatory neuron onto an unclassified neuron, EU1; and (h) unidirectional inhibition from an inhibitory neuron onto an unclassified neuron, IU1. The most abundant connection types in mPFC are excitatory connections (a–d, g). Their detection probability increases with longer recording times except for EI1, which seem to be already reliably detected at shorter recording times (a). Inhibitory connections are rarely detected in our dataset and their detection probability does not improve significantly with longer recording times.

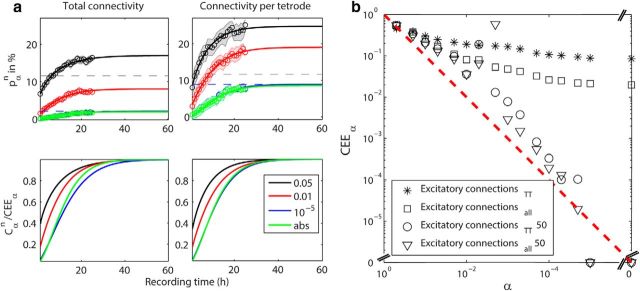
Figure 3a (top, data points) shows how the experimentally derived detection probabilities of excitatory connections p_αⁿ changes from 1 h recordings to 25 h recordings for four representative α levels: 0.05, 0.01, 10⁻⁵, and the absolute limit. The data points represent the median and the background band shows the range for the 84^th and 16^th percentile estimated by bootstrapping. The detection probabilities increased with longer recording times for both ways of calculating the connection probability. For α = 0.05, the detection probability increased from 6.7% (N_AllEx) and 8% (N_AllExTT) for 1 h recording segments to 16.4% (N_AllEx) and 25% (N_AllExTT) for 25 h recording segments, respectively. For α = 0.01, the detection probability increased from 1.6% (N_AllEx) and 2.9% (N_AllExTT) to 7.2% (N_AllEx) and 17.6% (N_AllExTT), respectively. For the stricter α values, 10⁻⁵ and the absolute limit, which show very similar trends for both ways of normalization, the detection probability increased from 0.1% (N_AllEx) and 0.5% (N_AllExTT), to 1.7% (N_AllEx) and 7.6% (N_AllExTT), respectively.

Figure 3.

a, Top, The experimentally derived detection probability p_αⁿ of excitatory connections. The median (circles) and 16^th and 84^th percentile (shaded area) of the detection probability are plotted for recording lengths of 1–25 h. The data in the left plot was normalized by the total number of possible excitatory neuron pairs (N_AllEx) and the data in the right plot by the total number of possible excitatory neuron pairs per tetrode (N_AllExTT). The results for four different significance α levels (color coded) are shown: 0.05, 0.01, 10⁻⁵, abs (note: the curves for the latter two levels largely overlap). The detection probabilities (C_αⁿ, solid lines) were extrapolated until asymptote (CEE_α) as estimated by the fitting of the statistical power function. The gray dashed horizontal line at 11.6% denotes the local connectivity as detected by Song et al. (2005) between pyramidal neurons in layer 5 of rat visual cortex. The blue dashed line indicates the asymptote as approached by α = 10⁻⁵. All R² values indicating the goodness of fit are between 0.98 and 0.99. Bottom, The fitted detection probabilities (C_αⁿ) divided by CEE_α are plotted for N_AllEx normalization (left) and for N_AllExTT normalization (right). b, The asymptotes (CEE_α) are plotted against the α levels on a log–log scale. Open squares and asterisks correspond to CEE_α normalized by N_AllEx and by N_AllExTT, respectively. Both ways of CEE_α estimation seem to approach a lower limit. Triangles and circles correspond to CEE_α normalized by N_AllEx and by N_AllExTT, respectively, for the alternative window at ±50 ms. CEE_α approaches zero as α becomes stricter. This is expected because no monosynaptic interactions are expected to be detected in the time interval of ±50 ms.

Curve fitting and extrapolation of the relationship between statistical power and sample size

Next, we investigated how the detection probability of excitatory connections between putative pyramidal neurons would improve beyond the recording duration of 25 h. The fitting of Equation 8 was applied to the experimentally derived detection probabilities p_αⁿ with 16 different α levels (0.5 to the absolute limit) to obtain the fitted detection probabilities C_αⁿ beyond 25 h. The optimization results are summarized in Table 2. Figure 3a (top) show the fitted results for four representative significance thresholds (α levels for 0.05, 0.01, 10⁻⁵, and abs). The corresponding power function, defined by C_αⁿ/CEE_α, where CEE_α is the asymptotic value of p_αⁿ, was also obtained (Fig. 3a, bottom). We found that the fitted functions converge to different asymptotic values of the experimentally derived detection probability of excitatory connections p_αⁿ but the difference becomes very small for stricter α levels (10⁻⁵ and absolute limit). There indeed appears to exist a lower limit asymptote as the threshold becomes stringent (∼2%, N_AllEx; ∼8.5%, N_AllExTT), indicated by the blue dashed lines in the plots. The CEE_α values for the stricter α levels (∼2% with N_AllEx and ∼8.5% with N_AllExTT) reach ∼20 and 70% of the local connectivity as reported by Song et al. (2005), respectively. As was discussed in the previous section, we consider that N_AllExTT is more directly comparable to their study. Therefore, we conclude that ∼70% of local E–E connections could be detected by long extracellular recordings.

For α levels of 0.05 and 0.01, the power function (C_αⁿ/CEE_α) approaches 1 more quickly than that of 10⁻⁵ and absolute limit (Fig. 3a, bottom); ∼90% of power could be achieved with 20 h of recording. However, their detection probability also increases quickly and exceeds Song et al.'s (2005) detection probability of 11.6%; α = 0.05 with N_AllEx normalization and α = 0.05 and 0.01 with N_AllExTT normalization (Fig. 3a, top). Because intracellular recordings have intrinsically a higher chance of detecting monosynaptic connections, as the presynaptic neurons are stimulated and even subthreshold responses in the postsynaptic neurons recorded, the overshoot for α levels 0.05 and 0.01 suggests that these acceptance criteria detect excessive false-positives.

To assess how the same asymptote could be possibly reached, CEE_α are plotted against the α levels in percentage on a log–log scale (Fig. 3b). We found that as α levels get stricter, the slope of the consecutive data points for both ways of the CEE_α estimation gets increasingly smaller (open square and asterisk correspond to N_AllEx and N_AllExTT normalization, respectively). This result indicates there is a lower limit asymptote. In contrast, when choosing a window of identical size at longer latency lags (±50 ms), the CEE_α estimation approaches zero almost following a diagonal line (open circle and open triangle correspond to N_AllEx and N_AllExTT normalization, respectively). A similar result was also obtained for the latency lags of ±25 ms. These results demonstrate that the windows at the latency lags outside of monosynaptic interactions (e.g., ±25 ms or ±50 ms) do not contain monosynaptic interactions.

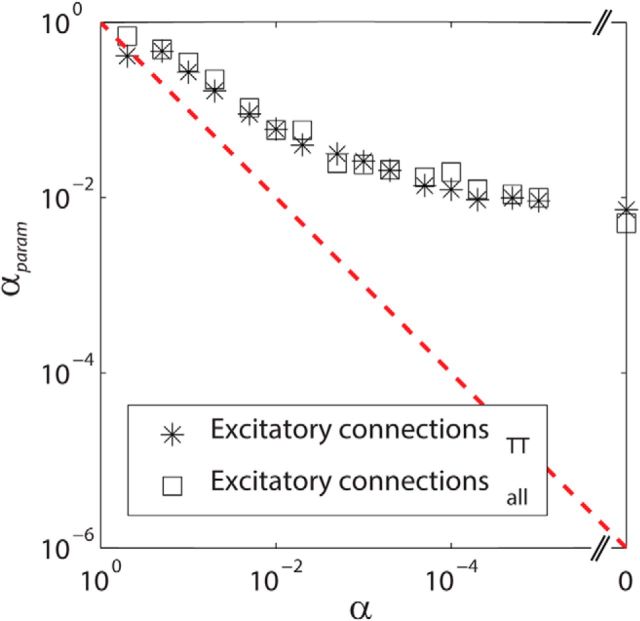
In the final form of the fitting function (Eq. 8), the significance level α was treated as a fitting parameter α_param to obtain a better fit. We confirmed that α and α_param were monotonically related, indicating that fitting α_param does not violate the original relationship of α = α_param significantly (Fig. 4). However, α_param deviates gradually when α gets smaller. This could be due to the fact that μ₁ will follow a skewed distribution, which is not accounted for in Equation 8. Thus, Equation 8 would need to be rewritten accordingly but it is beyond the scope of the present paper. Together, these results show that our method using short-latency peaks of cross-correlations with strict α levels and using the approach of fitting a statistical power function is valid for detecting monosynaptic E–E interactions and estimating their asymptotic detection probability in local networks.

Figure 4.

The relationship between the significance level α and the fitting parameter α_param, obtained from Equation 8. Asterisks depict the results obtained with N_AllEx and open squares depict the results obtained with N_AllExTT. α_param deviates gradually when α gets smaller. This is likely due to the fact that μ₁ is not a single value, but a distribution, which is not accounted for in Equation 8. However, α and α_param maintained a monotonically decreasing relationship. This suggests that separating α_param from α does not violate the original relationship of α = α_param substantially.

False-positives and the distribution of effect size

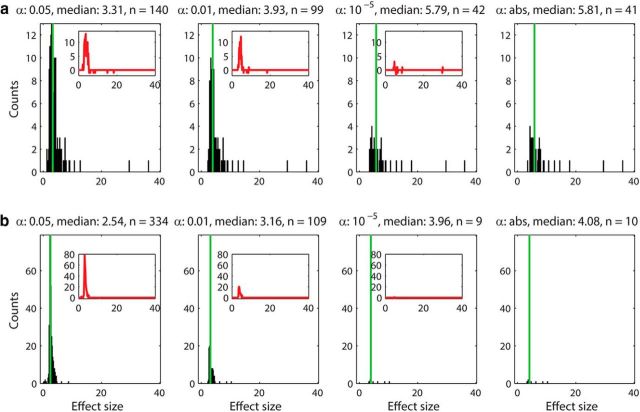
We investigated whether the connections detected by less stringent α levels (e.g., 0.05 and 0.01) were contaminated by false-positives by plotting the distribution of the effect size h (Eq. 9). The distribution of the effect size within tetrodes (short range) and between tetrodes (long range) for four representative α levels (0.05, 0.01, 10⁻⁵, and abs) are plotted in Figure 5a and b, respectively. Both unidirectional (EE1) and reciprocal excitatory connections (EE2) are included in the analysis. The results show that the distributions for the stricter α levels (10⁻⁵ and abs) were almost identical and contained strong effects only (Fig. 5, right columns). On the contrary, less strict α levels (0.05 and 0.01) contained additional large counts of smaller effect sizes (Fig. 5, left columns). Subtraction of the most stringent distribution (α = abs) from less stringent groups (α = 10⁻⁵, 0.01, and 0.05) confirmed that the stricter α levels (10⁻⁵ and abs) are very similar to each other but less stringent α levels (0.05 and 0.01) have higher counts of weak effect sizes (Fig. 5, insets). This is likely due to peak counts being contaminated by a large proportion of false-positives. Because false-positives would occur randomly, their distribution is expected to be Gaussian-like, which is consistent with what we obtained (Fig. 5, insets). In addition, most of the stronger effects are found in short range interactions (within tetrodes; Fig. 5a), not in long-range interactions (between tetrodes; Fig. 5b), suggesting that the strongest connections are mostly local. We also investigated the distribution of the effect size for unidirectional (EE1) and bidirectional connections (EE2) separately; Figure 6a for EE1 (within tetrodes), Figure 6b for EE1 (between tetrodes), Figure 6c for EE2 (within tetrodes), and Figure 6d for EE2 (between tetrodes). We found that the majority of strong effects for both EE1 and EE2 are local and that the long-range excitatory connections are predominantly unidirectional (EE1).

Figure 5.

The distribution of effect sizes (h) for short-range (a) and long-range (b) connections plotted for four different α values. The distribution of effect size for both unidirectional and reciprocal connections (EE1 and EE2) recorded within tetrodes (a) and between tetrodes (b) for four different α levels (0.05, 0.01, 10⁻⁵, and abs) are depicted. The number of peaks included, as well as the medians of the distributions are indicated above each histogram. The median is also plotted as a green vertical line. The results for α levels 10⁻⁵ and absolute limit are comparable. The distributions of effect size for α levels 0.05 and 0.01 are also similar. The insets show the difference between the most stringent group (α abs) and the less stringent groups (α levels 0.05 and 0.01). These counts correspond to weak effect sizes (<5) and most likely false-positives. The strong effect sizes (>10) are found in correlations between excitatory neurons recorded on the same tetrode, indicating that the strongest connections are mostly local.

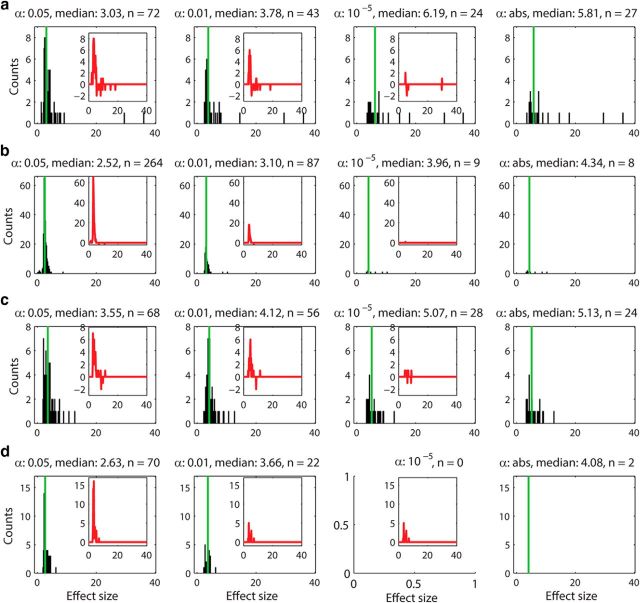
Figure 6.

The distribution of effect sizes (h) for unidirectional connections (EE1) within (a) and between (b) tetrodes and for reciprocal connections (EE2) within (c) and between (d) tetrodes for α levels 0.05, 0.01, 10⁻⁵, and abs. The significance levels as well as the median of the distributions are indicated above the histograms. The insets show the difference between higher α (0.05, 0.01, and 10⁻⁵) and α abs, indicating the amount of likely false-positives included in the counts. The strongest effect sizes of unidirectional connections seem to be distributed among short-range connections rather than long-range connections (a). The long-range connections appear to be predominantly single directed excitatory connections (b). As the significance level is determined by a jitter method over a distribution of 1000 jitter trials that can differ for different α levels, it is possible that not all pairs detected with α abs are included in the pairs detected with α 10⁻⁵ (even though they are mostly identical). In other words, occasionally a few more pairs can be detected with α abs than with α 10⁻⁵, which in the extreme case leads to no peaks detected at α 10⁻⁵, but still two peaks detected at α abs (d). Reciprocal excitatory connections seem to be mostly local (c) and according to α levels 10⁻⁵, and abs, there are hardly any reciprocal excitatory connections detectable between excitatory neurons recorded on different tetrodes (d). This also suggests that the peaks in α levels 0.01 and 0.05 are likely to be false-positives.

Hyper-reciprocity in mPFC

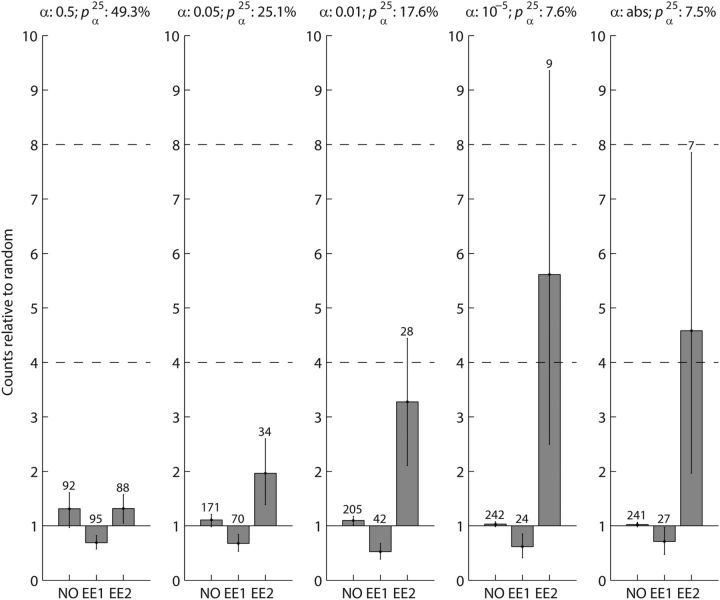
Further support of the conclusion that less stringent α levels (e.g., 0.01 and 0.05) are massively contaminated by false-positives came from comparing the counts of significant connection pairs at different α levels and the number of connection pairs predicted by a random connection assumption (Fig. 7). Given that a network is randomly connected by a connection probability p_αⁿ (Eq. 1), the expected number of unconnected pairs is N(1 − p_αⁿ)², the expected number of unidirectionally connected pairs is 2Np_αⁿ (1 − p_αⁿ), and the expected number of reciprocally connected pairs is N (p_αⁿ)². Song et al. (2005) reported that the count of reciprocally connected excitatory neuron pairs (EE2) in rat visual cortex is four times higher than the number predicted. Wang et al. (2006) reported 3.5 and 7.9 times more EE2 connections than predicted in visual cortex and prefrontal cortex, respectively, in young ferrets. The ratios of observed EE2 to predicted EE2 are comparable in visual cortex for both rodent studies (4 in rat and 3.5 in ferret). EE2 connections are twice as likely in ferret medial prefrontal cortex than in visual cortex (7.9/3.5 = 2.3) and if the relationship holds true for rat, we would expect the EE2 connection probability in rat medial prefrontal cortex to be up to eight times higher than predicted by a random connectivity assumption. Based on these considerations, we predicted that the EE2 connection in rat medial prefrontal cortex would be four to eight times higher than predicted. For the stringent α levels of the absolute limit and 10⁻⁵, we found that medians of observed EE2 connections are 4.6 and 5.6 times higher than the number predicted, respectively (Fig. 7, right columns). In addition, their 95% confidence intervals (Fig. 7, error bars) overlap with the predicted four to eight times range, suggesting that these results are consistent with what we predicted based on the numbers by Song et al. (2005) and Wang et al. (2006). However, for less stringent α levels, the difference between observed EE2 counts and predicted EE2 counts became lower than predicted; 3.2 times for α = 0.01, 2 times for α = 0.05 and 1.3 for α = 0.5 (Fig. 7, left three columns). Furthermore, their 95% confidence intervals do not overlap with the four to eight times range, except for α = 0.01, where there is a small overlap, indicating that the statistics of the observed EE2 connections were different for less stringent α levels. Because false-positives detected in cross correlograms are expected to occur randomly, the observed decrease of hyper-reciprocity suggests that more false-positives are included if less stringent α levels were used. We therefore conclude that stricter α levels together with long-term recordings are necessary for reliable detection of weak E–E interactions in extracellular recordings.

Figure 7.

The counts of unconnected (NO), single directed excitatory (EE1), and reciprocal excitatory (EE2) neuron pairs for five representative α levels (left to right; 0.5, 0.05, 0.01, 10⁻⁵, and abs), relative to the prediction of the random-connection null hypothesis are shown. The connection probability p_αⁿ as well as the α levels are indicated above the individual bar plots. The absolute counts of connections are indicated above the bars. Error bars represent the 2.5th and 97.5th percentiles of the medians of 1000 bootstrapped distributions. The dashed horizontal lines at 4 and 8 indicate the expected counts of observed EE2 connections relative to the null hypothesis in the Song et al. (2005) and Wang et al. (2006) studies. For stricter α levels (abs and 10⁻⁵), reciprocally connected excitatory neuron pairs (EE2) with the N_AllExTT normalization are 4.6–5.6 times more likely than expected. This is in the four to eight times range calculated from Song et al. (2005) and Wang et al. (2006). As α becomes less stringent (0.01, 0.05, and 0.5), the difference becomes less striking because more false-positive counts are likely to be included. The counts of single directed excitatory neuron pairs (EE1) and of unconnected neuron pairs (NO) are close to the expected numbers.

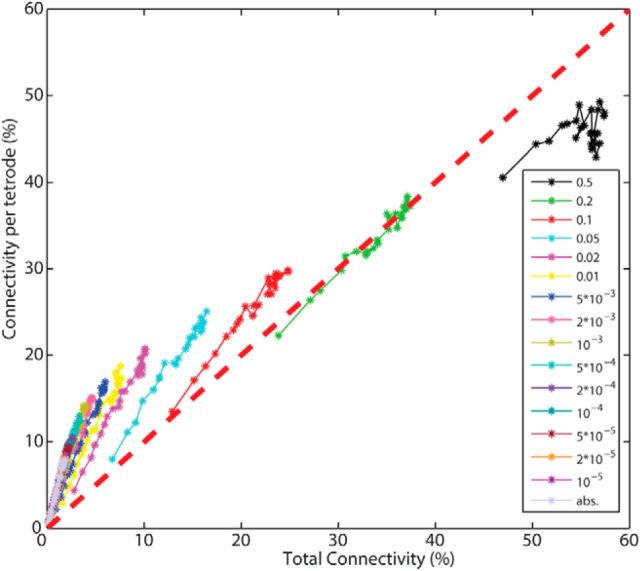
Excitatory connectivity in mPFC is predominantly local

The relationship between local excitatory connectivity (within tetrode connections, normalized by N_AllExTT) and total excitatory connectivity (within and between tetrode connections, normalized by N_AllEx) can be further investigated by plotting them against each other for different α levels (Fig. 8). For stricter α levels, observed connections were localized within the upper-left triangle, suggesting that predominantly local connections were detected. With increasingly relaxed α levels the difference between local and total connectivity disappeared (at α = 0.2, indicating that the difference was masked by an increasing number of false-positives. Interestingly, total connectivity became larger than local connectivity for α = 0.5. If there was a general tendency of underestimating the local connectivity and overestimating the total connectivity, then this could explain why the total connectivity is larger than the local connectivity for α = 0.5. One could speculate that over elimination of spikes during spike sorting resulting in decreased correlations (Cohen and Kohn, 2011) could lead to the observed effect as this would affect the detection of significant cross-correlations within tetrodes more than between tetrodes. Incapability of recording overlapping spikes within tetrodes may also enhance this tendency.

Figure 8.

The number of excitatory connections per tetrode (local connectivity, normalized with N_AllExTT) is plotted against the total number of excitatory connections (total connectivity, normalized with N_AllEx) for all investigated α levels. The red diagonal dashed line indicates equal probability between local and total connectivity (including within and between tetrode connections). The detected connections are predominantly local.

Various types of excitatory connections are the most abundant in mPFC and their detection probability increases with sample size

In addition to E–E interactions (EE1 and EE2), our 25 h recordings also allowed us to investigate six additional connection categories (EI1, EI2, IE1, II1, EU1 and IU1, see Materials and Methods); Although, II2, reciprocal inhibition between putative inhibitory neurons, could be defined as well, we excluded this connection probability from our analysis because its cross-correlation cannot be easily distinguished from the case of common inhibitory input. The detection probabilities of connection categories involving excitatory neurons (EE1, EE2, EI1, EI2, IE1, and EU1) change with increased recording duration for two representative α levels (10⁻⁵ and abs; Fig. 9). Note that the normalization by all recorded neuron pairs (N_All) was used because all neuron types (excitatory, inhibitory, and unclassified) were included. We also found that EE1 (Fig. 9b) and EU1 (Fig. 9g) are the most abundant connection types followed by EE2 (Fig. 9c), EI1 (Fig. 9a), and EI2 (Fig. 9d), suggesting that excitatory interactions are the major portion of cortical connections in rat prefrontal cortex. Inhibitory interactions, IE1 (Fig. 9e), II1 (Fig. 9f), and IU1 (Fig. 9 h), are detected much less frequently.

Discussion

Pyramidal neurons are the most abundant cell type in neocortex. Pyramid–pyramid connections (E–E interactions) provide the majority of intracortical and extracortical projections. However, most E–E synapses are extremely weak (McNaughton, 1980; Mason et al., 1991; Deuchars et al., 1994; Markram et al., 1997; Thomson and Deuchars, 1997; Reyes and Sakmann, 1999; Thomson et al., 2002). With long-term continuous recordings, we tried to capture weak connections between pyramidal neurons. As opposed to most electrophysiological studies that generally record for ∼0.5–2 h per session, we were able to detect excitatory interactions between putative pyramidal cells in 8.5% of cell pairs with recording lengths up to 25 h. This connection probability of 8.5%, estimated using the number of putative excitatory neuron pairs per tetrode, corresponds to ∼70% of the local E–E connections reported in Song et al. (2005). As was discussed, this normalization is considered to be most comparable to Song et al. (2005). The smaller connection probability (2%) found for the total excitatory connectivity indicates that on average the connection probability falls off with distance (Song et al., 2005; Fujisawa et al., 2008). In addition, 1 h fragments of our recordings yielded a consistent number of monosynaptically coupled pairs (0.2% for strictest α levels: abs and 10⁻⁵ and 1.04% for α 0.01; counts were normalized using all recorded neuron pairs, Fig. 9) to previously reported studies (0.2–0.8%; Csicsvari et al., 1998; Barthó et al., 2004; Maurer et al., 2006; Fujisawa et al., 2008).

The strength of a pyramidal–pyramidal connection is partly determined by the location of the synapse and the type of receptors activated (Deuchars et al., 1994). For instance, because lateral connections between pyramidal neurons in cortex are predominantly on distal parts of the dendrites, they are weakened as the potential propagates toward the soma. Those inputs are nearly only transferred if they coincide with other inputs (Deuchars et al., 1994). Therefore the E–E interactions detected by relatively short duration electrophysiological recordings are presumably the strongest ones. However, those are embedded in a much larger matrix of weak connections, which are difficult to capture with extracellular recordings that only detect action potential transmission. With regard to successful spike transmission, pyramidal–interneuron pairs have been shown to be more reliable (Mizumori et al., 1989; Marshall et al., 2002; Holmgren et al., 2003; Swadlow, 2003). Using a less stringent detection threshold, such as 1%, as used in many previous studies, is therefore less likely to be severely affected by false-positives. A higher convergence of excitatory inputs among pyramidal neurons is necessary to bring a postsynaptic pyramidal neuron to firing threshold (McNaughton et al., 1981; Markram et al., 1997). In this respect, long-term recordings dramatically increased the detection probability of the statistically rare E–E events.

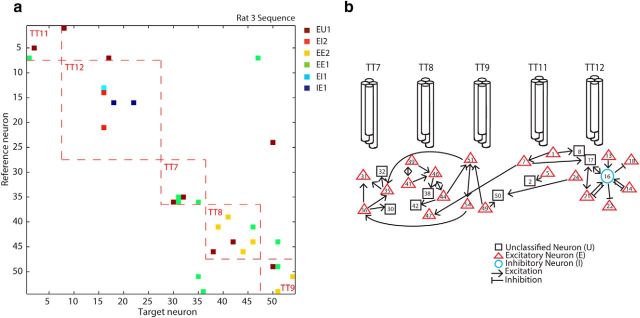
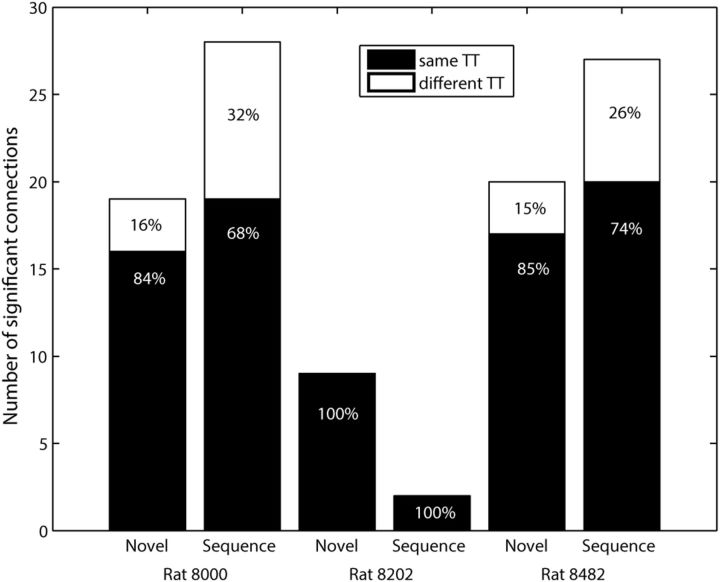
In Figure 5, we reported that most connections are local, i.e., both presynaptic and postsynaptic neurons are within the recording radius of a single tetrode. In the hippocampus, monosynaptically coupled pairs of pyramidal neurons and interneurons were also more frequently observed on the same tetrode than on different tetrodes (Csicsvari et al., 1998; Maurer et al., 2006). Connection strength tends to cluster around a few neurons (Barthó et al., 2004; Song et al., 2005; Fujisawa et al., 2008), often referred to as hub neurons. We also observed that many connections converge onto a few neurons. The majority of detected connections are local (Figs. 10a, 11), recorded on the same tetrode (Fig. 10a, red dashed lines). A schematic diagram created from Figure 10a also confirmed that there exists a hub neuron (Fig. 10b, neuron #16). Its inhibitory property (a hub neuron is an inhibitory neuron) is consistent with previous studies (Barthó et al., 2004; Fujisawa et al., 2008).

Figure 10.

a, The cross-correlogram matrix for all (n = 54) simultaneously recorded neurons in one session (rat 3, sequence task). Red dashed lines indicate correlations between neurons recorded on the same tetrode. Different colors denote different types of connections (see Fig. 9 legend) based on significant short-latency peaks or troughs in the cross correlogram at α abs. (b) Schematic mapping of the connections in the cross correlogram matrix in a between the neurons recorded on five different tetrodes. This animal had a “split bundle” hyperdrive with six recording tetrodes targeting the hippocampus (not included in this paper) and five tetrodes targeting the medial prefrontal cortex (b).

Figure 11.

Summary of local and long range connections per dataset. The number of significant excitatory connections within (same TT) and between (different TT) tetrodes for the individual datasets for α abs. Numbers are given in absolute (y-axis) and percentage (written on bars) values.

In this study, we showed that the detection probability of weak E–E connections can be significantly improved by long-term recordings (25 h) due to the substantially improved signal-to-noise ratio reflected in smoother cross-correlation signals for 25 h compared with 1 h recordings (Fig. 2). We were also able to detect the hyper-reciprocity of excitatory connections in medial prefrontal cortex with our long-term extracellular recordings (Song et al., 2005; Wang et al., 2006; Fig. 7). This strongly suggests that connectivity is not random, but highly structured. Despite the fact that increased recording times improve the detection of connections among excitatory neurons, extracellular recordings still underestimate the local connectivity as is reported by paired intracellular recordings. At best, they identify ∼70% of local excitatory connections at an α level that is strict enough to exclude most type I errors (Fig. 3). This limitation can be partly attributed to the fact that extracellular recordings in behaving and resting animals are bound to the brain state spaces visited over the duration of recordings, which the experimenter has only limited control over. In contrast, through direct stimulation of the presynaptic neuron, any subthreshold response in the postsynaptic neuron can be monitored in paired intracellular recordings. In addition, our analysis indicates that, to estimate reliably an asymptotic value for the local connectivity, stable recordings of at least 20–25 h, ideally longer, have to be used. This can be a challenge under many experimental conditions. A further caveat of the correlation method is the fact that the nature of the measure is a correlation and therefore reflects synaptic interactions only indirectly. Consequently, the cross-correlation analysis of extracellularly recorded spike trains should not be considered a definitive tool for estimating connectivity and should be used with caution. Despite this caveat, the method can provide important preliminary information for within- and inter-regional circuit connectivity and changes in their connectivity due to experimental manipulations that may not be obtainable with other current methods.

The cross-correlogram, like all other statistical methods, has limitations in terms of its applicability to the interference of causal interactions from spike-train data. First, the method assumes that the spike trains are stationary, meaning that their stochastic properties do not change over time. This assumption is not always easy to justify; for example, with repeated stimulus presentations neurons tend to adapt their responses (Fairhall et al., 2001). Second, cross-correlations are affected by firing rate differences between the neurons (de la Rocha et al., 2007; Amari, 2009). Appropriate normalization, however, can alleviate this problem (Hirase et al., 2001). It has been proposed that the information-geometric measure could be an alternative correlation measure that is statistically orthogonal to the change of firing probability (Amari and Nagaoka, 2000; Amari, 2001). In addition, recent theoretical studies show that an information-geometric measure could be more directly related to synaptic interactions (Tatsuno and Okada, 2004; Tatsuno et al., 2009; Nie and Tatsuno, 2012) and that it can be applied to nonstationary data (Shimazaki et al., 2012). Other promising methods would include a Bayesian approach (Brown et al., 2004; Eldawlatly et al., 2010) and a regularized logistic approach (Zhao et al., 2012). These measures may perform well in identifying causal, nonlinear relationships between neurons. Further investigation of long-term electrophysiological data by such statistical methods would promote the detection of neural interaction and hence contribute to the understanding of the circuit dynamics underlying complex behavior.