Mapping the Perceptual Grain of the Human Retina

Abstract

In humans, experimental access to single sensory receptors is difficult to achieve, yet it is crucial for learning how the signals arising from each receptor are transformed into perception. By combining adaptive optics microstimulation with high-speed eye tracking, we show that retinal function can be probed at the level of the individual cone photoreceptor in living eyes. Classical psychometric functions were obtained from cone-sized microstimuli targeted to single photoreceptors. Revealed psychophysically, the cone mosaic also manifests a variable sensitivity to light across its surface that accords with a simple model of cone light capture. Because this microscopic grain of vision could be detected on the perceptual level, it suggests that photoreceptors can act individually to shape perception, if the normally suboptimal relay of light by the eye's optics is corrected. Thus the precise arrangement of cones and the exact placement of stimuli onto those cones create the initial retinal limits on signals mediating spatial vision.

Introduction

Every sensory system has evolved tissue containing an array of specialized neurons to detect and transduce particular physical stimuli. Much of our knowledge about how each type of sensory neuron works has been learned in dissected preparations, which offer precise control over experimental conditions. To understand the next important step—how the signals that arise from single sensory neurons are handled downstream by the nervous system—an in vivo approach is unavoidable. The challenge here is that stimulation of individual neurons is difficult when they sit within an array of similar receptors, with the array itself hidden inside a sensory organ. The eye offers one exception to this situation, with the cornea and lens affording a view of the retina that is only obscured by imperfections in the optics. Recent advances in ocular imaging now make it possible to overcome these imperfections and image individual photoreceptors in the living retina (Williams, 2011). We have taken advantage of this unique access to directly probe the cellular basis of vision.

In humans, photopic vision begins with the ∼5 million cone photoreceptors that line the back of the retina (Curcio et al., 1990). Understanding how perception is mediated by any one of these cones is hampered primarily by the eye's aberrations (Liang and Williams, 1997), and secondarily by fixational eye motion that constantly translates any visual stimulus over many cones (Rolfs, 2009). Nonetheless, key insights about single cone function have been learned via techniques that bypass the optics of the eye. For instance, using interference fringes, investigators have found that cones appear to integrate light over a Gaussian aperture that is smaller than a cone diameter (MacLeod et al., 1992; Chen et al., 1993). This occurs because photoreceptors act as optical fibers, exhibiting waveguide behavior that gives rise to angular sensitivity tuning in the retina (Stiles and Crawford, 1933; Enoch, 1961; Roorda and Williams, 2002). These psychophysical findings are drawn from stimulation of large patches of retina, pooling signals from hundreds of cones. Thus it remains unclear if perception is ultimately constrained by the light capturing properties of single cones, by downstream retinal circuitry that requires pooling of cone signals, or both.

Here we use an adaptive optics scanning laser ophthalmoscope (AOSLO), which allows simultaneous retinal imaging and psychophysics to be conducted with an optical resolution approaching the diffraction limit (Roorda et al., 2002; Yang et al., 2010). Combined with real-time retinal tracking to compensate for eye motion (Yang et al., 2010), we aimed to confine light delivery to individual cones to assess the contribution of single photoreceptors to visual perception. If photoreceptor waveguiding effectively sets light capture, then stimuli should be most easily seen when delivered to the cone's center, and less so when displaced from the center. Physiological support for this idea has already been found in primate retinal ganglion cells (Field et al., 2010) and in neurons in the lateral geniculate nucleus (Sincich et al., 2009), where neural responses peak when stimuli land on the center of a cone. Our findings suggest that such micron-scale positional sensitivity is indeed preserved up to the perceptual level. With this psychophysical approach to studying single cone function, the neural underpinnings of vision can now be accessed at the elementary level of the photoreceptor.

Materials and Methods

AOSLO imaging and stimulation.

We used a multiwavelength AOSLO for imaging the cone mosaic (Roorda et al., 2002; Harmening et al., 2012). The details of imaging and conducting psychophysics with an AOSLO have been described previously (Rossi et al., 2007; Rossi and Roorda, 2010; Tuten et al., 2012). The light source was a supercontinuum laser (SuperK Extreme; NKT Photonics) whose output was bandpass filtered to provide an infrared (IR) imaging wavelength of 842 ± 25 nm, and a visible green stimulation wavelength of 543 ± 11 nm that minimized the sensitivity difference between long and medium wavelength-sensitive cones (L and M, respectively). For imaging, a focused spot from the IR beam was raster scanned across the retina, and the high-order aberrations encoded in the beam emerging from the eye were measured with a Shack–Hartmann wavefront sensor. The wavefront error of the eye was computed and used to drive a 144-actuator, 5.5 μm stroke deformable MEMS mirror (Boston Micromachines) into a compensatory shape, which corrected the wavefront on its way into, and out of, the eye. The returning light was sensed continuously by a photomultiplier tube (PMT) located behind a confocal pinhole conjugate with the retina. The voltage output of the PMT combined with positional signals from the scanning mirrors was used to render a 512 × 512 pixel imaging video at 30 frames per second.

Independent 10-bit modulation of the imaging and stimulus channels was achieved by passing them through dedicated acousto-optic modulators (AOMs) operating at 50 MHz before their entry into the scanning and corrective portions of the optical path. High-speed switching allows custom stimuli to be delivered to the retina, pixel by pixel, in correspondence with the acquired image. Stimulus delivery to selectable locations was achieved by real-time stabilization of fixational eye movements (Arathorn et al., 2007; Yang et al., 2010). Because pixel position and time are linked in scanning systems, a digital marker was placed in the retinal video on the pixel location corresponding to the time of AOM-triggered stimulus delivery. This mark could be retrieved during analysis and served as a record of stimulus location with respect to the photoreceptor mosaic imaged in the IR channel, the effects of chromatic dispersion notwithstanding (see next section). All imaging and psychophysical testing was conducted using a 5.6 mm system pupil and 1.28° imaging field (400 image pixels per degree of visual angle).

Chromatic dispersion correction in a multiwavelength AOSLO.

The multiwavelength nature of our psychophysical apparatus renders it susceptible to the effects of chromatic aberration: even if the imaging and stimulus beams of our system are perfectly aligned as they enter the eye, chromatic dispersion within the eye itself will cause them to come to a focus in different axial planes (longitudinal chromatic aberration, LCA) and at different locations in the transverse plane (transverse chromatic aberration, TCA). LCA has been shown to be relatively consistent between individuals (Atchison and Smith, 2005), and can be compensated by adjusting the relative vergences of the fiber optic point sources as they enter the system. The fidelity of LCA correction can be confirmed by recording interleaved images from the IR and green channels; when LCA is properly compensated, both images are in focus at the same time. The remaining individual differences in LCA between subjects were accounted for by prioritizing focus to maximize sharpness in the green stimulation channel.

Unlike LCA, the direction and magnitude of TCA is more idiosyncratic, and will in part depend on the position of the imaging and stimulation beams relative to the eye's entrance pupil. Since it is difficult to infer chromatic offsets on the retina solely from pupil position, we used an objective method for measuring TCA from the recorded retinal videos directly (Harmening et al., 2012). Individual TCA compensation offsets used in the experiments ranged from −15 to +20 pixels in x and y dimension in the image, corresponding to shifts of up to13 μm on the retina, which is greater than the cone diameter for all eccentricities tested in this study. One consequence of using an image-based measure of TCA is that a significant amount of light (∼50,000 cd/m²) is required in the green channel to capture a retinal image. Because these light levels are too high to run threshold psychophysics in parallel, TCA measurements were restricted to the beginning and end of each testing session. Subjects were allowed 15 min to re-adapt before testing commenced, and a bite bar was used to quell pupil motion relative to the instrument beams in the intervening period. TCA measurement differences between before and after an experiment were much smaller than typical cone diameters (mean in both x and y image dimension: 1.4 pixels). Because this difference was close to the noise limit of repeated TCA measurements, and because TCA could not be monitored during the experiment, we assumed TCA to be constant in the calculation of light delivery. Sessions where TCA shifted more than one-half of a cone diameter (∼4 pixels, ∼2.9 μm) between the two TCA measurements were excluded from all analyses.

Subjects and psychophysical procedures.

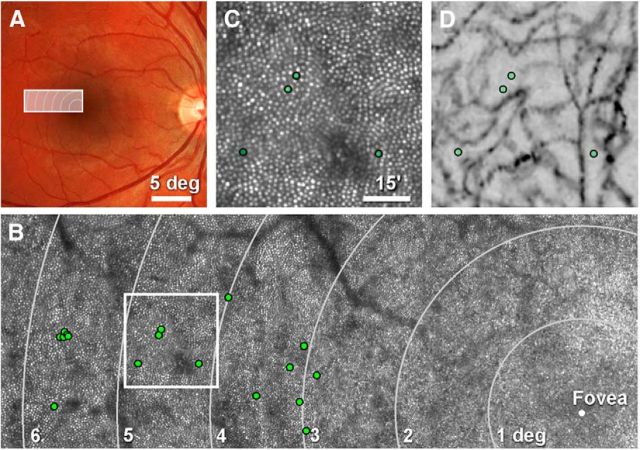
Subjects were four adults (one female, three males) with normal color vision. Mydriasis and cycloplegia were achieved by instilling one drop of 1% tropicamide and 2.5% phenylephrine 15 min before testing. Informed consent was obtained from each subject and all experimental procedures adhered to the tenets of the Declaration of Helsinki. Retinal stimulation sites were chosen on an approximately horizontal meridian, 2.5–5.5° temporally from the fovea. Eccentricity was taken from a large montage of scaled AOSLO images that included the fovea (Fig. 1B), and measured as the distance from the cone of interest to the subject's preferred retinal locus (plotted from a 5 s episode of fixation on a small flashing target). At each test eccentricity, high-resolution images of the vasculature were generated using an adaptive optics-based technique (Tam et al., 2010), and test sites were chosen from capillary-free regions to avoid screening by blood vessels (Fig. 1D).

Figure 1.

Selection of cones for targeted microstimulation. A, Right eye fundus photograph of Subject 2, with outlined area indicating where cones were selected for testing. B, Cone-resolved retinal montage of AOSLO images, with stimulation sites marked (green circles). Meandering dark structures are shadows cast by large retinal blood vessels. C, Field of cones from the outline in B, with four tested cones indicated. D, Vascular perfusion maps of the same region imaged in C, illustrating that stimulation sites were not situated under normally invisible capillaries (see Materials and Methods).

Visual sensitivity was assessed using an increment threshold approach. Throughout this study, light intensity values are expressed in arbitrary units (a.u.), between 0 and 1, where 0 corresponds to stimulation that contained only the constant 1.28° background field. A value of 1 corresponds to the background field plus the maximum available light intensity created by modulation of the smaller test stimulus on the retina. In radiometric terms, this value of 1 was typically ∼15 nW incident on the cornea for a 1.28° imaging field. For a 3 × 3 pixel stimulus presented for one frame, this equaled ∼4.28 log quanta. Residual light leak through the green channel AOM produced a background field of ∼4.3 cd/m², equaling ∼4100 rhodopsin isomerizations per second (Geller and Sieving, 1993), which effectively eliminated any rod contribution to the visual response (Aguilar and Stiles, 1954; Tamura et al., 1991). The background light produced ∼2.74 log quanta incident on the cornea for an area comparable in size and time to the stimulus. Thus, if a threshold was measured to be 0.5 a.u., the stimulus contained ∼17 times more photons than the background field covering the same stimulus area. The task required fixation on a small external spot produced by a bright LED. While fixating, subjects reported seeing or not seeing a small green stimulus square flashed during one video frame, accompanied by an audible cue. Stimulus edge length ranged from 3 pixels up to 9 pixels in the scanning raster [3.9–9.2 μm full-width at half-maximum (FWHM) on the retina], with 90% of tests performed with either 3 or 5 pixel squares. Due to the scanning nature of the AOSLO, stimulus light was delivered very briefly, during a time span of ∼120 μs for a 3 × 3 pixel stimulus, for example. Occasionally, after an experiment began, subjects reported never seeing a stimulus (possibly due to targeting an S cone); when this occurred, a new cone was selected for study.

In one experiment, we used a method of constant stimuli to derive thresholds from complete psychometric functions (n = 140 trials). For each test location, seven predefined and equally spaced stimulus intensities were presented 20 times in a randomly interleaved order, and the subjects responded in a yes–no paradigm. Subject responses for all intensity levels were used to construct psychometric functions by fitting a four-parameter logarithmic function to the data by using a maximum likelihood criterion with nonrestricted intervals for lapse and guess rates (Palamedes function PAL_PFML_FIT; Prins and Kingdom, 2009). Thresholds for these experiments were defined as the stimulus intensity where the function inflects. In all other experiments, we used a self-paced, yes–no Bayesian staircase algorithm to measure threshold after 22 trials at one location, with threshold of seeing set to 50% (Watson and Pelli, 1983; King-Smith et al., 1994). Staircase runs were repeated three to five times for all conditions. Trials were randomly interleaved, with the stimulus placed either on a cone or in the space directly adjacent to it (referred to as gap condition throughout this paper). For one experiment, patterned stimuli were generated at locations corresponding to multiple cones (2, 3, or 5 cones). The gap condition in this experiment was the same pattern shifted along a single vector to place stimuli in the multiple gaps next to the targeted cones (Fig. 7).

Figure 7.

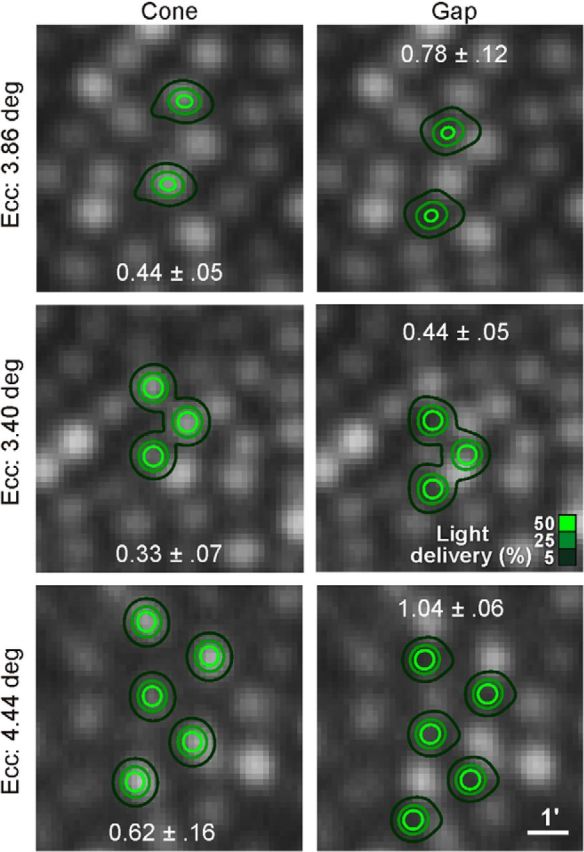
Revealing perceptual grain with patterned stimulation. In two subjects at three eccentricities, cone and gap thresholds were measured when 2, 3, or 5 cones were stimulated simultaneously, again with interleaved trials. In all cases, cone thresholds were significantly lower than gap thresholds (p ≤ 0.01). Numbers indicate mean threshold values ±1 SD from five repeated runs. Light delivery contours derived as in Figure 2.

Data analysis and cone modeling.

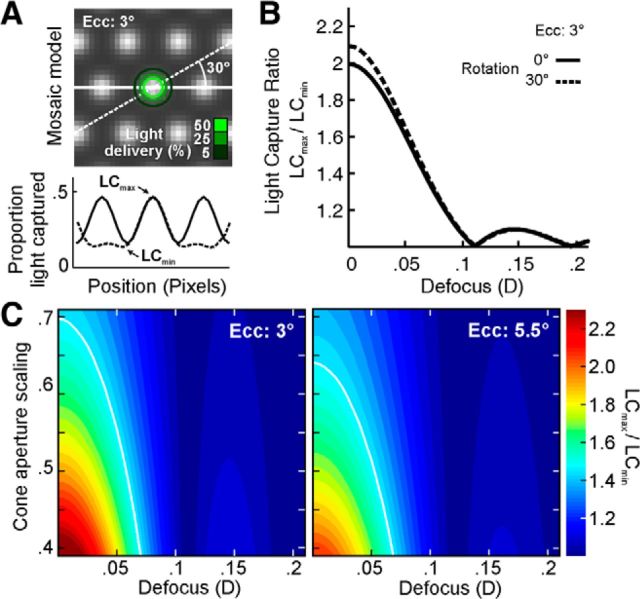
We examined the effect of stimulus position on light capture in a model cone mosaic while varying two parameters: cone aperture size and defocus (Fig. 8). Model arrays of cones were generated corresponding to retinal eccentricities of 3.0 and 5.5° (the bounds of our testing, approximately) using cone spacing measures from the literature (Curcio et al., 1990) and assuming perfect hexagonal packing (Fig. 8A, top). The profile of each cone aperture was represented by a 2D Gaussian whose FWHM was a fixed fraction of the inner segment diameter for that eccentricity (Hirsch and Curcio, 1989). Excitation of higher order modes due to off-center stimulation might cause the cone acceptance aperture to be non-Gaussian, but a complete model is not well defined and is beyond the scope of this paper. After blurring by a given amount of defocus, an image of our stimulus was convolved with a 2D Gaussian function with an SD equal to the average SD of stimulus delivery for our entire pool of data (28 arcsec). Next, the resulting stimulus representation was filtered by the model cone array as its position was varied along the horizontal meridian or a 30° oblique; for each location, the summed intensity in the filtered image represents the amount of light integrated into the cone array. Light capture (LC) as a function of stimulus position was plotted (Fig. 8A, bottom) and the light capture ratio, defined as LC_max/LC_min, was calculated. Figure 8B shows the light capture ratio as a function of stimulus defocus for a single cone aperture scaling (0.48). Light capture ratios across a range of aperture scaling factors and defocuses are shown in Figure 8C for the 3.0 and 5.5° eccentricities. The limits of our stimulus sizes were taken into account by using the smallest stimulus square (3 pixels) for the 3° eccentricity and the most frequently used of the larger stimuli (7 pixels) for the 5.5° eccentricity model calculation.

Figure 8.

Model of cone light acceptance and optical defocus. A, A hexagonally packed array of Gaussian cone apertures serves as a light capturing model (top). Translation of a 3 × 3 pixel stimulus (contours as in Fig. 2) along a horizontal or 30° oblique line produces LC that varies with position (bottom). B, The ratio LC_max/LC_min derived from the light capture peaks and troughs in A is plotted as a function of added stimulus defocus (solid line). The 30° orientation is indicated by dashed line. Zero defocus corresponds to a diffraction-limited stimulus geometry (as in Fig. 2C). Given the mean psychophysical gap/cone ratio of 1.48 (corresponding to LC_max/LC_min in the model), the model suggests that our stimulus was blurred by ∼0.06 diopters. C, Same analysis as in B, with cone aperture (proportion of inner segment diameter) as a free parameter (ordinate). The mean gap/cone ratio (1.48) is superimposed as white line. The full spectrum of scaling versus defocus was calculated for 3 and 5.5° eccentricity (left and right, respectively).

To facilitate comparison with our experimental data, our model adopts the following assumptions: (1) threshold is reached when some fixed amount of light is captured by the photoreceptor mosaic; (2) within a local patch of retina, each cone has the same inner segment diameter (and, thus, light acceptance profile); (3) each cone exhibits equal sensitivity to the green stimulus viewed upon the green background; and (4) the responses of adjacent cones sum linearly in the parafovea. On the basis of these assumptions, the light capture ratio represents the maximum gap/cone threshold ratio one might expect for a given set of aperture scaling and defocus parameters. The average threshold ratio for all data were then plotted as contour lines, defining our estimate of residual optical defocus for a range of aperture scaling factors (Fig. 8C).

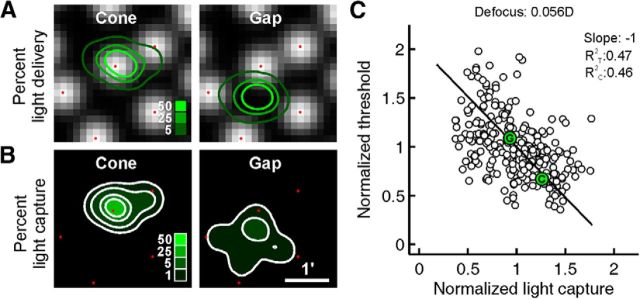
To account for light absorption based on actual stimulus delivery (Fig. 9), the following model was used. For each trial in a given psychophysical staircase, the precise location of the stimulus relative to the local cone mosaic could be determined by searching for the digital mark in the simultaneously recorded retinal video, and these locations could be plotted onto a reference image comprising registered frames from each trial video, with the spread of locations representing stimulus delivery errors. The effects of blur were modeled by convolving our stimulus with point-spread functions (PSFs) for the diffraction-limited case. The cumulative light distribution over the course of the staircase was computed by stacking these convolved stimulus profiles at the delivery location for each trial and scaling by the total number of trials (Fig. 2E). The cumulative light distribution over the 22 trials was then filtered by the model of the cone mosaic, with the intensity in the resulting image summed to estimate the amount of light coupled into the photoreceptors (Fig. 8B). For this analysis, a cone aperture scaling of 0.48 was used, which falls within the bounds of the data in Figure 8C and is supported by previous psychophysical studies (MacLeod et al., 1992).

Figure 9.

Light absorption model based on experimental stimulus delivery. A, Cone locations from high-magnification cone images around the stimulus location were replaced by Gaussian apertures (locations indicated by red dots). Light delivery from an example 22-trial run is shown as contours over the idealized cone apertures at this 3° test site for the cone and gap conditions. B, Proportion of captured light at each stimulus location is shown, calculated by the product of the stimulus location contours with the model apertures. C, The spatially summed light capture in B is computed for each threshold location, normalized against the mean within each group of repeated runs, and plotted against the similarly normalized threshold measurements. A residual stimulus blur of 0.056 diopters was applied (see Results) to arrive at unity slope for an orthogonal regression (solid line). The coefficients of determination are given for both threshold (R²_T) and light capture (R²_C) variance. The example cone (C) and gap (G) pair from A and B is indicated within their respective data points.

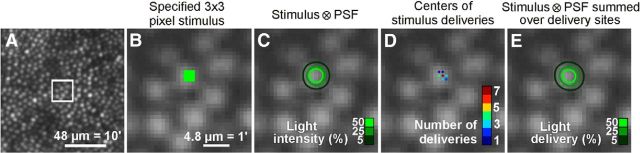
Figure 2.

Stimulus geometry and delivered light distribution. A, AOSLO image of cone mosaic at 3.1° eccentricity, with outlined area scaled up in B–E. B, Cone reflectance profiles at this eccentricity span ∼7 pixels, nearly 5 μm in diameter. Stimuli were specified in image pixels, a 3 × 3 pixel square stimulus in this example. C, Light intensity delivered to the retina is estimated by convolving the stimulus geometry with the diffraction-limited PSF of the eye (see Materials and Methods). Intensity contours show that the light spreads over a broader area than the 3 × 3 specification. D, Plot of actual delivery locations of the stimulus center relative to the targeted cone for a 22-trial psychophysical run. Positional delivery errors in eye motion correction caused stimulus deliveries to be jittered from trial to trial. E, Cumulative distribution of light delivery on the retina during the run in D, derived from the diffraction-limited stimulus integrated over the actual delivery locations. TCA was assumed to be constant for this analysis (see Materials and Methods).

To facilitate comparison across data collected at various parafoveal eccentricities, we normalized our light capture estimates and threshold data to their respective mean cone and gap values at each test site. After normalizing to these means, thresholds were plotted as a function of estimated capture for all four subjects for a range of residual blur (0.0–0.1 D) derived from Figure 8C. The resulting graph for a mean blur condition of 0.056 D is shown in Figure 9C. Because we expect variance in both our measures of light capture and increment threshold, we computed an orthogonal regression fit to the data. The resulting fit explains how much of the variance in the data can be explained by a linear model of light capture wherein all cones have equal weights. Because cones are known to have different weights (Field et al., 2010; Li et al., 2014), we estimated how much of the remaining variance may be due to cones with variable weights, using a Monte Carlo simulation. Light capture was computed as before, except each cone weight was drawn from a distribution that varied by 20% SD from a mean cone weight of 1. The variance of these data, computed from a fit where all cone weights were equal, was then averaged over 500 simulations. This yielded an estimate of the variance that could be caused by cone weight variability alone.

Results

Cone-sized microstimulation

To conduct psychophysical testing on identified photoreceptors, several technical hurdles need to be overcome, including: (1) the cones must be visualized at the microscopic level; (2) the retinal vasculature ought to be avoided, as it tends to shadow and uncontrollably scatter light; (3) the effects of chromatic aberrations have to be taken into account; and (4) ever-present eye motion must be counteracted so that stimuli land on the same retinal location on every trial. In this section, we show how these criteria were met. We first selected a region in the temporal retina along the horizontal meridian where overlying vessels are smallest and present the least interference for testing (Fig. 1A). In this area, we used AOSLO imaging to map the cone mosaic with subcellular resolution (Fig. 1B,C). All cones, except those within 0.25° of the fovea, were well resolved. We note here that variability in cone reflectance in AOSLO images is always observed, and is unlikely to significantly affect a cone's ability to capture light (Roorda and Williams, 2002; Pallikaris et al., 2003). The dark branched structures in the AOSLO montage (Fig. 1B) are shadows cast by larger blood vessels. What cannot be resolved in these AOSLO images, however, are the capillaries, which are mainly invisible to the 840 nm wavelength used for imaging when focused on the photoreceptor layer. To ensure that we did not test any cones lying beneath capillaries (which cover a substantial portion of retinal area; Snodderly et al., 1992), we also generated vascular maps in areas where cones were selected (Tam et al., 2010). All the cones analyzed in this study were located in capillary-free patches of retina (compare images of the same field with selected sites in Fig. 1C,D).

The stimulation light followed the same adaptive optics-corrected path as the imaging beam. Thus, in practice, we specified stimuli in terms of image pixels, with the spatial resolution constrained by the resolution of the AOSLO images. However, there are optical factors to consider when making the transition from a stimulus defined in image space to the actual distribution of light as it lands on the retina. First, since the eye's ocular media disperse light, wavelengths used for imaging and stimulation include chromatic offsets that need to be compensated (see Materials and Methods). We used an image-based method for measuring and correction of these offsets with sub-pixel precision (Harmening et al., 2012), ensuring that the stimulus location corresponded to the location defined in image space. Next, for the field size used (1.2° square), the sampling resolution was high enough that each photoreceptor was imaged within ∼10 pixels (Fig. 2A,B). A stimulus defined in image pixels could thus be well placed within the visible margins of a single cell (Fig. 2B).

As in any optical device, diffraction effects pose the limits to resolution and will change the geometry of the stimulus. With adaptive optics correction, the incident beam aperture (5.6 mm) yields a PSF with FWHM of 24 arcsec at the stimulation wavelength (543 nm). Expressed in image space, this corresponds to a FWHM of 2.6 pixels (1.9 μm on the retina). With optimal wavefront correction, a nominal 3 × 3 pixel stimulus (Fig. 2B) convolved by the system PSF produced a light intensity profile on the retina where the 5% intensity contour corresponded to a nearly circular area 7.3 pixels in diameter (5.3 μm on the retina), approximately matching the diameter of imaged cone apertures at 3° eccentricity (Fig. 2C). Similar agreement between cone and stimulus size was observed with larger test stimuli that were required at higher eccentricities due to reduced detection.

Repeated stimulation under constant conditions is mandatory in any psychophysical testing. Consequently, we further characterized light delivery by taking into account spatial delivery errors over each set of stimulus trials after fixational eye movements had been compensated for with real-time eye tracking (see Materials and Methods). When a selected cone was identified and tracked during an experiment, it was possible to repeatedly deliver stimuli within 1–2 pixels (0.73–1.46 μm) of the targeted location (Fig. 2D). In the given example, 7 of 22 deliveries landed exactly at the targeted image pixel, with the remaining 15 deliveries distributed over the immediately neighboring pixels. Across all 324 staircase experiments performed in the study (a total of 7128 stimulus trials), the average SD of delivery jitter was 2.2 pixels, in both x and y image coordinates (1.6 μm on the retina). For a single threshold experiment comprised of 22 repeated trials, the actual light delivery was calculated as the PSF-convolved nominal stimulus definition summed across the actual delivery locations (Fig. 2E). The resulting light delivery distribution is the final estimation of actual light distribution during one threshold experiment. The 5% delivery contour had a radially averaged diameter of 7.9 pixels (5.7 μm on the retina). Integrating the light distribution within this 5% contour showed that 82% of all the delivered light fell within this contour. Although this suggests that, even after repeated presentation, most of the delivered light was constrained to a retinal area the size of a single cone, we note that this does not take into account uncontrollable light scatter (see Discussion). Nonetheless, the following results suggest that most of the stimulus light during a set of trials was confined to a single cone.

Single-cone increment thresholds

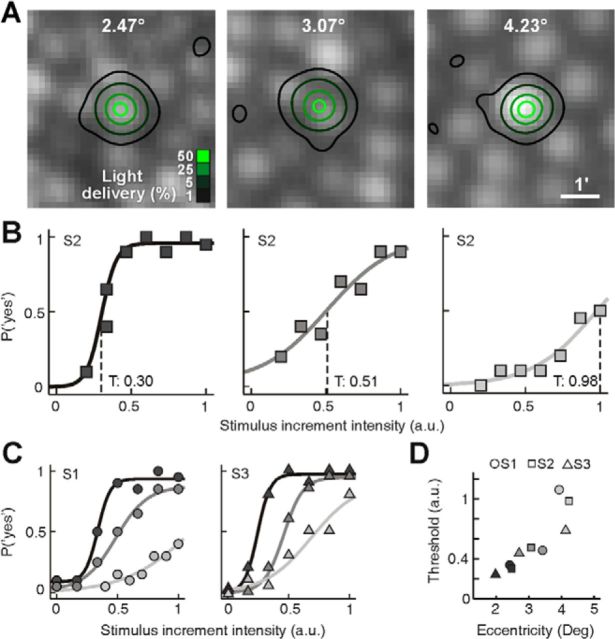
With the ability to repeatedly direct light to targeted cones, we first examined whether psychometric functions could be obtained from microstimulation. Luminance increment thresholds were measured in three subjects (S1–S3) at three different eccentricities, each with a method of constant stimuli. Tested eccentricities were similar for all subjects (S1: 2.41°, 3.42°, 3.93°; S2: 2.47°, 3.07°, 4.23°; S3: 1.98°, 2.7°, 4.13°). For each test location, seven predefined and equally spaced stimulus intensities were presented 20 times in a randomly interleaved order, and the subjects responded in a yes–no paradigm. Figure 3A shows the light delivery distributions for each 140 trial run in subject S2. Note that the 1% delivery contour is included to document single delivery outliers in the course of the experiment. It is also worth noting that cone size and spacing increased with eccentricity, as expected from known anatomy. At each eccentricity in subject S2, psychometric functions were obtained that showed increasing thresholds and shallower slopes with increasing eccentricity (Fig. 3B). Similar data were found for the other two subjects (Fig. 3C), with the correlation between threshold and eccentricity being fairly consistent between subjects (Fig. 3D). In subject S3, the same cone at 1.98° eccentricity was tested on different days and yielded very similar thresholds (0.25 and 0.27), suggesting that the experimental conditions were stable over time. Across subjects and eccentricities, the diameter of the 5% light delivery contour was typically 8.5 pixels (6.2 μm on the retina).

Figure 3.

Microstimulation threshold measurements. A, Light delivery distribution achieved in Subject 2 at three eccentricities, for 140-trial runs using the method-of-constant-stimuli approach. Note the increase in cone size and spacing with eccentricity. B, Psychometric functions were constructed by fitting a logarithmic function (lines) to the frequency-of-seeing data at each eccentricity (coded by gray level here and in C and D). Threshold, T, was defined as the intensity where the function inflects (dashed lines). C, Same as in B plotted for subjects S1 and S3. For the most eccentric test sites, modulation limits in the light delivery system (see Materials and Methods) result in a clipping of the upper portion of the psychometric function. D, Increment threshold was calculated from each psychometric fit and was plotted against eccentricity for all subjects, revealing a strong correlation between retinal eccentricity and threshold.

Our findings agree with prior studies showing that photopic thresholds are higher for a constantly sized stimulus as one tests further from the fovea (Wilson, 1970; Lie, 1980; Inui et al., 1981), the difference here is that most of the light was delivered to only one cone. The steepness of the psychometric functions also became shallower with increasing eccentricity, which indicates increases in signal uncertainty (Pelli, 1985; Tyler and Chen, 2000). The most likely retinal source of this uncertainty is increased cone convergence onto bipolar or ganglion cells with eccentricity (Anderson et al., 1991; Dacey, 1993; Volbrecht et al., 2000; Drasdo et al., 2007). These data suggest that standard psychometric assessment of visual function can be performed in the parafovea with cone-sized microstimulation.

Positional effect of stimulus placement

The structures seen in the AOSLO images mostly stem from light emitted at the inner aperture (near the external limiting membrane) of the optical fiber component of the photoreceptor. Because these act as optical waveguides for light traveling to the photopigment-filled outer segments, we tested whether perceptual sensitivity was dependent on the exact placement of the stimulus with respect to the individual cone apertures. The center of the inner segment is where light is captured most efficiently, and that efficiency drops off as a Gaussian function as the edge of the inner segment is reached. If this light-capturing profile is detectable psychophysically, it would imply that (1) our visual performance is ultimately determined by exactly where on this mosaic light falls and (2) stimulus energy can be effectively constrained to a cone-sized area despite the optical and technical obstacles outlined above.

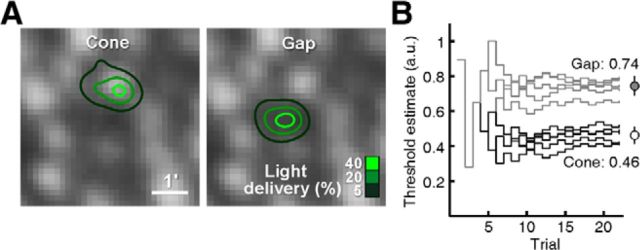
We measured increment thresholds in four subjects (S1–S4), this time using a Bayesian staircase method to allow more rapid estimation of threshold (see Materials and Methods). Stimuli were delivered either to the center of a targeted cone or to an adjacent gap between the targeted cone and a neighboring one (referred to as cone and gap conditions, respectively). Stimulus trials were randomly interleaved, drawn from two staircases operating simultaneously for the two conditions. Figure 4A shows an example of the light delivery distributions in one subject for a cone/gap pair (S2, 3.5° eccentricity). Threshold estimates were measured multiple times by repeating runs of interleaved staircases (Fig. 4B). In this example, all of the threshold estimates in the cone condition were lower than in the gap condition, and the difference between means was significant (cone: 0.46 ± 0.04 a.u.; gap 0.74 ± 0.06; p < 0.01, two-tailed t test). For the cone/gap pair in Figure 4, 61% more light had to be delivered to reach threshold when light was not centered on the cone. In the model described below, we consider how threshold is still attainable in the gap condition, despite it being counterintuitive.

Figure 4.

Comparing cone versus gap thresholds. A, Light delivery profiles for two stimulus conditions, either on a cone (left) or in the adjacent dark gap between cones (right), achieved during randomly interleaved trials (22 trials per condition, 3.5° eccentricity). B, Trial-by-trial stimulus intensity progress during five Bayesian adaptive staircases for each condition. Mean threshold measured for the cone condition was lower than for the gap condition (circles; mean ±1 SD).

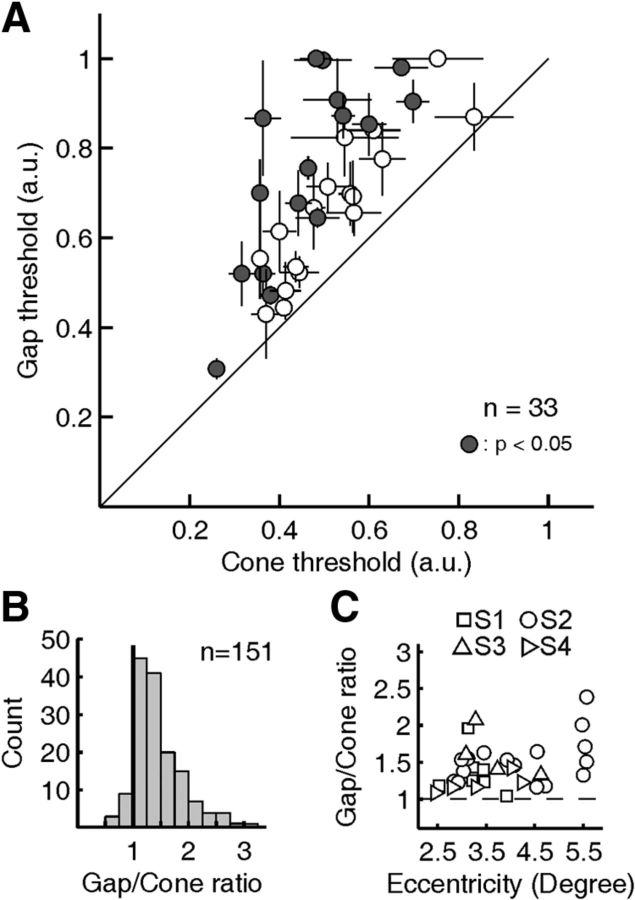
The pronounced difference between cone and gap thresholds was present in all sites tested (n = 33, 2.5–5.5° eccentricity), in all subjects (S1: n = 8; S2: n = 16; S3: n = 4; S4: n = 5), and with different stimulus sizes (tested range: 3–9 pixels square). To present these data as a population, we calculated a threshold ratio, comparing the mean gap condition against the mean cone condition for each test site. This ratio normalizes the data by removing the effects of eccentricity and day-to-day variation in background on threshold. A threshold ratio >1 signifies relatively worse sensitivity for the gap condition, while a ratio near 1 indicates no effect of stimulus placement. As evident in Figure 5A, all mean gap/cone ratios were >1, with an overall average ratio of 1.48 (range: 1.04–2.39) and with 16 of 33 of individual sites reaching significance (p < 0.05, two-tailed t test). Across the population, therefore, increment thresholds were generally 1.5 times higher when the light was directed between cones than when it was delivered directly on a cone.

Figure 5.

Population data for cone versus gap thresholds. A, Mean cone thresholds plotted against mean gap thresholds for 33 sites tested in four subjects. Horizontal and vertical bars represent ±1 SEM. Filled circles indicate a significant difference between cone and gap thresholds (two-tailed t test, p ≤ 0.05). B, Distribution of gap/cone threshold ratios measured during each pair of staircase runs is skewed toward higher values, with a mean gap/cone ratio of 1.48 (median: 1.38). C, Gap/cone threshold ratios plotted as a function of retinal eccentricity for each subject.

The mean ratio data obtained from repeated runs at any one location obscure the wider range of gap/cone ratios we observed during single pairs of runs. The distribution of pairwise gap/cone ratios, measured from each individual pair of runs, ranged from 0.46 to 3.13, and was skewed toward higher values (Fig. 5B). Analyzed in this way, 138 of the 151 threshold pairs (91%) had a ratio greater than one. This distribution may underestimate the true extent of the higher gap/cone ratios given that stimulus modulation constraints may lead to ceiling effects in the algorithm used to estimate thresholds (see Materials and Methods). Because we tested sites over a range of retinal eccentricities, it was possible that threshold ratios would increase with eccentricity, as the gap between cones tends to widen. At higher eccentricities we used larger stimuli to ensure detection (mostly 5 pixel square compared with 3 pixel square at lower eccentricity), possibly rivaling the effect of increased spacing. A plot of the mean gap/cone ratios as a function of eccentricity revealed a mild positive eccentricity effect with little predictive power (linear regression slope: 0.12, R²: 0.14; Fig. 5C). Given the low sample count at higher eccentricities, we used the mean gap/cone ratio of 1.48 as a best estimate for the positional effect of stimulus placement in the analysis below.

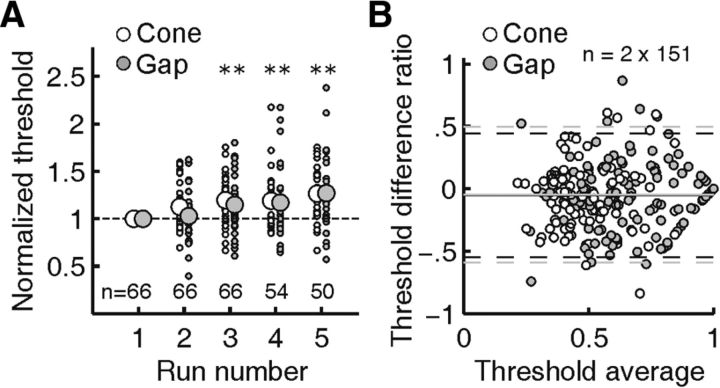
As a means of quantifying possible adaptation or fatigue effects that would alter thresholds with time (Frome et al., 1981), we tested whether threshold values changed over the course of repeated testing. Normalizing thresholds with respect to the values found in the first run, we found that across subjects and conditions, mean normalized thresholds rose by 7% between repeated runs (Fig. 6A). This threshold drift toward higher values reached significance (p < 0.01, two-tailed t test) after the second repetition. Because the threshold drift rate was not significantly different for cone and gap conditions, our analysis of a gap/cone threshold ratio was not affected. A Bland–Altman analysis of measurement repeatability (Altman and Bland, 1983) did not indicate any systematic threshold differences between repeated measurements (Fig. 6B).

Figure 6.

Threshold drift and Bland–Altman analysis. A, For each stimulus location, repeated threshold measurements were normalized against the threshold measured during the first run, for cone and gap stimulations separately. Thresholds increased by ∼7% with each run, suggesting fatigue or adaptation effects. Asterisks mark significant mean threshold increases (p ≤ 0.01); threshold drift over multiple runs did not differ between cone and gap conditions. Small dots correspond to individual thresholds, larger circles are mean values. B, Bland–Altman analysis reveals no significant systematic change between pairs of repeated threshold measurements. The V-shaped arrangement of data points toward higher average values is expected due to our maximum displayable stimulus intensity of 1. Solid lines are the mean; dashed lines encompass 95% of difference ratios.

If perceptual thresholds for a single cone are sensitive to the exact placement of stimulus light, then instances where multiple cones are stimulated should also exhibit a positional effect. We selected test conditions and eccentricities where the subjects reported seeing the stimulus only when two or more cones were stimulated. In two subjects (S3 and S4), increment thresholds were measured as described before, with the exception that two, three, or five cones were targeted for simultaneous stimulation (Fig. 7). In all cases, mean cone thresholds were significantly lower than mean gap thresholds (p ≤ 0.01, two-tailed t test). With two cone stimuli at 3.86° eccentricity, the mean gap/cone ratio was 1.8; with three stimuli at 3.40° the ratio was 1.3; and with five stimuli at 4.44° the gap/cone ratio was 1.7 (in this last example, a 3-cone stimulus was not visible to the subject). Thus, while the patterned stimulation required that cone signals combine to reach threshold, it was still the case that delivering light to areas between the cones profoundly compromised detection. It suggests that, even at the perceptual level, the cone mosaic cannot be treated as a uniform sheet of sensitivity; rather, it has peaks and troughs of sensitivity defined by the position of each cone.

Light capture model

The gap/cone threshold ratios we observed support the hypothesis that light capture—and consequently, visual sensitivity—in the parafovea is governed by the microscopic gradient manifest in the waveguiding properties of individual photoreceptors. One limitation to expressing the data in this fashion is that it requires a continuous variable—stimulus position—to be allocated to one of two categories (viz. cone or gap). To explain the effect of stimulus position on threshold quantitatively, we developed a model of light capture that incorporated data from the trial-by-trial stimulus positions over the course of each psychophysical staircase and the local arrangement of retinal receptors imaged during testing.

The first task in creating the model required validating our estimates of the spatiotemporal distribution of our stimulus on the retina (Fig. 2). For a number of reasons (see Discussion), residual optical blur not sensed or corrected by our AOSLO system could lead to significant light absorption in neighboring cones. The blur may arise from defocus or uncorrected aberrations; hereafter we will refer to this as equivalent defocus since both effects are essentially the same when the errors are small (Zhang and Roorda, 2006). To estimate the magnitude of this residual blur, we examined the effect of stimulus position on light capture in a model cone mosaic (Fig. 8A; for details, see figure legend and Materials and Methods). We adopted the assumption that, for neighboring cones in the parafovea, cone signals sum linearly and with equal perceptual weight (differential contribution of L and M cones is negligible because we used an equally driving wavelength, 543 nm), such that threshold will be reached when some fixed amount of light is captured by the photoreceptor array. Thus, as the position of a cone-sized stimulus is varied with respect to the cone mosaic, threshold will scale inversely with light capture. For example, when light capture is low (e.g., in the gap condition), more light must be delivered to reach the detection criterion. We compared the ratio of light capture for stimuli landing on a cone and in its adjacent gap at a given eccentricity to the mean gap/cone threshold ratios measured at similar eccentricities. Any remaining discrepancy between the estimated light capture and psychophysical ratios was attributed to residual blur, which has the effect of flattening the light capture gradient (Fig. 8B). After accounting for diffraction and additional motion blur introduced by stimulus delivery errors (jitter SD = 1.8 pixels), and using an estimate of cone aperture scaling (MacLeod et al., 1992), we estimated our equivalent defocus to be between 0.057 and 0.061 diopters (Fig. 8B). When the size of the cone aperture was allowed to vary over a reasonable range of Gaussian profile widths (MacLeod et al., 1992), the model yielded defocus estimates ranging from 0 to no greater than 0.08 diopters (Fig. 8C). These results imply that equivalent defocus was not a major factor contributing to the observed gap/cone threshold ratios. It is worth noting that under natural viewing conditions the cone/gap ratios would tend to unity, because normal ocular aberrations would lead to much larger optical spread than what is found here (Fig. 8C, points > 0.1 D); this indicates that the finest grain of light capture would only be perceptible when aberrations are minimized.

Having arrived at an estimate of the equivalent defocus of the stimulus, a model of light capture identical to the one described in the previous section was generated, with the exception that the actual experimental stimulus locations and receptor arrangements were used in place of their idealized counterparts. Spatial stimulus representations were generated in the same manner as Figure 2 and filtered by the cone mosaic to give an estimate of light capture (Fig. 9A,B). To facilitate comparison across data collected at various parafoveal eccentricities—where photopic threshold and the geometry of retinal light capture both change—it was necessary to normalize our light capture estimates and threshold data. For capture, data were normalized by the mean light capture for the local arrangement of receptors and delivery at each test site; for threshold, data were normalized to the mean value of the cone and gap condition at each test location. After such normalization, thresholds were plotted as a function of estimated light capture, and showed that threshold decreased with increasing light capture (Fig. 9C). If sensitivity thresholds were primarily governed by light capture in single cones, we would expect a negative unity slope in such a plot. Because the residual blur must be nonzero in a real eye in our experiments, we determined what amount of equivalent defocus would yield a slope of −1 from an orthogonal regression to the data (R²_T: 0.47, R²_C: 0.46). This residual stimulus blur had an equivalent defocus of 0.056 diopters, a value that agrees with our estimate of residual blur in the model analysis (Fig. 8). We conclude from these results that perceptual thresholds for cone and gap conditions can be explained directly by cone light capture that includes a small amount of defocus or uncorrected aberrations.

The linear fit in Figure 9C, which captures 47% of the variance in the data, assumes that cones are equally weighted in the model, leaving about half of the variance unexplained. It was recently shown that cone inputs converging onto single ganglion cells in primate retina have quite variable weighting (Li et al., 2014). So it is likely that some of the variance not explained by the linear model was due to cones having different weights. To estimate the impact of this variation, we simulated light capture in our data with cone weights that randomly varied by 20% SD from a mean cone weight (see Materials and Methods). This simulation showed that 25% of the variance in the data could arise from variable cone weighting alone. Although we have no estimate of the true distribution of cone weights, the simulation suggests that half of the unexplained variance in our linear model could result from a modest variability in cone weights. The remaining variance is likely due to nonlinear summation occurring downstream from the cones and from noise in the psychophysical measurement itself.

Discussion

By detecting visual sensitivity to positional shifts on the order of a photoreceptor's size, we demonstrated that fundamental properties of the waveguiding retina can be revealed by microstimulation. Sensitivity decreased when light was directed into gaps between cones, and increased when light was delivered to cone centers. Because it was accounted for by a model of cone acceptance apertures, the detection of microstimuli appears to be governed simply by cone light capture geometry.

Whether the increment thresholds we measured were derived solely from the activation of one cone remains, however, an open question. Although the trial-averaged stimulus diameters suggest that photon delivery was largely restricted to one cone, possible sources of undetectable stimulus blur exist that could result in photon absorption in more than one cone. These sources include inadequate correction of longitudinal chromatic aberration (Atchison and Smith, 2005), and predominantly, local intra-ocular scatter (Vos and Bouman, 1964; Vos et al., 1976). Such stray light arises from the corneal and lens interfaces, the vitreous humor, and the retinal tissue lying in front of the photoreceptors (Boynton and Clarke, 1964; Franssen et al., 2007; van den Berg et al., 2013). It is also possible that light reflecting off the retinal pigment epithelium could be detected by neighboring cones and contributing to the percept. These scattering sources cannot be sensed or controlled by the AOSLO. We minimized the effect of scatter by using thresholds as our metric, as this uses the least amount of light to perform a perceptual task. Nonetheless, even for the cone-targeted condition, we have no direct evidence that activity arising from only one cone suffices for reaching perceptual threshold.

However, indirect evidence from the multicone patterned stimulus experiments suggests that single cones do contribute in a straightforward way to perception. To achieve threshold in these experiments, more than one cone had to be stimulated. The recruitment of multiple cones to reach threshold at greater eccentricities (Fig. 7) is consistent with spatial summation, and with the convergence of cone inputs onto downstream retinal cells where the signals combine (Wilson, 1970; Inui et al., 1981; Volbrecht et al., 2000). Stimulation of multiple cones often shows linear summation up to some critical area (Ricco's Law; Ricco, 1877). Although this critical area changes with background intensity and stimulus duration (Barlow, 1958), our stimuli likely fell within the critical area for the eccentricities tested (Volbrecht et al., 2000). Together with the results from our light capture model, these data suggest that if a cone is capturing light, it adds to the signal driving threshold.

Our adaptive optics instrument cannot correct for forward light scatter arising from discontinuities in the optics. Although this light scatter may be significant, the energy is distributed widely and uniformly, such that the contribution onto any individual cone—even neighboring cones—is estimated to be <10⁻³ of the peak intensity for young eyes (van den Berg et al., 2010). In comparison, the intensity of the first Airy disk PSF ring is ∼1% of the peak. Moreover, when the focused PSF location is shifted, its energy distribution is altered dramatically relative to the cone mosaic, whereas the distribution of scattered energy is not. Assuming that light is summed linearly over the six adjacent cones that typically surround a single cone, then the total scattered light absorbed in these cones will be far less than that resulting from the blur arising from diffraction plus motion, which the model suggests is already lower than 5% of the light absorbed by the mosaic. The fact that threshold in the gap condition was essentially explained by the light capture model provides further support that intraretinal scatter does not play a significant role, and that pooling of signals from surrounding cones receiving very small amounts of light contribute negligibly to the threshold. Some of the variance in the data in Figure 9C arises from other sources of residual stimulus blur, but it cannot be readily separated from the many postreceptor sources of noise that accompany threshold tasks.

Prior visual testing with adaptive optics-corrected microstimuli suggests indirectly that percepts can be mediated by the activity of individual cones. Cone-sized scotomas caused by photoreceptor dysfunction in a deuteranopic subject were detected psychophysically with briefly flashed microstimuli (Makous et al., 2006). A recent model to explain color-naming variability arising from microstimuli suggests that the percepts are accounted for by signals from one cone (Hofer et al., 2005; Brainard et al., 2008). Psychophysical results derived from laser interferometry that bypass the eye's optical limitations identify the finest channels of visual perception as matching receptive fields that are about the size of foveal cone photoreceptors (Smallman et al., 1996). Other studies used small spots without adaptive optics correction to assess single cone perception. Williams et al. (1981) reported perceptual S cone mapping by probing just outside the foveola. Absolute threshold measurements determined L/M cone ratios in the fovea and mid periphery, derived from the fact that only a few cones are likely required for such thresholds (Cicerone and Nerger, 1989; Wesner et al., 1991; Otake and Cicerone, 2000). Our results build upon these earlier studies showing that percepts can be shaped by signals originating from single cones. The major advantages reported here are that the specific cone being tested is known and it can be stimulated repeatedly; thus perceptual sequelae can be measured directly from the cone of interest.

It has been known for some time that the waveguiding property of cones determines their light capture geometry. The Stiles–Crawford effect is a prime example. Light entering off-axis (at the pupil's edge) is harder to detect than light entering along the eye's optical axis (Stiles and Crawford, 1933). The effect is a consequence of cones behaving as optical waveguides with a Gaussian-shaped light acceptance profile (Enoch and Tobey, 1981; Vohnsen, 2007). It is thought that waveguiding occurs in the cone inner segment, where the higher internal refractive index—combined with photoreceptor tapering—leads to enhanced funneling of photons into the pigment-laden outer segment (Enoch, 1961; Miller and Bernard, 1983; Hoang et al., 2002). The size of the light acceptance profile defined by the inner segment remains a matter of debate. Studies using gratings as stimuli suggest light is integrated over the full diameter of the inner segment, both in the fovea (Miller and Bernard, 1983) and periphery (Anderson et al., 1991). In contrast, when studying the distortion percepts generated by high-frequency interference fringes, the inferred cone aperture was ∼48% of the inner segment diameter (MacLeod et al., 1992; Chen et al., 1993). We now show that such light capture profiles can be measured perceptually across just one cone. Along with the light capture model, the decreased sensitivity in the gaps between cones support the conclusion that the light-collecting aperture is smaller than the diameter of the inner segment. This result also obviates any prominent role for Muller cells in coupling light to the photoreceptors, at least near the fovea (Franze et al., 2007).

Given that many combinations of cone aperture size and residual blur can produce agreement between the psychophysical data and the light capture model, we can only set limits on the likely size of the cone apertures. The maximum residual blur estimated by our model (equivalent defocus of 0.08 diopters) is less than the subjective depth-of-focus for the parafovea (Wang and Ciuffreda, 2006), but, given it is at the upper limit of the range of the axial resolution for our system (computed to be ±0.1 diopter [∼74 μm] with 543 nm light and a confocal aperture of 3 Airy disk radii for a 5.6 mm pupil; Venkateswaran et al., 2004), our focus error is <0.1 diopters. This yields a minimal cone aperture of 10% of the inner segment diameter, an unlikely value considering earlier findings (MacLeod et al., 1992). At the upper limit, in perfect focus, the cone aperture is unlikely to be >70% of the inner segment diameter (Fig. 8C). Only nonlinear pooling of cone signals would necessitate shifting this estimate upward. Given such limits on the aperture sizes, it is clear that the spatial grain of perception should initially be determined by the exact arrangement of cones in any patch of retina and the exact placement of stimuli onto those waveguiding cones.

Functional testing at the cellular level in the retina creates new opportunities for vision science and retinal disease assessment. It has not been possible previously to stimulate single sensory receptors in any modality in vivo, yet one of the major goals in neuroscience is to understand how perception is mediated by the activity of single neurons (Parker and Newsome, 1998). The stage is now set for probing how signals from multiple cones interact to generate percepts, and how different retinal ganglion cell types might best be stimulated. In the ophthalmological clinic, functional testing of damaged cones may prove useful (Roorda, 2011; Carroll et al., 2013). In many retinopathies the fundus can appear unremarkable, yet cone waveguiding is disrupted and light detection is likely impaired (Birch et al., 1982; Smith et al., 1988). Cone-targeted stimulation may become a tool for better characterization of disease progression and offer a way to evaluate the efficiency of novel treatments at the microscopic level in the living eye.