The Impact of Cortical Deafferentation on the Neocortical Slow Oscillation

Abstract

Slow oscillation is the main brain rhythm observed during deep sleep in mammals. Although several studies have demonstrated its neocortical origin, the extent of the thalamic contribution is still a matter of discussion. Using electrophysiological recordings in vivo on cats and computational modeling, we found that the local thalamic inactivation or the complete isolation of the neocortical slabs maintained within the brain dramatically reduced the expression of slow and fast oscillations in affected cortical areas. The slow oscillation began to recover 12 h after thalamic inactivation. The slow oscillation, but not faster activities, nearly recovered after 30 h and persisted for weeks in the isolated slabs. We also observed an increase of the membrane potential fluctuations recorded in vivo several hours after thalamic inactivation. Mimicking this enhancement in a network computational model with an increased postsynaptic activity of long-range intracortical afferents or scaling K⁺ leak current, but not several other Na⁺ and K⁺ intrinsic currents was sufficient for recovering the slow oscillation. We conclude that, in the intact brain, the thalamus contributes to the generation of cortical active states of the slow oscillation and mediates its large-scale synchronization. Our study also suggests that the deafferentation-induced alterations of the sleep slow oscillation can be counteracted by compensatory intracortical mechanisms and that the sleep slow oscillation is a fundamental and intrinsic state of the neocortex.

Introduction

Sleep occupies approximately one-third to one-half of each day in the majority of mammalian species (Siegel, 2005). Thalamocortical activities during deep sleep are dominated by a slow oscillation (<1 Hz; Blake and Gerard, 1937) that appears as an alternation of active (UP) and silent (DOWN) states of cortical neurons (Steriade et al., 1993b; Steriade et al., 2001; Timofeev et al., 2001). This synchronous neuronal activity generates the EEG slow waves (Contreras and Steriade, 1995; Chauvette et al., 2010). The slow-wave sleep is essential for memory formation and consolidation (Gais et al., 2000; Stickgold et al., 2000; Maquet, 2001; Huber et al., 2004; Marshall et al., 2006) and it has been proposed that synaptic plasticity associated with different brain rhythms contributes to memory consolidation (Timofeev et al., 2000; Steriade and Timofeev, 2003; Tononi and Cirelli, 2006; Diekelmann and Born, 2010; Timofeev, 2011; Vyazovskiy et al., 2011; Chauvette et al., 2012).

Despite recent progress, the role and mechanisms of sleep (Steriade et al., 1993c; Destexhe and Sejnowski, 2001; Maquet, 2001; Steriade and Timofeev, 2003; Tononi and Cirelli, 2006; Diekelmann and Born, 2010) and the origin of the synchronous sleep slow oscillation remains a controversial topic. A number of studies (Timofeev and Steriade, 1996; Sanchez-Vives and McCormick, 2000; Timofeev et al., 2000; Bazhenov et al., 2002; Shu et al., 2003; Hasenstaub et al., 2005; MacLean et al., 2005; Rudolph et al., 2007; Csercsa et al., 2010) have suggested that the neocortex is, in itself, sufficient to generate the slow activity characteristic of slow-wave sleep via recurrent excitatory and inhibitory intracortical interactions. Other studies, however, have shown that the thalamus might actively contribute to the generation of the slow oscillation (Hughes et al., 2002; Crunelli and Hughes, 2010; David et al., 2013). These results argue for significant role of the thalamus in patterning the slow oscillation during deep sleep (Crunelli and Hughes, 2010).

The sleep slow oscillation groups other faster brain rhythms (Steriade et al., 1993a; Steriade, 2006), including fast oscillations in the β and γ frequency ranges (Steriade et al., 1996a; Steriade et al., 1996b; Dickson et al., 2003). Similar to the cortical slow oscillation, gamma oscillations can also be generated in isolated cortical structures in a condition of increased cortical excitability (Whittington et al., 1995; Draguhn et al., 1998).

In this study, we demonstrate that thalamocortical inputs critically contribute to maintaining both the slow and fast (β-γ) oscillations in the intact thalamocortical system. Full or partial cortical deafferentation that removes thalamocortical inputs also disrupts the slow and fast rhythms in the neocortical network, although rare spontaneous active states persisted in the cortex. The slow but not the fast oscillation started to recover within hours after disruption of the thalamocortical connectivity. We found in vivo evidence of recovery of the slow oscillation after cortical deafferentation and our modeling data indicate that an increase in intracortical excitatory synaptic drive may be one of the mechanisms underlying this phenomenon.

Materials and Methods

Surgery

Experiments were performed on cats of either sex in accordance with the guidelines published in the National Institutes of Health's Guide for the Care and Use of Laboratory Animals (NIH publication no. 86-23, revised 1987) and were approved by the Committee for Animal Care of Université Laval.

Acute experiments were conducted on cats anesthetized by intramuscular injection of ketamine and xylazine (10 and 2 mg/kg, respectively). All recordings were obtained in areas 5 and 7 of the suprasylvian gyrus. Animals were continuously supplied with lactated Ringer's solution at a rate of 10 ml/kg intravascularly. Ketamine was added to the lactated Ringer's solution to insure a supplementary dose of 20 μg/kg/min. The EEG was monitored throughout experiments, which lasted 8–36 h, and additional doses of ketamine-xylazine were administered intravenously when the EEG tended slightly toward activated pattern. Lidocaine (0.5%) was injected in all incision points. Animals were paralyzed with gallaminetriethiodide 2% and maintained under artificial ventilation. The ventilation rate and oxygenation were adjusted to keep an end-tidal CO₂ at 3–3.5%. Body temperature was maintained between 36.5 and 38°C throughout the experiment. The heart rate was continuously monitored (90–110 beats/min). The stability of intracellular recording was obtained by draining the cisterna magna, bilateral pneumothorax, and hip suspension and filling the hole made in the skull with agar 4% in saline 0.9%.

For experiments consisting in inactivating the thalamus (n = 10 cats), a stimulating electrode was stereotaxically inserted in the lateral posterior (LP) thalamic nucleus at the following coordinates: F 8, L 4.5, H 4.5 (Reinoso-Suarez, 1961). Cortical response to 5 current pulses (10 Hz, 1.5 mA, 0.2 ms) delivered to the LP nucleus was assessed before the inactivation of LP nucleus (Fig. 1a). LP was inactivated by injection of 2 μl of 20% lidocaine N-ethyl bromide (QX-314; Sigma) at 5 different coordinates: F7, L3, H3; F7, L3.75, H4.3; F7, L6, H4; F9, L6, H5; and F9, L6.75, H6.3. Coomassie blue (0.5%) was added to the QX-314 solution to confirm the sites of injection histologically (Fig. 1a). Inactivation of LP was confirmed by the absence of cortical response to LP stimulation (Fig. 1a). The preparation of neocortical slabs (∼6 × 10 mm) was described in detail previously (Timofeev et al., 2000). Slabs were isolated in acute cats (n = 7) and in chronically implanted cats (n = 2). The chronic surgery was described previously (Steriade et al., 2001; Timofeev et al., 2001).

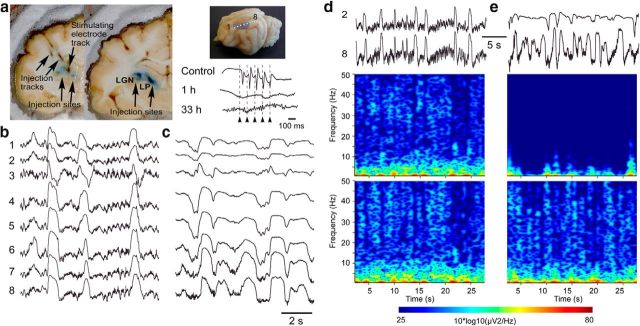
Figure 1.

Effects of partial thalamic inactivation on cortical slow oscillation. a, Left, Location of QX-314 injection sites (violet area) and stimulating electrode in LP nucleus. Top right, Location of cortical recording electrodes 1–8. Bottom right, Cortical response to LP stimulation in control and its abolition 1 and 33 h after inactivation. Multisite LFP recordings before (b) and 1 h after (c) LP inactivation. d, e, Wavelet transform of the LFP signal from electrodes 2 and 8 d before (d) and after (e) LP inactivation.

At the end of the experiment, animals were transcardiacally perfused with saline 0.9%, followed by paraformaldehyde 4%/glutaraldehyde 0.05% and then by sucrose 10% in PB 0.1 m. Brains were removed and kept in PB 0.1 m sucrose 30% until they sank and were subsequently cryosectioned (80 μm).

Electrophysiology

To record multisite field potential, an array of 8 low-impedance coaxial electrodes (Rhodes Medical Instruments), each spaced by 1.5 mm, was inserted in the medial portion of the suprasylvian gyrus (band-pass filter: 0.1 Hz-10 kHz). A high-impedance amplifier (low-pass filter at 10 kHz) with an active bridge circuitry was used to record and inject current in cells. Single, dual, and triple intracellular recordings were obtained with sharp glass micropipettes filled with 2 m potassium acetate (DC resistance of 30–75 MΩ). Signals were recorded with a 16-channel data acquisition system (Vision; Nicolet) at a sampling rate of 20 kHz.

Data analysis

Analyses were performed offline on a personal computer using IgorPro (WaveMetrics) and MATLAB (MathWorks) software. Statistical analyses were performed in Prism 6 software (GraphPad). Depending on the normality of data and the equality of variances, we used either parametric (Student's t test, ANOVA with Tukey's multiple-comparisons test) or nonparametric (Mann–Whitney test, Kruskall-Wallis test with post hoc Dunn's multiple correction) tests.

Wavelet transforms were computed for epochs of 15 s for frequency range of 0.1–70 Hz with the open source MATLAB toolbox EEGlab (Schwartz Center for Computational Neuroscience, University of California–San Diego). Fast Fourier transform was calculated for local field potential (LFP) recordings from the most and the least affected cortical sites.

Formal thresholds to determine the exact timing of onset of intracellular active and silent states were set as follows: the average and the SD of membrane potentials (V_m) were sampled in 25 ms time windows for epochs of at least 20 s. Values were plotted in a frequency matrix (see Fig. 3c) and displayed two distributions corresponding to active and silent states. An initial threshold between these two distributions was chosen by visual inspection to split values in two new hyperpolarized and depolarized distributions. Average and SD were computed for these distributions. The active state onset occurred when V_m crossed the average value of the depolarized distribution minus its SD and stayed above this threshold for at least 50 ms. Transition to the silent state began when V_m went below the average value of the hyperpolarized distribution plus its SD and stayed below this threshold for at least 50 ms. The number of active states per minute, the percentage of time spent in active states, and the mean duration of silent states were averaged for each cell. To characterize the intensity of postsynaptic activity before and after the onset of active states, we measured the SD of the membrane potential in bins of 200 ms and averaged it over several cycles.

Figure 3.

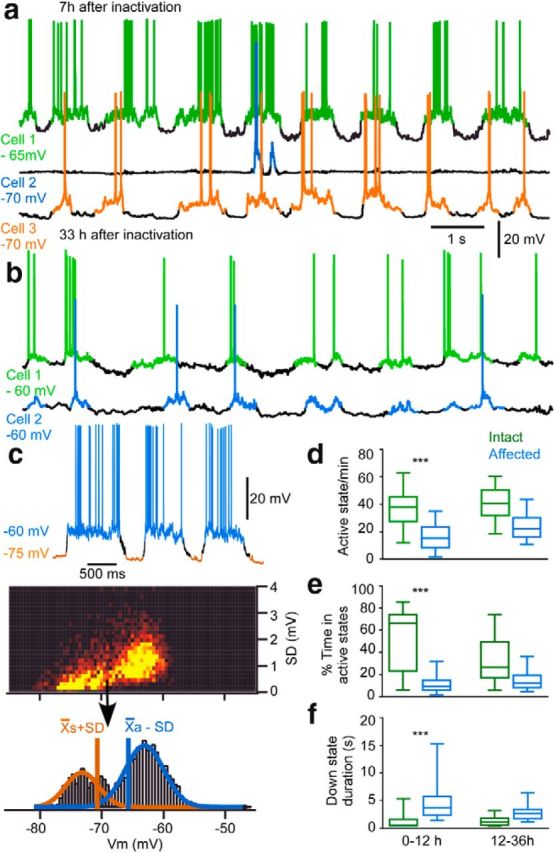
Intracellular activity in intact and partially deafferented cortical areas after inactivation of thalamic LP nucleus. a, Triple intracellular recordings from affected (blue) and unaffected regions (anterior = green, posterior = orange) 7 h after LP inactivation. b, Dual intracellular recording from unaffected (green) and recovering regions (blue) 33 h after inactivation. c, Detection method for active and silent states in intracellular recordings. V_m and SD is computed in for each 25 ms window from intracellular recordings (top traces) and presented as a color-coded frequency matrix. Active and silent states clusters are split according to an initial threshold (arrow) visually selected. Frequency histograms of these new V_m distributions are fitted with Gaussian curves. Silent state threshold (orange) is defined as the mean of its distribution (Xs) plus SD and active state threshold (blue) as the mean of its distribution (Xa) minus SD. d–f, Boxplots of active states occurrence (d), percentage of time in active state (e), and silent state duration (f) of neurons from intact and affected (0–12 vs 12–36 h) regions. Statistical significance was tested with ANOVA post hoc Dunn multiple-comparisons test: ***p < 0.001.

Computational models

Intrinsic currents: thalamus.

Conductance-based models of thalamocortical (TC) and thalamic reticular (RE) neurons include one compartment described by the equation:

where the membrane capacitance (C_m) = 1 μF/cm², nonspecific (mixed Na⁺, K⁺, Cl⁻) leakage conductance (g_leak) = 0.01 mS/cm² for TC cells and 0.05 mS/cm² for RE cells, and the reversal potential (E_leak) = −70 mV for TC cells and −77 mV for RE cells. I^int is the sum of active intrinsic currents, and I^syn is the sum of synaptic currents. The area of a RE cell and a TC cell was 1.43 × 10⁻⁴ and 2.9 × 10⁻⁴ cm², respectively (Bazhenov et al., 2002).

Both RE and TC cells include fast sodium current (I_Na), a fast potassium current (I_K), a low-threshold Ca²⁺ current (I_T), and a potassium leak current (I_KL) = g_KL (V − E_KL)_, where E_KL = −95 mV. In addition, a hyperpolarization-activated cation current (I_h) was also included in TC cells. For TC cells, the maximal conductances were as follows: g_K = 10 mS/cm², g_Na = 90 mS/cm², g_T = 2.2 mS/cm², g_h = 0.017 mS/cm², and g_KL = −0.03 mS/cm². For RE cells, the maximal conductances were as follows: g_K = 10 mS/cm², g_Na = 100 mS/cm², g_T = 2.3 mS/cm², and g_leak = 0.005 mS/cm². The expressions of voltage- and Ca²⁺-dependent transition rates for all currents have been described previously (Bazhenov et al., 2002).

Intrinsic currents: cortex.

The cortical pyramidal cells (PYs) and interneurons (INs) were represented by two-compartment models with channels simulated by Hodgkin–Huxley kinetics. Each compartment was described by Equation 1 with the addition of the current from adjacent compartment, I^d,s=g_c(V_d,s − V_s,d), where V_d(resp. V_s) is the voltage of the dendritic (resp. axosomatic) compartment. Based on our previous studies (Bazhenov et al., 2002; Chen et al., 2012), we assumed that the current dynamics in axosomatic compartment are fast enough to ensure that V_S is always at equilibrium state and can be defined by the equation g(V_S − V_D) = −I_S^int. The axosomatic and dendritic compartments were coupled by an axial current with conductance g_c.

The PY neurons and INs contained the fast Na⁺ channels, I_Na, with a higher density in the axosomatic compartment than in dendritic compartment. In addition, a fast delayed rectifier potassium K⁺ current (I_K) was present in the axosomatic compartment. A persistent sodium current (I_Na(p)) was included in both axosomatic and dendritic compartments. A slow-voltage-dependent noninactivating K⁺ current (I_Km), a slow Ca²⁺-dependent K⁺ current (I_Kca), a high-threshold Ca²⁺ current (I_HVA), and a potassium leak current (I_{KL =} g_KL(V − E_KL)) were included in the dendritic compartment only. The expressions of the voltage- and Ca²⁺-dependent transition rates for all currents are given in Timofeev et al. (2000). For the axosomatic compartment, the maximal conductances and passive properties were S_soma = 1.0 × 10 ⁻⁶ cm², g_Na = 3000 mS/cm², g_K = 200 mS/cm², and g_Na(p) = 0.07 mS/cm². For the dendritic compartment: C_m = 0.75 μF/cm², g_L = 0.033 mS/cm², g_KL = 0.0025 mS/cm², S_dend = S_somar, g_HVA = 0.01 mS/cm², g_Na = 1.5 mS/cm², g_Kca = 0.3 mS/cm², g_Km = 0.01 mS/cm², g_Na(p) = 0.07 mS/cm², and E_KL= −95 mV. E_leak was −68 mV for PYs and −75 mV for INs (Bazhenov et al., 2002). For INs, no I_Na(p) was included. The resistance (r) between compartments was set to 10 MΩ.

The firing properties of this model depended on the coupling conductance between compartments (g_c = 1/r) and the ratio of the dendritic area to the axosomatic area R (Mainen and Sejnowski, 1996). We used a model of a regular-spiking neuron for PY cells (R = 165) and a model of a fast-spiking neuron for IN cells (R = 50).

Synaptic currents.

All synaptic currents were calculated according to the following equation:

where g_syn is the maximal conductance, [O] is the fraction of open channels, and E^syn is the reversal potential. In RE and PY cells, the reversal potential was 0 mV for AMPA and NMDA receptors and −70 mV for GABA_A receptors. For TC cells, the reversal potential was −80 mV for GABA_A receptors and −95 mV for GABA_B receptors. A simple phenomenological model characterizing short-term depression of intracortical excitatory connections was also included in the model. According to this, a maximal synaptic conductance was multiplied to a depression variable (D), which represents the amount of available synaptic resources. Here, D = 1 − (1 − D_i (1 − U)) exp(−(t − t_i)/τ), where U = 0.2 is the fraction of resources used per action potential, τ = 500 ms is the time constant of recovery of the synaptic resources, D_i is the value of D immediately before the i_th event, and (t − t_i) is the time after i_th event.

GABA_A, NMDA, and AMPA synaptic currents were modeled by the first-order activation schemes. Dependence of postsynaptic voltage for NMDA receptors was 1/(1 + exp(V_post − V_th)/σ)), where V_th= −25 mV and σ = 12.5 mV. GABA_B receptors were modeled by a higher-order reaction scheme that considers the activation of K⁺ channels by G-proteins. The equations for all synaptic currents have been described previously (Bazhenov et al., 1998; Timofeev et al., 2000). The values of maximal conductance for each synapse are listed in Table 1.

Table 1.

Detailed geometry of thalamocortical network

Presynaptic cell	Postsynaptic cell	Connection type and strength (ms/cm2)	Connection radius (no. of cells)
TC (matrix)	PY (layer V)	AMPA = 1.212	45
TC (matrix)	IN (layer V)	AMPA = 0.606	10
TC (matrix)	RE	AMPA = 2.424	6
TC (core)	PY (II, III, IV)	AMPA = 1.212	10
TC (core)	IN (II, III, IV)	AMPA = 0.606	4
TC (core)	RE	AMPA = 2.424	6
RE	TC (matrix)	GABAa = 0.181	6
RE	TC (core)	GABAa = 0.181	6
RE	RE	GABAa = 1.06	4
PY (II, III, IV)	IN (II, III, IV)	AMPA = 1.212	1
		NMDA = 0.121
PY (II, III, IV)	PY (II, III, IV)	AMPA = 0.484	5
		NMDA = 0.042
PY (II, III, IV)	PY (V)	AMPA = 0.072	5
		NMDA = 0.015
PY (II, III, IV)	PY (VI)	AMPA = 0.072	5
		NMDA = 0.015
PY (V)	IN (V)	AMPA = 1.212	1
		NMDA = 0.121
PY (V)	PY (II, III, IV)	AMPA = 0.072	5
		NMDA = 0.015
PY (V)	PY (V)	AMPA = 0.484	5
		NMDA = 0.042
PY (V)	PY (VI)	AMPA = 0.072	5
		NMDA = 0.015
PY (V)	RE	AMPA = 4.242	5
PY (V)	TC (matrix)	AMPA = 0.606	8
PY (VI)	IN (VI)	AMPA = 1.212	1
		NMDA = 0.121
PY (VI)	PY (II, III, IV)	AMPA = 0.072	5
		NMDA = 0.015
PY (VI)	PY (V)	AMPA = 0.072	5
		NMDA = 0.015
PY (VI)	PY (VI)	AMPA = 0.484	5
		NMDA = 0.042
PY (VI)	RE	AMPA = 4.242	5
PY (VI)	TC (core)	AMPA = 0.606	8
PY (II, III, IV) (across columns)	PY (II, III, IV) (across columns)	AMPA = 0.212	Random (300 pairs in total)
		NMDA = 0.042
PY (V) (across columns)	PY (V) (across columns)	AMPA = 0.212	Random (300 pairs in total)
		NMDA = 0.042
PY (VI) (across columns)	PY (VI) (across columns)	AMPA = 0.212	Random (300 pairs in total)
		NMDA = 0.042
IN (II, III, IV)	PY (II, III, IV)	GABAa = 1.515	5
IN (V)	PY (V)	GABAa = 1.515	5
IN (VI)	PY (VI)	GABAa = 1.515	5
IN (II, III, IV)	IN (II, III, IV)	Gap junction = 0.06	1
IN (V)	IN (V)	Gap junction = 0.06	1
IN (VI)	IN (VI)	Gap junction = 0.06	1

Spontaneous miniature EPSPs and IPSPs were also set in the present model. The arrival times of miniature EPSPs and IPSPs followed the Poisson process (Stevens, 1993), with time-dependent mean rate μ = (2/(1 + exp(−(t − t₀)/400)) − 1)/250, where t is real time and t₀ is the timing of the last presynaptic spike.

Network geometry.

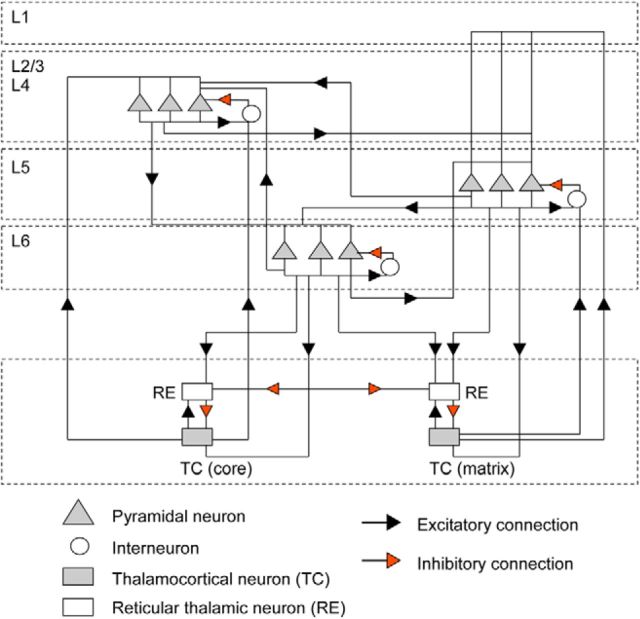
The thalamocortical network model was constructed using several populations of neurons, including cortical pyramidal cells (layers II-IV, layer V, and layer VI), cortical interneurons (layer II–IV, layer V, and layer VI), thalamocortical neurons (with matrix and core subsystems), and thalamic reticular neurons. A general connecting scheme among different populations of neurons is introduced in Figure 7. In total, there were 1500 pyramidal neurons (500 in each population), 360 interneurons (120 in each population), 250 thalamic reticular neurons, and 500 thalamocortical neurons (250 in each structure).

Figure 7.

Geometry of the thalamocortical network model. The thalamortical network model includes a cortical layer II/III/IV, cortical layer V, cortical layer VI, RE, and TC neurons. In each cortical layer, there are 500 PYs and 120 INs. They are evenly divided into 10 cortical columns (50 PY and 12 IN in each column). The thalamic network includes layer of thalamic reticular neurons (250 neurons) and relay cells (500 neurons) divided into two nuclei: specific (core) and diffusive (matrix). The black arrowhead represents excitatory connections and the red arrowhead indicates inhibitory connections. The connectivity radius (fan-out) information is listed in Table 1.

In addition, in this model, cortical layers were evenly split into 10 cortical columns, with a high density of short-range (within a predetermined footprint; Table 1) connections within each column and low-density, low-strength random connections between columns. Details of the network architecture (including the probability of connections and synaptic weights) are provided in Table 1.

In computational models, the LFP of an individual column was estimated by averaging membrane voltages of all neurons within this column.

Upregulation of synaptic efficacy and intrinsic conductances.

The increase in the SD of V_m was implemented by adjusting the strength of PY-PY connection, the strength of IN-PY connection, and the amplitude and frequency of the spontaneous miniature EPSPs (Fröhlich et al., 2008; Volman et al., 2011a; Volman et al., 2011b). Excitatory factors were increased (decreased) and inhibitory factors were decreased (increased) if the average PY firing rate was below (above) the target rate that was estimated by averaging the firing rate in the intact network. The adjusting parameters were ±0.5% for the strength of PY-PY connections and ±0.3% for the amplitude of miniature EPSP. The updating cycle was 2 s.

In addition, we also tested the following five different scaling models by manipulating different biophysical variables in the model: (1) conductance of leaking potassium current (g_KL) at the dendritic compartment of pyramidal neurons (the adjusting scale was ±0.5%); (2) conductance of the fast sodium current (g_Na) and voltage-dependent potassium current (g_Km) simultaneously at dendritic compartment of pyramidal neuron (the adjusting scale was ±0.25% for both of them); (3) conductance of persistent sodium current (g_Nap) and calcium-dependent potassium current (g_KCa) simultaneously at dendritic compartment of pyramidal neuron (the adjusting scale was ±0.1% for both of them); (4) strength of IN-PY connection (g_GABA-A) alone (the adjusting scale was ±2%); and (5) strength of PY-PY connection (g_AMPA) and minis amplitude (the adjusting scale was ±0.5% for g_AMPA and ±0.3% for minis amplitude).

Results

Thalamic inactivation disrupts cortical slow and fast activities

We chose to study the contribution of thalamic and cortical circuits to the slow oscillatory activity by inactivating the LP thalamic nucleus with the use-dependent sodium channels blocker QX-314 and recording the resulting activity in the respective cortical area (suprasylvian gyrus) in cats. In an intact preparation, LFP recordings (array of 8 electrodes separated by 1.5 mm; Fig. 1a) from the suprasylvian gyrus under ketamine-xylazine anesthesia demonstrated the presence of a robust and synchronized slow oscillation (Fig. 1b). Electrical pulse-trains applied through an electrode located within the (LP) nucleus of the thalamus at 10 Hz elicited a cortical augmenting response (Fig. 1a, inset, top trace). Wavelet transform analysis also pointed to the presence of a robust high-frequency component in the β-gamma frequency range during slow oscillation (Fig. 1d). In agreement with a previous study (Doi et al., 2007), when the LP thalamic nucleus was inactivated (Fig. 1a, left), the slow waves and fast rhythms in the targeted cortical regions were reduced dramatically (Figs. 1c,e, 4a). Electrical stimuli applied to the inactivated thalamic site (Fig. 1a) did not elicit any cortical response after QX-314 injection (Fig. 1a, inset, middle and bottom trace), indicating that these thalamic sites were functionally inactivated. In the affected cortical regions, both slow oscillation and β-gamma activity, which typically occurs during active cortical states, were virtually abolished (Fig. 1e, top) and were only slightly reduced in the periphery of the affected sites (Fig. 1e, bottom). This suggests that thalamic inputs are required for the generation and synchronization of cortical active states during slow oscillation. To verify whether thalamic injection of QX-314 effects were not attributed to a leak of QX-314 to cortical locations, in control experiments, we injected intracortically 0.1 μl of 20% QX-314. This induced local and complete cortical inactivation with a radius of 1.5 mm (data not shown).

Figure 4.

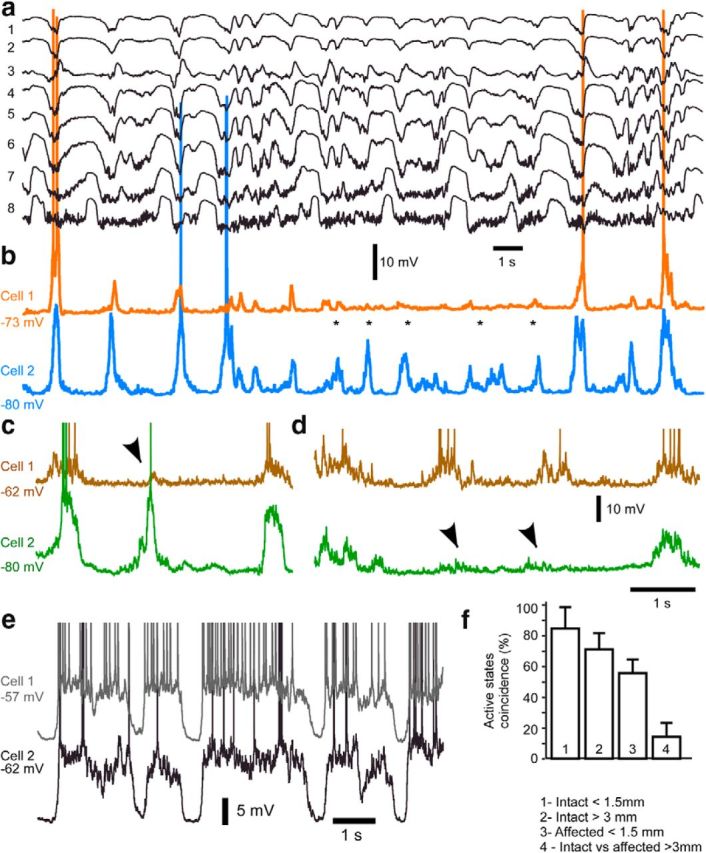
Alternating involvement in active states of closely located cortical neurons in the cortical area affected by thalamic inactivation. a, b, Multisite LFP (a) and dual (b) intracellular recordings of closely located neurons in affected regions (between sites 1 and 2). Multiple active states (*) occurred in Cell 2 but not in Cell 1. c, d, Dual intracellular recordings from another pair of closely located neurons from affected area. Active states occurred either simultaneously or in alternation (arrows). e, Dual intracellular recording of closely located neurons in the intact brain. f, Mean coincidence of active states occurrence for cortical neurons in four conditions.

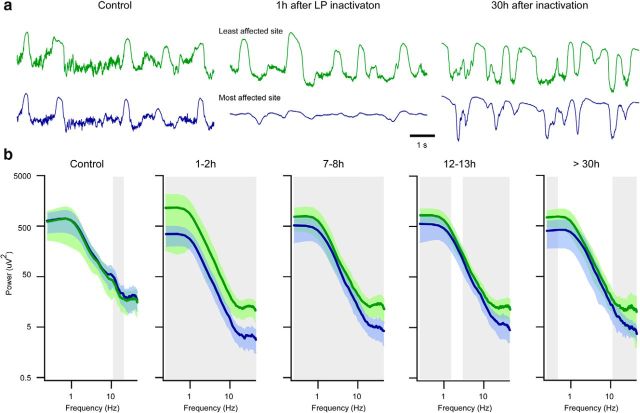
To quantify changes in slow and fast rhythms induced by thalamic inactivation, we performed power spectral analysis from 10 animals (Fig. 2) in which we compared activities in the most versus the least affected electrodes over time. Before thalamic inactivation, the differences were restricted to frequencies 12–17 Hz, which might be explained by a particular network organization of the two cortical sites. After thalamic inactivation, the power spectra of all investigated frequencies was reduced (Mann–Whitney, p < 0.05; Fig. 2b, 1–2 and 7–8 h).

Figure 2.

LFP power distribution in intact cortical regions versus cortical regions affected by thalamic inactivation. a, Examples of LFP recordings from suprasylvian gyrus of cats from intact (green) and affected (blue) regions. b, Power spectra distribution of LFP activities recorded in intact (green) and affected (blue) regions for frequencies 0.25–45 Hz. Bin is 0.25 Hz. Light green and blue indicate SD. Gray underlines significantly different bins (Mann–Whitney test, p = 0.05).

We performed multisite intracellular recordings to investigate the source of the reduction of the LFP signal in the affected region (Figs. 3, 4). Of 86 neurons recorded in this study, 59 were located in the territory with disturbed slow oscillatory activity, as estimated from the LFP recording. In the example shown in Figure 3a, the intracellular pattern in the affected region (intra 2) showed only one active state during 10 s epoch of recording, whereas active states cooccurred every 1–2 s in unaffected regions (intra 1 [anterior suprasylvian gyrus] and intra 3 [posterior suprasylvian gyrus]) separated by a distance of 11 mm.

To characterize the impact of thalamocortical inputs functional removal on the occurrence of active states and the percentage of time spent in this state, we detected active and silent states in each neuron according to formal thresholds (Fig. 3c, see Materials and Methods). In the affected region (0–12 h from time of inactivation), active states occurred with a mean frequency of 16.1 ± 9.1 per minute, lower than in intact regions (37.1 ± 12.1, p < 0.0001; Fig. 3d, Kruskal–Wallis post hoc Dunn's multiple-comparisons test). Overall, active states in regions with disrupted slow oscillation occupied 11.0 ± 6.9% of the total time, whereas, in intact regions, they occupied 51.6 ± 26.6% of the total time (Fig. 3e, p < 0.0001, Kruskal–Wallis post hoc Dunn's multiple-comparisons test). The down-state duration was also longer in neurons located in the affected region (Fig. 3f, p < 0.0001, Kruskal–Wallis post hoc Dunn's multiple-comparisons test). These results suggest that the thalamocortical neurons contribute significantly to the generation of the cortical active states of the slow oscillation.

Dual recordings from closely located neurons (0.5–1.5 mm) in affected areas demonstrate that active states can be generated in neighboring neurons either in alternation (Fig. 4c,d, arrowheads) or a large number of them can be recorded in one neuron but not in another one (Fig. 4b, asterisks). This contrasts to observations in intact cortical areas, in which alternating active and silent states occurred with a high degree of synchrony in neighboring neurons (Fig. 4e). Using coincidence analysis (Mukovski et al., 2007), we found that, in the intact suprasylvian gyrus, neurons within a distance of <1.5 mm (n = 10 pairs) spent coincidentally 84.4 ± 13.1% of the time in active states. In contrast, neurons within a similar interneuronal distance in the affected area displayed a lower coincidence of active states (n = 15 pairs, p < 0.001, ANOVA post hoc Tukey's multiple-comparisons test; Fig. 4f3). This synchronicity was significantly lower even than for neurons recorded in intact areas separated by >3 mm (n = 10 pairs, p = 0.005, ANOVA post hoc Tukey's multiple-comparisons test; Fig. 4f2). The lowest synchronicity of active states was observed between neurons located in intact area and those in the affected area (n = 11 pairs, p < 0.0001, ANOVA post hoc Tukey's multiple-comparisons test; Fig. 4f4). The reduced amplitude of the slow waves in the affected region (Fig. 1) can be attributed to the lack of actives state synchronicity among neurons devoid of thalamocortical inputs. In addition to its role in generating active states, these results reveal that blocking the activity of a thalamic region dramatically reduced the synchronization of cortically generated active states.

Time-dependent recovery of slow oscillation

Twelve to 13 hours after thalamic inactivation, the field potential activities started to recover progressively. The absence of cortical response to thalamic stimuli (Fig. 1a, inset, bottom trace) indicated that the inactivation by QX314 was still effective. After 30 h (n = 4 cats), the activities in low-frequency range of 0.5–12.0 Hz were similar in intact and affected cortical regions (Fig. 2b). In contrast, the power for the faster activities (>12.0 Hz) were significantly depressed in the most affected by thalamic inactivation site. The remaining differences in the infraslow range (<0.5 Hz) are likely attributed to the metabolic alterations induced by prolonged anesthesia (Aladjalova, 1957).

We also recorded the intracellular activity of neurons in the affected region 12–36 h after inactivation of the thalamus. As shown in Figure 3b, 33 h after thalamic inactivation, the simultaneously recorded intracellular activity of two cortical neurons from the intact and affected areas revealed a similar pattern of the slow oscillation. For the neurons recorded in the late period in the affected region (12–36 h), the difference in the number of active states, the time spent in active states, and the down state duration was not significant compared with the intact region (Kruskal–Wallis post hoc Dunn's multiple-comparisons test; Fig. 3d–f). These results suggest that the slow oscillation gradually recovers in the absence of thalamocortical input and point to the presence of intracortical compensatory mechanisms.

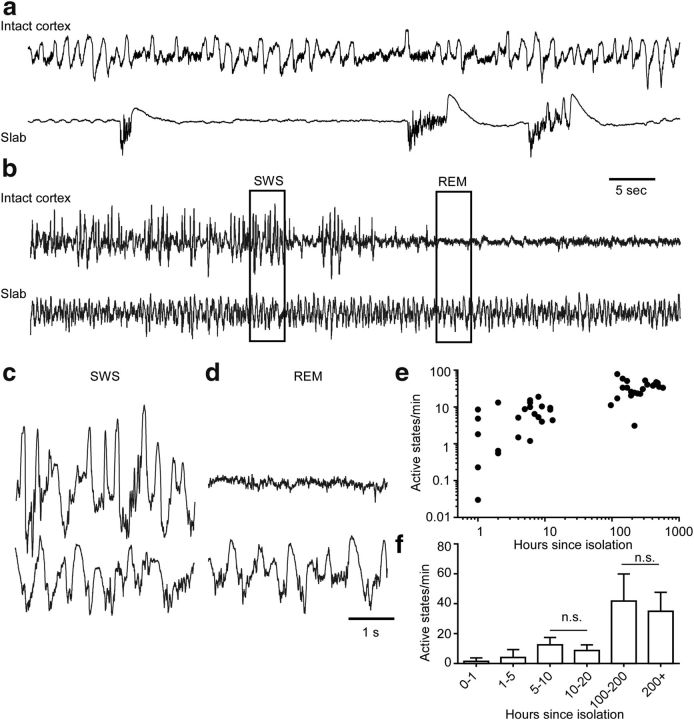
We extended our investigation of the cortical recovery of the slow oscillation to fully isolated neocortical slabs (Timofeev et al., 2000; Fig. 5). In the first hour after isolation, we detected in the LFP recordings of slabs of anesthetized cats an average of 1.4 ± 2.3 active states per minute (Fig. 5a,e,f), which was even lower than after thalamic inactivation. In total, we analyzed time-dependent changes in the active state generation in seven acute and two chronic slabs. Within time window segments selected for analysis (Fig. 5f), there was a highly significant increase in the number of active states after ∼100 h after isolation (Kruskal–Wallis test, p < 0.0001). Dunn's multiple-comparisons test shows that changes were found between all investigated groups except for two pairs of data indicated in Figure 5f. In chronic slabs, electrographic activities were not recorded during recovery from surgery. Recordings performed 100 or more hours from isolation revealed 35–45 active states per minute (Fig. 5b–f), which is comparable to the slow oscillation in naturally sleeping cats with intact cortex (Steriade et al., 1993b). The slow oscillation in the slab did not depend on the state of vigilance; it was present during both slow-wave sleep (Fig. 5b,c) and brain-activated states (Fig. 5b,d). These results suggest that the normal slow oscillation in the intact brain arises through interactions between thalamic and cortical circuits and that it gradually recovers in the absence of any extracortical inputs.

Figure 5.

LFP activities in acute and chronically isolated neocortical slabs. a, Ketamine-xylazine anesthesia. LFPs recorded from intact anterior suprasylvian gyrus (top trace) and from neocortical slab (bottom trace) 1 h after isolation. b, LFPs recorded from intact cortex (top trace) and isolated neocortical slab (bottom trace) 7 d (168 h) after isolation during a transition from SWS to REM. c, d, Expanded fragments of activity shown in b. e, Active states per minute in the slab versus time since isolation in hours. Each point is an average for an hour and an animal. f, Histogram showing active states per minute grouped in time segments used for statistical analysis.

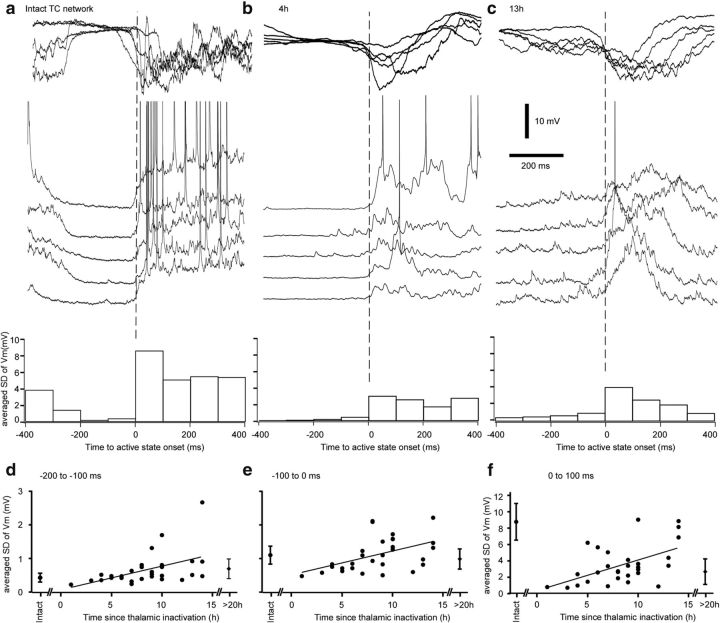
Concurrent to the recovery of the slow oscillation in partially deafferented cortical regions, we observed an increase in both the frequency and amplitude of postsynaptic events occurring before the active states as a function of time from thalamic inactivation (Fig. 6a–c). Because active states are associated with intense excitatory and inhibitory synaptic activities originating from a large number of interconnecting neurons, the extraction and quantification of individual events might give unreliable results with a bias toward larger amplitude events. Therefore, we analyzed segments of intracellular recordings that contained a silent state and its transition to an active state at different times from thalamic inactivation (Fig. 6) and measured the SD of the membrane potential fluctuations in bins of 100 ms near the onset of the active states (Fig. 6a–c, histograms). The analysis was performed on 10 neurons in control conditions (no inactivation), 29 cells in period 0–15 h, and 13 cells >20 h from thalamic inactivation (Fig. 6d–f). We found a progressive increase in the SD of membrane potential fluctuations over time in different segments preceding and immediately after the onset of an active state (Fig. 6d–f). The Kruskal–Wallis test further showed a highly significant increase in synaptic activities as a function of time from thalamic inactivation (−200 ms to −100 ms, p = 0.0136; −100 to 0 ms, p < 0.0001; and 0 to 100 ms, p < 0,0001). Dunn's multiple-comparisons test revealed that the values returned to control levels after 10–14 h from thalamic inactivation, closely matching our findings with LFP recordings (Fig. 2). We attribute the lower values of synaptic noise after 20 h to the long-lasting effects of ketamine-xylazine anesthesia. Overall, these results show that the progressive recovery of the neocortical slow oscillation is accompanied by an increase in neocortical postsynaptic activity.

Figure 6.

Upregulation of synaptic activites after thalamic inactivation. Examples of LFP and intracellular recordings at the transition to the active state before inactivation (a), 4 h (b), and 13 h (c) after thalamic inactivation. Below traces are the corresponding averaged SD of membrane potential in bins of 100 ms. d–f, Averaged SDs are plotted against the time since the thalamic inactivation for the period −200 to −100 ms before active state onset (d), −100 ms to active state onset (e), and the first 100 ms of the active states (f).

Modeling experiments of the synchronization and scaling of cortical slow oscillation

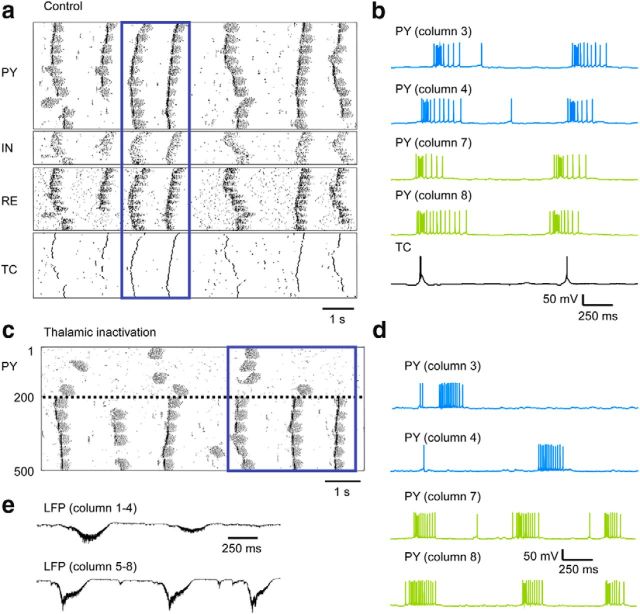
Previous models of the thalamocortical slow oscillation were based on uniform synaptic connectivity (Timofeev et al., 2000; Bazhenov et al., 2002; Compte et al., 2003). In light of our experimental findings, we implemented in a large-scale thalamocortical network model a more realistic columnar organization (Fig. 7, Table 1, see model description in Materials and Methods). Specifically, we implemented a high-density local connectivity and sparse long-range connections as observed in vivo (Thomson and Bannister, 2003). The model displayed an alternation of active and silent states at a frequency of 0.62 ± 0.08 Hz. The active-state initiation was driven by spontaneous transmitter release at excitatory synapses, whereas termination was mediated by synaptic depression, activation of intrinsic hyperpolarizing conductances, and synaptic inhibition (Timofeev et al., 2000; Bazhenov et al., 2002; Chen et al., 2012). This produced rhythmic activity resembling sleep slow oscillation in vivo that was synchronized across the thalamocortical network (Fig. 8a,b).

Figure 8.

Modeling study of the effect of thalamic deafferentation on the neocortical slow oscillation. a, Slow oscillation in large-scale thalamocortical model. Rastergrams of PYs, INs, REs, and TCs (top). b, Examples of membrane voltage of PY neurons from selected columns and of a TC neuron in control condition. c, Removal of synaptic connectivity from TC neurons to the first four cortical columns (top) reduced active states occurrence. d, Examples of membrane voltage of pyramidal neurons from selected columns after removal of thalamic inputs. e, LFPs in deafferented columns 1–4 were reduced in amplitude compared with intact columns 5–8.

Upon complete thalamic deafferentation of the first four cortical columns, the regular slow oscillation pattern was disrupted in affected cortical areas (Fig. 8c,d). In the intact network, both cortico-thalamo-cortical projections and long-range intracortical connectivity contributed to the synchrony of slow oscillation. However, immediately after thalamic inactivation, the remaining intracortical connections were not sufficient to drive rhythmic activity in the deafferented areas. Therefore, in agreement with experimental data (Figs. 3a,4b–d), deafferented cortical neurons were mostly silent and only displayed occasional and irregular active states that were limited to specific columns and did not propagate to the rest of the network. The simulated LFP amplitude was reduced in deafferented areas (Fig. 8e), as in experiments (Figs. 1c,e, 2). Occasionally, active states in the deafferented area occurred simultaneously with the intact network; however, in many cases, as in experimental observations (Fig. 4), these events were local, explaining the low amplitude of the simulated LFP (Fig. 8e). In this model, the generation of the active states was driven by intracortical mechanisms; however, active state synchronization depended on the thalamocortical projections and was severely diminished in the affected cortical areas after thalamic inactivation.

To describe more precisely the role of the thalamocortical projections in maintaining the normal pattern of the slow oscillation, we next evaluated the contribution of thalamocortical diffuse (matrix) versus specific (core) projections to the synchronization of the cortical active states. When the thalamocortical diffuse projections were fully dissected (Fig. 9a, left), transitions between active and silent states occurred independently among columns, as demonstrated by lower peak amplitude and longer time lag to the main peak of cross-correlation function (Fig. 9b,c). In contrast, removing only specific projections had no impact on the synchrony among columns (p < 0.001, two-sample t test based on population of maximum cross-correlation among columns; Fig. 9a,b, right). To further assess the impact of the thalamocortical input on the cortical synchronization of the slow waves, we varied the radius of thalamocortical connectivity in intact model and found that the intracortical synchrony increased as a function of the radius (Fig. 9d,e). This suggests that widespread thalamocortical projections play a critical role in the synchronization of the active cortical states across the entire cortical network.

Figure 9.

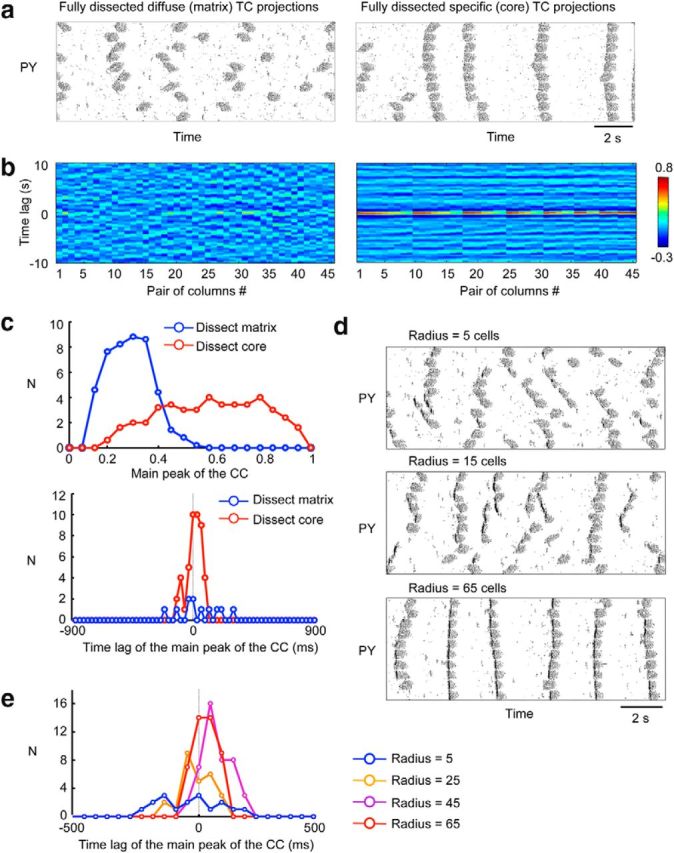
Impact of thalamocortical diffuse (matrix) versus specific (core) projections and the target radii on the synchronization of the slow oscillation. a, Rastergrams of the layer IV PY neurons after full dissection of thalamocortical diffuse projections (left) or full dissection of thalamocortical specific projections (right). b, Cross-correlation analysis of the LFP signals between all possible LFP pairs (y-axis) from 10 columns after the full dissection of diffuse matrix (left) or specific core (right) projections. c, Distributions of the peak amplitude (top) and time lag to the main peak (bottom) of cross-correlation function for simulations with dissected diffuse (blue) and specific (red) projections. d, Raster plots obtained from three different settings of the fan-out radius from the thalamocortical matrix structure to the cortex. e, Distribution of time lags to the main peak of cross-correlation function calculated for all pairs of LFPs in different spatial locations plotted for various radii of thalamocortical projections. Broader distribution indicates less synchronous spatiotemporal activity.

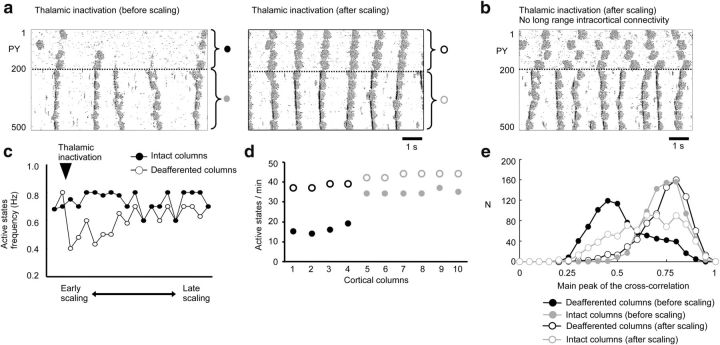
We reproduced in the model the increase in the SD of the V_m fluctuations (Fig. 6) by adjusting the strength of long-range intracortical excitatory synapses. When thalamic inputs were blocked, the overall firing rate of the cortical neurons decreased due to lower levels of excitability. This matched the reduction in synaptic activity levels at the onset of active states recorded in vivo (Fig. 6e). Based on previous models of homeostatic changes in the neocortical network (Houweling et al., 2005; Volman et al., 2011a), the efficacy of excitatory (inhibitory) intracortical synapses was progressively upregulated (downregulated) until the mean firing rate reached the target value corresponding to the slow oscillation in the baseline model (Volman et al., 2011a). These processes led to a progressive recovery of the normal pattern of the sleep slow oscillation in the deafferented columns (Fig. 10a). The average frequency of active states increased with time (Fig. 10c) and the number of active state occurrence in affected columns was similar to the one observed in intact columns after the progressive upregulation of the intracortical excitatory drive to target value (Fig. 10d). The synchronization of activity across cortical columns was also recovered (Fig. 10e). However, when long-range intracortical synaptic connectivity was excluded from the upregulation of excitability, the frequency of active states recovered but synchronization was lost (Fig. 10b). These results suggest that the scaling of the long-range corticocortical synaptic connectivity could compensate for the loss of the thalamocortical feedback loop.

Figure 10.

Modeling study of scaling the intracortical connectivity on the recovery of the neocortical slow oscillation. a, Cortical slow oscillation after thalamic inactivation. Left, No synaptic scaling. Right, Pattern of cortical activity during late phase of synaptic scaling. Synaptic scaling was modeled as decrease of inhibition from IN to PY and increase of excitation and minis amplitude between PYs. b, Network activity after synaptic scaling in the model without long-range intracortical connectivity. c, Time course of active states frequency recovery in simulations with synaptic scaling. Arrowhead indicates the time of deafferentation. d, Number of active states per minute after deafferentation without scaling (filled circle) or during the late phase of scaling (open circles). e, Distribution of main peak of the cross-correlation function between V_m of neurons within deafferented columns (black) or intact columns (gray) without scaling (filled circles) or after scaling (open circles).

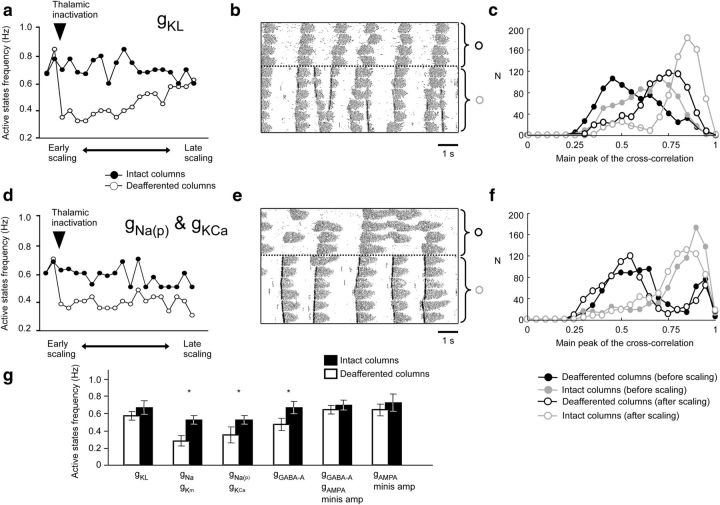
Synaptic scaling was suggested as a common mechanism of homeostatic plasticity (Turrigiano et al., 1998). However, other factors may contribute to the recovery of slow oscillation after the thalamic inactivation. This includes a homeostatic effect on neuromodulation, which can increase excitability by blocking K⁺ leak currents (McCormick, 1992), and on intrinsic conductances, which can affect the expression of intracellular excitatory and inhibitory conductances (Desai et al., 1999). To test these mechanisms, we implemented the scaling of various biophysical properties in the model. The results of these experiments for the intact and deafferented columns are shown in Figure 11. We first tested the downregulation of the g_KL in the dendritic compartment of all pyramidal neurons (Fig. 11a). We found that this mechanism was sufficient to recover the frequency and with somewhat lower synchrony of slow oscillation (Fig. 11b,c). In contrast, the scaling of the persistent Na⁺- and Ca²⁺-activated K⁺ currents failed to recover normal slow oscillation (Fig. 11d). Although activity of pyramidal neurons increased along the simulation, it did not form a regular slow oscillation pattern; instead, it led to very long active states, which could last longer than 3 s (Fig. 11e). Furthermore, synchronization level across deafferented columns was not improved along the recovery process (Fig. 11f). Similar results were obtained with scaling of g_Na and g_Km or g_GABA-A (Fig. 11g).

Figure 11.

Role of different biophysical features in the recovery of the slow oscillation. a, Scaling was modeled by adjusting the conductance of a leak potassium current (g_KL) in cortical neurons. Averaged active state frequency of intact columns (filled circle) and deafferented columns (open circle) along simulation. b, Representative example of the network activity during the late phase of scaling. c, Distribution of the peaks of cross-correlation function between pyramidal neurons in deafferented (black) or intact (gray) columns during initial (filled circles) or late (open circles) phase of scaling. d–f, Similar to a–c, however, scaling was modeled by adjusting conductance of the slow intrinsic currents: persistent sodium current (g_Nap) and calcium-dependent potassium current (g_KCa). g, Frequency of active states in deafferented (open blocks) and intact (filled blocks) columns during the late phase of HSP. Six different settings of scaling are shown: (1) potassium leak current (g_KL) in PYs, (2) fast intrinsic currents (g_Na and g_Km) in PYs, (3) slow intrinsic current (g_Nap and g_KCa) in PYs, (4) fast synaptic inhibition (g_GABA-A) from INs to PYs, (5) fast synaptic currents (g_GABA-A from INs to PYs, g_AMPA and minis amplitude between PYs), and (6) fast synaptic excitation (g_AMPA and minis amplitude between PYs). Asterisk indicates experiments in which no recovery was found.

In sum, we found that scaling the strength of the excitatory connections between pyramidal neurons and the minis amplitude at these excitatory synapses (Figs. 10, 11g) was sufficient for the slow oscillation recovery. Furthermore, changing the passive intrinsic properties (such as leaking K⁺ current) in pyramidal neurons was also able to mediate the recovery, likely because of the overall increase of excitability, although with lower levels of synchrony between neurons. Conversely, when scaling was applied to the active intrinsic conductances of the pyramidal neurons, the average firing rate of the network tended to increase, but the normal pattern of slow oscillation failed to recover.

Discussion

Using recordings from anesthetized and behaving cats, we found that the functional removal of thalamic inputs to the neocortex dramatically reduced the occurrence of active states of the slow oscillation. The remaining active states in the affected region were infrequent and local, explaining the low-amplitude LFP in that region. The slow oscillation started to recover 12 h after thalamic inactivation. Extending our investigation of this phenomenon to completely deafferented neocortical slabs, we observed a complete recovery of the slow oscillation within 2 weeks. This recovery of the slow oscillation occurred in parallel with an increase in spontaneous fluctuations of the membrane potential before the active states several hours after deafferentation, suggesting upregulation of excitatory synaptic drive. In a large-scale thalamocortical network model analysis, we replicated the disruption of the neocortical slow oscillation induced by removing the thalamic inputs to the cortex. We tested the effect of scaling various biophysical features of the model and found that the scaling of synaptic connectivity restored the frequency and synchrony of the slow oscillation. Upregulation of g_KL could restore the frequency of the slow oscillation, whereas the scaling of both fast and slow intrinsic Na⁺ and K⁺ conductances failed to recover the cortical slow oscillation. Collectively, our experimental and modeling results show that the normal pattern of the neocortical slow oscillation requires thalamic inputs, but suggests that there are cortical compensatory mechanisms to maintain the slow oscillation if thalamic input is damaged.

Thalamic and neocortical contribution to the slow oscillation

The relative contribution of the neocortex and the thalamus in the expression of the slow oscillation has been debated over the last two decades. Our results confirm previous studies demonstrating that the neocortical network was sufficient to generate the slow waves (Steriade et al., 1993b; Timofeev and Steriade, 1996; Sanchez-Vives and McCormick, 2000; Timofeev et al., 2000; MacLean et al., 2005; Hinard et al., 2012). The other evidence suggests that the full expression of slow oscillation requires a contribution from the thalamus (Hughes et al., 2002; Doi et al., 2007; Crunelli and Hughes, 2010; David et al., 2013). Computer models revealed that the interaction between thalamic and cortical networks may be necessary for maintaining regular transitions between active and silent states (Destexhe, 2009). The present study clearly shows that, after the removal of thalamic inputs (∼6% of excitatory synapses in the cortical network; Ahmed et al., 1994), the slow oscillation was replaced by local active states of much shorter duration that occurred irregularly and at a low rate. Similar results were obtained after complete isolation of a cortical area (slab), with regular active states having been replaced by irregular and infrequent events. We propose that the thalamocortical neurons: (1) participate in the generation of active states, (2) contribute to the normal duration of the active states by maintaining recurrent activity, and (3) play a major role in synchronizing the slow oscillation across cortical columns.

The thalamocortical network is tightly interconnected, which makes thalamocortical oscillations synchronous. Previous experimental (Contreras et al., 1996) and computational (Destexhe et al., 1998) studies have demonstrated that the removal of the cortex leads to the desynchronization of the spindle activity in the thalamus. Here, we show that thalamic inactivation desynchronizes the cortically generated slow oscillation without abolishing the generation of isolated cortical slow waves (Fig. 4). Importantly, several hours after deafferentation, the cortical plasticity processes reestablish the synchronization of slow waves (Fig. 3). In contrast, the recovery of a synchronous spindle activity with time was not demonstrated for thalamus in decorticated animals.

It was demonstrated previously in different species that, once slow waves are initiated in a specific location, they propagate to involve large cortical territories (Massimini et al., 2004; Volgushev et al., 2006; Mohajerani et al., 2010; Ruiz-Mejias et al., 2011). The fact that we observed isolated (local) cortical slow waves, which did not even propagate to neighboring regions, after the first hours after thalamic inactivation suggests that, in intact network, the thalamus plays a critical role in the generation of cortical propagation patterns. However, several hours after thalamic inactivation, the slow rhythm recovered in affected areas, indicating that, after a period of reorganization, the cortical network has functionally changed to promote the propagation of the slow waves.

In a large-scale model of the thalamocortical network with realistic network structure, we found that the dense local connectivity was sufficient to generate spontaneous active states, but widespread cortico-thalamo-cortical projections were required to ensure the propagation of the locally generated active states to the rest of the network. These results are in agreement with previous studies suggesting the role of the wide-spread (matrix) thalamocortical projections in the synchronization of cortical sleep spindle oscillations (Bonjean et al., 2012). When this connectivity was abolished to model the thalamic inactivation, the synchrony of active states was lost in the affected cortical areas. After a decrease in the overall level of activity, we found that the normal pattern of the slow oscillation could not be recovered by the scaling several Na⁺ and K⁺ conductances. However, an upregulation of excitatory synaptic conductances or a decrease in the potassium leak current recovered the slow oscillation, suggesting that these are the critical factors in the maintenance of cortical slow oscillation.

Unlike slow rhythms, the virtual abolition of fast rhythms in the neocortex did not recover over the investigated period of 36 h. Furthermore, the coincidence among neurons (based on fast rhythms grouped by the slow oscillation) was greatly diminished in the absence of thalamic inputs. These findings further suggest a role for the thalamus in the long-range synchrony of fast cortical activities. Although the synchronization of fast rhythms between thalamus and cortex was not investigated in detail, some studies have shown a coherence of these rhythms within the thalamocortical network (Steriade et al., 1996b; Castelo-Branco et al., 1998).

Slow oscillation as the intrinsic property of the neocortex

In the intact brain, the slow oscillation emerges as an alternation of active and silent states and occurs exclusively during slow-wave sleep (Steriade et al., 2001; Timofeev et al., 2001; Vyazovskiy et al., 2009). However, the patterns resembling the slow oscillation appear as a common feature of isolated cortical networks that develop with different time courses from initially “silent” cell primary cultures (Sun et al., 2010; Hinard et al., 2012), acute (Compte et al., 2008) and organotypic (Johnson and Buonomano, 2007) cortical slices, and neocortical slabs (Fig. 5). The main difference between the slow oscillation recorded in vivo during sleep or anesthesia and similar patterns recorded in isolated structures is the duration of silent states. Quantification of the duration of silent states in vivo demonstrate that they occupy 10–20% of the total sleep time (Chauvette et al., 2011), whereas available examples of recordings in acute, organotypic slices or cultures (Johnson and Buonomano, 2007; Compte et al., 2008; Sun et al., 2010; Hinard et al., 2012) show that the silent phase occupies >80% of the time, which brings the overall frequency of slow oscillation to much lower values. In acute isolated neocortical slabs (Timofeev et al., 2000; Fig. 5a), the silent states are also long. However, field potential recordings from chronic slabs (Fig. 5c) demonstrate that, after a sufficient period of time, the duration of silent states becomes similar to the one recorded in the intact cortex. These observations suggest that some minimal level of connectivity is needed to generate slow waves with parameters found in the intact cortex. Such a minimal level of connectivity is absent in acute and organotypic slices.

We found that ongoing plastic changes in the intracortical network had begun the recovery of the slow oscillation pattern 12 h after surgery independently of thalamic inputs, thus matching the time course of homeostatic plasticity (Turrigiano et al., 1998; Turrigiano, 1999; Murthy et al., 2001; Desai et al., 2002). Experimental findings and a modeling approach further suggested that the homeostatic upregulation of the intracortical excitatory synapses was sufficient to restore the normal slow oscillation pattern (Fig. 10). In such conditions, long-range intracortical connectivity played a critical role in the synchronization of active states across the entire network.

The activities similar to the slow oscillation occur in the majority of neurons in the human brain even before birth (André et al., 2010; Moore et al., 2011). Although a role for the sleep slow oscillation in brain functions remains controversial, our results suggest that the slow oscillation is an intrinsic and a fundamental state of the thalamocortical system. This state is prominent during slow-wave sleep and we propose that it is maintained by intracortical plasticity mechanisms. A reduction in critical elements of the cortical network reduces the spontaneous slow-wave activity. However, it then recovers up to a normal sleep pattern after a period of time lasting from minutes to days. Conversely, after a sustained period of wakefulness, the sleep pressure increases (Achermann et al., 1993) and the local populations of cortical neurons start to display local sleep-like activities even if the whole brain is in a waking state (Vyazovskiy et al., 2011). Collectively, these results demonstrate that any factor leading to a reduction of the slow oscillation triggers plastic changes that bring back this intrinsic cortical rhythm.