Predicting the Timing of Maturational Spurts in Skeletal Age

Abstract

Measures of maturity provide windows into the timing and tempo of childhood growth and maturation. Delayed maturation in a single child, or systemically in a population, can result from either genetic or environmental factors. In terms of the skeleton, delayed maturation may result in short stature or indicate another underlying issue. Thus, prediction of the timing of a maturational spurt is often desirable in order to determine the likelihood that a child will catch up to their chronological age peers. Serial data from the Fels Longitudinal Study were used to predict future skeletal age conditional on current skeletal age and to predict the timing of maturational spurts. For children who were delayed relative to their chronological age peers, the like-lihood of catch-up maturation increased through the average age of onset of puberty and decreased prior to the average age of peak height velocity. For boys, the probability of an imminent maturational spurt was higher for those who were less mature. For girls aged 11 to 13 years, however, this probability was higher for those who were more mature, potentially indicating the presence of a skeletal maturation plateau between multiple spurts. The prediction model, available on the web, is most relevant to children of European ancestry living in the Midwestern US. Our model may also provide insight into the tempo of maturation for children in other populations, but must be applied with caution if those populations are known to have high burdens of environmental stressors not typical of the Midwestern US. Am J Phys Anthropol 150:68–75, 2013.

The timing and tempo of growth and maturation are important areas of inquiry in physical anthropology and human biology. Historically, anthropologists have been at the forefront of the science of human growth and development, with some of the early publications in the AJPA concerning somatic growth and variation in maturation among various indigenous groups (Krogman, 1939; Michelson, 1946; Weiner and Thambipillai, 1952). Skeletal maturation, in particular, is significant to physical anthropologists and human biologists as it provides a window into the developmental processes of bone, which may or may not be strongly associated with other developmental milestones such as sexual maturation and somatic growth (Marshall, 1974; Flor-Cisneros et al., 2006).

Skeletal age (SA) is a measure of skeletal maturation allowing for an assessment of developmental progress. Children develop at different rates, and thus there exists variation in skeletal maturation at a given chronological age (CA). The difference between CA and SA, known as relative skeletal age (RSA), can be used on an individual level to compare a child to his CA peers, and also to compare a population to the reference population used to develop the particular SA assessment tool used (in the reference population, average SA at a given CA is approximately equal to CA, so RSA is zero on average). Delayed maturation (negative RSA) or accelerated maturation (positive RSA) in a given child or pediatric population can be interpreted as the result of genetic or environmental factors. For example, lower socioeconomic status (including poor nutrition) resulting in delayed maturation has been observed in many populations (Greulich, 1951; Chan et al., 1961; Garn et al., 1966; Garn et al., 1973; Cole and Cole, 1992; Hawley et al., 2009), and in some populations the magnitude of this delay differs between childhood and adolescence (Low et al., 1964; Frisancho et al., 1970). As another example, some populations in a higher altitude environment have been shown to have average RSA < 0 throughout childhood and adolescence (Clegg et al., 1972; Pawson, 1976; Pawson, 1977).

A lag in maturation on the individual level, however, can also be consistent with normal variation in the timing of maturational events, and there may be a high likelihood of an imminent maturational spurt (“catch-up maturation”). Knowledge of the timing of achievement of full skeletal maturity (commonly designated as SA = 18 years) and the timing of maturational spurts can be particularly important for children who require treatments that interact with bone growth (e.g., orthodontic appliances or dental implants). Catch-up maturation is difficult to predict, especially when given a single snapshot in time of a child’s SA.

Two questions arise when considering the timing and tempo of skeletal changes during growth and development, particularly in children of a delayed maturational status. First, what is the likelihood that a “delayed” child will catch up to their peers? Second, over what time span can such “catch-up maturation” be expected? Answers to these questions are not straightforward and depend heavily upon current chronological age and the magnitude of maturational delay, and may differ between populations.

The purpose of this article is to predict future skeletal age given a current skeletal maturity assessment with specific applications to predicting the timing of a spurt in skeletal maturation and the timing of reaching full skeletal maturity. SA was assessed using the FELS Method (Roche et al., 1988; Chumlea et al., 1989), the prediction model was estimated using data from the Fels Longitudinal Study (Roche, 1992), and we discuss the potential applicability of the results to other populations.

METHODS

Study sample

To adequately characterize normal changes in the timing and tempo of skeletal maturation, a large group of healthy children is needed for whom serial assessments of skeletal maturity are available across their childhood and adolescent years. The data in this study were derived from white participants of the Fels Longitudinal Study, the majority of who live in or near southwestern Ohio. Initiated in 1929, the Fels Longitudinal Study is currently the world’s longest running study of human growth and body composition changes over the lifespan (Roche, 1992). This is a randomly ascertained cohort in that participants were not selected for any specific feature or trait, and is, therefore, a study of normal variation. Signed informed consent has been obtained from all participants and all protocols and procedures are approved by the Wright State University Institutional Review Board.

Over the course of the study, children have generally been scheduled for visits at target ages 1, 3, 6, and 9 months, and every 6 months from ages 1–18 years. Data for the current study consist of skeletal ages derived from 9,497 hand-wrist radiographs, taken between 1940 and 2010, of 940 participants born 1932 to 1992 (478 boys; 462 girls) age 7.75 years to < 19 years (target visit ages 8 to 18 years). From 1932 to 1974, hand-wrist radiographs were collected from children at all target ages from 1 month to 18 years. However, starting in 1975, hand-wrist radiographs were not regularly collected prior to age 8 years. Additionally, children born later than 1992 were not used in the current analyses because they had not reached age 18 by 2010 (our sample cut-off date).

Each child’s hand-wrist radiograph was assessed via the FELS Method for skeletal maturity, a maximum-like-lihood based method that provides both a skeletal age estimate and a standard error, which represent the estimated mean and standard deviation of chronological age among children in the reference sample (Fels Longitudinal Study participants born prior to 1975) with a given level of skeletal maturity. The FELS Method is based on assessment of as many as 98 individual indicators of bone maturity of 32 bones of the hand-wrist. Of these 98 indicators, only 20–66 are assessed at any one chronological age. Details on the development and implementation of the FELS Method are published elsewhere (Roche et al., 1988; Chumlea et al., 1989).

Prediction model

To predict the timing of maturational spurts, we need a model for future skeletal age given a current assessment. To build this prediction model, we first grouped the observations into “bins” according to earlier SA and CA (SA₀ and t₀) and later CA (t₁), rounded to the nearest 0.5 year. Second, we estimated the mean and standard deviation of later SA (SA₁) within each bin. Finally, we regressed these mean and (log) standard deviation estimates on SA₀, t₀, and t₁. The regression relationships were nonlinear and there were covariate interactions. We allowed the data to determine the correct form of the relationship (rather than assuming linearity) by using semiparametric regression with natural spline (Hastie, 1992) functions of SA₀, t₀, and dt = t₁ – t₀, as well as all possible interactions. The model was used to predict the distribution of SA₁ given any combination of SA₀, t₀, and t₁ (not just rounded values) within the range of the observed data, assuming a normal distribution (an assumption which we assessed visually). The prediction model was fit separately for boys and girls.

We apply this prediction model to determine (1) the distribution of future skeletal age given an earlier assessment, (2) the probability of a spurt in maturation within a specified number of years, and (3) the probability of reaching full skeletal maturity (SA = 18) within a specified number of years.

Missing data

Not all participants were observed at every half-year, which creates missing data. In addition to participants occasionally missing a visit, the design of the Fels Longitudinal Study changed over the years such that at some periods of time participants were scheduled for visits every 6 months and at other periods every 12 months. There are 21 possible target ages from 8 to 18 years and participants in the study sample were radiographed from 1 to 21 times (median = 10). This imbalance potentially could lead to bias in the prediction model. To minimize this bias, we used multiple imputation (MI) (Little and Rubin, 2002). While the participants were observed at only 48% of the target ages, a large portion of the missing data imputation is essentially interpolation for a half-year visit where there are radiographs available at a visit 6 months prior and a visit 6 months later.

Both the prediction and imputation models require SA to be normally distributed. SA, however, is a semicontinuous variable; while it can take on any value between 0 and 18, it can also take on the exact values 0 and 18. Particularly for chronological ages near 0 and 18 years, the normality assumption fails. We solved this problem by imputing values above 18 for SA = 18 using a censored normal model (Tobin, 1958) prior to multiple imputation for missing data.

Censored normal imputation was carried out in R v2.13.1 (R Development Core Team, 2011), and MI for missing data was carried out using SAS PROC MI in SAS v9.2 (SAS Institute Inc., 2009). Ten imputations were carried out, resulting in 10 datasets in which every individual had a SA estimate at every target age and with no censoring at age 18 years. For all postanalysis calculations, the probability that SA = 18 (skeletal maturity using the FELS Method) was computed as the probability that imputed SA is ≥ 18. Complete details on the modeling and imputation procedures can be found in the Supporting Information.

RESULTS

Conditional predictions of skeletal age

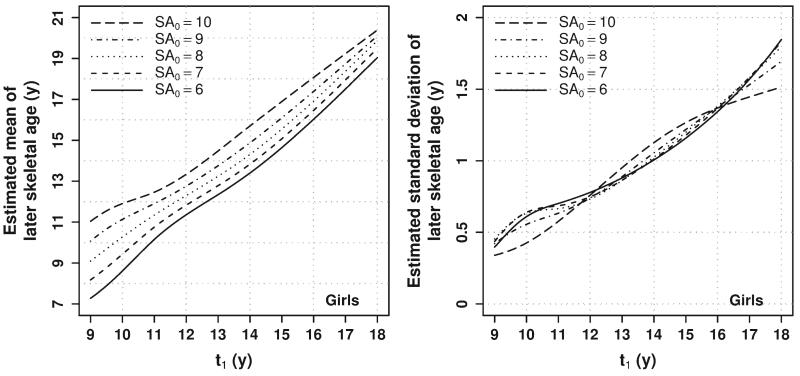
Predictions of skeletal age not conditioned on previous assessments can be presented in tabular or chart form (e.g., similar to growth charts for attained stature given age). The conditional predictions developed here depend on three variables (t₀, SA₀, and t₁) that can take on any value from 8 to 18 years and are thus impossible to present concisely in a set of tables or charts. Therefore, to facilitate usage, an online form was created (somtest3.wright.edu/PredictSA.html) where one can enter any (not just rounded) values for t₀, SA₀, and t₁ and obtain a table displaying the predicted mean and standard deviation for SA₁. For example, Figures 1 (for boys) and 2 (for girls) display the predicted mean and standard deviation of (uncensored) SA₁ at age t₁ from 9 to 18 years given a range of SA₀ values at t₀ = 8 years. The further in the future the prediction, the smaller the impact of current SA on the prediction, and the larger the variability in the prediction.

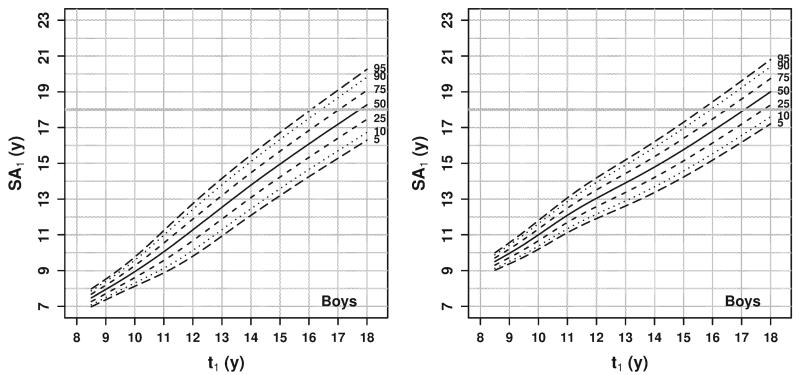
Fig. 1.

Estimated mean (left panel) and standard deviation (right panel) of (uncensored) SA₁ for boys at age t₁ given SA₀ at t₀ = 8 years. Each line represents the prediction at a different value of SA₀ representing relative skeletal ages from −2 to 2 years.

While SA itself cannot be greater than 18, the fitted model is for uncensored SA which can take on any value. Thus, given a predicted mean and standard deviation, one cannot simply compute probabilities for SA₁ based on a normal distribution. The online form can be used to calculate probabilities based on the fitted means and standard deviations. Details on these procedures are given in the Supporting Information.

Distribution of later SA given earlier SA

Given an estimated mean $\widehat{\mu }$ and standard deviation $\widehat{\sigma }$ for censored SA₁ one can compute the pth percentile for uncensored SA₁ as ${\mathrm{SA}}_1^{\left(\mathrm{p}\right)}=\widehat{\mu }+\widehat{\sigma }{\mathrm{z}}_{\mathrm{p}}$ where z_p is the pth percentile of a standard normal distribution. Two examples are illustrated in each of Figures 3 (boys) and 4 (girls) which display the estimated percentiles at age t₁ from 8.5 to 18 years given SA₀ = 7 years (left panel) and SA₀ = 9 years (right panel) at t₀ = 8 years. Any values above the thick horizontal gray line are considered to be full skeletal maturity (SA = 18 years). For girls, note the small probability in the right panel of Figure 4 that SA will actually decrease from 9 years at t₀ = 8 years to < 9 years at t₀ = 8.5 years (where the 5th percentile line is below 9 years). This is due to measurement error in both the earlier and later SA assessments; maturity is not decreasing, but the assessed values, which are estimates, can decrease. Percentiles for the distribution of SA₁ conditional on any combination of (t₀, SA₀, t₁) can be obtained via the online form.

Fig. 3.

Estimated percentiles of (uncensored) SA₁ for boys at age t₁ given SA₀ = 7 years (left panel) and SA₀ = 9 years (right panel) at t₀ = 8 years. Any value above the thick horizontal gray line is considered to be full skeletal maturity (SA₁= 18 years).

Fig. 4.

Estimated percentiles of (uncensored) SA₁ for girls at age t₁ given SA₀ = 7 years (left panel) and SA₀ = 9 years (right panel) at t₀ = 8 years. Any value above the thick horizontal gray line is considered to be full skeletal maturity (SA₁ = 18 years).

Probability of a maturational spurt within a specified number of years

The probability of a spurt in skeletal maturation is relevant in the clinical setting where a treatment is safer and/or more effective when the child is not undergoing rapid skeletal development or, as is the case in orthodontic treatment, is more effective when the child is growing at or near peak velocity. The prediction model can be used to estimate this probability for many different definitions of a “spurt” and “a specified number of years”, but here we present results for two examples: (1) For those with RSA < 0, what is the probability of being at RSA ≥ 0 after 2 years? and (2) Given current RSA, what is the probability of an increase in SA of ≥ 1.5 years within the next 1 year?

Probability of catch-up maturation

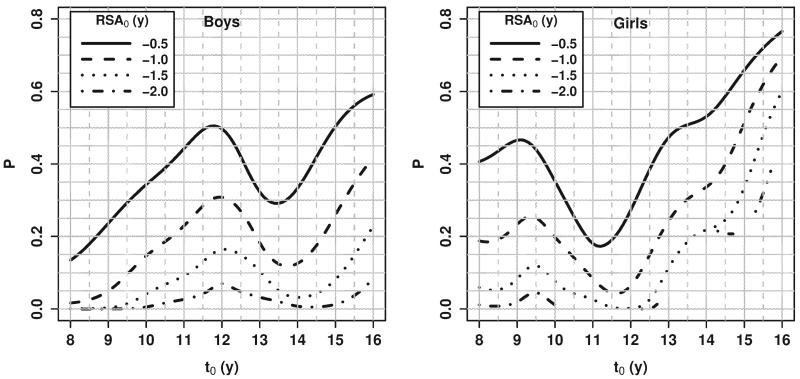
The first question (Fig. 5) is of interest for children who are delayed relative to their peers (RSA < 0), “What is the likelihood of “catch-up” maturation (getting to RSA ≥ 0) in the next two years?” For those who were most delayed (more negative RSA), the likelihood of catching up within the next two years was very low at most ages. Our data suggest that, for those who are delayed in skeletal maturation, the probability of catching up to one’s CA-matched peers (1) increases until after the average age of onset of the pubertal growth spurt in stature (10.7 years for boys, 8.7 years for girls, based on Fels Longitudinal Study data), (2) decreases prior to the average age at peak height velocity (13.8 years for boys, 11.5 years for girls, based on Fels Longitudinal Study data), and (3) then increases again, since all healthy individuals eventually reach the mature state.

Fig. 5.

Probability of “catch-up” maturation (RSA₁ ≥ 0 at t₁ = t₀ + 2 years given RSA₀ < 0).

Broken lines in Figure = (and in Fig. 6 below) result from the fact that probabilities for extreme RSA values were not estimated at all ages due to insufficient information at some combinations of (t₀, SA₀, t₁).

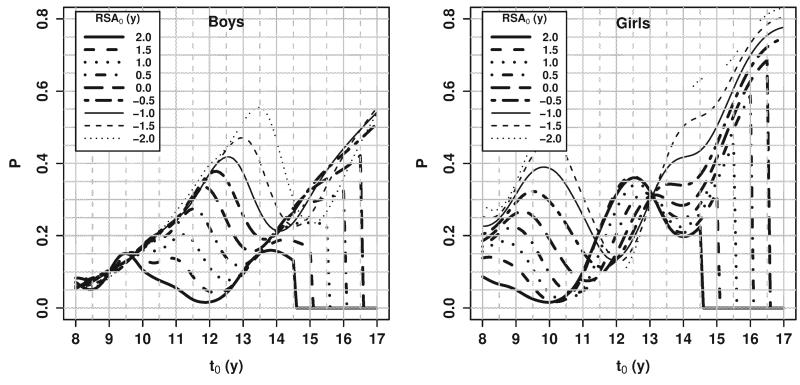
Fig. 6.

Probability of a maturational spurt (an SA increase of at least 1.5 years within the next 1 year), by RSA₀.

Probability of an imminent spurt

The second question is more general, namely, “What is the probability of an imminent spurt in skeletal maturation?” For example, Figure 6 illustrates the probability that SA increases by at least 1.5 years within the next year as a function of current CA (t₀), by current RSA (RSA₀). Regarding the question of the likelihood of a spurt, an initial guess is that that those who are less skeletally mature should have a greater chance of a spurt in the near future. The value of Figure 6 is to illustrate the magnitude of the probability for those at different levels of skeletal maturation, how the probability changes with age, and at what ages the initial guess is, in fact, incorrect.

For boys, this probability increased from ages 8 to 9.5 years and was very similar for all values of RSA₀. That is, at these ages, all boys had about the same chance of a maturational spurt, no matter how advanced or delayed they were relative to their peers. After age 9.5 years, however, the probability demonstrated a pattern that reflects the variability in the timing of a spurt in skeletal maturation, coinciding roughly with the adolescent pubertal growth spurt. For example, at age 11 years, boys with SA = 13 years (RSA = 2) have only a 5% chance of a spurt in the next year, presumably because they had recently experienced a maturational spurt, while boys with RSA :S 0.5 have a 25% chance of a spurt in the next year. At successively older ages, the probability of a spurt continues to increase for those who were more delayed/less advanced and begins to decrease for those who were less delayed/more advanced. Note that these curves do not reflect individual trajectories over time. When an individual experiences a spurt (or a delay) such that their rate of change in SA is other than 1 year/year, that individual will jump from one line to another. Each curve drops to zero probability at the age at which an increase of 1.5 years in skeletal age is impossible (since SA cannot exceed 18 years). For boys, then, the initial guess—that the likelihood of a spurt is larger for boys who are more delayed relative to their peers—was in general correct (the lines, for the most part, do not cross).

It is well known that girls mature earlier than boys, and this is reflected in Figure 6. At younger ages, the likelihood of a spurt was higher for girls than for boys. The pattern of probabilities for girls aged 8 to 10 years looks similar to the pattern for boys aged 10–12 years. For boys, the probability of a spurt in general decreased with current RSA at all ages (more mature implies less likely to have a spurt). For girls, however, from ages 11 to 13 years, this pattern was reversed, with the probability of a spurt often being higher for those who were more skeletally mature. This may indicate the presence of two maturational spurts, one around puberty and another towards the end of skeletal maturation which pushes girls closer to full maturity, with a maturational plateau in between. If this is true, then at age 12 years, for example, a girl with lower RSA is typically one who has experienced her pubertal spurt in skeletal maturation fairly recently but who is still far from her later spurt to full maturity, while a girl with higher RSA experienced her pubertal spurt much earlier and is now close to experiencing another spurt. Thus, for girls, the initial guess is not correct; at ages 11–13 years girls who were less mature skeletally were not more likely to experience a maturational spurt.

Probability of reaching full skeletal maturity within a specified number of years

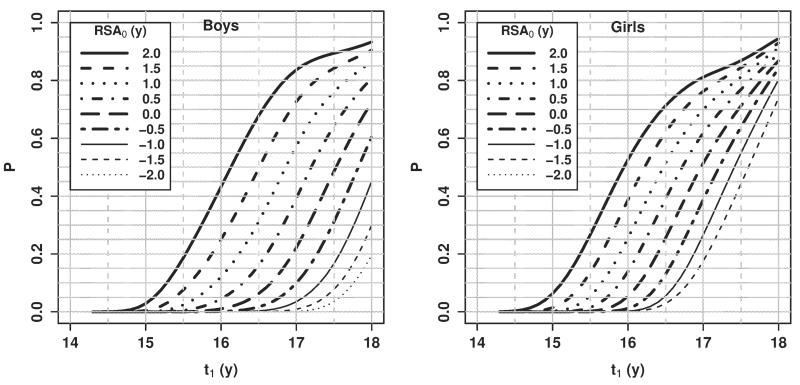
Another relevant question is when a child will reach full skeletal maturity. Within the context of this model, this question can be answered by finding the probability of reaching SA = 18 within a specified time frame. Here we present results for a single example. For 14 year old boys and girls, Figure 7 plots the probability of full skeletal maturation vs. future chronological age (t₁). These probabilities represent the estimated proportion of 14-year-olds with a given RSA who reached full skeletal maturity by the future chronological age on the x-axis.

Fig. 7.

Probability of reaching full skeletal maturity (SA = 18) by a specified age for 14 year olds, by RSA₀.

DISCUSSION

The rate at which a child’s skeleton develops is influenced by genetic, nutritional and other environmental factors. The timing of skeletal maturation is an important measure of life history and can be used to identify children as either accelerated or delayed in their bone development, signaling potential problems. Additionally, prediction of the timing of future maturational spurts is valuable in a variety of settings in which the impact of a treatment on growth and development is to be minimized (or maximized, depending on the nature of the problem to be treated).

Assessment of skeletal maturity in other populations has identified variation in maturational timing, as well as association of delayed maturation with social and geographic environmental factors such as poor nutrition, lower socioeconomic status in general, and high altitude (Greulich, 1951; Chan et al., 1961; Low et al., 1964; Garn et al., 1966; Frisancho et al., 1970; Garn et al., 1973; Cole and Cole, 1992; Hawley et al., 2009). Assessments in these populations were typically done using the Greulich-Pyle atlas method (Greulich and Pyle, 1959). That method was based on children of European descent, as are the more rigorous FELS Method and older versions of the Tanner-Whitehouse method (TW1 and TW2) (Tanner et al., 2001). Thus, any identified trend of delayed or accelerated maturation in a sample outside the reference populations for these methods may be simply normal interpopulation variation. While this would affect chronological age specific comparisons of skeletal age between populations, the current study is designed to assess the probability of catch-up maturation for an individual conditional upon a previous skeletal age assessment. Our results may, in fact, be applicable to other populations. Variation in skeletal maturation at a given age across populations does not necessarily imply that there is a similar magnitude of variation in conditional skeletal maturation.

Consider an overly simplified scenario in which there are only two possible skeletal maturity trajectories, “slow maturers” who have RSA < 0 for most of their childhood before getting to SA = 18 and “fast maturers” who have RSA > 0 for most of their childhood before getting to SA = 18. Suppose that in the reference population 50% of kids are “slow” and 50% are “fast”, and suppose that in some other population with different environmental conditions the distribution is 75% “slow” and 25% “fast”. At any given age, we would observe a difference in average skeletal maturity between these two populations, but within each of the “slow” and “fast” subgroups, the two populations would be identical in terms of their skeletal maturity trajectories. In this simplified scenario, a model, fit to the reference population, predicting a child’s RSA conditional on an earlier assessment would be applicable to the other population, even though the unconditional distributions of RSA are very different between the two populations.

Our study excluded children born after 1992 since they had not yet reached age 18 years by 2010. Their inclusion in this analysis would have required an untestable assumption of no recent secular trend in the relationship between earlier and later skeletal age. Research indicates, however, that there may be a trend towards earlier maturation in both sexes (Himes, 1984; So and Yen, 1990; Lejarraga et al., 1997; Pludowski et al., 2004; Hawley et al., 2009; Duren et al., 2010), and if the trend is of different magnitude at different ages, then prediction of future SA will also exhibit a secular trend. In addition to the possibility that the sample is not representative of children born more recently, a potential limitation of this study is the possibility of a secular trend within the sample used. However, for the same reasons that our predictions may be applicable to other populations, they may be robust to the presence of a secular trend. Within the same population, it is reasonable to entertain the possibility that changes in the distribution of skeletal maturity at a given age over time reflect changes in the distribution of children with varying levels of environmental factors that cause developmental delay or acceleration. Going back to the overly simplified example above, while the environmental factors themselves do not change, their distribution within the population has changed over time, thus changing the distribution of “slow” and “fast” maturers but not changing the relationship between current and future skeletal age within each subgroup. To check this, we included a birth year effect when estimating the conditional means and standard deviations (results not shown) and found this effect to be generally near zero and not dependent on the ages of assessment. On average, the secular trend was about one month in SA per 10 years difference in birth year; even the largest effects were only on the order of three months in SA for a 10 year difference in birth year.

In many cases, RSA of children in a given population is likely to be affected by external factors (e.g., environmental, nutritional, or disease stressors) not experienced by our relatively homogenous Midwestern United States population, and thus predictions based on the presented model would be erroneous. A case in point is a study of high altitude populations (Pawson, 1976), where it was estimated that 8 year old Quechua boys in Peru had a mean SA of 7 years (RSA = 21 year). In the Fels Longitudinal Study population, the predicted mean RSA for boys with RSA = 21 year at age 8 years reaches zero (that is, mean SA catches up to CA) at age 15 years. For the Quechua sample, however, the mean SA at age 15 years was only 13.5 years (RSA has decreased rather than increased). While these results are for unconditional means, they indicate that conditional skeletal maturity predictions based on the Fels Longitudinal Study may not apply to the Quechua population.

The behavior of conditional skeletal age in non-Caucasian populations has not been studied. Future work will include SA assessment of a larger sample of more racially diverse children. Analyses will also include sampling children born more recently. This will allow a more careful investigation of secular trends in skeletal maturity, as well as of racial differences in patterns of maturity. Additionally, by investigating individual-level trajectories of SA, we will be able to determine if, in fact, two skeletal maturational spurts exist for girls; and, by examining the concurrent stature trajectory, we will be able to elucidate the relationship between the timings of skeletal maturation and growth in size.

CONCLUSIONS

Using serial childhood data from the Fels Longitudinal study, we estimated prediction models for change in skeletal maturation. In the introduction we posed two broad questions regarding the use of this model to predict future skeletal age for an individual with delayed maturation. While answers to these questions depend upon many things, including the child’s chronological age and magnitude of maturational delay (RSA), some generalizations can be made.

Regarding the likelihood of a skeletally delayed child catching up to their peers:

• Prior to the pubertal growth spurt, the probability of “catch-up maturation” increased with chronological age.

• Between the pubertal growth spurt and average age of peak height velocity, the probability of “catch-up maturation” decreased with chronological age.

• Subsequent to the average age of peak height velocity, the probability of “catch-up maturation” increased.

• This increase was partly out of necessity, since all individuals are expected to reach full skeletal maturity at some point.

Regarding how soon such catch-up maturation will occur:

• For boys age 10–18 years, and for girls age 8–10 years and 14–18 years, the probability of an imminent maturational spurt was, in general, higher for those who were less mature.

• For girls aged 11–13 years, however, this probability was higher for those who were more mature, potentially indicating the presence of a skeletal maturation plateau between multiple spurts.

The model presented represents a novel tool for the assessment of an important measure of life history, skeletal maturation. Access to the model’s predictions is available online at somtest3.wright.edu/PredictSA.html. The nature of a conditional prediction model is such that it is impossible to table all the possibly relevant results. While some example predictions have been highlighted here, the interested reader can access additional results using the online form, providing prediction of and reference values for later SA over any time interval given an existing SA assessment. These predictions are most relevant to populations similar to the Fels Longitudinal Study, namely children of European ancestry. They may not be applicable to other populations with factors affecting the tempo of maturation that are not present in the Midwestern United States (e.g., high altitude, extreme nutritional or disease stressors).

Fig. 2.

Estimated mean (left panel) and standard deviation (right panel) of (uncensored) SA₁ for girls at age t₁ given SA₀ at t₀ = 8 years. Each line represents the prediction at a different value of SA₀ representing relative skeletal ages from –2 to 2 years.