Delivering systems pharmacogenomics towards precision medicine through mathematics

Abstract

The latest developments of pharmacology in the post-genomic era foster the emergence of new biomarkers that represent the future of drug targets. To identify these biomarkers, we need a major shift from traditional genomic analyses alone, moving the focus towards systems approaches to elucidating genetic variation in biochemical pathways of drug response. Is there any general model that can accelerate this shift via a merger of systems biology and pharmacogenomics? Here we describe a statistical framework for mapping dynamic genes that affect drug response by incorporating its pharmacokinetic and pharmacodynamic pathways. This framework is expanded to shed light on the mechanistic and therapeutic differences of drug response based on pharmacogenetic information, coupled with genomic, proteomic and metabolic data, allowing novel therapeutic targets and genetic biomarkers to be characterized and utilized for drug discovery.

Introduction

Response to a drug is highly variable among individuals.¹ Pharmacogenomics, attempting to explain the interindividual variability in drug response due to genetic variants, has been widely used as an approach to study and predict how an individual will respond to a particular drug/dose combination.^2,3 However, there is increasing recognition of the limitation of using pharmacogenomic approaches alone to achieve this goal. First, in addition to genetics, many other factors can play a role in the response to pharmacotherapy, including metabolic, environmental, and developmental factors.⁴ It is unclear how all these factors interact with genes in a complex web to determine drug efficacy and toxicity at the organ and patient level. Second, current pharmacogenomic studies are based on a direct relationship between genotype and phenotype, neglecting the causal networks inside the “black box” that lies between genotype and drug response.^5,6 The paucity of knowledge of the complex and subtle interconnectedness of signaling, transcriptional and metabolic networks that guide the distribution and action of drugs would greatly limit our capacity to tailor-make drugs for individual patients according to their characteristics.

We describe a dynamic framework to study the genetic architecture of drug response and quantify drug reactions as a coordinated network of genes, proteins and biochemical reactions. This framework incorporates pharmacokinetic (PK) and pharmacodynamic (PD) models that are derived to understand how drugs modulate cellular reactions in space and time and how they impact human pathophysiology into genetic mapping, allowing the landscape of genetic actions to be characterized in a precise, predictive manner. The integration of the “omics” data into this framework can study the pattern of gene expression (regulation, inhibition and induction) and systematically screen the pathways that could be involved in drug reactions. The results from this framework will facilitate the quantitative prediction of the responses of individual subjects as well as the design of optimal drug treatments that maximize therapeutic efficacy while minimizing the number and severity of adverse drug reactions.

In recent years, personalized medicine has emerged as an important research focus in medicine to provide knowledge about the delivery of the right drug at the right dose at the right time for the patient.^7,8 Our framework organizes systems biology into pharmacogenomics, providing powerful tools for designing personalized medicine.

Mechanistic modeling of drug response

Over the past decade, there has been rapid growth of using DNA-based markers to identify genes for drug response.^1,9,10 If significant associations are detected between marker genotype and drug-response phenotype through statistical tests, these markers are regarded as the genetic variants that affect drug response. This approach, although simple and widely applied in practice, cannot provide a mechanistic explanation about how the genes interact with biochemical pathways to determine drug response at the level of human patients.

By viewing drug response as a dynamic system involving drug transport, drug metabolism and drug targets, one mechanistic approach has been derived to map genes for each of these components using PK and PD equations.^11-13 This approach founded on biochemical reactions can not only identify how genes interact with each other and with developmental and environmental stimuli in a patient's body, but also quantify the dynamic effects of individual genes and gene-environment interactions on various biochemical pathways and reactions that contribute to drug response (Fig. 1A).

Figure 1.

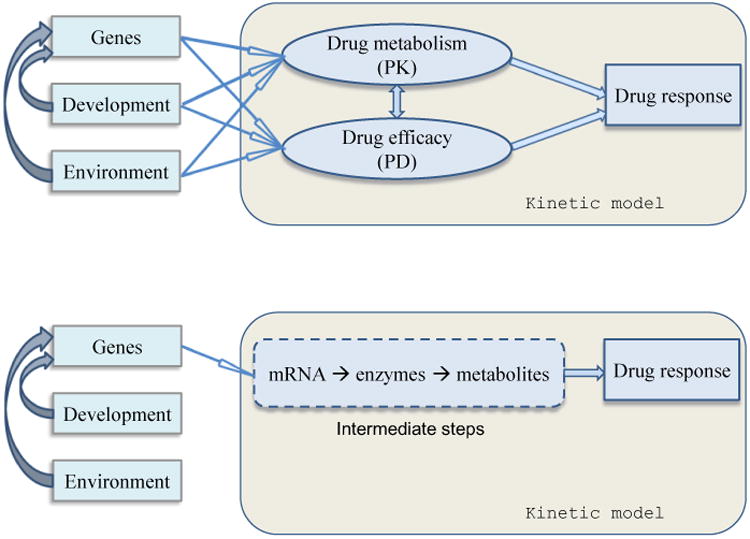
Kinetic modeling of drug response. Upper panel (A): Causal effects of genetic, developmental and environmental factors and their interactions on the outcome of drug response. All these effects operate through PK and PD reactions. Lower panel (B): Intermediate steps linking signaling, transcriptional and metabolic networks involved in the distribution and action of drugs.

As a phenotype, drug response should include regulatory and genetic mechanisms between genotype and phenotype. The “Central Dogma” of biology, DNA → mRNA → enzyme (inactive) → enzyme (active) → metabolite(s) → metabolism → cellular physiology → phenotype, subjected to continuous addendums and modifications in the recent past, is thought to be a fundamental rule to the form and control of every aspect of a phenotype. Regulatory control is exerted to affect virtually all these levels. A second mechanistic approach based on regulatory control has been developed,¹⁴ aimed to identify the “black box” that lies between genotype and drug response through transcript abundance and other intermediate molecular processes (Fig. 1B).

The mechanistic modeling of drug response capitalizes on specific modules which are linked through mathematical models. Below, we show how these modules are modeled from genetic, biochemical and engineering perspectives.

Genetic architecture modeling

Genetic architecture, the structure of the mapping from genotype to phenotype, builds and controls a given phenotypic character and its variational properties.¹⁵ Traditional approaches for linkage and association-based studies have been instrumental in the elucidation of the genetic architecture of complex traits or diseases, such as cardiovascular diseases, metabolic disturbances, diabetes, lipids, inflammation, and cancer. These approaches enable geneticists to address several fundamental questions, i.e., what mode of actions individual genes exert, additive or dominant; whether there are interactions (epistasis) among different genes; and what is the pleiotropic effect of genes on different traits; what is the distribution of allelic effects.¹⁶

Beyond these traditional descriptions, we need to integrate the molecular mechanisms involved in pharmacogenomic effects into drug response. Quantitative genetic theory should be refined to define the molecular effects of genes through mutations, insertions, deletions, copy number variations and, more recently, epigenetic events, such as histone and DNA methylation, and gene expression. In order to describe the pharmacogenetic control of drug response, the genetic architecture should not be only regarded as a given set of genetic effect parameters, but it should also reflect dynamic trajectories of genetic alteration over time and space and environmental changes.

Kinetic Models of Drug Reactions

Traditional pharmacogenomics investigates the genetic control of drug response measured as a static state of drug effect. However, when a drug is administered to a patient, it must be absorbed, distributed to its site of action, interact with its targets, undergo metabolism, and finally be excreted.¹⁷ This process, called pharmacokinetics (PK), influences the concentration of a drug reaching its target, and it interacts with another process associated with the drug target, called pharmacodynamics (PD), to determine drug response (Fig. 1A). Since functionally important genetic variation also occurs in the drug target itself, or in signaling cascades downstream from the target, the ability to take into account all of the factors that can influence drug response in the cell would help to better understand the mechanisms involved in the variation of drug response.

Previous work has modeled the genetic control of drug response by implementing mathematical aspects of PK and PD processes into a genetic mapping framework.^11-13,18 This so-called functional mapping model allows the detection of genes associated with drug response at varying doses or over a time course. A more powerful approach to modeling drug response is to treat its formation as a dynamic system in which various biochemical parts are linked through a system of differential equations (DE). Thus, by developing and implementing innovative statistical methods for estimating DE parameters,¹⁹ we can test and quantify the genetic and genomic control of biochemical pathways involved in drug response.

Dynamic Models of Genetic Network

Current pharmacogenomic studies are based on a direct relationship between genotype and phenotype through simple statistical models that are relatively opaque to biological interpretation. Such “black box” approaches are less helpful in revealing regulatory and genetic mechanisms between genotype and phenotype. As the cost of methods for measuring mRNA, protein and other indicators continues to fall, it becomes reasonable to design experiments that capture the dynamic processes of phenotypic formation across timescales. With these data, the respective systems disciplines arise from the study of the transcriptome (the set of RNA transcripts) and the metabolome (the entire range of metabolites taking part in a biological process). Other omes (sets) that may also be of interest include: the interactome (complete set of interactions between proteins or between these and other molecules), the localizome (localization of transcripts, proteins, etc.) or even the phenome (complete set of phenotypes) of a given organism.⁵ New models are needed to reconstruct biological networks by incorporating interactome, localizome, and phenome related to drug response. Coupling with DNA polymorphism information, these models are capable of mapping quantitative trait loci (QTLs) that control transcriptional (eQTL), proteomic (pQTL), and metabolomic (mQTL) expressions²⁰ and their interaction networks among these different types of QTLs.

Implementing Systems Approaches

Systems biology studies the relationships among elements of a system, aimed to better understand its emergent properties. A systems analysis can be applied to molecules, cells, organs, individuals or even ecosystems. For instance, a system may include just a few protein molecules that together serve a defined task (e.g., fatty acid synthesis), a more complex molecular machine (e.g., a transcription complex) or a cell or group of cells executing a particular function, such as an immune response.²¹ In each case, a systems analysis describes all of the elements of the system, defines the biological networks that interrelate the elements of a system, and characterizes the flow of information that links these elements to an emergent biological process through their networks. A particular response to medications emerges when the operation of networks is perturbed to some degree. By comparing responsive and non-responsive networks, we can identify critical nodal points (proteins) which, if modulated, are likely to reconfigure the perturbed network structure back toward its non-responsive state.²¹ These nodal proteins are likely to represent drug targets.

The detection and identification of nodal proteins in complicated networks is critical in developing the solutions of the models. A system of differential equations can be implemented to model the structure of regulatory networks involved in drug response. Although previous work has utilized ordinary differential equations to model the change in each gene's expression,^22-24 these models are structurally too simple to capture the complexity of networks. Also, statistical issues on parameter estimation for differential equations have never been adequately explored. Innovative statistical methods need to be developed for estimating the mathematical parameters defining differential equations with noisy measurements by combining a modified data smoothing method and the generalization of profiled estimation. Also, these statistical methods should be expanded to handle non-linear differential equations (including stochastic, delay, and partial types) that better describe the complexity of regulatory networks.

Modeling dynamic systems of drug response

Functional Mapping

By incorporating PK/PD principles into a genetic mapping framework, functional mapping provides a statistical tool for mapping dynamic genes.^11-13 Functional mapping was founded on finite mixture models, a type of density model that comprises a number of component functions. According to the mixture models, each dose-response curve, fitted by a finite set of measurements at L doses for subject i, arrayed by y_i = (y_i(C₁), …, y_i(C_L)), where (C₁, …, C_L) is a vector of dose level, is assumed to have arisen from one of a known or unknown number of components, each component being modeled by a multivariate normal distribution. Assuming that there are 3^J genotypes, derived from J genes, contributing to the variation among different curves, such a mixture model is expressed as

$$\mathbf{y}\sim p(\mathbf{y}|\mathit{\omega },\mathit{\phi },\eta )=\sum _{j=1}^{3^J}{\omega }_j{f}_j(y_i;{\phi }_j,\eta )$$ (1)

where ω = (ω₁,…,ω_3^J) are the mixture proportions (i.e., genotype frequencies) which are constrained to be non-negative and sum to unity; φ = (φ₁,…,φ_3^J) are the component- (or genotype) specific parameters, with φ_j being specific to component j; η are parameters which are common to all components; and f_j(y_i;φ_j,η) is a multivariate normal distribution (although other types of distributions can be substituted for the multivariate normal) with mean vector u_j = (u_j(C₁), …, u_j(C_L)) and covariance matrix Σ.

The unknown parameters being estimated include 3^JL time-specific means, L(L+1)/2 variances and covariances and J gene positions. Functional mapping does not estimate all elements of the mean vector and matrix directly. Instead, it estimates the biologically relevant parameters (φ_j) that model the mean vector¹⁸ and parsimonious parameters (η) that model the covariance structure. General approaches for covariance structure can be parametric, nonparametric, or semiparametric.²⁵ An optimal covariance-structuring approach that best fits a specific data should be tested and obtained from model selection criteria.

For drug response, genotypic means at a dose C_l can be model by the Emax function,¹⁸ i.e.,

$$E(C_l)=E_0+\frac{E_{max}{C}_l^H}{E{C}_{50}^H+C_l^H}$$ (2)

where E₀ is the baseline, E_max is the asymptotic drug response, EC₅₀ is the drug concentration at which drug effect is the half of E_max, and H is the slope of drug response curve. By estimating drug effect-related curve parameters φ_j = (E_0j, E_maxj, EC_50j, H_j) for each genotype j, one can determine how a gene affects drug response and, further, how individual patients respond to drug therapy based on their genotypes (Fig. 2). The covariance (Σ) structure can be modeled by a statistical approach, which could be parametric, nonparametric, and semiparametric. The best approach for the covariance structure can balance the trade-off between model parsimony and flexibility through a model selection procedure.

Figure 2.

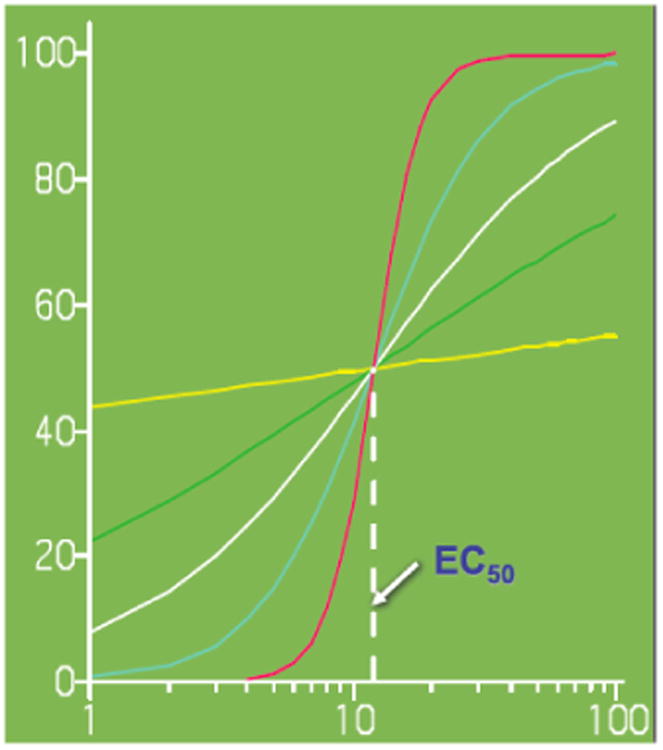
Different drug response curves determined by Eq. (2). The x- and y-axis is the concentration of a drug and its effect, respectively. The differences in the curve shape of drug response are determined by parameters (E₀, E_max, H), although all curves have the same EC₅₀ value. Our model can detect such shape differences among different genotypes.

In an application of functional mapping to map drug response, SNP haplotypes, derived from the β₁AR and β₂AR receptor genes, were detected to alter patients' heart rate in response to a drug called dobutamine.¹⁸ The study genotyped 107 patients for two SNPs within the β₂AR receptor gene and measured their heart rates in a response to different doses of dobutamine, 0 (baseline), 5, 10, 20, 30, and 40 mcg/min. Race, age and gender were considered as covariates.

Body mass is an important developmental factor for drug response. It can integrated with functional mapping based on allometric scaling principles. Allometric scaling, described by a simple power equation, provides a good predictor of a variety of biological variables including metabolic rate, lifespan, growth rate, heart rate, DNA nucleotide substitution rates, and length of aortas.²⁶ It can also be used for the scaling preclinical evaluation of drug metabolism and response.²⁷ A power equation was used to model E_max in equation (2) by E_max = αM^β, where α and β are the power coefficients that specify the allometry of E_max over body mass (M).

This model was used to estimate and test haplotype effects on drug response modified by this scaling law. Of four possible haplotypes (GG, GA, CG, and CA), derived from the β₂AR receptor gene, GG was found to be a risk haplotype that produced the best fit to the data. The combination between risk haplotype GG (expressed as A) and other non-risk haplotypes GA, CG, and CA (collectively expressed as B) forms three composite diplotypes AA, AB, and BB. Our model produced the following results:

• With lighter body mass, the two homozygotes (AA or BB) respond to the dose of dobutamine more rapidly than the heterozygote (AB).

• When body mass increases, the slope of the responsiveness is much larger for the heterozygote than the two homozygotes.

• The power to detect a significant genetic effect on drug response is increased when allometric scaling is incorporated (p = 0.002) than when it is not incorporated (p = 0.021).

It should be pointed out that functional mapping can be integrated with genome-wide association studies (GWAS) to characterize a complete picture of the genetic architecture of drug response. GWAS allows all SNPs and their interactions to be analyzed simultaneously.

Systems Mapping

Drug response is the consequence of interactions among drug, disease, and body (Fig. 3). The interactions between drug and body can be quantified by pharmacokinetics (focusing on how the body processes a drug, resulting in a drug concentration) and pharmacodynamics (concerned with how the drug acts on the body, resulting in a measurable drug effect). Through PK-PD modeling and simulation, a drug's absorption, distribution, and elimination properties can be characterized. Differential equations and stochastic models, which provide detailed descriptions of dynamic systems that include physically relevant units, can be used to simulate the dynamic behavior of drug response and link the exposure of a drug and the modulation of pharmacological targets, physiological pathways and ultimately disease systems.²⁸ For example, Wang et al.¹⁷ implement a system of ordinary differential equations (ODEs) to quantify the flow of the drug in the body, its interaction with the disease, and its pharmacological effect, which is expressed as

Figure 3.

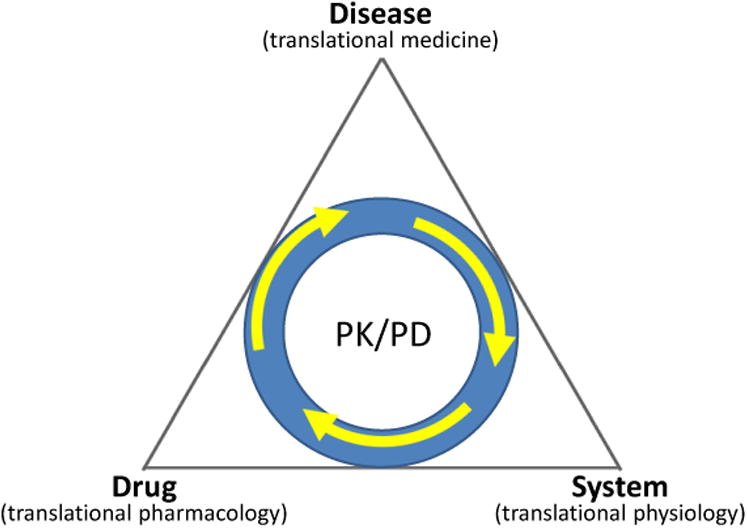
Drug response as a system with interactions between the drug, disease, and body through PK-PD processes. Thus, translational research in drug discovery and development could be considered to be divided into three broad disciplines – translational physiology, pharmacology and pathology. Mechanism-based PK-PD modelling, by quantitatively combining system and drug-specific physiological, pharmacological and pathological properties, has the potential to facilitate translational research. Adapted from ref 28.

$$\begin{array}{l}\mathrm{P}\mathrm{K}\{\begin{array}{l}\frac{dQ}{dt}=-k_{A}Q\\ \frac{dC}{dt}=\frac{k_{A}Q}{V}-\frac{V_{max}C}{k_m+C}\end{array}\\ \mathrm{P}\mathrm{D}\{\begin{array}{l}\frac{dC}{dt}=-\frac{C_l}{V}C\\ \frac{dR}{dt}=-k_{\text{in}}(1+\frac{E_{max}C}{E{C}_{50}+C})-k_{\text{out}}R\end{array}\end{array}$$ (3)

where time t is the independent variable, Q is the amount of drug in the digestive system, C is the plasma drug concentration, V is the distribution volume, k_A is the decay rate of the drug, k_m is the Michaelis-Menten constant, V_max is the maximum rate of the reaction, R is drug response that can be viewed as blood pressure, body temperature or other pharmacologic response, k_in and k_out are the zero-order and the first-order rate constant for production and loss of an effect, respectively, and E_max and EC₅₀ are the maximum effect of the drug and the drug concentrations producing 50% of the maximum stimulation, respectively.

By integrating these two systems of ODEs (3) into the mixture model (1), a new model, called systems mapping, has been developed.¹⁹ Systems mapping is implemented with a mathematical or statistical algorithm to estimate and test the PK and PD parameters, allowing us to ask and address new hypotheses about the genetic control of drug response and pleiotropic effects of individual genes on PK and PD processes. If two types of environmental and developmental covariates, those that are discrete (such as gender, race, and smoke/no smoke) and continuous (such as age, nutrient level, and body mass), are incorporated, we will have power to quantify gene-gene interactions, gene-environment interactions and gene-development interactions.

Network Mapping

Gene regulatory networks play a pivotal role in every process of drug response, including cell differentiation, cell cycle, metabolism, and signal transduction.²⁹ By studying the dynamics of these networks, we can better understand the mechanisms of altering these cellular processes through medications and more precisely predict drug response. With the aid of powerful computational tools, the following specific questions can be addressed: what is the full range of behavior for this system under different conditions? How does the system change when certain parts stop functioning? How robust is the system under extreme conditions?

Many models have been developed for regulatory network analysis. The Boolean network is one of the most popular models, in which the level of gene expression is either 1 (on) or 0 (off) and the relationship among genes is represented by a Boolean function. This discrete model provides a qualitative understanding of different functionalities of a given network under different conditions, but it is too simple to capture the complexity of the network. A more general and flexible model of regulation is based on a system of ordinary differential equations (ODEs) that is originally used to model electronic networks in engineering(Fig. 4).^22,23,30,31 These equations describe an instantaneous change in each component as a function of the levels of other network components. For simple ODE systems, an analytical solution based on the Hill and Michaelis– Menten functions can be formulated, whereas larger networks, which are constructed by these functions and various linear and bilinear functions, can only be solved by a numerical solution.

Figure 4.

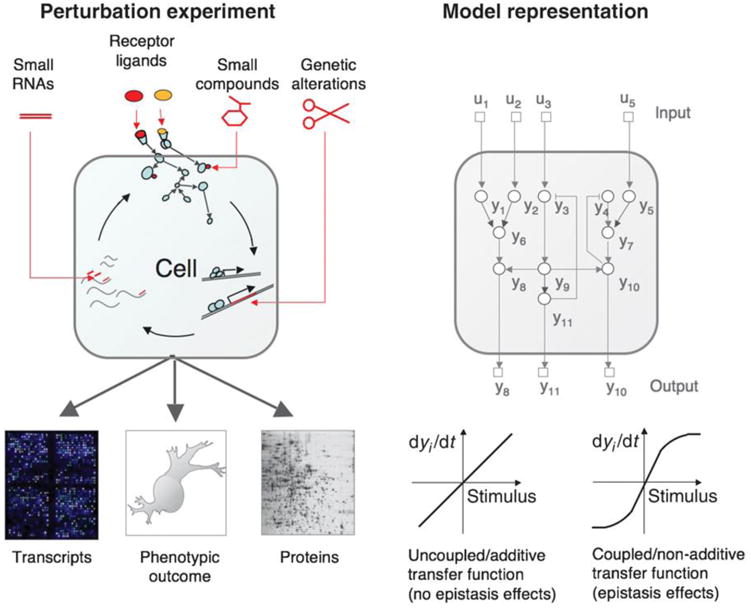
Phenotypic changes by the perturbation of a drug. In the left panel, perturbations and their points of action are shown. Small inhibitory RNAs alter gene expression; natural protein ligands and small compounds act, e.g., on receptors, transporters or enzymes. Genetic alterations have diverse functional effects. Perturbations can be natural or investigational. Observations (readouts) typically focus on a phenotype of interest, such as growth or differentiation, and on observation points that are both practical and informative, such as transcripts, protein levels or covalent modifications, e.g., phosphorylation. In the right panel, models for studying drug response are demonstrated in which all key system variables are represented as real number variables, the combinatorial perturbations u_i as well as their targets, internal variables, observation points and phenotypic outputs y_i. Inputs (upper layer, squares) affect the different dynamical variables of the system (circles), some of which can be observed (lower layer, squares). The model represents a processing system that relates the input to the output through the interacting dynamical variables. Representation of coupled perturbations (nonlinear effects) is a key requirement of the modeling method. Adapted from ref 33.

The ODE methods have been applied to model the regulatory network of Halobacterium salinarum,³¹ human regulatory networks (mediating TLR-5–mediated stimulation of macrophages) and several other microbial networks.³² The ODE approach provides detailed information about the network's dynamics and, also, can generate predictions that may subsequently be compared to cellular phenotypes.

Below, we show how ODEs can be used to model the regulatory network of drug response by a system of differential equations. In drug discovery, we seek for a targeted perturbation that can typically inhibit or activate function of biomolecules related to a disease.³³ We describe the pathways related to drug action as a system characterized by a particular type of cell, its environment, its points of intervention (such as drug targets), time points of observation (such as the phosphorylation state of proteins involved in signaling processes) and a phenotypic change (such as cell death or growth) (Fig. 4). Mathematical models are used to describe the regulatory network of the system in which nodes denote levels of molecular activity and edges reflect the impact of one node on the time derivative of another. As shown in Fig. 4, the time evolution of the system can be modeled by a first-order differential equation

$$\frac{dy}{dt}=f(y(t),u(t))$$ (4)

where the vector y(t) represents the activities of the system's components; the vector u(t) represents perturbations of drugs on the components; and f is a linear or nonlinear transfer function. In practice, y(t) can be the abundances of specific mRNAs or proteins, whereas u(t) can be the concentrations of different chemical compounds to which the cells are exposed (Fig. 4).³³ Equation (4) can be linear differential equations for a system, but they can further be modified by a nonlinear transfer function to reflect properties of the system that are not explicitly modeled.

The application of differential equations to the detection of drug targets can be made by inferring functional interactions between pathway components, predicting phenotypic consequences of drug combinations, and controlling the behavior of the system. By incorporating systems modeling of transcriptome, proteome, protein-protein, protein-DNA interactions into a genome-wide association studies, we will gain better insights into the genetic architecture of drug response in which specific eQTL, pQTL, and mQTLs and their interactions can be identified to better predict the efficacy of drugs. All this constitutes a concrete step toward the active development of network-oriented pharmacology.

Future Prospects

Compared to their capabilities only a few years ago, new biotechnologies now hold the potential to accurately and inexpensively produce terabytes of genotype, gene expression, protein and metabolic data for complex traits, such as drug response. With various platforms able to generate vast amounts of information, these advances demand an effective approach to analyze and interpret the high-dimensional data by developing powerful computational tools. The development of these tools should be based on solid biological relevance. Their applications should be tested and validated by multiple experiments in which various data are collected and analyzed. Only in this manner can the pace of groundbreaking discovery be accelerated. First, we need to develop a warehouse of computational tools for mapping genes and their interactions with other factors involved in drug response. The flow of a drug through the body (pharmacokinetics) and its pharmacological reactions (pharmacodynamics) are modeled by a system of differential equations. These physiologically meaningful equations are incorporated to quantify the temporal-spatial pattern of genetic actions for drug response and understand the mechanisms of how genes interact with developmental and environmental factors to determine drug efficacy and toxicity. Since proper statistical inference of dynamic genetic effects depends on robust modeling of longitudinal covariance structure, parsimonious and flexible approaches for the covariance structure of longitudinal and repeated measures data will enhance the efficiency of the models.

Second, we need to devise a systems approach for understanding the genetic network of drug response by integrating genetic, genomic, proteomic, and metabolic data. A network of genetic and metabolic control should be constructed for drug response with the “omics” data. The nodes and edges are linked through a system of differential equations (DE) of high complexity under fundamental biological principles. Powerful mathematical algorithms can be implemented within a statistical model framework to solve the DE parameters that define the network and the perturbation of the system. A quantitative framework can be formulated to test biologically interesting hypotheses about the interacting pattern of biological parts for a system and the dynamic behavior of the system.

Our hope is to use an increasingly growing amount of complete genome sequences for engineering new biotechnological solutions to the design and discovery of new drugs. Although in principle it is possible to re-engineer new processes by selectively combining otherwise distinct biochemical capabilities, this will very much rely on our profound understanding of how the proteins encoded in each individual genome dynamically assemble into biological circuits through interactions with the environment. To achieve this goal, we need powerful computational tools for systems approaches to understand how a simple genetic change or environmental perturbation influences the behavior of an organism at the molecular level and ultimately its phenotype and how we can enable re-engineering of cellular circuits for the system through quantitative alterations. To this end, computational approaches will be coordinated and implemented with experimental data to construct a predictive gene regulatory network model for drug response.