Abstract
Fundamental to increasing our understanding of the role of white matter microstructure in normal/abnormal function in the living human is the development of MR-based metrics that provide increased specificity to distinct attributes of the white matter (e.g., local fibre architecture, axon morphology, and myelin content). In recent years, different approaches have been developed to enhance this specificity, and the Tractometry framework was introduced to combine the resulting multi-parametric data for a comprehensive assessment of white matter properties.
The present work exploits that framework to characterise the statistical properties, specifically the variance and covariance, of these advanced microstructural indices across the major white matter pathways, with the aim of giving clear indications on the preferred metric(s) given the specific research question.
A cohort of healthy subjects was scanned with a protocol that combined multi-component relaxometry with conventional and advanced diffusion MRI acquisitions to build the first comprehensive MRI atlas of white matter microstructure. The mean and standard deviation of the different metrics were analysed in order to understand how they vary across different brain regions/individuals and the correlation between them. Characterising the fibre architectural complexity (in terms of number of fibre populations in a voxel) provides clear insights into correlation/lack of correlation between the different metrics and explains why DT-MRI is a good model for white matter only some of the time. The study also identifies the metrics that account for the largest inter-subject variability and reports the minimal sample size required to detect differences in means, showing that, on the other hand, conventional DT-MRI indices might still be the safest choice in many contexts.
Keywords: Diffusion tensor MRI, Myelin, CHARMED, White matter microstructure
Highlights
-
•
We report an atlas of key white matter pathways in standard space.
-
•
CHARMED provide more specific measures of axonal properties than DT-MRI metrics.
-
•
Crossing fibres explain the correlation between myelin and diffusion indices.
-
•
DT-MRI metrics need the smallest sample size to detect differences between groups.
Introduction
Diffusion tensor MRI (DT-MRI) has proven to be an incredibly powerful tool over recent years (Basser, 1995; Basser et al., 1994). Numerous studies have been performed documenting the clinical utility of DT-MRI in various brain diseases (Assaf and Pasternak, 2008) and its ability to track specific patterns in the developing (Hüppi et al., 1998) as well as in the ageing brain (Pfefferbaum et al., 2000). In addition, the ability to recover voxel-wise the orientation of the fibre pathways has widespread implications in the fields of cognitive neuroscience and neurobiology (Ulmer et al., 2005).
To increase the anatomical specificity of DT-MRI, an approach for obtaining ‘tract-specific’ measurements of tissue microstructure was developed by mapping specific microstructural parameters along pathways reconstructed by tractography (Jones et al., 2005). However, while anatomical specificity can be improved with this approach (compared to voxel-wise estimates), and despite the growing popularity of DT-MRI, the two most-widely reported indices, the fractional anisotropy (FA) and mean diffusivity (MD) (Basser and Pierpaoli, 1996) have a notorious lack of specificity to different sub-components of white matter (WM) microstructure. Axonal membranes play the primary role in determining FA, but myelination also modulates FA (Beaulieu, 2002). Moreover, the fibre architectural paradigm (Pierpaoli et al., 1996) has a huge impact, where intra-voxel orientational dispersion of fibre populations leads to a reduction in the measured anisotropy (Budde and Annese, 2013). Finally, water diffusivity parallel to the axon and the axon morphology and density will also modulate FA.
Understanding the role of WM microstructure in brain function in health and disease demands more specific indices that tap into these sub-components. Different approaches have recently been proposed to disentangle the role of the fiber architectural paradigm from the axon morphology. For example, the composite hindered and restricted model of diffusion, or CHARMED (Assaf and Basser, 2005; Assaf et al., 2004), explains the signal as the contribution of two different pools: a hindered extra-axonal compartment and one or more intra-axonal compartments, whose properties are characterised by a model of restricted diffusion perpendicular to fibre axis within impermeable cylinders (Neuman, 1974). This model recovers both the fibre arrangements and distinct axon-specific parameters, e.g., the restricted fraction (RF), sometimes interpreted as axonal density, and the intra-axonal longitudinal diffusivity (IAD), holding great promise for increasing the specificity of diffusion MRI. For example, CHARMED indices have been shown to be more sensitive than DT-MRI in characterising tissue changes arising during short term neuro-plasticity (Tavor et al., 2013).
Characterising myelin properties is also crucial for understanding brain function, since myelin serves multiple roles, which include reducing conductive leak, reducing charging time of the axonal segment and increasing conduction velocity. Several ways of quantifying the myelin content using MRI have been proposed over recent years (MacKay et al., 1994; Mehta et al., 1996; Sled et al., 2004). An approach that is considered particularly useful, due to its efficiency in term of scan duration, is the multi-component driven equilibrium single pulse observation of T1 and T2, or mcDESPOT analysis (Deoni et al., 2008). McDESPOT produces whole brain maps of the myelin water fraction (MWF) and the intrinsic relaxation times T1 and T2 in a clinically feasible time, i.e. typically less than 10 min on most human MRI scanners.
Combining different microstructural indices for a comprehensive assessment of WM is at the basis of the Tractometry philosophy introduced recently (Bells et al., 2011a). This method combines macromolecular measurements from optimized magnetization transfer imaging (Cercignani and Alexander, 2006), multicomponent T2 species from relaxometry (Deoni et al., 2008) and axonal density measurements from CHARMED (Assaf and Basser, 2005) along specific white matter pathways reconstructed from diffusion MRI, providing a comprehensive assessment of multiple microstructural metrics.
The aim of the current work is to deploy the Tractometry approach in a cohort of healthy participants and extract the mean and standard deviation of the different microstructural indices, in order to understand how they vary across different brain regions/individuals, the correlation between them and their statistical power in detecting differences between groups.
Specific goals are: 1) to create an atlas of axon-specific characteristics measuring CHARMED metrics, conventional DT-MRI indices, the myelin water fraction and the relaxation times T1 and T2; 2) to investigate correlations between the different metrics and find the indices that account for the largest variability; and 3) to evaluate the minimal group size required to detect a true difference in means at a predefined probability using a statistical power analysis (Maxwell et al., 2008).
We report mean values and confidence intervals of multi-variate data for a number of major white matter fasciculi. To capture salient characteristics of the microstructural indices and to compare the trends for the different tracts irrespectively of their length/width, the parameters are also projected along the tract profile. We explain the correlations between the different metrics in terms of the underlying fibre architecture. In addition, we identify the indices that account for the largest inter-subject variability and evaluate the minimal sample size required to detect differences in means, with the aim of ensuring that future studies are sufficiently powered to detect effects robustly. The information gained is used to speculate about the most appropriate metrics to be used, suggesting that DT-MRI is the best choice for characterising white matter microstructure only some of the time.
Materials and methods
Data acquisition
Seventeen healthy right-handed participants (mean age/standard deviation = 24.2/2.8 y) were included in this study. Informed consent was obtained prior to scanning and the study was performed with approval from the local ethics review board. MRI data were acquired on a 3 T General Electric HDx MRI system (GE Medical Systems, Milwaukee, WI) using an eight channel receive only head RF coil.
The MRI protocol comprised: cardiac-gated DT-MRI protocol (TE = 87 ms, 45 gradient orientations (Jones et al., 1999), b-value = 1200 s/mm2, spatial resolution (SR) 1.9 × 1.9 × 2.4 mm, total acquisition time (AT) ~ 20 min depending on the heart rate), CHARMED protocol (TE/TR = 114/17000 ms, 130 gradient orientations distributed on 8 shells, maximum b-value = 7500 s/mm2, SR 2.4 isotropic, AT 35 min) (De Santis et al., in press), mcDESPOT protocol (spoiled gradient recalled, or SPGR, acquisitions: TE/TR = 2.1/4.7 ms, flip angles = [3, 4, 5, 6, 7, 9, 13, 18°]; balanced Steady-State Free Precession, or bSSFP, acquisitions: TE/TR = 1.6/3.2 ms, flip angles = [10.6, 14.1, 18.5, 23.8, 29.1, 35.3, 45, 60°], SR 2.4 isotropic, AT 10 min) (Deoni et al., 2008), and high resolution T1-weighted anatomical scan (FSPGR). bSSFP acquisitions were repeated with and without 180 RF phase alteration to remove SSFP banding artefacts, B0 and B1-induced errors in the derived myelin water fraction estimates (Deoni, 2011).
Data analysis
DT-MRI analysis was performed with ExploreDTI (Leemans et al., 2009) to obtain FA, MD, AD and RD maps (fractional anisotropy, mean diffusivity, axial and radial diffusivity, respectively). Whole brain tractography was obtained for each subject in native space using constrained spherical harmonic deconvolution (Tournier et al., 2004). Track termination was based on a fibre orientation density amplitude threshold of 0.1.
Waypoints were then defined to virtually dissect (Catani et al., 2002) the cingulum, arcuate, uncinate, superior longitudinal, inferior longitudinal, inferior fronto-occipital, fornix and thalamo-cortical fasciculi in each hemisphere. A binary map was computed for each reconstructed fasciculus, with the same matrix size as the FA, but taking a value of one in each voxel intersected by a streamline, zero elsewhere.
CHARMED data were corrected for motion and distortions using a previously-reported CHARMED-specific registration routine (Ben-Amitay et al., 2012). An in-house program coded in Matlab (The MathWorks, Natick, MA) was used to calculate CHARMED parameters RF and IAD (restricted fraction and intra-axonal diffusivity, respectively) according to De Santis et al. (2013). Using a model selection approach (De Santis et al., in press), the number of predominant fibre orientations present in the voxel was obtained.
SPGR and bSSFP images for each participant were corrected for motion using FMRIB's Linear Image Registration Tool (Jenkinson and Smith, 2001) to the first acquired image; maps of MWF, T1 and T2 (the myelin water fraction and the intrinsic relaxation times T1 and T2, respectively) were obtained fitting the mcDESPOT model using a script coded in C++ (Deoni et al., 2008).
DT-MRI, CHARMED and mcDESPOT parameters were corrected for partial volume effects due to CSF contamination (Bells et al., 2011b; Pasternak et al., 2009).
Tract reconstruction and normalisation
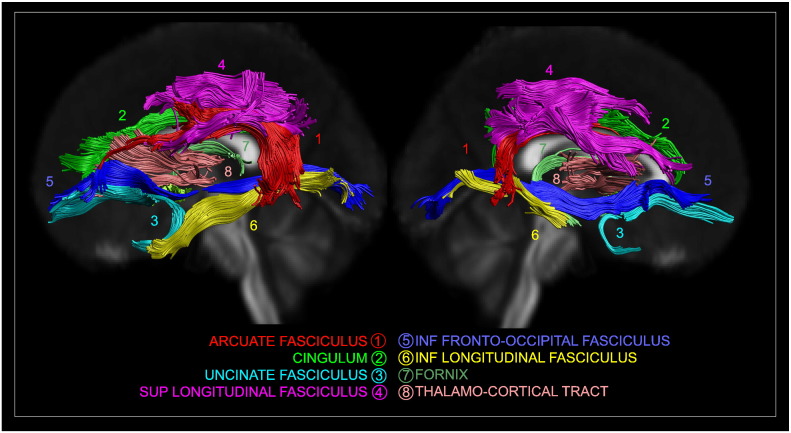
For each subject, all the parametric maps were non-linearly registered to the T1-weighted anatomical scan using the FNIRT routine from the FSL package (Jenkinson et al., 2012) to remove EPI distortions. The latter was used to normalize the brain in MNI space again via non-linear warping. The combined transformations were then applied to the parametric maps (FA, MD, AD, RD, MWF, T1, T2, RF, IAD) and to the binarised tract maps (see below). The population mean and standard deviation were calculated in each voxel for all parameters. For each tract, the binary maps for each individual were overlaid and summed to generate a probabilistic map of the tract location, which we refer to as a tract commonality map (TCM). The TCM was thresholded at 70% (i.e., > 70% of population had a streamline passing through the voxel). The entire set of streamlines from a whole brain tractography result of one subject was then warped non-linearly to MNI space. Only the portions of streamlines passing through non-zero voxels in the TCM for each tract were retained for the fibre atlas. The result is shown in Fig. 1.
Fig. 1.
Tractography reconstruction superimposed on the normalised FA map for eight different tracts: the arcuate fasciculus (ARC) (1), the cingulum (CING) (2), the uncinate fasciculus (UNC) (3) the superior longitudinal fasciculus (SLF) (4), the inferior longitudinal fasciculus (ILF) (5), the inferior fronto-occipital fasciculus (IFOF) (6), the fornix (FX) (7) and the thalamo-cortical (TC) tract (8).
The parametric maps were projected onto the reconstructed tracts. To capture the salient characteristics of each tract, the parametric maps were also evaluated as a function of position along the tract by calculating the tract profile. To obtain the profile, a single mean tract was created by fitting a curve in 3D to the point cloud generated by all the coordinates of each tract taken together. The mean tract was sampled along 100 equally spaced points and the mean of the metrics on the planes orthogonal to the mean tract was evaluated for each step at each point. The mean profiles were used to compare left and right tracts by calculating the asymmetry along the tract as the percentage difference between left and right values for each step.
Correlation between different microstructural metrics
The correlation between DT-MRI, CHARMED and mcDESPOT metrics was evaluated in 42 ROIs obtained from the intersection of the FA-derived skeleton from the tract-based spatial statistics pipeline (Smith et al., 2006) and standardised WM labels in standard space (Mori et al., 2008), according to the method described in De Santis et al. (2012). Out of the 45 ROIs used in the study, we selected ROIs 3–5, 7, 14–50 due to the incomplete overlap of the standardised WM labels and the acquired brain volume of the CHARMED acquisition. A principal component analysis (PCA) was applied to analyse the contribution to the inter-subject variability of the metrics.
Power analysis
The sample size needed to obtain a statistical power of 0.9 at a relative effect size of 10% was also evaluated assuming that the difference in group mean values was tested using a two-tailed Students t-test (Szczepankiewicz et al., 2013). The sample size was calculated by inputting mean values and standard deviations, calculated for each tract, into the formula reported in Szczepankiewicz et al. (2013). To generalise the outcome to different experimental setups, we calculated the contribution to the total variance introduced by imaging and post-processing noise (Szczepankiewicz et al., 2013). 200 datasets were generated using a residual bootstrap approach and the noise variance was evaluated as the mean variance over the different runs. A single number for each microstructural parameter was obtained as the average over all the WM ROIs.
Results
The mean values and the associated standard deviations of the microstructural parameters are reported in Table 1. The fornix shows a significant degree of contamination from cerebro-spinal fluid for all the DT-MRI and the mcDESPOT-derived indices (i.e., abnormally low FA/high diffusivity, low MWF and high relaxation times), but not so for the CHARMED parameters. Consequently, this tract has been excluded from the following analyses.
Table 1.
Mean values, standard deviations (SD) and coefficient of variation (CV) across individuals of the different microstructural metrics, calculated on the eight different reconstructed tracts (data for left and right are averaged): the arcuate fasciculus (ARC),the cingulum (CING), the uncinate fasciculus (UNC), the superior longitudinal fasciculus (SLF), the inferior longitudinal fasciculus (ILF), the inferior fronto-occipital fasciculus (IFOF), the fornix (FX) and the thalamo-cortical (TC) tract. MD, AD, RD and IAD are expressed in units of 10− 3 mm2/s. T1 and T2 are expressed in ms. CV is expressed in percentage.
| ARC | CING | IFOF | ILF | SLF | UNC | FX | TC | ||
|---|---|---|---|---|---|---|---|---|---|
| FA | Mean | 0.40 | 0.38 | 0.41 | 0.42 | 0.40 | 0.35 | 0.28 | 0.35 |
| SD | 0.07 | 0.17 | 0.10 | 0.10 | 0.08 | 0.10 | 0.09 | 0.11 | |
| CV | 18 | 45 | 24 | 24 | 20 | 29 | 32 | 31 | |
| MD | Mean | 0.75 | 0.81 | 0.83 | 0.79 | 0.75 | 0.84 | 1.35 | 0.87 |
| SD | 0.03 | 0.08 | 0.10 | 0.08 | 0.03 | 0.04 | 0.45 | 0.20 | |
| CV | 4 | 10 | 12 | 10 | 4 | 5 | 33 | 23 | |
| AD | Mean | 1.09 | 1.18 | 1.22 | 1.18 | 1.09 | 1.17 | 1.71 | 1.19 |
| Std | 0.07 | 0.20 | 0.14 | 0.15 | 0.08 | 0.09 | 0.48 | 0.24 | |
| CV | 6 | 17 | 11 | 13 | 7 | 8 | 28 | 20 | |
| RD | Mean | 0.58 | 0.63 | 0.63 | 0.60 | 0.58 | 0.67 | 1.16 | 0.70 |
| Std | 0.05 | 0.14 | 0.12 | 0.09 | 0.06 | 0.08 | 0.44 | 0.22 | |
| CV | 9 | 22 | 19 | 15 | 10 | 12 | 38 | 31 | |
| MWF | Mean | 0.20 | 0.14 | 0.15 | 0.17 | 0.21 | 0.11 | 0.06 | 0.12 |
| Std | 0.02 | 0.06 | 0.04 | 0.04 | 0.03 | 0.04 | 0.03 | 0.05 | |
| CV | 10 | 43 | 27 | 24 | 14 | 36 | 50 | 42 | |
| T1 | Mean | 1187 | 1547 | 1364 | 1303 | 1175 | 1618 | 2284 | 1573 |
| Std | 123 | 367 | 180 | 188 | 146 | 244 | 566 | 382 | |
| CV | 10 | 24 | 13 | 14 | 12 | 15 | 25 | 24 | |
| T2 | Mean | 35 | 59 | 47 | 41 | 35 | 50 | 129 | 60 |
| Std | 5 | 25 | 13 | 10 | 5 | 11 | 43 | 30 | |
| CV | 14 | 42 | 28 | 24 | 14 | 22 | 33 | 50 | |
| RF | Mean | 0.28 | 0.20 | 0.21 | 0.23 | 0.29 | 0.13 | 0.09 | 0.17 |
| Std | 0.06 | 0.10 | 0.06 | 0.06 | 0.07 | 0.04 | 0.04 | 0.07 | |
| CV | 21 | 50 | 29 | 26 | 24 | 31 | 44 | 41 | |
| IAD | Mean | 0.91 | 1.06 | 0.92 | 0.87 | 0.88 | 1.03 | 1.05 | 1.08 |
| Std | 0.15 | 0.25 | 0.17 | 0.19 | 0.17 | 0.21 | 0.29 | 0.30 | |
| CV | 16 | 24 | 18 | 22 | 19 | 20 | 28 | 28 |
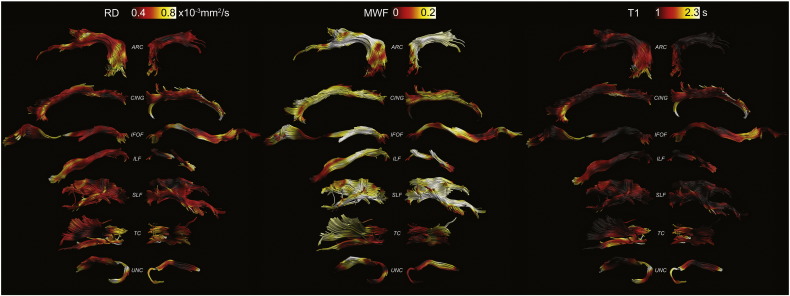
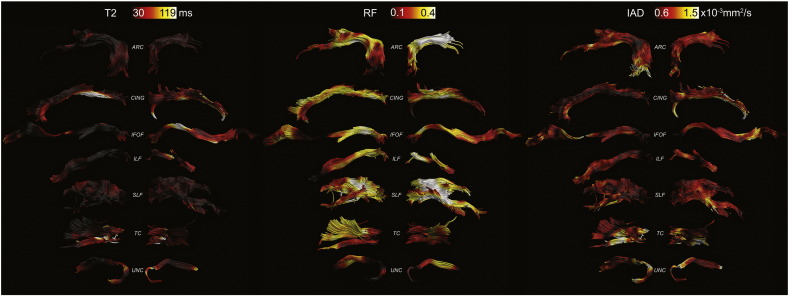
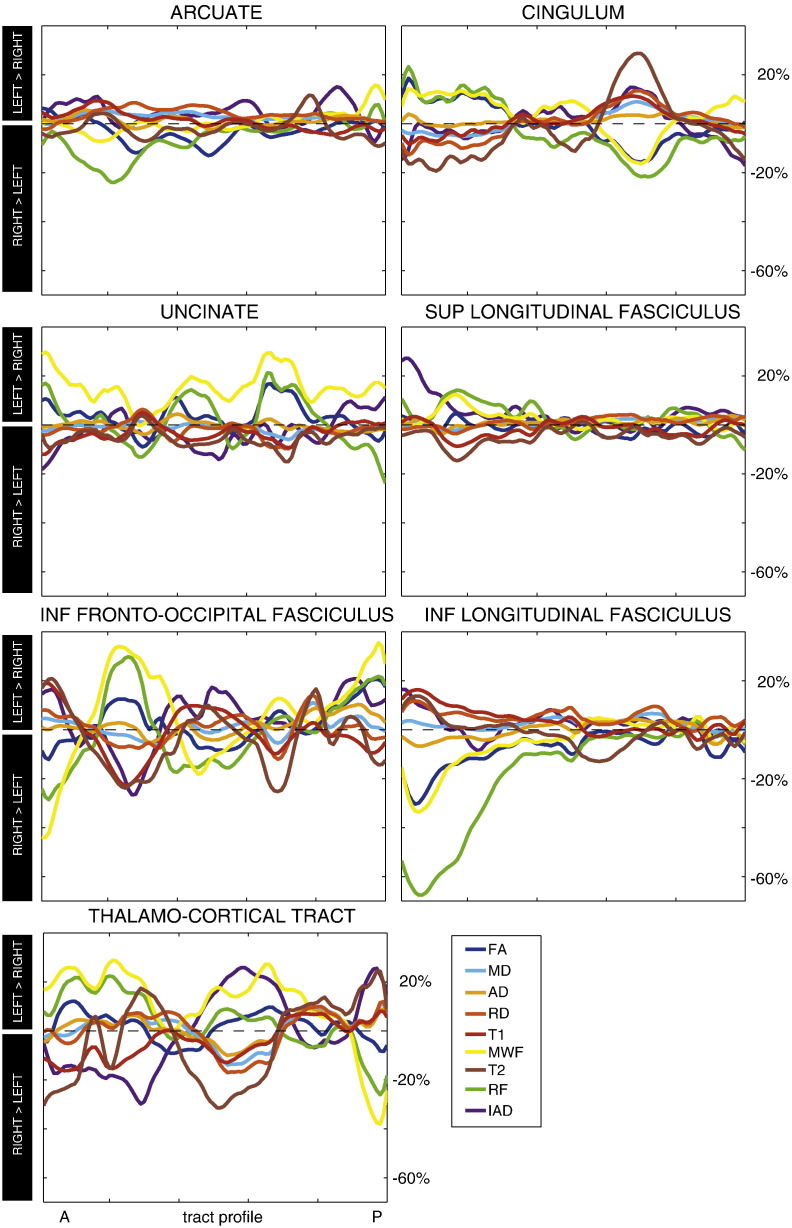
Figs. 2–4 show the tract projections of the microstructural parameters. The range of the colour bar for each microstructural parameter is chosen to be within the 5th and the 95th percentile. The profiles of the asymmetry along the different tracts are reported in Fig. 5 for all metrics. The asymmetry has different patterns for different microstructural indices, e.g., RF is the micro structural index that has the largest asymmetry while diffusivity metrics have a more symmetric behaviour in the two hemispheres. The asymmetry profiles also vary from one tract to another. The arcuate fasciculus, for example, has very symmetric profiles while the inferior longitudinal fasciculus shows considerable asymmetry in the anterior part.
Fig. 2.
FA, MD and AD maps projected onto the reconstructed left and right tracts, respectively.
Fig. 3.
RD, MWF and T1 maps projected onto the reconstructed left and right tracts, respectively.
Fig. 4.
T2, RF and IAD maps projected onto the reconstructed left and right tracts, respectively.
Fig. 5.
Asymmetry profiles along the different tracts for the microstructural parameters.
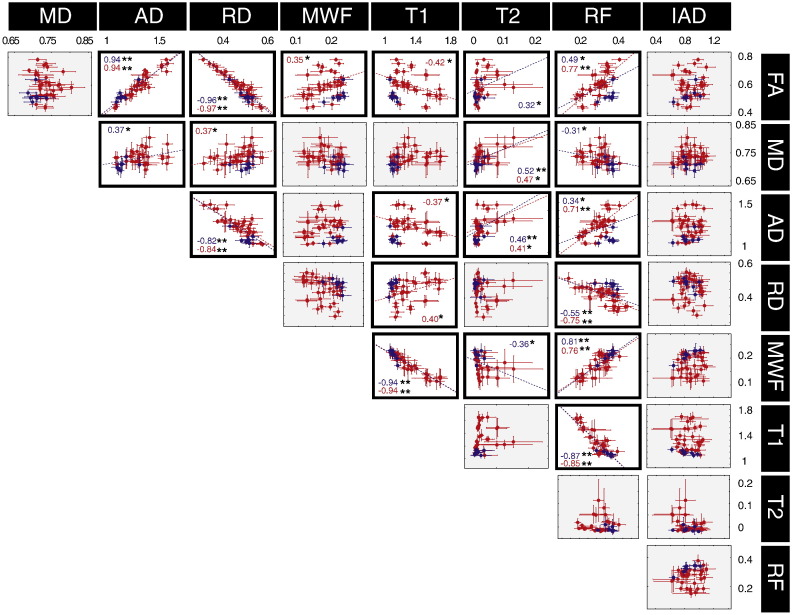
Fig. 6 shows the correlation between the different microstructural parameters. To disentangle the role of the architectural paradigm (i.e., the extent to which the presence of multiple fibre orientations within the voxel impacts on the microstructural parameters), the results are colour-coded according to the number of predominant orientations in the ROI, as obtained using the model parsimony testing framework described elsewhere (De Santis et al., in press). Hence, red indicates a single fibre population (SFP), blue indicates multiple fibre populations (MFP).
Fig. 6.
Correlation between the different microstructural metrics. Grey boxes indicates non-significant correlation. One asterisk indicates p < 0.05 while two asterisks indicate p < 0.001. The correlations are calculated on 42 ROIs obtained from the intersection of the FA-derived skeleton from the tract-based spatial statistics pipeline. Each dot is colour-coded according to the number of predominant orientations in the ROI: red indicates a single fibre orientation; blue indicates more than one predominant orientations.
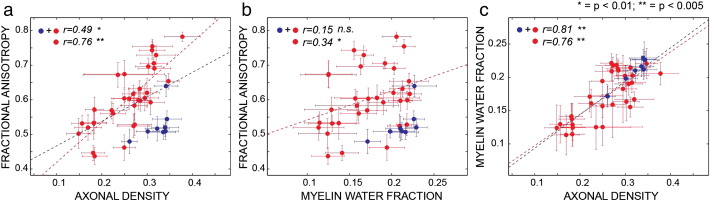
In some cases, the extent to which two metrics were significantly correlated (p < 0.05) depended on whether there was a single fibre configuration or a more complex architectural paradigm. The following pairs of metrics were only significantly correlated in SFP configurations: FA/MWF, FA/T1, MD/RD, AD/T1. In contrast, the following pairs of metrics were correlated at the p < 0.05 level irrespective of whether the voxels contains SFP or MFP configurations: FA/AD, FA/RD, FA/RF, MD/T2, AD/RD, AD/T2, AD/RF, RD/RF, MWF/T1, MWF/RF, T1/RF. In some pairs belonging to the second group, the fibre configuration still has an impact on the strength of the correlation, i.e., the correlation between FA/RF and AD/RF becomes highly significant (p < 0.001) when only SFP regions are considered. In order to highlight the crucial results of the present study, the correlations between FA, RF and MWF are also reported in Fig. 7.
Fig. 7.
Correlation between FA and RF (panel a), FA and MWF (panel b), FR and MWF (panel c) (zoom of three elements of the matrix in Fig. 6). One asterisk indicates p < 0.05 while two asterisks indicate p < 0.001. The results are colour-coded according to the number of predominant orientations in the ROI: red indicates a single fibre orientation; blue indicates more than one predominant orientations.
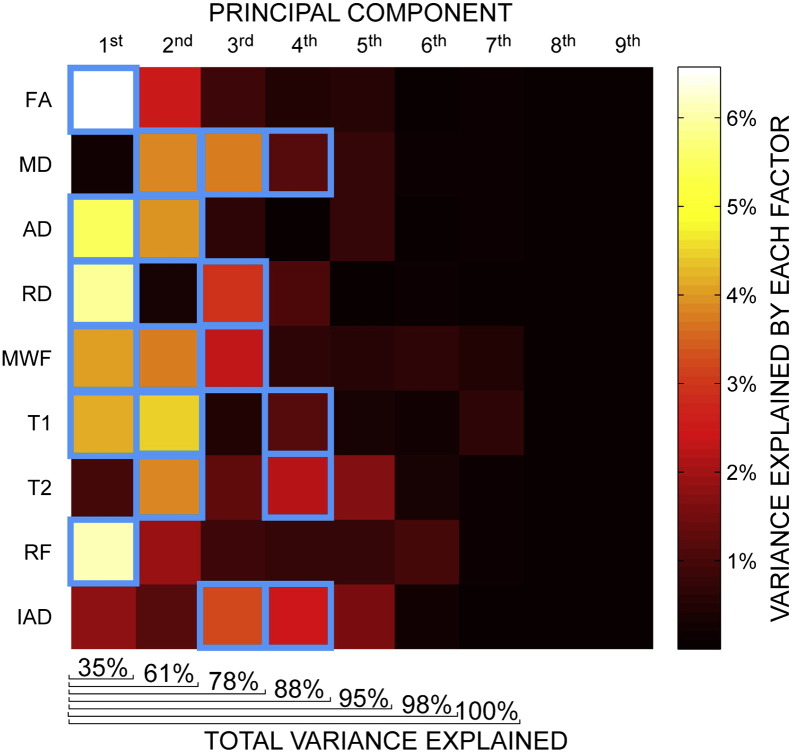
A PCA was used to analyse the contribution of each metric to the inter-subject variability (Fig. 8). The principal component (PC) that explains the largest part of the variability comprises mostly FA, RF and RD. The largest contribution to the second PC is given by T1 while diffusivity measurements (MD and IAD) play a role in the third PC.
Fig. 8.
Principal component analysis of the inter-subject variability in different microstructural indices. Columns represent the principal components while rows correspond to the factor loadings of the different microstructural indices. Blue squares indicate that the factor contributes to the variability more than it would if each factor had equal weight.
Fig. 9 shows the sample size needed to obtain a statistical power of 0.9 at a relative effect size of 10%. The cingulum and the uncinate fasciculus are the tracts that require more subjects to detect subtle difference between means. Amongst the microstructural parameters, MD and T1 are the ones that require the smallest sample size. FA, T2, RF and IAD require the largest sample size. MWF requires variable sample sizes, depending on the specific tracts: the arcuate fasciculus and the inferior longitudinal fasciculus need much less subjects than the others to detect the same effect size. Table 2 reports the contribution of imaging and post-processing noise to the total variance. This allows one to use previously reported findings (Szczepankiewicz et al., 2013) to generalise the sample size to arbitrary experimental setups.
Fig. 9.
Tract-averaged sample size needed to obtain a statistical power of 0.9 at a relative effect size of 10%.
Table 2.
Noise variance (NV) of the micro structural indices calculated using a residual bootstrap approach. MD, AD, RD and IAD are expressed in units of 10− 3 mm2/s. T1 and T2 are expressed in ms.
| NV | |
|---|---|
| FA | 0.08 |
| MD | 0.02 |
| AD | 0.03 |
| RD | 0.09 |
| MWF | 0.02 |
| T1 | 87 |
| T2 | 4 |
| FR | 0.02 |
| IAD | 0.15 |
Discussion
In this paper, we report the first atlas of WM microstructure in standard space that includes not just DT-MRI indices, but also the axonal density, intra-axonal diffusivity, myelin water fraction and the number of fibre populations within the voxel to reach the comprehensive assessment of WM microstructure that characterises the Tractometry philosophy (Bells et al., 2011a). The atlas comprises mean and standard deviation of the microstructural indices for the major association, projection and commissural pathways, and their asymmetry profiles along each tract.
Despite the fact that all metrics were corrected for partial volume contamination, the fornix still shows a significant degree of contamination from cerebro-spinal fluid for all the DT-MRI and the mcDESPOT-derived indices, but not so for the CHARMED parameters, suggesting that partial volume effects are encapsulated in the hindered part of the multi-compartment fit, while the results for the restricted compartments reflect true axonal features.
We investigate variance and covariance of the multivariate data to study correlations between the microstructural measures and find the parameters that account for the largest variance. To prove the robustness of the approach, the correlation analysis was not only performed within the whole brain skeleton, but also repeated within the entire WM volume as defined and parcelled by Mori et al. (2008), showing similar results (data not shown). The correlation analysis gives insight about the influence of the fibre architectural paradigm on the measured biomarkers. While FA is clearly dependent on the number of main fibre orientations in the voxel (Budde and Annese, 2013; Pierpaoli and Basser, 1996), so that fibre dispersion lowers the FA, the restricted fraction (RF) shows independence, and hence provides a more direct measure of interesting microstructural properties. The correlation between FA and RF is higher when only SFP regions are considered (r = 0.49, p < 0.05 versus r = 0.77, p < 0.001), while regions characterised by fibre dispersion cluster in the high-AD/low-FA area of the plot. Accounting for the number of fibre populations also allows better interpretation of the correlation between FA and MWF, which is significant when only single fibre population regions are selected (r = 0.35, p < 0.05). This is in agreement with, and helps explaining, previously published results. For example, Mädler et al. (2008) found some degree of linear correlation between DT-MRI and relaxometry measures in structure characterised by coherent fibre orientation, but reported deviation from linearity in disorganised bundles characterised by multiple fibre crossings.
Interestingly, the radial diffusivity, which is often considered as an index of myelination (Janve et al., 2013; Song et al., 2005), did not correlate significantly with MWF. This lack of correlation in the human datasets reported here may be explained by the architectural paradigm, as most of the previous studies linking the radial diffusivity with myelination were performed in the rodent models, where the white matter follows a simple architectural paradigm, or in very homogeneous fibre systems. The fact that FA correlates well with MWF (which has previously been validated against histological markers of myelin) only when SFP configurations are considered is an extremely important result for interpreting previous studies. If it were the case that cognition/symptomatology were dependent on myelination, then our ability to detect changes (or individual differences) in myelin, using FA, would be highly dependent on the local fibre architecture. Correlations will be most likely found in the simplest fibre architectures, and less so in complex fibre arrangements. This potential source of heterogeneity in the ability to detect differences in FA, or in the ability to detect correlations with FA, is not discussed in literature. RF has the highest correlation with MWF for both single and multiple fibre populations (r = 0.76, p < 0.001 for SFP and r = 0.81, p < 0.001 for all the regions). There is no significant correlation between MD and IAD, nor between AD and IAD, but regions of high fibre dispersion have consistently lower MD/AD. RF is negatively correlated with MD (r = − 0.31, p < 0.05) and positively correlated with AD (r = 0.34, p < 0.05 and r = 0.71, p < 0.001 for SFP regions). IAD and RF are instead not correlated and ROIs with more than one fibre, characterised by high RF are spread homogeneously along the IAD axis. This suggests that IAD may be a more specific measure of axonal properties in that it does not depend on the density of axons, nor on their spatial arrangement. The lack of correlation between intra and extra-axonal diffusivities can be interpreted as evidence of the fact that, to assume that intra- and extra-axonal diffusivities are the same, one has to effectively assume that the axon is an empty cylinder placed inside an empty space, but this is clearly not the case. This outcome is in agreement with the kurtosis literature, that reported non-zero kurtosis values parallel to the fibres (Hui et al., 2008), most likely due to the intra-axonal diffusivity and extra-axonal diffusivity having different values, for example because of the presence of oligodendrocytes and other cells in the extra-axonal space.
Myelin content and T1, as well as myelin content and the relaxation rate R1 = 1/T1 (data not shown), are highly correlated. This is consistent with previous reports in the literature (Lee et al., 2012; Lutti et al., 2013).
Disentangling the different contributions to the measured diffusion properties is vital to increasing the specificity of diffusion MRI in health and disease. Advanced, multi-compartment models of the diffusion signal, such as the CHARMED model (Assaf et al., 2004) and multi-component relaxometry approaches (Deoni et al., 2008) used here have the ability to move beyond the limitations of the single tensor model and tease apart the architectural paradigm, by fitting more than one fibre population per voxel, and morphological parameters like the intra-axonal diffusivity and the axonal density. Both these parameters are independent of the local fibre architecture and not mutually correlated. Conversely, DT-MRI indices are both strongly dependent on the fibre architecture and mutually correlated, making it difficult to interpret a change in the measured values over time, or a difference between groups (De Santis et al., in press).
While there is almost certainly a strong reporting bias in the literature, in that negative results are less frequently reported (Rosenthal, 1979), a point that needs to be addressed is why DT-MRI metrics such as FA have proven to be so useful in separating diseased from healthy brains, or explaining individual differences in brain function, despite our findings here about the general lack of correlation with more specific microstructural indices of WM subcomponents. It is clear from Fig. 7 that in cases where there is a single fibre population, then FA (for example) does a reasonable job of indexing axonal density (r = 0.77, p < 0.001), and provides moderate correlation with myelination metrics (r = 0.35, p < 0.05). If investigators happen to study a cognitive process that relies on a pathway that contains predominantly a single fibre population, or a disease happens to have foci in areas where there are substantial portions of the tract for which voxels contain just a single fibre population, then modulations to axonal density and/or myelination could well be detected with DT-MRI-based metrics. This could explain the reported utility of DT-MRI to date. However, on the flip-side, the prevalence of multiple fibre populations within a voxel is very high, with estimates as large as 90% of voxels (Jeurissen et al., 2012) which, on the basis of the present findings, clearly presents a problem for wide-spread use of DT-MRI metrics.
A strong correlation between indices of myelination (myelin water fraction) and axon density (restricted volume fraction) suggests that these measures are closely linked and is in agreement with previous findings (Takahashi et al., 2002). Crucially, as seen in Fig. 7, the correlation between the axon density and myelin water fraction is rather insensitive to whether there is a single fibre population or whether there is a more complex configuration. Several studies have suggested that conduction is optimized when the ratio of the inner to outer diameter of the axon, also referred to as the g-ratio, is fixed (at around 0.6) (Paus and Toro, 2009; Rushton, 1951), implying that axon and myelin characteristics should be strongly correlated. The CHARMED model assumes a fixed distribution of the axonal diameter for the whole white matter, but variability exists amongst different brain areas (Alexander et al., 2010). The axonal diameter is expected to play a role in modulating FA, but simulations show that its contribution is only marginal, given the range of axonal radii commonly found in human white matter (Dell'acqua et al., 2012; Ford et al., 1998).
The correlation analysis was also repeated within each tract (data not shown), confirming that in areas of predominantly coherent fibre orientation DT-MRI indices and CHARMED both correlate with the myelin content.
Principal component analysis indicates that the metrics that account for the largest variability in the data are those proportional to the amount of restricted signal like FA, RD and RF. The longitudinal relaxation time, proportional to the myelin content in WM, is important in determining the second PC while the metrics proportional to the magnitude of the diffusivity (MD and IAD) affect the third component. When very limited experimental time is available, and when there is no a priori information about the microstructural index that is sensitive to the investigated condition, this analysis suggests that FA or RF should be prioritized, as these metrics determine the first PC that alone accounts for over one third of the total variability.
Finally, we infer the sample size needed to detect differences between groups, in order to ensure that future studies are sufficiently powered to detect effects robustly. Different WM tracts are characterised by specific patterns of microstructure, and they also require different sample sizes when looking for differences between two groups, as shown in Fig. 5. The results, in agreement with Szczepankiewicz et al. (2013), clearly indicate that despite the lack of specificity of DT-MRI derived indices, DT-MRI requires smaller sample sizes than the other more advanced metrics, and may therefore be the best choice for clinics, at least when the investigator is only interested in detecting the effect. On the other hand, the same biological phenomena can have different effect sizes depending on the indices with which the effect is measured: e.g., tissue changes arising during short term neuro-plasticity produce a 1.5% change in MD and a 5% change in RF (Tavor et al., 2013). Such considerations are important and help in the debate over current (and future) utility of non-tensor metrics in the clinic. The calculation of the sample size presented in this work is clearly dependent on the SNR of the experimental setup used, but can be easily expended by accounting for different setups using the formula calculated by Szczepankiewicz et al. (2013).
Conclusions
In summary, we have constructed an atlas of key white matter pathways in standard space, reporting mean and standard deviations of tissue microstructural indices. By analysing statistical properties of the WM metrics, we draw the following conclusions:
-
1)
multi-compartment models provide more specific measures of axonal properties that are far less dependent on the architectural paradigm than DT-MRI-based metrics
-
2)
the correlation between myelin and diffusion metric is better explained when accounting for the presence of multiple fibres within a voxel
-
3)
the metrics that account for the largest variability in the data are those proportional to the amount of restriction within the voxel, and may be preferred when very limited scan time is available
-
4)
on the other hand, if the investigator is only interested in detecting the effect, MD is the metric that needs the smallest sample size to successfully detect differences between groups.
Acknowledgments
The authors wish to thank Tim Vivian-Griffiths and Marloes Jansen for acquiring the data, Sean Deoni and Ofer Pasternak for sharing the code to analyse the data and all the members of the CONNECT consortium. This work was funded by the EU-FP7 FET programme of the European Commission which supported the CONNECT consortium. This work was also founded by the Wellcome Trust through a Sir Henry Wellcome Postdoctoral Fellowship (to SDS) and a New Investigator Award (to DKJ).
Footnotes
This is an open-access article distributed under the terms of the Creative Commons Attribution-NonCommercial-No Derivative Works License, which permits non-commercial use, distribution, and reproduction in any medium, provided the original author and source are credited.
References
- Alexander D.C., Hubbard P.L., Hall M.G., Moore E.A., Ptito M., Parker G.J.M., Dyrby T.B. Orientationally invariant indices of axon diameter and density from diffusion MRI. Neuroimage. 2010;52(4):1374–1389. doi: 10.1016/j.neuroimage.2010.05.043. [DOI] [PubMed] [Google Scholar]
- Assaf Y., Basser P.J. Composite hindered and restricted model of diffusion (CHARMED) MR imaging of the human brain. Neuroimage. 2005;27(1):48–58. doi: 10.1016/j.neuroimage.2005.03.042. [DOI] [PubMed] [Google Scholar]
- Assaf Y., Pasternak O. Diffusion tensor imaging (DTI)-based white matter mapping in brain research: a review. J. Mol. Neurosci. 2008;34(1):51–61. doi: 10.1007/s12031-007-0029-0. [DOI] [PubMed] [Google Scholar]
- Assaf Y., Freidlin R.Z., Rohde G.K., Basser P.J. New modeling and experimental framework to characterize hindered and restricted water diffusion in brain white matter. Magn. Reson. Med. 2004;52(5):965–978. doi: 10.1002/mrm.20274. [DOI] [PubMed] [Google Scholar]
- Basser P.J. Inferring microstructural features and the physiological state of tissues from diffusion-weighted images. NMR Biomed. 1995;8(7-8):333–344. doi: 10.1002/nbm.1940080707. [DOI] [PubMed] [Google Scholar]
- Basser P.J., Pierpaoli C. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. J. Magn. Reson. B. 1996;111(3):209–219. doi: 10.1006/jmrb.1996.0086. [DOI] [PubMed] [Google Scholar]
- Basser P.J., Mattiello J., LeBihan D. Estimation of the effective self-diffusion tensor from the NMR spin echo. J. Magn. Reson. B. 1994;103(3):247–254. doi: 10.1006/jmrb.1994.1037. [DOI] [PubMed] [Google Scholar]
- Beaulieu C. The basis of anisotropic water diffusion in the nervous system —a technical review. NMR Biomed. 2002;15(7-8):435–455. doi: 10.1002/nbm.782. [DOI] [PubMed] [Google Scholar]
- Bells S., Cercignani M., Deoni S., Assaf Y., Pasternak O., Evans C.J., Leemans A., Jones D.K. Proc. Int. Soc. Magn. Res. Med. 2011. Tractometry: comprehensive multi-modal quantitative assessment of white matter along specific tracts. [Google Scholar]
- Bells S., Deoni S., Pasternak O., Jones D. Proc ISMRM 19th Annual Meeting, Montreal. 2011. Partial volume corrections of myelin water fraction values. [Google Scholar]
- Ben-Amitay S., Jones D.K., Assaf Y. Motion correction and registration of high b-value diffusion weighted images. Magn. Reson. Med. 2012;67(6):1694–1702. doi: 10.1002/mrm.23186. [DOI] [PubMed] [Google Scholar]
- Budde M.D., Annese J. Quantification of anisotropy and fiber orientation in human brain histological sections. Front. Integr. Neurosci. 2013;7:3. doi: 10.3389/fnint.2013.00003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catani M., Howard R.J., Pajevic S., Jones D.K. Virtual in vivo interactive dissection of white matter fasciculi in the human brain. Neuroimage. 2002;17(1):77–94. doi: 10.1006/nimg.2002.1136. [DOI] [PubMed] [Google Scholar]
- Cercignani M., Alexander D.C. Optimal acquisition schemes for in vivo quantitative magnetization transfer MRI. Magn. Reson. Med. 2006;56:803–810. doi: 10.1002/mrm.21003. [DOI] [PubMed] [Google Scholar]
- De Santis S., Assaf Y., Jones D.K. Using the biophysical charmed model to elucidate the underpinnings of contrast in diffusional kurtosis analysis of diffusion-weighted MRI. MAGMA. 2012;25(4):267–276. doi: 10.1007/s10334-011-0292-5. [DOI] [PubMed] [Google Scholar]
- De Santis S., Assaf Y., Evans C., Jones D.K. Improved precision in charmed assessment of white matter through sampling scheme optimisation and model parsimony testing. Magn. Res. Med. 2013 doi: 10.1002/mrm.24717. (Epub ahead of print) (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dell'acqua F., Simmons A., Williams S.C.R., Catani M. Can spherical deconvolution provide more information than fiber orientations? Hindrance modulated orientational anisotropy, a true-tract specific index to characterize white matter diffusion. Hum. Brain Mapp. 2012 doi: 10.1002/hbm.22080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deoni S.C.L. Correction of main and transmit magnetic field (B0 and B1) inhomogeneity effects in multicomponent-driven equilibrium single-pulse observation of T1 and T2. Magn. Reson. Med. 2011;65(4):1021–1035. doi: 10.1002/mrm.22685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deoni S.C.L., Rutt B.K., Arun T., Pierpaoli C., Jones D.K. Gleaning multicomponent T1 and T2 information from steady-state imaging data. Magn. Reson. Med. 2008;60(6):1372–1387. doi: 10.1002/mrm.21704. [DOI] [PubMed] [Google Scholar]
- Ford J.C., Hackney D.B., Lavi E., Phillips M., Patel U. Dependence of apparent diffusion coefficients on axonal spacing, membrane permeability, and diffusion time in spinal cord white matter. J. Magn. Reson. Imaging. 1998;8(4):775–782. doi: 10.1002/jmri.1880080405. [DOI] [PubMed] [Google Scholar]
- Hui E.S., Cheung M.M., Qi L., Wu E.X. Towards better MR characterization of neural tissues using directional diffusion kurtosis analysis. Neuroimage. 2008;42:122–134. doi: 10.1016/j.neuroimage.2008.04.237. [DOI] [PubMed] [Google Scholar]
- Hüppi P.S., Maier S.E., Peled S., Zientara G.P., Barnes P.D., Jolesz F.A., Volpe J.J. Microstructural development of human newborn cerebral white matter assessed in vivo by diffusion tensor magnetic resonance imaging. Pediatr. Res. 1998;44(4):584–590. doi: 10.1203/00006450-199810000-00019. [DOI] [PubMed] [Google Scholar]
- Janve V.A., Zu Z., Yao S.Y., Li K., Zhang F.L., Wilson K.J., Ou X., Does M.D., Subramaniam S., Gochberg D.F. The radial diffusivity and magnetization transfer pool size ratio are sensitive markers for demyelination in a rat model of type III multiple sclerosis (MS) lesions. Neuroimage. 2013;74:298–305. doi: 10.1016/j.neuroimage.2013.02.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkinson M., Smith S. A global optimisation method for robust affine registration of brain images. Med. Image Anal. 2001;5(2):143–156. doi: 10.1016/s1361-8415(01)00036-6. [DOI] [PubMed] [Google Scholar]
- Jenkinson M., Beckmann C.F., Behrens T.E.J., Woolrich M.W., Smith S.M. FSL. Neuroimage. 2012;62(2):782–790. doi: 10.1016/j.neuroimage.2011.09.015. (URL: http://dx.doi.org/.015, doi:015) [DOI] [PubMed] [Google Scholar]
- Jeurissen B., Leemans A., Tournier J.D., Jones D.K., Sijbers J. Investigating the prevalence of complex fiber configurations in white matter tissue with diffusion magnetic resonance imaging. Hum. Brain Mapp. 2012 doi: 10.1002/hbm.22099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones D.K., Horsfield M.A., Simmons A. Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magn. Reson. Med. 1999;42(3):515–525. [PubMed] [Google Scholar]
- Jones D.K., Catani M., Pierpaoli C., Reeves S.J., Shergill S.S., O'Sullivan M., Maguire P., Horsfield M.A., Simmons A., Williams S.C.R., Howard R.J. A diffusion tensor magnetic resonance imaging study of frontal cortex connections in very-late-onset schizophrenia-like psychosis. Am J Geriatr Psychiatry. 2005;13(12):1092–1099. doi: 10.1176/appi.ajgp.13.12.1092. [DOI] [PubMed] [Google Scholar]
- Lee J., Shmueli K., Kang B.T., Yao B., Fukunaga M., van Gelderen P., Palumbo S., Bosetti F., Silva A.C., Duyn J.H. The contribution of myelin to magnetic susceptibility-weighted contrasts in high-field MRI of the brain. Neuroimage. 2012;59(4):3967–3975. doi: 10.1016/j.neuroimage.2011.10.076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leemans A., Jeurissen B., Sijbers J., Jones D. 17th Annual Meeting of Intl Soc Mag Reson Med. 2009. ExploreDTI: a graphical toolbox for processing, analyzing, and visualizing diffusion MR data. [Google Scholar]
- Lutti A., Dick F., Sereno M.I., Weiskopf N. Using high-resolution quantitative mapping of R1 as an index of cortical myelination. Neuroimage. 2013 doi: 10.1016/j.neuroimage.2013.06.005. [DOI] [PubMed] [Google Scholar]
- MacKay A., Whittall K., Adler J., Li D., Paty D., Graeb D. In vivo visualization of myelin water in brain by magnetic resonance. Magn. Reson. Med. 1994;31(6):673–677. doi: 10.1002/mrm.1910310614. [DOI] [PubMed] [Google Scholar]
- Mädler B., Drabycz S.A., Kolind S.H., Whittall K.P., MacKay A.L. Is diffusion anisotropy an accurate monitor of myelination? Correlation of multicomponent T2 relaxation and diffusion tensor anisotropy in human brain. Magn. Reson. Imaging. 2008;26(7):874–888. doi: 10.1016/j.mri.2008.01.047. [DOI] [PubMed] [Google Scholar]
- Maxwell S.E., Kelley K., Rausch J.R. Sample size planning for statistical power and accuracy in parameter estimation. Annu. Rev. Psychol. 2008;59:537–563. doi: 10.1146/annurev.psych.59.103006.093735. [DOI] [PubMed] [Google Scholar]
- Mehta R.C., Pike G.B., Enzmann D.R. Magnetization transfer magnetic resonance imaging: a clinical review. Top. Magn. Reson. Imaging. 1996;8(4):214–230. [PubMed] [Google Scholar]
- Mori S., Oishi K., Jiang H., Jiang L., Li X., Akhter K., Hua K., Faria A.V., Mahmood A., Woods R., Toga A.W., Pike G.B., Neto P.R., Evans A., Zhang J., Huang H., Miller M.I., van Zijl P., Mazziotta J. Stereotaxic white matter atlas based on diffusion tensor imaging in an ICBM template. Neuroimage. 2008;40(2):570–582. doi: 10.1016/j.neuroimage.2007.12.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neuman C.H. Spin echo of spins diffusing in a bounded medium. J. Chem. Phys. 1974;60:4508–4511. [Google Scholar]
- Pasternak O., Sochen N., Gur Y., Intrator N., Assaf Y. Free water elimination and mapping from diffusion MRI. Magn. Reson. Med. 2009;62(3):717–730. doi: 10.1002/mrm.22055. [DOI] [PubMed] [Google Scholar]
- Paus T., Toro R. Could sex differences in white matter be explained by g ratio? Front. Neuroanat. 2009;3:14. doi: 10.3389/neuro.05.014.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfefferbaum A., Sullivan E.V., Hedehus M., Lim K.O., Adalsteinsson E., Moseley M. Age-related decline in brain white matter anisotropy measured with spatially corrected echo-planar diffusion tensor imaging. Magn. Reson. Med. 2000;44(2):259–268. doi: 10.1002/1522-2594(200008)44:2<259::aid-mrm13>3.0.co;2-6. [DOI] [PubMed] [Google Scholar]
- Pierpaoli C., Basser P.J. Toward a quantitative assessment of diffusion anisotropy. Magn. Reson. Med. 1996;36(6):893–906. doi: 10.1002/mrm.1910360612. [DOI] [PubMed] [Google Scholar]
- Pierpaoli C., Jezzard P., Basser P.J., Barnett A., Chiro G.D. Diffusion tensor MR imaging of the human brain. Radiology. 1996;201(3):637–648. doi: 10.1148/radiology.201.3.8939209. [DOI] [PubMed] [Google Scholar]
- Rosenthal r. Psychol. Bull. 1979;86(3):638–641. [Google Scholar]
- Rushton W.A. A theory of the effect of fibre size in medullated nerves. J. Physiol. 1951;115:101–122. doi: 10.1113/jphysiol.1951.sp004655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sled J.G., Levesque I., Santos A.C., Francis S.J., Narayanan S., Brass S.D., Arnold D.L., Pike G.B. Regional variations in normal brain shown by quantitative magnetization transfer imaging. Magn. Reson. Med. 2004;51(2):299–303. doi: 10.1002/mrm.10701. [DOI] [PubMed] [Google Scholar]
- Smith S.M., Jenkinson M., Johansen-Berg H., Rueckert D., Nichols T.E., Mackay C.E., Watkins K.E., Ciccarelli O., Cader M.Z., Matthews P.M., Behrens T.E.J. Tract-based spatial statistics: voxelwise analysis of multi-subject diffusion data. Neuroimage. 2006;31(4):1487–1505. doi: 10.1016/j.neuroimage.2006.02.024. [DOI] [PubMed] [Google Scholar]
- Song S.K., Yoshino J., Le T.Q., Lin S.J., Sun S.W., Cross A.H., Armstrong R.C. Demyelination increases radial diffusivity in corpus callosum of mouse brain. Neuroimage. 2005;26(1):132–140. doi: 10.1016/j.neuroimage.2005.01.028. [DOI] [PubMed] [Google Scholar]
- Szczepankiewicz F., Lätt J., Wirestam R., Leemans A., Sundgren P., van Westen D., Ståhlberg F., Nilsson M. Variability in diffusion kurtosis imaging: impact on study design, statistical power and interpretation. Neuroimage. 2013;76:145–154. doi: 10.1016/j.neuroimage.2013.02.078. [DOI] [PubMed] [Google Scholar]
- Takahashi M., Hackney D.B., Zhang G., Wehrli S.L., Wright A.C., O'Brien W.T., Uematsu H., Wehrli F.W., Selzer M.E. Magnetic resonance microimaging of intraaxonal water diffusion in live excised lamprey spinal cord. Proc. Natl. Acad. Sci. U. S. A. 2002;99(25):16192–16196. doi: 10.1073/pnas.252249999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tavor I., Hofstetter S., Assaf Y. Micro-structural assessment of short term plasticity dynamics. Neuroimage. 2013;81C:1–7. doi: 10.1016/j.neuroimage.2013.05.050. [DOI] [PubMed] [Google Scholar]
- Tournier J.D., Calamante F., Gadian D.G., Connelly A. Direct estimation of the fiber orientation density function from diffusion-weighted MRI data using spherical deconvolution. Neuroimage. 2004;23(3):1176–1185. doi: 10.1016/j.neuroimage.2004.07.037. [DOI] [PubMed] [Google Scholar]
- Ulmer J.L., Parsons L., Moseley M., Gabrieli J., editors. White Matter in Cognitive Neuroscience: Advances in Diffusion Tensor Imaging and Its Applications. 1st edition. Wiley-Blackwell; 2005. (December 23, 2005) [Google Scholar]