Skip to main content
PMC home page
Elsevier Sponsored Documents logoLink to Elsevier Sponsored Documents
. 2014 Apr 11;47(6):1465–1471. doi: 10.1016/j.jbiomech.2014.01.030

The influence of computational strategy on prediction of mechanical stress in carotid atherosclerotic plaques: Comparison of 2D structure-only, 3D structure-only, one-way and fully coupled fluid-structure interaction analyses

Yuan Huang a, Zhongzhao Teng a,b,⁎, Umar Sadat c, Martin J Graves a, Martin R Bennett d, Jonathan H Gillard a
PMCID: PMC3989027  PMID: 24529358

Abstract

Background

Compositional and morphological features of carotid atherosclerotic plaques provide complementary information to luminal stenosis in predicting clinical presentations. However, they alone cannot predict cerebrovascular risk. Mechanical stress within the plaque induced by cyclical changes in blood pressure has potential to assess plaque vulnerability. Various modeling strategies have been employed to predict stress, including 2D and 3D structure-only, 3D one-way and fully coupled fluid-structure interaction (FSI) simulations. However, differences in stress predictions using different strategies have not been assessed.

Methods

Maximum principal stress (Stress-P1) within 8 human carotid atherosclerotic plaques was calculated based on geometry reconstructed from in vivo computerized tomography and high resolution, multi-sequence magnetic resonance images. Stress-P1 within the diseased region predicted by 2D and 3D structure-only, and 3D one-way FSI simulations were compared to 3D fully coupled FSI analysis.

Results

Compared to 3D fully coupled FSI, 2D structure-only simulation significantly overestimated stress level (94.1 kPa [65.2, 117.3] vs. 85.5 kPa [64.4, 113.6]; median [inter-quartile range], p=0.0004). However, when slices around the bifurcation region were excluded, stresses predicted by 2D structure-only simulations showed a good correlation (R2=0.69) with values obtained from 3D fully coupled FSI analysis. 3D structure-only model produced a small yet statistically significant stress overestimation compared to 3D fully coupled FSI (86.8 kPa [66.3, 115.8] vs. 85.5 kPa [64.4, 113.6]; p<0.0001). In contrast, one-way FSI underestimated stress compared to 3D fully coupled FSI (78.8 kPa [61.1, 100.4] vs. 85.5 kPa [64.4, 113.7]; p<0.0001).

Conclusions

A 3D structure-only model seems to be a computationally inexpensive yet reasonably accurate approximation for stress within carotid atherosclerotic plaques with mild to moderate luminal stenosis as compared to fully coupled FSI analysis.

Keywords: Carotid, Atherosclerosis, Stroke, Mechanics, Stress

1. Introduction

Carotid atherosclerotic disease is responsible for 25–30% of all strokes (Levy et al., 2008). Currently, luminal stenosis is the only validated diagnostic criterion for risk stratification, but this criterion becomes less reliable in patients with mild to moderate stenoses that underlie the majority of clinical events (Barnett et al., 1998; Rothwell et al., 2003). A ‘vulnerable’ carotid atherosclerotic plaque (i.e. one likely to rupture and cause a stroke) is characterized by the presence of plaque hemorrhage (PH), a large lipid-rich necrotic core (LRNC), and fibrous cap (FC) rupture. These compositional and morphological features provide complementary information to luminal stenosis in predicting clinical presentations in both symptomatic (Altaf et al., 2008; Eliasziw et al., 1994; Sadat et al., 2010) and asymptomatic (Singh et al., 2009; Takaya et al., 2006) patients. However, although ~60% symptomatic patients exhibit PH or FC rupture at baseline (Gao et al., 2007; Milei et al., 2003), only about 15% will experience a recurrent event at 1 year (U-King-Im et al., 2009). It is thus clear that plaque composition detected by imaging alone cannot predict future cerebrovascular risk, and additional analyses or biomarkers are required.

Under physiological conditions, carotid plaques are subjected to mechanical loading from pulsatile blood pressure. FC rupture may occur when this loading exceeds its material strength. Indeed, plaques with high mechanical stress concentrations are associated with fissuring in both coronary (Richardson et al., 1989) and carotid (Sadat et al., 2010; Tang et al., 2009b) plaques. As a consequence, many studies have tried to predict mechanical stress within the plaque structure (Bluestein et al., 2008; Kiousis et al., 2009; Kock et al., 2008; Leach et al., 2010; Lee et al., 2004; Tang et al., 2004), and to assess its clinical significance (Gao et al., 2011; Sadat et al., 2011; Zhu et al., 2010). However, atherosclerotic plaques are multi-component structures with irregular geometries and highly non-linear material properties, and plaques undergo large deformations due to pulsatile blood pressure; it is therefore challenging to predict mechanical loading within the structure. Different computational strategies have been employed to examine plaque stress, including 2 dimensional (2D) structure-only (Kaazempur-Mofrad et al., 2003; Sadat et al., 2010; Tang et al., 2009a; Zhu et al., 2010), 2D longitudinal fluid-structure interaction (FSI) (Kock et al., 2008; Thrysoe et al., 2010), 3 dimensional (3D) structure-only (Kiousis et al., 2009; Teng et al., 2011), 3D one-way (Gao and Long, 2008; Gao et al., 2009) and fully coupled FSI (Bluestein et al., 2008; Leach et al., 2010; Tang et al., 2009b; Teng et al., 2013). However, differences in assessing mechanical stress within carotid atherosclerotic plaques using different computational strategies have not been comprehensively analyzed (Ohayon et al., 2005; Tang et al., 2009a, 2008; Yang et al., 2007). This study assessed maximum principal stress (Stress-P1) obtained from 4 commonly used strategies in patient-specific modeling, namely 2D structure-only, 3D structure-only, 3D one-way and fully coupled FSI analysis.

2. Material and methods

2.1. Data acquisition

Computerized tomography (CT) and electrocardiograph-gated, high-resolution, multi-sequence in vivo magnetic resonance (MR; Fig. 1) images were obtained from 8 patients with symptomatic carotid atherosclerotic disease. Patient demographic details are listed in Table 1. Images were acquired at Addenbrooke′s Hospital (a university teaching hospital), Cambridge, UK using a previously published protocol (Teng et al., 2013). The research study was approved by the Cambridge Regional Ethics Committee and patients gave written, informed consent. In brief, the following MR sequences were used: T1-weighted (repetition time/echo time: 1×RR/7.8 ms); Proton Density (PD)-weighted (repetition time/echo time: 2×RR/7.8 ms); T2-weighted (repetition time/echo time: 2×RR/85 ms); and short tau inversion recovery (STIR) (repetition time/echo time/inversion time: 2×RR/42 ms/150 ms); the field of view was 100×100 mm2 and matrix size 256×256. Multi-detector CT angiography acquisition was performed either on a 16 or 64-section multi-detector CT scanner (Siemens Somatom Sensation 16 or 64, Siemens Medical Solutions, Germany). Scanning started after a 25-s delay following non-ionic contrast administration of Iopamidol (Niopam 300; Bracco Diagnostics, Rome, Italy). CT parameters settings included: tube voltage 120 kV; tube current 220–256 mA; rotation time 0.33 s (64-section) or 0.5 s (16-section); 0.6/0.8 mm slice thickness with 0.3/0.4 mm increment; matrix 512×512; field of view 190–210 mm. Co-registration of CT and MR images was undertaken with reference to the carotid bifurcation, and considering the slice thickness (slice thickness of MRI was 3 mm and 0.6–0.8 mm for CT) and luminal shape. Plaque atherosclerotic components, including FC, lipid, calcium and PH were manually segmented using CMRTools (London, UK).

Fig. 1.

Fig. 1

Open in a new tab

Carotid atherosclerotic plaque images (72-year old, female). CT (upper panels), T1-weighted MR images (middle panels) and corresponding segmented contours (lower panels). (Red asterisk=lumen). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Table 1.

Patient demographic details (n=8).

n (%)/Mean±SD
Sex(Male) 5(62.5)
Age 64.4±10.6
Diastolic pressure(mmHg) 83.9±18.4
Systolic pressure(mmHg) 143.8±29.8
Heart rate(/minute) 72.5±10.4
Hypertension 5(62.5)
Atrial fibrillation 0(0)
Ischemic heart disease 2(25.0)
Diabetes 0(0)
High cholesterol 4(50.0)
Peripheral vascular disease 1(12.5)
Previous TIA/Stroke 3(37.5)
Aspirin used before recruitment 5(62.5)
ECST defined stenosis (%) 54.6±13.8
Open in a new tab

2.2. Plaque geometry reconstruction

Under physiological conditions, the plaque is pressurized and axially stretched. An appropriate computational starting shape needs to be determined to accurately predict stress distribution (de Putter et al., 2007; Huang et al., 2009). In this study, a patient-specific shrinkage procedure was employed to process the segmented plaque contour to obtain the computational starting shape both for 2D (Huang et al., 2011; Tang et al., 2009a) and 3D (Huang et al., 2009; Tang et al., 2009b) analyses. 2D slices were stacked together and axially interpolated using a cubic spline function to reconstruct the 3D plaque geometry. A component-fitting mesh generation technique was used to generate structured mesh for these models (Tang et al., 2009b). In brief, the 3D geometry was divided into many small six-face volumes and the entire structure was meshed using hexahedron elements to deal with models involving highly non-linear material properties and large deformation.

2.3. Finite element simulation

The arterial wall and all plaque components were assumed to be hyperelastic, isotropic, incompressible, and piecewise homogeneous. The modified Mooney–Rivlin formulation was used to describe the material property of each component,

W=c1(I1−3)+D1[exp(D2(I1−3))−1]

where I1 is the first strain invariant, and c1, D1 and D2 are material parameters from earlier studies (Yang et al., 2007): vessel material, c1=36.8 kPa, D1=14.4 kPa, D2=2; FC, c1=73.6 kPa, D1=28.8 kPa, D2=2.5; LRNC, c1=2 kPa, D1=2 kPa, D2=1.5; calcium, c1=368 kPa, D1=144 kPa, D2=2.0; loose matrix, c1=18.4 kPa, D1=7.2 kPa, D2=1.5; connective tissue, c1=29.4 kPa, D1=11.5 kPa, D2=1.5; fresh PH, c1=1 kPa, D1=1 kPa, D2=0.25 and chronic PH, c1=9 kPa, D1=9 kPa, D2=0.25.

The deformation of each atherosclerotic component was governed by the Cauchy momentum equation,

ρsU¨=∇⋅σ

where U is the displacement vector, σ is the stress tensor and ρs is the density of each component.

For both 2D and 3D structure-only models, a single data set of blood pressure waveform, which was scaled according to the diastolic and systolic pressures of each patient, was used to apply over the lumen contour/surface. In addition, the assumption of plane strain was used in 2D structure-only simulations.

In 3D FSI simulation, the blood flow was assumed to be laminar, Newtonian, viscous, and incompressible. A no-slip condition between fluid and the vessel wall was applied. The incompressible Navier–Stokes equations with an arbitrary Lagrangian–Eulerian formulation were used as the governing equation,

ρb∂v∂t+ρb[(v−vg)⋅∇]v=−∇p+μ∇2v

where v is the flow velocity, vg is the mesh velocity, p is the pressure, and μ and ρb stand for blood viscosity and density, respectively. For simplicity, constant material properties were used in this study, with μ=4×10−3 Pa s and ρb=1000 kg/m3. The loading condition for the fluid domain was

p|inlet=pin(t),p|outlet=pout(t),

with pressure waveforms shown in Fig. 2. In the one-way FSI simulation, the fluid model was solved first and the obtained pressure was then transferred to the solid domain as the external loading, and structural stress was calculated accordingly. There was no further iteration between the fluid and solid domains. In contrast, non-linear incremental iterative procedures were used to handle the interaction between these two domains in the fully coupled FSI analysis (Adina R & D Inc, 2009).

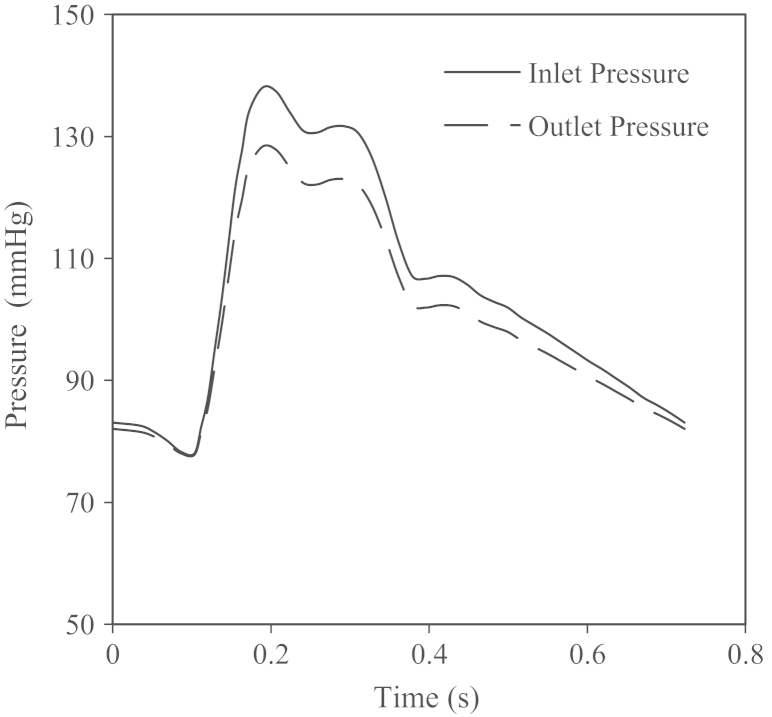
Fig. 2.

Fig. 2

Open in a new tab

Waveform of pressure at the inlet and outlet. Pressure conditions specified at the inlet and outlet as a function of time. For each patient, the waveform was scaled according to the pressure at diastole and systole.

For all types of models, the computational simulation was performed using the commercial finite element package ADINA8.6.1 (ADINA R&D Inc, USA) and 5% pre-axial stretch (Holzapfel et al., 2000, 2005) was applied for all 3D analyses. A connective region was added between the internal and external carotid arteries, which mimics the supporting tissue in human body and minimizes the bending effect caused by the pre-axial stretch.

2.4. Data analysis

Stress-P1 within the plaque structure was computed and its peak value over the diseased region was used for analysis. Data normality was assessed by Shapiro–Wilk test. A two-tailed paired t test was used for normally distributed data and a two-tailed Wilcoxon matched pair test for non-normal data. Data are presented as mean±standard deviation (SD) and median [inter-quartile range (IQR)], respectively. A significant difference was assumed if p<0.05.

3. Results

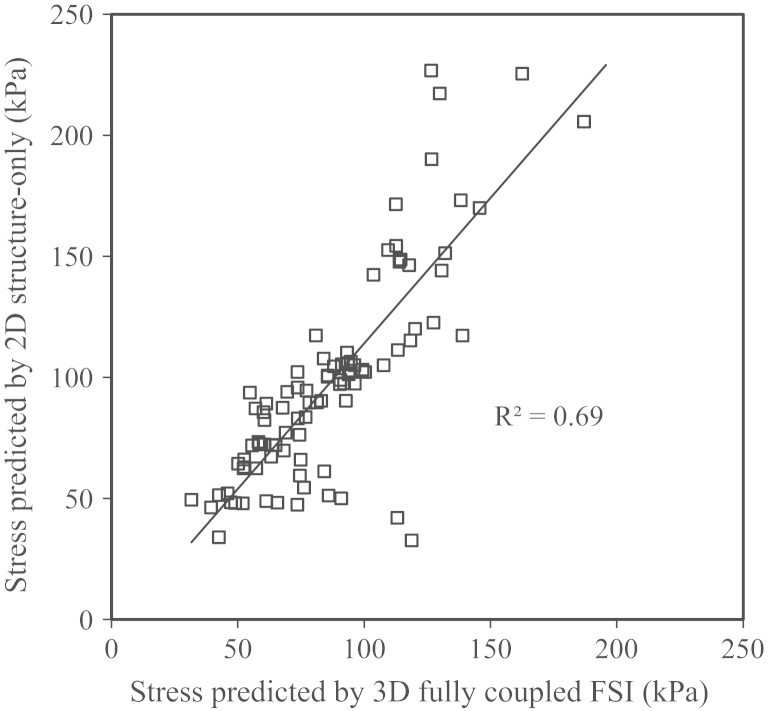
Results obtained were assessed against 3D fully coupled FSI as the gold standard. 2D structure-only simulations resulted in a significant stress overestimation (94.1 kPa [65.2, 117.3] vs. 85.5 kPa [64.4, 113.6], p=0.0004) with wide scattering near the bifurcation region (Figs. 3 and 4a). If results obtained from slices around the bifurcation region were excluded, stress predicted by 2D structure-only simulations showed a good correlation (R2=0.69) with the value obtained from 3D fully coupled FSI analyses (Fig. 5).

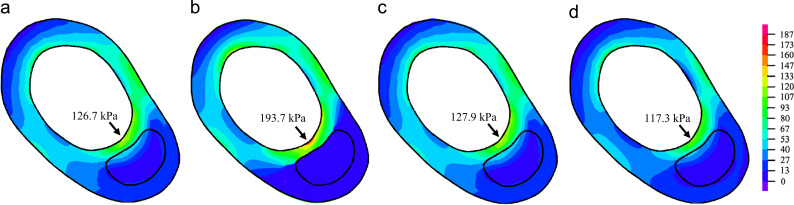
Fig. 3.

Fig. 3

Open in a new tab

Comparison of plaque wall stress on a transverse slice. Stress-P1 predicted by 3D fully coupled FSI (a), 2D structure-only (b), 3D one-way FSI (c) and 3D structure-only (d) models. Unit: kPa.

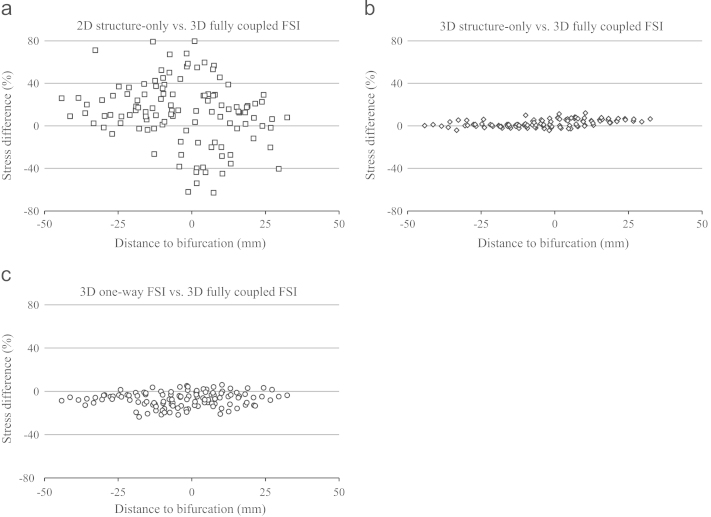
Fig. 4.

Fig. 4

Open in a new tab

Comparison of stresses. Bland-Altman plots comparing stress predicted by various modeling strategies with 3D fully coupled FSI models for (a) 2D structure-only, (b) 3D structure-only or (c) 3D one-way FSI. The vertical axes show the percentage error and the horizontal axes show the slice position to the bifurcation.

Fig. 5.

Fig. 5

Open in a new tab

Stress correlation. Correlation between stresses predicted by 2D structure-only and 3D fully coupled FSI models.

The 3D models, including 3D structure-only, one-way FSI and fully coupled FSI analysis demonstrated a good qualitative agreement in predicting stress within the plaque structure (Fig. 4b and c). The 3D structure-only model produced a small yet statistically significant overestimation of stress levels (86.8 kPa [66.3, 115.8] vs. 85.5 kPa [64.4, 113.6], p<0.0001 (Fig. 4b)). In contrast, one-way FSI underestimated stress levels (78.8 kPa [61.1, 100.4] vs. 85.5 kPa [64.4, 113.7], p<0.0001 (Fig. 4c)).

4. Discussion

The numerical accuracy and reliability of fully coupled FSI analysis have been previously demonstrated and validated, showing good agreement with both analytical solutions (Huang, 2009) and experimental data (Tang et al., 2003). Therefore, results obtained from fully coupled FSI models were used as the gold standard for the assessment of other numerical approaches.

In this study, we found a large difference (24.3% [11.9%, 41.4%]) in stress predicted by 2D models compared to 3D fully coupled FSI models. Moreover, the location predicted by the 2D model where high stress concentrations appeared was different from that predicted by 3D models. Our findings are consistent with those by Ohayon et al. (2005) based on one patient data set, who found that 2D structure-only orthotropic elastic models failed to predict the location of rupture accurately, whilst the 3D model showed much better agreement. These investigators also found that the 2D simulations overestimated peak wall stress by over 70% compared to the 3D model (Ohayon et al., 2005). A similar phenomenon was observed by Tang et al. (2009a, 2008) from two carotid plaques, who found a similar pattern of stress distribution between 2D structure-only and 3D fully coupled FSI models (Tang et al. 2009a, 2008), despite 3D FSI demonstrating a much higher stress throughout the structure (Tang et al., 2008). In contrast, in a different study the same authors found that 2D structure-only models overestimated stress around the luminal region (Huang et al., 2009). In addition to the overall overestimation, we also found that 2D structure-only models had a wider scatter of prediction error near the bifurcation region (Fig. 4a). When results in the bifurcation region were excluded, the stress predicted by 2D models had a good correlation with 3D fully coupled FSI models (Fig. 5). The relatively poor performance of 2D structure-only models arose as a result of the over-simplification of the biomechanical scenario (Ohayon et al., 2005; Tang et al., 2008). Firstly, the lack of axial tissue bounding and support in 2D models could lead to unrealistic deformations, which further resulted in a scattered distribution (in most cases an overestimation due to large deformations) of stress level. Secondly, the assumption of plane strain would require the cross-sectional plane morphology to be very similar; so that strains in the third direction could be constrained by nearby material. However this assumption was often inappropriate and sometimes severely violated due to the plaque heterogeneity and axial curvature changes.

We found that 3D structure-only models demonstrated only a small albeit statistically significant difference (2.2% [0.7%, 5.7%]) of stress levels compared to 3D fully coupled models. Considering the much-reduced computational cost, this indicates that 3D structure-only models can provide a temporally efficient yet still accurate approximation of a fully coupled FSI. As shown in Fig. 4b, the agreement between 3D structure-only and fully coupled FSI was better in the proximal than the distal region, with a gradual change towards overestimation of critical stress (p<0.0001) proximal to distal. This reflects one of the major limitations of 3D structure-only models, which neglect the axial pressure drop throughout the artery. The pulsatile blood pressure, being the only loading applied to the 3D structure-only models, dominates the deformation and stress distributions within the plaque. Therefore, neglecting the axial pressure drop would over-inflate the structure and lead to the gradual overestimation of stress levels. As all plaques involved in this study demonstrated moderate degrees of luminal stenosis, the pressure gradient across these plaques was relatively small. However a significant pressure drop may occur across a plaque with severe stenosis (Yang et al., 2007) and 3D structure-only models may therefore lead to poor predictions under such circumstances.

One-way FSI can be regarded as a simplified method of a fully coupled FSI. Compared to 3D structure-only analysis, one-way FSI incorporates the flow information without performing iterations between the fluid and solid domains. However, one of the key underlying assumptions of one-way FSI is that the structural deformation should be nearly negligible. This assumption may be severely violated in analyses involving highly-deformable biological tissues, including atherosclerotic plaque. Fig. 6 compares the pressure at the boundary between fluid and solid domains at systole. It can be seen that the assumption of rigid wall in one-way FSI leads to a lower pressure profile in the majority of fluid domains. The arterial elasticity allows radial distension of the vessel, which reduces the resistance to flow according to Poiseuille′s Law. Moreover, the deformable conduit acts as a capacitor when subject to pulsatile flow, which also modifies the flow characteristics. Therefore, a rigid vessel model will overestimate the pressure drop of blood flow and hence underestimate the pressure profile. This pressure profile, used as the loading condition of structural simulation, consequently results in a difference of wall stress by 7.4% [3.6%, 14.3%] compared to 3D fully coupled FSI.

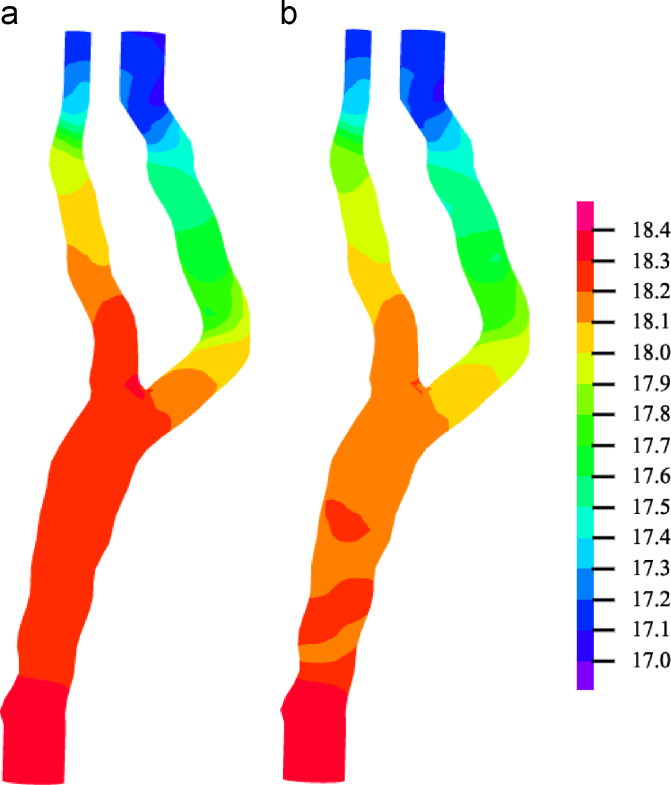
Fig. 6.

Fig. 6

Open in a new tab

Pressure in fluid domain. Comparison of predicted flow-induced pressure at the boundary between fluid and solid domains in (a) 3D fully coupled FSI and (b) 3D one-way FSI models at systole. Despite the same pressure-specified boundary condition, the 3D one-way FSI model showed a much faster pressure drop in the proximal region. Unit: kPa.

Despite the drawbacks of oversimplification of plane strain and absence of flow-induced pressure changes, 2D plaque models require minimal pre-processing from histological or imaging slices to numerical models. The technique is much easier to implement compared to 3D modeling, and has been used extensively in clinical atherosclerosis studies to identify the rupture site (Richardson et al., 1989), investigate high-risk features (Huang et al., 2001; Sadat et al., 2011), differentiate patient groups (Sadat et al., 2011) and correlate with biological activity (Howarth et al., 2007; Lee et al., 1996). As discussed previously, if 2D structure-only modeling is used, the bifurcation region should be excluded from the analysis. 3D structure-only models can be reconstructed from interpolation of a stack of delineated image slices (Nieuwstadt et al., 2013; Ohayon et al., 2005). Such models allow better description of plaque geometry and hence more reliable prediction of stress and strain. In addition, this technique does not require the assumption of plane strain, and anisotropic properties, such as fiber orientation, can be incorporated into the model (Gasser and Holzapfel, 2007). In reality, the deformable plaque and the internal pulsatile blood flow influence each other assembling a typical environment of FSI. Therefore, 3D fully coupled FSI is believed to be the most accurate modeling strategy for the assessment of plaque vulnerability. However, it should be emphasized that residual stress within the plaque structure could affect the stress level significantly (Ohayon et al., 2007); this has been ignored in most studies as it is not measureable using current non-invasive techniques.

In conclusion, four different modeling strategies (2D structure-only, 3D structure-only, 3D one-way and fully coupled FSI) were compared in patient-specific plaque models. 2D simulations yielded the poorest performance with a significant overestimation of plaque stress. 3D structural models showed good qualitative and quantitative agreement with the 3D fully coupled FSI, and are recommended as computationally inexpensive yet accurate approximations of fully coupled FSI analysis for plaques with mild to moderate stenoses.

Conflict of interest statement

None.

Acknowledgments

This research is supported by BHF PG/11/74/29100 and the NIHR Cambridge Biomedical Research Centre.

References

  1. Adina R & D Inc,2009. ADINA Theory and Modeling Guide. Vol III: ADINA CFD &FSI. Watertown.
  2. Altaf N., Daniels L., Morgan P.S., Auer D., MacSweeney S.T., Moody A.R., Gladman J.R. Detection of intraplaque hemorrhage by magnetic resonance imaging in symptomatic patients with mild to moderate carotid stenosis predicts recurrent neurological events. J. Vasc. Surg. 2008;47:337–342. doi: 10.1016/j.jvs.2007.09.064. [DOI] [PubMed] [Google Scholar]
  3. Barnett H.J., Taylor D.W., Eliasziw M., Fox A.J., Ferguson G.G., Haynes R.B., Rankin R.N., Clagett G.P., Hachinski V.C., Sackett D.L., Thorpe K.E., Meldrum H.E., Spence J.D. Benefit of carotid endarterectomy in patients with symptomatic moderate or severe stenosis. North American Symptomatic Carotid Endarterectomy Trial Collaborators. N. Engl. J. Med. 1998;339:1415–1425. doi: 10.1056/NEJM199811123392002. [DOI] [PubMed] [Google Scholar]
  4. Bluestein D., Alemu Y., Avrahami I., Gharib M., Dumont K., Ricotta J.J., Einav S. Influence of microcalcifications on vulnerable plaque mechanics using FSI modeling. J. Biomech. 2008;41:1111–1118. doi: 10.1016/j.jbiomech.2007.11.029. [DOI] [PubMed] [Google Scholar]
  5. de Putter S., Wolters B.J., Rutten M.C., Breeuwer M., Gerritsen F.A., van de Vosse F.N. Patient-specific initial wall stress in abdominal aortic aneurysms with a backward incremental method. J. Biomech. 2007;40:1081–1090. doi: 10.1016/j.jbiomech.2006.04.019. [DOI] [PubMed] [Google Scholar]
  6. Eliasziw M., Streifler J.Y., Fox A.J., Hachinski V.C., Ferguson G.G., Barnett H.J. Significance of plaque ulceration in symptomatic patients with high-grade carotid stenosis. North American Symptomatic Carotid Endarterectomy Trial. Stroke. 1994;25:304–308. doi: 10.1161/01.str.25.2.304. [DOI] [PubMed] [Google Scholar]
  7. Gao H., Long Q. Effects of varied lipid core volume and fibrous cap thickness on stress distribution in carotid arterial plaques. J. Biomech. 2008;41:3053–3059. doi: 10.1016/j.jbiomech.2008.07.011. [DOI] [PubMed] [Google Scholar]
  8. Gao H., Long Q., Graves M., Gillard J.H., Li Z.Y. Carotid arterial plaque stress analysis using fluid-structure interactive simulation based on in-vivo magnetic resonance images of four patients. J. Biomech. 2009;42:1416–1423. doi: 10.1016/j.jbiomech.2009.04.010. [DOI] [PubMed] [Google Scholar]
  9. Gao H., Long Q., Kumar Das S., Halls J., Graves M., Gillard J.H., Li Z.Y. Study of carotid arterial plaque stress for symptomatic and asymptomatic patients. J. Biomech. 2011;44:2551–2557. doi: 10.1016/j.jbiomech.2011.07.012. [DOI] [PubMed] [Google Scholar]
  10. Gao P., Chen Z.Q., Bao Y.H., Jiao L.Q., Ling F. Correlation between carotid intraplaque hemorrhage and clinical symptoms: systematic review of observational studies. Stroke. 2007;38:2382–2390. doi: 10.1161/STROKEAHA.107.482760. [DOI] [PubMed] [Google Scholar]
  11. Gasser T.C., Holzapfel G.A. Modeling plaque fissuring and dissection during balloon angioplasty intervention. Ann. Biomed. Eng. 2007;35:711–723. doi: 10.1007/s10439-007-9258-1. [DOI] [PubMed] [Google Scholar]
  12. Holzapfel G.A., Schulze-Bauer C.A.J., Stadler M. Vol AMD-242. American Society of Mechanical Engineers (ASME); New York: 2000. Mechanics of Angioplasty: Wall, Balloon and Stent. [Google Scholar]
  13. Holzapfel G.A., Sommer G., Gasser C.T., Regitnig P. Determination of layer-specific mechanical properties of human coronary arteries with nonatherosclerotic intimal thickening and related constitutive modeling. Am. J. Physiol. Heart Circ. Physiol. 2005;289:H2048–H2058. doi: 10.1152/ajpheart.00934.2004. [DOI] [PubMed] [Google Scholar]
  14. Howarth S., Li Z.Y., Trivedi R.A., Graves JM U.K.-I., Kirkpatrick M.J., Gillard J.H. P.J. Correlation of macrophage location and plaque stress distribution using USPIO-enhanced MRI in a patient with symptomatic severe carotid stenosis: a new insight into risk stratification. Br. J. Neurosurg. 2007;21:396–398. doi: 10.1080/02688690701400775. [DOI] [PubMed] [Google Scholar]
  15. Huang H. Department of Mathematical Science, Worcester Polytechnic Institute; Worcester, USA: 2009. In vivo MRI-Based Three-Dimensional Fluid-Structure Interaction Models and Mechanical Image Analysis for Human Carotid Atherosclerotic Plaques. [Google Scholar]
  16. Huang H., Virmani R., Younis H., Burke A.P., Kamm R.D., Lee R.T. The impact of calcification on the biomechanical stability of atherosclerotic plaques. Circulation. 2001;103:1051–1056. doi: 10.1161/01.cir.103.8.1051. [DOI] [PubMed] [Google Scholar]
  17. Huang X., Yang C., Yuan C., Liu F., Canton G., Zheng J., Woodard P.K., Sicard G.A., Tang D. Patient-specific artery shrinkage and 3D zero-stress state in multi-component 3D FSI models for carotid atherosclerotic plaques based on in vivo MRI data. Mol. Cell. Biomech. 2009;6:121–134. [PMC free article] [PubMed] [Google Scholar]
  18. Huang Y., Teng Z., Sadat U., Hilborne S., Young V.E., Graves M.J., Gillard J.H. Non-uniform shrinkage for obtaining computational start shape for in-vivo MRI-based plaque vulnerability assessment. J. Biomech. 2011;44:2316–2319. doi: 10.1016/j.jbiomech.2011.06.014. [DOI] [PubMed] [Google Scholar]
  19. Kaazempur-Mofrad M.P., Younis H.F., Patel S., Isasi A., Chung C., Chan R.C., Hinton D.P., Lee R.T., Kamm R.D. Cyclic strain in human carotid bifurcation and its potential correlation to atherogenesis: Idealized and anatomically-realistic models. J. Eng. Math. 2003;47:299–314. [Google Scholar]
  20. Kiousis D.E., Rubinigg S.F., Auer M., Holzapfel G.A. A methodology to analyze changes in lipid core and calcification onto fibrous cap vulnerability: the human atherosclerotic carotid bifurcation as an illustratory example. J. Biomech. Eng. 2009;131:121002. doi: 10.1115/1.4000078. [DOI] [PubMed] [Google Scholar]
  21. Kock S.A., Nygaard J.V., Eldrup N., Frund E.T., Klaerke A., Paaske W.P., Falk E., Yong Kim W. Mechanical stresses in carotid plaques using MRI-based fluid-structure interaction models. J. Biomech. 2008;41:1651–1658. doi: 10.1016/j.jbiomech.2008.03.019. [DOI] [PubMed] [Google Scholar]
  22. Leach J.R., Rayz V.L., Soares B., Wintermark M., Mofrad M.R., Saloner D. Carotid atheroma rupture observed in vivo and FSI-predicted stress distribution based on pre-rupture imaging. Ann. Biomed. Eng. 2010;38:2748–2765. doi: 10.1007/s10439-010-0004-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Lee K.W., Wood N.B., Xu X.Y. Ultrasound image-based computer model of a common carotid artery with a plaque. Med. Eng. Phys. 2004;26:823–840. doi: 10.1016/j.medengphy.2004.08.013. [DOI] [PubMed] [Google Scholar]
  24. Lee R.T., Schoen F.J., Loree H.M., Lark M.W., Libby P. Circumferential stress and matrix metalloproteinase 1 in human coronary atherosclerosis. Implications for plaque rupture. Arterioscler. Thromb. Vasc. Biol. 1996;16:1070–1073. doi: 10.1161/01.atv.16.8.1070. [DOI] [PubMed] [Google Scholar]
  25. Levy E.I., Mocco J., Samuelson R.M., Ecker R.D., Jahromi B.S., Hopkins L.N. Optimal treatment of carotid artery disease. J. Am. Coll. Cardiol. 2008;51:979–985. doi: 10.1016/j.jacc.2007.10.052. [DOI] [PubMed] [Google Scholar]
  26. Milei J., Parodi J.C., Ferreira M., Barrone A., Grana D.R., Matturri L. Atherosclerotic plaque rupture and intraplaque hemorrhage do not correlate with symptoms in carotid artery stenosis. J. Vasc. Surg. 2003;38:1241–1247. doi: 10.1016/s0741-5214(03)00910-8. [DOI] [PubMed] [Google Scholar]
  27. Nieuwstadt H.A., Akyildiz A.C., Speelman L., Virmani R., van der Lugt A., van der Steen A.F., Wentzel J.J., Gijsen F.J. The influence of axial image resolution on atherosclerotic plaque stress computations. J. Biomech. 2013;46:689–695. doi: 10.1016/j.jbiomech.2012.11.042. [DOI] [PubMed] [Google Scholar]
  28. Ohayon J., Dubreuil O., Tracqui P., Le Floc’h S., Rioufol G., Chalabreysse L., Thivolet F., Pettigrew R.I., Finet G. Influence of residual stress/strain on the biomechanical stability of vulnerable coronary plaques: potential impact for evaluating the risk of plaque rupture. Am. J. Physiol. Heart Circ. Physiol. 2007;293:H1987–H1996. doi: 10.1152/ajpheart.00018.2007. [DOI] [PubMed] [Google Scholar]
  29. Ohayon J., Finet G., Treyve F., Rioufol G., Dubreuil O. A three-dimensional finite element analysis of stress distribution in a coronary atherosclerotic plaque: in-vivo prediction of plaque rupture location. In: Payan Y., editor. Biomechanics Applied to Computer Assisted Surgery. 2005. pp. 225–241. [Google Scholar]
  30. Richardson P.D., Davies M.J., Born G.V. Influence of plaque configuration and stress distribution on fissuring of coronary atherosclerotic plaques. Lancet. 1989;2:941–944. doi: 10.1016/s0140-6736(89)90953-7. [DOI] [PubMed] [Google Scholar]
  31. Rothwell P.M., Eliasziw M., Gutnikov S.A., Fox A.J., Taylor D.W., Mayberg M.R., Warlow C.P., Barnett H.J. Analysis of pooled data from the randomised controlled trials of endarterectomy for symptomatic carotid stenosis. Lancet. 2003;361:107–116. doi: 10.1016/s0140-6736(03)12228-3. [DOI] [PubMed] [Google Scholar]
  32. Sadat U., Teng Z., Young V.E., Graves M.J., Gaunt M.E., Gillard J.H. High-resolution magnetic resonance imaging-based biomechanical stress analysis of carotid atheroma: a comparison of single transient ischaemic attack, recurrent transient ischaemic attacks, non-disabling stroke and asymptomatic patient groups. Eur. J. Vasc. Endovasc. Surg. 2011;41:83–90. doi: 10.1016/j.ejvs.2010.09.006. [DOI] [PubMed] [Google Scholar]
  33. Sadat U., Teng Z., Young V.E., Walsh S.R., Li Z.Y., Graves M.J., Varty K., Gillard J.H. Association between biomechanical structural stresses of atherosclerotic carotid plaques and subsequent ischaemic cerebrovascular events--a longitudinal in vivo magnetic resonance imaging-based finite element study. Eur. J. Vasc. Endovasc. Surg. 2010;40:485–491. doi: 10.1016/j.ejvs.2010.07.015. [DOI] [PubMed] [Google Scholar]
  34. Singh N., Moody A.R., Gladstone D.J., Leung G., Ravikumar R., Zhan J., Maggisano R. Moderate carotid artery stenosis: MR imaging-depicted intraplaque hemorrhage predicts risk of cerebrovascular ischemic events in asymptomatic men. Radiology. 2009;252:502–508. doi: 10.1148/radiol.2522080792. [DOI] [PubMed] [Google Scholar]
  35. Takaya N., Yuan C., Chu B., Saam T., Underhill H., Cai J., Tran N., Polissar N.L., Isaac C., Ferguson M.S., Garden G.A., Cramer S.C., Maravilla K.R., Hashimoto B., Hatsukami T.S. Association between carotid plaque characteristics and subsequent ischemic cerebrovascular events: a prospective assessment with MRI—initial results. Stroke. 2006;37:818–823. doi: 10.1161/01.STR.0000204638.91099.91. [DOI] [PubMed] [Google Scholar]
  36. Tang D., Teng Z., Canton G., Hatsukami T.S., Dong L., Huang X., Yuan C. Local critical stress correlates better than global maximum stress with plaque morphological features linked to atherosclerotic plaque vulnerability: an in vivo multi-patient study. Biomed. Eng. Online. 2009;8:15. doi: 10.1186/1475-925X-8-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Tang D., Teng Z., Canton G., Yang C., Ferguson M., Huang X., Zheng J., Woodard P.K., Yuan C. Sites of rupture in human atherosclerotic carotid plaques are associated with high structural stresses: an in vivo MRI-based 3D fluid-structure interaction study. Stroke. 2009;40:3258–3263. doi: 10.1161/STROKEAHA.109.558676. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Tang D., Yang C., Kobayashi S., Zheng J., Vito R.P. Effect of stenosis asymmetry on blood flow and artery compression: a three-dimensional fluid-structure interaction model. Ann. Biomed. Eng. 2003;31:1182–1193. doi: 10.1114/1.1615577. [DOI] [PubMed] [Google Scholar]
  39. Tang D., Yang C., Mondal S., Liu F., Canton G., Hatsukami T.S., Yuan C. A negative correlation between human carotid atherosclerotic plaque progression and plaque wall stress: in vivo MRI-based 2D/3D FSI models. J. Biomech. 2008;41:727–736. doi: 10.1016/j.jbiomech.2007.11.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Tang D., Yang C., Zheng J., Woodard P.K., Sicard G.A., Saffitz J.E., Yuan C. 3D MRI-based multicomponent FSI models for atherosclerotic plaques. Ann. Biomed. Eng. 2004;32:947–960. doi: 10.1023/b:abme.0000032457.10191.e0. [DOI] [PubMed] [Google Scholar]
  41. Teng Z., He J., Sadat U., Mercer J., Wang X., Bahaei N., Thomas O., Gillard J. How does juxtaluminal calcium affect critical mechanical conditions in carotid atherosclerotic plaque? an exploratory study. IEEE. Trans. Biomed. Eng. 2013 doi: 10.1109/TBME.2013.2275078. [DOI] [PubMed] [Google Scholar]
  42. Teng Z., Sadat U., Huang Y., Young V.E., Graves M.J., Lu J., Gillard J.H. In vivo MRI-based 3D mechanical stress-strain profiles of carotid plaques with juxtaluminal plaque haemorrhage: an exploratory study for the mechanism of subsequent cerebrovascular events. Eur. J. Vasc. Endovasc. Surg. 2011;42:427–433. doi: 10.1016/j.ejvs.2011.05.009. [DOI] [PubMed] [Google Scholar]
  43. Thrysoe S.A., Oikawa M., Yuan C., Eldrup N., Klaerke A., Paaske W.P., Falk E., Kim W.Y., Nygaard J.V. Longitudinal distribution of mechanical stresses in carotid plaques of symptomatic patients. Stroke. 2010;41:1041–1043. doi: 10.1161/STROKEAHA.109.571588. [DOI] [PubMed] [Google Scholar]
  44. U-King-Im J.M., Young V., Gillard J.H. Carotid-artery imaging in the diagnosis and management of patients at risk of stroke. Lancet Neurol. 2009;8:569–580. doi: 10.1016/S1474-4422(09)70092-4. [DOI] [PubMed] [Google Scholar]
  45. Yang C., Tang D., Yuan C., Hatsukami T.S., Zheng J., Woodard P.K. In vivo/ex vivo MRI-based 3D non-newtonian FSI models for human atherosclerotic plaques compared with fluid/wall-only models. Comput. Model. Eng. Sci. 2007;19:233–246. [PMC free article] [PubMed] [Google Scholar]
  46. Zhu C., Teng Z., Sadat U., Young V.E., Graves M.J., Li Z.Y., Gillard J.H. Normalized wall index specific and MRI-based stress analysis of atherosclerotic carotid plaques: a study comparing acutely symptomatic and asymptomatic patients. Circ. J. 2010;74:2360–2364. doi: 10.1253/circj.cj-10-0305. [DOI] [PubMed] [Google Scholar]

RESOURCES